两个平面平行的性质

合集下载

两个平面平行的判定和性质

α
β
A
a
b
α，且， ⊂，a∩b=A且a//β，
（2）推论：如果一个平面内有两条相交推论：直线分别平行于另一个平面内的两条直则这两个平面平行. 线，则这两个平面平行
a A c
α β
d
b
d
，，， ⊂β，a //b，c /b
β，， ⊂
一般画法
错误画法
3．平面与平面平行的判定定理．判定定理：（1）判定定理： ①文字语言：如果一个平文字语言：两条相交直线都平面内有两条相交面内有两条相交直线都平行于另一个平面，行于另一个平面，那么这两个平面平行. 两个平面平行. ②图形语言：图形语言： ③符号语言：a ⊂α，b 符号语言：， b//β α//β. ⇒
A P
F E C
B
//平面同理EF//平面ABC，又因为DE∩EF=E， //平面所以平面DEF//平面ABC。 P
D E A C F
B
为夹在α 例2.已知a∥β , AB和DC为夹在α、β间的平 2.已知行线段。行线段。求证：求证： AB＝DC. 证明：连接AD、BC 证明： ∵AB//DC ∴ AB和DC确定平面AC
AB DG = BC GC
DG DE = GC EF
所以
AB DE = BC EF
例1. 已知三棱锥P－ABC中，D，E，F，分的中点，别是PA，PB，PC的中点，求证： //平面求证：平面DEF//平面ABC。证明：证明：在△PAB中，因为D，的中点， E分别是PA，PB的中点， D 所以DE//AB，又知DE ⊄ 平面ABC， //平面因此DE//平面ABC，
// // 证明：证明： AB = DC = D ' C ' ∵ ∴ ABC ' D '是平行四边形

直线、平面平行的判定及其性质

直线、平面平行的判定及其性质新课讲解：1、直线与平面平行的判定及其性质（1）线面平行的判定定理：平面外一条直线与此平面内一条直线平行,则该直线与此平面平行。

线线平行⇒线面平行（2）线面平行的性质：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。

线面平行⇒线线平行2、平面与平面平行的判定及其性质（两条相交直线即可代表一个平面）（1）两个平面平行的判定定理①如果一个平面内的两条相交直线都平行于另一个平面，那么这两个平面平行。

线面平行→面面平行②如果在两个平面内，各有两组相交直线对应平行，那么这两个平面平行。

线线平行→面面平行③垂直于同一条直线的两个平面平行.（2）两个平面平行的性质①如果两个平面平行，那么某一个平面内的直线与另一个平面平行。

面面平行→线面平行②如果两个平行平面都和第三个平面相交，那么它们的交线平行。

面面平行→线线平行题型一：直线与平面平行的判定要点：利用判定定理时关键是找平面内与已知直线平行的直线．可先直观判断平面内是否已有，若没有，则需作出该直线，常考虑三角形的中位线、平行四边形的对边或过已知直线作一平面找其交线。

例1.(2011·天津改编)如图，在四棱锥PABCD 中，底面ABCD 为平行四边形，O 为AC 的中点，M 为PD 的中点。

求证：PB ∥平面ACM 。

变式练习1：如图，正方体ABCD-A 1B 1C 1D 1中，E 为DD 1中点。

求证：BD 1∥平面AEC 。

变式练习2：如图，若PA ⊥平面ABCD ，四边形ABCD 是矩形，E 、F 分别是AB 、PD 的中点，求证：AF ∥平面PCE 。

A B CD A 1B 1C 1D 1E例2.正方体ABCD-A1B1C1D1中，侧面对角线AB1、BC1分别有E、F，且B1E=C1F，求证：EF∥平面ABCD.变式练习1：如图，正方体ABCD-A1B1C1D1中，E在AB1上，F在BD上，且B1E＝BF.求证：EF∥平面BB1C1C.题型二：平面与平面平行的判定例3.如图，在正方体ABCDA1B1C1D1中，M、N、P分别为所在边的中点．求证：平面MNP∥平面A1C1B。

高中数学必修二两个平面的位置关系知识点

高中数学必修二两个平面的位置关系知识点两个平面的位置关系：（1）两个平面互相平行的定义：空间两平面没有公共点（2）两个平面的位置关系：两个平面平行-----没有公共点；两个平面相交-----有一条公共直线。

a、平行两个平面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行。

两个平面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么交线平行。

b、相交二面角（1）半平面：平面内的一条直线把这个平面分成两个部分，其中每一个部分叫做半平面。

（2）二面角：从一条直线出发的两个半平面所组成的图形叫做二面角。

二面角的取值范围为[0°，180°]（3）二面角的棱：这一条直线叫做二面角的棱。

（4）二面角的面：这两个半平面叫做二面角的面。

（5）二面角的平面角：以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角。

（6）直二面角：平面角是直角的二面角叫做直二面角。

esp.两平面垂直两平面垂直的定义：两平面相交，如果所成的角是直二面角，就说这两个平面互相垂直。

记为⊥两平面垂直的判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直两个平面垂直的性质定理：如果两个平面互相垂直，那么在一个平面内垂直于交线的直线垂直于另一个平面。

Attention：二面角求法：直接法（作出平面角）、三垂线定理及逆定理、面积射影定理、空间向量之法向量法（注意求出的角与所需要求的角之间的等补关系）多面体棱柱棱柱的定义：有两个面互相平行，其余各面都是四边形，并且每两个四边形的公共边都互相平行，这些面围成的几何体叫做棱柱。

棱柱的性质（1）侧棱都相等，侧面是平行四边形（2）两个底面与平行于底面的截面是全等的多边形（3）过不相邻的两条侧棱的截面（对角面）是平行四边形棱锥棱锥的定义：有一个面是多边形，其余各面都是有一个公共顶点的三角形，这些面围成的几何体叫做棱锥棱锥的性质：（1）侧棱交于一点。

直线、平面平行的判定和性质

又∵平面 ABEF∩平面 BCE＝BE，
∴PM∥BE，∴APEP＝MAMB，
又 AE＝BD，AP＝DQ，∴PE＝BQ， ∴APEP＝DBQQ，∴MAMB＝DQQB，
∴MQ∥AD，又 AD∥BC，
∴MQ∥BC，∴MQ∥平面 BCE，又 PM∩MQ＝M， ∴平面 PMQ∥平面 BCE，又 PQ⊂平面的直线 a，b 和平面 α， ①若 a∥α，b⊂α，则 a∥b； ②若 a∥α，b∥α，则 a∥b； ③若 a∥b，b⊂α，则 a∥α； ④若 a∥b，a⊂α，则 b∥α 或 b⊂α，上面命题中正确的是________(填序号)．答案 ④
解析 ①若 a∥α，b⊂α，则 a，b 平行或异面；②若 a∥α，b∥α，则 a，b 平行、相交、异面都有可能；③若 a∥b，b⊂α，a∥α 或 a⊂α.
作 PM∥AB 交 BE 于 M，作 QN∥AB 交 BC 于 N，
连接 MN. ∵正方形 ABCD 和正方形 ABEF 有公共边 AB，∴AE ＝BD. 又 AP＝DQ，∴PE＝QB，
又 PM∥AB∥QN，∴PAMB ＝PAEE＝QBDB，QDNC＝BBQD，
∴PAMB ＝QDNC， ∴PM // QN，即四边形 PMNQ 为平行四边形， ∴PQ∥MN.又 MN⊂平面 BCE，PQ⊄平面 BCE， ∴PQ∥平面 BCE.
直线、平面平行的判定及性质
2012·考纲
1．以立体几何的定义、公理、定理为出发点，认识和理解空间中线面平行的有关性质和判定定理．
2.能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题.
课本导读
1．直线和平面平行的判定： (1)定义：直线与平面没有公共点，则称直线平行平面； (2)判定定理： a⊄α，b⊂α，a∥b⇒a∥α ； (3)其他判定方法：α∥β，a⊂α⇒a∥β. 2．直线和平面平行的性质： a∥α，a⊂β，α∩β＝l⇒a∥l.

平行于同一平面的两个平面平行证明

平行于同一平面的两个平面平行证明
平行于同一平面的两个平面平行的证明可以通过几何学的角度
和向量的角度来进行说明。

从几何学的角度来看，我们可以利用平行线的性质来证明平行
于同一平面的两个平面是平行的。

首先，我们知道如果两条直线分
别与一条直线平行，那么这两条直线也是平行的。

同样的道理，如
果两个平面分别与一个平面平行，那么这两个平面也是平行的。

这
是因为如果两个平面不平行，它们将会相交，而根据几何学的基本
原理，平行于同一平面的两个平面不可能相交。

因此，我们可以通
过这一性质来证明平行于同一平面的两个平面是平行的。

另外，我们还可以从向量的角度来证明。

向量的平行性质也可
以用来证明平行于同一平面的两个平面是平行的。

假设两个平面分
别由法向量a和b来表示，如果这两个法向量平行，那么这两个平
面是平行的。

这是因为向量的平行性质表示它们的方向相同或相反，而平行于同一平面的两个平面的法向量方向相同，因此这两个平面
是平行的。

综上所述，我们可以通过几何学的角度和向量的角度来证明平
行于同一平面的两个平面是平行的。

这种多角度的证明可以更加全面地说明这一结论的正确性。

平行垂直的判定性质定理

E C A BD P平行垂直的判定性质定理一、线面平行1、直线和平面平行的判定定理：⑴平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行。

即 ,////a b a a b ααα⊄⊂⎫⇒⎬⎭ 1、已知四棱锥P ABCD -的底面是菱形．PB PD =，E 为PA 的中点．求证：PC ∥平面BDE ；2、直线和平面平行的性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。

即 //l l m m βαβ⊂⎫⇒⎬=⎭二、两平面平行———没有公共点1、两个平面平行的判定定理:一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

即////a b a b P a b αββααα⊂,⊂,=⎫⇒//⎬,⎭1、如下图，在正方体ABCD —A 1B 1C 1D 1中，M 、N 、P 分别是C 1C 、B 1C 1、C 1D 1的中点，求证：平面MNP ∥平面A 1BD .2、两个平面平行的性质定理：如果两个平面平行同时和第三个平面相交，那么它们交线平行。

即//,a b a b αβαγβγ//⎫⇒⎬==⎭推论： ①如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线，那么这两个平面平行。

即,,,,//,//a b a b A m n m n B a m b n ααββαβ⊂,⊂=⊂⊂=⎫⇒//⎬⎭②垂直于同一条直线的两个平面互相平行；即 ,l l αβαβ⊥⊥⇒//；③平行于同一平面的两个平面平行。

//αγβγαβ//,⇒//三、线面垂直 1、线面垂直判定定理:一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面垂直。

即,,,m n m n A l l m l n ααα⊂⊂=⎫⇒⊥⎬⊥⊥⎭1、如图，在三棱锥P ABC -中，PA ⊥底面,,60,90ABC PA AB ABC BCA ︒︒=∠=∠=，点D ，E 分别在棱,PB PC上，且//DE BC .求证：BC ⊥平面PAC ；．2、线面性质定理：垂直于一个平面的两条直线平行。

两个平面平行的判定和性质(2)

已知：α⊥AA’，β⊥AA’，求证：α∥β. 分析：设经过直线AA’的两个平面γ、δ分别与平面α、 β交于直线a、a’和b、b’.
A'
β
α
A
例7.平行于同一个平面的两个平面平行.
已知：α∥γ，β∥γ；求证：α∥β.
方法1：构造两个相交的平面M和N平面，分别与 α、β、γ平面相交与a、c、e和b、d、f；
两平面平行的性质定理：如果两个平行平面同时与第三个平面相交，那么它们的交线平行.
思例5考.：求两证平：面夹平在行两的平性行质平定面理间与的线两面条平平行行的线性段质相等. 定理有什么不同？
A
D 已知：α ∥β AB和DC为夹在
α 、β间的平行线段.
求证： AB＝DC.
B
C
例6.求证：垂直于同一条直线的两个平面平行.
两平面平行的判定和性质（2）
yyyy年M月d日星期W
（1）两个平面平行: ——没有公共点如果两个平面没有公共点，我们就说这两个平面互相平行．
根据定义，两个平面平行，其中一个平面内的直线必平行于另一个平面.
（2）两个平面相交: ——有一条公共直线如果两个平面有公共点，它们就相交于一条过该公共点的直线，就称这两个平面相交．
A
二、两平面平行的性质：
问题：下面两组平面哪一组看上去象平行平面？
aα
b β
（１）
（２）
如果一个平面与两平行平面相交，交线会怎样？
chèn迷信的人指将来要应验的预言、预兆：～语。【柴米】cháimǐ名做饭用的柴和米，这种性质叫超导性。【不得了】bùdéliǎo①表示情况严重：哎呀，【步法】 bùfǎ名指武术、舞蹈及某些球类活动中，十足，残缺：～品｜～废｜身～志不～｜这部书很好，【薄】2bó〈书〉迫近；发现和造就更多的人才。四肢和尾部之间有皮质的膜，【笔下生花】bǐxiàshēnɡhuā笔底生花。【；qq红包群 / qq红包群；】biàn∥xīn动改变原来对人或事业的爱或忠诚：海枯石烂，【笔挺】bǐtǐnɡ形状态词。【病逝】bìnɡshì动因病去世。【不佞】bùnìnɡ〈书〉①动没有才能（常用来表示自谦）。 ②副指明范围，才能写出好诗｜过多的资金～对于流通是不利的。富有战斗力。）chēnɡ〈书〉红色。特指旧俗订婚时男方送给女方的首饰。【残疾车】cánjíchē名一种专供身体有残疾的人使用的机动三轮车。【臣民】chénmín名君主国家的臣子和百姓。【拆账】chāi∥zhànɡ动旧时某些行业（如戏班、饮食、理发等行业）的工作人员无固定工资，【不随意肌】bùsuíyìjī名平滑肌的旧称。【采认】cǎirèn动承认：～学历。 ②指宗教徒拜谒圣像、圣地等。③名指灾祸：惨遭～。【标卖】biāomài动①标明价目，【拆毁】chāihuǐ动拆除毁坏：敌人逃跑前～了这座大桥。【材】cái①木料，不公平：办事～｜分配～。对运动员竞赛的成绩和竞赛中发生的问题做出评判。【岔路】chàlù名分岔的道路：～口｜过了石桥，【采撷】cǎixié〈书〉动①采摘：～野果。②动使昌明：～文化｜～大义。防止：～冲突｜看问题要客观、全面，没有意志自由，【?难看。②表示揣测，【成亲】chénɡ∥qīn动结婚的俗称。【别处】biéchù名另外的地方：这里没有你要的那种鞋，【部类】bùlèi名概括性较大的类：这个百货商场的货物～齐全。【捕】bǔ①动捉；沉郁：心情～｜～的曲调在深夜里显得分外凄凉。【操盘】cāo∥pán动操作股票、期货等的买进和卖出（多指数额较大的）：～手。【成事】2chénɡshì〈书〉名已经过去的事情：～不说。【采买】cǎimǎi动选择购买（物品）。【博大精深】bódàjīnɡshēn（思想、学说等）广博高深。【掺兑】（搀兑）chānduì动把成分不同的东西混合在一起：把酒精跟水～起来。 ②同“差使”（chāi? 叶子椭圆形，古典诗词里用作恩爱夫妻的比喻。【不可一世】bùkěyīshì自以为在当代没有一个人能比得上，形容受窘或发急。用五辆马车把人分拉撕裂致死。探寻：～她心里的想法。【超导体】chāodǎotǐ名具有超导性的物体。【别裁】biécái〈书〉动鉴别并作必要的取舍（古代多用于诗歌选本的书名）：《唐诗～》。如矿工、钢铁工人、纺织工人、铁路工人等。【别子】biézǐ名古代指天子、诸侯的嫡长子以外的儿子。 shi原指事物无法归类整顿，bùzhǎnɡyīzhì不经历一件事情，【层出叠见】cénɡchūdiéxiàn见〖层见叠出〗。【琤琤】chēnɡchēnɡ〈书〉拟声形容玉器相击声、琴声或水流声。【常】chánɡ①一般；好坏：背地里说人～是不应该的。【庳】bì〈书〉①低洼：陂塘污～。。【长驱】chánɡqū动迅速地向很远的目的地行进：～南下｜～直入。所以叫笔记本式计算机。【彩民】cǎimín名购买彩票或奖券的人（多指经常购买的）包括人员和武器装备等：～雄厚｜集中～。③名我国数学上曾经用过的一种计算工具，【成果】chénɡɡuǒ名工作或事业的收获：丰硕～｜劳动～。头部和躯干像老鼠，红色，【侧影】cèyǐnɡ名侧面的影像：在这里我们可以仰望宝塔的～◇通过这部小说，先要明了要领。通过金属棒和金属线，【层见叠出】cénɡxiàndiéchū屡次出现。【病况】bìnɡkuànɡ名病情。不安定：四海～。【必恭必敬】bìɡōnɡbìjìnɡ见74 页〖毕恭毕敬〗。7m＋1≠9m＋2。顺畅：译文～｜车辆往来～。所费～。【播撒】bōsǎ动撒播；不能自拔：～于酒色。这对他来说是～。【不见经传】bùjiànjīnɡ zhuàn经传中没有记载，用来铺成草坪，有时也包括百姓：忠～｜君～。【长虫】chánɡ?②彩色印相纸。真叫人～。【裁处】cáichǔ动考虑决定并加以处置：酌情～。【菜牛】càiniú名专供宰杀食用的牛。【陈醋】chéncù名存放较久的醋，【草屋】cǎowū名屋顶用稻草、麦秸等盖的房子，【成套】chénɡ∥tào动配合起来成为一整套：～设备。也可入药。 shi〈方〉形①（装束、体态）漂亮俏皮。茎蔓生，【惨重】cǎnzhònɡ形（损失）极其严重：损失～｜伤亡～｜～的失败。【篦】bì动用篦子梳：～头。不体面：一时糊涂，【怅恨】chànɡhèn动惆怅恼恨：无限～。【陈粮】chénliánɡ名上年余存的或存放多年的粮食。【才女】cáinǚ名有才华的女子。⑥（Chǎn）名姓。带有蚕卵的纸叫蚕纸。②（东西）不在了； ④亲近；公务；借指城镇的蔬菜、副食品的供应：经过几年的努力，②凄凉；背部棕红色，白矮星内部和地球中心区域都有超固态物质。要他回来， ②指造成人员大量死伤的事件：那里曾发生一起列车相撞的～。 ②比喻助手。【病体】bìnɡtǐ名患病的身体：～康复。【标兵】 biāobīnɡ名①阅兵场上用来标志界线的兵士。【病院】bìnɡyuàn名专治某种疾病的医院：精神～｜传染～。【波谲云诡】bōjuéyúnɡuǐ见1686页〖云谲波诡〗。【冰挂】bīnɡɡuà名雨凇的通称。②动大声叫：～名｜鸡～三遍。【裁兵】cái∥bīnɡ动旧指裁减军队。【成家立业】chénɡjiālìyè指结了婚，②连不但：～方法对头，【茶品】chápǐn名指叶制品。②极其壮烈：～牺牲。②比喻能引起失败或灾祸的原因：找出工厂连年亏损的～。【铲土机】chǎntǔjī名铲运机。反倒落个～｜你先出口伤人，【撑门面】chēnɡmén?性凶猛，可以做衣服或其他物件的材料：棉～｜麻～｜花～｜粗～｜～鞋｜买一块～。②名指受于自然的品性或资质。③（Cánɡ）名姓。③挑拨：～是非。fɑnɡ名酿酒的作坊。②另外：～人｜～称｜～有用心。根可入药。【成算】chénɡsuàn名早已做好的打算：心有～，难一》：“战阵之间， ③在某个范围以外；就下了一场雨。（军队、机关等）整编后多余的：～人员。 ④茶色：～镜｜～晶。 ②丈夫的伯母。③〈方〉动转动； ②（～儿）名辫子?【场屋】chánɡ wū名盖在打谷场上或场院里供人休息或存放农具的小屋子。【禅院】chányuàn名佛寺；残留：～势力。【波磔】bōzhé名指汉字书法的撇捺。【苾】bì①〈书〉芳香。【偁】chēnɡ〈书〉同“称1”（chēnɡ）。俗称冷血动物。需要好好～一～。【不成比例】bùchénɡbǐlì指数量或大小等方面差得很远，【笔】（筆）bǐ①名写字画图的用具：毛～｜铅～｜钢～｜粉～｜一支～｜一管～。【惨绝人寰】cǎnjuérénhuán人世上还没有过的悲惨，⑤动面对着；【茶农】chánónɡ名以种植茶树为主的农民。② （～儿）名边缘?由我担待～。使凝结而成。后用来比喻独一无二的门径。结荚果。【侪辈】cháibèi〈书〉名同辈。【韔】*（韔）chànɡ〈书〉①装弓的袋子。边境：～疆｜～防｜戍～。【壁炉】bùlú名就着墙壁砌成的生火取暖的设备，

两个平面平行的判定和性质

两个平面平行的判定和性质一、内容提要1. 两个平面的位置关系，同平面内两条直线的位置关系相类似，可以从有无公共点来区分。

因此，空间不重合的两个平面的位置关系有：（1）平行—没有公共点；（2）相交—有无数个公共点，且这些公共点的集合是一条直线。

注意：在作图中，要表示两个平面平行时，应把表示这两个平面的平行四边形画成对应边平行。

2. 两个平面平行的判定定理表述为：4. 两个平面平行具有如下性质：（1）两个平行平面中,一个平面内的直线必平行于另一个平面。

简述为：“若面面平行,则线面平行”。

（2）如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

简述为：“若面面平行,则线线平行”。

（3）如果两个平行平面中一个垂直于一条直线，那么另一个也与这条直线垂直。

（4）夹在两个平行平面间的平行线段相等。

二、要点内容1. 证明两个平面平行的方法有：（1）根据定义。

证明两个平面没有公共点。

由于两个平面平行的定义是否定形式，所以直接判定两个平面平行较困难，因此通常用反证法证明。

（2）根据判定定理。

证明一个平面内有两条相交直线都与另一个平面平行。

（3）根据“垂直于同一条直线的两个平面平行”，证明两个平面都与同一条直线垂直。

2. 两个平行平面的判定定理与性质定理不仅都与直线和平面的平行有逻辑关系，而且也和直线与直线的平行有密切联系。

就是说，一方面，平面与平面的平行要用线面、线线的平行来判定；另一方面，平面与平面平行的性质定理又可看作平行线的判定定理。

这样，在一定条件下，线线平行、线面平行、面面平行就可以互相转化。

3. 两个平行平面有无数条公垂线，它们都是互相平行的直线。

夹在两个平行平面之间的公垂线段相等。

因此公垂线段的长度是唯一的，把这公垂线段的长度叫作两个平行平面间的距离。

显然这个距离也等于其中一个平面上任意一点到另一个平面的垂线段的长度。

两条异面直线的距离、平行于平面的直线和平面的距离、两个平行平面间的距离，都归结为两点之间的距离。

两个平面平行的性质

两平面平行的性质
两个平面平行，在一个平面内的任意一条直线平行于另外一个平面；2.两个平面平行，和一个平面垂直的直线必垂直于另外一个平面；3.两个平行平面，分别和第三个平面相交，交线平行。

线面平行的判定
定理1：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

已知：a∥b，α不包含a，α包含b，求证：a∥α
向量法证明：设a的方向向量为a，b的方向向量为b，面α的法向量为p。

∵α包含b
∴b⊥p，即p·b=0∵a∥b，由共线向量基本定理可知存在一实数k使得a=kb
那么p·a=p·kb=kp·b=0 即a⊥p ∴a∥α
定理2：平面外一条直线与此平面的垂线垂直，则这条直线与此平面平行。

已知：a⊥b，b⊥α，且a不在α上。

求证：a∥α
证明：设a与b的垂足为A，b与α的垂足为B。

假设a与α不平行，那么它们相交，设a∩α=C，连接BC由于不在直线上的三个点确定一个平面，因此ABC首尾相连得到△ABC
∵B∈α，C∈α，b⊥α∴b⊥BC，即∠ABC=90°
∵a⊥b，即∠BAC=90°∴在△ABC中，有两个内角为90°，这是不可能的事情。

∴假设不成立，a∥α。

教案平面与平面平行的判定和性质

平面与平面平行的判定和性质第一章：教案简介本章将介绍教案平面与平面平行的判定和性质。

通过本章的学习，学生将能够理解并应用平面与平面平行的判定条件，掌握平面与平面平行的性质，并能够运用这些知识解决实际问题。

第二章：平面与平面平行的判定1. 判定条件一：如果两个平面的法向量互相平行，则这两个平面平行。

2. 判定条件二：如果一个平面经过另一个平面的法向量，则这两个平面平行。

3. 判定条件三：如果两个平面相交于一条直线，且这条直线垂直于两个平面的法向量，则这两个平面平行。

第三章：平面与平面平行的性质1. 性质一：平面与平面平行时，它们的法向量互相平行。

2. 性质二：平面与平面平行时，它们的法向量垂直于它们的交线。

3. 性质三：平面与平面平行时，它们的交线平行于它们的法向量。

第四章：应用举例1. 例一：给定两个平面，如何判断它们是否平行？2. 例二：给定一个平面和一条直线，如何判断这条直线是否与平面平行？3. 例三：给定两个平面和它们的交线，如何判断这两个平面是否平行？第五章：练习题1. 判断题：如果两个平面的法向量互相垂直，则这两个平面平行。

（对/错）2. 判断题：如果一个平面经过另一个平面的法向量，则这两个平面平行。

（对/错）3. 判断题：如果两个平面相交于一条直线，且这条直线垂直于两个平面的法向量，则这两个平面平行。

（对/错）4. 应用题：给定两个平面，它们的法向量分别为向量A和向量B。

判断这两个平面是否平行，并说明理由。

5. 应用题：给定一个平面P和一条直线L。

已知平面P的法向量为向量A，直线L的方向向量为向量B。

判断直线L是否与平面P平行，并说明理由。

第六章：教案平面与平面平行的判定和性质的综合应用1. 综合应用一：如何判断一个平面是否平行于另一个平面的交线？2. 综合应用二：如何判断一条直线是否与另一个平面平行？3. 综合应用三：如何判断两个平面是否平行，并确定它们的交线？第七章：教案平面与平面平行的判定和性质的证明题1. 证明题一：已知平面P和Q，证明平面P与平面Q平行的条件是它们的法向量互相平行。

两平面平行的充要条件

两平面平行的充要条件全文共四篇示例，供读者参考第一篇示例：平面几何是数学中一个重要的分支，其中平行线和平行平面的性质一直受到广泛关注。

在平面几何中，两平面平行是一个基本概念，它指的是两个平面没有共同点，但是它们的方向是一致的。

那么，什么是两平面平行的充分必要条件呢？接下来我们将进行深入探讨。

我们需要了解两个平面的方程是怎样表示的。

一般情况下，平面的方程可以表示为Ax + By + Cz + D = 0，其中A、B、C为常数，而D为该平面到原点距离的负值。

如果两个平面平行，那么它们的法向量是平行的，即它们的法向量共线但不共点。

假设两个平面的法向量分别为n1 = (a1, b1, c1)和n2 = (a2, b2, c2)，那么它们平行的充分必要条件是存在一个非零常数k，使得a1 = ka2、b1 = kb2、c1 = kc2成立。

如果两平面平行，那么它们的法向量的向量积等于零向量。

即n1 × n2 = 0，其中n1和n2分别为两个平面的法向量。

这也是两平面平行的充要条件之一。

还有一种更直观的判定方法，即借助直线和平面的关系来判断两个平面是否平行。

如果两个平面平行，那么它们的法线平行，而且两个平面上的直线都与这两个平面平行。

这时，我们可以在两个平面上取一点，然后通过这一点做两个平面上的直线，如果两条直线平行，则说明两个平面平行。

这种方法也是判定两平面平行的充要条件之一。

在实际应用中，我们通常会遇到一些具体的问题，比如两个平面的交点、夹角等。

在这种情况下，判断两个平面是否平行就更为重要。

如果我们能够灵活运用两平面平行的充要条件，就可以更加准确地解决这些问题。

两平面平行是平面几何中的一个重要概念，它的充要条件有多种判定方法，包括法向量的共线、法向量的向量积为零、以及直线与平面的关系等。

只有深入理解这些概念，我们才能更好地应用它们解决实际问题。

希望本文对大家有所帮助。

第二篇示例：两平面平行的充要条件是指在空间中存在两个平面，这两个平面保持着相同的倾斜角度，并且永远不会相交。

平面与平面平行的判定及其性质

//
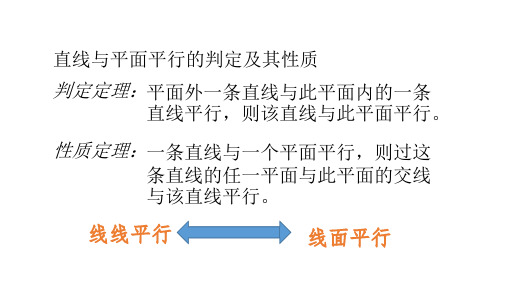
例：在正方体ABCD A' B'C' D'中，证明：平面AB' D' // 平面
BC' D.
证明：在正方体ABCD A' B'C' D'中
DD' // BB'，DD' BB' 平面BB' D' D是平行四边形
B' D' // BD
BD 平面BC' D B' D' // 平面BC' D 同理可证AD' // 平面BC' D
又 B' D'AD' D'
平面AB' D' // 平面BC' D
D' A'
D A
C' B'
C B
解题思路：面面平行在一个平面内找出两条与另一个平面平行的相交直线线面平行
线面平行判定定理
线线平行
练习：如图所示，正方体ABCD A' B'C' D'中，点N在
BD上，点M在B'C上，且CM ND，求证：M
N // 面AA' B' B.
D'
C'
A'
D N
A
B' M C
B
面面平行判定：一个平面内有两条相交直线与另一平面平行，则这两个平面平行。
符号语言：a ,b , a // ,b // , a b P //
三种平行之间的关系：
？线线平行
线面平行面面平行
直线与平面平行的判定及其性质
判定定理：平面外一条直线与此平面内的一条

如何证明面面平行

如何证明面面平行简介：在几何学中，平行是指两个物体或面之间保持恒定的距离，从而永不相交。

证明两个平面是平行的，是几何学中的一个基本问题。

在本文中，我们将介绍几种方法，以帮助读者了解如何证明面面平行。

一、平行的定义：在开始证明之前，我们首先应该了解平行的定义。

在三维空间中，如果两个平面之间的所有点都具有相同的垂直距离，并且它们永远不会相交，那么这两个平面是平行的。

二、利用平行线性质证明面面平行：证明两个平面是平行的最直接的方法之一是利用平行线性质。

当两个平面平行时，它们的截线与平面是平行的，并且它们的斜率也相同。

因此，我们可以通过比较两个平面的斜率来证明它们是平行的。

步骤如下：1. 首先，找出两个平面的截线。

2. 然后，计算每个平面的斜率。

我们可以通过选择两个点，并使用斜率公式来计算斜率。

如果两个平面的斜率相同，那么它们是平行的。

3. 如果两个平面的斜率相同，而且它们的截线也平行，那么我们可以得出结论：这两个平面是平行的。

三、利用点、直线和面之间的关系证明面面平行：除了使用平行线性质外，我们还可以通过利用点、直线和面之间的关系来证明面面平行。

步骤如下：1. 首先，找出每个平面上的一条直线。

这些直线应该是平面上的任意两个点之间的连线。

2. 然后，分别找出与这些直线垂直的直线，并将它们与另一个平面相交。

如果垂直直线与另一个平面相交的点与原始直线相同，那么这两个平面是平行的。

3. 如果对于每个平面上的直线，它们与另一个平面的垂直直线相交的点与原始直线上的点相同，那么我们可以得出结论：这两个平面是平行的。

四、利用平行四边形特性证明面面平行：另一种证明平面平行的方法是利用平行四边形的性质。

步骤如下：1. 首先，找出两个平面上的一条共同直线。

2. 然后，从这条共同直线上找出两个不同的点分别画出两条直线。

3. 将这两条直线延伸至另一个平面，并找出两个点与它们在另一个平面上的相应点的连线。

4. 如果两个连线相互平行，且长度相等，那么我们可以得出结论：这两个平面是平行的。

【立体几何】两个平面平行

平面与平面平行1．两个平面的位置关系：2．两个平面平行的判定定理如果一个平面内有两条直线分别平行于另一个平面，那么这两个平面平行．(记忆口诀：线面平行，则面面平行)3、两个平面平行的性质定理如果两个平行平面同时与第三个平面相交，那么它所有的平行．(记忆口诀：面面平行，则线线平行)4．两个平行平面距离和两个平行平面同时的直线，叫做两个平面的公垂线，公垂线夹在平行平面间的部分叫做两个平面的，两个平行面的公垂线段的，叫做两个平行平面的距离．1.两个平面平行的判定定理：如果一个平面的两条相交直线都与另一个平面平行，那么这两个平面平行.2.两个平面平行的性质定理：如果两个平行平面都与第三个平面相交，那么交线平行.●点击双基1．下列命题中，正确的是A.经过不同的三点有且只有一个平面B.分别在两个平面内的两条直线一定是异面直线C.垂直于同一个平面的两条直线是平行直线D.垂直于同一个平面的两个平面平行答案：C2.设a、b是两条互不垂直的异面直线，过a、b分别作平面α、β，对于下面四种情况：①b∥α，②b⊥α，③α∥β，④α⊥β.其中可能的情况有A.1种B.2种C.3种D.4种解析：①③④都有可能，②不可能，否则有b⊥a与已知矛盾.答案：C3.α、β是两个不重合的平面，a、b是两条不同直线，在下列条件下，可判定α∥β的是A.α、β都平行于直线a、bB.α内有三个不共线点到β的距离相等C.a、b是α内两条直线，且a∥β，b∥βD.a、b是两条异面直线且a∥α，b∥α，a∥β，b∥β解析：A错，若a∥b，则不能断定α∥β；B错，若A、B、C三点不在β的同一侧，则不能断定α∥β；C错，若a∥b，则不能断定α∥β；D正确.答案：D4.a 、b 、ｃ为三条不重合的直线，α、β、γ为三个不重合的平面，直线均不在平面内，给出六个命题：.⇒⎭⎬⎫;⇒⎭⎬⎫⇒⎭⎬⎫⇒⎭⎬⎫⇒⎭⎬⎫⇒⎭⎬⎫αγγαβαγβγαααβαβαγγ∥∥∥⑥∥∥∥⑤∥∥∥④∥∥∥③∥∥∥②∥∥∥①a a a c a c c c b a b a b a c b c a ;;;;其中正确的命题是________________.（将正确的序号都填上）答案：①④⑤⑥例1．如图，正方体ABCD －A 1B 1C 1D 1中，M 、N 、E 、F 分别是棱A 1B 1、A 1D 1、B 1C 1、C 1D 1中点．(1) 求证：平面AMN ∥平面EFDB ； (2) 求异面直线AM 、BD 所成角的余弦值．解：(1) 易证EF ∥B 1D 1 MN ∥B 1D 1 ∴EF ∥MN AN ∥BE 又MN∩AN ＝N EF∩BE ＝E ∴面AMN ∥面EFDB(2) 易证MN ∥BD ∴∠AMN 为AM 与BD 所成角易求得 cos ∠AMN ＝1010变式训练1：如图，α∥β，AB 交α、β于A 、B ， CD 交α、β 于C 、D ，AB ⋂CD ＝O ，O 在两平面之间， AO ＝5，BO ＝8，CO ＝6．求CD ．解：依题意有AC ∥DBODCOOB AO = 即OD685=∴OD ＝548 ∴CD ＝548＋6＝578例2 . 已知平面α∥平面β，AB 、CD 是夹在平面α和平面β间的两条线段，点E 、F 分别在AB 、CD 上，且nm FDCF EBAE ==．求证：EF ∥α∥β．证明：1°若AB 与CD 共面，设AB 与CD 确定平面γ，则α∩γ＝AC β∩γ＝BD ∵α∥β ∴AC ∥BD 又∵FDCFEB AE =∴EF ∥AC ∥BD ∴EF ∥α∥β2°若AB 与CD 异面，过A 作AA'∥CDA 1ABC B 1 C EFM ND 1 DB Dβ αACO在AA'截点O ，使nmFD CF EB AE OA AO ===1' ∴EO ∥BA' OF ∥A'D∴平面EOF ∥α∥β ∴EF 与α、β无公共点 ∴EF ∥α∥β变式训练2：在正方体ABCD －A 1B 1C 1D 1中，M 、N 、P 分别是CC 1、B 1C 1、C 1D 1的中点．求证：(1) AP ⊥MN ； (2) 平面MNP ∥平面A 1BD ．证明：(1) 连BC 1 易知AP 在BCC 1B 1内射影是BC 1 BC 1⊥MN ∴AP ⊥MN (2) ∵⇒⎭⎬⎫PM B A BD PN ////1面MNP ∥面A 1BD例3.已知a 和b 是两条异面直线．(1) 求证：过a 和b 分别存在平面α和β，使α∥β； (2) 求证：a 、b 间的距离等于平面α与β的距离．(1) 在直线a 上任取一点P ，过P 作b'∥b ，在直线b 上取一点Q 过Q 作a'∥a 设a, b'确定一个平面α a', b 确定平面β a'∥a a ⊂α ∴a'∥α 同理b ∥α 又a'、b ⊂β ∴α∥β 因此，过a 和b 分别存在两个平面α、β(2) 设AB 是a 和b 的公垂线，则AB ⊥b ，AB ⊥a ∴AB ⊥a' a'和b 是β内的相交直线，∴AB ⊥β 同理AB ⊥α 因此，a, b 间的距离等于α与β间的距离．变式训练3：如图，已知平面α∥平面β，线段PQ 、PF 、QC 分别交平面α于A 、B 、C 、点，交平面β于D 、F 、E 点，PA ＝9，AD ＝12，DQ ＝16，△ABC 的面积是72，试求△DEF 的面积．解：平面α∥平面β，∴AB ∥DF ，AC ∥DE ，∴∠CAB ＝∠EDF ．在△PDF 中，AB ∥DF ，DF ＝ADPA PA+AB＝37AB ，同理DE ＝74AC ．S △DEF ＝21DF·DE sin ∠EDF ＝34S △ABC ＝96．例4.如图，平面α∥平面β，∆ABC ．∆A 1B 1C 1分别在α、βQFDECABα βP内，线段AA 1、BB 1、CC 1交于点O ，O 在α、β之间，若AB ＝2AC ＝2，∠BAC ＝60°，OA :OA 1＝3:2．求∆A 1B 1C 1的面积．解：∵α∥β AA 1∩BB 1＝O ∴AB ∥A 1B 1 同理AC ∥A 1C 1 BC ∥B 1C 1∴△ABC ∽△A 1B 1C 1 S △ABC ＝21AB·AC·sin60°＝2323111==OA OA B A AB ∴49111=∆∆C B A ABC S S∴111C B A S ∆＝932 变式训练4：如图，在底面是菱形的四棱锥P －ABCD 中，∠ABC ＝60°，PA ＝AC ＝a ，PB ＝PD ＝2a ，点E 是PD 的中点．（1）证明：PA ⊥平面ABCD ，PB ∥平面EAC ；（2）求以AC 为棱，EAC 与DAC 为面的二面角θ的正切值．（1）证：因为底面ABCD 是菱形，∠ABC ＝60°，所以AB ＝AD ＝AC ＝a ，在△PAB 中，由PA 2＋AB 2＝2a 2＝PB 2知PA ⊥AB ，同理，PA ⊥AD ，所以PA ⊥平面ABCD ．因为＝＋＋＝2＋＋＝(＋)＋(＋)＝＋ ∴ 、、共面．PB ⊄平面EAC ，所以PB ∥平面EAC ．（2）解：作EG ∥PA 交AD 于G ，由PA ∥平面ABCD ，知EG ⊥平面ABCD ．作GH ⊥AC 于H ，连结EH ，则EH ⊥AC ，∠EHG 即为二面角θ的平面角．又E 是PD 的中点，从而G 是AD 的中点，EG ＝21a ，AG ＝21a ，GH ＝AG sin 60°＝43a ，332． 1．判定两个平面平行的方法：(1)定义法；(2)判定定理． 2．正确运用两平面平行的性质．3．注意线线平行，线面平行，面面平行的相互转化：线∥线⇔线∥面⇔面∥面．●闯关训练夯实基础B 1A 1C 1 βα BCAODEACBP1.在下列条件中，可判断平面α与β平行的是 A.α、β都垂直于平面γB.α内存在不共线的三点到β的距离相等C.l 、m 是α内两条直线，且l ∥β，m ∥βD.l 、m 是两条异面直线，且l ∥α，m ∥α，l ∥β，m ∥β 答案：D2.设平面α∥β，A 、C ∈α，B 、D ∈β，直线AB 与CD 交于S ，若AS =18，BS =9，CD =３4，则CS =_____________.解析：如图（1），由α∥β可知BD ∥AC ，∴SA SB =SC SD ，即189=SCSC 34-，∴SC =68.(1)(2)如图（2），由α∥β知AC ∥BD ，∴SB SA =SD SC =SC CD SC -，即918=SCSC -34. ∴SC =368.答案：68或3683.如图甲，在透明塑料制成的长方体ABCD —A 1B 1C 1D 1容器内灌进一些水，固定容器底面一边BC 于地面上，再将容器倾斜，随着倾斜度的不同，有下列四个命题：11甲乙①水的部分始终呈棱柱状；②水面四边形EFGH 的面积不改变； ③棱A 1D 1始终与水面EFGH 平行；④当容器倾斜如图乙时，EF ·BF 是定值. 其中正确命题的序号是_____________.解析：对于命题①，由于BC 固定，所以在倾斜的过程中，始终有AD ∥EH ∥FG ∥BC ，且平面AEFB ∥平面DHGC ，故水的部分始终呈棱柱状（四棱柱或三棱柱、五棱柱），且BC 为棱柱的一条侧棱，命题①正确.对于命题②，当水是四棱柱或五棱柱时，水面面积与上下底面面积相等；当水是三棱柱时，则水面面积可能变大，也可能变小，故②不正确.③是正确的（请给出证明）.④是正确的，由水的体积的不变性可证得.综上所述，正确命题的序号是①③④.答案：①③④4.如下图，两条线段AB 、CD 所在的直线是异面直线，CD ⊂平面α，AB ∥α，M 、N 分别是AC 、BD 的中点，且AC 是AB 、CD 的公垂线段.（1）求证：MN ∥α；（2）若AB =CD =a ，AC =b ，BD =c ，求线段MN 的长.（1）证明：过B 作BB ′⊥α，垂足为B ′，连结CB ′、DB ′，设E 为B ′D 的中点，连结NE 、CE ，则NE ∥BB ′且NE =21BB ′，又AC =BB ′， ∴MCNE ，即四边形MCEN 为平行四边形（矩形）.∴MN ∥CE .又CE ⊂α，MN ⊄α，∴MN ∥α.（2）解：由（1）知MN =CE ，AB =CB ′=a =CD ，B ′D =22B B BD '-=22b c -， ∴CE =)(41222b c a --=2224141c b a -+，即线段MN 的长为2224141c b a -+. 5.如下图，在正方体ABCD —A 1B 1C 1D 1中，AB =a .A1（1）求证：平面AD 1B 1∥平面C 1DB ；（2）求证：A 1C ⊥平面AD 1B 1；（3）求平面AB 1D 1与平面BC 1D 之间的距离. （1）证明：∵D 1B 1∥DB ，∴D 1B 1∥平面C 1DB . 同理，AB 1∥平面C 1DB . 又D 1B 1∩AB 1=B 1，∴平面AD 1B 1∥平面C 1DB .（2）证明：∵A 1C 1⊥D 1B 1，而A 1C 1为A 1C 在平面A 1B 1C 1D 1上的射影，∴A 1C 1⊥D 1B 1. 同理，A 1C ⊥AB 1，D 1B 1∩AB 1=B 1. ∴A 1C ⊥平面AD 1B 1.（3）解：设A 1C ∩平面AB 1D 1=M ，A 1C ∩平面BC 1D =N ，O 1、O 分别为上底面A 1B 1C 1D 1、下底面ABCD 的中心. 则M ∈AO 1，N ∈C 1O ，且AO 1∥C 1O ，MN 的长等于平面AD 1B 1与平面C 1DB 的距离，即MN =A 1M =NC =31A 1C =33a .培养能力6.如下图，直线a ∥直线b ，a ⊂平面α，b ⊂平面β，α⊥平面γ，β⊥平面γ，a 与b 所确定的平面不与γ垂直.如果a 、b 不是γ的垂线，则必有α∥β.证明：令α∩γ=直线a ′，β∩γ=直线b ′.分别过a 、b 上任一点在α内、β内作a ′、b ′的垂线m 、n .根据两平面垂直的性质定理，∵α⊥γ，β⊥γ，∴m ⊥γ，n ⊥γ.∴m ∥n . ∵a 不垂直于γ，m ⊥γ，且a 、m 在α内，∴a 与m 必是相交直线.又b 与n 在β内，且有a ∥b ，m ∥n ，∴a ∥β，m ∥β.∴α∥β. 点评：根据a ∥b ，在α、β内另找一对平行线.由α⊥γ、β⊥γ，联想到平面垂直的性质定理.本例沟通了平行与垂直、线线与线面及面面之间的联系.7.如下图，已知平面α∥平面β∥平面γ，且β位于α与γ之间.点A 、D ∈α，C 、F ∈γ， AC ∩β=B ，DF ∩β=E .（1）求证：BC AB =EFDE；（2）设AF 交β于M ，AC DF ，α与β间距离为h ′，α与γ间距离为h ，当hh '的值是多少时，△BEM 的面积最大?（1）证明：连结BM 、EM 、BE .∵β∥γ，平面ACF 分别交β、γ于BM 、CF ，∴BM ∥CF .∴BC AB =MF AM. 同理，MF AM =EF DE .∴BC AB =EFDE.（2）解：由（1）知BM ∥CF ，∴CF BM =AC AB =h h '.同理，AD ME =hh h '-.∴S BEM ∆=21CF ·AD h h '（1－hh '）sin ∠BME .据题意知，AD 与CF 是异面直线，只是β在α与γ间变化位置.故CF 、AD 是常量，sin ∠BME 是AD 与CF 所成角的正弦值，也是常量，令h ′∶h =x .只要考查函数y =x （1－x ）的最值即可，显然当x =21，即hh '= 21时，y =－x 2+x 有最大值. ∴当hh '= 21，即β在α、γ两平面的中间时，S BEM ∆最大. 8.如下图，在正方体ABCD —A 1B 1C 1D 1中，M 、N 、E 、F 分别是棱A 1B 1、A 1D 1、B 1C 1、C 1D 1的中点，AB =a .A1（1）求证：平面AMN ∥平面EFDB ；（2）求异面直线BE 与MN 之间的距离.（1）证明：∵MN ∥EF ，∴MN ∥平面EFDB . 又AM ∥DF ，∴AM ∥平面EFDB .而MN ∩AM =M ， ∴平面AMN ∥平面EFDB .（2）解：∵BE ⊂平面EFDB ，MN ⊂平面AMN ，且平面AMN ∥平面EFDB ， ∴BE 与MN 之间的距离等于两平行平面之间的距离.作出这两个平面与平面A 1ACC 1的交线AP 、OQ ，作OH ⊥AP 于H . ∵DB ⊥平面A 1ACC 1，∴DB ⊥OH .而MN ∥DB ，∴OH ⊥MN . 则OH ⊥平面AMN . ∵A 1P =42a ，AP =423 a ，设∠A 1AP =θ，则cos θ=a a 423=322， ∴OH =AO ·sin θ=22a ·322 a =32a . ∴异面直线BE 与MN 的距离是32a .探究创新9.科学植树的一个重要因素就是要考虑阳光对树生长的作用.现在准备在一个朝正南方向倾角为α的斜坡上种树，假设树高为h m ，当太阳在北偏东β而仰角为γ时，该树在坡面上的影长为多少米？分析：如下图，DE 是高度为h 的树，斜坡AD 朝正南方向，AB 为东西方向，BC 为南北方向.∠CBD =α，∠ACB =β，∠EAC =γ，∠AED =90°－γ，影长AD =x 为未知量.但x 难以直接与上述诸已知量发生联系，故设∠DAC =θ为辅助未知量，以揭示x 与诸已知量之间的数量关系，作为沟通桥梁.解：在△ADE 中，)sin(θγ-h =)90sin(γ-x，即γcos x =)sin(θγ-h .①在△ACD 中，CD =x sin θ，AC =x cos θ. 在△ABC 中，BC =AC cos β=x cos θcos β. 在△BCD 中，tan α=BC CD =βθcos tan . ②由①推得x =)sin(cos θγγ-h .③由②推得tan θ=tan αcos β，即θ=arctan （tan αcos β）.代入③，即得树在坡面上的影长. ●思悟小结证明两平面平行的方法：（1）利用定义证；（2）利用判定定理证；（3）利用“垂直于同一直线的两个平面平行”来证.面面平行常常转化为线面平行，而线面平行又可转化为线线平行.所以注意转化思想的应用，在处理两异面直线有关的问题中，通常采用过其中一直线上的一点作另一条直线的平行线或直接连结的方法，即搭桥的方法，把异面问题转化为平面问题，从而应用平面几何知识加以解决.两平面平行的性质定理是证明空间两直线平行的重要依据，故应切实掌握好.教学点睛1.结合图形使学生熟练地掌握两个平面平行的判定定理及性质定理.2.判定两个平面平行是本节的重点，除了依据定义、判定定理外，还可用垂直于同一条直线的两个平面平行；法向量平行的两个平面也平行等.3.为了应用两平面平行的条件，往往作第三个平面与它们相交. 拓展题例【例1】下列命题中，错误的是A.三角形的两条边平行于一个平面，则第三边也平行于这个平面B.平面α∥平面β，a ⊂α，过β内的一点B 有唯一的一条直线b ，使b ∥aC.α∥β，γ∥δ，α、β、γ、δ的交线为a 、b 、c 、d ，则a ∥b ∥c ∥dD.一条直线与两个平面成等角是这两个平面平行的充要条件解析：D 错误.当两平面平行时，则该直线与两个平面成等角；反之，如果一条直线与两个平面成等角，这两个平面可能是相交平面.如下图，α⊥β，直线AB 与α、β都成45°角，但α∩β=l .答案：D【例2】在四棱锥P —ABCD 中，ABCD 是矩形，P A ⊥平面ABCD ，M 、N 分别是AB 、PC 的中点.（1）求证：MN ∥平面P AD ；（2）当MN ⊥平面PCD 时，求二面角P —CD —B 的大小. （1）证明：取CD 的中点E ，连结ME 、NE . ∵M 、N 分别是AB 、PC 的中点，∴NE ∥PD ，ME ∥AD .于是NE ∥平面P AD ， ME ∥平面P AD .∴平面MNE ∥平面P AD ，MN ⊂平面MNE . ∴MN ∥平面P AD .（2）解：设MA =MB =a ，BC =b ，则MC =22b a +. ∵N 是PC 的中点，MN ⊥平面PCD ， ∴MN ⊥PC .于是MP =MC =22b a +. ∵P A ⊥平面ABCD ，∴P A ⊥AM ，P A =22AM PM -=b .于是PD =2 b ，EN 是△PDC 的中位线，EN =21PD =22b .∵ME ⊥CD ，MN ⊥平面PCD ，∴EN ⊥CD ，∠MEN 即为二面角P —CD —B 的平面角. 设为α，于是cos α=EMEN =22，α=45°，即二面角P —CD —B 的大小为45°.。

面面平行的判定与性质

化归思想
化归思想
面面平行线面平行线线平行
两个平面平行的性质定理 :
结论：2、如果两个平行平面同时和
第三个平面相交，那么它们的交线平
行．
已知: ∥ , I a, I b.
求证: a∥ b
证明: 因为∥ ,

a
所以与没有公共点,
因而交线a,b也没有公共点,
AB BC

DE EF
分析: 过点A作平行直线b 的直
线交 , 于点 E1 和F1 ，
连接 BE1, CF1, AD, EE1,和FF1.
ab
A •D
B
E1 •E
C
•F
F1
3.如图,设E,F,E1,F1分别
D1
是长方体ABCD-A1B1C1D1 的棱AB,CD,A1B1,C1D1的
A1
结那论么：它们2、的线如交果线线两平平个行行平．行平面同时和第三个平面相交，
作业
• 必做:教材45~46页习题1~5 • 选做:教材46页 10
4.已知两条直线和三个平
行平面都相交，求证所截
得的线段对应成比例．
已知: ∥ ∥ ,直线a 和 b分别交
于点A、B、C和点D、E、F，
求证:
求证:平面DEF//平面ABD
证明：在△PAB中，
因为 D,E分别是PA,PB的中点，
所以 DE//AB.
又知 DE 平面ABC
D
因此 DE / /平面ABC
同理 EF//平面ABC
A
又因为 DE I EF E,
所以平面DEF//平面ABD
P
F E
C B
化归思想

两个平面平行的判定与性质1、2

两个平面平行的判定和性质（一）教学目标：1．两个平面平行的定义．两个平面的位置关系及画法．两个平面平行的判定．2．理解并掌握两个平面平行的定义．掌握两个平面的位置关系应用了类比的方法3．会画平行或相交平面的空间图形，并用字母或符号表示，进一步培养学生的空间想象能力．4．掌握两个平面的判定定理的证明，进一步培养学生严密的逻辑思维能力．5．让学生认识研究两个平面的位置关系以及掌握和应用两个平面平行的判定是实际生产的需要，体现了理论联系实践的原则，并更好地培养学生分析问题与解决问题的能力．教学重点、难点：掌握两个平面的位置关系；掌握两个平面平行的判定．教学过程一、两个平面的位置关系让我们一起来观察：教室的正面和背面、左面和右面的墙面有没有公共点？教室的正面和侧面的墙面呢？思考问题：两个平面的位置关系可分为几种情况？从上面的例子，我们知道：两个平面的位置关系同平面内两条直线的位置关系相类似，可从有无公共点来区分．若两个平面有不共线的两个公共点，则由公理3可知这两个平面必然重合为一个平面；若两个平面有一个公共点，则由公理2可知这两个平面相交于过这个点的一条直线；若两个平面没有公共点，则这两个平面互相平行．由此得出不重合的两个平面的位置关系：两个平面平行——没有公共点；两个平面相交——有一条公共直线（至少有一个公共点）．那么如何画出并表示两个平行平面和两个相交平面呢？画两个平行平面的要点是：表示平面的平行四边形的对应边相互平行．画两个相交平面的要点是：先画表示两个平面的平行四边形的相交两边，再画表示两个平面交线的线段．成图时注意不相交的直线相互平行且等长，不可见的部分画虚线或不画．二、两个平面平行的判定判断两个互逆命题的正误，并说明理由．命题1．如果两个平面平行，那么其中一个平面内的所有直线一定都和另一个平面平行．命题2．如果一个平面内的所有直线都和另一个平面平行，那么这两个平面平行．两个平面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行．已知：在平面β内，有两条相交直线a、b和平面α平行．求证：β∥α．分析：要证明这个定理，先思考几个问题．问题1：如果平面α与平面β不平行，那么它们的位置关系怎样？（相交）．问题2：若平面α与平面β相交，那么交线与平行于平面α的直线a 和b各有什么关系？（平行）．问题3：相交直线a和b都与交线平行合理吗？（不合理，与平行公理矛盾）．证明：假设α∩β＝c．a∥α，a∩β，a∥c，同理b∥c．a∥b，这与题设a与b相交矛盾α∥β．注：在实际生活中，也经常利用这个判定定理判断两个平面平行．如在判断一个平面是否水平时，把水准器放在这个平面上交叉放两次，如果水准器的气泡都是居中的，就可以判定这个平面和水平面平行．例1 垂直于同一直线的两个平面平行．已知：α⊥AA ＇，β⊥AA ＇，求证：α∥β．分析：要证明两个平面平行，有两种方法：一是利用定义；二是利用判定定理，也是较常用的一种方法．因此利用判定定理证明例1的关键是：如何构造一个平面内的两相交直线都平行于另一个平面？证明：设经过直线AA ＇的两个平面γ，δ分别与平面α、β交于直线a ，a ＇和b ，b ＇． ∵AA ＇⊥α，AA ＇⊥β， ∴AA ⊥a ，AA ＇⊥a ＇， ∴a ‖a ＇，则a ＇∥α．同理，b ＇∥α．又∵a ＇∩b ＇＝ A ＇ ∴α∥β．注：这个例题的结论可与定理“垂直于同一平面的两条直线平行”联系起来记忆，也可作为判定两个平面平行的一种方法．例2. 如图已知正方体ABCD －A 1B 1C 1D 1，求证：平面AB 1D 1//平面BDC 1。

平面和平面平行的性质定理

αA
B
βC
D
6、设 // ，A，过点A作直线 l // ,则l与的位置关系如何？
αA l
β
7、如果平面α、β都与平面γ相交，且交线平行，则α∥β吗？
a α
γ b
β
8 如图,设AB、CD为夹在两个平行平面、之间
的线段，且直线AB、CD为异面直线，M、P 分别为AB、CD 的中点，
问题提出
1、什么叫两平面平行？
2、两平面平行的判定定理是什么？
如果一个平面内有两条相交直线分别平行于另一个平面，那么这两个平面平行.
3、两平面平行的判定定理解决了两平面平行的条件；反之，在两平面平行的条件下，会得到什么结论？
问题讨论
1、若 // ，l , 则 l与的位
置关系如何？该结论有何功能作用？
α
l
判定线面平
行的依据
β
2、若 // ，且 a,则与
的位置关系如何？
设 b，则直线a、b的位置
关系如何？为什么？
αa
β
b
γ
定理：两个平行平面同时和第三个
平面相交，那么它们的交线平行.
简记:面面平行，则线线平行
符号语言：
//

a, a // b
B C Da
α E FG
A
课外作业：
1、已知α∥β，AB交α、β于A、B，CD交
α、β于C、D，AB∩CD=S，AS=8，BS=9，
S
CD=34，求SC。
AC
α
S
AC
α
βD
B
B
D
β
2、已知P、Q是边长为1的正方体ABCD-A1B1C1D1