正多边形,扇形,圆锥侧面展开图正多边形,扇形,圆锥侧面展开图共33页
2013年全国名校中考模拟试卷分类汇编36正多边形、扇形和圆锥侧面展开图

正多边形、扇形和圆锥侧面展开图一、选择题1、(2013安徽芜湖一模)圆锥的底面直径是80cm ,母线长90cm ,则它的侧面展开图的圆心角是 ( ). A .3200B.400C .1600D.800答案:C2、(2013江苏射阴特庸中学)如右图,正五边形ABCDE 中,对角线AC 、AD 与BE 分别相交于点N 、M .下列结论错误..的是( ) A .四边形NCDE 是菱形 B .四边形MNCD 是等腰梯形 C .△AEM 与△CBN 相似 D .△AEN 与△EDM 全等 答案:C3、(2013江苏扬州弘扬中学二模)如图所示的平面图形中,不可能围成圆锥的是( )答案:D4、(2013·温州市中考模拟)已知:圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于A .11πB .10πC .9πD .8π 答案:D 5、(2013·湖州市中考模拟试卷10)如图是一个空心圆柱形纸筒,高为3,底面圆周长为4,若将这个纸筒沿圆筒侧面线路B M A →→剪开铺平,所得图形可能为( )A .边长为3和4的矩形B .边长为5和4的矩形C .边长为5和3的平行四边形D .边长为5和4的平行四边形答案:D6、10.(2013年河北二摸)在综合实践活动课上,小明同学用纸板制作了一个圆锥形漏斗模型.如图所示,它的底面半径OB =6cm ,高OC =8cm ,则这个圆锥漏斗的侧面积是 A .30cm B .30πcm C .60πcm D .120cm答案:C7、(2013年温州一摸)已知:圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于N M ED CB A BCDA B AC O 第10题图A .11πB .10πC .9πD .8π 答案:D二、填空题1、(2013江苏东台实中)已知圆锥的侧面积为π8cm 2,侧面展开图的圆心角为45°,则该圆锥的母线长为 cm 。
答案:82、 (2013·吉林中考模拟)一个圆锥的母线长为4,侧面积为8错误!未找到引用源。
常见几何体的表面展开图
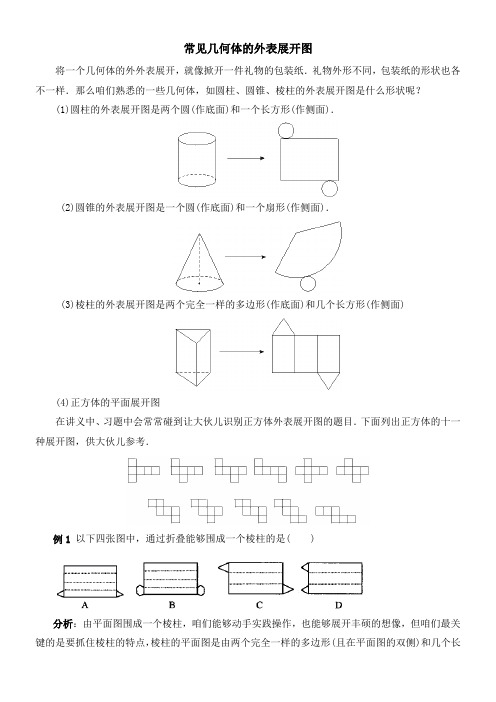
常见几何体的外表展开图将一个几何体的外外表展开,就像掀开一件礼物的包装纸.礼物外形不同,包装纸的形状也各不一样.那么咱们熟悉的一些几何体,如圆柱、圆锥、棱柱的外表展开图是什么形状呢?(1)圆柱的外表展开图是两个圆(作底面)和一个长方形(作侧面).(2)圆锥的外表展开图是一个圆(作底面)和一个扇形(作侧面).(3)棱柱的外表展开图是两个完全一样的多边形(作底面)和几个长方形(作侧面)(4)正方体的平面展开图在讲义中、习题中会常常碰到让大伙儿识别正方体外表展开图的题目.下面列出正方体的十一种展开图,供大伙儿参考.例1 以下四张图中,通过折叠能够围成一个棱柱的是( )分析:由平面图围成一个棱柱,咱们能够动手实践操作,也能够展开丰硕的想像,但咱们最关键的是要抓住棱柱的特点,棱柱的平面图是由两个完全一样的多边形(且在平面图的双侧)和几个长方形组成的.解:正确答案选C.点评:专门要注意的是两个完全一样的多边形是棱柱的上下两个底面图形(棱柱展开后,这两个图形是位于展开图的双侧),故不选D,另外定几个长方形,究竟是几个呢,它的个数确实是上下底多边形的边数,应选C.例2如以下图的平面图形是由哪几种几何体的外表展开的?(1) (2) (3)分析:找几何体的外表展开图,关键是看侧面和底面的形状.底面是圆的几何体有圆柱、圆锥、圆台.侧面是扇形的几何体是圆锥.侧面是长方形的几何体是棱柱、圆柱.解答:(1)圆锥;(2)圆柱;(3)圆台.例3如以下图,在正方体的两个相距最远的极点处停留着一只苍蝇和一只蜘蛛,蜘蛛能够从哪条最短的途径爬到苍蝇处?说明你的理由.分析:在解这道题时,正方体的展开图对解题有专门大的帮忙,由于作展开图有各类不同的方式,因此从蜘蛛到苍蝇能够用6种不同方式选择最短途径,而其中每一条途径都通过连结正方体2个极点的棱的中点.解:由于蜘蛛只能在正方体的外表爬行,因此只需作出那个正方体的展开图并用点标出苍蝇和蜘蛛的位置,依照“两点之间线段最短〞这一常识可知,连结这两个点的线段确实是最短的途径.点评:这种求最短路程是多少及求与棱的夹角是多少等问题,同窗们容易犯的错误是:用棱柱来计算路程,可求出的却不是最短的.通过对该节内容的学习,咱们必然要养成擅长观看,随时寻觅规律的良好适应,只有如此,才能把所学知识融会贯穿.。
数学 4直棱柱和圆锥的侧面展开图-课件

例1
解
根据图示可知该包装盒的侧面是矩形,又已知上、下底面是正六边形,因此这个几何体是正六棱柱(如图所示).
由已知数据可知它的底面周长为2×6=12,因此它的侧面积为12×6=72.
课堂小结
下列各图是几何体的平面展开图,猜想下列展开图可折成什么立体图形,并指出围成的几何体的形状.
当堂训练
某个立体图形的侧面展开图如图所示,它的 底面是正三角形,那么这个立体图形是( )(A)三棱柱 (B)四棱柱 (C)三棱锥.
A
我们,还在路上……
You made my day!
观察下图中的立体图形把上述这样的立体图形称为直棱柱,其中“棱”是指两个面的公共边,它具有以下特征:(1) 有两个面互相平行,称它们为底面;(2)其余各个面均为矩形,称它们为侧面;(3)侧棱(指两个侧面的公共边)垂直于底面.
根据底面图形的边数,我们分别称图中的立体图形为直三棱柱、直四棱柱、直五棱柱、直六棱柱.例如,长方体和正方体都是直四棱柱.底面是正多边形的棱柱叫作正棱柱.
下图是雕塑与斗笠的形象,它们的形状有什么特点?
在几何中,我们把上述这样的立体图形称为圆锥,圆锥是由一个底面和一个侧面围成的图形,它的底面是一个圆,连接顶点与底面圆心的线段叫作圆锥的高,圆锥顶点与底面圆上任意一点的连线段都叫作圆锥的母线,母线的长度均相等.
把圆锥沿它的一条母线剪开,它的侧面可以展开成平面图形,像这样的平面图形称为圆锥的侧面展开图,如图所示.
收集几个直棱柱模型,再把侧面沿一条侧棱剪开,它们的侧面能否展开成平面图形,是矩形吗?
将直棱柱的侧面沿着一条侧棱剪开,可以展开成平面图形,像这样的平面图形称为直棱柱的侧面展开图.如下图所示是一个直四棱柱的侧面展开图.
简单旋转体与多面体PPT课件

A' D
B'
L
c
C
=A B 2A D 2D D 2
=a2b2c2
A
a
b
B
L= a2b2c2
第36页/共38页
B组---2、
第37页/共38页
感谢您的观看!
第38页/共38页
球
半圆 直径 所在的直线
第31页/共38页
二、多面体的结构特征
多面体
结构特征
棱柱
有两个面 互相平行 ,其余各面都是四边形,并 且每相邻两个面的交线都_平__行__且__相_等___
有一个面是 多边形 ,而其余各面都是有一个公共 棱锥 __顶__点
的三角形
棱台
棱锥被平行于 底面 的平面所截, 截面 和 底面 之间的部分
三棱锥 四面体 直棱锥
四棱锥 正棱锥
第27页/共38页
五棱锥
2. 棱台
用一个平行于棱锥底面的平面去截棱锥 ,底面与截面之间的部分的多面体叫做棱台.
A1
D1
C1
B1
上底面
侧棱 侧面
下底面
正棱台:用正棱椎截得的棱 台叫正棱台
四棱台ABCD--A'B'C'D'
顶点
第28页/共38页
几何体的分类
柱体
锥体
D.圆锥所有的轴截面是全等的等腰三角形
2. 下列命题是真命题的是( )
A 以直角三角形的一直角边所在的直线为轴旋转所得 的几何体为圆锥;
B 以直角梯形的一腰所在的直线为轴旋转所得的旋转 体为圆柱;
C 圆柱、圆锥、棱锥的底面都是圆;
D 有一个面为多边形,其他各面都是三角形的几何体 是棱锥。
立体图形的表面展开图例题与讲解

立体图形的表面展开图例题与讲解(总4页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--立体图形的表面展开图1.圆柱、圆锥、棱柱的表面展开图将一个几何体的外表面展开,就像打开一件礼物的包装纸.礼物外形不同,包装纸的形状也各不相同.那么我们熟悉的一些几何体,如圆柱、圆锥、棱柱的表面展开图是什么形状呢(1)圆柱的表面展开图是两个圆(作底面)和一个长方形(作侧面).(2)圆锥的表面展开图是一个圆(作底面)和一个扇形(作侧面).(3)棱柱的表面展开图是两个完全相同的多边形(作底面)和几个长方形(作侧面).【例1】如图,将图中的阴影部分剪下来,围成一个几何体的侧面,使AB,DC重合,则所围成的几何体图形是().解析:此题可用排除法.因为阴影部分是个扇环,而圆柱的侧面展开图是长方形,所以排除A;圆锥的侧面展开图是扇形,所以排除B;长方体的侧面展开图是长方形,所以C 也要排除;故选D.答案:D2.正方体的表面展开图(1)正方体的表面展开图按展开图中正方形所在的行数及正方形的个数,归纳起来有四种情形,各种类型的共同特点是行与行之间有且只有一个“日”型结构,由此可知正方体的展开图不会出现如下面图形所示的“凹”字型和“田”字型结构,因为这里的行与行之间出现了两组“日”型结构.(2)正方体展开图中相对面的寻找技巧:相间的两个小正方形(中间隔着一个小正方形)是正方体的两个对面,如图1中的A面和B面;‘Z’字两端处的小正方形是正方体的对面,如图2、图3的A面和B面.此种方法简称为“相间、‘Z’端是对面”.解技巧正方体的表面展开图的判断思路(1)是否满足四种阵型中的一种;(2)行与行之间有且只有一个“日”型结构.【例2】一个正方形的每一个面上都写有一个汉字,其平面展开图如图所示,那么在该正方形中,与“爱”相对的字是().A.家B.乡C.孝D.感解析:本题以热爱家乡为素材,考查正方体的表面展开图.解题时可亲自动手剪一剪、折一折,即可得到与“爱”相对的字是“乡”;另外也可对展开图加以分析,根据展开图对面之间不能有公共边或公共的顶点,“爱”的对面不可能是“我”或“家”,折叠起来后“孝”、“感”与“爱”相邻,所以“爱”的对面不可能是“孝”、“感”,所以与“爱”相对的字是“乡”;但如果本题应用正方体展开图的对面寻找技巧——“相间、‘Z’端是对面”来解决,会非常简单,由相间的两个小正方形(中间隔着一个小正方形)是正方体的两个对面易知“爱”与“乡”相对.答案:B【例3】如图是正方体的展开图,则原正方体相对两个面上的数字和最小是().A.4 B.6 C.7D.8解析:将展开图还原成正方体,2和6相对,3和4相对,1和5相对,则原正方体相对两个面上的数字和最小为6.答案:B谈重点解决正方体展开图问题的关键熟练掌握正方体展开图的对面寻找技巧可以有效降低解题的难度,起到事半功倍的效果.3.正方体表面展开图的应用如果不考虑由于旋转等造成的相对位置的不同,正方体表面展开图一共有11个.正方体表面展开图的特点是每一个顶点周围的棱不超过三条.(1)“1–4–1”型有6个,其中通过“1”的移动可以由一个得到另外的5个,如图.(2)“1–3–2”型有3个,其中通过“1”的移动可以由1个得到另外的2个,如图.(3)“3–3”型有一个,“2–2–2”型有一个,如图.【例3-1】一个正方体的每一个面上都写着一个汉字,其表面展开图如图所示,那么,在该正方体中和“超”所对的汉字是__________.解析:这是“1–3–2”型的正方体表面展开图.根据展开图可知对面之间不能有公共边或公共顶点,所以“超”字的对面不能是“沉”、“着”、“越”,根据上下相对和左右相对,由于“信”和“着”相对,“着”和“超”相邻,所以“信”和“超”相邻.这样和“超”相对的字只能是“自”.答案:自【例3-2】六一儿童节时,阿兰准备用硬纸片通过裁剪、折叠制作一个封闭的正方体礼盒.她先在硬纸片上设计了一个如图1所示的裁剪方案(实线部分),经裁剪、折叠后成为一个封闭的正方体礼盒.请你参照如图,帮她设计另外两种不同的裁剪方案,使之经裁剪、折叠后也能成为一个封闭的正方体礼盒.图1 图2分析:阿兰设计的是正方体的11种展开图中的一种,可以从剩下的10种展开图中任选两种在如图的小方格中画出.解:如图2所示.4.其他立体图形展开图的应用由平面图形围成的立体图形叫多面体,其表面展开图可以有不同的形状.应多实践,观察,并大胆想象立体图形与表面展开图的关系.立体图形的表面展开图包括侧面展开图和底面展开图,画立体图形的展开图时,一定先观察立体图形的每一个面的形状.圆柱的侧面展开图是长方形,底面是圆;圆锥的侧面展开图是扇形,底面是圆;n棱柱的侧面展开图是n个高相等的长方形,底面是n边形;n棱锥的侧面展开图是n个三角形,底面是n边形.【例4】小新的茶杯是圆柱形,如图所示.左边下方有一只蜘蛛,从A处爬行到对面的中点B处,如果蜘蛛爬行路线最短,请画出这条最短路线图.分析:先画出圆柱的侧面展开图,再连接得到最短路线.解:如图所示.5.立体图形展开图的应用立体图形展开图的考查一般以选择题为主要方式,答案的获得需要学生经历一定的实验操作过程,当然学生也可以将操作活动转化为思维活动,在头脑中模拟(想象)折纸、翻转活动,较好地考查了学生的空间观念.解决此类问题,要充分考虑带有各种符号和各种图案的面的特点及位置,解题时,先正确画出立体图形的表面展开图,再仔细观察图案以及符号的不同特点,从而选出正确的答案.有时,根据图案的位置和方向可以先把一些很明显的不符合题目要求的选择项先排除掉,再一步步的寻找正确的选项.要想灵活解决此类问题,一要熟练掌握立体图形展开图的基本知识和解题技巧;二要充分发挥自己的空间想象力;三要不断积累生活经验和解题经验.【例5-1】如图所示的正方体的展开图是().解析:利用正方体及其表面展开图的特点解题.选项A和选项D折叠后,箭头不指向白三角形,C项折叠后与原正方体不符.B折叠后与原正方体相同.故选B.答案:B【例5-2】图1是由白色纸板拼成,将其中两面涂上颜色,如图2所示.下列四个中哪一个是图2的表面展开图().解析:由图中阴影部分的位置,首先可以排除B,D,又阴影部分正方形在左,三角形在右.故选A.答案:A。
常见几何体的表面展开图

常见几何体的表面展开图作者:王长颖来源:《初中生世界·七年级》2018年第12期研究立体图形的时候,我们可以通过研究平面图形(如三视图)的性质来研究几何体的性质.几何体转化为平面图形还有一种方法,那就是将几何体的表面展开,得到平面图形.我们可以通过研究立体圖形的表面展开图来研究立体图形的性质,但并不是所有几何体的表面都可以展开成平面,如球的表面就不能展开成平面.这里我们列举几种常见立体图形的表面展开图供同学们学习.一、常见几何体的展开图1.圆柱的表面展开图.圆柱的表面展开图由两个大小完全一样的圆(底面)和一个长方形(侧面)组成,如图1.友情提醒:圆柱展开图得到的两个圆的周长和长方形的一边长相等,长方形的另一边的长等于原来圆柱的高.2.圆台的表面展开图.圆台的表面展开图由大小不同的两个圆(底面)和扇形的一部分(侧面)组成,如图2.友情提醒:展开后的两个圆的周长分别等于两段弧的长度.3.圆锥的表面展开图.圆锥的表面展开图由一个圆(底面)和一个扇形(侧面)组成,如图3.4.棱锥的表面展开图.棱锥的表面展开图由一个多边形(底面)和几个三角形(侧面)组成.三棱锥的表面展开图如图4,四棱锥的表面展开图如图5.5.棱柱的表面展开图.直棱柱的表面展开图由两个完全相同的多边形(底面)和几个长方形(侧面)组成.直三棱柱的表面展开图由两个大小一样的三角形和三个长方形组成,如图6.直四棱柱的表面展开图由两个完全一样的四边形和四个长方形组成,如图7.二、几何体展开图1.正三棱锥的两种展开图之间的关系.不同几何体的表面展开图不相同,同一个几何体不同展开方式得到的平面图形也有所不同,但组成这些图形的基本图形往往又是一致的.例如:将图8的正三棱锥沿AB、AC、AD三条棱剪开,得到的平面展开图为图9,若沿着AB、BC、AD三条棱剪开,得到的平面展开图为图10.上述两个三棱锥的表面展开图,虽然形状不同,但组成元素都是三角形.由此我们可以猜测由四个三角形组成的几何体的展开图可能是三棱锥.无论是哪种形式的展开图,只要能将其围成一个立体图形,它就是该立体图形的平面展开图.2.正方体的十一种展开图.正方体的展开图详见本期第50页文章《借用口诀识记正方体展开图》.(作者单位:南京市第一中学江北新区学校)。
2010年中考试题最新分类汇总-42.正多边形、扇形和圆锥侧面展开图2

一、选择题1.(2010天水)在综合实践活动中,小明同学有纸板制作了一个圆锥形漏斗模型,如图所示,它的底面半径OB=6cm,高0C=8cm,则这个圆锥形漏斗的侧面面积是( ) A.30cm 2B. 60 cm 2C. 180cm 2D. 30 cm 2【答案】B2.(2010云南西双版纳)已知:一个圆锥的底面直径是6cm,母线长是8cm,求它的表面积为( )A 、224cm π B 、233cm C 、224cmD 、233cm π【答案】B3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20. 二、填空题1.(2010青海)圆锥的底面直径为12cm ,母线长为30cm ,则圆锥的侧面积为 cm 2(结果用π表示)。
【答案】180π2.(2010广东清远)在半径是20cm 的圆中,90°的圆心角所对的弧长为 cm .(精确到0.1 cm )【答案】31.4 3.(2010天水)如图,在Rt △ABC 中,∠ABC=90°,AB=8cm ,BC=6cm ,分别以A ,C 为圆心,以2A C 的长为半径作圆,将Rt △ABC 截去两个扇形,则剩余(阴影)部分的面积为 cm 2。
【答案】24-254π4.(2010年广西崇左)一个形状如圆锥的冰淇淋纸筒的底面直径为6cm 、母线长5cm ,围成这样的冰淇淋纸筒所需纸片的面积是 cm 2. 【答案】15π5.(2010云南大理)已知扇形的弧长为20π,所在圆的半径是10,那么这个扇形的面积为 。
【答案】100π.6.(2010辽宁阜新)如图所示,在以O 为圆心的两个同心圆中,大圆的直径AB 交小圆于C 、D 两点,AC =CD =DB ,分别以C ,D 为圆心,以CD 为半径作半圆.若AB =6㎝,则图中阴影部分的面积为 cm 2.【答案】4π7.(2010岳阳市)如图,我国南方一些地区农民戴的斗笠是一个底面圆半径为24厘米,高为厘米的圆椎形,这个斗笠的侧面积是(用含π的数表示) .【答案】672πcm28.9.10.11.12.13.14.15.16.17.18.19.20. 三、解答题1.(2010甘肃定西)如图,点D 在O ⊙的直径A B 的延长线上,点C 在O ⊙上,CD AC =,120=∠ACD ,(1)求证:C D 是O ⊙的切线;(2)若O ⊙的半径为2,求图中阴影部分的面积.【答案】(1)证明:连结O C . ………………1分∵ CD AC =,120ACD ︒∠=,∴ 30A D ︒∠=∠=. ………………2分 ∵ OC OA =,∴ 230A ︒∠=∠=. ………………3分∴ 290OCD ACD ︒∠=∠-∠=. …………………………………………………4分 ∴ C D 是O ⊙的切线. ……………………………………………………………5分 (2)解:∵∠A=30o , ∴ 1260A ︒∠=∠=. ……………………………6分∴ 323602602ππ=⨯=OBC S 扇形. …………………………………………………7分在Rt △OCD 中, ∵ tan 60C D O C︒=, ∴ 32=CD . …………………………8分∴ 323222121=⨯⨯=⨯=∆CD OC S OCD Rt . …………………………9分 ∴ 图中阴影部分的面积为-3232π. ………………………………………10分2.(2010辽宁省丹东)如图,已知在⊙O 中,ABAC 是⊙O 的直径,AC ⊥BD 于F ,∠A =30°.(1)求图中阴影部分的面积;(2)若用阴影扇形OBD 围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.【答案】(1)连结AD .由轴对称性可知:∠DAC=∠BAC=30,AB=AD ,△ABD 是一个边长为∠BOD=∠BAD=120°,AC ⊥BD ,故BF =21AB =23,由等腰△BOD ,∠OBF=30°.利用勾股定理求得:OB =4.∴S 阴影=31S 圆=16π3.(2)设圆锥的底面圆的半径为r ,则周长为2πr ,∴1202ππ4180r = .∴43r =.3.(2010贵州黔东南州)如图,水平放置的圈柱形水管道的截面半径是0.6m ,其中水面高0.3m ,求截面上有水部分的面积(结果保留π)【答案】取圆心O, 设截面上水面所在的弦为AB , 过O 作OC ⊥AB , 垂足为C ,连接OA ,∵OA第22题图=0.6m, 水面高0.3m, ∴OC =0.3m, AC =22OCOA -=0.33m ,∴cos ∠AOC =21,∴∠AOC =60°,∠AOB =120°. 则截面上有水部分的面积大小为1806.01202∙∙π-21×0.63×0.3=0.24π-0.093.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.。
正多边形,扇形,圆锥侧面展开图 正多边形,扇形,圆锥侧面展开图

考
限
点 管
限时集训
时 集
理
训
归
类
单击此处进入 限时集训
探
究
考
限
点
时
管
集
理
训
归 类 探 究
图37-8
考
限
点
时
管
集
理
【预测理由】 平面图形的滚动问题,实质上是物体 训
的旋转,考查动点移动的路线或围成的面积,难度较大,
归
类 创新性很强,是中考的热点考题和容易丢分的考题.
探
究
[预测变形 1] 如图 37-9 所示,Rt△ABC 的边 BC 位
考 于直线 l 上,AC= 3,∠ACB=90°,∠A=30°,若 Rt 限
类
探 后作出边心距即可.
究
类型之二 扇形的弧长计算
考 点
[2012·湛江]一个扇形的圆心角为60°,它
限 时
管 理
所对的弧长为2π cm,则这个扇形的半径为
A
集 训
(
)
归
AC..62 cm3 cm
BD.. 612ccmm
类 探 究
【解析】 由扇形的圆心角为 60°,它所对的弧长为 2 π cm,
即 n=60,l=2π,
考 点 管 理
∠C=60°,菱形 ABCD 在直线 l 上向右作无滑动地翻滚, 限
每绕着一个顶点旋转 60°叫一次操作,则经过 36 次这样 的操作,菱形中心 O 所经过的路径总长为__(8___3_+__4_)π___(结
时 集 训
果保留π).
归 类 探 究
图37-10
考
限
点 管
【解析】 每操作 3 次一个循环,而 3 次当中 O 点经
湘教版九年级下册数学课件第3章3.2直棱柱圆锥的侧面展开图
基础巩固练
6.【中考·云南】一个圆锥的侧面展开图是半径为 8 的半圆形, 则该圆锥的表面积(侧面积与底面积的和)是( A ) A.48π B.45π C.36π D.32π
基础巩固练 7.【中考·自贡】已知圆锥的侧面积是 8π cm2,若圆锥底面半径
为 R(cm),母线长为 l(cm),则 R 关于 l 的函数图象大致是 ()
素养核心练 13.【中考·邵阳】如图①,在等腰三角形 ABC 中,∠BAC=120°,
AD 是∠BAC 的平分线,且 AD=6,以点 A 为圆心,AD 长 为半径画弧 EF,交 AB 于点 E,AC 于点 F. (1)求由弧 EF 及线段 FC,CB,BE 围成的图形(图中阴影部分) 的面积;
素养核心练
能力提升练
12.一个正六棱柱模型如图所示,它的底面边长是 6 cm,侧棱 长是 4 cm,观察这个模型,回答下列问题:
(1)这个六棱柱一共有多少个面?它们的形状分别是什么?它的 哪些面的形状、面积完全相同?
能力提升练
解:这个六棱柱一共有 8 个面.上、下底面是正六边形,侧面都 是矩形.上、下底面的形状、面积完全相同,6 个侧面的形状、 面积完全相同.
新知笔记 2.(1)圆锥:如图是一个圆锥,它是由一个底面和一个侧面围成
的图形,它的底面是一个___圆_____,连接顶点和底面圆心的 线段叫作圆锥的高,圆锥顶点与底面圆上任意一点的连线段 都叫作圆锥的母线,母线的长度均相等. (2)圆锥的侧面展开图是一个__扇__形____, 展开图的半径是圆锥的_母__线__长___,弧 长是圆锥底面圆的周长.
素养核心练
(2)将阴影部分剪掉,余下扇形 AEF,将扇形 AEF 围成一个圆锥 的侧面,如图②,AE 与 AF 正好重合,圆锥侧面无重叠,求 这个圆锥的高 h.
立体图形的表面展开图例题与讲解

立体图形的表面展开图1.圆柱、圆锥、棱柱的表面展开图将一个几何体的外表面展开,就像打开一件礼物的包装纸.礼物外形不同,包装纸的形状也各不相同.那么我们熟悉的一些几何体,如圆柱、圆锥、棱柱的表面展开图是什么形状呢(1)圆柱的表面展开图是两个圆(作底面)和一个长方形(作侧面).(2)圆锥的表面展开图是一个圆(作底面)和一个扇形(作侧面).(3)棱柱的表面展开图是两个完全相同的多边形(作底面)和几个长方形(作侧面).【例1】如图,将图中的阴影部分剪下来,围成一个几何体的侧面,使AB,DC重合,则所围成的几何体图形是( ).解析:此题可用排除法.因为阴影部分是个扇环,而圆柱的侧面展开图是长方形,所以排除A;圆锥的侧面展开图是扇形,所以排除B;长方体的侧面展开图是长方形,所以C也要排除;故选D.答案:D2.正方体的表面展开图(1)正方体的表面展开图按展开图中正方形所在的行数及正方形的个数,归纳起来有四种情形,各种类型的共同特点是行与行之间有且只有一个“日”型结构,由此可知正方体的展开图不会出现如下面图形所示的“凹”字型和“田”字型结构,因为这里的行与行之间出现了两组“日”型结构.(2)正方体展开图中相对面的寻找技巧:相间的两个小正方形(中间隔着一个小正方形)是正方体的两个对面,如图1中的A面和B面;‘Z’字两端处的小正方形是正方体的对面,如图2、图3的A面和B面.此种方法简称为“相间、‘Z’端是对面”.解技巧正方体的表面展开图的判断思路(1)是否满足四种阵型中的一种;(2)行与行之间有且只有一个“日”型结构.【例2】一个正方形的每一个面上都写有一个汉字,其平面展开图如图所示,那么在该正方形中,与“爱”相对的字是( ).A.家B.乡C.孝D.感解析:本题以热爱家乡为素材,考查正方体的表面展开图.解题时可亲自动手剪一剪、折一折,即可得到与“爱”相对的字是“乡”;另外也可对展开图加以分析,根据展开图对面之间不能有公共边或公共的顶点,“爱”的对面不可能是“我”或“家”,折叠起来后“孝”、“感”与“爱”相邻,所以“爱”的对面不可能是“孝”、“感”,所以与“爱”相对的字是“乡”;但如果本题应用正方体展开图的对面寻找技巧——“相间、‘Z’端是对面”来解决,会非常简单,由相间的两个小正方形(中间隔着一个小正方形)是正方体的两个对面易知“爱”与“乡”相对.答案:B【例3】如图是正方体的展开图,则原正方体相对两个面上的数字和最小是( ).A.4 B.6 C.7 D.8解析:将展开图还原成正方体,2和6相对,3和4相对,1和5相对,则原正方体相对两个面上的数字和最小为6.答案:B谈重点解决正方体展开图问题的关键熟练掌握正方体展开图的对面寻找技巧可以有效降低解题的难度,起到事半功倍的效果.3.正方体表面展开图的应用如果不考虑由于旋转等造成的相对位置的不同,正方体表面展开图一共有11个.正方体表面展开图的特点是每一个顶点周围的棱不超过三条.(1)“1–4–1”型有6个,其中通过“1”的移动可以由一个得到另外的5个,如图.(2)“1–3–2”型有3个,其中通过“1”的移动可以由1个得到另外的2个,如图.(3)“3–3”型有一个,“2–2–2”型有一个,如图.【例3-1】一个正方体的每一个面上都写着一个汉字,其表面展开图如图所示,那么,在该正方体中和“超”所对的汉字是__________.解析:这是“1–3–2”型的正方体表面展开图.根据展开图可知对面之间不能有公共边或公共顶点,所以“超”字的对面不能是“沉”、“着”、“越”,根据上下相对和左右相对,由于“信”和“着”相对,“着”和“超”相邻,所以“信”和“超”相邻.这样和“超”相对的字只能是“自”.答案:自【例3-2】六一儿童节时,阿兰准备用硬纸片通过裁剪、折叠制作一个封闭的正方体礼盒.她先在硬纸片上设计了一个如图1所示的裁剪方案(实线部分),经裁剪、折叠后成为一个封闭的正方体礼盒.请你参照如图,帮她设计另外两种不同的裁剪方案,使之经裁剪、折叠后也能成为一个封闭的正方体礼盒.图1 图2分析:阿兰设计的是正方体的11种展开图中的一种,可以从剩下的10种展开图中任选两种在如图的小方格中画出.解:如图2所示.4.其他立体图形展开图的应用由平面图形围成的立体图形叫多面体,其表面展开图可以有不同的形状.应多实践,观察,并大胆想象立体图形与表面展开图的关系.立体图形的表面展开图包括侧面展开图和底面展开图,画立体图形的展开图时,一定先观察立体图形的每一个面的形状.圆柱的侧面展开图是长方形,底面是圆;圆锥的侧面展开图是扇形,底面是圆;n棱柱的侧面展开图是n个高相等的长方形,底面是n边形;n棱锥的侧面展开图是n个三角形,底面是n边形.【例4】小新的茶杯是圆柱形,如图所示.左边下方有一只蜘蛛,从A处爬行到对面的中点B处,如果蜘蛛爬行路线最短,请画出这条最短路线图.分析:先画出圆柱的侧面展开图,再连接得到最短路线.解:如图所示.5.立体图形展开图的应用立体图形展开图的考查一般以选择题为主要方式,答案的获得需要学生经历一定的实验操作过程,当然学生也可以将操作活动转化为思维活动,在头脑中模拟(想象)折纸、翻转活动,较好地考查了学生的空间观念.解决此类问题,要充分考虑带有各种符号和各种图案的面的特点及位置,解题时,先正确画出立体图形的表面展开图,再仔细观察图案以及符号的不同特点,从而选出正确的答案.有时,根据图案的位置和方向可以先把一些很明显的不符合题目要求的选择项先排除掉,再一步步的寻找正确的选项.要想灵活解决此类问题,一要熟练掌握立体图形展开图的基本知识和解题技巧;二要充分发挥自己的空间想象力;三要不断积累生活经验和解题经验.【例5-1】如图所示的正方体的展开图是( ).解析:利用正方体及其表面展开图的特点解题.选项A和选项D折叠后,箭头不指向白三角形,C项折叠后与原正方体不符.B折叠后与原正方体相同.故选B.答案:B【例5-2】图1是由白色纸板拼成,将其中两面涂上颜色,如图2所示.下列四个中哪一个是图2的表面展开图( ).解析:由图中阴影部分的位置,首先可以排除B,D,又阴影部分正方形在左,三角形在右.故选A.答案:A。
九年级数学扇形面积公式、圆柱、圆锥侧面展开图人教版知识精讲

九年级数学扇形面积公式、圆柱、圆锥侧面展开图人教版【本讲教育信息】一. 教学内容:扇形面积公式、圆柱、圆锥侧面展开图[学习目标]1. 掌握基本概念:正多边形,正多边形的中心角、半径、边心距以及平面镶嵌等。
2. 扇形面积公式:S n R lR 扇==π236012n 是圆心角度数,R 是扇形半径,l 是扇形中弧长。
3. 圆柱是由矩形绕一边旋转360°形成的几何体,侧面展开是矩形,长为底面圆周长,宽为圆柱的高S rh 圆柱侧=2π r 底面半径 h 圆柱高4. 圆锥侧面积圆锥是由直角三角形绕一直角边旋转360°形成的几何体。
侧面展开是扇形,扇形半径是圆锥的母线,弧长是底面圆周长。
5. 了解圆柱由两平行圆面和一曲面围成,明确圆柱的高和母线,它们相等。
6. 了解圆锥由一个曲面和一个底面圆围成,明确圆锥的高和母线,知道可以通过解高、母线、底面半径所围直角三角形,解决圆锥的有关问题。
7. 圆柱圆柱的侧面展开图是两邻边分别为圆柱的高和圆柱底面周长的矩形。
圆柱的侧面积等于底面周长乘以圆柱的高。
如图所示,若圆柱的底面半径为r ,高为h ,则:S rh 侧=2π,S S S rh r r h r 表侧底=+=+=+22222πππ()。
8. 圆锥圆锥是由一个底面和一个侧面组成的。
圆锥的底面是一个圆,侧面是一个曲面,这个曲面在一个平面上展开后是一个扇形,这个扇形的半径是圆锥的母线,扇形的弧长是圆锥底面的周长。
因此,圆锥的侧面积是圆锥的母线与底面周长积的一半。
如图所示,若圆锥的底面半径为r ,母线长为l ,则S l r rl 侧·,==122ππ S S S rl r r l r 表侧底=+=+=+πππ2()。
[重点、难点]扇形面积公式及圆柱、圆锥侧面积公式的理解和灵活应用。
【典型例题】例1. 已知如图1,矩形ABCD 中,AB =1cm ,BC =2cm ,以B 为圆心,BC 为半径作14圆弧交AD 于F ,交BA 延长线于E ,求扇形BCE 被矩形所截剩余部分的面积。
圆锥的侧面展开图汇总

圆锥的侧面展开图汇总圆锥是一种由平面形状和锥体组合而成的立体几何体,其侧面展开图可以展开成一个平面图形。
本文将为您介绍几种常见的圆锥侧面展开图,以及计算圆锥侧面展开图面积和体积的方法。
圆锥的侧面展开图直角圆锥展开图直角圆锥是指其底面和母线之间夹角为90度的圆锥。
在展开图中,圆锥的底面展开成一个圆形,侧面展开成一条斜线和两个扇形。
直角圆锥展开图直角圆锥展开图在计算直角圆锥侧面展开图面积时,可以将侧面分解成两个扇形和一条三角形。
设圆锥的半径为r,侧面直线段长度为l,则展开图面积为:A = πr² + πrl在计算直角圆锥体积时,可使用下列公式:V = (1/3)πr²h其中,h为圆锥高度。
正圆锥展开图当圆锥的底面和母线之间的夹角不为90度时,被称为正圆锥。
在正圆锥展开图中,圆锥的底面展开成一个圆形,侧面展开成一个扇形。
正圆锥展开图正圆锥展开图在计算正圆锥侧面展开图面积时,可使用下列公式:A = πr² + πrl其中,r为圆锥的半径,l为圆锥侧面直线段长度。
在计算正圆锥体积时,可使用下列公式:V = (1/3)πr²h其中,h为圆锥的高度。
倒圆锥展开图倒圆锥是指圆锥的底面反转的立体几何体。
在展开图中,倒圆锥的底面展开后成为一个带有三角形开口的圆形,侧面展开成两条直线段和两个扇形。
倒圆锥展开图倒圆锥展开图在计算倒圆锥侧面展开图面积时,可使用下列公式:A = πr² - πrl其中,r为圆锥的半径,l为圆锥侧面直线段长度。
在计算倒圆锥体积时,可使用下列公式:V = (1/3)πr²h其中,h为圆锥的高度。
本文介绍了三种常见的圆锥侧面展开图,包括直角圆锥展开图、正圆锥展开图和倒圆锥展开图。
此外,还介绍了计算圆锥侧面展开图面积和体积的方法。
希望本文能够对您有所帮助。
