垂径定理第二课时
2.3垂径定理(第2课时)课件(共12张ppt)

D D
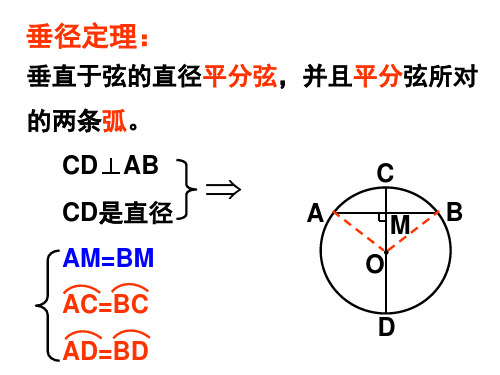
由 ① CD是直径 ③ AM=BM
可推得
②CD⊥AB, ④A⌒C=B⌒C,
·O
A (E)
B 推论1:
⑤A⌒D=B⌒D.
平分弦(不是直径)的直径垂直于弦, C 并且平分弦所对的两条弧.
探究二:AB是⊙O的一条弦,且AM=BM。且CD⊥AB
于点M,CD与圆心有何位置关系?还有什么结论?
为什么?
C
ED F B
设圆弧的半径OA为r,OD=r-2.4 在Rt△OAD中,由勾股定理,
r
O
得: r≈3.9(m)
在Rt△ONH中,由勾股定理,得:
OH=√ON2-NH2=√3.92-1.52=3.6
∴ DH=OH-OD=3.6-1.5=2.1>2 ∴此货船能顺利通过这座拱桥.
1、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的
谢谢观赏
You made my day!
我们,还在路上……
∠ CEB=30°=∠ FEO OF=1.5
A F
O· E C
B
AF=√OA2-OF2=√62-1.52=
3√15 2
AB=2AF= 3√15
9.如图,圆O与矩形ABCD交
AH
于E、F、G、H,EF=10, HG=6,AH=4,求BE的长.
BE
BE=2
MG D
·ON F C
10、如图,在⊙O中,AB为⊙O的弦
M
B
图中相等的线段有 :AE=EB CF=FD . 图中相等的劣弧有: A⌒MC⌒=NB⌒=MN⌒D. .A⌒C=B⌒D. .
A
E
O·F
D
CN
3、如图,点P是半径为5cm的⊙O内一点,且OP=3cm,
九年级数学下册精品教学课件27.1.2-第2课时-垂径定理

O
A
PB
课堂小结
垂径定理
内容 推论 辅助线
垂直于弦的直径平分弦, 并且平分弦所对的两条弧
一条直线满足:①过圆心;②垂直于弦; ③平 分弦(不是直径); ④平分弦所对的优弧; ⑤平分弦所对的劣弧.满足其中两个条件就 可以推出其它三个结论(“知二推三”)
两条辅助线: 连半径,作弦心距
基本图形及 构造Rt△利用勾股定 变 式 图 形 理计算或建立方程.
证明:
∴四边形ADOE为矩形,
又 ∵AC=AB
C
∴ AE=AD E
∴ 四边形ADOE为正方形.
A
·O
D
B
5.已知:如图,在以O为圆心的两个同心圆中,大圆 的弦AB交小圆于C,D两点。你认为AC和BD有什么 关系?为什么?
证明:过O作OE⊥AB,垂足为E
,
O.
则AE=BE,CE=DE.
A CED B
(1)连接AO,BO,则AO=BO,
又AE=BE,∴△AOE≌△BOE(SSS),
∴∠AEO=∠BEO=90°,
A
∴CD⊥AB.
(2)由垂径定理可得A⌒C =B⌒C, A⌒D =B⌒D.
·O
E B
D
归纳总结
垂径定理的推论
平分弦(不是直径)的直径垂直于这条弦,并 且平分这条弦所对的两条弧;
平分弧的直径垂直平分这条弧所对的弦.
O·
102 62 8 cm
.
∴ AB=2AE=16cm.
例2 如图, ⊙ O的弦AB=8cm ,直径CE⊥AB
于D,DC=2cm,求半径OC的长.
解:连接OA,∵ CE⊥AB于D,
E
∴ AD 1 AB 1 8 4 (cm)
垂径定理第二课时

你会四等分弧AB吗?
赵州石拱桥
• 1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱 是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高 (弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半 径(精确到0.1m).
随堂练习P92 4
赵州石拱桥
解:如图,用 AB 表示桥拱,AB 所在圆的圆心为O,半径为Rm, 经过圆心O作弦AB的垂线OD,D为垂足,与 AB 相交于点C.根 据垂径定理,D是AB的中点,C是AB 的中点,CD就是拱高. 37.4 由题设 AB 37.4, CD 7.2, C
• . 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶 高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并 高出水面2米的货船要经过这里,此货船能顺利通过这 座拱桥吗?
船能过拱桥吗
• 解:如图,用 AB 表示桥拱, AB 所在圆的圆心为O,半径为Rm, 经过圆心O作弦AB的垂线OD,D为垂足,与 AB 相交于点C.根 据垂径定理,D是AB的中点,C是 AB的中点,CD就是拱高. 1 由题设得 AB 7.2, CD 2.4, HN MN 1.5.
a 2 ⑵ r d ( ) 2
2 2
(1)如图,已知⊙O的半径为 6 cm,弦 AB与半径 OA的 夹角为 30 °,求弦 AB 的长.
O 6 A
30°
E
A
O M C
B
(2)如图,已知⊙O的半径为 6 cm,弦 AB与半径 OC互 相平分,交点为 M , 求 弦 AB 的长.
• 在直径为650mm的圆柱形油槽内装入一些油后,截 面如图所示.若油面宽AB = 600mm,求油的最大深 度.
O
挑战自我
• 1、要把实际问题转变成一个数学问题来解决.
《垂径定理》课件2
例题:
2、如图,AB是半圆的直径,O是圆心, C是半圆上一点,D是弦AC的中点,OD 交弧AC于E,若AC=8cm,DE=2cm,则 OD的长为____cm。
E D A
C
O
B
例题: 3.你能破镜重
n A
圆吗?
m C B
·
O
作弦AB.AC及它们的垂直平
分线m.n,交于O点;以O为圆 心,OA为半径作圆。
O
D A B
C
练习2:在圆O中,直径CE⊥AB于D,OD=4 ㎝,弦AC= ㎝ , 求圆O的半径。
E
10
O
D A B
C
E
练习1: 如图,圆O的弦AB=8 ㎝ , DC=2㎝,直径CE⊥AB于D, 求半径OC的长。
O
D A B
C
练习2:在圆O中,直径CE⊥AB于D,OD=4 ㎝,弦AC= ㎝ , 求圆O的半径。
4.如图为一圆弧形拱桥,半径OA=10m, 拱高为4m,求拱桥跨度AB的长。
C A D O B
判断下列说法的正误
①平分弧的直径必平分弧所对的弦
②平分弦的直线必垂直弦
③垂直于弦的直径平分这条弦 ④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线是圆的直径
⑥平分弦所对的一条弧的直径必垂直这条弦 ⑦在圆中,如果一条直线经过圆心且平
D
O
练习
1、将一个两边都带有刻度的直尺放在半圆形纸 片上,使其一边经过圆心O,另一边所在直线 与半圆交于点D、E, 量出半径 OC = 5cm,弦 DE=8cm。求直尺的宽度。
D C A
O
E B
如图,⊙O的直径为10,弦AB=8,P为AB上的一 个动点,那么OP长的取值范围 是 。
垂径定理第二课时

⌒ ⌒ ⑤AD=BD. 只要具备其中两个条件,就可推出其余三个结论. 为了便于理解,不出错误,定理 C 和推论可以这样记:对于一个圆 及一条直线来说,如果具备下列 A B M└ 5个条件中的任何2个,那么其它 ●O 三个也成立。
D
你可以写出相应的命题吗? 相信自己是最棒的!
垂径定理及逆定理
① CD是直径 ② CD⊥AB, ③ AM=BM, , ⌒ ⌒ ⌒ ⌒ ⑤AD=BD. ④AC=BC,来自CA·
O
D
B
船能过拱桥吗?
例3.如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱 顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方 形并高出水面2米的货船要经过这里,此货船能顺利通 过这座拱桥吗?
船能过拱桥吗
解:如图,用 AB 表示桥拱, AB 所在圆的圆心为O,半径为Rm, 经过圆心O作弦AB的垂线OD,D为垂足,与 AB 相交于点C.根 据垂径定理,D是AB的中点,C是 AB 的中点,CD就是拱高. 由题设得 1
求证:AC=BD
⌒
⌒
推论2.
圆的两条平行弦所夹 的弧相等。
挑战自我画一画
例:平分已知弧
已知:弧AB E 求作:弧AB的中点
C
AB
A
作法: ⒈ 连结AB.
B
⒉作AB的垂直平分线 CD,交弧AB于点E. D
点E就是所求弧AB的中点。
变式一: 求弧AB的四等分点。
C m n
F
A
E
G
B
D
C m E A n
2
C
E F
●
O
(1)如图,已知⊙O的半径为 6 cm,弦 AB与半径 OA的夹角为 30 °,求弦 AB 的长.
垂径定理1-3课时

BB24.1.2 垂直于弦的直径——垂径定理(第一课时)一、知识探究1、圆既是 图形,又是 图形。
对称轴是 ,对称中心是 。
2、按要求作图(1)作⊙O 的任意一条弦AB ;(2)过圆心O ,作垂直于弦AB 的直径CD ,交AB 于点E 。
观察并回答:问题1:通过观察,在该图中有没有相等的线段:问题2:通过观察,在该图中有没有相等的弧: 证明过程:已知:CD 是⊙O 的直径,且CD ⊥AB 。
求证:AE=BE结论:垂径定理: 的直径 ,并且 。
几何语言的写法:∵ ∴强调:(1) ;(2) ;(3) (4) ;(5) 二、例题解析例1:在⊙O 中,弦AB 长8cm ,圆心O 到AB 的距离为3cm ,则⊙O 半径为例2:⊙O 的半径为5,M 是⊙O 内一点,OM=3,则过M 点的最短弦的长为例3:如图:已知线段AB 交⊙O 于C 、D 两点,若AC=BD ,求证:OA=OB 。
三、课堂练习:1、在⊙O 中,弦AB 长8cm ,⊙O 半径为5cm ,圆心O 到AB 的距离为2、在⊙O 中,⊙O 半径为5cm ,圆心O 到弦AB 的距离3cm ,则弦AB 的长为3、在半径为R 的⊙O 中,有长为R 的弦AB ,那么O 到AB 的距离为4、如图,在以O 为圆心的两个同心圆中,大圆的弦AB 交小圆与C 、D 两点。
求证:AC=BD 。
5、如图,AB 是⊙O 的直径,弦CD ⊥AB 于点P ,CD=10cm ,AP ∶PB=1∶5 ,求的⊙O 半径。
24.1.2 垂直于弦的直径——垂径定理的推论(第二课时)一、知识回顾垂径定理: 的直径 ,并且 。
按要求作图(1)在⊙O (2)作弦(3)连接问题1:⊙O 的直径CD 与弦AB 有怎样的位置关系: 问题2:该图中有没有相等的弧 证明过程:已知:CD 是⊙O 的直径,并且平分弦AB ,求证:CD ⊥AB 。
结论:垂径定理的推论: 的直径 ,并且 三、例题解析例1:已知⊙O 的半径OA=10㎝,弦AB=16㎝,P 为弦AB 上的一个动点,则OP 的最短距离为典型练习:1、下面四个命题中正确的一个是( )A .平分一条直径的弦必垂直于这条直径B .平分一条弧的直线垂直于这条弧所对的弦C .弦的垂线必过这条弦所在圆的圆心D .圆内平分一条弧和它所对弦的直线必过这个圆的圆心 2、下列命题中,正确的是( ).A .过弦的中点的直线平分弦所对的弧B .过弦的中点的直线必过圆心C .弦所对的两条弧的中点连线垂直平分弦,且过圆心D .弦的垂线平分弦所对的弧3、⊙O 的直径为10,弦AB 的长为8,M 是弦AB 上的动点,则OM 的长的取值范围是( ) (A )5OM 3≤≤ (B )5OM 4≤≤ (C )5OM 3<< (D )5OM 4<<4、如图所示,若⊙O 的半径为13cm ,点P 是弦AB 上一动点,且到圆心的最短距离5cm ,则弦AB 的长为______________ . 四、课堂练习1、已知:如图,AB 是⊙O 的弦,半径OC ⊥AB 于点D ,且AB=8m ,OC=5m ,则DC 的长为(1) (2) (3)2、如图,在⊙O 中,直径AB 丄弦CD 于点M ,AM=18,BM=8,则CD 的长为__________ . 3、如图,∠PAC=30°,在射线AC 上顺次截取AD=3cm ,DB=10cm ,以DB 为直径作⊙O 交射线AP 于E 、F 两点,则线段EF 的长是_________ cm .4、已知圆的半径为5cm ,一弦长为8cm ,则弦的中点到弦所对弧的中点的距离为__ _____。
部编人教版数学九年级上册垂径定理2市级公开课ppt课件

A
B
E
O
A
E
B
C
F
D
O
C
F
D
记住:圆的两条平行弦之间的距离有两种情况。
8.在直径为650mm的圆柱形油槽内装入一些油后,截面如 图所示.若油面宽AB = 600mm,求油的最大深度.
9、在直径为650mm的圆柱形油槽内装入一些油后,截面的 油面宽AB = 600mm,求油的最大深度.
(4)弦的垂直平分线一定是圆的直径。
(5)平分弧的直线,平分这条弧所对的 弦。 (6)弦垂直于直径,这条直径就被弦平分。
O ACB
(4)
B
O D
C
A
(5)
C
O A EB
D (6)
知识运用
A
B
例1. 平分已知弧 AB .
你会四等分弧AB吗?
思考:已知一个圆或一条弧,如何找出它的圆心? 作两条弦的垂直平分线,它们的交点就是圆心。
O
A
┌E
D
B
D
600
C
D
A
600
B
O ø650
C
10、如图,在⊙O中,AB为⊙O的弦,C、D是直线AB上 两点,且AC=BD求证:△OCD为等腰三角形。
11、如图,在⊙O中,AB为⊙O的弦,C、D是直线AB上两点, 且△OCD为等腰三角形,求证AC=BD。
O
∟
E
CA
BD
O
∟
E
CA
BD
12. 如图,将半径为2cm的圆形纸片折叠后,圆 弧恰好经过圆心,则折痕AB的长为( C )
O A
B C
D P
2.3《垂径定理》课件2 (共19张PPT)

该定理的题设是: 垂直于弦的直径 该定理的结论是: 平分这条弦,并且平 分弦所对的弧 几何语言叙述定理:
∵CD为⊙O的直径,且CD⊥AB,(条件) . (结论) , ∴AM=BM, = BC AC AD = BD
C A M O B
D
D
在下列图形,符合垂径定理的条件吗?
A C B D E O (2) A E O D (3) D O A E C (6) B A O E B (7) B A E O (4) B
2
在Rt△AEO中,由勾股定理 得 OA2 =OE 2 +AE 2 .
即
r 2 =(r -2)2 +4.
解得 r=5.
∴ CD = 2r = 10 (cm).
E A 例2.如图,已知在⊙O中,弦AB的长为 .O 8cm,圆心O到AB的距离为3cm,求⊙O 的半径。 解:连结OA ∵OE ┴ AB于E. OE=3 1 ∴AE= 2 AB=4 由勾股定理得: ∴OA=√AE2+OE2=5
C
圆是轴对称图形, 对称轴是任意一条过 圆心的直线(直径).
O
D
2.在对折⊙O后,用针在半圆上刺一个小孔,得 两个重合的点 A、B (如图①).把对折的圆摊平,那么 折痕 CD 是直径,点 A、B 是关于直线 CD 的一对对 称点.连接 AB,得弦 AB(如图②),这时直径 CD 与弦 AB有怎样的位置关系?
B
O
练一练 如图a、b,一弓形弦长为 4 6 cm,弓形所在的
2cm或____ 12cm 圆的半径为7cm,则弓形的高为___ _.
C
A
C B A
D
O 图a
O
D 图b
B
1、从知识上学习了什么? 垂径定理:垂直于弦的直径平分弦,并且平分弦对的 两条弧。 2、从方法上学习了什么? (1).垂径定理是圆中一个重要的结论,叙述语言要准确, 一条直线只要满足①过圆心;②垂直于弦;则可得 ③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧。 (2).垂径定理和勾股定理有机结合计算弦长、半径、弦 心距等问题的方法,构造直角三角形 (3).解决有关弦的问题时,经常 ①连结半径; ②过圆心作一条与弦垂直的线段等辅助线,为应用 垂径定理创造条件。
24.1垂径定理(第二课时)

24.1垂径定理第2课时教学目标:通过练习进一步掌握圆的垂径定理及应用重点、难点:重点、垂径定理难点:垂径定理的应用教学过程一、教师导学1、圆是:()图形2、垂径定理()(1)(2):;3、根据垂径定理填空:(1)若CD是直径,CD⊥AB于P,则:;(2)若CD是直径,AB不是直径且AP=BP,则:(3)若CD是直径,弧AP=弧BP则:(4)若CD⊥AB于P且AP=BP则:二、自学探究如图24-11,AB为⊙O的直径,CD为弦,过C、D分别作CN⊥CD、DM⊥CD,分别交AB于N、M,请问图中的AN与BM是否相等,说明理由.方法:三、学生展示1、选择题.(1).如图1,如果AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下列结论中,错误的是().A.CE=DE B. C.∠BAC=∠BAD D.AC>AD(1) (2) (3)(2).如图2,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是()A.4 B.6 C.7 D.8(3).如图3,在⊙O中,P是弦AB的中点,CD是过点P的直径,则下列结论中不正确的是()A.AB⊥CD B.∠AOB=4∠ACD C. D.PO=PD2、填空题(1).如图4,AB为⊙O直径,E是中点,OE交BC于点D,BD=3,AB=10,则AC=_____.(4) (5)(2).P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短弦长为________;最长弦长为_______.(3).如图5,OE、OF分别为⊙O的弦AB、CD的弦心距,如果OE=OF,那么_______(只需写一个正确的结论)四、测评小结(1).如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.方法:(2).(开放题)AB是⊙O的直径,AC、AD是⊙O的两弦,已知AB=16,AC=8,AD=8,求∠DAC的度数.(选做)课堂小结知识与方法:五、作业:课本88页8、9、10。
九年级数学上册(浙教版)课件 3.3 垂径定理 第2课时 垂

︵ 7.如图,⊙O 的直径 AB 平分CAD,AB 交 CD 于 E,AE 与 BE 的 长度之比为 5∶1,CD=16 cm,则⊙O 的半径为__2_4__5__cm.
5
8.如图,AB是半圆的直径,点O是圆心,点C是半圆上一点,点 E是弧AC的中点,OE交弦AC于点D,若AC=8 cm,DE=2 cm, 则OD的长为__3__cm.
9.如图,AB 为⊙O 的直径,从圆上一点 C 作弦 CD⊥AB,∠OCD ︵︵
的平分线交⊙O 于 P,求证:AP=BP.
解:连结 OP,∵OC=OP,∴∠OCP=∠P,又 ∠DCP=∠OCP,∴∠DCP=∠P,∴CD∥OP,
︵︵ ∵CD⊥AB,∴OP⊥AB,∴AP=BP
10.在半径为5 cm的⊙O中,弦AB的长为6 cm,当弦AB的两个端点A, B在⊙O上滑动时,AB的中点在滑动过程中所经过的路线为( )C A.正方形 B.直线 C.圆 D.多边形
第3章 圆的基本性质
3.3 垂径定理
第2课时 垂径定理的推论
垂直
平分
1.定理1:平分弦(不是直径)的直径_______于弦,并且_______弦所
对的弧.
2.定理2:平分弧的直径__垂__直__平__分____弧所对的__弦__.
知识点一:垂径定理的推论 1.已知⊙O 的半径为 2 cm,弦 AB 长 2 3 cm,则这条弦的中点 到弦所对劣弧的中点的距离为( A ) A.1 cm B.3 cm C.1 cm 或 3 cm D. 3 cm 或 3 cm
15.某居民小区一处圆形下水管道破裂,修理人员准备更换一段新 管道,如图,污水水面宽度为60厘米,水面至管道顶部距离为10厘 米,问修理人员应准备内径多大的管道?
解:100厘米
3.3垂径定理(2)课件公开课课件教案教学设计
2.如图所示,AB 是半圆的直径,E 是B︵C的中点, OE 交弦 BC 于点 D.已知 BC=8 cm,DE=2 cm, 则 AB 的长为__1_0___cm.
【解析】 E 是B︵C的中点,OE 交弦 BC 于点 D,∴ OE⊥BC,CD=BD=4 cm.设 OB=x cm,则 OD=(x- 2)cm.在 Rt△ODB 中,OD2+BD2=OB2,∴(x-2)2+42 =x2,解得 x=5,2x=10.
定理2 平分弧的直径垂直于弧所对的弦.
⌒⌒
已知:如图,⊙O的直径交弦AB(不是直径)于点P,AC=BC
求证:CD⊥AB 证明:连结OA,OB,则AO=BO
∴△AOB是等腰三角形⌒⌒ ∵ຫໍສະໝຸດ C=BC∴∠AOC=∠BOC
∴CD⊥AB
新知讲解
典例精讲
例3 赵州桥的跨径(桥拱圆弧所对的弦的长)为 37.02 m,拱高 (桥拱圆弧的中点到弦的距离)为7.23m, 求赵州桥的桥拱圆弧的半 径(精确到0.01m).
作业布置
教材课后作业题第1-6题。
并且AM=BM.
你能说说这样找的理由?
●M ●O
想一想 垂径定理的逆命题是什么?
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
条件
结论1
结论2
逆命题1:平分弦的直径垂直于弦.
逆命题2:平分弧的直径垂直于弧所对的弦.
C
探索规律
AB是⊙O的一条弦,且AM=BM. 过点M作直径CD. 右图是轴对称图形吗? 如果是,其对称轴是什么? 你能发现图中有哪些等量关系? 与同伴说说你的想法和理由.
4.某一公路隧道的形状如图所示,半圆拱的圆心距离地面2m,半径为 1.5m.一辆高3m,宽2.3m的集装箱卡车能顺利通过这个隧道吗?如果要 使高度不超过4m,宽为2.3m的大货车也能顺利通过这个隧道,且不改 变圆心到地面的距离,半圆拱的半径至少为多少米?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2. 讲解规则:老师这儿有两个漏斗和两个乒乓球。现在请两位同学每人拿起一个漏斗,力气大的同 学将漏斗口朝上,把乒乓球放在漏斗口内,用力向上吹漏斗口;力气小的同学将漏斗口朝下,把乒 乓球放在漏斗把上,用力向上吹,看看谁能把乒乓球球吹走,谁就获胜。大家猜一猜,谁能把乒乓 球吹走? 3. 学生猜测: 4. 验证猜测: 5. 自由探索:教师引导学生分析现象,提出问题,猜测原因。 6. 教师小结:这个小游戏包含着科学道理,在我们的身边到处可见,只要你细心观察,你就会体验 到,今天这节课我们就从探究身边的科学开始。 (板书科学) [设计意图:通过此环节能调动学生的学习兴趣,激发学生探索科学的积极性,让学生感受到自主学 习的快乐。 ]
(四)课外拓展,继续探索 一节课的时间总是这么短暂,但我们探索科学的脚步不会因为下课铃声响起而停止。课下,就让我 们以“身边的科学”为主题进行一次调查活动,继续我们探索科学的脚步吧!
下面是赠送的团队管理名言学习,
4、管理工作中最重要的是:人正确的事,而不是正确的做事。 5、管理就是沟通、沟通再沟通。 6、管理就是界定企业的使命,并激励和组织人力资源去实现这个使命。界定使命是企 业家的任务,而激励与组织人力资源是领导力的范畴,二者的结合就是管理。 7、管理是一 种实践,其本质不在于“知”而在于“行”;其验证不在于逻辑,而在于成果;其唯一权 威就是成就。 8、管理者的最基本能力:有效沟通。 9、合作是一切团队繁荣的根本。 10、将合适的人请上车,不合适的人请下车。 11、领导不是某个人坐在马上指挥他的部队,而是通过别人的成功来获得自己的成功。 12、企业的成功靠团队,而不是靠个人。 13、企业管理过去是沟通,现在是沟通,未来还是沟通。 14、赏善而不罚恶,则乱。罚恶而不赏善,亦乱。 15、赏识导致成功,抱怨导致失败。 16、世界上没有两个人是完全相同的,但是我们 期待每个人工作时,都拥有许多相同的特质。 17、首先是管好自己,对自己言行的管理,
(青岛版五年制)三年级科学上册教案科学在我们身边
一、教材分析 : 科学技术的飞速发展与小学生的日常生活没有太直接的关系,为了让学生建立起关注科学的态
度,本课从做科学小游戏、科学小实验以及介绍科技新产品、科研新成果的角度编排的探究内容。 其目的是引导学生学会观察生活中的现象,感受科技的进步;强化“我也能做科学”的意识,增强 学科学的信心;形成科学的思维方式,进一步明确什么是科学。
(二)实验探究,深入体验 活动一:“能否站起来”实验 1. 热身活动:听老师的口令:起立 . 坐下. 起立 . 坐下。 2. 讲解实验要求:指一名学生端坐在讲台前的椅子上,双脚往前放。老师把手指放在他的额头前, 不让他的身子向前倾,试一试,这位同学能站起来吗? 3. 学生猜测并说出理由。 4. 分组实验,教师巡视指导 。 5. 交流. 分析实验结果 6. 教师小结:这个游戏含有一定的科学道理。至于究竟怎么回事,大家的猜想对不对呢?在以后 的学习中我们会解决这些问题。课下,同学们也可以继续研究,看还能发现哪些问题。 [设计意图:起与坐本来是很平常的一件事,在平常中又含有科学道理,这就让学生不由自主地去探
并要填好实验记录 (课件展示实验记录 )
实验材料
瓶子
漏斗
木块
书本
能否吹灭蜡烛
理由
小组合作进行实验,教师巡回指导。 3. 汇报交流: 4. 学生讨论:(1)为什么隔着漏斗 . 瓶子能吹灭蜡烛?( 2)为什么隔着木块 . 书本等不能吹灭蜡 烛?(教师引导学生从物体的形状上寻找答案,并鼓励学生课下找更多的实验材料进行研究。 ) [设计意图:此环节 进一步让学生体会什么是科学,进一步让学生了解探究的快乐。 ] 活动三:“吸饮料”实验 1. 教师导入:我们在生活中喝饮料 . 喝牛奶时,常常用到吸管,利用吸管可以很方便地喝到饮料牛 奶。今天,我们用两根吸管来试一试。 2. 提出实验要求:请同学把自备的杯子里倒上矿泉水,再用两根吸管来吸,一根插到水里,一根放 在杯外,用嘴同时吸两根吸管,看能否吸到饮料。 3. 学生猜想:猜想的结果让学生通过实验来验证。 4. 学生实验,教师巡回指导。 5. 交流汇报:在实验过程中你们有什么发现?为什么?引导学生说出实验中的发现, 并猜猜其中的 原因。 6. 教师小结:同学们,刚才的游戏和实验就是科学探究的过程。而科学就是提出问题,然后想办法
20、团队精神要从经理人自身做起,经理人更要带头遵守企业规定,让技术及素质较 高的指导较差的,以团队的荣誉就是个人的骄傲启能启智,互利共生,互惠成长,不断地 逐渐培养员工的团队意识和集体观念。
(3)教师小结:看来科学就在我们身边,我们身边处处有科学(板书在我们身边) ,只要你是个有 心人,我们身边的科学就不难发现。 2. 交流资料,感悟科学 (1)教师谈话:课前大家已经搜集了一些有关科技方面的资料,下面咱们来交流一下。 (2)学生交流资料: (3)教师总结:同学们带来的资料很好,老师也带来了一些这方面的资料。 (课件出示资料:播放 登月图片 . 无土栽培 . 克隆羊多利 . 磁悬浮列车 . 海上石油开采 . 风力发电等)让学生感悟到身边 处处有科学,我们的生活离不开科学。 [设计意图:科学来源于生活,这一环节就是让学生从生活中发现科学,为科学的探索和研究奠定基 础。从而让学生理解“我们身边处处有科学,我们的生活离不开科学”的道理。 ]
二、学情分析: 科学就在我们身边,但大部分却与学生的日常生活关系不大,所以本课提出了“身边处处有科
学,我们一起找一找”的活动要求,让学生在游戏中感受到科学的存在,让学生明白“我也能够做 科学”的意识。学生通过体验游戏中的科学来激发他们学科学的兴趣。
三、教学目标: 1.能力目标:经历科学探究的一般过程,即:提出问题、研 .究问题、解答问题; 2.知识目标:认识到科技是不断发展的,喜欢大胆想象与未来科技有关的内容;关心日常生活中的 科技新产品、新事物。 3.情感目标:学会观察生活中的现象,理解我们身边处处有科学,我们生活离不开科学的道理,提 高学科学、用科学的积极性、主动性。
