分块矩阵的初等变换及其应用[含论文、综述、开题-可编辑]

合集下载

分块矩阵的应用论文

分块矩阵的应用引言矩阵作为数学工具之一有其重要的实用价值，它常见于很多学科中，如：线性代数、线性规划、统计分析，以及组合数学等，在实际生活中，很多问题都可以借用矩阵抽象出来进行表述并进行运算，如在各循环赛中常用的赛格表格等，矩阵的概念和性质相对矩阵的运算较容易理解和掌握，对于矩阵的运算和应用，那么有很多的问题值得我们去研究，其中当矩阵的行数和列数都相当大时，矩阵的计算和证明中会是很烦琐的过程，因此这时我们得有一个新的矩阵处理工具，来使这些问题得到更好的解释，矩阵分块的思想由此产生.矩阵分块,就是把一个大矩阵看成是由一些小矩阵组成的.就如矩阵的元素(数) 一样,特别是在运算中,把这些小矩阵当作数一样来处理.把矩阵分块运算有许多方便之处.因为在分块之后,矩阵间的相互关系可以看得更清楚,在实际操作中与其他方法相比,一般来说,不仅非常简洁,而且方法也很统一,具有较大的优越性,是在处理级数较高的矩阵时常用的方法.比方，从行列式的性质出发，可以推导出分块矩阵的假设干性质，并可以利用这些性质在行列式计算和证明中的应用分块矩阵；也可以借助分块矩阵的初等变换求逆矩阵及矩阵的秩等；再如利用分块矩阵求高阶行列式，如设A 、C 都是n 阶矩阵，其中0A ≠，并且AC CA =，那么可求得A B AD BC C D =-；分块矩阵也可以在求解线性方程组应用.本文将通过对分块矩阵性质的研究，比较系统的总结讨论分块矩阵在计算和证明方面的应用，从而确认分块矩阵为处理很多代数问题带来很大的便利.1 分块矩阵的定义及相关运算性质1.1分块矩阵的定义矩阵分块,就是把一个大矩阵看成是由一些小矩阵组成的.就如矩阵的元素(数) 一样,特别是在运算中,把这些小矩阵当作数一样来处理.定义1设A 是一个m n ⨯矩阵，假设用假设干横线条将它分成r 块，再用假设干纵线条将它分成s 块，于是有rs 块的分块矩阵，即1111...............s r rs A A A A A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，其中ij A 表示的是一个矩阵.1.2分块矩阵的相关运算性质 1.2.1加法设()ij m n A a ⨯=()ij m n B b ⨯=，用同样的方法对,A B 进行分块()ij r sA A ⨯=，()ij r sB B ⨯=，其中ij A ，ij B 的级数相同，那么 ()ij ij r s A B A B ⨯+=+. 1.2.2数乘设是任()(),ij ij m n r s A a A k ⨯⨯==为任意数，定义分块矩阵()ij r s A A ⨯=与k 的数乘为()ij r skA kA ⨯=1.2.3乘法设()(),ij ij s n n m A a B b ⨯⨯==分块为()(),ij ij r l l r A A B B ⨯⨯==，其中ij A 是i j s n ⨯矩阵，ij B 是i j n m ⨯矩阵，定义分块矩阵()ij r l A A ⨯=和()ij l r B B ⨯=的乘积为()1122...,1,2,...;1,2,3,...,ij i j i j il lj C A B A B A B i t j l =+++==.、1.2.4转置设()ij s n A a ⨯=分块为()ij r s A A ⨯=，定义分块矩阵()ij r s A A ⨯=的转置为()ji s rA A ⨯''=1.2.5分块矩阵的初等变换分块矩阵A 的以下三种变换称为初等行变换： (1) 对调A 的两行(用i j r r ↔表示对调i 、j 两行)；(2) 用一个可逆阵K 左乘A 的某一行的所有子矩阵(用i K r ⨯表示用K 左乘第i 行)； (3) 将A 的某一行的所有子矩阵左乘一个矩阵K 再加到另一行的对应子矩阵上去(i j r K r +⨯表示将第j 行左乘K 再加到第i 行).将上述定义中的“行〞换成“列〞,“左乘〞换成“右乘〞, 即得分块矩阵的初等列变换的定义, 分块矩阵的初等行变换和初等列变换统称为初等变换.2 分块矩阵的应用2.1用分块矩阵解决行列式的问题利用矩阵分块的方法求行列式的值是行列式求值的常用方法之一, 但通常所用的?高等代数?教材中对能够用矩阵分块法求值的行列式要求较为严格, 多数为形式较特殊的行列式.下面给出了一个应用范围较为广泛的行列式的分块矩阵求值方法.引理2.1([3])假设A 为k 阶方阵，B 为r 阶方阵，C 为r k ⨯矩阵, 那么有A ABC B= 在上述引理中,要求子块当中有一个为零矩阵, 更一般的有如下的结论. 定理2.2([3])假设n 阶方阵P 可分为A B P CD ⎡⎤=⎢⎥⎣⎦其中A 为r 阶方阵, B 为()r n r ⨯-矩阵, C 为()n r r -⨯矩阵, D 为()n r -阶方阵, 那么有〔1〕当A 为可逆矩时1P A D CA B -=-；〔2〕当D 为可逆矩阵时1P D A BD C -=-.在进行行列式的求值运算时, 假设能找到符合本定理条件要求的矩阵分块方法, 就可应用定理的结论进行行列式的计算, 现举例说明如下：例2.3 计算行列式 013c ...0 (00)...0.........0...nb b b ac P ac a c =其中10,123...c i n ≠=.解设 0()A c =，()...B b b b =，()...TC a a a =130...00...0,0,1,2,,.........00 (i)n c c D c i n c ⎡⎤⎢⎥⎢⎥=≠=⋅⋅⋅⎢⎥⎢⎥⎣⎦ 那么D 为可逆矩阵，由定理1的结论〔2〕知1A BP D A BD C C D-==- ，将 1111210...00...0.........00...n c c D c ----⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦及,A B C D ,,代入得 1111212...((...))n n P c c c a ab c c c ---=-+++.例2.4 矩阵()ij ai j P a bi j =⎧==⎨≠⎩当时当时，求行列式P 的值.解：行列式P 的主对角线元素为a ，其余元素为b ，因此：〔1〕当a b =时，由行列式的性质知P =0；〔2〕当a b ≠时，从第一行开始，将行列式的前行减去后行得...000 (00).........000......a b b a a b b a P a b b abbbb a ----=--，令...000...000.........,, 000 000...0a b b a a b b a A B a b b a o a b b a --⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦()()...,,C b b b b D a ==由定理2.2可知 1P A D CA B -=-，而 ()1n A a b -=- ，()011,,,>a b i jA i j --⎧-≤⎪=⎨⎪⎩计算结果得 ()()()()()()111+1n n P a b a n b a b a n b --=---=--.假设定理中的矩阵A 和D 均为可逆矩阵时，定理的两个结论均成立，可以利用公式11D A BD C A D CA B---=-进行转换求行列式的值，举例说明如下.推论2.5 假设,,,A B C D 均为n 阶方阵，且A 可逆，AC CA =，那么 ABT AD CB C D==-. 例2.6 计算行列式 1111122310250121T -=.解对T 进行分块A B T C D ⎡⎤=⎢⎥⎣⎦，其中 11111025,,,,12230121A B C D ⎡⎤⎡⎤⎡⎤⎡⎤====⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦ 显然A 可逆，且AC CA =，所以T AD CB =-，而 4667AD ⎡⎤=⎢⎥⎣⎦，1123CB ⎡⎤=⎢⎥-⎣⎦ 所以， 3510410T ==. 定理2.7 假设,A B 均为n 阶方阵，那么A BA B A B B A =+-.. 例2.8 计算行列式 1234234134124123T =.解对矩阵T 进行分块A B T C D ⎡⎤=⎢⎥⎣⎦，其中 1234,,2341A B ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦由于 4664A B ⎡⎤+=⎢⎥⎣⎦ ，22,22A B --⎡⎤-=⎢⎥-⎣⎦ 所以 (20)(8)160T A B A B =+-=-⨯-=. 2.2 分块矩阵在解线性方程组中的应用例2.9设n 个未知数m 个方程的线性方程组为11112211211222221122...............n n n n m m mn n ma x a x a xb a x a x a x b a x a x a x b +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩ 〔1〕记()ij m n A a ⨯=,()12X=,,...,Tn x x x 〔其中T 表示矩阵的转置〕, ()12,,...,Tm B b b b = ,那么方程〔1〕的矩阵形式为 AX B =.把方程〔1〕的矩阵形式改写成如下分块矩阵的形式111211212222AA XB A A X B ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，其中 111111........................r r rr a a A a a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，111121........................r n rr rn a a A a a ++⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，()11112A A A =，111211........................r r r m mr a a A a a ++⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，111221........................r r r n mr mn a a A a a ++++⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，()22122A A A =，()112...Tr X x x x =，()212...Tr r n X x x x ++=，()112...T r B b b b =，()212...Tr r m B b b b ++=，方程组〔1〕有解时，我们解方程组〔1〕时总是把〔1〕化成简单的同解方程组，从而求出其解.定理2.10. 设方程组〔1〕有解且()()11,r A r n r A r =≤=，那么方程组()1112A A X B =与AX B =同解.例2.11．方程组1112132223243132333441424344212212330x x x x x x x x x x x x x x ++=⎧⎪--=⎪⎨+++=-⎪⎪+++=⎩ 〔2〕求此方程组的解并证明此方程组和方程组111213222324212x x x x x x ++=⎧⎨--=⎩ 〔3〕同解.解：令1210011111212331A ⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥⎣⎦，11121210()0111A A ⎡⎤=⎢⎥--⎣⎦，其中 111201A ⎡⎤=⎢⎥⎣⎦，121011A ⎡⎤=⎢⎥--⎣⎦，1210B ⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦，112B ⎡⎤=⎢⎥⎣⎦，121011210112101011120111201112112110111200000233100111200000⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥------⎢⎥⎢⎥⎢⎥→→⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦，所以此方程组的齐次线性方程组的解为1232111001c c --⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦，又3200-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦是方程组的一个特解，所以此方程组的解为 12323112100010c c ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，由上可知()2r A =并且11()2r A =，所以由定理3可证方程组〔2〕和〔3〕同解. 2.3分块矩阵在相似问题中的应用定理2.12.如果方阵~A B ，方阵~C D ，那么00~00A B C D ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦. 证明因为方阵~A B ，方阵~C D ，所以 110000000000E A XE X Y C E Y E --⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦11110000000000A XB X X AXC YD Y Y CY ----⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ ，而 1110000E XY E ---⎧⎫⎡⎤⎡⎤⎪⎪⎨⎬⎢⎥⎢⎥⎪⎪⎣⎦⎣⎦⎩⎭1100E Y --⎡⎤⎢⎥⎣⎦1100X E --⎡⎤=⎢⎥⎣⎦0000XE E Y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦，所以 00~00A B C D ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦. 2.4用分块矩阵证明矩阵秩的问题定理2.13.设0A M C B ⎡⎤=⎢⎥⎣⎦,A 为m n ⨯矩阵，B 为k l ⨯矩阵，那么有()()()r M r A r B ≥+，且0C =时，()()()0A r M r r A r B C B ⎡⎤==+⎢⎥⎣⎦ 证明设A 在初等变换下的标准形为1000rE D ⎡⎤=⎢⎥⎣⎦，()r r A =，又设B 在初等变换下的标准形为 2000sED ⎡⎤=⎢⎥⎣⎦，()s r B =，那么，对M 前m 行前n 列作初等变换，对它的后k 行后l 列也作初等变换可把M 化为11120D C M D ⎡⎤=⎢⎥⎣⎦，现在利用1D 左上角的1经列初等变换消去1C 位置中的非零元；再用2D 左上角的1经行初等变换消去它上面1C 处的非零元素，于是把1M 再化作220000000000000r s E C M E ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦，那么有 ()()()()()()122r M r M r M r s r C r s r A r B ===++≥+=+.利用这个定理及初等变换可证明一些秩的不等式.例2.14. 设A 为m n ⨯矩阵，B 为n l ⨯矩阵，假设0AB =，那么()()r A r B n +≤. 证明因为()()00000000n n n n A AB A r A r B r r r r r n E B E B E B E B ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+=≤====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦，所以 ()()r A r B n +≤.例2.15. 设A 、B 都是n 阶矩阵，求证：()()()r AB A B r A r B ++≤+.证明：因为 0A AB A B B ++⎡⎤⎢⎥⎣⎦(2)(1)E -⨯+−−−−→0A AB A B +⎡⎤⎢⎥⎣⎦(1)()(2)B E ⨯--+−−−−−→00A B ⎡⎤⎢⎥⎣⎦，所以 0E E E -⎡⎤⎢⎥⎣⎦0E B E E --⎡⎤⎢⎥⎣⎦00A B ⎡⎤=⎢⎥⎣⎦，又0E E E -⎡⎤⎢⎥⎣⎦，0E B E E --⎡⎤⎢⎥⎣⎦都可逆，所以 000A AB A B A r r B B ++⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦，而 ()0A AB A B r r AB A B B ++⎡⎤≥++⎢⎥⎣⎦ 又 ()()00A r r A r B B ⎡⎤=+⎢⎥⎣⎦，所以 ()()()r AB A B r A r B ++≤+. 2.5 用分块矩阵求逆矩阵的问题分块矩阵是高等代数中的一个重要的工具，在求解高阶矩阵问题中的应用尤为广泛.求矩阵的逆矩阵可以用伴随矩阵或初等变换的方法来解决，而此类方法对于级数较高的矩阵运算量较大，对某些矩阵可以适当分块后再进行运算，可起到事半功倍的作用.定理2.16. 对于n 阶矩阵A ，如果存在n 阶矩阵B ，使得 AB BA I == 那么矩阵称为可逆矩阵，而B 称为A 的逆矩阵.假设,A B 都可逆，那么 100A B -⎡⎤⎢⎥⎣⎦1100A B --⎡⎤=⎢⎥⎣⎦10A C B -⎡⎤⎢⎥⎣⎦11110A A CB B ----⎡⎤-=⎢⎥⎣⎦,10A C B -⎡⎤⎢⎥⎣⎦11110A B CAB ----⎡⎤=⎢⎥-⎣⎦, 1111110000kk n k n k E A B E A B A CA E C D E D -------⎡⎤⎡⎤-⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦其中1D 1D CA B -=-.以下举些例子具体说明分块矩阵在矩阵求逆中的具体应用.例2.17. 矩阵1200210000120025A ⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥-⎣⎦，求1A -. 解：可以将矩阵A 分成四块12A 00A A ⎡⎤=⎢⎥⎣⎦，其中1A 1221⎡⎤=⎢⎥-⎣⎦，2A 1225-⎡⎤=⎢⎥-⎣⎦，根据分块矩阵的性质，1A -111200A A --⎡⎤=⎢⎥⎣⎦，而1A ，2A 为二级矩阵，其逆矩阵易求出，分别为 11A -12552155⎡⎤⎢⎥=⎢⎥-⎣⎦，12A -5221--⎡⎤=⎢⎥--⎣⎦，所以 1A -12005521005500520021⎡⎤⎢⎥⎢⎥-=⎢⎥⎢⎥--⎢⎥--⎣⎦ 2.6 分块矩阵在矩阵的特征值问题中的应用在高等代数中，矩阵的特征值问题是一项非常重要的内容，特征值对于线性变换的研究具有根本的重要性．而我们在求一些阶数较高和较复杂的矩阵特征值时，经常会用矩阵的分块去解决，这样可以使问题的解决更简明.定理2.18. 设A 为n 阶矩阵，λ是一个数，如方程AX X λ=,存在非零解向量，那么称λ为A 的一个特征值，相应的非零解向量X 称为与特征值λ对应的特征向量.定理2.19.设A 为n 阶矩阵，含有未知量λ的矩阵I A λ-称为A 的特征矩阵，其行列式I A λ-为λ的n 次多项式，称为A 的特征多项式0I A λ-=称为A 的特征方程，λ是矩阵A 的一个特征值，那么一定是0I A λ-=的根，因此又称为特征根.假设λ是0I A λ-=的i n 重根，那么λ称为A 的i n 重特征值.引理2.20.设A 为n 阶矩阵，那么A 为幂等矩阵的充要条件()()r A E r A n -+=，这里E 为n 阶单位矩阵，()r A 表示A 的秩.引理2.21.幂等矩阵()1112A A X B = 与000rE ⎡⎤⎢⎥⎣⎦ 或000r E ⎡⎤⎢⎥⎣⎦相似，其中()r r A =. 例2.22. 设12,,A A A 均为n 阶方阵，且12A A A =+，()()(),1,2i i r A r r A r i ===，求证：假设212,A A r r r ==+，那么12,,A A A 的特征值为1或0，且1的个数和它们的秩相等.证明：〔1〕当A 可逆时，即()r A n =，因为2A A =，所以A E =，又 12r r r =+，12E A A =+，由得()()()12r A r A r A n =+=，由引理2.20得到211A A =.同理222A A =，所以1A ，2A 是幂等矩阵，由引理2.21得10~00rEA ⎡⎤⎢⎥⎣⎦，200~0r A E ⎡⎤⎢⎥⎣⎦， 12,,A A A 和E ，000rE⎡⎤⎢⎥⎣⎦，000r E ⎡⎤⎢⎥⎣⎦有相同的特征根，所以12,,A A A 的特征值为1或0，且特征值1的个数和它们的秩相等.〔2〕当()0r A =时，即0A =，结论显然成立.〔3〕设0r n <<，即A 为非零由布可逆矩阵，又因为2A A =，故存在可逆矩阵P 使11112P AP P A P P A P ---=+，()r r A =，令 000rE⎡⎤⎢⎥⎣⎦1112111221222122A A B B A A B B ⎡⎤⎡⎤=+⎢⎥⎢⎥⎣⎦⎣⎦这里 ()1ij P AP A -= ()121111ij r P A P B E A B -=⇒=+，所以 ()()()()()1111111111=r r A B r A r B r A r B r +≤+≤+=，从而 ()()()()()1111111112=r r A B r A r B r A r A r +≤+≤+=，又因为 ()()()11121100r A r A A B -≥-≥， r ，从而 ()()111r A r A =，()211r A B =，这样1111Er A B =+，且()1111r A B r +=，由定理2.18的证明可知，存在可逆矩阵Q ，使11110Q=00r E Q A -⎡⎤⎢⎥⎣⎦ ，211100Q=0r Q B E -⎡⎤⎢⎥⎣⎦， 111112n-n-n-n-00000000000rr r r r E Q QQ Q P A P P A P E E E E ----⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦11111112111221222122n-n-n-n-00000000r r r r A A B B Q Q Q Q A A B B E E E E ----⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦11111112111221222122Q A Q Q A Q B Q Q B A Q A B QB ----⎡⎤⎡⎤=+⎢⎥⎢⎥⎣⎦⎣⎦，设 1111122122Q A Q Q A A Q A --⎡⎤⎢⎥⎣⎦1121111222000r E C C G G A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，又因为11211111222000r E C r C r G G A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，所以21120,0G G ==，设 211111112r 212122*********W Q B QQ B E W B QB Z Z B --⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦，同上可得110Z =，110W = ，故111121120,0,0,0C G W Z ====，又1111112212222000000r E Q A Q Q A A Q A A --⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦，从而220A =，同理 211111221220000000r Q B QQ B E B QB --⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦，100n r Q T P E --⎡⎤=⎢⎥⎣⎦，故有1210000,000rrET AT E-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦12111200000000,00000000rrET AT T A T E--⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦，综上所述,结论成立.小结本文通过例题对分块矩阵在证明和计算中两方面的应用进行了总结分析，在证明方面涉及了矩阵秩的相关问题和矩阵列行向量线性相关性问题，在证明线性相关问题上，利用分块矩阵的解可以很清晰动的描述线性方程组的解和相关内容，对一些具体的解与矩阵行列相关性之间的关系做出了总结；在分块矩阵计算方面我们主要解决了求逆矩阵与高级行列式的问题.通过本文的表达充分表达了分块矩阵在代数计算和证明方面的优越，也给出了分块矩阵在线性代数中所具有的重要地位，当然在分块矩阵的应用的表达中，本文并不是对所有的证明和计算都进行讨论，所以在应用的完整性上有待改进，并可以继续进行探讨和研究.参考文献[1] 蓝以中.高等代数简明教程[M].北京：北京大学出版社，2007：141-149.[2] 杜之韩,刘丽,吴曦.线性代数[M].成都：西南财经大学出版社，2003：61-68.[3] 郝玉琴.利用矩阵的分块法解线性方程组[J].唐山师专学报，1999(5):37-38.[4] 王萼芳.线性代数学习指导[M].北京：清华大学出版社，2021：104-108.[5] 祁秋菊.分块矩阵的相关应用[J].科技信息，2021：1-4.[6] 孔庆兰.分块矩阵的应用[J].枣庄学院报，2006〔5〕：24-25.[7] 王秀芳.分块矩阵的应用讨论[J].连云港师范高等专科学校学报，2021〔3〕：98-99.[8] 严坤妹.分块矩阵的应用[J].福建播送电视大学学报，2006〔59〕：71-73.[9] 张敏.分块矩阵的应用[J].吉林师范大学学报，2003〔1〕：118-120.[10] 周兴建.分块矩阵及其应用[J].科技资讯，2007〔35〕：126-126.[11] 陈晓兰，杨子胥.分块矩阵的一些应用[J].德州师专学报，1995〔4〕：1-14.[12] 钱钶.用分块矩阵证明矩阵秩的假设干定理[J].景德镇高专学报，1995〔4〕：11-14.[13] 徐常青，杜先能.高等代数方法与应用[M].合肥：安徽大学出版社，2002：66-67.[14] 林瑾瑜.分块矩阵的假设干性质及其在行列式计算中的应用[J].广东播送电视大学学报,2006,15(2):109-112.[15] 张敏.分块矩阵的应用[J].吉林师范大学学报〔自然科学版〕，2003，1(1):120.[16] 刘力.分块矩阵在证明矩阵秩的性质上的应用[J].沧州师范专科学校学报,2006,22(4):40-41.[17] 李玉梅.分块矩阵的几个重要应用[J].怀化师专学报，2000，19(4)：77-78.。

分块矩阵的应用论文

所以，
又，都可逆，
所以，
而
又，
所以 .
2.5用分块矩阵求逆矩阵的问题
分块矩阵是高等代数中的一个重要的工具，在求解高阶矩阵问题中的应用尤为广泛.求矩阵的逆矩阵可以用伴随矩阵或初等变换的方法来解决，而此类方法对于级数较高的矩阵运算量较大，对某些矩阵可以适当分块后再进行运算，可起到事半功倍的作用.
[16]刘力.分块矩阵在证明矩阵秩的性质上的应用[J].沧州师范专科学校学报,2006,22(4):40-41.
[17]李玉梅.分块矩阵的几个重要应用[J].怀化师专学报，2000，19(4)：77-78.
综上所述,结论成立.
小结
本文通过例题对分块矩阵在证明和计算中两方面的应用进行了总结分析，在证明方面涉及了矩阵秩的相关问题和矩阵列行向量线性相关性问题，在证明线性相关问题上，利用分块矩阵的解可以很清晰动的描述线性方程组的解和相关内容，对一些具体的解与矩阵行列相关性之间的关系做出了总结；在分块矩阵计算方面我们主要解决了求逆矩阵与高级行列式的问题.通过本文的叙述充分体现了分块矩阵在代数计算和证明方面的优越，也给出了分块矩阵在线性代数中所具有的重要地位，当然在分块矩阵的应用的叙述中，本文并不是对所有的证明和计算都进行讨论，所以在应用的完整性上有待改进，并可以继续进行探讨和研究.
[5]祁秋菊.分块矩阵的相关应用[J].科技信息，2009：1-4.
[6]孔庆兰.分块矩阵的应用[J].枣庄学院报，2006（5）：24-25.
[7]王秀芳.分块矩阵的应用讨论[J].连云港师范高等专科学校学报，2008（3）：98-99.
[8]严坤妹.分块矩阵的应用[J].福建广播电视大学学报，2006（59）：71-73.
计算结果得 .

分块矩阵的初等变换及其若干应用

⎛E 解将 T 与分块单位矩阵 ⎜ m ⎝O O⎞ ⎛A O 排成分块矩阵 ⎜ ⎟ En ⎠ ⎝C D
4
Em O
O⎞ .对上述分块 En ⎟ ⎠
矩阵进行分块矩阵的初等行变换，将“ T ”的部分变为单位矩阵:
⎛A O ⎜C D ⎝
第1块行左乘A−1
Em O O
O ⎞ 第1块行左乘-CA−1加到第2块行 ⎛ A O Em ⎯⎯⎯⎯⎯⎯⎯⎯⎯ →⎜ ⎟ −1 En ⎠ ⎝ O D −CA A−1
⎛E （1）交换分块单位阵 ⎜ m ⎝ 0t × m
用此矩阵左乘 T ，有
3
⎛ 0t × m ⎜ ⎝ Em
Et ⎞ ⎛ A B ⎞ ⎛ C D ⎞ ⎟ ⎟=⎜ ⎟, 0m×t ⎠ ⎜ ⎝C D⎠ ⎝ A B ⎠
这正是交换 T 的两块行得到的矩阵.
⎛E （2）用 P 乘分块单位阵 ⎜ m ⎝ 0t × m 0m×t ⎞ ⎟ 的第一块行，得分块初等矩阵 Et ⎠ ⎛ P ⎜ ⎝ 0t × m 0m×t ⎞ ⎟. Et ⎠
⎛ En1 ⎜O ⎜ ⎜O ⎜ ⎜O ⎝ O En2 O O O ⎞ O O ⎟ ⎟ % O ⎟ ⎟ O E ns ⎟ ⎠ O
1
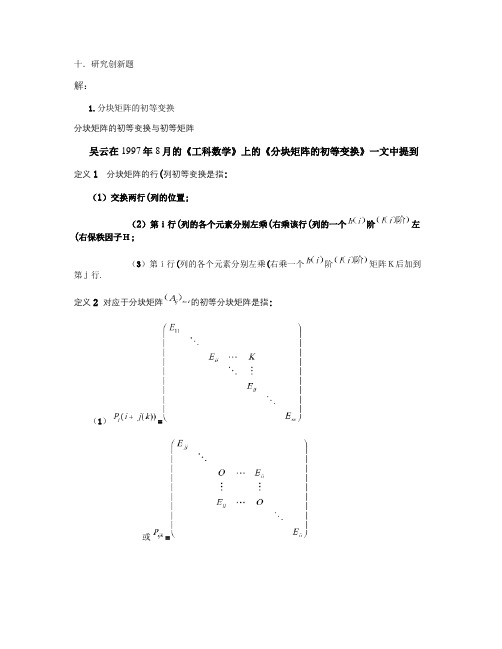
的分块矩阵称为分块单位矩阵. 定义分块单位矩阵经过一次分块矩阵的初等行（列）变换后得到分块矩阵就叫做分块初等矩阵.因为分块矩阵的初等变换有三种形式，因此分块初等矩阵也相应的有以下三种类型：（1）交换分块单位矩阵的第 i , j 块行（或块列）得到的分块矩阵.例如,
T 的左边乘上相应的 2×2 分块初等矩阵.同理可证对一个 2×2 分块矩阵
⎛A B⎞ T =⎜ ⎟ 作一分块矩阵的初等列变换就相当于在 T 的右边乘上相应的 2×2 分 ⎝C D⎠ 块初等矩阵. 2．分块矩阵初等变换的应用 ⎛ A O⎞ 例求T = ⎜ ⎟ 的逆,其中 A 是 m 阶可逆矩阵, B 是 n 阶可逆矩阵. ⎝C D⎠

分块矩阵的初等变换及应用

十．研究创新题解：1.分块矩阵的初等变换分块矩阵的初等变换与初等矩阵吴云在1997年8月的《工科数学》上的《分块矩阵的初等变换》一文中提到定义1 分块矩阵的行(列)初等变换是指: （1）交换两行(列)的位置;（2）第ｉ行(列)的各个元素分别左乘(右乘)该行(列)的一个）（i h 阶）阶）（（i l 左(右)保秩因子Ｈ;（3）第ｉ行(列)的各个元素分别左乘(右乘)一个）（i h 阶）阶）（（i l 矩阵Ｋ后加到第ｊ行. 定义2 对应于分块矩阵t s ij A ⨯）（的初等分块矩阵是指:（1）))((k j i P i +=⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ss ll ii E E K E E11或ijk P =⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ii ll ii jj E O E E O E（2） )(H P il =⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ss llE H E 或)(H P ik =⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ii E H E 11其中Ｈ为第ｉ行(列)的一个左(右)保秩因子；(1) ))((k j i P i +=⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ss ll ii E E K E E11(2) 或))((k j i P k +=⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ll ll ii E E K E E11 初等分块矩阵与通常的初等矩阵类似,但由于矩阵乘法不满足交换律,故需要分为左、右两种.直接验算可得: 定理1 (1)交换t s ij A ⨯）（的第ｉ行与第ｊ行,相当于左乘一个ｍ阶初等分块矩阵ijL P,其中ijL P 中的元素ii E 为ｈ(i)阶单位矩阵, jj E 为ｈ(j)阶单位矩阵,当ｒ≠ｉ且ｒ≠ｊ时, rr E 为ｈ(ｒ)阶单位矩阵;交换t s ij A ⨯）（的第ｉ列与第ｊ列相当于右乘一个ｎ阶初等分块矩阵ijk P ,其中ii E 为ｌ(i)阶单位矩阵, jj E 为ｌ(j)阶单位矩阵, 当ｒ≠ｉ且ｒ≠ｊ时, rr E 为ｌ(ｒ)阶单位矩阵；(2) t s ij A ⨯）（的第ｉ行的每一个元素左乘一个矩阵Ｈ相当于t s ij A ⨯）（左乘一个ｍ阶分块矩阵）（H P iL 中Ｈ为ｈ(ｉ)阶方阵; t s ij A ⨯）（的第ｉ列的每一个元素右乘一个矩阵Ｈ,相当于t s ij A ⨯）（右乘一个ｎ阶初等到变换矩阵）（H P ik ,其中Ｈ为ｌ(ｉ)阶方阵； (3) t s ij A ⨯）（的第ｊ行的每个元素分别左乘一个ｈ(ｉ)×ｈ(ｊ)矩阵Ｋ后加到第ｉ行,相当于t s ij A ⨯）（左乘一个初等分块矩阵））（（k j i P L +;第ｊ列的每一个元素分别右乘ｌ(ｊ)×ｌ(ｉ)矩阵Ｋ后加到第ｉ列,相当于t s ij A ⨯）（右乘））（（k j i P k +. 定理2设Ａ为方阵,则分块矩阵t s ij A ⨯）（施行第一种行初等变换后,对应的行列式为A j i h ），（）（1-,其中h(i,j)=h(i)h(j)-l+h(i+l)]+…+h(j)[h(i)+h(i+j)+…+h(j-l)], l(i,j)=l(i)h(j)-l+l(i+l)]+…+l(j)[l(i)+l(i+j)+…+l(j-l)],施行第二种初等变换后,对应的行列式为|Ｈ|·|Ａ|;施行第三种初等变换后,对应的行列式的值不变.证明: H H P i =）（,A k j i P =+））（（显然成立. 下证），（）（j i h irL P 1-=,ii E 所在的第1行逐次与它相邻的行交换,移至jj E 前,共进行ｈ(ｉ)-1+ｈ(ｉ+1)+…+ｈ(ｊ-1)次交换两行,第2行逐次与它相邻的行交换,移至jj E 前,同样进行相同次交换两行,依此类推,把ii E 所在的行移至jj E 所在的行前,共进行ｈ(ｉ)[ｈ(ｉ)-1+ｈ(ｉ+1)+…+ｈ(ｊ-1)]次交换两行,然后把jj E 移至适当的位置,同理共进行ｈ(ｊ)[ｈ(ｉ)+ｈ(ｉ+1)+…+ｈ(ｊ-1)]次交换两行,所以交换两行的总次数为ｈ(ｉ,ｊ),故），（）（j i h irL P 1-=;同理），（）（j i l irR P 1-=. 所以有A P ilj =ilj P ∙A =(-1)),(l i h A 或ilk AP =A ∙ilkP =（-1）),(j i l AA H P il )(=)(H P il A =H ∙A 或A )(H P ik =H ∙AA k j i p l ))((+=)((k j i P l +A ∙=A ))((k j i AP K +=A ))((k j i P k +=A定理3 分块矩阵进行初等变换后,秩不变.证明: 对于(1),相当于对n m ij a A ⨯=)(进行若干次行(列)的交换,故命题成立;对于(2),根据定义1,显然成立;对于(3),相当于进行若干次把n m ij a A ⨯=)(行(列)乘以一个倍数后加到另一行(列),故命题成立.定理4 (1)设Ａ,Ｂ的行数均为ｍ,则矩阵方程ＡＸ=Ｂ,当rank (Ａ)= rank (Ａ,Ｂ)=ｍ时有唯一解,当rank (Ａ)= rank (Ａ,Ｂ)<ｍ时有无穷多解, 当rank (Ａ)< rank (Ａ,Ｂ)时无解;(2)设Ａ,Ｂ的列数均为ｎ,则矩阵方程ＸＡ=Ｂ,当rank (Ａ)= ）（T T B A rank ,=ｎ时有唯一解,当rank (Ａ)= ）（T T B A rank ,<ｎ有无穷多解, 当rank (Ａ)< ）（T T B A rank ,时无解. 证明: (1)设rank (Ａ)= rank (Ａ,Ｂ)<ｍ,则存在可逆矩阵Ｐ,Ｑ,使Q O O O I P A r ⎢⎢⎣⎡⎥⎦⎤=，Q O OB B P B ⎢⎢⎣⎡⎥⎦⎤=21 其中r I 为ｒ阶单位矩阵, 1B 为ｒ阶方阵,设Q B B B B Q X o⎢⎣⎡⎥⎦⎤=-43211,则有: Q O O O I P AX r o ⎢⎢⎣⎡⎥⎦⎤= Q B B B B Q ⎢⎣⎡⎥⎦⎤-43211= []⎢⎣⎡⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤4321B B B B O O O I P r = Q O O B B P ⎢⎢⎣⎡⎥⎦⎤21=B所以o X 为ＡＸ=Ｂ的解,其中3B , 4B 是任意的.当rank (Ａ)= rank (Ａ,Ｂ)=ｍ时,Ａ=Ｐ(m I Ｏ)Ｑ,Ｂ=( 1B 2B ),显然,ＡＸ=Ｂ有唯一解: Q B B Q X o ）（211-=;当rank (Ａ)< rank (Ａ,Ｂ)时,ＡＸ=Ｂ无解.同理可证(2)成立(当rank (Ａ)= rank ( tA , TB )<ｎ时,X=P ⎢⎢⎣⎡⎥⎦⎤O OO I r1-P ) 定义3 对于任意的ｕ,ｖ,如果rank ( ij A )= rank ( ij A ,iv A )= rank (T ij A ,Tiv A ),则称ij A 为极大元.定理5 分块矩阵22　ij A ⨯）（可以用分块矩阵的初等变换对角化的充要条件是:它有一个极大元.证明: 充分性.不妨设11A 为极大元(否则可以通过第一种分块矩阵的初等变换把极大元移到第一行,第一列交叉位置).由定理4,存在可逆矩阵Ｐ,Ｑ,使Q O O O I P A r⎢⎢⎣⎡⎥⎦⎤=11Q O B O A P A ⎢⎣⎡⎥⎦⎤=2121，Q O O A A P A ⎢⎢⎣⎡⎥⎦⎤=2'1'12,令Ｋ=-Ｐ⎢⎣⎡⎥⎦⎤4321A A A A 1-P ,其中3A , 4A 为适当阶数的任意矩阵.则 K 11A + 21A =P -⎢⎣⎡⎥⎦⎤4321A A A A 1-P P ⎢⎢⎣⎡⎥⎦⎤O O O I r Q ，所以22　ij A ⨯）（第一行左乘Ｋ加到第二行,得⎢⎢⎣⎡⎥⎦⎤+22121211A KA O A A .同理,令Ｋ＇=-1-Q ⎢⎢⎣⎡⎥⎥⎦⎤4231，，，，A A A A Q , 则11A Ｋ′+12A =0,所以⎢⎢⎣⎡⎥⎦⎤+22121211A KA OA A 的第一列右乘Ｋ′后加到第二列,得⎢⎢⎣⎡⎥⎥⎦⎤+221211A KA OO A .(如先进行列变换,再进行行变换,得⎢⎢⎣⎡⎥⎥⎦⎤+222111A K A OO A ，, 因为2221A KA +=⎢⎢⎣⎡⎥⎥⎦⎤-2'21'22'11'1A A A A A A A A +22A =21'A K +22A ,故两种运算顺序结果相同) 必要性.反证法,不妨设rank (11A )≠rank (T A 11,T A 21)或rank (T A 11,TA 221)rank (21A ),则由定理4, X 11A =-21A 或X 21A =-11A 无解,从而不存在Ｋ,使22　ij A ⨯）（对角化.同理,当rank (11A )≠rank (11A ,12A )或rank (11A ,12A )≠rank (12A )时,不存在'K 使 -A 11K '=A 12或-'12K A =11A 成立.定理5表明:并不是所有的2×2分块矩阵都可以用分块矩阵初等变换对角化,如果分块矩阵没有极大元,则需分得更细,才能对角化.定理 6 矩阵n m A ⨯的一种分块方法t s ij A ⨯)(可以用分块矩阵的初等变换对角化的充分条件是:存在ｓ-1行且存在ｔ-1列有极大元.证明: 用数学归纳法.当ｓ=ｔ=1时,只有一块,命题成立;设ｓ ≤ｅ,ｔ≤ ｆ时命题成立.当ｓ=ｅ+1,ｔ=ｆ时,存在ｅ行且存在ｆ-1列有极大元,显然可以用第一种分块矩阵的初等变换,通过交换两行或两列的位置,使t s ij A ⨯）（的前ｅ行与前ｆ-1列都有极大元,再把前ｅ行,前ｆ-1列看成一块,得到一个新的2×2分块矩阵,记为22　ij B ⨯）（.显然11B 为极大元,根据定理4, 22　ij B ⨯）（可以化成对角形:⎥⎦⎤⎢⎣⎡+2221B KB O OB ,又）（）（111-⨯=f e ij A B ,它的每行、列都有极大,故由假设11B 可以对角化,从而f e ij A ⨯=）（）（1可以对角化.同理可证当ｓ=ｅ,ｔ=ｆ+1时, ）（）（1+⨯f e ij A 可以对角化.由此命题成立.下面讨论对角化后的非零块ii A 进一步化简的方法.设Q O OO I P A i ii ⎥⎦⎤⎢⎣⎡=,121-⎥⎦⎤⎢⎣⎡=P B O B I L i i 与⎥⎦⎤⎢⎣⎡=-211C C O I Q R Ri .根据定理1, i L ,i R 为ii A 的左(右)保秩因子,显然也是ii A 所在行(列)的左(右)保秩因子,故对角化后的分块矩阵第ｉ行、第ｉ列分别左乘i L ,右乘i R 后, ii A 可以化成⎥⎦⎤⎢⎣⎡O O O I i讨论分块方阵行列式的计算,先讨论分块初等阵的行列式. 设I 为S ×S 分块单位阵:I=⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛s r r r r I I I I321 其中I r i 为r i 阶单位阵(1≤i ≤S),对I 施行一次初等变换可得定义2所述的三种分块初等阵,它们的行列式有下列计算公式.引理分块初等阵的行列式有以下性质:(1)|I(i,j)|= τ)1(-,其中τ=r i (r i +1+…+r j )+ r j (r i +1+…+ r j -1)(i<j). 特别地,若j=i+1,则| I(i,j)|=(-1) r i r j ; (2)|I(i(K))|=|k|,其中K 是r i 阶可逆阵; (3)|I(j(K),i)|=1,其中K 是r i ×r j 矩阵.证(1)不难验证,将I(i,j)的元素行进行τ次相邻的对调可将I(i,j)变成I,由行列式的性质,|I(i,j)|= τ)1(-|I|=τ)1(-.(2),(3)由对角分块方阵及三角形分块方阵的行列式计算方法即知.由于对分块方阵A 施行一次初等行变换,相当于用相应的分块初等阵左乘A,由上述引理,我们有下列分块方阵的行列式计算性质. 定理7 设A 是一个分块方阵.(1)交换|A|的i,j 两行(列),行列式变为(-1)τ|A|,其中τ= r i (r i +1+…+ r j )+ r j (r i +1+…+ r j -1);特别地,交换|A|的相邻两行(列)(i 行和i+1行),行列式变为(-1) r i r i +1|A|; (2)用一个r i 阶可逆阵K 左(右)乘|A|的第i 行(列)的所有矩阵,等于用|K|乘以|A|; (3)用一个矩阵左(右)乘|A|的某一行(列)的所有矩阵再加到另一行(列)的对应元素上,行列式不变. 由定理7的(2)可得推论分块行列式|A|的某一行(列)的所有矩阵的可逆左(右)因子K,可以行列式|K|的形式提到行列式符号外.2．分块矩阵初等变换的应用一、利用分块矩阵的初等变换求矩阵的逆.廖中行在2002年05期《四川教育学院学报》上的《初等变换在分块矩阵乘法》的一文中提到例1: 已知⎥⎦⎤⎢⎣⎡=C OD BP 其中Ｂ是ｒ×ｒ可逆阵,Ｃ是ｓ×ｓ可逆阵,求证:Ｐ可逆,并求1-P .分析:本题是一个分块阵的求逆问题,一般可用待定子块法,也可利用广义初等变换,还可用左乘分块初等阵的方法.解:因Ｂ、Ｃ可逆,故|Ｂ|≠0,|Ｃ|≠0.根据拉普拉斯展开,有C B CO DB P ·==≠0,故Ｐ可逆.求C 有三种办法:解法一:利用广义初等行变换法.⎪⎭⎝E C 0012⎪⎭ ⎝-100C E (B 1-D)2r ⨯+r 1 ⎪⎪⎭⎫ ⎝⎛-----1111000C DC B E B E 故P 1-=⎪⎪⎭⎫ ⎝⎛-----11110C DC B B 本题对分块矩阵进行广义初等变换是一般矩阵的初等变换的一种推广,其方法和一般矩阵相同.作初等行(列)变换时,对矩阵Ｐ应左(右)乘相应的分块单位阵.上述分块初等变换的过程也可用分块阵左乘相应的分块初等阵,可表示如下: 解法二: 可用左乘分块初等阵的方法求1-P⎪⎪⎭⎫ ⎝⎛--1100C B ⎪⎪⎭⎫ ⎝⎛C D B 0=⎪⎪⎭⎫⎝⎛--110C D B E有 ⎪⎪⎭⎫ ⎝⎛--E D B E 01⎪⎪⎭⎫ ⎝⎛-E D B E 01=⎪⎪⎭⎫⎝⎛E E 00 即：⎪⎪⎭⎫ ⎝⎛--E D B E 01⎪⎪⎭⎫ ⎝⎛-C B 001⎪⎪⎭⎫ ⎝⎛C D B 0=⎪⎪⎭⎫⎝⎛E E 00=E 故有P 1-=⎪⎪⎭⎫ ⎝⎛C D B 01-=⎪⎪⎭⎫ ⎝⎛--E D B E 01⎪⎪⎭⎫ ⎝⎛--1100C B =⎪⎪⎭⎫⎝⎛-----11110C DC B B 例2：已知A=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--1001000000643521100010001，求A 1-.分析:本题是一个矩阵的求逆问题,一般可用公式法,矩阵的初等变换法求;可块矩阵初等变换法求1-A .利用分块矩阵初等变换法先A 化分成分块矩阵，即A=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--1001000000643521100010001=⎪⎪⎭⎫ ⎝⎛C D B 0 其中B=⎪⎪⎪⎭⎫ ⎝⎛100010001，C=⎪⎪⎭⎫ ⎝⎛--1001，D=⎪⎪⎪⎭⎫ ⎝⎛654321 从而求得B 1-=⎪⎪⎪⎭⎫ ⎝⎛100010001，C 1-=⎪⎪⎭⎫ ⎝⎛--1001然后对A 进行广义初等变换，即：⎪⎭⎝E C 0012⎪⎭⎝-100C E(B 1-D)⨯r 2+r 1 ⎪⎪⎭⎫⎝⎛-----111100C DC B E B E ∴A 1-=⎪⎪⎭⎫ ⎝⎛-----11110C DC B B =⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--1000001000651004201031001如果用其它方法来求解将会变得很繁琐，用分块矩阵的初等变换发来求解就显的比较简单.二、利用分块矩阵初等变换求行列式的值宋玉英在2002年04期的《兰州教育学院学报》上的《“用广义初等变换”法求“分块矩阵”的逆矩阵》一文中提到例3 设P=⎪⎪⎭⎫⎝⎛D C B A 是一个分块方阵,其中A 是r 阶可逆阵,求|P|. 解: 由推论及定理7的(3):P =D C B A =A DCB A Ir 1-=ABCA D B A I r 110---=A B CA D 1-- 若A 与D 可乘,则|P|=|AD-ACAB|;又若A 与C 可交换(即AC=CA),则|P|=|AD-CB|.例例4 设D n 2=d c d c b a b a, 其中a ≠0,求|A|解： D n 2=dcd c b a ba=DC BA由于A,C 可交换,所以D n 2=CB AD -=⎪⎪⎪⎭⎫⎝⎛∙⎪⎪⎪⎭⎫ ⎝⎛bc bc ad ad = =|(ad-bc)I|=(ad-bc)n例5 设A,B,C 和D 是n 阶方阵,试证明DC B A =AB CD证两次利用定理4的(1),得D C B A =（-1）2n B A D C =（-1）2n （-1）2n A B C D =AB C D三、利用分块矩阵的初等变换求矩阵的秩史永铨在2002年02期《淮南师范学院学报》上的《分块矩阵初等变换及其应用》一文中提到：矩阵的秩有以下初等性质:设Ａ与Ｂ分别是ｒ×ｓ与ｐ×ｑ矩阵，则ｒBC A 0≥ｒ(Ａ)+ｒ(Ｂ)并且当Ａ(或Ｂ)是方阵且非异时,或者Ｃ=0时上式的等号成立.例6. 设Ａ是ｍ×ｎ阵DC BA 的非异顺序主子阵,则r DC B A =ｒ(Ａ)+ｒ(Ｄ-ＣＡ1-Ｂ)证： ⎥⎦⎤⎢⎣⎡---r m rI CA I 10∙⎥⎦⎤⎢⎣⎡D C B A =⎥⎦⎤⎢⎣⎡--B CA D B A10而Ａ是非异阵,由以上性质知ｒ⎥⎦⎤⎢⎣⎡D C B A =⎥⎦⎤⎢⎣⎡--B CA D B A 10≥ｒ(Ａ)+ｒ(Ｄ-CA 1-B) 例7. 设ｎ阶方阵Ａ=(Ｑij )为反对称矩阵,证明:ｒ(Ａ)必为偶数证: 对ｎ用归纳法ｎ=1,2是命题显然成立设阶数小于ｎ时命题为真则对ｎ阶及对称矩阵Ａ,将Ａ分块成Ａ=DBCA 1,其中Ａ1=01212a a -不妨设12a ≠0.⎥⎦⎤⎢⎣⎡--I BA I 110⎥⎦⎤⎢⎣⎡D B C A 1⎥⎦⎤⎢⎣⎡--I C A I 011=⎥⎦⎤⎢⎣⎡--C BA D A 11100∴ｒ(Ａ)=ｒ⎥⎦⎤⎢⎣⎡D BC A 1=ｒ⎥⎦⎤⎢⎣⎡--C BA D A 11100 =ｒ(Ａ1)+ｒ(Ｄ-ＢＡ11-Ｃ) =2+ｒ(Ｄ-ＢＡ11-Ｃ)但Ｄ-ＢA 11-Ｃ为阶数比Ａ低的反对称矩阵,由归纳假设ｒ(Ｄ-ＢＡ11-Ｃ)为偶数,故ｒ(Ａ)为偶数.四、分块矩阵的初等变换在矩阵分解中的应用例8. 设Ａ=(ａij )是ｎ阶方阵,它的顺序主子式全不为零,证明: 存在非异下三角形矩阵Ｂ与非异上三角形矩阵Ｃ,使Ａ=ＢＣ证: 对ｎ用归纳法ｎ=1时显然成立设当ｎ-1时,结论成立,则对ｎ,将Ａ分块成Ａ=⎥⎦⎤⎢⎣⎡-nn n a A βα1由归纳假设对Ａ1-n =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----1,11,11,11,1n n n n a a a a 有Ａ1-n =Ｂ1Ｃ1其中Ｂ1Ｃ1分别是ｎ-1阶非异下三角形与上三角形矩阵⎥⎦⎤⎢⎣⎡----10111n n A I β∙⎥⎦⎤⎢⎣⎡-b a A n 01,其中b=a nn -11--n A βa 上式两端取行列式有：A =1-n A ∙b, ∴ b ≠0∴ ⎥⎦⎤⎢⎣⎡-b A n 001=⎥⎦⎤⎢⎣⎡I C B 0011∙⎥⎦⎤⎢⎣⎡-b a B C 0111 于是得：A ⎥⎦⎤⎢⎣⎡-m n a A βα1=⎥⎦⎤⎢⎣⎡----10111n n A I β∙⎥⎦⎤⎢⎣⎡1001B ⎥⎦⎤⎢⎣⎡-b B C 0111α=BC 其中B=⎥⎦⎤⎢⎣⎡----10111n n A I β1-∙⎥⎦⎤⎢⎣⎡1001B =⎥⎦⎤⎢⎣⎡---10111n n A I β⎥⎦⎤⎢⎣⎡1001B =⎥⎦⎤⎢⎣⎡-10111C B β, C=⎥⎦⎤⎢⎣⎡-b B C 0111αB =1B ≠0,C =b 1C 0≠∴B 与C 分别是非奇异的下三角与上三角形矩阵.类似的例子还可以举出很多,由于篇幅有限,不再赘述.总之,在矩阵乘法中,只要对矩阵进行恰当的分块,结合矩阵初等变换的方法,就能大大的简化其运算.。

分块矩阵的初等变换及应用_百度文库.

十．研究创新题解：1.分块矩阵的初等变换分块矩阵的初等变换与初等矩阵吴云在1997年8月的《工科数学》上的《分块矩阵的初等变换》一文中提到定义1分块矩阵的行(列初等变换是指:（1）交换两行(列的位置;（2）第ｉ行(列的各个元素分别左乘(右乘该行(列的一个阶左(右保秩因子Ｈ;（3）第ｉ行(列的各个元素分别左乘(右乘一个阶矩阵Ｋ后加到第ｊ行.定义2 对应于分块矩阵的初等分块矩阵是指:（1）=或=（2）=或=其中Ｈ为第ｉ行(列的一个左(右保秩因子；(1 =(2 或=初等分块矩阵与通常的初等矩阵类似,但由于矩阵乘法不满足交换律,故需要分为左、右两种.直接验算可得:定理1(1交换的第ｉ行与第ｊ行,相当于左乘一个ｍ阶初等分块矩阵,其中中的元素为ｈ(i阶单位矩阵,为ｈ(j阶单位矩阵,当ｒ≠ｉ且ｒ≠ｊ时,为ｈ(ｒ阶单位矩阵;交换的第ｉ列与第ｊ列相当于右乘一个ｎ阶初等分块矩阵,其中为ｌ(i阶单位矩阵,为ｌ(j阶单位矩阵,当ｒ≠ｉ且ｒ≠ｊ时,为ｌ(ｒ阶单位矩阵；(2 的第ｉ行的每一个元素左乘一个矩阵Ｈ相当于左乘一个ｍ阶分块矩阵中Ｈ为ｈ(ｉ阶方阵; 的第ｉ列的每一个元素右乘一个矩阵Ｈ,相当于右乘一个ｎ阶初等到变换矩阵,其中Ｈ为ｌ(ｉ阶方阵；(3 的第ｊ行的每个元素分别左乘一个ｈ(ｉ×ｈ(ｊ矩阵Ｋ后加到第ｉ行,相当于左乘一个初等分块矩阵;第ｊ列的每一个元素分别右乘ｌ(ｊ×ｌ(ｉ矩阵Ｋ后加到第ｉ列,相当于右乘.定理2设Ａ为方阵,则分块矩阵施行第一种行初等变换后,对应的行列式为,其中h(i,j=h(ih(j-l+h(i+l]+…+h(j[h(i+h(i+j+…+h(j-l],l(i,j=l(ih(j-l+l(i+l]+…+l(j[l(i+l(i+j+…+l(j-l],施行第二种初等变换后,对应的行列式为|Ｈ|·|Ａ|;施行第三种初等变换后,对应的行列式的值不变.证明: ,显然成立.下证,所在的第1行逐次与它相邻的行交换,移至前,共进行ｈ(ｉ-1+ｈ(ｉ+1+…+ｈ(ｊ-1次交换两行,第2行逐次与它相邻的行交换,移至前,同样进行相同次交换两行,依此类推,把所在的行移至所在的行前,共进行ｈ(ｉ[ｈ(ｉ-1+ｈ(ｉ+1+…+ｈ(ｊ-1]次交换两行,然后把移至适当的位置,同理共进行ｈ(ｊ[ｈ(ｉ+ｈ(ｉ+1+…+ｈ(ｊ-1]次交换两行,所以交换两行的总次数为ｈ(ｉ,ｊ,故;同理.所以有==(-1或==（-1）==或=====定理3 分块矩阵进行初等变换后,秩不变.证明: 对于(1,相当于对进行若干次行(列的交换,故命题成立;对于(2,根据定义1,显然成立;对于(3,相当于进行若干次把行(列乘以一个倍数后加到另一行(列,故命题成立.定理4 (1设Ａ,Ｂ的行数均为ｍ,则矩阵方程ＡＸ=Ｂ,当(Ａ= (Ａ,Ｂ=ｍ时有唯一解,当(Ａ= (Ａ,Ｂ<ｍ时有无穷多解,当(Ａ< (Ａ,Ｂ时无解;(2设Ａ,Ｂ的列数均为ｎ,则矩阵方程ＸＡ=Ｂ,当(Ａ= =ｎ时有唯一解,当(Ａ= <ｎ有无穷多解,当(Ａ< 时无解.证明: (1设(Ａ= (Ａ,Ｂ<ｍ,则存在可逆矩阵Ｐ,Ｑ,使，其中为ｒ阶单位矩阵, 为ｒ阶方阵,设,则有: == =B所以为ＡＸ=Ｂ的解,其中, 是任意的.当(Ａ= (Ａ,Ｂ=ｍ时,Ａ=Ｐ(ＯＱ,Ｂ=( ,显然,ＡＸ=Ｂ有唯一解: ;当(Ａ< (Ａ,Ｂ时,ＡＸ=Ｂ无解.同理可证(2成立(当(Ａ= ( , <ｎ时,X=P定义3 对于任意的ｕ,ｖ,如果( = ( ,= (,,则称为极大元.定理5 分块矩阵可以用分块矩阵的初等变换对角化的充要条件是: 它有一个极大元.证明: 充分性.不妨设为极大元(否则可以通过第一种分块矩阵的初等变换把极大元移到第一行,第一列交叉位置.由定理4,存在可逆矩阵Ｐ,Ｑ,使，,令Ｋ=-Ｐ,其中, 为适当阶数的任意矩阵.则K+ =，所以第一行左乘Ｋ加到第二行,得.同理,令Ｋ＇=-, 则Ｋ′+ =0,所以的第一列右乘Ｋ′后加到第二列,得.(如先进行列变换,再进行行变换,得,因为=+=+,故两种运算顺序结果相同必要性.反证法,不妨设(≠(,或(,(,则由定理4, =-或=-无解,从而不存在Ｋ,使对角化.同理,当(≠(,或(,≠(时,不存在使-A K=A或-=成立.定理5表明:并不是所有的2×2分块矩阵都可以用分块矩阵初等变换对角化,如果分块矩阵没有极大元,则需分得更细,才能对角化.定理6 矩阵的一种分块方法可以用分块矩阵的初等变换对角化的充分条件是:存在ｓ-1行且存在ｔ-1列有极大元.证明: 用数学归纳法.当ｓ=ｔ=1时,只有一块,命题成立;设ｓ≤ｅ,ｔ≤ ｆ时命题成立.当ｓ=ｅ+1,ｔ=ｆ时,存在ｅ行且存在ｆ-1列有极大元,显然可以用第一种分块矩阵的初等变换,通过交换两行或两列的位置,使的前ｅ行与前ｆ-1列都有极大元,再把前ｅ行,前ｆ-1列看成一块,得到一个新的2×2分块矩阵,记为.显然为极大元,根据定理4, 可以化成对角形: ,又,它的每行、列都有极大,故由假设可以对角化,从而可以对角化.同理可证当ｓ=ｅ,ｔ=ｆ+1时, 可以对角化.由此命题成立.下面讨论对角化后的非零块进一步化简的方法.设,与.根据定理1, ,为的左(右保秩因子,显然也是所在行(列的左(右保秩因子,故对角化后的分块矩阵第ｉ行、第ｉ列分别左乘,右乘后, 可以化成讨论分块方阵行列式的计算,先讨论分块初等阵的行列式.设I为S×S分块单位阵:I=其中I r为r阶单位阵(1≤i≤S,对I施行一次初等变换可得定义2所述的三种分块初等阵,它们的行列式有下列计算公式.引理分块初等阵的行列式有以下性质:(1|I(i,j|= ,其中τ=r (r+1+…+r+ r (r+1+…+ r-1(i特别地,若j=i+1,则| I(i,j|=(-1 r r;(2|I(i(K|=|k|,其中K是r阶可逆阵;(3|I(j(K,i|=1,其中K是r×r矩阵.证(1不难验证,将I(i,j的元素行进行τ次相邻的对调可将I(i,j变成I,由行列式的性质,|I(i,j|= |I|=.(2,(3由对角分块方阵及三角形分块方阵的行列式计算方法即知.由于对分块方阵A施行一次初等行变换,相当于用相应的分块初等阵左乘A,由上述引理,我们有下列分块方阵的行列式计算性质.定理7 设A是一个分块方阵.(1交换|A|的i,j两行(列,行列式变为(-1τ|A|,其中τ= r (r+1+…+ r+ r (r+1+…+ r-1;特别地,交换|A|的相邻两行(列(i行和i+1行,行列式变为(-1 r r+1|A|;(2用一个r阶可逆阵K左(右乘|A|的第i行(列的所有矩阵,等于用|K|乘以|A|;(3用一个矩阵左(右乘|A|的某一行(列的所有矩阵再加到另一行(列的对应元素上,行列式不变.由定理7的(2可得推论分块行列式|A|的某一行(列的所有矩阵的可逆左(右因子K,可以行列式|K|的形式提到行列式符号外.2．分块矩阵初等变换的应用一、利用分块矩阵的初等变换求矩阵的逆.廖中行在2002年05期《四川教育学院学报》上的《初等变换在分块矩阵乘法》的一文中提到例1: 已知其中Ｂ是ｒ×ｒ可逆阵,Ｃ是ｓ×ｓ可逆阵,求证:Ｐ可逆,并求.分析:本题是一个分块阵的求逆问题,一般可用待定子块法,也可利用广义初等变换span,还可用左乘分块初等阵的方法.解:因Ｂ、Ｃ可逆,故|Ｂ|≠0,|Ｃ|≠0.根据拉普拉斯展开,有≠0,故Ｐ可逆.求C有三种办法:解法一:利用广义初等行变换法.B r,C r(B D+r故P=本题对分块矩阵进行广义初等变换是一般矩阵的初等变换的一种推广,其方法和一般矩阵相同.作初等行(列变换时,对矩阵Ｐ应左(右乘相应的分块单位阵.上述分块初等变换的过程也可用分块阵左乘相应的分块初等阵,可表示如下:解法二: 可用左乘分块初等阵的方法求=有=即：==E故有P===例2：已知A=，求A.分析:本题是一个矩阵的求逆问题,一般可用公式法,矩阵的初等变换法求;可以用分块矩阵初等变换法求.利用分块矩阵初等变换法先A化分成分块矩阵，即A==其中B=，C=，D=从而求得B=，C=然后对A进行广义初等变换，即：B r,C r(B D r+rA==如果用其它方法来求解将会变得很繁琐，用分块矩阵的初等变换发来求解就显的比较简单.二、利用分块矩阵初等变换求行列式的值宋玉英在2002年04期的《兰州教育学院学报》上的《“用广义初等变换”法求“分块矩阵”的逆矩阵》一文中提到例3设P=是一个分块方阵,其中A是r阶可逆阵,求|P|.解: 由推论及定理7的(3:====若A与D可乘,则|P|=|AD-ACAB|;又若A与C可交换(即AC=CA,则|P|=|AD-CB|.例例4 设D=, 其中a≠0,求|A|解： D==由于A,C可交换,所以D=== =|(ad-bcI|=(ad-bc例5 设A,B,C和D是n阶方阵,试证明=证两次利用定理4的(1,得=（-1）=（-1）（-1）=三、利用分块矩阵的初等变换求矩阵的秩史永铨在2002年02期《淮南师范学院学报》上的《分块矩阵初等变换及其应用》一文中提到：矩阵的秩有以下初等性质:设Ａ与Ｂ分别是ｒ×ｓ与ｐ×ｑ矩阵，则ｒ≥ｒ(Ａ+ｒ(Ｂ并且当Ａ(或Ｂ是方阵且非异时,或者Ｃ=0时上式的等号成立.例6. 设Ａ是ｍ×ｎ阵的非异顺序主子阵,则r=ｒ(Ａ+ｒ(Ｄ-ＣＡＢ证：=而Ａ是非异阵,由以上性质知ｒ=≥ｒ(Ａ+ｒ(Ｄ考情解读B例7. 设ｎ阶方阵Ａ=(Ｑ为反对称矩阵,证明:ｒ2必为偶数(1: 对ｎ用归纳法ｎ=1,2是命题显然成立设阶数小于ｎ时命题为真则对ｎ阶及对称矩阵Ａ,将Ａ分块成Ａ=,其中Ａ=不妨设(30.=∴ｒ(Ａ=ｒ=ｒ=ｒ(Ａ+ｒ作函数图象有两种基本方法：一是描点法，二是图象变换法，其中图象变换有平移变换、伸缩变换、对称变换．Ｃ4=2+ｒ(Ｄ-ＢＡＣ但Ｄ-ＢAＣ为阶数比Ａ低的反对称矩阵,由归纳假设ｒ(Ｄ-ＢＡＣ为偶数,故ｒ(Ａ为偶数.四、分块矩阵的初等变换在矩阵分解中的应用例8. 设Ａ=(ａ是ｎ阶方阵,它的顺序主子式全不为零,证明: 存在非异下三角形矩阵Ｂ与非异上三角形矩阵Ｃ,使Ａ=ＢＣ证: 对ｎ用归纳法ｎ=1时显然成立设当ｎ-1时,结论成立,则对ｎ,将Ａ分块成Ａ=由归纳假设对Ａ=有Ａ=ＢＣ其中ＢＣ分别是ｎ-1阶非异下三角形与上三角形矩阵,其中b=-上式两端取行列式有：=b,b0=于是得：A==BC其中B===,C==0,=bB与C分别是非奇异的下三角与上三角形矩阵.类似的例子还可以举出很多,由于篇幅有限,不再赘述.总之,在矩阵乘法中,只要对矩阵进行恰当的分块,结合矩阵初等变换的方法,就能大大的简化其运算.。

矩阵初等变换及其应用毕业论文

矩阵初等变换及其应用毕业论文矩阵初等变换及其应用毕业论文摘要：初等变换是高等代数和线性代数学习过程中非常重要的，使用非常广泛的一种工具。

本文列举了矩阵初等变换的几种应用，包括求矩阵的秩、判断矩阵是否可逆及求逆矩阵、判断线性方程组解的状况、求解线性方程组的一般解及基础解系、证向量的线性相关性及求向量的极大无关组、求向量空间两个基的过渡矩阵、化二次型为标准形。

并用具体例子说明矩阵初等变换在以上几种应用中是如何运用的。

关键词：矩阵初等变换初等矩阵在代数的学习过程中，我发现矩阵的初等变换有许多应用，几乎贯穿着始终。

本文将对矩阵的初等变换进行介绍并以具体例子说明矩阵初等变换的七种应用。

虽然这些计算格式有不少类似之处，但是也指出由于这些计算格式有不同的原理，所以它们的应用也有一些明显的区别。

定义1：矩阵的行（列）初等变换是指对一个矩阵施行的下列变换：（1）交换矩阵的两行（列）(交换第i ，j 两行（列），记作()ij ij r c ）；（2）用一个不等于零的数乘矩阵的某一行（列）即用一个不等于零的数乘矩阵的某一行（列）的每一个元素（用数k 乘以第i 行（列），记作()(())i i r k c k ；（3）用某一个数乘矩阵的某一行（列）后加到另一行（列），即用某一数乘矩阵的某一行（列）的每一个元素再加到另一行（列）的对应元素上(第i 行（列）k 倍加到第j 行（列），记作()(())ij ij r k c k 。

初等行、列变换统称为初等变换。

定义2：对单位矩阵I 仅施以一次初等变换后得到的矩阵称为相应的初等矩阵，分别记为第1、2、3类行（列）初等矩阵为()ij ij R C ，()(())i i R k C k ，()(())ij ij R k C k ，有ij R =ij C =10111⎛⎫ ⎪ ⎪ ⎪⎪⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ ()i R k =()i C k =1k1⎛⎫ ⎪⎪⎪ ⎪ ⎪ ⎪⎝⎭()ij R k =()ij C k =11j 11i k⎛⎫ ⎪ ⎪ ⎪⎪⎪ ⎪ ⎪ ⎪ ⎪⎝⎭行行初等变换与初等矩阵之间有下列基本性质。

分块矩阵的初等变换及其应用

分块矩阵的初等变换及其应用一、引言分块矩阵作为矩阵的一种特殊形式，具有重要的数学应用。

在线性代数中，我们学习到了矩阵的初等变换，它们是一类重要的矩阵操作，可以通过一系列的行变换和列变换来改变矩阵的形态。

而分块矩阵的初等变换则是在分块矩阵中进行的一种特殊的操作，本文将详细介绍分块矩阵的初等变换及其应用。

二、分块矩阵的初等变换分块矩阵的初等变换是指对分块矩阵进行一系列的操作，包括交换分块的位置、对某个分块进行乘法变换和加法变换等。

这些操作可以通过矩阵的行变换和列变换来实现。

1. 交换分块的位置交换分块的位置是指将分块矩阵中的两个分块进行位置交换。

这种操作可以通过交换两个分块所在的行或列来实现。

2. 对某个分块进行乘法变换对某个分块进行乘法变换是指对分块矩阵中的某个分块进行乘以一个非零标量的操作。

这种操作可以通过将分块矩阵中对应的行或列乘以一个非零标量来实现。

3. 对某个分块进行加法变换对某个分块进行加法变换是指对分块矩阵中的某个分块进行加上另一个分块的操作。

这种操作可以通过将分块矩阵中对应的行或列加上另一个分块所在的行或列来实现。

三、分块矩阵的应用分块矩阵的初等变换在数学和工程领域中有着广泛的应用。

下面将介绍几个典型的应用场景。

1. 线性代数中的矩阵运算在线性代数中，我们经常需要对矩阵进行运算，如求逆矩阵、求特征值等。

分块矩阵的初等变换可以简化这些运算的过程，使得计算更加简便和高效。

2. 线性方程组的求解线性方程组的求解是数学中的一个重要问题。

分块矩阵的初等变换可以通过行变换和列变换将线性方程组转化为简化的形式，从而更容易求解。

3. 矩阵的相似性在矩阵的相似性中，我们经常需要对矩阵进行相似变换。

分块矩阵的初等变换可以通过对分块矩阵进行相似变换，从而得到相似的简化矩阵。

4. 矩阵的分解矩阵的分解是数学中的一个重要问题，可以帮助我们更好地理解矩阵的结构和性质。

分块矩阵的初等变换可以通过对分块矩阵进行分解，从而得到更简化的形式。

分块矩阵的初等变换及其应用开题报告 [开题报告]

毕业论文开题报告信息与计算科学分块矩阵的初等变换及其应用一、选题的背景、意义1．选题的背景在数学的矩阵理论中，一个分块矩阵或是分段矩阵就是将矩阵分割出较小的矩形矩阵，这些较小的矩阵就称为区块。

换个方式来说，就是以较小的矩阵组合成一个矩阵。

分块矩阵的分割原则是以水平线和垂直线进行划分。

分块矩阵中，位在同一行（列）的每一个子矩阵，都拥有相同的列数（行数）。

通过将大的矩阵通过分块的方式划分，并将每个分块看做另一个矩阵的元素，这样之后再参与运算，通常可以让计算变得清晰甚至得以大幅简化。

例如，有的大矩阵可以通过分块变为对角矩阵或者是三角矩阵等特殊形式的矩阵。

2．选题的意义矩阵的分块是处理较高阶矩阵时常用的方法，用一些贯穿于矩阵的纵线和横线将矩阵分成若干子块，使得阶数较高的矩阵化为阶数较低的分块矩阵。

在运算中，我们有时把这些子块当作元素一样来处理，从而简化了表示，便于计算。

分块矩阵初等变换是线性代数中重要而基本的运算，它在研究矩阵行列式、特征值、秩等各种性质及求矩阵的逆、解线性代数方程中有着广泛的应用。

因此，如何直接对分块矩阵实行初等变换显得非常重要，本文的目的就是讨论分块矩阵的初等变换及其应用[1]。

二、研究的基本内容与拟解决的主要问题2.1 分块矩阵及其初等变换2.1.1 分块矩阵的定义：将一个分块矩阵A用若干条纵线和横线分成许多块的低阶矩阵，每一块低阶矩阵称为A 的子块。

以子块为元素的矩阵A称为分块矩阵。

我们将单位矩阵E分块：⎪⎪⎪⎭⎫⎝⎛=s r r E E E 000001O ，其中E r 是r i 阶单位矩阵(1<i<s) 称E 为分块单位矩阵[2]。

2.1.2 分块矩阵与广义初等变换[3]分块矩阵可以解释为矩阵中的矩阵,而对这个矩阵进行初等变换, 相应的初等矩阵也要变为可计算的分块矩阵,所进行的变换陈维广义初等变换.其目的在于简化计算和证明.定义 1 矩阵称为分块矩阵,如果元素A ij 为阶矩阵,其中m 1+m 2+m 3+…+m r =M 注释：定义规定分块矩阵为与同行的矩阵有相同的行数,位于同列的元素有相同的列数.它们的行数之和构成分块矩阵的行数, 列数之和构成分块矩阵的列数. 分块矩阵的运算满足矩阵的运算定义,由于它的特殊性,故此给出各自的定义.•设 A,B 为两个分块矩阵,则定义它们的加法为 A+B=(A ij + B ij )条件：A,B 为同阶矩阵而且A ij , B ij 也为同阶矩阵.•设 A=(A ij )rxt , B=(B ij )txs 为两个分块矩阵,则定义它们的乘法为A X B=(C ij )其中∑==tj kj ikij B AC 1的列数t 等于B 的行数而且A ij x B ij 也存在.同样地,广义初等变换与广义初等矩阵可简单叙述如下：定义 2 广义初等变换是对分块矩阵进行以下的变换的统称.• 交换矩阵的两行(列)； • 将某行(列)左(右)乘可逆矩阵；•将某行(列)左(右)乘矩阵加到另一行(列)上；定义 3 设E nXn 为分块的单位矩阵,对其进行一次广义初等变换所得到的矩阵称为广义初等矩阵[4].例子 1 广义初等矩阵具体形式⎪⎪⎭⎫ ⎝⎛→⎪⎪⎭⎫ ⎝⎛0000mn n mE E E E , ⎪⎪⎭⎫ ⎝⎛→⎪⎪⎭⎫ ⎝⎛n n mE P E E 0000, ⎪⎪⎭⎫⎝⎛→⎪⎪⎭⎫ ⎝⎛En Q E E E mn m000 广义初等矩阵(变换)的作用如同一般的初等矩阵(变换),遵守"左行右列"原则. 例子 2 设 ⎪⎪⎭⎫ ⎝⎛=D C B A M那么 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛B A D C D C B A EE m n 00, ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛D C PB PA D C B A En P 00 ⎪⎪⎭⎫ ⎝⎛++=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛D QB C QA B A D C B A En Q E m 02.1.3 分块矩阵的初等行（列）变换的定义[5]与普通矩阵的初等行变换类似，分块矩阵也有三种类型的初等行变换：1.把一个块行的左P 倍（P 是矩阵）加到另一个块行上；2.换两个块行的位置；3.用一个可逆矩阵左乘某一块行。

分块矩阵的初等变换及其应用

2
证明syvester不等式：设A、 B分别是s×n、 n×m矩阵，则只要证n+rank （AB ） ≥rank （A ） +rank （B ）。根据（3 ）式有 0 I 。 0 0 0 AB
n
rank （AB ） ≥rank （A ） +rank （B ） -n。〔 6〕
n+rank （AB ） =rank
分块矩阵的初等变换及其应用分块矩阵的初等变换矩阵初等变换的应用矩阵的初等变换矩阵初等变换矩阵的初等变换技巧初等变换法求逆矩阵利用初等变换求逆矩阵矩阵的初等行变换矩阵初等行变换
大理学院学报
J OURNAL OF DALI UNIVERS ITY
第 8 卷第 8 期 2009 年 8 月 Vol.8 No.8 Aug. 2009
高等代数教材中的许多问题都可以用分块矩阵来解决，而且过程简单，容易理解。2×2分块矩阵形式简单，但如果与分块矩阵的初等变换结合起来却变得非常有用。
1 分块矩阵的初等变换
1.1 分块矩阵的初等行（列）变换的定义与普通矩阵的初等行变换类似，分块矩阵也有三种类型的初等行变换〔 1〕： ①把一个块行的左P倍（P是矩阵）加到另一个块行上； ②换两个块行的位置； ③用一个可逆矩阵左乘某一块行。类似地有分块矩阵的初等列变换： ①把一个块列的右P倍（P是矩阵）加到另一个块列上； ②互换两个块列的位置； ③用一个可逆矩阵右乘某一块列。 1.2 分块矩阵的初等变换与分块初等矩阵的关系把单位矩阵分块得到的矩阵 I 0 经过一次分块矩阵 0 0 0 I
B Is B Is -B Is In A In A =｜Is-AB｜。
（1 ）
另一方面，又有 In A 于是有 In 0 B Is = In-BA A 0 Is ，

分块矩阵初等变换的妙用

分块矩阵初等变换的妙用分块矩阵初等变换是线性代数中的一个重要概念，在数学和工程领域都有着广泛的应用。

它通过将矩阵分成若干块，对每个块进行初等变换，从而对整个矩阵进行操作和分析。

分块矩阵初等变换的妙用不仅可以简化矩阵运算，还可以方便地对矩阵进行性质分析和求解。

本文将通过详细的介绍和实例分析，展示分块矩阵初等变换在实际应用中的重要性和妙用之处。

一、分块矩阵初等变换的基本概念分块矩阵初等变换是指将一个矩阵按照一定规则分成若干个子矩阵，并对每个子矩阵进行初等变换。

常见的分块方式包括按行分块和按列分块，每种分块方式都有其特定的应用场景和操作规则。

按行分块是指将一个矩阵按照行进行分割，形成若干个子矩阵。

对于一个m×n的矩阵A，可以按行分块为r行和s行两部分，分别记为A = [A11 A12; A21 A22]，其中A11是r×s 的子矩阵，A12是r×(n-s)的子矩阵，A21是(m-r)×s的子矩阵，A22是(m-r)×(n-s)的子矩阵。

分块矩阵初等变换的基本操作包括矩阵加减法、数乘、转置和乘法等，通过这些操作可以对子矩阵进行初等变换，从而实现对整个矩阵的变换和分析。

1. 简化矩阵运算分块矩阵初等变换可以显著简化矩阵的运算和求解过程。

通过将大矩阵分成若干个小块，可以分别对每个小块进行操作，然后将结果整合在一起，从而减少了计算量和复杂度。

尤其是在大规模矩阵的运算中，分块矩阵初等变换可以大大提高计算效率。

2. 方便性质分析和求解分块矩阵初等变换还可以方便地对矩阵的性质进行分析和求解。

通过分块的方式，可以更加清晰地观察矩阵的结构和特点，从而更容易得出结论和推断。

对角块矩阵的分块初等变换可以方便地求出特征值和特征向量，从而分析矩阵的性质和行为。

3. 实际应用分块矩阵初等变换在工程和科学领域有着广泛的应用。

在控制系统中，经常需要对大规模矩阵进行运算和分析，而分块矩阵初等变换可以使得控制系统的设计和分析更加简洁和高效；在信号处理领域，分块矩阵初等变换可以方便地处理多维信号和图像数据，从而实现对图像的分析和处理。

分块矩阵初等变换的妙用

分块矩阵初等变换的妙用分块矩阵是线性代数中常用的重要工具之一，它在矩阵运算和变换中有广泛的应用。

在实际应用中，我们经常遇到大规模矩阵的运算和变换，而分块矩阵可以通过对矩阵进行分块处理，使得复杂的运算变得简单直观。

本文将介绍分块矩阵初等变换的妙用，探讨其在线性代数中的重要作用。

一、分块矩阵初等变换的基本概念分块矩阵是将一个矩阵按照行或列进行划分，每个小块可以是一个数、一个向量、一个行/列向量，也可以是一个矩阵。

分块矩阵初等变换是指对分块矩阵进行的行/列交换、数乘、行/列加减操作。

在分块矩阵初等变换中，我们通常有以下三种基本操作：1. 行/列交换：即将两行/列进行互换。

2. 数乘：即将矩阵的某一行/列中的元素乘以一个非零数。

3. 行/列加减：即将矩阵的某一行/列加上或减去另一行/列的若干倍。

通过这些基本操作，我们可以对分块矩阵进行各种变换，从而达到简化运算、求解方程组、矩阵的相似变换等目的。

1. 矩阵的分块运算分块矩阵初等变换可以简化矩阵的运算。

对于一个大规模矩阵进行求逆运算时，可以将其分块为多个小规模的矩阵，然后对每个小矩阵进行求逆运算，最后组合起来，避免了对整个大矩阵进行求逆的复杂运算。

这样一来，不仅简化了运算，还提高了计算效率。

2. 方程组的求解分块矩阵初等变换也常用于解决方程组。

对于形如AX=B的线性方程组，其中A是一个大规模矩阵，B是一个向量，X是未知向量。

我们可以将矩阵A根据其特点进行分块处理，比如按照系数矩阵的形式进行分块，然后通过初等变换将系数矩阵化为上三角矩阵或对角矩阵，从而简化了方程组的求解过程。

3. 矩阵的相似变换在线性代数中，矩阵的相似变换是一个重要的概念。

而分块矩阵初等变换可以帮助我们更直观地理解矩阵的相似性。

通过对分块矩阵进行初等变换，我们可以将一个矩阵化为对角阵或者标准型，从而得到矩阵的一些特征信息，如特征值、秩等，为矩阵的进一步研究提供了便利。

4. 线性变换的表示在线性代数中，我们经常需要研究线性变换的性质和特点。

分块矩阵的初等变换及其应用(1)

分块矩阵的初等变换及其在行列式、逆和秩中的应用

／：Ｉ１０２、０．
ｆ？
１
ｆ００／＼１＼２
单位矩阵Ｉ过一次初等变换得到的矩阵叫初等矩阵．经初等矩阵有以下三种：（）Ｉ以第１初等变换得到１对施种
则＝？Ｍ１
如能捕捉生活点滴，生写作素材是丰富的，作文时学生就学写会少些无奈。学中要努力培养学生广泛的阅读兴趣，导学教引生积累丰富的写作素材，展各种有趣的活动，发学生写作开激的欲望．学生感受写作文如同说话一般，吐不快。在习作使不指导的过程中，师的职责不是传授技法和知识，是激励、教而唤醒、舞，学生学会生活、会积累、会运用。每一天都鼓让学学带着健康的情感生活，着友爱的情态关注身边的人和事，带每次都带着积极的情绪动笔，就一定能写出富有个性和真情
摘要：文把矩阵的初等变换推广到分块矩阵．用本并分块矩阵的初等变换解决了许多有关分块矩阵的问题．关键词：等变换分块矩阵分块初等矩阵初
一
定理１设Ａ＝ａ）（ …
，
一
的文章
４４
初等矩阵记为ＩｉＫ）；（（）
（）矩阵Ｋ乘Ｉ３用左的第ｊ加到第ｉ所得到的分块初等矩行行阵记为Ｉｊｋ，，时表示用矩阵Ｋ乘Ｉ第ｉ加到第ｊ所（（）ｉ同）右的列列得到的分块初等矩阵．与定理１类似，们有：我定理２对分块矩阵Ｍ做一次分块初等行（）换相当列变于在Ｍ的左边（）乘以一个相应的分块初等矩阵．右边

毕业设计--分块矩阵的初等运算及其应用-精品

太原科技大学毕业设计（论文）设计(论文)题目：分块矩阵的初等运算及其应用姓名___ 姬君君__学院（系）应用科学学院专业_数学与应用数学班级 081801指导教师___ 王银珠___年月日太原科技大学毕业设计（论文）任务书（由指导教师填写发给学生）学院（直属系）：应用科学学院时间： 2012年3月1日学生姓名姬君君指导教师王银珠设计（论文）题目分块矩阵的初等运算及其应用主要研究内容1、翻译相关英文科技文献；2、了解分块矩阵常用的各种运算，探讨其应用；3、深入研究分块矩阵的新的运算，探讨研究其在实际中的应用.研究方法通过查找文献、特别是英文文献，培养翻译数学相关英文文献的能力，进一步查找文献，结合所学知识解决分块矩阵的初等运算以及实际应用的问题．主要技术指标(或研究目标)深入研究分块矩阵的新的运算，探讨研究其在实际中的应用。

主要参考文献1.《线性代数与矩阵论》，许以超主编，高等教育出版社，2008.2.《矩阵论》，杨明，刘先忠著，华中科技大学出版社，2005.说明：一式两份，一份装订入学生毕业设计（论文）内，一份交学院（直属系）.目录摘要 (Ⅲ)ABSTRACT (Ⅳ)第1章绪论 (1)第2章分块矩阵的定义及相关运算 (16)2.1 分块矩阵的定义 (18)2.2 分块矩阵的运算 (20)2.2.1 加法与数量乘法运算 (21)2.2.2乘法运算 (22)2.2.3 转置运算 (23)2.3 分块矩阵的初等变换 (28)2.3.1定义.....................................................................................................................2.3.2运算..................................................................................................... 第3章分块矩阵的应用 (29)3.1分块矩阵在解线性方程组中的应用..................................................................3.2 遗传算法运行参数分析 (32)3.2.1 确立评价目标函数 (36)3.2.2 分析各参数的影响 (38)3.3 对基本遗传算法的改进 (40)3.3.1适应值函数的改进 (42)3.3.2 自适应遗传算法 (46)结论............................................................................ .... (48)参考文献 (49)致谢 (50)附录 (55)附录Ⅰ中文译文....................................................................................... ..55 附录Ⅱ英文原文 (62)(注1：如果还有其他附录，可放在中文译文之前，中文译文、英文原文编号顺延) (注2：先将目录排好，基本对齐，然后选择段落-对齐方式-分散对齐)分块矩阵的初等运算及其应用摘要作为高等代数中的一个工具，矩阵是高等代数中的一个重要概念，分块矩阵是矩阵中的一个重要内容，在高等代数中有着很重要的应用，本文详细且全面论述了分块矩阵阵的概念和算法，包括用分块矩阵来算矩阵的乘积，利用分块矩阵求逆矩阵的问题，用分块矩阵求矩阵的行列式问题。

分块矩阵的应用研究文献综述

毕业论文文献综述数学与应用数学分块矩阵的应用研究一、前言部分（说明写作的目的，介绍有关概念、综述范围，扼要说明有关主题争论焦点）本论文的重要目的是通过查阅各种相关文献，寻找各种相关信息，来研究分块矩阵的计算方法和分块矩阵在化简行列式、行列式运算、求矩阵的特征值等方面的应用，首先我们先来介绍一些概念：分块矩阵的概念[]1：当矩阵的行数与列数较大时, 为便于运算, 有时把它分成若干个小块, 每个小块是行数与列数较小的矩阵.把一个矩阵看作是由一些小块矩阵所构成, 这就是矩阵的分块.构成分块矩阵的每个小矩阵, 称为子块.如对矩阵A 分块如下⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=1011012100100001A 其中记⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=1121,0000,10011A O E ,则A 可表示为分块矩阵⎥⎦⎤⎢⎣⎡=E A O E A 1 矩阵的分块可以有各种不同的分法.如矩阵A 也可分块如下:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=1011012100100001A 通过分块矩阵的定义和概念，我们将探讨分块矩阵的计算，并利用分块矩阵的思想把分块矩阵的应用联系到其它问题中.二、主题部分（阐明有关主题的历史背景、现状和发展方向，以及对这些问题的评述）作为解决线性方程的工具，矩阵已有不短的历史.拉丁方阵和幻方在史前年代已有人研究.矩阵这一具体概念是由19世纪英国数学家凯利首先提出并形成矩阵代数这一系统理论的.但是追根溯源，矩阵最早出现在我国的＜九章算术＞中，在＜九章算术＞方程一章中，就提出了解线性方程各项的系数、常数按顺序排列成一个长方形的形状.随后移动处筹，就可以求出这个方程的解.在欧洲，运用这种方法来解线性方程组，比我国要晚2000多年.1693年，微积分的发现者之一戈特弗里德•威廉•莱布尼茨建立了行列式论(theory of determinants).1750年，加布里尔•克拉默其后又定下了克拉默法则.1800年，高斯和威廉•若尔当建立了高斯—若尔当消去法.1848年詹姆斯•约瑟夫•西尔维斯特首先创出matrix 一词.研究过矩阵论的著名数学家有凯莱、威廉•卢云•哈密顿、格拉斯曼、弗罗贝尼乌斯和冯•诺伊曼.分块矩阵的引进使得矩阵这一工具的使用更加便利，解决问题的作用更强有力，其应用也就更广泛.在矩阵的某些运算中，对于级数比较高的矩阵，常采用分块的方法将一个矩阵分割成若干个小矩阵，在运算过程中将小矩阵看成元素来处理，对问题的解决往往起到简化的作用.本文通过一些例子来说明分块矩阵的一些应用.预备知识[][]32-分块矩阵的运算: 矩阵的分块技巧性较强，要根据不通的问题进行不同的分块，常见的方法有四种：（1）列向量分法),,2,1(),,,,(21n i a a a a A i n ΛΛ==为A 的列向量.（2）行向量分发),,2,1(21n i A i n ΛM =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=ββββ为A 的行向量.（3）分成两块),,(21A A A =其中21,A A 分别为B 的若干行.（4）分成四块⎥⎦⎤⎢⎣⎡=4321C C C C A 对分块矩阵可以进行广义初等变换，广义初等变换分为三种：（1）交换分块阵的两行（或列）；（2）用一可逆矩阵乘以分块矩阵的某一行（或列）；（3）用某一矩阵乘以某一行（或列）加到另一行（或列）. 根据广义初等变换的类型对应三种广义初等阵（1）⎥⎦⎤⎢⎣⎡00nm E E ; （2）G D G E E D ,,00,00⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡均为可逆阵；（3）⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡E H E E ME,0. 分块矩阵的加法计算B A +时，若对AB 分块,则要求用子块表出的AB 应同型且对应位置的子块也应同型.如对矩阵A 分块为⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=E C O E A 1011012100100001则对B 也应予以同型的分块⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=E G O D B 1026013600020021从而按分块相加，有⎥⎦⎤⎢⎣⎡+=+O G C D E B A由于⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=+122202211001D E 因此⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=+0026003642123122B A 分块矩阵的乘法计算AB 时，若对B A ,分块，则要求用子块表出的A 的列数等于用子块表出的B 的行数且对应的子块ij A 与pq B 应满足.p j =如对矩阵A 分块如下：⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=E CO E A 1011012100100001可对B 分块如下：⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=E G O D B 1026013600020021则有⎥⎦⎤⎢⎣⎡--+=⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡-=E GC CGDE G O D E O C E AB 由于⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=+238125263642310221CG D 所以⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------=102601364223831125AB 分块矩阵在矩阵中是一块重要内容，它是解决许多实际问题的提供方法，下面介绍个分块矩阵在解决线性代数问题中的一些简单应用[][]153-1. 用分块矩阵解决行列式问题在线性代数中,分块矩阵是一个十分重要的概念,它可以使矩阵的表示简单明了,使矩阵的运算得以简化. 而且还可以利用分块矩阵解决某些行列式的计算问题. 而事实上,利用分块矩阵方法计算行列式,时常会使行列式的计算变得简单,并能收到意想不到的效果.这里给出利用分块矩阵计算行列式的几种方法.引理1：设x ，y 为任意矩阵，则⎥⎦⎤⎢⎣⎡p mI x I 0与⎥⎦⎤⎢⎣⎡p mI y I 0都可分解为第三类初等矩阵的乘积.（即对单位矩阵仅仅施行第三类初等变换就可使它的右上角或左下角变成给定的任何矩阵）.证明：任取)(max ij y y =，把单位矩阵⎥⎦⎤⎢⎣⎡=p mI I I 00的第一列的11y 倍，第2列的21y 倍，……第m 列的1m y 倍，都加到第1+m 列上去；这时，I 的右上角第一列变化成y 的第一列.这相当于对单位矩阵作了m 次第三类列的初等变换.类似地，m 次列的第三类初等列变换，可使I 的右上角第二列化为y 的第二列，……因此⎥⎥⎦⎤⎢⎢⎣⎡=p mm I y I Q Q IQ 021Λ. 定理1（拉普拉斯定理）：设在行列式D 中任意取定了()11-≤≤n k k 行，由这k 行元素所组成的一切k 级子式与它们的代数余子式的乘积之和等于行列式D .定理2 设B A ,都是n 阶矩阵，则B A AB =证：由于⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-000n n nn I AB AI B I B I A，由引理⎥⎦⎤⎢⎣⎡n nI B I 0可分解为第三类初等矩阵的乘积.因此，用它右乘一个矩阵M ，相当于对M 进行一系列的第三类初等列变换.从而不改变M 的值.所以0nnI AB A BI A -=-两边均对后n 列用拉普拉斯定理，得左边==B A 右边AB I AB n nn n =--=++++++)()1(2)1()21(ΛΛ.例1 求证：()n n nnβαβαβααααβββ+++-=ΛΛΛΛΛΛΛΛΛΛ22112121010010001证明：由于⎥⎦⎤⎢⎣⎡-+=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡B A B BA I I I AB B A I I I 000由引理和拉普拉斯定理，两边取得列式，得B A B A A B B A -+=⎥⎦⎤⎢⎣⎡. 例2 计算下面2n 阶行列式()02≠=a bcb c d a da H n ON N O解令.,,,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=d dD c c C b bB a aA O O O O 为n 阶方阵.由于0≠a ，故A 为可逆方阵.又易知⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡---=-----d ca b dca b d ca b D CA B 1111O从而得出()().112nnn n cd ab d ca b a D CA B A B C D A H -=-=-⋅=⎥⎦⎤⎢⎣⎡=--2. 利用矩阵分块的方法求逆矩阵求矩阵的逆矩阵可以用伴随矩阵或初等变换的方法来解决, 而此类方法对于级数较高的矩阵运算量较大, 对某些矩阵可以适当分块后再进行运算, 可起到事半功倍的作用.例3 设⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=6000004000001001095201473M ，求1-M .解：令⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--=600040001,000000,109014,3275D C B A 则很容易求得，,61000410001,327511⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡--=--D A且.21211967454361000410001109014327511⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-⋅⎥⎦⎤⎢⎣⎡--⋅⎥⎦⎤⎢⎣⎡---=---BD A .610000041000001002121193267454375011111⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-------=⎥⎦⎤⎢⎣⎡-=∴-----D BD A A M例4：求矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0043000020000045300021000M 的逆矩阵.解：设.000000,430020004,5321,000000⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=D C B A则,4183002100041,13251⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡--=-C B 由定理可得，.001300025418300002100000410000111⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---=⎥⎦⎤⎢⎣⎡=---BC M 3. 用分块矩阵求解非齐次线性方程组在线性代数中，我们知道：如果A 是一个n 阶非奇异阵(),,,3,2,1,,n j i a A ij Λ==将A进行分块,22211211⎥⎦⎤⎢⎣⎡=A A A A A 其中22211211,,,A A A A 分别是k m m k k k ⨯⨯⨯,,和m m ⨯矩阵.若22A 是非奇异方阵，那么一定可以找到一个上三角分块矩阵,012212⎥⎦⎤⎢⎣⎡-=-m kI A A IM 使得,02221⎥⎦⎤⎢⎣⎡=A AG MA 其中,211221211A A A A G --=且G 是非奇异阵.对于该结论，如果用来求解n 个方程的非齐次线性方程组是比较方便的.可按如下过程求解：设非齐次线性方程组为：⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++nn nn n n n n n n b x a x a x a b x a x a x a b x a x a x a ΛΛΛΛΛΛ22112222212111212111 （1）将（1）式写成矩阵方程为B AX = （2）这里A 为系数矩阵.,2121⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n n b b b B x x x X M M 若A 是非奇异阵，即,0≠A 则方程组（1）有唯一确定的解. 将阶阵A 分块：,22211211⎥⎦⎤⎢⎣⎡=A A A A A 并注意22A 是非奇异阶阵，同时将X 及B 进行相应的分块.可令：⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=2121,B B B X X X ,1B 的行数等于1211,A A 的行数，2B 的行数等于1211,A A 的行数.则矩形方程（2）可写成⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡212122211211B B X X A A A A （3）将（3）式两端分别左乘上三角分块矩阵,012212⎥⎦⎤⎢⎣⎡-=-m kI A A IM 有⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-21221212122210B A A B X X A A G（4）其中211221211A A A A G --= ()0≠G .方程（4）分解成以下两个矩阵方程⎩⎨⎧=+-=-22221211221211B X A X A A A B GX （5）因()0≠G ，故(),212212111B A A B G X ---=再将1X 代入2222121B X A X A =+中，得.1212222X A B X A -= ().12121222X A B A X -=-由此，得.21⎥⎦⎤⎢⎣⎡=X X X例5 已知,82593122⎥⎦⎤⎢⎣⎡--=A 求一个24⨯的矩阵B ，使得0=AB ，并且秩()2=B 解：我们把矩阵B 按列分块()21,B B B ，由0=AB 即是()0,21=B B A 所以B 的每一列即是0=AX 的解，又因为秩()2=B ，所以21,B B 线性无关由⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→⎥⎥⎦⎤⎢⎢⎣⎡--→⎥⎦⎤⎢⎣⎡--81185102321112112540232111825923211182593122⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→8118510818101 所以⎪⎩⎪⎨⎧+=-=432431811858181x x x x x x （43,x x 为自由未知量）现分别令1,043==x x 及0,143==x x 得⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=018581,108118121X X 事实上21,X X 就是0=AX 方程组的基础解系，显然21,X X 线性无关.故我们方可令2211,X B X B ==,所以()⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--==0110858118181,21B B B例6 求解方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-+---=-+++=-+-+=+-+--=-+-+332224343238243214225432154321543215432154321x x x x x x x x x x x x x x x x x x x x x x x x x解将方程写成矩阵方程，并进行分块，有.212122211211⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡B B X X A A A A 这里.321224121,113413,243142,122122211211⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡-=A A A A 先求出22A 的逆矩阵.21021101101211035121122⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=-A 计算.10351252102512212⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=--A A 将方程（2）两段左乘以矩阵,03122122⎥⎦⎤⎢⎣⎡-=-I A A IM 得到：.32358410321112243412113000565420001654321⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-------x x x x x 解矩阵方程 .21245144113413323,144584105654216,584105654216121212121⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=-⎥⎦⎤⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡-⎥⎥⎦⎤⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡---X A B x x x x 所以().137421245210211011012110351211212122543⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-X A B A x x x 所求方程组的解为.13,7,4,14,454321==-=-==x x x x x4. 用分块矩阵证明秩的问题例7 设A,B 分别是p n n m ⨯⨯,的矩阵，则()()(){}B r A r AB r m in ≤矩阵乘积的秩不超过各因子矩阵的秩.证明：先证()()B r B A r ≤⋅.⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=mn ma in i n a L a L L La L a L L L a L a A 1111 ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=m i B M B M B B 1 ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=m i C M C M C AB 1 其中n B B ,,1Λ分别表示B 的1，2，…，n 行，n C C ,,1Λ分别表示AB 的1，2，…，m 行，由分块矩阵乘法性质得()m L i B a C nj iij i ,,11==∑=，即AB 的行向量组可由B 的行向量组线性表示，在高等代数中我们知道如果向量组r i a a ,,Λ可以经向量组i i b b ,,Λ线性表出，则()()i r b L b r a L a r ,,,,11≤，所以()()B r AB r ≤.再证()()A r AB r ≤设(),,,,,1111121⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==np nj n p j n n L b L b L L L L Lb L b L b B A A A A Λ ()p j D D D AB ΛΛ1=则由分块矩阵乘法规则可得()∑===ni i j p L j A b D 1,,2,1即AB的行向量组可由A 的列向量线性表出，所以()()A r AB r ≤由此得()()(){}.,m in B r A r B A r ≤⋅三、总结部分（将全文主题进行扼要总结，提出自己的见解并对进一步的发展方向做出预测）本论文论述了分块矩阵的概念，分析了分块矩阵的性质，讨论了分块矩阵的应用问题.最后对分块矩阵的重点、难点进行归纳，给出恰当的例子.本论文重点是研究分块矩阵的应用问题.查阅各种相关文献，对各文献进行归纳总结，提取各文献中关于定积分的相关内容，系统的进行总结.其中的难点在于如何利用分块矩阵解决相关问题.相信我经过跟多的研究分块矩阵会有更多的应用.四、参考文献（根据文中参阅和引用的先后次序按序编排）[1]张政修，曹承宾，王尚文．经济数学基础—线性代数[M]．北京：高等教育出版社，2003．[2]王秀芳．分块矩阵的应用讨论[J]．连云港师范高等专科学校学报，2008，9：97-99．[3]张敏．分块矩阵的应用[J]．吉林师范大学学报，2003，2：118-120．[4]严坤妹．分块矩阵的应用[J]．福建广播电视大学学报,2006：71-73．[5]王莲花，李念伟，梁志新．分块矩阵在行列式计算中的应用[J]．河南教育学院学报,2005，3：12-15．[6]刘红旭．利用分块矩阵求解非齐次线性方程组[J]．辽宁师专学报,2003，6：21-22．[7]周兴建．分块矩阵及其应用[J]．科技资讯,2007：126-127．[8]孔庆兰．分块矩阵的应用[J]．枣庄学院学报,2006，10：24 -26．[9]同济大学数学系．线性代数[M]．北京：高等教育出版社,2007．[10]孙要伟，郑远平[J]．牡丹江大学学报．2008，8：104 -107．[11]陈志杰．高等代数与解析几何[M]．北京：高等教育出版社,2000．[12]王萼芳．高等代数教程[M]．北京：北京大学出版社,2001．[13]丘维声．高等代数[M] ．北京：高等教育出版社，2000．[14]David C．Lay．Linear Algebra and Its Applications Third Edition [M]．BEIJING :Publishing House ofElectronics Industry ,2004．[15]彭国华，李德琅．Linear Algebra [M]．北京：高等教育出版社，2006，5．。

分块矩阵初等变换的妙用

分块矩阵初等变换的妙用分块矩阵是线性代数中的一个重要概念，它通过将矩阵分割成若干个小块，便于进行复杂的矩阵计算。

而分块矩阵初等变换则是利用分块矩阵的特性，来简化矩阵计算的一种方法。

在实际问题中，分块矩阵初等变换有着广泛的应用，本文将通过一些具体的例子，来展示分块矩阵初等变换的妙用之处。

我们需要了解分块矩阵的基本概念。

分块矩阵是将一个大矩阵分割成若干个小矩阵的形式，每个小矩阵称为一个块。

分块矩阵的表示形式通常是：\[ A = \begin{pmatrix}A_{11} & A_{12} \\A_{21} & A_{22}\end{pmatrix} \]A_{11}、A_{12}、A_{21}、A_{22}分别为小矩阵，可以是1x1的标量，也可以是任意大小的矩阵。

在进行分块矩阵初等变换时，我们可以分别对每个小块进行变换，然后根据变换的性质来对整个分块矩阵进行变换。

通过分块矩阵初等变换，我们可以简化复杂的矩阵计算，并且可以在一定程度上提高计算的效率。

下面，我们将通过一些具体的例子，来展示分块矩阵初等变换的妙用。

我们来看一个简单的例子：现在，我们需要计算矩阵 C = AB。

如果我们直接进行矩阵乘法，那么计算过程将会非常复杂。

如果我们利用分块矩阵初等变换，情况就会有所不同。

我们可以对矩阵 A 和 B 进行分块：\[ A = \begin{pmatrix}A_{11} & A_{12} \\A_{21} & A_{22}\end{pmatrix} = \begin{pmatrix}I & O \\A_{21} & A_{22}\end{pmatrix} \]\[ B = \begin{pmatrix}B_{11} & B_{12} \\B_{21} & B_{22}\end{pmatrix} = \begin{pmatrix}B_{11} & O \\B_{21} & I\end{pmatrix} \]I 为单位矩阵，O 为零矩阵。

分块矩阵的初等变换及其应用

分块矩阵的初等变换及其应用
李晓红;卜啸天
【期刊名称】《高等继续教育学报》
【年(卷),期】2007(021)004
【摘要】本文介绍了分块矩阵的初等变换概念,并通过它在求行列式、逆矩阵及矩阵的秩中的具体应用,说明了分块矩阵的初等变换能简洁、快速地解决一些矩阵问题,而且该方法容易理解和掌握.
【总页数】3页(P19-21)
【作者】李晓红;卜啸天
【作者单位】西安工业大学,数理系,西安,710032;西安昆仑工业集团有限责任公司,西安,710043
【正文语种】中文
【中图分类】O151.2
【相关文献】
1.分块矩阵的初等变换在行列式中的应用
2.分块矩阵的初等变换在分块矩阵中的应用
3.分块初等变换在矩阵的秩中的应用
4.分块矩阵广义初等变换的应用
5.分块矩阵的初等变换在求逆矩阵及行列式的值中的应用
因版权原因，仅展示原文概要，查看原文内容请购买。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

设计（20 届）分块矩阵的初等变换及其应用所在学院专业班级信息与计算科学学生姓名学号指导教师职称完成日期年月摘要：本文介绍了矩阵，分块矩阵的一些基本概念，同时也介绍了分块矩阵的初等变换，分块矩阵的初等变换在一些问题中的相关应用，如利用分块矩阵的初等变换计算矩阵的行列式，求矩阵的逆，在秩问题中的应用，在相似问题中的应用以及在其他方面的应用，用22分块矩阵的初等变换证明实对称矩阵的正定性。

并根据各种的应用给出了大量的例题，充分体现了分块矩阵的初等变换在代数学中所具有一定的优越性。

关键词：分块矩阵；初等变换；行列式；矩阵的逆；应用Elementary block matrix transform and its applicationAbstract：This article introduces some basic concepts of the matrix and partitioned matrix，also introduces the elementary transformation of partitioned matrix and the related application in some problems. For example, using the elementary transformation of partitioned matrix to compute matrix's determinant or get the inverse of a matrix. Also it introduces the application of partitioned matrix in some rank problems, similar problems and other problems, using the 22elementary transformation of partitioned matrix to prove the definiteness of symmetric matrix. According to different kinds of application, it lists a lot of examples, which fully indicate the superiority of partitioned matrix's elementary transformation in algebra.Key words：partitioned matrices; elementary transformation; determinant; the inverse of a matrix; Application目录1 绪论 (1)1.1问题的背景 (1)1.2问题的意义 (1)2 矩阵的介绍 (2)2.1矩阵的概念 (2)2.2矩阵的运算 (4)2.3矩阵的行列式与秩 (6)2.4矩阵的逆 (8)2.5初等矩阵 (8)3 分块矩阵的介绍 (10)3.1分块矩阵的定义 (10)3.2分块矩阵的分类 (10)3.3分块矩阵的运算 (11)3.4分块矩阵的初等变换和分块初等阵 (12)3.5分块方阵的行列式 (15)4 分块矩阵初等变换的相关应用 (18)4.1利用分块矩阵的初等变换计算行列式 (18)4.2利用分块矩阵的初等变换求矩阵的逆 (20)4.3分块矩阵的初等变换在秩问题中的应用 (23)分块矩阵的初等变换证明实对称矩阵的正定性 (25)4.4用224.5分块矩阵的初等变换在相似问题中的应用 (26)结论 (27)致谢 (28)参考文献 (29)1 绪论1.1 问题的背景在数学上，矩阵是指纵横排列的二维数据表格，最早来自于方程组的系数及常数所构成的方阵。

这一概念由19世纪英国数学家凯利首先提出。

矩阵概念在生产实践中也有许多应用，比如矩阵图法以及保护个人帐号的矩阵卡系统（有深圳网域提出）等等。

“矩阵”的本意也常被应用，比如监控系统中负责对前端视频源与控制线切换控制的模拟设备也叫矩阵。

矩阵理论是经典数学的基础，也是实用性最强的数学分支之一，是处理大量有限维空间形式与数学关系的强有力的工具。

矩阵理论在系统科学、优化方法、控制论、图论、稳定性理论等众多领域中都有广泛的应用。

计算机的普及进一步促进了矩阵理论的发展。

在数学的矩阵理论中，一个分块矩阵或是分段矩阵就是将矩阵分割出较小的矩形矩阵，这些较小的矩阵就称为区块。

换个方式来说，就是以较小的矩阵组合成一个矩阵。

分块矩阵的分割原则是以水平线和垂直线进行划分。

分块矩阵中，位在同一行（列）的每一个子矩阵，都拥有相同的列数（行数）。

将大的矩阵通过分块的方式划分，并将每个分块看做另一个矩阵的元素，这样之后再参与运算，通常可以让计算变得清晰甚至得以大幅简化。

例如，有的大矩阵可以通过分块变为对角矩阵或者是三角矩阵等特殊形式的矩阵。

1.2 问题的意义矩阵的分块是处理较高阶矩阵时常用的方法，用一些贯穿于矩阵的纵线和横线将矩阵分成若干子块，使得阶数较高的矩阵化为阶数较低的分块矩阵。

在运算中，我们有时把这些子块当作元素一样来处理，从而简化了表示，便于计算。

分块矩阵初等变换是线性代数中重要而基本的运算，它在研究矩阵行列式、特征值、秩等各种性质及求矩阵的逆、解线性代数方程中有着广泛的应用。

因此，如何直接对分块矩阵实行初等变换显得非常重要，本文的目的就是讨论分块矩阵的初等变换及其应用。

2 矩阵的介绍2.1 矩阵的概念线性方程组的一些重要性质反映在它的系数矩阵和增广矩阵的性质上，并且解方程组的过程也表现为变换这些矩阵的过程。

除线性方程组之外，还有大量的各种各样的问题也都提出矩阵的概念，并且这些问题的研究常常反映为有关矩阵的某些方面的研究，甚至于有些性质完全不同的、表面上完全没有联系的问题，归结成矩阵问题以后却是相同的。

这就使矩阵成为数学中一个极其重要的应用广泛的概念，因而也就使矩阵成为代数特别是线性代数的一个主要研究对象。

矩阵是指纵横排列的二维数据表格。

由mn 个复数ij a （其中1,2,,;1,2,,i m j n ==）构成的长方形阵111212122212n n m m mn A A A A A A A A A A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦，称为一个m 行n 列的矩阵，或m n ⨯矩阵，它共有m 个行和n 个列。

1.在解析几何中考虑坐标变换时，如果只考虑坐标系的转轴（反时针方向转轴），那么平面直角坐标变换的公式为''''cos sin ,(1)sin cos ,x x y y x y θθθθ⎧=-⎪⎨=+⎪⎩其中θ为x 轴与'x 轴的夹角。

显然，新旧坐标之间的关系，完全可以通过公式中系数所排成的22*矩阵cos sin ,(2)sin cos θθθθ-⎛⎫⎪⎝⎭表示出来。

通常，矩阵（2）称为坐标变换（1）的矩阵。

在空间的情形，保持原点不动的仿射坐标系的变换有公式'''111213'''212223'''313233,,(3).x a x a y a z y a x a y a z z a x a y a z ⎧=++⎪=++⎨⎪=++⎩同样，矩阵111213212223313233,(4)a a a a a a a a a ⎛⎫⎪ ⎪ ⎪⎝⎭就称为坐标变换（3）的矩阵。

2.在讨论国民经济的数学问题中也常常用到矩阵。

例如，假设在某一地区，某一种物资，比如说煤，有s 个产地12,,,s A A A 和n 个销地12,,,n B B B ，那么一个调运方案就可用一个矩阵来表示，其中ij a 表示有产地i A 运到销地j B 的数量。

3.二次曲线的一般方程为222220(5)ax bxy cy dx ey f +++++=（5）的左端可以用表来表示，其中每一个数就是它所在的行和列所对应的,x y 或1的乘积的系数，而（5）的左端就是按这样的约定所形成的项的和。

换句话说，只要规定了,,1x y 的次序，二次方程（5）的左端就可以简单地用矩阵a b d b c e d e f ⎛⎫⎪⎪ ⎪⎝⎭，（6）来表示。

通常，（6）称为二次曲线（5）的矩阵，以后我们会看到，这种表示法不只是形式的。

事实上，矩阵（6）的行列式就是解析几何中二次曲线的不变量3I ，这表明了矩阵（6）的性质确实反映了它所表示的二次曲线的性质。

4. n 维向量也可以看成矩阵的特殊情形。

n 维行向量就是1n ⨯矩阵，n 维列向量就是1n ⨯矩阵。

用大写的拉丁字母,,,A B 或者(),(),ij ij a b 来代表矩阵。

有时候，为了指明所讨论的矩阵的级数，可以把s n ⨯矩阵写成,,,sn sn A B 或者(),(),ij sn ij sn ab设(),(),ij mn ij lk A a B b ==如果,,ij ij m l n k a b ===且，对1,2,,;1,2,i m j n ==都成立，我们就说A B =.即只有完全一样的矩阵才叫做相等。

5.对方阵而言：两个下标相等的元素称为主对角线上的元素，简称为对角元素：除对角元素外其余元素均为0的方阵称为对角矩阵；主对角线以下均为0的矩阵称为上三角矩阵; 主对角线以上均为0的矩阵称为下三角矩阵;关于主对角线对称，即满足条件ij ji a a =的矩阵，称为对称矩阵；满足条件ij ji a a =-的矩阵，称为反对称矩阵，此时显然有112332,1243A D --⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，即主对角线为0。

复数域C 上m n ⨯矩阵全体常常记为m nC⨯，一般地，数域F 上m n ⨯矩阵全体记为m n F ⨯。

2.2 矩阵的运算矩阵的运算，它们可以认为是矩阵之间一些最基本的关系。

包括矩阵的加法、乘法、矩阵与数的乘法以及矩阵的转置。

为了确定起见，取定一个数域p ，以下所讨论的矩阵全是由数域p 中的数组成的。

1.加法定义2.1 设111212122212111212122212(),()n n ij sn s s sn n n ij sn s s sn a a a a a a A a a a a b b b b b b B b b b b ⎛⎫⎪ ⎪== ⎪⎪⎝⎭⎛⎫⎪ ⎪== ⎪⎪⎝⎭。

是两个s n ⨯矩阵，则矩阵111112121121212222221122()(),ij sn ij ij snn n n n s s s s sn sn C c a b a b a b a b a b a b a b a b a b a b ==++++⎛⎫⎪+++ ⎪= ⎪⎪+++⎝⎭称为A 和B 的和，记为C A B =+。