垂心、重心、内心、外心、旁心的定义和性质
三角形的重心、外心、垂心、内心和旁心(五心定理)

三角形五心定理(三角形的重心,外心,垂心,内心和旁心称之为三角形的五心)三角形五心定理是指三角形重心定理,外心定理,垂心定理,内心定理,旁心定理的总称。
一、三角形重心定理三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名)重心的性质:1、重心到顶点的距离与重心到对边中点的距离之比为2∶1。
2、重心和三角形3个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3。
二、三角形外心定理三角形外接圆的圆心,叫做三角形的外心。
外心的性质:1、三角形的三条边的垂直平分线交于一点,该点即为该三角形外心。
2、若O是△ABC的外心,则∠BOC=2∠A(∠A为锐角或直角)或∠BOC=360°-2∠A(∠A为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、计算外心的坐标应先计算下列临时变量:d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。
c1=d2d3,c2=d1d3,c3=d1d2;c=c1+c2+c3。
重心坐标:( (c2+c3)/2c,(c1+c3)/2c,(c1+c2)/2c )。
5、外心到三顶点的距离相等三、三角形垂心定理三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的性质:1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
2、三角形外心O、重心G和垂心H三点共线,且OG∶GH=1∶2。
(此直线称为三角形的欧拉线(Euler line))3、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的2倍。
内心、外心、重心、垂心定义及性质总结

内心、外心、重心、垂心定义及性质总结
1.内心:
(1)三条角平分线的交点,也是三角形内切圆的圆心。
(2)性质:到三边距离相等。
2外心:
(1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3重心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
4垂心:三条高所在直线的交点。
5重心:三条中线定相交,交点位置真奇巧,
交点命名为“重心”,重心性质要明了,
重心分割中线段,数段之比听分晓;
长短之比二比一,灵活运用掌握好.
6垂心:三角形上作三高,三高必于垂心交.
高线分割三角形,出现直角三对整,
直角三角形有十二,构成六对相似形,
四点共圆图中有,细心分析可找清.
7内心:三角对应三顶点,角角都有平分线,
三线相交定共点,叫做“内心”有根源;
8外心点至三边均等距,可作三角形内切圆,此圆圆心称“内心”如此定义理当然.
三角形有六元素,三个内角有三边.
作三边的中垂线,三线相交共一点.
此点定义为“外心”,用它可作外接圆.
“内心”“外心”莫记混,“内切”“外接”是关键.:。
内心、外心、重心、垂心定义及性质总结74139

内心、外心、重心、垂心定义及性质总结
74139
------------------------------------------作者xxxx
------------------------------------------日期xxxx
内心、外心、重心、垂心定义及性质总结
1.内心:
(1)三条角平分线的交点,也是三角形内切圆的圆心。
(2)性质:到三边距离相等。
2外心:
(1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3 重心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
4 垂心:三条高所在直线的交点。
5 重心 : 三条中线定相交,交点位置真奇巧,
交点命名为“重心”,重心性质要明了,
重心分割中线段,数段之比听分晓;
长短之比二比一,灵活运用掌握好.
6 垂心 : 三角形上作三高,三高必于垂心交.
高线分割三角形,出现直角三对整,
直角三角形有十二,构成六对相似形,
四点共圆图中有,细心分析可找清.
7内心 : 三角对应三顶点,角角都有平分线,
三线相交定共点,叫做“内心”有根源;
点至三边均等距,可作三角形内切圆,
此圆圆心称“内心”如此定义理当然.
8外心 : 三角形有六元素,三个内角有三边.
作三边的中垂线,三线相交共一点.
此点定义为“外心”,用它可作外接圆.
“内心”“外心”莫记混,“内切”“外接”是关键.。
三角形的内心,外心,重心,垂心,旁心及性质分别是指什么?
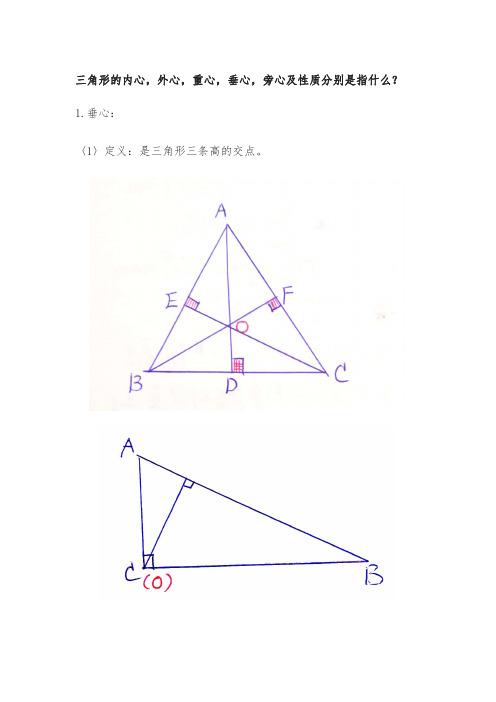
三角形的内心,外心,重心,垂心,旁心及性质分别是指什么?1.垂心:〈1〉定义:是三角形三条高的交点。
〈2〉性质:[性质1]锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外。
[性质2]三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心。
[性质3]垂心O关于三边的对称点,均在△ABC的外接圆圆上。
[性质4]△ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形,。
[性质5]O、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为--垂心组)。
[性质6]△ABC,△ABO,△BCO,△ACO的外接圆是等圆。
[性质7]三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍。
[性质8]设O、H分别为△ABC的外心和垂心,则∠BAO=∠HAC,∠ABH=∠OBC,∠BCO=∠HCA.[性质9]锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍,即AH+BH+CH=2(r+R)。
[性质10]锐角三角形的垂心是垂足三角形的内心;锐角三角形的内接三角形(顶点在原三角形的边上)中,以垂足三角形的周长最短。
[性质11]设H为非直角三角形的垂心,且D、E、F分别为H在BC,CA,AB.上的射影,H1,H2,H3分别为△AEF,△BDF,△CDE的垂心,则△DEF≌△H1H2H3.[性质12]三角形垂心H的垂足三角形的三边,分别平行于原三角形外接圆在各顶点的切线。
2.内心〈1〉定义:是三角形三条内角平分线的交点即内接圆的圆心。
交于点O,点O即为△ABC的内心。
〈2〉性质:[性质1]三角形的内心到三边的距离相等,都等于内切圆半径r. [性质2]∠BOC=90°+∠BAC/2。
[性质3]在Rt△ABC中,∠A=90°,三角形内切圆切BC于D,则S△ABC=BDxCD3.重心:〈1〉重心的定义:重心是三角形三条中线的交点。
三角形的重心、外心、垂心、内心和旁心(五心定理)[参照]
![三角形的重心、外心、垂心、内心和旁心(五心定理)[参照]](https://img.taocdn.com/s3/m/bff5d6ed6037ee06eff9aef8941ea76e59fa4a74.png)
三角形的重心、外心、垂心、内心和旁心(五心定理)[参照]
三角形的重心:是指三角形内任意一点,它到三条边上三个顶点连线的质心,即三角形的外心和所有顶点的重心。
外心:指三角形的外接圆心,也就是三条边的质心,即三角形的重心。
垂心:指三角形的垂心,也就是三角形所有内角的质心,即三角形的重心。
内心:指三角形内角平分线的交点,也就是三角形各内角的质心,即三角形的重心。
旁心:指三角形的垂直平分线的交点,也就是三角形各边的质心,即三角形的重心。
三角形的重心、外心、垂心、内心和旁心(五心定理)

三角形五心定理(三角形的重心,外心,垂心,内心和旁心称之为三角形的五心)三角形五心定理是指三角形重心定理,外心定理,垂心定理,内心定理,旁心定理的总称。
之二胡藕藤创作一、三角形重心定理三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名)重心的性质:1、重心到顶点的距离与重心到对边中点的距离之比为2∶1。
2、重心和三角形3个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3。
二、三角形外心定理三角形外接圆的圆心,叫做三角形的外心。
外心的性质:1、三角形的三条边的垂直平分线交于一点,该点即为该三角形外心。
2、若O是△ABC的外心,则∠BOC=2∠A(∠A为锐角或直角)或∠BOC=360°-2∠A(∠A为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、计算外心的坐标应先计算下列临时变量:d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。
c1=d2d3,c2=d1d3,c3=d1d2;c=c1+c2+c3。
重心坐标:( (c2+c3)/2c,(c1+c3)/2c,(c1+c2)/2c )。
5、外心到三顶点的距离相等三、三角形垂心定理三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的性质:1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
2、三角形外心O、重心G和垂心H三点共线,且OG∶GH=1∶2。
(此直线称为三角形的欧拉线(Euler line))3、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的2倍。
三角形重心、外心、垂心、内心的向量表示及其性质

向量的重心、垂心、内心、外心、旁心三角形重心、内心、垂心、外心的概念及简单的三角形形状判断方法。
重心:ABC 中、每条边上所对应的中线的交点;垂心:ABC 中、每条边上所对应的垂线上的交点;内心:ABC 中、每个角的角平分线的交点(内切圆的圆心);外心:ABC 中、每条边上所对应的中垂线的交点(外接圆的圆心)。
一、重心1、 O 是 ABC 的重心OA OB OC 0若 O 是 ABC 的重心,则BOC AOC AOB 1 ABC 故 OA OB OC 0 ,1 (PA 3PG PB PC) G 为 ABC 的重心 .3、 P 是△ ABC所在平面内任一点. G是△ ABC的重心 1 (PA) .2 PG PB PC3证明:PG PA AG PB BG PC CG 3PG ( AG BG CG) (PA PB PC) ∵ G是△ ABC的重心∴ GA GB GC 0 AG BG CG 0,即 3PG PA PB PC由此可得 PG 1 (PA PB PC ) . (反之亦然(证略))33、已知 O 是平面上一定点, A, B, C 是平面上不共线的三个点,动点P 满足OP OA ( AB AC) ,(0,) ,则 P 的轨迹一定通过△ ABC 的重心 .例 1 若 O 为ABC 内一点, OA OB OC 0 ,则 O 是ABC 的()A.内心 B .外心 C .垂心 D .重心第 1 页共 10 页二、垂心1、 O 是 ABC 的垂心OA OB OB OC OA OC若 O 是 ABC ( 非直角三角形 ) 的垂心,则故 tan AOA tan BOB tanCOC 02、H是面内任一点,HA HB HB HC HC HA 点 H 是△ ABC的垂心 .由 HA HB HB HC HB ( HC HA) 0 HB AC 0 HB AC ,同理 HC AB , HA BC . 故 H 是 ABC 的垂心 . (反之亦然(证略))3、 P 是△ ABC 所在平面上一点,若 PA PB PB PC PC PA ,则 P 是△ ABC 的垂心.由 PA PB PB PC ,得 PB (PA PC ) 0 ,即 PB CA 0 ,所以 PB⊥ CA .同理可证 PC ⊥ AB , PA ⊥ BC .∴ P 是△ ABC 的垂心.如图 1.A CCB PEMHPA FB图 1 O 图⑷4、已知 O 是平面上一定点,A, B, C 是平面上不共线的三个点,动点P 满足AB AC,(0,) ,则动点 P 的轨迹一定通过OP OAAC cos CAB cos B△ ABC 的垂心.例 2 P 是△ ABC所在平面上一点,若PA PB PB PC PC PA ,则 P 是△ ABC 的()A.外心B.内心C.重心D.垂心第 2 页共 10 页三、内心1、 O 是ABC 的内心的充要条件是OA AB ACOBBA BC CA CBOCAB AC BA BC CA CB Ae1e2B引进单位向量,使条件变得更简洁。
初中几何三角形的垂心、外心、内心、中心、旁心。

初中几何三角形的垂心、外心、内心、中心、旁心。
初中几何三角形的垂心、外心、内心、中心、旁心几何学是数学中非常重要的一个分支,而三角形是几何学中最基本的一种形状。
在研究三角形的过程中,我们会遇到一些特殊的点,它们被称为垂心、外心、内心、中心和旁心。
本文将就这些特殊点进行详细的介绍。
一、垂心垂心是指一个三角形内部的一个点,该点到三角形的三条边上的顶点分别作垂线,而且垂线交于一个点。
这个点就是垂心。
我们用H表示垂心。
垂心有以下几个重要性质:1. 垂心到三角形的三个顶点分别连线,这三线交于三角形的垂心。
2. 垂心到三角形三边的垂线长度相等,且等于垂心到三条边的距离之和。
3. 垂心到三角形三个顶点的距离之和最小。
二、外心外心是指一个三角形外部的一个点,该点到三角形的三个顶点的距离相等。
我们用O表示外心。
外心有以下几个重要性质:1. 外心是三角形的外接圆的圆心,也就是可以通过三角形顶点作圆周定出外接圆。
2. 外心到三角形的三个顶点连线的垂线交于外心。
3. 外心到三角形三边的距离相等,且等于外心到三边的垂线长度之和。
三、内心内心是指一个三角形内部的一个点,该点与三角形的三条边的距离之和是最小的。
我们用I表示内心。
内心有以下几个重要性质:1. 内心是三角形的内切圆的圆心,也就是可以通过三角形边作切线定出内切圆。
2. 内心到三角形的三个顶点的连线上,各个连线在内心处垂直,即内心是三角形的垂心。
3. 内心到三角形三边的距离之和最小。
四、中心中心是指一个三角形内部的一个点,该点到三角形的三个顶点的距离相等,且到三角形三边的距离之和最小。
我们用C表示中心。
中心有以下几个重要性质:1. 中心是三角形的外心、垂心和重心的交点。
2. 中心到三角形的三个顶点连线的垂线交于中心。
3. 中心到三角形三边的距离相等,且等于中心到三边的垂线长度之和。
五、旁心旁心是指一个三角形外部的一个点,该点到三角形的某两条边的距离相等,到另外一条边的距离比较大。
内心、外心、重心、垂心定义及性质总结

此文档收集于网络,如有侵权请联系网站删除
内心、外心、重心、垂心定义及性质总结
1. 内
心:(1)三条角平分线的交点,也是三角形内切圆的圆心。
(2)性质:到三边距离相等。
2 外
心:1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3 重
心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍
4 垂心:三条高所在直线的交点
5 重心: 三条中线定相交,交点位置真奇巧,交点命名为“重心”,重心性质要明了,重心分割中线段,数段之比听分晓;长短之比二比一,灵活运用掌握好.
6 垂心: 三角形上作三高,三高必于垂心交.高线分割三角形,出现直角三对整,直
角三角形有十二,构成六对相似形,四点共圆图中有,细心分析可找清.
7 内心: 三角对应三顶点,角角都有平分线,三线相交定共点,叫做“内心”有根
源;点至三边均等距,可作三角形内切圆,此圆圆心称“内心”如此定
义理当然.
8 外心: 三角形有六元素,三个内角有三边.作三边的中垂线,三线相交共一点.此点定义为“外心” ,用它可作外接圆.“内心”“外心”莫记混,“内切”“外接”是关键.。
三角形的重心、外心、垂心、内心和旁心(五心定理).doc

三角形五心定理(三角形的重心,外心,垂心,内心和旁心称Z为三角形的五心)三角形五心定理是指三角形重心定理,外心定理,垂心定理,内心定理, 旁心定理的总称。
、三角形重心定理三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点, 重心因而得名)重心的性质:1、重心到顶点的距离与重心到对边中点的距离Z比为2 : 1o2、重心和三角形3个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其重心坐标为((X1 +X2+X3)/3, (Y1 +Y2+Y3)/3o二、三角形外心定理三角形外接圆的圆心,叫做三角形的外心。
外心的性质:仁三角形的三条边的垂直平分线交于一点,该点即为该三角形外心。
2、若0是ZXABC的外心,则ZB0C=2ZA ( ZA为锐角或宜角)或Z BOC=360°-2ZA (ZA 为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时, 外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、计算外心的坐标应先计算下列临时变量:d1, d2, d3分别是三角形三个顶点连向另外两个顶点向量的点乘od=d2d3, c2=d1d3, c3=d1d2; c=c1+c2+c3o 重心坐标:((c2+c3)/2c, (c1+c3)/2c, (c1+c2)/2c )o5、外心到三顶点的距离相等三、三角形垂心定理三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的性质:1>三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
2、三角形外心O、重心G和垂心H三点共线,且0G : GH=1 : 2。
垂心、重心、内心、外心、旁心的定义和性质

垂心、重心、内心、外心、旁心的定义和性质1.定义垂心:三角形三条高的交点重心:三角形三条中线的交点内心:三角形三条内角平分线的交点即内接圆的圆心外心:三角形三条边的垂直平分线的交点即外接圆的圆心旁心:三角形两条外角平分线和一条内角平分线的交点注意:正三角形中重心、垂心、外心、内心重合,这个点叫中心。
2.性质垂心:1、锐角三角形垂心在三角形内部,直角三角形垂心在三角形直角顶点,钝角三角形垂心在三角形外部。
2、垂心H关于三边的对称点,均在△ABC的外接圆上。
3、锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。
4、从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
(西姆松线)重心:1、重心到顶点的距离与重心到对边中点的距离之比为2:1。
2、重心和三角形3个顶点组成的3个三角形面积相等。
3、重心和三角形3个顶点的连线的任意一条连线将三角形面积平分。
4、重心到三角形3个顶点距离的平方和最小。
5、重心是三角形内到三边距离之积最大的点。
6、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3);空间直角坐标系——横坐标:(X1+X2+X3)/3 纵坐标:(Y1+Y2+Y3)/3竖坐标:(Z1+Z2+Z3)/3内心:1、到三边的距离相等,都等于内切圆半径r。
2、内心都在三角形的内部。
3、设三角形的三个顶点坐标分别为A(x_1,y_1),B(x_2,y_2),C(x_3,y_3),其对边长分别为a,b,c,则内心坐标I((ax_1+bx_2+cx_3)/(a+b+c),(ay_1+by_2+cy_3)/(a+b+c))外心:1、到三角形三顶点的距离相等,都等于外接圆半径R。
2、直角三角形外心在斜边的中点,锐角三角形外心在内部,钝角三角形外心在外部。
旁心:1、旁心到三边的距离相等。
2、三角形有三个旁切圆,三个旁心。
三角形的五“心”及其性质

三角形的五“心”及其性质
三角形的五心是指三角形内部的五个特殊点,包括重心、外心、内心、垂心和旁心。
1. 重心:三角形三个顶点与其对边的中点连接所交于一点,这个点被
称为重心。
重心到三角形三边的距离相等,重心将三角形划分为三个
面积相等的小三角形。
2. 外心:三角形三个顶点的垂直平分线相交于一点,这个点被称为外心。
外心是三角形外接圆圆心,即三角形三个顶点与外心的连线的长
度相等。
3. 内心:三角形三个顶点的角平分线相交于一点,这个点被称为内心。
内心是三角形内切圆圆心,即三角形三条边与内心的连线的垂直距离
相等。
4. 垂心:三角形三个顶点的高的延长线相交于一点,这个点被称为垂心。
垂心是三角形三条高的交点,即垂心到三角形三个顶点所在的直
线距离相等。
5. 旁心:三角形的旁心有三个,分别对应三条边。
旁心是指三角形的
外切圆圆心,即三角形的一条边外边的一条角的角平分线与另外两条
边延长线的交点。
这些五心有一些重要的性质:
- 重心是三角形的重要重心之一,它将三角形分成三个面积相等的小三
角形。
- 外心是三角形外接圆圆心,外接圆的直径是三角形的边长,外心到三
个顶点的距离相等。
- 内心是三角形内切圆圆心,内接圆与三个边相切,内心到三个边的距
离相等。
- 垂心是三角形三条高的交点,垂心到三个顶点所在的直线距离相等。
- 旁心是三角形外切圆圆心,外切圆与三条边相切,旁心到相对应的边
的距离相等。
内心、外心、重心、垂心定义及性质总结[借鉴]
![内心、外心、重心、垂心定义及性质总结[借鉴]](https://img.taocdn.com/s3/m/78232147eef9aef8941ea76e58fafab069dc4404.png)
内心、外心、重心、垂心定义及性质总结[借鉴]内心、外心、重心、垂心是几何学中与三角形相关的四个重要概念。
以下是它们的定义及性质总结:1.内心(Incenter)定义:内心是三角形内切圆的圆心。
性质:o内心到三角形三个顶点的距离相等。
o内心与三角形各边之间的距离等于三角形半周长与内切圆半径之差的一半。
o在内心分线上,任意两边的向量之积等于另外两边向量之积的负值。
2.外心(Excenter)定义:外心是三角形外接圆的圆心。
性质:o外心到三角形三个顶点的距离相等。
o外心与三角形各顶点连线所成的角等于三角形内角和的一半。
o在外心分线上,任意两边的向量之积等于另外两边向量之积的值。
3.重心(Centroid)定义:重心是三角形三条中线的交点。
性质:o重心到三角形三个顶点的距离与到三条中线的距离相等。
o重心与三角形各边之间的距离等于三角形半周长与外接圆半径之差的一半。
o在重心分线上,任意两边的向量之积等于另外两边向量之积的值。
4.垂心(Hypotenuse)定义:垂心是三角形各边上的高线的交点。
性质:o垂心到三角形三个顶点的距离与到三条高的距离相等。
o垂心与三角形各顶点连线所成的角等于三角形内角和的一半。
o在垂心分线上,任意两边的向量之积等于另外两边向量之积的负值。
总结:内心、外心、重心和垂心在几何学中具有特殊的性质和重要性。
这些概念之间的关系可以用于证明定理和解决问题。
对于内心和外心,它们分别与三角形的内切圆和外接圆相关,而重心和垂心则分别与三角形的中线和高的交点相关。
这些概念及其性质在几何学中具有广泛的应用,例如在解决几何问题、绘制图形和证明定理等方面都有重要的应用价值。
三角形重心,垂心,外心,内心性质(可编辑)

三角形重心,垂心,外心,内心性质重心:三角形顶点与对边中点的连线交于一点,称为三角形重心; 垂心:三角形各边上的高交于一点,称为三角形垂心; 外心:三角形各边上的垂直平分线交于一点,称为三角形外心; 内心:三角形三内角平分线交于一点,称为三角形内心; 中心:正三角形的重心、垂心、外心、内心重合,称为正三角形的中心。
旁心三角形的旁切圆(与三角形的一边和其他两边的延长线相切的圆)的圆心叫做旁心。
旁心是一个三角形内角平分线与其不相邻的两个外角平分线的交点,它到三角形三边的距离相等。
如图,点M就是△ABC的一个旁心。
三角形任意两角的外角平分线和第三个角的内角平分线的交点。
一个三角形有三个旁心,而且一定在三角形外。
若设O为△ABC的旁心,用向量表示则有aOA=bOB+cOC 1、三角形一内角平分线和另外两顶点处的外角平分线交于一点,该点即为三角形的旁心。
2、每个三角形都有三个旁心。
三角形“五心歌”三角形有五颗心;重、垂、内、外和旁心,五心性质很重要,认真掌握莫记混.重心三条中线定相交,交点位置真奇巧,交点命名为“重心”,重心性质要明了,重心分割中线段,数段之比听分晓;长短之比二比一,灵活运用掌握好.垂心三角形上作三高,三高必于垂心交.高线分割三角形,出现直角三对整,直角三角形有十二,构成六对相似形,四点共圆图中有,细心分析可找清. 内心三角对应三顶点,角角都有平分线,三线相交定共点,叫做“内心”有根源;点至三边均等距,可作三角形内切圆,此圆圆心称“内心”如此定义理当然.外心三角形有六元素,三个内角有三边.作三边的中垂线,三线相交共一点.此点定义为“外心”,用它可作外接圆.“内心”“外心”莫记混,“内切”“外接”是关键.重心的几条性质:1、重心到顶点的距离与重心到对边中点的距离之比为2:1。
2、重心和三角形3个顶点组成的3个三角形面积相等。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3);空间直角坐标系――横坐标:(X1+X2+X3)/3 纵坐标:(Y1+Y2+Y3)/3 竖坐标:(z1+z2+z3)/35、三角形内到三边距离之积最大的点。
三角形重心、外心、垂心、内心的向量表示及其性质【医学模板】

向量的重心、垂心、内心、外心、旁心三角形重心、内心、垂心、外心的概念及简单的三角形形状判断方法。
重心:ABC ∆中、每条边上所对应的中线的交点; 垂心:ABC ∆中、每条边上所对应的垂线上的交点;内心:ABC ∆中、每个角的角平分线的交点(内切圆的圆心); 外心:ABC ∆中、每条边上所对应的中垂线的交点(外接圆的圆心)。
一、重心1、O 是ABC ∆的重心⇔=++若O 是ABC ∆的重心,则ABC AOB AOC BOC ∆=∆=∆=∆31故=++,)(31PC PB PA PG ++=⇔G 为ABC ∆的重心.2、 P 是△ABC 所在平面内任一点.G 是△ABC 的重心⇔)(31++=.证明:CG PC BG PB AG PA PG +=+=+=⇒)()(3+++++= ∵G 是△ABC 的重心∴=++⇒=++,即++=3由此可得)(31PC PB PA PG ++=.(反之亦然(证略))3、已知O 是平面上一定点,A B C ,,是平面上不共线的三个点,动点P 满足()OP OA AB AC λ=++,(0)λ∈+∞,,则P 的轨迹一定通过ABC △的重心.例1 若O 为ABC ∆内一点,0OA OB OC ++= ,则O 是ABC ∆ 的( )A .内心B .外心C .垂心D .重心二、垂心1、O 是ABC ∆的垂心⇔OC OA OC OB OB OA ∙=∙=∙若O 是ABC ∆(非直角三角形)的垂心,则 故tan tan tan =++C B A2、H 是面内任一点,HA HC HC HB HB HA ⋅=⋅=⋅⇔点H 是△ABC 的垂心. 由⊥⇔=⋅⇔=-⋅⇔⋅=⋅00)(, 同理⊥,⊥.故H 是ABC ∆的垂心. (反之亦然(证略))3、P 是ABC △所在平面上一点,若PA PC PC PB PB PA ⋅=⋅=⋅,则P 是ABC △的垂心.由PA PB PB PC ⋅=⋅,得()0P B P A P C ⋅-=,即0P B C A ⋅=,所以PB CA ⊥.同理可证PC AB ⊥,PA BC ⊥. ∴P 是ABC △的垂心.如图1.4、已知O 是平面上一定点,AB C ,,是平面上不共线的三个点,动点P 满足cos cos AB AC OP OA AB B AC C λ⎛⎫ ⎪=++ ⎪⎝⎭,(0)λ∈+∞,,则动点P 的轨迹一定通过ABC △的垂心.例2 P 是△ABC 所在平面上一点,若⋅=⋅=⋅,则P 是△ABC 的()图1AA.外心B.内心C.重心D.垂心三、内心1、O是ABC∆的内心的充要条件是=⎫⎛∙=⎫⎛∙=⎫⎛∙引进单位向量,使条件变得更简洁。
三角形五心及其性质

引言概述:三角形是几何学中最基本、最重要的图形之一,三角形的性质和特点被广泛研究和应用。
其中,三角形的五心是三角形内外最重要的五个点:重心、外心、垂心、内心和旁心。
五心之间的关系和性质对于解决三角形相关问题和证明定理具有重要的作用。
本文将详细介绍三角形的五心及其性质。
正文内容:一、重心1. 三角形的重心是三边中线的交点,也是中位线和高线的交点。
2. 重心到顶点的距离是中点到顶点距离的2/3,是高线的距离的2/3。
3. 重心将三角形分割为六个三角形,其中三个三角形的面积相等。
二、外心1. 三角形的外心是三边垂直平分线的交点,也是三角形的三条角平分线的交点。
2. 外心到顶点的距离等于外心到对边的距离,也等于外心到三角形内切圆的半径。
三、垂心1. 垂心是三边垂直平分线的交点,也是三角形内心和外心连线的中点。
2. 垂心到顶点的距离等于垂心到底边垂足的距离。
四、内心1. 三角形的内心是三边的内切圆的圆心,也是三边角平分线的交点。
2. 内心到三边的距离相等,等于三角形的内切圆的半径。
3. 内心到三角形各顶点的连线所围成的三个小三角形的面积相等。
五、旁心1. 旁心是三边的旁切圆的圆心,也是外角平分线的交点。
2. 旁心到其所在边的距离相等,等于旁切圆的半径。
3. 旁心和顶点之间的连线与三角形所在边垂直。
总结:三角形的五心(重心、外心、垂心、内心和旁心)是三角形内外部最重要的五个点,它们分别有着独特的性质和作用。
通过研究五心之间的关系和性质,可以更深入地理解三角形的结构和性质。
五心的位置和特点对于解决三角形相关问题和证明定理具有重要的作用。
理解和应用五心的性质可以帮助我们更好地理解和应用三角形的定理与性质,从而更好地解决相关问题。
旁心,垂心,重心,外心,内心

旁心,垂心,重心,外心,内心三角形内心是三条角平分线的交点,它到三边的距离相等。
外心是三条边垂直平分线的交点,它到三个顶点的距离相等。
重心是三条中线的交点,它到顶点的距离是它到对边中点距离的2倍。
垂心是三条高的交点,它能构成很多直角三角形相似。
旁心是一个内角平分线与其不相邻的两个外角平分线的交点,它到三边的距离相等。
(1)重心和三顶点的连线所构成的三个三角形面积相等;(2)外心到三顶点的距离相等;(3)垂心与三顶点这四点中,任一点是其余三点构成的三角形的垂心;(4)内心、旁心到三边距离相等;(5)垂心是三垂足构成的三角形的内心;(6)外心是中点三角形的垂心;(7)中心也是中点三角形的重心;(8)三角形的中点三角形的外心也是其垂足三角形的外心。
三角形的五心一定理重心定理:三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍,该点叫做三角形的重心。
外心定理:三角形的三边的垂直平分线交于一点,该点叫做三角形的外心。
垂心定理:三角形的三条高交于一点,该点叫做三角形的垂心。
内心定理:三角形的三内角平分线交于一点,该点叫做三角形的内心。
旁心定理:三角形一内角平分线和另外两顶点处的外角平分线交于一点,该点叫做三角形的旁心。
三角形有三个旁心。
三角形的重心、外心、垂心、内心、旁心称为三角形的五心,它们都是三角形的重要相关点。
上述的几个结论早在欧几里得时代均已被人发现,欧几里得除垂心定理外,均把它们作为重要定理收集在自己的《几何原本》里。
重心物理术语定义:一个物体的各部分都要受到重力的作用。
从效果上看,我们可以认为各部分受到的重力作用集中于一点,这一点叫做物体的重心。
物体的重心位置质量均匀分布的物体(均匀物体),重心的位置只跟物体的形状有关。
有规则形状的物体,它的重心就在几何重心上,例如,均匀细直棒的中心在棒的中点,均匀球体的重心在球心,均匀圆柱的重心在轴线的中点。
不规则物体的重心,可以用悬挂法来确定物体的重心,不一定在物体上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
垂心、重心、内心、外心、旁心的定义和性质
1.定义
垂心:三角形三条高的交点
重心:三角形三条中线的交点
内心:三角形三条内角平分线的交点即内接圆的圆心
外心:三角形三条边的垂直平分线的交点即外接圆的圆心
旁心:三角形两条外角平分线和一条内角平分线的交点
注意:正三角形中重心、垂心、外心、内心重合,这个点叫中心。
2.性质
垂心:1、锐角三角形垂心在三角形内部,直角三角形垂心在三角形直角顶点,钝角三角形垂心在三角形外部。
2、垂心H关于三边的对称点,均在△ABC的外接圆上。
3、锐角三角形的垂心到三顶点的距离之和等于其内切圆与外
接圆半径之和的2倍。
4、从一点向三角形的三边所引垂线的垂足共线的充要条件是
该点落在三角形的外接圆上。
(西姆松线)
重心:1、重心到顶点的距离与重心到对边中点的距离之比为2:1。
2、重心和三角形3个顶点组成的3个三角形面积相等。
3、重心和三角形3个顶点的连线的任意一条连线将三角
形面积平分。
4、重心到三角形3个顶点距离的平方和最小。
5、重心是三角形内到三边距离之积最大的点。
6、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,
即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3);空间直角坐
标系——横坐标:(X1+X2+X3)/3 纵坐标:(Y1+Y2+Y3)/
3 竖坐标:(Z1+Z2+Z3)/3
内心:1、到三边的距离相等,都等于内切圆半径r。
2、内心都在三角形的内部。
3、设三角形的三个顶点坐标分别为
A(x_1,y_1),B(x_2,y_2),C(x_3,y_3),其对边长分别为
a,b,c,则内心坐标
I((ax_1+bx_2+cx_3)/(a+b+c),(ay_1+by_2+cy_3)/(a+
b+c))
外心:1、到三角形三顶点的距离相等,都等于外接圆半径R。
2、直角三角形外心在斜边的中点,锐角三角形外心在内部,
钝角三角形外心在外部。
旁心:1、旁心到三边的距离相等。
2、三角形有三个旁切圆,三个旁心。
旁心一定在三角形外。
3、直角三角形斜边上的旁切圆的半径等于三角形周长的一半。
