信号与系统课后习题与解答第三章

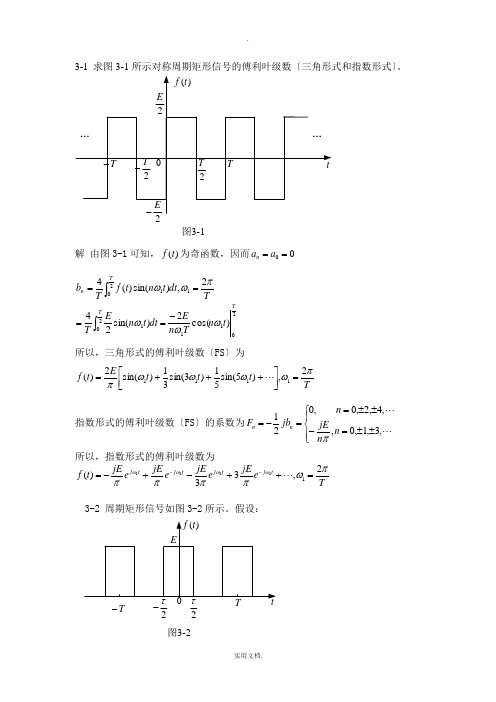
3-1 求图3-1所示对称周期矩形信号的傅利叶级数（三角形式和指数形式）。

图3-1

解 由图3-1可知，)(t f 为奇函数，因而00==a a n

2

1120

11201)cos(2)sin(242,)sin()(4T T T n t n T n E

dt t n E T T dt t n t f T b ωωωπωω-==

=

=⎰⎰

所以，三角形式的傅利叶级数（FS ）为

T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦

⎤

⎢⎣⎡+++=

指数形式的傅利叶级数（FS ）的系数为⎪⎩⎪

⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,

021n n jE n jb F n n π

所以，指数形式的傅利叶级数为

T e jE e jE e jE e jE t f t j t j t j t j π

ωππππωωωω2,33)(11111=

++-+-=--

3-2 周期矩形信号如图3-2所示。若：

图3-2

2

T

-2-

重复频率kHz f 5= 脉宽 s μτ20=

幅度 V E 10=

求直流分量大小以及基波、二次和三次谐波的有效值。

解 对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数（FS ）的系数

⎪⎭

⎫

⎝⎛=⎪⎭⎫ ⎝⎛==

=

=⎰⎰--22

sin 12,)(1112212211τωττωππωτ

τ

ωωn Sa T E n n E dt Ee T T dt e t f T F t

jn T

T t jn n

则的指数形式的傅利叶级数（FS ）为

∑∑∞

-∞

=∞

-∞

=⎪⎭

⎫

⎝

⎛==

n t

jn n t

jn n

e n Sa T

E e

F t f 112

)(1ωωτωτ 其直流分量为T E n Sa T E F n ττωτ=⎪⎭

⎫ ⎝⎛=→2lim

100 基波分量的幅度为⎪⎭⎫ ⎝

⎛

⋅=

+-2sin 2111τωπE

F F 二次谐波分量的幅度为⎪⎭⎫ ⎝

⎛

⋅=

+-22sin 122τωπE

F F 三次谐波分量的幅度为⎪⎭⎫ ⎝

⎛

⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得

s T s rad 441102,/10-⨯==πω 将各参数的值代入，可得

直流分量大小为

V 11021020104

6

=⨯⨯⨯--

基波的有效值为

()

)(39.118sin 2

10101010sin 210264V ≈=⨯⨯⨯- πππ

二次谐波分量的有效值为

()

)(32.136sin 2

51010102sin 21064V ≈=⨯⨯⨯- πππ

三次谐波分量的有效值为()

)(21.1524sin 32

101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ

3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示，)(1t f 的参数为s μτ5.0=，

s T μ1= ，V E 1=； )(2t f 的参数为s μτ5.1=，s T μ3= ，V E 3=，分别求：

（1）)(1t f 的谱线间隔和带宽（第一零点位置），频率单位以kHz 表示； （2）)(2t f 的谱线间隔和带宽； （3）)(1t f 与)(2t f 的基波幅度之比； （4）)(1t f 基波与)(2t f 三次谐波幅度之比。

解 由题3-2可知，图3-2所示周期矩形波形的傅利叶级数为

T e n Sa T

E t f t

jn πωτωτ

ω2,2)(1

11=⎪⎭⎫ ⎝⎛=

∑∞

∞

- 且基波幅度为

⎪⎭

⎫ ⎝⎛=⎪⎭⎫ ⎝⎛

⋅T t E E

ππτωπsin 22sin 21 三次谐波幅度为

⎪⎭

⎫

⎝⎛=⎪⎭⎫ ⎝⎛⋅T t E E ππτωπ3sin 3223sin 321 另外，周期信号的频谱是离散的，每两根相邻谱线间的间隔就是基频1ω。 周期矩形信号频谱的包络线是抽样函数，其第一个零点的位置为

⎪⎭

⎫ ⎝⎛

=⇒==τπωπτωτπω2n 2n 211令。注意，频谱还可以表示为频率f 的函数。由f πω2=可知，若以f 为频谱图的横轴，则谱线间隔就为，第一个零点的位置就为τ

1

=

f 。

依据以上结论，可得到题中个问题的答案如下： （1）)(1t f 的谱线间隔kHz s T 100011

1===

μ 带宽（第一零点位置）kHz s

20005.01

1==

=μτ

（2）)(2t f 的谱线间隔kHz s T 3103

1311⨯===

μ 带宽kHz s 3103

2

5.111

⨯==

=

μτ

（3）)(1t f 的基波幅度πμμππ215.0sin 1

2=⎪⎪⎭

⎫ ⎝⎛⨯⨯=

s s )(2t f 的基波幅度π

μμππ635.1sin 3

2=⎪⎪⎭⎫ ⎝⎛⨯⨯=

s s 因此)(1t f 的基波幅度：)(2t f 基波幅度3:16

:2=π

π

（4）)(2t f 的三次谐波幅度π

μμππ2

35.13sin 332=⎪⎪⎭⎫ ⎝⎛⨯⨯=

s s 因此)(1t f 基波幅度：)(2t f 三次谐波幅度

1:12

:2=π

π

3-4 求图3-3所示周期三角信号的傅利叶级数并画出幅度谱。

图3-3

2

解 由图3-3可知，该周期三角信号是偶函数，因而0=n b 即)(t f 不包含正弦谐波分量。

2

)(2220E dt t f T a T

T ==⎰-