给定边界面积最小的曲面的平均曲率为零的证明方法
极小曲面

极小曲面 设 2D R ⊂是有界开区域,边界为D ∂。
函数(,)x y ϕ在D ∂上有定义。
设2(,)()u u x y C D =∈,则曲面(,)zu x y =的面积为()DI u =⎰⎰。
设2{(,):(,)(),|}D W u x y u x y C D u ϕ∂=∈=, 考虑泛函I 在W 上的极小值是否存在的问题。
几何意义,以空间封闭曲线Γ为边界的曲面中,寻找其面积最小者。
这里{(,,):(,),(,)}x y z x y D z x y ϕΓ=∈∂= 。
这样的问题称为极小曲面问题。
假若泛函I 在u W ∈处达到最小值,我们考查其必要条件。
记20{(,):(,)(),|0}D W v x y v x y C D v ∂=∈=,显然,若I 在u W ∈处达到最小值, 则对任意0v W ∈,()I u tv +在0t =处达到最小值,所以0()|0t d I u tv dt =+=,而()DI u tv +=⎰⎰,()dI u tv dt +22Du v tv u v tv +++=⎰⎰,于是有x x y y Du v u v +=⎰⎰,设在xz平面上有一条显式曲线=≤≤≤。
z u x a x b(),(0)如果固定z轴不动,让xz平面绕着z 轴旋转360,那么这一条曲线就扫出一张旋转曲面,这个旋转曲面∑的方程为2222:)z u D a x y b=≤+≤。
r=。
我们寻找旋转的极小曲面。
历史资料极小曲面面积在法向变分下达到临界值的曲面,也即平均曲率(见曲面)为零的曲面。
目录简介研究同名图书简介研究同名图书展开小的曲面就是所谓极小曲面,从数学上求这膜曲面的问题称为普拉托问题。
这个问题可以用变分法来解。
从变分学观点看,可以考虑以已知闭曲线Γ为固定边界的曲面的法向变分。
由欧拉-拉格朗日方程(见变分法),对于任何这样的变分,曲面面积达到临界值的充要条件是曲面的平均曲率h=0。
因此,通常就用这个几何条件来定义极小曲面。
极小曲面浅谈
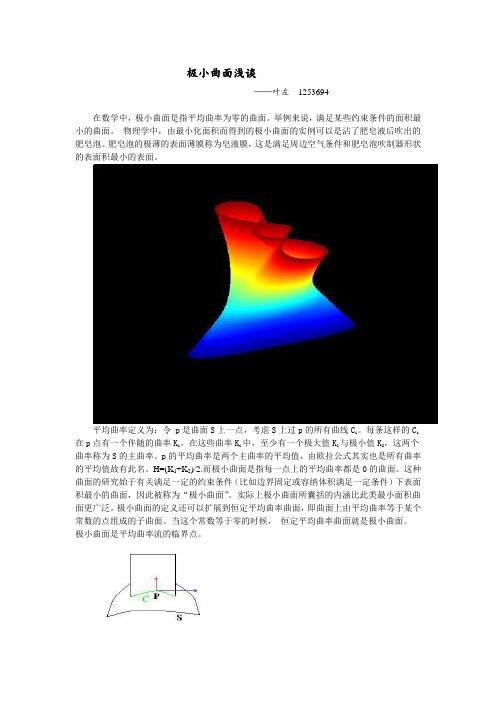
极小曲面浅谈——叶左1253694在数学中,极小曲面是指平均曲率为零的曲面。
举例来说,满足某些约束条件的面积最小的曲面。
物理学中,由最小化面积而得到的极小曲面的实例可以是沾了肥皂液后吹出的肥皂泡。
肥皂泡的极薄的表面薄膜称为皂液膜,这是满足周边空气条件和肥皂泡吹制器形状的表面积最小的表面。
平均曲率定义为:令 p是曲面S上一点,考虑S上过p的所有曲线C i。
每条这样的C i 在p点有一个伴随的曲率K i。
在这些曲率K i中,至少有一个极大值K1与极小值K2,这两个曲率称为S的主曲率。
p的平均曲率是两个主曲率的平均值,由欧拉公式其实也是所有曲率的平均值故有此名。
H=(K1+K2)/2.而极小曲面是指每一点上的平均曲率都是0的曲面。
这种曲面的研究始于有关满足一定的约束条件(比如边界固定或容纳体积满足一定条件)下表面积最小的曲面,因此被称为“极小曲面”。
实际上极小曲面所囊括的内涵比此类最小面积曲面更广泛。
极小曲面的定义还可以扩展到恒定平均曲率曲面,即曲面上由平均曲率等于某个常数的点组成的子曲面。
当这个常数等于零的时候,恒定平均曲率曲面就是极小曲面。
极小曲面是平均曲率流的临界点。
极小曲面的经典例子包括:1).欧几里得平面,无特别约束条件下最平常的极小曲面;2).悬链面:由悬链线围绕其水平准线旋转而得到的曲面。
这是最早发现的“不寻常”的极小曲面。
3).正螺面:一个线段沿着垂直于其中点的直线匀速螺旋上升时扫过的曲面。
这是继悬链曲面后发现的第二种不寻常的极小曲面;4).Enneper曲面。
4).Scheck曲面;5).Costa —Hoffman—Meeks曲面。
悬链面悬链曲面状的皂液膜可以由将两个等大的圆环紧贴放入肥皂水中,拿出后再缓慢分开得到.方程:z=cosh-1错误!.正螺面就是让一条直线l的初始位置与x轴重合,然后让直线l一边绕z轴作匀速转动,一边沿z轴方向作匀速运动,则直线在这两种运动的合成下扫出的曲面就是正螺旋面,它的方程为:z=arctan(y/x).显然正螺旋面可以看做是由直线形成的,即它是一个直纹面Costa面在三维欧氏空间E3中,若一张曲面可用方程z=z(x,y)来表示,则称它为图,或非参数化曲面。
曲面的基本形式与曲面上的曲率

第四章 曲面的第二基本形式与曲面上的曲率§5 曲面上的曲率概念利用上一节所作的准备,围绕曲面弯曲状况的刻画,本节将引入曲面上的基本的和重要的曲率概念,并简要讨论相关的几何体.一.主曲率定义1 曲面 S 上的点 P 处的法曲率关于切方向的两个最值,分别称为曲面 S 在点 P 处的主曲率;使得法曲率达到最值的两个切方向,分别称为曲面 S 在点 P 处的主方向.注记1 ① Weingarten 变换的特征值和特征方向,分别是曲面的主曲率和主方向.② 当两个主曲率 κ1(P ) ≠ κ2(P ) 时,曲面在点 P 处有且仅有正交的两组主方向,每一组的单位化向量分别就是Weingarten 变换的单位正交特征向量.而当两个主曲率 κ1(P ) = κ2(P ) 时,曲面在点 P 处的任何非零切向都是主方向,Weingarten 矩阵 ω(P ) = κ1(P )I 2 ,即 Ω(P ) = κ1(P )g (P ) .主曲率和主方向的计算,自然归结为Weingarten 变换的特征值和特征方向的计算,也就是Weingarten 矩阵的特征值和特征方向的计算.即: ① 对于主曲率的算法,当易知Weingarten 矩阵 ω 之时,方程为 (4.3) 式,或直接写为(5.1) |ω - λI 2 | = 0 ;等价地,当易知系数矩阵 Ω 和 g 之时,其方程可变形为(5.2) |Ω - λg | = 0 .② 对于主方向的算法,各种等价算式为a = a i r i ≠ 0 为主方向,即非零切方向 a 1:a 2 为主方向 ⇔ ∃λ , ∍(a 1, a 2)ω = λ(a 1, a 2) , (a 1, a 2) ≠ (0, 0)⇔ ∃λ , ∍(a 1, a 2)Ω = λ(a 1, a 2)g , (a 1, a 2) ≠ (0, 0)⇔ det. ⎝⎛⎭⎫(a 1, a 2)Ω (a 1, a 2)g = 0⇔(a2)2-a1a2 (a1)2g11g12g22Ω11Ω12Ω22= 0 .主方向所对应的微分方程通常写为(5.3)(d u2)2-d u1d u2 (d u1)2g11g12g22Ω11Ω12Ω22= 0 .定义2若曲面S在点P处的两个主曲率相等,则称点P为曲面S上的一个脐点.若曲面S处处为脐点,则称曲面S为全脐曲面.若脐点处的主曲率为零,则称之为平点;若脐点处的主曲率不为零,则称之为圆点.注记2全脐曲面S的法曲率只与点有关而不依赖于切向选取,故只有平面和球面两类;平面上各点为平点,球面上各点为圆点.全脐曲面主方向所对应的微分方程是蜕化的恒等式.二.Gauss曲率和平均曲率定义3对于正则曲面S,其在点P处的两个主曲率的乘积K,称为其在点P处的Gauss曲率或总曲率;其在点P处的两个主曲率的算术平均值H,称为其在点P处的平均曲率.注记3①注意到(4.4)-(4.5) 式,Gauss曲率和平均曲率分别具有用Weingarten矩阵或两个基本形式系数的表达式,分别列为(5.4)K=|ω|=|Ω||g|=LN-M2EG-F2,(5.5) H= tr.ω2=LG- 2MF+NE2(EG-F2).②主曲率方程 (4.3) 式现可改写为(5.6)λ2- 2Hλ+K= 0 ;其中H 2-K= (κ1-κ2)24≥ 0 .③Gauss曲率在容许参数变换下不变;平均曲率在保向参数变换下不变,在反向参数变换下变号.④当曲面三阶连续可微时,Gauss曲率和平均曲率分别是连续可微函数;此时,两个主曲率函数(5.7)κi=H±H2-K , i= 1, 2处处连续,并且在非脐点处连续可微.⑤ 平均曲率等于法曲率按切方向的积分平均值(留作习题). ⑥ 平均曲率不是等距不变量.反例如圆柱面和平面.例1 证明可展曲面的Gauss 曲率 K ≡ 0 .证明 对可展曲面 S 的直纹面参数化 r (u , v ) = a (u ) + v l (u ) ,由可展定义得知 n v ≡ 0 ,故其第二基本形式系数满足M = - r u ∙n v ≡ 0 , N = - r v ∙n v ≡ 0 ,于是K = LN - M 2 EG - F 2≡ 0 . □ 在上例中,若取准线使 a '∙l ≡ 0 且 |l | ≡ 1 ,则可展曲面 S 的第一和第二基本形式系数矩阵同时对角化,Weingarten 矩阵则为特征值对角阵,而且(5.8) κ1 = L E, κ2 ≡ 0 . 三.Gauss 映射和第三基本形式Gauss 在考察曲面的弯曲程度刻画时,注意到曲面的单位法向在单位球面上的行为对于曲面弯曲状况的反映,并进一步明确了两者的依赖程度,进而在曲面论中做出了卓有成效的工作.观察熟知的一些曲面,比如平面、圆柱面、圆锥面、椭球面、双叶双曲面、双曲抛物面等等,可以直观感受到单位法向不同的行为和曲面不同的弯曲状况之间有着密切联系.定义4 对于 C 3 正则曲面 S : r (u 1, u 2) 及其单位法向量场 n (u 1, u 2) ,曲面 S 到以原点为心的单位球面 S 2(1) 上的映射(5.9) G : S →S 2(1) r (u 1, u 2)→G (r (u 1, u 2)) = n (u 1, u 2)称为曲面 S 的Gauss 映射.二次微分形式(5.10) Ⅲ = d n ∙d n图4-5称为曲面S的第三基本形式.性质①n1⨯n2=K r1⨯r2.②|K(P)|=limU收缩至P A(G(U))A(U),其中P∈U⊂S, U为单连通区域,A(G(U)) 是G(U)⊂S2(1) 的面积,A(U) 是U⊂S的面积.③Ⅲ- 2HⅡ+KⅠ= 0 .证明①由Weingarten公式得n1⨯n2= [-(ω11r1+ω12r2)]⨯[-(ω21r1+ω22r2)]=|ω|r1⨯r2=K r1⨯r2.②A(U) =⎰⎰r-1(U)| r1⨯r2| d u1d u2 ,A(G(U)) =⎰⎰r-1(U) | n1⨯n2| d u1d u2=⎰⎰r-1(U)|K|| r1⨯r2| d u1d u2.而由积分中值定理,∃P*∈U使⎰⎰r-1(U) |K|| r1⨯r2| d u1d u2=|K (P*)|⎰⎰r-1(U)| r1⨯r2| d u1d u2.故而lim U收缩至P A(G(U))A(U)= limP*→P|K (P*)|=|K (P)|.③结论用系数矩阵等价表示为(Ω g-1)g(Ω g-1)T- 2HΩ+K g≡ 0⇔Ω g-1Ω- 2HΩ+K g≡ 0⇔Ω g-1Ω g-1- 2HΩ g-1+K I2≡ 0⇔ωω- (tr.ω)ω+|ω|I2≡ 0 .而最后的等式对于二阶方阵总成立(用特征值理论则知是显然的),用元素计算可直接验证为ωi kωk j- (tr.ω)ωi j+|ω|δi j=ωi1ω1j+ωi2ω2j- (ω11+ω22)ωi j+ (ω11ω22-ω12ω21)δi j≡ 0 .□习题⒈对于螺面r= (u cos v , u sin v , u+v) ,试求:①主曲率κ1和κ2;②Gauss曲率和平均曲率.⒉试求球面的Gauss曲率和平均曲率与球面半径的关系.⒊试证:平均曲率等于法曲率按切方向的积分平均值,即 2πH(P) =⎰2πκ(P, θ) dθ.⒋试证:直纹面的Gauss曲率处处非正.⒌设正则曲面S: r(u1, u2) 当常数μ足够小时 1 - 2μH+μ2K> 0 .按参数相同作对应曲面S*: r*(u1, u2) =r(u1, u2) +μn(u1, u2) ,其中n为曲面S的单位法向量场.试证:①S和S* 在对应点具有相同的单位法向和法线;②S和S* 在对应点的Weingarten矩阵具有关系式ω* =ω (I2-μω )-1;③S和S* 在对应点的Gauss曲率和平均曲率具有关系式K* =K1 - 2μH+μ2K,H* =H-μK1 - 2μH+μ2K;④S的曲率线对应于S* 的曲率线.⒍已知曲面S在一点处沿着一组等分周角的m个切方向的法曲率分别为κn(1), …,κn(m),m> 2 .试证:S在该点的平均曲率H=κn(1)+…+κn(m)m.⒎试证:曲面S的第三基本形式恒为零的充要条件为S是平面.。
微分几何(第三版)【梅向明_黄敬之_编】第三章课后题答案[1]
![微分几何(第三版)【梅向明_黄敬之_编】第三章课后题答案[1]](https://img.taocdn.com/s3/m/ec2031ed524de518974b7d0c.png)
§4.直纹面和可展曲面1. 证明曲面r =}32,2,31{2432v u u uv u v u +++是可展曲面.证法一: 已知曲面方程可改写为r =},2,{432u u u +v }32,,31{2u u ,令()a u =},2,{432u u u ,()b u =}32,,31{2u u ,则r =()a u + v ()b u ,且()b u ≠0,这是直纹面的方程 ,它满足(',,')a b b =23226412334013u u u u u u =0 ,所以所给曲面为可展曲面。
证法二:证明曲面的高斯曲率为零。
(略)2。
证明曲面r={cosv-(u+v)sinv, sinv+(u+v)cosv,u+2v}是可展曲面。
证法一: 曲面的方程可改写为 r=()a v + u ()b v ,其中()a v ={cosv-vsinv,sinv+vcosv, 2v},()b v ={-sinv, cosv,1} ,易见()b v ≠0,所以曲面为直纹面,又因为(',,')a b b =2sin cos 2cos sin 2sin cos 1cos sin 0v v v v v v v v vv ------=0,所以所给曲面为可展曲面。
证法二:证明曲面的高斯曲率为零。
(略)3.证明正螺面r={vcosu,vsinu,au+b}(a ≠0)不是可展曲面。
证法一:原曲面的方程可改写为r=()a u + v ()b u ,其中()a u ={0,0,au+b},()b u ={cosu,sinu,0}.易见()b u ≠0, 所以曲面为直纹面,又因为(',,')a b b =00cos sin 0sin cos 0au u u u -=a ≠0.故正螺面不是可展曲面。
证法二:证明曲面的高斯曲率为零。
(略)4.证明挠曲线的主法线曲面与副法线曲面不是可展曲面。
极小曲面

第一章 肥皂膜实验如果你把一根铜丝弯成一条封闭的空间曲线(留出一个把手),将这个框架浸入配制好的肥皂液,然后将它轻轻地提取出来,那么肥皂液就会在铜丝框架上张成一个处于平衡状态的绚丽多彩的薄膜,这个薄膜所成的曲面有哪些性质?它是什么样的曲面?这是一些令人神往的问题.我们知道,在数学发展史上有许多生动的例子说明,物理实验经常为数学模型的形成及数学理论的完善和发展提供极有价值的启示和刺激.前面所提到的实验由19世纪的比利时物理学家J.Plateau 作了仔细的观察和详细的描述.如果我们忽略不计肥皂膜液本身的重量,也不考虑除了肥皂膜表面张力以外的其它干扰因素(例如外界的风力等),则薄膜的势能在表面张力作用下便会达到最小值,从而必定使肥皂膜采取的曲面形状具有最小的面积.Plateau 通过肥皂膜的有趣实验,确定了肥皂膜曲面和肥皂泡曲面的许多几何性质.因此,Plateau 至少是用实验的手段产生了以非常一般的任意空间曲线为边界的面积最小的曲面.现在,通常把寻求一给定的空间曲线C 为边界的面积最小的问题称为Plateau 问题,当然,要在数学上把这个问题讲清楚绝非易事,以后我们会介绍Plateau 问题在数学上的正确提法.上面的问题命名为Plateau 问题,是因为Plateau 系统地对于这个问题作了实验研究和观察.但是早在18世纪,Euler 就提出过这类问题.Euler 在1744年发表的《寻求具有某种极大或极小性质的曲线的技巧》一书中举出了一个例子,要求决定出介于点(00,y x )和点(11,y x )之间的平面曲线)(x f y ,使得它在绕x 轴旋转时所产生的曲面的面积最小.Euler 证明了函数)(x f 必须是一段悬链线,生成的旋转面叫悬链面.Euler 所得到的实际上就是以位于两个平行的平面上,且连心线与平面垂直的两个圆周为边界的面积“最小”的曲面.尽管如此,一般都认为这类曲面的研究是grange 在1760年开始的,因为他第一次给出了这类曲面应该满足的偏微分方程.他所考虑的是三维欧式空间3R 中由函数),(y x f Z =给出的图像M ,其中点),(y x 的变化范围是xy 平面上的一个区域grange 利用他所创立的变分法原理证明了:如果在所有定义在区域D 上,并且在边界D ∂上取值相同的函数的图像中M 的面积最小,则函数),(y x f Z =必须满足偏微分方程0)1(2122=++-+yy y xy y x xx y f f f f f f f )( 这就是著名的所谓极小曲面的方程.在1776年,几何学家J.B.Meusnier 证明了函数),(y x f Z =的图像M 的平均曲率是}.)1(2)1{(121222322yy x xy y x xx y yx f f f f f f f f f H ++-+++=)(因此,Meusnier 给出了Lagrange 的方程的几何解释:满足偏微分方程的曲面就是其平均曲率为零的曲面.此外,他还指出悬链面和正螺旋面是满足极小曲面的两个非线性函数的图像.现在,把3R 中平均曲率为零的曲面称为极小曲面.第二章 极小曲面方程这一节,首先要把曲面在他它的邻近变形的概念正确地表达出来.然后据此导出lagrange 的极小曲面方程.假定我们所考虑的曲面M 是连续可微函数Z=f(x,y)的图象,其中点(x,y )的变动范围是xy 平面上的一个区域D.今后称M 为定义在区域D 上的一张图.若有连续可微函数Z=F (x,y,t ),…………(2.1)其中(x,y,t )∈D ⨯(-ε,ε),ε是任意一个正数,并且F (x,y,0)=f(x,y) …………(2.2)对于任意的(x,y )∈D 成立,则称函数Z=F (x,y,t )是Z=f(x,y)的一个变分. 每当t 取定一个属于(-ε,ε)的数值t 0,函数Z=F (x,y,t 0)就给出定义在区域D 上的一张图M 0t .条件(2.2)说明M 0=M.所以,给定函数Z=f(x,y)的一个变分,就是给出了图M 在它邻近的一个变形M t ,有时,我们也称M t 是M 的一个变分.如果变分(2.1)除了满足条件外,还满足 F (x,y,t )=f(x,y) …………(2.3)其中(x,y,t )是∂D ⨯(-εε,)中的任意点,则变形曲面M t 与图M 有共同的边界曲线.这时,我们称(2.1)是Z=f(x,y)的有相同的边界值的变分,或称M t 是图M 的有固定边界的变分.将函数线性化是研究函数的最简单的方法之一.对于变分(2.1)也可以作同样的考虑.令g(x,y)=0,,=∂∂t tt y x F )(,…………(2.4)则g(x,y)是定义在D 上的连续可微函数.它的几何意义是变分曲面M t 在点(x,y )处在t=0时刻变形的速率.令F 0(x,y,t)=f(x,y)+tg(x,y),…………(2.5)则Z=F 0(x,y,t)仍是Z=f(x,y)的一个变分.而且Z=F 0(x,y,t)是函数Z=F(x,y,t)关于变量t 的Taylor 展开式中略去t 的二次以上的项所得到得表达式.下面的计算会告诉我们,在变分计算中起本质作用的是变分Z=F(x,y,t)关于t 的一此近似值,也就是定义在区域D 上的函数g(x,y),为了把变形的速度形象地表示出来,我们引进向量场V=(x,y,g(x,y)) …………(2.6)它定义在D 上,也可以认为定义在图形M 上,我们称V 为图M 的变分向量场.如果图M 的变分M t 有固定的边界,则从(2.3)式得g(x,y)=0, ∀(x,y)∈∂D曲面面积的定义对于极小曲面理论而言自然是十分重要的基本问题.事实上,在极小曲面理论的发展过程中,关于曲面面积定义的讨论占据重要的位置,几何测度论就是这个过程中十分重要的产物.在这里我们先承认函数Z=f(x,y)的图M 的面积为A(M)=…………(2.7)此式的几何意义将在第三节介绍,同时在那里还要对曲面面积的定义作一些讨论.对于M 的一个变分M t .命A(M t)=, 它是一个以t 为自变量的函数.我们知道,如果把M 看成张在边界曲线∂M 上的肥皂膜.那么当M 在它邻近作保持边界曲线不动的变形时,即当M 作固定边界的变分M t 时,M 的面积取最小值,也就是对任意的t ∈(-,εε)有A(M)≤A(M t ) …………(2..8)我们已经假定F(x,y,t)是连续可微函数,所以A(M t )是t 的连续可微函数.(2.8)式意味着函数A(M t )在t=0时达到最小值.故有t ddt=A(M t )=0 …………(2.9)我们的任务是把上式的左端计算出来,由(2.5)式知 F(x,y,t)=f(x,y)+tg(x,y)+t 2h(x,y,t), 因此 F x ∂∂=f x ∂∂+t g x ∂∂+t 2h x∂∂F y ∂∂=f y ∂∂+t g y ∂∂+t 2h y∂∂ 1+2F x ∂⎛⎫ ⎪∂⎝⎭+2F y ⎛⎫∂ ⎪∂⎝⎭=(1+f 2x +f 2y )+2t(f x g x +f y g y )+t 2h (x,y,t)⋅ 其中Q(x,y,t)是有界函数,且 P(x,y)=222()1x x y y x y f g f g f f +++t=0附近的Taylor 展式,我们得到~2(1(,)(,,))2t P x y t Q x y t ++, 其中~Q (x,y,t )是有界函数.由此可得0t d dt=A(M t)=0t Dt =∂∂⎰dxdy=f g f g +dxdy条件(2.9)成为:对D 上任意的连续可微函数g(x,y),都应该有f g f g +dxdy=0 …………(2.10)为了用分部积分法从(2.10)导出f 应满足的偏微分方程, 命 p=f x ∂∂, q=f y∂∂ 并且把(2.10)被积表达式写成g gp q ∂∂⋅+⋅=x y ⎛⎫⎛⎫∂∂+∂∂()qg x y x ⎡⎤⎛⎫⎢⎥ ⎪∂∂⎢⎥⎪-+⋅∂∂∂⎡⎤⎢⎥ ⎪- ⎪⎢⎥⎢⎥∂⎣⎦⎝⎭⎣⎦ 对于右端前两项在D 上的积分可以用Green 公式:(,)(,)D D B A A x y dx B x y dy dxdy x y ∂⎛⎫∂∂+=- ⎪∂∂⎝⎭⎰⎰,…………(2.11) 其中A(x,y),B(x,y)是定义在D 上的连续可微函数,边界∂D 的正定向要求沿曲线∂D 正向行进时区域D 落在它的左边,所以我们有0()t t d A M dt=∂=⎰-D gdxdy x y ⎡⎤⎛⎫⎛⎫∂∂⎢⎥+∂∂⎢⎥⎣⎦⎰ 前面已假定M t 是M 的固定边界的变分,故 g0D∂≡,于是(2.10)式成为0()t t d A M dt==-0D gdxdy x y ⎡⎤⎛⎫⎛⎫∂∂⎢⎥+=∂∂⎢⎥⎣⎦⎰………(2.12)如果上面的条件对任意的在边界D ∂上的值为零的连续可微函数g(x,y)恒成立,则容易导出函数Z=f(x,y)在区域D 上满足微分方程2x y ⎡⎤⎛⎫⎛⎫∂∂⎢⎥+∂∂⎢⎥⎣⎦=0 …………(2.13) 为此只要证明(2.13)式在任意一点(0,0x y )∈D 成立.在这里关键是要找出一个非负连续可微函数,使得它在一个固定点的某领域内恒等于1.而支集包含在区域D 内,这样的函数是存在的,我们可以具体地构造出来.例如:设0,εδ<<命1e x p ,()()0,()x x x x x εδεδεδα⎧<<⎨--⎩≤≥⎧⎪=⎨⎪⎩或x()x β=()()xx dxx dxdx αα+∞+∞-∞⎰⎰显然,函数(),()x x αβ都是实轴R 上的光滑函数,满足0()1x β≤≤,且{1,0,()x x x εδβ≤≥=这些性质 不难从下图看出来,不需另行验证函数()x β通常称为截断函数,其功能是把函数在某一点的邻域上的部分分离出来,而保持函数在整体上的可微性不变.比如,对于(0,0x y )∈D ,可以取0εδ<<,使得已(0,0x y )为中心,以为边长的正方形0000x x y y ⎡⎡⨯⎣⎣整个落在区域D 内,命g(x,y)=x y ⎡⎤⎛⎫⎛⎫∂∂⎢⎥+∂∂⎢⎥⎣⎦2200()()x x y y ββ--则g 是整个D 上的连续可微函数.并且 g0D∂≡.此外,g在0000x x y y ⎡⎡+⨯-+⎣⎣内恒等于方括号内的表达式. 将上面构造的g(x,y) 代入(2.12)式边得到00x x x y y y -≤-≤⎡⎤⎛⎫⎛⎫∂∂⎢⎥+∂∂⎥⎦⎰2⋅2200()()0x x y y dxdy ββ--=由于被积表达式为非负函数,其积分为零,蕴含着被积表达式必定恒等于零.于是在点(x 0,y 0)有0,0()0x y x y =⎛⎫⎛⎫∂∂+∂∂由(x 0,y 0)在D 内的任意性得(2..13)式在D 内成立. 将(2.13)式展开可得x y ⎛⎫⎛⎫∂∂+∂∂=32221(1)x y f f ++22(1)2(1)0y xx x y xy x yy f f f f f f f ⎡⎤+-+++=⎣⎦此即极小曲面方程.上面得讨论可以归纳如下得结论:设M 是定义在区域D ⊂R 2上得连续可微函数Z=f(x,y)的图.如果对于M 的任意一个保持边界不动的变分M t ,都有A(M)≤A(M t ).则函数Z=f(x,y)必须满足方程22(1)2(1)0y xx x y xy x yy f f f f f f f +-++= …………(2.14)第三章 曲面的面积前面所讨论的曲面都表示为函数Z=f(x,y)的图象.这种表示是有局限性的,它要求曲面与平行于Z 轴的直线只能有一个交点.更常用的表示曲面的方法是用参数方程.假定在3微欧氏空间R 3中取定一个笛卡儿直角坐标系[0,i,j,k],那么曲面M 上的点P (x,y,z )可以用三个函数(,)(,)(,)x xu v y y u v z z u v =⎧⎪=⎨⎪=⎩…………(3.1) 表示,其中(u,v )称为曲面的参数,它的变化范围是平面R 2的一个区域D ,通常,我们用r 表示向径op →,于是曲面(3.1)可以记成r=r(x(u,v), y(u,v),z(u,v)) …………(3.2)参数(u,v )是区域D 上的点的坐标,同时也是曲面M 上的点的坐标.这是因为把参数u,v 的值代入方程(3.1),便得到曲面上的对应点的笛卡儿坐标(x,y,z ),所以曲面上的点是由u,v 的值通过方程(3.1)而确定的.我们把(u,v )称为曲面M 上的点的曲纹坐标.对于能用微积分进行研究的曲面,一般要求(3.1)式中的函数x(u,v),y(u,v),z(u,v)有连续的三阶以上的偏导数.另外,为了使方程(3.1)确定给出一张曲面,通常还要求在曲面上每一点处u-曲线合v-曲线的切向量r u =(,,u u u x y z )和r v =(,,)v v v x y z 不共线,即u v r r ⨯=,,0uu uu uu vv vv vvy z z x x y y z z x x y ⎡⎤≠⎢⎥⎣⎦…………(3.3) 满足以上条件的曲面称为正则曲面.函数Z=f(x,y)的图象可以看作(x,y )为参数的正则曲面: r=(x,y,f(x,y)) …………(3.4) 这时 r x =(1,0,f x ), r y =(0,1,f y ),所以 x y r r ⨯=(,,1)0x y f f --≠. 由向量的定义可知()0,()u u v v u v r r r r r r ⋅⨯=⋅⨯=0 然而,切向量u r 和v r 在曲面上张成在该点的切平面,所以上式表明u v r r ⨯与曲面的切平面垂直;利用正则曲面M 上就有一个完全确定的单位法向量场 n=u vu vr r r r ⨯⨯ …………(3.5) 这样,在正则曲面M 上的每一点r(u,v)附加了一个标架{,,,}u v r r r n .它的原点就是曲面M 上的点r ,标架的前两个向量,u v r r 是曲面在该点的两个切向量,它们分别是参数曲线的切向量,n 是曲面在该点的单位法向量.我们称{},,,u v r r r n 为曲面在该点的自然标架.为了利用自然标架场来研究曲面,知道该标架场的度量系数是十分重要的,所谓一个标架的度量系数是指标架向量之间的内积的值.我们记:222222u u u u u u v v u u v u v u v u v v v v E r r x y z F r r r r x x y y z z G r r x y z ⎧=⋅=++⎪=⋅=⋅=++⎨⎪==++⎩…………(3.7) 其余的系数量0u v r n r n ⋅=⋅=, 1n n ⋅=.如果我们用dr 表示曲面M 在点r(u,v)的切向量,它可以表示为 u v dr r du r dv =+ …………(3.7)因此,,u v d d 恰好是切向量r d 关于自然标架的分量,向量r d 的长度平方为2dr =222dr dr Edu Fdudv Gdv ⋅=++…………(3.8)右端即为曲面的第一基本形式,通常用I 表示.下面我们要讨论曲面面积的概念,并且把它用第一基本形式的系数表示出来.关于连续曲面面积的定义,Lebesque 给出的定义如下:对每一个连续曲面S 都指定了一个数A(S),称为S 的面积,要求满足以下条件:(1)如果S 是多面体的表面,则A (S )是S 的通常意义下的面积,即它等于组成S 的多个多边形面积之和;(2)若有一系列曲面S n →S ,则l i m n →∞A(S n )≥A(S);(3)对于每一个连续曲面S ,必能找到一串多面体的表面P n 使P n →S 且l i m ()()n n A P A S →∞=定义中涉及到曲面序列S n 趋于曲面S 的概念,后来由Frechet 所澄清.在Frechet 意义下,两块连续曲面之间的距离是这样定义的:假定两块曲面S 1,S 2是从单位圆盘D 到R 3的两个连续映射的象即: 311:f D S R →⊂ 322:f D S R →⊂命 1212(,)((),())x Df f Sup d f x f x δ∈= 其中),(∙∙d 是R 3中距离函数.显然,如果12(,)0f f δ=.则12f f =.但我们要考虑的是两个曲面的接近程度,而不是它们参数表示的接近程度,所以需要在它们所有可能的参数表示中取12(,)f f δ的下确界.于是命1212(,)inf (,)Td S S f f T δ= ,其中T 遍历了所有的从D 到自身的同胚.12(,)d S S 称为曲面S 1和S 2之间的距离.应该指出的是,在Frechet 意义下考虑两个曲面之间的距离时,这两个曲面必须有相同的拓补类型.在前面的叙述中12,S S 都是与圆同胚的曲面.现在,Lebesque 的定义中的A(S)可以这样取:设{}n P 是任意的在Frechet 意义下收敛于S 的多面体表面的序列,命{}()i n f l i m ()n n P n A S AP →∞=, 其中()n n A P P 是在通常意义下的面积,那么A(S)适合Lebesque 定义的要求,可以证明,当曲面M 是连续可微的时候,上面定义的()A M 可以表示成二重积分:()A M =⎰,…………(3.10)由于证明过程相当复杂,这里不予以证明.但是我们要指出两点.一是表达式(3.10)与曲面参数表示的选择无关,在就是表达式有明显的直观意义.假定曲面M 有参数变换(,)(,)u uu v v v u v =⎧⎨=⎩(,)u v D∈ …………(3.11) 在新参数,uv 下.曲面M 的参数方程(3.1)成为 ((,),(,)((,),(,)),((,),(,)),x x u u v v u v y y u u v v u v z z u u v vu v === 直接计算得到 22()2(),u u v v EE F G u u u u∂∂∂∂=+⋅+∂∂∂∂22(),()2().u v u v u v v v FE F G u v u v v u uv u u v u G E F G v v v v∂∂∂∂∂∂∂∂=⋅+⋅+⋅+⋅∂∂∂∂∂∂∂∂∂∂∂∂=+⋅+∂∂∂∂(,),(,)u v uv ∂=∂ …………(3.12) 其中(,)(,)u v uv ∂∂ =,uuu v v v uv∂∂∂∂∂∂∂∂ 是参数变换(3.11)的Jacobi 行列式.根据二重积分的变量替换公式,我们有(,)(,)u v dudvu v ∂==∂⎰⎰⎰ . 由此可见,(3.10)式尽管是用曲面的参数方程给出的,但是它与参数的选择是无关的.设所考虑的小曲面片是σ适当地选取R 3中的笛卡儿直角坐标系使得σ 在指定点P 的切平面恰好是xy-平面.设σ的参数方程是: x=x(u,v), y=y(u,v), z=z(u,v),其中(u,v )σ∈D ⊂,则σ在点P 的切平面上的正交投影σ的方程是: x=x(u,v), y=y(u,v), z=0.其中(u,v )σ∈.当σ的直径充分小时,上面的方程建立了σ与σ之间的一一对应.即(u,v )可以看作投影区域σ上的曲纹坐标;所以根据二重积分的变量替换公式.σ的面积可表示为:(,)().(,)x y A dxdy dudv u v σσσ∂==∂⎰⎰注意到曲面σ在点P 的法线与Z 轴重合,即 ,(,)()(,0,0)(,)u v P Px y r r u v ∂⨯=∂ 故(,).(,)u v P Px y r r u v ∂⨯=∂于是根据曲面的法向量u v r r ⨯的连续性,在σ上任意一点有(,)(,),(,)u v x y r r u v u v σε∂=⨯+∂ 其中(,)u v σε在σ的直径很小时可以任意地小,特别是,对于任意给定的ε>0,只要分割得相当细,从而σ得直径充分地小,总可以使对于任意得(u,v )σ∈有(,)u v σε<ε因而A(σ)=(,)u v r r dudv u v dudv σσσε⨯+⎰⎰()()u v A r r dudv A σσεσ-⨯≤⋅⎰ …………(3.13)要指出的是表达式u v r r dudv σ⨯⎰不再与R 3中笛卡儿直角坐标系的特殊取法有关系,因此从(3.13)式得到()u vDA r r dudv σσ-⨯≤∑⎰(,)()u v dudv A D σσσεε≤⋅∑⎰ 由此可见,若用()d σ表示σ的直径,则有m a x ()l i m().uvd A r r dudv σσσσ→=⨯∑⎰…………(3.14) 但是,由向量积的定义,我们知道sin (,)u v u v u v r r r r r r ⨯=<=所以(3.14)式的右端就是(3.10)式右端的二重积分. 函数Z=f(x,y)的图象可以看作方程(3.4)给出的参数曲面, 所以(,,1),x y x y r r f f ⨯=--x y r r ⨯=故函数Z=f(x,y), (x,y)D ∈的图象的面积是A(M)=.⎰这就是前面的(2.7)式.第四章 曲面的曲率再上一节我们已经讨论了参数曲面上的度量,也就是曲面的第一基本形式,可以计算曲面上曲线的长度,以及计算曲面的面积,现在,简要叙述以下曲面曲率的概念.先给出曲面的第二基本形式:Ⅱ2222r u v n d Ld Mdudv Nd =⋅=++…………(4.1)它的系数L ,M ,N 称为曲面的第二类基本量. 现在把曲面的单位法向量u v u v r r n r r ⨯==⨯代入(4.1) 式中,就有u u u v vv L r n M r n N r n =⋅==⋅==⋅=设正则曲面S 的参数方程是(,)r r u v =,I 和Ⅱ分别是它的第一基本形式和第二基本形式,则n k II =I =2222()2()()2()L du Mdudv N dv E du Fdudv G dv ++++ …………(4.2)称为曲面S 在点(u,v )处沿切线方向(du,dv )的法曲率.于是,曲面S 在点(u,v )处沿切线方向(du,dv )的法曲率恰好等于曲面S 上经过点(u,v )以(du,dv )为切方向的曲线在该点的法曲率.曲面S 在点(u,v )处由切方向(du,dv )和法向量n(u,v)决定了一个平面.称为曲面S 在该点处由切方向(du,dv )确定的法截面,法截面与曲面S 本身相交成一条平面曲线,称为曲面在该点的一条法截线.在直观上,可以把法截面想象为与曲面在一点处垂直的“刀”,法截线就是用这把刀在曲面上切割出来的剖面线.法曲率恰好是曲面在该点沿相应的切方向的剖面线的相对曲率,这正是Euler 研究形状的基本出发点,下面我们要导处Euler 公式.不妨假定在给定点P 的附近取参数系(u,v ),使得参数曲线网在点P 使彼此正交的(显然,这总是能做到的).即在P 点有0u v r r ⨯=或F=0,假设切向量(du,dv ),u v r du r dv +与u-曲线切向量u r 的夹角是θ.则有c o s u v u u v u rd u r d vr d u r d v θ+=⋅+因而sin θ=于是曲面在P 点沿切方向(du,dv )的法曲率是22222n Ldu Mdudv Ndv k Edu Gdv ++=+=22cos sin sin L N E G θθθθ++在P 点,E ,G ,L ,M ,N 都是确定的数值,所以上式明确地把法曲率n k 表示为方向角θ的函数,它还可以改写为11cos2222n L N L N k E G E G θθ⎛⎫⎛⎫=-++ ⎪ ⎪⎝⎭⎝⎭.如果10,2L N E G ⎛⎛⎫-≠ ⎪ ⎝⎭⎝则有20θ使得01c o s 2L N θ⎛⎫- ⎪=0s i n 2θ=于是012().2n L N k E G θθ⎛⎫=-++ ⎪⎝⎭…………(4.3) 由此可见,当0θθ=或0θπ+时,n k 取最大值112L N k E G ⎛⎫=++⎪⎝⎭ 4.4) 当00322πθθθπ=++或时,n k 取最小值212L N k E G ⎛⎫=+ ⎪⎝⎭…………(4.5) 我们把曲面在P 点得最大法曲率1k 和最小法曲率2k 称为曲面在P 点得主曲率.用21,k k 代入(4.3)式得)(s i n )(c o s 022021θθθθ-+-=k k k n .…………(4.6)此即Euler 公式.如果0,21=⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-EG M G N E L ,则得⎪⎭⎫ ⎝⎛+=G N E L k n 21. 它与切方向θ无关,这时,曲面的主方向不确定,这样的点称为曲面的脐点. 命 2121),(21k k K k k H =+=…………(4.7) 分别称为曲面在P 点的平均曲率和Gauss 曲率.根据21,k k 的表达式(4.4),(4.5),在F=0时我们有H 和K 的表达式:⎪⎭⎫⎝⎛+=G N E L H 21 EG M LN K 2-=要强调指出的是,我们在上面计算曲面在点P 的主曲率21,k k .平均曲率H 和Gauss 曲率K 时.预先假定参数曲线网在P 点正交.即在P 点有F=0.如果去掉这个假定,则不难导出 )(222F EG NGMF LG H -+-=…………(4.8)22FEG M LN K --= …………(4.9) 下面,我们来看一下函数Z=f(x,y)的图像的平均曲率,Gauss 曲率的表达式,在第三节中已经指出Z=f(x,y)的图像可以看作一下的参数曲面 )),(,,(y x f y x r = …………(4.10) 直接微分得到),0,1(x x f r =, ),1,0(y y f r =, ).1,,(y x y x f f r r --=⨯ 因此曲面的单位法向量是,11,1,1222222⎪⎪⎪⎭⎫ ⎝⎛++++-++-=y x y x y y x x f f f f f f f f n 第一基本形式和第二基本形式的系数分别是221,,1y y x x f G f f F f E +==+=.1,1,1222222yxyy yxxy yxxx ff f N ff f M ff f L ++=++=++=所以平面的平均曲率是])1(2)1[()1(21)(222223222yy x xy y x xx y yxf f f f f f f f f F EG NEMF LG H ++-+++=-+-=…………(4.11) Gauss 曲率是)1(22222y x xy yy xx f f f f f F EG M LN K ++-=--= …………(4.12) 比较H 的表达式(4.11)和Lagrang 的极小曲面方程(2.14)可知,方程(2.14)等价于:H=0 …………(4.13)这是完全几何化的条件,与表示曲面的方式是无关的,因此我们给极小曲面下一个正式的定义:3R 中平均曲率恒等于零的曲面称为极小曲面.第五章 极小曲面的Weierstrass 公式本节我们要指出极小曲面与复变函数论有密切的联系,从极小曲面理论的发展和现状来看,复变函数论在其中起着不可替代的作用,原因是Weierstrass 发现了极小曲面方程的用复变函数给出的通解,即所谓的Weierstrass 公式,从而揭示了极小曲面与全纯函数,亚全纯函数之间的本质联系.关于曲面论的一个特别重要的事实是,在有向的正则曲面上可以引进复坐标,而且当两个复坐标域有彼此重叠的部分时,这两种复坐标之间有互为全纯函数(或称复解析函数)的关系.用现代的语言说,有向的正则曲面是一个一维复流行,至于在有向正则曲面上可以引进复坐标的根据在于曲面上存在局部的等温参数系.在第三节,我们对于正则参数曲面 2),(),,(R D v u v u r r ⊂∈=定义了第一基本形式: 222Gdv Fdudv Edu I ++=.其中G F E ,,恰好是自然标架的切向量v u r r ,的度量系数,即 .,,v v v u u u r r G r r F r r E ⋅=⋅=⋅=如果,0≡F 并且G E ≡则我们称(u,v)为曲面的等温参数系.在等温参数系(u,v)下,自然标架的切向量v u r r ,是彼此正交的,并且它们的长度相等.此时,曲面的第一基本形式成为)(22dv du I +=λ 其中 0),(),(>==v u G v u E λ.我们知道( u,v)本来是区域2R D ⊂ 内的笛卡儿直角坐标系,平面区域D 本身的第一基本形式是 22dv du +.我们所考虑的曲面实际上是从3R D 到内的一个映射,所以(u,v)是曲面上的等温参数系的意思是上面的映射是保角的,即在每一点(u,v)的两个切向量的夹角在映射下保持不变, 并且在该点的各个方向的切向量的长度在映射下按照同一个比例系数),(v u λ伸缩,既然每一个有向正则曲面在局部上总是存在等温系数的.因此任意两个正则曲面在局部上都是彼此成保角对应的,这是二维曲面特有的性质.对于曲面上的等温参数系(u,v),引进复变量v u 1-+=ω,则ω是极小曲面上的局部复坐标系.重要的是,如果M 在有重叠部分的两个区域上分别有等温参数系(u,v)和)~,~(v u,命ω~=v u ~1~-+,则在这个区域的重叠部分,复坐标ω~是ω的全纯函数,反过来ω也是ω~的全纯函数.实际上,由于)~,~(),,(v u v u 都是等温参数系,故在公共区域上有)~~(~)(2222vd u d dv du I +=+=λλ, 其中0~,>λλ.所以2222222222~~~~~~~~~~)(dv v v v u dudv u v v v v u u u du u v u u v d u d dv du ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=+=+ρ故有ρ=⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂2222~~~~v v v u u v u u ,0~~~~=∂∂∂∂+∂∂∂∂uv v v v u u u, 其中0~>=λλρ.由此可见,Jacobi 矩阵是T v v uv v u u u ⋅=⎪⎪⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂∂∂ρ~~~~, 其中T 是一个2阶正交矩阵.由于M 的有向性,从)~,~(),(v uv u →的参数变换是保持定向的,所以⎪⎪⎭⎫⎝⎛-=θθθθc o s s i n s i n c o s T , 这意味着 uv v u v v u u ∂∂-=∂∂∂∂=∂∂~~,~~. 上面的方程正好是函数),(~~),,(~~v u v v v u u u== 的Cauchy-Riemann 方程,故复坐标ω~写成ω的函数时是复解析函数,或全纯函数.同时这也说明参数变换)~,~(),(v uv u 必定是实解析的. 一般地,如果M 是一个Hausdorff 拓补空间,并且M 上的每一个点都有一个领域能够与复平面上的一个开区域建立同胚关系,那么通过上述同胚关系在这个邻域内建立了复坐标系.再进一步,如果M 上有非空交集的两个复坐标域上的复坐标都是全纯的.则我们称M 是一维复流行.或称M 为一个黎曼曲面.依照这个说法,空间3R 中任意一个有向的正则曲面都是一个黎曼曲面.在研究黎曼曲面的时候,引进复坐标系常常可以使问题边的简单.现在假定M 是用等温参数u,v 表示的一块曲面),(v u r r =.其中),(v u 的定义域D 是2R 内的一个区域,其第一基本形式为)(22dv du I +=λ.设复坐标为v u 1-+=ω,…………(5.1) 并且引进复化的偏微分算子,121121⎪⎭⎫ ⎝⎛∂∂-+∂∂=∂∂⎪⎭⎫ ⎝⎛∂∂--∂∂=∂∂v u v u ωω…………(5.2) 若f 是定义在D 上的可微函数,则ωωωωωωωωd fd f d d v f d d u f dv v f du u f df ∂∂+∂∂=--⋅∂∂++⋅∂∂=∂∂+∂∂=)(121)(21.…………(5.3)这个公式表明,可微函数),(v u f 可以看成变量ωω,的函数,而微分df 可以展开成ωωd d ,的一次形式,其系数是形式偏导数ω∂∂f 和ω∂∂f,函数f 是全纯函数的条件是f 的实部和虚部满足Cauchy-Riemann 方程.,)(I m )(R e ,)(I m )(R e uf v f v f u f ∂∂-=∂∂∂∂=∂∂ 这等价于.0Im 1Re 1Im 1Re 21=⎥⎦⎤⎢⎣⎡∂∂-+⎪⎭⎫⎝⎛∂∂-+⎪⎭⎫ ⎝⎛∂∂-+∂∂=∂∂v f v f u f u f f ω 由此可见,全纯函数f 有关于ω的导数,并且ωω∂∂=fd df …………(5.4) 利用上面的记号,把),(v u r 看成向量函数,命 v u r r r12--=∂∂=ωφ,…………(5.5) 它是曲面M 的切向量v u r r ,的复线性组合,即φ是一个复化的切向量.将φ对ω求偏导数,并且利用vu uv r r =,我们有)(21)1(121vv uu v u r r r r v u +=--⎪⎭⎫ ⎝⎛∂∂-+∂∂=∂∂ωφ.…………(5.6)容易看出ωφ∂∂是曲面的法向量.实际上0)(21)()(2121)(21=⎥⎦⎤⎢⎣⎡⋅∂∂-⋅∂∂+⋅∂∂=⋅+⋅=⋅∂∂v v v u u u u vv u uu u r r u r r v r r u r r r r r ωφ, 这里用到了),(v u 是等温参数的假定.同理有 0=⋅∂∂v r ωφ. 于是ωφ∂∂必定是曲面的单位法向量n 的倍数,该倍数是 ,)(21)(21H N L n r n r n vv uu λωφ=+=⋅+⋅=⋅∂∂ 因此 .Hn λωφ=∂∂…………(5.7) 如果M 是一块极小曲面,则上式成为,0242=+=∂∂=∂∂∂vv uu r r r ωφωω…………(5.8) 因此,曲面M 是极小曲面的充分必要条件是它的参数方程),(v u r 是等温参数v u ,的调和函数.这是Weierstrass 给出的定理.(5.8)式还说明,复化切向量φ作为向量函数是复变量ω的全纯函数.我们的目的是通过φ这样的全纯函数重建极小曲面的参数方程.我们先给出函数φ的几个性质.将φ与它自身作内积得到,12)1()1(22v u vuv u v u r r r r r r r r ---=--⋅--=⋅φφ所以),(v u 是曲面M 的等温参数的条件化为φ满足方程0=⋅φφ …………(5.9) 另外,,02)1()1(22>=+=-+⋅--=⋅λφφvu v u v u r r r r r r …………(5.10)这意味着函数φ不能有零点.现在记φ的分量分别为,,,321ϕϕϕ即,1,1,1321v u v u v u z z y y x x --=--=--=ϕϕϕ则方程(5.9)成为.0232221=++ϕϕϕ…………(5.11)条件(5.10)成为,0232221≠++ϕϕϕ即321,,ϕϕϕ没有公共零点. 将(5.11)改写成232121)1)(1(ϕϕϕϕϕ-=---+,命 211ϕϕ--=f …………(5.12) 如果f 恒等于零,则03≡ϕ,故 ,0≡=v u z z这说明M 是平行于xy-坐标面的一块平面.下面假定f 不恒等于零,因为f 是全纯函数,故它的零点都是孤立的,这样2131ϕϕϕ--=g …………(5.13)是ω的亚纯函数,g 的极点是f 的零点.此时,从(5.11)式得到 221232111g f ⋅-=---=-+ϕϕϕϕϕ …………(5.14)从(5.12),(5.13),(5.14)可以解出 ⎪⎪⎪⎩⎪⎪⎪⎨⎧=+-=-=fg g f g f 32221),1(21),1(21ϕϕϕ …………(5.15) 现在,这个过程可以倒过来,设f 是定义在D 上的全纯函数,g 是定义在D 上的亚纯函数.如果g 的极点集包含在f 的零点集内,并且g 的极点阶数的两倍不大于该点作为f 的零点的阶数,则由(5.15)式给出的321,,ϕϕϕ都是ω的全纯函数,并且它们自动地适合方程(5.11).另外,从(5.15)式得到,)1(21222232221g f +=++ϕϕϕ…………(5.16) 所以要321,,ϕϕϕ没有公共零点,必须使f 没有除g 的极点以外的零点,并且f 的零点的阶数不能大于该点作为g 的极点的阶数的两倍.把这两个方面结合起来,g 的极点集和f 的零点集恰好是一致的,并且g 的极点阶数的两倍等于该点作为f 的零点的阶数.最后,从ωφ∂∂=r2得到⎪⎭⎫ ⎝⎛∂∂+∂∂=-+⎪⎭⎫⎝⎛∂∂--∂∂=dv v r du u r dv du v r u r d )1(1ωφ+.1⎪⎭⎫ ⎝⎛∂∂+∂∂--dv u r du v r如果已经给出了参数方程),(v u r ,则 ⎰⎰∂∂+∂∂==),(),(),(),(0000),(v u v u v u v u dv vrdu u r dr v u r与积分路径无关,所以积分⎰ωφd 没有实周期,即对于区域D 内的任意一条闭路径C ,,0Re =⎰Cd ωφ并且⎰=ωωωφ0Re ),(d v u r .把上面的讨论总括起来得到下面的结果:设M :D v u v u r r ∈=),(),,(是以),(v u 为等温参数系的极小曲面,并且M 不是平行于xy-坐标面的一块平面,则有定义在D 上的全纯函数f 和亚纯函数g ,f 的零点集与g 的极点集是重合的,并且f 的零点阶数等于该点作为g 的极点的阶数的两倍,使得曲面M 的参数方程),(v u r 可以表示为⎪⎪⎪⎩⎪⎪⎪⎨⎧=+-=-=⎰⎰⎰ωωωωωωωωω00.Re ,)1(21Re ,)1(21Re 22fgd z d g f y d g f x …………(5.17)反过来,任意给定满足上述条件的全纯函数f 和亚纯函数g ,只要(5.17)式右边的积分没有实周期,则(5.17)式便给出了以(v u ,)为等温参数的极小曲面.由此可见,(5.17)给出了3R 中极小曲面的通解,称为极小曲面的Weierstrass 公式,通常把(5.17)中的函数g f ,称为W -因子.参考文献[1] 梅向明,黄敬之. 微分几何.第三版. 北京:高等教育出版社, 2003.[2] 陈维桓. 极小曲面. 湖南:湖南教育出版社,1993.[3] 陈维桓. 微分几何初步. 北京:北京大学出版社,1990.[4] L. V. 阿尔福斯, 复分析, 上海:上海科学技术出版社, 1984.[5] 陈维桓. 夏仁龙. 赵国松. 关于3R中极小曲面的一个注记. 北京大学学报, 1987, 第一期:12~15.[6] L.Xiao. Some results on pseudo-embedded minimal surfaces in3R.Acta Math. Sinica,1984. 3:116~120[7] M. Struwe. Plateau’s Problem and the Calculus of Varia-tions. PrincetonUniv. Press,1998.[8] 华东师范大学数学系. 数学分析. 第三版. 北京:高等教育出版社,2003.[9] J. L. M. Barbosa, M. Do Carmo ,On the size of a stable minimal surfacesin 3R.Amer. J. Math. ,1976, 98:515~528[10] J. L. M. Barbosa, A. G. Colares, Minimal surfaces in 3R.Lecture Notesin Math,1195.[11] 熊金城. 点集拓补讲义. 第三版. 北京:高等教育出版社. 2003.[12] M. do Carmo, C.K. Peng. Stable complete minimal surfaces in3R areplane, Bull. AMS,1979, 1:903~906[13] R. Courant. Dirichlet’s Principle,Conformal Mapping, and MinimalSurfaces. Interscience, New York, 1950.[14] R. Courant. Soap film experiments with minimal surfaces. Amer. Math.Monthly ,1940.[15] H. B. Lawson, Jr. ,Lectures on Minimal Surfaces. Publish or Perish,Berkeley,1980.谢辞本研究及学位论文是在我的导师郑老师的亲切关怀和悉心指导下完成的。
COMSOL寻找最小曲面案例

COMSOL寻找最小曲面案例
觉得这个例子有点意思。
参考《COMSOL Mulitiphysics基本操作指南和常见问题解答》P71
问题提出:
给定一个空间曲线,通过这条曲线的曲面有无数个,那么哪个曲面的面积最小呢?
数学处理:
曲线在XY平面上有一个投影,在这个投影区域Ω的边界∂Ω上给定函数值u|∂Ω=Φ(x,y),则曲面的最小面积为:
采用Euler-Lagrange方程,上式转化为:
变分法:
采用试函数法求解该问题为:
相当于输入:
引入边界条件:
u|∂Ω =Φ(x,y)即可求解。
这个算例告诉我们如何求解最小值问题,如果用COMSOL的弱形式,那么只须将求解函数丢到test()中,加上合适的边界条件即可。
求解设置:
引入边界条件:
取Ω={(x,y)|x^2+y^2<1},u|∂Ω=x^2。
即求解域为一个半径为1的圆,边界值用dirichlet条件r=x^2,其空间曲线为一个马鞍线,解的边缘为该曲线,而显示的曲面为最小面积的曲面。
另外的例子:矩形求解域,边界值为 (x-0.5)^2+(y-0.5)^2
THANKS !!!
致力为企业和个人提供合同协议,策划案计划书,学习课件等等
打造全网一站式需求
欢迎您的下载,资料仅供参考。
34高斯曲率与平均曲率

3.4 高斯曲率与平均曲率-高斯映射
高斯映射的参数表示为 g0 = g0(u,v),其中 g0(u,v) = g(r(u,v)) = n(u,v). 我们也把 g0 叫曲面 S 的高斯映射或球面表 示. n(u,v)
g
n(u,v)
S
r (u,v) S2 g0
3.4 高斯曲率与平均曲率-高斯映射
因为 g0 是从 G 到 R3 的一个映射,因此是 一张参数曲面,但不一定是正则的.
3.4高斯曲率与平均曲率
内容:高斯曲率、平均曲率、高斯映射、 第三基本形式、极小曲面、常高斯曲率曲 面 重点:高斯曲率与平均曲率的计算
3.4 高斯曲率与平均曲率-高斯曲率与平均曲率的概念
曲面的两个主曲率之积 K = k1k2 叫曲面的 高斯曲率,两个主曲率的平均值 H = ½(k1 + k2) 叫曲面的平均曲率. 椭圆点即高斯曲率大于零的点,双曲点即 高斯曲率小于零的点,抛物点即高斯曲率 等于零的点.
3.4 高斯曲率与平均曲率-第三基本形式
曲面的第三基本形式定义为 III = dn ⋅ dn. 将第三基本形式写成 III = edu2 + 2f dudv + gdv2, 则有 e = nu ⋅ nu,f = nu ⋅ nv,g = nv ⋅ nv. 定理. 设有曲面 S: r = r(u,v),其平均曲率 为 H,高斯曲率为 K,则有 III – 2H II + K I = 0. 看证明
3.4 高斯曲率与平均曲率-旋转常高斯曲率曲面
设旋转曲面 S: r = (ucosv, usinv, y(u)),这 是一张由 Oxz 平面上的曲线 z = y (x) 绕 z 轴旋转而成的曲面.试求y 使得 S 的高斯 曲率 K 为常数. 详情
最速降线问题解的充分条件的证明

最速降线问题解的充分条件的证明邢家省;杨义川【摘要】将最速降线问题转化为求一个泛函的最小值问题,给出了泛函临界点是泛函最小值点的直接证明和泛函临界点唯一性的证明.【期刊名称】《吉首大学学报(自然科学版)》【年(卷),期】2019(040)002【总页数】4页(P1-4)【关键词】最速降线问题;泛函;临界点;最小值;充分条件【作者】邢家省;杨义川【作者单位】北京航空航天大学数学与系统科学学院,北京100191;北京航空航天大学数学、信息与行为教育部重点实验室,北京100191;北京航空航天大学数学与系统科学学院,北京100191;北京航空航天大学数学、信息与行为教育部重点实验室,北京100191【正文语种】中文【中图分类】O175.29最速降线问题[1-6]是变分法起源的一个古典问题.在解决最速降线问题的过程中,人们只关注最速降线问题的必要条件,而没有考虑其充分条件.文献[2-4]研究了一般变分泛函临界点为泛函最小值点的充分条件,虽然给出了相当复杂的理论方法,但是都没有直接证明最速降线问题的充分条件.笔者拟在文献[7-12]的基础上,给出泛函临界点为泛函最小值点的简洁证明和泛函临界点的唯一性的证明,对最速降线问题作出完善的解答.1 最速降线问题转化为泛函的最小值问题最速降线问题描述如下:在一铅直平面上,给定不在同一铅直直线上的两点A,B.在重力作用下,一质点沿着过A,B两点的光滑轨道L下滑,下滑的轨道L不同,质点由A点下滑到B点所需的滑动时间T也就不同.问当L是什么曲线时,所需的滑动时间T最短?具体到坐标系中,最速降线问题的描述如下:建立xoy坐标系,ox轴正向水平向右,oy轴正向竖直向下,将o点设在A点,B点坐标为(a,b),a,b>0.设一质点沿某曲线y=y(x)由点o(0,0)无摩擦地滑动到点(a,b),问当y=y(x)是什么曲线时,所需的滑动时间T最短?质点沿曲线y=y(x)由点o(0,0)无摩擦地滑动到点(a,b),所需的时间是设函数集合M={y∈C2[0,a],y(0)=0,y(a)=b,y(x)>0,x∈(0,a]},则T(y)就是定义在M上的一个泛函.于是,最速降线问题转化为在M上求函数y=y(x),使得泛函T(u)在y处有最小值,即求y∈M,使得2 泛函在某函数处有最小值的必要条件令M0={v∈C2[0,a],v(0)=0,v(a)=0},若泛函T(u)在y处有最小值,则对于∀v∈M0,T(y+εv)都在ε=0处达到最小值,于是令则T(y+εv)=F(y(x)+εv(x),(y(x)+εv(x))′)dx,从而∀v∈M0.(1)经过分部积分,得到∀v∈M0.(2)(1)式就是泛函T(u)在y处有最小值的必要条件,显然(1)式与(2)式是等价的.下面证明(2)式的解的存在性.因为(2)式中v∈M0是任意的,所以因为所以(C为常数).对于有于是(3)(3)式可化简成y(1+(y′)2)=c2(c为常数),由此得到令则令w=ccos θ,则令t=2θ,则由条件“当x=0时y=0”可知,对应的c1=0,从而得到曲线的参数方程其中常数k可由另一条件“当x=a时y=b”来确定.显然,最速降线为摆线的一部分[1-6].至此,泛函临界点的存在性得证,但这只是泛函有最小值的必要条件.3 泛函临界点为泛函最小值点的充分条件的证明对于y+εv∈M,有因为在(y(x)+εv(x),(y(x)+εv(x))′)处是正定矩阵,所以∀v∈M0且v不恒为0.由此可知,T(u)在M上的最小值在y∈M处达到.4 泛函临界点方程解的唯一性的证明设y1,y2∈M是问题(1)的2个解,即∀v∈M0,i=1,2,于是注意到从而特别地,取v=y2-y1,则因为在处是正定矩阵,必有所以y2-y1=0,即y2=y1.由此可知,问题(1)的解是唯一的.参考文献:【相关文献】[1] 陆文端.微分方程中的变分方法[M].北京:科学出版社,2003:1-4.[2] 张恭庆.变分学讲义[M].北京:高等教育出版社,2011:30-41.[3] OPREA J.Differential Geometry and Its Applications[M].北京:机械工业出版社,2005:360-367.[4] COURANT R,HILBERT D.数学物理方法(Ⅰ)[M].钱敏,郭敦仁,译.北京:科学出版社,2011:137-176.[5] 陈国旺,陈翔英.非线性高阶发展方程[M].北京:科学出版社,2017:1-24.[6] 谢建华.最速降线问题解充分性的证明[J].力学与实践,2009,31(3):82-84.[7] 刘建新,曲安京.高斯建立绝妙定理的历史过程[J].自然辩证法研究,2017,33(9):108-113.[8] 张光照,邢家省,贺慧霞.曲面上曲线为短程线的必要条件的证明方法[J].河南科学,2013,31(12):2 126-2 132.[9] 邢家省,贺慧霞,高建全.给定边界面积最小的曲面的平均曲率为零的证明方法[J].四川理工学院学报(自然科学版),2014,27(2):83-86.[10] 邢家省,杨小远.一类欧拉积分公式与广义菲涅尔积分的计算[J].吉首大学学报(自然科学版),2018,39(1):1-6.[11] 邢家省,杨义川.分布函数列的一致收敛性[J].吉首大学学报(自然科学版),2018,39(2):1-4.[12] 陈祖墀.偏微分方程[M].合肥:中国科学技术大学出版社,2002:236-258.。
微分几何第二章曲面论曲面的概念

VS
高斯曲率
设曲面$S$在点$P$处的两个主曲率分别为 $k_1, k_2$,则称$K = k_1k_2$为曲面在 点$P$处的高斯曲率。高斯曲率是曲面内蕴 几何量的重要代表,反映了曲面在一点处 的弯曲程度。
法截线和法截线族
法截线
设曲面$S$在点$P$处的法向量为 $mathbf{n}$,过点$P$且与法向量 $mathbf{n}$垂直的平面称为法截面。 法截面与曲面交于一条曲线,该曲线 称为法截线。
曲面性质
曲面具有连续性、光滑性、可定向性等性质。其中连续性指 曲面上任意两点都可以用一条连续曲线连接;光滑性指曲面 上任意一点都存在切线平面;可定向性指曲面存在连续的单 位法向量场。
曲面分类与举例
曲面分类
根据曲面的形状和性质,可以将曲面分为闭曲面、开曲面、紧致曲面、非紧致曲面等类 型。
举例
球面、环面、柱面、锥面等都是常见的曲面类型。例如,球面可以表示为 $mathbf{r}(theta, varphi) = (Rcosthetasinvarphi, Rsinthetasinvarphi,
法截线族
过曲面上一点的所有法截线构成的集 合称为该点的法截线族。法截线族在 微分几何中具有重要的研究价值,与 曲面的形状和性质密切相关。
04
曲面局部理论:可 展曲面与极小曲面
可展曲面定义及性质
定义
可展曲面是一类特殊的曲面,它可以在不改 变距离的情况下完全展开到一个平面上。也 就是说,它的高斯曲率为零。
02
第一基本形式与度 量性质
第一基本形式定义及性质
第一基本形式定义
第一基本形式是微分几何中曲面论的基本概念,用于描述曲面上的度量性质。它是一个二次微分形式,记作$I = Edu^2 + 2Fdudv + Gdv^2$,其中$E, F, G$是曲面上的系数函数。
谱半径平均度证明

谱半径平均度证明要证明一个有向图的谱半径与平均度存在关系,需要从图论和线性代数两个方面进行证明。
1. 图论证明:设有向图G的邻接矩阵为A,G中共有n个顶点。
邻接矩阵的元素a[i][j]表示顶点i到顶点j的有向边的权重,如果没有边连接i和j,则a[i][j]=0。
图G的度矩阵D是一个对角矩阵,其对角线元素d[i][i]表示顶点i的度数。
那么,G的拉普拉斯矩阵L=D-A。
根据图论中拉普拉斯矩阵的性质,拉普拉斯矩阵具有以下两个性质:(1)拉普拉斯矩阵是一个实对称矩阵。
(2)拉普拉斯矩阵的最小特征值为0,其对应的特征向量为1的倍数。
由于G是有向图,拉普拉斯矩阵不一定是对称矩阵,但是可以通过构造一个新的矩阵H,使得H=QT LQ是一个对称矩阵,其中Q是一个辅助矩阵。
所以我们考虑证明H的最小特征值为0。
由于L=D-A,所以有DL=L+DL。
考虑H的一个特征向量x,对应特征值为λ。
则有:Hx=(QT LQ)x=QT(DL-A)Qx = QTDLQ-QTAQx = λx即:DLQx-λQx - QTAQx = 0令y=Qx,则上述等式可变形为:DLy-λy-QTAy = 0左右乘以QT:QTLQTDLy-λQTLQy - QTLQTAy = 0由于QTLQ是对称矩阵,所以有:QTLQTDLy-λQTLQy - QTLQTAy = 0即:D(Ly)-λ(Ly)-AT(Ly) = 0所以我们可以得到,y是拉普拉斯矩阵DL−λI−AT的特征向量。
由于图G的谱半径是拉普拉斯矩阵的最大特征值,我们可以得到λ的范围为0 ≤ λ ≤ Δ(G),其中Δ(G)表示G的最大度数。
2. 线性代数证明:由于拉普拉斯矩阵L是实对称矩阵,所以它的特征值一定是实数。
我们知道,对于一个对称矩阵,存在n个正交归一的特征向量,它们对应的特征值构成一个实数集合。
设G的特征值为λ1,λ2,...,λn,则谱半径ρ(G)=max{|λ1|,|λ2|,...,|λn|}。
曲率推导过程

曲率推导过程一、引言曲率是微分几何学中一个重要的概念,用于描述曲线或曲面的弯曲程度。
曲率推导是研究曲线或曲面曲率性质的基础。
本文将详细介绍曲率推导的过程,并深入探讨相关概念和算法。
二、曲率的定义曲线的曲率在数学上有多种不同的定义,其中一种较为常见的定义是使用切线和曲率圆。
设曲线上一点P,以P为圆心,曲线上的一条切线为切线L,切线L与曲线的交点为Q,则曲线在点P处的曲率定义为切线L的切线段OQ相对于OP的夹角的倒数。
三、平面曲线曲率的推导对于平面曲线,其曲率可以通过一系列计算步骤推导得到。
具体推导过程如下:1. 参数表示假设平面曲线C可以用参数方程x(t)和y(t)表示,其中t为参数。
则点P的坐标为(x(t), y(t)),切线向量为(Tx, Ty)。
2. 切线向量的表示切线向量的计算公式为:Tx = dx / dtTy = dy / dt其中,dx / dt和dy / dt为曲线在点P处的导数。
3. 曲率圆推导建立坐标系,以点P为原点。
设曲率圆的半径为R,曲率圆与曲线相切于点Q。
连接点P和Q,则向量PQ的方向为法向量N。
曲线在点P处的曲率C定义为切线L的切线段OP相对于N的夹角的倒数。
4. 坐标表示设曲率圆的中心坐标为(a, b),则曲线在点P处的曲率C的计算公式为:C = lim (x -> a) (1 / R) = lim (x -> a) (y - b) / sqrt((x - a)^2 + (y - b)^2)5. 曲率计算根据曲线参数表示和曲率圆推导的结果,可以计算曲率C。
首先计算曲率圆中心坐标(a, b),然后计算曲率圆半径R,最后代入曲率公式即可得到曲率C的值。
四、空间曲面曲率的推导与平面曲线类似,空间曲面的曲率也可以通过一系列计算步骤推导得到。
具体推导过程如下:1. 参数表示假设空间曲面S可以用参数方程x(u, v)、y(u, v)和z(u, v)表示,其中u和v为参数。
曲率及其计算方法

曲率及其计算方法曲率是求解曲线弯曲程度的一种数学概念,可以十分精确地描述曲线的形态。
在物理、工程、制图等领域中,曲率的计算十分重要,可以用来精确描述曲线的性质和特征。
这篇文章将介绍曲率的概念、定义和计算方法,并通过实例来说明它对于现实问题的应用。
一、曲率的概念和定义在平面或者空间中,曲线上的每一个点都可以定义一个曲率。
曲率是该点所在曲线的弯曲程度的度量。
在数学中,曲率的定义如下:(1) 平面曲线上一点的曲率:曲率k是切线方向上一阶导数 |v'(t)| 与切向量方向上一阶导数|v(t)| 之比的绝对值:k = |v'(t)| / |v(t)|其中v(t)是曲线的弧长参数表示,v'(t)是v(t)关于t的一阶导数。
曲率k的单位是1/长度。
(2) 空间曲线上一点的曲率:空间曲线上一点的曲率是该点在曲线切平面中切向量的曲率。
二、曲率的计算方法有了前面的曲率概念和定义的基础,接下来我们将介绍如何计算曲线的曲率。
首先,我们需要了解两个概念:弧长和参数式。
(1) 弧长弧长是曲线长度的测量量。
对于参数式 r(t) = (x(t),y(t)), t∈[a,b]的曲线,它的弧长可以通过下式计算:s = ∫(a,b) |r'(t)| dt其中 |r'(t)| 表示 r(t) 的变化率,s 为曲线长度。
通过弧长可以确定曲线上每一点的位置以及曲线围成面积的大小。
(2) 参数式对于平面曲线,我们可以用参数式来表示曲线上的点,即x(t) = x,y(t) = y其中t作为参数。
通过变化t的值,我们可以确定曲线上的每一个点。
同理,对于空间曲线,我们也可以用参数式来表示曲线上的每一个点。
现在我们已经具备了曲率计算的前置知识,接下来我们将详细介绍两种曲率的计算方法。
(1) 弧长参数曲率计算法对于参数式表示的曲线,我们可以通过弧长参数求解其曲率,具体计算方法如下:1. 计算弧长s:s = ∫(a,t) |r'(t)| dt其中r'(t)为r(t)的一阶导数。
极小曲面方程黎曼几何

极小曲面方程黎曼几何全文共四篇示例,供读者参考第一篇示例:极小曲面方程是黎曼几何中一个重要的概念,它研究的是曲面上的特殊曲面,这些曲面在曲率非常小的情况下表现出特殊的几何性质。
在黎曼几何中,曲面的曲率是一个重要的性质,它描述了曲面的变曲性,即在曲面上任意一点处的曲线的曲率。
极小曲面是指曲率几乎为零的曲面,它们在曲率几乎为零的情况下表现出来的性质是非常特殊的。
我们来看极小曲面的定义。
一个曲面被称为极小曲面,如果它的高斯曲率等于零,即K = 0。
在曲面的参数化表示下,极小曲面的方程通常是一个非线性偏微分方程,其解可能是很复杂的。
极小曲面的权力意味着其具有一些特殊的性质,比如在其上的曲线的长度最小等。
那么极小曲面在黎曼几何中有什么重要性呢?极小曲面的研究在几何学和拓扑学中占有重要地位。
极小曲面的研究可以帮助我们理解曲面的局部结构。
极小曲面存在的条件对于拓扑学中的一些问题具有重要的应用价值。
在黎曼几何中常常用极小曲面来研究拓扑空间的不变量,比如欧拉数等。
极小曲面方程在黎曼几何中的研究是一个重要的课题,它不仅有着深刻的理论意义,还具有广泛的应用价值。
通过研究极小曲面方程,我们可以更深入地理解曲面的几何性质,进而推动几何学和拓扑学等领域的发展。
希望未来能有更多的学者投入到极小曲面方程的研究中,为这一领域的发展带来更多的新的突破和进展。
第二篇示例:极小曲面方程是黎曼几何中一个非常重要的概念。
在黎曼几何中,我们研究的对象是曲面和流形,而极小曲面则是其中的一类特殊的曲面。
极小曲面在数学和物理领域都具有重要的应用价值,它们在微分几何、微分方程、拓扑学等领域都有着广泛的应用。
我们来介绍一下什么是极小曲面。
在黎曼几何中,给定一个曲面,我们可以通过测量曲面上的长度、角度等几何量来描述这个曲面。
极小曲面是指在给定度量下表面积最小的曲面。
具体来说,对于一个曲面上的曲线,我们可以通过积分来计算这个曲线的长度,而曲面上的面积则可以通过这些曲线的长度来计算。
泊松公式:描述在曲面上平均值的积分公式

泊松公式:描述在曲面上平均值的积分公式第一章:引言在数学中,曲面的平均值是一个重要的概念。
通过平均值,我们可以描述曲面上的各种性质,并进行计算和分析。
泊松公式就是一种用来计算曲面上平均值的积分公式。
在本文中,我们将介绍泊松公式的定义、推导方法和应用。
第二章:泊松公式的定义泊松公式是由法国数学家西莫恩·泊松于19世纪初提出的。
在曲面上,泊松公式将一个函数的平均值与该函数在曲面上的积分联系起来。
具体而言,设曲面S 的方程为F(x, y, z) = 0,函数f(x, y, z)在曲面上的平均值为M,曲面S的面积为A,则泊松公式可以表示为:M = 1/A ∬S f(x, y, z) dS其中∬S表示对曲面S进行面积积分,dS表示曲面S上的面积元素。
第三章:泊松公式的推导为了推导泊松公式,我们首先将曲面S分成无数个小面元,每个小面元的面积为dS。
然后,我们可以将函数f在每个小面元上的取值视为常数,即f(x, y, z) ≈c。
根据积分的定义,我们可以将曲面上的积分拆分为对每个小面元的积分,即:∬S f(x, y, z) dS = ∑c dS其中∑表示对所有小面元求和。
由于每个小面元的面积相等,我们可以将dS提取出来,并用曲面S的面积A代替每个小面元的面积,即:∑c dS = c ∑dS = cA因此,泊松公式可以改写为:M = 1/A ∬S f(x, y, z) dS ≈1/A cA = c也就是说,曲面上的平均值M近似等于函数f在曲面S上的任意一点的取值c。
第四章:泊松公式的应用泊松公式在数学和物理学中有广泛的应用。
其中一种重要的应用是计算曲面上的质心坐标。
设曲面S的方程为F(x, y, z) = 0,函数f(x, y, z)表示曲面S上的密度分布,则曲面S的质心坐标可以通过泊松公式计算得到:(xc, yc, zc) = (1/M) ∬S (xf(x, y, z), yf(x, y, z), zf(x, y, z)) dS其中M表示曲面S的质量。
.一般曲面

§ 12一般曲面一、曲面的方程与曲线的坐标曲面方程的形式有隐 式 F (x ,y ,z )=0 显 式 z =f (x ,y )参数式⎪⎩⎪⎨⎧===),(),(),(υυυu z z u y y u x x 矢量式 r =r (u ,υ) 或 r =x (u ,υ)i +y (u ,υ)j +z (u ,υ)k对于参数式或矢量式表示的曲面,如果取υ为一系列数值,,21υυ ,而让u 连续变动,则r (u ,i υ)(i =1,2, )表示一族曲线,称为u 线(图7.23);同样,如果取u 为一系列数值u 1,u 2, ,而让υ连续变动,则r (u i ,υ)(i =1,2, )表示另一族连续曲线,称为υ线.u 线与υ线在曲面上构成曲线网,称为坐标线或坐标网.于是u =u i , υ=j υ这个数对就可以确定曲面上一点M ,这数对(u i ,j υ)称为点M 的曲线坐标(或高斯坐标).二、 切面、法线与曲面的方向[法线单位矢量] 通过曲面上一的M 所有曲面曲线(即该曲面上的曲线),在点M 的切线落在同一平面上(奇点除外),称这平面为曲面在点M 的切面通过点M 与切面垂直的直线称为曲面在点M 的法线.切面通过的矢量r u =u ∂∂r和υυ∂∂=r r 称为坐标矢量,它们分别是u 线和υ线在点M 的切矢量(图7.24)曲面上点的法线单位矢量为υυr r r r N ⨯⨯=u u这里为了区别曲线的法线单位矢量和曲面的法线单位矢量,前者以n 表示,后者以N 表示.[曲面的方向] 曲面的方向规定如下:朝N 的正向那一面是曲面的正面(图7.24中看到的一面);另一面为反面.[曲面的切线方程与法线方程] 曲面方程切面方程法线方程),,(='z y x Fz =f (x ,y ))()()(000000=-+-⋅+-⋅z z F y y F x x F z y x )()(00000y y z x x z z z y x -⋅+-⋅=-00000z y x F z z F y y F x x -=-=-图 7.23图 7.24表中000,,u x x x z F 分别表示ux x ∂∂∂,,在点M (x 0,y 0,z 0)的值,r 0是点M 的矢径,00,υr r u 分别表示υ∂∂∂∂r r ,u 在点M 的值,N 0为点M 的法线单位矢量.[曲面的奇点] 若曲面F (x ,y ,z )=0上一点M (x 0,y 0,z 0)的三个偏导数同时等于零,即0000===z y x F F F则称点M 为该曲面的奇点.三、 第一基本二次型与曲面的度量[第一基本二次型与第一基本量]各量与图形计算公式曲面曲线的弧长L⎩⎨⎧==)()(t t u u υυ 曲面面积S (由曲线围成)曲线夹角α(两条曲线交于点M )⎰⎰++==1010d 2d 22tt t t t G u F uE s L υυ⎰⎰⎰⎰-==SSu F EG S S υd d d 2Θα=δδ⋅=22)()(d d cos r r rr式中 22222d d d 2d υυυυΘδ+δδ+δ++=G u F u E G u F u EE ,F ,G 为曲面的第一基本量(在点M 取值)。
给定边界面积最小的曲面的平均曲率为零的证明方法

记
引 言
以空间封闭曲线 ,为边界的曲面中 , 寻找其面积最 小者 , 这样的问题称为极小 曲面问题 。这涉及 到面
g = ‘ , i , j= 1 , 2
积最小曲面的存在性 、 唯一 性等问题 , 人们 通过考察 面 积最小 曲 面 的必 要 条 件 , 试 图 寻 找 到 面 积最 小 的 曲 面 “ m ] 。现已证明 , 在 固定边界的曲面族中, 假若存 在面 积最小的曲面, 则面积最小的曲面的平均曲率为零¨ 。 这个结果 已被人 们用多种方 式给予 了证 明 , 文献 [ 1 - 9 ] 中给出的原始传统证明过于繁琐 , 有些证 明过程也 不太 全面。本文在文献 [ 1 - 9 ] 的基础上 , 给 光滑 曲线 , 是过 厂的一 曲面 , 且以
厂 为 边界 。
是 A =( g )的逆矩阵 0
0 2
“
O u i a — u
j I ×
l × r2
一 网
b = 。 , i d =1 , 2
设正则曲面 的参数表示为 :
坠
曲面 的面积为 :
2, 3
墨 堂堕堂垫! 鱼签 兰 2
g - -
.
! !±!
+ g ): ∑ 2 g I j
、
)
— r
邸
— — — 丁 —
2
,
gl l
一
- gl 2
一
厂
广
—
一
¨
’
坦 √ ‘ : ‘ ‘ ¨ ; 一 ‘ “ J 1 d u l d u 2
』 ! 工 (
沿任意闭曲面的曲面积分为零的条件

2. 闭曲面积分为零的充要条件
定理2. 设 P(x, y, z),Q(x, y, z), R(x, y, z)在空间二维单
连通域G内具有连续一阶偏导数, 为G内任一闭曲面, 则
P d y d z Q d z d x R d x d y 0
①
的充要条件是:
P Q R 0 , (x, y, z) G
1. 连通区域的类型 设有空间区域 G , • 若 G 内任一闭曲面所围成的区域全属于 G, 则称 G 为空间二维单连通域 ;
• 若 G 内任一闭曲线总可以张一片全属于 G 的曲面, 则称 G 为空间一维单连通域 .
例如, 球面所围区域 既是一维也是二维单连通区域 ; 环面所围区域 是二维但不是一维单连通区域 ; 立方体中挖去一个小球所成的区域 是一维但
②
x y z
证: “充分性”.根据高斯公式可知②是①的充分条件.
“必要性”. 用反证法已. 知①成立, 假设存在 M 0 G, 使
P Q R x y z
M 0
0
因P, Q, R 在G内具有连续一阶偏导数 , 则存在邻域
U (M0 ) G, 使在U (M 0 )上, P Q R 0 x y z
设U (M 0 )的边界为 取外侧, 则由 高斯公式 得
P d y d z Q d z d x R d x d y
U (M0)
P Q R x y z
d xd yd z
0
与①矛盾, 故假设不真.ห้องสมุดไป่ตู้因此条件②是必要的.
证明闭合曲面上外法向的积分为0

证明闭合曲面上外法向的积分为0在数学中,证明闭合曲面上外法向的积分为0是一个重要的定理,它涉及到向量场和曲面积分的概念。
在这篇文章中,我将详细解释这个定理的含义和证明过程。
首先,让我们来解释一下什么是闭合曲面上外法向的积分。
闭合曲面是一个没有边界的曲面,外法向是与曲面垂直的方向。
外法向的积分是指向量场在曲面上的法向分量的积分。
如果这个积分等于0,就意味着向量场在曲面上的法向分量的总和为0,即向量场沿着曲面的法向的总和为0。
现在让我们来证明闭合曲面上外法向的积分为0。
首先,我们可以将闭合曲面分割成许多小的曲面片段,然后对每个曲面片段进行积分。
根据高斯定理,闭合曲面上的外法向的积分等于向量场在整个曲面的散度的积分。
由于向量场在闭合曲面上的散度等于0(因为闭合曲面没有内部或外部),所以闭合曲面上外法向的积分为0。
另一种证明闭合曲面上外法向的积分为0的方法是利用斯托克斯定理。
根据斯托克斯定理,闭合曲面上外法向的积分等于曲面的边界曲线上的环绕向量场的曲线积分。
由于闭合曲面没有边界,所以曲线积分为0,即闭合曲面上外法向的积分为0。
总的来说,证明闭合曲面上外法向的积分为0的关键在于利用高斯定理或斯托克斯定理,将曲面分割成小的曲面片段,然后证明向量场的散度为0或曲线积分为0。
这个定理在数学和物理领域都有广泛的应用,可以帮助我们理解向量场在曲面上的性质和行为。
在实际问题中,证明闭合曲面上外法向的积分为0的定理可以帮助我们分析流体的流动、电场的分布等问题,为我们提供了一种重要的分析工具。
希望这篇文章能够帮助您更好地理解这个定理的含义和证明过程。
如果您有任何疑问或者需要进一步的解释,欢迎向我提问。
谢谢!。
固定边界的曲面中面积最小曲面的必要条件

固定边界的曲面中面积最小曲面的必要条件罗秀华;张光照;邢家省【期刊名称】《河南科学》【年(卷),期】2015(033)010【摘要】The proof method of the necessary condition of minimal curved surface within the curved surface with fixed boundary is discussed in this paper. In three-dimensional Euclidean space,the mean curvature of minimal curved surface within the closed curved surface with fixed boundary is bound to be zero. The proof process of the necessary condition of minimal curved surface within the curved surface with fixed boundary is demonstrated by means of the direct perturbation method of the surface vector equation.%考虑固定边界的曲面中面积最小曲面的必要条件的证明方法问题. 在三维欧氏空间中,给定边界的闭曲面中面积最小的曲面,其平均曲率一定为零. 采用直接的曲面向量方程的扰动方法,给出了固定边界面积最小曲面的必要条件的证明过程.【总页数】5页(P1691-1695)【作者】罗秀华;张光照;邢家省【作者单位】平顶山教育学院,河南平顶山 467000;河南经贸职业学院技术科学系,郑州 450000;北京航空航天大学数学与系统科学学院,数学、信息与行为教育部重点实验室,北京 100191【正文语种】中文【中图分类】O186.1【相关文献】1.曲面间最小距离及其在曲面求交中的应用 [J], 李学艺;陈松;王小椿2.边界稳定化Heegaard曲面具有临界性的一个必要条件 [J], 孙艳红3.给定边界面积最小的曲面的平均曲率为零的证明方法 [J], 邢家省;贺慧霞;高建全4.曲线曲面积分中利用对称性及曲线曲面方程化简 [J], 魏连鑫5.边界元素法中有关积分的计算方法(Ⅱ)柱状边界条件下对曲面积分及椭圆积分的计算 [J], 刘福平;李善军;张庚骥因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( (
'$$ '!$ '$$ '
!$
'$! '!! '$! '
!!
) )
"
(
'!! )'$!
)'$! '$$
)
"
( "! ' & %
$ 参数分量表示的面积最小的曲面的平均 曲率为零的证明
设 !是一封闭空间光滑曲线" "是过 ! 的一曲面" 且以 !为边界( 设正则曲面 "的参数表示为) !" ! ! # $ "# ! % " !$ $ ! # $ "# ! % "$ ! ! # $ "# ! % "$ B ! #$ "
! ! ! !
$#$
;& < < $ # "-"$ B # ;& B# % < #$ < #!
$ ! !
'% ! % ' %槡
= " $ ! > " $ ( " $ !
> = >
= (
> ( $ '% ! % '= ! > =; & # )% 槡
(
= " $
( " $
> " $
显然"若 / 在 !$ $ "$ ! "$ B % 处达到最小值 " 则对任意 < &" : # "&"$ "! "B ( / !!$ !< $ "$ ! "$ B % ;& $ "< ! "< B%% 在 & "# 处达到最小值"所以 < / !!$ !< $ "$ ! "$ B % ;& $ "< ! "< B%% <& 经计算"得 #3 !% < & #4
( (
!
!
!
假若泛函 / 在某处达到最小值"考查其必要条件(
! 由变分引理"设 %为 6 中的开集" 7 !% % " 若对 "8 ! 任意 %" 8 % " 都有 #!%
!
'% ' %槡
( " $
= (
! #$ & ## = ## (
7 ! # "9 %% ! # "9 % < # < 9"# " 则必 &
$# ' ( 现已证明"在固定边界的曲面族中"假若存在面 面 &$C $$ ' 积最小的曲面"则面积最小的曲面的平均曲率为零 &$C (
(
'$$ '!$
) $
'$! '!!
)
$ '
这个结果已被人们用多种方式给予了证明" 文献 & $C D' 中给出的原始传统证明过于繁琐" 有些证明过程也不太 全面( 本文在文献 & $C D ' 的基础上" 给出几种完备的证 明过程"便于人们查找确认使用(
第 !" 卷第 ! 期 !#$% 年 % 月
四川理工学院学报 自然科学版
& ' () *+ , ' ./ 0 1(+ *2 */ 3 4 ) 5 / 6 7' .0 / 4 *0 489 *: / *4 4 ) / *: ; + 6 () + , .0 / 4 *0 49 </ 6 / ' *
邢家省$! 贺慧霞$! 高建全B
! $K 北京航空航天大学数学与系统科学学院" 北京 $##$D$ #!K 数学$信息与行为教育部重点实验室" 北京 $##$D$ # BK 平顶山教育学院" 河南 平顶山 %E"### %
55摘5要在曲面论几何中定义平均曲率为零的曲面为极小曲面 而在三维欧氏空间中 给定边界 的闭曲面中面积最小的曲面 其平均曲率一定为零 即给定边界的闭曲面中面积最小的曲面为极小曲 面 文章用变分理论给出几种新的证明使证明过程更加直接明了 关键词极小曲面正则曲面平均曲率变分方法 中图分类号L $ME> $ 记 ! & "! # "
&
文献标志码@
引 言
以空间封闭曲线 !为边界的曲面中"寻找其面积最
$# ' ( 这涉及到面 小者"这样的问题称为极小曲面问题 &$C
! #! ## &
'& *! "& "( "$ "! ( "! & ( '$$ '!! )'$! '!$ "' % " *"! ' & ( 命
) $ * "
积最小曲面的存在性$ 唯一性等问题" 人们通过考察面 积最小 曲 面 的 必 要 条 件" 试 图 寻 找 到 面 积 最 小 的 曲
= (
+& = (
其中 + $"! +$ "+! "+B % 是曲面上的单位法向量( 于是
! !
'' %% 槡
= " $ ( " $
= (
+ & "# = (
而
第 !" 卷第 ! 期?? ???邢家省等固定边界面积最小的曲面的平均曲率为零的证明方法 ." 所以有 '! . + & "# "&"$ "! "B 槡 从而 . "# ( 定理 ! 对于过空间光滑闭曲线 ! 的曲面 " " 如果 !所围的曲面 "的面积最小"则曲面 "的平均曲率恒等 于零( 平均曲率为零的曲面"未必是面积最小的曲面( < 考察 ! / !!$ !< $ "$ ! "$ B % ;& $ "< ! "< B % % " 可知其为 <& 不定型"若想为正定型是需要条件的(
!
MN
#
$ !
!
"$ " $ #
%- '
# $
# $
$*! ! ! ,+ $*! ! ! ,+ &? % )? % ' <#<9 $ $ &
# 9 9
%
$ "' 利用格林公式"注意到 ? A "得 #% $* $ ? ! ! ,$ +% <#<9"( ? *! ! ,$ +% 0 ' 5 !! "#% <B ) &
."
"$ " $ #
%- '
# $
# $
收稿日期 !#$BC $$C !B 基金项目国家自然科学基金资助项目 $$$"$#$B 作者简介邢家省 $DE%C 男河南泌阳人副教授博士主要从事偏微分方程微分几何方面的研究 9 C F + / , G H 5 1IJ(+ + K 4 <(K 0 *
B B B
槡
小值(
! % 4% ! % 5% )! % 4 5 % & &
& " $ & " $ & " $
! &
! &
!
'% ' % ## ! 槡
= " $ !
#
!
= (
$ & #% "
(
=
( " $
过曲线 !的曲面 "满足什么条件"使 / 取到局部极
%
= " $ ! = " $
= ( ' #槡 #' ( '= $ '% $ % & # ;% 槡 & # ; ## = ( " $ = " $ ( " $ ## =
> " $
利用格林公式"得 # #3 # #3 !%&! ! % ; ! % ' % << # < # & ## #4 ## #5
& $
% & " $ B
得
!
"#
!
!
$
&
!
&
( '' = ! %% 槡
= " $ ! ( " $ !
! ! #$ & & > #$ )% ! % " ( = ## = ## ( > ## > " $
%
由于 + ! "+ ! " 曲面的平均 $ $ # ")C ! # )9 9 ")D # )E ! 9 曲率 ." 所以 )! ! % "C ! $ $ 9 ,+ # % ;! ! # ,+ 9 9 ,! # )E ! # ,! 9 " C $ $ F ! " ! C ;E % ! ! D E
