2011江苏高考数学冲刺小练(4)

合集下载

2011高考数学押题卷及答案如皋中学4月

2011高考数学押题卷及答案如皋中学4月一、填空题：本大题共14小题，每小题5分，共计70分．1．为了检查某超市货架上的奶粉是否含有三聚氰胺，要从编号依次为01到50的袋装奶粉中抽取5袋进行检验，现将50袋奶粉按编号顺序平均分成5组，用每组选取的号码间隔一样的系统抽样方法确定所选取的5袋奶粉的编号，若第4组抽出的号码为36，则第1组中用抽签的方法确定的号码是 ▲ .2．若复数1z mi =-(i 为虚数单位，m ∈R )，若22z i =-，则复数z 的虚部为 ▲ .3．若函数()2sin()(0)f x x =ω+ϕω>的图象的相邻两条对称轴的距离是π，则ω的值为 ▲ .4．若双曲线焦点为(5,0)，渐近线方程为2x y =±，则此双曲线的标准方程为 ▲ ．5．已知向量a → = (sin 55°，sin 35°)，b → = (sin 25°，sin 65°)，则向量 a → 与 b → 的夹角为 ▲ ．6．已知a ，b ，c 是锐角△ABC 中∠A ，∠B ，∠C 的对边，若a = 3，b = 4，△ABC 的面积为33，则c = ▲ ．7．作为对数运算法则：lg()lg lg (0,0)a b a b a b +=+>>是不正确的.但对一些专门值是成立的，例如：lg(22)lg 2lg 2+=+. 则关于所有使lg()lg lg a b a b +=+（0a >，0b >）成立的,a b 应满足函数()a f b =表达式为▲ .8．两游客坐火车旅行，期望座位连在一起，且有一个靠窗，已知火车内的座位的排法如图，则下列座位号码中符合要求的有 ▲ .①48，49 ②54，55 ③62，63④75，76 ⑤84，85 ⑥96，979．已知关于x 的不等式 x + 1x + a 2的解集为P ，若1P ，则实数a 的取值范畴为 ▲ ．窗口 1 2过道 345窗口67 8 9 10 11 12 13 14 15 16 17 … … …10．已知集合(){}22,|2009x y x y Ω=+≤，若点),(y x P 、点),(y x P '''满足x x '≤且y y '≥，则称点P 优于P '. 如果集合Ω中的点Q 满足：不存在Ω中的其它点优于Q ，则所有如此的点Q 构成的集合为 ▲ .11．若实数x 、y 满足114422x y x y +++=+，则22x y S =+的取值范畴是 ▲ .12．已知集合P ={ x | x = 2n ，n ∈N}，Q ={ x | x = 2n ，n ∈N}，将集合P ∪Q 中的所有元素从小到大依次排列，构成一个数列{an}，则数列{an}的前20项之和S20 = ▲ ．13．记集合{}0,1,2,3,4,5,6=T ，3124234,1,2,3,47777⎧⎫=+++∈=⎨⎬⎩⎭i a a a a Ma T i ，将M中的元素按从大到小的顺序排列，则第2009个数是 ▲ .14．已知抛物线()y g x =通过点(0,0)O 、(,0)A m 与点(1,1)P m m ++，其中0>>n m ，a b <，设函数)()()(x g n x x f -=在a x =和b x =处取到极值，则n m b a ,,,的大小关系为 ▲ .二、解答题：本大题共6小题，共计90分．解承诺写出必要的文字讲明步骤．15．（本小题共14分）已知在等边三角形ABC 中，点P 为线段AB 上一点，且(01)AP AB =≤≤u u u r u u u rλλ.（1）若等边三角形边长为6，且13=λCP ；（2）若CP AB PA PB ⋅≥⋅u u u r u u u r u u u r u u u r，求实数λ的取值范畴.16．（本小题共14分）如图所示，在直三棱柱111C B A ABC -中，1AB BB =，1AC ⊥平面D BD A ,1为AC 的中点．（1）求证：//1C B 平面BD A 1；（2）求证：⊥11C B 平面11A ABB ；（3）设E 是1CC 上一点，试确定E 的位置使平面⊥BD A 1平面BDE ，并讲明理由．17．（本小题共14分）椭圆C ：12222=+by a x )0(>>b a 的一个焦点)0,2(1-F ，右准线方程8=x ．（1）求椭圆C 的方程；（2）若M 为右准线上一点，A 为椭圆C 的左顶点，连结AM 交椭圆于点P ，求APPM的取值范畴；（3）设圆Q ：22()1(4)x t y t -+=>与椭圆C 有且只有一个公共点，过椭圆C 上一点B 作圆Q 的切线BS 、BT ，切点为,S T ，求BS BT ⋅u u u r u u u r的最大值．A 1B 1C 1AB CD18．（本小题共16分）在金融危机中,某钢材公司积压了部分圆钢,经清理知共有2009根.现将它们堆放在一起.(1)若堆放成纵断面为正三角形(每一层的根数比上一层根数多1根),并使剩余的圆钢尽可能地少,则剩余了多少根圆钢?(2)若堆成纵断面为等腰梯形(每一层的根数比上一层根数多1根),且许多于七层，（Ⅰ）共有几种不同的方案?（Ⅱ）已知每根圆钢的直径为10cm ，为考虑安全隐患，堆放高度不得高于4m ，则选择哪个方案，最能节约堆放场地？19．（本小题共16分）已知函数21()ln (4)2f x x x a x =++-在(1,)+∞上是增函数.（1）求实数a 的取值范畴；（2）在（1）的结论下，设2()||,[0,ln 3]2xa g x e a x =-+∈，求函数)(x g 的最小值．20．（本小题共16分）已知数列{}n a ，{}n b 满足12a =，121n n n a a a +=+，1n n b a =-数列{}n b 的前n 项和为n S ，2n n n T S S =-.（1）求证：数列1n b ⎧⎫⎨⎬⎩⎭为等差数列，并求通项n b ；（2）求证：1n n T T +>；（3）求证：当2n ≥时，271112n n S +≥．数学附加题21.为了保证信息安全传输，设计一种密码系统，其加密、解密原理如下图：现在加密方式为：把发送的数字信息X ，写为“11211222a a a a ”的形式，先左乘矩阵1422A ⎡⎤=⎢⎥-⎣⎦，再左乘矩阵625514855B ⎡⎤-⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦，得到密文Y ，现在已知接收方得到的密文是4,12,36,72，试破解该密码.22.以直角坐标系的原点O 为极点，x 轴的正半轴为极轴．已知点P 的直角坐标为(1,5)-，[来源:学科网]点M 的极坐标为(4,)2π．若直线l 过点P ，且倾斜角为3π，圆C 以M 为圆心、4为半径.（1）求直线l 的参数方程和圆C 的极坐标方程；（2）试判定直线l 和圆C 的位置关系.23．在2009年春运期间，一名大学生要从南京回到徐州老家有两种选择，即坐火车或汽车.已知该大学生先去买火车票的概率是先去买汽车票概率的3倍，汽车票随时都能买到.若先去买火车票，则买到火车票的概率为0.6，买不到火车票，再去买汽车票.（1）求这名大学生先去买火车票的概率；（2）若火车票的价格为120元，汽车票的价格为280元，设该大学生购买车票所花费钞票数为ξ，求ξ的数学期望值.24．已知抛物线223y x =，过其对称轴上一点(23,0)P 作一直线交抛物线于,A B 两点，若60OBA ∠=︒，求OB 的斜率.答案1、062、1-3、1 5．30° 6.137、(1)1ba b b =>- 8、“通过椭圆)0(12222>>=+b a by a x 中心的任意弦的两端点与椭圆上除这两个端点外的任意一点P 的连线的斜率之积为定值22b a-”.②⑤⑥9.[−1，0] 10、答案：(){}22,|2009,00且x y x y x y +=≤≥提示：P 优于P '，即P 位于P '的左上方，“不存在Ω中的其它点优于Q ”，即“点Q 的左上方不存在Ω中的点”.故满足条件的点集合为(){}22,|2009,00且x y xy x y +=≤≥.11、答案：24S <≤提示：设12122,2(0,0)x y t t t t ==>>，则22121222t t t t +=+，2121212()22()t t t t t t +-=+，∴2121212()2()20t t t t t t +-+=>，得112t t +>或120t t +<（舍去），又2212121212()2()222t t t t t t t t +⎛⎫+-+=≤ ⎪⎝⎭，得1204t t ≤+≤，∴1224t t <+≤.12. 343 13、答案：3922401[来源:学科网] 提示：3124234,1,2,3,47777⎧⎫=+++∈=⎨⎬⎩⎭i a a a a M a T i 中的元素为44444401237,,,,,77777⋅⋅⋅，故从大到小排列第2009个数是3922401. 14、答案：b n a m <<<提示：由抛物线通过点(0,0)O 、(,0)A m 设抛物线方程(),0y kx x m k =-≠，又抛物线过点(1,1)P m m ++，则1(1)(1)m k m m m +=++-，得1k =，则2()()y g x x x m x mx ==-=-，∴)()()(x g n x x f -=32()()()x x m x n x m n x mnx =--=-++，[来源:学&科&网] ∴/2()32()f x x m n x mn =-++，又函数()f x 在a x =和b x =处取到极值，故//()0,()0f a f b ==，Q 0>>n m ，∴/22()32()()0f m m m n m mn m mn m m n =-++=-=->，/22()32()()0f n n m n n mn n mn n n m =-++=-=-<，又a b <，故b n a m <<<.15、解：（1）当13=λ时，13AP AB =u u u r u u u r ，2222221()262622282CP CA AP CA CA AP AP =+=+⋅+=-⨯⨯⨯+=u u u r u u u r u u u r u u u r u u u r u u u r u u u r.∴||7CP =u u u r……………………………………………………………………7分（2）设等边三角形的边长为a ，则221()()2CP AB CA AP AB CA AB AB a a ⋅=+⋅=+λ⋅=-+λu u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ，222()()PA PB PA AB AP AB AB AB a a ⋅=⋅-=λ⋅-λ=-λ+λu u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r…………………12分即2222212a a a -+λ≥-λ，∴21202λ-λ+≤，∴222222≤λ≤. 又00≤λ≤，∴2212≤λ≤. ……………………………………………………14分16、解：（1）证明：连接1AB 与B A 1相交于M ，则M 为B A 1的中点，连结MD ，又D 为AC 的中点，∴1//B C MD ，又⊄C B 1平面BD A 1，∴1//B C 平面BD A 1．…………4分（2）∵1AB B B =，∴四边形11A ABB 为正方形，∴11A B AB ⊥，又∵1AC ⊥面BD A 1，∴11AC A B ⊥，∴1A B ⊥面11C AB ，∴111A B B C ⊥，又在直棱柱111C B A ABC -中111C B BB ⊥，∴11B C ⊥平面A ABB 1．………………8分（3）当点E 为C C 1的中点时，平面⊥BD A 1平面BDE ，D Θ、E 分不为AC 、C C 1的中点，∴1//DE AC ，1AC Θ平面BD A 1，∴DE ⊥平面BD A 1，又⊂DE 平面BDE ，∴平面⊥BD A 1平面BDE ．…………14分17、解：（1）由题意得，2=c ，82=ca 得，216a =，212b =，∴所求椭圆方程为1121622=+y x ．………………………………………………………4分（2）设P 点横坐标为0x ，则141248000-+=+-=x x x AP PM ， ∵440≤<-x ，∴21141248000≥-+=+-=x x x AP PM ． ∴AP PM 的取值范畴是⎪⎭⎫⎢⎣⎡+∞,21 ………………………………………………………9分（3）由题意得，5t =，即圆心Q 为(5,0)，设BQ x =，则||||cos BS BT BS BT SBT ⋅=⋅∠u u u r u u u r u u u r u u u r[来源:学科网] 2||||(12sin )BS BT SBQ =⋅-∠u u u r u u u r221(1)[12()]x x=--2223x x=+-，∵19BQ <≤，即19x <≤，∴2181x <≤，易得函数2y x x =+在(1,2)上单调递减，在(2,81]上单调递增，∴281x =时，max 6320()81BS BT ⋅=u u u r u u u r . …………………………………14分18、(1) 当62=n 时，使剩余的圆钢尽可能地少，现在剩余了56根圆钢；-----4分(2) 当纵断面为等腰梯形时，设共堆放n 层,则从上到下每层圆钢根数是以x 为首项、1为公差的等差数列，从而2009)1(21=-+n n nx ，即4177220092)12(⨯⨯⨯=⨯=-+n x n ，因1-n 与n 的奇偶性不同，因此12-+n x 与n 的奇偶性也不同，且12-+<n x n ，从而由上述等式得： ⎩⎨⎧=-+=574127n x n 或⎩⎨⎧=-+=2871214n x n 或⎩⎨⎧=-+=981241n x n 或⎩⎨⎧=-+=821249n x n ，因此共有4种方案可供选择。

【步步高】江苏专用2011高考数学二轮复习专题限实规范训练4 理苏教版

专题四立体几何(时间∶120分钟满分∶160分)一、填空题(本大题共14小题，每小题5分，共70分)1．(2010·湖南)图中的三个直角三角形是一个体积为20 cm3的几何体的三视图，则h＝________cm.2.已知m，n是不重合的直线，α，β是不重合的平面，有下列命题：①若α∩β＝n，m∥n，则m∥α，m∥β；②若m⊥α，m⊥β，则α∥β；③若m∥α，m⊥n，则n⊥α；④若m⊥α，n⊂α，则m⊥n，其中所有真命题的序号是________．3．设三棱柱的侧棱垂直于底面，所有棱的长都为a，顶点都在一个球面上，则该球的表面积为________．4．有一棱长为a的正方体骨架，其内放置一气球，使其充气且尽可能地大(仍保持为球的形状)，则气球表面积的最大值为________．5.如图所示，用平行于AD且过BC的平面BCFE截长方体，得到几何体ABCD－A1EFD1，设AB＝BC＝5，B1E＝4，其主视图的面积为6，则其左视图的面积为________．6．α、β是两个不同的平面，m、n是平面α及β之外的两条不同的直线，给出四个论断：①m⊥n；②α⊥β；③n⊥β；④m⊥α，以其中三个论断作为条件，剩余的一个论断作为结论，写出你认为正确的一个命题______________．7．已知平面α⊥β，α∩β＝l，P是空间一点，且P到平面α、β的距离分别是1、2，则点P到l的距离为________．8．已知几何体的三视图(如图)，则该几何体的体积为______________．9．如图，在长方体ABCD－A1B1C1D1中，AD＝AA1＝1，AB＝2，E为AB的中点，则点E到平面ACD1的距离为___________________________________．10.如图，设平面α∩β＝EF，AB⊥α，CD⊥α，垂足分别为B、D.若增加一个条件，就能推出BD⊥EF.现有：①AC⊥β；②AC与α，β的夹角相等；③AC与CD在β内的射影在同一条直线上；④AC∥EF.那么上述几个条件中能成为增加条件的是________(填上你认为正确的所有答案序号)．11．已知直线a，b和平面α，β，试利用上述元素并借助于它们之间的位置关系，构造出一个判断α∥β的真命题：___________________________.12.如图，在正三棱柱ABC－A1B1C1中，D为棱AA1的中点，若截面△BC1D是面积为6的直角三角形，则此三棱柱的体积为____________．13．如图，在长方体ABCD －A 1B 1C 1D 1中，AB ＝BC ＝2，AA 1＝1，则BC 1与平面BB 1D 1D 所成角的正弦值为________．14.三棱锥S －ABC 中，∠SBA ＝∠SCA ＝90°，△ABC 是斜边AB ＝a 的等腰直角三角形，则以下结论中：①异面直线SB 与AC 所成的角为90°；②直线SB ⊥平面ABC ；③平面SBC ⊥平面SAC ；④点C 到平面SAB 的距离是12a . 其中正确结论的序号是______________．二、解答题(本大题共6小题，共90分)15.(14分)(2010·安徽)如图，在多面体ABCDEF 中，四边形ABCD 是正方形，EF ∥AB ，EF ⊥FB ，AB ＝2EF ，∠BFC ＝90°，BF ＝FC ，H 为BC 的中点．(1)求证：FH ∥平面EDB ；(2)求证：AC ⊥平面EDB ；(3)求二面角B －DE －C 的大小．16.(14分)如图，PA ⊥平面ABCD ，ABCD 是矩形，PA ＝AB ＝1，AD＝3，点F 是PB 的中点，点E 在边BC 上移动．(1)求三棱锥E －PAD 的体积；(2)当点E 为BC 的中点时，试判断EF 与平面PAC 的位置关系，并说明理由；(3)证明：无论点E 在边BC 的何处，都有PE ⊥AF .17.(14分)如图：四棱锥P －ABCD 中，ABCD 为矩形，△PAD 为等腰直角三角形，∠APD ＝90°，面PAD ⊥面ABCD ，AB ＝1，AD ＝2，E 、F 分别为PC和BD 的中点．(1)证明：EF ∥面PAD ；(2)证明：面PDC ⊥面PAD ；(3)求四棱锥P －ABCD 的体积．18.(16分)如图，在四棱锥P －ABCD 中，底面ABCD 为菱形，∠BAD ＝60°，Q 为AD 的中点．(1)若PA ＝PD ，求证：平面PQB ⊥平面PAD ；(2)点M 在线段PC 上，PM ＝tPC ，试确定实数t 的值，使得PA ∥平面MQB .19.(16分)如图所示，四棱锥P —ABCD 中，PA ⊥平面ABCD ，PB 与底面所成的角为45°，底面ABCD 为直角梯形，∠ABC ＝∠BAD ＝90°，PA ＝BC ＝12AD .(1)求证：平面PAC ⊥平面PCD ；(2)在棱PD 上是否存在一点E ，使CE ∥平面PAB ？若存在，请确定E 点的位置；若不存在，请说明理由．20．(16分)如图所示，在四棱锥O —ABCD 中，底面ABCD 是边长为1的菱形，∠ABC ＝π4，OA ⊥底面ABCD ，OA ＝2，M 为OA 的中点， N 为BC 的中点．(1)证明：直线MN ∥平面OCD ；(2)求异面直线AB 与MD 所成角的大小；(3)求点B 到平面OCD 的距离．答案1.42.②④3.73πa 2 4.2πa 2 5.10 6．可填①③④⇒②与②③④⇒①中的一个7. 5 8.423 9.13 10.①③ 11.a ⊥α，a ⊥β⇒α∥β 12.8 3 13.10514．①②③④15．方法一 (1)证明如图(1)，设AC 与BD 交于点G ，则G 为AC 的中点，连接EG ，GH .又H 为BC 的中点，∴GH 綊12AB .又EF 綊12AB ，∴EF 綊GH .∴四边形EFHG 为平行四边形．∴EG ∥FH .而EG ⊂平面EDB ，∴FH ∥平面EDB .(2)证明由四边形ABCD 为正方形，有AB ⊥BC .又EF ∥AB ，∴EF ⊥BC .而EF ⊥FB ，∴EF ⊥平面BFC ，∴EF ⊥FH ，∴AB ⊥FH .又BF ＝FC ，H 为BC 的中点，∴FH ⊥BC .∴FH ⊥平面ABCD .∴FH ⊥AC .又FH ∥EG ，∴AC ⊥EG .又AC ⊥BD ，EG ∩BD ＝G ，∴AC ⊥平面EDB .(3)解 EF ⊥FB ，∠BFC ＝90°，∴BF ⊥平面CDEF .在平面CDEF 内过点F 作FK ⊥DE 交DE 的延长线于K ，则∠FKB 为二面角B －DE －C 的一个平面角．设EF ＝1，则AB ＝2，FC ＝2，DE ＝ 3.又EF ∥DC ，∴∠KEF ＝∠EDC ，∴sin∠EDC ＝sin∠KEF ＝23.∴FK ＝EF sin∠KEF ＝23，tan∠FKB ＝BFFK ＝3，∴∠FKB ＝60°.∴二面角B －DE －C 为60°.方法二 (1)证明 ∵四边形ABCD 为正方形，∴AB ⊥BC .又EF ∥AB ，∴EF ⊥BC .又EF ⊥FB ，∴EF ⊥平面BFC .∴EF ⊥FH ，∴AB ⊥FH .又BF ＝FC ，H 为BC 的中点，∴FH ⊥BC .∴FH ⊥平面ABC .以H 为坐标原点，HB →为x 轴正方向， HF →为z 轴正方向，建立如图(2)所示的坐标系．设BH ＝1，则A (1，－2,0)，B (1,0,0)，C (－1,0,0)，D (－1，－2,0)，E (0，－1,1)，F (0,0,1)．设AC 与BD 的交点为G ，连接GE ，GH ，则G (0，－1,0)，∴GE →＝(0,0,1)．又HF →＝(0,0,1)，∴HF →∥GE →.又GE ⊂平面EDB ，HF ⊄平面EDB ，∴FH ∥平面EBD .（2）证明 AC →＝(－2,2,0)，GE →＝(0,0,1)，AC →·GE →＝0，∴AC ⊥GE .又AC ⊥BD ，EG ∩BD ＝G ，∴AC ⊥平面EDB .（3）解 BE →＝(－1，－1,1)，BD →＝(－2，－2，0)，设平面BDE 的法向量为n 1＝(1，y 1，z 1)，则BE →·n 1＝－1－y 1＋z 1＝0，BD →·n 1＝－2－2y 1＝0，∴y 1＝－1，z 1＝0，即n 1＝(1，－1,0)．CD →＝(0，－2,0)，CE →＝(1，－1,1)．设平面CDE 的法向量为n 2＝(1，y 2，z 2)，则n 2·CD →＝0，y 2＝0，n 2·CE →＝0,1－y 2＋z 2＝0， z 2＝－1，故n 2＝(1,0，－1)．cos 〈n 1，n 2〉＝n 1·n 2|n 1|·|n 2|＝12×2＝12，又0°≤〈n 1，n 2〉≤180°，∴〈n 1，n 2〉＝60°，即二面角B －DE －C 为60°.16．(1)解三棱锥E －PAD 的体积V ＝13PA ·S △ADE ＝13PA ·(12·AD ·AB )＝36. (2)解当点E 为BC 的中点时，EF 与平面PAC 平行.∵在△PBC 中，E 、F 分别为BC 、PB 的中点，∴EF ∥PC ，又EF ⊄平面PAC ，PC ⊂平面PAC ，∴EF ∥平面PAC .(3)证明 ∵PA ⊥平面ABCD ，BE ⊂平面ABCD ，∴BE ⊥PA ，又BE ⊥AB ，AB ∩PA ＝A ，AB ，PA ⊂平面PAB ，∴BE ⊥平面PAB .又AF ⊂平面PAB ，∴AF ⊥BE .又PA ＝AB ＝1，点F 是PB 的中点，∴PB ⊥AF ，又∵PB ∩BE ＝B ，PB ，BE ⊂平面PBE ，∴AF ⊥平面PBE .∵PE ⊂平面PBE ，∴AF ⊥PE .17．(1)证明如图，连接AC ，∵ABCD 为矩形且F 是BD 的中点，∴AC 必经过F ，又E 是PC 的中点，所以EF ∥AP ，∵EF 在面PAD 外，AP 在面PAD 内，∴EF ∥面PAD .(2)证明 ∵面PAD ⊥面ABCD ，CD ⊥AD ，面PAD ∩面ABCD ＝AD ，∴CD ⊥面PAD ，∴CD ⊥AP .∵AP ⊥PD ，PD 和CD 是相交直线，∴AP ⊥面PCD ，又AP 在面PAD 内，所以面PDC ⊥面PAD .(3)解作PH ⊥AD 于H ，∵△PAD 为等腰直角三角形，∠APD ＝90°，AD ＝2，∴PH ＝12AD ＝1.又面PAD ⊥面ABCD ，∴PH ⊥面ABCD ，即PH 为棱锥P －ABCD 的高．S ABCD ＝2×1＝2.∴V P －ABCD ＝13×2×1＝23.18．(1)证明底面ABCD 为菱形，∠BAD ＝60°，Q 为AD 的中点，所以AD ⊥QB ，又PA ＝ PD ，则PQ ⊥AD ，所以AD ⊥平面PQB ，而AD ⊂面PAD ，∴平面PQB ⊥平面PAD .(2)解连接AC ，交QB 于O 点，连接OM ，BM ，QM ，若使得PA ∥平面MQB ，则PA ∥OM ，∵PM ＝tPC ，∴AO ＝tAC ，在底面菱形ABCD 中，可得t ＝13. 19．(1)证明设PA ＝1，由题意BC ＝PA ＝1，AD ＝2.∵PA ⊥平面ABCD ，∴PB 与平面ABCD 所成的角为∠PBA ＝45°，∴AB ＝1，由∠ABC ＝∠BAD ＝90°，易得CD ＝AC ＝2，由勾股定理逆定理得AC ⊥CD .又∵PA ⊥CD ，PA ∩AC ＝A ，∴CD ⊥平面PAC ，又CD ⊂平面PCD ，∴平面PAC ⊥平面PCD .(2)解存在点E 使CE ∥平面PAB .理由如下：分别以AB 、AD 、AP 为x 轴、y 轴、z 轴建立空间直角坐标系如图所示，则P (0,0,1)，C (1,1,0)，D (0,2,0)，设E(0，y ，z )，则PE →=(0，y ，z-1), PD →＝(0,2，－1)．∵PE →//PD →,∴y ·(－1)－2(z －1)＝0. ①∵AD →＝(0,2,0)是平面PAB 的法向量，又CE →＝(－1，y －1，z )，若使CE ∥平面PAB ，则CE →⊥AD →.∴(－1，y －1，z )·(0,2,0)＝0，∴y ＝1.把y ＝1代入①，得z ＝12. ∴E 是PD 的中点，∴存在E 点使CE ∥平面PAB ，此时E 为PD 的中点．20．(1)证明作AP ⊥CD 于点P ，并且连结OP ，如图，分别以AB 、AP 、AO 所在直线为x 、y 、z 轴建立空间直角坐标系．则A (0,0,0)，B (1,0,0)，P (0，22，0)，D (－22，22，0)，O (0,0,2)，M (0,0,1)．如图，取OB 中点E ，连接ME 、EN ，则ME ∥AB ，又∵AB ∥CD ，∴ME ∥CD .又NE ∥OC ，且ME ∩NE ＝E ，CD ∩OC ＝C ，∴平面MNE ∥平面OCD .∴MN ∥平面OCD .(2)解设AB 与MD 所成角为θ，∵AB →＝(1,0,0)，MD →＝(－22，22，－1)，.21||||cos =•=∴MD AB θ又θ∈(0，π2]，∴θ＝π3.∴AB 与MD 所成角的大小为π3.（3）解 C(1－22，22，0)，OD →＝(－22，22，－2)，CD →＝(－1,0,0)．设平面OCD 的一个法向量n ＝(x ，y ，z )． ⎪⎩⎪⎨⎧=-=-+-⎪⎩⎪⎨⎧=•=•∴.,,,002222200x z y x CD n OD n 即 ∴x ＝0，令y ＝2，则z ＝12.∴n ＝(0，2，12)又BP →＝(－1，22，0)，,||||32=•=∴n n BP d即点B 到平面OCD 的距离为23.。

江苏省2011年高考数学最后冲刺(一)

江苏省2011年高考数学最后冲刺（一)江苏省涟水中学汪显林（一)知识及题型1。

集合：定义域与值域,交并补（可能的题号：5～10。

难易度：B）. 2。

复数：关注几何性质(可能题号:2～3,难易度：A）。

3。

简易逻辑：充要条件、或且非的真假（可能题号：5～10, 难易度：B）。

4。

三角函数图象及性质：重点变换（可能题号:1～5，难易度：A，）5。

解三角形与和差角：注意二倍角及变角关注求值题（可能题号：16，17, 难易度:B或C）.6.向量的数量积：注重基底表示与共线问题（可能会涉及不等式等知识)（可能题号：8～12, 难易度：B、C）。

7。

向量与三角：可能涉及解三角形（可能题号:8～12，难易度：B、C）。

8.向量与不等式:（可能题号：10～14, 难易度:B、C）。

9。

推理与证明：（可能题号：8～12，难易度:B）。

10。

算法：注重选择结构与推理相结合(可能题号：3～5, 难易度：A).11。

概率与统计：重视总体特征数的估计（频率分布及其求平均数方差），古典概型（可能题号：2～5,15，难易度:A、B)。

12.直线与圆：可能题号:5~12，17,18，难易度:B、C。

13。

立体几何:注重棱柱、长方体（正方体)，求点面距离及体面积，一证一计算，（注意三垂线定理的运用)可能题号：16，难易度：A、B.14.圆锥曲线:其中抛物线与双曲线可能题号：3～8, 难易度:A。

直线与椭圆或圆，关注：轨迹、直线与椭圆，解方程组，以及探究题,可能题号：17、18, 难易度：B、C。

15。

数列：等差等比性质（重点等比），和与通项及递推关系，研究单调性及相关的不等式（关注分式线性、等比放缩）,注重应用题。

考察两题可能题号：10~14，18～20，难易度：B，C.16。

导数：切线有关问题,在单调性、极值、最值、不等式方面应用，考察两题，可能题号：8~14，19，20, 难易度:B、C。

17.函数:重点定义域、值域，单调性、最值，分段函数、绝对值函数、对数函数、指数函数，关注与定比分点及凹凸函数有关的问题含参问题以及方程的研究；考察三题,可能题号：5～14,19，20, 难易度：B、C。

江苏省2011届高三数学小题训练23-24

江苏省2011届高三数学小题训练0231。

命题“x ∀∈R ，2x ≥”的否定是 .2。

已知集合{}1,0A =-，集合{}0,1,2B x =+，且A B ⊆，则实数x 的值为 .3。

在ABC ∆中，5,8,60a b C ===, 则CB CA ⋅的值为。

4. 计算机的价格大约每3年下降23，那么今年花8100元买的一台计算机，9年后的价格大约是元. 5。

已知复数122i,12iz z =+=+，则21z z z=在复平面内所对应的点位于第象限。

6. 已知向量a ＝(1，2），b ＝(2-，1)，若正数k 和t ，使得x ＝a ＋（t 2＋1）b 与y ＝－k a ＋1tb 垂直，则k 的最小值是。

7。

将函数()πsin 23y x =-的图象先向左平移π6,然后将所得图象上所有点的横坐标变为原来的2倍(纵坐标不变),则所得到的图象对应的函数解析式为 . 8．若关于x 的不等式2260axx a -+<的解集为(1， m ),则实数m = 。

9．已知()*3211nan n =∈-N ，数列{}na 的前n 项和为nS ,则使0nS>的n 的最小值是10。

函数()f x 的定义域为开区间（a ,b )，其导函数()f 'x 在（a ，b ）内的图象如图所示，则函数()f x 在开区间(a ，b ）内有个极大值点。

11. 利用绝对值符号将分段函数3, 2,()21, 12,3, 1x f x x x x ->⎧⎪=-+-≤≤⎨⎪<-⎩改写为非分段函数的解析式是()f x= .12. 已知实数a，b，c，d满足：a〈b，c〈d,()()1,()()1--=--=，则a c a dbc b da，b，c，d的大小关系是(用“<"连接)。

13. 某商品的单价为5000元，若一次性购买超过5件，但不超过10件时，每件优惠500元；若一次性购买超过10件，则每件优惠1000元。

2011江苏高考数学押题试卷

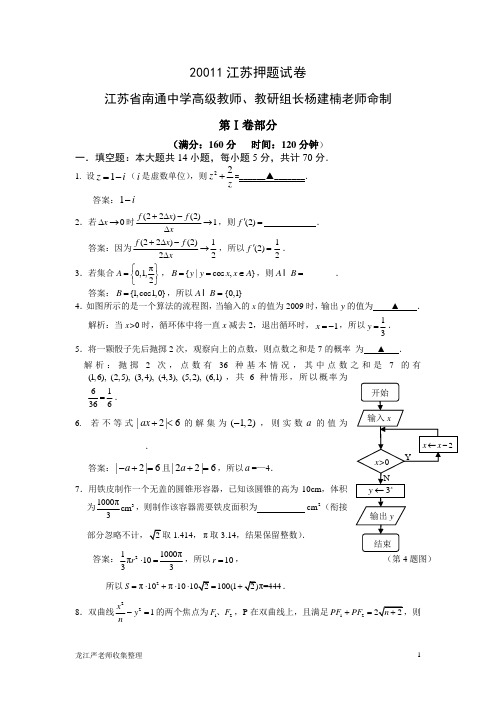
（第4题图）20011江苏押题试卷江苏省南通中学高级教师、教研组长杨建楠老师命制第Ⅰ卷部分（满分：160分时间：120分钟）一．填空题：本大题共14小题，每小题5分，共计70分．1. 设1z i =-（i 是虚数单位），则22z z+=______▲_______．答案：1i - 2．若0x ∆→时(22)(2)1f x f x+∆-→∆，则(2)f '= ．答案：因为(22)(2)122f x f x +∆-→∆，所以(2)f '=12．3．若集合0,1,2A π⎧⎫=⎨⎬⎩⎭，{|cos ,}B y y x x A ==∈，则A B = _______．答案：{1,cos1,0}B =，所以A B = {0,1} 4．如图所示的是一个算法的流程图，当输入的x 的值为2009时，输出y 的值为 ▲ ．解析：当x>0时，循环体中将一直x 减去2，退出循环时，1x =-，所以13y =． 5．将一颗骰子先后抛掷2次，观察向上的点数，则点数之和是7的概率为 ▲ ．解析：抛掷2次，点数有36种基本情况，其中点数之和是7的有(1,6),(2,5),(3,4),(4,3)，共6种情形，所以概率为61366=． 6. 若不等式|2|6ax +<的解集为(1,2)-，则实数a 的值为_____________．答案：|2|6a -+=且|22|6a +=，所以a =—4．7．用铁皮制作一个无盖的圆锥形容器，已知该圆锥的高为10cm ，体积为31000πcm 3，则制作该容器需要铁皮面积为 2cm （衔接1.414，π取3.14，结果保留整数）．答案：211000ππ1033r ⋅=，所以10r =，所以2π10π10100(1π=444S =⋅+⋅⋅．8．双曲线221x y n-=的两个焦点为12F F 、，P 在双曲线上，且满足12PF PF +=C△12PF F 的面积为．答案：12||PFPF -=12PF PF +=22121244,2PF PF n PF PF +=+⋅=， 22212121212cos 02PF PF F F F PF PF PF +-∠==⋅，所以12π2F PF ∠=，所以12112S PF PF =⋅=． 9. 2009年北京国庆阅兵式上举行升旗仪式．如图，在坡度为15 的观礼台上，某一列座位与旗杆在同一个垂直于地面的平面上，在该列的第一排和最后一排测得旗杆顶端的仰角分别为60和30，且第一排和最后一排的距离为米，则旗杆的高度为米．答案：设旗杆高度为x 米，则x =所以151)2x =10．已知数列{}n a 共有6项，若其中三项是1，两项是2，一项是3，则满足上述条件的数列共有个．答案：列举法（树形图）即可得到结论6011．已知()(1)(2)(3)f x x x x =---，则'()0f x =在区间（1，3）内的解的个数为．答案：()(1)(2)(3)f x x x x =---的3个零点为1，2，3，所以，在(1,2),(2,3)之间各有一个极值点，所以'()0f x =在区间（1，3）内的解的个数为2个． 12．若()f n 为()2*1n n N +∈的各数位上的数字之和，如：2141197+=，1＋9＋7＝17，则()1417f =，记()()1f n f n =，()()()21f n f f n =，，()()()()*1k k f n f f n k N +=∈，则()20108f ＝．答案：123(8)11,(8)4,(8)8f f f ===，所以3(8)(8)n n f f +=，所以20103(8)(8)8f f ==． 13．如图，△ABC 中，4AB =，AC =8，60BAC ∠= ，延长CB 到D ，使BA BD =，当E 点在线段AB 上移动时，若AE AC AD λμ=+，当λ取最大值时，λμ-的值是．答案：当λ取最大值时，AE AB =，,A B A C C B A B A D D B =+=+，所以(1AB AC =+ ，旗杆E所以λμ==2λμ-=．14．设函数()f x (0)a <的定义域为D ，值域为A ，若所有点(,)s t (,)s D t A ∈∈构成一个正方形区域，则a 的值为．答案：定义域的长度为12x x -=可得a =4-．二、解答题：本大题共6小题，共计90分．15．（本小题14分）已知向量()()()cos ,1,,cos a x x b f x x ωωω==，其中ω＞0，且，又函数()f x 的图像两相邻对称轴之间的距离为32π (1)求的值ω；(2) 求函数在区间上的最大值与最小值及相应的值．解：(1) //a b，()cos (cos )f x x x x ωωω∴=1cos 22x ω+=1πsin(2)26x ω=++． …………………………………………… 4分由题意，函数()f x 的最小正周期为3π，又ω＞0，2π3π=2ω∴13ω∴=． …………6分 (2) 由(1)知12()sin(236f x x π=++， 5,2x π⎡⎤∈π⎢⎥⎣⎦ ，2511,,3666x πππ⎡⎤+∈⎢⎥⎣⎦ ∴当25,366x ππ+=即x =π时，()f x 取得最大值1, …………………………… 12分当29,366x ππ+=即2x =π时，()f x 取得最小值1.2- ……………………14分16．（本小题满分14分）如图，空间四边形BEDF 在平面α的射影是一个边长为 2a 、∠A =60°的菱形ABCD ，其中A 、C 分别为E 、F 在平面α的射影，且 AE =3a ，CF =a ．（1）求证：EF BD ⊥；（2）求证：平面 EBD ⊥平面FBD ．证明：（1）因为FC ⊥面ABCD ，CB CD = 所以FB FD =，……………………2分又因为O 为BD 的中点，所以FO BD ⊥，同理EO BD ⊥，……………………4分又EO FO O = ，所以BD ⊥面EFO ，………………………………………5分所以EF BD ⊥；…………………………………………………………………6分（2）因为FC ⊥面ABCD ，EA ⊥面ABCD ，所以//FC EA ，所以,,,E A C F 四点共面， ………………………………………………………8分在菱形ABCD 中，边长为 2a 、∠A =60°，所以AO CO =，则tan tan COF AOE ∠=∠=，所以，在平面EACF 内，30,60COF AOE ∠=∠= ，则EO FO ⊥， …………………………………………………………………10分由（1）可知，EO BD ⊥ 又BD FO O = ，所以EO ⊥面BDF ，……………………………………………………………12分因为EO ⊂面BDE ，所以平面 EBD ⊥平面FBD ．……………………………14分 17（本小题15分）已知圆O 的方程为），，过点直线03(,1122A l y x =+且与圆O 相切．（1）求直线1l 的方程；（2）设圆O 与x 轴交与P,Q 两点，M 是圆O 上异于P,Q 的任意一点，过点A 且与x 轴垂直的直线为2l ，直线PM 交直线2l 于点'P ，直线QM 交直线2l 于点'Q ．求证：以''Q P 为直径的圆C 总过定点，并求出定点坐标．解：（1）∵直线1l 过点(3,0)A ，且与圆C ：221x y +=相切，设直线1l 的方程为(3)y k x =-，即30kx y k --=，则圆心(0,0)O 到直线1l 的距离为1d ==，解得42±=k ， ……………4分∴直线1l 的方程为3)y x =-，即3)y x =-． …………………………7分（2）对于圆方程122=+y x ,令0y =，得1x =±,即(1,0),(1,0)P Q -．又直线2l 过点A 且与x 轴垂直，∴直线2l 方程为3x =，设(,)M s t ，则直线PM 方程为).1(1++=x s ty 解方程组3,(1)1x ty x s =⎧⎪⎨=+⎪+⎩,得).14,3('+s t P 同理可得,).12,3('-s t Q …………………9分 ∴以P Q ''为直径的圆C '的方程为0)12)(14()3)(3(=--+-+--s ty s t y x x ，又122=+t s ，∴整理得2262(61)0s x y x y t-+-++=， 13分若圆C '经过定点，只需令0y =，从而有2610x x -+=，解得3x =±，∴圆C '总经过定点坐标为(3±．……………………………………………15分18．（本小题满分15分）某生产旅游纪念品的工厂，拟在2010年度将进行系列促销活动．经市场调查和测算，该纪念品的年销售量x 万件与年促销费用t 万元之间满足3－x 与t +1成反比例．若不搞促销活动，纪念品的年销售量只有1万件．已知工厂2010年生产纪念品的固定投资为3万元，每生产1万件纪念品另外需要投资32万元．当工厂把每件纪念品的售价定为：“年平均每件生产成本的150%”与“年平均每件所占促销费一半”之和时，则当年的产量和销量相等．(利润=收入－生产成本－促销费用)(1)求出x 与t 所满足的关系式；(2)请把该工厂2010年的年利润y 万元表示成促销费t 万元的函数； (3)试问：当2010年的促销费投入多少万元时，该工厂的年利润最大？解：(1) 设比例系数为k )0(≠k ．由题知，有13+=-t kx ．……………………………2分又．时，10==x t21013=+=-∴k k，．……………………………………………………………4分 )0(123≥+-=∴t t x t x 的关系是与．…………………………………………5分 (2) 依据题意，可知工厂生产x 万件纪念品的生产成本为)323(x +万元，促销费用为t 万元，则每件纪念品的定价为：(xtx x 2%150323+⋅+)元/件．……………………8分于是，t x xtx x x y -+-+⋅+⋅=)323()2%150323(，进一步化简，得 )0(2132299≥-+-=t t t y ．……………………………………………………………11分因此，工厂2010年的年利润)0(2132299≥-+-=t t t y 万元．(3) 由(2)知，)0(2132299≥-+-=t t t y )713221(4221132250)21132(50时，等号成立，即当=+=+=+⋅+-≤+++-=t t t t t t t …13分所以，当2010年的促销费用投入7万元时，工厂的年利润最大，最大利润为42万元．…………………………………………………………………………………………15分 19.（本题满分16分）已知等差数列{}n a 中，公差0d >，其前n 项和为n S ，且满足2345a a ⋅=，1414a a +=. （1）求数列{}n a 的通项公式；（2）设由n n S b n c =+（0c ≠）构成的新数列为{}n b ，求证：当且仅当12c =-时，数列{}n b 是等差数列；（3）对于（2）中的等差数列{}n b ，设8(7)n n n c a b =+⋅（*n ∈N ），数列{}n c 的前n 项和为n T ，现有数列{}()f n ，()22nn n b f n T a =--（*n ∈N ），求证：存在整数M ，使()f n M ≤对一切*n ∈N 都成立，并求出M 的最小值．解：（1）∵等差数列{}n a 中，公差0d >， ∴23232323144545544391414n a a a a a d a n a a a a a ⋅=⋅==⎧⎧⎧⇒⇒⇒=⇒=-⎨⎨⎨=+=+=⎩⎩⎩………………………………4分（2）()()143212n n n S n n +-==-，nn S b n c =+()21n n n c -=+，………………………………6分由2132b b b =+得12115213c c c =++++，化简得220,0c c c +=≠，∴12c =-………………8分反之，令12c =-，即得2n b n =，显然数列{}n b 为等差数列，∴ 当且仅当12c =-时，数列{}n b 为等差数列. ………………………………………10分（3） ()()8111711n n n c a b n n n n ===-+⋅++∴11111122311n nT n n n =-+-++-=++ ()245151112451451451n n n b n n f n T a n n n n n n =-=-=+-+=+--+-+-+…………………12分9(1),2f =-而2n ≥时()()()()5151201(1)()0412451414521f n f n n n n n n n n n -+-=+--=-<-+-+--++ ∴(){}f n 在2n ≥时为单调递减数列，此时max ()(2)2f n f ==…………………………14分 ∴存在不小于2的整数，使()2f n ≤对一切*n ∈N 都成立， min 2M =．………………16分 20.（本题满分16分）已知2()ln ,()3f x x x g x x ax ==-+-．（1）求函数()f x 在[,2](0)t t t +>上的最小值；（2）对一切(0,)x ∈+∞，2()()f x g x ≥恒成立，求实数a 的取值范围；（3）证明对一切(0,)x ∈+∞，都有12ln xx e ex>-成立．解：⑴ '()ln 1f x x =+，当1(0,)x e ∈，'()0f x <，()f x 单调递减，当1(,)x e∈+∞，'()0f x >，()f x 单调递增． …………………………2分① 102t t e<<+<，t 无解； …………………………3分 ② 102t t e <<<+，即10t e <<时，min 11()()f x f e e ==-；…………………………4分 ③12t t e ≤<+，即1t e≥时，()f x 在[,2]t t +上单调递增，min ()()ln f x f t t t ==； …………………………5分所以min110()1ln t e ef x t t t e ⎧-<<⎪⎪=⎨⎪≥⎪⎩，，． …………………………6分 ⑵ 22ln 3x x x ax ≥-+-，则32l n a x x x≤++，设3()2l n(0)h x x x x x=++>，则2(3)(1)'()x x h x x+-=，(0,1)x ∈，'()0h x <，()h x 单调递增，(1,)x ∈+∞，'()0h x >，()h x 单调递减，所以min ()(1)4h x h ==，因为对一切(0,)x ∈+∞，2()()f x g x ≥恒成立，所以min ()4a h x ≤=； …………………………10分⑶ 问题等价于证明2ln ((0,))xx x x x e e>-∈+∞，由⑴可知()ln ((0,))f x x x x =∈+∞的最小值是1e -，当且仅当1x e =时取到，设2()((0,))x x m x x e e =-∈+∞，则1'()x xm x e-=，易得max 1()(1)m x m e ==-，当且仅当1x =时取到，从而对一切(0,)x ∈+∞，都有12ln x x e ex>-成立．…………………………16分第Ⅱ卷部分（满分：40分时间：30分钟）一、选做题（从中任选两题作答，每小题10分）21．A （4-1几何证明）如图所示，已知PA 与⊙O 相切，A 为切点，PBC 为割线，弦CD ∥AP ，AD ，BC 相交于E 点，F 为CE 上一点，且2DE EF EC =⋅．（1）求证：∠P=∠EDF ；（2）求证：CE·EB=EF·EP ．证明：（1）∵2DE EF EC =⋅， ∴DE CE EF ED =::． ∴DEF ∽CED ．∴∠DEF=∠C ，又∵CD ∥AP ，∴∠C=∠P ．∴∠P=∠EDF ．………………………4分（2）∵∠P=∠EDF ，∠DEF=∠PEA ，∴DEF ∽PEA ∆， ∴DE ︰PE=EF ︰EA ． ∴EF·EP=DE·EA ．又因为弦AD ，BC 相交于点E ， ∴DE·EA=CE·EB ． ∴CE·EB=EF·EP ．………………………10分 B （4-2矩阵变换）二阶矩阵M 对应的变换将点（1，-1）与（-2，1）分别变换成（-1，-1）与（0，-2）．（1）求二阶矩阵M ；（2）设直线L 在变换M 作用下得到了直线m ：x -y =4，求直线L 的方程．解：（1）设M =a b c d ⎡⎤⎢⎥⎣⎦，则1111a b c d -⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦，且2012a b c d -⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦ 1,1,a b c d -=-⎧⎨-=-⎩且20,2 2.a b c d -+=⎧⎨-+=-⎩解之得1,2,3,4,a b c d =⎧⎪=⎪⎨=⎪⎪=⎩∴M =1234⎡⎤⎢⎥⎣⎦．………………………5分（2）∵1223434x x x y y y x y '+⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥'+⎣⎦⎣⎦⎣⎦⎣⎦，且直线m ：4x y ''-=， ∴(2)(34)4x y x y +-+=，即20x y ++=为所求直线L 的方程．…………………10分 C （4-4极坐标与参数方程）已知直线的极坐标方程为sin()4πρθ+=，圆M 的参数方程2cos ,22sin ,x y θθ=⎧⎨=-+⎩（其中θ为参数）．（1）将直线的极坐标方程化为直角坐标方程；（2）求圆M 上的点到直线的距离的最小值．解：（1）极点为直角坐标原点O，sin()s )4πρθρθθ+=+=∴sin cos 1ρθρθ+=，可化为直角坐标方程：x+y-1=0. ………………………5分（2）将圆的参数方程化为普通方程：22(2)4x y ++=，圆心为C （0，-2）， ∴点C到直线的距离为d ==， ∴．……………………………………10分 21 D （4-5不等式选讲）（本小题为选做题．．．，满分10分）已知(0,)2x π∈，求函数2sin y x =+的最小值以及取最小值时所对应的x 值解：由(0,)2x π∈知：2sin y x =+21111sin x =+54≥=1=2sin x 即1sin 2x =时取等号， ∴当6x π=时min 54y =。

江苏省2011年高考数学最后冲刺(四)

610141020 30 y 温度/ ℃Ox第56题江苏省2011年高考数学最后冲刺（四)江苏省涟水中学汪显林(五）一、填空题 1. 已知的两根为，且，则的取值范围是2。

如图,，若，则= 。

3。

若b b a 2121-+与是的等比中项,则||2||2b a ab +的最大值为 4.已知函数f(x）满足1(2),2()()()()(),2f f x f y f x y f x y f x y ==++-+则f(2012）=5。

P 为ABC ∆所在平面内一点,并且1277AP AB AC =+,则ABP ∆的面积与ABC ∆的面积之比＝。

6.已知椭圆2221(0)x y m m m m+=>+的右焦点为F ，右准线为l ，且直线y=x与l 相交于A 点，另有定点B （—1，1），若5AF AB <,则椭圆的离心率的范围是 . 7。

设a 1=2，*122,,11n n nn n a ab n N a a ++=∈+-，则数列{}n b 的通项公式b n = .的模为边长构成三角8。

设向量,a b 满足3,4,0,a b ab ===以,,,a b a b -形，则他的边与半径为1的圆的公共点个数最多为。

9.过三角形的重心G 的直线分别交边AB,AC 于P ，Q ，设AP ,,AB AQ AC λμ==则11λμ+＝。

10. 如上图,某地一天从6时到14时的温度变化曲线近似满足函数sin()y A x B ωϕ=++，,则温度变化曲线的函数解析式为 ▲ .11。

设定义在R 上的函数()f x 满足对,x t R ∀∈,且0t ≠，都有(()())0t f x t f x +->,则{}{}(,)|()(,)|x y y f x x y y a ==的元素个数为．二、解答题 12. 如图，过圆224x y +=与x 的两个交点A 、B ，作圆的切线AC 、BD ,再过圆上任意一点H 作圆的切线，交AC 、BD 于C 、D 两点,设AD 、BC 的交点为R .⑴求动点R 的轨迹E 方程；⑵过曲线E 的右焦点作直线l 交曲线E 于M 、N 两点，交y 轴于P 点，记1PM MFλ=，2PN NFλ=，求证：12λλ+为定值13。

2011高考数学小题冲刺训练(详细解析)(二)

2011高考数学小题狂做冲刺训练（详细解析）高中数学姓名：__________班级：__________考号：__________题号一二总分得分、选择题（本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一个选项是符合题目要求的）设集合M＝{x|x-m≤0},N＝{y|y＝(x-1)2-1,x∈R},若M∩N＝,则实数m的取值范围是（）A.m≥-1B.m＞-1C.m≤-1D.m＜-1把1＋（1＋x）＋（1＋x）＋…＋（1＋x）展开成关于x的多项式,其各项系数和为a n,则等于（）A．2n B．2n－1 C．2 D．解析：令x＝1,得a n＝1＋2＋22＋…＋2n＝.答案：D数列{a n}的前n项和为S n,若,则S5等于( )A.1B.C.D.解析: ,∴S5＝a1+a2+a3+a4+a5＝.答案:B平面α⊥平面β,α∩β＝l,点P∈α,点Q∈l,那么PQ⊥l是PQ⊥β的( )A.充分但不必要条件B.必要但不充分条件C.充要条件D.既不充分也不必要条件解析:根据线面垂直、面面垂直的判定定理可知,PQ⊥l是PQ⊥β成立的充要条件.答案:C一间民房的屋顶有如图三种不同的盖法：①单向倾斜；②双向倾斜；③四向倾斜.记三种盖法屋顶面积分别为P1、P2、P3.若屋顶斜面与水平面所成的角都是α,则( )A.P3＞P2＞P1B.P3＞P2＝P1C.P3＝P2＞P1D.P3＝P2＝P1解析:该题是二面角知识在实际生活中的应用，首先应明确三种盖法的屋顶斜面与水平面所成二面角都相等，又三种盖法的屋顶在水平面上的射影面积均相等，由面积射影公式S影=S·cosα，知屋顶面积P1、P2、P3均相等.答案:D从一群参加志愿者活动的学生中抽取k人,每人分一件纪念品,然后让他们继续参与志愿者活动.过一会儿,再从中任取m人,发现其中有n人已领取纪念品,估计共有志愿者______________人.（）A. B. C.k＋m-n D.解析：设共有x名志愿者学生（x≥k）,则x名学生中,每名学生有纪念品的概率为,∴与应较接近.∴.故选A.答案：A若a=(2,2,0),b=(1,3,z),〈a，b〉=60°,则z等于( )A. B.- C.± D.±解析:∵a·b=8，|a|·|b|=2，cos〈a,b〉=,∴z=±.答案:C由1,3,5,…,2n-1,…构成数列{a n},数列{b n}满足b1＝2,当n≥2时,,则b5等于（）A.17B.15C.33D.63解析：根据题意,得b2＝＝a2＝3b3＝＝a3＝5b4＝＝a5＝9b5＝＝a9＝17.答案：A某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为L1＝5.06x-0.15x2和L2＝2x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为( )A.45.606B.45.6C.45.56D.45.51解析:依题意,可设甲销售x辆,则乙销售(15-x)辆,∴总利润S＝5.06x-0.15x2+2(15-x)＝-0.15x2+3.06x+30(x≥0).∴当x＝10.2时,S max＝45.6(万元).答案:B设A为圆(x-1)2+y2＝1上的动点,PA是圆的切线且|PA|＝1,则P点的轨迹方程是… ( )A.(x-1)2+y2＝4B.(x-1)2+y2＝2C.y2＝2xD.y2＝-2x解析:作图可知圆心(1,0)到P点距离为,所以P在以(1,0)为圆心,以为半径的圆上,其轨迹方程为(x-1)2+y2＝2.答案:B、填空题（本大题共5小题，每小题5分，共25分）如果0＜a＜b＜c＜d＜e,,则把变量______________的值增加1会使S的值增加最大.(填入a,b,c,d,e中的某个字母)解析：经分析可知,只有将a、c增大,才能使S增大.若a增加1,则,若c增加1,则.又0＜b＜d,则,∴S1＞S2.答案：a已知数列{a n}是递增数列,且a n＝n2+λn,则实数λ的范围是__________.解法一:a n+1-a n＝(n+1)2+λ(n+1)-n2-λn＝2n+1+λ,∵数列{a n}是单调递增的,∴a n+1-a n＝2n+1+λ＞0恒成立.只要2n+1+λ的最小值大于0即可,∴3+λ＞0.∴λ＞-3.解法二：a n＝n2+λn且{a n}是单调递增的,∴.∴λ＞-3.答案:λ＞-3设向量a＝(-1,3,2),b＝(4,-6,2),c＝(-3,12,t),若c＝ma+nb,则t＝_________,m+n＝______.解析:ma+nb＝(-m+4n,3m-6n,2m+2n),∴(-m+4n,3m-6n,2m+2n)＝(-3,12,t).∴解得∴.答案:11若,则的值是____________.解析：∵,∴.答案：某市2007年底有出租车10万辆,计划从2008年起,每年报废0.2万辆旧出租车,假定该市每年新增加出租车数量是上年年底的10%,若到2010年底该市的出租车数量在［k,k+1］(k∈N*)内,则k＝________万辆.解析:由题设可得a n+1＝a n×1.1-0.2,变形为a n+1-2＝1.1(a n-2),∴{a n-2}是以8为首项,1.1为公比的等比数列.∴2010年底是a4-2＝8×1.13,即a4＝2+8×1.13＝12.648∈［12,13］.∴k＝12.答案:12。

数学_2011年江苏省南通市某校高考数学最后冲刺试卷(含答案)

2011年江苏省南通市某校高考数学最后冲刺试卷一、填空题（共14小题，每小题5分，满分70分）1. 已知z(1−i)=1，则复数z 在复平面上对应的点位于第________象限．2. 已知△ABC 中，A ，B ，C 的对边分别为a ，b ，c ．若a =c =√6+√2，且A =75∘，则b =________．3. 命题：“∀x ∈(0,π2),sinx <x”的否定是________．4. 抛物线y 2=4mx(m >0)的焦点到双曲线x 216−y 29=l 的一条渐近线的距离为3，则此抛物线的准线方程为________．5. 已知流程图如右图所示，该程序运行后，为使输出的b 值为16，则循环体的判断框内①处应填________．6. 设a ，b 为互不相等的正整数，方程ax 2+8x +b =0的两个实根为x 1，x 2(x 1≠x 2)，且|x 1|<|x 2|<1，则a +b 的最小值为________．7. 已知正数x 、y 满足{2x −y ≤0x −3y +5≥0，则z =4−x ⋅(12)y 的最小值为________．8. 在棱长为1的正四面体ABCD 中，E 是BC 的中点，则AE →⋅CD →=________．9. 若关于x 的不等式组{x 2−x −2>02x 2+(2k +5)x +5k <0的整数解集为{−2}，则实数k 的取值范围是________．10. 已知a >0，设函数f(x)=2009x+1+20072009x +1+sinx(x ∈[−a,a])的最大值为M ，最小值为N ，那么M +N =________．11. 已知P 为抛物线y 2=4x 的焦点，过P 的直线l 与抛物线交与A ，B 两点，若Q 在直线l 上，且满足|AP →||QB →|=|AQ →||PB →|，则点Q 总在定直线x =−1上．试猜测如果P 为椭圆x 225+y 29=1的左焦点，过P 的直线l 与椭圆交与A ，B 两点，若Q 在直线l 上，且满足|AP →||QB →|=|AQ →||PB →|，则点Q 总在定直线________上．12. 曲边梯形由曲线y =e x ，y =0，x =1，x =5所围成，过曲线y =e x ，x ∈[1, 5]上一点P 作切线，使得此切线从曲边梯形上切出一个面积最大的普通梯形，这时点P 的坐标是________．13.如图在三角形ABC 中，E 为斜边AB 的中点，CD ⊥AB ，AB =1，则(CA →⋅CD →)(CA →⋅CE →)的最大值是________．14. 如图，线段AB =8，点C 在线段AB 上，且AC =2，P 为线段BC 上的一动点，点A 绕点C 旋转后与点B 绕点P 旋转后重合于点D ，设CP =x ，△PCD 的面积为f(x)，则f(x)的最大值为________．二、解答题（共6小题，满分90分）15. 在△ABC 中，角A ，B ，C 所对边分别为x 且1+tanAtanB =2c b．（1）求角f(x)=ax 2−4bx +1；（2）若a =(0, −1)，b(cosB, 2cos 2C2)，试求|y =f(x)|的最小值．16. 如图，已知三棱锥A −BPC 中，AP ⊥PC ，AC ⊥BC ，M 为AB 中点，D 为PB 中点，且△PMB 为正三角形．（1）求证：DM // 平面APC ；（2）求证：平面ABC ⊥平面APC ；（3）若BC ＝4，AB ＝20，求三棱锥D −BCM 的体积． 17. 已知关于x 的一元二次函数f(x)=ax 2−4bx +1．（1）设集合P ={1, 2, 3}和Q ={−1, 1, 2, 3, 4}，分别从集合P 和Q 中随机取一个数作为a 和b ，求函数y =f(x)在区间[|m +n|2上是增函数的概率；（2）设点(12, |m +n|min =√22)是区域{x +y −8≤0x >0y >0内的随机点，求MD 上是增函数的概率． 18. 已知矩形ABCD 中，AB =2√2，BC =1．以AB 的中点O 为原点建立如图所示的平面直角坐标系xoy．（1）求以A，B为焦点，且过C，D两点的椭圆的标准方程；（2）过点P(0, 2)的直线l与（1）中的椭圆交于M，N两点，是否存在直线l，使得以线段MN为直径的圆恰好过原点？若存在，求出直线l的方程；若不存在，说明理由．19. 定义：对于任意n∈N∗，满足条件a n+a n+22≤a n+1且a n≤M（M是与n无关的常数）的无穷数列a n称为T数列．（1）若a n＝−n2+9n(n∈N∗)，证明：数列a n是T数列；（2）设数列b n的通项为b n=50n−(32)n，且数列b n是T数列，求常数M的取值范围；（3）设数列c n=|pn−1|(n∈N∗, p>1)，问数列b n是否是T数列？请说明理由．20. 对于正整数a，b，存在唯一一对整数q和r，使得a＝bq+r，0≤r<b．特别地，当r ＝0时，称b能整除a，记作b|a，已知A＝{1, 2, 3, ..., 23}．(Ⅰ)存在q∈A，使得2011＝91q+r(0≤r<91)，试求q，r的值；(Ⅱ)求证：不存在这样的函数f:A→{1, 2, 3}，使得对任意的整数x1，x2∈A，若|x1−x2|∈{1, 2, 3}，则f(x1)≠f(x2)；(Ⅲ)若B⊆A，card(B)＝12（card(B)指集合B中的元素的个数），且存在a，b∈B，b< a，b|a，则称B为“和谐集”．求最大的m∈A，使含m的集合A的有12个元素的任意子集为“和谐集”，并说明理由．2011年江苏省南通市某校高考数学最后冲刺试卷答案1. 一2. 23. ∃x∈(0,π2),sinx≥x4. x=−55. 36. 97. 1168. −149. −3≤k<210. 401611. x=−25412. (2, e2)13. 22714. 2√215. 解：（1）已知的等式1+tanAtanB =2cb化简得：1+sinAcosB sinBcosA =2sinCsinB即sinBcosA+sincosBsinBcosA=2sinC sinB，∴ sin(A+B)sinBcosA =2sinC sinB，又sinC =sin[π−(A +B)]=sin(A +B)，∴ cosA =12，∵ 0<A <π，∴ A =π3；（2）a →+b →=(cosB, 2cos 2C 2−1)=(cosB, cosC)，∴ |a →+b →|2=cos 2B +cos 2C =cos 2B +cos 2(2π3−B)=1−12sin(2B −π6)， ∵ A =π3，∴ B +C =2π3，∴ B ∈(0, 2π3)，从而−π6<2B −π6<7π6，∴ 当sin(2B −π6)=1，即B =π3时，|a →+b →|2取得最小值12，所以|a →+b →|min =√22． 16. （II ）∵ △PMB 为正三角形，D 为PB 的中点∴ MD ⊥PB ，∴ AP ⊥PB 又∵ AP ⊥PC ，PB ∩PC ＝P ∴ AP ⊥面PBC∵ BC ⊂面PBC∴ AP ⊥BC 又∵ BC ⊥AC ，AC ∩AP ＝A∴ BC ⊥面APC ， ∵ BC ⊂面ABC∴ 平面ABC ⊥平面APC（III ）由题意可知，三棱锥A −BPC 中，AP ⊥PC ，AC ⊥BC ，M 为AB 中点，D 为PB 中点，且△PMB 为正三角形．MD ⊥面PBC ，BC ＝4，AB ＝20，MB ＝10，DM ＝5√3，PB ＝10，PC =√100−16=2√21，∴ MD 是三棱锥D −BCM 的高，S △BCD =12×4×2√21×12=2√21，∴ V M−DBC =13Sℎ=13×5√3×2√21=10√7．17. 解：（1）∵ 函数f(x)=ax 2−4bx +1的图象的对称轴为x =2b a，要使f(x)=ax 2−4bx +1在区间[1, +∞)上为增函数，当且仅当a >0且2ba ≤1，即2b ≤a若a =1则b =−1，若a =2则b =−1或1；若a =3则b =−1或1； ∴ 事件包含基本事件的个数是1+2+2=5∴ 所求事件的概率为515=13．（2）由（1）知当且仅当2b ≤a 且a >0时，函数f(x)=ax 2−4bx +1在区是间[1, +∞)上为增函数，依条件可知试验的全部结果所构成的区域为{(a,b)|{a +b −8≤0a >0b >0} 构成所求事件的区域为三角形部分．由{a +b −8=0b =a 2得交点坐标为(163,83)， ∴ 所求事件的概率为P =12×8×8312×8×8=13．18. 解：（1）由题意可得点A ，B ，C 的坐标分别为(−√2，0)，(√2,0)，(√2,1)．设椭圆的标准方程是x 2a 2+y 2b 2=1(a >b >0)．则2a =AC +BC ，即2a =√(2√2)2+12+1=4>2√2，所以a =2．所以b 2=a 2−c 2=4−2=2．所以椭圆的标准方程是x 24+y 22=1．（2）由题意知，直线l 的斜率存在，可设直线l 的方程为y =kx +2．由{y =kx +2x 2+2y 2=4.得(1+2k 2)x 2+8kx +4=0．因为M ，N 在椭圆上，所以△=64k 2−16(1+2k 2)>0．设M ，N 两点坐标分别为(x 1, y 1)，(x 2, y 2)．则x 1+x 2=−8k1+2k 2x 1x 2=41+2k 2，若以MN 为直径的圆恰好过原点，则OM →⊥ON →，所以x 1x 2+y 1y 2=0，所以，x 1x 2+(kx 1+2)(kx 2+2)=0，即(1+k 2)x 1x 2+2k(x 1+x 2)+4=0，所以，4(1+k 2)1+2k 2−16k 21+2k 2+4=0，即8−4k 21+2k 2=0，得k 2=2，k =±√2经验证，此时△=48>0．所以直线l 的方程为y =√2x +2，或y =−√2x +2．即所求直线存在，其方程为y =±√2x +2．19. 由a n ＝−n 2+9n ，得a n +a n+2−2a n+1＝−n 2+9n −(n +2)2+9(n +2)+2(n +1)2−18(n +1)＝−2 所以数列a n 满足a n +a n+22≤a n+1．又a n =−(n −92)2+814，当n ＝4或5时，a n 取得最大值20，即a n ≤20．综上，数列a n 是T 数列．因为b n+1−b n =50(n +1)−(32)n+1−50n +(32)n =50−12(32)n ，所以当50−12(32)n ≥0即n ≤11时，b n+1−b n >0，此时数列b n 单调递增当n ≥12时，b n+1−b n <0，此时数列b n 单调递减；故数列b n 的最大项是b 12，所以，M 的取值范围是M ≥600−(32)12①当1<p ≤2时，当n ＝1时c 1=p −1,c 2=1−p 2,c 3=1−p3，由c 1+c 3−2c 2=5p 3−2≤0得p ≤65，即当1<p ≤65时符合c n +c n+22≤c n+1条件．若n ≥2，则p n≤1，此时c n =1−p n于是c n +c n+2−2c n+1=(1−pn )+(1−p n+2)−2(1−pn+1)=−2p n(n+1)(n+2)<0又对于n ∈N ∗有c n =|pn −1|<1，所以当1<p ≤65时数列c n 是T 数列； ②当2<p ≤3时，取n ＝1则：c 1=p −1,c 2=p2−1,c 3=1−p3，由c 1+c 3−2c 2=2−p3>0，所以2<p ≤3时数列c n 不是T 数列．③当p >3时，取n ＝1则c 1=p −1,c 2=p2−1,c 3=p3−1，由c 1+c 3−2c 2=5p 6>0，所以p >3时数列c n 不是T 数列．综上：当1<p ≤65时数列c n 是T 数列；当p >65时数列c n 不是T 数列．20. （1）因为2011＝91×22+9，所以q ＝22，r ＝9．（2）证明：假设存在这样的函数f:A →{1, 2, 3}，使得对任意的整数x ，y ，若|x −y|∈{1, 2, 3}，则f(x)≠f(y)．设f(1)＝a ，a ∈{1, 2, 3}，f(2)＝b ，b ∈{1, 2, 3}，由已知a ≠b ，由于|3−1|＝2，|3−2|＝1，所以f(3)≠f(1)，f(3)≠f(2)．不妨令f(3)＝c，c∈{1, 2, 3}，这里c≠a，且c≠b，同理，f(4)≠b，且f(4)≠c，因为{1, 2, 3}只有三个元素，所以f(4)＝a．即f(1)＝f(4)，但是|4−1|＝3，与已知矛盾．因此假设不成立，即不存在这样的函数f:A→{1, 2, 3}，使得对任意的整数x，y，若|x−y|∈{1, 2, 3}，则f(x)≠f(y)．(Ⅲ)当m＝8时，记M＝{7+i|i＝1, 2, ..., 16}，N＝{2(7+i)|i＝1, 2, 3, 4}记P＝∁M N，则card(P)＝12，显然对任意1≤i<j≤16，不存在n≥3，使得7+j＝n(7+i)成立．故P是非“和谐集”，此时P＝{8, 9, 10, 11, 12, 13, 14, 15, 17, 19, 21, 23}．同样的，当m＝9，10，11，12时，存在含m的集合A的有12个元素的子集为非“和谐集”．因此m≤7．下面证明：含7的任意集合A的有12个元素的子集为“和谐集”．设B＝{a1, a2, ..., a11, 7}，若1，14，21中之一为集合B的元素，显然为“和谐集”．现考虑1，14，21都不属于集合B，构造集合B1＝{2, 4, 8, 16}，B2＝{3, 6, 12}，B3＝{5, 10, 20}，B4＝{9, 18}，B5＝{11, 22}，B′＝{13, 15, 17, 19, 23}．以上B1，B2，B3，B4，B5每个集合中的元素都是倍数关系．考虑B′⊆B的情况，也即B′中5个元素全都是B的元素，B中剩下6个元素必须从B1，B2，B3，B4，B5这5个集合中选取6个元素，那么至少有一个集合有两个元素被选，即集合B中至少有两个元素存在倍数关系．综上所述，含7的任意集合A的有12个元素的子集B为“和谐集”，即m的最大值为7．。

高三数学江苏省2011届小题训练(4)

江苏省2011届高三数学小题训练004 １．2)11(i ai -+为实数，则实数a 的值是２．已知5()lg ,f x x =则(2)f =３．若角α的终边落在直线y ＝－x 上，则ααααcos cos 1sin 1sin 22-+-的值等于___________４．已知,αβ是两个不同平面，,m n 是两条不同直线。

给出下列命题: ①若m ∥,,n m n αα⊥⊥则 ②若m ∥,,n m ααβ=则∥n③若,,m m αβα⊥⊥则∥β ④若,,m n m n α⊥⊥则∥α其中不正确的是（填写你认为正确的序号) ５．过点)2,3(-的直线l 经过圆0222=-+y y x 的圆心，则直线l 的倾斜角大小为６．已知x 、y 满足约束条件⎪⎩⎪⎨⎧≥+-≤--≥-+06y 3x 201y x 02y 2x ,则22y 1x ++)(的最小值为７．已知S n 是数列{a n ｝的前n 项和，且S n = 3n －2，则a n = ８．若函数432--=x x y 的定义域为[0，m ],值域为]4,425[--,则m 的取值范围是９．函数)34cos(x y -=π的单调递增区间为１０．如果三棱锥的三个侧面两两垂直，它们面积分别为6cm 2、4cm 2、3cm 2，那么它的外接球体积是。

１１．阅读流程图填空:(1）最后一次输出的i = ；（2）一共输出i 的个数为。

１２．如图，在ABC △中，12021BAC AB AC ∠===，，°,D 是边BC 上一点，2DC BD =，则AD BC ⋅=_________．１３．已知椭圆19822=++y a x 的离心率21=e ，则a 的值等于１４．给出下面类比推理命题（其中Q 为有理数集,R 为实数集，C 为复数集）:①“若b a b a R b a =⇒=-∈0，则、”类比推出“b a b a C c a =⇒=-∈0,则、” ②“若d b c a di c bi a R d c b a ==⇒+=+∈,，则复数、、、”类比推出 “d b c a d c b a Q d c b a ==⇒+=+∈,22，则、、、”③“若b a b a R b a >⇒>-∈0，则、、”类比推出“若b a b a C b a >⇒>-∈0,则、” ④“若111||<<-⇒<∈x x R x ，则”类比推出“若111||<<-⇒<∈z z C z ，则"其中类比结论正确．．．．的有（填写序号）１、１２、1lg 25 ３、０４、②④５、120° ６、553 ７、 ⎩⎨⎧≥⋅==-2n 321n 11n n ,,a ８、]3,23[ ９、 R k k k ∈⎥⎦⎤⎢⎣⎡+-,436,496ππππ １０、 329629cm π １１、５７，８１２、38 １３、或45 １４、① ②A B D C。

37033_2011届江苏省苏州高级中学高考数学押题卷(苏教版)

江苏省苏州高级中学2011年高考数学押题卷（满分160分，考试时间120分钟）一、填空题：本大题共14小题，每小题5分，共计70分．1．集合A ＝{x |1＜x ≤3，x ∈R }，B ＝{x |－1≤x ≤2，x ∈R }，则A B ＝． 2．已知||a ＝3，||b ＝2．若⋅a b ＝－3，则a 与b 夹角的大小为． 3．设x ，y 为实数，且1i x -＋12i y -＝513i-，则x ＋y ＝． 4．椭圆2x ＋2my ＝1的焦点在y 轴上，长轴长是短轴长的两倍，则m 的值为．5．若θ∈42ππ⎛⎫⎪⎝⎭，，sin2θ＝116，则cos θ－sin θ的值是．6．已知Ω＝{(x ，y )|x ＋y ＜6，x ＞0，y ＞0}，A ＝{(x ，y )|x ＜4，y ＞0，x －2y ＞0}，若向区域Ω上随机投掷一点P ，则点P 落入区域A 的概率为．7．已知a ，b 为异面直线，直线c ∥a ，则直线c 与b 的位置关系是． 8．一个算法的流程图如右图所示则输出S 的值为．9．将20个数平均分为两组，第一组的平均数为50，方差为33；第二组的平均数为40，方差为45，则整个数组的标准差是．10．某同学在借助题设给出的数据求方程lg x ＝2－x 的近似数(精确到0.1)时，设()f x ＝lg x ＋x －2，得出(1)f ＜0，且(2)f ＞0，他用“二分法”取到了4个x 的值，计算其函数值的正负，并得出判断：方程的近似解为x ≈1.8，那么他所取的4个值中的第二个值为．11．设OM ＝112⎛⎫⎪⎝⎭，，ON ＝(0，1)，O 为坐标原点，动点P (x ，y )满足0≤OP OM ⋅≤1，0≤OP ON ⋅≤1，则z ＝y －x 的最小值是．12．设周期函数()f x 是定义在R 上的奇函数，若()f x 的最小正周期为3，且满足(1)f ＞－2，(2)f ＝m －3m，则m 的取值范围是． 13．等差数列{}n a 的公差为d ，关于x 的不等式22d x ＋12d a x ⎛⎫- ⎪⎝⎭＋c ≥0的解集为[0，22]，则使数列{}n a 的前n 项和n S 最大的正整数n 的值是．14．方程2x ＋2x －1＝0的解可视为函数y ＝x ＋2的图象与函数y ＝1x的图象交点的横坐标．若4x ＋ax －9＝0的各个实根1x ，2x ，…，k x (k ≤4)所对应的点9()i ix x ，(i ＝1，2，…，k )均在直线y ＝x 的同侧，则实数a 的取值范围是．二、填空题：本大题共6小题，共计70分．请在指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．（本小题满分14分）已知函数()f x ＝sin()A x ωϕ+，x ∈R (其中A ＞0，ω＞0，0＜ϕ＜2π)的图象与x 轴的交点中，相邻两个交点之间的距离为2π，且图象上一个最低点为2(2)3M π-，．（1）求()f x 的解析式；（2）当x ∈[]122ππ，时，求()f x 的值域．16．（本小题满分14分）如图，在四棱锥P －ABCD 中，PD ⊥底面ABCD ，底面ABCD 是直角梯形，DC ∥AB ，∠BAD ＝90︒，且AB ＝2AD ＝2DC ＝2PD ＝4，E 为PA 的中点．（1）证明：DE ∥平面PBC ；（2）证明：DE ⊥平面PAB ． 17．（本小题满分14分）有一气球以v (m/s)的速度由地面上升(假设气球在上升过程中的速度大小恒定)，10分钟后由观察点P 测得气球在P 的正东方向S 处，仰角为45︒；再过10分钟后，测得气球在P 的东偏北30︒方向T 处，其仰角为60︒(如图，其中Q 、R 分别为气球在S 、T 处时的正投影)．求风向和风速(风速用v 表示)．18．（本小题满分16分）已知圆C 过点P (1，1)，且与圆M ：2(2)x +＋2(2)y +＝2r (r ＞0)关于直线x ＋y ＋2＝0对称．（1）求圆C 的方程；（2）设Q 为圆C 上的一个动点，求PQ MQ ⋅的最小值；（3）过点P 作两条相异直线分别与圆C 相交于A ，B ，且直线PA 和直线PB 的倾斜角互补，O 为坐标原点，试判断直线OP 和AB 是否平行？请说明理由．19．（本小题满分16分）设数列{}n a 的前n 项和为n S ，且满足n S ＝2－n a ，n ＝1，2，3，…．（1）求数列{}n a 的通项公式；（2）若数列{}n b 满足1b ＝1，且1n b +＝n b ＋n a ，求数列{}n b 的通项公式；（3）设n c ＝n (3－n b )，求数列{}n c 的前n 项和为n T ．20．（本小题满分16分）已知集合M 是满足下列性质的函数()f x 的全体：存在非零常数k ，对定义域中的任意x ，等式()f kx ＝2k＋()f x 恒成立．（1）判断一次函数()f x ＝ax ＋b (a ≠0)是否属于集合M ；（2）证明函数()f x ＝2log x 属于集合M ，并找出一个常数k ；（3）已知函数()f x ＝log a x (a ＞1)与y ＝x 的图象有公共点，证明()f x ＝log a x ∈M ．参考答案1．[－1，3]2．120︒3．44．145．154-6．297．相交或异面8．459．810．1.75 11．－112．(-∞，1)(0-，3)13．1114．(-∞，24)(24-，)+∞15．（1）由最低点为M (23π，－2)得A ＝2．由x 轴上相邻两个交点之间的距离为2π得2T＝2π，即T ＝π，ω＝2T π＝2ππ＝2．由点M (23π，－2)在图象上得22sin(2)3πϕ⨯+＝－2，即4sin()3πϕ+＝－1．故43πϕ+＝2k π－2π，k ∈Z ．所以ϕ＝k π－116π．又0＜ϕ＜2π，所以ϕ＝6π，故()f x ＝2sin(2)6x π+．（2）因为x ∈[]122ππ，，所以(2)6x π+∈7[]36ππ，．当26x π+＝2π，即x ＝6π时，()f x 取得最大值2；当26x π+＝76π，即x ＝2π时，()f x 取得最小值－1．故()f x 的值域为[－1，2]．16．（1）设PB 的中点为F ，连结EF 、CF ，EF ∥AB ，DC ∥AB ，所以EF ∥DC ，且EF ＝DC ＝12AB ．故四边形CDEF 为平行四边形，可得ED ∥CF ．又ED ⊄平面PBC ，CF ⊂平面PBC ，故DE ∥平面PBC ．（2）因为PD ⊥底面ABCD ，AB ⊂平面ABCD ，所以AB ⊥PD ．又因为AB ⊥AD ，PD AD ＝D ，AD ⊂平面PAD ，PD ⊂平面PAD ，所以AB ⊥平面PAD ．ED ⊂平面PAD ，故ED ⊥AB ．又PD ＝AD ，E 为PA 的中点，故ED ⊥PA ；PAAB ＝A ，PA ⊂平面PAB ，AB ⊂平面PAB ，所以ED ⊥平面PAB ．17．10分钟后由观察点P 测得气球在P 的正东方向S 处，仰角为45︒的S 点处，即∠SPQ ＝4π，所以PQ ＝QS ＝600v (m)．又10分钟后测得气球在P 的东偏北30︒方向，其仰角为60︒的T 点处，即∠RPQ ＝6π，∠TPR ＝3π，RT ＝2QS ＝1200v (m)，于是PR ＝tan 3RT π＝4003v (m)．在△PQR 中由余弦定理，得QR ＝222cos PQ PR PQ PR QPR +-⋅∠＝2003v (m)．因为2PR ＝2(4003)v ＝2(600)v ＋2(2003)v ＝2PQ ＋2QR ．所以∠PQR ＝2π，即风向为正南风．因为气球从S 点到T 点经历10分钟，即600s ，所以风速为||600QR ＝33v (m/s)．18．（1）设圆心C (a ，b )，则2220222 1.2a b b a --⎧++=⎪⎪⎨+⎪=⎪+⎩，解得00.a b =⎧⎨=⎩，则圆C 的方程为2x ＋2y ＝2r ，将点P 的坐标代入，得2r ＝2，故圆C 的方程为2x ＋2y ＝2．（2）设Q (x ，y )，则2x ＋2y ＝2，且PQ MQ ⋅＝(x －1，y －1)·(x ＋2，y ＋2)＝2x ＋2y ＋x ＋y －4＝x ＋y －2，所以PQ MQ ⋅的最小值为－4(可由线性规划或三角代换求得)．（3）由题意，知直线PA 和直线PB 的斜率存在，且互为相反数，故可设 PA ：y －1＝k (x －1)，PB ：y －1＝－k (x －1)．由221(1)2y k x x y -=-⎧⎨+=⎩，，得22(1)k x +＋2k (1－k )x ＋2(1)k -－2＝0．因为点P 的横坐标x ＝1一定是该方程的解，故可得A x ＝22211k k k --+，同理B x ＝22211k k k +-+．所以ABk ＝B A B A y y x x --＝(1)(1)B A B A k x k x x x -----＝2()B A B A k k x x x x -+-＝1＝OP k ．所以直线OP 和AB 一定平行．19．（1）因为n ＝1时，1a ＋1S ＝1a ＋1a ＝2，所以1a ＝1．因为n S ＝2－n a ，即n a ＋n S ＝2，所以1n a +＋1n S +＝2．两式相减：1n a +－n a ＋1n S +－n S ＝0，即1n a +－n a ＋1n a +＝0，故有12n a +＝n a ．因为n a ≠0，所以1n n a a +＝12(n ∈*N )．所以数列{}n a 是首项1a ＝1，公比为12的等比数列，n a ＝112n -⎛⎫⎪⎝⎭(n ∈*N )．（2）因为1n b +＝n b ＋n a (n ＝1，2，3，…)，所以1n b +－n b ＝112n -⎛⎫⎪⎝⎭．从而有21b b -＝1，32b b -＝12，43b b -＝212⎛⎫⎪⎝⎭，…，1n n b b --＝212n -⎛⎫ ⎪⎝⎭(n ＝2，3，…)．将这n －1个等式相加，得n b －1b ＝1＋12＋212⎛⎫ ⎪⎝⎭＋…＋212n -⎛⎫⎪⎝⎭＝1112112n -⎛⎫- ⎪⎝⎭-＝2－1122n -⎛⎫⎪⎝⎭．又因为1b ＝1，所以n b ＝3－1122n -⎛⎫⎪⎝⎭(n ＝1，2，3，…)．（3）因为n c ＝n (3－n b )＝1122n n -⎛⎫⎪⎝⎭，所以n T ＝022111111223(1)22222n n n n --⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++-+⎢⎥ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦．① 12n T ＝123111111223(1)22222n nn n -⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++-+⎢⎥ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦．② ①－②，得12n T ＝021111122222n -⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫++++⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦－122nn ⎛⎫ ⎪⎝⎭．故n T ＝1124112n⎛⎫- ⎪⎝⎭-－142n n ⎛⎫ ⎪⎝⎭＝8－82n －142nn ⎛⎫ ⎪⎝⎭＝8－1(84)2n n +(n ＝1，2，3，…)．20．（1）若()f x ＝ax ＋b ∈M ，则存在非零常数k ，对任意x ∈D 均有()f kx ＝akx ＋b ＝2k＋()f x ，即a (k －1)x ＝2k恒成立，得100k k -=⎧⎨=⎩，，无解，所以()f x ∉M ．（2）2log ()kx ＝2k＋2log x ，则2l og k ＝2k ，k ＝4，k ＝2时等式恒成立，所以()f x ＝2log x ∈M ．（3）因为y ＝log a x (a ＞1)与y ＝x 有交点，由图象知，y ＝log a x 与y ＝2x必有交点．设log a k ＝2k ，则()f kx ＝log ()a kx ＝log a k ＋log a x ＝2k＋()f x ，所以()f x ∈M ．。

2011届江苏高考数学权威预测题

2011届某某高考数学权威预测题一、填空题（每小题5分，共70分）1、设复数122,2()z i z x i x R =+=-∈，若12z z •为实数，则x 为▲.2、*()RN N ＝▲．3、半径为1的半球的表面积为▲.4、“cos y x =是周期函数”写成三段论是：大前提：三角函数都是周期函数小前提：▲．结论：函数cos y x =是周期函数5、若某程序框图如所示，则该程序运作后输出的y 等于▲.6、在锐角ABC ∆中，2,,A B B C ∠=∠∠∠的对边长分别是,b c ，则bb c+的取值X 围是▲. 7、若双曲线22221(0,0)x y a b a b -=>>的一个焦点到一条渐近线的距离等于焦距的14，则该双曲线的渐近线方程是▲.8、已知各项均为正数的等比数列765{}:2,n a a a a =+满足1192,a m n=+则的最小值为▲.9、已知定义在R 上的可导函数()y f x =的导函数为/()f x ，满足/()()f x f x <且(1)y f x =+为偶函数，(2)1f =，则不等式()x f x e <的解集为▲.10、两圆2240()x y a a R ++++-=∈和22140()x y b b R ++--+=∈恰有三条共切线，则11a b+的最小值为▲. 11、设定义在R 上的函数()f x 满足对,x t R ∀∈，且0t ≠，都有(()())0t f x t f x +->，则{}{}(,)|()(,)|x y y f x x y y a ==的元素个数为 ▲．Q12、设点()a b ,在平面区域{()||1||1}D a b a b =,≤,≤中按均匀分布出现，则椭圆22221x y a b +=（a ＞b ＞0）的离心率e＜2的概率为▲． 13已知ABC ∆中，I 为内心，2,3,4,AC BC AB AI xAB y AC ====+且，则x y +的值为▲.14、已知数列{}n a 的各项都是正整数，且1352n n nka a a ++⎧⎪=⎨⎪⎩1n n n a a a +为奇数为偶数，k 是使为奇数的正整数若存在*m N ∈，当n m >且n a 为奇数时，n a 恒为常数p ，则p =▲．二、解答题15、(14分) 如图，正△ABC 的边长为15，1235AP AB AC =+，1255BQ AB AC =+．（1）求证：四边形APQB 为梯形；（2）求梯形APQB 的面积．16、（14分）如图，已知正四面体ABCD 的棱长为3cm ．（1）求证：AD ⊥BC ；（2）已知点E 是CD 的中点，点P 在△ABC 的内部及边界上运动，且满足EP ∥平面ABD ，试求点P 的轨迹；（3）有一个小虫从点A 开始按以下规则前进：在每一个顶点处等可能地选择通过这个顶点的三条棱之一，并且沿着这条棱爬到尽头，当它爬了12cm 之后，求恰好回到A 点的概率．17、（14分）在海岸A 处，发现北偏东045方向、距离A 处13-海里的B 处有一艘走私船；在A 处北偏西075方向、距离A 处2海里的C 处的辑私船奉命以310海里/小时的速度追截走私船.同时，走私船正以10海里/小时的速度从B 处向北偏东030方向逃窜，问辑私船沿什么方向能最快追上走私船？最少要花多少时间？18、（16分）如图，在平面直角坐标系中，方程为220x y Dx Ey F ++++=的圆M 的内接四边形ABCD 的对角线AC 和BD 互相垂直，且AC 和BD 分别在x 轴和y 轴上 . （1）求证：0F <；（2）若四边形ABCD 的面积为8，对角线AC 的长为2，且0AB AD ⋅=，求224D E F +-的值；（3）设四边形ABCD 的一条边CD 的中点为G ，OH AB ⊥且垂足为H .试用平面解析几何的研究方法判断点O 、G 、H 是否共线，并说明理由.B AC D19、（16分）定义：对于任意*n ∈N ，满足条件212n n n a a a +++≤且n a M ≤（M 是与n 无关的常数）的无穷数列{}n a 称为T 数列．（1）若2n a n =-(*n ∈N )，证明：数列{}n a 是T 数列；（2）设数列{}n b 的通项为243nn b n =-，且数列{}n b 是T 数列，求M 的取值X 围；（3）设数列1n c q n p=--(*n ∈N )，问数列{}n c 是否是T 数列？请说明理由．20、（16分）对于正整数,a b ，存在唯一一对整数q r 和，使得,0a bq r r q =+≤<.特别地，当0r =时，称b 能整除a ，记作|b a ，已知{1,2,3,,23}A =.（1）存在q A ∈，使得201191(091)q r r =+≤<，试求,q r 的值；（2）求证：不存在这样的函数:{1,2,3}f A →，使得对任意的整数12,x x A ∈，若12||{1,2,3}x x -∈，则12()()f x f x ≠；（3）若,()12(()B A card B card B ⊆=指集合B 中元素的个数），且存在,,,|a b B b a b a ∈<，则称B 为“和谐集”.求最大的m A ∈，使含m 的集合A 的有12个元素的任意子集为“和谐集”，并说明理由.答案一、填空题1、4；2、{0}；3、53π；4、cos y x =是三角函数； 5、63； 6、11(,)32； 7、0x ±=； 8、4； 9、(0,)+∞； 10、1； 11、０或１； 12、116；13、23； 14、1或5.二、解答题15、解：（1）因PQ PA AB BQ =++=1235AB AC --1255AB AB AC +++=1315AB ，…4分故PQ ∥AB ，且|PQ |=13，|AB |=15，|PQ |≠|AB |，于是四边形APQB 为梯形．…7分（2）设直线PQ 交AC 于点M ，则25AM AC =，故梯形APQB 的高h 为正△ABC 的AB 边上高的25，即2155h ==11分从而，梯形APQB 的面积为1(1315)2+⨯=14分16、解：（1）取BC 中点M ，连AM ，DM ．因△ABC 及△BCD 均为正三角形，故BC ⊥AM ，BC ⊥DM ．因AM ，DM 为平面ADM 内的两条相交直线，故BC ⊥平面ADM ，于是BC ⊥AD ．…4分（2）连接EM ，并取AC 的中点Q ，连QE ，QM ．于是EQ ∥AD ，故EQ ∥平面ABD ．同理MQ ∥平面ABD ．因EQ ，MQ 为平面QEM 内的两条相交直线，故平面QEM ∥平面ABD ，从而点P 的轨迹为线段QM ． ……………………8分（3）依题设小虫共走过了4条棱，每次走某条棱均有3种选择，故所有等可能基本事件总数为34=81． ……………………10分走第1条棱时，有3种选择，不妨设走了AB ，然后走第2条棱为：或BA 或BC 或BD ．若第2条棱走的为BA ，则第3条棱可以选择走AB ，AC ，AD ，计3种可能；若第2条棱走的为BC ，则第3条棱可以选择走CB ，CD ，计2种可能；同理第2条棱走BD 时，第3棱的走法亦有2种选择． ……………………12分故小虫走12cm 后仍回到A 点的选择有3×(3+2+2)=21种可能．于是，所求的概率为2178127=． ……………………14分 17、解：设辑私船t 小时后在D 处追上走私船，则有t BD t CD 10,310==.在ABC ∆中，0120,2,13=∠=-=ABC AC AB .利用余弦定理可得6=BC .…4分由正弦定理，222362sin sin =⋅=∠=∠BAC BC AC ABC , 得045=∠ABC ，即BC 与正北方向垂直.于是0120=∠CBD .……………8分在BCD ∆中，由正弦定理得，21310120sin 10sin sin 0=⋅=∠=∠tt CD CBD BD BCD 得030=∠BCD , 又030sin 120sin BC CD =，63310=t，得106=t .……………12分答：当辑私船沿东偏北︒30.……14分 18、解:（1）证法一：由题意，原点O 必定在圆M 内，即点(0,0)代入方程220x y Dx Ey F ++++=的左边后的值小于0，于是有0F <，即证.…………4分证法二：由题意，不难发现A 、C 两点分别在x 轴正负半轴上. 设两点坐标分别为(),0A a ，(),0C c ，则有0ac <.对于圆方程220x y Dx Ey F ++++=，当0y =时，可得20x Dx F ++=，其中方程的两根分别为点A 和点C 的横坐标，于是有A C x x ac F ==.因为0ac <，故0F <.………………4分（2）不难发现，对角线互相垂直的四边形ABCD 面积2AC BDS ⋅=，因为8S =，2AC =，可得8BD =.………………6分又因为0AB AD ⋅=，所以A ∠为直角，而因为四边形是圆M 的内接四边形，故284BD r r ==⇒=.………………8分对于方程220x y Dx Ey F ++++=所表示的圆，可知22244D E F r +-=，所以2224464D E F r +-==.………………10分（3）证：设四边形四个顶点的坐标分别为(),0A a ，()0,B b ，(),0C c ，()0,D d . 则可得点G 的坐标为,22c d ⎛⎫⎪⎝⎭，即,22c d OG ⎛⎫= ⎪⎝⎭.………………12分又(),AB a b =-，且AB OH ⊥，故要使G 、O 、H 三点共线，只需证0AB OG ⋅=即可. 而2bd ac AB OG -⋅=，且对于圆M 的一般方程220x y Dx Ey F ++++=，当0y =时可得20x Dx F ++=，其中方程的两根分别为点A 和点C 的横坐标，于是有A C x x ac F ==.………………14分同理，当0x =时，可得20y Ey F ++=，其中方程的两根分别为点B 和点D 的纵坐标，于是有B D y y bd F ==. 所以，02bd acAB OG -⋅==，即AB OG ⊥. 故O 、G 、H 必定三点共线.………………16分19、解：(1) 由2n a n =-得222212(2)2(1)20n n n a a a n n n +++-=--+++=-<所以数列{}n a 满足212n n n a a a +++≤. 2n a n =-(*n ∈N )单调递减,所以当n =1时，n a 取得最大值-1，即1n a ≤-.所以，数列{}n a 是T 数列.……4分(2) 由243n n b n =-得()1124132432423n n nn n b b n n ++-=+--+=-⋅，当24230n-⋅≥,即2n ≤时，10n n b b +->，此时数列{}n b 单调递增；……………6分而当3n ≥时，10n n b b +-<，此时数列{}n b 单调递减；因此数列{}n b 中的最大项是3b ，所以，M 的取值X 围是 3494M b ≥=. ……………9分（3）假设数列{}n c 是T 数列，依题意有：2111222(2)(1)()(1)(2)n n n c c c p n p n p n p n p n p n +++-=+-=--+-+-----…11分因为*n ∈N ,所以当且仅当p 小于n 的最小值时,2102n n n c c c +++-≤对任意n 恒成立，即可得1p <. ……………14分又当1p <时，0n p ->,1n c q q n p=-<-，故M q ≥ 综上所述：当1p <且M q ≥时，数列{}n c 是T 数列．……………16分 20、（1）解：因为201191229=⨯+，所以22,9q r ==.……………3分（2）证明：假设存在这样的函数:{1,2,3}f A →，使得对任意的整数,x y ，若12||{1,2,3}x x -∈，则12()()f x f x ≠.设(1),{1,2,3},(2),{1,2,3}f a a f b b =∈=∈，由已知a b ≠.由于|31|2,|32|1-=-=，所以(3)(1),(3)(2)f f f f ≠≠. ……………6分不妨令(3),{1,2,3}f c c =∈，这里,c a ≠且c b ≠，同理，(4),(4)f b f c ≠≠且, 因为{1,2,3}只有三个元素，所以(4)f a =. 即(1)(4)f f =，但|41|3-=，与已知矛盾. 因此，假设不成立，即不存在这样的函数:{1,2,3}f A →，使得对任意的整数12,x x A ∈，若12||{1,2,3}x x -∈，则12()()f x f x ≠.……………9分（3）解：当8m =时，记{7|1,2,,16},{2(7)|1,2,3,4}M i i N i i =+==+=，记MP N =，则()12card P =，显然对任意116i j ≤<≤，不存在3n ≥，使得7(7)j n i +=+成立.故P 是非 “和谐集”，此时，{8,9,10,11,12,13,14,15,17,19,21,23}P =.同理，当9,10,11,12m =时，存在含m 的集合A 的有12个元素的子集为“和谐集”. 因此7m ≤.……………12分下面证明：含7的任意集合A 的有12个元素的子集为“和谐集”. 设1211{,,,,7}B a a a =.若1，14，21都不属于集合B ，构造集合123{2,4,8,16},{3,6,12},{5,10,20}B B B ===，/45{9,18},{11,22},{13,15,17,19,23}B B B ===.以上12345,,,,B B B B B 每个集合中的元素都是倍数关系.考虑/B B ⊆的情况，也即/B 中5个元素全都是B 的元素，B 中剩下6个元素必须从12345,,,,B B B B B 这5个集合中选取6个元素，那么至少有一个集合有两个元素被选，即集合B 中至少有两个元素存在倍数关系.综上所述，含7的任意集合A 的有12个元素的子集B 为“和谐集”，即m 的最大值为7.……16分。

2011届高考数学冲刺小题训练

高考冲刺小题训练11．若集合{1,2,3,4},{1,2},{2,3}U M N ===，则()U C M N = ▲ .2．已知命题:,sin 1p x R x ∀∈≤, 则p ⌝为 ▲ . 3.已知平面向量()1,2=a ，()2,2x x =+b ，若⊥a b ，则实数x = ▲ .4.复数1ii+在复平面内对应的点位于第 ▲ 象限．5.已知等差数列}{n a 的公差为2，若134,,a a a 成等比数列，则1a 等于 ▲ .6.如图，ABC ∆中，2CD DB =，设AD mAB nAC =+（,m n 为实数），则m n += ▲ .7.若一个长方体的长、宽、高分别为5米、4米、3米，则其外接球的表面积为 ▲ 米2.8.若实数y x ,满足⎪⎩⎪⎨⎧≤+≥≥622y x y x ，则y x z 3+=的最大值为 ▲ . 9.已知平面向量a 与b 的夹角为120°，5=a ,8=b ，则+a b = ▲ .10.已知等差数列}{n a 的前n 项和为n S ，若3766a a =-=，，则下列四个命题中真命题的序号为 ▲ ．① 46S S > ② 45S S = ③ 65S S = ④ 65S S >11.设,αβ为互不重合的平面，,m n 为互不重合的直线，给出下列四个命题：①若,,m n m n αα⊥⊂⊥则； ②若,,m n m αα⊂⊂∥,n β∥β，则α∥β；③若,,,,m n n m n αβαβαβ⊥⋂=⊂⊥⊥则；④若,,//,//m m n n ααββ⊥⊥则.其中正确命题的序号为 ▲ .12.在△ABC 中，AB ＝3，AC ＝1，D 为BC 的中点，则ADBC =· ▲ .13.已知关于x 的一元二次不等式022>++b x ax 的解集为}1|{ax x -≠，则227a b a b ++-（其中b a >）的最小值为 ▲ .14.设等差数列{}n a 的各项均为整数，其公差0d ≠，65=a ，若，，，，，，t n n n a a a a a 2153 )5(21 <<<<<t n n n 成等比数列，则1n 的值为 ▲ .高考冲刺小题训练2一、填空题（本大题共14小题，每小题5分，共70分）． 1、集合{}21,2≤≤--==x x y y A ，则集合A= ▲__ .2.设m,n 为整数，则“m,n 均为偶数”是“m+n 是偶数”的______▲_____条件3.已知),,2(,31)4sin(ππθπθ∈=+则θsin =____▲_____ 4．设f(x)=52ax bsin x+x +，且f(-2)=3，则f(2)= _▲___5.已知O 是坐标原点，A ()1,2-，()8,4-B ，且03=+BC AB ，则=OC __▲____6.如图，在任意四边形ABCD 中，E ，F 分别是AD ，BC 的中点，若0=-+EF CD AB λ，则λ= ▲__ .7.设函数)(x f 是定义在R 上的周期为3的奇函数，若112)2(,1)1(+-=<a a f f ，则a 的取值范围是 ▲__ .8、若0,0≥≥y x ,且1≤+y x ，则y x z -=的最大值是____▲____ 9.在等比数列}{n a 中，5,4133115=+=•a a a a ,则=414a a ___▲___ 10.已知直线03:,02:21=+=-y x l y x l ，则这两条直线的夹角为___▲_____ 11.把函数)32sin(π+=x y 的图像向右平移ϕ（ϕ>0）个单位，所得图像关于直线6π=x 对称，则ϕ的最小值为____▲___12.若对于a>0,b>0,c>0,有33abc c b a ≥++，当且仅当a=b=c 时取等号。

江苏南通2011高考数学二轮冲刺小练参考答案

江苏南通2011高考数学二轮冲刺小练参考答案（1）1．}2,0{； 2．14； 3．0； 4．－25 ； 5．3 ； 6．7 ；78．4i ；93； 10．30（或31或32）． 11．解（1）∵依题意知CD ⊥AD ，又平面PAD ⊥平面ABCD ， ∴CD ⊥平面PAD ．又∵CD ⊂平面PCD ， ∴平面PAD ⊥平面PCD ．（2）由（1）知PA ⊥平面ABCD ，∴平面PAB ⊥平面ABCD ．在棱PB 上取一点M ，在平面PAB 内作MN ⊥AB ，垂足为N ，则MN ⊥平面ABCD ，设MN=h ，则V M-ABC =111213323A B C hS h h ∆=⨯⨯⨯⨯=，又V P-ABCD =11(12)1113322A B C D S P A +=⨯⨯⨯=，要使V PDCMA :V MACB =2:1，则1():2:1233h h -=，解得12h =，即M 为PB 的中点．12．解（1）设椭圆C 的焦距为2c ，Q （x 0，0），P （x 1，y 1），由F （－c ，0），A （0，b ）得0(,),(,)FA c b AQ x b ==- ．∵FA AQ ⊥ ，∴200cx b -=，即20b x c=．又∵85A P P Q = ，∴211118(0,)(,0)5b x y b x y c --=--，∴21185,1313b bx y c ==．又∵点P 在椭圆上，∴2222285()()13131bbcab+=，整理得223b ac =，又∵222b ac =-，∴222()3a c ac -=，即22320e e +-=，解得12e =，故椭圆的离心率为12．（2）由（1）知223b ac =，12c a=，故23,22ba a c c==，于是Q （3,02a ）、F （,02a -），△AQF 的外接圆圆心为（,02a ），半径1||2r F Q a ==．∵△AQF 的外接圆与直线033=++y x 相切，1|03|a a ++=，解得a =2，∴1b c ==，故椭圆C 的方程为22143xy+=．（2）1．2-；2．(1,2]-； 3．716； 4．322； 5．1-； 6．[-；7．1b a+；8．2211612xy+=； 9．9； 10．4．11．解（1）由题设知01()1sin 22f x x x x =+=因为，是函数)(x f y =图象的一条对称轴，所以02()2x k ,k ππ=+∈Z ，)]32cos(1[21)]62cos(1[21)(00πππ++=++=k x x g当k 为偶数时，41)32cos 1(21)(0=+=πx g ；当k 为奇数时，43)3cos 1(21)(0=+=πx g ．（2）因为)]6cos(1[21)sin 211()(πωω++++=x x x h23)3sin(2123)sin 21cos 23(sin 21++=+-+=πωωωωx x x x ，当22[,] [,]3333333x x πππωππωππω∈-+∈-++时，，因为2()[,]33h x ππ-在上是增函数，且 ,0>ω 所以 ],2,2[]33,332[πππωππωπ-⊆++-即2,332,332ωπππωπππ⎧-+-⎪⎪⎨⎪+⎪⎩≥≤ 12ω解得≤，所以ω的最大值为21．12．解（1）∵23(*)n n S a n n =-∈N ，∴11123a S a ==-，∴13a =．又由1123,23(1)n n n n S a n S a n ++=-⎧⎨=-+⎩得111223n n n n n a S S a a +++=-=--，∴132(3)n n a a ++=+，∴{3}n a +是首项为136a +=，公比为2的等比数列， ∴1362n n a -+=⨯，即3(21)nn a =-．（2）假设数列{}n a 中存在三项,,()r s t a a a r s t <<，它们可以构成等差数列．由（1）知r s t a a a <<，则2s r t a a a =+， ∴6(21)3(21)3(21)srt-=-+-，即1222s r t+=+，∴1212s r t r+--=+（*）． ∵,,r s t 均为正整数且r s t <<， ∴（*）左边为偶数而右边为奇数，（或由1t s +≥，∴122ts +≥，∴1222t r s +>+） ∴假设不成立，即数列{a n }不存在三项使它们按原顺序可以构成等差数列．（3）1．5； 2．2+i ； 3．(,1]-∞； 4．216y x =或28x y =-；5．充分不必要；6．14； 7．22(2)(1)4x y -+-=； 8； 9．1； 10．65． 11．证（1）连结BD ．在长方体AC 1中，对角线BD ∥B 1D 1．又∵E 、F 为棱AD 、AB 的中点， ∴EF ∥BD ，∴EF ∥B 1D 1．又B 1D 1⊂平面C B 1D 1，EF ⊄平面C B 1D 1，∴EF ∥平面C B 1D 1．（2）∵在长方体AC 1中，AA 1⊥平面A 1B 1C 1D 1，而B 1D 1⊂平面A 1B 1C 1D 1，∴AA 1⊥B 1D 1．又在正方形A 1B 1C 1D 1中，A 1C 1⊥B 1D 1，∴B 1D 1⊥平面CAA 1C 1．又∵平面C B 1D 1⊂平面平面C B 1D 1，∴平面CAA 1C 1⊥平面CB 1D 1． 12．解（1）∵((cos ,sin )A A =-=m n ，∴1cos cos )2sin()226A A A A A π⋅=-+=-=-m n ．又∵1⋅=m n ，∴1sin()62A π-=．又∵0A π<<，∴66A ππ-=，∴3A π=．（2）∵2222cos ,,3ab c bc A A a π=+-==∴2232cos3b c bc π=+-，∴223b c bc +=+．又∵222b c bc +≥（当且仅当b c =时取等号）， ∴32bc bc +≥，∴3bc ≤，∴1sin 244ABC S bc A ∆==≤，∴△ABC的面积的最大值为4．（4）1．（0，0，－3）； 2．（0，73）； 3．（－1，0）； 4．4 ； 5．23；6．1n； 7．2-； 8．3； 9．1； 10．[8,．11．解（1）∵,cos ),(cos ,cos )x x x x ==a b ，∴()221f x m =⋅+-ab 2cos 2cos 21x x x m =++-2cos 22x x m =++ 2sin(2)26x m π=++∴()f x 的最小正周期是π．（2）∵]2,0[π∈x ，∴]67,6[62πππ∈+x ．∴当6762ππ=+x 即2π=x 时，函数()f x 取得最小值是12-m ．∵512=-m ，∴3=m ．12．证（1）∵底面ABCD 是菱形，O 为中心．∴AC ⊥BD ，又∵SA=SC ，∴AC ⊥SO ，而SO BD=O ，∴AC ⊥面SBD ．（2）取棱SC 中点M ，CD 中点N ，连接MN ，则动点P 的轨迹即是线段MN ．证明如下：连结EM 、EN ，∵E 是BC 中点，M 是SC 中点， ∴EM//SB ，同理EN//BD ．又∵AC ⊥平面SBD ∴AC ⊥SB ， ∴AC ⊥EM ，同理AC ⊥EN ，又EM EN=E ， ∴AC ⊥平面EMN ，因此，当P 点在线段MN 上运动时，总有AC ⊥EP ． P 点不在线段MN 上时，不可能有AC ⊥EP ．（5）1．a ≤2 ； 2．2；3．①②； 4．－4； 5．3[,1)4； 6．(,1)-∞-； 72；8．49；9．115；10．1(,0)3-．11．解（1）}{n a 为等差数列，4352a a a a +=+∴，252515,54,a a a a +=⎧∴⎨⋅=⎩解得256,9,a a =⎧⎨=⎩（因d<0，舍去）或259,6,a a =⎧⎨=⎩ 11,10,d a =-⎧⇒⎨=⎩ 11n a n ∴=-．（2）n a a n -==11,101 ， 21()121222n n n a a S n n +∴==-+．又021<-，对称轴为221，故当n = 10或11时，S n 取得最大值，其最大值为55．12．解如图，设βα=∠=∠BCO ACB ,，再设A （0，a ）、B （0，b ）、C （x ，0），则,)tan(xa=+βα xb =βtan ．])tan[(tan ββαα-+=21tan )tan(1tan )tan(x abx bxa+-=⋅++-+=ββαββαa b a b a b ab x x---==+≤（当且仅当ab x x=时取等号）．∵2x ab =，x >0，∴,时ab x =αtan 有最大值，最大值为abb a 2-，又∵x y tan =在)2,0(π内为增函数，∴αtan 有最大值时，角α最大．∴使∠ACB 取得最大值的点C的坐标为0)．（6）1．4；2．1；3．132()2n -⨯； 4．4 ； 5．58； 6．113；7．10k ≤（或11k <）； 8．(,8]-∞； 9．2； 10．①③④．11．12．解（1）∵4sin 2)(x x x f +=，∴1cos ()24x f x '=+，∴13()[,]44f x '∈，满足条件0()1f x '<<．又∵(0)0f =，∴方程0)(=-x x f 有实数根0，∴函数4sin 2)(x x x f +=是集合M 中的元素．（2）假设方程0)(=-x x f 存在两个实数根,()αβαβ<，则[,]D αβ⊆，故存在0[,]x αβ∈，使得等式0()()()()f f f x βαβα'-=-成立．又∵()f αα=，()f ββ=，∴0()1f x '=，这与0()1f x '<<矛盾，故假设不成立，即方程0)(=-x x f 只有一个实数根．（7）1．(1,1)-； 2．0.8 ； 3．－1； 4．12a >； 5．60； 6．7．034a a <或≤≤； 8．2 ； 9．32； 10．11．解（1）1, 2k b ==．（2）由)()(x g x f >得24x -<<，y =)(1)(x f x g +=252x x x --+．设2 (06)t x t =+<<，则153y t t=+--≥，当且仅当1t =，即1x =-时，等号成立．12．解（1）∵E 、F 分别为AB 1、BC 1的中点，∴EF ∥A 1C 1．又∵A 1C 1∥AC ，∴EF ∥AC ．又∵EF ⊄平面ABC ，∴EF ∥平面ABC ．（2）∵AB=AA 1，∴AB 1⊥A 1B ．又∵AB 1⊥BC 1，∴AB 1⊥平面A 1BC 1， ∴AB 1⊥A 1C 1，∴AB 1⊥AC ，又∵BB 1⊥AC ，∴AC ⊥平面ABB 1A 1，∴AC ⊥AB ．（3）∵AB=CC 1=a ，BC=b ，∴，112B A AB S a =，∴1111111111223BABC C B A AB B A AB V V S AC -==⨯⨯⨯=．（8）1．23-； 2．1； 3．40； 4．134π-； 5．（-2，15）； 6．若①②④，则③；7．相离； 8．32； 9．2010； 10．(,3][3,)-∞-+∞ ．11．12．解 ∵a =(cos32x ，sin32x )，b =(2sin 2cosx x -，)，∴⋅a b x x x x x 2cos 21sin 23sin21cos23cos=-=，||2|cos |x ===a +b ．又∵[0]2x π∈，，∴cos x ≥0，∴||a +b =2cos x ，∴()2||f x λ=⋅-a b a +b 即2221)(cos 2)(λλ---=x x f ． ∵[0]2x π∈，，∴0≤cos x ≤1．①若λ＜0，则当且仅当cos x =0时，f (x )取得最小值－1，这与已知矛盾； ②若0≤λ≤1，则当且仅当cos x =λ时，f (x )取得最小值221λ--，由已知得 23212-=--λ，解得21=λ；③若λ＞1，则当且仅当cos x =1时，f (x )取得最小值λ41-，由已知得2341-=-λ，解得85=λ，这与1>λ相矛盾．综上所述，21=λ．（9）1．π； 2．a >12； 3．56； 4．－6； 5．－4 ；6．440x y --=或20x y -+=；7．12；8．33[0,[,)22-++∞ ； 9．30； 10．[7，8]．11．解 ∵DE ∥AC ，DF ∥AB ，∴四边形DEAF 是平行四边形，∴||||D E D F A D += ，即||D E D F +的最小值就是线段AD 长的最小值，显然，当AD ⊥BC时AD 最小，即AD 长的最小值为BC 边上的高d BC ．在△ABC 中，∵AB=5，AC=4，∠BAC=60°，∴由余弦定理得，BC ==又∵11sin 22A B C B C S A B A C B A C B C d ∆=⋅∠=⋅，∴sin 7BC AB AC BACd BC⋅∠===，∴||D E D F +7．12．解（1）∵数列{}n a 的前n 项和22n S n n =+，∴12213,(1)(2)[(1)2(1)]21,(2)n n n S n a S S n n n n n n -⎧==⎪=⎨-=+--+-=+⎪⎩≥21(*)n n =+∈N ．（2）由（1）得1121n b n a b --=+．∵数列{}n b 中，第n 项n b 是数列{}n a 的第1n b -项(2)n ≥， ∴121n n b b -=+，(2)n ≥，∴112(1)n n b b -+=+，(2)n ≥ 又∵11b =，∴112b +=，∴数列{1}n b +是以2为首项，2为公比的等比数列， ∴11222n nn b -+=⨯=，∴21nn b =-．（3）231231111111111111122222nnn b b b b +++⋅⋅⋅+=++++=-++++∵对任意的*n ∈N ，1112n-<，∴要使不等式2123111111111n m m b b b b +++⋅⋅⋅<-+++++恒成立，只需211m m -+≥，解得：0m ≤或1m ≥， ∴m 的取值范围为(,0][1,)-∞+∞ ．（10）1．2-； 22； 3．43-； 4．1,42-； 5．16a -≤≤； 6．5 ；7．8π； 8．51630x y -+=； 9．27 ； 10．③④．11．证（1）设AC BD O = ，连OE ．由题意可得11,22===E M E F A C A O又∵//E M A O ，∴四边形EOAM 为平行四边形，∴//.E O A M⊂⊄ EO EBD AM EBD 平面,平面//AM EBD ∴平面．（2）连DM ，BM ，MO,,AF AC EC AC AFEC ABCD ⊥⊥⊥ 平面平面，,,,,AF ABCD EC ABCD AF AD EC DC ∴⊥⊥∴⊥⊥平面平面又ABCD 为菱形，∴AD=DC ，∴DF=DE ．又点M 是EF 的中点，∴D M EF ⊥．12,2B D A F D O B D A F M O =∴=== ，∴45D M O ∠=︒，同理45BM O ∠=︒， ∴D M BM ⊥．又E F B M M = DM BEF ∴⊥平面．,DM EFD EFD BEF ⊂∴⊥ 平面平面平面．12．解（1） A 、B 、C 成等差数列，2,B A C ∴=+又A B C π++=,3π=∴B ，由23-=⋅BC AB 得，2332cos-=⋅πa c ， 3ac ∴=． ①又由余弦定理得ac c a ac c a b-+=∴-+=222223,3cos2π，622=+∴c a ． ② 由①、②得，32=+c a ．（2）2sin sin A C -=22sin sin()3A A π--12sin cos sin )22A A A =-+=3sin )226A A A π-=-，20,,3662A A ππππ<<∴-<-<∴2sin sin A C -的取值范围为(2-．（11）1．3； 2．1316； 3．①②③； 4．0； 5．[3,2)-； 62；7．平行；8．3； 9．x =－1或5x +12y －31=0；10．①③④．11．解（1）因为k =2，2()(1)4ln f x x x =+-，所以()f x '=422x x+-．由()f x '＞0得2(1)(2)x x x-+＞0，（此处用“≥”同样可以）又x ＞0，故x ＞1，于是函数的增区间为(1,)+∞．（或[1,)+∞）（2）当k ＜0时，g (x )=()f x '=222k x x+-．g (x )=2()2k x x-++≥2，当且仅当x=”．①若(0,2]，即当k ∈[4,0)-时,函数g (x )在区间(0,2]上的最小值为2；②若k ＜－4，则2()2(1)kg x x'=+在(0,2]上为负恒成立，故g (x )在区间(0,2]上为减函数，于是g (x )在区间(0,2]上的最小值为(2)=6－k ．综上所述，当k ∈[4,0)-时，函数g (x )在区间(0,2]上的最小值为2+；当k ＜－4时，函数g (x )在区间(0,2]上的最小值为6－k ．12．解（1）由题意得：222222294115103a b a a b c b c a⎧+=⎪⎪⎧=⎪⎪=+∴⎨⎨=⎪⎩⎪⎪=⎪⎩ 所以椭圆的方程为1101522=+y x ．（2）由题可知当直线PA 过圆M 的圆心（8，6）时，弦PQ 最大,因为直线PA 的斜率一定存在，设直线PA 的方程为：y －6=k (x －8)，又因为P A 与圆O 相切，所以圆心（0，0）到直线PA 的距离为10，即101|68|2=+-kk ，解得13k =或139，直线PA 的方程为：3100139500x y x y -+=--=或．（3）设α=∠AOP , 则α2,=∠∠=∠AOB BOP AOP ，则1201)(21cos 2cos 222-=-=-=∠OPOPOA AOB α．8210||,12210||minmax =-==+=OP OP ，2200||||cos 10O A O B O A O B A O B O P∴⋅=⋅∠=-，m ax m in 55155(),()818O A O B O A O B ∴⋅=-⋅=- ．（12）1．3i --；2．（－1，3）； 3．2 ； 4．5 ； 5．3 ； 6．350 ；7．2a π； 8．0； 9．②④； 10．48．11．解（1）由a 11=2，得a 13= a 11×m 2=2m 2，a 61= a 11+5m =2+5m ．又a 13=a 61+1，所以2m 2=2+5m +1，解得m =3或m =0.5-（舍去）．所以111111[(1)](31)3j j j ij i a a ma i m mi ---=⋅=+-=-．（2）S=111212122212()()()n n n nnn a a a a a a a a a ++++++++++ =1112111211(13)(13)(13)1(31)()1313132nnnnn n a a a a a a ---+++=-+++---=1(231)1(31)(31)(31)224nnn nn n +--⋅=+-．12．解 ∵ f （x ）=－2x 2＋bx ＋c 在x =1时有最大值1，∴2()2(1)1f x x =--+，∴f （x ）≤1．又∵ x ∈[m ，n ]（0＜m ＜n ）时，f （x ）的取值范围是11[]n m ，， ∴ f （x ）在[m ，n ]上是减函数，∴m ≥1，∴ f （m ）=1m，f （n ）=1n，∴ m ，n 是方程2()2(1)1f x x =--+=1x的两个解，解方程结合1≤m ＜n 得m =1，n=12+．（13）1．i ；2．x +y －5=0； 3．(2,)+∞；4．（1，1），（2，2），（3，4），（4，8）；5．赔14元； 6．0.2； 7．①②③； 8．23； 9．191622=-xy； 10．③④． 11．解（1）由 0)12(21020103010=++-S S S 得 ,)(21020203010S S S S -=-即,)(220121130222110a a a a a a +++=+++ 可得.)(22012112012111010a a a a a a q+++=+++⋅因为0>n a ，所以 ,121010=q解得21=q ，因而.,2,1,2111 ===-n qa a nn n（2）因为}{n a 是首项211=a ，公比21=q 的等比数列，故11(1)1221,.12212nn n nnn S nS n -==-=--则数列}{n nS 的前n 项和),22221()21(2nn n n T +++-+++=).2212221()21(212132++-+++-+++=n nn n n n T前两式相减，得122)212121()21(212+++++-+++=n nn nn T12211)211(214)1(++---+=n nnn n ，即 1(1)12222n n n n n nT -+=++-． 12．解（1）∵AD ⊥平面ABE ，AD ∥BC ，∴BC ⊥平面ABE ，则AE ⊥BC ．又∵BF ⊥平面ACE ，∴AE ⊥BF ， ∴AE ⊥平面BCE ．又∵BE ⊂平面BCE ，∴AE ⊥BE ．（2）111422233D AE C E A D C E A B C D V V V ---===⨯⨯⨯=．（3）在三角形ABE 中，过M 点作MG ∥AE 交BE 于G 点，在三角形BEC 中，过G 点作GN ∥BC交EC 于N 点，连MN ，则由比例关系易得CN ＝CE 31．MG ∥AE ，MG ⊄平面ADE, AE ⊂平面ADE ， ∴MG ∥平面ADE ，同理，GN ∥平面ADE ， ∴平面MGN ∥平面ADE ．又∵MN ⊂平面MGN ，∴MN ∥平面ADE ， ∴N 点为线段CE 上靠近C 点的一个三等分点．（14）1．{－1，0，1} ； 2．①②③； 3．－3 ； 4．45°； 5．3，－17 ；6．16.5； 7．－4；8．(b ； 9．0.6； 10．14x =．11．解 2221(1)2xxxy aa a =+-=+-．① 当1a >时，∵11x -<<，∴1xa a a≤≤，∴2m ax (1)2y a =+-．由21,(1)214a a >⎧⎨+-=⎩得3a =； ② 当01a <<时，∵11x -<<，∴1xa a a≤≤，∴2m ax 1(1)2y a=+-．由201,1(1)214a a<<⎧⎪⎨+-=⎪⎩得13a =．综上所得， 13a =或3．12．解（1）∵1r =，∴(cos 3,sin ),(cos ,sin 3)AC BC αααα=-=-．又∵1AC BC ⋅=-，∴(cos 3)cos sin (sin 3)1αααα-+-=-，∴2sin cos 3αα+=，∴5sin 29a =-．（2）方法一：∵3r =，A ，B ，C 在以原点为圆心，3为半径的圆上．又∵∠AOB=90°，∴∠ACB=45°．又∵∠ABC=60°，AB=∴由正弦定理得sin sin 2A B A B C A C A C B∠===∠方法二：∵∠ABC=60°，∴∠AOBC=120°．又∵OA=OB=3r =，∴由余弦定理得AC ===．（15）1．23-；2．充要；3．1(,1)(,)2-∞-+∞ ； 4．122--； 5．5；6．14； 7．2；8．9-；9．{4，5，6}； 10．①④．11．解：（1）∵(cos sin )x x ==，，a b ，85⋅=a b ，85x x +=，即cos()x -=π445．又∵42x ππ<<，∴044x ππ<-<，∴3sin()45x π-=，∴3tan()44x π-=．（2）由（1）得sin cos()cos ()2222417252x x x =-=--=ππ．又∵111141313()144tan x tan xtan xtan x tan x π+====-----+，∴2(1)7428()125375sin x tan x tan x +=⨯-=--． 12．解设AB=c ，AC=b ，BC=a ．（1）∵9AB AC ⋅=，S △ABC =6，∴cos 9,sin 12,bc A bc A =⎧⎨=⎩ 两式平方相加得bc =15，∴43sin ,cos 55A A ==．又∵sin cos sin B A C =， ∴sin cos sin C A B =，∴35c b =，由35c b =与bc =15得b =3，c =5，∴4a ==．（2）∵2S △ABC ∴121(2)55x y z x y ++=++，设2t x y =+，则3412,0,0,x y x y +⎧⎪⎨⎪⎩≤≥≥由线性规划得08t ≤≤，∴1245x y z ++≤≤．（本题也可建立平面直角坐标系解之）（16）1．（0，1]； 2．0ad bc +=； 3．无数； 4．4； 5．70x y +-=或250x y -=； 6．－3； 7．23； 8．②③； 9．[1,5)(5,)+∞ ；10．①②⑥．11．解设f (m )=(x 2－1)m －2x +1，f (m )是m 的函数，其图象是直线．依题意，f (m )<0对m ∈[－2，2]恒成立．由于y =f (m )，当－2≤m ≤2时的图象是线段，该线段应全部位于x 轴下方，其充要条件是端点的纵坐标小于0，即(2)0,(2)0.f f -<⎧⎨<⎩由f (－2)<0得22(1)210x x ---+<，解得2x <或2x >；由f (2)<0得22(1)210x x --+<，解得1122x -+<<，所以(2)0,(2)0f f -<⎧⎨<⎩的解集为1122x -++<<，即适合题意的x的取值范围是11(22-++．12．解（1）设P(x ，y )是)(x f 图象上的任意一点，P 关于点A 的对称点为Q(x 0，y 0)，则000,2,x x y y +=⎧⎨+=⎩即00,2.x x y y =-⎧⎨=-⎩据题意知Q(x 0，y 0)在21)(++=xx x h 的图象上，所以00012y x x =++，即122y x x-=-++-，即1y x x =+，所以1()f x x x=+．（2）由（1）知1()()a a g x f x x x x+=+=+，所以21()1a g x x+'=-．又因为)(x g 在区间（0，2）上为减函数，所以2110a x+-<即21a x >- 当(0,2)x ∈时恒成立．又因为(0,2)x ∈时，213x -<，所以3a ≥．（17）1．1，1 ；2．(0,1)； 3．19； 4．23； 5．3m 和1.5m ； 6．3π；7．（0，4）； 8．22136xy-=； 9．[2,)-+∞； 10．97300.11．解（1）∵{}n a 是等差数列，∴212,i i i a a a +++=∴方程21220i i i a x a x a ++++=可化为222()0.i i i i a x a a x a +++++=即2(1)()0i i x a x a +++=，有一解1x =-为公共解．（2）由（1）知以上方程另一解为()21,2,,,i ia x i n a +=-=⋅⋅⋅所以2i iia a a +=-，所以321111111111n n n n n na a a a a a ++++-=---++++1132n n n n n n a a a a a a ++++=---112222n n a a d ddd+=-==----，故数列1{}1n a +是以111a +为首项，12-为公差的等差数列．12．解（1）易得直线l 的方程为()2t y x a =+，代入椭圆方程并整理得：222(4)40.a t y aty +-=所以224,4M at y a t =+S=2S △AOM =2×22214.24M a t OA y a t ⋅=+（2）由（1）得，22244aS a a t t==+≤，当且仅当2t a=时等号成立．所以，当2[1,2]a∈时，即[1,2]a ∈时，m ax S a =；当2a >时，设224u a t t=+，则224u a t'=-．∵[1,2]t ∈，∴0,u '>∴u 在[1,2]t ∈上单调递增，∴S 在[1，2]上单调递减，∴1t =时，2max 24.4aS a =+综上得，2m ax2,(12),4,(2).4a a S a a a ⎧⎪=⎨>⎪+⎩≤≤ （18）1．9.2； 2．充要； 3．40； 4．－3； 5．0； 6．[2010,2011)，I ←I +2 ；7．154；8．13； 9．4； 10．3{4,,6}2--． 11．解设事件A 为函数()f x 有零点．当0,0a b >>时，函数()f x 有零点的充要条件为a b ≥．（1）用正六面体骰子从1，2，3，4，5，6这六个数中掷出的一个数，再用正四面体骰子从1，2，3，4这四个数中掷出的一个数，共有基本事件24个．设事件A 包含下列基本事件：当a =1时，b =1；当a =2时，b =1，2；当a =3时，b =1，2，3；当a =4时，b =1，2，3，4；当a =5时，b =1，2，3，4；当a =6时，b =1，2，3，4．所以事件A 发生的概率为1234443()244P A +++++==．（2）实验的全部结果所构成的区域为16,{(,)|}14a a b b ⎧⎨⎩≤≤≤≤，构成事件A 的区域为16,{(,)|14,}a a b b a b ⎧⎪⎨⎪⎩≤≤≤≤≥，所以事件A 发生的概率为1(52)372()5310P A +⨯==⨯．12．解（1）R x t t t x x t x x f ∈+-++--=,4342cos 2sin 4cos )(23223223sin 12sin 434(sin )433x t x t t t x t t t =--++-+=-+-+．∵|t |≤1，|sin x |≤1，∴当sin x t =时，)(x f 取得最小值g(t )，即3()433g t t t =-+．（2）∵2()1233(21)(21)g t t t t '=-=+-，|t |≤1，列表如下：∴由此可见，g(t )的单调增区间为（―1，―12）和（12，1），单调减区间为（―12，12），故g(t )的极大值为1()42g -=，极小值为1()22g =．（19）1．－2； 2．m n k；3．1(,1)2； 4．12+5．左，8π； 6．三；7．1[0,]2a； 8．911，22；9．2214xy -=； 10．22221111habc=++．11．证（1）因为()lnln(0)x x f x aaa=-=-+>，所以1322111()()22a f x x x x a --'=⋅-+-20=-<，所以，()f x 在区间(,)a +∞上是减函数．（2）因为b a >，由（1）得()()f b f a <，即ln0ba-<，所以ln ln b ab a-<-12．证（1）连接A 1D ．∵A 1D 1DA 是正方形，∴AD 1⊥DA 1．又∵AD 1⊥A 1C ，∴AD l ⊥平面A 1CD ，∴AD 1⊥CD ．又∵DD 1⊥CD ， ∴CD ⊥平面AD l ， ∴CD ⊥平面AD ．（2）设AC BD=O ．∵AD=DC ，AB=BC ，∴BO ⊥AC ．又∵BO ⊥C 1C ，AC C 1C=C ，∴BO ⊥平面AA 1C 1C ．在BD 上取点M ，使得OM=OD ，连接AM ，CM ． ∵AD=DC ，∠ADC=90°，又DO ⊥AC ，且AO=OC ，∴CM=AM=AD ，∴四边形AMCD 是一个正方形，∴AM ∥CD ． ∴A 1D ⊥AM ．又∵AD 1⊥A 1D ，∴A 1D ⊥平面AD 1M ，D 1M ⊥A 1D ．又∵A 1C 1⊥平面DD 1B 1B ，∴D 1M ⊥A 1C 1．又∵A 1D A 1C 1=A 1，∴D 1M ⊥平面A 1C 1D ，此时DM=，∴当DM=D 1M ⊥平面A 1C 1D ．（20）1． x ∀∈R ，x 2+ x +1≥0； 2．一； 3．0.01； 4．24； 5．①④；6．13R(S 1＋S 2＋S 3＋S 4)； 7．； 8．32； 9．(1,1)--； 101．11．解（1）因为各组的频率和等于1，故第四组的频率：41(0.0250.01520.010.005)100.3f -+⨯++⨯==，直方图如下图所示．（2）依题意，60及以上的分数所在的第三、四、五、六组，频率和为(0.0150.030.0250.005)100.75+++⨯=，所以，抽样学生成绩的及格率是75%．利用组中值估算抽样学生的平均分123456455565758595f f f f f f ⋅+⋅+⋅+⋅+⋅+⋅＝450.1550.15650.15750.3850.25950.05⨯+⨯+⨯+⨯+⨯+⨯＝71，估计这次考试的平均分约是71分．12．解（1）由//m n 得0cos cos )2(=-⋅-C a A c b ，由正弦定理得0cos sin cos sin cos sin 2=--C A A C A B ， ∴0)sin(cos sin 2=+-C A A B ，∴0sin cos sin 2=-B A B ．1,(0,),sin 0,cos ,23A B B A A ππ∈∴≠=∴=．（2）22sin coscos 2sinsin 233y B B B ππ=++11cos 2cos 2222B B B =-++11cos 2222B B =-+s i n (2)16B π=-+，由（1）得67626320ππππ<-<-∴<<B B ，∴1sin(2)(,1]62B π-∈-，∴1(,2]2y ∈．（21）1．1或3；2．2； 3．[1,1]-； 4．13-； 5．14； 6．4π； 7．2572；8．1；9．11； 10．②③④． 11．解 ∵32(),3xf x bx cx =++∴2()2.f x x bx c '=++由(1)0f '=得210.b c ++=∵1是()f x '的零点，且()f x '的图象关于x b =-对称，∴21b --也是()f x '的零点，即c 也是()f x '的零点．又∵112b -<<，∴30.c -<<又∵0x 是()2c y f x x =-的一个极值点，∴0()02c f x '=<，∴0(,1)x c ∈，∴043x c -<-<，∴0(4)(3)f x f -<-．12．解（1）∵13(23)3n n tS t S t --+=，∴123(23)3n n tS t S t ---+=，两式相减得13(23)0n n ta t a --+=．又∵0t >，∴1233n n a t a t -+=，∴{a n }是以1为首项，233t t +为公比的等比数列．（2）由（1）得()f t 232133t t t+==+，∴1112()3n n n b f b b --==+， ∴{bn }是以1为首项，23为公差的等差数列，∴2211(1)333n b n n =+-=+．（3））由（2）得2462,,,,n b b b b 是以53为首项，43为公差的等差数列，∴12233445212221n n n n b b b b b b b b b b b b -+-+-++-21343522121()()()n n n b b b b b b b b b -+=-+-++- 242225142()2[(1)]33323n b b b n n n =-⨯+++=-⨯⨯⨯+⨯-⨯ 22193n n =--．（22）1．42．84； 3． 45．1(,0)(0,2)2-； 6．6 ；7．1或－1； 8．8； 9． 10．100π．11．解（1）连接AF ，∵E ， F 分别为CC 1，DD 1的中点，∴EF ∥AB ，且EF=AB ，∴四边形ABEF 为平行四边形．又在四棱柱ABCD －A 1B 1C 1D 1中，AB ⊥平面AA l D 1D ， ∴EF ⊥A 1F ．由已知得，A 1A=2，∴A 1F 2+AF 2=AA 12，∴AF ⊥A l F ．又AF EF=F ，∴A 1F ⊥平面ABEF ，即A 1F ⊥面BEF ．（2）由A 1F ⊥平面BEF 得A 1B 在平面BEF 上的射影为BF ，∴∠A 1BF 为直线A 1B 与平面BEF 所成的角．由已知，A 1A 11sin 5A BF ∠=．12．解（1）∵方程20n n x a x a --=有一根为1n S -，1(2)n n n a S S n -=-≥，∴211(1)()(1)()0n n n n n n S S S S S S --------=，化简得112n n S S -=-，∴11111121111111111112n n n n n n n S S S S S S S --------=-=--------11111n n S S ---==--，∴数列1{}1n S -为等差数列，其公差为－1 ；（2）由2(1)(1)0n n n n S a S a ----=，令n=1，得21111(1)(1)0a a a a ----=，解得112a =，∴1111211S a ==---．由（1）得12(1)(1)(1)1n n n S =-+-⋅-=-+-，∴1n nS n =+，∴2n ≥时，1111(1)n n n n n a S S n nn n --=-=-=++，又112a =也符合上式，∴1(*)(1)n a n n n =∈+N ．（23）1．12； 2．[1,2)； 3．12-； 4．（-13，13）；5．2212xy -=；6．②④； 78．； 9．48；10．12-．11．解（1）∵(cos ,sin )αα=a ，(cos ,sin )ββ=b ，∴||||1==a b ．又∵|||k k +=-a b a b ，∴22||3||k k +=-a b a b ，∴2222222363k k k k ++=-+⋅⋅a a b b a a b b ，∴22(3)1(31)18k k k-+-⋅=⋅⋅a b kk kk 4182222+=+=．（2）∵k ＞0，∴由（1）⋅ab 21114442k k kk+==+=≥，当且仅当kk 414=，即1=k 时取等号．此时，⋅a b 1||||cos 2θ==⋅⋅a b ，∴21cos =θ，∴3πθ=，即⋅a b 的最小值为21，此时a 与b 的夹角θ为3π．12．解（1）12n n a S += ，12n n n S S S +∴-=，13n nS S +∴=．又111S a == ，∴数列{}n S 是首项为1，公比为3的等比数列，1*3()n n S n -=∈N ．当2n ≥时，21223(2)n n n a S n --==⨯≥，21132n n n a n -=⎧∴=⎨2⨯⎩，，，≥．（2）12323n n T a a a na =++++ ，当1n =时，11T =；当2n ≥时，0121436323n n T n -=+⨯+⨯++⨯ ， ①所以 12133436323n n T n -=+⨯+⨯++⨯， ②①－②得：12212242(333)23n n n T n ---=-+++++-⨯213(13)222313n n n ---=+⨯-⨯-11(12)3n n -=-+-⨯．111()3(2)22n n T n n -∴=+-≥．又111T a == 也满足上式，1*11()3()22n n T n n -∴=+-∈N ．（24）1．4； 2．四； 3 4．①②； 5．34(,)55-或34(,)55-； 6．2e ； 7．364； 8．7； 9．222231)(3)(5)[(1)2(1)](n n n n n n n n n n -++-++-++++-++-= ； 10．4．11．证（1）在图1中，过C 作CF ⊥EB ．∵DE ⊥EB ，∴四边形CDEF 是矩形．∵CD=l ，∴EF=1．∵四边形ABCD 是等腰梯形，AB=3， ∴AE=BF=1．∵∠BAD=45°，∴DE=CF=1．连结CE ，则CE=CB=∵EB=2，∴∠BCE=90°．则BC ⊥CE ．在图2中，∵AE ⊥EB ，AE ⊥ED ，EB ED=E ， ∴AE ⊥平面BCDE ．∵BC ⊂平面BCDE ，∴AE ⊥BC ．∵AE CE=E ，∴BC ⊥平面AEC ．（2）用反证法．假设EM // 平面ACD ．∵EB // CD ，CD ⊂平面ACD ，EB ⊄平面ACD ， ∴EB // 平面ACD ．∵EB EM=E ，∴平面AEB // 平面ACD ．而A ∈平面AEB ，A ∈平面ACD ，与平面AEB // 平面ACD 矛盾．∴假设不成立，∴EM 与平面ACD 不平行．12．（25）1．充要； 2．（0，3）； 3．3； 4．－1； 5．0.7； 6．－2； 7．40 dm 2；8．(,)33-∞-+∞ ； 9．41；10．(,2][2,){0}-∞-+∞ ．11．证切化弦后用和角公式得2sin sin cos 1sin A B CC=，再用正弦定理得2cos 1ab C c=，再用余弦定理得222212ab a b c c ab+-⋅=，即2223a b c +=． 12．解（1）∵对任意的实数y x ,都有()()()2()1f x y f x f y y x y +=++++，1)1(=f ，∴(1)()(1)2(1)1()24f x f x f x f x x +=++++=++，(1)()24f x f x x +-=+， ∴当*x ∈N 时，()[()(1)][(1)(2)][(2)(1)](1)f x f x f x f x f x f f f =--+---++-+2[(22)286]133x x x x =++++++=+- ．（2）由（1）得，*x ∈N 时，不等式()f x ≥)10()7(+-+a x a 可化为233x x +-≥(1)(71a x x -+-，即247x x -+≥(1)a x -． ∵2x ≥，∴2471x x a x -+-≥．∵2474(1)22211x x x x x -+=-+-=--≥（当且仅当411x x -=-即32x =>取等号），∴要使原不等式恒成立，只需a 2≤，即实数a 的取值范围为(,2]-∞．（26）1．[0，2]； 2．2； 3．－2；4．①④； 5．相切； 6．)6,2[-；7．1b <-或2b >； 8．①②④；9．7；10．③．11．解（1）设021<<x x ，则2133x x <，1321<+x x ∵1212112212121222()()333333()()91919191x x x x xx x x x x x x x x f f +++---=-=++++121212()()()()331309191xx x xx x +--=<++，∴12()()f x f x <，即)(x f y =在)0,(-∞上是增函数．（2）∵3110191233xx xx<=++≤，∴当0x ≤时，()311(,0]9122xxf x =-∈-+．又∵函数)(x f y =是R 上的奇函数，∴当0>x 时，19321)(+-=xxx f 1(0,)2∈．综上得 )(x f y =的值域为 11(,)22- ．12．解（1）因为2a e ==，所以c =1，则b =1，即椭圆C 的标准方程为2212xy +=．（2）因为P （1，1），所以12PF k =，所以2O Q k =-，所以直线OQ 的方程为y =－又椭圆的左准线方程为x =－2,所以点Q （－2，所以1P Q k =-，又1O P k =,所以1k k PQ OP -=⊥,即OP PQ ⊥，故直线PQ 与圆O 相切．（3）当点P 在圆O 上运动时，直线PQ 与圆O 保持相切．证明如下：设00(,)P x y (0x ≠，则22002y x =-，所以001PF y k x =+，001O Q x k y +=-，所以直线OQ 的方程为001x y x y +=-，所以点Q(－2,0022x y +) ，所以0022000000000022(22)22(2)(2)PQ x y y y x x x x k x x y x y y +--+--====-+++，又因为00O P y k x =，所以1k k PQ OP -=⊥，即OP PQ ⊥，故直线PQ 始终与圆O 相切．（27）1．2； 2．{|0}x x ≥； 3．8； 4．4； 5．120°； 6．92；7．13+； 8．23-；9．5∶1；10．)37,53(． 11．证明（1）取PD 中点G ，易证FG 21CD AE ，∴四边形AEFG 为平行四边形，∴EF ∥AG ，∴EF ∥平面PAD ．（2）分别取DE 、BC 中点M 、N ．由PD=PE ，PB=PC ，则PM ⊥DE ，PN ⊥BC ．在直角梯形BCDE 中，∵BC ⊥MN ，∴BC ⊥平面PMN ．∥ ＝ ∥ ＝∵BC ⊥PN ，∴BC ⊥PM ．又∵DE ⊥PM ，∴PM ⊥面ABCD ， ∴平面PDE ⊥平面ABCD ．12．解（1）∵)2sin(sin 3βαβ+=，∴3sin[()]sin[()]αβααβα+-=++．∴3sin()cos 3cos()sin αβααβα+-+=sin()cos cos()sin αβααβα+++ ∴αβααβαsin )cos(2cos )sin(+=+ 又∵βα,为锐角，2πβα≠+，∴αβαtan 2)tan(=+．（2）由（1）可得αβαβαtan 2tan tan 1tan tan =-+，∴22tan 2tan 112tan 42tan tan αβααα==++≤（当且仅当12tan tan αα=，即tan 2α=时取等号），∴βtan 的最大值为42．（28）1．（－∞，2）； 2．1或2； 3．a ≥－8； 4．60； 5．4π； 6．150° ；7．b =8．32-；910．（3，＋∞）．11．解（1）22,cos ),(1,2cos ),x x x =+= m n2()222cos 2cos 23f x x x x x ∴=⋅=++=++m n3)62sin(2++=πx ，ππ==∴22T ，32222(),()26263k x k k k x k k πππππππππ+++∈∴++∈Z Z 令≤≤≤≤，2()[,]()63f x k k k ππππ∴++∈Z 的单调减区间为．（2）由4)(=A f 得，1()2sin(2)34,sin(2).662f A A A ππ=++=∴+=A ABC ∆ 为的内角又， 752,266666A A πππππ∴<+<∴+=，3π=∴A ．11,sin 322ABC S b bc A ∆==∴=2=∴c ，。

江苏省2011年高考数学最后冲刺(三)

江苏省2011年高考数学最后冲刺（三）江苏省涟水中学汪显林（四）一、填空题1. 如图，在OAB ∆中，点P 是线段OB 及线段AB 延长线所围成的阴影区域(含边界)的任意一点，且OP xOA yOB =+则在直角坐标平面内，实数对(,)x y 所示的区域在直线4y =的下侧部分的面积是2. 已知点集}|),{(n m y y x L ⋅==,其中(2,2)m x b =-,(1,1)n b =+，点(,)n n n P a b L ∈，1{(,)|1}P L x y x ==，且11n n a a +-=,则数列{}n b 的通项公式为_______。

3. 已知点P （x ，y ）是直线kx+y+4 = 0（k 〉 0)上一动点，PA 、PB 是圆C ：2220x y y +-=的两条切线，A 、B 是切点，若四边形PACB 的最小面积是2,则k 的值为4. 设直线3x ＋4y －5＝0与圆C 1: 422=+y x 交于A , B 两点, 若圆C 2的圆心在线段AB 上, 且圆C 2与圆C 1相切, 切点在圆C 1的劣弧⌒AB 上，则圆C 2的半径的最大值是_______. 5。

已知关于的方程有且只有一个实根，则实数的取值范围是 6. 直线12=+by ax 与圆122=+y x 相交于A ，B 两点,（b a ,是实数）,且△AOB是直角三角形（O 是坐标原点)，则点),(b a P 与点)1,0(之间的距离的最大值为 7。

设集合，函数，若，且的取值范围是。

BAO P8. 已知A ，B ，P 是双曲线上不同的三点，且A,B 连线经过坐标原点，若直线PA ，PB 的斜率乘积，则该双曲线的离心率为。

9. 如图，,点P 在线段AB 的垂直平分线上,记向量的值为_______.10。

有一个数阵排列如下：则第20行从左至右第10个数字为________。

11。

在ABC ∆中，过中线AD 中点E 任作一直线分别交边AB ，AC 于点M,N 两点，设AN (0),AM xAB yAC xy ==≠，则4x+y 的最小值为。

江苏省南通市2011高考数学二轮小练(4)

江苏南通2011高考数学二轮冲刺小练（4）班级学号姓名1．已知空间的点A （1，0，2），B （1，－3，1），M 是z 轴上的点，AM=BM ，则点M 的坐标是．2．已知平面上的点A （－2，1），B （1，3），AP AB 23=，则点P的坐标是．3．不等式2log ()x -<1+x 的解集是． 4．若右边的程序流程图输出数对i ，j ，则这两个数的和是．5．某商场举行抽奖活动，从装有编为0，1，2，3四个小球的抽奖箱中同时抽出两个小球，两个小球号码相加之和等于5中一等奖，等于4中二等奖，等于3中三等奖．中奖的概率是．6．已知正项数列{a n }的首项为l ，且对于一切正整数n 都有na n 2=[(n +1)a n +1+a n ]a n +1，则数列的通项公式是a n = ．7．关于x 的方程x 2－2ax +a 2－4a =0有模为3的虚数根，则实数a 的值是． 8．已知以F 1，F 2为焦点的椭圆，其离心率为e ，以F 1为顶点、F 2为焦点的抛物线与椭圆的一个交点是P ，若e PF PF =||||21，则e 的值为．9．若))(2)(1()(a x x x x f ---=，其中1＜a ＜2，则='+'+')()2(4)1(12a f a f f ． 10．如图长方体中，O 在AD 上，AB=8，AD=10，DO=AA 1=6．若以O 为球心，r 为半径作球面，使其与长方体的六个面都有公共点，则r 的取值范围是．11．已知：(3sin ,cos ),(cos ,cos )x x x x ==a b ，()221f x m =⋅+-a b （,x m ∈R ）. （1）求()f x 关于x 的表达式，并求()f x 的最小正周期；（2）若]2,0[π∈x 时()f x 的最小值为5，求m 的值.开始 i ←5 结束j ←－2 i ←i + j j ←i + j输出i, j12．如图，在四棱锥S—ABCD中，侧棱SA=SB=SC=SD，底面ABCD是菱形，AC与BD交于O点．（1）求证：AC⊥平面SBD；（2）若E为BC中点，点P在侧面△SCD内及其边界上运动，并保持PE⊥AC，试指出动点P的轨迹，并证明你的结论．SCBDO E。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

江苏南通2011高考数学冲刺小练（4）
班级学号姓名
1．已知空间的点A （1，0，2），B （1，－3，1），M 是z 轴上的点，AM=BM ，则点M 的坐标是．
2．已知平面上的点A （－2，1），B （1，3），2
3=，则点P
的坐标是．
3．不等式2log ()x -<1+x 的解集是． 4．若右边的程序流程图输出数对i ，j ，则这两个数的和是．
5．某商场举行抽奖活动，从装有编为0，1，2，3四个小球的抽奖
箱中同时抽出两个小球，两个小球号码相加之和等于5中一等奖，等于4中二等奖，等于3中三等奖．中奖的概率是．
6．已知正项数列{a n }的首项为l ，且对于一切正整数n 都有na n 2=[(n +1)a n +1+a n ]a n +1，则数列的通项公式是a n = ．
7．关于x 的方程x 2－2ax +a 2－4a =0有模为3的虚数根，则实数a 的值是． 8．已知以F 1，F 2为焦点的椭圆，其离心率为e ，以F 1为顶点、F 2为焦点的抛物线与椭圆的一个交点是P ，若
e PF PF =|
||
|21，则e 的值为．
9．若))(2)(1()(a x x x x f ---=，其中1＜a ＜2，则='+'+')
()2(4)1(12
a f a f f ． 10．如图长方体中，O 在AD 上，AB=8，AD=10，DO=AA 1
=6．若以O 为球心，r 为半径作球面，使其与长方体的六个面都有公共点，则r 的取值范围是．
11．
已知：,cos ),(cos ,cos )x x x x ==a b ，()221f x m =⋅+-a b （,x m ∈R ）. （1）求()f x 关于x 的表达式，并求()f x 的最小正周期；（2）若]2
,
0[π
∈x 时()f x 的最小值为5，求m 的值.
12．如图，在四棱锥S —ABCD 中，侧棱SA=SB=SC=SD ，
底面ABCD 是菱形，AC 与BD 交于O 点．（1）求证：AC ⊥平面SBD ；
（2）若E 为BC 中点，点P 在侧面△SCD 内及其边界
上运动，并保持PE ⊥AC ，试指出动点P 的轨迹，并证明你的结论．
S
C
B
D O E。