2020年高考数学满分突破:立体图形中的动点问题
专题3.2 动点轨迹成曲线,坐标关系是关键-2020届高考数学压轴题讲义(解答题)(解析版)

【题型综述】1.动点轨迹问题解题策略一般有以下几种:(1)直译法:一般步骤为:①建系,建立适当的坐标系;②设点,设轨迹上的任一点P(x ,y);③列式,列出动点P 所满足的关系式;④代换,依条件式的特点,选用距离公式、斜率公式等将其转化为x ,y 的方程式,并化简;⑤证明,证明所求方程即为符合条件的动点轨迹方程.(2)定义法:先根据条件得出动点的轨迹是某种已知曲线,再由曲线的定义直接写出动点的轨迹方程; (3)代入法(相关点法):动点P (x ,y )依赖于另一动点Q (x 0,y 0)的变化而变化,并且Q (x 0,y 0)又在某已知曲线上,则可先用x ,y 的代数式表示x 0,y 0,再将x 0,y 0代入已知曲线得要求的轨迹方程;(4)参数法:当动点P (x ,y )坐标之间的关系不易直接找到,也没有相关动点可用时,可考虑将x ,y 均用一中间变量(参数)表示,得参数方程,再消去参数得普通方程. 2.解轨迹问题注意:(1)求点的轨迹与求轨迹方程是不同的要求,求轨迹时,应先求轨迹方程,然后根据方程说明轨迹的形状、位置、大小等.(2)要验证曲线上的点是否都满足方程,以方程解为坐标点是否都在曲线上,补上在曲线上而不满足方程解得点,去掉满足方程的解而不再曲线上的点.【典例指引】类型一 代点法求轨迹方程例1 【2017课标II ,理】设O 为坐标原点,动点M 在椭圆C :2212x y +=上,过M 作x 轴的垂线,垂足为N ,点P 满足2NP NM =。
(1) 求点P 的轨迹方程;(2)设点Q 在直线3x =-上,且1OP PQ ⋅=。
证明:过点P 且垂直于OQ 的直线l 过C 的左焦点F 。
因此点P 的轨迹方程为222x y +=。
(2)由题意知()1,0F -。
设()()3,,,Q t P m n -,则()()3,,1,,33OQ t PF m n OQ PF m tn =-=---⋅=+-, ()(),,3,OP m n PQ m t n ==---。
2020年中考数学压轴题专题七《几何图形动点运动问题》

专题七几何图形动点运动问题【考题研究】几何动点运动问题,是以几何知识和具体的几何图形为背景,渗透运动变化的观点,通过点、线、形的运动,图形的平移、翻折、旋转等把图形的有关性质和图形之间的数量关系位置关系看作是在变化的、相互依存的状态之中,要求对运动变化过程伴随的数量关系的图形的位置关系等进行探究.对学生分析问题的能力,对图形的想象能力,动态思维能力的培养和提高有着积极的促进作用.动态问题,以运动中的几何图形为载体所构建成的综合题,它能把几何、三角、函数、方程等知识集于一身,题型新颖、灵活性强、有区分度,受到了人们的高度关注,同时也得到了命题者的青睐,动态几何问题,常常出现在各地的中考数学试卷中.【解题攻略】几何动点运动问题通常包括动点问题、动线问题、面动问题,在考查图形变换(含三角形的全等与相似)的同时常用到的不同几何图形的性质,以三角形四边形为主,主要运用方程、函数、数形结合、分类讨论等数学思想.【解题类型及其思路】动态几何特点 - 问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
)动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。
利用动点(图形)位置进行分类,把运动问题分割成几个静态问题,然后运用转化的思想和方法将几何问题转化为函数和方程问题, 利用函数与方程的思想和方法将所解决图形的性质(或所求图形面积)直接转化为函数或方程。
解题类型:几何动点运动问题常见有两种常见类型:(1)利用函数与方程的思想和方法将所解决图形的性质直接转化为函数或方程;(2)根据运动图形的位置分类,把动态问题分割成几个静态问题,再将几何问题转化为函数和方程问题【典例指引】类型一【探究动点运动过程中线段之间的数量关系】【典例指引1】在4ABC中,/ACB =45°,点D为射线BC上一动点(与点B、C不重合),连接AD ,以AD为一边在AD右侧作正方形ADEF .(1)如果AB=AC ,如图1,且点D在线段BC上运动,判断/ BAD/CAF (填'=” 或F,并证明:CFXBD(2)如果A4AC ,且点D在线段BC的延长线上运动,请在图2中画出相应的示意图,此时(1)中的结论是否成立?请说明理由;(3)设正方形ADEF的边DE所在直线与直线CF相交于点P,若AC = 4j2, CD = 2,求线段CP的长.【举一反三】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE ,连接AE、BD交于点P(1)观察猜想:①线段AE与BD的数量关系为;②/ APC的度数为(2)数学思考:如图2,当点C在线段AB外时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明(3)拓展应用:如图3,分别以AC、BC为边在AB同侧作等腰直角三角形ACD和等腰直角三角形BCE,其中/ ACD = Z BCE=90° , CA=CD , CB = CE,连接AE = BD 交于点P,贝U 线段AE与BD的关系为图1 图工图3类型二【确定动点运动过程中的运动时间】【典例指引2】已知:如图,在平面直角坐标系中,长方形OABC的项点B的坐标是(6,4). 牛C-------------- |B~ A x(1)直接写出A点坐标(, ), C点坐标(, );(2)如图,D为OC中点.连接BD , AD ,如果在第二象限内有一点P m,1 ,且四边形OADP的面积是ABC面积的2倍,求满足条件的点P的坐标;0I -A 艾(3)如图,动点M从点C出发,以每钞1个单位的速度沿线段CB运动,同时动点N从点A出发.以每秒2个单位的速度沿线段AO运动,当N到达O点时,M , N同时停止运动,运动时间是t秒t 0 ,在M , N运动过程中.当MN 5时,直接写出时间t的值.AC、BD 相交于点O, AB,AC, AB =3, BC = 5,点P从点A出发,沿AD以每秒1个单位的速度向终点D运动.连结PO并延长交BC于点Q.设点P的运动时间为t秒.(1)求BQ的长,(用含t的代数式表示)(2)当四边形ABQP是平行四边形时,求t的值(3)当点O在线段AP的垂直平分线上时,直接写出t的值.类型三【探究动点运动过程中图形的形状或图形之间的关系】【典例指引3】已知矩形ABCD中,AB 10cm, BC 20cm,现有两只蚂蚁P和Q同时分别从A、B出发,沿AB BC CD DA方向前进,蚂蚁P每秒走1cm,蚂蚁Q每秒走2cm.问:A --------------------- \DA----------------------B----- 5 ----- C B ----- 5 ----- C"w(1)蚂蚁出发后△ PBQ第一次是等腰三角形需要爬行几秒?(2)P、Q两只蚂蚁最快爬行几秒后,直线PQ与边AB平行?【举一反三】如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(AO AB)且AO、AB的长分别是一元二次方程x23x 2 0的两个根,点C在x轴负半轴上,且AB: AC=1:2.(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM ,设4ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.类型四【探究动点运动过程中图形的最值问题】【典例指引4】如图,抛物线y=ax2- 3x+c与x轴相交于点A ( - 2, 0)、B (4, 0),与4y轴相交于点C,连接AC, BC,以线段BC为直径作。
高考数学 立体几何-2020年高考数学(理)破题之道与答题规范

B→C=(- 3,1,0),BB→′=AA→′=(0,1, 3).
8分
设平面BCC′B′的一个法向量为m=(x,y,z),
则m·B→C=0,m·B→ B′=0,
所以-y+
3x+y=0, 3z=0,
取x=1,y=
3,z=-1,
所以m=(1, 3,-1).
[满分体验]
10分
[满分体验]
又平面ABC的一个法向量为n=(0,0,1),故cos〈m,n〉=
5 5.
11 分
所以平面
MAB
与平面
MCD
所成二面角的正弦值是2
5
5 .
12 分
[满分心得]
❶写全得分步骤,踩点得分:对于解题过程中踩分点的步骤有则给分,无则没分.如 第(1)问中缺少交线为CD,扣分,忽视DM⊂平面DMA也要扣分. ❷正确计算是得分的保证:建系指出原点和坐标轴正方向,关键点坐标要准确.
专题04 立体几何
[破题之道] 立体几何解答题的基本模式是论证推理与计算相结合,以 某个几何体为依托,分步设问,逐层加深.解决这类题目的原则是建 模、建系. (1)建模——将问题转化为平行模型、垂直模型、平面化模型或角度、 距离等的计算模型; (2)建系——依托于题中的垂直条件,建立空间直角坐标系,利用空间 向量求解. .
1.(2018·全国卷Ⅰ)如图,四边形 ABCD 为正方形,E,F 分别为 AD,BC 的中点, 以 DF 为折痕把△DFC 折起,使点 C 到达 点 P 的位置,且 PF⊥BF.
(1)证明:平面 PEF⊥平面 ABFD; (2)求 DP 与平面 ABFD 所成角的正弦值.
[满分体验]
[满分体验]
设DP与平面ABFD所成角为θ,
立体几何中的最值与动态问题

,
故当 x
a 1 时,MN有最小值 (1 cos ) a . 2 2
C
例 4.如图, 正方形 ABCD、 ABEF 的边长都是 1,而且平面 ABCD、 ABEF 互相垂直。点 M 在 AC 上移动,点 N 在 BF 上移动,若 CM=x ,BN=y,
D
M P
(0 x, y 2 ). (1)求 MN 的长(用 x,y 表示); (2)求 MN 长的
4 3 .
例 2.如图,正方形 ABCD、ABEF 的边长都是 1,而且平面 ABCD、ABEF 互相垂直。点 M 在 AC 上移动,点 N 在 BF 上移动,若 CM=BN= a
(0 a 2 ). (1)求 MN 的长;
(2)当 a 为何值时,MN 的长最小; (3)当 MN 长最小时,求面 MNA 与面 MNB 所成的二面角 的大小。 解析: (1)作 MP∥AB 交 BC 于点 P,NQ∥AB 交 BE 于点 Q,连接 PQ,依题意可得 MP∥NQ,且 MP=NQ, 即 MNQP 是平行四边形。∴MN=PQ,由已知,CM=BN=a,CB=AB=BE=1,
(2)如图 2, ∵ΔBEF 等腰, 取 EF 中点 G, 连 BG, 则 BG⊥EF.∴BG=
BE 2 EG 2
=
3 a 2 ( a) 2 8
=
55 a 8
∴SΔBEF=
55 3 55 1 1 3 ·EF·BG= · a· a= 2 2 4 8 64
a.
2
(3)∵VA-BCD=VB-ACD,而三棱锥 B—AEF,三棱锥 B—ACD 的两个高相同,所以它们体积之比于( )2 1 1 。故所求二面角 4 4 cos 3 6 6 2 4 4
2020年中考数学压轴题突破之动态问题(几何)(含详解)

2020年中考数学压轴题突破之动态问题(几何)1.如图,点O是等边ABC内一点,AOB 110 , BOC .以OC为一边作等边三角形OCD,连接AC、AD .(1)若120 ,判断OB OD BD (填“,或”)(2)当150 ,试判断AOD的形状,并说明理由;(3)探究:当时,AOD是等腰三角形.(请直接写出答案)【答案】(1) 二; (2) ADO是直角三角形,证明见详解;(3) 125、110、140 .【分析】(1)根据等边三角形性质得出COD 60 ,利用?BOC a = 120。
求出BOD 180 ,所以B, 0, D三点共线,即有OB+ OD = BD ;(2)首先根据已知条件可以证明BOC ADC ,然后利用全等三角形的性质可以求出ADO的度数,由此即可判定AOD的形状;(3)分三种情况讨论,利用已知条件及等腰三角形的性质即可求解.2 .如图,在平面直角坐标系中,矩形ABCO的顶点O与坐标原点重合,顶点A C在坐标轴上,B(18,6),将矩形沿EF折叠,使点A与点C重合.图3 G(1)求点E的坐标;(2)P O O A E2E时停止运动,设P的运动时间为t, VPCE的面积为S,求S与t的关系式,直接写出t 的取值范围;3(3)在(2)的条件下,当PA=]PE 时,在平面直角坐标系中是否存在点Q,使得以点P 、E 、G Q 为顶点的四边形为平行四边形?若不存在,请说明理由;若存在,请求出点Q 的坐标.【答案】(1) E (10, 6); (2) S= -8t+54 (0<t<3)或 S=-6t+48 (3vtW8); (3)存 在,Q (14.4 , -4.8 )或(18.4 , -4.8 ). 【详解】解:(1)如图 1,矩形 ABO, B (18, 6),• .AB=18 BC=6,设 AE=x,贝U EC=x BE=18-x,Rt^EBC 中,由勾股定理得: EB"+BC 2=EC 2,(18-x) 2+62=x 2, x=10,即 AE=10,①当P 在OA 上时,0WtW3,如图 2,=18X 6-1X10(62) — - X8X6 - 1X 18X2t , 2 2 2=-8t+54 ,②当P 在AE 上时,3<t<8,如图3,S = S 矩形 OABC S △ PAE -S △ BEC -S △OPCj• •E ( 10, 6);(2)分两种情况:S=1PE?BC=1 X 6X(16-2t)=3 (16-2t ) =-6t+48 ;2 2(3)存在,由PA=3PE可知:P在AE上,如图4,过G作GHLOC于H,2•.AP+PE=10.•.AP=6 PE=4,设OF=y,则FG=y, FC=18-y,由折叠得:/ CGFW AOF=90 ,由勾股定理得:FC2=FC+CG,•. ( 18-y) 2=y2+62,y=8,•.FG=8 FC=18-8=10,1FC?GH= 1FG?CG221X10XGH= 1 X6X8,22GH=4.8,由勾股定理得:FH=J82 4 82 =6.4 ,• .OH=8+6.4=14.4,.•.G ( 14.4 , -4.8 ),•・•点P、E G Q为顶点的四边形为平行四边形,且PE=4,.•.Q ( 14.4 , -4.8 )或(18.4 , -4.8 ). k ,3.如图1,平面直角坐标系xoy中,A(-4, 3),反比例函数y —(k 0)的图象分别x交矩形ABOC勺两边AC, BC于E, F (E, F不与A重合),沿着EF将矩形ABO所叠使A, D重合.②若折叠后点 D 落在矩形ABOCrt (不包括边界),求线段CE 长度的取值范围.(2)若折叠后,△ ABD 是等腰三角形,请直接写出此时点 D 的坐标.7 . 23 3. 11 3.【答案】(1)①EC= 2;②3 CE 4; (2)点D 的坐标为(一,一)或(一,一)88 2 5 5【详解】,k k解:(1)①由题意得E(k,3) , F( 4,-), 3 4k kk 0 ,则 EC — , FB 一, 3 4AF 3 一, 417(12 k) 4 3 1 3 4(12 k) 3..由 A(-4, 3)得:AC 4, AB 3,,AC 4一 --- 一,AB 3 AE AC AF AB '又A=Z A,・ .△AE% AACB ・ •/AEF4 ACB ・ •.EF// CB如图2,连接AD 交EF 于点H ,••• AE.AE (1)①如图2,当点D 恰好在矩形 ABOC 勺对角线BC 上时,求CE 的长;②由折叠得EF 垂直平分AD,••• /AHE 90 ,则 EAH AEF又• BAD EAH BAC 90 ,BAD AEF ,・ .△AE% ABAQAE AF 口"AB AE 4--- ----- ,则 ----- ------ -,AB BD BD AF 34 3 9 BDAB - 3 - 3 4 4设 AF=x,贝U FB=3— x, FD=AF=x 在Rt^BDF 中,由勾股定理得:FB 2 BD 2 FD 2,r i图2由折叠的性质得: •••D 在 BC 上, ,AE AHEC DH 1 EC AC 2AH=DH 1,则 AE EC 2;即(3 x)2x 2 ,解得:如图,当D 落在BO 上时,: EAF ABD 90 ,B力。
2022高考数学立体几何—空间中的动点问题全文

可编辑修改精选全文完整版立体几何—空间中的动点问题专题综述空间中的动点问题是指在一定的约束条件下,点的位置发生变化,在变化过程中找出规律,将动点问题转化为“定点”问题、将空间问题转化为平面问题、将立体几何的问题转化为解析几何的问题等,目的是把问题回归到最本质的定义、定理或现有的结论中去.立体几何中考查动点问题,往往题目难度较大,渗透化归与转化思想,对学生的逻辑推理能力要求较高.一般考查动点轨迹、动点的存在性、定值、范围、最值等问题,除了利用化动为定、空间问题平面化等方法,在几何体中由动点的变化过程推理出结果以外,也可以通过建系,坐标法构建函数,求得结果.专题探究探究1:坐标法解决动点问题建立空间直角坐标系,使几何元素的关系数量化,借助空间向量求解,省去中间繁琐的推理过程.解题步骤与空间向量解决立体几何问题一致,建立适当的空间直角坐标系由动点的位置关系,如在棱上或面内,转化为向量的关系,用参数表示动点的坐标通过空间向量的坐标运算表示出待求的量若求最值或取值范围,转化为函数问题,但要注意自变量的取值范围.一般坐标法用于解决动点的存在性问题、求最值、求范围问题.说明:对于求最值、范围问题,也可以直接通过几何体中的某个变量,构建函数,求最值或范围.(2022湖北省宜昌市模拟) (多选)在正方体1111ABCD A B C D -中,点为线段1AD 上一动点,则( ) A. 对任意的点,都有1B D CQ ⊥ B. 三棱锥1B B CQ -的体积为定值 C. 当为1AD 中点时,异面直线1B Q 与所成的角最小D. 当为1AD 中点时,直线1B Q 与平面11BCC B 所成的角最大【审题视点】以正方体为载体考查定点的定值、最值问题,正方体便于建立空间直角坐标系,可选择用坐标法解决.【思维引导】选项,可以用几何知识证明;选项,设出点坐标,用坐标表示出异面直线成角的余弦值或线面角的正弦值,求最值,得出点位置.【规范解析】解:对于:连接,1.CD因为在正方体1111ABCD A B C D -中, 1B D ⊥平面1ACD ,CQ ⊂平面1ACD , 1B D CQ ⊥,故正确; 对于:平面11//ADD A 平面11BCC B ,平面11ADD A 与平面11BCC B 的距离为正方体棱长,1123111326B B CQ Q BCB V V a a a --==⨯⋅=,为定值,故正确;对于:以为坐标原点,直线分别轴,建立空间直角坐标系如下图:设正方体1111ABCD A B C D -的棱长为2, ()[](),0,20,2Q x x x -∈,则1(2,2,2)B , ()2,2,0B , (0,2,0)C , 因此()12,2,B Q x x =---, ()2,0,0BC =-, 设异面直线1B Q 与所成的角为θ,则当时,,当时,当时,故当与1D 重合时,异面直线1B Q 与所成的角最小,故不正确;对于: ()12,2,B Q x x =---, 又是平面11BCC B 的一个法向量,设直线1B Q 与平面11BCC B 所成的角为α,则,所以当1x =时,sin α取得最大值63,而0,2πα⎡⎤∈⎢⎥⎣⎦, 因此α取得最大值,即当为1AD 中点时,直线1B Q 与平面11BCC B 所成的角最大, 故正确. 故选.ABD用一个参数表示动点的坐标,并求出参数范围,即为函数定义域转化为函数求最值,求出当函数取最值时的x 的值【探究总结】典例1是一道典型的研究动点问题的多选题,难度中等,但能够反映出坐标法研究最值范围问题的思路.建系设坐标,写出参数范围 根据向量运算构造函数求最值.(2021安徽省蚌埠市联考) 已知圆柱1OO 底面半径为1,高为π,是圆柱的一个轴截面,动点从点出发沿着圆柱的侧面到达点,其距离最短时在侧面留下的曲线Γ如图所示.将轴截面绕着轴1OO 逆时针旋转(0)θθπ<<后,边11B C 与曲线Γ相交于点.P(1)求曲线Γ长度; (2)当2πθ=时,求点1C 到平面的距离;(3)证明:不存在(0)θθπ<<,使得二面角D AB P --的大小为.4π探究2:化动为定点的位置在变化的过程中,有些量或位置关系是不变的,比如点到平面的距离不变,从而使几何体的体积不变;动点与另外一定点的连线与某条直线始终垂直,与某个平面始终平行.在证明体积为定值、证明位置关系时,要动中寻定,将动态的问题静态化:将动点转化为定点,寻找动直线所在的确定平面,从而解决问题.答题思路:1.动点到平面的距离为定值:证明平面,动点到平面的距离即为定点到平面的距离;2.为动点,为定点,证明:证明所在平面与垂直;3.为动点,为定点,证明平面:证明所在平面与平面平行.(2021湖南省四校联考) 在正三棱柱中,,,分别为的中点,P 是线段DF 上的一点.有下列三个结论:①平面;②;③三棱锥的体积时定值,其中所有正确结论的编号是 A. ①②B. ①③C. ②③D. ①②③【审题视点】求证关于动直线的线面平行或线线垂直,三棱锥的体积为定值问题,要化动为定.【思维引导】证明动直线所在平面与已知平面平行;证明定直线与动直线所在平面垂直;寻找过点与平面平行的直线,即得出点到平面的距离.【规范解析】解:如图,对于①,在正三棱柱中,,分别为的中点,平面平面,由平面,得平面,故①正确;对于②,在正三棱柱中,平面平面,平面平面平面,,平面平面,故②正确;对于③,平面平面,平面到平面的距离为定值,而有为定值,故是定值,线面平行,转化为面面平行异面直线垂直,转化为线面垂直体积的定值问题,转化点到平面的距离是定值,即通过线面平行或面面平行,得出动点到平面距离为定值故③正确.故选D .【探究总结】立体几何证明中经常出现,求证关于动直线的线面平行与线线垂直问题,其思路是转化为证明动直线所在的定平面与其他平面或直线的位置关系.关键是分析动点,动线或动面间的联系,在移动变化的同时寻求规律.(2021云南省曲靖市联考) 如图所示的几何体中,111ABC A B C -为直三棱柱,四边形为平行四边形,2CD AD =,60ADC ∠=︒,1.AA AC =(1)证明:,1C ,1B 四点共面,且11A C DC ⊥;(2)若1AD =,点是上一点,求四棱锥的体积,并判断点到平面11ADC B 的距离是否为定值?请说明理由.探究3: 巧用极端位置由于点位置连续变化,使研究的图形发生连续的变化,利用点的位置变化“极端”位置,避开抽象及复杂的运算,得到结论.常见题型:1.定值问题:几何体中存在动点,但所求结果是确定的,即随着动点位置的改变不会影响所求的量,故可以考虑动点在极端位置的情况,优化解题过程.2.范围问题:几何体中存在动点,结果会随着动点位置改变而改变,当动点从一侧极端位置移动到令一个极端位置的过程中,所求量在增大、或减小、或先增后减、或先减后增,通过求出极端位置处的值,及最值,从而得出范围;3.探究问题:探究满足条件的点是否存在,也可以转化为求出范围,从而得出结论.(2021湖南省株洲市模拟) 在正四面体中, 为棱的中点, 为直线上的动点,则平面与平面夹角的正弦值的取值范围是 .【审题视点】本例可用极端位置法分析,也可以建系,用坐标法解决.【思维引导】借助极端位置分析,不难看出经过和底边中线的平面与平面垂直,点在移动的过程中,存在一个位置使平面与经过和底边中线的平面平行,即平面平面,此时两平面所成角为,角最大;当点移动到无穷远时,平面平面,此时两平面所成角最小.【规范解析】解:由下左图 设为的中心,为的中点, 则在正四面体中平面, 为中点,为的中点,,故平面连接,并延长交于点, 连接,并延长交于点, 则过点的平面交直线于点. 则平面平面 即平面与平面的夹角的正弦值为1,点从取最值的位置处移动至直线的无穷远处的过程中, 平面与平面的夹角逐渐减小,即当点在无穷远处时,看作, 如下右图 故平面与平面的夹角即为平面与平面的夹角,求出其正弦值为. 综上可知:面与面的夹角的正弦值的取值范围为.【探究总结】借助极端位置解决典例3中的问题,首先利用几何知识,明确点在移动的过程中 ,所求量的变化情况,若在极端位置处取“最值”,问题就简化为求出极端位置处的值.(2021浙江省杭州市高三模拟)高为1的正三棱锥的底面边长为,二面角与二面角A PB C --之和记为,则在从小到大的变化过程中,的变化情况是( )A .一直增大B .一直减小C .先增大后减小D .先减小后增大专题升华结合几何知识,两平面成角的变化过程,即动点从一个极端位置变化到另一极端位置时,夹角大小的增减情况在极端位置处取“最值”,直接求出点该处时的夹角的正弦值,即为范围区间的一个端点几何体中研究动点问题往往难度较大,开放性强,技巧性高.总体思路是:用几何知识,经过逻辑推理,证明位置关系或求出表示出所求量;或者建立空间直角坐标系,将几何问题代数化,用空间向量研究动点问题,省去了繁杂的推理环节,但计算量较大.解决动点问题的策略不局限与上述方法,常用的的方法还有:运用条件直接推算,借助条件将几何体还原到长方体中去;构造函数,数形结合;还将空间问题转化为平面几何解决,如化折为直、利用解析几何的知识解决. 但只要我们熟练掌握这些基本方法,并灵活加以应用,不仅能化繁为简,化难为易,而且还可以得到简捷巧妙的解法.【答案详解】 变式训练1【解答】解:(1)在侧面展开图中为的长,其中AB AD π==,∴曲线Γ的长为2;π(2)当2πθ=时,建立如图所示的空间直角坐标系,则有()0,1,0A -、()0,1,0B 、1,0,2P π⎛⎫- ⎪⎝⎭、()11,0,C π-, 、(1,1,)2AP π=-、1(1,0,)OC π=-设平面的法向量为(,,)n x y z =,则2002n AB y n AP x y z π⎧⋅==⎪⎨⋅=-++=⎪⎩, 取2z =得(,0,2)n π=,所以点1C 到平面的距离为12||||4OC n d n ππ⋅==+; (3)假设存在满足要求的(0)θθπ<<, 在(2)的坐标系中,()sin ,cos ,P θθθ-,,设平面的法向量为111(,,)m x y z =,则111120sin (cos 1)0y x y z θθθ=⎧⎨-+++=⎩,取11x =得sin (1,0,)m θθ=,又平面的法向量为(1,0,0)k =,由二面角D AB P --的大小为4π, 则|cos ⟨,m k ⟩2212|sin .21sin θθθθ==⇒=+ sin (0)2πθθθ<<<,0θπ∴<<时,均有sin θθ<,与上式矛盾.所以不存在(0)θθπ<<使得二面角D AB P --的大小为.4π 变式训练2【解答】(1)证明:因为111ABC A B C -为直三棱柱, 所以,且,又四边形为平行四边形,//BC AD ,且BC AD =,,且,四边形为平行四边形,,1B 四点共面;,又1AA ⊥平面,AC ⊂平面,,四边形11A ACC 为正方形,连接1AC 交1A C 于,,在ADC ∆中,2CD AD =,,由余弦定理得,,所以,AD AC ⊥,又1AA ⊥平面ABCD ,AD ⊂平面ABCD ,1AA AD ⊥,,1AA ⊂平面11A ACC ,,AD ⊥平面11A ACC ,1AC ⊂平面11A ACC ,所以,又,平面,1A C ⊥平面, 1DC ⊂平面,(2)解:由(1)知:1A C ⊥平面,在Rt DAC 中,由已知得3AC =,,四棱锥的体积,//BC AD ,点到平面的距离为定值,即为点到平面的距离变式训练3【解析】解:设二面角为,二面角A PB C --为,当时,正三棱锥趋向于变为正三棱柱,;当时,正三棱锥趋向变为平面,.当正三棱锥为正四面体时,且,,故.当从小变大时,要经过从变为小于的角,然后变为的过程, 故只有选项符合.故选:.静夜思[ 唐] 李白原文译文对照床前明月光,疑是地上霜。
2020高考立体几何动点最值问题压轴选填题

立体几何新颖问题压轴填空题以立体几何为背景的新颖问题常见的有折叠问题,与函数图象相结合问题、最值问题,探索性问题等. 对探索、开放、存在型问题的考查,探索性试题使问题具有不确定性、探究性和开放性,对学生的能力要求较高,有利于考查学生的探究能力以及思维的创造性,是新课程下高考命题改革的重要方向之一;开放性问题,一般将平面几何问题类比推广到立体几何的中,不过并非所有平面几何中的性质都可以类比推广到立体几何中,这需要具有较好的基础知识和敏锐的洞察力;对折叠、展开问题的考查,图形的折叠与展开问题(三视图问题可看作是特殊的图形变换)蕴涵了“二维——三维——二维” 的维数升降变化,求解时须对变化前后的图形作“同中求异、异中求同”的思辩,考查空间想象能力和分析辨别能力,是立几解答题的重要题型.类型一 几何体在变化过程中体积的最值问题典例1 在棱长为6的正方体1111ABCD A B C D -中,M 是BC 的中点,点P 是面11DCC D 所在的平面内的动点,且满足APD MPC ∠=∠,则三棱锥P BCD -的体积最大值是( )A .36B . C.24 D .【名师指点】在运动变化过程中,当变量达到某一个特殊位置时,要所求的变量的最值达到. 这就要求看准变化中的临界点,从而确定最值. 空间问题平面化是解题关键.【举一反三】表面积为π60的球面上有四点C B A S 、、、且ABC ∆是等边三角形,球心O 到平面ABC 的距离为3,若ABC SAB 面⊥,则棱锥ABC S -体积的最大值为 .类型二 几何体的外接球或者内切球问题典例2 已知长方体1111D C B A ABCD -的外接球O 的体积为332π,其中21=BB ,则三棱锥ABC O -的体积的最大值为( )A.1B.3C.2D.4【举一反三】在三棱锥P ABC -中,PA ⊥平面ABC ,02,2,1,60PA AB AC BAC ===∠=,则该三棱锥的外接球的表面积为 .类型三 立体几何与函数的结合典例3 如图,在棱长为1的正方体1111ABCD A B C D -的对角线1AC 上取一点P ,以A 为球心,AP 为半径作一个球,设AP x =,记该球面与正方体表面的交线的长度和为()f x ,则函数()f x 的图像最有可能的是( )【名师指点】本题考查数形结合的数学思想方法,考查特殊值、小题小作的小题技巧.【举一反三】如图所示,正方体''''ABCD A B C D -的棱长为1,,E F 分别是棱'AA ,'CC 的中点,过直线EF 的平面分别与棱'BB 、'DD 分别交于,M N 两点,设BM x =,[0,1]x ∈,给出以下四个结论:①平面MENF ⊥平面BDD B '';②直线AC ∥平面MENF 始终成立;③四边形MENF 周长()L f x =,[0,1]x ∈是单调函数;④四棱锥C MENF '-的体积()V h x =为常数;以上结论正确的是___________.【精选名校模拟】1. 如图,正方体1111D C B A ABCD -的棱长为3,以顶点A 为球心, 2为半径作一个球,则图中球面与正方体的表面相交得到的两段弧长之和等于( )A .65πB .32π C. π D .67π2. 在三棱锥ABC P -中,PC PB PA ,,两两垂直,且1,2,3===PC PB PA ,设M 是底面ABC ∆内一点,定义),,()(p n m M f =,其中p n m ,,分别是三棱锥PAB M -,三棱锥PBC M -,三棱锥PCA M -的体积,若),,21()(y x M f =,且81≥+y ax ,则正实数a 的最小值为________.F EA'B'ABCD C'D'M N2. 已知5 2.236≈,如图,在矩形ABCD 中,5,3,AD AB E F ==、分别为AB 边、CD 边上一点,且1AE DF ==,现将矩形ABCD 沿EF 折起,使得ADEF BCFE ⊥平面平面,连接AB CD 、,则所得三棱柱ABE DCF -的侧面积比原矩形ABCD 的面积大约多( )A.68%B.70%C.72%D.75% 3. 如图四边形ABCD ,2AB BD DA ===,2BC CD ==.现将ABD ∆沿BD 折起,当二面角A BD C --处于5[,]66ππ过程中,直线AB 与CD 所成角的余弦值取值范围是( ) A .522[,]88- B .252[,]88 C .2[0,]8D .52[0,]84. 如图,90ACB ∠=︒,DA ⊥平面ABC ,AE DB ⊥交DB 于E ,AF DC ⊥交DC 于F ,且2AD AB ==,则三棱锥D AEF -体积的最大值为 .5. 已知四面体ABCD 的每个顶点都在球O 的表面上,5AB AC ==,8BC =,AD ⊥底面ABC ,G 为ABC ∆的重心,且直线DG 与底面ABC 所成角的正切值为12,则球O 的表面积为_________.7.已知ABC ∆的三边长分别为5=AB ,4=BC ,3=AC ,M 是AB 边上的点,P 是平面ABC 外一点.给出下列四个命题:①若⊥PM 平面ABC ,且M 是AB 边中点,则有PC PB PA ==;②若5=PC ,⊥PC 平面ABC ,则PCM ∆面积的最小值为215;③若5=PB ,⊥PB 平面ABC ,则三棱锥ABC P -的外接球体积为π62125;④若5=PC ,P 在平面ABC 上的射影是ABC ∆内切圆的圆心,则三棱锥ABC P -的体积为232;其中正确命题的序号是 (把你认为正确命题的序号都填上).ABCDEF8. 将矩形ABCD 绕边AB 旋转一周得到一个圆柱,3AB =,2BC =,圆柱上底面圆心为O ,EFG ∆为下底面圆的一个内接直角三角形,则三棱锥O EFG -体积的最大值是 .9. 我国南北朝时代的数学家祖恒提出体积的计算原理(祖恒原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等.类比祖恒原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为1的梯形,且当实数t 取[]0,3上的任意值时,直线y t =被图1和图2所截得的两线段长始终相等,则图1的面积为 ____________.10. 已知平面α截一球面得圆M ,过圆M 的圆心的平面β与平面α所成二面角的大小为60°,平面β截该球面得圆N ,若该球的表面积为64π,圆M 的面积为4π,则圆N 的半径为__________.12.如图所示,在正方体1111ABCD A B C D -中,点E 是棱1CC 上的一个动点,平面1BED 交棱1AA 于点F .给出下列四个结论:①存在点E ,使得11C A //平面F BED 1;②存在点E ,使得⊥D B 1平面F BED 1;③对于任意的点E ,平面⊥D C A 11平面F BED 1;④对于任意的点E ,四棱锥F BED B 11-的体积均不变. 其中,所有正确结论的序号是___________.13.已知三棱锥S ABC -,满足,,SA SB SC 两两垂直,且2SA SB SC ===,Q 是三棱锥S ABC -外接球上一动点,则点Q 到平面ABC 的距离的最大值为 .15. 正三角形ABC 的边长为2,将它沿高AD 翻折,使点B 与点C 间的距离为1,此时四面体ABCD 外接球表面积为____________ .。
2020高考立体几何动点最值问题压轴选填题

2020高考立体几何动点最值问题压轴选填题立体几何问题中常见的探索性问题包括折叠问题、与函数图象相结合问题、最值问题和探索性问题。
探索性试题通常具有不确定性、探究性和开放性,要求学生具有较高的探究能力和创造性思维。
开放性问题需要学生具备扎实的基础知识和敏锐的洞察力,将平面几何问题类比推广到立体几何中。
折叠和展开问题则考查学生的空间想象能力和分析辨别能力,要求学生在“二维——三维——二维”的维数升降变化中进行思考。
典例1:在棱长为6的正方体ABCD中,点M是BC的中点,点P是面DCC所在的平面内的动点,且满足∠APD=∠MPC,则三棱锥P-BCD的体积最大值是多少?解题关键在于找到变化过程中的临界点,从而确定最值。
在这道题中,需要将空间问题平面化,同时注意到当P点位于D点时,三棱锥P-BCD的体积最大。
典例2:已知长方体ABCD的外接球O的体积为32π,其中BB1=2,则三棱锥O-ABC的体积的最大值是多少?类似于典例1,需要找到变化过程中的临界点。
在这道题中,可以通过求长方体ABCD的对角线长度,进而求出三棱锥O-ABC的高,从而求出体积。
注意到当三棱锥O-ABC的高等于长方体ABCD的对角线长度时,体积最大。
典例3:在棱长为1的正方体ABCD的对角线AC上取一点P,以A为球心,AP为半径作一个球,设AP=x,记该球面与正方体表面的交线的长度和为f(x),则函数f(x)的图像最有可能的是什么?这道题需要将立体几何和函数图象相结合,考查学生的数形结合能力和小题小作的技巧。
可以通过画图求出交线长度和f(x),然后根据函数图象的特点进行判断。
举一反三】正方体ABCD A'B'C'D'的棱长为1,E,F分别是棱AA',CC'的中点。
过直线EF的平面分别与棱BB'、DD'分别交于M,N两点,设BM x,x[0,1]。
给出以下四个结论:①平面MENF平面BDD B;②直线AC∥平面MENF始终成立;③四边形MENF周长L f(x),x[0,1]是单调函数;④四棱锥C MENF的体积V h(x)为常数。
【精品高考数学】2020年江苏省高考数学三轮冲刺专项突破-专题02 立体几何+答案

2020年江苏省高考数学三轮冲刺专项突破专题02 立体几何2020年江苏高考核心考点1.线线与线面的平行与垂直:线线与线面的平行与垂直一定要熟练掌握它们的判定定理和性质定理。
利用几何方法证明垂直与平行问题是立体几何的重要内容,也是高考考查的重点,求解的关键是根据线线垂直(平行)、线面垂直(平行)、面面垂直(平行)这三者之间的互化关系,借助辅助线与面,找出符号语言与图形语言之间的关系,从而将问题解决。
2.平面与平面的平行与垂直:熟练掌握平面与平面的平行与垂直的判定定理和性质定理,注意判定定理和性质定理的条件。
3.多面体的表面积与体积:求多面体的表面积与体积常用方法:1、公式法:可以运用规则的几何体;2、割补法:把不规则的图形分割成规则的图形,或者把几何体补成熟悉的几何体。
3、等积法:通过转换顶点,换成底面积或者高易求的几何体。
专项突破一、填空题(本大题共14小题,每小题5分,共计70分.)1.(江苏省南通市2020届四校联盟)在正四棱锥S ﹣ABC D 中,点O 是底面中心,SO =2,侧棱SA =2√3,则该棱锥的体积为 .2.(江苏省丹阳市2020届高三年级下学期3月质量检测卷)已知圆锥的侧面展开图是一个半径为6cm ,圆心角为23π的扇形,则此圆锥的体积为 cm 3. 3.(2020届天一中学高三年级第二学期期初调研测试)某种圆柱形的如罐的容积为128π个立方单位,当它的底面半径和高的比值为 时,可使得所用材料最省.4.(2019~2020学年度如皋高三年级第二学期期初调研测试)已知正四棱柱1111ABCD A B C D -中12,3AB AA ==,O 为上底面中心.设正四棱柱1111ABCD A B C D -与正四棱锥1111O A B C D -的侧面积分别为12,S S ,则21S S = . 5.(江苏省张家港市2020届高三阶段性调研测试)在三棱锥P ABC -中,底面ABC 是边长为3的等边三角形,PA PC ⊥,PB PC ⊥,2PA PB ==,则该三棱锥的体积为_______.6.(江苏省苏北七市2020届高三第二次调研考试)如图,在体积为V 的圆柱O 1O 2中,以线段O 1O 2上的点O 为项点,上下底面为底面的两个圆锥的体积分别为V 1,V 2,则12V V V+的值是 . 7.(江苏省南京市、盐城市2020届高三年级第二次模拟考试)在△AB C 中,AB =25AC 5∠BAC =90°,则△ABC 绕BC 所在直线旋转一周所形成的几何体的表面积为 .8.(2020年南师附中高考模拟数学试卷)设m ,n 为空间两条不同的直线,α,β为空间两个不同的平面,给出下列命题:①若m ∥α,m ∥β,则α∥β; ②若m ⊥α,m ∥β,则α⊥β; ③若m ∥α,m ∥n ,则n ∥α; ④若m ⊥α,α∥β,则m ⊥β. 其中的正确命题序号是 .9.(2019—2020学年度扬州中学第二学期阶段性检测改编)将一个底面半径为4,高为2的圆锥锻造成一个球体,则球体的表面积为 .10.(江苏省海安中学高三3月数学模拟考试数学试卷)现有一个橡皮泥制作的圆锥,底面半径为1,高为4.若将它制作成一个总体积不变的球,则该球的表面积为 .11.(2019—2020学年度镇江市九校2020届高三年级3月模拟考试)如图,是一个四棱锥的平面展开图,其中间是边长为2的正方形,上面三角形是等边三角形,左、右三角形是等腰直角三角形,则此四棱锥的体积为 .12.(江苏省常熟市2020届高三3月“线上教育”学习情况调查)四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是边长为2的正方形,2PA =,则四棱锥的侧面积是_________.13.(2020年江苏沭阳高级中学高考模拟试卷高考数学百日冲刺数学试卷(3月份))如图,从一个边长为12的正三角形纸片的三个角上,沿图中虚线剪出三个全等的四边形,余下部分再以虚线为折痕折起,恰好围成一个缺少上底的正三棱柱,而剪出的三个相同的四边形恰好拼成这个正三棱柱的上底,则所得正三棱柱的体积为.14.(2019—2020学年度苏、锡、常、镇四市高三教学情况调查(一))如图在矩形ABC D中,E为边AD 的中点,AB=1,BC=2.分别以A,D为圆心,1为半经作圆弧EB,EC,将两圆弧EB,EC及边BC所围成的平面图形(阴影部分)绕直线AD旋转一周,所形成的几何体的体积为.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤.15.(江苏省南通市2020届四校联盟)如图,在直四棱柱ABCD﹣A1B1C1D1中,已知底面ABCD是菱形,点P是侧棱C1C的中点.(1)求证:AC1∥平面PBD;(2)求证:BD⊥A1P.16.(江苏省南京市、盐城市2020届高三年级第二次模拟考试)在如图,三棱锥P—AB C中,点D,E分别为AB,BC的中点,且平面PDE⊥平面AB C.(1)求证:AC ∥平面PDE ;(3)若PD =AC =2,PE 3PBC ⊥平面AB C .17.(江苏省如皋中学高三3月数学模拟考试数学试卷)如图,在四棱锥P ABC D 中,底面ABCD 为平行四边形,面PAD ABCD ⊥面,三角形PAD 为正三角形.(1)若,E F 为,PB CD 中点,证明://EF PAD 面; (2)若90PAB ∠=︒,证明:面PAD PAB ⊥面.18.(2020年江苏沭阳高级中学高考模拟试卷高考数学百日冲刺数学试卷(3月份))如图,在四棱锥P ﹣ABC D 中.(1)若AD ⊥平面PAB ,PB ⊥PD ,求证:平面PBD ⊥平面PAD ;(2)若AD ∥BC ,E 为PA 的中点,当BE ∥平面PCD 时,求BCAD的值.19.(2019—2020学年度苏、锡、常、镇四市高三教学情况调查(一))如图,在四棱锥P —ABC D 中,四边形ABCD 为平行四边形,BD ⊥DC ,△PCD 为正三角形,平面PCD ⊥平面ABCD ,E 为PC 的中点.(1)证明:AP ∥平面EBD ;FEPDCBA(2)证明:BE⊥P C.20.(江苏省苏北七市2020届高三第二次调研考试)如图,在直三棱柱ABC—A1B1C1中,CA=CB,点P,Q 分别为AB 1,CC1的中点.求证:(1)PQ∥平面ABC;(2)PQ⊥平面ABB1A1.2020年江苏省高考数学三轮冲刺专项突破专题02 立体几何2020年江苏高考核心考点1.线线与线面的平行与垂直:线线与线面的平行与垂直一定要熟练掌握它们的判定定理和性质定理。
2020高考—立体几何(解答+答案)
2020年高考——立体几何1.(20全国Ⅰ文19)(12分)如图,D为圆锥的顶点,O是圆锥底面的圆心,ABC△是底面的内接正三角形,P为DO 上一点,∠APC=90°.(1)证明:平面PAB⊥平面PAC;(2)设DO=2,圆锥的侧面积为3π,求三棱锥P−ABC的体积.2.(20全国Ⅰ理18)(12分)如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE AD=.ABC△是底面的内接正三角形,P为DO上一点,66PO DO=.(1)证明:PA⊥平面PBC;(2)求二面角B PC E--的余弦值.3.(20全国Ⅱ文20)(12分)如图,已知三棱柱ABC–A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点.过B1C1和P的平面交AB于E,交AC于F.(1)证明:AA1//MN,且平面A1AMN⊥平面EB1C1F;(2)设O为△A1B1C1的中心,若AO=AB=6,AO//平面EB1C1F,且∠MPN=π3,求四棱锥B–EB1C1F的体积.4.(20全国Ⅱ理20)(12分)如图,已知三棱柱ABC -A 1B 1C 1的底面是正三角形,侧面BB 1C 1C 是矩形,M ,N 分别为BC ,B 1C 1的中点,P 为AM 上一点,过B 1C 1和P 的平面交AB 于E ,交AC 于F .(1)证明:AA 1∥MN ,且平面A 1AMN ⊥EB 1C 1F ;(2)设O 为△A 1B 1C 1的中心,若AO ∥平面EB 1C 1F ,且AO =AB ,求直线B 1E 与平面A 1AMN 所成角的正弦值.5.(20全国Ⅲ文 19)(12分)如图,在长方体1111ABCD A B C D -中,点E ,F 分别在棱1DD ,1BB 上,且12DE ED =,12BF FB =.证明:(1)当AB BC =时,EF AC ⊥; (2)点1C 在平面AEF 内.6.(20全国Ⅲ理19)(12分)如图,在长方体1111ABCD A B C D -中,点,E F 分别在棱11,DD BB 上,且12DE ED =,12BF FB =.(1)证明:点1C 在平面AEF 内;(2)若2AB =,1AD =,13AA =,求二面角1A EF A --的正弦值.7.(20新高考Ⅰ20)(12分)如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.(1)证明:l⊥平面PDC;(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.8.(20天津17)(本小题满分15分)如图,在三棱柱111ABC A B C -中,1CC ⊥平面,,2ABC AC BC AC BC ⊥==,13CC =,点,D E 分别在棱1AA 和棱1CC 上,且2,1,AD CE M ==为棱11A B 的中点.(Ⅰ)求证:11C M B D ⊥;(Ⅱ)求二面角1B B E D --的正弦值;(Ⅲ)求直线AB 与平面1DB E 所成角的正弦值.9.(20浙江19)(本题满分15分)如图,在三棱台ABC —DEF 中,平面ACFD ⊥平面ABC ,∠ACB =∠ACD =45°,DC =2BC . (Ⅰ)证明:EF ⊥DB ;(Ⅱ)求直线DF 与平面DBC 所成角的正弦值.10.(20江苏15)(本小题满分14分)在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.(1)求证:EF∥平面AB1C1;(2)求证:平面AB1C⊥平面ABB1.11.(20江苏22)(本小题满分10分)在三棱锥A —BCD 中,已知CB =CD =5,BD =2,O 为BD 的中点,AO ⊥平面BCD ,AO =2,E 为AC 的中点.(1)求直线AB 与DE 所成角的余弦值; (2)若点F 在BC 上,满足BF =14BC ,设二面角F —DE —C 的大小为θ,求sin θ的值.12.(20北京16)(本小题13分)如图,在正方体1111ABCD A B C D 中,E 为1BB 的中点.(Ⅰ)求证:1//BC 平面1AD E ;(Ⅱ)求直线1AA 与平面1AD E 所成角的正弦值.参考答案:1.解:(1)由题设可知,PA =PB = PC .由于△ABC 是正三角形,故可得△PAC ≌△PAB . △PAC ≌△PBC .又∠APC =90°,故∠APB =90°,∠BPC =90°.从而PB ⊥PA ,PB ⊥PC ,故PB ⊥平面PAC ,所以平面PAB ⊥平面PAC . (2)设圆锥的底面半径为r ,母线长为l . 由题设可得rl =3,222l r -=. 解得r =1,l =3,从而3AB =.由(1)可得222PA PB AB +=,故62PA PB PC ===. 所以三棱锥P -ABC 的体积为3111166()323228PA PB PC ⨯⨯⨯⨯=⨯⨯=.2.解:(1)设DO a =,由题设可得63,,63PO a AO a AB a ===,22PA PB PC a ===. 因此222PA PB AB +=,从而PA PB ⊥. 又222PA PC AC +=,故PA PC ⊥. 所以PA ⊥平面PBC .(2)以O 为坐标原点,OE 的方向为y 轴正方向,||OE 为单位长,建立如图所示的空间直角坐标系O xyz -.由题设可得312(0,1,0),(0,1,0),(,0),(0,0,)222E A C P --. 所以312(,,0),(0,1,)222EC EP =--=-. 设(,,)x y z =m 是平面PCE 的法向量,则00EP EC ⎧⋅=⎪⎨⋅=⎪⎩m m ,即20231022y z x y ⎧-+=⎪⎪⎨⎪--=⎪⎩,可取3(2)=m . 由(1)知2(0,1,2AP =是平面PCB 的一个法向量,记AP =n , 则25cos ,|||5⋅==n m n m n m |.所以二面角B PC E --的余弦值为255.3.解:(1)因为M ,N 分别为BC ,B 1C 1的中点,所以MN ∥CC 1.又由已知得AA 1∥CC 1,故AA 1∥MN .因为△A 1B 1C 1是正三角形,所以B 1C 1⊥A 1N .又B 1C 1⊥MN ,故B 1C 1⊥平面A 1AMN . 所以平面A 1AMN ⊥平面EB 1C 1F .(2)AO ∥平面EB 1C 1F ,AO ⊂平面A 1AMN ,平面A 1AMN ⋂平面EB 1C 1F = PN , 故AO ∥PN ,又AP ∥ON ,故四边形APNO 是平行四边形,所以PN =AO =6,AP = ON =13AM =3,PM =23AM =23,EF =13BC =2.因为BC ∥平面EB 1C 1F ,所以四棱锥B -EB 1C 1F 的顶点B 到底面EB 1C 1F 的距离等于点M 到底面EB 1C 1F 的距离.作MT ⊥PN ,垂足为T ,则由(1)知,MT ⊥平面EB 1C 1F ,故MT =PM sin ∠MPN =3.底面EB 1C 1F 的面积为1111()(62)624.22B C EF PN ⨯+⨯=+⨯=所以四棱锥B -EB 1C 1F 的体积为1243243⨯⨯=.4.解:(1)因为M ,N 分别为BC ,B 1C 1的中点,所以MN ∥CC .又由已知得AA 1∥CC 1,故AA 1∥MN .因为△A 1B 1C 1是正三角形,所以B 1C 1⊥A 1N .又B 1C 1⊥MN ,故B 1C 1⊥平面A 1AMN . 所以平面A 1AMN ⊥平面EB 1CF .(2)由己知得AM ⊥BC .以M 为坐标原点,MA 的方向为x 轴正方向, MB 为单位长,建立如图所示的空间直角坐标系M -xyz ,则AB =2,AM =3. 连接NP ,则四边形AONP 为平行四边形,故23231,(,,0)333PM E =.由(1)知平面A 1AMN ⊥平面ABC ,作NQ ⊥AM ,垂足为Q ,则NQ ⊥平面ABC . 设(,0,0)Q a ,则22123234(),(,1,4())33NQ a B a a =----, 故21123223210(,,4()),||3333B E a a B E =-----=. 又(0,1,0)=-n 是平面A 1AM 的法向量,故1111,π10sin(,)cos ,210||B E B E B E B E -===⋅n n n |n |.所以直线B 1E 与平面A 1AMN 所成角的正弦值为1010.5.解:(1)如图,连结BD ,11B D .因为AB BC =,所以四边形ABCD 为正方形,故AC BD ⊥.又因为1BB ⊥平面ABCD ,于是1AC BB ⊥.所以AC ⊥平面11BB D D . 由于EF ⊂平面11BB D D ,所以EF AC ⊥.(2)如图,在棱1AA 上取点G ,使得12AG GA =,连结1GD ,1FC ,FG ,因为1123D E DD =,123AG AA =,11DD AA =∥,所以1ED AG =∥,于是四边形1ED GA 为平行四边形,故1AE GD ∥.因为1113B F BB =,1113AG AA =,11BB AA =∥,所以11FG A B =∥,11FG C D =∥,四边形11FGD C 为平行四边形,故11GD FC ∥.于是1AE FC ∥.所以1,,,A E F C 四点共面,即点1C 在平面AEF 内.6.解:设AB a =,AD b =,1AA c =,如图,以1C 为坐标原点,11C D 的方向为x 轴正方向,建立空间直角坐标系1C xyz -.(1)连结1C F ,则1(0,0,0)C ,(,,)A a b c ,2(,0,)3E a c ,1(0,,)3F b c ,1(0,,)3EA b c =,11(0,,)3C F b c =,得1EA C F =.因此1EA C F ∥,即1,,,A E F C 四点共面,所以点1C 在平面AEF 内. (2)由已知得(2,1,3)A ,(2,0,2)E ,(0,1,1)F ,1(2,1,0)A ,(0,1,1)AE =--,(2,0,2)AF =--,1(0,1,2)A E =-,1(2,0,1)A F =-.设1(,,)x y z =n 为平面AEF 的法向量,则 110,0,AE AF ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,220,y z x z --=⎧⎨--=⎩可取1(1,1,1)=--n . 设2n 为平面1A EF 的法向量,则 22110,0,A E A F ⎧⋅=⎪⎨⋅=⎪⎩n n 同理可取21(,2,1)2=n .因为1212127cos ,||||7⋅〈〉==-⋅n n n n n n ,所以二面角1A EF A --的正弦值为427.7.解:(1)因为PD ⊥底面ABCD ,所以PD AD ⊥.又底面ABCD 为正方形,所以AD DC ⊥,因此AD ⊥底面PDC . 因为AD BC ∥,AD ⊄平面PBC ,所以AD ∥平面PBC . 由已知得l AD ∥.因此l ⊥平面PDC . (2)以D 为坐标原点,DA 的方向为x 轴正方向,建立如图所示的空间直角坐标系D xyz -.则(0,0,0),(0,1,0),(1,1,0),(0,0,1)D C B P ,(0,1,0)DC =,(1,1,1)PB =-. 由(1)可设(,0,1)Q a ,则(,0,1)DQ a =.设(,,)x y z =n 是平面QCD 的法向量,则0,0,DQ DC ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,0.ax z y +=⎧⎨=⎩ 可取(1,0,)a =-n . 所以2cos ,||||31PB PB PB a⋅-〈〉==⋅+n n n . 设PB 与平面QCD 所成角为θ,则22332sin 1311aa a θ==+++ 2326131a a ++当且仅当1a =时等号成立,所以PB 与平面QCD 所成角的正6.8.依题意,以C 为原点,分别以1,,CA CB CC 的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系(如图),可得1(0,0,0),(2,0,0),(0,2,0),(0,0,3)C A B C ,11(2,0,3),(0,2,3),(2,0,1),(0,0,2)A B D E ,(1,1,3)M .(Ⅰ)证明:依题意,1(1,1,0)C M =,1(2,2,2)B D =--,从而112200C M B D ⋅=-+=,所以11C M B D ⊥.(Ⅱ)解:依题意,(2,0,0)CA =是平面1BB E 的一个法向量,1(0,2,1)EB =,(2,0,1)ED =-.设(,,)x y z =n 为平面1DB E 的法向量,则10,0,EB ED ⎧⋅=⎪⎨⋅=⎪⎩n n 即20,20.y z x z +=⎧⎨-=⎩不妨设1x =,可得(1,1,2)=-n . 因此有|||6cos ,|A CA C CA ⋅〈〉==n n n 30sin ,6CA 〈〉=n . 所以,二面角1B B E D --30(Ⅲ)解:依题意,(2,2,0)AB =-.由(Ⅱ)知(1,1,2)=-n 为平面1DB E 的一个法向量,于是3cos ,||||AB AB AB ⋅==n n n . 所以,直线AB 与平面1DB E 39.(Ⅰ)如图,过点D 作DO AC ⊥,交直线AC 于点O ,连结OB .由45ACD ∠=︒,DO AC ⊥得2CD CO =,由平面ACFD ⊥平面ABC 得DO ⊥平面ABC ,所以DO BC ⊥. 由45ACB ∠=︒,122BC CD ==得BO BC ⊥.所以BC ⊥平面BDO ,故BC ⊥DB .由三棱台ABC DEF -得BC EF ∥,所以EF DB ⊥. (Ⅱ)方法一:过点O 作OH BD ⊥,交直线BD 于点H ,连结CH .由三棱台ABC DEF -得DF CO ∥,所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角.由BC ⊥平面BDO 得OH BC ⊥,故OH ⊥平面BCD ,所以OCH ∠为直线CO 与平面DBC 所成角. 设22CD =.由2,2DO OC BO BC ====,得26,33BD OH = 所以3sin OH OCH OC ∠==, 因此,直线DF 与平面DBC 3. 方法二:由三棱台ABC DEF -得DF CO ∥,所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角,记为θ.如图,以O 为原点,分别以射线OC ,OD 为y ,z 轴的正半轴,建立空间直角坐标系O xyz -.设22CD =.由题意知各点坐标如下:(0,0,0),(1,1,0),(0,2,0),(0,0,2)O B C D .因此(0,2,0),(1,1,0),(0,2,2)OC BC CD ==-=-. 设平面BCD 的法向量(,,z)x y =n .由0,0,BC CD ⎧⋅=⎪⎨⋅=⎪⎩n n 即0220x y y z -+=⎧⎨-+=⎩,可取(1,1,1)=n .所以|3sin |cos ,|3|||OC OC OC θ⋅===⋅n |n n |.因此,直线DF 与平面DBC 所成角的正弦值为33.10.证明:因为,E F 分别是1,AC B C 的中点,所以1EF AB ∥.又/EF ⊂平面11AB C ,1AB ⊂平面11AB C , 所以EF ∥平面11AB C .(2)因为1B C ⊥平面ABC ,AB ⊂平面ABC ,所以1B C AB ⊥.又AB AC ⊥,1B C ⊂平面11AB C ,AC ⊂平面1AB C ,1,B C AC C =所以AB ⊥平面1AB C .又因为AB ⊂平面1ABB ,所以平面1AB C ⊥平面1ABB .11.解:(1)连结OC ,因为CB =CD ,O 为BD 中点,所以CO ⊥B D .又AO ⊥平面BCD ,所以AO ⊥OB ,AO ⊥O C .以{}OB OC OA ,,为基底,建立空间直角坐标系O –xyz . 因为BD =2,CB CD ==,AO =2,所以B (1,0,0),D (–1,0,0),C (0,2,0),A (0,0,2). 因为E 为AC 的中点,所以E (0,1,1). 则AB =(1,0,–2),DE =(1,1,1),所以|||1||||||5cos AB DE AB DE AB DE +=⋅⋅==<>,.因此,直线AB 与DE . (2)因为点F 在BC 上,14BF BC =,BC =(–1,2,0). 所以111(,,0)442BF BC ==-. 又20,0DB =(,), 故71(,,0)42DF DB BF =+=.设1111()x y z =,,n 为平面DEF 的一个法向量, 则1100,DE DF ⎧⎪⎨⎪⎩⋅=⋅=,n n 即111110710,42x y z x y +⎧+=⎪+=⎪⎨⎩, 取12x =,得1–7y =,15z =,所以1(275)n =-,,. 设2222()x y z =,,n 为平面DEC 的一个法向量,又DC =(1,2,0),则2200,DE DC ⎧⎪⎨⎪⎩⋅=⋅=,n n 即22222020,x y z x y ++=+=⎧⎨⎩,取22x =,得2–1y =,2–1z =,所以2(211)n =--,,. 故2112|||475|13|||||co |13786s θ+-⋅===⋅⨯n n n n .所以22391cos s n 13i θθ=-=.12.。
2020年高考理科数学《立体几何》题型归纳与训练及答案解析

12020年高考理科数学《立体几何》题型归纳与训练【题型归纳】题型一线面平行的证明1例1如图,高为1的等腰梯形 ABCD 中,AM = CD = 3AB = 1•现将△AMD 沿MD 折起,使平面 AMD 丄 平面 MBCD ,连接 AB , AC.试判断:在AB 边上是否存在点【解析】线面平行,可以线线平行或者面面平行推出。
此类题的难点就是如何构造辅助线。
构造完辅助线,证明过程只须注意规范的符号语言描述即可。
本题用到的是线线平行推出面面平行。
【易错点】不能正确地分析DN 与BN 的比例关系,导致结果错误。
【思维点拨】此类题有两大类方法: 1.构造线线平行,然后推出线面平行。
此类方法的辅助线的构造须要学生理解线面平行的判定定理与线面平行的性质之间的矛盾转化关系。
在此,我们需要借助倒推法进行分析。
首先,此类型题目大部分为证明题,结论必定是正确的,我们以此 为前提可以得到线面平行。
再次由线面平行的性质可知,过已知直线的平面与已知平面的交线必定平行于该直线,而交线就是我们要找的线,从而做出辅助线。
从这个角度上看我们可以看出线线平行推线面 平行的本质就是过已知直线做一个平面与已知平面相交即可。
如本题中即是过AD 做了一个平面ADB与平面MPC 相交于线PN 。
最后我们只须严格使用正确的符号语言将证明过程反向写一遍即可。
即先证1【答案】当AP = 3AB 时,有AD //平面MPC. 理由如下:连接BD 交MC 于点N ,连接NP.在梯形 MBCD 中,DC // MB ,DN NB DC MB 12,Ap 1在△ADB 中,pp 二」AD 〃 PN . •/ AD?平面 MPC , PN?平面 MPC , ••• AD //平面 MPC.P ,使AD //平面 MPC?并说明理由AD平行于PN,最后得到结论。
构造交线的方法我们可总结为如下三个图形。
PP上一方法二方法三2.构造面面平行,然后推出线面平行。
2020高考立体几何动点最值问题压轴选填题

立体几何新颖问题压轴填空题以立体几何为背景的新颖问题常见的有折叠问题,与函数图象相结合问题、最值问题,探索性问题等. 对探索、开放、存在型问题的考查,探索性试题使问题具有不确定性、探究性和开放性,对学生的能力要求较高,有利于考查学生的探究能力以及思维的创造性,是新课程下高考命题改革的重要方向之一;开放性问题,一般将平面几何问题类比推广到立体几何的中,不过并非所有平面几何中的性质都可以类比推广到立体几何中,这需要具有较好的基础知识和敏锐的洞察力;对折叠、展开问题的考查,图形的折叠与展开问题(三视图问题可看作是特殊的图形变换)蕴涵了“二维——三维——二维” 的维数升降变化,求解时须对变化前后的图形作“同中求异、异中求同”的思辩,考查空间想象能力和分析辨别能力,是立几解答题的重要题型.类型一 几何体在变化过程中体积的最值问题典例1 在棱长为6的正方体1111ABCD A B C D -中,M 是BC 的中点,点P 是面11DCC D 所在的平面内的动点,且满足APD MPC ∠=∠,则三棱锥P BCD -的体积最大值是( )A .36B . C.24 D .【名师指点】在运动变化过程中,当变量达到某一个特殊位置时,要所求的变量的最值达到. 这就要求看准变化中的临界点,从而确定最值. 空间问题平面化是解题关键.【举一反三】表面积为π60的球面上有四点C B A S 、、、且ABC ∆是等边三角形,球心O 到平面ABC 的距离为3,若ABC SAB 面⊥,则棱锥ABC S -体积的最大值为 .类型二 几何体的外接球或者内切球问题典例2 已知长方体1111D C B A ABCD -的外接球O 的体积为332π,其中21=BB ,则三棱锥ABC O -的体积的最大值为( )A.1B.3C.2D.4【举一反三】在三棱锥P ABC -中,PA ⊥平面ABC ,02,2,1,60PA AB AC BAC ===∠=,则该三棱锥的外接球的表面积为 .类型三 立体几何与函数的结合典例3 如图,在棱长为1的正方体1111ABCD A B C D -的对角线1AC 上取一点P ,以A 为球心,AP 为半径作一个球,设AP x =,记该球面与正方体表面的交线的长度和为()f x ,则函数()f x 的图像最有可能的是( )【名师指点】本题考查数形结合的数学思想方法,考查特殊值、小题小作的小题技巧.【举一反三】如图所示,正方体''''ABCD A B C D -的棱长为1,,E F 分别是棱'AA ,'CC 的中点,过直线EF 的平面分别与棱'BB 、'DD 分别交于,M N 两点,设BM x =,[0,1]x ∈,给出以下四个结论:①平面MENF ⊥平面BDD B '';②直线AC ∥平面MENF 始终成立;③四边形MENF 周长()L f x =,[0,1]x ∈是单调函数;④四棱锥C MENF '-的体积()V h x =为常数;以上结论正确的是___________.【精选名校模拟】1. 如图,正方体1111D C B A ABCD -的棱长为3,以顶点A 为球心, 2为半径作一个球,则图中球面与正方体的表面相交得到的两段弧长之和等于( )A .65πB .32π C. π D .67π2. 在三棱锥ABC P -中,PC PB PA ,,两两垂直,且1,2,3===PC PB PA ,设M 是底面ABC ∆内一点,定义),,()(p n m M f =,其中p n m ,,分别是三棱锥PAB M -,三棱锥PBC M -,三棱锥PCA M -的体积,若),,21()(y x M f =,且81≥+y ax ,则正实数a 的最小值为________.F EA'B'ABCD C'D'M N2. 已知5 2.236≈,如图,在矩形ABCD 中,5,3,AD AB E F ==、分别为AB 边、CD 边上一点,且1AE DF ==,现将矩形ABCD 沿EF 折起,使得ADEF BCFE ⊥平面平面,连接AB CD 、,则所得三棱柱ABE DCF -的侧面积比原矩形ABCD 的面积大约多( )A.68%B.70%C.72%D.75% 3. 如图四边形ABCD ,2AB BD DA ===,2BC CD ==.现将ABD ∆沿BD 折起,当二面角A BD C --处于5[,]66ππ过程中,直线AB 与CD 所成角的余弦值取值范围是( ) A .522[,]88- B .252[,]88 C .2[0,]8D .52[0,]84. 如图,90ACB ∠=︒,DA ⊥平面ABC ,AE DB ⊥交DB 于E ,AF DC ⊥交DC 于F ,且2AD AB ==,则三棱锥D AEF -体积的最大值为 .5. 已知四面体ABCD 的每个顶点都在球O 的表面上,5AB AC ==,8BC =,AD ⊥底面ABC ,G 为ABC ∆的重心,且直线DG 与底面ABC 所成角的正切值为12,则球O 的表面积为_________.7.已知ABC ∆的三边长分别为5=AB ,4=BC ,3=AC ,M 是AB 边上的点,P 是平面ABC 外一点.给出下列四个命题:①若⊥PM 平面ABC ,且M 是AB 边中点,则有PC PB PA ==;②若5=PC ,⊥PC 平面ABC ,则PCM ∆面积的最小值为215;③若5=PB ,⊥PB 平面ABC ,则三棱锥ABC P -的外接球体积为π62125;④若5=PC ,P 在平面ABC 上的射影是ABC ∆内切圆的圆心,则三棱锥ABC P -的体积为232;其中正确命题的序号是 (把你认为正确命题的序号都填上).ABCDEF8. 将矩形ABCD 绕边AB 旋转一周得到一个圆柱,3AB =,2BC =,圆柱上底面圆心为O ,EFG ∆为下底面圆的一个内接直角三角形,则三棱锥O EFG -体积的最大值是 .9. 我国南北朝时代的数学家祖恒提出体积的计算原理(祖恒原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等.类比祖恒原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为1的梯形,且当实数t 取[]0,3上的任意值时,直线y t =被图1和图2所截得的两线段长始终相等,则图1的面积为 ____________.10. 已知平面α截一球面得圆M ,过圆M 的圆心的平面β与平面α所成二面角的大小为60°,平面β截该球面得圆N ,若该球的表面积为64π,圆M 的面积为4π,则圆N 的半径为__________.12.如图所示,在正方体1111ABCD A B C D -中,点E 是棱1CC 上的一个动点,平面1BED 交棱1AA 于点F .给出下列四个结论:①存在点E ,使得11C A //平面F BED 1;②存在点E ,使得⊥D B 1平面F BED 1;③对于任意的点E ,平面⊥D C A 11平面F BED 1;④对于任意的点E ,四棱锥F BED B 11-的体积均不变. 其中,所有正确结论的序号是___________.13.已知三棱锥S ABC -,满足,,SA SB SC 两两垂直,且2SA SB SC ===,Q 是三棱锥S ABC -外接球上一动点,则点Q 到平面ABC 的距离的最大值为 .15. 正三角形ABC 的边长为2,将它沿高AD 翻折,使点B 与点C 间的距离为1,此时四面体ABCD 外接球表面积为____________ .。
2020年中考数学必考考点 专题34 动态问题(含解析)

专题34 动态问题专题知识回顾一、动态问题概述1.就运动类型而言,有函数中的动点问题、图象问题、面积问题、最值问题、和差问题、定值问题和存在性问题等。
2.就运动对象而言,几何图形中的动点问题,有点动、线动、面动三大类。
3.就图形变化而言,有轴对称(翻折)、平移、旋转(中心对称、滚动)等。
4.动态问题一般分两类,一类是代数综合方面,在坐标系中有动点,动直线,一般是利用多种函数交叉求解。
另一类就是几何综合题,在梯形,矩形,三角形中设立动点、线以及整体平移翻转,对考生的综合分析能力进行考察。
所以说,动态问题是中考数学当中的重中之重,只完全掌握才能拿高分。
另一类就是几何综合题,在梯形,矩形,三角形中设立动点、线以及整体平移翻转,对考生的综合分析能力进行考察。
所以说,动态问题是中考数学当中的重中之重,只完全掌握才能拿高分。
二、动点与函数图象问题常见的四种类型:1.三角形中的动点问题:动点沿三角形的边运动,根据问题中的常量与变量之间的关系,判断函数图2.四边形中的动点问题:动点沿四边形的边运动,根据问题中的常量与变量之间的关系,判断函数图象。
3.圆中的动点问题:动点沿圆周运动,根据问题中的常量与变量之间的关系,判断函数图象。
4.直线、双曲线、抛物线中的动点问题:动点沿直线、双曲线、抛物线运动,根据问题中的常量与变量之间的关系,判断函数图象。
三、图形运动与函数图象问题常见的三种类型:1.线段与多边形的运动图形问题:把一条线段沿一定方向运动经过三角形或四边形,根据问题中的常量与变量之间的关系,进行分段,判断函数图象。
2.多边形与多边形的运动图形问题:把一个三角形或四边形沿一定方向运动经过另一个多边形,根据问题中的常量与变量之间的关系,进行分段,判断函数图象。
3.多边形与圆的运动图形问题:把一个圆沿一定方向运动经过一个三角形或四边形,或把一个三角形或四边形沿一定方向运动经过一个圆,根据问题中的常量与变量之间的关系,进行分段,判断函数图象。
专题06 立体几何中的动点及最值范围问题(解析版)

专题06 立体几何中动点及最值范围问题题型一、角度、长度最值范围问题(多选)1、设动点P 在正方体1111ABCD A B C D -的对角线1BD 上,记11D P D B λ=当APC ∠为钝角时,则实数可能的取值是( ) A .12B .23C .13D .1【答案】AB【分析】首先以D 为原点,DA ,DC ,1DD 分别为x ,y ,z 轴建立空间直角坐标系,根据题意得到0PA PC ⋅<,再解不等式即可得到答案.【解析】以D 为原点,DA ,DC ,1DD 分别为x ,y ,z 轴建立空间直角坐标系,如图所示:设正方体的边长为1,则()1,0,0A ,()1,1,0B ,()0,1,0C ,()10,0,1D ,()11,0,1D A =-,()10,1,1D C =-,()11,1,1D B =-,所以()11,,D P D B λλλλ==-. 又因为()()()11,,1,0,11,,1PA PD D A λλλλλλ=+=--+-=---,()()()11,,0,1,1,1,1PC PD DC λλλλλλ=+=--+-=---, 因为APC ∠为钝角,所以0PA PC ⋅<,即()()()()()()()2111=1310λλλλλλλ--+--+---<,解得113λ<<.故选AB【名师点睛】本题主要考查空间向量的数量积运算,属于简单题.2、如图,正方体1111ABCD A B C D -,点P 在1AB 上运动(不含端点),点E 是AC 上一点(不含端点),设EP 与平面1ACD 所成角为θ,则cosθ的最小值为( )A .13B .33C .53D .63答案: A 解析:由已知求出AC 的中点1E 与1B 的连线与平面1ACD 所成角的余弦值,在1AB 上(不含端点)任取一点P ,在平面1AB E 内过P 作11//PE B E ,则EP 与平面1ACD 所成角11OE B θ=∠,可得1cos 3θ=,结合选项即可得答案.详解:解:如图,由正方体的性质,可得1B D ⊥平面1AD C ,且1B 在平面1AD C 上的射影O 为△1AD C 的外心.设正方体的棱长为1,则△1AD C 的边长为2, 当1E 为AC 的中点时,11162326OE =-=, 1116122B E =+=,此时11616cos 362OE B ==. 在1AB 上(不含端点)任取一点P ,在平面1AB E 内过P 作11//PE B E ,则EP 与平面1ACD 所成角11OE B θ=∠,可得1cos 3θ=.结合选项可知,cos θ的最小值为13.故选:A .3、三棱柱111ABC A B C -的侧棱与底面垂直,11AA AB AC ===,AB AC ⊥,N 是BC 的中点,点P 在11A B 上,且满足111A P A B λ=,当直线PN 与平面ABC 所成的角取最大值时,λ的值为( )A .12B .22C .32D .255【答案】A【分析】建立空间直角坐标系,利用向量的夹角公式,求出直线PN 与平面ABC 所成的角,即可求得结论.【解析】如图,以AB ,AC ,1AA 分别为x ,y ,z 轴,建立空间直角坐标系A xyz -,则(,P λ0,1),11,,122PN λ⎛⎫=-- ⎪⎝⎭,平面ABC 的一个法向量为(0,n =0,1)设直线PN 与平面ABC 所成的角为θ,21sin 15()24PN nPN nθλ⋅∴==⋅-+, ∴当12λ=时,25(sin )5max θ=,此时角θ最大.故选A . 【名师点睛】本题考查了向量法求线面角的求法,考查了函数最值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.4、如图所示,在正方体1111ABCD A B C D -中,点E 为线段AB 的中点,点F 在线段AD 上移动,异面直线1B C 与EF 所成角最小时,其余弦值为( )A .0B .12C .105D .1116【答案】C【分析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,利用向量法能求出异面直线1B C 与EF 的夹角的余弦值,根据夹角最小即可求得结果.【解析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,在正方体1111ABCD A B C D -中, 点E 为线段AB 的中点,设正方体棱长为2, 则1(0,0,0),(2,1,0),(2,2,2),(0,2,0)D E B C ,1(2,0,2)B C =--,设(),0,0F m ()02m ≤≤,(2,1,0)EF m =--,设异面直线1B C 与EF 的夹角为θ,则1212|||2(2)|cos ||||122(2)1211(2)EF B C m EF B C m m θ⋅-⨯-===⋅⋅-+⋅+-, 异面直线1B C 与EF 所成角最小时,则cos θ最大,即0m =时,210cos 51102141θ===⋅+.故选C .【名师点睛】本题考查异面直线及其所成的角的余弦值,解题方法是建立空间直角坐标系,用空间向量法表示距离、求角,属于中档题.5、如图,已知正方体1111ABCD A B C D -的棱长为1,,E F 分别是棱11,AD B C 上的中点.若点P 为侧面正方形11ADD A 内(含边)动点,且存在,x y R ∈使1B P xBE yBF =+成立,则点P 的轨迹长度为A .12B .1C 5D .2π 【答案】C【分析】根据向量共面判断出1//B P 平面BEF ,由面面平行得到P 点的轨迹,在直角三角形中求出边长即可.【解析】因为1B P xBE yBF =+成立,所以1B P BE BF 、、共面,即1//B P 平面BEF , 如图,取11A D 中点Q ,连接1B Q 、1B A 、AQ , 根据正方体的性质得,1//B Q BE ,1//B A FE , 且111=B QB A B ,=FEBE E ,所以平面1//B AQ 平面BEF ,所以点P 在AQ 上运动,点P 的轨迹为线段AQ ,因为11A A =,112AQ =, 由勾股定理得151+=42QA =,故选C .题型二、动点问题(多选)1、如图,棱长为1的正方体1111ABCD A B C D -中,P 为线段1A B 上的动点(不含端点),则下列结论正确的是A .平面11D A P ⊥平面1A APB .//BC 平面11AD PC .三棱锥1D CDP -的体积为定值 D .直线1D P 与AC 所成的角可能是6π【答案】AC【解析】对于A 中,在正方体1111ABCD A B C D -中,可得1111,A D AA A D AB ⊥⊥,又由1AA AB A =,所以11A D ⊥平面1A AP ,因为11A D ⊂平面11D A P ,所以平面11D A P ⊥平面1A AP ,所以A 正确; 对于B 中,在正方体1111ABCD A B C D -中,可得11//BC A D , 所以11,,,B C A D 四点共面,所以B 不正确; 对于C 中,因为1111122CDD S=⨯⨯=,点P 到平面1CDD 的距离为1BC =, 所以三棱锥1D CDP -的体积为定值,所以C 正确;对于D 中,以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,可得1(0,0,1),(1,0,0),(0,1,0)D A C ,设(1,,)(01,01)P a b a b <<<<, 则1(1,,1),(1,1,0)D P a b AC =-=-, 则11221cos ,01(1)2D P AC D P AC D P ACa b ⋅==<⋅++-⋅,当1a =时,1,2D P AC π=;当0,1a b ==时,13,4D P AC π=, 所以直线1D P 与AC 所成的角的范围是(,)42ππ,所以D 不正确.故选AC【名师点睛】此类问题解答中熟记正方体的几何结构特征,熟练应用转化顶点,利用等体积法求解三棱锥的体积,以及合理利用空间向量的夹角公式求解异面直线所成的角是解答的关键.(多选)2、如图,在三棱柱111ABC A B C -中,侧棱1AA ⊥底面111A B C ,90BAC ︒∠=,11AB AC AA ===,D 是棱1CC 的中点,P 是AD 的延长线与11A C 的延长线的交点.若点Q 在直线1B P 上,则下列结论错误的是( ).A .当Q 为线段1B P 的中点时,DQ ⊥平面1A BD B .当Q 为线段1B P 的三等分点时,DQ ⊥平面1A BDC .在线段1B P 的延长线上,存在一点Q ,使得DQ ⊥平面1A BD D .不存在点Q ,使DQ 与平面1A BD 垂直 【答案】ABC【分析】以1A 为坐标原点,11A B ,11A C ,1A A 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,求得平面1A BD 的一个法向量(,,)n x y z =,假设DQ ⊥平面1A BD ,且11B Q B P λ=,得到11DQ DB BQ =+=11,12,2λλ⎛⎫--+- ⎪⎝⎭,则(2,1,2)n =-与11,12,2DQ λλ⎛⎫=--+- ⎪⎝⎭共线,研究1112122124λλ---+===-是否有解即可. 【解析】以1A 为坐标原点,11A B ,11A C ,1A A 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,则由1(0,0,0)A ,1(1,0,0)B ,1(0,1,0)C ,(1,0,1)B ,10,1,2D ⎛⎫ ⎪⎝⎭,(0,2,0)P ,所以1(1,0,1)A B =,110,1,2A D ⎛⎫= ⎪⎝⎭,1(1,2,0)B P =-,111,1,2DB ⎛⎫=-- ⎪⎝⎭.设平面1A BD 的一个法向量为(,,)n x y z =,则11012n A B x z n A D y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩, 取2z =-,则2x =,1y =,所以平面1A BD 的一个法向量为(2,1,2)n =-.假设DQ ⊥平面1A BD ,且11(1,2,0)(,2,0)BQ B P λλλλ==-=-, 则11DQ DB BQ =+=11,12,2λλ⎛⎫--+- ⎪⎝⎭. 因为DQ 也是平面1A BD 的法向量,所以(2,1,2)n =-与11,12,2DQ λλ⎛⎫=--+- ⎪⎝⎭共线,所以1112122124λλ---+===-成立,但此方程关于λ无解. 因此不存在点Q ,使DQ 与平面1A BD 垂直,故选ABC .(多选)3、在长方体1111ABCD A B C D -中,23AB =12AD AA ==,,,P Q R 分别是11,,AB BB AC 上的动点,下列结论正确的是 A .对于任意给定的点P ,存在点Q 使得1D P CQ ⊥ B .对于任意给定的点Q ,存在点R 使得1D R CQ ⊥ C .当1AR A C ⊥时,1AR D R ⊥D .当113AC A R =时,1//D R 平面1BDC 【答案】ABD【分析】如图所示建立空间直角坐标系,计算142D P CQ b ⋅=-,()12222D R CQ b λλ⋅=--,134AR D R ⋅=-,10D R n ⋅=,得到答案.【解析】如图所示,建立空间直角坐标系,设()2,,0P a ,0,23a ⎡⎤∈⎣⎦,()2,23,Q b ,[]0,2b ∈,设11A R AC λ=,得到()22,23,22R λλλ--,[]0,1λ∈. ()12,,2P a D -=,()2,0,CQ b =,142D P CQ b ⋅=-,当2b =时,1D P CQ ⊥,A 正确;()122,23,2D R λλλ=--,()12222D R CQ b λλ⋅=--,取22bλ=+时,1D R CQ ⊥,B 正确;1AR A C⊥,则()()12,23,222,23,2212440AR AC λλλλλλ⋅=--⋅--=-+-+=, 14λ=,此时11333313,,,,02222224AR D R ⎛⎫⎛⎫⋅=-⋅-=-≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,C 错误; 113AC A R =,则4234,,333R ⎛⎫ ⎪ ⎪⎝⎭,14232,,333D R ⎛⎫=- ⎪ ⎪⎝⎭,设平面1BDC 的法向量为(),,n x y z =,则10n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩,解得()3,1,3n =-,故10D R n ⋅=,故1//D R 平面1BDC ,D 正确. 故选ABD .【点睛】本题考查了空间中的线线垂直,线面平行,意在考查学生的计算能力和空间想象能力,推断能力. 题型三、确定点的位置1、如图,在三棱柱111ABC A B C -中,四边形11AAC C 是边长为3的正方形,1CC BC ⊥,1BC =,2AB =.(1)证明:平面1A BC ⊥平面1ABC ;(2)在线段1A B 上是否存在点M ,使得1CM BC ⊥,若存在,求1BMBA 的值;若不存在,请说明理由.【答案】(1)证明见解析;(2)14. 【解析】(1)在ABC 中,3AC =1BC =,2AB =,满足222AC BC AB +=,所以AC BC ⊥,又1CC BC ⊥,1CC AC C =,所以BC ⊥面11ACC A ,又1AC ⊂面11ACC A ,所以1BC A C ⊥,又四边形11AAC C 是边长为3的正方形,所以11AC AC ⊥,又1BCAC C =,所以1AC ⊥面1A CB ,又1AC ⊂平面1ABC ,所以平面1A BC ⊥平面1ABC ;(2)在线段1A B 上存在点M ,使得1CM BC ⊥,且114BM BA =, 理由如下:由(1)得,以点C 为原点,1,,CA CB CC 所在直线分别为,,x y z 轴建立空间直角坐标系,如图所示,则()3,0,0A,()0,0,0C ,()0,1,0B ,13,0,3A ,(13C ,设(),,M x y z ,1BM BA λ=,所以(),1,3,3x y z λ-=-,解得3x λ=,1y λ=-,3z λ=,所以()3,13CM λλλ=-,(10,1,3C B =-,要使1CM BC ⊥,则需10CM BC ⋅=,即130λλ--=,解得14λ=,故114BM BA =.2、如图,在多面体ABCDP 中,ABC 是边长为4的等边三角形,PA AC =,22BD CD ==,42PC PB ==,点E 为BC 的中点,平面BDC ⊥平面ABC .(1)求证://DE 平面PAC(2)线段BC 上是否存在一点T ,使得二面角T DA B --为直二面角?若存在,试指出点T 的位置;若不存在,请说明理由.【答案】(1)证明见解析;(2)存在,T 为线段BC 上靠近点C 的八等分点. 【分析】(1)根据题目条件证明DE ⊥平面ACE ,从而得到DE //PA ,得出DE //平面PAC ;(2)建立空间直角坐标系,假设存在点(),0,0T λ,计算平面TDA 和平面BDA 的法向量,使法向量数量积为零,然后求解λ,根据λ的值确定点T 的位置. 【解析】(1)因为22BD CD ==ABC 是边长为4的等边三角形, 所以((2222222216BD CD BC +=+==,所以BDC 是等腰直角三角形,90BDC ∠=︒.又点E 为BC 的中点,所以DE BC ⊥.因为平面BDC ⊥平面ABC ,平面BDC ⋂平面ABC BC =,所以DE ⊥平面ABC . 因为42PC PB ==,4PA AC AB ===,所以222224432PA AC PC +=+==,222224432PA AB PB +=+==,所以PAB △与PAC 都是直角三角形,故PA AC ⊥,PA AB ⊥. 又AC AB A ⋂=,所以PA ⊥平面ABC ,所以DE PA ∥. 因为PA ⊂平面PAC ,DE ⊄平面PAC ,所以DE 平面PAC .(2)连接AE ,以E 为原点,EC ,EA ,ED 所在直线分别为x ,y ,z 轴,建立如图所示的空间直角坐标系,则()0,23,0A ,()2,0,0B -,()2,0,0C ,()0,0,2D ,设存在(),0,0T λ,使得二面角T DA B --为直二面角,易知22λ-≤≤,且0λ≠. 设平面BAD 的法向量为()1111,,n x y z =,则由()2,0,2BD =,()0,23,2AD =-,得1111030x z y z +=⎧⎪⎨-+=⎪⎩,令11z =,得111x x =-,133y =,故131,,13n ⎛⎫=- ⎪ ⎪⎝⎭.设平面TAD 的法向量为()2222,,n x y z =,则由(),0,2DT λ=-,(),23,0AT λ=-,得222220,230x z x y λλ-=⎧⎪⎨-=⎪⎩,令21z =,得22x λ=,233y =,故223,,13n λ⎛⎫= ⎪ ⎪⎝⎭. 由122233133cos ,074433n n λλ-+⨯+==⨯+,得12103λ-+=,故32λ=. 所以当T 为线段BC 上靠近点C 的八等分点时,二面角T DA B --为直二面角.3、如图,三棱柱111ABC A B C -中,AB ⊥侧面11BB C C ,已知13BCC π∠=,1BC =,12AB C C ==,点E 是棱1C C 的中点.(1)求证:1C B ⊥平面ABC ; (2)求二面角11A EB A --的余弦值;(3)在棱CA 上是否存在一点M ,使得EM 与平面11A B E 所成角的正弦值为21111,若存在,求出CM CA 的值;若不存在,请说明理由.【答案】(1)证明见解析(225(3)存在,13CM CA =或523CM CA =.【解析】(1)由题意,因为1BC =,12CC =,13BCC π∠=,所以13BC又所以22211BC BC CC +=,所以1BC BC ⊥,因为AB ⊥侧面11BB C C ,所以1AB BC ⊥.又因为AB BC B ⋂=,AB ,BC ⊂平面ABC ,所以直线1C B ⊥平面ABC . (2)以B 为原点,分别以BC ,1BC 和BA 的方向为x ,y 和z 轴的正方向建立如图所示的空间直角坐标系,则()0,0,2A ,()13,0B -,132E ⎛⎫⎪ ⎪⎝⎭,()13,2A -,设平面1AB E 的一个法向量为()111,,n x y z =,()13,2AB =--,13,,222AE ⎛⎫=- ⎪ ⎪⎝⎭因为100n AB n AE ⎧⋅=⎨⋅=⎩,所以11111132013202x z x y z ⎧--=⎪⎨-=⎪⎩,令13y =,则11x =,所以()1,3,1n =设平面11A B E 的一个法向量为(),,m x y z =,()110,0,2A B =-,133,,222A E ⎛⎫=-- ⎪ ⎪⎝⎭, 因为11100m A B m A E ⎧⋅=⎪⎨⋅=⎪⎩,所以20332022z x y z -=⎧⎪⎨--=⎪⎩,令3y =,则1x =,所以()1,3,0m =,2m =,5n =,4m n ⋅=,所以425cos ,525m n m n m n⋅===.设二面角11A EB A --为α,则25cos cos ,5m n α==. 所以设二面角11A EB A --的余弦值为255. (3)假设存在点M ,设(),,M x y z ,因为CM CA λ=,[]0,1λ∈,所以()()1,,1,0,2x y z λ-=-,所以()1,0,2M λλ-所以13,,222EM λλ⎛⎫=-- ⎪ ⎪⎝⎭设平面11A B E 的一个法向量为()1,3,0m =,所以22132112211132424λλλ--=⎛⎫-++ ⎪⎝⎭,得2693850λλ-+=.即()()312350λλ--=,所以13λ=或523λ=,所以13CM CA =或523CM CA =.【名师点睛】本题考查了线面平行的判定与证明,以及空间角的求解问题,意在考查学生的空间想象能力和逻辑推理能力,解答中熟记线面位置关系的判定定理和性质定理,通过严密推理是线面位置关系判定的关键,同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解. 强化训练(多选)1、如图所示,正方体1111ABCD A B C D -中,1AB =,点P 在侧面11BCC B 及其边界上运动,并且总是保持1AP BD ⊥,则以下四个结论正确的是A .113P AA D V -=B .点P 必在线段1BC 上 C .1AP BC ⊥D .//AP 平面11AC D【答案】BD【分析】根据三棱锥体积公式求得116P AA D V -=,知A 错误;以D 为坐标原点建立空间直角坐标系,利用空间向量法可得到1CP x B C →→=-,11AP BC →→⋅=,AP →垂直于平面11AC D 的法向量n →,由此可确定,,B C D 的正误.【解析】对于A ,P 在平面11BCC B 上,平面11//BCC B 平面1AA D ,P ∴到平面1AA D 即为C 到平面1AA D 的距离,即为正方体棱长,1111111113326P AA D AA D V S CD -∴=⋅=⨯⨯⨯⨯=△,A 错误;对于B ,以D 为坐标原点可建立如下图所示的空间直角坐标系:则()1,0,0A ,(),1,P x z ,()1,1,0B ,()10,0,1D ,()11,1,1B ,()0,1,0C()1,1,AP x z →∴=-,()11,1,1BD →=--,()11,0,1B C →=--,1AP BD ⊥,1110AP BD x z →→∴⋅=--+=,x z ∴=,即(),1,P x x ,(),0,CP x x →∴=,1CP x B C →→∴=-,即1,,B P C 三点共线,P ∴必在线段1B C 上,B 正确;对于C ,()1,1,AP x x →=-,()11,0,1BC →=-,111AP BC x x →→∴⋅=-+=,AP ∴与1BC 不垂直,C 错误;对于D ,()11,0,1A ,()10,1,1C ,()0,0,0D ,()11,0,1DA →∴=,()10,1,1DC →=, 设平面11AC D 的法向量(),,n x y z →=,1100n DA x z n DC y z ⎧⋅=+=⎪∴⎨⋅=+=⎪⎩,令1x =,则1z =-,1y =,()1,1,1n →∴=-, 110AP n x x →→∴⋅=-+-=,即AP n →→⊥,//AP ∴平面11ACD ,D 正确. 故选BD .【点睛】本题考查立体几何中动点问题相关命题的辨析,涉及到三棱锥体积公式、动点轨迹、线线垂直关系和线面平行关系等知识;解题关键是熟练应用空间向量法来验证相关结论.2、如图,在边长为2的正方体1111ABCD A B C D -中,E 为BC 的中点,点P 在底面ABCD 上移动,且满足11B P D E ⊥,则线段1B P 的长度的最大值为( )A .45B .2C .2D .3【答案】D【分析】以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系,设点(),,0P x y ,根据110B P D E ⋅=得出x 、y 满足的关系式,并求出y 的取值范围,利用二次函数的基本性质求得1B P 的最大值.【解析】如下图所示,以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系D xyz -,则点()12,2,2B 、()10,0,2D 、()1,2,0E ,设点()(),,002,02P x y x y ≤≤≤≤,()11,2,2D E =-,()12,2,2B P x y =---,11D E B P ⊥,()112224220B P D E x y x y ∴⋅=-+-+=+-=,得22x y =-,由0202x y ≤≤⎧⎨≤≤⎩,得022202y y ≤-≤⎧⎨≤≤⎩,得01y ≤≤, ()()2221224548B P x y y y ∴=-+-+=-+01y ≤≤,当1y =时,1B P 取得最大值3.故选D .3、在长方体1111ABCD A B C D -中,已知底面ABCD 为正方形,P 为11A D 的中点,2AD =,13AA =,点Q 为正方形ABCD 所在平面内的一个动点,且满足2QC QP =.则线段BQ 的长度的最大值是( )A .2B .4C .6D .前三个答案都不对【答案】C【分析】先以D 点为坐标原点,分别以DA ,DC ,1DD 所在方向为x 轴,y 轴,z 轴正方向,建立空间直角坐标系,由题意得到(0,2,0)C ,()1,0,3P ,(2,2,0)B ,设(,,0)Q x y ,由2QC QP =,得到22(2)(2)4-++=x y ,再由圆上的点与定点距离的问题,即可求出结果.【解析】以D 点为坐标原点,分别以DA ,DC ,1DD 所在方向为x 轴,y 轴,z 轴正方向,建立如图所示的空间直角坐标系,因为在长方体1111ABCD A B C D -中,已知底面ABCD 为正方形,P 为11A D 的中点,2AD =,13AA =(0,2,0)C ,(1,3P ,(2,2,0)B ,因为点Q 为正方形ABCD 所在平面内的一个动点,设(,,0)Q x y , 因为2QC QP =,所以()2222(2)213+-=⋅-++x y x y ,整理得:22(2)(2)4-++=x y ,即点Q 可看作圆22(2)(2)4-++=x y 上的点, 又22(2)(2)=-+-BQ x y ,所以BQ 表示圆22(2)(2)4-++=x y 上的点与定点(2,2)之间的距离, 因此22max (22)(22)426=-+--+=+=BQ r (其中r表示圆22(2)(2)4-++=x y 的半径.)故选C . 【名师点睛】本题主要考查立体几何中的轨迹问题,涉及圆上的点到定点距离的最值,灵活运用转化与化归的思想即可,属于常考题型.4、如图,已知正方体ABCD -A 1B 1C 1D 1棱长为8,点H 在棱AA 1上,且HA 1=2,在侧面BCC 1B 1内作边长为2的正方形EFGC 1,P 是侧面BCC 1B 1内一动点,且点P 到平面CDD 1C 1距离等于线段PF 的长,则当点P 在侧面BCC 1B 1运动时,2HP 的最小值是( )A .87B .88C .89D .90【答案】B【分析】建立空间直角坐标系,过点H 作1HM BB ⊥,垂足为M ,连接MP ,得出222HP HM MP =+,当MP 最小时,2HP 最小,利用空间直角坐标系求2HP 的最小值.【解析】如图,建立空间直角坐标系,过点H 作1HM BB ⊥,垂足为M ,连接MP ,则HM PM ⊥,所以222HP HM MP =+,当MP 最小时,2HP 最小, 过P 作1PN CC ⊥,垂足为N ,设(,8,)P x z ,则(2,8,6),(8,8,6),(0,8,)F M N z ,且08,08x z ≤≤≤≤,因为PN PF =,所以22(2)(6)x z x -+-=,化简得244(6)x z -=-,所以222222(8)(6)(8)441260(6)2424MP x z x x x x x =-+-=-+-=-+=-+≥, 当6x =时,2MP 取得最小值24,此时222282488HP HM MP =+=+=, 所以2HP 的最小值为88,故选B .5、如图,在棱长为2的正方体1111ABCD A B C D -中,E 为BC 的中点,点P 在底面ABCD 上(包括边界....)移动,且满足11B P D E ⊥,则线段1B P 的长度的最大值为A .55B .25C .2D .3【答案】D【分析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,利用向量法能求出线段1B P 的长度的最大值.【解析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,设P (a ,b ,0),则1D (0,0,2),E (1,2,0),1B (2,2,2),1B P =(a −2,b −2,−2),1D E =(1,2,−2), 因为1B P ⊥1D E ,()1122240B P D E a b ∴⋅=-+-+=, 所以a +2b −2=0,01b ≤≤,所以点P 的轨迹是一条线段,()()()()2222221224224548a b b B P b b b -+-+==+-+=-+, 由二次函数的性质可得当1b =时,2548b b -+可取到最大值9, 所以线段1B P 的长度的最大值为3.故选D .6、如图所示,在正方体1111ABCD A B C D -中,点P 是底面1111D C B A 内(含边界)的一点,且//AP 平面1DBC ,则异面直线1A P 与BD 所成角的取值范围为A .3,44ππ⎡⎤⎢⎥⎣⎦B .,42ππ⎡⎤⎢⎥⎣⎦C .,32ππ⎡⎤⎢⎥⎣⎦D .2,33ππ⎡⎤⎢⎥⎣⎦【答案】C【分析】连接111,,AB AD B D ,则点P 在线段11B D 上,以D 为坐标原点建立坐标系,利用向量方法可求出范围. 【解析】过A 作平面α平面1DBC ,点P 是底面1111D C B A 内(含边界)的一点,且//AP 平面1DBC ,则P ∈平面α,即P 在α与平面1111D C B A 的交线上,连接111,,AB AD B D ,11DD BB =,则四边形11BDD B 是平行四边形,11B D BD ∴,11B D ∴平面1DBC ,同理可证1AB ∥平面1DBC ,∴平面11AB D ∥平面1DBC ,则平面11AB D 即为α,点P 在线段11B D 上,以D 为坐标原点,1,,DA DC DD 建立如图坐标系,设正方体棱长为1,则()0,0,0D ,()1,1,0B ,()1,0,0A ,设(),,1P λλ,[]0,1λ∈,()1,1,0DB ∴=,()1,,1AP λλ=-,21DB AP λ∴⋅=-,2DB =,2222AP λλ=-+,设1A P 与BD 所成角为θ,则()22221211cos 2121DB APDB AP λλθλλλλ⋅--===-+⋅-+ 221313442121324λλλ=-=--+⎛⎫-+ ⎪⎝⎭,当12λ=时,cos θ取得最小值为0, 当0λ=或1时,cos θ取得最大值为12,10cos 2θ∴≤≤,则32ππθ≤≤.故选C .7、如图,三棱锥V ABC -的侧棱长都相等,底面ABC 与侧面VAC 都是以AC 为斜边的等腰直角三角形,E 为线段AC 的中点,F 为直线AB 上的动点,若平面VEF 与平面VBC 所成锐二面角的平面角为θ,则cos θ的最大值是A .33 B .23C 5D 6【答案】D【分析】连接BE ,以E 为原点,EB 为x 轴,EC 为y 轴,EV 为z 轴,建立空间直角坐标系,求出平面VBC 的一个法向量m ,平面VEF 的一个法向量n ,利用cos m n m nθ⋅=即可求解.【解析】底面ABC 与侧面VAC 都是以AC 为斜边的等腰直角三角形, 则Rt ABC Rt VAC ≅,所以VA VC BA BC === 设2VA VC BA BC VB =====,由E 为线段AC 的中点,则2VE BV ==, 由222VE BE VB +=,所以VE EB ⊥,以E 为原点,EB 为x 轴,EC 为y 轴,EV 为z 轴, 建立空间直角坐标系,如图所示:则()2,0C ,)2,0,0B,(2V ,设(),2,0F x x -,(0,2,2VC =-,(2,0,2VB =-,(2EV =,(,2,2VF x x =,设平面VBC 的一个法向量()111,,m x y z =,则00m VC m VB ⎧⋅=⎨⋅=⎩,即1111220220z x ⎧+=⎪⎨-=⎪⎩,令11x =,则11y =,11z =,所以()1,1,1m =. 设平面VEF 的一个法向量()222,,n x y z =,则00n EV n VF ⎧⋅=⎨⋅=⎩,即(222220220z x x x y z ⎧=⎪⋅+-⋅+=⎪⎩,解得20z =,令21y =,则221x x =-, 所以21,1,0n x ⎛⎫=- ⎪ ⎪⎝⎭, 平面VEF 与平面VBC 所成锐二面角的平面角为θ,则22cos 22232m n x m n x xθ⋅==-+,将分子、分母同除以1x,可得=令()2266632f x x x ⎛=-+=-+ ⎝⎭,当2x =时,()min 3f x =,则cos θ3=. 故选D【点睛】本题考查了空间向量法求二面角、考查了基本运算求解能力,解题的关键是建立恰当的空间直角坐标系,属于中档题.8、已知MN 是正方体内切球的一条直径,点P 在正方体表面上运动,正方体的棱长是2,则PM PN →→⋅的取值范围为 A .[]0,4 B .[]0,2C .[]1,4D .[]1,2【答案】B【分析】利用向量的线性运算和数量积运算律可将所求数量积化为21PO →-,根据正方体的特点可确定PO →的最大值和最小值,代入即可得到所求范围. 【解析】设正方体内切球的球心为O ,则1OM ON ==,2PM PN PO OM PO ON PO PO OM ON OM ON →→→→→→→→→→→→⎛⎫⎛⎫⎛⎫⋅=+⋅+=+⋅++⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,MN 为球O 的直径,0OM ON →→∴+=,1OM ON →→⋅=-,21PM PN PO →→→∴⋅=-,又P 在正方体表面上移动,∴当P 为正方体顶点时,PO →最大,最大值为;当P 为内切球与正方体的切点时,PO →最小,最小值为1,[]210,2PO →∴-∈,即PM PN →→⋅的取值范围为[]0,2.故选B .【点睛】本题考查向量数量积的取值范围的求解问题,关键是能够通过向量的线性运算将问题转化为向量模长的取值范围的求解问题.7、在正四面体D ABC -(所有棱长均相等的三棱锥)中,点E 在棱AB 上,满足2AE EB =,点F 为线段AC 上的动点.设直线DE 与平面DBF 所成的角为α,则A .存在某个位置,使得DE BF ⊥B .存在某个位置,使得4FDB π∠=C .存在某个位置,使得平面DEF ⊥平面DACD .存在某个位置,使得6πα=【答案】C【分析】设正四面体D ABC -的底面中心为点O ,连接DO ,则DO ⊥平面ABC ,以点O 为坐标原点,OB 、OD 所在直线分别为x 、z 轴建立空间直角坐标系,设正四面体D ABC -的棱长为2,然后利用空间向量法逐一分析求解可得结果. 【解析】如下图所示,设正四面体D ABC -的底面中心为点O ,连接DO ,则DO ⊥平面ABC ,以点O 为坐标原点,OB 、OD 所在直线分别为x 、z 轴建立空间直角坐标系, 设正四面体D ABC -的棱长为2,则31,0A ⎛⎫- ⎪ ⎪⎝⎭、23B ⎫⎪⎪⎝⎭、3C ⎛⎫ ⎪ ⎪⎝⎭、26D ⎛ ⎝⎭、31,03E ⎫-⎪⎪⎝⎭,设,03F λ⎛⎫- ⎪ ⎪⎝⎭,其中11λ-≤≤, 对于A 选项,若存在某个位置使得DE BF ⊥,31,333DE ⎛⎫=-- ⎪ ⎪⎝⎭,(),0BF λ=-,1103DE BF λ∴⋅=--=,解得3λ=-,不合乎题意,A 选项错误;对于B 选项,若存在某个位置使得4FDB π∠=,,33DF λ⎛=-- ⎝⎭,23DB ⎛=⎝⎭,cos ,DF DB DF DB DF DBλ⋅<>====⋅B选项错误;对于C 选项,设平面DAC 的一个法向量为()111,,m x y z =,1,DA ⎛=-- ⎝⎭,DC ⎛=-⎝⎭,由1111113033303m DA x y z m DC x y z ⎧⋅=---=⎪⎪⎨⎪⋅=-+-=⎪⎩,取11z =-,得()22,0,1m =-,设平面DEF 的一个法向量为()222,,n x y z =,31,3DE ⎛=- ⎝⎭,,DF λ⎛=- ⎝⎭, 由22222231033333n DE x y z n DF x y z λ⎧⋅=--=⎪⎪⎨⎪⋅=-+=⎪⎩,取y =,则()221n λ=+-,若存在某个位置,使得平面DEF ⊥平面DAC ,则2190m n λ⋅=+=,解得[]31,17λ=-∈-,合乎题意,C 选项正确;对于D 选项,设平面DBF 的一个法向量为()333,,u x y z =,2326,0,33DB ⎛⎫=- ⎪ ⎪⎝⎭,326,,33DF λ⎛⎫=-- ⎪ ⎪⎝⎭, 由333332326033326033u DB x z u DF x y z λ⎧⋅=-=⎪⎪⎨⎪⋅=-+-=⎪⎩,令z λ=,则()2,6,u λλ=,若存在某个位置,使得6πα=,即()()22612131sin cos ,6227272363u DE u DE u DEλλπλλ++⋅==<>===⋅⨯++⨯,整理得254120λλ-+=,162400∆=-<,该方程无解,D 选项错误. 故选C.【点评】本题考查利用空间向量法求解空间角以及利用空间向量法处理动点问题,计算量大,属于难题.10、如图,直三棱柱111ABC A B C -的底面是边长为6的等边三角形,侧棱长为2,E 是棱BC 上的动点,F 是棱11B C 上靠近1C 点的三分点,M 是棱1CC 上的动点,则二面角A FM E --的正切值不可能...是A .3155B .2155C .6D .5【答案】B【分析】建立空间直角坐标系,求得二面角A FM E --的余弦值,进而求得二面角A FM E --的正切值,求得正切值的最小值,由此判断出正确选项.【解析】取BC 的中点O ,连接OA ,根据等边三角形的性质可知OA BC ⊥,根据直三棱柱的性质,以O 为原点建立如图所示的空间直角坐标系.则()()0,33,0,1,0,2A F ,设()()3,0,02M t t ≤≤. 则()()1,33,2,2,0,2AF FM t =-=-. 设平面AMF 的一个法向量为(),,m x y z =,则()3320220m AF x z m FM x t z ⎧⋅=-+=⎪⎨⋅=+-=⎪⎩,令1y =,得633363,1,66t m t t ⎛= --⎝⎭. 平面FME 的一个法向量是()0,1,0n =,所以222cos ,28120252633363166m n m n m nt t t t t ⋅===⋅-+⎛⎫⎛⎫-++ ⎪ ⎪--⎝⎭⎝⎭,所以2sin ,1cos ,m n m n =-222710821628120252t t t t -+=-+所以二面角A FM E--的正切值为()sin ,27 cos,m nf tm n===因为02t≤≤,所以111466t-≤≤--,216125405-=-⨯结合二次函数的性质可知当1165t=--时,()f t5=;当1166t=--时,()f t=,所以()f t∈⎣,所以二面角A FM E--.故选B.【点睛】本小题主要考查二面角的求法,考查数形结合的数学思想方法,属于难题.11、直四棱柱ABCD﹣A1B1C1D1中,侧棱长为6,底面是边长为8的菱形,且∠ABC =120°,点E在边BC上,且满足BE=3EC,动点M在该四棱柱的表面上运动,并且总保持ME⊥BD1,则动点M的轨迹围成的图形的面积为_____;当MC与平面ABCD所成角最大时,异面直线MC1与AC所成角的余弦值为_____.【答案】,17【分析】由题意可知M的轨迹为过E且与直线1BD垂直的平面与直四棱柱的截面的边界,根据直棱柱的结构特征和底面棱形的性质,由线面垂直的定义可得截面与下底面的截线是与AC平行的,进而确定截面与与AB的交点F,建立空间直角坐标系,利用坐标方法求得截面与1BB的交点G,进而得到所求面积,根据线面角的定义可得M与G重合时MC与平面ABCD所成角最大,利用空间向量可求异面直线所成角的余弦值.【解析】如图,在直四棱柱1111ABCD A B C D-中,因为底面是菱形,侧棱垂直底面,所以AC ⊥平面11BDD B ,所以1BD AC ⊥.在AB 上取F ,使得3BF FA =,连接EF ,则//EF AC ,1⊥BD EF .记AC 与BD 的交点为O ,以O 为坐标原点,建立如图所示的空间直角坐标系O xyz -,则()4,0,0B ,()14,0,6D -,()1,33,0E .在1BB 上取一点G ,记为()4,0,G t ,于是()18,0,6BD =-,()3,33,EG t =-. 由12460BD EG t ⋅=-+=,得4t =,即12BG GB =, 所以EFG 的边为点M 的运动轨迹. 由题意得22213FG BF BG =+=33836344EF AC ==⨯= 动点M 的轨迹围成的图形的面积为()()22163213331532⨯-=显然当M 与G 重合时,MC 与平面ABCD 所成角最大. 因为()4,0,4M ,()10,43,6C ,所以()14,43,2MC =-. 因为AC 的一个方向向量为()0,1,0n =,所以1251cos ,17MC n =即异面直线1MC 与AC 251. 【点睛】本题考查点、线、面的位置关系,考查空间动点的轨迹,涉及线面垂直的判定与性质,异面直线所成的角,线面角,利用空间直角坐标系和空间向量确定点的位置和求异面直线所成的角,考查直观想象与数学运算的核心素养.属中档题,难度较大.12、如图,在直三棱柱111ABC A B C -中,已知90ABC ∠=︒,P 为侧棱1CC 上任意一点,Q 为棱AB 上任意一点,PQ 与AB 所成角为α,PQ 与平面ABC 所成的角为β,则α与β的大小关系为( )A .αβ=B .αβ<C .αβ>D .不能确定【答案】C【分析】建立空间直角坐标系设()()(),0,,0,,00,0,0P x z Q y x y z >≥≥,利用空间向量法分别求得cos ,cos αβ,然后根据(0,],0,22ππαβ⎡⎤∈∈⎢⎥⎣⎦,利用余弦函数的单调性求解.【解析】建立如图所示空间直角坐标系:设()()(),0,,0,,00,0,0P x z Q y x y z >≥≥,则()(),,,0,,0QP x y z QB y =-=-,所以2222,,QP QB y QP x y z QB y ⋅==++=,所以222cos QP QB y QP QBx y zα⋅==⋅++,又(0,],0,22ππαβ⎡⎤∈∈⎢⎥⎣⎦,222sin QP CP z QPx y zβ⋅==++,所以22222cos x y x y zβ+=++,所以cos cos βα>,因为cos y x = 在0,2π⎛⎫⎪⎝⎭上递减,所以αβ>,故选C 13、如图,在四棱柱1111ABCD A B C D -中,底面ABCD 为正方形,侧棱1AA ⊥底面ABCD ,3AB =,14AA =,P 是侧面11BCC B 内的动点,且1AP BD ⊥,记AP 与平面11BCC B 所成的角为θ,则tan θ的最大值为( )A .43B .53C .2D .259【答案】B【分析】建立空间直角坐标系,利用向量法能求出线面角的正切值的最大值. 【解析】以1,,DA DC DD 所在直线分别为,,x y z 轴,建立空间直角坐标系, 设(,3,)P x z ,则1(3,3,),(3,3,4)AP x z BD =-=--,11,0AP BD AP BD ⊥∴⋅=,33(3)3340,4x z z x ∴---⨯+=∴=, 22225||(3)6916BP x z x x ∴=-+=-+225488191625255x ⎛⎫=-+ ⎪⎝⎭, ||5tan ||3AB BP θ∴=,tan θ∴的最大值为53.故选B .14、如图,在棱长都相等的正三棱柱111ABC A B C -中,D 是棱1CC 的中点,E 是棱1AA 上的动点.设AE x =,随着x 增大,平面BDE 与底面ABC 所成锐二面角的平面角是( )A .增大B .先增大再减小C .减小D .先减小再增大【答案】D【解析】设正三棱柱111ABC A B C -棱长为2,,02AE x x =≤≤, 设平面BDE 与底面ABC 所成锐二面角为α,以A 为坐标原点,过点A 在底面ABC 内与AC 垂直的直线为x 轴,1,AC AA 所在的直线分别为,y z 轴建立空间直角坐标系,则3,1,0),(0,2,1),(0,0,),(3,1,1),(0,2,1)B D E x BD ED x =-=-,设平面BDE 的法向量(,,)m s t k =,则m BDm ED⎧⊥⎨⊥⎩,即302(1)0s t k t x k ⎧-++=⎪⎨+-=⎪⎩,令3k =33,1t x s x =-=+,所以平面BDE 的一个法向量(1,33,23)m x x =+-, 底面ABC 的一个法向量为(0,0,1)n =,222233cos |cos ,|115(1)3(1)12()24m n x x x α=<>==++-+-+当1(0,)2x ∈,cos α随着x 增大而增大,则α随着x 的增大而减小,当1(,2)2x ∈,cos α随着x 增大而减小,则α随着x 的增大而增大.故选D .【点睛】本题考查空间向量法求二面角,应用函数思想讨论二面角的大小,考查直观想象、数学计算能力,素养中档题.15、如图所示,在正方体1111ABCD A B C D -中,点P 是底面1111D C B A 内(含边界)的一点,且//AP 平面1DBC ,则异面直线1A P 与BD 所成角的取值范围为( )A .3,44ππ⎡⎤⎢⎥⎣⎦B .,42ππ⎡⎤⎢⎥⎣⎦C .,32ππ⎡⎤⎢⎥⎣⎦D .2,33ππ⎡⎤⎢⎥⎣⎦【答案】C【解析】过A 作平面α平面1DBC ,点P 是底面1111D C B A 内(含边界)的一点,且//AP 平面1DBC ,则P ∈平面α,即P 在α与平面1111D C B A 的交线上,连接111,,AB AD B D ,11DD BB =,则四边形11BDD B 是平行四边形,11B D BD ∴,11B D ∴平面1DBC ,同理可证1AB ∥平面1DBC ,∴平面11AB D ∥平面1DBC ,则平面11AB D 即为α,点P 在线段11B D 上,以D 为坐标原点,1,,DA DC DD 建立如图坐标系,设正方体棱长为1,则()0,0,0D ,()1,1,0B ,()1,0,0A ,设(),,1P λλ,[]0,1λ∈,()1,1,0DB ∴=,()1,,1AP λλ=-,21DB AP λ∴⋅=-,2DB =,2222AP λλ=-+,设1A P 与BD 所成角为θ,则()22221211cos 2121DB APDB AP λλθλλλλ⋅--===-+⋅-+221313442121324λλλ=-=--+⎛⎫-+⎪⎝⎭12λ=时,cos θ取得最小值为0, 当0λ=或1时,cos θ取得最大值为12,10cos 2θ∴≤≤,则32ππθ≤≤.故选C .16、如图,矩形ABCD 中,222AB AD ==E 为边AB 的中点,将ADE 沿直线DE 翻折成1A DE △.在翻折过程中,直线1A C 与平面ABCD 所成角的正弦值最大为( )A .1024- B .66C .514-D .55【答案】A【解析】分别取DE ,DC 的中点O ,F ,则点A 的轨迹是以AF 为直径的圆, 以,OA OE 为,x y 轴,过O 与平面AOE 垂直的直线为z 轴建立坐标系,则()2,1,0C -,平面ABCD 的其中一个法向量为n = (0,0.1), 由11A O =,设()1cos ,0,sin A αα,则()1cos 2,1,sin CA αα=+-, 记直线1A C与平面ABCD 所成角为θ,则211|sin 1cos sin 4cos 64cos 6||CA nCA n αθαα⋅-===++⋅,设3153535102cos ,,sin 222416444t t t αθ-⎡⎤⎛⎫=+∈=-+≤-=⎪⎢⎥⎣⎦⎝⎭ 所以直线1A C 与平面ABCD 所成角的正弦值最大为1024-,故选A . (多选)17、在正方体1111ABCD A B C D -中,若棱长为1,点,E F 分别为线段11B D 、1BC 上的动点,则下列结论正确结论的是( )A .1DB ⊥面1ACD B .面11//AC B 面1ACDC .点F 到面1ACD 的距离为定值33D .直线AE 与面11BB D D 所成角的正弦值为定值13【答案】ABC【分析】以A 为坐标原点建立空间直角坐标系,利用共线向量可表示出动点,E F 的坐标,利用空间向量判断线面垂直、面面平行、求解点到面的距离和直线与平面所成角的方法依次验证各个选项即可得到结果.【解析】以A 为坐标原点可建立如下图所示的空间直角坐标系:由题意知:()0,0,0A ,()1,0,0B ,()1,1,0C ,()0,1,0D ,()10,0,1A ,()11,0,1B ,()11,1,1C ,()10,1,1D ,设(),,1E x y ,111B E B D λ→→=,即()()1,,0,,0x y λλ-=-,()1,,1E λλ∴-, 设()1,,F y z '',1BF BC μ→→=,即()()0,,0,,y z μμ''=,()1,,F μμ∴. 对于A ,()11,1,1DB →=-,()1,1,0AC →=,()10,1,1AD →=,11100DB AC DB AD ⎧⋅=⎪∴⎨⋅=⎪⎩,1DB AC ∴⊥,11DB AD ⊥, 又1,AC AD ⊂平面1ACD ,1AC AD A =,1DB ∴⊥平面1ACD ,A 正确;对于B ,1DB ⊥平面1ACD ,()11,1,1DB →∴=-为平面1ACD 的一个法向量,()111,1,0A C →=,()11,0,1A B →=-,111110DB A C DB A B ⎧⋅=⎪∴⎨⋅=⎪⎩,111DB AC ∴⊥,11DB A B ⊥, 又111,A C A B ⊂平面11A C B ,1111AC A B A =,1DB ∴⊥平面11A C B ,∴平面11//AC B平面1ACD ,B 正确;对于C ,()1,,AF μμ→=,∴点F 到面1ACD 的距离111333AF DB d DB →→→⋅===,为定值,C 正确;对于D ,几何体为正方体,AC ∴⊥平面11BB D D ,()1,1,0AC →∴=是平面11BB D D 的一个法向量,又()1,,1AE λλ→=-,设直线AE 与平面11BB D D 所成角为θ,则21sin 2222AC AEAC AEθλλ→→→→⋅==⋅-+⋅,不是定值,D 错误.故选ABC .(多选)18、如图所示,正方体1111ABCD A B C D -中,1AB =,点P 在侧面11BCC B 及其边界上运动,并且总是保持1AP BD ⊥,则以下四个结论正确的是( )A .113P AA D V -=B .点P 必在线段1BC 上 C .1AP BC ⊥D .//AP 平面11AC D【答案】BD【分析】根据三棱锥体积公式求得116P AA D V -=,知A 错误;以D 为坐标原点建立空间直角坐标系,利用空间向量法可得到1CP x B C →→=-,11AP BC →→⋅=,AP →垂直于平面11AC D 的法向量n →,由此可确定,,B C D 的正误.【解析】对于A ,P 在平面11BCC B 上,平面11//BCC B 平面1AA D ,P ∴到平面1AA D 即为C 到平面1AA D 的距离,即为正方体棱长,1111111113326P AA D AA D V S CD -∴=⋅=⨯⨯⨯⨯=△,A 错误;对于B ,以D 为坐标原点可建立如下图所示的空间直角坐标系:则()1,0,0A ,(),1,P x z ,()1,1,0B ,()10,0,1D ,()11,1,1B ,()0,1,0C()1,1,AP x z →∴=-,()11,1,1BD →=--,()11,0,1B C →=--,1AP BD ⊥,1110AP BD x z →→∴⋅=--+=,x z ∴=,即(),1,P x x ,(),0,CP x x →∴=,1CP x B C →→∴=-,即1,,B P C 三点共线,P ∴必在线段1B C 上,B 正确; 对于C ,()1,1,AP x x →=-,()11,0,1BC →=-,111AP BC x x →→∴⋅=-+=,AP ∴与1BC 不垂直,C 错误;对于D ,()11,0,1A ,()10,1,1C ,()0,0,0D ,()11,0,1DA →∴=,()10,1,1DC →=,设平面11AC D 的法向量(),,n x y z →=,1100n DA x z n DC y z ⎧⋅=+=⎪∴⎨⋅=+=⎪⎩,令1x =,则1z =-,1y =,()1,1,1n →∴=-, 110AP n x x →→∴⋅=-+-=,即AP n →→⊥,//AP ∴平面11ACD ,D 正确.故选BD . (多选)19、如图所示,棱长为1的正方体1111ABCD A B C D -中,P 为线段1A B 上的动点(不含端点),则下列结论正确的是( )。
2020届高考数学(理科)大题高分突破3 解析几何中的最值问题(理) 含解析

解析几何中的最值问题例1.已知在平面直角坐标系xOy 中的一个椭圆,中心在原点,左焦点为(2,0)F -,上顶点为(0,2)D , 设点(2,1)A .(1)求该椭圆的标准方程;(2)过原点O 的直线交椭圆于点B ,C ,求ABC △面积的最大值.【答案】(1)22184x y +=;(2)最大值是4. 【解析】(1)由已知得2b =,2c =,则22a =,又椭圆的焦点在x 轴上,所以椭圆的标准方程为22184x y +=. (2)当直线BC 垂直于x 轴时,4BC =,因此ABC △的面积22ABC S =△;当直线BC 不垂直于x 轴时,该直线方程为y kx =,代入22184x y +=, 解得222222(,)2121k B k k ++,222222(,)2121k C k k --++,则2242221k BC k +=+,精选大题又点A 到直线BC的距离d∴ABC △的面积12ABC S BC d =⋅=△,于是ABC S ==△.由211221k kk +=≥-+,得4ABC S ≤△,其中当k =时,等号成立. ∴ABC S △的最大值是4.例2.在平面直角坐标系中,顶点为原点的抛物线C ,它是焦点为椭圆22143x y +=的右焦点. (1)求抛物线C 的标准方程;(2)过抛物线C 的焦点作互相垂直的两条直线分别交抛物线C 于,,,A B P Q 四点,求四边形ABPQ 的面积的最小值.【答案】(1)24y x =;(2)最小值为32.【解析】(1)椭圆22143x y +=的右焦点为(1,0), 所以抛物线的焦点为(1,0),顶点为原点,抛物线的方程为24y x =.(2)由(1)知,抛物线C 的焦点是()1,0,设直线():10AB x my m =+≠,则直线1:1PQ x y m=-+, 联立214x my y x=+⎧⎨=⎩,消去x ,得2440y my --=, 设()11,A x y ,()22,B x y ,则124y y m +=,124y y =-,所以2121222244AB x x my my m =++=+++=+,设点()33,P x y ,()44,Q x y ,同理可得244PQ m=+, 所以()2222114844416822APBQ S AB PQ m m m m ⎛⎫=⋅=++=++ ⎪⎝⎭四边形 228162832m m≥+⋅=, 当且仅当2288m m =,即1m =±时等号成立. 即四边形APBQ 的面积的最小值为32.1.已知椭圆22221(0)x y a b a b +=>>,短轴长为2,且过点3(2,). (1)求椭圆方程;(2)设直线l 为圆221:x C y +=的切线,且与椭圆交于,A B 两点,求AB 的最大值.模拟精做2.已知椭圆2222:1x y C a b+=(0a b >>)的焦距与短轴等长,长轴长为 (1)求椭圆C 的标准方程;(2)设直线l 与x 轴交于点(1,0)D -,与椭圆交于,M N 两点,求OMN △的面积的最大值.1.【答案】(1)2213x y +=;(2)最大值为3. 【解析】(1)椭圆短轴长为2,∴1b =,把点3(2,)3代入222+1x y a =,解得3a =, 所以椭圆的标准方程为2213x y +=. (2)由已知,切线l 与x 轴不平行,所以设直线:l x my n =+, 由直线l 与圆相切得211nm =+,221n m =+,设()11,A x y ,()22,B x y ,联立方程22+13x x m n y y ⎧⎪⎨⎪=+⎩=,得2223023()m m y ny n ++-+=,0Δ>,12223mn y y m -+=+,212233n y y m -=+. 所以2222121222221()41()4(33)3n m mn AB m y y y y m m -=++-⋅=+-+-+222613m m ++=, 因为22222222(1)23[]232(13)2612333m m m m m m +++++≤++==, 当且仅当221m =+,即1m =±时取等号,所以AB 的最大值为3.2.【答案】(1)2212x y +=;(2)最大值为22. 答案与解析【解析】(1)由题意得2222a b c a b c ⎧=+⎪⎪=⎨⎪=⎪⎩,解得11a b c ⎧=⎪=⎨⎪=⎩, 椭圆的方程为2212x y +=. (2)当直线l 与y 轴垂直时,OMN △的面积为0;设直线l 的方程为1x my =-,代入椭圆的方程22121x y +=, 有()222210m y my +--=,设()11M x y ,,()22N x y ,,12222m y y m +=+由韦达定理:,12212y y m -=+,1212OMN S OD y y =-===△, ()1t t =≥,则有221m t =-,代入上式有221212OMN S m t t t===≤+++△, 当且仅当1t =,即0m =时等号成立,所以OMN△的面积的最大值为2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
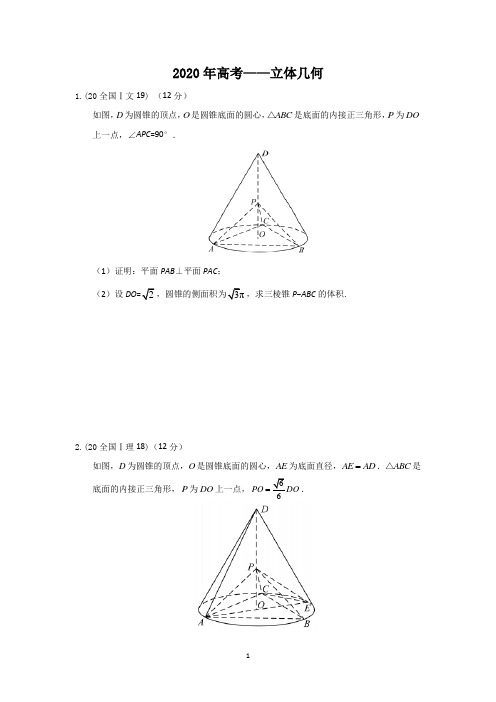
第 1 页 共 4 页 2020年高考数学满分突破:立体图形中的动点问题
1. 已知正方体1111ABCD A B C D -的棱长为a ,定点M 在棱AB 上(但不在端点A ,B 上),点P 是平面ABCD 内的动点,且点P 到直线11A D 的距离与点P 到点M 的距离的平方差为2a ,则点P 的轨迹所在曲线为( )
A. 抛物线
B. 双曲线 C . 直线 D. 圆
2. 如图,已知平面l αβ=,A 、B 是l 上的两个点,C 、D 在平面β内,且AD α⊥,
BC α⊥4AD =,6AB =,8BC =,
在平面α上有一个动点P ,使得APD BPC ∠=∠,则四棱锥P ABCD -体积的最大值是 。
3. 已知正方体1111ABCD A B C D -的棱长为1,点P 是底面ABCD 内的动点,若点P 到直线11A D 的距离等于点P 到直线CD
倍,则动点P 的轨迹所在的曲线是( )
A. 抛物线
B. 双曲线
C. 椭圆
D. 直线
4. 已知正方体1111ABCD A B C D -的棱长为1,动点P 在正方体1111ABCD A B C D -表面上运动,且AP r =
(0r <<,记点P 的轨迹的长度为()f r ,则1
()2
f =______;关于r 的方程()f r k =的解的个数可以为_______________(填上所有可能的值)。
5. 已知棱长为2的正方体ABCD A B C D -1111中,长为2的线段MN 的一个端点M 在DD 1上运动,另一个端点N 在底面ABCD 上运动,求MN 中点P 的轨迹与正方体的面所围成的几何体的体积。
参考答案。
