数学建模 对偶问题和灵敏度分析资料讲解
大纲解读第三章对偶问题与灵敏度分析

2、领会:(1)对称性,(2)弱对偶性,(3) 无界性,(4)强对偶定理,(5)互补松弛性定理 及其应用。
3、应用:运用互补松弛性定理求解线性规划问题。
(三)对偶解的经济解释
1、识记:(1)对偶解与影子价格,(2)影子价 格的特点。
一、考核知识点 (一)对偶模型 (二)对偶性质 (三)对偶解的经济解释 (四)灵敏度分析
பைடு நூலகம்
(一)对偶模型 1、识记:(1)原问题与对偶问题的关系,(2)
对偶问题的转换。 2、领会:(1)研究对偶问题的原因, (2)原问题与对偶问题的关系。
(二)对偶性质
1、识记:(1)对偶问题的对偶就是原问题,(2) 弱对偶性,(3)对偶(原)问题无可行解则原 (对偶)问题不可能有最优解,(4)对偶(原)
2、领会:影子价格的经济指导意义和管理决策价 值。
3、应用:怎样利用影子价格改善经营策略。
(四)敏感性分析
1、识记:(1)约束方程右边项变化的敏感分析, (2)增加新的决策变量的敏感性分析,(3)目标 函数系数变化的敏感性分析,(4)投入或技术系 数变化的敏感性分析。
2、领会:(1)敏感性分析的意义及其必要性, (2)如何进行敏感性分析。
对偶问题与灵敏度分析课件

第一讲 对偶理论 第二讲 灵敏度分析
对偶问题与灵敏度分析
第一一讲、对偶对问偶题 理论
车间
产品 工时单耗
甲
乙
生产能力
A
1
0
8
B
0
2
12
C
3
4
36
单位产品获利 3
5
• 例1中该厂的产品销售,现有另一企业想租赁其设备。 厂方为了在谈判时心中有数,需掌握设备台时费用的 最低价码,以便衡量对方出价,对是否出租做出抉择。
• 对偶问题的最优解: y1=0,y2=1/2,y3=1 对应于原问题最优 单纯型法表中,初始基变量x3 , x4 , x5的检验数的负值。
对偶问题与灵敏度分析
对称形式下对偶问题的一般形式
对称形式:变量均为非负,其约束条件当目标函数求极
大时均取“≤”,当目标函数取极小时均取“≥”。
线性规划原问题(P)
S.t. 4x1 +x2 - x3 ≤10 x1 + x2 - x3 = 4 x1 ≥0, x2 ≤0, x3 无限制
Max W= 5y1+10y2+4y3
S.t.
y1+ 4y2+ 1y3 ≤ 5 -y1+ y2+ y3 ≥ 3
2y1 - y2 - y3 =-1
y1≥0, y2≤0, y3 无限制
对偶问题与灵敏度分析
• 问题 ①的最优解:x1=4,x2=6,Z*=42。
对偶问题与灵敏度分析
第一讲 对偶理论 第二个问题:出让定价
• 假设出让设备A、B、C所得利润分别为y1、y2、y3
• 原本用于生产甲产品的设备台时,如若出让,不应低于自行生 产带来的利润,否则宁愿自己生产。于是有对甲产品
对偶理论及灵敏度分析

问 题 的 导 出
工 时 材 料 单件利润
1 1 2
•出卖资源获利应不少于生产产品的获利; 约束 •价格应该尽量低,这样,才能有竞争力; 目标
•价格应该是非负的
A
B
1
4 3
C
1
7 3
拥有量
问 题 的 导 出
工 时 材 料 单件利润
1
1 2
3
9
用y1和y2分别表示工时和材料的出售价格 总利润最小 保证A产品利润 min W=3y1+9y2 y1+y2≥2
保证B产品利润
保证C产品利润
y1+4y2≥3
y1+7y2≥3
售价非负
y1≥0
y2≥0
A
B
1
4 3
C
1
7 3
拥有量
问 题 的 导 出
工 时 材 料 单件利润
1
1 2
3
9
minW 3 y1 9 y2
y1 y 2 2 y 4y 3 1 2 s.t. y1 7 y 2 3 y1 0, y 2 0
对 称 形 式 的 对 偶 问 题
max Z CX
对 偶 问 题 的 定 义
AX b s.t. X 0
minW b Y
T
T
T T T A Y C s.t. T Y 0
或 min Yb
YA C s.t. Y 0
对 称 形 式 的 对 偶 问 题
4 y1 8 y 2 12 y 3 4 5 y 9 y 13y 2 1 2 3 3 6 y1 10 y 2 y1符号不限, y 2 0, y 3 0
对偶理论与灵敏度分析课件

航空航天领域
飞机和航天器的设计过程中需要 对气动性能、结构性能等进行灵
敏度分析,以优化设计方案。
机械工程领域
在机械设计中,需要对机构性能 、动力学特性等进行灵敏度分析 ,以提高机械设备的性能和稳定
性。
环境工程领域
在环境治理和生态保护方面,需 要对污染物扩散、水体自净等进 行灵敏度分析,以制定有效的环
详细描述
在机器学习中,我们通常会使用各种模型来预测未知数据。对偶理论和灵敏度分析可以 帮助我们理解这些模型的预测能力和泛化性能。例如,通过对偶理论,我们可以将一个 复杂的模型转化为一个更简单的模型,从而更容易理解和使用。同时,灵敏度分析可以
用来研究模型参数变化对预测结果的影响,从而更好地调整模型参数。
详细描述
在优化问题中,对偶理论可以将原问题转化为一个等价的优 化问题,有时这个新问题可能更容易求解。同时,灵敏度分 析可以用来研究原问题的参数变化对最优解的影响,从而更 好地理解问题的性质和最优解的稳定性。
金融问题中的对偶与灵敏度分析
总结词
在金融领域,对偶理论和灵敏度分析可 以用于风险评估、投资组合优化等问题 。
对偶理论的应用场景
资源分配问题
对偶理论可以应用于资源分配问 题,通过求解对偶问题来获得最
优解。
运输问题
对偶理论可以应用于运输问题,通 过求解对偶问题来获得最优解。
投资组合优化
对偶理论可以应用于投资组合优化 问题,通过求解对偶问题来获得最 优解。
02
灵敏度分析简介
灵敏度分析的定义
01
灵敏度分析是指对系统参数变化 引起系统性能变化的程度进行分 析,旨在了解系统对参数变化的 敏感程度。2
灵敏度分析算法的改进
3对偶问题与灵敏度分析解析

max z=70x1+120x2 s.t. 9x1+4x2≤360
4x1+5x2≤200 3x1+10x2≤300 x1,x2≥0
对偶的定义
(LP) Max z = CX (DP) Min w = Yb
s.t. AX ≤ b
s.t. YA ≥ C
X≥0
Y≥0
若一个问题的某约束为等式, 那么对应的对偶问题的相应变量无非负限制; 反之, 若一个问题的某变量无非负限制, 那么对应的对偶问题的相应约束为等式。
影子价格非资源的市场价格,而是指系统达到 最优状态时,资源的单位变化引起目标最优值的变化
什么是对偶单纯形法?
对偶单纯形法是求解线性规划的另一的基本方法。 它是根据对偶原理和单纯形法的原理而设计出来的, 因此称为对偶单纯形法。不要简单理解为是求解对偶 问题的单纯形法。
由对偶理论可以知道,对于一个线性规划问题,我 们能够通过求解它的对偶问题来找到它的最优解。
运筹学 ——第3章 对偶问题与灵敏度分析
本讲内容
什么是对偶问题 单纯形法的矩阵描述 对偶问题的性质 线性规划的灵敏度分析
什么是对偶问题?
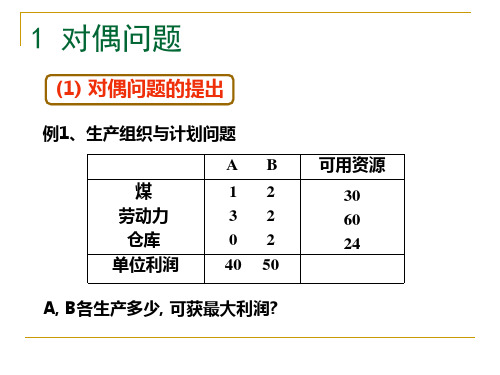
对偶问题的提出
考虑上一讲的生产计划问题,若设备和原料都用 于对外加工,工厂收取加工费。试问:该厂设备 工时、劳动力和原料该如何定价?
显然,工厂给这些生产要素定价,既要保证自己的利益, 又要使自己的价格具有竞争力
原问题(或对偶问题)
目标函数 max
约
m个
束
≤
条
≥
件
=
n个
变
≥0
量
≤0
无约束
约束条件右端项
目标函数变量的系数
ch2对偶与灵敏度分析

机会成本
a y + a y +⋯+ a y +⋯+ a y
1j 1 2j 2 ij i mj
m
表示减少一件产品所节省的资源可以增加的利润
13
(3)对偶松弛变量的经济解释——产品的差额成本(Reduced Cost)
机会成本 差额成本
m m
min w = b y s.t. ay
(2)对偶约束的经济解释——产品的机会成本 (Opportunity Cost)
增加单位资源可以增加的利润
m z = c1x1 ax s.t.
+ c2x2 ⋯ + cjx j ⋯ + cn xn
a11x1 + a12x2 ⋯ + a1jx j ⋯ + a1nxn ≤ b1 y1 a21x1 + a22x2 ⋯ + a2jx j ⋯ + a2nxn ≤ b2 y2 ⋯ ⋯⋯ ⋯⋯ ⋯ ⋯ am1 x1 + am2 x2 ⋯ + amj x j ⋯ + amn xn ≤ bm ym x1 x2 ⋯ xj ⋯ xn ≥0
16
2. 若计算原问题的单纯形终 表如下
Cj CB 12 5 XB X2 X1 σ(σj≤0?) B-1b 8/5 9/5 5 X1 P1 0 1 0 12 X2 P2 1 0 0 4 X3 P3 -1/5 7/5 -3/5 0 X4 P4 2/5 1/5 -29/5 -M X5 P5 -1/5 2/5 -M+2/5 θ
问原问题的最优解和对偶模型的最优解. 问原问题的最优解和对偶模型的最优解 3. 原问题的最优基的逆矩阵B-1 原问题的最优基的逆矩阵 4. 当两种资源分别单独增加一个单位 目标函数值分 当两种资源分别单独增加一个单位,目标函数值分 别增加多少? 别增加多少
对偶问题与灵敏度分析

第一讲 对偶理论
解释例1的对偶问题的数学模型
Max Z= 3x1 +5 x2
x1
≤8
S.t.
2x2 ≤12 3x1 +4 x2 ≤36
x1 , x2 ≥0
第一讲 对偶理论
一、对偶问题
• 对原企业而言,它用于出租或转让的资源收益不应 低于自行生产产品所获得的利润,才肯出租或转让。
• 在这个问题上厂长面临着两种选择:自行生产或出 租设备。首先要弄清两个问题:
①如何合理安排生产,取得最大利润? ②为保持利润水平不降低,资源转让的最低价格是多少?
• 问题 ①的最优解:x1=4,x2=6,Z*=42。
(3) 按照θ=Min{j /alj | alj<0 }= k /alk确定xk进基变量。 (4) 以alk为主元素,按单纯形法的方法进行迭代,得到新的表重复
(2).
第一讲 对偶理论
例题:使用对偶单纯形法
• Min W= 8y1+12y2+36y3
y1 + 0y2 + 3y3 ≥ 3 S.t. 0y1 + 2y2 + 4y3 ≥ 5
此时,同时达到最优解
j 1
i 1
Z bi
*
yi*
bi为第i种资源的拥有量
• 说明yi是右端项bi每增加一个单位的第i种资源对目标函数Z的贡献。 • 对偶变量 yi在经济上表示原问题第i种资源的边际价值。
• 对偶变量的值 yi*所表示的第i种资源的边际价值,称为影子价值。
对偶理论与灵敏度分析(1)

17
对偶定理
是揭示原始问题的解与对偶问 题的解之间重要关系的一系列定理。
18
2.4.4 对偶单纯形法
什麽是对偶单纯形法? 对偶单纯形法是应用对偶原理求解原始 线性规划的一种方法——在原始问题的单 纯形表格上进行对偶处理。 注意:不是解对偶问题的单纯形法!
19
2.4.4 对偶单纯形法
1、两种方法的特点 单纯形法特点:在保持基可行解的情况下,
显然:对称形式的对偶问题,若已知其中 一个问题,立即就可以写出相应的对偶问 题。
11
表2.13 对偶变换的规则
原问题 (max)
技术系数矩阵 A 价值系数 C 右端项 b
第 i 行约束条件为 型 第 i 行约束条件为 型 第 i 行约束条件为 = 型
决策变量 xj 0 决策变量 xj 0 决策变量 xj 不限
0 J
1/6 -1/6 0
[-2/3] -1/3 1
1 40
0 -1/4 1/4
1 1/2 -3/2
w
-17/2 15/2 0
0 2/7 3/2 25
原问题的最优解为(0,1/4,1/2),最优值为17/2
由上例得结论:
(1)当约束条件为“≥”时,不必引进人工变量, 使计算简化。
(2)由对偶问题的性质知道:用单纯形法求解L.P 问题时,每一次迭代可得一个基解,这时检验数 行的数是对偶问题的一个基解。原问题的松驰变 量对应着对偶问题的决策变量,对偶问题的松驰 变量对应着原问题的决策变量。在一个问题中是 基变量,则在另一个问题中就是非基变量 ,反之 亦然。
• (一)对称形式的对偶问题 • 比较上述的两个互为对偶问题:
max Z 3x1 5x2 4x3
2x1 3x2 1500 s.t. 2x2 4x3 800
第二章 对偶问题和灵敏度分析1
1
1 2
2
y1 y3
x 2x 2 可直接寫出此問題的對偶問題如下:
1 2
7 x1 6 x2 42 y2
x1 0, x2 0
D:Max y0 32 y1 42 y2 2 y3 可直接寫出此問題的對偶問題如下: :Max y x 32 s.t. 4 y1 7 y2 y3 D10 1 y 42 y 2 y
W = 30y1 + 60 y2 + 24y3
根据原则2 ,对方能够接受的价格显然是越低越好,因此 此问题可归结为以下数学模型:
目标函数 Min W = 30y1 + 60 y2 + 24y3 y1 + 3y2 约束条件 s.t y1 , y2 , y3 0 原线性规划问题称为原问题,此问题为对偶问题, y1 , y2 , y3 称为影子价格
y,,v v))是 行解, , ((y 是D D的可行解。 的可行解。 这两个 x,,s s) )是 令 令((x 是P P 的可 的可行解 这两个 可行 且只当 只当 可行解均为 解均为最佳 最佳解当 解当且 0 ii yi sii 0
x jjv jj 0 0 jj
原始问题的变量
极个别(B)
数学建模---对偶问题和灵敏度分析

对偶问题例题1:某养鸡场所用的混合饲料由n 种天然饲料配合而成。
要求在这批配合饲料中必须含有m 种不同的营养成分,且第i 种营养成分的含量不低于bi 。
已知第i 种营养成分在每单位第j 种天然饲料中的含量为a ij ,每单位第j 天然饲料的价格为c j 。
试问,应如何对这n 种饲料配方,使这批饲料的费用最小? 解 设x j 为第j 种天然饲料的用量。
显然,a ij x j 即为所用第j 种天然饲料中第i 种营养成分的含量,1nij j j a x =∑为这批混合饲料中第i 种营养成分的总含量;它不应低于bi 。
于是,我们得下列线性规划模型(1—1):1min nj jj f c x ==∑11,,..01,,nij j i j j a x b i m s t x j n=⎧≥=⎪⎨⎪≥=⎩∑现设想有一个饲料加工厂欲把这m 种营养成分分别制成m 种营养丸。
设第i 种营养丸的价格为ui(i =1,…,m)。
则养鸡场采购一个单位的第j 种天然饲料,就相当于对这m 种营养丸分别采购数量a 1j ,…a mj ,所化费用为1mij ii a u =∑养鸡场自然希望在用营养丸代替天然饲料时,在价格上能相对地比较便宜,故而饲料加工厂为了能与天然饲料供应者竞争,在制订价格时必然满足下述条件:11,,mij ij i a uc j n =≤=∑另一方面,养鸡场如果全部采购营养丸来代替天然饲料进行配料,则第i 种营养丸就需采购bi 个单位,所化费用为b i u i ,总费用为z=∑b i u i饲料加工厂面临的问题是:应把这m 种营养丸的单价ui(f=1,…,m)定为多少,才能使养鸡场乐意全部采用该厂生产的营养丸来取代这批天然饲料,且使本厂在竞争中得到最大收益。
为该问题建立数学模型,即得如下线性规划(1—2):1max mi i i z b u ==∑11,,..01,,mij i j i ia u c j n s t u i m =⎧≤=⎪⎨⎪≥=⎩∑我们称问题(1—2)为原有问题 (1—1)的对偶问题(记为(D))。
对偶理论和灵敏度分析(新)

W=Y’b=CBB-1b=Z
所以当原问题为最优解时,对偶问题为可行解且具有相 同的目标函数值。
非对称形式的原—对偶问题
minz=2x1+3x2-5x3+x4 s.t. x1+x2-3x3+x4≥5 2x1 +2x3-x4≤4 x2+x3+x4=6 x1≤0,x2,x3≥0
x2+x3+x4≥6 x2+x3+x4≤6
A(3,0)
B(1.8,0.4)
C(0,4)
D(2,2)
可行解
z
最优解
A
6
B
4.8
是
C
12
D
10
3 2 1
A(1,0)
B(0.8,0.6)
C(0,1)
O(0,0)
可行解
w
最优解
O
0
A
3
B
4.8
是
C
4
单纯形法计算的矩阵描述
Max Z=CX AX≤b
Max Z=CX+0Xs AX+IXs=b
I 为m×m的单位矩阵
≤
≥
=
≥
Free
≤
≥
≥
=
≤
≥
x1≥0
x2≤0
x3: Free
原始问题变量的个数(3)等于对偶问题约束条件的个数(3); 原始问题约束条件的个数(4)等于对偶问题变量的个数(4)。 原始问题变量的性质影响对偶问题约束条件的性质。 原始问题约束条件的性质影响对偶问题变量的性质。
*
写对偶问题的练习(2)
原始和对偶问题可行解目标函数值比较
对偶问题与灵敏分析

y1,y2,… ,ym ≥0
y1,y2,… ,ym ≥0
原问题为:
Max Z= c1x1+c2x2+…+cnxn Min (-Z)= -c1x1-c2x2-…-cnxn
a11x1 + a12x2+…+a1n xn ≤ b1 a21x1 + a22x2+…+a2n xn ≤ b2
MaxZ(X)= 2x2-5x3
y1 -x1
-x3 ≤- 2
y2 2x1 + x2+6x3 ≤ 6
y3/
x1 - x2+3x3 ≤ 0
y3// -x1 + x2-3x3 ≤ 0
x1,x2,x3≥0
其对偶问题为:
Min W(y)= -2y1+6y2
x1
-y1 +2y2 +y3/ -y3//
≥x02
y2 -y3/ +y3// ≥2
4
4 x4
6
x1 0, x2 , x3 0, x4无限制
s.t约无2变y束符1y量4方号y1≤1y≥程约01003≤束7,≥=2yyy13y22y22约40y束y3无,332变y方y符3y3量程号无31≥≥≤≤约=00限53束2制
2.1.4对偶问题的基本性质
以对称型为例
设原问题(P)为 其对偶问题(D)为
无符号约束
约束方程≥ ≤
=
原问题( P)为
对偶规划问题(D)为:
max z c1x1 c2 x2 c3 x3 c4 x4
s.t aa2111xx11
a12 x2 a22 x2
a13 x3 a23 x3
a14 x4 a24 x4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模对偶问题和灵敏度分析
对偶问题
例题1:某养鸡场所用的混合饲料由n 种天然饲料配合而成。
要求在这批配合饲料中必须含有m 种不同的营养成分,且第i 种营养成分的含量不低于bi 。
已知第i 种营养成分在每单位第j 种天然饲料中的含量为a ij ,每单位第j 天然饲料的价格为c j 。
试问,应如何对这n 种饲料配方,使这批饲料的费用最小? 解 设x j 为第j 种天然饲料的用量。
显然,a ij x j 即为所用第j 种天然饲料中第i 种营养成分的含量,1n
ij j j a x =∑为这批混
合饲料中第i 种营养成分的总含量;它不应低于bi 。
于是,我们得下列线性规划模型(1—1):
1
min n
j j
j f c x ==∑
1
1,,..01,,n
ij j i j j a x b i m s t x j n
=⎧≥=⎪⎨⎪≥=⎩
∑
现设想有一个饲料加工厂欲把这m 种营养成分分别制成m 种营养丸。
设第i 种营养丸的价格为ui(i =1,…,m)。
则养鸡场采购一个单位的第j 种天然饲料,就相当于对这m 种营养丸分别采购数量a 1j ,…a mj ,所化费用为1m
ij i i a u =∑养
鸡场自然希望在用营养丸代替天然饲料时,在价格上能相对地比较便宜,故而饲料加工厂为了能与天然饲料供应者竞争,在制订价格时必然满足下述条件:
1
1,
,m
ij i
j i a u
c j n =≤=∑
另一方面,养鸡场如果全部采购营养丸来代替天然饲料进行配料,则第i 种营养丸就需采购bi 个单位,所化费用为b i u i ,总费用为z=∑b i u i
饲料加工厂面临的问题是:应把这m 种营养丸的单价ui(f=1,…,m)定为多少,才能使养鸡场乐意全部采用该厂生产的营养丸来取代这批天然饲料,且使本厂在竞争中得到最大收益。
为该问题建立数学模型,即得如下线性规划(1—2):
1
max m
i i i z b u ==∑
1
1,,..01,,m
ij i j i i
a u c j n s t u i m =⎧≤=⎪⎨⎪≥=⎩∑
我们称问题(1—2)为原有问题 (1—1)的对偶问题(记为(D))。
,n
影子价格(Shadow Price )
例题2:某工厂计划在下一生产周期生产
3种产品A 1, A 2, A 3,这些产品都要在甲、乙、丙、丁4种设备上加工,根据设备性能和以往的生产情况知道单位产品的加工工时、各种设备的最大加工工时限制,以及每种产品的单位利润,如下表。
问如何安排生产计划,才能使工厂得到最大利润?
解:设x1, x2, x3为产品A1, A2, A3的产量
线性规划模型为:
Max f=8x1+10x2+2x3
s.t. 2x1+x2+3x3≤70
4x1+2x2+2x3≤80
3x1 + x3≤15
2x1+2x2 ≤50
最优单纯形表为:
最优方案为:x1=0,x2=25, x3=15, x4=0
最大利润为280千元
现在从另一个角度来讨论问题
假设工厂考虑不安排生产,而准备将所有设备出租,收取租费。
于是需要为每种设备的台时进行估价。
设y1, y2, y3, y4分别表示甲、乙、丙、丁4种设备的台时估价。
由例1中的表可知,生产一件产品A1需要各设备台时分别为2h,4h,3h,2h,如果将2h,
4h ,3h ,2h 不用于生产产品A 1,而是用于出租,租费应满足(为了不蚀本,租费不能少于利润) 2 y 1+4y 2+3 y 3+2 y 4≥8,依次可分析得线性规划模型如下
123412341
23123
12370801550243282210..322,,0
Min f y y y y y y y y y y y s t y y y y y y =++++++≥⎧⎪++≥⎪⎨++≥⎪⎪≥⎩
说明:企业为了能够得到租用设备的用户,使出租设备的计划成交,在价格满足约束条件下,应将设备价格定得尽可能低(why ?)
最优解:y 1=2/3, y 2=0, y 3=0, y 4=14/3 最小租费:280千元 定义:
,n
设***
*12ˆ(,,,)T
m y
y y y =为对偶问题(D )的最优解,则称*i y 为原有问题(P )
第i 个约束对应的影子价格(Shadow Price )
由例2知*i y 是对第i 种资源(设备台时)的一种估价,这个价格不是市场价格,而是针对具体企业在一定时期内存在的一种特殊价格,它蕴含在求最大利润的生产计划模型中。
影子价格的经济含义:
(1)影子价格是对现有资源实现最大效益的一种估价。
根据例2的讨论,企业可以根据现有资源的影子价格,对资源的使用有两种考虑:第一,是否将设备用于外加工或出租,若租费高于某设备的影子价格,可考虑出租该设备,否则不宜出租;第二,是否将投资用于购买设备,以扩大生产能力,若市价低于某设备的影子价格,可考虑买进该设备,否则不宜买进。
(2)影子价格表明资源增加对总效益产生的影响。
易见有
****
*
1122m m f z b y b y b y ==++
+
从而,如果i b 增加一个单位,目标函数值的增量将是*i y ,据此,由影子价格的大小可以知道哪种资源的增加可以给企业带来较大的收益。
如例2中四种设备的影子价格分别为2/3,0,0,14/3,因此,在同样的条件下,增加设备丁是最有利的,不应增加设备乙和丙。
例3:某外贸公司准备购进两种产品A 1, A 2。
购进产品A 1每件需要10元,占用5m 3的空间,待每件A 1卖出后,可获纯利润3元;购进产品A 2每件需要15元,占用3m 3的空间,待每件A 2卖出后,可获纯利润4元。
公司现有资金1400元,有430 m 3的仓库空间存放产品,从而可得线性规划模型如下:
12
1212123410151400
..53430,0Max z x x x x s t x x x x =++≤⎧⎪
+≤⎨⎪≥⎩ 最优单纯形表
最优方案:x 1=50,x 2=60
最大利润:390
现在公司有另外一笔资金585元,准备用于投资,到底是购买产品呢?还是增加仓库容量?(假设增加1m3的仓库空间需要0.8元)
由上表知,仓库的影子价格y2=1/9,即增加1m3的仓库空间,公司可多获利1/9元,又增加1m3的仓库空间需要0.8元,从而,每增加1元投资可多获利
10/72元,近似为0.14元;购买产品的资金的影子价格y1=11/45,每增加1元购买产品可多获利11/45元,近似为0.24元。
因此,投资应该用于购买产品而不是增加仓库容量。
585元进行投资之后,最大利润为585 y1=143元(???????)
灵敏度分析(Sensitivity Analysis)
最优解是在参数cj、bi、aij都固定不变的条件下取得的。
但是,在实际问题中,对一个具体的企业来说,参数cj、bi、aij不是固定不变的。
例如,产品的市场价格可能有所变动;国家分配的原材料可能有所增减;动力供应情况可能随季审而变化f添置新设备而使生产台时增加;由于产品设计结构有所改进,使单位产品的原材料消耗定额有所增减……,现实诸因素的种种变化都会引起已建立的数学模型的参数变化。
或者,当运用线性规划编制完生产计划并即将付诸应用时,又发生了新的情况,某些原来未加限制的资源现在有了限制,从而出现一个新的追加约束条件。
或者,企业准备增加新产品,使工厂的生产计划发生整个变化。
从而,我们面临这样的问题:上述种种情况的发生,将对已求得的最优解产生什么影响?或者说,我们如何在原有的最优单纯形表的基础上用最少的计算量,去获得修改后的线性规划问题的最优解?这就是下面我们要讨论的灵敏度分析问题。
一般分下面几个问题来进行灵敏度分析(Sensitivity Analysis):
1.变量x s的目标函数系数c s在何范围内变动,问题(LP)的最优基(最优解)不变?如果超出这个范围,如何求最优解?
2.第s种资源bs在何范围内变动,最优基不变?如果bs超出这个范围,如何求最优解?
3.变量x s在矩阵A中的系数列向量发生变化,如何求新问题的最优解?
4.追加新的约束条件,如何求新的线性规划的最优解?
5.增加新的变量x s,如何求新问题的最优解?。
