【名师原创全国通用】2014-2015学年高一寒假作业数学(八)Word版含答案

合集下载

【名师原创全国通用】2014-2015学年高三寒假作业数学(二)Word版含答案

【原创】高三数学寒假作业（二）一、选择题，每小题只有一项是正确的。

1.设集合{}{}212,log 2A x x B x x =-≤=<，则A B ⋃=A. []1,3-B. [)1,4-C. (]0,3D. (),4-∞ 2.已知函数sin ,0,()(1),0,x x f x f x x π≤⎧=⎨->⎩那么)32(f 的值为 A. 21- B. 23- C. 21 D. 23 3.已知函数f (x)＝267,0,100,,x x x x x ++<≥⎧⎪⎨⎪⎩ 则 f (0)＋f (-1)＝（） (A) 9 (B)7110 (C) 3 (D) 1110 4.已知函数()22x f x =-，则函数|()|y f x =的图像可能是………………………………..（）5.若互不相等的实数c b a ,,成等差数列，b a c ,,成等比数列，且103=++c b a ，则=a （）A. 4B. 2C. -2D. -46.下列各式中值为的是（）A ． sin45°cos15°+cos45°sin15°B ． sin45°cos15°﹣cos45°sin15°C ． cos75°cos30°+sin75°sin30°D ．7.设实数x ，y 满足条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,00820104y x y x y x ,若目标函数z ＝ax ＋by(a ＞0，b ＞0)的最大值为12，则23a b +的最小值为()8.已知函数()f x 满足1()()f x f x =, 当[]1,3x ∈时,()ln f x x =,若在区间1,33⎡⎤⎢⎥⎣⎦内,曲线()()g x f x ax =-与x 轴有三个不同的交点,则实数a 的取值范围是 ( ) A.10,e ⎛⎫ ⎪⎝⎭ B.10,2e ⎛⎫ ⎪⎝⎭ C.ln 31,3e ⎡⎫⎪⎢⎣⎭ D.ln 31,32e ⎡⎫⎪⎢⎣⎭9.圆心在直线y ＝x 上，经过原点，且在x 轴上截得弦长为2的圆的方程为() A ．(x －1)2＋(y －1)2＝2B ．(x －1)2＋(y ＋1)2＝2C ．(x －1)2＋(y －1)2＝2或(x ＋1)2＋(y ＋1)2＝2D ．(x －1)2＋(y ＋1)2＝或(x ＋1)2＋(y －1)2＝2二、填空题10.已知集合{}|1A x x =≤，{}|B x x a =≥，且A B R ⋃=，则实数a 的取值范围是__________ .11.理：已知集合{}0,2>==x x y y M ，{})2lg(2x x y x N -==，则=N M .12.已知等差数列{}n a 的前n 项和为n S ，且1533a a a +=，1014a =，则12S =13.抛物线241x y -=上的动点M 到两定点（0，-1）、（1，-3）的距离之和的最小值为三、计算题14.（本小题满分13分）已知函数)12(log )(21--=x ax x f (a 为常数).(1)若常数2a <且0a ≠,求()f x 的定义域;(2)若()f x 在区间(2,4)上是减函数,求a 的取值范围.15.（本小题满分12分）已知直三棱柱111C B A ABC -中，△ABC 为等腰直角三角形，∠BAC ＝90°，且AB ＝1AA ，D 、E 、F 分别为A B 1、C C 1、BC 的中点．（1）求证：DE ∥平面ABC ；（2）求证：F B 1⊥平面AEF ；（3）求二面角F AE B --1的余弦值．16.（本小题满分12分）已知椭圆()2222:10x y C a b a b+=>>的离心率为2，短轴端点到焦点的距离为2。

高一寒假作业数学试题(8) 含答案

高一数学寒假作业81．已知集合{}3A x N x =∈≤，{}26160B x x x =+-<，则A B =I （） A.{}82x x -<< B.{}1 C.{}0 1，D.{}0 1 2，， 2．下列四个函数中，在定义域上不是单调函数的是（）A ．21y x =-+B ．1y x= C ．lg y x = D ．3y x = 3．为了得到3sin 23y x π⎛⎫=+ ⎪⎝⎭函数的图象，只需把3sin y x =上所有的点（） A.先把横坐标缩短到原来的12倍，然后向左平移6π个单位 B.先把横坐标缩短到原来的2倍，然后向左平移6π个单位 C. 先把横坐标缩短到原来的2倍，然后向左右移3π个单位 D.先把横坐标缩短到原来的12倍，然后向右平移3π个单位 4．函数54)(2+-=x x x f 在区间],0[m 上的最大值为5，最小值为1，则实数m 的取值范围是( )A.),2[+∞B.[2,4]C.[0,4]D.]4,2(5．设02log 2log <<b a ，则( )A.10<<<b aB.10<<<a bC.1>>b aD.1>>a b 6．已知向量(1,),(3,2)a m b ==-r r ，且()a b b +⊥r r r ，则m =( )A.8-B.6-C.6D.87．已知函数的定义域是[-2，3],则的定义域是8．若函数12(log )x y a =在R 上是减函数，则实数a 取值集合是9．已知()f x 对任意实数x 满足()(2)1f x f x +=，且(1)5f =-，则[]()f f x = ．10．已知tan 3α=，则3sin sin 2παα⎛⎫- ⎪⎝⎭的值是 .11．若sin cos 3sin cos αααα+=-，tan()2αβ-=，则tan(2)βα-= . 13．已知向量()()1,3,2,0a b ==-r r . （1）求a b -r r ；（2）求向量a b -r r 与a r 的夹角；（3）当t ∈[－1，1]时，求a tb -r r 的取值范围.12．已知某海滨浴场海浪的高度y （米）是时间t （0≤t ≤24，单位：小时）的函数，记作：y ＝f （t ），下表是某日各时的浪高数据：经长期观测，y ＝f （t ）的曲线可近似地看成是函数b t A y +=ωcos（1）根据以上数据，求函数b t A y +=ωcos 的最小正周期T ，振幅A 及函数表达式；（2）依据规定，当海浪高度高于1米时才对冲浪爱好者开放，请依据（1）的结论，判断一天内的上午8∶00时至晚上20∶00时之间，有多少时间可供冲浪者进行运动？数学寒假作业8 1．C 2．B 3．A 4．B 5．B 6．D 7．[0,52] 8．），（121 9．15-10．310 11． 12．（1）232）π6（3）[]3,12 13.（1）1cos 126y t π=+；（2）上午9∶00至下午3∶00．。

高一年级(必修1)寒假作业8Word版含答案

高一年级（必修1）寒假作业8第Ⅰ卷（共60分）一、选择题：本大题共10个小题.在每小题给出的四个选项中，只有一项是符合题目要求的.1.集合{}2|70,*A x x x x N =-<∈，则6|*,B y N y A y ⎧⎫=∈∈⎨⎬⎩⎭中元素的个数为（） A ．1个B ．2个C ．3个D ．4个2.满足{}{},,,,,a b M a b c d e ≠≠⊂⊂的集合M 的个数为（） A ．6B ．7C ．8D ．93.已知{}|,A x y x x R ==∈，{}2|,B y y x x R ==∈，则A B = （）A ．{}0,1B ．{}|0y y ≥C ．()(){}0,0,1,1D ．∅4.定义集合A 、B 的一种运算：{}1212*|,,A B x x x x A x B =⋅∈∈，若{}1,2,3A =，{}1,2B =，则集合*A B 的子集个数为（） A ．15B ．16C ．31D ．325.下面各组函数中为相等函数的是（）A ．()f x =，()1g x x =-B ．()f x =()g x =C ．()1f x x =-，()1g t t =-D ．()f x x =，2()x g x x=6.若A 、B 、C 为三个集合，A B B C = ，则一定有（） A ．A C ⊆ B ．C A ⊆C ．A C ≠D ．A =∅7.函数2()232f x x x =--的定义域是（） A ．(],2-∞B ．(],1-∞C ．11(,)(,2]22-∞--D ．11(,)(,2)22-∞-- 8.设集合{}|010,*U x x x N =<<∈，若{}2,3A B = ，{}()1,5,7U A B = ð，{}()()9U U A B = 痧，则集合B =（） A ．{}2,3,4B ．{}2,3,4,6C ．{}2,4,6,8D ．{}2,3,4,6,89.已知集合{}|21,A x x n n Z ==-∈，{}|21,B y y n n Z ==+∈，{}|21,C s s k k Z ==±∈，{}|41D t t k ==±，则四者间的关系是（）A ．ABCD =⊆=B ．A BCD =⊇= C ．A B C D ⊆⊆⊆ D ．A B C D ===10.已知{}|40A m m =-<<，|B m y R ⎧⎫==⎨⎬⎩⎭，则下列关系正确的是（）A ．AB =B ．A B ≠⊃C ．A B ≠⊂D ．A B =∅第Ⅱ卷二、填空题（本题共4个小题，将答案填在答题纸上）11.设集合{}23,A m =、{}1,3,21B m =-，若A B ≠⊂，则实数m = ．12.2(21)31f x x -=+，则(3)f = ．13.设A ，B 是非空集合，定义{}|A B x x A B x A B ⨯=∈∉ 且，已知{}|02A x x =≤≤，{}|1B x x =≥，则A B ⨯= ．14.已知集合{}2|20P x x x =-->，{}2|0Q x x ax b =++≤，若P Q R = ，(]2,3P Q = ，则a b += ．三、解答题（本大题共2小题.解答应写出文字说明、证明过程或演算步骤.）15.设集合{}2|320A x x x =-+=，{}22|2(1)(5)0B x x a x a =+++-=．（1）若{}2A B = ，求实数a 的值；（2）若A B A = ，求实数a 的取值范围．16.设实数集R 为全集，{}|0215A x x =≤-≤，{}2|0B x x a =+<．（1）当4a =-时，求A B 及A B ；（2）若()R B A B = ð，求实数a 的取值范围．高一年级（必修1）寒假作业8答案一、选择题二、填空题11.1- 12.13 13.{}|012x x x ≤<>或 14.5- 三、解答题15.解：因为{}{}2|3201,2A x x x =-+==．（1）由{}2A B = 知，2B ∈，从而得2224(1)(5)0a a +++-=，即2430a a ++=，解得1a =-或3a =-.（2）对于集合B ，由224(1)4(5)8(3)a a a ∆=+--=+，因为A B A = ，所以B A ⊆．①当0∆<，即3a <-时，B =∅，满足条件； ②当0∆=，即3a =-时，{}2B =，满足条件； ③当0∆>，即3a >-时，{}1,2B A ==才能满足条件．由根与系数的关系得2122(1),125,a a +=-+⎧⎨⨯=-⎩解得25,27,a a ⎧=-⎪⎨⎪=⎩矛盾，故实数a 的取值范围是3a ≤-． 16.解：（1）∵{}|0215A x x =≤-≤，∴15|22A x x ⎧⎫=≤≤⎨⎬⎩⎭．当4a =-时，{}{}2|40|22B x x x x =-<=-<<，所以1|22A B x x ⎧⎫=≤<⎨⎬⎩⎭ ，所以5|22A B x x ⎧⎫=-<≤⎨⎬⎩⎭ ．（2）由（1）可知15|22R A x x x ⎧⎫=<>⎨⎬⎩⎭或ð，由()R B A B = ð，可知B C ⊂；当B =∅时，即0a ≥时成立；当B ≠∅，即0a <时，{|B x x =<，此时要使()R B A ⊂ð12≤，即104a -≤<．综上可知a 的取值范围是14a ≥-．。

高一寒假作业数学试题(8) Word版含答案

高一数学寒假作业
命题人：卜全力学生训练日期：
．已知集合，，则（） . . . .
．下列四个函数中，在定义域上不是单调函数的是（）．．．．．为了得到函数的图象，只需把上所有的点（）
.先把横坐标缩短到原来的倍，然后向左平移个单位
.先把横坐标缩短到原来的倍，然后向左平移个单位
. 先把横坐标缩短到原来的倍，然后向左右移个单位
.先把横坐标缩短到原来的倍，然后向右平移个单位．函数在区间上的最大值为，最小值为，则实数的取值范围是( ) . .[] .[] . ．设，则( ) . . . . ．已知向量，且，则( )
. .
．已知函数的定义域是[，],则的定义域是
．若函数在上是减函数，则实数取值集合是．已知对任意实数满足，且，则．
．已知，则的值是.
．若，，则.
．已知向量.
（）求；
（）求向量与的夹角；
（）当∈[－，]时，求的取值范围.
．已知某海滨浴场海浪的高度（米）是时间（≤≤，单位：小时）的函数，记作：＝（），下表是某日各时的浪高数据：
经长期观测，＝（）的曲线可近似地看成是函数
（）根据以上数据，求函数的最小正周期，振幅及函数表达式；
（）依据规定，当海浪高度高于米时才对冲浪爱好者开放，请依据（）的结论，判断一天内的上午∶时至晚上∶时之间，有多少时间可供冲浪者进行运动？。

高一寒假作业数学试题第八天 Word版含答案

第八天一．选择题．已知幂函数为奇函数，且在（，∞）上单调递增，则实数的值可能为（）．﹣．．﹣．．已知指数函数（）﹣（＞且≠）的图象恒过定点，若定点在幂函数（）的图象上，则幂函数（）的图象是（）．下列命题中：①幂函数的图象都经过点（，）和点（，）；②幂函数的图象不可能在第四象限；③当时，幂函数的图象是一条直线；④当＞时，幂函数是增函数；⑤当＜时，幂函数在第一象限内的函数值随的值增大而减小．其中正确的是（）．①和④．④和⑤．②和③．②和⑤．已知函数（）（﹣﹣）﹣﹣是幂函数且是（，∞）上的增函数，则的值为（）．．﹣．﹣或．．已知函数（）是幂函数，则对函数的单调区间描述正确的是（）．.单调减区间为（﹣∞，∞）．单调减区间为（，∞）．单调减区间为（﹣∞，）∪（，∞）．单调减区间为（﹣∞，）和（，∞）．若，，，则，，的大小关系为（）．＞＞．＜＜．＜＜．＞＞．如图是函数（，∈*，，互质）的图象，则下述结论正确的是（）．，是奇数，且＜．是偶数，是奇数，且＞．是偶数，是奇数，且＜．是奇数，是偶数，且＞．已知幂函数在（，∞）上单调递增，函数（）﹣，∀∈[，）时，总存在∈[，）使得（）（），则的取值范围是（）．∅．≥或≤．＞或＜．≤≤．函数是幂函数，对任意，∈（，∞），且≠，满足，若，∈，且＞，＜，则（）（）的值（）．恒大于．恒小于．等于．无法判断．已知函数是幂函数，且在（，∞）上为增函数，若，∈，且＞，＜，则（）（）的值（）．恒等于．恒小于．恒大于．无法判断二．填空题．已知幂函数（）（∈*）的图象不与轴、轴相交，且关于原点对称，则．．已知（）是定义在上的奇函数，当＞时，（）是幂函数，且图象过点，则（）在上的解析式为．．已知函数，那么不等式（﹣）＜（）的解集为．．对于函数（）定义域内的任意，且≠，给出下列结论：（）（）（）•（）（）（•）（）•（）（）＞（）（）＞其中正确结论为：．三．解答题．已知函数（）（∈）为偶函数，且在（，∞）上为增函数．（）求的值，并确定（）的解析式；（）若函数（）（（）﹣）在区间（，∞）上恒为正值，求实数的取值范围．答案：。

【名师原创全国通用】2014-2015学年高三寒假作业数学(十)Word版含答案

【原创】高三数学寒假作业（十）一、选择题，每小题只有一项是正确的。

1.已知集合A={2，0，1，4}，{}2,2,2B k k R k A k A =∈-∈-∉，则集合B 中所有的元素之和为( )A.2B.－2.已知命题p ：x ∈A B ，则非p 是A ．x 不属于AB B ．x 不属于A 或x 不属于BC ．x 不属于A 且x 不属于BD ．x ∈A B 3.已知函数)1(+=x f y 定义域是[]3,2-，则y f x =-()21的定义域是（）Ａ.[]-14，Ｂ.[]052，Ｃ.[]-55，Ｄ.]73[，- 4.在等差数列{a n }中，若,23=a ,85=a ，则9a 等于 ( )A ．16B ．18C ．20D ．225.已知函数()sin()1()4f x x x x R π=+-∈. 则函数()f x 在区间[,]44ππ-上的最大值和最小值分别是A. , 最小值为1-B. , 最小值为C. 最大值为1, 最小值为1--D. 最大值为1, 最小值为1-6.平面向量(1,1)AB =-，(1,2)n =(1,2)n =，且3n AC ⋅=，则n BC ⋅= （）A ．2-B ．2C ．3D ．47.已知点(,)P a b 与点(1,0)Q 在直线2310x y +-=的两侧，且0, 0a b >>，则1a b -的取值范围是A ．(,3)-∞-B ．1(,0)3-C ．(3,)+∞D ．1(0,)38.在下列关于点P ，直线l 、m 与平面α、β的命题中,正确的是A. 若m α⊥,l m ⊥，则l ∥αB. 若αβ⊥，m =⋂βα，l P P ∈∈,α，且l m ⊥，则l β⊥C. 若l 、m 是异面直线，m α, m ∥β, l β, l ∥α,则α∥β.D. 若αβ⊥，且l β⊥,l m ⊥，则m α⊥9.已知A ，B ，P 是双曲线12222=-by a x 上不同的三点，且A ，B 的连线经过坐标原点，若直线PA ，PB 的斜率乘积32=⋅PB PA k k ，则该双曲线的离心率为（） A ．25 B. 26 C. 2 D. 315二、填空题10.已知函数212log (1)y x =-的单调递增区间为．11.已知各项都是正数的等比数列{}n a 满足437371234++=+a a a a ，那么7837a a + 的最小值为12.下列命题：①若()f x 是定义在[—1，1]上的偶函数，且在[—1，0]上是增函数，[,]42ππθ∈，则(sin )(sin )f f θθ> ②若锐角,αβ满足cos sin ,.2παβαβ>+<则 ③若2()2cos 1,2x f x =-则()()f x f x π+=对x R ∈恒成立。

高一年级(必修一)寒假作业8Word版含答案

高一年级（必修一）寒假作业8一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合M={x|﹣1＜x ＜3}，N={x|﹣2＜x ＜1}，则N M =（）A ．（﹣2，1）B ．（﹣1，1）C ．（1，3）D ．（﹣2，3）2．满足A∪{﹣1，1}={﹣1，0，1}的集合A 共有（）A ． 4个B ．3个C ．2个D ．1个 3．已知集合}.02|{2R a a x ax x A ∈=++=，若集合A 有且仅有2个子集，则a 的取值是（）A ． 1B ．﹣1C ．0或1D ．﹣1，0或14．下列图形中，不能表示以x 为自变量的函数图象的是（）(A) (B) (C) (D)5．下列各组函数表示相同函数的是( )．A ． f (x )＝x 2，g (x )＝(x )2B ．f (x )＝1，g (x )＝x 2C ．f (x )＝⎩⎪⎨⎪⎧ x ，x ≥0，－x ，x <0，||)(t t g =D ．f (x )＝x ＋1，g (x )＝x 2－1x －16．若)(x f 满足关系式x x f x f 3)1(2)(=+，则)2(f 的值为（）A ． 1B ．1-C ．23-D ．237．已知函数)(x f 的定义域为（﹣1，0），则函数)12(-x f 的定义域为（）A ． )1,1(-B ．（0，）C ．)0,1(-D ．（，1）8．函数f (x )＝cx2x ＋3(x ≠－32)满足x x f f =))((，则常数c 等于( )．A ．3B ．－3C ．3或－3D ．5或－39．若f (x )＝－x 2＋2ax 与g (x )＝ax ＋1在区间[1,2]上都是减函数，则a 的取值范围是( )．A ．(－1,0)∪(0,1) B．(－1,0)∪(0,1] C．(0,1) D ．(0,1]10．)(x f 是定义在),0(+∞上的增函数，则不等式)]2(8[)(->x f x f 的解集是（）A ． ),0(+∞B ．（0，2）C ．（2，+∞）D ．)716,2(11．已知函数313)(23-+-=ax ax x x f 的定义域是R ，则实数a 的取值范围是（） A ． 012≤<-a B ．31>a C ．012<<-a D ．31≤a 12．已知函数⎪⎩⎪⎨⎧>≤---=)1()1(5)(2x xa x ax x x f 是R 上的增函数，则a 的取值范围是（） A ． 03<≤-a B ．23-≤≤-a C ．2-≤aD ． 0≤a二、填空题：本大题共4小题，每小题5分，共20分． 13．已知⎩⎨⎧≤+>+=）（）（11215)(2x x x x x f ，则)]1([f f =________． 14．函数1124)(++-=x x x f 的定义域是______________.15．设集合A ＝{x |x 2＋2x －8＜0}，B ＝{x |x ＜1}，则右图中阴影部分表示的集合为_________. 16．对任意两个实数x 1，x 2，定义⎩⎨⎧<≥=21221121,,},max{x x x x x x x x ,若f (x )＝x 2－2，x x g -=)(，则max{f (x )，g (x )}的最小值为__________．三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．17．（本小题10分）已知A ＝{x |x 2＋(2＋p )x ＋1＝0，x ∈R}，若A ∩(0，＋∞)＝∅，求p 的取值范围．18．（本小题12分）已知集合}10,12|{≤<-==x x y y A ，B ＝{x |(x －a )[x －(a ＋3)]＜0}．分别根据下列条件，求实数a 的取值范围．(1)A ∩B ＝A ；(2)φ≠B A .19．（本小题12分）已知函数22)(2++=ax x x f ，]5,5[-∈x ．（1）当1-=a 时，求)(x f 的最大值与最小值；（2）求函数)(x f 的最小值)(a g ．20．（本小题12分）甲同学家到乙同学家的途中有一公园，甲从家到公园的距离与乙从家到公园的距离都是2km ，甲10时出发前往乙家．如图：所示，表示甲从家出发到乙家为止经过的路程y （km ）与时间x （分）的关系．试写出)(x f y =的函数解析式．21．（本小题12分）已知函数f (x )＝ax －1x ＋1. (1)若a ＝－2，试证：f (x )在(－∞，－2)上单调递减．(2)函数f (x )在(－∞，－1)上单调递减，求实数a 的取值范围．22．（本小题12分）对于集合C B A ,,{}052≥+-=a x x x A ，{}7+≤≤=m x m x B ，若对于R m C a ∈∃∈∀，，使得R B A = .求集合C .高一年级（必修一）寒假作业8答案一、选择题：1-6 BADBCB 7-12 BBDDAB二、填空题：13．8 14．（﹣∞，﹣1）∪（﹣1，2]15．{x |1≤x ＜2} 16．－117．解析：①若A ＝∅，则Δ＝(p ＋2)2－4<0，得－4<p <0.………………………4分②若方程的两个根为非正实数，则⎩⎪⎨⎪⎧Δ≥0，x 1＋x 2＝－ p ＋2 ≤0，x 1x 2＝1>0.解得p ≥0. ………………………………9分综上所述，p 的取值范围是{p |p >－4}．…………………………………………10分 18．解析：因为集合A 是函数y ＝2x －1(0＜x ≤1)的值域，所以A ＝(－1,1]，B ＝(a ，a ＋3)． (1)A ∩B ＝A ⇔A ⊆B ⇔⎩⎪⎨⎪⎧a ≤－1，a ＋3＞1，即－2＜a ≤－1，故当A ∩B ＝A 时，a 的取值范围是(－2，－1]．……6分(2)当φ=B A 时，结合数轴知，a ≥1或a ＋3≤－1，即a ≥1或a ≤－4.故当φ≠B A 时，a 的取值范围是(－4,1). ……12分19．解析：（1）当a=﹣1时，∵函数1)1(22)(22+-=+-=x x x x f ，x∈[﹣5，5]，故当x=1时，函数)(x f 取得最小值为1，当x=﹣5时，函数)(x f 取得最大值为 37． …………………………2分（2）当5-<-a ，即5>a 时，函数)(x f 在区间[﹣5，5]上是单调增函数，最小值a f a g 1027)5()(-=-=． …………………………5分当55≤-≤-a ，即55≤≤-a 时，函数)(x f 在区间[﹣5，5]上的最小值22)()(a a f a g -=-=． …………………………8分当5>-a ，即5-<a 时，函数)(x f 在区间[﹣5，5]上是单调减函数，故最小值a f a g 1027)5()(+==． …………………………11分综上可得，)5()55()5(102721027)(2>≤≤--<⎪⎩⎪⎨⎧--+=a a a a aa a g ………………………………12分 20．解析：当0≤x ≤30时，设)(x f =kx ，将（30，2）代入可得k =， ∴x x f 151)(= ……………………………………………………4分当30＜x≤40时，)(x f =2； ………………………………………………2分当40＜x≤60时，设b mx x f +=)(，则将（40，2），（60，4）代入可得， ∴，解得，即2101)(-=x x f ．………………………10分综上． ………………………………12分21．解析：(1)证明任设x 1＜x 2＜－2，则f (x 1)－f (x 2)＝－2x 1－1x 1＋1－－2x 2－1x 2＋1＝－ x 1－x 2 x 1＋1 x 2＋1. ∵(x 1＋1)(x 2＋1)＞0，x 1－x 2＜0，∴f (x 1)－f (x 2)＞0，∴f (x 1)＞f (x 2)，∴f (x )在(－∞，－2)上单调递减． ………………………………………………6分(2)f (x )＝ax －1x ＋1＝a －a ＋1x ＋1，设x 1<x 2<－1，则f (x 1)－f (x 2)＝⎝ ⎛⎭⎪⎫a －a ＋1x 1＋1－⎝ ⎛⎭⎪⎫a －a ＋1x 2＋1 ＝a ＋1x 2＋1－a ＋1x 1＋1＝ a ＋1 x 1－x 2 x 1＋1 x 2＋1，又函数f (x )在(－∞，－1)上是减函数，所以f (x 1)－f (x 2)>0.由于x 1<x 2<－1，∴x 1－x 2<0，x 1＋1<0，x 2＋1<0，∴a ＋1<0，即a <－1.故a 的取值范围是(－∞，－1)． ………………………………………………12分22.解：由题意知⎩⎨⎧≤->∆≤∆70021x x 或即⎪⎩⎪⎨⎧≤-+<≥494)(42542521221x x x x a a 或4256<≤-⇒a 综上6-≥a。

高一数学寒假作业8

高一寒假作业8（答案解析）一、选择题1．已知互不重合的直线a ，b ，互不重合的平面α，β，给出下列四个命题，正确．．命题的个数是（） ①若a α∥，a β∥，b αβ=，则a b ∥②若αβ⊥，a α⊥，b β⊥，则a b ⊥ ③若αβ⊥，αγ⊥，a βλ=，则a α⊥④若αβ∥，a α∥，则a β∥ A ．1B ．2C ．3D ．42．若α、β是两个不同的平面，m 、n 是两条不同的直线，则下列结论错误的是（） A ．如果m n ∥，αβ∥那么，m 与α所成的角和n 与β所成的角相等 B ．如果m n ⊥，m α⊥，n β∥那么αβ⊥ C ．如果αβ∥，m α⊂，那么m β∥ D ．如果m α⊥，n α∥，那么m n ⊥3．下列四个正方体图形中，A ，B ，C 为正方体所在棱的中点，则能得出平面ABC ∥平面DEF 的是（）A ．B ．C ．D ．4．如图所示，在正方体1111ABCD A B C D -中，若E 是11A C 的中点，则直线CE 垂直于（）A ．ACB ．BDC ．1A DD ．11A D5．如图，在正方形123SG G G 中，E 、F 分别是12G G 、23G G 的中点，现在沿SE 、SF 、EF 把这个正方形折成一个四面体，使1G 、2G 、3G 重合，重合后的点记为G ．给出下列关系：①SG ⊥平面EFG ；②SE ⊥平面EFG ；③GF SE ⊥；④EF ⊥平面SEG ．其中成立的有（） A ．①与②B ．①与③C ．②与③D ．③与④6．如图所示，在三棱锥P ABC -中，平面ABC ⊥平面PAB ，PA PB =，AD DB =，则（）A ．PD ⊂平面ABCB ．PD ⊥平面ABC C ．PD 与平面ABC 相交但不垂直D ．PD ∥平面ABC7．如下图，梯形ABCD 中，AD BC ∥，1AD AB ==，AD AB ⊥，45BCD ∠=︒，将ABD △沿对角线BD 折起．设折起后点A 的位置为A '，并且平面A BD '⊥平面BCD ．给出下面四个命题：①A D BC '⊥；②三棱锥A BCD '-的体积为2；③CD ⊥平面A BD '； ④平面A BC '⊥平面A DC '．其中正确命题的序号是（）A ．①②B ．③④C ．①③D ．②④8．如图，正方体的棱长为1，线段11A C 上有两个动点E ，F ，且12EF =；则下列结论错误的是（）A ．BD CE ⊥B ．EF ABCD ∥平面C ．三棱锥E FBC -的体积为定值D ．BEF △的面积与CEF △的面积相等9．如图，PA ⊥矩形ABCD ，下列结论中不正确的是（）A ．PD BD ⊥B ．PD CD ⊥C ．PB BC ⊥D ．PA BD ⊥10．如图，已知四边形ABCD 是正方形，ABP △，BCQ △，CDR △，DAS △都是等边三角形，E 、F 、G 、H 分别是线段AP 、DS 、CQ 、BQ 的中点，分别以AB 、BC 、CD 、DA 为折痕将四个等边三角形折起，使得P 、Q 、R 、S 四点重合于一点P ，得到一个四棱锥．对于下面四个结论：①EF 与GH 为异面直线；②直线EF 与直线PB 所成的角为60︒； ③EF ∥平面PBC ；④平面EFGH ∥平面ABCD ．其中正确结论的个数有（）A．0个B．1个C．2个D．3个11．某正方体的平面展开图如图所示，则在这个正方体中（）A．NC与DE相交B．CM与ED平行C．AF与CN平行D．AF与CM异面⊥于E，12．如图，PA O☉上的一点，AE PB☉的直径，C是O⊥☉所在的平面，AB是O⊥于，给出下列结论：①BC⊥平面PAC；②AF⊥平面PCB；③EF PBAF PC F⊥；④AE⊥平面PBC．其中正确命题的个数是（）A．1B．2C．3D．4二、填空题13．已知m，n是两条不重合的直线，α，β，γ是三个两两不重合的平面给出下列四个命题：（1）若mα⊥，mβ∥⊥，则αβ（2）若αγ⊥，βγ⊥，则αβ∥（3）若m α⊂，n β⊂，m n ∥，则αβ∥ （4）若m β∥，βγ∥，则m γ∥其中正确的命题是________．(填上所有正确命题的序号)14．如图，直三棱柱111ABC A B C -中，2AB =，BC =1AC =，13AA =，F 为线段1AA 上的一动点，则当1BF FC +最小时，1BFC △的面积为_______．15．α，β是两个平面，m ，n 是两条直线，有下列四个命题： ①如果m α∥，n α∥，m β⊂，n β⊂，那么αβ∥； ②如果m α⊥，n α∥，那么m n ⊥； ③如果αβ∥，m α⊂，那么m β∥；④如果m n ∥，αβ∥，那么m 与α所成的角和n 与β所成的角相等．16．正方体1111ABCD A B C D -中，M ，N ，Q 分别是棱11C D ，11A D ，BC 的中点，点P 在对角线1BD 上，给出以下命题：①当P 在线段1BD 上运动时，恒有MN ∥平面APC ； ②当P 在线段1BD 上运动时，恒有1AB ⊥平面BPC ；③过点P 且与直线1AB 和11A C 所成的角都为60︒的直线有且只有3条．其中正确命题为________．三、解答题17．如图，在四棱锥P ABCD -中，底面ABCD 是正方形，PD ABCD ⊥底面，2PD AB ==，E ，F 分别为AB ，PC 的中点．（1）证明：直线EF PAD ∥平面；（2）求三棱锥B EFC -的体积．18．如图，三棱柱111ABC A B C -，1A A ⊥底面ABC ，且ABC △为正三角形，16A A AB ==，D 为AC 中点．（1）求三棱锥1C BCD -的体积；（2）求证：平面1BC D ⊥平面11ACC A ；（3）求证：直线1AB ∥平面1BC D ．高一寒假作业8（答案解析）一、选择题 1．【答案】C【解析】由题意，已知互不重合的直线a ，b 和互不重合的平面α，β，在A 中，由于b αβ=，a α∥，a β∥，过直线a 与平面α，β都相交的平面γ，记d αγ=，c βγ=，则a d ∥且a c ∥，所以d c ∥，又d b ∥，所以a b ∥，故A 是正确的；在B 中，若αβ⊥，a α⊥，b β⊥，则由面面垂直和线面垂直的性质得a b ⊥，所以是正确；在C 中，若αβ⊥，αγ⊥，a βλ=，则由线面垂直的判定定理得a α⊥，所以是正确；在D 中，若αβ∥，a α∥，则a β∥或a β⊂，所以是不正确的，故选C ． 2．【答案】B【解析】A ，如果m n ∥，αβ∥，根据线面角的定义可知m ，n 与α所成的角和m ，n 与β所成的角均相等，故A 正确；B ，如果m n ⊥，m α⊥，n β∥，α、β可平行也可以相交，不能得出αβ⊥，故B 错误；C ，如果αβ∥，m α⊂，那么m 与β无公共点，则m β∥，故C 正确；D ，如果n α∥，则存在直线l α⊂，使n l ∥，由m α⊥，可得m l ⊥，那么m n ⊥，故D 正确，故选B ． 3．【答案】B【解析】B 中，可证AB DE ∥，BC DF ∥，故可以证明AB ∥平面DEF ，BC ∥平面DEF ．又ABBC B =，所以平面ABC ∥平面DEF ．故选B ．4．【答案】B【解析】以A 为原点，AB ，AD ，1AA 所在直线分别为x ，y ，z 轴建立空间直角坐标系，设正方体棱长为1，则()0,0,0A ，()1,1,0C ，()1,0,0B ，()0,1,0D ，()10,0,1A ，11,,122E ⎛⎫ ⎪⎝⎭，11,,122CE ⎛⎫∴=-- ⎪⎝⎭，()1,1,0AC =，()1,1,0BD =-，()10,1,1A D =-，()10,0,1AA =，110022CE BD ∴=-+=⋅，则CE BD ⊥，即CE BD ⊥，故选B ． 5．【答案】B【解析】∵11SG G E ⊥，33SG G F ⊥，∴SG GE ⊥，SG GF ⊥，∴SG ⊥平面EFG ，故①正确；同理可得GF ⊥平面EGS ，又∵SE 平面EGS ，根据线面垂直的性质定理，得GF SE ⊥，故③正确，故选B ． 6．【答案】B【解析】∵PA PB =，AD DB =，∴PD AB ⊥．又∵平面ABC ⊥平面PAB ，平面ABC 平面PAB AB =，∴PD ⊥平面ABC ，故选B ． 7．【答案】B【解析】①90BAD ∠=︒，AD AB =，45ADB ABD ∴∠=∠=︒，AD BC ∥，45BCD ∠=︒，BD DC ∴⊥，平面A BD '⊥平面BCD ，且平面A BD'平面BCD BD =，CD ∴⊥平面A BD '，A D ⊂'平面A BD '，CD A D ∴⊥'，故A D BC '⊥不成立，故①错误；②棱锥A BCD '-的体积为1132⋅=③由①知CD ⊥平面A BD '，故③正确； ④由①知CD ⊥平面A BD '，又A B ⊂'平面A BD '，CD A B ∴⊥'，又A B A D '⊥'，且A D '、CD ⊂平面A DC '，A D CD D '=，A B ∴'⊥平面A DC '，又A B '⊂平面A BC '，∴平面A BC '⊥平面A DC '，故④正确．故选B ．8．【答案】D【解析】在正方体1111ABCD A B C D -中，BD ⊥平面11A ACC ，而CE ⊂平面11A ACC ，故BD CE ⊥，故A 正确．又11A C ∥平面ABCD ，因此EF ∥平面ABCD ，故B 正确．当EF 变化时，三角形CEF 的面积不变，点B 到平面CEF 的距离就是B 到平面11A CCC 的距离，它是一个定值，故三棱锥E FBC -的体积为定值（此时可看成三棱锥B CEF -的体积），故C 正确．在正方体中，点B 到EF C 到EF 的距离为1，D 是错误的．综上，故选D ． 9．【答案】A【解析】∵PA ⊥矩形ABCD ，∴PA BD ⊥，若PD BD ⊥，则BD ⊥平面PAD ，又BA ⊥平面PAD ，则过平面外一面有两条直线与平面垂直，不成立，故PD BD ⊥不正确，故A 不正确；∵PA ⊥矩形ABCD ，∴PA CD ⊥，AD CD ⊥， ∴CD ⊥平面PAD ，∴PD CD ⊥，故B 正确；∵PA ⊥矩形ABCD ，∴由三垂线定理得PB BC ⊥，故C 正确；∵PA ⊥矩形ABCD ，∴由直线与平面垂直的性质得PA BD ⊥，故D 正确．故选A ． 10．【答案】D【解析】①错误．所得四棱锥中，设AS 中点为I ，则E 、I 两点重合， ∵FI GH ∥，即EF GH ∥，即EF 与GH 不是异面直线；②正确．∵FI GH ∥，PB 与BQ 重合，且GH 与BQ 所成角为60︒，说明EF 与PB 所成角为60︒；③正确．∵FI GH BC ∥∥，BC ⊂平面PBC ，FI ⊄平面PBC ， ∴FI ∥平面PBC ，∴FE ∥平面PBC ；④正确．∵FI ∥平面ABCD ，IH ∥平面ABCD ，FIHI I =点，∴平面FIHG ∥平面ABCD ，即平面EFGH ∥平面ABCD ，故选D ． 11．【答案】B【解析】根据题意得到立体图如图所示：A ．NC 与DE 是异面直线，故不相交；B ．CM 与ED 平行，由立体图知是正确的；C ．AF 与CN 位于两个平行平面内，故不正确；D ．AF 与CM 是相交的．故答案为B ． 12．【答案】C【解析】因为PA O ⊥☉所在的平面，BC O ⊂☉所在的平面，所以PA BC ⊥，而BC AC ⊥，ACPA A =，所以BC ⊥平面PAC ，故①正确；又因为AF ⊂平面PAC ，所以AF BC ⊥，而AF PC ⊥，PC BC C =，所以AF ⊥平面PCB ，故②正确；而PB ⊂平面PCB ，所以AF PB ⊥，而AE PB ⊥，AEAF A =，所以PB ⊥平面AEF ，而EF ⊂平面AEF ，所以EF PB ⊥，故③正确；因为AF ⊥平面PCB ，假设AE ⊥平面PBC ，所以AF AE ∥，显然不成立，故④不正确；故选C ．二、填空题 13．【答案】（1）【解析】（1）根据线面垂直的性质可知若m α⊥，m β⊥，则αβ∥成立；（2）若αγ⊥，βγ⊥，则αβ∥或α与β相交；故（2）不成立；（3）根据面面平行的可知，当m 与n 相交时，αβ∥，若两直线不相交时，结论不成立；（4）若m β∥，βγ∥，则m γ∥或m γ⊂，故（4）不成立．故正确的是（1），故答案为（1）．14．【解析】将直三棱柱111ABC A B C -沿棱1AA 展开成平面连接1BC ，与1AA 的交点即为满足1BF FC +最小时的点F ，由于2AB =，1AC =，13AA =，再结合棱柱的性质，可得122AF FA ==，由图形及棱柱的性质，可得BF =1FC =1BC =，1cosFC B ∠==．∴1sin FC B ∠1BFC △的面积为12=． 15．【答案】②③④【解析】①如果m ，n 不一定相交，不能得出αβ∥，故错误； ②如果n α∥，则存在直线l α⊂，使n l ∥，由m α⊥，可得m l ⊥，那么m n ⊥．故正确； ③如果αβ∥，m α⊂，那么m 与β无公共点，则m β∥．故正确； ④如果m n ∥，αβ∥，那么m ，n 与α所成的角和m ，n 与β所成的角均相等．故正确；故答案是②③④．16．【答案】②③【解析】①当P 位于1BD 与平面MNAC 的交点处时，MN 在平面APC 内， ②因为1AB 垂直于BC 和1BD ，所以成立，③1AB 和11A C 成60︒角，过P 点与两直线成60︒的直线有三条故答案为②③．三、解答题17．【答案】（1）详见解析；（2）13．【解析】（1）证明：取PD 的中点G ，连FG ，AG ，∵F 为PC 的中点，∴FG CD ∥，12FG CD =且，又AE CD ∥，12AE CD =且，∴AEFG 四边形为平行四边形，∴EF AG ∥， EF PAD ⊄又平面，AG PAD ⊂平面，∴EF PAD ∥平面．（2）∵PD ABCD ⊥底面，F 为PC 的中点，∴点112F BCE d PD ==到平面的距离为．又1112122BCE S BE BC =⋅⋅=⨯⨯=△，∴11111333B EFC F BCE BCE V V S d --===⨯⨯=⋅△，即三棱锥B EFC -的体积为13．18．【答案】（1）（2）见解析；（3）见解析．【解析】（1）∵ABC △为正三角形，D 为AC 中点，∴BD AC ⊥，由6AB =可知，3CD =，BD =12BCD S CD BD ⋅⋅=△ 又∵1A A ⊥底面ABC ，且16A A AB ==，∴1C C ⊥底面ABC ，且16C C =， ∴1113C BCD BCD V S C C -⋅⋅==△ （2）∵1A A ⊥底面ABC ，∴1A A BD ⊥．又BD AC ⊥，∴BD ⊥平面11ACC A ．又BD ⊂平面1BC D ，∴平面1BC D ⊥平面11ACC A ．（3）连接1B C 交1BC 于O ，连接OD ，在1B AC △中，D 为AC 中点，O 为1B C 中点，所以1OD AB ∥，又OD 平面1BC D ，∴直线1AB ∥平面1BC D ．。

2014-2015学年高三寒假作业数学(八)Word版含答案

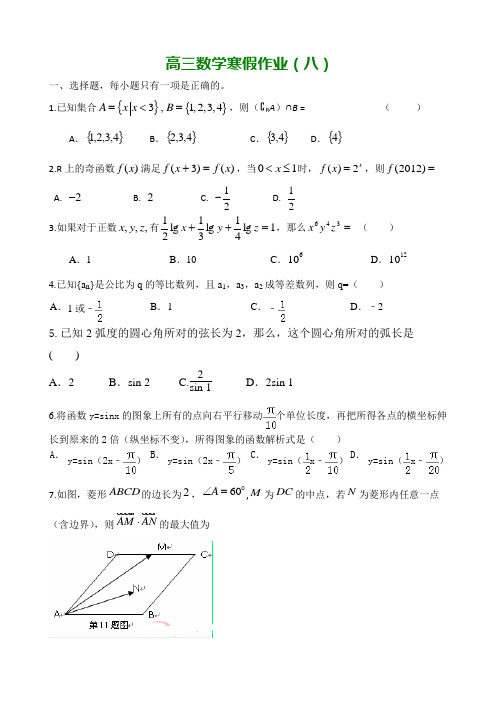
高三数学寒假作业（八）一、选择题，每小题只有一项是正确的。

1.已知集合{}{}3,1,2,3,4A x x B =<=，则（R A ）∩B = （）A ．{}4,3,2,1B ．{}4,3,2C ．{}4,3D ．{}4 2.R 上的奇函数()f x 满足)()3(x f x f =+，当01x <≤时，()2x f x =，则(2012)f =A. 2-B. 2C. 12-D. 123.如果对于正数,,,z y x 有1lg 41lg 31lg 21=++z y x ，那么=346z y x （） A ．1 B ．10 C ．610 D ．1210 4.已知{a n }是公比为q 的等比数列，且a 1，a 3，a 2成等差数列，则q=（）( )A ．2B ．sin 2 C.2sin 1 D ．2sin 16.将函数y=sinx 的图象上所有的点向右平行移动个单位长度，再把所得各点的横坐标伸）﹣（﹣x ）7.如图，菱形ABCD 的边长为2，60A ∠=,M 为DC 的中点，若N 为菱形内任意一点（含边界），则AM AN ⋅的最大值为A.3B.C.6D.98.设,,,,,a b c x y z 是正数，且22210a b c ++=，22240x y z ++=，20ax by cz ++=，则a b c x y z++=++ A ．14B ．13C ．12D ．349.在平面直角坐标系xoy 中，圆C 的方程为228150x y x +-+=，若直线2y kx =-上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，则k 的最大值为（）A ．2B ．43 C ．23D ． 3二、填空题10.若某程序框图如图所示，则该程序运行后输出的值是．11.已知α，β为平面，m ，n 为直线，下列命题：①若m ∥n ，n ∥α，则m ∥α； ②若m ⊥α，m ⊥β，则α∥β；③若α∩β＝n ，m ∥α， m ∥β，则m ∥n ； ④若α⊥β，m ⊥α，n ⊥β，则m ⊥n ．其中是真命题的有 ▲ ．(填写所有正确命题的序号)12.在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知C=2A ，cosA=，b=5，则△ABC 的面积为．13.（5分）（2011•陕西）设f （x ）=若f （f （1））=1，则a= ．三、计算题14.（本题满分14分）本大题共有2小题，第1小题7分，第2小题7分。

2014-2015学年高一寒假作业数学含答案

【原创】高一数学寒假作业（八）一、选择题，每小题只有一项是正确的。

1.若2log 030x x x f x x >⎧=⎨≤⎩（）（）（），则1[]4f f =（）（） A 9 B 19 C 9- D 19- 2.函数()f x 是定义在[6,6]-上的偶函数，且(3)(1)f f >，则下列各式一定成立的是（）A 、(0)(6)f f <B 、(1)(3)f f -<C 、(3)(2)f f >D (2)(0)f f >3.已知直线⊥l 平面α，直线m ⊆平面β，给出下列命题,其中正确的是①m l ⊥⇒βα// ②m l //⇒⊥βα③βα⊥⇒m l // ④βα//⇒⊥m lA ．①③ B.②③④ C.②④ D.①②③4.已知a ，b 是异面直线，直线c 平行于直线a ，那么c 与b ( )．AC5.的圆，则圆的半径r =．46.A ．B ．40x -=C ．D ．20x +=7.关于直线m 、n 与平面α、β，有下列四个命题：①若//,//m n αβ且//αβ，则//m n ； ②若,m n αβ⊥⊥且αβ⊥，则m n ⊥；③若,//m n αβ⊥且//αβ，则m n ⊥； ④若//,m n αβ⊥且αβ⊥，则//m n ；其中真命题的序号是 ( ).A ．①②B ．②③C ．①④D ．③④8.在正方体1111ABCD A BC D -中，下列几种说法正确的是A 、11AC AD ⊥B 、11DC AB ⊥C 、1AC 与DC 成45角D 、11AC 与1BC 成60角9.已知集合A ＝{x|0<log 4x<1}，B ＝{x|x≤3}，则A∩B＝( )A ．(0,1)B ．(0,3]C ．(1,3)D ．(1,3]二、填空题10.函数[]241,3,5y x x x =-+∈-的值域是 X|k |B | 1 . c|O |m11.已知()bx ax x f +=2是定义在[a-1,2a]上的偶函数，那么a+b 的值是____________． 12.计算121log 43-⎛⎫+ ⎪⎝⎭的结果为 ▲ . 13.已知奇函数)(x f 在0≥x 时的图象如图所示，则不等式0)(<x f 的解集是．（2）如果()216f =，求log 4a 的值。

名师原创全国通用2014-2015学年高三寒假作业数学(七)Word版含答案.pdf

（I）求 a，b 的值；
（II）若对 x [−1,2] ， f (x) c2 恒成立，求 c 的取值范围。
16.（本小题满分 12 分）
在△ABC 中，角 A,B,C 的对边分别是 a，b，c，若 3 acos C=csin A．
（1）求角 C 的大小；
（2）若 a=3，△ABC 的面积为 3 3 ，求 CA · AB 的值． 2
率为
．
x2 13.已知双曲线 C： a2
−
y2 b2
=1
(a＞0，b＞0)的一条渐近线与直线 l： x +
3y = 0 垂直，C
的一个焦点到 l 的距离为 1，则 C 的方程为__________________.
三、计算题 14.（本小题满分 12 分）
( ) 如图，已知椭 E: x2 + y2 a2 b2
（2）由（1）知： f (x) = x3 − 1 x2 − 2x + c 2
f '(x) = 3x2 − x − 2 = (x −1)(3x + 2)
x [-1，
−2
（ − 2 ，1） 1
3
3
(1，2]
学海无涯
−2) 3
y' ＋
－
＋
y
极大值
f (−1) ， f (− 2) ， f (2) 中的最大值 f (2) = 2 + c 3
A. ⊥ , = n, m ⊥ n
B. = m, ⊥ , ⊥
C. ⊥ , ⊥ , m ⊥
D. n ⊥ , n ⊥ , m ⊥
3.已知
U＝{y|y＝
log
2
x
}，P＝{y|y＝
1 x

高一数学寒假作业 08 Word版含解析

作业范围:必修综合测试
姓名学校班级
时间: 分钟分值分
第Ⅰ卷
一、选择题(本卷共小题，在每小题给出的四个选项中，只有一项是符合题目要求的.）
．已知，，则（）
.．．．
】届福建省厦门市高三月适应性考试文科数学试卷
【答案】
考点：平方关系、商数关系、两角差的正切.
【题型】选择题
【难度】较易
．在边长为的正中，是边的两个三等分点（靠近于点），则等于（）．．．．
】【百强校】届河北武邑中学高三文上期中数学试卷
【答案】
【解析】因,故
,故选．
考点：向量的几何运算及数量积公式的运用．
【题型】选择题
【难度】较易
．已知，则（）
．．．．
】【百强校】届广西河池课改联盟高三上联考二试（文）试卷
【答案】
考点：二倍角公式.
【题型】选择题
【难度】较易
．已知向量，，若，
则（）
．．．．
】【百强校】届河北冀州中学高三复习班上段考二（理）试卷
【答案】
【解析】
，
所以．所以．
考点：向量的数量积公式；三角恒等变换公式．
【题型】选择题
【难度】较易
．函数的图象如图所示，则的表达式为（）。

【名师原创全国通用】2014-2015学年高一寒假作业数学(六)Word版含答案

【原创】高一数学寒假作业（六）一、选择题，每小题只有一项是正确的。

1.函数1()()12xf x =-的定义域、值域分别是 A ．定义域是R ，值域是RB ．定义域是R ，值域是(0,)+∞C ．定义域是(0,)+∞ ，值域是RD ．定义域是R ，值域是(1,)-+∞2.若函数11)(-+=xe mx f 是奇函数，则m 的值为（） A 0 B21C 1D 2 3.若函数()x x f x ka a -=-(0a >且1)a ≠在(,)-∞+∞上既是奇函数又是增函数，则()log ()a g x x k =+的图象是（）4.由表格中的数据，可以判定方程20xe x --=的一个根所在的区间为(),1k k +()k N ∈，则k 的值为（）A ．-1B ．0C ．1D ．25.已知两条直线m n ，，两个平面αβ，．下面四个命题中不正确．．．的是（） A ． ,//,,n m m ααββ⊥⊆⇒⊥n B ．αβ∥，m n ∥，m n αβ⇒⊥⊥； C ． ,α⊥m m n ⊥,βαβ⊥⇒⊥n D ．m n ∥，m n αα⇒∥∥；6.下面命题正确的是（）（A ）经过定点00(,)P x y 的直线都可以用方程00()y y k x x -=-表示（B ）经过任意两个不同的点112222(,),(,)P x y P x y 的直线都可以用方程121121()()()()y y x x x x y y --=--表示（C ）不经过原点的直线都可以用方程1=+bya x 表示（D ）经过点(0,)Bb 的直线都可以用方程y kx b =+表示7.函数)3(log )(22a ax x x f +-=在),2[+∞上是增函数，则实数a 的取值范围是（）Ａ. 4≤a Ｂ. 2≤a Ｃ.44≤<-a Ｄ.42≤≤-a 8.设,m n 是不同的直线，γβα,,是不同的平面，有以下四个命题： ①//////αββγαγ⎫⇒⎬⎭ ②//m m αββα⊥⎫⇒⊥⎬⎭③//m m ααββ⊥⎫⇒⊥⎬⎭ ④////m n m n αα⎫⇒⎬⊂⎭其中，真命题是（）A.①④B.②③C.①③D. ②④ 9.满足条件{1}{1,2,3}M=的集合M 的个数是（）A.4B.3C.2D.1二、填空题10.已知m 、n 是不同的直线，α、β是不重合的平面，给出下列命题：① 若α//β，m ⊂α，n ⊂β，则m//n ；② 若m ，n ⊂α， m//β，n//β，则α//β；③若m//α，n ⊂α，则m//n ；④若m//n, m ⊥α,则n ⊥α。

【名师原创全国通用】2014-2015学年高三寒假作业数学(四)Word版含答案

【原创】高三数学寒假作业（四）一、选择题，每小题只有一项是正确的。

1.设全集{|0}=≥U x x ，集合{1}=P ，则U P =ð（A ）[0,1)(1,)+∞ （B ）(,1)-∞ （C ）(,1)(1,)-∞+∞ （D ）(1,)+∞2.已知1,0≠>a a ，xa x x f -=2)(，当)1,1(-∈x 时，均有21)(<x f ，则实数a 的取值范围是（）Ａ.[)∞+⋃⎥⎦⎤ ⎝⎛，，2210 Ｂ.(]2,1121⋃⎪⎭⎫⎢⎣⎡，Ｃ.[)∞+⋃⎥⎦⎤ ⎝⎛，，4410 Ｄ.(]4,1141⋃⎪⎭⎫⎢⎣⎡，3.若函数f(x)=e x(x ≤0)的反函数为y=f -1(x),则函数y=f -1(2x─1)的定义域为( )(A)(0,1] (B)(-1,1] (C)(-∞,12] (D)(12,1] 4.已知整数数列{}n a 共5项，其中51,4a a ==，且对任意14i ≤≤都有12i i a a +-≤，则符合条件的数列个数为（）A ．24B ．36C ．48D ．525.若3sin()5πα+=，α是第三象限的角，则sincos22sin cos 22παπαπαπα++-=--- （） A ．12 B ．12- C ．2 D ．2- 6.如图，已知,,3AB a AC b BD DC ===，用,a b 表示AD ，则AD =（）A ．34a b +B ．1344a b +C ．1144a b +D ．3144a b +7. 已知,x y 满足不等式420,280,2,x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩设y z x =，则z 的最大值与最小值的差为（）A. 4B. 3C. 2D. 18.抛物线22y x =上两点1122(x ,y ),(x ,y )A B 关于直线y x m =+对称,且121x x 2=-,则m =（）A ．32 B ．2 C ．52D ．3 9.甲乙两人进行乒乓球比赛，约定每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满6局时停止．设甲在每局中获胜的概率为23，乙在每局中获胜的概率为13，且各局胜负相互独立，则比赛停止时已打局数ξ的期望E ξ为（ ▲ ）。

【名师原创全国通用】2014-2015学年高一寒假作业物理(八)Word版含答案

【原创】高一物理寒假作业（八）一、选择题1.下列关于惯性的说法中正确的是（）A．人走路时没有惯性，被绊倒时有惯性B．物体的惯性是指物体不受外力作用时才表现出来的保持原来直线运动状态或静止状态的性质C．惯性是物体的固有属性，与运动状态和是否受力无关D．物体受力大时惯性大，受力小时惯性小，不受力作用时无惯性2.如图所示，轻弹簧下端固定在水平面上.一个小球从弹簧正上方某一高度处由静止开始自由下落，接触弹簧后把弹簧压缩到一定程度后停止下落.在小球下落的这一全过程中，下列说法中不正确．．．的是( )A.小球刚接触弹簧瞬间速度最大B.从小球接触弹簧到到达最低点，加速度方向先向下后向上C.从小球接触弹簧到到达最低点，小球的速度先增大后减小D.从小球接触弹簧到到达最低点，小球的加速度先减小后增大3.在水平桌面上放置一台电脑，下列说法正确的是( )A．电脑所受重力与电脑对桌面的压力是一对平衡力B．电脑对桌面的压力与桌面对电脑的支持力是一对平衡力C．电脑所受重力与桌面对电脑的支持力是一对作用力与反作用力D．电脑对桌面的压力与桌面对电脑的支持力是一对作用力与反作用力4.根据你对物理概念和规律的理解，下列说法中正确的是（）A．静止的物体可能受滑动摩擦力作用，运动的物体可以受静摩擦力作用B．枪膛中的子弹的加速度约为105m/s2，射出的速度可达1000m/s左右，所以加速度大，速度变化就越大C．高速行驶的火车很难停下来，所以速度越大物体的惯性越大D．竖直上抛运动的物体到达最高点时速度为零，加速度也为零5.如图所示，弹簧秤和细线的重力及一切摩擦不计，物重G=5N，则弹簧秤A和B的示数分别( )A．5N，0 B．0，5N C．10N，5N D．5N ，5N6.两个共点力F l、F2大小不同，它们的合力大小为F，则（）A．F1、F2同时增大一倍，F也增大一倍B．F1、F2同时增加10 N，F也增加10 N C．F1增加10 N，F2减少10 N，F一定不变D．若F1、F2中的一个增大，F不一定增大二、实验题7.某同学尝试用橡皮筋等器材探究力的平行四边形定则，他找到两条相同的橡皮筋(遵循胡克定律)和若干小重物，以及刻度尺、三角板、铅笔、细绳、白纸、钉子，设计了如下实验：将两条橡皮筋的一端与细绳连接，结点为O，细绳下挂一重物，两橡皮筋的另一端也都连有细绳．实验时，先将一条橡皮筋的另一端的细绳固定在墙上的钉子A上，另一条橡皮筋任其下垂，如图甲所示；再将另一条橡皮筋的另一端的细绳也固定在墙上的钉子B上，如图乙所示．①为完成实验，下述操作中必需的是________．a．两橡皮筋的另一端连接的细绳a、b长度要相同b．要测量橡皮筋的原长c．要测量图甲和图乙中橡皮筋的长度d．要记录图甲中结点O的位置及过结点O的竖直方向e．要记录图乙中结点O的位置及过结点O的竖直方向②对该实验“两条相同的橡皮筋”的要求的理解正确的为________．a．橡皮筋的材料和原长相同即可b．橡皮筋的材料和粗细相同即可c．橡皮筋的材料、原长和粗细均要相同8.某同学用打点计时器研究小车的匀变速直线运动，他将打点计时器接到频率是50Hz的交流电源上，实验中得到一条纸带，如图所示．他在纸带上便于测量的地方选取第1个计数点，在该点下标明A，第6个点下标明B，第11个点下标明C，第16个点下标明D，第21个点下标明E，测量时发现B点已模糊不清，测得AC长为14.56cm，CD长为11.15cm，DE长为13.73cm．（1）A.C两个计数点的时间间隔为。

【名师原创 全国通用】2014-2015学年高一寒假作业 数学(八)Word版含答案

【名师原创 全国通用】2014-2015学年高三寒假作业 数学(二)Word版含答案

高一寒假作业数学试题(8) 含答案

高一年级(必修1)寒假作业8Word版含答案

高一寒假作业数学试题(8) Word版含答案

高一寒假作业数学试题第八天 Word版含答案

【名师原创 全国通用】2014-2015学年高三寒假作业 数学(十)Word版含答案

高一年级(必修一)寒假作业8Word版含答案

高一数学寒假作业8

2014-2015学年高三寒假作业 数学(八)Word版含答案

2014-2015学年高一寒假作业 数学 含答案

名师原创 全国通用2014-2015学年高三寒假作业 数学(七)Word版含答案.pdf