空间直线与平面平行的判定 PPT
合集下载
直线、平面平行的判定及其性质课件

思考6:设直线a,b为异面直线,经过
直线a可作几个平面与直线b平行?过a,
b外一点P可作几个平面与直线a,b都
平行?
a
b
p
b a a
p b
理论迁移
例1 在空间四边形ABCD中,E,F分别是 AB,AD的中点,求证:EF//平面BCD.
A E B
F D
C
例2 在长方体ABCD—A1B1C1D1中. (1)作出过直线AC且与直线BD1平行的
思考4:有一块木料如图,
E
P为面BCEF内一点,要求 过点P在平面BCEF内画一
F
P D
条直线和平面ABCD平行,
那么应如何画线?
A
C B
思考5:如图,设直线b在平面α内,直 线a在平面α外,猜想在什么条件下直线 a与平面α平行?
a
a//b
α
b
探究(二):直线与平面平行的判断定理
思考1:如果直线a与平面α内的一条直 线b平行,则直线a与平面α一定平行吗?
D′
A′
P
C′
B′ D
C
A
B
例2 已知平面外的两条平行直线中的 一条平行于这个平面,求证另一条也 平行于这个平面.
如图,已知直线a,b
和平面α ,a∥b,
a
b
a∥α , a,b都在 平面α外 .
c α
求证:b∥α .
作业: P61练习,习题2.2A组:1,2. (做在书上) P62习题2.2A组:5,6. P63习题2.2B组:1,2.
由此可得什么推论?
推论 如果一个平 面内有两条相交直 线分别平行于另一
a
b
α
个平面内的两条直
线,那么这两个平 β
7.3空间直线平面的平行课件高三数学一轮复习

训练1 如图所示,已知四边形ABCD是正方形,四边形 ACEF是矩形,M是线段EF的中点. (1)求证:AM∥平面BDE;
证明 如图,记AC与BD的交点为O,连接OE. 因为O,M分别为AC,EF的中点, 四边形ACEF是矩形, 所以四边形AOEM是平行四边形,所以AM∥OE. 又因为OE⊂平面BDE,AM⊄平面BDE, 所以AM∥平面BDE.
(2)平面BDE∥平面MNG. 证明 因为N,G分别为平行四边形ADEF的边AD,EF的中点, 所以DE∥NG, 又DE⊄平面MNG,NG⊂平面MNG, 所以DE∥平面MNG. 因为M为AB的中点,N为AD的中点, 所以MN为△ABD的中位线, 所以BD∥MN, 又BD⊄平面MNG,MN⊂平面MNG, 所以BD∥平面MNG, 又DE与BD为平面BDE内的两条相交直线, 所以平面BDE∥平面MNG.
行
图形表示
符号表示
a⊂β,b⊂β, a∩b=P,a∥α, b∥α⇒α∥β
两个平面平行,则其中一 性质 个平面内的直线__平__行__于
另一个平面
两个平面平行,如果另一 性质 个平面与这两个平面_相__交__, 定理 那么两条__交__线__平行
α∥β, a⊂α⇒a∥β
α∥β,α∩γ=a, β∩γ=b⇒a∥b
例 4 如图,在四棱锥 P-ABCD 中,AD∥BC,AB=BC=21AD,E,F,H 分别
为线段 AD,PC,CD 的中点,AC 与 BE 交于 O 点,G 是线段 OF 上一点.
(1)求证:AP∥平面 BEF;
证明 如图,连接 EC,因为 AD∥BC,BC=12AD, 所以BC∥AE,BC=AE, 所以四边形ABCE是平行四边形,所以O为AC的中点. 又因为F是PC的中点,所以FO∥AP, 因为FO⊂平面BEF,AP⊄平面BEF, 所以AP∥平面BEF.
直线和平面平行的判定定理ppt课件

直线和平面平行的判定 定理ppt课件
2024/1/28
1
目录
2024/1/28
• 直线与平面平行基本概念 • 判定定理一:斜率相等法 • 判定定理二:向量共线法 • 判定定理三:距离相等法 • 综合应用与拓展 • 总结回顾与课堂互动
2
直线与平面平行基
01
本概念
2024/1/28
3
直线与平面定义
及特殊情况的处理。
15
判定定理三:距离
04
相等法
2024/1/28
16
距离相等法原理
直线与平面平行时,直线上任意一点 到平面的距离都相等。
利用这一性质,可以通过比较直线上 不同点到平面的距离是否相等来判断 直线与平面是否平行。
2024/1/28
17
点到直线距离公式
点$P(x_0, y_0, z_0)$到平面 $Ax + By + Cz + D = 0$的距 离公式为
2024/1/28
$d = frac{|Ax_0 + By_0 + Cz_0 + D|}{sqrt{A^2 + B^2 + C^2}}$
其中,$A, B, C$是平面方程中 的系数,$D$是常数项。
18
实例分析与讨论
实例1
已知直线$l$的方程为$frac{x-1}{2} = frac{y-2}{3} = frac{z-3}{4}$,平 面$pi$的方程为$x + y + z = 6$, 判断直线$l$与平面$pi$是否平行。
解
在直线$m$上任取两点$Q_1(-1,2,0)$和$Q_2(0,1,1)$,分别计算它们到平面 $alpha$的距离$d_3$和$d_4$。根据点到平面的距离公式,有
2024/1/28
1
目录
2024/1/28
• 直线与平面平行基本概念 • 判定定理一:斜率相等法 • 判定定理二:向量共线法 • 判定定理三:距离相等法 • 综合应用与拓展 • 总结回顾与课堂互动
2
直线与平面平行基
01
本概念
2024/1/28
3
直线与平面定义
及特殊情况的处理。
15
判定定理三:距离
04
相等法
2024/1/28
16
距离相等法原理
直线与平面平行时,直线上任意一点 到平面的距离都相等。
利用这一性质,可以通过比较直线上 不同点到平面的距离是否相等来判断 直线与平面是否平行。
2024/1/28
17
点到直线距离公式
点$P(x_0, y_0, z_0)$到平面 $Ax + By + Cz + D = 0$的距 离公式为
2024/1/28
$d = frac{|Ax_0 + By_0 + Cz_0 + D|}{sqrt{A^2 + B^2 + C^2}}$
其中,$A, B, C$是平面方程中 的系数,$D$是常数项。
18
实例分析与讨论
实例1
已知直线$l$的方程为$frac{x-1}{2} = frac{y-2}{3} = frac{z-3}{4}$,平 面$pi$的方程为$x + y + z = 6$, 判断直线$l$与平面$pi$是否平行。
解
在直线$m$上任取两点$Q_1(-1,2,0)$和$Q_2(0,1,1)$,分别计算它们到平面 $alpha$的距离$d_3$和$d_4$。根据点到平面的距离公式,有
直线与平面平行及性质课件-高一下学期数学人教A版(2019)必修第二册

D C
O
A
B
技巧点拨:中点问题可考虑利用中位线的性质解决.
例3、如图,四棱锥P-ABCD中,底面ABCD是平行四边形,E、F 分别是AB,PC的中点, 求证:EF//平面PAD
技巧点拨:可通过构造平行四边形寻找平行线.
如果一条直线和一个平面平行,那么这条直线和这个平面内的 直线有怎样的位置关系?
•CD//AB →→ •CD//平面α
直线与平面平行的判定定理:
如果平面外一条直线与此平面内的一条直线平行,那么该直线与 此平面平行
例2、求证:空间四边形相邻两边中点的连线,平行于经过另两边的平面. 解题流程:画图→写出已知求证→作出辅助线→证明
已知:空间四边形ABCD中,E、F分别是AB,AD的中 点. 求证:EF∥平面BCD.
点,求证:四边形EFGH是平行四边形.
A
EH // GF
H E
D
B
G
F C
探究:若加上条件AC=BD,那么四边形EFGH为什么图形?
2.等角定理
A’
E’
D’
A
E
D
如果空间中两个角的两条边分别对应平行, 那么这两个角相等或互补.
推论:
如果两条相交直线和另两条相交直线分别平行, 那么这两组直线所成的锐角(或直角)相等.
a
α
平行或异面
三、直线与平面平行的性质定理
一条直线与一个平面平行,则过这条直线的任一平面与此 平面的交线与该直线平行.
βa
αb
线面平行
先找平面再线找线两平平行 面的交线
例4、有一块木料如图,已知棱BC平行于面A′C′ (1)要经过木料表面A′B′C′D′内的一点P和棱BC将木料
锯开,应怎样画线? (2)所画的线和面AC有什么关系?
直线与平面平行的判定说课课件_图文

随堂练习
活动:
①让学生准备一张便于折叠的三 角形的纸,沿顶点任意折叠,做成 空间四边形,并标出相邻两边的 中点,观察连线与另外一个三角 形所在平面的位置关系. ②再让学生标出相邻两边的三等 分点、四等分点,观察连线与另 外一个三角形所在平面的位置关 系.
例1:
求证:空间四边形 相邻两边中点的连 线平行于经过另外 两边所在的平面.
变式:
1.如图,在空间四边形ABCD中,E、F分
别为AB、AD上的点,若
,则EF
与平面BCD的位置关系是_E_F_/_/平__面__B_C__D__.
A
F E
D
B
C
1.证明直线与平面平行的方法:
(1)利用定义;
(2)利用判定定理.
线线平行
线面平行
2.数学思想方法:直线与直线平行
平面与平面平行
直线与平面平行
承上启下
说学情 说教材 说目标 说教法 说学法
教师教法
启发式
问
题
引导式
为
载
探究式
体
学生学法
活
观察猜想
动
方法探究
为
主
小组合作
线
归纳总结
问题引入
作业布置
实 例 感 受
探究结论
说 过程
回 顾 反 思
数学应用
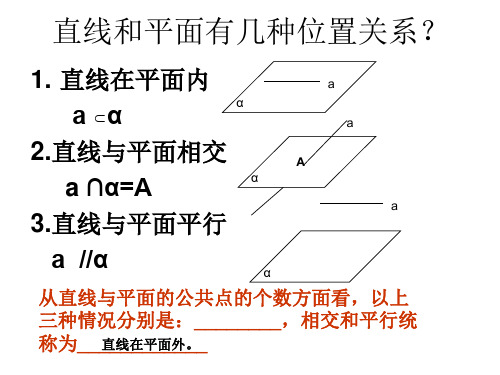
根据公共点的情况,空间中直线a和 平面 有哪几种位置关系?
直线与平面平行的判定说课课件_图文.ppt
说学情 说教材 说目标 说教法 说学法
初步了解
空间点、线、面 及其位置关系
基本熟悉 直观感知 操作确认
提供丰富和直观的观察材料
解决方法
恰当的教学方式和方法
直线与平面平行判定定理课件
A
平面CC’D’D 答:1)平面 )平面A’B’C’D’, 平面 答:2)平面 )平面A’B’C’D’,平面 ,平面ADD’A’
答:3)平面 )平面ADD’A’
问问1 问问2 问问3
D' B'
M D N
C'
若 M, N分 分 , 分 为 D'A,D'B的 , 的 中 中 , 则 MN 与 平 平_____ 平 平?
如何判断直线与平面平行? 如何判断直线与平面平行?
• 思考1:请大家利用手中的模型, 思考1 请大家利用手中的模型, 看看有哪些直线与平面是平行的, 看看有哪些直线与平面是平行的, 理由又是什么? 理由又是什么?
如何判断直线与平面平行? 如何判断直线与平面平行?
• 思考2:观察门扇转动,或者翻动 思考2 观察门扇转动, 书的封面这一运动变化过程中, 书的封面这一运动变化过程中,有 没有某些直线与某些平面平行? 没有某些直线与某些平面平行?为 什么? 什么? • 观察演示,想想在转动过程中,橡 观察演示,想想在转动过程中, 皮筋所在的直线与底面是否平行? 皮筋所在的直线与底面是否平行? 如何摆就能使它们平行? 如何摆就能使它们平行?
• 例1、求证:空间四边形相邻两 、求证: 边中点的连线平行于经过另外 两边所在的平面。 两边所在的平面。
A E B C F D
例2:P是平行四边形ABCD所在平面外 是平行四边形ABCD所在平面外 ABCD 一点, PA的中点 求证:PC//平 的中点, 一点,Q是PA的中点,求证:PC//平 面BDQ.
如何判断直线与平面平行? 如何判断直线与平面平行?
a
• 思考4: 思考4 如果平面外 b α 的一条直线a 的一条直线a与 平面内的直线b 平面内的直线b 平行,那么a 平行,那么a平行于平面α吗?
8.5空间直线、平面的平行(1)PPT课件(人教版)

形,BD∩AC=G,∴G是BD的中点.又∵E是
BB1的中点,∴DB1∥GE.又DB1⊄平面
ACE,GE⊂平面ACE,∴B1D∥平面ACE.
变式 (1)如图,四棱锥P-ABCD的底面为平行四边形,M为棱PC的中点.
求证:(1)BC∥平面PAD;
(2)AP∥平面MBD.
证明:(1)因为四棱锥P-ABCD的底面为平行四边形,所以BC∥AD,又BC⊄平面
意可知四边形ABC1D1为平行四边形,则AD1∥BC1.又AD1∥EF,所以EF∥BC1.因
为EF⊄平面BCC1B1,BC1⊂平面BCC1B1,所以EF∥平面BCC1B1.显然正方体的其
余4个面都不与EF平行.故选B.
变式 (3)如图所示,四棱锥S - ABCD的底面是平行四边
形,M,N分别是SA,BD上的点,且 = .求证:MN∥平面
SBC.
证明:连接AN并延长,使之交BC于点P,连接SP.因为AD∥BC,所以 = .又
= ,所以 = ,所以MN∥SP.
因为MN⊄平面SBC,SP⊂平面SBC,所以MN∥平面SBC.
小结
1.利用直线与平面平行的判定定理证明线面平行的一般步骤
解析
思考►►►
如何判定一条直线与一个平面平行?
【解析】 如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面
平行.
解析
直线与平面平行的判定定理:
表示定理
直线与平面
平行的
判定定理
图形
文字
符号
如果平面外一条直线
a⊄α,
与此平面内的一条直
b⊂α,
线平行,那么该直线
空间直线平面的平行课件-2024届高三数学一轮复习

D.A1B1∥NE
)
答案 B
解析 ∵在▱AA1B1B中,AM=MA1,BN=NB1,∴AM=BN.又AM∥BN,
∴四边形ABNM是平行四边形,∴MN∥AB.
又MN⊄平面ABC,AB⊂平面ABC,∴MN∥平面ABC.又MN⊂平面MNEF,平面
MNEF∩平面ABC=EF,∴MN∥EF,∴EF∥AB.在△ABC中,EF≠AB,
∴EF≠MN,∴四边形MNEF为梯形.故选B.
3.设m,n是不同的直线,α,β是不同的平面,则下列命题正确的是(
A.若m∥α,n∥α,则m∥n
B.若m∥α,m∥β,则α∥β
C.若m⊥α,α⊥β,则m∥β
D.若m⊥α,m⊥β,则α∥β
答案 D
解析 A选项,若m∥α,n∥α,则m∥n,或m,n相交或m,n异面,A错误;
EMGHIJ∥平面ACD1,EF∥平面ACD1,则F⊂平面EMGHIJ,观察各选项,ACD
满足.
考点二
线面平行的判定与性质(多考向探究)
考向1.直线与平面平行的判定
典例突破
例2.(2023江西南昌三模)如图,在多面体ABCDEF中,四边形ABCD与ABEF
均为直角梯形,AD∥BC,AF∥BE,DA⊥平面
∴BB1=2CD, =2,
∴OE∥GD,又OE⊄平面AA1C1C,GD⊂平面AA1C1C,
∴OE∥平面AA1C1C.
(2)解连接AC1,则GD∥AC1,OE∥AC1,
∴A,C1,O,E四点共面.
又AO∩BC=F,∴F∈AO,F∈平面AC1EO.
又F∈BC,BC⊂平面BB1C1C,
∴F∈平面BB1C1C.
系如何?
提示 平行或异面.
2.面面平行的判定与性质
)
答案 B
解析 ∵在▱AA1B1B中,AM=MA1,BN=NB1,∴AM=BN.又AM∥BN,
∴四边形ABNM是平行四边形,∴MN∥AB.
又MN⊄平面ABC,AB⊂平面ABC,∴MN∥平面ABC.又MN⊂平面MNEF,平面
MNEF∩平面ABC=EF,∴MN∥EF,∴EF∥AB.在△ABC中,EF≠AB,
∴EF≠MN,∴四边形MNEF为梯形.故选B.
3.设m,n是不同的直线,α,β是不同的平面,则下列命题正确的是(
A.若m∥α,n∥α,则m∥n
B.若m∥α,m∥β,则α∥β
C.若m⊥α,α⊥β,则m∥β
D.若m⊥α,m⊥β,则α∥β
答案 D
解析 A选项,若m∥α,n∥α,则m∥n,或m,n相交或m,n异面,A错误;
EMGHIJ∥平面ACD1,EF∥平面ACD1,则F⊂平面EMGHIJ,观察各选项,ACD
满足.
考点二
线面平行的判定与性质(多考向探究)
考向1.直线与平面平行的判定
典例突破
例2.(2023江西南昌三模)如图,在多面体ABCDEF中,四边形ABCD与ABEF
均为直角梯形,AD∥BC,AF∥BE,DA⊥平面
∴BB1=2CD, =2,
∴OE∥GD,又OE⊄平面AA1C1C,GD⊂平面AA1C1C,
∴OE∥平面AA1C1C.
(2)解连接AC1,则GD∥AC1,OE∥AC1,
∴A,C1,O,E四点共面.
又AO∩BC=F,∴F∈AO,F∈平面AC1EO.
又F∈BC,BC⊂平面BB1C1C,
∴F∈平面BB1C1C.
系如何?
提示 平行或异面.
2.面面平行的判定与性质
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D1
A1
E
G
D A
大家好
C1
B1
F
C B
11
练习 3. 如图,已知公共边为 AB 的两个全等的矩形 ABCD 和 ABEF 不在同一平面内,P,Q 分别是对角线 AE,BD 上的点,且 AP=DQ. 求证:PQ∥平面 CBE.
G H
大家好
12
反思~领悟
1.线面平行,通常可以转化为线线平行来处理.
4
归纳结论
直线与平面平行的判定定理:
平面外的一条直线与此平面内的一条直线平行,
则该直线与此平面平行 .
a
(线线平行 线面平行)
符号表示:
b
①内 b
②外
a
a / /
③平行 a / / b
大家好
5
例1 下列说法中正确的是( ) A.若直线l平行于平面α内的无数条直线,则l∥α B.若直线a在平面α外,则a∥α C.若直线a∥b,b⊂α,则a∥α
大家好
9
练习 1.如图,P 是▱ABCD 所在平面外一点,E,F 分别为 AB,PD 的 中点,求证:AF∥平面 PEC.
P
A BE
F
G
D
C
大家好
10
练习 2.如图,在长方体 ABCD-A1B1C1D1中,E, F, G 分别是棱 A1B1, B1C1, DD1 的中点,求证:EF∥平面 ACG.
例1. 如图,空间四边形ABCD中,E、F分别是
AB,AD的中点.
A
求证:EF∥平面BCD.
分析:只要证一个平面内有
两条相交直线和另一个平面平 行即可.
F
E
D
B
线线平行
线面平行
大家好
8
例 2.如图,空间四边形 ABCD 中,E、F、G、H 分别是 AB、BC、CD、 DA 的中点.
求证:(1)EH∥平面 BCD;(2)BD∥平面 EFGH.
块木板绕AB转动,在转动过程中,AB的对边CD(不落在α内) 是否都和平面α平行?
大家好
3
探究问题,归纳结论
如图,平面外的直线 a平行于平面 内的直线b。
(1)这两条直线共面吗?
(2)直线 a与平面 相交吗?
a
b
猜想:如果平面外一条直线和这个平面内的一条直
线平行,那么这条直线和大家这好 个平面平行。
2.2.1
直线与平面平行的判定
大家好
1
复习旧知
直线和平面的位置关系
位置 关系
公共点
直线 a 在平 面α内
有无数个
公共点
直线 a 与平 面 α 相交
直线 a 与平 面 α 平行
有且只有一个
公共点
没有
公共点
符号表示
a⊂α
a∩α=A
a∥α
图形 表示
大家好
2
新课导入
【问题导思】 如图,一块矩形木板ABCD的一边AB在平面α内,把这
D.若直线a∥b,b⊂α, a ⊄ α,那么直线a平行于平面α
内的无数条直线
大家好
6
若直线 a 不平行于平面 α,则下列结论成立的是( ) A.α 内的所有直线均与 a 异面 B.α 内不存在与 a 平行的直线 C.α 内直线均与 a 相交 D.直线 a 与平面 α 有公共点
大家好
7
线面平行的判定定理的运用
2.寻找平行直线可以通过三角形的中位线、 梯形的中位线、平行线的判定等来完成。
3.证明的书写三个条件“内”、“外”、“平 行”,缺一不可。
大家好
13
Bye Bye
大家好
14
