二自由度机械臂动力学分析培训资料
ch3 (二自由度机械系统动力学)

二自由度机械系统动力学
1
第3章 二自由度机械系统动力学
本章内容 3.1 引言——力学的发展过程 3.2 自由度与广义坐标 3.3 虚位移原理与广义力 3.4 拉格朗日方程(重点) 3.5 二自由度机械系统动力学方程 3.6 二自由度机械手动力学问题
2
前一章主要内容:
21
第三个100年,以爱因斯坦的狭义相对论为先导,进入 现代物理学研究阶段。 二十世纪三大科学发现: 1. 相对论(Principle of relativity, Special Principle of relativity, General Principle of relativity, Einstein) 2. 量子力学(Quantum mechanics, Bohr ) Quantum theory, especially the quantum theory of the structure and behavior of atoms and molecules. 3 . 混沌学(Chaos, Poincare )
5
6
7
8
本章采用的方法:拉格郎日方程(重点) 二自由度机械系统动力学不采用等效 力学模型法,一般采用拉格郎日方程来建 模。 在学习拉格郎日方程之前,必须掌握 一些重要的概念,如广义坐标、广义力、 虚位移等。首先了解一些科学史观,培养 科学精神。
9
《易》曰:形而上者谓之道,形而下者谓之器。
力学发展过程 3个100年 第一个100年,从牛顿的《自然哲学的数学原理》开 始(1687),到18世纪后期。本阶段还有伯努利、 欧拉、达朗伯等人。
22
微观力学最新研究成果: 1在微观领域内,不确定性是固有的; 2观察结果受观察者精神作用的影响; 3前卫科学家研究发现,研究成果与东 方哲学(佛学)相吻合。
机械系统动力学作业---平面二自由度机械臂运动学分析资料讲解

机械系统动力学作业---平面二自由度机械臂运动学分析平面二自由度机械臂动力学分析[摘要]机器臂是一个非线性的复杂动力学系统。
动力学问题的求解比较困难,而且需要较长的运算时间,因此,这里主要对平面二自由度机械臂进行动力学研究。
本文采用拉格朗日方程在多刚体系统动力学的应用方法分析平面二自由度机械臂的正向动力学。
经过研究得出平面二自由度机械臂的动力学方程,为后续更深入研究做铺垫。
[关键字]平面二自由度机械臂动力学拉格朗日方程一、介绍机器人是一个非线性的复杂动力学系统。
动力学问题的求解比较困难,而且需要较长的运算时间,因此,简化解的过程,最大限度地减少工业机器人动力学在线计算的时间是一个受到关注的研究课题。
机器人动力学问题有两类:■ ■■(1)给出已知的轨迹点上的■J- ■■■■■■,即机器人关节位置、速度和加速度,求相应的关节力矩向量Q。
这对实现机器人动态控制是相当有用的。
(2)已知关节驱动力矩,求机器人系统相应的各瞬时的运动。
也就是说,给出关节力矩■ ■■向量T求机器人所产生的运动風&及&。
这对模拟机器人的运动是非常有用的。
二、二自由度机器臂动力学方程的推导过程机器人是结构复杂的连杆系统,一般采用齐次变换的方法,用拉格朗日方程建立其系统动力学方程,对其位姿和运动状态进行描述。
机器人动力学方程的具体推导过程如下:(1)选取坐标系,选定完全而且独立的广义关节变量O r , r=l, 2,…,n。
(2)选定相应关节上的广义力F r :当O r是位移变量时,F r为力;当O r是角度变量时, F r为力矩。
(3)求出机器人各构件的动能和势能,构造拉格朗日函数。
(4)代入拉格朗日方程求得机器人系统的动力学方程。
下面以图1所示说明机器人二自由度机械臂动力学方程的推导过程。
1平更二自由度机械臂1、分别求出两杆的动能和势能设齐、B 2是广义坐标,Q i、Q2是广义力。
两个杆的动能和势能分别为:式中,’是杆1质心C i.,\ )的速度向量,\是杆2质心C i ( ' , J )的速度向量。
两自由度机械手动力学问题
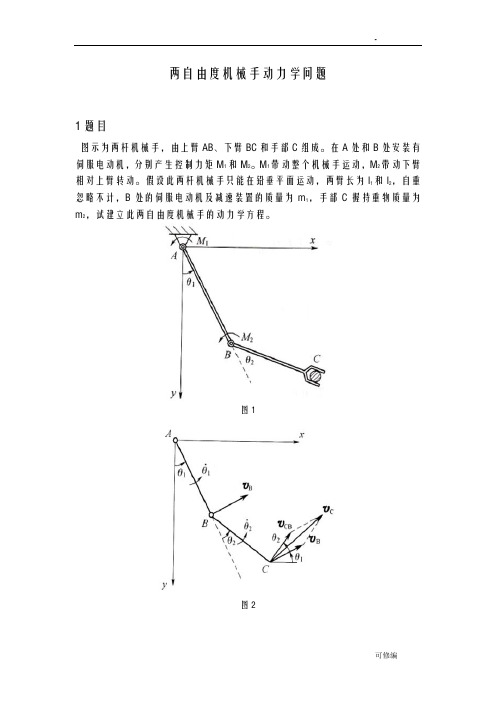
两自由度机械手动力学问题1题目图示为两杆机械手,由上臂AB、下臂BC和手部C组成。
在A处和B处安装有伺服电动机,分别产生控制力矩M1和M2。
M1带动整个机械手运动,M2带动下臂相对上臂转动。
假设此两杆机械手只能在铅垂平面运动,两臂长为l1和l2,自重忽略不计,B处的伺服电动机及减速装置的质量为m1,手部C握持重物质量为m2,试建立此两自由度机械手的动力学方程。
图1图22数值法求解2.1拉格朗日方程此两杆机械手可以简化为一个双摆系统,改双摆系统在B 、C 出具有质量m 1,m 2,在A 、B 处有控制力矩M 1和M 2作用。
考虑到控制力矩M 2的作用与杆2相对杆1的相对转角θ2有关,故取广义力矩坐标为2211,θθ==q q系统的动能为二质点m 1、m 2的动能之和,即由图2所示的速度矢量关系图可知以A 处为零势能位置,则系统的势能为由拉格朗日函数,动势为:广义力2211,M Q M Q ==求出拉格朗日方程中的偏导数,即代入拉格朗日方程式,整理得:2.2 给定条件 (1)角位移运动规律()231*52335.0*1163.0t t t +-=θ,()232*52335.0*1163.0t t t +-=θ21θθ和都是从0到90°,角位移曲线为三次函数曲线。
(2)质量m 1=4㎏ m 2=5kg (3)杆长l 1=0.5m l 2=0.4m2.3 MATLAB 程序t=0:0.1:3;theta1=-0.1163*t.^3+0.52335*t.^2; w1=-0.3489*t.^2+1.0467*t; a1=-0.6978*t+1.0467;theta2=-0.1163*t.^3+0.52335*t.^2; w2=-0.3489*t.^2+1.0467*t; a2=-0.6978*t+1.0467;m1=4; m2=5;l1=0.5; l2=0.4; g=9.8;D11=(m1+m2)*l1.^2+m2*l2.^2+2*m2*l1*l2*cos(theta2); D22=m2*l2.^2;D12=m2*l2.^2+m2*l1*l2*cos(theta2); D21=m2*l2.^2+m2*l1*l2*cos(theta2); D111=0;D122=-m2*l1*l2*sin(theta2); D222=0;D211=m2*l1*l2*sin(theta2); D112=-m2*l1*l2*sin(theta2); D121=-m2*l1*l2*sin(theta2); D212=0; D221=0;D1=(m1+m2)*g*l1*sin(theta1)+m2*g*l2*sin(theta1+theta2); D2=m2*g*l2*sin(theta1+theta2);M1=D11.*a1+D12.*a2+D111.*w1.^2+D122.*w2.^2+D112.*w1.*w2+D121.*w2.*w1+D1; M2=D21.*a2+D22.*a2+D211.*w1.^2+D222.*w2.^2+D212.*w1.*w2+D221.*w2.*w1+D2; T1=polyfit(t,M1,3) T2=polyfit(t,M2,3)subplot(2,1,1),plot(t,M1),grid on,xlabel('时间(s )'),ylabel('控制力矩(N ·m )'),title('motion1') subplot(2,1,2),plot(t,M2),grid on,xlabel('时间(s )'),ylabel('控制力矩(N ·m )'),title('motion2')2.4 数值计算结果()6167.1*7993.31*7329.3*5685.3t 231+++-=t t t M ()5449.1*9801.25*9481.8*0679.0t 232-+--=t t t M图3 M 1变化规律图图4 M2变化规律图3 ADAMS仿真3.1模型建立图5 模型图3.2 施加运动在两个关节处分别施加位移函数图6 关节运动施加图位移函数为:step(time,0,0,3,pi/2)运动规律如下图所示:图7 关节处运动规律图3.3 运动仿真设置仿真时间为3s,步数为300步,仿真结果如下图所示:图8 关节1处控制力矩仿真结果图图9 关节2处控制力矩仿真结果图4 结果对比图10 控制力矩M1结果对比图图11控制力矩M2结果对比图从函数规律上看,两种求解方法得出的结果几乎一样;从数值上看:t 0 0.5 1.0 1.5 2 2.5 3.0 数值计算M1 7.1699 14.3348 33.4367 49.4650 51.6557 44.8470 40.0971 仿真求解M1 7.4526 14.5646 33.5798 49.5093 51.5775 44.6398 39.8039表2 控制力矩M2数值结果对比由上两表可以看出:数值计算结果与仿真求解结果相差很小,误差围为0.437%-0.731%,出现这种结果的原因可能是因为两种方法计算的精度不同,或者是算法存在差异。
机械动力学第二章——两自由度振动讲解

k1 c1
F1(t)
m1
x1 k2
c2
F2(t)
m2
x2 k3
c3
建立坐标:x1,x2的原点分别取在m1,m 2的静平衡位置
受力分析:
F1(t)
F2(t)
k1x1
c1 x1
k2(x2-x1) m1
k2(x2-x1) m2
c2 (x2 x1) c2 (x2 x1)
k3x2
c3 x2
8
两自由度系统的振动微分方程
特解 2: x12 (t) sin 02t 2 , x22 (t) 2 sin 02t 2
由特解线性叠加可以得到通解:
x1(t) C1 sin 01t 1 C2 sin 02t 2
x2
(t
)
1C1
sin
01t
1
2C2
sin
02t
2
20
教学内容
两自由度系统的振动微分方程 两自由度系统的无阻尼自由振动 两自由度系统的强迫振动
21
两自由度系统的强迫振动
装在梁上或者板上的的转动电机,由于转子的不 平衡,或者说转子质量不均匀,在电机高速转动下,梁 或者板将发生上下振动。试问如何减小振动。 (1)提高电机质量 (2)增加阻尼 (3)动力吸振器
14
两自由度系统的无阻尼自由振动
图示两自由度系统,无阻尼,无激励
k1
k2
k3
m1
m2
振动微分方程为:
m1x1 (k1 k2 )x1 k2 x2 0 m2 x2 (k2 k3 )x2 k2 x1 0
令:
机械设计基础中的机器人学机械手臂的动力学与控制

机械设计基础中的机器人学机械手臂的动力学与控制机器人学是机械设计基础领域中的重要学科之一,它涉及到机器人的动力学、控制、感知和计划等方面。
在机器人学中,机械手臂的动力学与控制是一个核心问题。
本文将重点探讨机器人学中机械手臂的动力学与控制,并介绍相关的理论和方法。
一、机械手臂的动力学机械手臂的动力学研究的是机械手臂在运动过程中的力学特性和力学行为。
它主要包括运动学和动力学两个方面。
1. 运动学机械手臂的运动学研究的是机械手臂的位置、速度和加速度等运动参数之间的关系。
在运动学中,常用的描述方法是使用欧拉角或四元数来表示机械手臂的姿态。
2. 动力学机械手臂的动力学研究的是机械手臂的运动与外部力之间的关系。
在动力学中,常用的描述方法是使用牛顿-欧拉方程,它可以描述机械手臂的加速度与外部力矩之间的关系。
二、机械手臂的控制机械手臂的控制研究的是通过控制器对机械手臂进行运动和姿态的控制。
在机器人学中,常用的控制方法有位置控制、速度控制、力控制和姿态控制等。
1. 位置控制位置控制是一种基本的控制方法,它通过控制机械手臂的关节位置,实现对机械手臂的精确控制。
常用的位置控制方法有PID控制和模糊控制等。
2. 速度控制速度控制是一种对机械手臂的运动速度进行控制的方法,它可以实现对机械手臂的定速和变速控制。
常用的速度控制方法有PID控制和预测控制等。
3. 力控制力控制是一种对机械手臂的外部力进行控制的方法,它可以实现对机械手臂的力保持和力调节控制。
常用的力控制方法有阻抗控制和自适应控制等。
4. 姿态控制姿态控制是一种对机械手臂的姿态进行控制的方法,它可以实现对机械手臂的方向和角度的控制。
常用的姿态控制方法有模型预测控制和滑模控制等。
三、机械手臂的应用机械手臂广泛应用于工业生产、医疗护理、军事应用等领域。
在工业生产中,机械手臂可以代替人工完成重复性、繁琐或危险的工作任务,提高生产效率和产品质量。
在医疗护理中,机械手臂可以用于手术操作、康复训练等,帮助医生提高精确度和安全性。
第二章两自由度机构动力学分析
r
17
F2 s2
M1
r
计算广义力:
动力学方程:
r 1 2m2 r Q1 J11q 2 J q m r Q2 2 22 2
18
1 J12 q 2 Q1 J11q 动力学方程: J q 2 Q2 21 1 J 22 q
差动轮系动力学方程,可以直接应用此结论式。
16
例5:已知:J1 A , m2 , J s 2 , M 1 , F2
重力略,建立运动方程。
s2
M1
F2
分析:选广义坐标: q1 , q2 r
方法1:
1 2 1 3 i21 , i22 2 2
2 0, 即H不动,则: 方法2: 令q
同理
1 0, 令q
1 i 即1轮不动,则: 2 H i22
3 i22 2
求:i31 , ห้องสมุดไป่ตู้32
1 1 ( ) 8
15
2 J H iH 2
计算广义力:
此为二阶非线性微分方程,用数值解法求解。
13
例4:已知差动轮系中:
,各轮质量略。
1 , H 求:
分析:取广义坐标: q1 1 , q 2 H
1 q1 2, 2 ', 3 q1 , q2
H q2
则:
1 H
14
求:i21 , i22
第二章 两自由度机构动力学分析
§2-1 两自由度机构的运动分析 例:五杆机构,取 q1 1 , q2 S 4
分析:构件1由 q1 (1 ) 控制,q2 0
构件4由 q2 ( s4 ) 控制,q1 0 件2、3由
机械手臂运动学分析与控制

机械手臂运动学分析与控制机械手臂从上个世纪50年代开始出现,经过多年的发展,已经成为自动化行业中必不可少的一项技术。
机械手臂是由众多执行器和传感器组成的复杂系统,其实现的主要功能是将任务空间中指令位置的物体移动到所需位置。
然而,在实际应用中,由于环境和物体的不同,机械手臂的运动必须按一定的方式控制,因此机械手臂的运动学分析和控制显得非常重要。
一、机械手臂的运动学分析机械手臂的运动学分析主要研究机械手臂在工作空间中的运动方式及其各个关节的旋转角度、速度和加速度等因素。
机械手臂的运动学分析涉及到多学科的知识,主要包括几何学、向量分析和矩阵代数等。
几何学方面,机械手臂可以看作是由多个链接和关节组成的一系列构型,每个构型的重要特征是长度和联接方式。
根据机械手臂的构型及其几何形状,可以推导出机械手臂运动的解析式,从而得到机械手臂的运动学模型。
向量分析方面,机械手臂的运动可用向量描述。
通常机械手臂的位置和运动可用三维向量表示。
对于链式机械臂,可以构成向量链模型。
采用向量链模型,可通过向量之间的线性组合表达机械手臂的运动学模型,并和座标变换相结合,得到机械手臂的位置解析式。
矩阵代数方面,机械手臂运动学的矩阵描述主要是为了便于计算和控制。
通过将构造模型中各个链接和关节的位移、旋转关系表达为矩阵形式,结合每个关节的角位移,可以计算出机械手臂的位置以及各个关节的坐标值,并用于机械手臂控制。
二、机械手臂的运动控制机械手臂的运动控制是指通过控制各个关节的运动状态,实现机械手臂在不同载体上的任务操作。
机械手臂控制包括开环控制和闭环控制两种。
开环控制即使在不考虑反馈信息的情况下,通过输入某个指令,控制机械臂达到预定位置。
开环控制的优点是简单易行,应用广泛,而且在一些不精确的应用中已经得到充分的证明。
但是缺点也显而易见,由于不考虑环境和物体的不同,造成了控制误差,机械手臂无法达到精确的移动,并且当机械手臂受到外力干扰时,控制误差将会更加显著。
机械臂运动学动力学

机械臂运动学动力学机械臂是一种用于模拟人类手臂运动的机械装置,广泛应用于工业生产线、医疗手术、仓储物流等领域。
机械臂的运动学和动力学是研究机械臂运动规律和力学性能的重要方面。
机械臂的运动学研究了机械臂的几何结构和运动规律之间的关系。
它主要包括正解和逆解两个方面。
正解是指通过已知机械臂各个关节的角度,来求解末端执行器的位置和姿态。
逆解则是通过已知末端执行器的位置和姿态,来求解各个关节的角度。
机械臂的正解和逆解是机械臂运动规划和控制的基础,可以帮助我们确定机械臂的姿态以及如何控制机械臂的运动。
机械臂的动力学研究了机械臂运动时的力学特性和力的分布。
它主要包括运动学力学和动力学两个方面。
运动学力学是研究机械臂的关节角度、速度和加速度之间的关系,通过求解运动学方程可以得到机械臂的关节运动特性。
动力学则是研究机械臂在运动过程中所受到的力和力矩,通过求解动力学方程可以得到机械臂的力学性能。
机械臂的动力学研究可以帮助我们确定机械臂所需的驱动力和力矩,以及如何控制机械臂的力。
机械臂的运动学和动力学研究对于机械臂的设计、控制和优化具有重要意义。
通过运动学分析,我们可以确定机械臂的可达空间和工作空间,从而为机械臂的路径规划和避障算法提供依据。
通过动力学分析,我们可以确定机械臂所需的驱动力和力矩,从而为机械臂的选型和控制提供依据。
此外,运动学和动力学的研究还可以帮助我们改进机械臂的设计和优化控制算法,提高机械臂的运动精度和工作效率。
机械臂的运动学和动力学是研究机械臂运动规律和力学性能的重要方面。
通过运动学和动力学的研究,我们可以确定机械臂的运动规划和力学控制策略,从而实现机械臂的高效运动和精准操作。
机械臂的运动学和动力学研究不仅对于机械臂的设计和控制具有重要意义,也对于提高工业生产效率和人类生活质量具有积极影响。
机械臂培训资料
按MODE键保存
3、按ENTER进入到程序的第4步
[指令模式]
OUT
OUT:27=OFF\ON
点胶的开胶指令
1、CMD按下2 和 0
2、输入等待时间
3、按ENTER进入到程序的第5步
[指令模式]
计数器
等待时间=0.00s
输入等待时间(这个时间大于控制器的定时时间)
1、按CMD再按4和0
2、使用↓和→调节光标到OFF
模式
0执行模式[程序模式]
1程序模式
2测试模式频道.001
步数0001
复位完成调到程序模式
[程序模式]
频道.101
步数00001
复位完成
频道. 101 [END]
步数0001Biblioteka END]操作步骤(Step)
程序指令(Command)
程序说明(Description)
1、按CMD再按0和0
2、ABS改为INC输入移动Z数据
3、按ENTER进入到程序的第3步
[指令模式]
PTP移动
ABS
X=+0000.000
Y=+0000.000
Z=+0000.000
移动针头到产品点胶开始位置
然后Z值高度值减去2mm(当前z值减去2mm方便子程序的解决拉丝现象)
1、按CMD再按4和0
2、使用↓和→调节光标到ON
3、按ENTER进入到程序的第4步
N1:行数
N2:列数
CW:顺时针
CCW:逆时针
倾斜角-360---+360之间
呼叫:子程序的代码数
1、按CMD再按0和2
2、按ENTER进入到程序的第5步
机械动力学2自由度机构动力学分析

关键问题
• 二自由度机械手我们这里分析的是平面 的动力学相关问题而还有较复杂空间动 力学问题 • 对于数值计算结果与仿真求解结果存在 些差异,还有待更严谨的计算。
解决方案
1.应用拉格朗日方程也能解决只是计算较复杂 2.需要重新查错验算。
小组成员分工
• • • • • • • PPT制作与课堂介绍:李孟禹、许云猛 三维及二维建模几何参数确定:庞乂铭、薛琨 MATLAB仿真:薛琨、李孟禹 ADAMS仿真:孙铭权、庞乂铭 动力学建模:许云猛、孙文浩 关键问题解决与资料查找:孙文浩、孙铭权 方案讨论与确定:全体成员
The end!
二自由度机械手 动力学分析
小组成员:孙文浩、许云猛、薛琨、孙 铭权、庞乂铭、李孟禹 日期:2018.10.13 指导教师:庞永刚
目录
• • • • • • 三维建模 机构简图 几何参数的确定 动力学建模及数值分析 ADMS仿真分析 关键问题
三 维 建 模
机 构 简 图
A点的位置及速度
B点的位置及速度
广义力:
2
J12 m2l1ls 2 cos 2 1
Q1 M1 m1 gl1 sin 1 Fl1 sin 1 m2 gl1 sin 1 Q2 M 2 Fl3 sin 2 m2 gls 2 sin 2
• MATLAB求解
• 给定条件 角位移运动规律:
l3 l2 l2 1.201 0.750 1.951 m l 1.044 l 1.201 ls1 1 0.522 m ls 2 2 0.6005 m 2 2 2 2
MATLAB求解程序:
• t=0:0.1:3; • D111=0; theta1=-0.1163*t.^3+0.52335*t.^2; D122=-m2*l1*l2*sin(theta2); w1=-0.3489*t.^2+1.0467*t; D222=0; a1=-0.6978*t+1.0467; D211=m2*l1*l2*sin(theta2); theta2=-0.1163*t.^3+0.52335*t.^2; D112=-m2*l1*l2*sin(theta2); w2=-0.3489*t.^2+1.0467*t; D121=-m2*l1*l2*sin(theta2); a2=-0.6978*t+1.0467; D212=0; m1=72.259; D221=0; m2=79.555; D1=(m1+m2)*g*l1*sin(theta1)+m2*g*l2*sin(theta1+theta2); l1=1.044; D2=m2*g*l2*sin(theta1+theta2); l2=1.201; M1=D11.*a1+D12.*a2+D111.*w1.^2+D122.*w2.^2+D112.*w1.*w2+D121.*w2.*w1+D1; g=9.8; M2=D21.*a2+D22.*a2+D211.*w1.^2+D222.*w2.^2+D212.*w1.*w2+D221.*w2.*w1+D2; D11=(m1+m2)*l1.^2+m2*l2.^2+2*m2*l1*l2*cos(theta2); T1=polyfit(t,M1,3) D22=m2*l2.^2; T2=polyfit(t,M2,3) D12=m2*l2.^2+m2*l1*l2*cos(theta2); subplot(2,1,1),plot(t,M1),grid on,xlabel('时间(s)'),ylabel('控制力矩(N· m)'),title('motion1') D21=m2*l2.^2+m2*l1*l2*cos(theta2); subplot(2,1,2),plot(t,M2),grid on,xlabel('时间(s)'),ylabel('控制力矩(N· m)') title('motion2')
第6讲两自由度刚体

xsj xsj ysj ysj sj sj m j q1q2 J sj q1 q2 q1 q2 q1 q2
等 效 转 动 惯 量
2 x 2 y 2 j sj sj J sj J11 m j q1 q1 j 1 q1 N
d E E Qi dt qi qi
注意点: 1)
qi 必须是独立的广义坐标;
2)约束力的处理; 3)保守系统的第二类方程:
d L L 0 dt qi qi
L E V
三、二自由度的机械系统动力学方程及求解
1、运动学分析
(m m1 ) ml F Dx x x 4 2 mlx ml mgl D 3
Assignment
1)列出利用龙格库塔法求解二自由度机械系统动 力学方程的 K1i , K 2i , K3i , K 4i 系数。(选作) 2)写出机械系统动力学分析的一般步骤。
rk Qi Fk qi k 1
m
rk Fk q i 1 k 1 i
n m
qi
Q q
i 1 i
n
i
0
Q q
i 1 i
m
n
i
0
Qi 0
m rk xk yk Qi Fk Fkx Fky qi k 1 qi qi k 1
Fx Dx xx
mgl sin D F Dx x x
Qx F Dx x
Q mgl sin D
两自由度机械臂动力学模型的建模与控制

2020(Sum. No 207)2020年第03期(总第207期)信息通信INFORMATION & COMMUNICATIONS两自由度机械臂动力学模型的建模与控制王磊,陈辰生,张文文(同济大学中德学院,上海202001)摘要:机器人系统建模在布局评估、合理性研究、动画展示以及离线编程等方面有越来越广的应用。
文章对两个自由度 机械臂基于拉格朗日动力学方程,进行建模。
通过建立的模型,分析了重力对两自由度机械臂的影响以及在重力作用下不在稳定位置的机械臂的运动轨迹。
基于机械臂的数学模型,基于Simulink 仿真环境,建立机械臂的仿真模型。
采用逆 动力学方法对机械臂进行控制,观察其对机械臂的控制效果⑴。
通过仿真建模,可以了解机械臂动力学模型以及机械臂动态模型的控制问题。
关键词:动力学模型;数学模型推导;机器人建模;重力分析;逆动力学控制中图分类号:TP241 文献标识码:A 文章编号:1673-1131(2020 )03-0040-03The simulation and control of two ・degree-of freedom robot armWang Lei, Chen Chensheng, Zhang Wenwen(Sino German College of Tongji University, Shanghai 201804)Abstract: The simulation of robot systems is becoming very popular, it can be used for layout evaluation, feasibility studies, presentations with animation and off-line programming 121. In this paper, two degrees of freedom manipulators are modeled based on Lagrange^ dynamic equation. Through the established model, the influence of g ravity on the two-degree-of-freedom manip ulator and the trajectory of the manipulator that is not in a stable position under the action of gravity are analyzed. Based on the mathematical model of the robotic arm and the Simulink simulation environment, a simulation model of the robotic arm is es tablished. The inverse dynamics method was used to control the manipulator, and the control effect on the manipulator was observed. Through simulation modeling, you can understand the dynamics model of the robotic arm and the control problems of the dynamic model of t he robotic arm.Key words: dynamic model; mathematical model derivation; robot modeling; gravity analysis; inverse dynamic control0引言机器人学是一门特殊的工程科学,其中包括机器人设计、建模、控制以及使用。
机械臂动力学与控制

描述物体角动量的变化与力矩的关系,即力矩等于角动量变化率 。
关节型机械臂动力学
连杆长度与速度关系
根据刚体动力学原理,分析连杆长度变化对末端执行 器速度的影响。
力矩与关节角度关系
研究关节驱动力矩与关节角度之间的关系,建立动力 学模型。
动态平衡与稳定性
分析机械臂在运动过程中的动态平衡与稳定性问题。
操作臂动力学
操作臂建模
根据操作臂的结构和运动特点,建立操作臂的动 力学模型。
动态特性分析
分析操作臂的动态特性,如固有频率、阻尼比等 。
控制策略设计
基于操作臂的动力学模型,设计合适的控制策略 ,实现精确的运动控制。
02
机械臂控制方法
经典控制理论
01
02
03
04
PID控制
PID控制器是一种线性控制器 ,通过比较期望输出与实际输 出的误差来调整系统参数。
发展更安全、更自然的人机协作模式 ,使机械臂能够更好地适应人类的操 作习惯和工作流程。
模块化设计
通过模块化设计,使机械臂能够根据 特定任务技术
利用新型材料和先进的制造技术,优 化机械臂的结构和性能。
技术前沿与展望
柔性机械臂
自适应控制算法
结合柔性材料和传感器技术,实现更自然 、更安全的机械臂设计。
通过训练神经网络或其他机器学习模型,基于学习的轨迹规划能够自适应地处理各种复杂环境和任务,提高机械臂的适应性 和灵活性。
04
机械臂应用与实例
工业机械臂
工业机械臂是用于自动化生产 线上的重要设备,能够执行重 复性、高强度的工作,提高生 产效率和降低成本。
工业机械臂通常具有较高的负 载能力和精度,能够完成搬运 、装配、焊接等复杂任务。
机械臂动力学与控制

力控制
总结词
力控制是一种基于末端执行器与环境相互作用力的控制策略。
详细描述
力控制的目标是使末端执行器与环境之间的作用力保持在预定范围内,或者根据任务需求进行精确的力控制。它 通常需要使用力传感器来测量末端执行器与环境之间的作用力,并通过反馈机制调整关节角度以实现力的控制。 力控制在机器人操作任务中具有重要应用,如抓取、装配和人机交互。
运动学模型是描述机械臂末端 执行器与关节角度之间关系的 数学模型。
正运动学
正运动学是确定机械臂末端执行器位置和姿态的问题,给定关节角度,求解末端执 行器的位置和姿态。
正运动学可以通过几何学和线性代数的知识进行求解,常用的方法有解析法和数值 法。
正运动学模型是机械臂控制和路径规划的基础。
逆运动学
逆运动学是确定关节角度以实现特定 位置和姿态的末端执行器的问题,给 定末端执行器的位置和姿态,求解关 节角度。பைடு நூலகம்
随着人工智能技术的不断发展,机械臂的智能化控制已成为未来的发展趋势。通过引入 深度学习、强化学习等算法,机械臂能够自主地适应不同的任务和环境,提高自身的决
策能力和工作效率。
详细描述
智能化控制的核心在于让机械臂具备自主学习和决策的能力。通过训练机械臂识别任务 目标、理解环境信息,并自主规划运动轨迹,可以显著提高机械臂在复杂环境中的适应 性和鲁棒性。此外,智能化控制还可以降低对人工干预的依赖,减少人力成本,为自动
医疗机械臂
手术辅助
医疗机械臂在手术中起到 稳定、精准的操作作用, 提高手术成功率,减少患 者创伤。
康复训练
针对肢体残疾患者,医疗 机械臂可以辅助进行康复 训练,帮助患者恢复肌肉 功能和运动能力。
药物投送
在药物投送方面,机械臂 能够精确控制药物的投放 位置和剂量,提高治疗效 果。
2自由度及几何分析PPT课件

3、逐步扩大法:由一基本刚片开始,逐步增加二元体,扩大刚片的范围 ,将体系归结为两个刚片或三个刚片相连,再用规则判定。
三刚片用不共线 三铰相连,故原 体系为无多余约 束的几何不变体 系。
Ⅲ
O23
Ⅱ
O13
Ⅰ
O12
①抛开基础,只分析上部。 ②在体系内确定三个刚片。 ③三刚片用三个不共线的
三铰相连。 ④该体系为无多余约束的
1、去掉二元体,将体系化简单,然后再分析。
D
A
两根不共线的链杆联结
一点称为二元体。
C
B
依次去掉二元体A、B、C、D后, 剩下大地。故该体系为无多余约
规则三、在一个体系上 增加或拿掉二元体,不会改变
束的几何不变体系。
原体系的几何构造性质。
48
A O12 、O13、 O23
Ⅰ
Ⅱ
Ⅲ
三个刚片用共点的三个铰相连,
2.2.5稳定分析
22
E② D
F ① ⑤⑥
③ ⑧⑨
C
⑦
④
A
B
①
②
⑥
⑨
⑤
③
⑦
⑧
④
例a:j=6;b=9;r=3。 所以:W=2×6-9-3=0
例b:j=6;b=9;r=3。 所以:W=2×6-9-3=0
学而时习之,不亦悦乎。 習
24
例1
刚片法: W=3m-(2n+r) 铰结点法: W=2J-(b+r)
铰 相联,组成无多余约束的几何不变体
B
系。 如约束不满足限制条件,将出现下列几种形式的瞬变体系
三铰共线瞬变体系
三刚片以三对平行链杆相联瞬变体系 两平行链杆于两铰连线平行, 瞬变体系
01-3 两自由度刚性构件机械系统动力学

上式对θ1求偏导数,得
同理 可得
各杆转动角速度
燕山大学
Yanshan University
θ2和θ3速度是广 义坐标与广义速度的函数。
F (q , q , q 1 , q 2 ) 2 1 1 2 F (q , q , q 1 , q 2 ) 3 2 1 2
燕山大学
Yanshan University
Fx F cos(3 90) Fy F sin(3 90) δθ1≠0, δθ4=0,非保守力所做的虚 功。
Q11 M11 Fx x3 Fy y3
同理可以求得Q2。
3 x3 s3 sin 3 1 1 y s cos 3 3 3 3 1 1
33cos90sin90xyffff???????????1??11??133x?y?qmfxfy???333311333311sincosxsys??????????????????????????q1同理可以求得q2
1.4 两自由度刚性构件机械系统动力学
燕山大学
Yanshan University
Q1
燕山大学
Yanshan University
运动微分方程组:
刚性构件机械系统动力学小结 1、系统描述,力学模型
燕山大学
Yanshan University
抽油系统示意图
1、系统描述,力学模型
燕山大学
Yanshan University
H-G
曲柄
2、数学模型 数学模型:模型参数确定、运动微分方程。
运动微分方程的矩阵形式:
燕山大学
Yanshan University
6、系数矩阵的物理意义 (1)有效惯量Dii
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二自由度机械臂动力
学分析
平面二自由度机械臂动力学分析
姓名:黄辉龙 专业年级:13级机电 单位:汕头大学
摘要:机器臂是一个非线性的复杂动力学系统。
动力学问题的求解比较困难,而且需要较长的运算时间,因此,这里主要对平面二自由度机械臂进行动力学研究。
拉格朗日方程在多刚体系统动力学的应用方法分析平面二自由度机械臂的正向动力学。
经过分析,得出平面二自由度机械臂的动力学方程,为后续更深入研究做铺垫。
关键字:平面二自由度 动力学方程 拉格朗日方程
相关介绍
机器人动力学的研究有牛顿-欧拉(Newton-Euler )法、拉格朗日
(Langrange)法、高斯(Gauss )法等,但一般在构建机器人动力学方程中,多采用牛顿-欧拉法及拉格朗日法。
欧拉方程又称牛顿-欧拉方程,应用欧拉方程建立机器人机构的动力学方程是指研究构件质心的运动使用牛顿方程,研究相对于构件质心的转动使用欧拉方程,欧拉方程表征了力、力矩、惯性张量和加速度之间的关系。
在机器人的动力学研究中,主要应用拉格朗日方程建立机器人的动力学方程,这类方程可直接表示为系统控制输入的函数,若采用齐次坐标,递推的拉格朗日方程也可以建立比较方便且有效的动力学方程。
在求解机器人动力学方程过程中,其问题有两类:
1)给出已知轨迹点上•
••θθθ、及、
,即机器人关节位置、速度和加速度,求相应的关节力矩矢量τ。
这对实现机器人动态控制是相当有用的。
2)已知关节驱动力矩,求机器人系统相应各瞬时的运动。
也就是说,给出关节力矩矢量τ,求机器人所产生的运动•
••θθθ、及、。
这对模拟机器人的运动是非常有用的。
平面二自由度机械臂动力学方程分析及推导过程
1、机器人是结构复杂的连杆系统,一般采用齐次变换的方法,用拉格朗日方程建立其系统动力学方程,对其位姿和运动状态进行描述。
机器人动力学方程的具体推导过程如下:
1) 选取坐标系,选定完全而且独立的广义关节变量n r ,,2,1,r ⋅⋅⋅=θ。
2) 选定相应关节上的广义力r F :当r θ是位移变量时,r F 为力;当r θ是角度变量时,r F 为力矩。
3)求出机器人各构件的动能和势能,构造拉格朗日函数。
4) 代入拉格朗日方程求得机器人系统的动力学方程。
2、下面以图1所示说明机器人二自由度机械臂动力学方程的推导过程。
1)如图1,设21,θθ是广义坐标,21,Q Q 是广义力。
2)分别求出两杆的动能和势能 11112111111sin ,2
121:1θθc c c T c gl m U I v v m E =+=•杆 (1-1) ]sin [,2
121:22112222122222)()(杆θθθθ+=++=••l g m U I v v m E c c T c (1-2)
式中,1c v 是杆1质心),(111c c y x C 的速度向量,2c v 是杆2质心),(222c c y x C 的速度向量。
它们可以根据质心21,C C 的位置方程导出。
3)分别求出两杆的速度 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=)sin ()cos (1111111θθl dt
d l dt d dt dy dt dx v c c c (1-3)
[][]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=)sin(sin )cos(cos 2121121211222θθθθθθc c c c c l l dt
d l l dt d dt dy dt dx v (1-4)
4)代入拉格朗日方程求得机械臂动力学方程
根据具有完整理想约束的有N 个广义坐标系统的拉格朗日方程 n r Q q U q E q E dt d r r r r ,2,1,⋅⋅⋅==∂∂+∂∂-⎪⎪⎪⎭
⎫ ⎝⎛∂∂• (1-5)
式中,r q 是第r 个广义坐标,E 是系统动能,U 是系统势能,r Q 是对第r 个广义坐标的广义力。
该问题为二自由度的动力学研究,所以n=2,由于势能函数U 与广义速度无关,即•∂∂r q U
=0。
由(1-5)式可写成: r r r Q q L q L dt d =∂∂-⎪⎪⎪⎭
⎫ ⎝⎛∂∂• (1-6)
其中,是拉格朗日算子L U E L ,-=
可知在这里拉格朗日算子为:2121U U E E L --+=
代入式(1-6)可导出相应的式子,经过整理得:
Q g C M =++•
••)(),()(θθθθθ (1-7)
式中 ⎥⎦
⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=•21212122211211
,)(,),(,)(Q Q Q g g g C C C M M M M M θθθθ
[]⎪⎪⎪⎪⎩
⎪⎪⎪⎪⎨⎧+=+++==+-=+==++=+++++=•
••)cos()cos(cos cos sin ),2(sin ,)cos ()cos 2(212222*********
22122212221212222221221222122221222122212121111θθθθθθθθθθθθθc c c c c c c c c c c c c gl m g l l g m gl m g l l m C l l m C I l m M M M I l l l m M I l l l l m I l m M 式(1-7)为机械臂在关节空间的动力学方程的一般结构形式,它反映了关节力矩和关节变量、速度、加速度之间的函数关系。
对于n 个关节的机械臂,)(θM 是n n ⨯的正定对称矩阵,是θ的函数,称为机械臂的惯性矩阵;),(•θθC 是nx1的离心力和科氏力矢量;)(θg 是nx1的重力矢量,与机械臂的形位θ有关。
