华东师大版初三数学下册二次函数单元知识点总结

华师大版九年级下册数学知识点总结

华师大版九年级下册数学知识点总结第二十六章二次函数一、二次函数概念：1、二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零。

二次函数的定义域是全体实数。

2、二次函数2y ax bx c =++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2。

⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项。

二、二次函数的基本形式1. 二次函数基本形式：2y ax =的性质：a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质：3. ()2y a x h =-的性质：4. ()2y a x h k =-+的性质：三、二次函数图象的平移 1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下： 2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”。

概括成八个字“左加右减，上加下减”。

方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭，其中2424b ac b h k a a -=-=，。

华师大版九年级下册数学知识点总结

华师大版九年级下册数学知识点总结第二十六章二次函数一、二次函数概念：1、二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零。

二次函数的定义域是全体实数。

2、二次函数2y ax bx c =++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2。

⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项。

二、二次函数的基本形式1. 二次函数基本形式：2y ax =的性质：a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质：3. ()2y a x h =-的性质：4. ()2y a x h k =-+的性质：三、二次函数图象的平移 1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”。

概括成八个字“左加右减，上加下减”。

方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭，其中2424b ac b h k a a -=-=，。

华师大版九年级下册数学知识点总结

华师大版九年级下册数学知识点总结第二十六章二次函数一、二次函数概念：1、二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零。

二次函数的定义域是全体实数。

2、二次函数2y ax bx c =++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2。

⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项。

二、二次函数的基本形式1. 二次函数基本形式：2y ax =的性质：a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质：3. ()2y a x h =-的性质：4.()2y a x h k=-+的性质：三、二次函数图象的平移1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，；⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”。

概括成八个字“左加右减，上加下减”。

方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭，其中2424b ac b h k a a -=-=，。

华东师范大学出版社九年级下册数学知识点总结

华师大版九年级下册数学知识点总结第二十六章二次函数一、二次函数概念：1、二次函数的概念：一般地，形如2=++（a b cy ax bx c，，是常数，0a≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a≠，而b c，可以为零。

二次函数的定义域是全体实数。

2、二次函数2=++的结构特征：y ax bx c⑴等号左边是函数，右边是关于自变量x的二次式，x的最高次数是2。

⑵a b c，，是常数，a是二次项系数，b是一次项系数，c是常数项。

二、二次函数的基本形式1. 二次函数基本形式：2=的性质：a 的绝对值越大，抛物线的开口越小。

y ax2. 2=+的性质：y ax c Array3. ()2=-的性质：y a x h4. ()2y a x h k=-+的性质：三、二次函数图象的平移 1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k=-+，确定其顶点坐标()h k ，；⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”。

概括成八个字“左加右减，上加下减”。

方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k=-+与2y ax bx c =++的比较从解析式上看，()2y a x h k=-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭，其中2424b ac b h k a a-=-=，。

华师大版九年级下册数学知识点总结

华师大版九年级下册数学知识点总结第二十六章二次函数一、二次函数概念：1、二次函数的概念：一般地，形如2=++（a b cy ax bx c，，是常数，0a≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a≠，而b c，可以为零。

二次函数的定义域是全体实数。

2、二次函数2=++的结构特征：y ax bx c⑴等号左边是函数，右边是关于自变量x的二次式，x的最高次数是2。

⑵a b c，，是常数，a是二次项系数，b是一次项系数，c是常数项。

二、二次函数的基本形式y ax=的性质：a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质：3. ()2y a x h =-的性质：4. ()2y a x h k =-+的性质：三、二次函数图象的平移 1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，；⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下： 2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”。

概括成八个字“左加右减，上加下减”。

方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭，其中2424b ac b h k a a-=-=，。

华东师范大学九年级下册数学知识点总结

华师大版九年级下册数学知识点总结第二十六章二次函数一、二次函数概念：1、二次函数的概念：一般地，形如2=++（a b cy ax bx c，，是常数，0a≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a≠，而b c，可以为零。

二次函数的定义域是全体实数。

2、二次函数2=++的结构特征：y ax bx c⑴等号左边是函数，右边是关于自变量x的二次式，x的最高次数是2。

⑵a b c，，是常数，a是二次项系数，b是一次项系数，c是常数项。

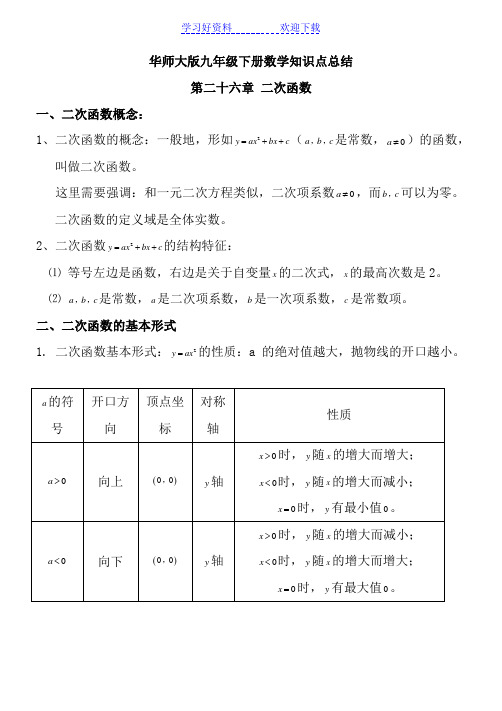
二、二次函数的基本形式1. 二次函数基本形式：2=的性质：a 的绝对值越大，抛物线的开口越小。

y ax2. 2=+的性质：y ax c Array3. ()2=-的性质：y a x h4. ()2y a x h k=-+的性质：三、二次函数图象的平移 1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k=-+，确定其顶点坐标()h k ，；⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”。

概括成八个字“左加右减，上加下减”。

方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k=-+与2y ax bx c =++的比较从解析式上看，()2y a x h k=-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭，其中2424b ac b h k a a-=-=，。

华师大版九年级下册数学知识点总结

华师大版九年级下册数学知识点总结第二十六章二次函数一、二次函数概念：1、二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零。

二次函数的定义域是全体实数。

2、二次函数2y ax bx c =++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2。

⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项。

二、二次函数的基本形式1. 二次函数基本形式：2y ax =的性质：a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质：3. ()2y a x h =-的性质：4.()2y a x h k=-+的性质：三、二次函数图象的平移1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，；⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”。

概括成八个字“左加右减，上加下减”。

方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭，其中2424b ac b h k a a -=-=，。

华东师大版九年级数学下26章二次函数知识点总结及经典例题

二次函数知识点总结一、二次函数概念:1二次函数的概念：一般地，形如y ax2 bx c（ a, b , c是常数，a 0 ）的函数，叫做二次函数。

里需要强调：和一元二次方程类似，二次项系数 a 0，而b，c可以为零•二次函数的定义域是全体实数•--22. 二次函数y ax bx c的结构特征：⑴等号左边是函数，右边是关于自变量x的二次式，x的最高次数是2.⑵a ,b, c是常数，a是二次项系数，b是一次项系数，c是常数项.二、二次函数的基本形式1. 二次函数基本形式：y ax2的性质:a的绝对值越大，抛物线的开口越小。

22. y ax c的性质:上加下减。

23. y a x h的性质:左加右减。

六、四、二次函数从解析式上看,b a x2a二次函数 4ac b 24a，其中 ax 2bx c 的性质ax 22axbx c 的比较 bx c 是两种不同的表达形式,4ac b 24a 后者通过配方可以得到前者,a 0向下 h , 0 X=hx h 时，y 随x 的增大而减小；x h 时，y 随 x 的增大而增大；x h 时，y 有最大值0 •24. y ax hk 的性质:a 的符号开口方向顶点坐标对称轴性质a 0向上h , kX=hx h 时，y 随x 的增大而增大；x h 时，y 随 x 的增大而减小；x h 时，y 有最小值k •a 0向下 h , k X=hx h 时，y 随x 的增大而减小；x h 时，y 随 x 的增大而增大；x h 时，y 有最大值k •三、二次函数图象的平移1. 平移步骤：⑴将抛物线解析式转化成顶点式⑵ 保持抛物线y ax 2的形状不变，将其顶点平移到h ，k 处，具体平移方法如下:2y a x h k ，确定其顶点坐标 h, k ；y=ax 2 A y=ax 2+k向右(h>0)【或左(*0)] 平移|k|个单位向右(h>0)【或左(h<0)] 平移|k|个单位2. 平移规律在原有函数的基础上概括成八个字“左加右减, h 值正右移，负左移;上加下减” •k 值正上移，负下移”向上(k>0)【或向下(k<0)】平移|k|个单位向上(k>0)【或下(k<0)】平移|k 个单位向上(k>0)【或下(k<0)] 平移|k 个单位y=a(x h)2y=a(x h)2+k向右(h>0)【或左(h<0)]平移|k|个单位七、二次函数解析式的表示方法21. 一般式：y ax bx c （ a , b , c 为常数，a 0）； 2•顶点式：y a （x h ）2 k （ a , h , k 为常数，a 0）;3. 两根式（交点式）：y a （x x i ）（x 血）（a 0, x , X 2是抛物线与x 轴两交点的横坐标）注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即b 2 4ac 0时，抛物线的解析式才可以用交点式表示. 二次函数解析式的这三种形式可以互化.二次函数的图象与各项系数之间的关系二次项系数a当a 0时，抛物线开口向上，当a 0时，抛物线开口向下，九、二次函数与一元二次方程:1.二次函数与一元二次方程的关系（二次函数与二次方程ax bx c 0是二次函数y x 轴的交点个数：兀图象与 2ax x 轴交点情况）： bx c 当函数值 y 0时的特殊情况. 2b 4ac 0时，图象与x 轴交于两点A X i , 0 , B x 2 , 0 (X i X 2），其中的X i , X 2是一元二次方2ax bx 0的两根.. 1' 2' 0时, 0时, 当a 当a x 轴只有一个交点; x 轴没有交点. 图象与图象与 0时，图象落在x 轴的上方，无论 0时，图象落在x 轴的下方，无论x 为任何实数，都有 x 为任何实数，都有2•当a2时,2a 2时，2a2ba 时， y 随x 的增大而减小; y 随x 的增大而增大;y 有最小值 24ac b4a0时，抛物线开口向下, 对称轴为暑，顶点坐标为b 4ac b 2 2a' 4a•当x —时，y 随2ax的增大而增大；当x时，y 随x 的增大而减小；当 x2—时，y 有最大值4^-b -2a4a八、 1. ⑴ ⑵a 的值越大，开口越小，反之 a 的值越小，开口越大; a 的值越小，开口越小，反之 a 的值越大，开口越大.2. 一次项系数b在二次项系数a 确定的前提下, 3. 常数项c⑴当c ⑵当c ⑶当c总结起来， b 决定了抛物线的对称轴.（同左异右 b 为0对称轴为y 轴）抛物线与y 轴的交点在x 轴上方，即抛物线与抛物线与y 轴的交点为坐标原点，即抛物线与抛物线与0时，0时， 0时， c 决定了抛物线与y 轴交点的位置.y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为正； y轴交点的纵坐标为0 ； y 轴交点的纵坐标为负.22. 抛物线y ax bx c的图象与y 轴一定相交，交点坐标为(0 , c)；二次函数对应练习试题一、选择题1. 二次函数y x2 4x 7的顶点坐标是()A.(2, —11)B. (- 2, 7)C. (2, 11)D. (2, - 3)2. 把抛物线y 2x2向上平移1个单位，得到的抛物线是( )2 2 2 2A. y 2(x 1)B. y 2(x 1)C. y 2x 1D. y 2x 12 k3. 函数y kx k和y (k 0)在同一直角坐标系中图象可能是图中的()x4.已知二次函数y ax2bx c(a 0)的图象如图所示当x 1和x 3时，函数值相等；③4a b 0④当y确的个数是()A.1个B.2 个C. 35.已知二次函数ax2 bx c(a由图象可知关于兀二次方程axA. — 1 .6.已知二次函数A.第一象限C.第三象限7.方程2x x2A.0个8.已知抛物线过点,则下列结论：①a,b同号；②2时,x的值只能取0.其中正个个D. 4B.-2.3C.-0.3D.-3.32ax bx c的图象如图所示，则点(ac,bc)在(B.第二象限D.第四象限-的正根的个数为( )xB. 1C.2A(2,0),B(-1,0), 与y轴交于点C,且OC=2.则这条抛物线的解析式为2A.y2x2x 2B.y2x2x 2C.y x2 x 2 或y 2 小x x 2 D.y2 2x x 2 或y x x 2二、填空题9•二次函数y x2 bx 3的对称轴是x 2，则b ______________ 。

华师大版九年级下册数学知识点总结

华师大版九年级下册数学知识点总结第二十六章二次函数一、二次函数概念：1、二次函数的概念:一般地，形如2y ax bx c =++（a b c ，，是常数,0a ≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似,二次项系数0a ≠,而b c ，可以为零。

二次函数的定义域是全体实数。

2、二次函数2y ax bx c =++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2。

⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项。

二、二次函数的基本形式1。

二次函数基本形式：2y ax =的性质：a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质：3. ()2y a x h =-的性质：4。

()2y a x h k =-+的性质：三、二次函数图象的平移 1. 平移步骤：方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移;k 值正上移,负下移”。

概括成八个字“左加右减，上加下减”。

方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下)平移m 个单位,c bx ax y ++=2变成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭，其中2424b ac b h k a a -=-=，。

华师大版九年级下册数学知识点总结

华师大版九年级下册数学知识点总结第二十六章二次函数一、二次函数概念：1、二次函数的概念：一般地，形如2y axbx c=++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c，可以为零。

二次函数的定义域是全体实数。

2、二次函数2y ax bx c=++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2。

⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项。

二、二次函数的基本形式1. 二次函数基本形式：2y ax =的性质：a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质：3. ()2y a x h =-的性质：4. ()2y a x h k =-+的性质：三、二次函数图象的平移 1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”。

概括成八个字“左加右减，上加下减”。

方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭，其中2424b ac b h k a a -=-=，。

华师大版九年级下册数学知识点总结

华师大版九年级下册数学知识点总结第二十六章二次函数一、二次函数概念：1、二次函数的概念：一般地，形如2y ax bx c=++（a b ca≠）的函数，叫做二次函，，是常数，0数。

这里需要强调：和一元二次方程类似，二次项系数0a≠，而b c，可以为零。

二次函数的定义域是全体实数。

2、二次函数2=++的结构特征：y ax bx c⑴等号左边是函数，右边是关于自变量x的二次式，x的最高次数是2。

⑵a b c，，是常数，a是二次项系数，b是一次项系数，c是常数项。

二、二次函数的基本形式1. 二次函数基本形式：2=的性质：a 的绝对值越大，抛物线的开口越小。

y ax2. 2=+的性质：y ax c3. ()2=-的性质：y a x h4. ()2y a x h k =-+的性质：三、二次函数图象的平移 1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”。

概括成八个字“左加右减，上加下减”。

方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭，其中2424b ac b h k a a -=-=，。

华师大版九年级下册数学知识点总结

华师大版九年级下册数学知识点总结第二十六章二次函数一、二次函数概念：1、二次函数的概念：一般地，形如2=++（a b cy ax bx ca≠）的，，是常数，0函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a≠，而b c，可以为零。

二次函数的定义域是全体实数。

2、二次函数2=++的结构特征：y ax bx c⑴等号左边是函数，右边是关于自变量x的二次式，x的最高次数是2。

⑵a b c，，是常数，a是二次项系数，b是一次项系数，c是常数项。

二、二次函数的基本形式1. 二次函数基本形式：2=的性质：a 的绝对值越大，抛物线的开口越y ax小。

2. 2=+的性质：y ax c3. ()2=-的性质：y a x h4. ()2=-+的性质：y a x h k三、二次函数图象的平移1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，；⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”。

概括成八个字“左加右减，上加下减”。

方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭，其中2424b ac b h k a a-=-=，。