单纯形法原理推导过程
第二章 单纯形法

第二章单纯形法第二章单纯形法单纯形法的一般原理表格单纯形法借助人工变量求初始的基本可行解单纯形表与线性规划问题的讨论改进单纯形法考虑到如下线性规划问题其中A一个m×n矩阵,且秩为m,b总可以被调整为一个m维非负列向量,C为n维行向量,X为n维列向量。
根据线性规划基本定理:如果可行域D={ X∈Rn / AX=b,X≥0}非空有界,则D上的最优目标函数值Z=CX一定可以在D的一个顶点上达到。
这个重要的定理启发了Dantzig的单纯形法,即将寻优的目标集中在D的各个顶点上。
单纯形法的一般原理Dantzig的单纯形法把寻优的目标集中在所有基本可行解(即可行域顶点)中。
其基本思路是从一个初始的基本可行解出发,寻找一条达到最优基本可行解的最佳途径。
单纯形法的一般步骤如下:(1)寻找一个初始的基本可行解。
(2)检查现行的基本可行解是否最优,如果为最优,则停止迭代,已找到最优解,否则转一步。
(3)移至目标函数值有所改善的另一个基本可行解,然后转会到步骤(2)。
确定初始的基本可行解确定初始的基本可行解等价于确定初始的可行基,一旦初始的可行基确定了,那么对应的初始基本可行解也就唯一确定为了讨论方便,不妨假设在标准型线性规划中,系数矩阵A中前m个系数列向量恰好构成一个可行基,即A=(BN),其中B=(P1,P2,…Pm)为基变量x1,x2,…xm的系数列向量构成的可行基,N=(Pm+1,Pm+2,…Pn)为非基变量xm+1,xm+2,…xn的系数列向量构成的矩阵。
所以约束方程就可以表示为用可行基B的逆阵B-1左乘等式两端,再通过移项可推得:若令所有非基变量, 则基变量由此可得初始的基本可行解问题:要判断m个系数列向量是否恰好构成一个基并不是一件容易的事。
基由系数矩阵A中m个线性无关的系数列向量构成。
但是要判断m个系数列向量是否线性无关并非易事。
即使系数矩阵A中找到了一个基B,也不能保证该基恰好是可行基。
因为不能保证基变量XB=B-1b≥0。
单纯形法基本原理

否
含 有xa
是 无可行解
(a对ik
0 任一
j 0)
否
是 无界解
有某个 否 非基变量的
j 0
唯一 最优解
是
无穷多
最优解
循
环
停止
计 算 i
( bi alk
alk
0)
用 非 基 变 量xk 替 换 基 变 量xl
列出下一个 新单纯形表
单纯形法的进一步讨论-人工变量法 Page 17
解的判别: 1)唯一最优解判别:最优表中所有非基变量的检验数非零, 则线 规划具有唯一最优解。 2)多重最优解判别:最优表中存在非基变量的检验数为零, 则线则性规划具有多重最优解(或无穷多最优解)。 3)无界解判别:某个λk>0且aik≤0(i=1,2,…,m)则线性 规划具有无界解。 4)无可行解的判断:当用大M单纯形法计算得到最优解并 且存在Ri>0时,则表明原线性规划无可行解。 5)退化解的判别:存在某个基变量为零的基本可行解。
max Z 3 x1 4 x2
2x1 x2 40
x1
3x2
30
x1
,
x2
0
解:1)将问题化为标准型,加入松驰变量x3、x4则标准型为:
max Z 3 x1 4 x2
2 x1 x2 x3 40
ቤተ መጻሕፍቲ ባይዱ
x
1
3x2
x4
30
x1
,
x2
,
x3
换
x3
x4
出
1
0
40 行
0
1
第5章_单纯形法

初始可行解:第一个找到的可行域的顶点。
三、单纯形法试算程序框图(见图5—1)
开始
转变为标准型[增加额外 变量(松弛、剩余、人工 变量)]
建立初始单纯形表
最优
是
停
否 找出“换入”“换出”变量
修正单纯形表
图5—1
5.2 线性规划模型的变换
一、线性规划模型标准型的特点 ⑴目标函数是求极大值或极小值; ⑵所有的变量都是非负的; ⑶除变量的非负约束外,其余的约束条件都
ABCD 含量(单位/千克)
最低需求量 (单位)
糖
5 2 4 2 60
蛋白质
3 2 1 4 40
脂肪
3 1 2 5 35
单价(元/千克) 1.5 0.7 0.9 1.2
例3是例2的对偶问题,例3与例2互为对偶线性规 划原规划与对偶规划具有对称性,如图所示:
食品
单一营
养成分单价
AB C D
单一营养
(x1) (x2) (x3) (x4) 成分需求量
m
c a Z j
i ij
i 1
解b
b 1
b 2
…… b
n
目标函 数
例1
求max Z=7x1+10x2 满足 7x1+7x2≤49 10x1+5x2≤50 x1,x2≥0
用单纯形法求解。
例2
第2章例1中我们得线性规划模型为: 目标函数:max Z = 50x1+100x2
满足 x1 + x2 ≤300 2x1 + x2 ≤400 x2 ≤250 x1,x2 ≥0
…… am1x1 + am2x2 + ……+ amnxn ≤(≥,=) bm x1,x2 …… xn≥ 0
系统工程导论_09单纯形法

(1)
第三、第一次迭代,得到初始基本可行解后,就进入迭代过程,但在开始迭代前应建立 一个判断标准, 以便决定每次迭代后的基本可行解是否是最优解, 从而决定迭代过程是停止 还是继续。选取临近顶点,如果能使目标函数值增大,则为新的基础可行解。 1)选择引入变量:选大原则; 考虑目标函数 f x 13x1 11x 2 ,由于 x1 的系数 13 比 x 2 的系数 11 大,故选 x1 为 引入变量; 2)选择退出变量:最小比值规则(或 规则) ;
x3 1500 4 x1 41500 / 4 x1 4375 x1 由于 x 2 0 ,根据(1)有: x 4 1575 5 x1 51575 / 5 x1 5315 x1 ,取 x 420 x 1420 / 1 x 1420 x 1 1 1 5
x1 2 x 2 x3 10 s.t. 2 x1 3 x 2 3 x3 10 (Ⅰ) x 0, x 0, x 0 2 3 1
线性规划问题(Ⅰ)和(Ⅱ)之间有如下关系: ① 一个问题的目标函数系数是另一个问题约束条件的右端常数; ② 一个问题的第 i 个约束条件的各系数是另一个问题第 i 个变量的约束条件系数(或, 一个问题的约束条件的系数矩阵是另一个问题的约束条件系数矩阵的转置) ; ③ 一个问题是求目标函数的极大值,约束条件全都是“≤”形式,而另一个问题是求 目标函数的极小值,约束条件全都是“≥”形式; ④ 两个问题的变量均非负。 一般情况:
3 x1 6 x2 24 s.t. 2 x1 x2 10 x 0, x 0 2 1
解:最优解为 x1 4 , x2 2 ,最优值为 f x 14 。
单纯形法原理

单纯形法原理及步骤单纯形法,求解线性规划问题的通用方法。
单纯形是美国数学家G.B.丹齐克于1947年首先提出来的。
它的理论根据是:线性规划问题的可行域是n维向量空间Rn中的多面凸集,其最优值如果存在必在该凸集的某顶点处达到。
顶点所对应的可行解称为基本可行解。
单纯形法的基本思想是:先找出一个基本可行解,对它进行鉴别,看是否是最优解;若不是,则按照一定法则转换到另一改进的基本可行解,再鉴别;若仍不是,则再转换,按此重复进行。
因基本可行解的个数有限,故经有限次转换必能得出问题的最优解。
如果问题无最优解也可用此法判别。
单纯形法是从某一基可行解出发,连续地寻找相邻的基可行解,直到达到最优的迭代过程,其实质是解线性方程组。
概述:根据单纯形法的原理,在线性规划问题中,决策变量(控制变量)x1,x2,…x n的值称为一个解,满足所有的约束条件的解称为可行解。
使目标函数达到最大值(或最小值)的可行解称为最优解。
这样,一个最优解能在整个由约束条件所确定的可行区域内使目标函数达到最大值(或最小值)。
求解线性规划问题的目的就是要找出最优解。
最优解可能出现下列情况之一:①存在着一个最优解;②存在着无穷多个最优解;③不存在最优解,这只在两种情况下发生,即没有可行解或各项约束条件不阻止目标函数的值无限增大(或向负的方向无限增大)。
单纯形法的一般解题步骤可归纳如下:①把线性规划问题的约束方程组表达成典范型方程组,找出基本可行解作为初始基本可行解。
②若基本可行解不存在,即约束条件有矛盾,则问题无解。
③若基本可行解存在,从初始基本可行解作为起点,根据最优性条件和可行性条件,引入非基变量取代某一基变量,找出目标函数值更优的另一基本可行解。
④按步骤3进行迭代,直到对应检验数满足最优性条件(这时目标函数值不能再改善),即得到问题的最优解。
⑤若迭代过程中发现问题的目标函数值无界,则终止迭代。
用单纯形法求解线性规划问题所需的迭代次数主要取决于约束条件的个数。
02.1-4 单纯形法

定理2.2(解的收敛定理 ) 定理 . (解的收敛定理
在已知一个基本可行解(初始基本可行 在已知一个基本可行解 初始基本可行 的前提下, 解)的前提下,使用单纯形法求解线性规划 的前提下 时,若每次迭代得出的基本可行解的基变量 均大于零(称为非退化),则算法必有限步终 均大于零 -1 1
-4 3
1 6 0 5
概念:单位子块——每行, 每行, 概念:单位子块 每行 每列均有一个元素为l, 每列均有一个元素为 ,其 余元素均为0的子块 的子块. 余元素均为 的子块.
取x1,x3为自由未知量 ,则可得
x 4 = 6 2 x1 + 4 x 3 x 2 = 5 + x1 3 x 3
二,确定初始的基本可行解
确定初始的基本可行解等价于确定初始的 可行基,一旦初始的可行基确定了, 可行基,一旦初始的可行基确定了,那么对应 的初始基本可行解也就唯一确定.
1.求基本可行解即为求解线性方程组Ax=b, .求基本可行解即为求解线性方程组 = , 方法: 含有n个未知量 的秩R(A)= 方法:设Ax=b含有 个未知量,A的秩R(A)= , 含有 个未知量, 的秩R(A)=m, 故由它可解出m个变量 称为基本变量),剩下的nm个变量 故由它可解出 个变量(称为基本变量 ,剩下的 个变量 称为基本变量 个变量 为自由取值的变量(称为自由变量 为自由取值的变量 称为自由变量 ,而所谓基本解即解中 称为自由变量), 取零的变量个数不少于nm个,于是,最简便的方法是: 个 于是,最简便的方法是: 取零的变量个数不少于
算法终止包括两种情况: 算法终止包括两种情况:
使表具有四个特点而得到了最优解和最 优值 在执行2步时, 在执行 步时,在所选列底线以上的元素 步时 中根本没有正元素, 中根本没有正元素,这时算法亦终止
单纯形法

单纯形法一、单纯形法的原理线性方程组的解:⎩⎨⎧=----=+-+-4322425432154321x x x x x x x x x x (1) 5个未知数,两个方程组。
方程的解多于1个。
两种初等变换:51)方程组的任一方程乘上一个不为零的数。
2)方程组的任一方程两边同乘上一个常数,分别加到另一个方程的两边。
式(1)做变换得到:(①×-1)⎩⎨⎧=-+-=+-+-2322242543254321x x x x x x x x x (2) 式(2)做变换得到:(②×2)⎩⎨⎧=-+-=---232642354325431x x x x x x x x (3)方程组(1)、(2)、(3)同解,可令0543===x x x 。
得到:61=x ,22=x 。
选择3x ,4x ,5x 不同的值,相应地有不同的1x 和2x 的值,因此方程组有多组解。
基本变量:如果变量i x 的系数在某一个方程为1,而在其它所有方程为0,则称i x 为该方程组中的基本变量。
非基本变量:凡不是基本变量的变量都叫做非基本变量。
1x ,2x 为基本变量;3x ,4x ,5x 为非基本变量。
旋转运算:运用初等变换,可使一给定变量化为基本变量,这一运算,成为旋转运算。
基本变量的个数,与方程的个数相同。
基本解:设非基本变量为0,求得相应的基本变量的值,得到一组解,这组解称为基本解。
基本可行解:基变量的值为非负时的基本解称为基本可行解。
单纯形法的思路;1)先不考虑目标函数,从满足约束条件开始,寻求一个初始基本可行解; 2)求具有较佳目标函数值的另一个基本可行解,以改进初始解;3)对目标函数做有限次的改善。
当某一个基本可行解不能再得到改善时,即求得最优解,单纯形法结束。
二、单纯形算法例:54321325max x x x x x Z +-++= 约束条件为:⎪⎩⎪⎨⎧≥≥≥≥≥=+++=+++0,0,0,0,0743********53214321x x x x x x x x x x x x x (5) 以上线性规划问题中,具有: 1)全部变量非负;2)全部约束条件都是等式;5 3)右端常数都是正的。
单纯形法求解原理过程

单纯形法求解原理过程第一篇:单纯形法求解原理过程单纯形法需要解决的问题:如何确定初始基本可行解;如何由一个基本可行解迭代出另一个基本可行解,同时使目标函数获得较大的下降;如何判断一个基本可行解是否为最优解。
min f(X)=-60x1-120x2 s.t.9x1+4x2+x3=360 3x1+10x2+x4=300 4x1+5x2+x5=200 xi≥0(i=1,2,3,4,5)(1)初始基本可行解的求法。
当用添加松弛变量的方法把不等式约束换成等式约束时,我们往往会发现这些松弛变量就可以作为初始基本可行解中的一部分基本变量。
例如:x1-x2+x3≤5 x1+2x2+x3≤10xi≥0 引入松弛变量x4,x5后,可将前两个不等式约束换成标准形式 x1-x2+x3+x4=5 x1+2x2+x3+x5=10xi≥0(i=1,2,3,4,5)令x1=x2=x3=0,则可立即得到一组基本可行解x1=x2=x3=0,x4=5,x5=10 同理在该实例中,从约束方程式的系数矩阵⎡94100⎤⎥A=[P1,P2,P3,P4,P5]=⎢310010⎢⎥⎢⎣45001⎥⎦中可以看出其中有个标准基,即⎡100⎤⎥B=⎢010⎢⎥⎢⎣001⎥⎦与B对应的变量x3,x4,x5为基本变量,所以可将约束方程写成X3=360-9x1-4x2 x4=300-3x1-10x2 x5=200-4x1-5x20 若令非基变量x1=x2=0,则可得到一个初始基本可行解X0 TX=[0,0,360,300,200]判别初始基本可行解是否是最优解。
此时可将上式代入到目标函数中,得: F(X)=-60x1-120x20对应的函数值为f(X)=0。
0由于上式中x1,x2系数为负,因而f(X)=0不是最小值。
因此所得的解不是最优解。
011(2)从初始基本可行解X迭代出另一个基本可行解X,并判断X 是否为最优解。
从一个基本可行解迭代出另一个基本可行解可分为两步进行:第一步,从原来的非基变量中选一个(称为进基变量)使其成为基本变量;第二步,从原来的基本变量中选一个(称为离基变量)使其成为新的非基变量。
运筹学-第一章-单纯形法基本原理
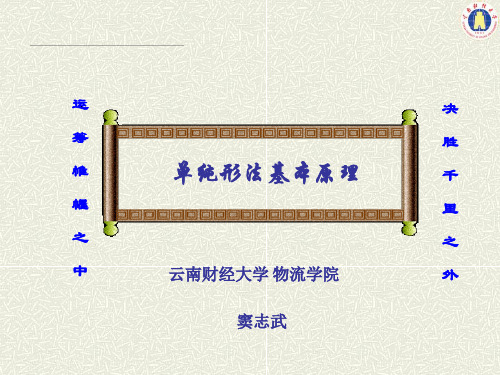
因为p1,…,pm,是一个基,其他向量pj可以这个基 的线性组合表示:
p j aij pi
i 1
m
单纯形法基本原理
m
( p j aij pi ) 0
i 1
m
p j aij pi 相减,然后乘上一个正数θ ,加上
i 1
p x
i 1
m
( 0)
i i
b 经过整理得到:
凸集
顶点
凸集
不是凸集
顶点:如果凸集C中不存在任何两个不同的点X1,X2,使X 成为这两个点连线上的一个点
单纯形法基本原理
定理1:若线性规划问题存在可行解,则该问题的可行域是 凸集。 定理2:线性规划问题的基可行解X对应可行域(凸集)的顶 点。 定理3:若问题存在最优解,一定存在一个基可行解是最优 解。(或在某个顶点取得)
( 0)
( x , x2 ,...xm , o,...o)
n j 1
0 1
0x j
n Pj x j b s.t. j 1 x j 0( j 1,2,3...n)
代入约束条件有
px
i 1
m
0
i i
b
单纯形法基本原理
系数矩阵的增广矩阵
bb列正好就是基变量的取值因此称列正好就是基变量的取值因此称bb列列为为解答列解答列单纯形法基本原理单纯形法基本原理令非基变量取非基变量取00基变量对应基变量对应bbii一起构一起构成初始基可行解成初始基可行解单纯形法基本原理单纯形法基本原理lplp单纯形法基本原理单纯形法基本原理在约束条件中的变量系数矩阵中总会有一个单位矩阵在约束条件中的变量系数矩阵中总会有一个单位矩阵初始可行基初始可行基当线性规划的约束条件均为其松弛变量的系数矩阵为单位矩阵
运筹学课件1-3单纯形法原理

理论方法 算法步骤 单纯形表
算例
第1页
一、基本概念
考虑线性规划标准形式 max z CX s .t . AX b X 0 :
其中A为m×n阶矩阵
可行解:满足AX=b,且X≥0的解称为可行解。 可行域:全部可行解的集合称为可行域。 最优解:使目标函数达到最大值的可行解称为最 优解。 基:设B是系数矩阵A的一个m×n阶的满秩子矩阵, 称B是(LP)的一个基。
-5 0 0
2.5 0 4 4 0 3
1.5 17.5 22 19
-3 0 0 0
问:基解中零的个数至少有多少个? 至少n-m个
例3
x1=0, x3=0 x2=3, x4=-2 是基解,但不 是可行解
D
max z=x1+2x2 s.t. x1+x23 x2 1 x1, x2 0
max z=x1+2x2 s.t. x1+x2+ x3 =3 x2 +x4=1 x1, x2 ,x3, x40
第12页
三、几个基本定理
引理 线性规划问题的可行解为基可行解的充要条件 是它的正分量所对应的系数列向量线性无关。
证: (2)充分性
若向量 P1 , P2 , , Pk 线性无关,
则必有 k m
T
当 k m 时, P1 , P2 , , Pm 构成基
从而 X ( x1 , , x m , 0 , , 0 ) 为相应的基可行解
若X
(X
(0)
(0)
证。
(0)
不是基可行解
(0)
,由定理 2 知 X
到通过 X
) CX ) CX
单纯形法基本原理及实例演示

③计算各非基变量xj的检验数j=Cj-CBPj ′,若所有j≤0,则问题已得
到最优解,停止计算,否则转入下步。
④在大于0的检验数中,若某个k所对应的系数列向量Pk≤0,则此问
题是无界解,停止计算,否则转入下步。
⑤根据max{j|j>0}=k原则,确定xk为换入变量(进基变量),再按 规则计算:=min{bi/aik| aik>0}=bl/ aik 确定xBl为换出变量。建 立新的单纯形表,此时基变量中xk取代了xBl的位置。
⑥以aik为主元素进行迭代,把xk所对应的列向量变为单位列向量,即 aik变为1,同列中其它元素为0,转第③ 步。
线性规划的例子
max z 4x1 3x2 2x1 2x2 1600 5x1 2.5x2 2500 x1 400 x1, x2 0
线性规划--标准化
● 引入变量:s1,s2,s3
检验系数区
Z=CBB-1b
初始单纯形表
迭代 基变 次数 量
CB
x1
x2
s1
s2
s3
50 100 0 0 0
比值
b bi ai 2
1 Zj=CBNj j cj zj
Z=CBB-1b
初始单纯形表
基
迭代 次数
变
CB
x1
X2
s1
s2 S3
量
50 100 0 0 0
比值
b bi ai 2
1 1 1 0 0 300
C向量
max z 50 100 0 0
CB
CN
x1
x2
0•
1 1 1
1 0 0
0 1 0
03第三章 单纯形法

第三章 单纯形法在线性规划的计算求解中,应用最多且最著名的就是单纯形法。
这种方法是美国运筹学家G .B.Dantzig 丹捷格在1947年提出的。
后来经过人们多次改进,形成了许多变种。
实践证明单纯形法是一种使用方便、行之有效的算法。
§3.1 单纯形法的原理基本可行解的存在定理已经表明,若线性规划有最优解,则一定存在最优基本可行解,因此求线性规划问题就归结为寻找最优基本可行解。
单纯形法的基本思想就是从一个基本可行解出发,检查该基本可行解是否为最优解;若不是,则再设法求另一个未检查过的基本可行解,如此继续,直到查询到最优解为止。
按照以上的思路,需要解决三个难题: 1、 如何求出第一个基本可行解?2、 如何判断这个基本可行解就是最优解?3、 若不是最优解,如何从一个基本可行解过渡到另一个未检查过的基本可行解? 第一个问题的彻底解决尚需留待今后,但是我们知道,求基本可行解就是解线性方程组=A x B ,由于且()r m =A ,故可以解出m 个变量,称之为基本变量,剩下的n-m 个变量称之为自由变量。
于是,最简单的方法就是令所有的自由变量的值为零相应得到的解就是基本解。
例3.1 考虑线性规划1234134123m in 324..246350,1,2,3,4j z x x x x s t x x x x x x x j =-++-+=-++=≥= (3.1)把约束方程写成表格的形式,如表3-1:20 -4 1 6 -1 1 3 0 5从上述表格的左端可以看出,由第二、四列构成一个单位子矩阵,或曰子块,即对角元为1,其余为0,因此把2x 和4x 解出,即把2x 和4x 作为基本变量,余下1x 和3x 作为自由变量。
41321362453x x x x x x =-+=+- (3.2)令所有的自由变量130x x ==,而426,5x x ==,从而得到一个基本解(0,5,0,6)T 。
若需要判断该基本解是否基本可行解?只需看左端有单位子矩阵时,右列的元素是否都是非负,若是,则为基本可行解。
第五章 单纯形法

x4 0 1 0
x5 0 0 1
基变量
b
300 400 250
基向量
非基向量
0
对应基本解:(0,0,300,400,250)
一、问题的提出
基 B1=(p1 ,p2 ,p3) B2=(p1,p2 ,p4 ) B3=(p1 ,p2 ,p5) B4=(p1 ,p3 ,p4) B5=(p1 ,p3 ,p5) B6=(p1 ,p4 ,p5) B7=(p2 ,p3,p4) B8=(p2 ,p3,p5) 基向量 基变量 非基 向量 p4 ,p5 p3 ,p5 p3 ,p4 p2 ,p5 p2 ,p4 p2 ,p3 p1 ,p5 p1 ,p4 非基 变量 x4 ,x5 x3 ,x5 x3 ,x4 x2 ,x5 x2 ,x4 x2 ,x3 x1 ,x5 x1 ,x4 基本解 (75,250,-25,0,0) (50,250,0,50,0) (100,200,0,0,50) 不存在 (200,0,100,0,50) (300,0,0,-200,-50) (0,250,50,150,0) (0,400,-100,0,150) 是 否 是 否 是否可行 否 是 是 p1 ,p2 ,p3 x1 ,x2 ,x3 p1 ,p2 ,p4 x1 ,x2 ,x4 p1 ,p2 ,p5 x1 ,x2 ,x5 p1 ,p3 ,p4 x1 ,x3 ,x4 p1 ,p3 ,p5 x1 ,x3 ,x5 p1 ,p4 ,p5 x1 ,x4 ,x5 p2 ,p3 ,p4 x2 ,x3 ,x4 p2 ,p3 ,p5 x2 ,x3 ,x5
一、问题的提出
既然如此,如果我们在技术矩阵中取出三列, 组成一个可逆阵,令其余两列对应的变量为 零,则一定可以得到一个解。
一、问题的提出
单纯形法原理以及步骤
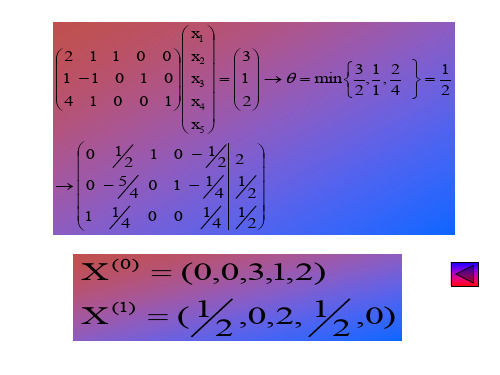
,0)
4、单纯形法迭代原理
单纯形法是沿顶点寻找线性规划问题最优解的一种有效方法。该方法主要包括: 确定初始基可行解(即起始顶点);从一个基可行解转移到另一个基可行解; 最优性检验三项内容。
1. 确定初始基可行解
对标准形式的线性规划问题
max z = ∑jn=1 cjxj
(1-6)
∑jn=1 Pjxj = b
0 0 … 0 amj 0 … 1 bm
bl alj
xj
min
bi aij
aij>
0
x1
2 1 1 1 4 1
1 0 0
0 1 0
0 0 1
x2 x3 x4
3 1 2
min
3, 2
1 1
,
2 4
1 2
x5
0
1 2
1
0
54
0
1
1 4
0
0
1 2
2
1
1 4
X (1) (x10 a1 j , x20 a2 j ,, xm0 amj ,0,, ,,0)T
由于Pj≤ 0,对任意的 0
xi0 aij 0
无限增大时,目标函数值无限增加,所以,线性规划问题具有无界解。
返回
第四节 单纯形法计算步骤
1.求初始基可行解,列出单纯形表 2. 最优性检验 3. 基变换(从一个基转换到另一个基) 4. 重复步骤2和3,求出最优解
…
xl 变为非基变量
xk 变为基变量
4 . 重复第2、3步,直到求出最优解(或计算结束)。
例:用表格式单纯形法求解下列线性规划问题。
max z =20x1 + 8x2 + 6x3
第4章 单纯形法

为0,求出了一组基本可行解。试想如果x1或者x2
不为0,是否会带来目标函数值变大? 需要最优性
检验,即如果x1或x2不论取其他任何非负值都不会
带来目标函数值增大,那该基本可行解就是最优解。
管理运筹学
20
§1 单纯形法的基本思路和原理
所谓最优性检验就是判断已求得的基本可行解是否是最优解。 (1) 最优性检验的依据——检验数σ j 一般来说目标函数中既包括基变量,又包括非基变量。现在我们要求 只用非基变量来表示目标函数,或者说目标函数中基变量的系数都为零了。 此时目标函数中所有变量的系数即为各变量的检验数,把变量xi的检验数 记为σ i。显然所有基变量的检验数必为零。在本例题中目标 函数为3x1+5x2。由于初始可行解中x1,x2为非基变量,所以此目标函 数已经用非基变量表示了,不需要再代换出基变量了。这样我们可知 σ 1=3,σ 2=5,σ 3=0,σ 4=0,σ 5=0。 检验数:用非基变量来代换基变量,使得目标函数只用非基变量来表示。
0 1 0 0 1
x1 +x2+s1
=300
2x1+x2+ s2 =400
x2+
s3=250
基向量:基B中的一列即称为一个基向量。基B中共有m个基向量。
非基向量:在A中除了基B之外的一列则称之为基B的非基向量。
基变量:与基向量pi对应的变量xi叫基变量,基变量有m个。(包 括松弛变量等,即标准化以后的所有变量)
为A的一个基,令这个基的
1 1 0
B3 1 0 0
1 0 1 x1 +x2+s1
=300
2x1+x2+ s2 =400
单纯形算法一般原理

单纯形算法的一般原理单纯形法的基本思路是有选择地取基本可行解,即是从可行域的一个极点出发,沿着可行域的边界移到另一个相邻的极点,要求新极点的目标函数值不比原目标函数值差。
考虑到如下线性规划问题:其中A一个m ×n 矩阵,且秩为m ,b总可以被调整为一个m 维非负列向量,C为n 维行向量,X为n 维列向量。
根据线性规划基本定理:如果可行域D={ X∈Rn / AX=b,X≥0}非空有界,则D上的最优目标函数值Z=CX一定可以在D的一个顶点上达到。
这个重要的定理启发了Dantzig 的单纯形法,即将寻优的目标集中在D 的各个顶点上。
Dantzig 的单纯形法把寻优的目标集中在所有基本可行解(即可行域顶点)中。
其基本思路是从一个初始的基本可行解出发,寻找一条达到 最优基本可行解的最佳途径。
单纯形法的一般步骤如下:(1)寻找一个初始的基本可行解。
(2)检查现行的基本可行解是否最优,如果为最优,则停止迭代,已找到最优解,否则转一步。
(3)移至目标函数值有所改善的另一个基本可行解,然后转会到步骤(2)。
求解思想如下图所示:maxZ=CX AX=b X 0⎧⎨≥⎩确定初始的基本可行解等价于确定初始的可行基,一旦初始的可行基确定了,那么对应的初始基本可行解也就唯一确定为了讨论方便,不妨假设在标准型线性规划中,系数矩阵A中前m 个系数列向量恰好构成一个可行基,即A=(BN),其中B=(P1,P2,…Pm )为基变量x1,x2,…xm 的系数列向量 构成的可行基,N=(Pm+1,Pm+2, …Pn)为非基变量xm+1,xm+2, …xn 的 系数列向量构成的矩阵。
那么约束方程AX=b 就可表示为:用可行基B的逆阵B-1左乘等式两端,再通过移项可推得:若令所有非基变量 ,则基变量由此可得初始的基本可行解B B N N X AX=(BN)=BX +NX =b X ⎛⎫ ⎪⎝⎭-1-1B N X =B b-B NX N X =0-1B X =B b 1B b X=0-⎛⎫ ⎪⎝⎭-1-1-1B N B N N B AX=b BX +NX =b X =B b-B NX X =0,X =B b →→→● 问题:➢ 要判断m 个系数列向量是否恰好构成一个基并不是一件容易的事。
单纯形法基本原理

2)求出线性规划的初始基可行解,列出初始单纯形表。
cj cB 0 基 x3 b 40 3 x1 2 4 x2 1 0 x3 1 0 x4 0
θi
0
j
x4
30
1
3
3
4
0
0
1
0
检验数
1 c1 (c3a11 c4a21 ) 3 (0 2 0 1) 3
单纯形法的计算步骤
单纯形法的计算步骤
cj
cB 0 0 基变量 x4 b 15 20
Page 11
1
x1 2 1/3
2
x2 -3 1
1
x3 2 5
0
x4 1 0
0
x5 0 1
θi
j
x5
- 20 25 60
2
0
j
1
2
x2
x1
Hale Waihona Puke x475 3 20 1/3 1/3
25 35/3
1
0 1 0 0 1
0
2
17 5
-9
1
1 0 0
Page 14
解:首先将数学模型化为标准形式
max Z 3 x1 2 x 2 x 3 4 x1 3 x 2 x 3 x 4 4 x1 x 2 2 x 3 x 5 10 2 x1 2 x 2 x 3 1 x j 0, j 1,2, ,5
Page 16
θi 4 5 1 3/5 8/3 —— —— 31/3 ——
j
→ →
j
→
j
j
单纯形法的进一步讨论-人工变量法
解的判别:
Page 17
2单纯形法

2 3 0 x1 x2 x3 2 1 0 1 (3) -1 1 1 0 -2m -4m m 5/3 0 1/3 1/3 1 -1/3 (2/3) 0 1/3
0 -1/3m
0 x4 1 0 0 0 1 0 0
0
-m x5 0 1 0 0
-m x6 0 16 0 20/3 1 10 0 0 28/5 0 20 1 5
例题(标准化模型的系数矩阵中能够找到单位阵 或排列阵作为初始基)
CB
0 0 5 0
c 3 XB B-1b x1 x3 x2 4 x5 8 12 6 36 12 0 1 0 3 -3
5 x2 0 2 1 4 0 -5 0
0 x3 1 0 0 0
0 x4 0 1 1/2 0 -2 0 5/2
0 x5 0 0 1 0
可行解。
第二阶段:将原目标函数换回,以第一阶段得到的 可行基为初始基进行迭代,直到找到最优解或判断 问题无界为止。 在第二阶段的迭代中可以删去所有人工变量。
例 用两阶段法求解:
max z 2 x1 3 x2 2 x1 x2 16 x 3 x 20 1 2 s.t. x1 x2 10 x1 , x2 0
max z 3x1 5 x2 x3 x1 2 x2 x4 s.t. x5 3x1 4 x2 x1 , x2 , x3 , x4 , x5
8 12 36 0
转换为典则形式: ① 目标方程中的所有基变量的系数全都为0; ② 基本可行解对应的可行基是一个m阶单位阵或排列 阵。
第二阶段寻找最优解或判断问题无界。
第一阶段:引入人工变量并找一个初始基,另构造
一个新的求极小值的目标函数,该目标函数除人工
