第三章分子对称性和分子点群资料
合集下载
第三章：分子对称性和点群
σv2 σv2 σd1 σv1 σd2 C42 E
C41 C43
σd1 σd1 σv1 σd2 σv2 C41 C43 E
C42
σd2 σd2 σv2 σd1 σv1 C43 C41 C42 E
第三章：分子对称性和点群
1
群元素 群
乘法
对称操作 点群
操作动作的连续
2
本章目录
3.1对称元素和对称操作 3.2 对称操作的乘积 3.3分子点群
3.3.1 构成群 3.3.2 点群乘法表 3.3.3 类和子群 3.3.4 分子点群的类型 ****
3
3.1对称元素和对称操作
• 对称元素的定义（Symmetry Elements） 几何实体，如一个点，一条直线，一个平面；
(x,y,z) -C-2-(-x-)-> (x,-y,-z)-C--2(-y-)> (-x,-y,z) (x,y,z) -C--2(-z-)-> (-x,-y,z)
so, C2(y)C2(x)= C2(z)
34
例3：C4（z）和σ (xz）的存在，自动地要求σ d的存在 普通点[x1,y1,z1]通过xz平面的反映效果可以表为
分子点群满足数学群四准则。
点群中点的含义：(1)这些对称操作都是点操作，操作时 分子中至少有一点不动；(2) 分子的全部对称元素至少通 过一个公共点。
37
满足群的四点要求：
• （1）群中任意两个元素的乘积必为群中的 一个元素。
以NH3为例，逐一求出所有的对称操作的二元乘 积，发现两个操作的乘积仍为集合中的一个操作。
Snm = hmCnm （1）若独立地存在一个Cn轴和一个垂直于它 的平面h，那么就存在Sn。 （2）当分别地既不存在Cn也不存在垂直的h 时，Sn也可以存在。
群论第3章
NH3
CO，NO，HCN
C3v
C∞v
③ Cnh 群 属于Cnh点群的分子中具有一个Cn轴和一个垂直于Cn轴的σh 对称元素：Cn和σh 因σhCn=Sn，故（n-1）个旋转必产生（n-1）个象转 实际上 Cnh群是Cn群和Cs群的直积，阶次为2n 。
Cnh Cn Cs E, Cn1 , Cn 2 ,..., Cn n1 E, h = E, Cn1 , Cn 2 ,..., Cn n1 , h , hCn1 Sn , hCn 2 ,..., hCn n1
第三章. 分子对称性与分子点群
3.1 分子对称性
利用对称性原理和概念探讨分子的结构和性质，是人们认 识分子的重要途径，是了解分子结构和性质的重要方法。 ① 能简明地表达分子的构型 Ni(CN)42-离子具有D4h点群的对称性，用D4h这个符号就可以 准确地表达 9 个原子在同一平面上， Ni 原子在中心位置， 周围4个-CN完全等同，Ni-C-N都是直线型，互为90°角。 ② 简化分子构型的测定工作
3.分子的对称操作和对称元素：
分子是有限物体，在进行对称操作时，分子中至少有一 点不动------点操作 只有四种类型的对称操作和对称元素 a. 旋转操作------旋转轴（Cn）
b. 反映操作------镜面（ σ ）
c. 反演操作------ 对称心（i） d. 象轴（旋转反映）操作------象转轴（反轴）Sn 右手坐标系：讨论对称操作时，常将分子定位在右手坐 标轴系上，分子的重心处在坐标原点，主轴与Z轴重合。 主轴：分子中轴次最高的轴。
Cnh 待 定 分 子 是 否 直 线 型 N Y i Td
例：有两个分子群 D2 { E，C2(x)，C2(y)，C2(z) }
第三章分子对称性和点群
A(c) A(a) A( f ) 0 1
0
0
001
cos 4
3
sin 4
3 0
sin 4
3
cos 4
3 0
0 0Βιβλιοθήκη cos 43sin 4
3
1 0
sin 4
3
cos 4
3 0
0
0
1
A (a) 1
A (b) 1
A (c) 1
表示的分类:
(1)等价表示 若A(g)是群G的一个表示, X是一正交变换矩阵, 则 B(g)=X-1A(g)X
规则二. 点群中所有不可约表示的维数的平方和等于群的阶 n. l12 l22 lk 2 n
在 D3中, l12 l22 l32 6
从而 l1 l2 1, l3 2
规则三. 点群中不可约表示特征标间的正交关系:
k
h j r (R j ) * s (R j ) n rs
j 1
对不可约表示: (R) 2 n
3
y2 a21 a22 a23 x2 , yi aij x j
y3 a31 a32 a33 x3
j 1
（i＝1,2,3)
矩阵的迹 (trace) 或特征标 (character):
( A) TrA aii
i
相似变换:
A S1AS
TrA TrA
(S为正交矩阵) St S SSt E
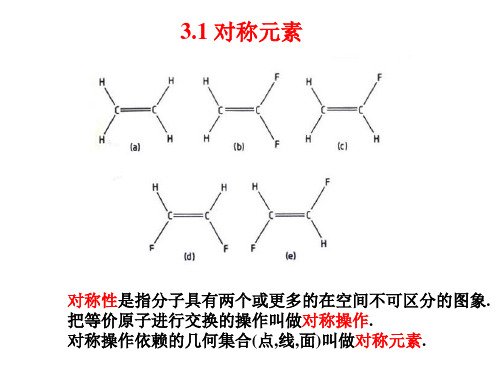
3.1 对称元素
对称性是指分子具有两个或更多的在空间不可区分的图象. 把等价原子进行交换的操作叫做对称操作. 对称操作依赖的几何集合(点,线,面)叫做对称元素.
3.1.1 n重对称轴, Cn (转动)
转角 2 / n
分子对称性和点群
例二：置换群（群元素为变换位置的操作，乘法规则为从右到左 相继操作）. S3 群 ( 三阶置换群 )
1 2 3 E 1 2 3 1 2 3 A 1 3 2
1 2 3 D 2 3 1 1 B 3 1 2 2 3 2 1 2 3 3 1
{E,D,F}构成S3的一个3阶子群
AA BB CC E
{E,A}、 {E,B}、 {E,C}分别构成S3的2阶子群
3.2.4 群的共轭类
共轭元素: B=X-1AX ( X,A,B都是群G的元素) (A和B共轭）
元素的共轭类: 一组彼此共轭的所有元素集合称为群的 一个类.
f 类 = { x-1fx,
第三章
分子对称性和点群
分子具有某种对称性. 它对于理解和应用分子 量子态及相关光谱有极大帮助. 确定光谱的选择定则需要用到对称性. 标记分子的量子态需要用到对称性.
3.1 对称元素
对称性是指分子具有两个或更多的在空间不可区分的图象. 把等价原子进行交换的操作叫做对称操作. 对称操作依赖的几何集合(点,线,面)叫做对称元素.
A4 =E
（2）非循环群
欲构成非循环群，只可能是各元素的逆元素为自身 即 A2 =B 2 =C 2 =E ,再根据重排定理即可得乘法表
3.2.3 群的子群
•子群: 设 H 是群 G 的非空子集, 若对于群 G 的乘法规则,集合 H 也 满足群的四个条件,则称 H 是 G 的子群. • 1) 封闭性 • 2) 结合律： H属于G并且为相同的乘法规则，因此结合律显然满足 • 3) 恒等元素：针对每个子群加入群G的恒等元素即可 • 4) 逆元素 因此满足条件1）与4）是证明子群成立的关键. 显然, 恒等元素 E 单独构成的群和群 G 自身是平庸子群.
(完整版)第三章-分子对称性和群论初步
操作A和B是可交换的。
两个或多个对称操作 的结果，等效于某个 对称操作。
例如,先作二重旋转，再对垂直 于该轴的镜面作反映，等于对 轴与镜面的交点作反演。
对称操作的乘积示意图
2.分子点群的确定
分子可以按 “点群”或“对称群”加以分 类。在一个分子上所进行的对称操作的完全组 合构成一个“点群”或“对称群”。
Third
确定分子是否具有象转轴Sn（n为偶数），如果只 存在Sn轴而别无其它对称元素，这时分子属于假轴 向群类的Sn群。
3. 分子点群的确定
Forth
假如分子均不属于上述各群，而且具有Cn旋转轴时 可进行第四步。当分子不具有垂直于Cn轴的C2轴时，
则属于轴向群类。有以下三种可能：
没有对称面 若有n个sv对称面 若有1个sh对称面
Z s2
Y
x
独立：可以通过其它对称元素或组合来产生。
CH4中的象转轴S4与旋转反映操作
4
3
43
旋转90◦
12
2
1
2
1 反映
43
3 4
2
1
注意: C4和与之垂直的σ都不独立存在
补充：反轴（In）和旋转反演操作(In )
反轴
如果分子图形绕轴旋转一定角度（θ=2π/n）后， 再按轴上的中心点进行反演，可以产生分子的 等价图形，则将该轴和反演组合所得到的对称 元素称为反轴。
对称中心的反演操作，能使分子中各相互对应的原子 彼此交换位置。即分子图形中任意一个原子的位置 A(x,y,z)将反射到点A’(-x,-y,-z)，同时A’点将反射到A点， 从而产生分子的等价图形。示意图.exe
对分子图形若连续反演n次，可以满足：
iˆ
nLeabharlann =E(n为偶数) ˆi(n为奇数)
两个或多个对称操作 的结果，等效于某个 对称操作。
例如,先作二重旋转，再对垂直 于该轴的镜面作反映，等于对 轴与镜面的交点作反演。
对称操作的乘积示意图
2.分子点群的确定
分子可以按 “点群”或“对称群”加以分 类。在一个分子上所进行的对称操作的完全组 合构成一个“点群”或“对称群”。
Third
确定分子是否具有象转轴Sn（n为偶数），如果只 存在Sn轴而别无其它对称元素，这时分子属于假轴 向群类的Sn群。
3. 分子点群的确定
Forth
假如分子均不属于上述各群，而且具有Cn旋转轴时 可进行第四步。当分子不具有垂直于Cn轴的C2轴时，
则属于轴向群类。有以下三种可能：
没有对称面 若有n个sv对称面 若有1个sh对称面
Z s2
Y
x
独立：可以通过其它对称元素或组合来产生。
CH4中的象转轴S4与旋转反映操作
4
3
43
旋转90◦
12
2
1
2
1 反映
43
3 4
2
1
注意: C4和与之垂直的σ都不独立存在
补充：反轴（In）和旋转反演操作(In )
反轴
如果分子图形绕轴旋转一定角度（θ=2π/n）后， 再按轴上的中心点进行反演，可以产生分子的 等价图形，则将该轴和反演组合所得到的对称 元素称为反轴。
对称中心的反演操作，能使分子中各相互对应的原子 彼此交换位置。即分子图形中任意一个原子的位置 A(x,y,z)将反射到点A’(-x,-y,-z)，同时A’点将反射到A点， 从而产生分子的等价图形。示意图.exe
对分子图形若连续反演n次，可以满足：
iˆ
nLeabharlann =E(n为偶数) ˆi(n为奇数)
chap3b第三章 分子的对称性和点群
C1 , Ci , Cs
有多条高阶轴分子（正四面体、正八面体 有多条高阶轴分子（正四面体、正八面体…) 只有镜面或对称中心, 或无对称性的分子: 只有镜面或对称中心 或无对称性的分子 只有S 为正整数） 只有 2n(n为正整数）分子 为正整数 分子:
S 4 , S 6 , S8 ,...
C n , C nh , C nv
Z
对称操作，共有 个对称操作 但每条S 必然也是C 个对称操作. 对称操作，共有9个对称操作 但每条 4必然也是 2， S42与C2对称操作等价，所以将 个S42划归 2， 对称操作等价，所以将3个 划归C ，
穿过正四面体每条棱 并将四面体分为两半 的是一个σd , 共有 个 共有6个 的是一个 σd 。
旋转反映
(具有 n的)分子 具有S 分子 具有 镜象 反映 旋转
分子
橙色虚线框表明，分子与其镜象能够通过实操作旋转完 橙色虚线框表明， 全迭合，而前提是“分子具有 全迭合，而前提是“分子具有Sn”. 根据n的不同可以写出 根据 的不同可以写出: S1=σ，S2=i，S4=S4。 的不同可以写出 结论： 的分子, 结论 ： 具有 σ、 或 i、 或 S4 的分子 , 可通过实际操作与其 镜象完全迭合，称为非手性分子。 镜象完全迭合，称为非手性分子。
夹角的镜面σ 夹角的镜面 d.
D2d : 丙二烯
D2d : B2Cl4
立方群：包括T 立方群：包括 d 、Th 、Oh 、Ih 等.
这类点群的共同特点是有多条高次(大于二次 旋转轴相交 这类点群的共同特点是有多条高次 大于二次)旋转轴相交 大于二次 旋转轴相交.
Td 群：属于该群的分子，对称性与正四面体完全相同。 属于该群的分子，对称性与正四面体完全相同。 正四面体完全相同
有多条高阶轴分子（正四面体、正八面体 有多条高阶轴分子（正四面体、正八面体…) 只有镜面或对称中心, 或无对称性的分子: 只有镜面或对称中心 或无对称性的分子 只有S 为正整数） 只有 2n(n为正整数）分子 为正整数 分子:
S 4 , S 6 , S8 ,...
C n , C nh , C nv
Z
对称操作，共有 个对称操作 但每条S 必然也是C 个对称操作. 对称操作，共有9个对称操作 但每条 4必然也是 2， S42与C2对称操作等价，所以将 个S42划归 2， 对称操作等价，所以将3个 划归C ，
穿过正四面体每条棱 并将四面体分为两半 的是一个σd , 共有 个 共有6个 的是一个 σd 。
旋转反映
(具有 n的)分子 具有S 分子 具有 镜象 反映 旋转
分子
橙色虚线框表明，分子与其镜象能够通过实操作旋转完 橙色虚线框表明， 全迭合，而前提是“分子具有 全迭合，而前提是“分子具有Sn”. 根据n的不同可以写出 根据 的不同可以写出: S1=σ，S2=i，S4=S4。 的不同可以写出 结论： 的分子, 结论 ： 具有 σ、 或 i、 或 S4 的分子 , 可通过实际操作与其 镜象完全迭合，称为非手性分子。 镜象完全迭合，称为非手性分子。
夹角的镜面σ 夹角的镜面 d.
D2d : 丙二烯
D2d : B2Cl4
立方群：包括T 立方群：包括 d 、Th 、Oh 、Ih 等.
这类点群的共同特点是有多条高次(大于二次 旋转轴相交 这类点群的共同特点是有多条高次 大于二次)旋转轴相交 大于二次 旋转轴相交.
Td 群：属于该群的分子，对称性与正四面体完全相同。 属于该群的分子，对称性与正四面体完全相同。 正四面体完全相同
第三章-分子的对称性
对称操作只能产生等价构型分子，不能改变其 物理性质（偶极矩）。因此，分子的偶极矩必定在 分子的每一个对称元素上。
(1) 若分子有一个Cn轴，则DM必在轴上； (2) 若分子有一个σ面，则DM必在面上； (3) 若分子有n个σ面，则DM必在面的交线上； (4) 若分子有n个Cn轴，则DM必在轴的交点上，DM=0； (5) 分子有对称中心 i ( Sn )，则DM=0。
群的乘法表
把群元素的乘积列为表，则得到乘法表。乘 积为列×行，行元素先作用，列元素后作用。群 的元素数目 n为群的阶数。 例：H2O，对称元素，C2, σv, σv’ ，对称操作
ˆ ˆ ˆ ˆ C2,σv ,σv ', E ， 属4阶群。
C2v
ˆ E ˆ C2 ˆ σv ˆ σv'
ˆ E ˆ ˆ σv σv' ˆ ˆ σv' σv
判据：若分子中有对称中心或有两个对称元素相交 于一点, 则分子不存在偶极矩。 推论：只有属于Cn 和Cnv(n=1,2,3,…,∞)这两类点群 的分子才具有偶极矩，而其他点群的分子偶极矩为 0。因C1v≡C1h≡Cs，Cs点群也包括在Cnv之中。
H C Cl
H C Cl
1,2 -二氯乙烯（顺式） , C2v，有
C60
闭合式[B12H12]2-
非真旋轴群: 包括Cs 、Ci 、S4 只有虚轴(不计包含在Sn中的Cn/2. 此外, i= S2 , σ = S1, 只有n为4的倍数时Sn是独立的).
Cs 群 ： 只有镜面 Ci 群: 只有对称中心 S4 群: 只有四次旋映轴
亚硝酸酐 N2O3
分子点群的确定
起点 线性分子
2
ˆ E ˆ E ˆ C
ˆ C2 ˆ C
第三章 分子的对称性和点群
3.1.1 分子的对称操作与对称元素
对称操作：不改变图形中 任何两点的距离而能使图形复 原的操作叫做对称操作；
对称元素: 旋转轴 对称操作: 旋转
对称操作据以进行的几何 要素叫做对称元素。如点、线、 面以及它们的组合。
分子中的四类对称操作及 相应的对称元素如下:
（1）旋转轴与旋转操作
借助一条直线，使分子旋转2/n后得到等价图形的操作称
3.2 点群
3.2.1 群的定义
设有一组元素的集合GA, B,C,...，定义一种称之为“乘
法”的运算，如果满足下列条件，则集合G构成群。
1）封闭性：集合G 中任何两个元素相“乘”（或称之为 组合），其结果仍然是G 中元素，也就是说，A、B分别 属于G，AB＝C 也属于 G。即 A∈G， B∈G， 则 AB＝ C∈G
邻菲罗啉、吡啶、环戊烯、甲醛 、丙酮、呋喃、顺式丁二烯和环 己烷(船式构象)等许多近似呈V 型的分子都属于C2v群。
C3v ： NH3 、NF3 C3v ：CHCl3
C3v群分子
无对称中心的线性分子属于C∞v群：如HCl
N2O C∞v群分子
(c) Sn群：只存在一个Sn轴 . n为偶数，如果为奇 数，就是Cnh群，不独立存在
又如，四个动作立正、向左转、向右转和向后转构成群, 这里定义的群元素之间的乘法就是一个动作之后接做另一 个动作。
例1. 实数加法群 元素为全体实数（因此是无限群），群乘
法为初等代数加法；（１）任意两实数之和仍是实数； （２）恒等元为０；（３）实数的代数加法满足结合律； （４）实数的逆元为其相反值。
生 物 界 的 对 称 性
文学中的对称性——回文
将这首诗从头朗诵到尾, 再反过来, 从尾到头去朗诵, 分别都是一首绝妙好诗. 它们可以 合成一首“对称性”的诗，其中每一首相当于一首“手性”诗.
第三章 分子的对成性与点群
群的举例： 例1：全体整数的集合对于加法运算构成一个群。 G={0、±1、±2、……} 不难看出，满足封闭性、缔合性，单位元素是0。每个元素R均 有逆元素(-R)，由R（-R）=0求得。 例2：全体整数的集合对于乘法运算是否构成一个群。 几个慨念： 群G的元有限——有限群 如群G中 AB = BA 可对易——交换群（Abel群） 群G中元的个数就是群G的阶（h） 群G中的元，如 R-1AR=B ， R-1BR=A，则A，B为 共轭元素，该变换称为相似变换。
48阶群
SF6
起点 线型分子
C∞v，D ∞h
有i 无i
D ∞h C∞v Td Oh CS Ci C1 Sn Cn Cnh Cnv Dn Dnh Dnv
正四面体 立方群 正八面体 有σ 有i 无轴群 无σ或i 有Sn(n为偶数，n是4的整数倍) (n为偶数， 的整数倍) 为偶数 无σ 有σh 有σv 无σ 有垂直Cn轴的C2 有垂直Cn轴的C2 Cn轴的 D群 有σh 有σd
相当于一个不动操作（获得全等图形的操作）。旋转360°也可 作为恒等操作。恒等操作和恒等元素是任何分子图形都具有的。
2.旋转轴Cn和旋转操作 ˆ 2.旋转轴Cn和旋转操作 cn 旋转轴Cn
旋转轴也叫对称轴 ，是通过分子的一条特定的直线，用记 号Cn表示。 旋转操作是以直线为轴旋转θ角能产生的等价图形。 θ=360/n ，n次旋转轴Cn 若旋转一次n=1（θ=360°）能使图形复原， 称为单重(一次)旋转轴，记为C1。 n=2 θ=180°,二次旋转轴C2。 。
ˆ ˆ 2) Ci 群：元素 E, i；操作 E i ，阶为2
H Cl F H
二氟二氯乙烷
F Cl
3) Cs 群：元素 E, σ；操作
第三章分子的对称性与点群PPT课件
C1 C2v
CCs1h
D3 D2h D2d
CSi2
Td Oh
典型类型
C2
C3
C3v
C∞v
C2h
C3h
D3h D3d
S4
D4h
D6h
D ∞h
1. Cn 点群
Cn群只有1个Cn 旋转轴。独立对称操作有n个。阶 次为n。
若分子只有n重旋转轴，它就属于Cn群，群元素为 {E，Cn1，Cn2…Cnn-1}。这是n阶循环群。
III. 1,3,5-三甲基苯
1,3,5-三甲基苯 （图III）是C3点 群的例子，若不考 虑甲基上H原子， 分子的对称性可以 很高，但整体考虑， C6H3(CH3)3只有C3 对称元素。C3轴位 于苯环中心，垂直 于苯环平面，分子 绕C3轴转动120°， 240°都能复原。
IV. CH3CCl3
如甲烷分子，一个
经过Ｃ原子的四次映转
轴S4，作用在分子上，H
１旋转到1’的位置后，
1’
经平面反映到H4的位置，
同时H2旋转到2’的位置
再反映到H3的位置……
整个分子图形不变，
S1 h ; S2 i ;
S C ; S 独立，包含C ;
3
3
h
4
2
S C ; S C i
5
5
h
6
3
即只有S4是独立的点群， 其余Sn 可化为 i, h 或 Cn i,Cn h
左图为D2对称性分子， C2主轴穿过联苯轴线，经过 2个O为水平面上的C2轴， 还有一个C2轴与这两个C2轴 垂直。
双乙二胺NH2CH2-CH2-NH2CH2-CH2-NH2可 对Co3+离子3配位 螯合，2个双乙二 胺与Co3+形成 Co(dien)2配合物， 具有D2对称性。 (右图）
第三章分子的对称性与点群详解演示文稿
个分子就具有对称中心 i。显然，正方形的PtCl42－离子
有对称中心，但四面体的SiF4分子就没有对称中心。
第十六页，共122页。
平面正方形的PtCl42－ 四面体SiF4不
具有对称中心
具对称中心
五、映转轴和旋转反映
映转轴也称为非真轴，与它联系的对称操作是旋转n 次轴再平面反映，两个动作组合成一个操作。
群的四个要求。
第二十二页，共122页。
一、对称点群分类
Cs
第二十三页，共122页。
Ci
S4
1. Cn 点群
Cn群只有1个Cn 旋转轴。独立对称操作有n个。阶次
为n。 若分子只有n重旋转轴，它就属于Cn群，群元素为{E，
Cn1，Cn2…Cnn-1}。这是n阶循环群。
H2O2
H2O2是C2点群，C2轴穿过O-O键的中心和 两个H连线的中心。
即只有S4是独立的点群，
其余Sn 可化为
i
,
或
h
Cn i,Cn h
第十八页，共122页。
对称元素与对称操作
对称元 素符号
E Cn
σ
对称元素
-旋转
镜面
基本对称操 作 符号
基本对称操作
E
恒等操作
C1n
绕C n轴按逆时针方向转
3600/n
σ
通过镜面反映
i
对称中心
i
按对称中心反演
Sn
映轴
S1n=σC1n 绕S n轴转3600/n，接着按
III. 1,3,5-三甲基苯
第二十六页，共122页。
1,3,5-三甲基苯（图
III）是C3点群的例
子，若不考虑甲基上 H原子，分子的对称 性可以很高，但整体
有对称中心，但四面体的SiF4分子就没有对称中心。
第十六页，共122页。
平面正方形的PtCl42－ 四面体SiF4不
具有对称中心
具对称中心
五、映转轴和旋转反映
映转轴也称为非真轴，与它联系的对称操作是旋转n 次轴再平面反映，两个动作组合成一个操作。
群的四个要求。
第二十二页，共122页。
一、对称点群分类
Cs
第二十三页，共122页。
Ci
S4
1. Cn 点群
Cn群只有1个Cn 旋转轴。独立对称操作有n个。阶次
为n。 若分子只有n重旋转轴，它就属于Cn群，群元素为{E，
Cn1，Cn2…Cnn-1}。这是n阶循环群。
H2O2
H2O2是C2点群，C2轴穿过O-O键的中心和 两个H连线的中心。
即只有S4是独立的点群，
其余Sn 可化为
i
,
或
h
Cn i,Cn h
第十八页，共122页。
对称元素与对称操作
对称元 素符号
E Cn
σ
对称元素
-旋转
镜面
基本对称操 作 符号
基本对称操作
E
恒等操作
C1n
绕C n轴按逆时针方向转
3600/n
σ
通过镜面反映
i
对称中心
i
按对称中心反演
Sn
映轴
S1n=σC1n 绕S n轴转3600/n，接着按
III. 1,3,5-三甲基苯
第二十六页，共122页。
1,3,5-三甲基苯（图
III）是C3点群的例
子，若不考虑甲基上 H原子，分子的对称 性可以很高，但整体
第三讲分子的对称性与群论基础群与分子点群
(AB)C=A(BC)
(3) 恒等元素 该集合必须含有一个元素 E，对于该集合中的任何元素 A， 都有：AE=EA=A (4) 逆元素 对于该集合的任何元素 A，一定有一个逆元素A-1，它也是 该集合的一个元素，使得： AA-1= A-1A = E 。
2
群与分子点群
1. 群的定义
* 群元素: 数、矩阵、对称操作、算符
群G与群H同构，则两者的阶相同，且乘法表相同。 群G： …., Ai , …, Aj , …., AiAj = Ak , ….
群H： …., Bi , …, Bj , …., BiBj = Bk , ….
26
群与分子点群
5、同构与同态
CS 群
Ci 群
CS与Ci 同构：元素一一对应，“乘积对应乘积”：
群G： …., {Aik} , …, {Aj l }, …., {AikAjl} , ….
群H： …., Bi , …, Bj , …., BiBj , ….
* 同态的群，其群元素的乘法关系相同。
* 若两个同态的群的阶相同，则两者同构。
28
群与分子点群
5、同构与同态
群 G = { 1, -1, i, -i }
（证毕）
由定理3，相互共轭的群元素组成一个封闭的子集合，称为 一个类（共轭类）。从而可以把一个群的元素按共轭类划 分，不同的类没有共同元素。
24
群与分子点群
4、子群与类
如果群的某个元素与其他元素的乘积都可交换，则该元素
自成一类（不与其他元素共轭）。
若：
PA = AP ,
PB =
BP , … ...
(4) 逆元素：相反数 （1 与 -1，2 与 -
2，…..）
分子对称性和分子点群课件
分子对称性的意义
预测和解释分子的物理和化学性质
分子对称性与分子的电子结构和化学键有关，因此可以用来预测和解释分子的性质，如稳 定性、反应活性等。
确定分子的点群
分子的点群是根据分子的对称性进行分类的，通过确定分子的点群可以更好地理解分子的 结构和性质。
指导药物设计和材料科学
分子对称性在药物设计和材料科学中具有重要意义，例如在药物设计中，可以利用分子对 称性来设计具有特定性质的化合物。
分子对称性在化学反应中的实例分析
以烷烃为例，烷烃的对称性越高，其化学反应选择性越低，因为它们具有更稳定的 分子结构。
以烯烃为例，烯烃的对称性较低，因此它们在加成反应中表现出较高的反应活性。
以芳香族化合物为例，由于芳香族化合物具有较低的对称性，它们在取代反应中表 现出较高的反应活性。
05
CATALOGUE
02
CATALOGUE
分子点群的基本概念
分子点群的分 类
01
02
03
04
第一类点群
包括1个线性群和3个二面体群。
第二类点群
包括4个四面体群、6个三方 柱群和1个六方柱群。
第三类点群
包括4个四方锥群、4个三角 锥群、2个八面体群、1个五 方双锥群和1个三方偏方面体
群。
第四类点群
包括1个二十面体群。
02
分子对称性是分子结构的一个重 要属性，它决定了分子的物理和 化学性质。
分子对称性的分类
01
02
03
点对称性
分子在三维空间中具有一 个或多个对称中心，这些 对称中心可以将分子分成 若干个相同的部分。
轴对称性
分子具有一个或多个对称 轴，这些对称轴可以将分 子分成若干个相同的部分。
分子对称性和分子点群PPT课件
完整版课件
28
2. Cn点群
C2
H
OO H
仅含有一个Cn轴。如：H2O2仅含有一个C2轴， 该轴平分两个平面的夹角，并交于O－O键的中点，
所以，该分子属于C2点群；类似的结构如：N2H4等
完整版课件
29
3. Cs点群
O
H
Cl
仅含有一个镜面。如：HOCl为一与水类似的
弯曲分子，只有一个对称面即分子平面，所以它属
完整版课件
2
对称元素和对称操作
元素符号
E C
σ
i
S
I
元素名称 单位元素 旋转轴
镜面 对称中心
映轴
反轴
操作符号
Ê
Ĉ σ∧
∧
i
Ŝ
Î
完整版课件
对称操作
恒等操作
绕中心旋转 2π/n
通过镜面反映
按分子中心反 演 绕中心旋转 2π/n 再镜面 对映 绕中心旋转 2π/n 再反演
下一页
3
分子点群的种类
点群
Cn群 C1 Cnv群 C2v Cnh群 C1h Dn群 D3 Dnh群 D2h Dnd群 D2d Sn群 S2 Td群 Td Oh群 Oh
同理，各个对称操作作用于Tx 、Tz，也可 以得到类似的结果。
Tx Tx
Tx
完整版课件
Tz
Tz
Tz
40
C2v
E
C2 (xz) (yz)
Γ1
1
-1
-1
1
Ty
Γ2
1
-1
1
-1
Tx
Γ3
1
1
1
1
Tz
上述数字的集合（矩阵）代表群，就是 群的表示。
第三章 群表示理论基础1
若{F 1，F 2，… F m }及{G 1，G 2，… G n }是两个函数集合，则函数集合｛F i G k ｝（m ×n 个）称为前两个函数集合的直积。
B 、表示的直积以函数集合｛F i G k ｝为基的表示ΓFG 称为以函数集合{F 1，F 2，… F m }为基的表示ΓF 与以函数集合{G 1，G 2，… G n }为基的表示ΓG 的直积。
记为：ΓFG = ΓF × ΓG2）定理：操作R 对应的矩阵中，以直积为基表示的特征标等于以单个函数为基表示的特征标的乘积。
χFG (R) = χF (R)χG (R)五、群表示间的关系小结1、群表示间的关系群表示Γa 的矩阵群为{A 1，A 2，A 3, …}，Γb 的矩阵群为{B 1，B 2，B 3, …}其中，A i 、B i 分别为Γa 与Γb 中对应于第i 个操作的矩阵 。
1）等价：若对每一个操作R 均能找到矩阵X ，使B(R) = X -1A(R)X ，则表示Γa与Γb 是等价的，记为Γa = Γb 。
2）约化： 若能找到矩阵X ，使表示Γ的任一矩阵C(R)，可通过相似变换X -1C(R)X= C´(R) 变为对角方阵C´(R)。
C´(R)中每一组对应的小方阵构成一个群的低维表示Γi ，则称表示Γ是可约化的。
记为：...2211+Γ+Γ=Γ=Γ∑a a a ii i3）直积：若ψa 和ψb 分别为Γa 及Γb 表示的基，则以（ψa ψb ）为基的表示Γab称为Γa 与Γb 的直积。
记为Γab =Γa ×Γb2、群表示的特征标间的关系若将上述关系中群表示符号Γ换为群表示中与某一对称操作对应的矩阵的特征标，则与上述群表示间关系相对应的特征标间的代数运算依然成立。
1）等价： Γa = Γb → χa (R) = χb (R)因为A(R)与B(R)为共轭矩阵，因此特征标应相等。
2）约化：∑∑=→Γ=Γi ii i i i R a R a )()(χχ这是显然的，因为与Γi 对应的矩阵在C´(R)里是沿对角线排列的，因此∑=ii i R a R )()('χχ又因为C(R)与C´(R) 共轭，因此χ(R) =χ´(R)。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
【教学要求】
1．熟练掌握对称元素和对称操作的概念。 2．掌握常见的对称元素和对称操作。 3．了解对称操作的乘积。 4．掌握点群的基本概念：群、子群、群的阶、对易
群与非对易群、共轭元素和群的类。 5．掌握常见分子所属点群的确定。 6．掌握分子旋光性和分子偶极矩的对称性判据。
上一页 下一页 回主目录
返回
后能够产生分子等价图形
的对称操作。将该轴和镜
面组合的对称元素称为象
转轴。
Sˆn Cˆnˆh ˆhCˆn
偶数次象转轴才独立
上一页 下一页 回主目录
返回
2020/11/18
CH4 的
四
旋转90°
重
象
转
轴
S4
相互 等价
及
旋
转
反映
反
映
操
作
仍代表 H
对称操作与对称元素
旋转是真操作, 其它对称操作为虚操作.
1. 对称性概念
对称(symmetry) 是一个很常见的现象。在 自然界我们可观察到五瓣对称的梅花、桃花， 六瓣的水仙花、雪花、松树叶沿枝干两侧对称， 槐树叶、榕树叶又是另一种对称……在人工建 筑中，北京的古皇城是中轴线对称。在化学中， 我们研究的分子、晶体等也有各种对称性。
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
§3.1 分子的对称性
轴旋转能产生 n 个旋转操作
Cˆn,Cˆn2,...,Cnn1,Cnn Eˆ
若取逆时针方向的旋转为
正操作，表示为 Cˆnk ，则
顺时针方向旋转为逆操作，
表示为 Cˆnk，有
Cˆnk
C (nk n
)
对称操作连续能使分
子图形完全复原的最少次
一个 h
反一式个Cl镜HC面=CHCl
两个 h
H2C=C=CH2
三个 v
H2O
NH3
CO2 , H2, HCl 等直线分子有无数个 v 镜面
E
C
C2
H
对称元素
v'
Cl
v''
E
E C2(x) C2(y) C2(z)
C2
h v v’ i
h
i
结构化学 精品课程
§3.1 分子的对称性
试找出分子中的镜面
上一页 下一页 回主目录
2020/11/18
结构化学 精品课程
【教学重难点】
1．重点：掌握对称元素和对称操作的概念， 学会确定简单分子的对称元素和对称操作 并确定其点群。
2．难点：Dn、Dnd、Sn群的判断；群的表示
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
§3.1 分子的对称性
一、对称元素和对称操作
将这首诗从头朗诵到尾, 再反过来, 从尾到头去朗诵, 分别都是一首绝妙好诗. 它 们可以合成一首“对称性”的诗，其中每一首相当于一首“手性”诗.
流游鹤鸥冷幽日悠 溪径伴飞井林落悠 远踏闲满寒古观绿 棹花亭浦泉回偎
结构化学 精品课程
§3.1 分子的对称性
数为该操作的周期。
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
§3.1 分子的对称性
Ĉ3
n 2
Ĉ3
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
§3.1 分子的对称性
③对称面和反映操作：
根据镜面与主旋转轴在空间排布方式的不同，镜面又分
为三类，通常以 的右下角标明镜面与主轴的关系：
返回
2020/11/18
结构化学 精品课程
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
§3.1 分子的对称性
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
上一页 下一页 回主目录
返回
2020/11/18
文学中的§对3称.1性分—子—的回对文称性
返回
2020/11/18
结构化学 精品课程
§3.1 分子的对称性
④对称中心（i）和反演操作 iˆ
对于具有对称中心的分子， 其中的任何一个原子，在中心的 另一侧，必能找到一个同它对应 的同类原子，互相对应的两个原 子和中心点同在一条直线上，且 距离相等。
y
i x
对分子图若连续反演n次，
iˆ2k1 iˆ iˆ2k Eˆ
§3.1 分子的对称性
① 恒等元素（Ｅ）和恒等操作（ Ê ） ② 旋转轴（Ｃn）和旋转操作 ( Ĉn)
对称轴 是分子中的一条特 定的直线，其相应的操作是
把分子图形以直线为轴旋转 能产生的等价图形，使分子 图形完全复原的最少次数为 n，分子可能有n个旋转轴， 其中n值最大的称为主轴。
上一页 下一页 回主目录
内江师范学院付孝锦
结构化学精品课程
第三章 分子对称性和分子点群
Chapter 3. Molecular Symmetry & Molecular Point Group
目 录 结构化学
精品课程
1 分子的对称性 2 点群 3 群的表示
上一页 下一页 回主目录
返回
2020/11/18
结构化学
精品课程 第三章 分子对称性和分子点群（8学时）
对称操作(symmetry operation ) 不改变图形中任何两点的距离而 能使图形复原的操作叫做对称操 作； 对称操作据以进行的几何要素叫 做对称元素. 分子中的四类对称操作及相应的 对称元素如下:
对称元素: 旋转轴 对称操作: 旋转
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
⊥Cn： 记为 h ，镜面垂直于主轴，即为
（horizontal，主轴为Z 轴 ）
// Cn ：记为 v ， 通过主轴（垂直 vertical）
// Cn ： 通过主轴且平分垂直主轴的 C2 轴，记为 d
（diagonal 对角线）
上一页 下一页 回主目录
返回
2020/11/18
平面型分子中至少有一个镜面，即 分子平面。
偎回月台泛来走开 林望明映舟客上篷 傍四孤碧渔仙烟一 水山寺泉浦亭花棹 绿观古寒满闲踏远 悠落林井飞伴径溪 悠日幽冷鸥鹤游流
上一页 下一页 回主目录
返回
2020/11/18
电荷对称:
一组带电粒子 极性互换, 其相互作 用不变(但在弱相互 作用下这种对称被 部分破坏).
结构化学 精品课程
§3.1 分子的对称性
(k 0,1,2...)
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
§3.1 分子的对称性
⑤象转轴（Sn）和旋转反映操作
^
Sn
象转：先将分子绕某轴旋
转 2 n 角度后，再凭借垂 直于该轴的平面进行反映
Sˆ2k1 2k 1
Cˆ 2k1 2k 1
ˆ
2k h
1
Eˆˆh ˆh
1．熟练掌握对称元素和对称操作的概念。 2．掌握常见的对称元素和对称操作。 3．了解对称操作的乘积。 4．掌握点群的基本概念：群、子群、群的阶、对易
群与非对易群、共轭元素和群的类。 5．掌握常见分子所属点群的确定。 6．掌握分子旋光性和分子偶极矩的对称性判据。
上一页 下一页 回主目录
返回
后能够产生分子等价图形
的对称操作。将该轴和镜
面组合的对称元素称为象
转轴。
Sˆn Cˆnˆh ˆhCˆn
偶数次象转轴才独立
上一页 下一页 回主目录
返回
2020/11/18
CH4 的
四
旋转90°
重
象
转
轴
S4
相互 等价
及
旋
转
反映
反
映
操
作
仍代表 H
对称操作与对称元素
旋转是真操作, 其它对称操作为虚操作.
1. 对称性概念
对称(symmetry) 是一个很常见的现象。在 自然界我们可观察到五瓣对称的梅花、桃花， 六瓣的水仙花、雪花、松树叶沿枝干两侧对称， 槐树叶、榕树叶又是另一种对称……在人工建 筑中，北京的古皇城是中轴线对称。在化学中， 我们研究的分子、晶体等也有各种对称性。
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
§3.1 分子的对称性
轴旋转能产生 n 个旋转操作
Cˆn,Cˆn2,...,Cnn1,Cnn Eˆ
若取逆时针方向的旋转为
正操作，表示为 Cˆnk ，则
顺时针方向旋转为逆操作，
表示为 Cˆnk，有
Cˆnk
C (nk n
)
对称操作连续能使分
子图形完全复原的最少次
一个 h
反一式个Cl镜HC面=CHCl
两个 h
H2C=C=CH2
三个 v
H2O
NH3
CO2 , H2, HCl 等直线分子有无数个 v 镜面
E
C
C2
H
对称元素
v'
Cl
v''
E
E C2(x) C2(y) C2(z)
C2
h v v’ i
h
i
结构化学 精品课程
§3.1 分子的对称性
试找出分子中的镜面
上一页 下一页 回主目录
2020/11/18
结构化学 精品课程
【教学重难点】
1．重点：掌握对称元素和对称操作的概念， 学会确定简单分子的对称元素和对称操作 并确定其点群。
2．难点：Dn、Dnd、Sn群的判断；群的表示
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
§3.1 分子的对称性
一、对称元素和对称操作
将这首诗从头朗诵到尾, 再反过来, 从尾到头去朗诵, 分别都是一首绝妙好诗. 它 们可以合成一首“对称性”的诗，其中每一首相当于一首“手性”诗.
流游鹤鸥冷幽日悠 溪径伴飞井林落悠 远踏闲满寒古观绿 棹花亭浦泉回偎
结构化学 精品课程
§3.1 分子的对称性
数为该操作的周期。
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
§3.1 分子的对称性
Ĉ3
n 2
Ĉ3
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
§3.1 分子的对称性
③对称面和反映操作：
根据镜面与主旋转轴在空间排布方式的不同，镜面又分
为三类，通常以 的右下角标明镜面与主轴的关系：
返回
2020/11/18
结构化学 精品课程
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
§3.1 分子的对称性
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
上一页 下一页 回主目录
返回
2020/11/18
文学中的§对3称.1性分—子—的回对文称性
返回
2020/11/18
结构化学 精品课程
§3.1 分子的对称性
④对称中心（i）和反演操作 iˆ
对于具有对称中心的分子， 其中的任何一个原子，在中心的 另一侧，必能找到一个同它对应 的同类原子，互相对应的两个原 子和中心点同在一条直线上，且 距离相等。
y
i x
对分子图若连续反演n次，
iˆ2k1 iˆ iˆ2k Eˆ
§3.1 分子的对称性
① 恒等元素（Ｅ）和恒等操作（ Ê ） ② 旋转轴（Ｃn）和旋转操作 ( Ĉn)
对称轴 是分子中的一条特 定的直线，其相应的操作是
把分子图形以直线为轴旋转 能产生的等价图形，使分子 图形完全复原的最少次数为 n，分子可能有n个旋转轴， 其中n值最大的称为主轴。
上一页 下一页 回主目录
内江师范学院付孝锦
结构化学精品课程
第三章 分子对称性和分子点群
Chapter 3. Molecular Symmetry & Molecular Point Group
目 录 结构化学
精品课程
1 分子的对称性 2 点群 3 群的表示
上一页 下一页 回主目录
返回
2020/11/18
结构化学
精品课程 第三章 分子对称性和分子点群（8学时）
对称操作(symmetry operation ) 不改变图形中任何两点的距离而 能使图形复原的操作叫做对称操 作； 对称操作据以进行的几何要素叫 做对称元素. 分子中的四类对称操作及相应的 对称元素如下:
对称元素: 旋转轴 对称操作: 旋转
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
⊥Cn： 记为 h ，镜面垂直于主轴，即为
（horizontal，主轴为Z 轴 ）
// Cn ：记为 v ， 通过主轴（垂直 vertical）
// Cn ： 通过主轴且平分垂直主轴的 C2 轴，记为 d
（diagonal 对角线）
上一页 下一页 回主目录
返回
2020/11/18
平面型分子中至少有一个镜面，即 分子平面。
偎回月台泛来走开 林望明映舟客上篷 傍四孤碧渔仙烟一 水山寺泉浦亭花棹 绿观古寒满闲踏远 悠落林井飞伴径溪 悠日幽冷鸥鹤游流
上一页 下一页 回主目录
返回
2020/11/18
电荷对称:
一组带电粒子 极性互换, 其相互作 用不变(但在弱相互 作用下这种对称被 部分破坏).
结构化学 精品课程
§3.1 分子的对称性
(k 0,1,2...)
上一页 下一页 回主目录
返回
2020/11/18
结构化学 精品课程
§3.1 分子的对称性
⑤象转轴（Sn）和旋转反映操作
^
Sn
象转：先将分子绕某轴旋
转 2 n 角度后，再凭借垂 直于该轴的平面进行反映
Sˆ2k1 2k 1
Cˆ 2k1 2k 1
ˆ
2k h
1
Eˆˆh ˆh