全等三角形判定2
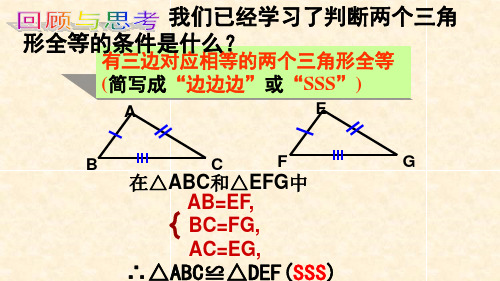
1.5全等三角形的判定(2)
以2.5cm,3.5cm为三角形的两边,长
度为2.5cm的边所对的角为40° ,情况
又怎样?动手画一画,你发现了什么?
C
F
A
40°
B
40°
D
E
结论:两边及其一边所对的角相
等,两个三角形不一定全等
课堂小结:
1. 目前有几种方法判定三角形全等?
2. 线段垂直平分线的概念
3. 线段垂直平分线的性质:线段垂直平分线上的点 到线段两端点的距离相等.
几何语言表述如下:
在A BC和ABC 中
AB AB(已知)
B B(已知)
BC
BC (已知)
ABC ABC(SAS)
例3 如图AC与BD相交于点O.已知
OA=OC,OB=OD,说△AOB≌△COD 的理
由.
解;在AOB和COD中 A
B
OA OC (已知) OBAOBODCO(D(已知对)顶角相等D)
将你画出的三角形和其他同学画的三角形进行比 较,它们互相重合吗?
由此,你得到了什么结论?
全等三角形的判定公理2:
两边及其夹角对应相等的两个三角形全等(简写 成“边角边”或“SAS”)
➢注 意 这个角一定要是两条边的夹角
有一个角和夹这个角的两边对应相等的两个
三角形全等(简写成“边角边”或“SAS”)
O C
∴△AOB≌△COD (SAS)
垂直于一条线段,并且平分这条线段 的直线叫做这条线段的垂直平分线,简 称中垂线.
点C是线段AB的垂直平分线上的特殊的
点,还是任意的点?由此你能得到什么结论?
线段垂直平分线
l
上的点到线段两
C
端的距离相等。 A
O
全等三角形的判定(SAS)2

探索三角形全等的条件(2)
灌南光明实验学校 孙老师
探 索
教学目标 1:教学目标
1:经历探索三角形全等条件的过程,体会分析问 题的方法。 2:掌握三角形全等的条件,并能利用这些条件判别 教学目标 1:经历探索三角形全等条件的过程,体会 两个三角形是否全等。 分析问题的方法。 2:掌握三角形全等的条件,并能利用这些条 3:了解三角形的稳定性及其在生活中的应用。经历 件判别两个三角形是否全等。 3:了解三角形的稳定性及其在生活中的应用。 探索三角形全等条件的过程,体会分析问题的方 法。 2:掌握三角形全等的条件,并能利用这些条件判别 两个三角形是否全等。 3:了解三角形的稳定性及其在生活中的应用。
独立训练
1、如图,已知∠1=∠2,要证明 △ABC≌ △ADE,还需补充的条件是( ) A、AB=AD,AC=AE B、AB=AD,BC=DE C、AC=AE,BC=DE D、以上都不对
5、如图所示,AB=AD,AC=AE, 如果想增加一个有关相等的条件,就 可以直接得到△ABC≌△ADE,那么 这个条件是( ) A、∠B=∠C B、∠B=∠D C、∠C=∠E D、∠BAC=∠DAE
三角形全等判定方法1.
全等三角形的两边和这两边所夹的角对应相等 的两个三角形全等。简写成“边角边”或
“SAS” 用符号语言表达为:
在△ABC与△DEF中 AB=DE
A
∠B=∠E BC=EF
B
C
D
∴△ABC≌△DEF(SAS)
E
F
一、自学反馈 (一)自学检查 1.观察下图中的三角形,先猜一猜, 再量一量,哪两个三角形是全等三角形?
拓展延伸
已知AB=AC,点D、E分别是AB、 AC边上的中点。 说明:△ABE≌△ACD. A D E
人教版八年级数学上册教学课件三角形全等的判定2

AB = CD
A EB
∴△ADE≌△CBF ( SSS )
② ∵ △ADE≌△CBF
∴ ∠A=∠C (
全等三角形 对应角相等 )
课堂小结
内容
有三边对应相等的两个三角形 全等(简写成 “SSS”)
谈谈本节课你有思哪路些分析收获以结现合有及图条形件存找,在隐证含准的条备件条困和件惑?
边边边 应 用
书写步骤
∴ ∠A=∠C (
)
B 有两个角对应相等的两个三角形
E
满足这六个条件可以保证△ABC ≌△DEF
有没有更简单的办法呢?
探索新知
思考 如果只满足这些 条件中的一部分,那么 能保证
△ABC ≌△DEF′吗?
互动探究
一个条件可以吗?
1. 有一条边相等的两个三角形 不一定全等 2. 有一个角相等的两个三角形 不一定全等
活,用智慧点亮人
生!
2、分别以A、B为圆心,4㎝和3㎝长为半径画弧,两弧交于点C;
为了庆祝国庆节,老师要求同学们回家制作三角形彩旗(如图),那么,老师应提供多少个数据了,能保证同学们制作出来的三角形彩旗全等呢?一定要知道所有的边长和所有的
真,让知识服务生 角度吗?
2、分别以A、B为圆心,4㎝和3㎝长为半径画弧,两弧交于点C; (简写为“边边边”或“SSS”)
情景问题
为了庆祝国庆节,老师要求同学们回家制 作三角形彩旗(如图),那么,老师应提 供多少个数据了,能保证同学们制作出来 的三角形彩旗全等呢?一定要知道所有的 边长和所有的角度吗?
新课导入
通过上节课的学习,大家知道:两个三角 形全等时,三条对应边相等,三组对应角相 等,那么判定两个三角形全等,是否一定需 要满足六个条件呢?如果只满足上述六个条 件中的一部分,是否也能保证两个三角形全 等呢?从这节课开始,我们来探究全等三角 形的判定.
全等三角形判定(二)

例01.如图,已知:21∠=∠,43∠=∠. 求证:BCD ADC ∆≅∆.分析:ADC ∆与BCD ∆的对应边是DC 与DC ,AD 与BC ,AC 与BD . 对应角是1∠与2∠,ADC ∠与BCD ∠,DAC ∠与CBD ∠. 由条件已有一对应边DC 与DC ,和一对应角1∠和2∠相等,只需证明BCD ADC ∠=∠,就可以证明两三角形全等.证明:21∠=∠,43∠=∠(已知),∴ 4231∠+∠=∠+∠. 即BCD ADC ∠=∠ 在ADC ∆与BCD ∆中,⎪⎩⎪⎨⎧∠=∠=∠=∠)(12)()(已知公共边已证CD DC BCD ADC ∴ )(ASA BCD ADC ∆≅∆例02.已知:如图,21∠=∠,C B ∠=∠. 求证:COD BOE ∆≅∆.分析:欲证COD BOE ∆≅∆,已有两组条件,即C B ∠=∠和COD BOE ∠=∠. 因此,必须再具备一组对应边相等这一条件. BE 和CD 是在BOE ∆和COD ∆中,但直接证明CE BE =比较困难. 若证OE 和OD 相等或OB 和OC 相等,可以分别转化到证明AOD AOE ∆≅∆和AOC AOB ∆≅∆. 由已知条件,不难证出这两对三角形分别全等.证明:∵ 21∠=∠(已知),DOC EOB ∠=∠(对顶角相等), ∴ DOC EOB ∠+∠=∠+∠21. 即 AOC AOB ∠=∠. 在AOB ∆与AOC ∆中,⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(公共边已证已知AO AO AOC AOB C B ∴ )(AAS AOC AOB ∆≅∆. ∴CO BO =在EOB ∆与COD ∆中⎪⎩⎪⎨⎧∠=∠=∠=∠)()()(已知已证对顶角相等C B CO BO COD EOB∴ COD BOE ∆≅∆(ASA )例03.如图,已知:AB 与CD 相交于点O ,且OD OC BD AC =,//,E 、F 为AB 上两点,且BF AE =.求证:DOF COE ∆≅∆.分析:欲证DOF COE ∆≅∆,已具备了两个条件,OD OC =和DOF COE ∠=∠. 所以只需证另一对角相等或证明OF OE =,即可. 证明另一对角相等,比较困难. 所以就证明OF OE =. 因为有BF AE =. 要证OF OE =只需证OB OA =即可. 由已知条件容易证得BOD AOC ∆≅∆,从而证明OB OA =.证明:∵BD AC //(已知)∴B A ∠=∠(两直线平行,内错角相等) 在AOC ∆与BOD ∆中,⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(已知对顶角相等已证OD OC BOD AOC B A ∴)(AAS BOD AOC ∆≅∆∴BO AO =(全等三角形的对应边相等) ∵BF AE =(已知), ∴BF BO AE AO -=-. 即OF OE =在COE ∆与DOF ∆中,⎪⎩⎪⎨⎧=∠=∠=)()()(已证对顶角相等已知OE OE DOE COE DO CO ∴)(SAS DOF COE ∆≅∆例04.如图,已知:CE BD ACE ABD DAE BAC =∠=∠∠=∠,,. 求证:AE AD =.分析:欲证相等的两条线段AD ,AE 分别在ABD ∆和ACE ∆中,由于CE BD =,ACE ABD ∠=∠,所以只需再证CAE BAD ∠=∠即可,这由已知条件DAE BAC ∠=∠容易得到.证明:∵DAE BAC ∠=∠(已知) ∴DAC DAE DAC BAC ∠-∠=∠-∠ 即CAE BAD ∠=∠ 在ABD ∆与ACE ∆中,⎪⎩⎪⎨⎧∠=∠∠=∠=)()()(已证已知已知CAE BAD ACE ABD CE BD ∴)(AAS ACE ABD ∆≅∆∴AE AD =(全等三角形的对应边相等)例05.已知:(如图)21,∠=∠∠=∠D A . 求证:DO AD =分析:要证DO AD =,只要证DOC AOB ∆≅∆即可,在AOB ∆和DOC ∆中,已知D A ∠=∠,DOC AOB ∆=∆,只要再证一边对应相等即可,根据已知可得DCB ABC ∆≅∆,从而可证DC AB =,进而可证DO AO =,思路即为:DO AO =⇐DOC AOB ∆≅∆⇐DC AB =⇐DCB ABC ∆≅∆⇐“AAS ”证明:在ABC ∆和DCB ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(21公共边已知已知CB BC D A ∴)(AAS DCB ABC ∆≅∆∴DC AB =(全等三角形的对应边相等)在AOB ∆和DOC ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(已证已知对顶角相等DC AB D A DOC AOB ∴ )(AAS DOC AOB ∆≅∆∴ DO AO =(全等三角形的对应边相等)例06.求证:三角形的一边的两端到这边的中线或中线的延长线的距离相等.分析:这是一道了题,必须先根据题意画出图形,再结合题意写出已知,求证,再证明.已知:AD 是ABC ∆的中线. 如图,且AD CF ⊥于F ,AD BE ⊥的延长线于E , 求证:CF BE =证明:∵AD 为ABC ∆的中线(已知) ∴ CD BD =(中线定义)∵ AD BE ⊥ AD CF ⊥(已知)∴ ︒=∠=∠90CFD BED (等于定义) 在BED ∆与CFD ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠)()(21)(已证对顶角相等已知CD BD CFD BED ∴CFD BED ∆≅∆(AAS )∴CF BE =(全等三角形对应边相等)说明 本题还可利用面积相等来证明,提示,过A 作BC AN ⊥于N ,希同学们自己来证明.例07.已知:如图,BC AD CD AB //,//, 求证:CD AB =.分析:因为四边形,我只学过三角形的有关知识,因此只要连结四边形的对角线从而把四边形的总是转化为三角形的总是来解决.证明:连结AC∵BC AD CD AB //,//(已知)∴43,21∠=∠∠=∠(两直线平行内错角相等)在ABC ∆和CDA ∆中⎪⎩⎪⎨⎧∠=∠=∠=∠)(43)()(21已证公共边已知CA AC∴ )(ASA CDA ABC ∆≅∆∴CD AB =(全等三角形的对应边相等)例08.已知:如图,AO CO DO BO ==,求证:OF OE =证明:在BOC ∆和DOA ∆中⎪⎩⎪⎨⎧=∠=∠=)()()(已知对顶角相等已知OA OC DOA BOC DO BO ∴ )(SAS DOA BOC ∆≅∆∴ D B ∠=∠(全等三角形的对应角相等) 在BOE ∆和DOF ∆中⎪⎩⎪⎨⎧∠=∠=∠=∠)()()(对顶角相等已知已证DOF BOE DO BO D B ∴)(ASA DOF BOE ∆≅∆∴OF OE =(全等三角形的对应边相等)说明 找到题目中的隐性条件并加以应用是关键.例09.如图,在ABC ∆和DBC ∆中,43,21∠=∠∠=∠,P 是BC 上任意一点, 求证:PD PA =.证明:在ABC ∆和DBC ∆中,⎪⎩⎪⎨⎧∠=∠=∠=∠)(43)()(21已知公共边已知BC BC ∴ )(ASA DBC ABC ∆=∆∴ DB AB =(全等三角形对应边相等) 在ABP ∆和DBP ∆中,⎪⎩⎪⎨⎧=∠=∠=)()(21)(公共边已知已证BP BP DB AB ∴ )(SAS DBP ABP ∆≅∆∴ PD PA =(全等三角形对应边相等)说明:本题也可通过DBC ABC ∆≅∆,得到DC AC =,从而证DCP ACP ∆≅∆,得到PD PA =.选择题(1)已知ABC Rt ∆与C B A Rt '''∆,︒=∠90C ,︒='∠90C ,B A '∠=∠.B A AB ''=.那么下列结论正确的是( )(A )C A AC ''= (B )C B BC ''= (C )C B AC ''= (D )以上答案都不对(2)在ABC ∆和C B A '''∆,甲:B A AB ''=;乙:C B BC ''=;丙:C A AC ''=;丁:A A '∠=∠;戊:B B '∠=∠;己:C C '∠=∠,则不能保证ABC ∆≌C B A '''∆成立的条件为( )(A )丙、丁、己 (B )甲、丙、戊 (C )甲、乙、戊 (D )乙、戊、己 (3)如图,已知ABD ∆和ACE ∆均为等边三角形,那么ADC ∆≌ABE ∆的根据是( )(A )ASA (B )SAS(C )AAS (D )以上都不对(4)如图,C 是BE 上一点,CD AB =,D A ∠=∠,E BCA ∠=∠,那么( )(A )ECD B ∠=∠ (B )C 是BE 的中点 (C )CD AB //(D )以上结论都正确参考答案:(1)C (2)B (3)B (4)D填空题(1)如图,已知:21∠=∠,D C ∠=∠. 求证:AD AC =.证明:在ACB ∆与ADB ∆中,⎪⎩⎪⎨⎧=∠=∠∠=∠) _______()()(21AB D C 已知已知 ∴ACB ∆≌ADB ∆( ) ∴AD AC =(2)如图,已知:BC AB ⊥,DC AD ⊥,垂足分别为B ,D .21∠=∠. 求证:AD AB =.证明:在ABC ∆与ADC ∆中,⎪⎩⎪⎨⎧=∠=∠∠=∠) ()(21)(AC AC ADC ABC ∴ ABC ∆≌ADC ∆( ) ∴AD AB =( )(3)如图,已知:CE AE =,C A ∠=∠.求证:ADE ∆≌CEB ∆.证明:在AED ∆与CEB ∆中,⎪⎩⎪⎨⎧==∠=∠) _____(______)()(已知CE AE C A ∴ AED ∆≌CEB ∆(ASA )(4)如图,已知:C B ∠=∠,AD AE =.求证:AEC ∆≌ADB ∆.证明:在AEC ∆与ADB ∆中,⎪⎩⎪⎨⎧=∠=∠∠=∠) ()()(AE AE C B A A 已知 ∴AEC ∆≌ADB ∆( )参考答案:(1)AB ;公共边;AAS ;全等三角形的对应边相等(2)垂直定义;已知;公共边;AAS ;全等三角形的对应边相等. (3)已知:AED ∠;CEB ∠;对顶角相等 (4)公共角;已知;AAS证明题1.如图,已知,21∠=∠,DCB ABC ∠=∠. 求证:DC AB =.2.如图,已知:E D ∠=∠,AM EM CN DN ===. 求证:点B 是线段AC 的中点.3.如图,已知:21∠=∠,AE AD =. 求证:OC OB =.4.如图,已知:在ABC ∆中,AD 是BAC ∠的平分线,AB DE ⊥于E ,AC DF ⊥于C ,求证:AF AE =.5.如图,已知:E 在AC 上,21∠=∠,43∠=∠. 求证:DE BE =.6.如图,已知:BC AD //,21∠=∠,43∠=∠,直线DC 过E 点交AD 于D ,交BC 于C .求证:AB BC AD =+.7.求证:三角形一边的两个端点到这边上的中线的距离相等. 8.如图,已知:DE AB =,直线AE ,BD 相交于点C ,︒=∠+∠180D B ,DE AF //,交BD 于F .求证:CD CF =.9.如图,已知:AB 与CD 相交于点O ,O 是AB ,CD 的中点,过点O 引直线EF 分别与AD ,BC 相交于E 、F 两点.求证:BF AE =.参考答案:1.证:由DCB ABC =∠,21∠=∠,可得ACB DBC ∠=∠.易证ABC ∆≌DCB ∆,∴ DC AB =2.证:易证DNB ∆≌EMB ∆,∴ EB DB =,由此可证:EA DC =.因此,可证DCB ∆≌EAB ∆.∴BC AB =,∴B 是AC 的中点.3.易证ABE ∆≌ACD ∆,∴C B ∠=∠,AC AB =,又∵AE AD =,∴CE BD =.由此可证BOD ∆≌COE ∆,∴OC OB =4.︒=∠=∠90AFD AED ,FAD EAD ∠=∠,AD AD =,∴AFD AED ∆≅∆,∴AF AE =.5.∵ 21∠=∠,AC AC =,43∠=∠,∴ABC ∆≌ADC ∆,∴AD AB =,又∵21∠=∠,AE AE =,∴ADE ABE ∆≅∆,∴DE BE =6.在AB 上取一点F ,使BF BC =,又∵43∠=∠,EB EB =,∴EC B EFB ∆≅∆,∴C EFB ∠=∠,又∵BC AD //,由此可推出D EFA ∠=∠.可证AFE ADE ∆≅∆,∴AF AD =,∴BC AD AB +=.7.已知:如图,AD 为ABC ∆的中线,AD BF ⊥于F ,AD CE ⊥于E . 求证:CE BF =.证:︒=∠=∠90BFD CED ,BDF CDE ∠=∠,BD CD =,∴ BFD CED ∆≅∆,∴ CE BF =8.证:∵ DE AF //, ∴AFC D ∠=∠,又∵︒=∠+∠180AFB AFC ,︒=∠+∠180D B ,∴ AFB B ∠=∠∴ DE AF AB ==,∴ 可证ECD ACF ∆≅∆,∴CD CF =9.证:BO AO =,BOC AOD ∠=∠,CO DO =,∴B O C A O D ∆≅∆,∴B A ∠=∠.而BOF AOE ∠=∠,BO AO =,∴BOF AOE ∆≅∆,∴ BF AE =能力:1、如图1,已知:AD 平分∠BAC ,AB=AC ,连接BD ,CD ,并延长相交AC 、AB 于F 、E 点.则图形中有( )对全等三角形.A 、2B 、3C 、4D 、5答案:C.2、如图2,已知:∠1=∠2,AB=DC ,图中全等三角形的对数是( )A 、0B 、1C 、2D 、3答案:A3、如图3,已知:△ABC 中,DF=FE ,BD=CE ,AF ⊥BC 于F ,则此图中全等三角形共有( )A 、5对B 、4对C 、3对 D2对答案:C.1、如图4,已知:在△ABC 中,AD 是BC 边上的高,AD=BD ,DE=DC ,延长BE 交AC 于F ,求证:BF 是△ABC 中边上的高. 图1 A B B 、E F D C AD B O C 1 2 图2 图3 D FE C AF C D B E 图4提示:关键证明△ADC ≌△BFC2、如图5,已知:∠D=∠E ,DN=EM ,AM=CN ,求证:点B 是线段AC 的中点.提示:欲证点B 是线段AC 的中点,只需证AB =BC.选择AB 、BC 所在的两个三角形,然后证这两个三角形△AMB ≌△CNB.由条件可得△EMB ≌△DNB ,所以得到∠EMB =∠DNB ,MB =NB由此易证△AMB ≌△CNB.3、如图6,已知:AB=CD ,∠A=∠D.求证:∠ABC=∠DCB提示:欲证∠ABC=∠DCB ,选择这两个角所在的三角形,只需证△ABC ≌△DBC由条件可知△ADC ≌△DAB ,所以得到∠DAC =∠ADB ,BD =AC ,加之条件利用边角边公理可证△ABC ≌△DBC4、如图7,已知:在△ABC 中,∠ACB=090,AC=BC ,AE 是BC 边上的中线过C 作CF ⊥AE ,垂足为F ,过B 作BD ⊥BC 交CF 的延长线于点D.(1)求证:AE=CD.(2)AC=12cm ,求BD 的长.提示:欲证AE=CD ,只需证△ACE ≌△CBD 由条件可知∠CAE =∠BCD (同角的余角相等)加之其它两个条件易证得结论.由E 是BC 的中点,EC =BE又BD =EC ,BC =AC 知BD =6 cm5、如图8,已知:在△ABC 中,AB=AC ,∠A=90,BD 平分∠ABC 交AC 于D ,CE ⊥BD 交BD 的延长线于E ,求证:BD=2CE提示:本题的关键是从结论BD=2CE 出发,想到构造线段CF =2CE ,再证BD =CFA M N E C DB 图5 A D BC 图6 O E ┛ ┓ ┏D A CF 图7 B A E C D 图8 F。
全等三角形判定二

两角和它们的夹边对应相等的两三角形全等(可以简写成“角边角”或“ASA ”). 【例】已知:如图点D 在AB 上,点E 在AC 上,AB AC B C =∠=∠,.求证:AD AE =.EDCB A分析:AD 和AE 分别在ADC △和AEB △中,所以要证AD AE =,只需证明ADC AEB ≌△△即可. 证明:在ADC △和AEB △中,A AAC AB C B ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ADC AEB ≌△△ ()ASA ∴AD AE =.问题:①在一个三角形中,两角确定,第三个角一定确定,对吗?为什么?②可不可以不作图,用“ASA ”推出“两角和其中一角的对边对应相等的两三角形全等”呢?如图,在ABC △和DEF △中,A D B E BC EF ∠=∠∠=∠=,,,ABC △与DEF △全等吗?能利用角边角条件证明你的结论吗?全等三角形判定(二)新知学习FED CBA证明:∵180A B C D E F ∠+∠+∠=∠+∠+∠=︒ A D B E ∠=∠∠=∠,∴A B D E ∠+∠=∠+∠∴C F ∠=∠在ABC △和DEF △中 B EBC EF C F ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABC DEF ≌△△ ()ASA两个角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS ”).【例1】在ABC △和A B C '''△中,A A'BC B'C'∠=∠=,,C C'∠=∠,则ABC △与'''A B C △ .【例2】如图,点CF 在BE 上,ACB DFE BC EF ∠=∠=,,请补充一个条件,使ABC DEF ≌△△,补充的条件是 .F EDC B A【例3】如图,已知MB ND =,MBA NDC ∠=∠,下列条件不能判定是ABM CDN ≌△△的是( )A .M N ∠=∠ B. AB CD =C .AM CN = D. AM CN ∥MNDC B A基础演练【例4】如图,90E F ∠=∠=︒,B C AE AF ∠=∠=,,给出下列结论:①CAD BAD ∠=∠ ②BE CF = ③ACN ABM ≌△△ ④CD DN =其中正确的结论是_________ _________NMFEDCB A【例5】如图,在ABC △和DCB △中,AB DC =,要使ABO DCO ≌△△,请你补充条件________________(只填写一个你认为合适的条件).ODC BA【例6】如图,已知A C ∠=∠,AF CE =,DE BF ∥,求证:ABF CDE ≌△△. FEDCBA【例7】如图,CD AB ⊥,BE AC ⊥,垂足分别为D E 、,BE 交CD 于F ,且AD DF = 求证:AC BF =FEDC BA【例8】已知:如图,AD AE =,ACD ABE ∠=∠求证:BD CE =.ED CB A【例9】如图,在t R ABC △中,AB AC =,90BAC ∠=︒,过点A 的任一直线AN ,BD AN ⊥于D ,BD AN ⊥于E ,求证:DE BD CE =-【例10】已知:如图,C D BAC ABD ∠=∠∠=∠,求证:OC OD =ODCBAN EDCBA【例11】如图,已知:AB CD =,AD BC =,O 是BD 中点,过O 点的直线分别交DA 和BC 的延长线于E F ,.求证:AE CF =.FOEDCBA斜边与一直角边对应相等的两个直角三角形全等.(HL ) 【例】已知:如图,AB BD ⊥,CD BD ⊥,AD BC =,求证:AB CD =.DBCA证明:∵AB BD ⊥,CD BD ⊥ ∴ABD CDB ∠=∠在Rt ABD △与Rt CDB △中 AD CBBD BD=⎧⎨=⎩ ∴Rt ABD Rt CDB ≌△△ ()HL ∴AB CD =【习题1】如图,已知321∠=∠=∠,AB AD =.求证:BC DE =.新知学习课后练习321O EDCBA【习题2】已知:如图,AB CD ∥,AE CF =求证:AB CD =OFEDCBA【习题3】如图,已知:BE CD =,B C ∠=∠,求证:12∠=∠21OED CBA【习题4】如图,ABC △中,D 是BC 上一点,DE AB ⊥,DF AC ⊥,E F 、分别为垂足,且AE AF =,求证:DE DF =,AD 平分BAC ∠.21FEDBA【习题5】如图,在ABC △中,D 是BC 的中点,DE AB ⊥,DF AC ⊥,垂足分别是E F 、,且DE DF =, 证明:AB AC =.FEDCBA【习题6】如图,AB CD=,DF AC⊥于F,BE AC⊥于E,DF BE=,求证:AF CE=.F EDCBA至此,我们有六种判定三角形全等的方法:1.全等三角形的定义2.判定定理边边边()SSS边角边()SAS角边角()ASA角角边()AAS HL(仅用在t R△中)推证两三角形全等时,要善于观察,寻求对应相等的条件,从而获得解题途径.知识总结。
数学人教版八年级上册12.2三角形全等的判定定理2(SAS).2 三角形全等的判定

A
A
B 图一 在图一中, ∠A 是AB和AC的夹角, 符合图一的条件,它可称为 “两边夹角”。
C
B
图二
C
符合图二的条件, 通常 说成“两边和其中一边的对角”
探索边角边
已知△ABC,画一个△A′B′C′使A B =A′B′,A C =A′ C ′, ∠A =∠A′。
画法: 1.画 ∠DA′ E= ∠A; ′ 2.在射线A D上截取A′ B′ =AB,在射线A′ E上截 取A ′C ′=AC; C C′ 3. 连接B ′C′.
补充题:
例1 如图AC与BD相交于点O, 已知OA=OC,OB=OD,说明 △AOB≌△COD的理由。 A B
O
D C C D
例2 如图,AC=BD, ∠CAB= ∠DBA,你能判断 BC=AD吗?说明理由。
A B 归纳:判定两条线段相等或二个角相等可以通 过从它们所在的两个三角形全等而得到。
课堂小结:
A B A′ B′ D
思考: ① △A′ B′ C′ 与 △ABC 全等吗?如何验正? 思考: ②这两个三角形全等是满足哪三个条件? 结论:两边及夹角对应相等的两个三角形全等
三角形全等判定方法2
两边和它们的夹角对应相等的两个三角形全
等。(可以简写成“边角边”或“ SAS ” )
用符号语言表达为:
A D
B
1
那么量出ED的长,就是A、B的 距离.为什么?【要求学生写出 理由即证明过程】
C
2
E
D
例2:点E、F在AC上,AD//BC,AD=CB,AE=CF
求证(1)△AFD≌△CEB
A 分析:证三角形全等的三个条件 边 AD = CB (已知) 角 ∠A=∠ 边 C AF = CE E F C D
三角形全等的判定2教学教案设计一等奖

3、三角形全等的判定2教学设计一等奖【教学目标】1.使学生理解边边边公理的内容,能运用边边边公理证明三角形全等,为证明线段相等或角相等创造条件;2.继续培养学生画图、实验,发现新知识的能力.【重点难点】1.难点:让学生掌握边边边公理的内容和运用公理的自觉性;2.重点:灵活运用SSS判定两个三角形是否全等.【教学过程】一、创设问题情境,引入新课请问同学,老师在黑板上画得两个三角形,△ABC与△全等吗?你是如何判定的.(同学们各抒己见,如:动手用纸剪下一个三角形,剪下叠到另一个三角形上,是否完全重合;测量两个三角形的所有边与角,观察是否有三条边对应相等,三个角对应相等.)上一节课我们已经探讨了两个三角形只满足一个或两个边、角对应相等条件时,两个三角形不一定全等.满足三个条件时,两个三角形是否全等呢?现在,我们就一起来探讨研究.二、实践探索,总结规律1、问题1:如果两个三角形的三条边分别相等,那么这两个三角形会全等吗?做一做:给你三条线段、、,分别为、、,你能画出这个三角形吗?先请几位同学说说画图思路后,教师指导,同学们动手画,教师演示并叙述书写出步骤.步骤:(1)画一线段AB使它的长度等于c(4.8cm).(2)以点A为圆心,以线段b(3cm)的'长为半径画圆弧;以点B为圆心,以线段a (4cm)的长为半径画圆弧;两弧交于点C.(3)连结AC、BC.△ABC即为所求把你画的三角形与其他同学的图形叠合在一起,你们会发现什么?换三条线段,再试试看,是否有同样的结论请你结合画图、对比,说说你发现了什么?同学们各抒己见,教师总结:给定三条线段,如果它们能组成三角形,那么所画的三角形都是全等的. 这样我们就得到判定三角形全等的一种简便的方法:如果两个三角形的三条边分别对应相等,那么这两个三角形全等.简写为“边边边”,或简记为(S.S.S.).2、问题2:你能用相似三角形的判定法解释这个(SSS)三角形全等的判定法吗?(我们已经知道,三条边对应成比例的两个三角形相似,而相似比为1时,三条边就分别对应相等了,这两个三角形不但形状相同,而且大小都一样,即为全等三角形.)3、问题3、你用这个“SSS”三角形全等的判定法解释三角形具有稳定性吗?(只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定了)4、范例:例1 如图19.2.2,四边形ABCD中,AD=BC,AB=DC,试说明△ABC≌△CDA. 解:已知AD=BC,AB=DC ,又因为AC是公共边,由(S.S.S.)全等判定法,可知△ABC ≌△CDA5、练习:6、试一试:已知一个三角形的三个内角分别为、、,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,你发现了什么?(所画出的三角形都是相似的,但大小不一定相同).三个对应角相等的两个三角形不一定全等.三、加强练习,巩固知识1、如图,,,△ABC≌△DCB全等吗?为什么?2、如图,AD是△ABC的中线, . 与相等吗?请说明理由.四、小结本节课探讨出可用(SSS)来判定两个三角形全等,并能灵活运用(SSS )来判定三角形全等.三个角对应相等的两个三角不一定会全等.五、作业4、三角形全等的判定2教学设计一等奖教学建议直角三角形全等的判定知识结构重点与难点分析:本节课教学方法主要是“自学辅导与发现探究法”。
三角形全等的判定

1. 全等三角形判定1:三边对应相等的两个三角形全等。
2. 全等三角形判定2:两边和它们的夹角对应相等的两个三角形全等。
3. 全等三角形判定3:两角和它们的夹边对应相等的两个三角形全等。
4. 全等三角形判定4:两个角和其中一个角的对边对应相等的两个三角形全等。
5. 全等三角形判定5:斜边和一条直角边对应相等的两个直角三角形全等。
典型例题知识点一:全等三角形判定1例1:如图,在△AFD和△EBC中,点A,E,F,C 在同一直线上,有下面四个论断:(1)AD=CB;(2)AE=CF;(3)DF=BE;(4)AD∥BC。
请将其中三个论断作为条件,余下的一个作为结论,编一道证明题,并写出证明过程。
解答过程:已知:如图,在△AFD和△EBC中,点A,E,F,C在同一直线上,AD=CB,AE=CF,DF=BE。
求证:AD∥BC。
知识点二:全等三角形判定2(2)由(1)知△OAB≌△OCD∴AB=CD例3:已知:如图,AB∥CD,AB=CD,求证:AD∥BC,AD=BC综上:AD∥BC,AD=BC例4:(1)在图1中,△ABC和△DEF满足AB=DE,AC=DF,∠A=∠D,这两个三角形全等吗?(2)在图2中,△ABC和△ABD满足AB=AB,AC=AD,∠B =∠B,这两个三角形全等吗?。
解答过程:(1)全等;(2)不全等。
解题后的思考:有两边和一角相等的两个三角形不一定全等,要根据所给的边与角的位置进行判断:(1)当两个三角形满足两边及夹角对应相等即“SAS”时,这两个三角形全等;(2)当两个三角形满足两边及其中一边的对角对应相等即“SSA”时,这两个三角形不一定全等。
在证明题中尤其要注意这一点。
知识点三:全等三角形判定3 例5:如图,BE⊥AE,CF⊥AE,ME=MF。
求证:AM是△ABC的中线。
解答过程:∵BE⊥AE,CF ⊥AE∴∠BEM=∠CFM=90°在△BME和△CMF中,解题后的思考:要证明AM是△ABC的中线,需要证明M是BC的中点,因此,转化为证明BM=CM,结合已知条件,应考虑证明与这两条相等线段有关的可能全等的两个三角形,结合题目中已有的条件和能够求出的相等关系,选择正确的判定方法来解决相关问题。
全等三角形性质与判定(二)-教师版

一、全等三角形的性质全等三角形对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,周长相等,面积相等.二、全等的性质和判定(1)全等三角形的判定方法:()tSSS SAS ASA AAS HL R、、、、△(2)全等三角形的图形变换形式:平移、对称、旋转(3)由全等可得到的相关定理:①角平分线定理②等腰、等边三角形性质和判定③垂直平分线定理共顶点等腰三角形旋转模型——“手拉手”模型证明全等的基本思想“SAS”等边三角形共顶点全等三角形性质与判定知识回顾知识讲解共顶点等腰直角三角形共顶点等腰三角形共顶点等腰三角形【例1】 如图,等边三角形ABC ∆与等边DEC ∆共顶点于C 点.求证:AE BD =.【解析】通过“SAS ”证明BCD ACE ≌△△,得到AE BD =.【例2】 已知:如图,点C 为线段AB 上一点,ACM ∆、CBN ∆是等边三角形. 求证:(1)AN BM =;(2)DE AB ∥;(3)CF 平分AFB ∠.同步练习【解析】通过“SAS ”证明MCB ACN ≌△△,得到AN BM =.通过“SAS ”证明MCE ACD ≌△△,得到CE CD =,从而推出DCE △为等边三角形, ︒=∠=∠60NCB DEC DE AB ∥.【变式练习】如图,B ,C ,E 三点共线,且ABC ∆与DCE ∆是等边三角形,连结BD ,AE 分别交AC ,DC 于M ,N 点.求证:CM CN =.【解析】通过“SAS ”证明BCD ACE ≌△△,得到CBD CAE ∠=∠. 再通过“SAS ”证明CAN CBM ≌△△,得到CM CN =.【例3】 如图,点C 为线段AB 上一点,ACM ∆、CBN ∆是等边三角形,D 是AN 中点,E 是BM 中点,求证:CDE ∆是等边三角形.【解析】通过“SAS ”证明MCB ACN ≌△△,得到CMB CAN MB AN ∠=∠=,.再通过“SAS ”证明CAD CME ≌△△,得到MCE ACD CE CD ∠=∠=,,从而推出︒=∠60DCE .【变式练习】(2008年全国初中数学联赛武汉CASIO 杯选拔赛)如图,ABD ∆和CED ∆均为等边三角形,AC BC =,AC BC ⊥.若2BE =,则CD = .【解析】通过“SAS ”证明BDE ADC ≌△△,得到1322-====CD AB BE AC ,,.【例4】 平面上三个正三角形ACF ,ABD ,BCE 两两共只有一个顶点,求证:EF 与CD 平分.【解析】通过“SAS ”证明,得到ACB AFD △≌△,DF CB CE ==; 再通过“SAS ”证明,得到BCA BED △≌△,DE AC CF ==; 得到四边形ABCD 为平行四边形,对角线互相平分.【例5】 已知:如图,ABC ∆、CDE ∆、EHK ∆都是等边三角形,且A 、D 、K 共线,AD DK =.求证:HBD ∆也是等边三角形.【解析】连接CH 交AD 于M通过“SAS ”证明FCH FDK △≌△,得到CH DK AD ==,60AMC ∠=︒,推出DAB HCB ∠=∠; 再通过“SAS ”证明,得到ABD CBH △≌△,HB HD BHC BDA =∠=∠,; 进一步推出HBD △也是等边三角形.【例6】 (2008年怀化市初中毕业学业考试试卷)如图,四边形ABCD 、DEFG 都是正方形,连接AE 、CG .求证:AE CG =.【解析】通过“SAS ”证明CDG ADE ≌△△,得到DG AE =.【变式练习】以△ABC 的两边AB 、AC 为边向外作正方形ABDE 、ACFG ,求证:CE =BG ,且CE ⊥BG .【解析】通过“SAS ”证明ABG AEC ≌△△,得到ABG AEC BG CE ∠=∠=,, 再通过“8”字图导角得到BG CE ⊥.【例7】 (2004河北)如图,已知点E 是正方形ABCD 的边CD 上一点,点F 是CB 的延长线上一点,且EA AF ⊥. 求证:DE BF =.【解析】通过“ASA ”证明ADE ABF △≌△,得到DE BF =.【变式练习】如图所示,在四边形ABCD 中,90ADC ABC ∠=∠=︒,AD CD =,DP AB ⊥于P ,若四边形ABCD 的面积是16,求DP 的长.【解析】过点D 作DE BC ⊥交BC 延长线于通过“AAS ”证明DPA DEC △≌△,得到DE DP =,从而推出四边形ABCD 是正方形 =164ABCD DPBE S S DP ==,【例8】 如图所示.正方形ABCD 中,在边CD 上任取一点Q ,连AQ ,过D 作DP ⊥AQ ,交AQ 于R ,交BC 于P ,正方形对角线交点为O ,连OP ,OQ .求证:OP ⊥OQ .QRPOD CBA【解析】通过“ASA ”证明ADQ DCP △≌△,得到DQ CP =,再通过“SAS ”证明,得到ODQ OCP △≌△,POC QOD ∠=∠从而推出OP OQ ⊥.【变式练习】如图,正方形OGHK 绕正方形ABCD 中点O 旋转,其交点为E 、F ,求证:AE CF AB +=.【解析】通过“ASA ”证明AOE BOF △≌△,得到AE BF =,从而推出AE CF AB +=.【例9】 如图,等腰直角三角形ABC 中,90B =︒∠,AB a =,O 为AC 中点,EO OF ⊥.求证:BE BF +为定值.【解析】连接OB通过“SAS ”证明BOE COF △≌△,得到BE CF =. BE BF BF CF BC a +=+==【变式练习】等腰直角三角形ABC ,90ABC =︒∠,AB a =,O 为AC 中点,45EOF =︒∠,试猜想,BE 、BF 、EF 三者的关系.【解析】过点O 作OD OE ⊥交BC 于D通过“SAS ”证明BOE COD △≌△,得到OE OD BE CD ==,. 再通过“SAS ”证明0E F DOF △≌△,得到EF DF =. 可以推出BE BF EF CD DF BF BC AB a ++=++===【例10】 已知E 、F 分别是正方形ABCD 的边BC 、CD 上的点,且45EAF =︒∠,AH EF ⊥,H 为垂足,求证:AH AB =.【解析】延长EB 至M ,使得BM DF =,通过“SAS ”证明ADF ABM △≌△,得到AM AF =. 再通过“SAS ”证明AME AFE △≌△,得到AB AH =.【例11】 (1997年安徽省竞赛题)如图,在△ABC 外面作正方形ABEF 与ACGH ,AD 为△ABC 的高,其反向延长线交FH 于M ,求证:(1)CF BH =;(2)MH MF =M EFHGD CBA【解析】(1)通过“SAS ”证明AFC ABH △≌△,得到CF BH =. (2)过F H 、分别作FN MD D HK MD K ⊥⊥于,于,再通过“AAS ”证明BDA ANF HKA ADC △≌△,△≌△,得到FN HK =. 再通过“8”字全等证明FNM HKM △≌△,从而得到MF MH =.【注】这道题有很多重要的结论,条件结论互换依然成立,2,ABC AFH BC AM S S ==△△【例12】 (1997年安徽省初中数学竞赛题)在等腰Rt ABC ∆的斜边AB 上取两点M 、N ,使45MCN ∠=︒,记AM m =,MN x =,BN n =,则以x 、m 、n 为边长的三角形的形状是( ).A .锐角三角形B .直角三角形C .钝角三角形D .随x 、m 、n 的变化而变化【解析】见下题 【答案】B【例13】 (通州区2009一模第25题)请阅读下列材料:已知:如图1在Rt ABC ∆中,90BAC ∠=︒,AB AC =,点D 、E 分别为线段BC 上两动点,若45DAE ∠=︒.探究线段BD 、DE 、EC 三条线段之间的数量关系. 小明的思路是:把AEC ∆绕点A 顺时针旋转90︒,得到ABE '∆,连结E D ', 使问题得到解决.请你参考小明的思路探究并解决下列问题:⑴ 猜想BD 、DE 、EC 三条线段之间存在的数量关系式,并对你的猜想给予证明; ⑵ 当动点E 在线段BC 上,动点D 运动在线段CB 延长线上时,如图2,其它条件不变,⑴中探究的结论是否发生改变?请说明你的猜想并给予证明.【解析】(1)过点A 作AD 的垂线AF ,使得AD AF =,连接EF CF 、通过“SAS ”证明ABD ACF △≌△,得到45B ACF BD CF ∠=∠==,. 再通过“SAS ”证明ADE AFE △≌△,得到DE EF =.在Rt ECF △中满足勾股定理,,得到222.CE CF EF +=,故222.CE BD DE += (2)同理可证222.CE BD DE +=【例14】 在等边ABC ∆的两边AB ,AC 所在直线上分别有两点M ,N ,D 为ABC ∆外一点,且60MDN ∠=︒,120BDC ∠=︒,BD CD =,探究:当点M ,N 分别爱直线AB ,AC 上移动时,BM ,NC ,MN之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系.⑴如图①,当点M ,N 在边AB ,AC 上,且DM =DN 时,BM ,NC ,MN 之间的数量关系式__________;此时LQ=_________ ⑵如图②,当点M ,N 在边AB ,AC 上,且DN DM ≠时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明;⑶如图③,当点M ,N 分别在边AB ,CA 的延长线上时,若AN =x ,则Q =_________(用x ,L 表示.图③图②图①ABCD MNABCD MNN MD CBA【解析】(1)MN BM CN =+,Q 2=L 3(2)延长AC 至E ,使得CE BM =,连接DE通过“SAS ”证明DBM DCE △≌△,得到DE DM =.再通过“SAS ”证明MDN EDN △≌△,得到MN NE BM CN ==+ 2223Q MN AN AM ME AN AC BM NC L x =++=+++==+ (3)在AC 上截取CE BM =,连接DE通过“SAS ”证明DBM DCE △≌△,得到DE DM =.再通过“SAS ”证明MDN EDN △≌△,得到MN NE CN BM ==- 2223Q MN AN AM NE AN AC BM NC L x =++=+++==+【变式练习】(1)如图,在四边形ABCD 中,AB =AD ,∠B =∠D =90°,E 、F 分别是边BC 、CD 上的点,且∠EAF =12∠BAD .求证:EF =BE +FD ; (2)如图在四边形ABCD 中,AB =AD ,∠B +∠D =180°,E 、F 分别是边BC 、CD 上的点,且∠EAF =12∠BAD , (1)中的结论是否仍然成立?不用证明. (3)如图在四边形ABCD 中,AB =AD ,∠B +∠ADC =180°,E 、F 分别是边BC 、CD 延长线上的点,且∠EAF =12∠BAD , (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.FED CBAF EDCBA【解析】(1)延长BC 至M ,使得DK BM =,连接AM 通过“SAS ”证明ADF ABM △≌△,得到AF AM =.再通过“SAS ”证明AME AFE △≌△,得到EF EM BE DF ==+ (2)同理可证 (3)同理可证【变式练习】如图所示,在四边形ABCD 中,AB =BC ,∠A =∠C =90°,∠B =135°,K 、N 分别是AB 、BC 上的点,若△BKN 的周长为AB 的2倍,求∠KDN 的度数.【解析】延长BC 至E ,使得CE AK =,连接DE 、BD 通过“HL ”证明ABD CBD △≌,得到AD CD =.通过“SAS ”证明ADK CDE △≌△,得到DK DE ADK CDE =∠=∠,.再通过“SSS ”证明KDN EDN △≌△,得到122.52NDK NDE KDN ADC ∠=∠∠=∠=,【例15】 (北京市初二数学竞赛试题) 如图所示,在五边形ABCDE 中,90B E ∠=∠=︒,AB CD AE ===1BC DE +=,求此五边形的面积.【解析】延长DE 至F ,使得BC EF =,连接AC 、AF 、AD 通过“SAS ”证明ABC AEF △≌△,得到AC AF =. 再通过“SSS ”证明ACD AFD △≌△, 12212ABCDE ADE S S DF AE==∙∙=△同步课程˙全等三角形性质与判定 【变式练习】(江苏省数学竞赛试题)如图,已知五边形ABCDE 中,∠ABC =∠AED =90°,AB =CD =AE =BC +DE =2.求该五边形的面积.【解析】延长DE 至F ,使得BC EF =,连接AC 、AF 、AD 通过“SAS ”证明ABC AEF △≌△,得到AC AF =. 再通过“SSS ”证明ACD AFD △≌△, 12242ABCDE ADE S S DF AE ==∙∙=△【变式练习】(希望杯全国数学邀请赛初二第二试试题) 在五边形ABCDE 中,已知AB AE =,BC DE CD +=,180ABC AED ∠+∠=,连接AD .求证:AD 平分CDE ∠.【解析】延长DE 至F ,使得BC EF =,连接AC 、AF 通过“SAS ”证明ABC AEF △≌△,得到AC AF =. 再通过“SSS ”证明ACD AFD △≌△,得到ADC ADF ∠=∠.【习题1】如图,已知ABC ∆和ADE ∆都是等边三角形,B 、C 、D 在一条直线上,试说明CE 与AC CD +相等的理由.【解析】通过“SAS ”证明ABD ACE △≌△,得到BD CE AC CD ==+.【习题2】已知:如图,点E 是正方形ABCD 的边AB 上任意一点,过点D 作DF DE ⊥交BC 的延长线于点F .求证:DE DF =.FEDCBA【解析】通过“ASA ”证明ADE CDF △≌△,得到DE DF =.【习题3】已知:如图,点C 为线段AB 上一点,ACM ∆、CBN ∆是等边三角形.CG 、CH 分别是ACN ∆、MCB ∆ 的高.求证:CG CH =.课后练习【解析】通过“SAS ”证明ACN MCB △≌△,得到CAN CMB ∠=∠. 再通过“AAS ”证明CAG CMH △≌△,得到CG CH =.【习题4】如图,正方形ABCD 的边长为1,AB 、AD 上各存一点P 、Q ,若△APQ 的周长为2,求∠PCQ 的度数.QP DCBA【解析】延长AB 至M ,使得BM DQ =,连接CM 依题可知:PQ DP BP =+通过“ASA ”证明CDQ CBM △≌△,得到,CQ CM DCQ BCM =∠=∠. 再通过“ASA ”证明CQP CMP △≌△,得到45QCP MCP ∠=∠=【习题5】在等腰直角ABC ∆中,90ACB ∠=,AC BC =,M 是AB 的中点,点P 从B 出发向C 运动,MQ MP ⊥ 交AC 于点Q ,试说明MPQ ∆的形状和面积将如何变化.【解析】通过“ASA ”证明MBP MCP △≌△,得到BMP CMQ BM CM ∠=∠=,,从而推出 MPQ ∆是等腰直角三角形,点P 从B 出发向C 运动,MP 先变小在变大, 故MPQ ∆的面积先变小再变大.同步课程˙全等三角形性质与判定【习题6】如图,正方形ABCD 中,FAD FAE ∠=∠.求证:BE DF AE +=.【解析】延长EB 至M ,使得BM DF =,通过“SAS ”证明ADF ABM △≌△,得到AFD M DAF BAM ∠=∠∠=∠,. 通过导角推出M EAM ∠=∠,从而推出AE ME =,故BE DF AE +=.【习题7】等边ABD ∆和等边CBD ∆的边长均为1,E 是BE AD ⊥上异于A D 、的任意一点,F 是CD 上一点,满足1AE CF +=,当E F 、移动时,试判断BEF ∆的形状.【解析】依题可知,AE DF =,通过“SAS ”证明ABE DBF △≌△,得到ABE DBF BE BF ∠=∠=,. 从而推出BEF △为等边三角形.【习题8】(北京市数学竞赛试题,天津市数学竞赛试题) 如图所示,ABC ∆是边长为1的正三角形,BDC∆是顶角为120的等腰三角形,以D 为顶点作一个60的MDN ∠,点M 、N 分别在AB 、AC 上,求AMN ∆的周长.同步课程˙全等三角形性质与判定【解析】延长AC 至E ,使得BM CE =,通过“SAS ”证明DBM DCE △≌△,得到BDM CDE ∠=∠. DM DE =,再通过“SAS ”证明MDN EDN △≌△,得到MN EN MN BM CN ==+,.。
(完整版)全等三角形判定2(SAS)学案及题型

C'B'A'CBACBADCBA2111.2三角形全等的判定(2)SAS营山希望学校任画一个△ABC求作:'''A B C∆,使''A B AB=,''B C BC=,'A A∠=∠作图步骤:(2) 把△'''A B C剪下来放到△ABC上,观察△'''A B C与△ABC是否能够完全重合?(3)归纳;由上面的画图和实验可以得出全等三角形判定(二):两边和它们的夹角对应相等的两个三角形(可以简写成“”或“”)(4)用数学语言表述全等三角形判定(二)在△ABC和'''A B C∆中,∵''AB A BBBC=⎧⎪∠=⎨⎪=⎩∴△ABC≌三、合作探究例如图,AC=BD,∠1=∠2,求证:BC=AD.1、如图,已知AC,BD相交于O,AO=DO,BO=CO,证明:∠A=∠D2.如图,AE是,BAC的平分线∠AB=AC.证明△ABD≌△ACD3 已知:如图,BD=CE,AD=AE,求证:BE=CD.5 如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,求证:BE=DCDABQCPE1图2图3图6 如图,点C 是AB 中点,CD ∥BE ,且CD=BE ,试探究AD 与CE 的关系。
7 如图:已知AC ,BD 相交于O ,OA=OB ,OC=OD.证明:△ABC ≌△BAD(提高题)如图,已知CA=CB,AD=BD,M 、N 分别是CA 、CB 的中点,求证:DM=DNAC E DDC12 O。
【数学课件】直角三角形全等的判定(2)

问题:判定一般三角形全等的方法有哪 几种?若这两个三角形是直角三角形, 那么这些判定方法适用吗? 答:SSS,SAS,ASA,AAS
• 如图,具有下列条件的Rt△ABC与Rt△DEF(其中∠C =∠F=90°)是否全等,在( )里填写理由;如果 不全等,在( )里打“×”: (1)AC=DF,∠A=∠D ( ASA) (2)AC=DF,BC=EF ( SAS ) (3)AB=DE,∠B=∠E (AAS ) (4)∠A=∠D,∠B=∠E ( × )
N
A′
Rt△ABC≌ Rt△A'B'C'
B
C
M
B′
C′
两个直角三角形全等的判定: 斜边和一直角边对应相等的两个直角三角形全等 (可以简写成“斜边、直角边公理”或“HL”)
注意:“HL”是仅适用于Rt△的特殊方法。应用HL判定时,虽只 有两个条件,但必须先有两个Rt△。书写格式为: 在Rt△______和Rt△_____和△A′B′C′中,CD、C′D′分别是高,并且AC=A′C′,CD= C′D′,∠ACB=∠A′C′B′。 求证:△ABC≌△A′B′C′ 证明:∵ CD、C′D′分别是高 ∴ ∠ADC= ∠A′D′C′=90° 在Rt△ ADC与Rt△ A′D′C′中 AC=A′C′ CD=C′D′ ∴ Rt△ ADC=Rt△ A′D′C′(HL) ∴ ∠A =∠A′ 在△ABC与△A′B′C′中 ∠A =∠A′ AC=A′C′ ∠ACB=∠A′C′B′ ∴ △ABC≌△A′B′C′(ASA)
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭 2、教育人就是要形成人的性格。——欧文 3、自我教育需要有非常重要而强有力的促进因素——自尊心、自我尊重感、上进心。——苏霍姆林斯基 4、追求理想是一个人进行自我教育的最初的动力,而没有自我教育就不能想象会有完美的精神生活。我认为,教会学生自己教育自己,这是一种 最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——(前苏联)苏霍姆林斯基 6、教育不是注满一桶水,而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的,但其果实是甜的。——亚里士多德 9、教育的目的,是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——(前苏联)苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美,人的关系的美而看到的精神的高尚、善良和诚实,并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知,而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品,就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心,这种道德上的自勉。要是儿童自己不求上进,不知自勉,任何教育者就都不能在他的身 上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方,儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲,最大的乐趣就在于:在其有生之年,能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情,就是爱。教育没有了情爱,就成了无水的池,任你四方形也罢、圆形也罢,总逃不出一个空虚。班主任广博的爱 心就是流淌在班级之池中的水,时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么,但它能启发儿童创造力以从事于创造工作。——陶行知
全等三角形的判定二(边角边)

第2课时三角形全等的判定(二)(SAS)1.理解和掌握全等三角形判定方法2——“边角边”.理解满足“边边角”的两个三角形不一定全等.2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.阅读教材P37-39页“探究3及例2”,掌握三角形全等的判定条件SAS,进一步掌握证明格式,学生独立完成下列问题:学习流程:1、了解感知合作探究一:同桌之间完成:三角形全等的判定“边角边”的探究定义:两边和他们的夹角分别相等的两个三角形全等.(可以简写成”边角边”或”SAS”)几何语言的书写:在△ABC 和△A’B’C’中∴△ABC≌△A’B’C’( )自学反馈(小组交流完成)(1)已知:如图,AB、CD相交于O点,AO=CO,OD=OB.求证:(1)△AOD≌△COB.(2)∠D=∠B(2)已知:如图,AB=AC,∠BAD=∠CAD.求证:∠B=∠C.变式:已知:如图,AB=AC,AD平分∠BAC. 求证:∠B=∠C.(3)如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是( )A.∠A=∠DB.∠E=∠CC.∠A=∠CD.∠ABD=∠EBC(4)有两边和一个角对应相等的两个三角形全等.(填“一定”或“不一定”)1.利用SAS证明全等时,要注意“角”只能是两组相等边的夹角;在书写证明过程时相等的角应写在中间;2.证明过程中注意隐含条件的挖掘,如“对顶角相等”、“公共角、公共边”等.阅读教材P39页“思考”,明白有两边和其中一边的对角对应相等的两个三角形不一定全等,并会通过画图举反例,BA CB’A’C’完成P39页练习题.独立完成后小组内交流思路1.如图,AB=AC,AE=AD,求证:∠B=∠C变式:AB=AC,BE=CD.求证:∠B=∠C.跟踪训练:(活动2)1.已知:如图,AB=AD,AC=AE,∠1=∠2.求证:BC=DE.2.已知:如图,AB∥CD,AB=CD.求证:AD∥BC.可从问题出发,要证线段平行只需证角相等即可(∠3=∠4),而证角相等可证角所在的三角形全等.合作探究三:迁移应用例2如图,将两个一大、一小的等腰直角三角尺拼接(A、B、D三点共线,AB=CB,EB=DB,∠ABC=∠EBD=90°),连接AE、CD,试确定AE与CD的关系,并证明你的结论.1.注意挖掘等腰直角三角形中的隐藏条件;2.线段的关系分数量与位置两种关系.3.分析已知条件,确定证三角形全等所缺少的条件,充分挖掘隐藏条件.活动3 课堂小结1.利用对顶角、公共角、直角用SAS证明三角形全等.2.用“分析法”寻找命题结论也是一种推理论证的方法,即从结论出发逐步递推到题中条件,常以此作为分析寻求推理论证的途径.。
人教版数学八年级上册 全等三角形的判定二

全等三角形的判定二(ASA ,AAS )(基础)要点一、全等三角形判定1——“角边角”全等三角形判定1——“角边角”两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA ”). 要点诠释:如图,如果∠A =∠,AB =,∠B =∠,则△ABC ≌△.要点二、全等三角形判定4——“角角边”1.全等三角形判定4——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS ”) 要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果DE ∥BC ,那么∠ADE =∠B ,∠AED =∠C ,又∠A =∠A ,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.要点三、判定方法的选择1.选择哪种判定方法,要根据具体的已知条件而定,见下表:'A ''A B 'B '''A B C【典型例题】类型一、全等三角形的判定1——“角边角”1、(2015•渝中区模拟)如图,已知AD,BC相交于点O,OB=OD,∠ABD=∠CDB求证:△AOB≌△COD.举一反三:【变式】如图,AB∥CD,AF∥DE,BE=CF.求证:AB=CD.类型二、全等三角形的判定4——“角角边”【高清课堂:379110 全等三角形的判定二,例6】2、已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.求证:AD=AC.举一反三:【变式】如图,AD是△ABC的中线,过C、B分别作AD及AD的延长线的垂线CF、BE.求证:BE=CF.3、(2015春•雅安期末)如图:AB=A′B′,∠A=∠A′,若△ABC≌△A′B′C′,则还需添加的一个条件有()种.A.1B. 2C.3D.4【思路点拨】本题要证明△ ABC≌△ A′B′C′,已知了AB=A′B′,∠A=∠ A′,可用的判别方法有ASA,AAS,及SAS,所以可添加一对角∠B=∠B′,或∠C=∠C′,或一对边AC=A′C′,分别由已知与所添的条件即可得证.类型三、全等三角形判定的实际应用4、“三月三,放风筝”.下图是小明制作的风筝,他根据DE=DF,EH=FH,不用度量,就知道∠DEH=∠DFH.请你用所学的知识证明.【巩固练习】一、选择题1.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中,和△ABC全等的图形是()图4-3A.甲和乙B.乙和丙C.只有乙D.只有丙2.如图,已知MB=ND,∠MBA=∠NDC,下列条件不能判定△ABM≌△CDN的是()A.∠M=∠N B.AB=CD C.AM=CN D.AM∥CN3. 某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是()A.带①去B.带②去C.带③去D.①②③都带去4. 如图,已知AB=CD,AD=BC,则下列结论中错误的是()A.AB∥DCB.∠B=∠DC.∠A=∠CD.AB=BC5. 如图,AB、CD、EF相交于O,且被O点平分,DF=CE,BF=AE,则图中全等三角形的对数共有()A. 1对B. 2对C. 3对D. 4对6.如图,∠1=∠2,∠3=∠4,下面结论中错误的是()A.△ADC≌△BCD B.△ABD≌△BACC.△ABO≌△CDO D.△AOD≌△BOC二、填空题7. 已知,如图,AB∥CD,AF∥DE,AF=DE,且BE=2,BC=10,则EF=________.8. 如图, 已知:∠1 =∠2 , ∠3 =∠4 , 要证BD =CD , 需先证△AEB ≌△AEC , 根据是,再证△BDE ≌△,根据是.9.(2014秋•大同期末)如下图∠1=∠2,由AAS判定△ABD≌△ACD,则需添加的条件是.10. 如图,AC=AD,CB=DB,∠2=30°,∠3=26°,则∠CBE=_______.11. 已知,如图,AB=CD,AC=BD,则△ABC≌,△ADC≌ .12. 已知:如图,∠B=∠DEF,AB=DE,要说明△ABC≌△DEF,(1)若以“ASA”为依据,还缺条件(2)若以“SAS”为依据,还缺条件三、解答题13.(2015•通辽)如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.14. 如图,已知D、E、B 三点共线,AE=CE ,AE⊥CE,∠D=∠B=90°.求证:CD+AB=DB.15. 如图,已知AB=DC,AC=DB,BE=CE求证:AE=DE.。
1.2直角三角形全等的判定2

1.2 直角三角形全等的判定Ⅰ.核心知识点扫描⑴直角三角形全等特有的方法:斜边和一条直角边对应相等的两个直角三角形全等。
(简写为“H L ”)⒈直角三角形的全等判定定理⑵与一般三角形公有的方法:SAS 、ASA 、AAS 、SSS. ⑴角平分线的性质:角平分线上的点到这个角两边的距离相等。
⒉直角三角形的全等的应用⑵角平分线的判定:在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上。
Ⅱ.知识点全面突破知识点1:直角三角形全等的判定方法(重点)⒈判定定理:斜边和一条直角边对应相等的两个直角三角形全等(简写:HL ). ⒉用数学语言表示为:如图1-2-1,在△ABC 和△A ˊB ˊC ˊ中,∵∠ACB=∠A ˊC ˊB ˊ=90°,AB= A ˊB ˊ,AC= A ˊC ˊ, ∴△ABC ≌△A ˊB ˊC ˊ. 3.定理的证明.已知如图1-2-1所示,在△ABC 和△A ′B ′C ′中,∠ACB=∠A ′B ′C ′=90°,AC=A ′C ′,AB=A ′B ′,求证:△ABC ≌△A ′B ′C ′. 证明:设 AC=A ′C ′=b ,AB=A ′B ′=c ,∵在△ABC 和△A ′B ′C ′中,∠ACB=∠A ′B ′C ′=90°,AC=A ′C ′=b ,AB=A ′B ′=c ∴BC=B ′C ′∵在△ABC 和△A ′B ′C ′中''''''AC A C AB A B BC B C ⎧=⎪=⎨⎪=⎩∴△ABC ≌△A ′B ′C ′(SSS)例 :(2010,北京)已知:如图1-1-2,点A 、B 、C 、D 在同一条直线上,EA⊥AD,FD⊥AD,AE=DF ,AB=DC .求证:∠ACE=∠DBF.{{C(CBA(AB'C'A'B CA图1-2-1证明:∵AB=DC∴AC=DB∵EA⊥AD,FD⊥AD∴∠A=∠D=90°在△EAC与△FDB中,EA=FD, ∠A=∠D,AC=DB∴△EAC≌△FDB(SAS) ∴∠ACE=∠DBF.点拨:□C要想证明∠ACE=∠DBF,则需要证明△EAC≌△FDB 即可,而两个三角形全等的条件题中易得.证明:能.∵AB=DC∴AC=DB∵EA⊥AD,FD⊥AD∴∠A=∠D=90°在Rt△EAC与Rt△FDB中AC=DB, EC=BF∴△EAC≌△FDB(HL)∴∠ACE=∠DBF.点拨:要想证明∠ACE=∠DBF,则需要证明△EAC≌△FDB即可,由EA⊥AD,FD⊥AD,可得∠ACB=∠DCE=90°,由AB=DC,可得AC=DB,再根据EC=BF可利用“HL”证明两个三角形全等.知识点2:角的平分线的性质定理及逆定理(重点)1. 角的平分线的性质定理及逆定理定理内容用数学语言表示定理作用角的平分线的性质定理角平分线上的点到这个角的两边的距离相等.∵□C PA⊥AO,PB⊥OB,OP是角平分线,∴PA=PB(角的平分线的性质定理)证明线段相等角的平分线的判定定理角内部到角的两边距离相等的点,在这个角的平分线上.∵□C PA⊥AO,PB⊥OB,PA=PB,∴OP是角平分线(角的平分线的判定定理)证明角相等2.角是轴对称图形,角平分线所在的直线是它的对称轴,用“折叠得到折痕(垂线段)重合”来证明角平分线定理1,再说明角平分线定理1逆命题是真命题.由此,角平分图1-2-2线的这两个定理可以归纳为:角平分线可以看着是到角的两边距离相等的所有点的集合. 例1:(2009,山东临沂)如图1-2-3,OP 平分AOB ∠, PA OA ⊥, PB OB ⊥,垂足分别为A ,B .下列结论中不一定成立的是( ) A .PA PB = B .PO 平分APB ∠C .OA OB =D .AB 垂直平分OP解:D点拨:本题考查的是三角形全等和角平分线的性质。
全等三角形的判定(二)边角边_课件

证明: ∵ AD平分∠BAC,
∴ ∠BAD=∠CAD. 在△ABD与△ACD中, AB=AC,(已知) ∵ ∠BAD=∠CAD,(已证) AD=AD,(公共边) ∴△ABD≌△ACD(S.A.S.)。
巩 固 一 下
1: 如图,已知AB和CD相交与O,
OA=OB, OC=OD.说明 △ OAD与
△ OBC全等的理由 解:在△OAD 和△OBC中
2.已知:AB=AC、AD=AE、∠1= ∠2.求证:△ABD≌△ACE.
3.如图所示:AB=AC,AD=AE,求证: ∠B=∠C
4.如图:AD平分∠BAC,AE=AC, AB=7,BC=6,AC=4求△BDE的周长。
达标测试:
1.、已知:如图 AB=AC,AD=AE,∠BAC=∠DAE,求证: A △ABD≌△ACE
你画的三角形与同伴画的一定全等吗?
全等
C 3cm A 3cm
实践 检验
F
45°
4cm
B
D
4cm
E
结论:
在两个三角形中,如果有 两条边及它们的夹角对应 相等,那么这两个三角形 全等。(简记为S.A.S)。
温馨提示:
例 1 在△ ABC中, AB= AC, AD平分∠ BAC , 求证: △ABD≌△ACD.
三角形全等的判定 ——边角边
二中 王丽
复习:全等三角形的性质
若△AOC≌△BOD, 对应边: AC= BD , AO= BO , CO= DO , 对应角有: ∠A= ∠B , ∠C= ∠D , ∠AOC= ∠BOD ;
A O B
D
C
今天我们来讨论两个三角形有两条边和一个角分 别对应相等,那么这两个三角形一定全等吗?又有几 种情况呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A B
C D E
课题:11.2 三角形全等的判定2)
教学目标
①经历探索三角形全等条件的过程,培养学生观察分析图形能力、动手能力. ②在探索三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理.
③通过对问题的共同探讨,培养学生的协作精神.
教学难点
指导学生分析问题,寻找判定三角形全等的条件.
知识重点
应用“边角边”证明两个三角形全等,进而得出线段或角相等.
教学过程(师生活动)
一、情境,引入课题
多媒体出示探究3:已知任意△ABC ,画△A'B'C',使A'B'=AB ,A'C'=AC ,∠A'=∠A .
教帅点拨,学生边学边画图,再让学生把画好的△A'B'C',剪下放在△ABC 上,观察这两个三角形是否全等.
二、交流对话,探求新知
根据前面的操作,鼓励学生用自己的语言来总结规律:
两边和它们的夹角对应相等的两个三角形全等.(SAS)
补充强调:角必须是两条相等的对应边的夹角,边必须是夹相等角的两对边.
三、应用新知,体验成功
出示例2,如图,有—池塘,要测池塘两端A 、B 的距离,可先在平地上取一个可以直接到达A 和B 的点C ,连接AC 并延长到D ,使CD =CA ,连接BC 并延长到E ,使CE =CB .连接DE ,那么量出DE 的长就是A 、B 的距离,为什么?
让学生充分思考后,书写推理过程,并说明每一步的依据.
(若学生不能顺利得到证明思路,教师也可作如下分析:
要想证AB =DE ,
只需证△ABC ≌△DEC
△ABC 与△DEC 全等的条件现有……还需要……)
明确证明分别属于两个三角形的线段相等或者角相等的问题,常常通过证明这两个三角形全等来解决.
补充例题: 1、已知:如图AB=AC,AD=AE,∠BAC=∠DAE
求证: △ABD ≌△ACE
证明:∵∠BAC=∠DAE (已知)
∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD
A B C D E F M ∴∠BAD=∠CAE
在△ABD 与△ACE
AB=AC (已知)
∠BAD= ∠CAE (已证)
AD=AE (已知)
∴△ABD ≌△ACE (SAS)
思考:
求证:1.BD=CE 2. ∠B= ∠C 3. ∠ADB= ∠AEC 变式1:已知:如图,AB ⊥AC,AD ⊥AE,AB=AC,AD=AE.
求证: △DAC ≌△EAB
BE=DC ∠B= ∠ C ∠ D= ∠ E BE ⊥CD 四、再次探究,释解疑惑 出示探究4,我们知道,两边和它们的夹角对应相等的两个
三角形全等.由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?
让学生模仿前面的探究方法,得出结论:两边及其中一边的对角对应相等的两个三角形不一定全等.
教师演示:方法(一)教科书10页图11.2-7.
方法(二)通过画图,让学生更直观地获得结论.
五、巩固练习
课本P10页,练习1、2.
六、小结提高
1.判定三角形全等的方法;
2.证明线段、角相等常见的方法有哪些?让学生自由表述,其他学生补充,让学生自己将知识系统化,以自己的方式进行建构.
七、布置作业
1.课本P15页,习题11.2第3、4题.
2.选作题:
(1)小明做了一个如图所示的风筝,测得DE =DF ,EH =FH ,你能发现哪些结沦?并说明理由.
(2)如图,∠1=∠2,AB =AD ,AE =AC ,求证BC =DE .。
