振型参与质量系数详解
局部震动问题

首先是收集的一些资料,关于局部振动的:资料一:控制结构的局部振动使有效质量系数满足规范要求在对结构进行整体控制设计的时候,我们有时会遇到这种情况,结构的“有效质量系数”达不到规范所要求的不小于90%的要求(见抗规5.2.2条文说明、高规5.1.13条2款),有时即使把“计算振型数”取得很大,也无法满足这个要求。
问题究竟出在哪里?我们又怎样来解决这个问题呢?对于存在这种情况的工程,我们通过继续观察其“结构空间振动简图”,可以发现这样一种现象,在我们所取“计算振型数”范围内的结构振型中,有的振型是结构的整体在振动,而有的振型只有结构的局部在振动。
继续分析下去,我们会发现,发生局部振动的部位,或空间刚度较差,或缺少约束。
如结构错层等原因形成的较长的越层柱;楼板开洞等原因形成的较长的无板梁段或无板墙段;悬臂端缺少约束的悬臂构件;没有设置屋脊梁的坡屋顶;楼顶设置刚度或约束较差的构架等。
因为上述问题的存在,使得这些部位的局部振动极易被激发。
由于这种振动是局部的,所以只有局部的构件参与其中,其参与的质量也只能是与这些构件有关的质量。
结构的有效质量是“计算振型数”所包含的各振型的有效质量由低阶到高阶的叠加,当其中存在较多的与局部振动有关的较低阶的振型时,结构的“有效质量系数”就不容易满足规范的要求。
笔者认为:发生低阶局部振型的部位是结构的薄弱部位,在地震中低阶局部振型容易被激发而在该部位产生较大的变形,当该部位的相关构件在结构中处于比较重要的位置时,可能影响结构的安全,故在设计中应采取措施尽量消除。
在结构设计时,可以加强与局部振动有关的构件沿振动方向的刚度,使相关局部振型由较低阶振型转变为较高阶振型,将其排除出“计算振型数”范围;也可以沿相关构件节点的振动方向增加约束,如加设拉梁等,以消除局部振动。
对于那些对结构安全没有影响或影响可以忽略不计的局部振动,可以强制采用“全楼刚性楼板假定”过滤掉局部振动,或增加“计算振型数”来增大结构的“有效质量系数”。
PKPM振型

PKPM中振型数量取值请列出各种结构中振型数怎样取值。
无所谓多少,通常以满足振型系量参与系数>=90%(用SATWE等相关软件计算时,其结果中会给出这个结果)所需要的振型数即可,其取值通常为3的倍数,也不能大于总层数的3倍,一般的民用建筑在9~30范围里即可满足要求。
但如果是空旷的结构以及层概念不太明显的结构,可能要受到高阶振型的影响比较大,取的计算振数也可能比较多,有60~90的都见过。
一般为结构层数的3倍,不包含地下室,多塔一般不应小于15,太大也没有多大意义,一般只要让XY两个方向的质量参与都达到90%就可以了,如果达不到就在加大计算振型个数如何取?计算震型个数:这个参数需要根据工程的实际情况来选择。
对于一般工程,不少于9个。
但如果是2层的结构,最多也就是6个,因为每层只有三个自由度,两层就是6个。
对复杂、多塔、平面不规则的就要多选,一般要求“有效质量系数”大于90%就可以了,证明我们的震型数取够了。
这个“有效质量系数”最先是美国的WILSON教授提出来的,并且将它用于著名的ETABS程序。
《高层建筑混凝土结构技术规程》的5.1.13-2条要求B级高度的建筑和复杂的高层建筑“抗震计算时,宜考虑平扭藕连计算结构的扭转效应,振型数不应小于15,对多塔楼结构的振型数不应少于塔数的9倍,且计算振型数应使振型参与质量不少于总质量的90%”-------------------------------------------规范规定要求震型参与质量达到总质量的90%以上这句话怎么理解?s一些概念,希望对你有帮助有关振型的几个概念振型参与系数:每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量(或者说该模态质量)之比,即为该振型的振型参与系数。
一阶振型自振频率最小(周期最长),二阶,三阶....振型的自振频率逐渐增大.地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。
自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意.在形状上如实反映实际结构在该周期下的振动形态.振型零点是指在该振型下结构的位移反应为0。
计算振型个数如何取

计算振型个数如何取?作者: sparrow 发布日期: 2006-8-13 查看数: 51 出自: 计算震型个数:这个参数需要根据工程的实际情况来选择。
对于一般工程,不少于9个。
但如果是2层的结构,最多也就是6个,因为每层只有三个自由度,两层就是6个。
对复杂、多塔、平面不规则的就要多选,一般要求“有效质量系数”大于90%就可以了,证明我们的震型数取够了。
这个“有效质量系数”最先是美国的WILSON教授提出来的,并且将它用于著名的ETABS程序。
《高层建筑混凝土结构技术规程》的5.1.13-2条要求B级高度的建筑和复杂的高层建筑“抗震计算时,宜考虑平扭藕连计算结构的扭转效应,振型数不应小于15,对多塔楼结构的振型数不应少于塔数的9倍,且计算振型数应使振型参与质量不少于总质量的90%”-------------------------------------------规范规定要求震型参与质量达到总质量的90%以上这句话怎么理解?一些概念,希望对你有帮助有关振型的几个概念振型参与系数:每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量(或者说该模态质量)之比,即为该振型的振型参与系数。
一阶振型自振频率最小(周期最长),二阶,三阶....振型的自振频率逐渐增大.地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。
自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意.在形状上如实反映实际结构在该周期下的振动形态.振型零点是指在该振型下结构的位移反应为0。
振型越高,周期越短,地震力越大,但由于我们地震反应是各振型的迭代,高振型的振型参与系数小。
特别是对规则的建筑物,由于高振型的参与系数小,一般忽略高振型的影响。
振型的有效质量:这个概念只对于串连刚片系模型有效(即基于刚性楼板假定的,不适用于一般结构。
)。
某一振型的某一方向的有效质量为各个质点质量与该质点在该一振型中相应方向对应坐标乘积之和的平方((∑mx)2)。
振型参与系数

关于振型参与系数
建筑结构2010-08-08 21:20:36 阅读631 评论0 字号:大中小订阅
在抗震设计中,经常会碰到振型参与系数这个概念,但很多人往往记不清或不理解振型参与系数到底表示什么意思。
这里将从振型分解法的求解过程来说明这个系数的含义。
振动方程:
对上式进行振型分解,即令
并应用瑞利阻尼:
得:
对上式两端左乘
得:
由正交性知,上式变为:
即:
方程两端除以
并注意到:
且令:
得:
式中
即为振型参与系数。
可见振型参与系数的真正含义为单位质点在第j振型中所分配到的地震作用的分配系数,即单位质点地震作用的分解(配)系数。
与单质点地震振动方程相比,以上以广义位移
为未知量的振动方程,其右端仅多了一个系数
若再令
则上式可变为与单质点地震振动方程完全一样的形式,即:
上式是一个常系数的二阶非齐次微分方程,其解由通解和特解组成。
通解可由高等数学求得,特解可由杜哈梅积分求得。
其最终解为:
式中,
求出了
由等效静力的抗震计算法知,第j振型作用到第i质点的地震作用为:
这就是《震规》式(5.2.2-1)求第j振型作用到第i质点的水平地震作用标准值的表达式。
由
的表达式容易知道:
地震作用按振型的分解可用图表示如下:。
二阶系统主振型公式

二阶系统主振型公式
振型参与系数:每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量(或者说该模态质量)之比,即为该振型的振型参与系数。
一阶振型自振频率最小(周期最长),二阶,三阶。
振型的自振频率逐渐增大. 地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。
自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意。
在形状上如实反映实际结构在该周期下的振动形态。
振型零点是指在该振型下结构的位移反应为0。
振型越高,周期越短,地震力越大,但由于我们地震反应是各振型的迭代,高振型的振型参与系数小。
特别是对规则的建筑物,由于高振型的参与系数小,一般忽略高振型的影响。
由于大开洞造成振型质量参与系数不够的调整方法

由于大开洞造成振型质量参与系数不够的调整方法首先是收集的一些资料,关于局部振动的:资料一:控制结构的局部振动使有效质量系数满足规范要求在对结构进行整体控制设计的时候,我们有时会遇到这种情况,结构的“有效质量系数”达不到规范所要求的不小于90%的要求(见抗规5.2.2条文说明、高规5.1.13条2款),有时即使把“计算振型数”取得很大,也无法满足这个要求。
问题究竟出在哪里?我们又怎样来解决这个问题呢?对于存在这种情况的工程,我们通过继续观察其“结构空间振动简图”,可以发现这样一种现象,在我们所取“计算振型数”范围内的结构振型中,有的振型是结构的整体在振动,而有的振型只有结构的局部在振动。
继续分析下去,我们会发现,发生局部振动的部位,或空间刚度较差,或缺少约束。
如结构错层等原因形成的较长的越层柱;楼板开洞等原因形成的较长的无板梁段或无板墙段;悬臂端缺少约束的悬臂构件;没有设置屋脊梁的坡屋顶;楼顶设置刚度或约束较差的构架等。
因为上述问题的存在,使得这些部位的局部振动极易被激发。
由于这种振动是局部的,所以只有局部的构件参与其中,其参与的质量也只能是与这些构件有关的质量。
结构的有效质量是“计算振型数”所包含的各振型的有效质量由低阶到高阶的叠加,当其中存在较多的与局部振动有关的较低阶的振型时,结构的“有效质量系数”就不容易满足规范的要求。
笔者认为:发生低阶局部振型的部位是结构的薄弱部位,在地震中低阶局部振型容易被激发而在该部位产生较大的变形,当该部位的相关构件在结构中处于比较重要的位置时,可能影响结构的安全,故在设计中应采取措施尽量消除。
在结构设计时,可以加强与局部振动有关的构件沿振动方向的刚度,使相关局部振型由较低阶振型转变为较高阶振型,将其排除出“计算振型数”范围;也可以沿相关构件节点的振动方向增加约束,如加设拉梁等,以消除局部振动。
对于那些对结构安全没有影响或影响可以忽略不计的局部振动,可以强制采用“全楼刚性楼板假定”过滤掉局部振动,或增加“计算振型数”来增大结构的“有效质量系数”。
振型参与质量系数详解

振型参与质量系数详解
马旭升
【期刊名称】《黑龙江科技信息》
【年(卷),期】2009(000)023
【摘要】现行抗震规范和高规都有这个系数,并牵涉到其他几个概念,与大家分享有关振型的几个概念
【总页数】1页(P299)
【作者】马旭升
【作者单位】黑龙江集盛建筑设计有限公司
【正文语种】中文
【中图分类】TU857
【相关文献】
1.隔震结构振型参与系数与有效质量系数的研究 [J], 王继红;唐兴荣
2.大跨度屋盖结构脉动风振响应的振型能量参与系数 [J], 田玉基;杨庆山
3.关于建筑结构地震反应分析中振型参与系数物理意义的讨论 [J], 曾敦弟
4.关于“结构振型参与系数和振型贡献的分析”一文的勘误 [J], 孙广俊;李爱群
5.关于结构振型参与系数和振型贡献的分析 [J], 孙广俊;李爱群
因版权原因,仅展示原文概要,查看原文内容请购买。
振型参与系数的物理意义

振型参与系数的物理意义振型参与系数,这个词听上去是不是有点拗口?它的意思就是在振动分析中,每种振型对于系统整体振动的贡献有多大。
听起来复杂?别担心,我们来慢慢聊聊,保证你听了也能会心一笑。
想象一下,你和朋友们在一起玩乐队,每个人都有自己的乐器。
你是主唱,另一位朋友打鼓,还有人弹吉他、拉小提琴。
每个人都在用心演奏,但如果主唱跑调了,整个乐队可就尴尬了。
这个时候,主唱的“参与系数”就特别高,因为他对乐曲的影响最大。
再想想如果吉他手太过火,音量一大,反而让人听不清主唱的声音,这样一来,吉他手的参与系数就得打个折扣。
振型参与系数的道理就像是乐队中的每个乐器,各自的贡献和影响力不一样,有的主导,有的辅助。
说到这里,咱们可以把这个系数想象成一个“重要性排行榜”。
在一场激烈的篮球比赛中,得分手就是那个重要的“主唱”。
他每次投篮,球进了,球队就能欢呼;投不进,那可真是有点哭笑不得。
相对来说,防守球员的参与度虽然重要,但他们的得分少,影响力稍微小一些。
振型参与系数就是这样评估每个“球员”在整体“比赛”中扮演的角色。
振动的时候,咱们的系统就像是一场热闹的聚会,每个振型都在跟着节奏晃动。
有的振型节奏快,像是在舞池中旋转;有的振型则是慢慢摆动,给人一种稳重的感觉。
不同的振型就像不同的舞蹈风格,有的活泼,有的端庄。
在分析振动的时候,搞清楚哪个振型在整个系统中贡献最大,才能更好地理解系统的表现。
咱们再深入一层,振型参与系数的计算其实就像是对这场聚会的“人气评分”。
如果某个振型的参与系数高,说明它在整个系统中占据了举足轻重的地位,起到了“定海神针”的作用。
反之,参与系数低的振型就像是聚会中那个默默无闻的角落,虽有存在,但不太引人注目。
可是,千万别小看那些低参与度的振型,它们也能在关键时刻闪耀光芒,像个黑马,给你一个意外的惊喜。
听到这里,你可能会想,振型参与系数能不能用在生活中呢?当然可以!比如,工作团队中,每个人的能力和贡献就像振型参与系数一样。
[整理].01.11结构动力学--振型参与系数
![[整理].01.11结构动力学--振型参与系数](https://img.taocdn.com/s3/m/353df6dc19e8b8f67c1cb9f7.png)
关于振型参与系数
建筑结构2010-08-08 21:20:36 阅读631 评论0 字号:大中小订阅
在抗震设计中,经常会碰到振型参与系数这个概念,但很多人往往记不清或不理解振型参与系数到底表示什么意思。
这里将从振型分解法的求解过程来说明这个系数的含义。
振动方程:
对上式进行振型分解,即令
并应用瑞利阻尼:
得:
对上式两端左乘
得:
由正交性知,上式变为:
即:
方程两端除以
并注意到:
且令:
得:
式中
即为振型参与系数。
可见振型参与系数的真正含义为单位质点在第j振型中所分配到的地震作用的分配系数,即单位质点地震作用的分解(配)系数。
与单质点地震振动方程相比,以上以广义位移
为未知量的振动方程,其右端仅多了一个系数
若再令
则上式可变为与单质点地震振动方程完全一样的形式,即:
上式是一个常系数的二阶非齐次微分方程,其解由通解和特解组成。
通解可由高等数学求得,特解可由杜哈梅积分求得。
其最终解为:
式中,
求出了
由等效静力的抗震计算法知,第j振型作用到第i质点的地震作用为:
这就是《震规》式(5.2.2-1)求第j振型作用到第i质点的水平地震作用标准值的表达式。
由
的表达式容易知道:
地震作用按振型的分解可用图表示如下:。
振型的有关概念

有关振型的几个概念振型参与系数:每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量(或者说该模态质量)之比,即为该振型的振型参与系数。
一阶振型自振频率最小(周期最长),二阶,三阶....振型的自振频率逐渐增大. 地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。
自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意.在形状上如实反映实际结构在该周期下的振动形态.振型零点是指在该振型下结构的位移反应为0。
振型越高,周期越短,地震力越大,但由于我们地震反应是各振型的迭代,高振型的振型参与系数小。
特别是对规则的建筑物,由于高振型的参与系数小,一般忽略高振型的影响。
振型的有效质量:这个概念只对于串连刚片系模型有效(即基于刚性楼板假定的,不适用于一般结构。
)。
某一振型的某一方向的有效质量为各个质点质量与该质点在该一振型中相应方向对应坐标乘积之和的平方((∑mx)2)。
一个振型有三个方向的有效质量,而且所有振型平动方向的有效质量之和等于各个质点的的质量之和,转动方向的有效质量之和等于各个质点的转动惯量之和。
有效质量系数:如果计算时只取了几个振型,那么这几个振型的有效质量之和与总质量之比即为有效质量系数。
这个概念是由WILSON E.L. 教授提出的,用于判断参与振型数足够与否,并将其用于ETABS程序。
振型参与质量:某一振型的主质量(或者说该模态质量)乘以该振型的振型参与系数的平方,即为该振型的振型参与质量。
振型参与质量系数:由于有效质量系数只实用于刚性楼板假设,现在不少结构因其复杂性需要考虑楼板的弹性变形,因此需要一种更为一般的方法,不但能够适用于刚性楼板,也应该能够适用于弹性楼板。
出于这个目的,我们从结构变形能的角度对此问题进行了研究,提出了一个通用方法来计算各地震方向的有效质量系数即振型参与质量系数,规范即是通过控制有效质量振型参与质量系数的大小来决定所取的振型数是否足够。
PKPM振型

PKPM中振型数量取值请列出各种结构中振型数怎样取值。
无所谓多少,通常以满足振型系量参与系数>=90%(用SATWE等相关软件计算时,其结果中会给出这个结果)所需要的振型数即可,其取值通常为3的倍数,也不能大于总层数的3倍,一般的民用建筑在9~30范围里即可满足要求。
但如果是空旷的结构以及层概念不太明显的结构,可能要受到高阶振型的影响比较大,取的计算振数也可能比较多,有60~90的都见过。
一般为结构层数的3倍,不包含地下室,多塔一般不应小于15,太大也没有多大意义,一般只要让XY两个方向的质量参与都达到90%就可以了,如果达不到就在加大计算振型个数如何取?计算震型个数:这个参数需要根据工程的实际情况来选择。
对于一般工程,不少于9个。
但如果是2层的结构,最多也就是6个,因为每层只有三个自由度,两层就是6个。
对复杂、多塔、平面不规则的就要多选,一般要求“有效质量系数”大于90%就可以了,证明我们的震型数取够了。
这个“有效质量系数”最先是美国的WILSON教授提出来的,并且将它用于著名的ETABS程序。
《高层建筑混凝土结构技术规程》的5.1.13-2条要求B级高度的建筑和复杂的高层建筑“抗震计算时,宜考虑平扭藕连计算结构的扭转效应,振型数不应小于15,对多塔楼结构的振型数不应少于塔数的9倍,且计算振型数应使振型参与质量不少于总质量的90%”-------------------------------------------规范规定要求震型参与质量达到总质量的90%以上这句话怎么理解?s一些概念,希望对你有帮助有关振型的几个概念振型参与系数:每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量(或者说该模态质量)之比,即为该振型的振型参与系数。
一阶振型自振频率最小(周期最长),二阶,三阶....振型的自振频率逐渐增大.地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。
自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意.在形状上如实反映实际结构在该周期下的振动形态.振型零点是指在该振型下结构的位移反应为0。
振型参与系数

振型参与系数振型参与系数每个质点质量mi与其在某一振型中相应坐标φij乘积之和与该振型的主质量(或者说该模态质量)之比,即为该振型的振型参与系数(表明地震反应中j振型位移对该振型质量点的某一方向的反应的加权系数) 。
一阶振型自振频率最小(周期最长),二阶,三阶....振型的自振频率逐渐增大。
地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。
自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意。
在形状上如实反映实际结构在该周期下的振动形态。
振型零点是指在该振型下结构的位移反应为0。
振型越高,周期越短,地震力越大,但由于我们地震反应是各振型的迭代,高振型的振型参与系数小。
特别是对规则的建筑物,由于高振型的参与系数小,一般忽略高振型的影响。
振型的有效质量:这个概念只对于串连刚片系模型有效(即基于刚性楼板假定的,不适用于一般结构)。
某一振型的某一方向的有效质量为各个质点质量mi与该质点在该一振型中相应方向对应坐标φij乘积之和的平方。
一个振型有三个方向的有效质量,而且所有振型平动方向的有效质量之和等于各个质点的的质量之和,转动方向的有效质量之和等于各个质点的转动惯量之和。
有效质量系数:如果计算时只取了几个振型,那么这几个振型的有效质量之和与总质量之比即为有效质量系数。
这个概念是由WILSON E.L. 教授提出的,用于判断参与振型数足够与否,并将其用于ETABS程序。
振型参与质量:某一振型的主质量(或者说该模态质量(φj)'Mφj )乘以该振型的振型参与系数的平方,即为该振型的振型参与质量。
振型参与质量系数:由于有效质量系数只实用于刚性楼板假设,现在不少结构因其复杂性需要考虑楼板的弹性变形,因此需要一种更为一般的方法,不但能够适用于刚性楼板,也应该能够适用于弹性楼板。
出于这个目的,我们从结构变形能的角度对此问题进行了研究,提出了一个通用方法来计算各地震方向的有效质量系数即振型参与质量系数,规范即是通过控制有效质量振型参与质量系数的大小来决定所取的振型数是否足够。
PKPM振型

PKPM中振型数量取值请列出各种结构中振型数怎样取值。
无所谓多少,通常以满足振型系量参与系数>=90%(用SATWE等相关软件计算时,其结果中会给出这个结果)所需要的振型数即可,其取值通常为3的倍数,也不能大于总层数的3倍,一般的民用建筑在9~30范围里即可满足要求。
但如果是空旷的结构以及层概念不太明显的结构,可能要受到高阶振型的影响比较大,取的计算振数也可能比较多,有60~90的都见过。
一般为结构层数的3倍,不包含地下室,多塔一般不应小于15,太大也没有多大意义,一般只要让XY两个方向的质量参与都达到90%就可以了,如果达不到就在加大计算振型个数如何取?计算震型个数:这个参数需要根据工程的实际情况来选择。
对于一般工程,不少于9个。
但如果是2层的结构,最多也就是6个,因为每层只有三个自由度,两层就是6个。
对复杂、多塔、平面不规则的就要多选,一般要求“有效质量系数”大于90%就可以了,证明我们的震型数取够了。
这个“有效质量系数”最先是美国的WILSON教授提出来的,并且将它用于著名的ETABS程序。
《高层建筑混凝土结构技术规程》的5.1.13-2条要求B级高度的建筑和复杂的高层建筑“抗震计算时,宜考虑平扭藕连计算结构的扭转效应,振型数不应小于15,对多塔楼结构的振型数不应少于塔数的9倍,且计算振型数应使振型参与质量不少于总质量的90%”-------------------------------------------规范规定要求震型参与质量达到总质量的90%以上这句话怎么理解?s一些概念,希望对你有帮助有关振型的几个概念振型参与系数:每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量(或者说该模态质量)之比,即为该振型的振型参与系数。
一阶振型自振频率最小(周期最长),二阶,三阶....振型的自振频率逐渐增大.地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。
自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意.在形状上如实反映实际结构在该周期下的振动形态.振型零点是指在该振型下结构的位移反应为0。
新的抗震规范将结构分为规则结构、一般不规则结构、特别不规则结构和严重不规则结构,而严重不规则结构是禁

SATWE中,有效质量的计算适用于弹性板和刚性板.当有效质量系数不足时,也会发生剪重比不够的情况.
======================================================================
考虑扭转耦联时的振动周期(秒)、X,Y方向的平动系数、扭转系数
振型号周期转角平动系数(X+Y)扭转系数
1 1.4877 179.67 0.99 ( 0.99+0.00 ) 0.01
周期比,位移比是通过数据来分析结构布置的合理性,另外更重要的是强调抗震较大,原则是离刚心越远的地方增加抗侧力构件的刚度,可调整边框梁柱,剪力墙断面。同时可减小X,Y向侧向刚度,总之Tt/T1,从分母,分子两个方面着手即可。
另外,多层只需满足抗规的要求,只有位移比控制,没有周期比控制,但可参考分析。
==============================================
3-Dimensional Vibration Period (Seconds)
and Vibration coefficient in X, Y direction and torsion
Mode NoPeriodAngleMovementTorsion
注释:
1)这里的“质量”的概念不同于通常意义上的质量。离散结构的振型总数是有限的,振型总个数等于独立质量的总个数。可以通过判断结构的独立质量数来了解结构的固有振型总数。具体地说:
振动周期(秒),XY方向的平动因子及Z向扭转因子,振型质量参与系数

功能说明该文件主要输出与结构整体性能相关的一些内容。
输出内容如下:(1)振动周期(秒),X、Y方向的平动因子及Z向扭转因子,振型质量参与系数其格式如下:振型号,周期,X向平动因子,Y向平动因子,Z向扭转因子振型号,X向平动质量系数,Y向平动质量系数,Z向扭转质量系数最后输出:X向平动振型质量参与系数总计Y向平动振型质量参与系数总计Z向扭转振型质量参与系数总计结构的周期比(Tt/T1)最不利地震作用方向= (度)注意事項(1)有效质量系数是判断结构振型数够否的重要指标,也就是地震作用够否的重要指标。
当有效质量系数大于90%时,表示振型数、地震作用满足规范要求,否则应该增加计算振型数量;(2)《高规》第4.3.5条控制结构的扭转效应,对第一扭转周期Tt与第一平动周期T1之比给出明确规定。
程序中对于第一周期是这样判断的:X或Y向平动因子最大对应振型的周期为第一平动周期;Z向扭转因子最大,且扭转因子大于0.5对应振型的周期为第一扭转周期;(3)用户对于第一周期的判断还应该结合振型图的形状,查看结构在该振型作用下是否为整体振动,第一周期对应的振型必须是整体振动的振型,而不是局部振动的振型。
因此建议对于程序自动计算的周期比结果还应该人为核算一下是否合理;(4)输出的最不利地震作用方向为与整体坐标系X轴的夹角,逆时针为正,顺时针为负。
功能说明(2)各振型的地震力及基底剪力的输出输出用户定义的各个方向地震作用工况(RS_*)及最不利地震作用工况(RS_C(*))下的地震力。
其格式如下:【RS_*】振型**的地震力塔号,层号,F.x,F.y,F.t其中:F.x:X方向的地震力分量(kN);F.y:Y方向的地震力分量(kN);F.t :X(Y)方向的地震力的扭矩(kN.m)。
【RS_*】各振型的基底剪力振型,基底剪力(kN)【RS_*】各层地震作用(CQC(耦联)或SRSS(非耦联))塔号,层号,层地震力,楼层剪力,剪重比,倾覆弯矩最后输出:抗震规范(5.2.5条)中要求的最小剪重比(%)= x.xx%。
由于大开洞造成振型质量参与系数不够的调整方法

由于大开洞造成振型质量参与系数不够的调整方法首先是收集的一些资料,关于局部振动的:资料一:控制结构的局部振动使有效质量系数满足规范要求在对结构进行整体控制设计的时候,我们有时会遇到这种情况,结构的“有效质量系数”达不到规范所要求的不小于90%的要求(见抗规5.2.2条文说明、高规5.1.13条2款),有时即使把“计算振型数”取得很大,也无法满足这个要求。
问题究竟出在哪里?我们又怎样来解决这个问题呢?对于存在这种情况的工程,我们通过继续观察其“结构空间振动简图”,可以发现这样一种现象,在我们所取“计算振型数”范围内的结构振型中,有的振型是结构的整体在振动,而有的振型只有结构的局部在振动。
继续分析下去,我们会发现,发生局部振动的部位,或空间刚度较差,或缺少约束。
如结构错层等原因形成的较长的越层柱;楼板开洞等原因形成的较长的无板梁段或无板墙段;悬臂端缺少约束的悬臂构件;没有设置屋脊梁的坡屋顶;楼顶设置刚度或约束较差的构架等。
因为上述问题的存在,使得这些部位的局部振动极易被激发。
由于这种振动是局部的,所以只有局部的构件参与其中,其参与的质量也只能是与这些构件有关的质量。
结构的有效质量是“计算振型数”所包含的各振型的有效质量由低阶到高阶的叠加,当其中存在较多的与局部振动有关的较低阶的振型时,结构的“有效质量系数”就不容易满足规范的要求。
笔者认为:发生低阶局部振型的部位是结构的薄弱部位,在地震中低阶局部振型容易被激发而在该部位产生较大的变形,当该部位的相关构件在结构中处于比较重要的位置时,可能影响结构的安全,故在设计中应采取措施尽量消除。
在结构设计时,可以加强与局部振动有关的构件沿振动方向的刚度,使相关局部振型由较低阶振型转变为较高阶振型,将其排除出“计算振型数”范围;也可以沿相关构件节点的振动方向增加约束,如加设拉梁等,以消除局部振动。
对于那些对结构安全没有影响或影响可以忽略不计的局部振动,可以强制采用“全楼刚性楼板假定”过滤掉局部振动,或增加“计算振型数”来增大结构的“有效质量系数”。
振型有效质量与参与质量

1振型有效质量(系数)对于刚性楼板的高楼模型,可以将楼层的质量集中到楼板处,以形成糖葫芦串结构。
并且只关心“糖葫芦”水平向的两个平动自由度和一个扭转自由度。
这样一来,当对其进行动力分析而需要设每个“糖葫芦”的质量时,就只需设其这三个方向的质量(两个平动方向均为其质量,扭转为其转动惯量)。
并且,质量矩阵不采用一致质量矩阵,而采用集中质量矩阵。
则其质量矩阵有如下的对角阵形式:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=nz nynxzyxJ m m J m m m 0...0][111 …………..(1) 式(1)中,iz iy ix J m m 、、分别为每个“糖葫芦”在x 、y 向的质量和扭转惯量。
一般情况下,两个平动质量是相等的。
若对上述结构进行模态分析,便可以得到振型向量矩阵,并对其关于质量矩阵][m 进行归一化得到归一化后的振型向量矩阵][Φ:][]][[][E m T =ΦΦ……………………………...…………………(2) ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=Φnnz nznz nznny ny ny ny nnx nx nx nx z n zz z y n y y y x n x x xθθθθφφφφφφφφθθθθφφφφφφφφ......................][321321321131211113121111312111. (3)式(3)中ijz ijy ijx θφφ、、分别为第i 振型第j 个“糖葫芦”在x 、y 方向上的位移和扭转角。
对于上述的“糖葫芦”串结构,每个节点处有三个方向的自由度,并且三个方向上的振型是相互独立的——也就是说,对于其任一振型,每个节点都最多只存在一个方向上的位移。
因此,下面将仅讨论这种结构的一个方向上的振型有效质量:可以将式(1)和式(3)表达成为如下形式:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=n m m m m .0.0][21………………………….…………(4) ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=Φnn nn n n n φφφφφφφφφφφφ.......][21323132221212111 (5)由式(2)有:][]][[][E m T =ΦΦ两边同时右乘1][-Φ后有:1][][][-Φ=Φm T再边再同时左乘][Φ有:][][]][[E m T =ΦΦ通过同样的方法(等式两边同时左乘或右乘一矩阵)可以得到如下式:}1]{[}1{}1]{[]][][[}1{m m m T T T =ΦΦ将上式写成这样的形式:}1]{[}1{})1]{[]([})1]{[]([m m m T T T T =ΦΦ (6)于是,容易得到如下的非矩阵表达式:∑∑∑====n i ni i nj ijj m m 1121))((φ (7)于是,有一天,Wilson 教授就将式(7)表达式中的21))((∑=nj ij j m φ定义为第i 阶振型的有效质量,并且将∑∑==ni i n j ij j m m 121/))((φ定义为第i 阶振型的质量系数。
振型参与系数
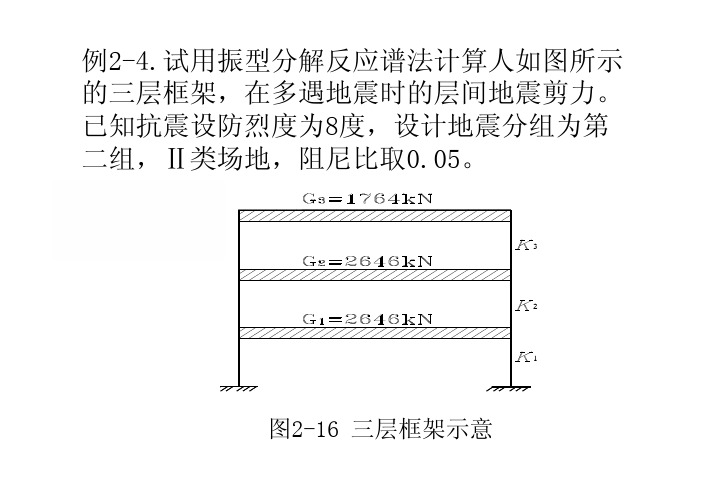
例2-4.试用振型分解反应谱法计算人如图所示的三层框架,在多遇地震时的层间地震剪力。
已知抗震设防烈度为8度,设计地震分组为第二组,Ⅱ类场地,阻尼比取0.05。
图2-16 三层框架示意解:(1)求解结构体系的周期和振型由矩阵迭代法(或雅可比法)可计算出结构体系的三个自振周期和振型分别为:第一振型{X }1 T=[0.334 0.667 1.000]T 1 =0.467s X T=[−0.667 −0.666 1.000]第二振型{T 2 }=2 0.208s第三振型{X }T 3=[4.019 −3.035 1.000]T 3 =0.134s(2) 计算各振型的地震影响系数查得多遇地震时设防烈度为8度的αmax =0.16 查得Ⅱ类场地、设计地震分组为第二组T g =0.40s 当阻尼比ξ=0.05 时,η2 =1.0 γ=0.9 第一振型,因T g <T 1 <5T g ,所以:⎛T g⎞γ⎛0.40 ⎞0.9α1 =⎜⎜⎟⎟η2αmax =⎜⎟×1.0 ×0.16 =0.139 ⎝T⎠⎝0.467 ⎠第二振型α2 =αmax=0.16 第三振型α3 =αmax =0.16(3)计算各振型的参与系数由式(2-84)计算各振型的振型参与系数第一振型:3∑X 1i G i 0.334×2646+0.667×2646+1.000×1764γ1 =i =31 =2 2 2=1.363 ∑X12G 0.334 ×2646+0.667 ×2646+1.000 ×1764iii =13X G ∑2i i第二振型:γ2 =i =31 XG =−0.428 ∑22iii =1第三振型:∑33i X G iγ3 =i =31 =0.063 XG ∑23ii(4) 计算各振型各楼层的水平地震作用1i =各振型各楼层的水平地震作用由式(2-96)计算:第一振型:F 1i =α1γ1 X 1iG iF11=0.139×1.363×0.334×2646 =167.4kNF12=0.139×1.363×0.667 ×2646 =334.4kNF13=0.139 ×1.363×1.000 ×1764 =334.2kN 第二振型:F2i=α2γ2 X2i G iF 21 =120.9kN F22=120.7kN F23=−120.8kN第三振型:F3i=α3γ3 X3i G iF31=107.2kN F32 =−80.9kN F33 =17.8kN(5)计算各振型的层间剪力第一振型:V 1 ∑=nk iF1=i k kN V 11 =167.4 +334.4 +334.2 =836.0 V 12 =334.4 +334.2 =668.6kNV 13 =334.2kN第二振型:V 2 ∑=nki F 2=ik 21V =120.8 k NV 22 =−0.1kNV 23 =−120.8kNn 第三振型:V 3i =∑F 3kk =iV 31 =44.1kNV 32 =−63.1kN V 33 =17.8kN(6)计算水平地震作用效应各层层间剪力由式(2-97)计算各层层间剪力V1==845.8kNV2=671.6kN V3=355.8kN图2-17 各振型的地震剪力(kN)(a)第一振型地震剪力;(b)第二振型地震剪力;(c)第三振型地震剪力和组合后各层地震剪力(kN)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
振型的有效质量:这个概念只对于串连刚片系模型有效(即基于刚性楼板假定的,不适用于一般结构。)。某一振型的某一方向的有效质量为各个质点质量与该质点在该一振型中相应方向对应坐标乘积之和的平方((∑mx)2)。一个振型有三个方向的有效质量,而且所有振型平动方向的有效质量之和等于各个质点的的质量之和,转动)若记结构固有振型总数是NM,那么参与振型数最多只能选NM个,选参与振型数大于NM是错误的,因为结构没那么多。
3)参与振型数与有效质量系数的关系:
3-1)参与振型数越多,有效质量系数越大;
3-2)参与振型数 =0 时,有效质量系数 =0
3-3)参与振型数 =NM 时,有效质量系数 =1.0
振型参与质量系数:由于有效质量系数只实用于刚性楼板假设,现在不少结构因其复杂性需要考虑楼板的弹性变形,因此需要一种更为一般的方法,不但能够适用于刚性楼板,也应该能够适用于弹性楼板。出于这个目的,我们从结构变形能的角度对此问题进行了研究,提出了一个通用方法来计算各地震方向的有效质量系数即振型参与质量系数,规范即是通过控制有效质量振型参与质量系数的大小来决定所取的振型数是否足够。(见高规(5.1.13)、抗规(5.2.2)条文说明)。这个概念不仅对糖葫芦串模型有效。一个结构所有振型的振型参与质量之和等于各个质点的质量之和。如果计算时只取了几个振型,那么这几个振型的振型参与质量之和与总质量之比即为振型参与质量系数。
注释:
1)这里的“质量”的概念不同于通常意义上的质量。离散结构的振型总数是有限的,振型总个数等于独立质量的总个数。可以通过判断结构的独立质量数来了解结构的固有振型总数。具体地说:
每块刚性楼板有三个独立质量Mx,My,Jz;
每个弹性节点有两个独立质量mx,my;
根据这两条,可以算出结构的独立质量总数,也就知道了结构的固有振型总数。
由此可见,有效质量系数与振型参与质量系数概念不同,但都可以用来确定振型叠加法所需的振型数。
我们注意到:ETABS6.1中,只有有效质量系数(effective mass ratio)的概念,而到了ETABS7.0以后,则出现了振型质量参与系数(modal participating mass ratio),可见,振型参与质量系数是有效质量系数的进一步发展,有效质量系数只适用于串连刚片系模型,分别有x方向 、y方向、rz方向的有效质量系数。振型参与质量系数则分别有x、y、z、rx、ry、rz六个方向的振型参与质量系数。
有效质量系数:如果计算时只取了几个振型,那么这几个振型的有效质量之和与总质量之比即为有效质量系数。这个概念是由WILSON E.L. 教授提出的,用于判断参与振型数足够与否,并将其用于ETABS程序。
振型参与质量:某一振型的主质量(或者说该模态质量)乘以该振型的振型参与系数的平方,即为该振型的振型参与质量。
zt)振型参与质量系数详解
抗震规范和高规都有这个系数,牵涉到其他几个概念,与大家分享
有关振型的几个概念
振型参与系数:每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量(或者说该模态质量)之比,即为该振型的振型参与系数。一阶振型自振频率最小(周期最长),二阶,三阶....振型的自振频率逐渐增大. 地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。 自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意.在形状上如实反映实际结构在该周期下的振动形态.振型零点是指在该振型下结构的位移反应为0。 振型越高,周期越短,地震力越大,但由于我们地震反应是各振型的迭代,高振型的振型参与系数小。 特别是对规则的建筑物,由于高振型的参与系数小,一般忽略高振型的影响。
4) 参与振型数 NP 如何确定?
4-1)参与振型数 NP 在 1-NM 之间选取。
4-2)NP应该足够大,使得有效质量系数大于0.9。
有些结构,需要较多振型才能准确计算地震作用,这时尤其要注意有效质量系数是否超过了0.9。比如平面复杂,楼面的刚度不是无穷大,振型整体性差,局部振动明显的结构,这种情况往往需要很多振型才能使有效质量系数满足要求。
