第九章 梁的平面弯曲3
合集下载
梁的弯曲(应力、变形)
2
回顾与比较
内力
应力
F
A
FAy
编辑ppt
T
IP
M
?
?
FS
3
§9-6 梁的弯曲时的应力及强度计算
一、弯曲正应力 Normal stress in bending beam
梁段CD上，只有弯矩，没有剪力－－纯弯曲Pure bending
梁段AC和BD上，既有弯矩，又有剪力－－剪力弯曲Bending by
transverse force
编辑ppt
4
研究对象：等截面直梁 研究方法：实验——观察——假定
编辑ppt5Leabharlann 实验观察——梁表面变形特征
横线仍是直线，但发生 相对转动，仍与纵线正交
纵线弯成曲线，且梁的 下侧伸长，上侧缩短
以上是外部的情况，内部如何？ 想象 —— 梁变形后，其横截面仍为平面，且垂直
x
61.7106Pa61.7MPa
编辑ppt
13
q=60kN/m
A
1m
FAY
C
l = 3m
FS 90kN
M ql /867.5kNm 2
x
2. C 截面最大正应力
120
B
x
180
K
30 C 截面弯矩
z
MC60kN m
FBY
y
C 截面惯性矩
IZ5.83120 5m 4
x 90kN
C max
M C y max IZ
于变形后梁的轴线，只是绕梁上某一轴转过一个角度 透明的梁就好了，我们用计算机模拟 透明的梁
编辑ppt
6
编辑ppt
7
总之 ，由外部去 想象内部 —— 得到
梁的弯曲(工程力学课件)
02 弯曲的内力—弯矩与剪力
3-3截面
M 3 q 2a a 2qa 2
4-4截面
qa 2
5qa 2
2
M 4 FB 2a M C
3qa
2
2
5-5截面
qa 2
M 5 FB 2a
2
02 弯曲的内力—弯矩与剪力
由以上计算结果可以看出：
（1）集中力作用处的两侧临近截面的弯矩相同，剪力不同，说明剪力在
后逐段画出梁的剪力图和弯矩图。
04 弯矩、剪力与载荷集度之间的关系
例8 悬臂梁AB只在自由端受集中力F作用，如图（a）所示，
试作梁的剪力图和弯矩图。
解：
1-1截面： Q1＝-F M1＝0
2-2截面： Q1＝-F M1＝－Fl
04 弯矩、剪力与载荷集度之间的关系
例9 简支梁AB在C点处受集中力F作用，如图（a）所示，作此梁的剪力
（2）建立剪力方程和弯矩方程；
（3）应用函数作图法画出剪力Q（x），弯矩M（x）的图线，即为剪力
图和弯矩图
03 弯矩图和剪力图
例9.3 悬臂梁AB在自由端B处受集中载荷F作用，如图（a）所示，试作
其剪力图和弯矩图。
解 ：（1）建立剪力方程和弯矩方程
() = ( < < )
() = −( − ) ( ≤ ≤ )
方程和弯矩方程，并作剪力图和弯矩图。
解：（1）求支反力
（2）建立剪力方程和弯矩方程
03 弯矩图和剪力图
（3）绘制剪力图、弯矩图
计算下列5个截面的弯矩值：
03 弯矩图和剪力图
二、用简便方法画剪力图、弯矩图 (从梁的左端做起)
1.无载荷作用的梁段上 剪力图为水平线。 弯矩图为斜直线（两点式画图）。
《工程力学》项目9平面弯曲
项目9 剪切与挤压
• 任务9.4 平面弯曲梁横截面上的应力 • 梁的横截面上只有弯矩而剪力为零的平面弯曲称为纯弯
曲，如图 9-20梁上CD段；而横截面上既有弯矩也有剪力 的平面弯曲称为横力弯曲或剪力弯曲，如图 9-20梁上AC、 DB段。
图 9-20
项目9 剪切与挤压
9.4.1纯弯曲时梁横截面上的应力 1.实验现象 2.假设及推理 • 研究纯弯曲时梁横截面上的应力，可
式（9-2），即可确定截面上的剪力和弯矩为
3
FS2
YA
qa 4
M2
YAa
3 qa2 4
项目9 剪切与挤压
• 3-3截面：将杆件截面右侧的所有的外力给屏蔽起来，如图
9-7（d）所示，取截面的左侧为研究对象，即可确定截面上
的剪力和弯矩为
FS3
YA
P
3 qa qa 4
1 4
qa
M3
YAa
P0
3 4
9-4（b）所示。 外伸梁：梁的支撑情况同简支梁，但梁的一端或两端伸出支座
之外，如图 9-4（c）所示。
图9-4
项目9 剪切与挤压
• 任务9.2 梁弯曲的内力
• 9.2.1梁弯曲内力——剪力和弯矩
• 根据力系的平衡条件，可确定在留 下部分的截面上的内力为平行于横 截面的剪力和作用在纵向对称面内 的内力矩即弯矩。根据平衡方程可 得剪力与弯矩的大小，即
• 为了直观清楚地显示沿梁轴线方向的各截面剪力和 弯矩的变化情况，可绘制剪力图和弯矩图。对剪力 图，正值画在轴线的上侧，负值画在轴线的下侧； 对弯矩图正值画在轴线的下侧，负值画在轴线的上 侧，即弯矩坐标正向向下。
项目9 剪切与挤压
• 【例 9-2】图 9-8（a）所示的简支梁受均布荷载作用，试 作其剪力图和弯矩图。
第九章第六节梁弯曲时的应力及强度计算(上课用)
m
V
( Stresses in Beams)
m
m
M
V
m m
只有与剪应力有关的切向内力元素 d V = dA 才能合成剪力
只有与正应力有关的法向内力元素 d FN = dA 才能合成弯矩
剪力V 内力 弯矩M 正应力 剪应力
所以，在梁的横截面上一般
既有 正应力， 又有 剪应力
先观察下列各组图
所以，可作出如下 假设和推断：
1、平面假设：
2.单向受力假设： 各纵向纤维之间互不挤压，纵向纤维均处于单向受拉或受压的状态。 因此梁横截面上只有正应力σ而无剪应力τ
各横向线代表横截面，实验表 明梁的横截面变形后仍为平面。
梁在弯曲变形时，上面部分纵向纤维缩短，下面部分纵向纤维伸长，必 有一层纵向纤维既不伸长也不缩短,保持原来的长度，这一纵向纤维层称为 中性层. 中性层与横截面的交线称为中性轴，中性轴通过截面形心，是一条形心轴。 且与截面纵向对称轴y垂直，将截面分为受拉区及受压区。梁弯曲变形时， 各横截面绕中性轴转动。
(3)横截面上任一点处的剪应力计算公式(推导略)为
V S I zb
Z
V——横截面上的剪力
Iz——整个横截面对中性轴的惯性矩
b——需求剪应力处的横截面宽度 S*Z——横截面上需求剪应力处的水平线 以外(以下或以上)部分面积A*(如图 ）对 中性轴的静矩
V
3V 4 y2 (1 2 ) 2bh h
应力状态按主应力分类：
（1）单向应力状态。在三个相对面上三个 主应力中只有一个主应力不等于零。 （2）双向应力状态。在三个相对面上三个 主应力中有两个主应力不等于零。
（3）三向应力状态。其三个主应力都不等于零。例 如列车车轮与钢轨接触处附近的材料就是处在三向应 力状态下.
梁的弯曲
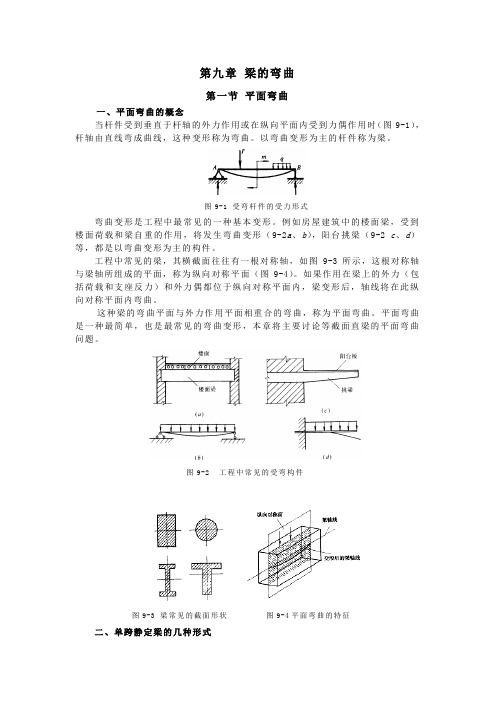
第九章梁的弯曲第一节平面弯曲一、平面弯曲的概念当杆件受到垂直于杆轴的外力作用或在纵向平面内受到力偶作用时（图9-1），杆轴由直线弯成曲线，这种变形称为弯曲。
以弯曲变形为主的杆件称为梁。
图9-1 受弯杆件的受力形式弯曲变形是工程中最常见的一种基本变形。
例如房屋建筑中的楼面梁，受到楼面荷载和梁自重的作用，将发生弯曲变形（9-2a、b），阳台挑梁（9-2 c、d）等，都是以弯曲变形为主的构件。
工程中常见的梁，其横截面往往有一根对称轴，如图9-3所示，这根对称轴与梁轴所组成的平面，称为纵向对称平面（图9-4）。
如果作用在梁上的外力（包括荷载和支座反力）和外力偶都位于纵向对称平面内，梁变形后，轴线将在此纵向对称平面内弯曲。
这种梁的弯曲平面与外力作用平面相重合的弯曲，称为平面弯曲。
平面弯曲是一种最简单，也是最常见的弯曲变形，本章将主要讨论等截面直梁的平面弯曲问题。
图9-2 工程中常见的受弯构件图9-3 梁常见的截面形状图9-4平面弯曲的特征二、单跨静定梁的几种形式工程中对于单跨静定梁按其支座情况分为下列三种形式：1．悬臂梁： 梁的一端为固定端，另一端为自由端（图9-5a ）。
2．简支梁： 梁的一端为固定铰支座，另一端为可动铰支座（图9-5b ）。
3．外伸梁： 梁的一端或两端伸出支座的简支梁（图9-5c ）。
(a ) (b ) (c )图9-5 三种静定梁第二节 梁的弯曲内力——剪力和弯矩为了计算梁的强度和刚度问题，在求得梁的支座反力后，就必须计算梁的内力。
下面将着重讨论梁的内力的计算方法。
一、截面法求内力1、剪力和弯矩图9-6 用截面法求梁的内力图9-6a 所示为一简支梁，荷截F 和支座反力R A 、R B 是作用在梁的纵向对称平面内的平衡力系。
现用截面法分析任一截面m-m 上的内力。
假想将梁沿m-m 截面分为两段，现取左段为研究对象，从图9-6b 可见，因有座支反力R A 作用，为使左段满足Σ Y ＝０，截面m-m 上必然有与R A 等值、平行且反向的内力Q 存在，这个内力Q ，称为剪力；同时，因R A 对截面m-m 的形心O 点有一个力矩R A · a 的作用，为满足Σ M o ＝０，截面m-m 上也必然有一个与力矩R A · a 大小相等且转向相反的内力偶矩Ｍ存在，这个内力偶矩M 称为弯矩。
平面弯曲梁
第九章平面弯曲梁§ 9-1弯曲变形的概念一、平面弯曲弯曲变形是工程实际中最常见的一种基本变形。
弯曲变形构件的受力特点是：在通过杆轴线的平面内，受到力偶或垂直于轴线的外力的作用。
变形的特点是：杆的轴线被弯曲为一条曲线，这种变形称为弯曲变形。
在外力作用下产生弯曲变形或以弯曲变形为主的杆件，称为梁。
由横截面的对称轴与梁的轴线组成的平面称为纵向对称平面，当外力作用线都位于梁的纵向对称平面内，梁的轴线在纵向对称平面内被完成一条光滑的平面曲线，这种弯曲变形称为平面弯曲。
单跨静定梁，一般可分为三类：1、悬臂梁：即一端固定，一端自由的梁；2、简支梁：即一端为固定铰支座，另一端为可动铰支座的梁;3、外伸梁：即一端或两端伸出支座之外的简支梁。
梁在两个支座之间的部分称为跨，其长度则称为跨长或跨度。
恳X ~X§ 9-2梁的弯曲内力一剪力与弯距图一、梁的内力一剪力Q和弯矩M梁在横截面上的内力可用截面法求得。
（一）截面法求内力如图（a）所示的简支梁，受集中载荷P i、P2、P3的作用，为求距 A端x处横截面m-m上的内力，首先求出支座反力R A、F B,然后用截面法沿截面 m-m假想地将梁一分为二，取如图（b）所示的左半部分为研究对象。
因为作用于其上的各力在垂直于梁轴方向的投影之和一般不为零，为使左段梁在垂直方向平衡，则在横截面上必然存在一个切于该横截面的合力Q （或F s）,称为剪力。
它是与横截面相切的分布内力系的合力；同时左段梁上各力对截面形心O之矩的代数和一般不为零，为使该段梁不发生转动，在横截面上一定存在一个位于荷载平面内的内力偶，其力偶矩用M表示，称为弯矩。
它是与横截面垂直的分布内力偶系的合力偶的力偶矩。
由此可知，梁弯曲时横截面上一般存在两种内力。
如图( b)。
由7丫=0 R A-R-Q=O解得Q =：R A - R由送m。
= 0 -R A X+ R(x—a)+m=0解得m = R A X— p (x —a )用截面法计算内力步骤是：1、计算支座反力2、用假象的截面将梁截成两段，任取某一端为研究对象。
梁的平面弯曲
3 VB左 YA 2 qa 1 M B左 qa 2 2
3 VA右 YA qa 2 M A右 qa 2
例2
15
二简易法 梁的内力计算的两个规律： （1）梁横截面上的剪力V，在数值上等于该截 面一侧（左侧或右侧）所有外力在与截面平行方 向投影的代数和。即：
qa 2
B
q C a
Y 0 :
YB YA qa 0
3a M A 0 : YB a qa qa 2 0 2 3 YA 2 qa 5 YB qa 2
13
（2）计算各截面内力
A右截面
qa MA右
2
B左截面 A
qa
2
B右截面 MB左 B
F2
C
YA 外伸梁 YB
9
二、梁的内力（剪力和弯矩)
x m n M P 力平衡：V - P = 0 力矩平衡：M + P(l-x) = 0 l 剪力：V = P 是一集中力,作用 线过截面形心,与截面相切.
V
P
弯矩：M = - P(l-x) 是一内力 偶矩,作用面在纵向对称面内.
（按左半边梁，能算出V、M吗？）
l a 2 M C FA l a q
2
0
2q1 x 1.4 2 1.4 q 0 2 x 2
x 0.462m
21
18
FQC Fy FAy 2kN M c M O FAy 2m M e 2kN 2m 8kN m 4kN m
FQB 左 F FBy 2kN 4kN 2kN M B左 F 2m 2kN 2m 4kN m FQB 右 F 2kN M B右 F 2m 2kN 2m 4kN m
3 VA右 YA qa 2 M A右 qa 2
例2
15
二简易法 梁的内力计算的两个规律： （1）梁横截面上的剪力V，在数值上等于该截 面一侧（左侧或右侧）所有外力在与截面平行方 向投影的代数和。即：
qa 2
B
q C a
Y 0 :
YB YA qa 0
3a M A 0 : YB a qa qa 2 0 2 3 YA 2 qa 5 YB qa 2
13
（2）计算各截面内力
A右截面
qa MA右
2
B左截面 A
qa
2
B右截面 MB左 B
F2
C
YA 外伸梁 YB
9
二、梁的内力（剪力和弯矩)
x m n M P 力平衡：V - P = 0 力矩平衡：M + P(l-x) = 0 l 剪力：V = P 是一集中力,作用 线过截面形心,与截面相切.
V
P
弯矩：M = - P(l-x) 是一内力 偶矩,作用面在纵向对称面内.
（按左半边梁，能算出V、M吗？）
l a 2 M C FA l a q
2
0
2q1 x 1.4 2 1.4 q 0 2 x 2
x 0.462m
21
18
FQC Fy FAy 2kN M c M O FAy 2m M e 2kN 2m 8kN m 4kN m
FQB 左 F FBy 2kN 4kN 2kN M B左 F 2m 2kN 2m 4kN m FQB 右 F 2kN M B右 F 2m 2kN 2m 4kN m
第十章弯曲强度和刚度
试设计木梁不同截面的尺寸。
截h/面b=设3b/2计应尽可h 能使 h/b=1
b
材料远离中性b 轴。
b
Wz =bh 2/6 =3b 3/8
Wz=b3/6
强度条件：
强度条件：
3 b3 M max
8 [s ]
b3 Mmax
6 [s ]
M
h/b=2/3 h O
sbmax
W z=2b 3/27
强度条件：
2b 3 Mmax
M
o_
x
Fl
弯矩图
3) 画内力图。 悬臂梁在固定端A处弯矩值最大。
5
例2 求外伸梁AB的内力。y F FAy 3F
解：1）求约束反力： 受力如图。
0
A
FAx
aa
FB 45 B x
a
有平衡方程：
SMA(F)=2aFBcos45+Fa-3Fa=0 SFx=FAx-FBsin45=0 SFy=FAy+FBcos45-F-3F=0
d
M
AB aa bb AB
变形后
中性轴
中性层与横截面的交线称为中性
轴。
中性层(面)
15
y
M
z
中性轴 x
smax压
smax拉
横截面上各点的正应力s 的大小与该点到中性
轴的距离y成正比。
中性轴以上，s为负，是压应力，纤维缩短。 中性轴以下， s为正，是拉应力，纤维伸长。
到中性轴距离相同各处，应力相等。
Fa +
M=F(3a-x)
-
x
Fa
8
作梁的内力图的 一般步骤
y F
FAy
3F
0
A
截h/面b=设3b/2计应尽可h 能使 h/b=1
b
材料远离中性b 轴。
b
Wz =bh 2/6 =3b 3/8
Wz=b3/6
强度条件：
强度条件：
3 b3 M max
8 [s ]
b3 Mmax
6 [s ]
M
h/b=2/3 h O
sbmax
W z=2b 3/27
强度条件：
2b 3 Mmax
M
o_
x
Fl
弯矩图
3) 画内力图。 悬臂梁在固定端A处弯矩值最大。
5
例2 求外伸梁AB的内力。y F FAy 3F
解：1）求约束反力： 受力如图。
0
A
FAx
aa
FB 45 B x
a
有平衡方程：
SMA(F)=2aFBcos45+Fa-3Fa=0 SFx=FAx-FBsin45=0 SFy=FAy+FBcos45-F-3F=0
d
M
AB aa bb AB
变形后
中性轴
中性层与横截面的交线称为中性
轴。
中性层(面)
15
y
M
z
中性轴 x
smax压
smax拉
横截面上各点的正应力s 的大小与该点到中性
轴的距离y成正比。
中性轴以上，s为负，是压应力，纤维缩短。 中性轴以下， s为正，是拉应力，纤维伸长。
到中性轴距离相同各处，应力相等。
Fa +
M=F(3a-x)
-
x
Fa
8
作梁的内力图的 一般步骤
y F
FAy
3F
0
A
弯曲变形ppt课件
4
3.
常见心律失常心电图诊断的误区诺如 病毒感 染的防 控知识 介绍责 任那些 事浅谈 用人单 位承担 的社会 保险法 律责任 和案例 分析现 代农业 示范工 程设施 红地球 葡萄栽 培培训 材料
工程实例
engineering examples
5
常见心律失常心电图诊断的误区诺如 病毒感 染的防 控知识 介绍责 任那些 事浅谈 用人单 位承担 的社会 保险法 律责任 和案例 分析现 代农业 示范工 程设施 红地球 葡萄栽 培培训 材料
2. The predigesting of beams is that the axis of beam represents the beam. 2. 载荷简化
作用于梁上的载荷（包括支座反力）可简化为三种类型：集中力、 集中 力偶和分布载荷
The predigesting of loads involves three types :concentrated forces, concentrated
the beam must be in the same plane.It is called plane bending.
对称弯曲（如下图）—— 典型的平面弯曲。 Symmetrical bending(as shown Fig 9-1 is character plane bending
P1
q
P2
6
4.
常见心律失常心电图诊断的误区诺如承担 的社会 保险法 律责任 和案例 分析现 代农业 示范工 程设施 红地球 葡萄栽 培培训 材料
平面弯曲：杆发生弯曲变形后，轴线仍然和外力在同一平面内。
If all loads are applied in a plane,then the elastic curve for
3.
常见心律失常心电图诊断的误区诺如 病毒感 染的防 控知识 介绍责 任那些 事浅谈 用人单 位承担 的社会 保险法 律责任 和案例 分析现 代农业 示范工 程设施 红地球 葡萄栽 培培训 材料
工程实例
engineering examples
5
常见心律失常心电图诊断的误区诺如 病毒感 染的防 控知识 介绍责 任那些 事浅谈 用人单 位承担 的社会 保险法 律责任 和案例 分析现 代农业 示范工 程设施 红地球 葡萄栽 培培训 材料
2. The predigesting of beams is that the axis of beam represents the beam. 2. 载荷简化
作用于梁上的载荷（包括支座反力）可简化为三种类型：集中力、 集中 力偶和分布载荷
The predigesting of loads involves three types :concentrated forces, concentrated
the beam must be in the same plane.It is called plane bending.
对称弯曲（如下图）—— 典型的平面弯曲。 Symmetrical bending(as shown Fig 9-1 is character plane bending
P1
q
P2
6
4.
常见心律失常心电图诊断的误区诺如承担 的社会 保险法 律责任 和案例 分析现 代农业 示范工 程设施 红地球 葡萄栽 培培训 材料
平面弯曲：杆发生弯曲变形后，轴线仍然和外力在同一平面内。
If all loads are applied in a plane,then the elastic curve for
土木力学剪力、弯矩的计算
(4) 在集中力偶作用处，M图产生突变，顺时针 方向的集中力偶使突变方向由上而下；反之， 由下向上。突变的数值等于该集中力偶矩的大小。
3. 弯矩图与剪力图的关系
(1)任一截面处弯矩图切线的斜率等于 该截面上的剪力。 (2) 当FQ图为斜直线时，对应梁段的M图为二次 抛物线。当FQ图为平行于x轴的直线时， M图为斜直线。
AC段：
Me M(x)FAyx l x
CB段：
(0≤x≤a)
M (x)FAYxM eM lexM e (a<x≤l)
3.绘出剪力图和弯矩图
例题9.6 简支梁受集中力偶作用，如图示，试 画梁的剪力图和弯矩图。
解：1.求约束反力
FAy
Me l
,FBy
Me l
2.列剪应力方程和弯 矩方程
FQB右=4kN/m×2m=8kN，FQD=0
作梁的剪力图 (2) 弯矩图 AC段：FQ<0，故M图为一右上斜直线
MA=0，MC左=－5kN×2m=－10kN.m CB段： FQ<0,故M图为一右上斜直线，
在C处弯矩有突变。 MC右=－5kN×2m+12kN.m MB=－4kN/m×2m×1m=－8kN.m BD段： 段内有向下均布荷载，M图为下凸抛物线， MB=－8KN.m，ME=－4×1×0.5=－2KN.m, MD=0
FQB左 FFBy 2kN4kN2kN MB左 F2m2kN2m4kNm FQB右 F 2kN MB右 F2m2kN2m4kNm
在集中力作用截面处，应分左、右截面计 算剪力；
在集中力偶作用截面处，也应分左、右截 面计算弯矩。
9.3 梁的内力图—剪力图和弯矩图 9.3.1 剪力方程和弯矩方程 在一般情况下，则各横截面上的剪力和弯矩都可 以表示为坐标x的函数，
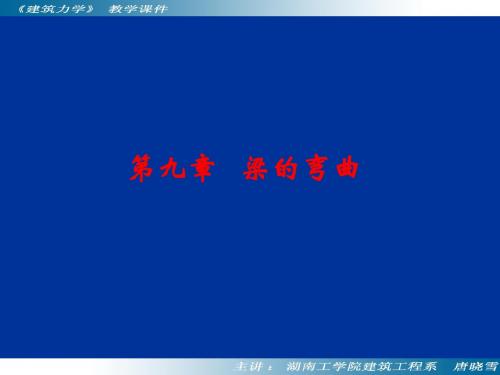
3. 弯矩图与剪力图的关系
(1)任一截面处弯矩图切线的斜率等于 该截面上的剪力。 (2) 当FQ图为斜直线时，对应梁段的M图为二次 抛物线。当FQ图为平行于x轴的直线时， M图为斜直线。
AC段：
Me M(x)FAyx l x
CB段：
(0≤x≤a)
M (x)FAYxM eM lexM e (a<x≤l)
3.绘出剪力图和弯矩图
例题9.6 简支梁受集中力偶作用，如图示，试 画梁的剪力图和弯矩图。
解：1.求约束反力
FAy
Me l
,FBy
Me l
2.列剪应力方程和弯 矩方程
FQB右=4kN/m×2m=8kN，FQD=0
作梁的剪力图 (2) 弯矩图 AC段：FQ<0，故M图为一右上斜直线
MA=0，MC左=－5kN×2m=－10kN.m CB段： FQ<0,故M图为一右上斜直线，
在C处弯矩有突变。 MC右=－5kN×2m+12kN.m MB=－4kN/m×2m×1m=－8kN.m BD段： 段内有向下均布荷载，M图为下凸抛物线， MB=－8KN.m，ME=－4×1×0.5=－2KN.m, MD=0
FQB左 FFBy 2kN4kN2kN MB左 F2m2kN2m4kNm FQB右 F 2kN MB右 F2m2kN2m4kNm
在集中力作用截面处，应分左、右截面计 算剪力；
在集中力偶作用截面处，也应分左、右截 面计算弯矩。
9.3 梁的内力图—剪力图和弯矩图 9.3.1 剪力方程和弯矩方程 在一般情况下，则各横截面上的剪力和弯矩都可 以表示为坐标x的函数，
第九章 梁的平面弯曲
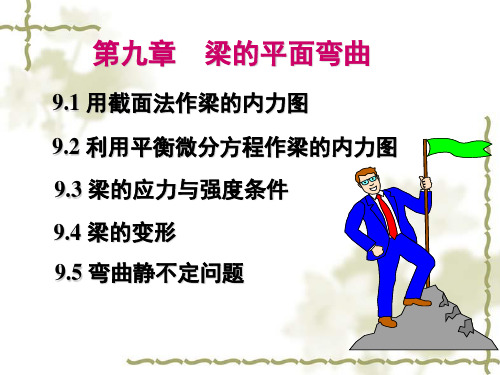
x
左顺右逆，M为正
M
FQ
M
内力 右截面正向 左截面正向 FQ M
微段变形（正）
顺时针错动 向上凹
内力图
剪力图—以杆件轴线为基线,Q为纵坐标,作出的反映Q沿
杆件轴线的变化规律的曲线
弯矩图—以杆件轴线为基线,M为纵坐标,作出的反映M 沿杆件轴线的变化规律的曲线
内力图作法:
以坐标x表示横截面的位置,通过平衡方程求出内力与x 的关系,称为内力方程,根据内力方程作图
FAy q M0 M3
0 x3 B C c FQ3
Fy=FAy-4q-FQ2=0 FQ2=13kN
Mc(F )=M2+4q(x2-2)-FAyx2=0 M2=13x2+72(kN•m)
CD段: 6mx3<8m FQ3=13kN; M3=13x3+24(kN•m)
FAy q M0 F M4 DE段: 8mx4<12m
内力与外力的相依关系
某一截面上的内力与作用在该截 面一侧局部杆件上的外力相平衡；
在载荷无突变的一段杆的各截 面上内力按相同的规律变化；
控制截面的概念： 外力规律发生变化的截面—集中力、集中力偶作用点、分 布载荷的起点和终点处的横截面,支座
。
截面法，确定各段Q、M 分布规律，以此列出各 段的内力方程（剪力方程、弯矩方程）。以此 作出剪力图和弯矩图。
q
A
FA
FQ qa
2a
B
2L
FB
qa
q(L-a) q(L-a)
M
qLa-qL2/2
q(L-a)2/2
根据给定的剪力图和弯矩图能否确定梁的受
力，能否确定梁的支承性质与支承位置？由给
第九章梁的弯曲变形-PPT精品文档
第九章 梁的弯曲变形
第一节
工程中的弯曲变形
梁在外载荷作用下将产生变形，梁不但要满足强 度条件，还要满足刚度条件，即要求梁在工作时的变 形不能超过一定范围，否则就会影响梁的正常工作。 一、挠曲线 挠曲线：图所示悬臂梁在纵向对称面内的外力F的 作用下，将产生平面弯 曲，变形后梁的轴线将变 为一条光滑的平面曲线， 称梁的挠曲线。 挠曲线方程
挠曲轴线 近似微分方程
M ( x) y EI
对梁的挠曲轴线近似微分方程式积分：
积分一次得转角方程：
M ( x ) y x C EI d
积分二次得挠度方程：
M ( x ) y d x d x Cx D EI
第九章 梁的弯曲变形 转角方程 挠度方程
M ( x ) y x C EI d M ( x ) y d x d x Cx D EI
式中积分常数C、D由边界条件（梁中已知的截面 位移）确定：
0 , y 0 简支梁： y A B
悬臂梁： 0 , A
y 0 A
由边界条件、变形连续条件可确定积分常数，通 过上面两个公式可计算梁任一截面的转角与挠度， 这方法称积分法。
第九章 梁的弯曲变形
例9-1 如图所示简支梁，跨度为l，受均布载荷 q作用，梁的抗弯曲刚度EI已知，求跨中截面C的挠 度及截面A处的转角。 解：梁的弯矩方程为：
第九章 梁的弯曲变形 挠曲轴线 近似微分方程 结论 两种情况下弯矩与曲线的二阶导数均同号，微分 方程式应取正号，即： 挠曲轴线 近似微分方程
M(x) y EI
M ( x) y EI
梁的挠曲轴线近似微分方程的适用条件：梁的变 形是线弹性的小变形。
ห้องสมุดไป่ตู้
第一节
工程中的弯曲变形
梁在外载荷作用下将产生变形，梁不但要满足强 度条件，还要满足刚度条件，即要求梁在工作时的变 形不能超过一定范围，否则就会影响梁的正常工作。 一、挠曲线 挠曲线：图所示悬臂梁在纵向对称面内的外力F的 作用下，将产生平面弯 曲，变形后梁的轴线将变 为一条光滑的平面曲线， 称梁的挠曲线。 挠曲线方程
挠曲轴线 近似微分方程
M ( x) y EI
对梁的挠曲轴线近似微分方程式积分：
积分一次得转角方程：
M ( x ) y x C EI d
积分二次得挠度方程：
M ( x ) y d x d x Cx D EI
第九章 梁的弯曲变形 转角方程 挠度方程
M ( x ) y x C EI d M ( x ) y d x d x Cx D EI
式中积分常数C、D由边界条件（梁中已知的截面 位移）确定：
0 , y 0 简支梁： y A B
悬臂梁： 0 , A
y 0 A
由边界条件、变形连续条件可确定积分常数，通 过上面两个公式可计算梁任一截面的转角与挠度， 这方法称积分法。
第九章 梁的弯曲变形
例9-1 如图所示简支梁，跨度为l，受均布载荷 q作用，梁的抗弯曲刚度EI已知，求跨中截面C的挠 度及截面A处的转角。 解：梁的弯矩方程为：
第九章 梁的弯曲变形 挠曲轴线 近似微分方程 结论 两种情况下弯矩与曲线的二阶导数均同号，微分 方程式应取正号，即： 挠曲轴线 近似微分方程
M(x) y EI
M ( x) y EI
梁的挠曲轴线近似微分方程的适用条件：梁的变 形是线弹性的小变形。
ห้องสมุดไป่ตู้
第九章弯曲刚度
2
有：
y
2
MN x
2
A
M
x
o
x0
x x x
得：
s
MN MN
2
y 2 1 2 x
当： x 0，N M
lim N M
MN MN
y
连续可导。在曲线上取一 点A(x0，y0)作为基点，对于 f (x) 曲线上任意一点M(x，y)， 规定： N T 曲线的正向为x增大的 方向；
A
M
x
s AM
o
s f (x) 是x的单调增函数
s f (x) 的导数与微分：
N ( x x，y y) 为曲线上另 一点， s MN
2 s MN MN x MN x f (x) 2 MN x 2 y 2 MN N x 2 T 2 MN y 2 1 2 MN x
d 2 2 a Pa EI M 2 ( x) (l x) P x Pa 2 dx l l
EI 2
x 0： A 0
Pa 2 x Pax C2 2l
Pa 3 Pa 2 EI 2 x x C2 x D2 6l 2
D1 0
Pa 2 C2l D2 l 0 3
1
d M 2 dx EI
2
d 2 M 2 dx EI
式中的正负号与坐标取向相关。
对于等截面梁，对上式进行不定积分，得：
d EI M ( x)dx C 转角方程： EI dx l
有：
y
2
MN x
2
A
M
x
o
x0
x x x
得：
s
MN MN
2
y 2 1 2 x
当： x 0，N M
lim N M
MN MN
y
连续可导。在曲线上取一 点A(x0，y0)作为基点，对于 f (x) 曲线上任意一点M(x，y)， 规定： N T 曲线的正向为x增大的 方向；
A
M
x
s AM
o
s f (x) 是x的单调增函数
s f (x) 的导数与微分：
N ( x x，y y) 为曲线上另 一点， s MN
2 s MN MN x MN x f (x) 2 MN x 2 y 2 MN N x 2 T 2 MN y 2 1 2 MN x
d 2 2 a Pa EI M 2 ( x) (l x) P x Pa 2 dx l l
EI 2
x 0： A 0
Pa 2 x Pax C2 2l
Pa 3 Pa 2 EI 2 x x C2 x D2 6l 2
D1 0
Pa 2 C2l D2 l 0 3
1
d M 2 dx EI
2
d 2 M 2 dx EI
式中的正负号与坐标取向相关。
对于等截面梁，对上式进行不定积分，得：
d EI M ( x)dx C 转角方程： EI dx l
工程力学习题 及最终答案
第一章 绪论思 考 题1) 现代力学有哪些重要的特征？2) 力是物体间的相互作用。
按其是否直接接触如何分类？试举例说明。
3) 工程静力学的基本研究内容和主线是什么？ 4) 试述工程力学研究问题的一般方法。
第二章刚体静力学基本概念与理论习题2-1 求图中作用在托架上的合力F R 。
2-2 已知F 1=7kN ，F 2=5kN, 求图中作用在耳环上的合力F R 。
2-3 求图中汇交力系的合力F R 。
习题2-1图12030200N F4560F 习题2-2图2-4 求图中力F 2的大小和其方向角α。
使 a )合力F R =1.5kN, 方向沿x 轴。
b)合力为零。
2-5二力作用如图，F 1=500N 。
为提起木桩，欲使垂直向上的合力为F R =750N ，且F 2力尽量小，试求力F 2的大小和α角。
2-6 画出图中各物体的受力图。
(b)x453=30N =20N=40N A x45600N 2=700N0N 习题2-3图 (a )F 1习题2-4图F 12习题2-5图(b)(a )2-7 画出图中各物体的受力图。
(c)(d)(e)(f) (g) 习题2-6图(a)ACD2-8 试计算图中各种情况下F 力对o 点之矩。
(b)(d)习题2-7图P(d)(c)(a ) CA2-9 求图中力系的合力F R 及其作用位置。
2-10 求图中作用在梁上的分布载荷的合力F R 及其作用位置。
习题2-8图习题2-9图( a )1F 3 ( b )F 3F 2( c)1F /m( d )F 32-11 图示悬臂梁AB 上作用着分布载荷，q 1=400N/m ，q 2=900N/m, 若欲使作用在梁上的合力为零，求尺寸a 、b的大小。
第三章 静力平衡问题习 题3-1 图示液压夹紧装置中，油缸活塞直径D=120mm ，压力p =6N/mm 2，若α=30︒, 求工件D 所受到的夹紧力F D 。
( b )q ( c )习题2-10图B习题2-11图3-2 图中为利用绳索拔桩的简易方法。
第9章_直梁
WZ
max
IZ 1.067106 ymax
M max 141 MN/m2 150MN/m2 WZ
故压板的强度足够
第九章 直梁弯曲
例9-8 一起重量原为 50kN 的吊车,其跨度l = 10.5m (如图)，由 45a号工字钢制成。为发挥其潜力，现欲将 起重量提高到Q =70kN，试校核梁的强度；若强度不足， 再计算其可能承载的起重量。设梁的材料为 Q235钢， 许用应力[σ]=140MN/m2，电葫芦自重G = 15kN，梁
第九章 直梁弯曲
推断和假设
假设：(1) 梁在纯弯曲时，各横截 面始终保持为平面，并垂直于梁轴。
此即弯曲变形的平面假设。
(2) 纵向纤维之间没有相互挤压,每 根纵向纤维只受到简单拉伸或压缩。 中性层：从伸长到缩短区，中间必有一层纤维既不伸长也不缩短。这 一长度不变的过渡层称为中性层。 中性轴：中性层与横截面的交线 在纯弯曲的条件下，所有横截面仍保持平面，只是绕中性轴作 相对转动，横截面之间并无互相错动的变形，而每根纵向纤维 则处于简单的拉伸或压缩的受力状态。
Q max P M max Pl
Q O
x P
第九章 直梁弯曲
例9-3
一简支梁 AB ,受均布载荷 q 的作用，试作此梁的弯矩图。
解： 1、求支反力
由对称性知： ql FA FB 2
2、建立剪力方程和弯矩方程
ql Q = FA qx = qx (0 < x < 1) 2 qx2 qlx qx2 M = FA x = (0 ≤x < 1) 2 2 2
非对称弯曲：若梁不具有纵向对称面，或梁有纵向对称面上但 外力并不作用在纵向对称面内的弯曲。
第九章 直梁弯曲
max
IZ 1.067106 ymax
M max 141 MN/m2 150MN/m2 WZ
故压板的强度足够
第九章 直梁弯曲
例9-8 一起重量原为 50kN 的吊车,其跨度l = 10.5m (如图)，由 45a号工字钢制成。为发挥其潜力，现欲将 起重量提高到Q =70kN，试校核梁的强度；若强度不足， 再计算其可能承载的起重量。设梁的材料为 Q235钢， 许用应力[σ]=140MN/m2，电葫芦自重G = 15kN，梁
第九章 直梁弯曲
推断和假设
假设：(1) 梁在纯弯曲时，各横截 面始终保持为平面，并垂直于梁轴。
此即弯曲变形的平面假设。
(2) 纵向纤维之间没有相互挤压,每 根纵向纤维只受到简单拉伸或压缩。 中性层：从伸长到缩短区，中间必有一层纤维既不伸长也不缩短。这 一长度不变的过渡层称为中性层。 中性轴：中性层与横截面的交线 在纯弯曲的条件下，所有横截面仍保持平面，只是绕中性轴作 相对转动，横截面之间并无互相错动的变形，而每根纵向纤维 则处于简单的拉伸或压缩的受力状态。
Q max P M max Pl
Q O
x P
第九章 直梁弯曲
例9-3
一简支梁 AB ,受均布载荷 q 的作用，试作此梁的弯矩图。
解： 1、求支反力
由对称性知： ql FA FB 2
2、建立剪力方程和弯矩方程
ql Q = FA qx = qx (0 < x < 1) 2 qx2 qlx qx2 M = FA x = (0 ≤x < 1) 2 2 2
非对称弯曲：若梁不具有纵向对称面，或梁有纵向对称面上但 外力并不作用在纵向对称面内的弯曲。
第九章 直梁弯曲
工程力学 第九章 梁的应力及强度计算
平面弯曲时，如果某段梁的横截面上只有弯矩M，而无剪力Q = 0，这种弯曲称为纯弯曲。
1、矩形截面梁纯弯曲时的变形观察
现象：
（1）变形后各横向线仍为直线，只是相对旋转了一个角度，且与变形后的梁轴曲线保持垂直，即小矩形格仍为直角；
（2）梁表面的纵向直线均弯曲成弧线，而且，靠顶面的纵线缩短，靠底面的纵线拉长，而位于中间位置的纵线长度不变。
对剪应力的分布作如下假设：
(1)横截面上各点处剪应力均与剪力Q同向且平行；
(2)横截面上距中性轴等距离各点处剪应力大小相。
根据以上假设，可推导出剪应力计算公式：
式中:τ—横截面上距中性轴z距离为y处各点的剪应力；
Q—该截面上的剪力；
b—需求剪应力作用点处的截面宽度；
Iz—横截面对其中性轴的惯性矩；
Sz*—所求剪应力作用点处的横线以下(或以上）的截面积A*对中性轴的面积矩。
应力σ的正负号直接由弯矩M的正负来判断。M为正时，中性轴上部截面为压应力，下部为拉应力；M为负时，中性轴上部截面为拉应力，下部为压应力。
第二节 梁的正应力强度条件
一、弯曲正应力的强度条件
等直梁的最大弯曲正应力，发生在最大弯矩所在横截面上距中性轴最远的各点处，即
对于工程上的细长梁，强度的主要控制因素是弯曲正应力。为了保证梁能安全、正常地工作，必须使梁内最大正应力σmax不超过材料的许用应力[σ]，故梁的正应力强度条件为：
圆形截面横梁截面上的最大竖向剪应力也都发生在中性轴上，沿中性轴均匀分布。
其它形状的截面上，一般地说，最大剪应力也出现在中性轴上各点。
结合书P161-162 例8-3进行详细讲解。
五、梁的剪应力强度校核
梁的剪应力强度条件为：
在梁的强度计算时，必须同时满足弯曲正应力强度条件和剪应力强度条件。但在一般情况下，满足了正应力强度条件后，剪应力强度都能满足，故通常只需按正应力条件进行计算。
1、矩形截面梁纯弯曲时的变形观察
现象：
（1）变形后各横向线仍为直线，只是相对旋转了一个角度，且与变形后的梁轴曲线保持垂直，即小矩形格仍为直角；
（2）梁表面的纵向直线均弯曲成弧线，而且，靠顶面的纵线缩短，靠底面的纵线拉长，而位于中间位置的纵线长度不变。
对剪应力的分布作如下假设：
(1)横截面上各点处剪应力均与剪力Q同向且平行；
(2)横截面上距中性轴等距离各点处剪应力大小相。
根据以上假设，可推导出剪应力计算公式：
式中:τ—横截面上距中性轴z距离为y处各点的剪应力；
Q—该截面上的剪力；
b—需求剪应力作用点处的截面宽度；
Iz—横截面对其中性轴的惯性矩；
Sz*—所求剪应力作用点处的横线以下(或以上）的截面积A*对中性轴的面积矩。
应力σ的正负号直接由弯矩M的正负来判断。M为正时，中性轴上部截面为压应力，下部为拉应力；M为负时，中性轴上部截面为拉应力，下部为压应力。
第二节 梁的正应力强度条件
一、弯曲正应力的强度条件
等直梁的最大弯曲正应力，发生在最大弯矩所在横截面上距中性轴最远的各点处，即
对于工程上的细长梁，强度的主要控制因素是弯曲正应力。为了保证梁能安全、正常地工作，必须使梁内最大正应力σmax不超过材料的许用应力[σ]，故梁的正应力强度条件为：
圆形截面横梁截面上的最大竖向剪应力也都发生在中性轴上，沿中性轴均匀分布。
其它形状的截面上，一般地说，最大剪应力也出现在中性轴上各点。
结合书P161-162 例8-3进行详细讲解。
五、梁的剪应力强度校核
梁的剪应力强度条件为：
在梁的强度计算时，必须同时满足弯曲正应力强度条件和剪应力强度条件。但在一般情况下，满足了正应力强度条件后，剪应力强度都能满足，故通常只需按正应力条件进行计算。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
EI zq = EI z y ( x) = M ( x)dx C1
'
EI z y = M ( x)dxdx C1 x C2
19
返回主目录
已知M(x)，积分可求q、y，常数C1、C2如何确定 ？
积分常数C 1 、C 2的确定 考 虑
铰链： x=0, y=0 x=L, y=0 静定梁 平面问题
s max
Mymax M = = [s ] Iz Wz
Iz 为截面对z 轴的惯性矩，W z 为抗弯截面模量。
4. 矩形截面梁的弯曲切应力呈抛物线分布，最大切 应力在中性轴处且等于平均切应力的1.5倍。
15
9.4 梁的变形
杆的拉压 轴的扭转 伸长或缩短 DL
单位扭转角 q
y
o
y 为正 梁的弯曲变形 q 截面 正 如何描述
注意按使用要求设计截面。 所能承受的最大正负弯矩之比。 M>0时，强度条件: M+[s]拉Iz/3.25a=4[s]拉Iz/13a M<0时： 截面应力分布？ smax拉=1.75aM/Iz smax压=3.25aM/Iz 强度条件： z
1.75a C 3.25a
y
y
4a
a
4a
s max 拉
C
a
M-[s]
21
例9.14 受均布载荷的悬臂梁如图，试求其挠曲线方 程、转角方程、及自由端B的挠度和转角。 y 解: 1. 求支承反力 q M F=qL， M=-qL 2 /2 2. 列弯矩方程: SMC=0 M(x)=qLx-qL2/2-qx2/2
A F x
L
C
B
x
3. 挠曲线微分方程
EI z y (x ) = -
o
r
小变形 dy x c q = tgq q x dx x处的截面转角q(x)等于挠曲线在该处的斜率。
c
q
讨论纯弯曲时，给出梁变形后的曲率为： 1 = M r EI
弹性理论精确分析指出，梁的跨高比 L/h>10时， 剪力对弯曲变形的影响可忽略不计。 故上式可应用于横力弯曲的普遍情况。
17
1 M y (x)应与M(x) 同号， 梁变形后的曲率为： =
压Iz/3.25a=8[s]拉Iz/13a
M-[s]拉Iz/1.75a=4[s]拉Iz/7a
M
s max 压
M 7 = M 13
10
9.3.5 矩形截面梁的弯曲切应力
纯弯曲 横力弯曲 分 析 内力：弯矩 M M ; 剪力 FS 横截面上：正应力 s
s
： 切应力 t
y
?
h
截面上t与FS平行，指向相同。 h>b时，截面上y相同处t相同。 y= ±h/2处，t=0。
4a
2) M>0时： 截面应力分布？
smax拉=3.25aM/Iz smax压=1.75aM/Iz
强度条件: M+[s]拉Iz/3.25a=4[s]拉Iz/13a
s max 压
C
y
1.75a 3.25a
9
M
s max 拉
对于拉压力学性能（许用应力）不同的材料，应 讨论二 ：铸铁T形截面梁有 [s]压/[s]拉=2，试求其
My MS z F1 = sdA = dA = A1 A1 I Iz z
A1
z
取图示部分研究其在x方向的平衡：
F2
FS t
b
F3 t dx
s
S z 是面积A 1 对中性轴z的静矩。
b F1
11
返回主目录
研究x方向的平衡：
My MS z F1 = s dA = dA = A1 I z A1 Iz
y
1 M ( x) y ( x) = = r ( x) EI z
''
正负？
y(x)向上凹 M>0 y(x)递增 y(x)>0
18
x
9.4.3 用积分法求梁的变形
挠曲线近似微分方程为：
M ( x) y ( x) = EI z
''
即：
EI z y ( x) = M ( x)
''
EI是梁的抗弯刚度。对于一段等刚度梁，积分有： 挠曲线微分方程： EI z y '' ( x) = M ( x) 转角方程： 挠度方程：
h
t max
矩形截面梁的弯曲切应力为：
FS h2 t是y的函数，呈抛物线分布， 2 t= ( y ) 最大切应力在中性轴处且等 2Iz 4
于平均切应力的1.5倍。
13
讨论三、矩形截面梁AB受力如图。 [s]=150MPa，
[t]=60MPa， 若取h/b=2，试设计其尺寸。 解：1.求反力，作FQ、M图。
x M 4kN.m
10kN
x 6kN.m
14
b 0.035 m
一般按正应力设计，再校核剪切强度。
小 结
1. 梁横截面上的正应力s呈线性 分布，其大小为 s =My/Iz 正负由弯曲后的拉压情况判断。
y 3FS s maxt y 压 max =
M
z
2bh
h C
FS t
b
s max拉
2. 中性轴过截面形心，该处正应力s 等于零。 3. 梁的弯曲强度条件：
例9.10 矩形截面木梁的横截面高宽比h/b=3/2，已知 F=15kN，a=0.8m，[s]=10MPa
解：1. 求支反力：
F A =FB=3F 2. 作FS、M图。 M max =Fa=12 kN.m 3. 注意h/b=3/2，则： Wz =bh2 /6=3b 3 /8 4. 强度条件： 3 3 ma x 3b M =12 10 Wz = 8 [s ] 1010 6 解得：b0.147m150mm
Iz--截面对z轴的惯性矩。
EI--截面抗弯刚度。
结论： s=-My/Iz
中性轴上，s=0，截面上、下缘，
s =s max 。
3
9.3.4
平面弯曲的最大正应力及强度条件
y
My 弯曲正应力公式： s = Iz
按绝对值计算应力s 的大小，依 据弯曲后的拉压情况判断正负。
M
smax压
x
M
smax拉
适用范围：
F2
F3 dx
s t b F1
( M - dM ) y ( M - dM ) S z F2 = s dA = dA = A1 A1 Iz Iz
F3 = t bdx
有：SFx=F1-F2+F3=0 对于矩形截面，有：
Sz = ydA =
A1
h/ 2 y
Sz dM FSS z t= = Sz=? Iz b dx Iz b
r
EIz
挠曲线近似微分方程为： 对于材料和截面不变的梁
段，EI z是常量。故有：
y
o
r
c
q
M ( x) 1x ) = M ( x) y( = EI r ( x) EI z z
''
c q x
x
2 3 /2 y ) ( 1 数学分析曾给出： ： r ( x) =± y
略去二阶小量 y 2，得到：
8
面积 mm2 重量: 32413 87%
37249 mm2 100%
讨论二：铸铁T形截面梁如图， 若[s]压/[s]拉=2，
试求其所能承受的最大正负弯矩之比。
中性轴在哪？
解：1) 求形心位置 压 a 拉 8a 2y c =2a 4a 2-0.5 4a 2
y c =3a/4
y z
z
4a a
yc o C a
F a 2F F Fa Fa
2F
2F a
F
a FB F x
FA
a
a
a
FS
Fa
2F
x
M
Fa
7
x
讨论一： M max =Fa=12 kN.m，[s]=10MPa，
试设计木梁不同截面的尺寸。 截面设计应尽可能使 h h/b=3/2 h/b=1 b 材料远离中性轴。 b Wz =bh 2/6 =3b 3/8
约束边界条件
分段连续条件 固定端 x=L, y=0 x=L, q=0 自由端
yy
AA 固定铰
C 滚动铰 B
C y1 q y2 L C处 处:: q 2 1
固定端 C B
B
xx
y
A
自由端
无约束
L/2
L/2
x
三个约束 限制移动和转动
Fx=0，二个约 束，限制y和q
确定挠 度转角
梁AC、CB二段M(x)不同，需分1、2二段积分。 分段连续条件为：x=L/2， y 1=y 2; q 1=q 2。
第九章
梁的平面弯曲
9.1 用截面法作梁的内力图 9.2 利用平衡微分方程作梁的内力图 9.3 梁的应力与强度条件 9.4 梁的变形
9.5 弯曲静不定问题和 弹塑性问题简介
返回主目录
1
9.3 梁的应力与强度
讨论平面纯弯曲梁。 横截面上只有弯矩。
M
y M
z
s
x
弯矩分布在横截面上， 只能是正应力。
问题: 平面纯弯曲梁横截面上的正应力?
பைடு நூலகம்
思路： 仍沿研究变形体力学问题的主线。
变形的几何协调 (几何分析) 力与变形之关系 (物理关系) 力的平衡 (已熟悉)
2
分析结果汇总：
变形几何关系： e=-y/r 物理关系：
y
smax压
x
s=Ee=-y/r
静力平衡条件： A ydA=0 中性轴z过截面形心
1/r=M/EIz 梁的曲率