青岛版数学七年级上册综合练习题(全册)
(青岛版)七年级数学上册第一章测试题
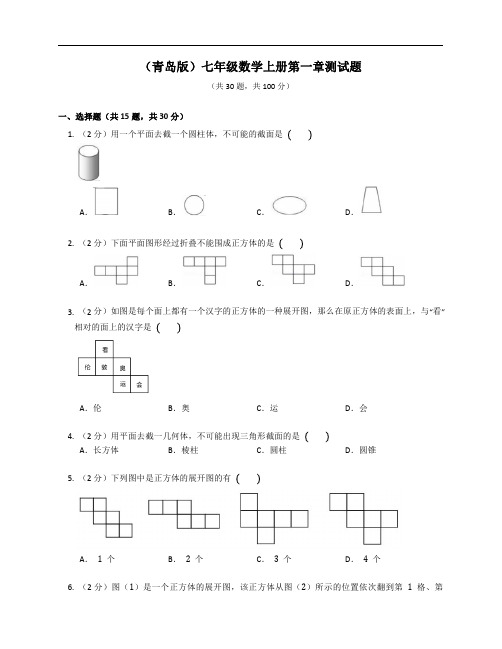
(青岛版)七年级数学上册第一章测试题(共30题,共100分)一、选择题(共15题,共30分)1.(2分)用一个平面去截一个圆柱体,不可能的截面是 A.B.C.D.2.(2分)下面平面图形经过折叠不能围成正方体的是 A.B.C.D.3.(2分)如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与“看”相对的面上的汉字是 A.伦B.奥C.运D.会4.(2分)用平面去截一几何体,不可能出现三角形截面的是 A.长方体B.棱柱C.圆柱D.圆锥5.(2分)下列图中是正方体的展开图的有 A.1个B.2个C.3个D.4个6.(2分)图(1)是一个正方体的展开图,该正方体从图(2)所示的位置依次翻到第1格、第2格、第3格、第4格,此时这个正方体朝上一面的字(不考虑文字的方向)是 A.梦B.中C.国D.我7.(2分)如图,一个几何体由5个大小相同,棱长为1的小正方体搭成,下列说法正确的是 A.从正面看到的形状图的面积为7B.从左面看到的形状图的面积为3C.从上面看到的形状图的面积为3D.这个几何体的表面积是138.(2分)某正方体的平面展开图如图所示.由此可知,正方体中“爱”字所在面的对面的汉字是 A.习B.会C.思D.考9.(2分)如图是由6个小正方体搭成的几何体,从该几何体上面看到的形状图是 A.B.C.D.10.(2分)下面几何体中,截面图形不可能是圆 A.圆柱B.圆锥C.球D.正方体11.(2分)下面平面图形经过折叠不能围成正方体的是 A .B .C .D .12.(2分)如图,是一个正方形盒子的展开图,若要在展开后的其中的三个正方形,,内分别填入适当的数,使得展开图折成正方体后相对的面上的两个数互为相反数,则填入正方形,,内的三个数依次为 A .1,−2,0B .0,−2,1C .−2,0,1D .−2,1,013.(2分)用一个平面去截一个几何体,得到的截面是五边形,这个几何体可能是 A .圆锥B .圆柱C .球体D .长方体14.(2分)下列平面图形经过折叠不能围成正方体的是 A .B .C .D .15.(2分)下面几何体中,截面图形不可能是圆的是 A .圆柱B .圆锥C .球D .正方体二、填空题(共10题,共20分)16.(2分)如图是一个正方体的展开图,它的六个面上分别写有“构建和谐社会”六个字,将其围成正方体后,与“社”在相对面上的字是.17.(2分)用一个平面去截三棱柱不可能截出以下图形中的(填序号).①等腰三角形,②等边三角形,③圆,④正方形,⑤五边形,⑥梯形18.(2分)一个直棱柱有八个面,所有侧棱长的和为24 cm ,则每条侧棱的长是cm .19.(2分)如果一个棱柱的底面是六边形,且侧棱长为5 cm,那么它所有的侧棱长之和是.20.(2分)用一个平面去截一个正方体,所得截面的边数最少是,最多是.21.(2分)如图,从一个棱长为4 cm的正方体的一个顶点挖去一个棱长为1 cm的正方体后,从任何角度所能看到的所有面的面积为.22.(2分)一个几何体,是由许多规格相同的小正方体堆积而成的,从正面看和从左面看的形状如图所示,要搭成这样的几何体,最少需用块小正方体.23.(2分)圆柱的侧面展开图是.24.(2分)将三棱柱沿它的棱剪成平面图形,至少要剪开条棱.25.(2分)一个几何体是由一些大小相同的小正方块摆成的.其从上面和正面看到的形状图如图所示,则组成这个几何体的小正方块最多有个.三、解答题(共5题,共50分)26.(10分)从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.27.(10分)下图是用小正方体搭成的几何体.请分别画出从左面、上面看到的几何体的形状图.28.(10分)从正面,左面,上面观察如图所示的几何体,分别画出所看到的几何体的形状图.29.(10分)如图是一个由若干个小正方体搭成的几何体从上面看到的形状图,其中小正方形内的数字是该位置小正方体的个数,请你画出它从正面和从左面看到的形状图.30.(10分)如图是一个由若干个小正方体搭成的几何体从上面看到的形状图,其中小正方形内的数字是该位置小正方体的个数,请你画出它从正面和从左面看到的形状图.答案一、选择题(共15题,共30分)1.【答案】D【解析】用一个平面去截一个圆柱体,轴截面是矩形;过平行于上下底面的面去截可得到圆;过侧面且不平行于上下底面的面去截可得到椭圆;不可能的截面是等腰梯形.故选D.【知识点】面截体2.【答案】B【解析】由分析可知不能折叠成正方体的是:B.故选:B.【知识点】正方体的展开图3.【答案】C【解析】这是一个正方体的平面展开图,共有六个面,其中面“伦”与“奥”相对,面“会”与“敦”相对,“看”与面“运”相对.【知识点】正方体相对两个面上的文字4.【答案】C【知识点】面截体5.【答案】D【解析】这四个图形全部都是正方体的展开图.【知识点】正方体的展开图6.【答案】D【解析】由图(1)可得,“中”和“的”相对;“国”和“我”相对;“梦”和“梦”相对;由图(2)可得,小正方体从图(2)的位置依次翻到第5格时,“国”在下面,则这时小正方体朝上面的字是“我”.故选D.【知识点】正方体相对两个面上的文字7.【答案】B【知识点】从不同方向看物体8.【答案】C【解析】由展开图可知,学与会相对,习与考相对,爱与思相对,故选C.【知识点】正方体相对两个面上的文字9.【答案】B【解析】从上往下看,该几何体的俯视图如下:【知识点】从不同方向看物体10.【答案】D【解析】本题中,用平面去截正方体,得的截面可能为三角形、四边形、五边形、六边形,无论如何,截面也不会有弧度不可能是圆.【知识点】面截体11.【答案】B【知识点】正方体的展开图12.【答案】A【解析】由于只有符号不同的两个数互为相反数,由正方体的展开图解题得填入正方形中,,内的三个数依次为1,−2,0.故选:A.【知识点】正方体相对两个面上的文字13.【答案】D【解析】A、用一个平面去截一个圆锥,得到的图形可能是圆形,椭圆,抛物线,双曲线的一支,三角形,故A选项错误;B、用一个平面去截一个圆柱,得到的图形只能是圆,椭圆,长方形,故B选项错误;C、用一个平面去截一个球体,得到的图形可能是圆,故C选项错误;D、用一个平面去截一个长方体,得到的图形可能是五边形,长方形,三角形,故D选项正确.故选:D.【知识点】面截体14.【答案】C【知识点】正方体的展开图15.【答案】D【知识点】面截体二、填空题(共10题,共20分)16.【答案】和【解析】正方体的表面展开图,相对的面之间一定相隔一个正方形,与“社”在相对面上的字是和.【知识点】正方体相对两个面上的文字17.【答案】③【解析】当截面与底面平行时,得到的截面形状是三角形故①②正确;当截面与底面垂直且经过三棱柱的四个面时,得到的截面形状是正方形,故④正确;当截面与底面斜交且经过三棱柱的四个面时,得到的截面形状是等腰梯形,故⑥正确;当截面与三棱柱的五个面相交时,得到的截面形状是五边形形,故⑤正确.【知识点】面截体18.【答案】4【解析】∵这个棱柱有八个面,∴这个棱柱是6棱柱,有6条侧棱,∵所有侧棱的和为24 cm,∴每条侧棱长为24÷6=4cm.【知识点】认识立体图形19.【答案】30 cm【解析】∵棱柱的底面是六边形∴棱柱有6条侧棱,∵侧棱长为5 cm,∴它所有的侧柱长之和是6×5=30cm,故答案为:30 cm.【知识点】认识立体图形20.【答案】3;6【解析】∵用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,∴所得截面的边数最少是3,最多是6.故答案为:3;6.【知识点】面截体21.【答案】96 cm2【解析】挖去小正方体后,剩下物体的表面积与原来的表面积相比较没变化,即从任何角度所能看到的所有面的面积为16×6=96 cm2.【知识点】从不同方向看物体22.【答案】6【解析】根据三视图可得:第二层有2个小正方块,根据主视图和左视图可得第一层最少有4个正方体,故最少需用2+4=6块正方体.【知识点】从不同方向看物体23.【答案】矩形【知识点】圆柱的展开图24.【答案】5【解析】由图形可知:没有剪开的棱的条数是4条,则至少需要剪开的棱的条数是:9−4=5(条),故至少需要剪开的棱的条数是5条.【知识点】直棱柱的展开图25.【答案】6【解析】利用俯视图标数法,标出小正方块最多的情况如下:21212+2+1+1=6.【知识点】从不同方向看物体三、解答题(共5题,共50分)26.【答案】如图所示.【知识点】从不同方向看物体27.【答案】该几何体从左面看和从上面看所得图形如图所示:【知识点】从不同方向看物体28.【答案】【知识点】从不同方向看物体29.【答案】如图所示:【知识点】从不同方向看物体30.【答案】【知识点】从不同方向看物体。
初中数学青岛版七年级上册第1章 基本的几何图形1.4线段的比较与作法-章节测试习题(1)

章节测试题1.【答题】已知点O是线段AB上的一点,且AB=12cm,点M、N分别是线段AO、线段BO的中点,那么线段MN的长度是( )A. 6cmB. 5cmC. 4cmD. 无法确定【答案】A【分析】根据线段中点的性质,可得OM,ON,根据线段的和差,可得答案.【解答】∵点O是线段AB上一点,∴AO+BO=AB=12∵点M、N分别是线段AO、线段BO的中点,∴MO=AO,NO=BO.∴MN=MO+NO=(AO+BO)=6(cm).选A.2.【答题】下列关系中,与图示不符合的式子是( )A. AD-CD=AB+BCB. AC-BC=AD-DBC. AC-BC=AC+BDD. AD-AC=BD-BC【答案】C【分析】根据线段之间的和差关系依次进行判断即可得出正确答案.【解答】解: A. AD-CD=AC=AB+BC,正确;B. AC-BC=AD-DB=AB,正确;C. AC-BC=AC+BD,错误;D. AD-AC=BD-BC=CD,正确.选C.3.【答题】平面上有四点,经过其中的两点画直线最多可画出( )A. 三条B. 四条C. 五条D. 六条【答案】D【分析】画出图形即可确定最多能画的直线的条数.【解答】解:如图,最多可画6条直线.选D.方法总结:此题考查直线问题,只有在任意三点不在同一直线时,才能画出最多的直线.4.【答题】为比较两条线段AB与CD的大小,小明将点A与点C重合使两条线段在一条直线上,点B在CD的延长线上,则( )A. AB<CDB. AB>CDC. AB=CDD. 以上都有可能【答案】B【分析】根据线段的比较,点A与点C重合使两条线段在一条直线上,点B在CD的延长线上,可得答案.【解答】解:由点A与点C重合使两条线段在一条直线上,点B在CD的延长线上,得AB>CD.选B.5.【答题】线段AB=2 cm,延长AB到C,使BC=AB,再延长BA到D,使BD =2AB,则线段DC的长为( )A. 4 cmB. 5 cmC. 6 cmD. 2 cm【答案】C【分析】由已知条件可知,BD=2AB,直接代入求值即可.【解答】解:∵BD=2AB,AB=2cm,∴BD=4cm,DC=DB+BC=4+2=6cm.选C.方法总结:在未画图类问题中,正确画图很重要.所以能画图的一定要画图这样才直观形象,便于思维.6.【答题】已知线段AB=1 cm,BC=3 cm,则点A到点C的距离为( )A. 4 cmB. 2 cmC. 2 cm或4 cmD. 无法确定【答案】D【分析】没有明确A、B、C三点是否在同一直线上,故点A到点C的距离无法确定.【解答】解:选D.7.【答题】下列说法正确的是( )A. 两点之间直线最短B. 画出A,B两点间的距离C. 连接点A与点B的线段,叫A,B两点间的距离D. 两点之间的距离是一个数,不是指线段本身【答案】D【分析】根据线段的性质,两点间的距离的定义对各选项分析判断利用排除法求解.【解答】解: A. 两点之间线段最短,故A错误;B. 量出A,B两点间的距离,故B错误;C. 连接点A与点B的线段的长,叫A,B两点间的距离,故C错误;D. 两点之间的距离是一个数,不是指线段本身,正确.选D.8.【答题】如图,C,D是线段AB上的两个点,CD=3 cm,M是AC的中点,N 是DB的中点,AB=7.8 cm,那么线段MN的长等于( )A. 5.4 cmB. 5.6 cmC. 5.8 cmD. 6 cm【答案】A【分析】由已知根据线段的和差和中点的性质可求得MC+DN的长度,再根据MN=MC+CD+DN不难求解.【解答】解:∵M是AC的中点,N是DB的中点,CD=3cm,AB=7.8cm,∴MC+DN=(AB-CD)=2.4cm,∴MN=MC+DN+CD=2.4+3=5..4cm.选A.9.【答题】C为AB的一个三等分点,D为AB的中点,若AB的长为6.6 cm,则CD的长为( )A. 0.8 cmB. 1.1 cmC. 3.3 cmD. 4.4 cm【答案】B【分析】题干中只是说C是线段AB的三等分点,并没有说是哪一个三等分点,线段的三等分点有两个,故应分类讨论,分为AC=AB和BC=AB两种情况.在不同的情况下根据线段之间的关系得出AB的长度.【解答】根据三等分点可得:AC=6.6÷3=2.2cm,根据中点的性质可得:AD=6.6÷2=3.3cm,则CD=AD-AC=3.3-2.2=1.1cm,故选择B.方法总结:本题主要考查的就是中点以及三等分点的性质,属于简单的题型,解决这个问题我们首先要能够根据给出的条件画出图形,然后根据所得的图形进行线段的长度计算.在求线段长度的题目中很多时候我们要根据点的位置关系来进行分类讨论,做题的时候一定要注意这个点是在线段上还是直线上.10.【答题】如图,AB=CD,那么AC与BD的大小关系是( )A. AC=BDB. AC<BDC. AC>BDD. 不能确定【答案】A【分析】由题意已知AB=CD,根据等式的基本性质,两边都减去BC,等式仍然成立.【解答】根据AB=CD可得:AC+BC=BD+BC,则AC=BD,故选择A.11.【答题】下列错误的判断是( )A. 任何一条线段都能度量长度B. 因为线段有长度,所以它们之间能比较大小C. 利用圆规配合尺子,也能比较线段的大小D. 两条直线也能进行度量和比较大小【答案】D【分析】根据直线、线段的性质:直线不可以度量,无法比较长短;线段可以度量,能比较长短,逐项判定即可.【解答】直线和射线的长度是无法度量的,则两条直线不能比较大小.12.【答题】如图,C是线段AB上的点,D是线段AC的中点,E是线段BC的中点,若DE=10,则AB的长为( )A. 10B. 20C. 30D. 40【答案】B【分析】灵活运用寻求到的解题线索,搞清图形中隐含的线段之间的和、倍、差的关系,并合理利用等量代换或消元处理等代数方法证明几何问题,用代数方法证明几何中的问题是很重要的方法.【解答】∵点D是线段AC的中点,∴CD=AC,∵点E是线段BC的中点,∴DE=CD+CE= (AC+BC),∴AC+BC=2DE=20.∴AB=AC+BC=20选B.13.【题文】如图,是线段上一点,M是线段的中点,N是线段BC的中点且MN=3cm,则的长为cm.【答案】6【分析】根据线段中点的性质,可得AC+CB=2MN的长,依此可得AB的长.【解答】解:∵M是线段AC的中点,N是线段BC的中点,∴AC=2MC,BC=2CN,∴AB=AC+BC=2(MC+CN)=2MN=6cm.故答案为:6.14.【题文】直线上有A,B,C三点,点M是线段AB的中点,点N是线段BC 的一个三等分点,如果AB=6,BC=12,求线段MN的长度.【答案】1或5或7或11.【分析】分类讨论点C在AB的延长线上,点C在B的左边,根据线段的中点,三等分点的性质,可得BM、BN的长,根据线段的和差,可得答案.【解答】解:(1)点C在射线AB上,如:点M是线段AB的中点,点N是线段BC的三等分点,MB=AB=3,BN=CB=4,或BN′=BC=8,MN=BM+BN=3+4=7,或MN′=BM+BN′=3+8=11;(2)点C在射线BA上,如:点M是线段AB的中点,点N是线段BC三等分点,MB=AB=3,BN=CB=4,或BN′=BC=8,MN=BN﹣BM=4﹣3=1,或MN′=BN′﹣BM=8﹣3=5.方法总结:本题考查了两点间的距离,分类讨论是解题的关键,根据线段中点的性质,线段的和差,可得出答案.15.【题文】已知x=﹣3是关于x的方程(k+3)x+2=3x﹣2k的解.(1)求k的值;(2)在(1)的条件下,已知线段AB=6cm,点C是直线AB上一点,且BC=kAC,若点D是AC的中点,求线段CD的长.【答案】(1)k=2;(2)CD的长为1cm或3cm.【分析】(1)把x=-3代入方程进行求解即可得k的值;(2)由于点C的位置不能确定,故应分点C在线段AB上与点C在BA的延长线上两种情况进行讨论即可得.【解答】解:(1)把x=﹣3代入方程(k+3)x+2=3x﹣2k得:﹣3(k+3)+2=﹣9﹣2k,解得:k=2;(2)当k=2时,BC=2AC,AB=6cm,∴AC=2cm,BC=4cm,当C在线段AB上时,如图1,∵D为AC的中点,∴CD=AC=1cm;当C在BA的延长线时,如图2,∵BC=2AC,AB=6cm,∴AC=6cm,∵D为AC的中点,∴CD=AC=3cm,即CD的长为1cm或3cm.16.【题文】(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,求线段MN的长度.(2)在(1)中,如果AC=acm,BC=bcm,其它条件不变,你能猜出MN的长度吗?请你用一句简洁的话表述你发现的规律.(3)对于(1)题,如果我们这样叙述它:“已知线段AC=6cm,BC=4cm,点C 在直线AB上,点M,N分别是AC,BC的中点,求MN的长度.”结果会有变化吗?如果有,求出结果.【答案】(1)5cm;(2)MN=,直线上相邻两线段中点间的距离为两线段长度和的一半;(3)有变化,会出现两种情况:①当点C在线段AB上时,MN==5cm;②当点C在AB或BA的延长线上时,MN=1cm.【分析】(1)(2)在一条直线或线段上的线段的加减运算和倍数运算,首先明确线段间的相互关系,最好准确画出几何图形,再根据题意进行计算;(3)会出现两种情况:①点C在线段AB上;②点C在AB或BA的延长线上.不要漏【解答】解:(1)∵AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,(2)直线上相邻两线段中点间的距离为两线段长度和的一半;(3)如图,有变化,会出现两种情况:①当点C在线段AB上时,②当点C在AB或BA的延长线上时,17.【题文】已知:线段a,b求作:线段AB,使AB=2a+b(用直尺、圆规作图,不写作法,但要保留作图痕迹)【答案】见解析【分析】先在射线上依次截取再截取,则线段【解答】解:如图:,线段AB即为所求.18.【题文】如图,已知B、C两点把线段AD分成2:4:3的三部分,M是AD 的中点,若CD=6,求:(1)线段MC的长.(2)AB:BM的值.【答案】(1)3(2)4:5【分析】(1)AB:BC:CD=2:4:3,可得线段、线段的长,根据线段的和差,可得线段的长,根据线段中点的性质,可得的长,根据线段的和差,可得答案;(2)根据线段中点的性质,可得的长,根据线段的和差,可得的长,根据比的意义,可得答案.【解答】解:(1)由AB:BC:CD=2:4:3,CD=6,得AB=4,BC=8.由线段的和差,得AD=AB+BC+CD=4+8+6=18.由线段中点的性质,得由线段的和差,得MC=MD−CD=9−6=3;(2)由线段的和差,得BM=AM−AB=9−4=5.由比的意义,得AB:BM=4:5.19.【题文】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣4,点C在数轴上表示的数是4,若线段AB以3个单位长度/秒的速度向右匀速运动,同时线段CD以1个单位长度/秒的速度向左匀速运动.(1)问运动多少秒时BC=2(单位长度)?(2)线段AB与线段CD从开始相遇到完全离开共经过多长时间?(3)P是线段AB上一点,当B点运动到线段CD上,且点P不在线段CD上时,是否存在关系式BD﹣AP=3PC.若存在,求线段PD的长;若不存在,请说明理由.【答案】(1)1或2;(2)1.5秒;(3)5或 3.5.【分析】(1)分点B在点C的左边和点B在点C的右边两种情况讨论;(2)所走路程为这两条线段的和,用路程,速度,时间之间的关系可求解;(3)随着点B的运动,分别讨论当点B和点C重合、点C在点A和B之间及点A与点C重合时的情况.【解答】解:(1)设运动t秒时,BC=2单位长度,①当点B在点C的左边时,由题意得:3t+2+t=6,解得:t=1;②当点B在点C的右边时,由题意得:3t﹣2+t=6,解得:t=2.(2)(2+4)÷(3+1)=1.5(秒).答:线段AB与线段CD从开始相遇到完全离开共经过1.5秒长时间.(3)存在关系式BD﹣AP=3PC.设运动时间为t秒,①当t=(4+2)÷(3+1)=1.5时,点B和点C重合,点P在线段AB上,0<PC≤2,且BD=CD=4,PA+3PC=AB+2PC=2+2PC,当PC=1时,BD=AP+3PC,即BD﹣AP=3PC;②当1.5<t<2.5时,点C在点A和点B之间,0<PC<2:当点P在线段BC上时,BD=CD﹣BC=4﹣BC,AP+3PC=AC+4PC=AB﹣BC+4PC=2﹣BC+4PC当PC=0.5时,有BD=AP+3PC,即 BD﹣AP=3PC,③当t=2.5时,点A与点C重合,0<PC≤2,BD=CD﹣AB=2,AP+3PC=4PC,当PC=0.5时,有BD=AP+3PC,即BD﹣AP=3PC,∵P在C点左侧或右侧,∴PD的长有2种可能,即5或3.5.20.【题文】已知线段AB=6cm,点P是线段AB的中点,E是线段AB延长线上的一点,BE=AB,求线段PE的长.【答案】5cm.【分析】根据线段的倍分关系与和差关系求解. 【解答】解:∵点P是线段AB的中点,AB=6cm,∴PB=AB=3cm,∵EB=AB,∴EB=2cm,∴PE=PB+BE=5cm.。
青岛版七年级数学上册相反数练习题

《相反数》同步练习一、随堂检测1、-(+5)表示 的相反数,即-(+5)= ; -(-5)表示 的相反数,即-(-5)= 。
2、-2的相反数是 ;75的相反数是 ; 0的相反数是 。
3、化简下列各数:-(-68)= -(+0.75)=-(-53)= -(+3.8)=+(-3)= +(+6)= 4、下列说法中正确的是( ) A 、正数和负数互为相反数B 、任何一个数的相反数都与它本身不相同C 、任何一个数都有它的相反数D 、数轴上原点两旁的两个点表示的数互为相反数 二、拓展提高1、-(-3)的相反数是 。
2、已知数轴上A 、B 表示的数互为相反数,并且两点间的距离是6,点A 在点B 的左边,则点A 、B 表示的数分别是 。
3、已知a 与b 互为相反数,b 与c 互为相反数,且c=-6,则a= 。
4、一个数a 的相反数是非负数,那么这个数a 与0的大小关系是a 0.5、数轴上A 点表示-3,B 、C 两点表示的数互为相反数,且点B 到点A 的距离是2,则点C 表示的数应该是 。
6、下列结论正确的有( )①任何数都不等于它的相反数;②符号相反的数互为相反数;③表示互为相反数的两个数的点到原点的距离相等;④若有理数a,b 互为相反数,那么a+b=0;⑤若有理数a,b 互为相反数,则它们一定异号。
A 、2个 B 、3个 C 、4个 D 、5个7、如果a=-a ,那么表示a 的点在数轴上的什么位置? 三、体验中考 1、(河南)-5的相反数是( ) A 、51B 、51C 、-5D 、52、(杭州)如果a+b=0,那么a,b 两个有理数一定是( )A 、都等于0B 、一正一负C 、互为相反数D 、互为倒数(原题是“那么两个实数一定是”此处改为“两个有理数是”)参考答案一、随堂检测1、5,-5,-5,5;2、2,75,0; 3、68,-0.75,53,-3.8,-3,6; 4、C 考查相反数的代数意义和几何意义 二、拓展提高 1、-3 2、-3,3 3、-6 4、≥ 5、1或56、A 根据相反数的定义。
青岛版七年级上册数学同步练习附答案2.3相反数与绝对值

2.3 相反数与绝对值一、选择题1. 下面各对数,互为相反数的是( )A. 2与-|-2|B. -2与-|2|C. |-2|与|2|D. 2与-(-2)2. 下列说法正确的是( )A. -|a |一定是负数B. 若|a |=|b |,则a =bC. 若|a |=|b |,则a 与b 互为相反数D. 若一个数小于它的绝对值,则这个数是负数3. 下面说法正确的个数为( )①π的相反数是-3.14;②-(-3.8)的相反数是3.8;③一个数和它的相反数不可能相等;④+(-2 014) 的相反数为-2 014.A. 0B. 1C. 2D. 34. 若一个数的相反数是非负数,则这个数一定是( )A. 正数或0B. 非零的数C. 负数或0D. 05. 如图,数轴上的A ,B ,C 三点所表示的数分别为a ,b ,c ,其中AB=BC ,如果|a|>|c|>|b|,那么该数轴的原点O 的位置应该在( )(第5题图)A.点A 的左侧B. 点A 与点B 之间C. 点B 与点C 之间D. 点C 的右侧 二、填空题6. 数a+b 的相反数是 ,-b 的相反数是 .7. 若a = +3.2,则-a= ;若a=-41,则-a= ;若-a=1,则a= ;若-a=-2,则a= .8. 若|a|=|-3|,则a= .9. 当a 为 时,式子8-|2a-6|有最大值,最大值是 .三、解答题10. 如图,数轴上的点A ,B ,C ,D ,E 分别表示什么数?其中哪些数互为相反数?(第10题图)11.(1)已知x的相反数是-2,且2x+3a=5,求a的值;(2)已知-[-(-a)]=8,求-a的相反数.12. 已知数a,b表示的点在数轴上的位置如图.(第12题图)(1)在数轴上表示出a,b的相反数的位置.(2)若数b与其相反数相距20个单位长度,则b表示的数是多少?(3)在(2)的条件下,若数a与数b的相反数表示的点相距5个单位长度,求a表示的数是多少.13. 北京航天研究院所属工厂,制造“嫦娥三号”上的一种螺母,要求螺母的内径可以有±0.02 mm的误差,抽查5个螺母,超过规定内径的毫米数记作正数,没有超过规定内径的毫米数记作负数,检查结果如下:+0.010,-0.018,+0.006,-0.002,+0.015.(1)指出哪些产品是合乎要求的?(即在误差范围内的)(2)指出合乎要求的产品中哪个质量好一些,哪个质量稍差一些?11. 某工厂为了组装学校的新桌椅,生产了一批配套的螺母. 产品质量的要求是:螺母的内径可以有±0.20 mm的误差. 抽查7只螺母,超过规定内径的毫米数记作正数,不足规定的毫米数记作负数,检测结果如下表:(单位:mm)(1)其中第几号螺母不合格?(2)第几号螺母的尺寸最标准?(3)误差最大的螺母与6号螺母相差多少毫米?答案一、1. A 【解析】因为-|-2| =-2,且2与-2互为相反数,所以A中 2与-|-2|互为相反数.故选A.【知识归纳】化简题中的括号与绝对值:化简或计算时,要按运算顺序进行,如果既有“括号”,又有“绝对值符号”,要注意运算顺序.(1)如果绝对值符号里有括号,应先化简括号,再求绝对值.(2)如果括号里有绝对值符号,可以先求绝对值,再化简括号,也可以先化简括号,再求绝对值.2. D 【解析】当a =0时,-|a |=0,故A 错误;若|a |=|b |,则a =b 或a =-b ,故B ,C 错误.故选D.3. A 【解析】π的相反数是-π(π≠3.14);-(-3.8)=3.8,3.8的相反数是-3.8;0的相反数是0,它们相等;+(-2 014)=-2 014,-2 014的相反数为2 014. 综上所述没有一个是正确的.故选A.4. C 【解析】负数的相反数是正数,0的相反数是0,所以所求的数为负数或0. 故选C.5. C 【解析】因为|a |>|c |>|b |,所以点A 到原点的距离最大,点C 到原点的距离其次,点B 到原点的距离最小. 又因为AB =BC ,所以原点O 的位置在点B 与点C 之间,且靠近点B 的地方.故选C.【一题多解】排除法:若原点在点A 的左侧,则|c |>|b |>|a |,因此排除选项A ;若原点在点A 与点B 之间,则|c |最大,因此排除选项B ;若原点在点B 与点C 之间,则|a |最大,此时,若原点靠近点B ,则|c |>|b |; 若原点在点C 的右侧,则|a |>|b |>|c |,因此排除选项D.故选C.二、6. -(a +b );b 【解析】求一个数的相反数,只要在它的前面加上“-”,然后化简即可.所以,数a +b 的相反数是-(a +b ),-b 的相反数是-(-b )=b .7. -3.2;41;-1;2 8. ±3 9. 3;8 【解析】因为|2a -6|≥0,所以当|2a -6|=0,即2a -6=0,a =3时,式子8-|2a -6|有最大值,最大值是8.【知识归纳】绝对值的两个应用:(1)若|a |+|b |=0,则a =b =0.(2)m -|a |有最大值m ,m +|a |有最小值m .三、10. 解:由数轴上各点到原点的距离的大小可知,各点所表示的数大致为A :-3.8;B :-2.2;C :-0.8;D :0.8;E :2.2.故互为相反数的数有-2.2和2.2;-0.8和0.8两组.11. 解:(1)因为2的相反数是-2,所以x =2.所以2×2+3a =5,所以a =31. (2)-[-(-a )]=8,所以-a =8.因为8的相反数是-8,所以-a 的相反数是-8.12. 解:(1)如答图.(第12题答图)13. 解:(1)其中第2,3号螺母不合格.(2)第5号螺母的尺寸最标准.(3)误差最大的螺母是2号,故|+0.30|+|-0.01|=0.31(mm),即误差最大的螺母与6号螺母相差0.31 mm.。
青岛版2020七年级数学上册期中综合复习基础过关练习题1(附答案详解)

青岛版2020七年级数学上册期中综合复习基础过关练习题1(附答案详解)1.下列各对数中,互为相反数的是( ).A .+(-8)和(-8)B .-(-8)和+8C .-(-8)和+(+8)D .+8和+(-8)2.a 、b 在数轴上的位置如图,则a+b 、a ﹣b 、ab 、b a 中负数是个数有( )个.A .4B .3C .2D .13.某市有一天的最高气温为2℃,最低气温为﹣8℃,则这天的最高气温比最低气温高( )A .10℃ B .6℃ C .﹣6℃ D .﹣10℃4.四种统计图:①条形图;②扇形图;③折线图;④直方图.四个特点:(a )易于比较数据之间的差异;(b )易于显示各组之间的频数的差别;(c )易于显示数据的变化趋势;(d )易于显示每组数据相对于总数的大小.统计图与特点选配方案分别是:①与(a );②与(c );③与(d );④与(b ). 其中选配方案正确的有( )A .1个B .2个C .3个D .4个5.7的相反数是 ( )A .7B .-7C .+7或-7D .0和7 6.下列图形中,棱锥是( )A .B .C .D . 7.运用去括号法则和加法交换律后,8-(-3)+(-5)+(-7)等于( )A .8-3+5-7B .3+8-7-5C .-5-7-3+8D .8+3-5+78.下列运算正确的是 ( )A .52(52)7-+=-+=-B .7229218--⨯=-⨯=-C .54331345÷⨯=÷= D .2(1)1--=- 9.在+2017,﹣3.2,0,227-,π,0.010010001…,﹣49这七个数中,有理数的个数为( )A .4 B .5 C .6 D .710.下列说法错误的是( )A .倒数和它本身相等的数,只有1和1?-B .相反数与本身相等的数只有0C .立方等于它本身的数只有0、1和1-D .绝对值等于本身的数是正数11.下列各式,计算结果为负数的是( )A .-[-(-6)]+6B .-|-5|-(+9)C .-32+(-3)2-(-5)D .[(-1)7+(-3)2]×(-1)412.下列各数中,为负数的是( )A .5.4B .0C .-3D .8%13.下列运算中,正确的是( ).A .2(2)4=--B .224-=C .236=D .3(3)27-=- 14.计算(-16)÷的结果等于A .32B .-32C .8D .-815.计算﹣3+10=( )A .﹣30B .﹣13C .﹣7D .7 16.在2-、0、14-、5这四个数中,最小的数是( ) A .2- B .0 C .14- D .5 17.在(3-),2,()23--,23-,3--,3-,2a 中,正数的个数为( )A .1个B .2个C .3个D .4个18.下列计算结果为负数的是( )A .-5+6B .-8÷(-4)C .2-(-3)D .-2×3 19.为贯彻落实觉中央、国务院关于推进城乡义务教育一体化发展的部署,教育部会同有关部门近五年来共新建、改扩建校舍186000000平方米,其中数据186000000用科学记数法表示是( )A .1.86×107B .186×106C .1.86×108D .0.186×10920.以下问题不适合采用全面调查的是( )A .调查某班学生每周课前预习的时间B .调查某中学在职教师的身体健康状况C .调查某电视节目的收视率D .调查某校篮球队员的身高21.近似数3.14精确到 位。
2019—2020年青岛版七年级上册数学《线段的比较与作法》综合课堂同步练习题及答案.docx

1.4 线段的比较与作法【知能点分类训练】知能点1 线段大小的比较方法1.如图1所示,AB=CD,则AC与BD的大小关系是().A.AC>BD B.AC<BD C.AC=BD D.无法确定(1)(2)2.已知线段AB=7厘米,在直线AB上画线段BC=1厘米,那么线段AC=________.3.如图2所示,已知B,C两点在线段AD上,AC=_____+BC=_____-______,AC+BC-BC=______.4.如果线段AB=13厘米,MA+MB=17厘米,那么下面说法正确的是().A.M点在线段AB上B.M点在直线AB上C.M点在直线AB外D.M点可能在直线AB上,也可能在直线AB外知能点2 线段的中点及等分5.已知点C是线段AB上一点,D是AC的中点,BC=4厘米,DB=7厘米,则AB=______•厘米,AC=_______厘米.6.如图3所示,C和D是线段的三等分点,M是AC的中点,那么CD=______BC,AB=______MC.(3)7.如果点B在线段AC上,那么下列表达式中:①AB=12AC,②AB=BC,③AC=2AB,④AB+BC=AC.能表示B是线段AC的中点的有().A.1个B.2个C.3个D.4个8.如图所示,点C在线段AB上,线段AC=6厘米,BC=4厘米,点M,N分别是AC,•BC的中点.(1)求线段MN的长度.(2)根据(1)的计算过程和结果,设AC+BC=a,其他条件不变,你能猜测出MN的长度吗?请用一句简洁的话表述你发现的规律.知能点3 线段的基本性质(线段公理)9.如图所示,由A到B有(1),(2),(3)三条路线,最短的路线选(1)的理由是(•).A.因为它直B.两点确定一条直线C.两点间距离的定义D.两点之间,线段最短10.如图所示,一条河流经过A,B两地,为缩短河道,现将河流改道,怎样才能使两地之间河道最短?11.如图所示,在△ABC中一定存在下面关系:AB+AC>BC,你能说明原因吗?由此你又能得到什么结论呢?12.如图所示,A,B是两个村庄,若要在河边L上修建一个水泵站往两村输水,问水泵站应修在河边的什么位置,才能使铺设的管道最短,并说明理由.【综合应用提高】13.C是线段AB上的中点,D是线段BC上一点,则下列说法不正确的是().A.CD=AC-BD B.CD=12AB-BDC.CD=AD-BC D.CD=12BC14.如图所示,已知线段AB=80厘米,M为AB的中点,P在MB上,N为PB的中点,且NB=14厘米,求PA的长.15.如图所示,一只昆虫要从正方体的一个顶点A•爬到相距它最远的另一个顶点B,哪条路径最短?说明理由.16.如图所示,已知BC=13AB=14CD,点E,F分别是AB,CD的中点,且EF=60•厘米,•求AB,CD的长.【开放探索创新】17.如图所示,七年级(2)班的孟飞同学在一张透明纸上画了一条长8厘米的线段MN,并在线段MN上任意找了一个不同于M,N的点C,然后用折纸的方法找出了线段MC,NC的中点A,B,并求出了线段AB的长,想一想,孟飞是如何找到线段MC,NC的中点的?又是如何求出线段AB的长度的?【中考真题实战】18.将一张长方形的纸对折,如图可以得到一条折痕,继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到_______条折痕,如果对折n次,可以得到______条折痕.19.已知线段AB ,C 是AB 的中点,D 是BC 的中点,下面等式不正确的是( ).A .CD=AC-DB B .CD=AD-BC C .CD=12AB-BD D .CD=13AB20.如图所示,从A 地到B 地有多条道路,一般地,人们会走中间的直路,而不会走其他的曲折的路线,这是因为( ).A .两点之间线段最短B .两直线相交只有一个交点C .两点确定一条直线D .垂线段最短参考答案:1.C (点拨:∵AB=CD,∴AB+BC=CD+BC,∴AC=BD)2.8厘米或6厘米(点拨:分两种情况:①C在线段AB内,②C在线段AB延长线上)3.AB AD CD AD4.D 5.10 6 6.126 7.C (点拨:①②③)8.解:(1)∵AC=6厘米,BC=4厘米,∴AB=AC+BC=10厘米又∵点M是AC的中点,点N是BC的中点,∴MC=AM=12AC,CN=BN=12BC,∴MN=MC+CN=12AC+12BC=12(AC+BC)=12AB=5厘米.(2)由(1)中已知AB=10厘米,求出MN=5厘米,分析(1)的推算过程可知MN=12AB,故当AB=a时,MN=12a,从而得到发现的规律:线段上任一点把线段分成的两部分的中点间的距离等于原线段长度的一半.9.D10.将A,B两点间的曲线河道改为线段.11.BA+AC与BC可看成由B到C的两条线,一条是折线,即曲线,另一条是直线.根据:两点之间,线段最短.结论:三角形两边之和大于第三边.12.过点A,B作线段AB,与直线L的交点P为所求水泵站的点,因为两点之间,线段最短.13.D (点拨:如图所示:CD=BC-BD=AC-BD=12AB-BD,CD=AD-AC=AD-BC,D•不是BC的中点,∴CD≠12BC,故选D)14.解:∵N 是BP 中点,M 是AB 中点, ∴PB=2NB=2×14=28(厘米), ∵AM=MB=12AB=12×80=40(厘米), ∴MP=MB-PB=40-28=12(厘米),∴PA=AM+MP=40+12=52(厘米).15.如图将正方体展开,根据“两点之间,线段最短”知,线段AB 即为最短路线.16.解:设BC=x 厘米,由题意得 AB=3x ,CD=4x .∵E ,F 分别是AB ,CD 的中点,∴BE=12AB=32x ,CF=12CD=2x ,∴EF=BE+CF-BC=32x+2x-x .即32x+2x-x=60解得x=24∴AB=3x=72(厘米),CD=4x=96(厘米)答:线段AB 长为72厘米,线段CD 长为96厘米.17.解:孟飞同学是将纸对折,使M ,C 重合,N ,C 重合,两个折痕与线段的交点就分别是中点A 和B ;他是根据AB=12MN ,求出AB=4厘米.18.15 2n -1 19.D 20.A.。
青岛版七年级数学上册《5.5 函数的初步认识》同步练习-带参考答案

青岛版七年级数学上册《5.5 函数的初步认识》同步练习-带参考答案一、选择题1.下面说法中正确的是( )A.两个变量间的关系只能用关系式表示B.图象不能直观的表示两个变量间的数量关系C.借助表格可以表示出因变量随自变量的变化情况D.以上说法都不对2.下列各曲线中表示y是x的函数的是( )3.关于变量x,y有如下关系:①x﹣y=5;②y2=2x;③:y=|x|;④y=1x.其中y是x函数的是( )A.①②③B.①②③④C.①③D.①③④4.在下列各图象中,y不是x函数的是( )A. B. C. D.5.若等腰三角形的周长为60 cm,底边长为x cm,一腰长为y cm,则y关于x的函数解析式及自变量x的取值范围是()A.y=60-2x(0<x<60)B.y=60-2x(0<x<30)C.y=12(60-x)(0<x<60) D.y=12(60-x)(0<x<30)6.汽车由北京驶往相距120千米的天津,它的平均速度是30千米/时,则汽车距天津的路程s(千米)与行驶时间t(时)之间的函数关系式及自变量的取值范围是( )A.s =120﹣30t(0≤t ≤4)B.s =30t(0≤t ≤4)C.s =120﹣30t(t>0)D.s =30t(t =4)7.如图,根据流程图中的程序,当输出数值y=5时,输入的数值x 是( )A.17B.-13C.17或-13D.17或-178.百货大楼进了一批花布,出售时要在进价(进货价格)的基础上加一定的利润,其长度x 与售价y 如下表:长度x/m 1 2 3 4 …售价y/元 8+0.3 16+0.6 24+0.9 32+1.2 …下列用长度x 表示售价y 的关系式中,正确的是( )A.y=8x+0.3B.y=(8+0.3)xC.y=8+0.3xD.y=8+0.3+x9.根据如图所示的程序计算函数y 的值,若输入x 的值是2时,则输出的y 的值是6,若输入x 的值是3,则输出的y 的值是( )A.6B.7C.8D.910.小亮家与姥姥家相距24 km ,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一平面直角坐标系中,小亮和妈妈的行进路程S(km)与时间t(h)的函数图象如图所示.根据图象得到下列结论,其中错误的是( )A.小亮骑自行车的平均速度是12 km/hB.妈妈比小亮提前0.5 h到达姥姥家C.妈妈在离家12 km处追上小亮D.9:30妈妈追上小亮二、填空题11.一个小球由静止开始沿一个斜坡向下滚动,通过仪器观察得到小球滚动的距离s(m)与时间t(s)的数据如下表:时间t(s) 1 2 3 4 …距离s(m) 2 8 18 32 …写出用t表示s的关系式:________.12.长方形的周长为24cm,其中一边为x(其中x>0),面积为ycm,则这样的长方形中y与x的关系可以写为 .13.如图所示的计算程序中,y与x之间的函数表达式为 .14.烧一壶水,假设冷水的水温为20℃,烧水时每分钟可使水温提高8℃,烧了x分钟后水壶的水温为y℃,当水开时就不再烧了.(1)y与x的关系式为________,其中自变量是________,它应在________变化.(2)x=1时,y=________,x=5时,y=________.(3)x=________时,y=48.15.已知y是x的一次函数,下表列出了部分对应值,则m=.x 1 0 2y 3 m 516.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数关系是y=95x+32,如果某一温度的摄氏度数是25℃,那么它的华氏度数是℉.三、解答题17.某剧院的观众席的座位为扇形,且按下列方式设置:排数(x) 1 2 3 4 …50 53 56 59 …座位数(y)(1)按照上表所示的规律,当x每增加1时,y如何变化?(2)写出座位数y与排数x之间函数的表达式.(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.18.为了增强居民的节水意识,某城区水价执行“阶梯式”计费,每月应缴水费y(元)与用水量x(t)之间的函数关系如图所示.若某用户去年5月缴水费18.05元,求该用户当月用水量.19.某超市为了方便顾客,将某品牌的瓜子散装出售时套上了包装袋,其质量x(千克)与售价y(元)之间的关系如下表所示(售价中的0.20元是包装袋的费用),观察表中y与x之间的关系:x 1 2 3 4 …y 6.0+0.20 12.0+0.20 18.0+0.20 24.0+0.20 …(2)写出售价y与数量x之间的关系式.(3)小王想用100元买15千克这种瓜子,请帮他算算钱够用吗?20.一根合金棒在不同的温度下,其长度也不同,合金棒的长度和温度之间有如下关系:温度℃…﹣5 0 5 10 15 …长度cm …9.995 10 10.005 10.01 10.015 …(1)上表反映了温度与长度两个变量之间的关系,其中_______是自变量,_______是函数.(2)当温度是10℃时,合金棒的长度是_______cm.(3)如果合金棒的长度大于10.05cm小于10.15cm,根据表中的数据推测,此时的温度应在______℃~_______℃的范围内.(4)假设温度为x℃时,合金棒的长度为ycm,根据表中数据写出y与x之间的关系式________.(5)当温度为﹣20℃或100℃,合金棒的长度分别为______cm或______cm.21.我们知道,海拔高度每上升1千米,温度下降6 ℃.某时刻,益阳地面温度为20 ℃,设高出地面x千米处的温度为y ℃.(1)写出y与x之间的函数关系式.(2)已知碧云峰高出地面约500米,求这时山顶的温度大约是多少度?(3)此刻,有一架飞机飞过上空,若机舱内仪表显示飞机外面的温度为﹣34 ℃,求飞机离地面的高度为多少千米?22.周末,小明和弟弟从家出发,步行去吉林省图书馆学习.出发2分钟后,小明发现弟弟的数学书忘记带了,弟弟继续按原速前往图书馆,小明按原路原速返回家取书,然后骑自行前往图书馆,恰好与弟弟同时到达图书馆.小明和弟弟各自距家的路程y(m)与小明步行的时间x(min)之间的函数图象如图所示.(1)求a的值.(2)求小明取回书后y与x的函数关系式.(3)直接写出小明取回书后与弟弟相距100m的时间.答案1.C2.D.3.D4.C5.D6.A.7.C8.B9.B.10.D.11.答案为:s=2t2(t≥0)12.答案为:y=(12﹣x)x13.答案为:y=-2x+414.答案为:(1)y=8x+20 x 在0﹣﹣10变化;(2)28 60;(3)3.515.答案为:1.16.答案为:7717.解:(1)由图表中数据可得,当x每增加1时,y增加3.(2)由题意,得y=50+3(x-1)=3x+47.(3)某一排不可能有90个座位.理由如下:令y=90,得3x+47=90,解得x=43 3.∵x为整数∴某一排不可能有90个座位.18.解:由图可知,当用水量在0~8 t时每吨水的价格为15.2÷8=1.9(元);当用水量超过8 t时超过8 t部分每吨水的价格为(23.75-15.2)÷(11-8)=2.85(元). ∴该用户当月用水量为(18.05-15.2)÷2.85+8=9(t).19.解:(1)表格中反映了瓜子质量与售价之间的关系.(2)y=6x+0.20.(3)当x=15时,y=6×15+0.20=90.20(元).∵90.20<100∴他的钱够用.20.解:(1)温度;长度(2)10.01(3)50;150(4)y=0.001x+10(5)9.98;10.121.解:(1)y=20﹣6x(x>0).(2)500米=0.5千米,y=20﹣6×0.5=17(℃).答:这时山顶的温度大约为17 ℃.(3)﹣34=20﹣6x,x=9.答:飞机离地面高度为9千米.22.解:(1) a=200÷2×8=800(2)设小明取回书后y与x的函数关系式是y=kx+b.由题意,得k=200,b=-800.∴小明取回书后y与x的函数关系式是y=200x﹣800.(3)由题意100x﹣(200x﹣800)=100,解得x=7∴7min后小明与弟弟相距100m.。
七年级数学上册《第五章 生活中的常量与变量》同步练习题及答案(青岛版)

七年级数学上册《第五章生活中的常量与变量》同步练习题及答案(青岛版)学校:___________班级:___________姓名:___________考号:___________一、选择题1.某人要在规定时间内加工100个零件,则工作效率y与时间t之间的关系中,下列说法正确的是( )A.y,t和100都是变量B.100和y都是常量C.y和t是变量D.100和t都是常量2.在圆的周长C=2πr中,常量与变量分别是( )A.2是常量,C、π、r是变量B.2是常量,C、r是变量C.C、2是常量,r是变量D.D.2是常量,C、r是变量3.人的身高h随时间t的变化而变化,那么下列说法正确的是( )A.h,t都是不变量B.t是自变量,h是因变量C.h,t都是自变量D.h是自变量,t是因变量①a是常量时,y是变量;②a是变量时,y是常量;③a是变量时,y也是变量;④a,y可以都是常量或都是变量.上述判断中,正确的有( )A.1个B.2个C.3个D.4个5.下表是某报纸公布的世界人口数情况:年份1957 1974 1987 1999 2010人口数30亿40亿50亿60亿70亿上表中的变量是( )A.仅有一个,是年份B.仅有一个,是人口数C.有两个变量,一个是人口数,另一个是年份D.一个变量也没有6.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:下列说法不正确的是( )A.x与y都是变量,且x是自变量,y是因变量B.弹簧不挂重物时的长度为0cmC.物体质量每增加1kg,弹簧长度y增加0.5cmD.所挂物体质量为7kg时,弹簧长度为13.5cm7.某物体一天中的温度是时间t的函数:T(t)=t3-3t+60,时间单位是小时,温度单位为℃,t=0表示12:00,其后t的取值为正,则上午8时的温度为( )A.8℃B.112℃C.58℃D.18℃8.笔记本每本a元,买3本笔记本共支出y元,在这个问题中:①a是常量时,y是变量;②a 是变量时,y是常量;③a是变量时,y也是变量;④a,y可以都是常量或都是变量.上述判断中,正确的有( )A.1个B.2个C.3个D.4个二、填空题9.某种报纸的价格是每份0.4元,买x份报纸的总价为y元,填写下表.份数/份 1 2 3 4 …价钱/元…在这个问题中, 是常量;是变量.10.圆柱的高是6cm,当圆柱的底面半径r由小到大变化时,圆柱的体积V也随之发生变化.在这个变化过程中,自变量是_____,因变量是_____.11.在关系式V=30-2t中,V随着t的变化而变化,其中自变量是_____,因变量是_____,当t=_____时,V=0.12.在关系式V=30-2t中,V随着t的变化而变化,其中自变量是________,因变量是________,当t=________时,V=0.13.声音在空气中传播的速度y(m/s)(简称声速)与气温x(℃)的关系如下表所示.气温x/℃0 5 10 15 20声速y/(m/s) 331 334 337 340 343上表中是自变量, 是因变量.照此规律可以发现,当气温x为℃时,声速y达到346 m/s.14.如图,一个四棱柱的底面是一个边长为10 cm的正方形.当它的高变化时,体积也随着变化.(1)若高为h(cm),体积v(cm3),则v与h之间的关系式为 .(2)变量是;常量是 .三、解答题15.已知高度每增加1000米,气温下降6℃,如果某地面气温为22℃(1)分别计算出该地1000米、2000米高空的气温.(2)若h米高空的气温为T,试写出T与h的关系,并指出关系式中的常量和变量.16.一种树苗的高度用h表示,树苗生长的年数用a表示,测得有关数据如下表:(树苗原高100 cm)年数a 高度h/cm1 100+52 100+103 100+154 100+20……(1)试用年数a的代数式表示h;(2)此树苗需多少年就可长到200 cm高?17.一种手机卡的缴费方式为:每月必须缴纳月租费20元,另外每通话1 min要缴费0.2元.(1)如果每月通话时间为x(min),每月缴费y(元),请用含x的代数式表示y.(2)在这个问题中,哪些是常量?哪些是变量?(3)当一个月通话时间为200 min时,应缴费多少元?(4)当某月缴费56元时,此人该月通话时间为多少分钟?18.地壳的厚度约为8到40km,在地表以下不太深的地方,温度可按y=3.5x+t算,其中x是深度,t是地球表面温度,y是所达深度的温度.(1)在这个变化过程中,自变量和因变量分别是什么?(2)如果地表温度为2℃,计算当x为5km时地壳的温度.19.在烧水时,水温达到100 ℃就会沸腾,下表是某同学做“观察水的沸腾”试验时记录的数据: 时间/min 0 2 4 6 8 10 12 14 …温度/℃30 44 58 72 86 100 100 100 …(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)水的温度是如何随着时间的变化而变化的?(3)时间每推移2 min,水的温度如何变化?(4)时间为8 min时,水的温度为多少?你能得出时间为9 min时水的温度吗?(5)根据表格,你认为时间为16 min和18 min时水的温度分别为多少?(6)为了节约能源,你认为应在什么时间停止烧水?20.父亲告诉小明:“距离地面越高,气温越低.”并给小明出示了下面的表格:距离地面高度/km 0 1 2 3 4 5气温/℃20 14 8 2 -4 -10根据上表,父亲还给小明出了下面几个问题,你和小明一起回答.(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?(3)你知道距离地面6 km的高空气温是多少吗?答案1.C2.B3.B4.B5.C6.B7.A8.B9.答案为:0.4;0.8;1.2;1.6;0.4;x,y10.答案为:自变量是:r,因变量是:V.11.答案为:t,V,15.12.答案为:t,V,15.13.答案为:气温;声速;25.14.答案为:v=100h;四棱柱的高、体积,四棱柱的底面边长.15.解:∵离地面距离每升高1 km,气温下降6℃∴该地空中气温T(℃)与高度h(km)之间的函数表达式为:T=22﹣6h;(1)把h=1km代入T=22﹣6h=16把h=2km代入T=22﹣6h=22﹣12=10答:该地1000米、2000米高空的气温分别为16℃、10℃;(2)T=22﹣6h,其中22,6是常量,T,h是变量.16.解:(1)由表可知h=100+5a.(2)当h=200 cm时,有200=100+5a,解得a=20.答:此树苗需20年就可长到200 cm高.17.解:(1)每月缴费y(元)与通话时间x(min)的关系式为y=15x+20.(2)在这个问题中,月租费20元和每分钟通话费15元是常量,每月通话时间x(min)与每月缴费y(元)是变量.(3)当x=200时,y=15×200+20=60(元).因此当一个月通话时间为200 min时,应缴费60元.(4)当y=56时,15x+20=56,解得x=180.因此当某月缴费为56元时,此人该月通话时间为180 min.18.解:(1)x,t;y;(2)19.5.19.解:(1)上表反映了水的温度与时间的关系,时间是自变量,水的温度是因变量.(2)水的温度随着时间的增加而增加,到100 ℃时恒定.(3)时间每推移2 min,水的温度增加14 ℃,到10 min时恒定.(4)时间为8 min时,水的温度是86 ℃,时间为9 min时,水的温度是93 ℃.(5)根据表格,时间为16 min和18 min时水的温度均为100 ℃.(6)为了节约能源,应在第10 min后停止烧水.20.解:(1)反映了距离地面高度与气温之间的关系.距离地面高度是自变量,气温是因变量.(2)随着h的升高,t逐渐降低.(3)观察表格,可得距离地面高度每上升1 km,气温下降6 ℃.当距离地面5 km时,气温为-10 ℃,故当距离地面6 km时,气温为-16 ℃.。
