水力学.恒定总流动量方程.
水力学恒定总流的动量方程

5.7 恒定总流的动量方程
对复杂的水流运动分析,特别是涉及分析水流和其固 体边界之间的作用力问题,应用动量方程进行分析和 计算更简便,直接.
如:求动水总压力,求水流作用于管道弯头上的动 水压力及射流冲击力等.
5.7 恒定总流的动量方程
一、恒定总流动量方程的推导
推导的原理: 动量定律
5.7 恒定总流的动量方程
一、恒定总流动量方程的推导
元流的动量: ρu1∆tdA1u1
所 以:
M11 A1 u1tdA1 u1 t A1 u1u1dA1 t Q u1dQ
用断面平均流速v代u,所产
生的误差用动量修正系数
α'修正.
于是
5.7 恒定总流的动量方程
一、恒定总流动量方程的推导
A1 1 1 1
(如c):作求1用动于水脱总离压体力内,求水水体流上作的用重于力管. 道弯头上的动水压力及射流冲击力等.
Qtv Qtv v v A 为动2解计量:恒算 定 因定方律弯总便:管流,单水动将位平量动时放方量间置程方内,的程物故1应写体此用成动弯三量管坐的液标变体轴化所上等受的于重投作力影1用在式于平该面物内体投上影的分1所量1有等外于1力零的,总沿和管轴线取基准面,则:
动量方程的应用条件及注意事项: 动量方程的应用条件与能量方程的应用条件相同: (1)必须是恒定流,且为不可压缩的均质流体.
(2)作用于流体上的质量力只有重力,所研究的流 体边界是静止的.
(3)所取的两个过流断面必须是均匀流断面或渐 变流断面,但两个断面之间可以不是渐变流. (4)一般地,所取两个断面间没有流量的汇入和分 出;也无能量的输入和输出.
(c5)作动用量于方脱程离只体能内求水解体一上个的未重知力数.,两个以上时,要与连续性方程以及能量方程联合求解.
水力学__主要知识点

第3章 流态与水头损失
水头损失以及与水头损失有关的液体的流态。
(一)水头损失的计算方法
1.总水头损失: hw= ∑hf + ∑hj 沿程水头损失:
通过尼古拉兹实验研究发现紊流三个流区内的沿程水力摩擦系数
的变化规律。
5. λ的变化规律 尼古拉兹实验 (人工粗糙管)
层流区: λ=f1(Re)=
64 Re
光滑区:λ= f2 (Re) 紊流粗糙区紊也称流为区紊:流粗过阻糙渡力区区平::方λλ==区,ff34沿((Rr0程e), 水r0 力) 摩擦系数λ与雷诺数无关,
忽略不计
j
hf
l d
2
2g
H
Q2 K2
l
K Ac R — 流量模数
1
l d
(5)水头线绘制 注意事项: (1)局部水头损失集中在一个断面; (2)管中流速不变,总水头线平行于测压管水头线; (3)总水头线总是下降,而测压管水头线可升可降; (4)当测压管水头线在管轴线(位置水头线)以下,表示该处存在负压; (5)注意出口的流速水头(自由出流)或局部损失(淹没出流)。
1.连续介质:液体是由液体质点组成的连续体,可以用连续函数描述
液体运动的物理量.
2.理想液体:忽略粘滞性、可压缩性的液体
(三)作用在液体上的两类作用力
第1章水静力学
水静力学包括静水压强和静水总压力两部分内容。通过静水压强和静水
总压力的计算,可以求作用在建筑物上的静水荷载。
水力学部分章节知识点

绪论1、密度是指单位体积液体所含有的质量 量纲为[M/L3],单位为kg/m32、容重是指单位体积液体所含有的重量 量纲为[F/L3],单位为N/m3一般取ρ水=1000 kg/m3,γ水=9800N/m3=9.8kN/m3第一章 水静力学1、静水压强的特性:①静水压强垂直指向受压面②作用于同一点上各方向的 静水压强的大小相等2、3、绝对压强——以设想没有大气存在的绝对真空状态作为零点计量的压强,用p ′表示(绝对压强恒为正值)相对压强——以当地大气压作为零点计量的压强,用p 表示。
(相对压强可正可负) 4、真空——当液体中某点的绝对压强小于当地大气压强pa , 即其相对压强为负值时,称为水力意义上的“真空”真空值(或真空压强)——指绝对压强小于大气压强的数值,用pk 来表示 5、压强的单位:1个工程大气压=98kN/㎡ =10m 水柱压=735mm 水银柱压6、压强的测量①测压管②U 形水银测压计③差压计7、静水压强分布图的绘制规则:1.按一定比例,用线段长度代表该点静水压强的大小 2.用箭头表示静水压强的方向,并与作用面垂直 8、平面的静水总压力的计算 ①图解法②解析法9、作用于曲面上的静水总压力(投影) 第二章 液体运动的流束理论1、迹线——某液体质点在运动过程中,不同时刻所流经的空间点所连成的线。
流线——是指某一瞬时,在流场中绘出的一条光滑曲线,其上所有各点的速度向量都与该曲线相切。
/流管——由流线构成的一个封闭的管状曲面 微小流束——充满以流管为边界的一束液流总流——在一定边界内具有一定大小尺寸的实际流动的水流,它是由无数多个微小流束组成2、水流的分类(1)按运动要素是否随时间变化①恒定流——运动要素不随时间变化②非恒定流——运动要素随时间变化(2)按同一流线上各质点的流速矢是否沿流程变化①均匀流——同一流线上流速矢沿流程不发生变化②非均匀流 a 、渐变流b 、急变流 3、均匀流的重要特性(1)过水断面为平面,且过水断面的形状和尺寸沿程不变(2) 同一流线上不同点的流速应相等,从而各过水断面上的流速分布相同,断面平均流速相等(3) 均匀流(包括非均匀的渐变流)过水断面上的动水压强分布规律与静水压强分布规律p z C gρ+=0p p ghρ=+相同,即在同一过水断面上各点的测压管水头为一常数推论:均匀流(包括非均匀的渐变流)过水断面上动水总压力的计算方法与静水总压力的计算方法相同。
恒定总流的动量方程

恒定总流的动量方程利用前面介绍的连续性方程和能量方程,已经能够解决许多实际水力学问题,但对于某些较复杂的水流运动问题,尤其是涉及到计算水流与固体边界间的相互作用力问题,如水流作用于闸门的动水总压力,以及水流经过弯管时,对管壁产生的作用力等计算问题,用连续性方程和能量方程则无法求解,而必须建立动量方程来解决这些问题。
动量方程实际上就是物理学中的动量定理在水力学中的具体体现,它反映了水流运动时动量变化与作用力间的相互关系,其特点是可避开计算急变流范围内水头损失这一复杂的问题,使急变流中的水流与边界面之间的相互作用力问题较方便地得以解决。
一、动量方程式的推导及适用条件(一)动量方程式的推导由物理学可知,物体的质量m 与速度υ的乘积称为物体的动量。
动量是矢量,其方向与流速方向相同。
物体在外力作用下,速度会发生改变,同时动量也随之变化。
动量定理可表述为:运动物体单位时间内动量的变化等于物体所受外力的合力。
现将动量定理用于恒定流中,推导恒定流的动量方程。
图3-29在不可压缩的恒定流中,任取一渐变流微小流束段1—2(图3-29)。
设1—1断面和2—2断面的过水断面面积和流速分别为21、dA dA 和1u 、2u ,经过dt 时段后,微小流束由原来的1—2位置运动到了新的位置21'-'处,从而发生了变化。
设其动量的变化为dk ,它应等于流段21'-'与流段1—2内的动量之差。
因为水流为不可压缩的恒定流,所以对于公共部分21-'段来讲,虽存在着质点的流动的替换现象,但它的形状、位置以衣液体的质量、流速等均不随时间发生变化,故动量也不随时间发生改变。
这样,在dt 时段内,21'-'段的水流动量与1—2段的动量之差实际上即为22'-段的动量与11'-段的动量之差。
在dt 时段内,通过11'-段的水体质量为11dtdA u ρ,通过22'-段的水体质量为22dtdA u ρ,对于不可压缩液体,根据连续性方程,可知dQdt dtdA u dtdA u ρρρ==2211,则微小流束段的动量变化为)(12u u dQdt k d -=ρ设总流两个过水断面的面积分别为21A A 与,将上述微小流束的动量变化k d 沿相应的总流过水断面进行积分,即可得到总流在dt 时段内动量的变化量为)()()(121112221212a dA u u dA u u dt u dQdt u dQdt u u dQdt k d A A QQ Q ⎰⎰⎰∑⎰⎰-=-=-=ρρρρ 由于实际液体过水断面上的流速分布均匀,且不易求得,故考虑用断面平均流速υ来代替断面上不均匀分布的流速u ,以便计算总流的动量。
水力学第二章思考题答案

2.1.恒定流:如果在流场中任何空间点上所有的运动要素都不随时间而改变。
非恒定流:如果在流场中任何空间点上有任何一个运动要素是随时间而变化。
均匀流:水流的流线为相互平行的直线。
非均匀流:水流的流线不是相互平行的直线。
渐变流:水流的流线虽然不是相互平行的直线,但几乎近于平行的直线。
急变流:水流的流线之间夹角很大或者流线的曲率半径很小。
按运动要素是否彼此平行的直线分为均匀流和非均匀流,而非均匀流按流线的不平行和弯曲程度又分为渐变流和急变流。
渐变流重要性质为:过水断面上近似服从静压分布:Z+P/y=C2.2.此时的A₁υ₁=A₂υ₂符合连续方程。
两个断面无支流,且上游水位恒定,则下游通过的流量一定,则流量保持平衡,满足该公式。
2.3能量方程:Ζ₁+Ρ₁/ρg+α₁(μ₁)²/2g=Ζ₂+Ρ₂/ρg+α₂(μ₂)²/2g+hw’。
Ζ₁:位置水头;Ρ₁/ρg:压强水头;(μ₁)²/2g:流速水头;Ζ₂:单位位能;Ρ₂/ρg:单位压能;(μ₂)²/2g:单位动能;hw’:水头损失。
能量意义:在总流中任意选取两个过水断面,该两断面上液流所具有的总水头若为H₁和H₂,则:H₁=H₂+hw。
2.4这些说法都不对。
对于理想液体来说,在无支流进去的情况下,其各断面的流量总和是相等的,根据能量方程:Ζ₁+Ρ₁/ρg+α₁(μ₁)²/2g=Ζ₂+Ρ₂/ρg+α₂(μ₂)²/2g+hw’,及连续方程:A₁υ₁=A₂υ₂。
可以看出:只要其流量不改变,能量的总和就不会变。
则水是由流速大地方向流速小的地方流这种说法就是错误的。
总流的动量方程:ΣF=ρQ(Β₂υ₂-Β₁υ₁),也说明了这一点。
2.5总水头线:把各断面H=Ζ+Ρ/ρg+α(μ)²/2g描出的点子连接起来得到的线就是总水头线;测压管水头线:把各断面的(Ζ+Ρ/ρg)值的点子连接起来得到的线就是测压管水头线。
水力学实验报告(动量方程验证实验)
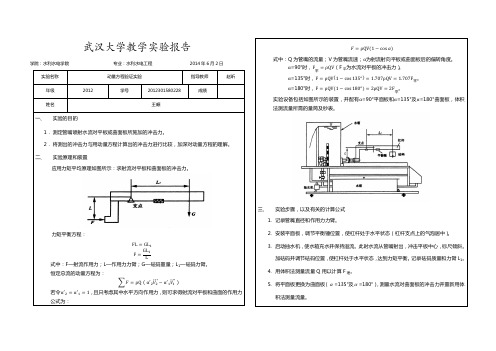
������ = ρQV(1 − cos ������)
式中:Q 为管嘴的流量;V 为管嘴流速;α为射流射向平板或曲面板后的偏转角度。 α=90°时,F平 = ρQV(F 平为水流对平板的冲击力)。 α=135°时,F = ρQV(1 − cos 135°) = 1.707ρQV = 1.707F 。
6. 关闭抽水机,将水箱中水排空,砝码从杠杆上取下,结束实验。 注意事项 1. 量测流量后,量筒内的水必须倒进接水器,以保证水箱循环水充足。 2. 测流量时,计时与量筒接水一定要同步进行,以减小流量的量测误差。 3. 测流量一般测两次取平均值,以消除误差。
四、 实测的数据(表)
1. 有关常数
喷管直径 d=0.92cm,作用力力臂 L=8cm。
2. 实验中,平衡锤产生的力矩没有加以考虑,为什么? 答:平衡锤在冲击开始前将杠杆平衡,用以平衡更换面板产生的作用力差异,在实验过 程中,可以视为是杠杆的一部分,不影响计算结果。
教
师
评
指导教师
年
月
日
语
稳,对流量法测验产生影响。 此外,由于实验时间长,水轮机工作状况发生改变;修正系数误差忽略等问题均会产生较小 误差。 七、 回答实验指导书中有关问题 1. F 实与 F 理有差异,除实验误差外还有什么原因?
答:理论误差(系统误差)。 实验数据处理时的参数,修正系数等忽略因素都是造成二者差异的非实验因素。
6 710 5.20 136.54
六、 对实验结果的分析与结论 实验测得α = 90°时,F 实=30625.00 N×10-5,F 理=30511.71 N×10-5,误差为 0.37% 实验测得α = 135°时,F 实=59718.75 N×10-5,F 理=54067.45 N×10-5,误差为 10.45% 实验测得α = 180°时,F 实=63700.00 N×10-5,F 理=55991.30 N×10-5,误差为 13.76% 实验测得在α = 90°时,理论值与实际值吻合较好,但在α = 135°和α = 180°时,偏差比较 大。 下面就实验过程进行误差分析。测量中误差产生原因有很多,主要有以下几种: (1) 实验时,杠杆是否水平。 尝试将实验数据中的 10.4cm 改变 0.2cm,算得与原数据计算的误差差别为 2%,故 杠杆读数是一个主要影响因素。 在实验中,主要面临两大问题影响杠杆平衡 ① 冲击引起的平衡困难。在无水流冲击时,平衡杠杆比较简单,但是在水流冲击下, 杠杆的平衡很难把握,且由于杠杆的颤动,引起砝码摆动,更加大了平衡难度, 使得平衡时容易出现微小误差;当使用α = 180°的曲面板时,杠杆颤动非常严重, 几乎难以确定平衡状态。 ② 平衡时的砝码和平衡锤的移位。由于平衡锤和砝码公用同一轨道,在移动砝码时, 极易引起平衡锤的微微移动,经由杠杆作用误差放大;另一方面,由于杠杆的颤 动,在平衡锤固定不牢固的区域,会引起其移动。 (2) 体积法测流量产生的误差。 由于此法测量时,需要测量者丰富的经验和敏捷的反应力,对于初学者易产生较大误 差。另一方面,由于在α = 180°时,曲面板在水流冲击下不断摆动,引起水流的不平
动量方程

8.动量方程应用注意事项:
(1) 作好“三步”:
(a)控制体的选取:--总流 一般选取总流边界为控制体边界, 横向边界一般取过水断面;
9.动量方程的应用
•求解固体边界的水流作用力 •求解射流冲击力
•求解水跃
恒定总流动量方程式应用举例
一、弯管内水流对管壁的作用力
弯管中水流为急变流,动水压强分布规律和静水 压强不同,因此不能用静水压力的计算方法来计算弯 管中液体对管壁的作用力。
取如图所示控制体,作用 于控制体上的力包括两端 断面上的 动水压力,还有 管壁对水流的反作用力。
Fp1 -Fp2cos α + R x =ρ Q (v2cosα -v1)
α R x= α -v1) -Fp1+Fp2 cos ρ Q (v 2cos
= -1983 N(方向与图示相反)
y方向的动量方程:
-F p2sin α + R y=ρ Q (v 2 sinα -0)
R y =ρ Q v 2 sinα +Fp2sinα
(b)绘计算简图:正确标示流速和作 用在水体上的力,注意各流速和 力矢量的投影方向及其正负号; (c)动量方程是矢量方程,建立坐标 系; (2)流出动量减去流入动量,未知力 的方向可以假设;
(3)∑F包括作用在控制体上的全部
外力,不能遗漏,也不能多选。当 未知力的方向不能事先确定时,可
以先假设其方向进行求解。如果求
水轮机: -HP= Pg/(γ Q ηg) (出力)
小 结:
水力学实验报告思考题答案

水力学实验报告实验一流体静力学实验实验二不可压缩流体恒定流能量方程(伯诺利方程)实验实验三不可压缩流体恒定流动量定律实验实验四毕托管测速实验实验五雷诺实验实验六文丘里流量计实验实验七沿程水头损失实验实验八局部阻力实验实验一流体静力学实验实验原理在重力作用下不可压缩流体静力学基本方程或 (1.1) 式中:z被测点在基准面的相对位置高度;p被测点的静水压强,用相对压强表示,以下同;p0水箱中液面的表面压强;γ液体容重;h被测点的液体深度。
另对装有水油(图1.2及图1.3)U型测管,应用等压面可得油的比重S0有下列关系:(1.2)据此可用仪器(不用另外尺)直接测得S0。
实验分析与讨论1.同一静止液体内的测管水头线是根什么线?测压管水头指,即静水力学实验仪显示的测管液面至基准面的垂直高度。
测压管水头线指测压管液面的连线。
实验直接观察可知,同一静止液面的测压管水头线是一根水平线。
2.当P B<0时,试根据记录数据,确定水箱内的真空区域。
,相应容器的真空区域包括以下三部分:(1)过测压管2液面作一水平面,由等压面原理知,相对测压管2及水箱内的水体而言,该水平面为等压面,均为大气压强,故该平面以上由密封的水、气所占的空间区域,均为真空区域。
(2)同理,过箱顶小水杯的液面作一水平面,测压管4中,该平面以上的水体亦为真空区域。
(3)在测压管5中,自水面向下深度某一段水柱亦为真空区。
这段高度与测压管2液面低于水箱液面的高度相等,亦与测压管4液面高于小水杯液面高度相等。
3.若再备一根直尺,试采用另外最简便的方法测定γ0。
最简单的方法,是用直尺分别测量水箱内通大气情况下,管5油水界面至水面和油水界面至油面的垂直高度h和h0,由式,从而求得γ0。
4.如测压管太细,对测压管液面的读数将有何影响?设被测液体为水,测压管太细,测压管液面因毛细现象而升高,造成测量误差,毛细高度由下式计算式中,为表面张力系数;为液体的容量;d为测压管的内径;h为毛细升高。
水力学 主要知识点

Px
第2章 液体运动的流束理论 1. 流线的特点:反映液体运动趋势的图线
流线的特征:流线不能相交;恒定流流线形状位置不变;恒定流 迹 线和流线重合。
2 .流动的分类:
液
非恒定流 均匀流
流 恒定流
非均匀流 渐变流
急变流 在均匀流和渐变流过水断面上,压强分布满足: z p c
hf
l 2
d 2g
达西公式
圆管
hf
l 2
4R 2g
λ—沿程水头损失系数
R—水力半径 R A 圆管 R d
局部水头损失
4
ζ—局部水头损失系数
hj
V2 2g
从沿程水头损失的达西公式可以知道,要计算沿程水头损失,
关键在于确定沿程水头损失系数λ。而λ值的确定与水流的
流态和边界的粗糙程度密切相关。
图解法:大小:P=Ωb, Ω--静水压强分布图面积
方向:垂直并指向受压平面 作用线:过压强分布图的形心,作用点位于对称轴上。
静水压强分布图是根据静水压强与水深成正比关系绘制的,只要用比例 线段分别画出平面上两点的静水压强,把它们端点联系起来,就是静水 压强分布图 解析法:大小:P=pcA, pc—形心处压强
g (二)液体运动基本方程
1.恒定总流连续方程
v 1A1= v 2A2
,
v2 A1 v1 A2
Q=vA
利用连续方程,已知流量可以求断面平均流速,或者通过两断面间
的几何关系求断面平均流速。
2.恒定总流能量方程
z1
p1g 1v12来自2gz2
p2
g
2v22
2g
hw
hw
水力学1(12)

R ′y = p 2 A 2 sinα − ρQv 2 sinα
Q= 1 1 2 πd1v 1 = × 3.14 × 0.25 2 × 2.45 = 0.12m 3 /s 4 4
π 2 3.14 d1 = 1.8 × 98 × × 0.25 2 = 8.65kN 4 4
A
代入
v v v v v dK = ∫ ρdt(u2 − u1 )dQ = ρdt( ∫ u2u2dA 2 − ∫ u1u1dA1 ) ∑
Q A2 A1
式得
v v v ∑ dK = ρdt(β2v 2v 2 A2 − β1v 1v 1A1)
由 于
v 1A1 = v 2 A 2 = Q 则
v v v ∑ dK = ρQdt(β2v 2 − β1v 1)
式中
p1A 1 = p1
v2 =
0.25 2 A1 d v 1 = ( 1 )2 v 1 = ( ) × 2.45 = 3.83m/s A2 d2 0.2
11
不计水流阻力时,以通过管轴的水平面为基准面,建立1 不计水流阻力时,以通过管轴的水平面为基准面,建立1-1和2-2 断面能量方程得
2 2 p1 v 1 p2 v 2 + = + ρg 2g ρg 2g
第十二讲
第六节
恒定流动量方程
液体恒定流动量方程是物体动量守恒原理在液体运动中的具体表 现,它反映了液体的动量变化与液体和固体边界间作用力的关系。 它反映了液体的动量变化与液体和固体边界间作用力的关系。 一、恒定流动量方程 物理学中的质点系动量定理可表述为: 物理学中的质点系动量定理可表述为:单位时间内质点系动量 的变化量
3第三章 水动力学基础

液体运动时的加速度:
du x u x u x dx u x dy u x dz dt t x dt y dt z dt
du x u x u u u ux x u y x uz x dt t x y z 同理可得 du y u y u y u y u y ux uy uz dt t x y z du z u z u u u ux z u y z uz z dt t x y z 即
1 A1 2 A2
Q1 Q2 总流连续性方程适用于连续的不可压缩液体作恒定流的
情况,对理想液体和实际液体的各种流动状态都适用。
第三节
一、理想液体 元流能量方程:
若令 上式即
恒定流元流能量方程
2 u12 p2 u 2 z1 z2 2g 2g
p1
u2 H z 2g p
均匀流具有下列特征:
1)过水断面为平面,且形状和大小沿程不变; 2)同一条流线上各点的流速相同,因此各过水断面上 平均流速 v 相等; 3)同一过水断面上各点的测压管水头为常数(即动水 压强分布与静水压强分布规律相同,具有z p C
的关
系),即在同一过水断面上各点测压管水头为一常数。 3.有压流与无压流(根据过水断面上的周线是否有自由 表面分类)
在管道均匀流中,同一断面上各测压管水面必上升至同一高 度,但不同断面上测压管水面所上升的高程是不相同的。
流动的恒定、非恒定是相对时间而言,均匀、
非均匀是相对空间而言;
恒定流可是均匀流,也可以是非均匀流,
非恒定流也是如此,但是明渠非恒定均匀流是不
可能存在的(为什么?)。
水力学常用知识讲解(笔记)

⽔⼒学常⽤知识讲解(笔记)《⽔⼒学》学习指南第⼀章绪论(⼀)液体的主要物理性质1.惯性与重⼒特性:掌握⽔的密度ρ和容重γ;2.粘滞性:液体的粘滞性是液体在流动中产⽣能量损失的根本原因。
描述液体内部的粘滞⼒规律的是⽜顿内摩擦定律 :注意⽜顿内摩擦定律适⽤范围:1)⽜顿流体, 2)层流运动3.可压缩性:在研究⽔击时需要考虑。
4.表⾯张⼒特性:进⾏模型试验时需要考虑。
下⾯我们介绍⽔⼒学的两个基本假设: (⼆)连续介质和理想液体假设1.连续介质:液体是由液体质点组成的连续体,可以⽤连续函数描述液体运动的物理量。
2.理想液体:忽略粘滞性的液体。
(三)作⽤在液体上的两类作⽤⼒第⼆章⽔静⼒学⽔静⼒学包括静⽔压强和静⽔总压⼒两部分内容。
通过静⽔压强和静⽔总压⼒的计算,我们可以求作⽤在建筑物上的静⽔荷载。
(⼀)静⽔压强:主要掌握静⽔压强特性,等压⾯,⽔头的概念,以及静⽔压强的计算和不同表⽰⽅法。
1.静⽔压强的两个特性:(1)静⽔压强的⽅向垂直且指向受压⾯(2)静⽔压强的⼤⼩仅与该点坐标有关,与受压⾯⽅向⽆关,2.等压⾯与连通器原理:在只受重⼒作⽤,连通的同种液体内, 等压⾯是⽔平⾯。
(它是静⽔压强计算和测量的依据)3.重⼒作⽤下静⽔压强基本公式(⽔静⼒学基本公式)p=p 0+γh 或其中: z —位置⽔头,p/γ—压强⽔头(z+p/γ)—测压管⽔头请注意,“⽔头”表⽰单位重量液体含有的能量。
4.压强的三种表⽰⽅法:绝对压强p ′,相对压强p ,真空度p v , ↑它们之间的关系为:p= p ′-p a p v =│p │(当p <0时p v 存在)↑相对压强:p=γh,可以是正值,也可以是负值。
要求掌握绝对压强、相对压强和真空度三者的概念和它们之间的转换关系。
1pa(⼯程⼤⽓压)=98000N/m 2=98KN/m2下⾯我们讨论静⽔总压⼒的计算。
计算静⽔总压⼒包括求⼒的⼤⼩、⽅向和作⽤点,受压⾯可以分为平⾯和曲⾯两类。
水力学实验

五、雷诺实验
Байду номын сангаас二、实验原理
同一种液体在同一管道中流动,当流速不同时,液 体在运行中有两种不同的流态。当流速较小时,管 中水流的全部质点以平行而不互相混杂的方式分层 流动,这种形态的游体流动称为层流。当流速较大 时,管中水流各质点间发生相互混杂的运动,这种 形态的液体流动称为紊流。
五、雷诺实验
二、实验原理
四、动量方程实验
四、实验步骤 4、用体积法测量流量 Q 用以计算 F理 ; 5、重复上述步骤一次; 6、将平面板更换为曲面板( 135及 180),
又可实测和计算不同流量的作用力; 7、关闭抽水机,将水箱中的水排空,砝码从
杠杆上 取下,实验结束。
四、动量方程实验
五、注意事项
1、量测流量后,量筒内的水必须倒进接水器, 以保证水箱循环水充足;
2
v
2 2
2g
hw
它表明:液体在流动的过程中,液体的各种机
械能(单位位能、单位压能和单位动能)是可以
相互转化的。但由于实际液体存在粘性,液体运
动时为克服阻力而要消耗一定的能量,也就是一 部分机械能转化为热能而散逸,即水头损失。因 而机械能应沿程减少。
三、能量(伯努利)方程实验
三、实验设备
三、能量(伯努利)方程实验
2.如果压差计用倾斜管安装,压差计的读数差 是不是沿程水头损失值?管内用什么性质的液体比 较好?其读数怎样换算为实际压强差值?
3.为什么上、下临界雷诺数值会有差别? 4.为什么不用临界流速来判别层流和紊流?
二、流线演示实验
2、在孔板前,流线逐渐收缩,汇集于孔板的 过流孔口处,只在拐角处有一小旋涡出现;孔板 后水流逐渐扩散,并在主流区周围形成较大的旋 涡回流区。
水力学基本公式3篇

水力学基本公式3篇以下是网友分享的关于水力学基本公式的资料3篇,希望对您有所帮助,就爱阅读感谢您的支持。
水力学基本公式篇1短管:既考虑局部损失又考虑沿程损失可分为自由出流和淹没出流水泵吸水管、虹吸管、铁路涵管、建筑给水管等。
长管:仅考虑沿程损失,不计流速水头和局部损失流:若在容器壁上开孔,水经孔口流出的水力现象。
仅考虑局部损失自由出流定义:水经孔口流入空气中ϕ=≈==0.97μ=εϕ=0.64⨯0.97=0.62薄壁小孔口在Re 很大时,局部阻力系数ζ0=0.06淹没出流:孔口流出的水流不是进入空气,而是流入下游水体中,致使孔口淹没在下游水面2222v v αv αv c 之下。
当Acse=1 H +0+11=H +0+22+ζc +ζ12g22g2gse在相同水头H0的作用下,同样断面面积的管嘴的过流能力是孔口的1.32倍,μn =ϕn =0.822g对管嘴的长度也有一定限制。
长度过短,流束收缩后来不及扩大到整个出口断面,收缩断面的真空不能形成,管嘴仍不能发挥作用;长度过长,沿程水头损失不容忽略,管嘴出流变为p v≤7m 短管流动。
ρg 圆柱形外管嘴正常工作条件作用水头:H0≤9m 管嘴长度:l = (3~4)l=3~4d短管的水力计算流量系数:自 2由自由出流出口中心以上的水头w 淹没出流:上下游水位差μ=自由出流c淹没出流μ=c管道轴线的一部分高出无压的上游供水水面,这样的管道称为虹吸管⎛l ⎫vH =h = λ+∑ζ⎪⎝d ⎭2g长管的水力计算:因为长管可以忽略不计,则w f长管的全部作用水头都消耗于沿程水头损失,总水头线H 是连续下降的直线,并与测压管水头线重合。
H =h =h2、简单管道的比阻计算方法比阻a 取决于λ、dH =h f =alQ 2=SQ 2串联管道:若节点处q1= q2 = …= 0,则Q1= Q2= Q3= …=Q 若有流量分出,Qi = qi + Qi +1n n n2总水头损失等于各管段水头损失的总和。
清华水力学实验:05动量方程

z 若射流冲击的是一块凹面板,则沿射流方向的动量方
程投影式为:
ρQ(α 02v2 cosβ − α 01v1) = −R′ , 取动量修正系数 α 01 = α 02 = 1.0 ,v1 = v2 = v 仍满足,所 以
R′ = ρQv(1 − cosβ) .
动量-1
z 本实验装置设计的射流方向是铅垂向上的,重力沿射 流方向有分量,考虑到重力的减速作用,射流冲击到 实验板上的速度小于喷嘴出口流速,为 v1 = v2 = v2 − 2gz , 故将实验板受力公式改为 R = ρQ v2 − 2gz (1 − cos β) , 其中 z 为射流喷射高程(喷嘴出口到实验板的距离)。
2. 学习用天平测力和用体积 法测流量的实验技能。
实验步骤
1. 认真阅读实验目的要求、实 验原理和注意事项。
2. 查阅用天平测力和用体积法(手工、自动)量测流量的原理和步骤。 3. 调天平,将微调砝码拨到零位,配重放到 A 盘,使天平处于平衡状态。调节天平位置,
使喷嘴中心与实验板中心在同一轴线上,然后用定位件将天平固定。在天平 B 盘放入砝 码,实验板为平板时放 60g 砝码,曲板时放 100g 砝码。 4. 接好自动量测仪,按自动量测操作步骤(另附)进行操作。 5. 将分流器泄水口拨向泄水槽(11),开大稳压箱调压阀,关闭进水调节阀,将量水箱存 水放空后,关闭量水箱泄水阀。启动水泵,待稳压箱内的气体全部排除后关小调压阀(不
清华大学水利水电工程系水力学实验室
水力学 流体力学
课程教学实验指示书
恒定总流动量方程验证实验
原理简介
z 对恒定总流运用动量守恒原理,可以得到动量方程
ρQ(−α
G 01v1
+
恒定总流的动量方程详解课件

充分混合和反应。
02
动量方程推导及意义
动量方程介绍
恒定总流
在流体力学中,当流体流经某一管道 或在某一区域内流动时,若其流速、 压强、密度等物理量均保持不流动时, 动量变化与外力之间的关系。
动量方程推导过程
控制体选取
在推导过程中,需要选取一个控 制体,该控制体可以是一段管道、 一个阀门或一个泵等。
边界条件和初始条件
解释数值模拟过程中所需的边界条件和初始条件的设置方法和依据。
实验与模拟结果对比分析
结果展示
分别展示实验和数值模拟的结果,如速度分布、 压力分布等。
结果对比
对比分析实验和数值模拟的结果,评估数值模拟 的准确性和可靠性。
误差分析
分析实验和数值模拟结果之间存在的误差及其来 源,提出改进方法和建议。
恒定总流的动量方程详解 课件
目录
• 恒定总流基本概念 • 动量方程推导及意义 • 恒定总流动量方程实例分析 • 动量方程在工程中的应用 • 实验验证与数值模拟方法 • 总结与展望
01
恒定总流基本概念
恒定总流定义
• 恒定总流是指在管道中流动的流体,其流量、流 速、压强等物理量在时间和空间上均保持不变的 流动状态。
方程简化与整理
通过对方程进行简化和整理,可 以得到常见的动量方程形式,如 欧拉方程、伯努利方程等。
01
假设条件
推导动量方程时,需要假设流体 为不可压缩流体,且流动过程中 无摩擦损失。
02
03
应用牛顿第二定律
通过对控制体内的流体应用牛顿 第二定律,可以得到动量方程的 基本形式。
04
动量方程物理意义
动量变化与外力关系
在供水系统中,恒定总流可以保证用户获得稳定的水压和水量,确保供
水力学 第3章液体一元恒定总流基本原理(下)

udA Q v
A
A
A
3.3.6
均匀流和非均匀流,均匀流的特性
均匀流和非均匀流:流速的大小和方向沿流线不变 的流动称为均匀流;否则称为非均匀流。
均匀流的特性:
1、流线是相互平行的直线,因此过水断面是平面,且过水断面面 积沿程不变。
2、同一根流线上各点的流速相等,流速分布沿流不变。 3、过水断面上的动水压强按静水压强分布。
2 p1 1v12 p2 2v2 z1 hp z2 hw g 2 g g 2 g
式中:hp为两断面间加入(取正 号)或支出(取负号) 的单位机械能。
例3.3文丘里管测流量
列1 1, 2断面的能量方程可得 2
2 p1 1v12 p2 2v2 z1 z2 hw g 2g g 2g
解
( )先分别求出两个断面 1 的流速
3.5
恒定元流的能量方程
3.5.1理想液体恒定元流的能量方程
由物理学中动能定理指出:运动物体在某一时段内动能的增量等 于各外力对物体所做的功之和。 Ek Ek12 Ek12 ( Ek12 Ek 22 ) ( Ek11 Ek12 ) Ek Ek 22 Ek11 根据质量守恒原理流段1-1’和2-2’的质量应相等,即 dm=ρu1dA1dt= ρu2dA2dt=ρdQdt
p v 2 d( z ) dh g 2 g 水力坡度J w ds ds
p d( z ) g 测管坡度J p ds
恒定总流能量方程的应用条件:
1.作用于液体上的质量力只有重力。
2.水流必须是恒定流。 3.所取过水断面应是均匀流或渐变流过水断面, 但两断面之间可以存在急变流。 4.两过水断面之间没有外界能量加入或支出,若 有需修正能量方程。
