D对面积曲面积分
高数第四节.对面积的曲面积分 (1)

1. f ( x, y, z)dS f ( x, y, z)dS f ( x, y, z)dS.
1
2
当为闭曲面时, f ( x, y, z)dS 可写成 f ( x, y, z)dS.
2. 当 f ( x, y, z) 1时, dS 是曲面的面积.
复习:
z n
设光滑曲面
M
则面积 A 可看成曲面上各点 M (x, y, z) S dA
处小切平面的面积 d A 无限积累而成. o
设它在 D 上的投影为 d , 则
x
y
d
d cos d A n ( fx( x0 , y0 ), fy( x0 , y0 ), 1 )
cos
1
1 fx2 (x, y) f y2 (x, y)
d A 1 fx2 (x, y) f y2 (x, y) d
z
h
oD xy
ay
x
因为dS
1
z
2 x
z
2 y
dxdy
a
dxdy,
a2 x2 y2
dS
a
dxdy,
a2 x2 y2
ห้องสมุดไป่ตู้
dS z
Dxy
a2
adxdy x2
y2
add Dxy a2 2
a
2π
d
0
a2 h2 0
d a2 2
2πa
1 2
ln( a 2
2
) 0
a2
h2
2πa ln a . h
f (i ,i , i )Si
积分曲面
面积元素
积分和式
以上积分也称为第一类曲面积分或对面积的 曲面积分.
高斯公式

应用: (1) 计算曲面积分
∫∫Σ Pd y d z + Qd z d x + Rd xd y = 0
∂P ∂Q ∂R + + =0 ∂x ∂ y ∂z
作业
273页 16(2)(6) 274页 (B) 6
沿任意闭曲面的曲面积分为零的条件
z = − 1 − x 2 − y 2 的上侧 计算 的上侧, 例5. 设∑为下半球面
解 :设
∑
∑1 : z = 0, x 2 + y 2 ≤ 1
z
,取上侧
I = ∫∫ x sin 2 (1 − z )dydz + y cos 2 (1 − z )dzdx
y
− z dxdy
∑1
′ P′ + Q′ + Rz = 0 x y
y
− z dxdy
=0
∑1
′ P′ + Q′ + Rz = 0 x y
x
= ∫∫ x sin 2 (1 − z )dydz + y cos 2 (1 − z )dzdx − z dxdy
y
∑
∴ I = I1 + ∫∫ ( − 6 z )dxdy
1 x
内容小结
1. 高斯公式及其应用 公式:
∫∫Σ Pd y d z + Qd z d x + Rd xd y ∂P ∂Q ∂R )d xd y d z = ∫∫∫ ( + + Ω ∂x ∂ y ∂z
= ∫∫ Pd y d z + Qd z d x + Rdx d y
Σ
(Gauss 公式 公式)
对面积的曲面积分习题解析
15 15
曲面上任一点的坐标满足曲面方程
(6) x2 dS ,其中 Σ 为球面 x2 y2 z2 a2 (a 0) ;
答案: 4 a4 3
解 析: 本 题中 Σ 为 球 面 x2 y2 z2 a2 (a 0) , 在 xOy 面 的投影 区域 为
Dx y {(x, y) | x2 y2 a2} . 可将球面方程化为 : z a2 x2 y2 . 如图 9 所示,球面 : x2 y2 z2 a2 对称地
答案: a(a2 h2 )
解析: 本题中 Σ 为 球面 z a2 x2 y2
上 z h (0 h a) 的部分,如图 4 所示.
此时 z
x
, z
y
,
x a2 x2 y2 y a2 x2 y2
图4
Σ 在 xOy 面上的投影区域为 Dx y {(x, y) | x2 y2 a2 h2 },
其中,
2 cos2 d
1
,
0
22
a 3
d 1 a
3
d
0 a2 2
a 0 1 ( )2
a
参照上册课本第 163 页例 4.3.16 结论
2 cosn xd x 2 sinn xd x
0
0
n 1 n 3
n n 1
n2 n3
n n 2
3 1 (n为偶数)
42 2
.
4 2 1 (n为奇数)
图 11
根据曲面积分的性质可知 dS S ,即此曲面积分等于积分曲面的面积. 本题中的旋
转抛物面 z 2 (x2 y2 ) 在 xOy 面上方四个卦限里是对称的,因此,只需求出第一卦限里
的面积,再乘以 4.
记
曲面积分

y
R( x, y, z) d x d y D
(S ) xy
说明: 如果积分曲面 取下侧, 则
R( x, y, z ) d x d y Dx y R( x, y, z( x, y)) d x d y
若记 正侧的单位法向量为 n ( cos , cos , cos )
令 d S n d S (d yd z, d zd x, d x d y )
A ( P( x, y, z ) , Q( x, y, z ) , R( x, y, z ) )
则对坐标的曲面积分也常写成如下向量形式
2
2
2 d
0
2
0
rdr 1 r cos
2
1 r
2
4
d 1 r2
cos 2 1 r 2 0
4 tan 1
例8 计算
其中Σ为平面x+y+z=1,与三坐标 平面所围
( x 1)dydz ydzdx dxdy,
4
立体的表面,取外侧
解:
z
I
o x Dx y
y
f ( x, y, z ) dS 存在, 且有
Dx y
f ( x, y ,
)
一代、二换、三投影 化为二重积分计算
Dx y
f ( x, y,
)
一代、二换、三投影, 化为二重积分计算 “一代”: 将z=z(x,y)代入被积函数f (x,y,z), 得f [x,y,z(x,y)]; “二换”:将dS换成相应的曲面面积元素的表达式: 2 如Σ:z=z(x,y),则 dS 1 z x z 2 dxdy y “三投影”:认清Σ在xOy平面上的投影区域Dxy,二 重积分是在区域上Dxy进行的。 说明: 如果曲面方程为
对面积的曲面积分

用平行于坐标轴的直线网 dS M
将 Dxy分割为若干小区域, o
任取一个小矩形 d x
相应地上有小曲面块dS,
Dxy
y
(x, y)
d
T为 上过 M( x, y, z( x, y))的切平面.
以 d 边界为准线,母线平行于z 轴的
小柱面,截曲面 为 dS;
z
对面积的曲面积分(或第一型曲面积分) 若积分曲面是封闭的,则相应的曲面积分
记为 f (x, y, z)dS
计算对面积的曲面积分 ——化为二重积分
f ( x, y, z)dS
x, y, z 在上变化 曲面面积元素
?
一、曲面的面积
设曲面 : z z x, y, x, y Dxy
Dxy是有界闭区域,
1 2 3
2 1
O Dxy
1
3
x
4
1
y
在4上:z 1 x y,
dS
1
z
2 x
z
2 y
d
3d
又 4 在xoy面上的投影区域 Dxy
z
是由 x 0, y 0, x y 1 1
4
围成的三角形.
Dxy : 0 y 1 x,0 x 1
1
x
O Dxy
1
y
x y 1
在4上:z 1 x y,
x,
y
z
2 y
x,
y
d
对面积的曲面积分的计算公式为
f x, y, zdS
f x, y, z x, y
1
z
2 x
z
2 y
d
Dxy
化为二重积分
5-6第二类曲面面积分

n
存在条件:
当 P ( x , y , z ), Q ( x , y , z ), R ( x , y , z ) 在有向光滑曲 面Σ 上连续时,对坐标的曲面积分存在.
组合形式:
P ( x, y, z )dydz Q( x, y, z )dzdx R( x, y, z )dxdy
1
2.
P ( x , y, z )dydz P ( x , y, z )dydz
Q( x , y, z )dzdx Q( x , y, z )dzdx
R( x , y, z )dxdy R( x , y, z )dxdy
o
Dxy
y
x
(s) xy
R( x, y, z )dxdy lim R( i , i , i )( Si ) xy 0 i 1
n
取上侧, cos 0, 又 i z ( i , i )
n
( Si ) xy ( ) xy ,
lim R( i , i , i )( Si ) xy
解
x
1
把分成1和 2两部分
1 : z1 1 x 2 y 2 ; 2 : z2 1 x 2 y 2 ,
xyzdxdy xyzdxdy xyzdxdy
2 1
xy 1 x y dxdy xy( 1 x y )dxdy
第六节 第二类曲面积分
• • • • • • 一、曲面的侧 二、概念的引入 三、概念及性质 四、计算法 五、两类曲面积分的联系 六、小结 思考题
一、曲面的侧
观察以下曲面的侧 (假设曲面是光滑的)
面积分及高斯公式2010

对称性
例5
计算
( x 3 x 2 y z )dS , 其中Σ为球面
z a 2 x 2 y 2 之位于平面 z h (0 h a )
上方的部分.
z
解 曲面Σ 的方程
Σ
z a2 x2 y2
Σ在xOy面上的投影域
x
O
y
Dxy : x 2 y 2 a 2 h2
(2 x 2 z ) d S 2 ( x z ) ydS
2 2 dS 1 z x z y dxdy
2dxdy
D
xy
上一页
下一页
例2 计算 | xyz |为抛物面z x y (0 z 1).
解 依对称性知
抛物面 z x y
2 2
z
关于xOz面、yOz面均对称; 被积函数 | xyz |
求
H dS ,
: x y z 1
答案
4 6 ai 5 i 1
上一页
下一页
例11.计算曲面积分
重心公式
中是球面x 2 y 2 z 2 2 x 2 z .
解:
I ( x 2 y 2 z 2 ) 2x y 2 y z dS
曲面积分的计算及证明
1.对面积的曲面积分的计算
(1)用公式直接计算
(2)用对称性
(3)两类面积分间的联系.
上一页
下一页
对面积的曲面积分时,首先应根据 曲面Σ选好投影面, 确定投影域并写出 曲面Σ的方程, 然后算出曲面面积元素; 最后将曲面方程代入被积函数, 化为二
重积分进行计算.
对面积的曲面积分

| xyz| dS 4 xyzdS d S 1 (2 x )2 (2 y )2 d x d y
1
4 xy (x2 y2) 1(2x)2(2y)2d xd y
D x y
42d1r2co ssinr21 4 r2rd r 00
极 坐 标
22sin2d1r5 14r2dr
0
0
u
(3) 若曲面 :xx(y,z)
则 f(x,y,z)dS f [x(y,z), y, z] 1x2 yxz2dydz D yz
对面积的曲面积分
计算面积的曲面积分的解题步骤:
1、应根据曲面Σ选好投影面. 2、确定投影域并写出 曲面Σ的显函数形式,
并算出曲面面积元素dS.
3、将曲面方程代入被积函数,化为二 重积分进行计算.
Dxy
对面积的曲面积分
补充
设分片光滑的 曲面Σ关于yOz面对称,则
f(x, y,z)dS
0,
当f(x,y,z)为x的奇函数
2f(x,y,z)dS.
当f(x,y,z)为x的偶函数
1
其中 1 :x x (y ,z ) 0 .
对面积的曲面积分
例 计算 |xy|zdS,
其为 中抛 zx 2物 y2 (0 面 z 1 ).
1 5 u(u1)2du 125 51
41
4
420
对面积的曲面积分
例 计算xdS, 其中 是圆x2柱 y2面 1,
平 z 面 x 2 及 z 0 所围成的空间立体的表面.
z
z
z
O
x
y
O
x
y
O
x
y
对面积的曲面积分
例 计算xdS, 其中 是圆x2柱 y2面 1,
对面积的曲面积分的几何意义

对面积的曲面积分的几何意义一、引言曲面积分是向量分析中的一个重要概念,它在物理学、工程学等领域中有着广泛的应用。
而对于曲面积分的几何意义,是我们在学习和应用曲面积分时必须深刻理解的。
二、曲面积分的定义在数学中,曲面积分是对一个向量场在给定曲面上的积分。
具体来说,如果我们有一个向量场F(x,y,z)=(P,Q,R),并且有一个参数化的曲面S,那么F在S上的曲面积分就可以表示为:∫∫S F·dS其中,“·”表示向量点乘,“dS”表示曲面元素。
三、曲面元素为了更好地理解曲面积分的几何意义,我们需要先了解一下什么是曲面元素。
对于任意给定点P(x,y,z)处定义一个切平面T,并且令dS为该平面上与z轴正方向夹角为θ(θ∈[0,π])时z轴投影区域dA,则dS=dA/cosθ。
这个定义可以帮助我们计算出曲面上每个点处与该点相关联的小区域。
四、曲线与流量在理解了曲面元素的概念后,我们可以更好地理解曲面积分的几何意义。
曲面积分实际上是将向量场F投影到曲面S上,然后计算在这个投影下的流量。
具体来说,我们可以将曲面S看作是一个容器,向量场F看作是液体流入该容器内部的速度场。
那么,在单位时间内流入该容器内部的液体体积就等于F在S上的曲面积分。
五、对比一般积分与一般积分不同的是,在一般积分中,我们对函数f(x)在一个区间[a,b]上进行求和或平均值计算。
而在曲面积分中,我们对向量场F在一个参数化的曲面S上进行求和或平均值计算。
因此,曲面积分更加复杂和抽象。
六、实际应用曲面积分在物理学、工程学等领域中有着广泛的应用。
例如,在电磁学中,我们可以利用曲面积分来计算电荷产生的电场强度;在流体力学中,我们可以利用曲面积分来计算涡旋流线等物理量;在机械工程中,我们可以利用曲面积分来计算物体的质心和转动惯量等。
七、总结在本文中,我们介绍了曲面积分的定义、曲面元素的概念以及曲面积分的几何意义。
通过对曲面积分的深入理解,我们可以更好地应用它来解决实际问题。
对面积的曲面积分的可代入性和对称性

对面积的曲面积分的可代入性和对称性第十二章 曲面积分一、对面积的曲面积分的可代入性对面积的曲面积分中被积函数可代入性:是指可以将曲面的表达式代入被积函数。
所以x , y , z 满足曲面的方程.是定义在曲(,,)f x y z面 上的,也就是说以 f (x , y , z ) 的自变量x , y , z 为坐标的点P 就是曲面Σ上,比如:设 f (x , y , z )=xyz 是定义在曲面Σ:z = x 2 + y 2 上,从而 f (x ,y ,z ) 就可以写成 xy (x 2+y 2),即f (x ,y ,z ) = xy (x 2+y 2).因为 f 中的x , y , z 是约定在曲面之上的,所以 z 的取值为x 2 + y 2 , 而点的坐标必须满足曲面的方程,而二重积分计算时则不能把边界曲线的表达式代入被积函数,满足的关系式通过不等式描述,一般含有“≤”或“≥”。
因为被积函数中的x , y 是平面区域D 内部的点对应的x , y ,此时x , y +≤+⎰⎰22221()d ,x y x y x y σ比如:中的取值限定在圆内,满足的是x 2 + y 2 ≤ 1,所以22221()d x y x y σ+≤+⎰⎰+≤≠⎰⎰2211d .x y σ二、对面积的曲面积分的对称性定义1设曲面∑上任取一点P(x, y, z),若(x, y, – z)对应的点Q也在∑上,或者说:将∑的关系式中“z”换成“–z”,而关系式不变,则称曲面∑关于xOy面对称.【曲面还可以关于yOz面对称或zOx面对称。
】例如: Σ的关系式为:x2 + y2 + z2= a2 (z ≥ 0), 若将z改成-z,则关系式变成了: x2 + y2 +(-z)2= a2 (-z ≥0),即x2 + y2 + z2= a2 (z ≤ 0),关系式发生了变化,即曲面发生了变化,所以曲面不关于xOy面对称。
当然,如果大家把x改成-x,则关系式不变,所以曲面关于yOz面对称。
高数 对面积的曲面积分讲解

如 : z z( x, y) ,则
dS
1
z
2 x
z
2 y
dxdy
“三投影”认清 在 二重积分是在区域上
xoy 平面上的投影区域 Dxy 进行的。
Dxy ,
10
2)如果曲面方程为 x x( y, z), ( y, z) Dyz
或 y y( x, z), ( x, z) Dxz
21
例5 设 : x2 y2 z2 a2
z 1
计算 I f ( x, y, z)dS
解 锥面 z x2 y2 与上半球面 z
x o Dx y y
a2 x2 y2 的
交线为
设 1为上半球面夹于锥面间的部分,它在 xoy 面上的
投影域为 Dx y ( x, y)
1
x x2
y2
2
y x2
y2
2
O
dxdy
a
2a x
2dxdy
I ( xy y x2 y2 x x2 y2 ) 2dxdy
Dxy
20
y
0 2 x x2 y2dxdy
Dxy
2a cos
2
两片, 则计算较繁。 解 取曲面面积元素
则
I
0H
2
R2
R dz z2
2 arctan H
R
H
z dz
o
y
x
28
例11 求椭圆柱面
位于xoy面上方及平面
z = y 下方那部分柱面 的侧面积 S 。
对面积的曲面积分的物理意义

对面积的曲面积分的物理意义
1. 对面积的曲面积分的物理意义之一就是计算流量啊!就好比家里的水龙头,水不断地流出来,那流过的水量不就可以用这个来算嘛!你说神奇不神奇?
2. 它还能表示质量分布呢!想象一下一块不均匀的面包,每一处的密度都不一样,通过对面积的曲面积分就能知道这块面包总的质量呀!这多有意思啊!
3. 嘿,对面积的曲面积分可以用来理解热量的传递哦!就像冬天我们靠近暖炉,热量从暖炉散发出来,这个散发的总量就和它有关呀!你难道不想搞清楚吗?
4. 它也是计算电荷量分布的好工具呀!好比一个带电的球体,不同地方电荷量不一样,用对面积的曲面积分就能算出总电荷量啦,这是不是很妙?
5. 对面积的曲面积分在研究电磁学方面可重要啦!就像探索宇宙中的神秘电波,能帮助我们了解那些奇妙的电磁现象呢,你不好奇吗?
6. 哇塞,在流体力学里,它能告诉我们流体流过一个曲面的总量呢!就像河水在河床上流淌,这个总量可有着大用处呢!
7. 你知道吗,对面积的曲面积分能衡量一个物体表面的力的分布哦!就如同风吹在旗帜上,不同地方受力不同,它能算出来呢,厉害吧!
8. 它还能帮我们搞清楚光学里的一些现象呢!比如光线在一个曲面上的分布情况,这就像在黑暗中寻找光明的线索呀,是不是很吸引人?
9. 对面积的曲面积分可以用来研究物体的辐射强度哦!想象一下太阳辐射到地球上的能量,通过它就能知道大概的情况啦,这多神奇呀!
10. 嘿呀,它甚至可以在研究声音的传播上发挥作用呢!就像声波在空间中扩散,对面积的曲面积分能算出相关的信息,你说牛不牛?
我的观点结论:对面积的曲面积分在各个领域都有着非常重要且有趣的应用,它就像一把神奇的钥匙,能打开很多科学奥秘的大门,让我们对世界有更深入的理解和认识。
对面积的曲面积分的计算方法(一)

对面积的曲面积分的计算方法(一)对面积的曲面积分的计算方法曲面积分是对曲面上的某个物理量的积分,计算曲面积分需要对曲面进行参数化,然后将积分变为对参数的积分。
针对计算对面积的曲面积分,需要注意以下几个方面。
曲面的参数化首先需要对曲面进行参数化,将曲面表示为一个参数方程,这样才能进行对参数的积分。
对于一个光滑曲面,可以采用以下方法进行参数化。
•隐式参数化:将曲面方程化为F(x,y,z)=0的形式,然后通过某些手段解得一个参数方程。
•显式参数化:即直接给出x,y,z三个自变量的函数表达式。
参数变换曲面积分需要对参数的积分,而参数变换可以将曲面积分转化为对一个标准区域D的积分,即曲面上的每一个点都与标准区域D上的一个点对应。
这样可以帮助我们更容易地对参数进行积分。
曲面积分的计算公式对于面积元素dσ,面积分的计算公式如下:∬fS (x,y,z)dσ=∬fD(x(u,v),y(u,v),z(u,v))|n|dudv其中|n|表示n向量在(x,y,z)点的模长,也即面积元素dσ的面积大小。
实例演示以球体 x 2+y 2+z 2=R 2 为例,设 f (x,y,z )=z ,现计算 f 在球体上的曲面积分。
首先可以把球体用下面的参数方程表示出来:{x =Rsinϕcosθy =Rsinϕsinθz =Rcosϕ然后可以计算出 dσ 及其对应的模长:dσ=R 2sinϕdϕdθ|n |=√(∂x ∂u ×∂x ∂v )2+(∂y ∂u ×∂y ∂v )2+(∂z ∂u ×∂z ∂v)2=√2Rsinϕ 所以曲面积分可以写成:∬z S dσ=∫∫(Rcosϕ)π02π0⋅(R 2sinϕ)dϕdθ=0 因此,f 在球体上的曲面积分等于 0。
综上,对面积的曲面积分的计算方法需要进行曲面的参数化、参数变换和计算公式的应用。
掌握这些知识,可以更好地解决曲面积分的问题。
注意事项在计算曲面积分的过程中,需要注意以下几个方面:• 对于面积元素 dσ,需要注意其符号,在计算曲面积分时要与曲面的法向量 n 的方向一致。
第四节对面积的积分

讨论3 时, 将投影域选在xoz 上.
(注意: y 1 x 分为左、右两片)
(左右两片投影相同)
2
xdS xdS xdS
3 31 32
2 x 1 y x y z dxdz
2 2 Dxz
x 2 x 1 2 dxdz 1 x Dxz
1.定义 设曲面 是光滑的, 函数 f ( x , y , z )在 上有界, 把 分成 n小块 S i ( S i 同时也表示 第 i 小块曲面的面积) ,设点 ( i , i , i ) 为 S i 上 任意取定的点,作乘积 f ( i , i , i ) S i ,
1
( x y ) 1 z z dxdy
2 2 2 x 2 y
1
2 ( x 2 y 2 )dxdy
D
D
o
y
2 2 d r rdr 2 0 0
2
2
1
x
(x
2
2
y )dS
2 2
( x y )dS d r rdr
I z 0 ( x 2 y 2 )dS
2 0 ( x 2 y 2 ) 1 z x z2 y dxdy D a 2 2 0 ( x y ) 2 dxdy 2 2 a x y D
4 1 4 0a 0 a d r 2 2 rdr 2 a r 3 0 0
xy
2. 若曲面 : y y( x, z )
则 f ( x , y , z )dS
D
xz
2 2 f [ x , y( x , z ), z ] 1 y x yz dxdz;
曲面积分的计算方法

曲面积分的计算方法
曲面积分是对曲面上某个量的积分,常用于物理学、工程学和数学等领域的问题求解。
计算曲面积分的方法包括两类:对面积元素的积分和对参数的积分。
方法一:对面积元素的积分
1. 将曲面划分为小面元,每个面元的面积为ΔS。
2. 在每个面元上选择一个点P,计算该点上的量F的值。
3. 计算量F在每个面元上的微元积分dΦ=F(P)ΔS。
4. 对所有面元上的微元积分进行求和,即可得到曲面积分的近似值。
方法二:对参数的积分
1. 将曲面用参数方程表示,即将曲面上的点P(x,y,z)表示为参数u和v的函数:P(u,v)=(x(u,v),y(u,v),z(u,v))。
2. 计算参数u和v的范围,并确定积分的积分区域D。
3. 计算向量积dS=|∂P/∂u × ∂P/∂v|dudv,其中∂P/∂u和∂P/∂v分别表示参数u和v对应的偏导数。
4. 将量F用参数表示,即F(P(x,y,z))=F(x(u,v),y(u,v),z(u,v))。
5. 计算量F在参数区域D上的积分:∬F(P)dS =
∫∫F(x(u,v),y(u,v),z(u,v))|∂P/∂u × ∂P/∂v|dudv。
这两种方法都可以用于计算曲面积分,根据具体的问题选用合适的方法。
需注意,在计算中要注意曲面的参数化表示和确定积分区域,以及正确计算面积元素或微元积分。
对面积的曲面积分

第四节 对面积的曲面积分4.1 学习目标了解对面积的曲面积分的概念、 性质,掌握对面积的曲面积分的计算方法, 会用曲面积分求一些几何量与物理量 .4.2 内容提要1.定义 设函数f x, y,z 在光滑曲面上有界,将曲面任意分成n 小块 s ( S i也表示第i 小块曲面的面积),在 S i 上任取一点 M i ( i , i , J ,作乘积f( i , i , i ) S i n (i 1,2,L ,n ),并作和 f i , i , is i ,记各小曲面直径的最大值为,如果对曲i 1面的任一分法和点(i , i , i )的任意取法,当 0时,上述和式的极限都存在且相等,则称此极限值为函数 f x,y,z 在曲面上对面积的曲面积分或第一类曲面积分,记nf(x, y,z)dS lim 0 i 1 f ( i , i , i ) S •【注】定义中的“ S i ”是面积元素,因此,S i 0 .2•性质f(x,y,z)dS f(x,y,z)dS f(x, y,z)dS ;1 2②当被积函数为1时,积分结果在数值上等于曲面的面积S ,即f (x, y, z)dS S .3.对面积的曲面积分的计算在xoy 面上的投影区域为 D xy ,函数z z x, y 在Dxy同样地:x x y,zf (x, y, z)dSD yzD xy 上具有连续偏导数,被积函数f (x, y,z)在 上连续,则f (x,y,z)dSf(x, y,z(x,y)h 1dxdy①关于曲面具有可加性,若12,且1与2没有公共的内点,则设曲面 由z z x, y 给出,x y,z , y,z dydz ,:y y z,xf(x,y,z)dS f x, yz,x ,zD xz4•对面积的曲面积分的应用设曲面上任意一点x, y, z处的面密度是x, y,z①曲面的质量x, y, zdS.②曲面的质心x,y,z 2 dzdx .x,y,z dS, x,y,z dS③曲面的转动惯量I x x,y,z dS Iyx, y,zI z x,y,z dS, I o z x, y, z dSdS,x, y,zdS.4.3 典型例题与方法基本题型I :计算对面积的曲面积分1 填空题:x2y2z24,则Q(X2y2)dS由积分区域的对称性知乙x2dS y2dS? z2dS而积分在上进行,乙(x2故应填12832 选择题(A) xdS (C) zdS乙(X2y2)dS - (x23z24,y2)dSa2(z 0),代入上式得,z2)dS .22128在第一卦限中的部分,则有()4 xdS ;( B) ydS 4 xdS ;1 14 xdS ;( D) xyzdS 4 xyzdS解因为曲面是上半球面, 关于yoz 面对称且被积函数f i (x, y,z) x ,f 2(x, y, z) xyz 都是变量X 的奇函数,于是 xdS xyzdS ° .类似地, 关于xoz面对称且f 3(x, y,z) y 是变量y 的奇函数,于是 yds 0 .而 xdS 0, xyzdS 0 ,1 1故应选(C ).事实上,由对称性,zdS 4zdS ,zdS xdS, (0正确.1 1 1【方法点击】 在计算对面积的曲面积分时,应注意下列技巧: (1) 利用对称性,但要注意,曲面 关于某坐标面对称,被积函数关于相应变量具有 奇偶性,两者缺一不可.(2)利用积分曲面 的方程化简被积函数.例3计算曲面积分 (2x 2y z)ds ,其中 是平面2x 2y z 2 0被三个坐标面所截下的在第一卦限的部分D : 0 x 1,0 y22dSJ 1~x ~ dxdy ^ 2dxdy ,解法2x 2y,z x2,Z y 2.在xoy 平面上的投影是三角形,记为(2x 2y z)ds2g 1 z x 2 z y 2 dxdy6dxdy 3.D解法(2x 2y z)ds 2dS22 3 .【方法点击】在解法二中,将曲面方程代入到了曲面积分里, 形,最后用到了三角形的面积公式 .例 4 计算 | (x2y 2)dS ,因为积分曲面是一个三角为立体.x 2 y2z 1的边界.【分析】]根据积分曲面 的方程, 分转化为投影区域上的二重积分进行计算.确定投影区域,计算曲面面积微元dS ,将曲面积1为锥面zx 2 y 2 , 0 z 1,在 1 上,图4-12为z 1上x 2y 21部分,在 2上,dS dxdy ,2 2i, 2在xOy 面的投影区域为D :x y 1,所以图4-2【注】该题不能将积分曲面向xoy 面作投影,因为投影为曲线,不是区域•基本题型II :对面积的曲面积分的应用(x 21y 2)dS + (x y 2)dS2 (x 2 2 y )、. 2dxdy (xD2y )dxdy(.2 1) (x 2y 2)dxdy (1D3d八2).例5计算 z 2dS ,其中 为 x 2 y 24介于z 0,z 6之间的部分•【分析】积分曲面 如图11-13所示,此积分为对面积的曲面积分,积分曲面关于xoz 面,yoz 面对称,被积函数是偶函数,则有z 2dS = 4 z 2dS , 1故可利用对称性解之•解 设1 : x 4 y 2,其在yoz 面的投影域为D yz :dS . 1 x y 2x z2dydzdydzz dS = 4 z ? dS =4Ddy 288 .1例6求物质曲面S: z (x2 y2)(0 z 1)的质量,其面密度z((x, y,z) S).2解S在xoy平面上的投影区域D : x2 y2(、‘2)2.解以球心为原点,铅锤直径为Z 轴建立直角坐标系,则球面方程为x 2y 2z 2R 2, 且任意点M (x,y, z)处的密度为x 2y 2.设球壳的质心坐标为(x,y,z),由对称性知,x y 0 .z dS于是球壳的质量为2 R43 R4R12 3 3,于是半球壳的质心坐标为-2R 3 324.4 教材习题解答1.有一个分布着质量的曲面,在点(X, y, z)处它的面密度u(x,y, z),用对面积的曲面积分表示这曲面对于 x 轴转动惯量。
8-4 第一型曲面积分
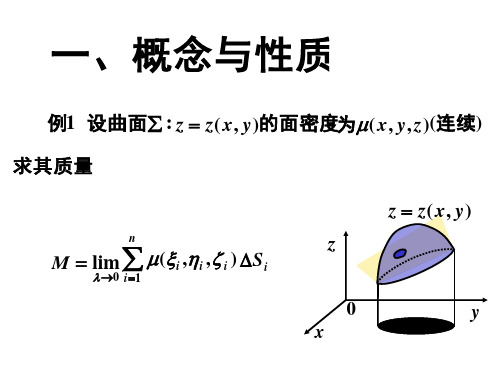
2. 若曲面 ∑ :
则
y = y( x , z )
∫∫
∑
f ( x , y , z )dS =
∫∫
D xz
f [ x , y( x , z ), z ] 1 + y′ + y′ dxdz; x z
2 2
3. 若曲面∑: x = x( y, z)
则
∫∫
∑
f ( x , y , z )dS =
∫∫
D yz
∑
可用参数方程: 讨论 ∑ 3 时, 可用参数方程:
x = cos θ y = sin θ z = z
(0 ≤ θ ≤ 2π , 0 ≤ z ≤ cos θ + 2)
易得:dS = EG F 2 dθ dz = dθ dz
∴ ∫∫ xdS = ∫ dθ ∫
∑3 0
2π
cosθ + 2
0
cos θ dz = π
h (0 ≤ θ ≤ 2π , 0 ≤ ≤ arccos ) a
易得:dS = EG F 2 d dθ = a 2 sin d dθ
∫∫
∑
dS = ∫ dθ ∫ 0 0 z
2π
arccos
h a
a sin a d = 2π a ln a cos h
2
例5
计算 ∫∫ ( x + y + z )ds , 其中∑ 为平面
z
例3
∑:
求 ∫∫ ( x 2 + y 2 + z 2 ) dS
∑
x 2 + y 2 = 1, 1 ≤ z ≤ 2的部分
解 化作 yz 的二重积分
0
y
x = ± 1 y2
第一类曲面积分

1zx2 z2y 1 ( 1 )2 ( 1 )23 ,
从而 xyzdS xyzdS
4
3x(y1xy)dxdy,
其中 Dxy是4在xO D 面 xyy 上的投, 影区域
即由直 x线 0, y0及xy1所围成的.闭区
因此
1 1 x
xyzdS 3x d x y (1 xy )d y
00
301x(1x)y22y331 0xdx
例2
计算曲面积分 1 dS ,其中是球面 x2y2z2a2 被平面
z
zh(0<h<a)截出的顶部.
解 的 方 程 为 z a 2 x 2 y 2 . 在 x O y 面 上 的 投 影 区 域
Dxy 为圆形闭区域:x2y2a 2h 2. 又
z
1 z x 2 z y 2 a 2 a x 2 y 2 . h
若 f(x , y , z ) 关于z(或 x ,或 y )是偶函数
f(x,y,z)d S2f(x,y,z)dS
1
其中 1是位于对称坐标 部面 分一侧
完全类似于三重积分的对称性
练习 计算积分:
(x y z)ds, 其中 S 是上半球面 x2y2z2a2,z0;
s
z
略解:z a2 x2 y2,
zx
31x(1x)3dx
0
6
31(x3x23x3x4)d x 3 .
60
120
例5
计算
x2
1
y2
dS
其中 是介于平面
z = 0 与 z = H 之间的圆柱面x2y2R2
解 y R 2 x 2 ,曲 面 分 为 左 右 两 片 。 令 1:y R2x2
1在zo面 x 的投影区 D z x域 :0 为 z H R x R
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2页/共26页
二、对面积的曲面积分的计算法
定理: 设续, 则曲面积分
o
y
f (x, y, z) dS 存在, 且有
x Dxy
( k )x y
f (x, y, Dx y
证明: 由定义知
)
n
lim
0 k 1
第3页/共26页
而
( k )xy 1 zx2 (x, y) z y2 (x, y) dxd y
曲面面积为
第1页/共26页
对面积的曲面积分与对弧长的曲线积分性质类似.
• 积分的存在性.
在光滑曲面上连续,
则对面积的曲面积分存在. • 对积分域的可加性.若是分片光滑的, 例如分成
两片光滑曲面 1, 2, 则有
f (x, y, z) d S 1 f (x, y, z) d S
• 线性性质.
k1 f (x, y, z) k2g(x, y, z)d S k1 f (x, y, z) dS k2 g(x, y, z) dS
定义:设为光滑曲面, f(x,y,z)是定义在上的一 个有界函数, 若对做任意分割和局部区域任意取点
“乘积和式极限”
记作 f (x, y, z)d S
都存在, 则称此极限为函数f(x,y,z)在曲面上对面积 的曲面积分或第一类曲面积分.其中f(x,y,z)叫做被积 函数, 叫做积分曲面.
据此定义, 曲面形构件的质量为M (x, y, z) d S
解: 锥面 z x2 y2与上半球面z a2 x2 y2 的
交线为
设 1为上半球面夹于锥面间的部分, 它在xoy面
上的投影域为
Dxy (x, y)
x2
y2
1 2
a2
,
则
I (x2 y2 ) d S 1
第9页/共26页
I (x2 y2 ) d S 1
(x2 y2)
Dx y
用球坐标 z R cos d S R2 sin d d
R3
2 d
2 sin cos d
0
0
R 2 d
2 sin d
0
0
思考题: 例3是否可用球面坐标计算?
第11页/共26页
例5.计算 解:取球面坐标系,则
: x2 y2 z2 R2.
2
d
R2 sin R cos
d
00
2
R
d( R cos R cos
z = y下方那部分柱面的侧面积S.
解: S dS
取 dS zds
L z ds L y ds
3
5 4cos2 t dcos t
0
z oz y
L ds x
第15页/共26页
例9.设有一颗地球同步轨道通讯卫星, 距地面高度
h=36000km,运行的角速度与地球自转角速度相同,
试计算该通讯卫星的覆盖面积与地球表面积的比.
1 x
1y
4 xyz d S
4 : z 1 x y,
(x,
y)
Dxy
:
0
0
y
x
1 1
x
1
1 x
3 x dx y(1 x y) dy
0
0
3 120
第8页/共26页
例3. 设 : x2 y2 z2 a2
z 1
计算 I f (x, y, z) d S .
x o Dx y y
a
dxd y
a2 x2 y2
2
d
1 2
2a
a r2
r dr
0
0
a2 r2
1 a4 (8 5 2)
6
思考: 若例3中被积函数改为
z 1 x o Dx y y
计算结果如何?
第10页/共26页
例4. 求半径为R的均匀半球壳的重心.
解: 设的方程为
利用对称性可知重心的坐标 x y 0 , 而
0
第6页/共26页
思考: 若是球面
出的上下两部分, 则
dS z
(
0
)
dS z
(
4 a ln a
h
)
被平行平面z =±h截
z
h o
y x h
第7页/共26页
例2. 计算
其中是由平面
与
坐标面所围成的四面体的表面.
z
解: 设 1, 2, 3, 4分别表示在平面 1
上的部分,则 o
原式= 1 2 3 4 xyz dS
(地球半径R=6400km)
z
解: 建立坐标系如图覆, 盖曲面的
Rh
半顶角为, 利用球坐标系, 则
d S R2 sin d d
卫星覆盖面积为
A d S
R
2
2
0
sin
d
0
d
2 R2 (1 cos ) 2 R2 h
Rh
o
R
y
x
cos R
Rh
第16页/共26页
故通讯卫星的覆盖面积与地球表面积的比为
)
0
第12页/共26页
例6. 计算
其中是球面 x2 y2
z2 2(x y z).
解: 显然球心为 (1,1,1), 半径为 3
利用对称性可知
I
2 3
(
x
2
y
2
z2)dS
4 3
(x
y z) d S
xd S yd S zd S 利用重心公式
4 xd S 4 x d S
1 zx2 (k , k ) z y2 (k , k ) ( k )xy
f (x, y, z) dS
f (k ,k , z(k ,k ))
1 zx2 (k , k ) z y2 (k , k ) ( k )xy
f (k ,k , z(k ,k ))
(光滑)
1
z
2 x
(k
,
k
)
z
y
2
(
k
,
k
)
x xd S d S
第13页/共26页
例7. 计算
其中是介于平面
之间的圆柱面
分析: 若将曲面分为前后(或左右) z
两片, 则计算较繁. 解: 取曲面面积元素
则
I
H 2 R dz
0 R2 z2
2 arctan H
R
H
z dz
o
y
x
第14页/共26页
例8. 求椭圆柱面
位于xoy面上方及平面
A
4 R2
h 2( R h)
36 106 2(36 6.4) 106
第5页/共26页
例1. 计算曲面积分
其中是球面
被平面
截出的顶部.
解:
z
Dxy : x2 y2 a2 h2
1
z
2 x
z
2 y
h o
Dxy a y x
dS z
a dxdy
2
Dxy a2 x2 y2 a 0 d
a2 h2 rd r
0
a2 r2
2
a
1 ln(a2 2
r2)
a2 h2
(
k
)
x
y
f (x, y, Dx y
) 1 zx2 (x, y) z y2 (x, y)dxdy
第4页/共26页
说明: 1)如果曲面方程为
x x( y, z), ( y, z) Dyz
或 y y(x, z), (x, z) Dxz 可有类似的公式. 2)若曲面为参数方程, 只要求出在参数意义下dS 的表达式, 也可将对面积的曲面积分转化为对参数 的二重积分. (见本节后面的例4, 例5)
