第三章 逻辑代数基础 作业题(参考答案)
第3章 逻辑代数(习题)

CD
AB
00 01 11 10
00 1 1
1
01
1
(1) F1 m(0,1,2,4) d(5,6)
BC
11 1
1
10 1 1
1
(2) F2 m(3,5,6,7,10) d(0,1,2,4,8)
CD
AB
00 01 11 10
00 x x 1 x
(a)
BC
A
00 01 11 10
0 11
表 T3.4(3表)T3.4(3) A B CA FB C F 0 0 00 0 0 0 0 0 10 10 1 1 0 1 00 01 0 0 0 1 10 1 1 1 1 0 01 0 0 0 1 0 11 0 1 0 1 1 01 1 0 1 1 1 11 1 1 1
(3)
A
表 T3.4(1)
ABCD ABCD ABCD ABC D ABCD ABCD
3.2 答案
(1) 左边 AB B AB AB B A B 右边 (2) 左边 A B CCD (B C)(ABD BC)
(A B C) CD ABCD BC
A B C C D ABCD BC A B 1 D ABCD BC 1 右边
0 0 0X 0Y 1Z 1F
O 000 0
B
0 0 1 0 10 01 01
O
010 1
C
011 0
0 1 0 1 10 00 10
O
101 1
F 0 1 0 1 11 00 00
O
111 1
表 T3.4(2)
1 1A B C F t 000 0
1 10 0 1 1
0 1 0t 1
《数字逻辑》第3章习题答案

题
【3-1】填空: (1) 逻辑代数中有三种最基本运算: 与 、 或 和 非 ,在此基础上又派生出五种基本运算, 分别为 与非 、 或非 、 异或 、 同或 、和 与或非 。 (2) 与运算的法则可概述为:有 0 出 0 ,全 1 出 1 ;类似地,或运算的法则为 有”1”出”1”, 全”0”出”0” 。 (3) 摩根定理表示为: A B = A B ; A B = A B 。 (4) 函数表达式 Y= AB C D ,则其对偶式为 Y ' = ( A B)C D 。 积的形式结果应为 M ( 0,1,2,4,5,8,9,10)。 (5) 函数式 F=AB+BC+CD 写成最小项之和的形式结果应为 m ((3,6,7,11,12,13,14,15)), 写成最大项之
0 0 1 1 1 1
1 1 0 0 1 1
0 1 0 1 0 1
1 1 0 0 1 0
【3-8】写出下列函数的反函数 F ,并将其化成最简与或式。 (1) F1 ( A D )( B C D)( AB C ) (2) F2 ( A B )( BCD E )( B C E )(C A) (3) F3 A B C A D (4) F4 ( A B)C ( B C ) D 解: (1) F1 AD C (2) F2 AB A C E (3) F3 AB AC A D (4) F4 BC C D ABD A B C 【3-9】用对偶规则,写出下列函数的对偶式 F ,再将 F 化为最简与或式。 (1) F1 AB B C A C (2) F2 A B C D (3) F3 ( A C )( B C D)( A B D) ABC (4) F4 ( A B )( A C )( B C )(C D) (5) F5 AB C CD BD C 解:题中各函数对偶函数的最简与或式如下: (1) F1 A BC AB C (2) F2 A B D A C D (3) F3 AC A BD (4) F4 A BC B C CD (5) F5 ABC D (6) F6 AB C D 【3-10】已知逻辑函数 F A B C , G=A⊙B⊙C,试用代数法证明: F G 。 解:
第3章 逻辑代数基础-习题答案

第3章 逻辑代数基础3.1 已知逻辑函数真值表如题表3.1所示,写出函数对应的标准与或表达式和标准或与表达式。
解: (0,1,4,5)()()()()(2,3,6,7)F A B C A B C A B C A B C A B C A B C A B C A B C =+++==++++++++=∑∏3.2 写出下列函数的标准与或式和标准或与式。
(1)()()()X A B D A C D B C D =++++++ 解:(先求标准或与式,得最大项;最大项中没有的编号构成最小项,组成标准与或式)()()()()()()()()(0,1,2,6,14)(3,4,5,7,8,9,10,11,12,13,15)X A B D A C D B C D A B C D A B C D A B C D A B C D A B C D =++++++=+++++++++++++++==∑∏ (2) X BCD AC D A C D A B D =+++ 解:(先求标准与或式,得最小项;最小项中没有的编号构成最大项,组成标准或与式)(0,2,4,7,8,12,15)(1,3,5,6,9,10,11,13,14)X BCD AC D A C D A B DABCD ABCD ABC D AB C D ABC D A B C D A BC D =+++=++++++==∑∏3.3 使逻辑函数()()()()()X A B B C A C A C B C =+++++为0的逻辑变量组合有哪些?使之为1的逻辑变量组合有哪些? 解:()()()()()()()()()()()(1,2,3,4,5,6)(0,7)X A B B C A C A C B C A B C A B C A B C A B C A B C A B C =+++++=++++++++++++==∑∏ 使函数为0的组合即最大项,有ABC =“110”,“101”,“100”,“011”,“010”,“001”;使之为1的逻辑变量组合有ABC =“000”,“111”。
第三章 逻辑代数基础 作业题(参考答案)

第三章逻辑代数基础(Basis of Logic Algebra)1.知识要点逻辑代数(Logic Algebra)的公理、定理及其在逻辑代数化简时的作用;逻辑函数的表达形式及相互转换;最小项(Minterm)和最大项(Maxterm)的基本概念和性质;利用卡诺图(Karnaugh Maps)化简逻辑函数的方法。
重点:1.逻辑代数的公理(Axioms)、定理(Theorems),正负逻辑(Positive Logic, Negative Logic)的概念与对偶关系(Duality Theorems)、反演关系(Complement Theorems)、香农展开定理,及其在逻辑代数化简时的作用;2.逻辑函数的表达形式:积之和与和之积标准型、真值表(Truth Table)、卡诺图(Karnaugh Maps)、最小逻辑表达式之间的关系及相互转换;3.最小项(Minterm)和最大项(Maxterm)的基本概念和性质;4.利用卡诺图化简逻辑函数的方法。
难点:利用卡诺图对逻辑函数进行化简与运算的方法(1)正逻辑(Positive Logic)、负逻辑(Negative Logic)的概念以及两者之间的关系。
数字电路中用电压的高低表示逻辑值1和0,将代数中低电压(一般为参考地0V)附近的信号称为低电平,将代数中高电压(一般为电源电压)附近的信号称为高电平。
以高电平表示1,低电平表示0,实现的逻辑关系称为正逻辑(Positive Logic),相反,以高电平表示0,低电平表示1,实现的逻辑关系称为负逻辑(Negative Logic),两者之间的逻辑关系为对偶关系。
(2)逻辑函数的标准表达式积之和标准形式(又称为标准和、最小项和式):每个与项都是最小项的与或表达式。
和之积标准形式(又称为标准积、最大项积式):每个或项都是最大项的或与表达式。
逻辑函数的表达形式具有多样性,但标准形式是唯一的,它们和真值表之间有严格的对应关系。
第3章 逻辑代数基础答案.docx

第3章逻辑代数习题33. 1求下列函数的反函数(1) F = AB + C(A + D)(2)y = A(万+ C万+ CD)解:(1)F = AB + C(A + D)=AB*C(A + D)= (A + B)*(C + AD)=AC + BC + ABD(2)F = AB + C(A + D)=AB*C(A + D)= (A + B)*(C + AD)=AC + BC + ABD3. 2求下列函数的对偶式(1)Y = AB* CD* DAB(2)Y = A + C + B + C + A + B + B + C解:(1)Y = AB* CD* DABY'=A + B + C + D + D + A + B(2)Y = A + C + B + C + A + B + B + CY'=ACB^CABB^C3. 3用基本定理和公式证明下列等式(1)ABC + ABC + ABC = AB + AC(2)AB+ AC+ BC AB + C(3)A万+ BD + AD + DC^A万+ Z)(4)BC + D +万(万 + C)(DA + B) = B + D(5)AB + AB + AB + AB = 1(6)(A + B)(A + B)(A + B)(A + B) = 0(7) AB + BC + CA = AB + BC + CA(8)(A + B + C) • AB + BC + CA + ABC = (A + 万 +。
・(AB + BC + CA) + 云万©(9)A©B©C=A0BOC(10)A®B = AQB证明:(1)ABC + ABC + ABC = AB + AC左式=ABC + ABC + ABC=(ABC + ABC) + (ABC + ABC)-AB(C + C) + AC(B + B)=AB + AC =右式(2)AB+ AC+ BC AB + C左式= AB + AC + BC=AB + AC(B + B) + BC=AB + ABC + ABC + BC= B(A + AC) + B(AC + C)=AB + BC + BC=AB + C =右式(3)A万+ BD + AD + DC^AB + D左式=A万+ 切+ l£)+ OC=AB + BD + A(B + B)D + DC=B(A + AZ)) + BD + ABD + DC=AB + BD + BD + ABD + DC=AB+D+ABD+DC=AB + D =右式(4)BC + D +万(万 + C)(DA + B) = B + D左式= BC + D + D(B + C)(DA + B)=BC + D + BD(B+ C}=BC+D+BCD=BC+D+BC=B + D =右式(5)AB + AB + AB + AB = 1&^ = AB + AB + AB + AB=A(B + B) + A(B + B)= A + A=]=右式(6)(A + B)(A + 万)Q + B)Q + 万)=0左式=(A + fi)(A + B)(A + B)(A + 万)=(A + B)(A + B)(A + B)(A + B)=(A + B) + (A + B) + (A + B) + (A + B)=AB + AB + AB + AB=1 = 0 =右式(7)AB + BC + CA = AB + BC + CA根据代入规则,令A=B,,B=C,,C=A,左式= AB + BC + CA= B'C'+C'A'+ A'B'再次利用代入规则可得左式= B'C'+C'A' + A'B'= XB + §C + C如右式(8)(A + 5 + C) • AB + BC + CA + ABC = (M + 万 + C)・(AB + BC + CA) + ~ABC左式=(A + B + C) • AB + BC + CA + ABC=(A + B + C) • AB + BC + CA + ABC= (A + B + C)*(AB + BC + CA) + ABC=右式(9)A©B©C=AOB©C左式=A㊉3㊉C= A©BC + (A ㊉B R= (AOB)C+(A©5)C=A©BOC=右式(10)万= AOB左式=A®B= AB + AB-AB+AB=A0B(11)若A®B = C则= A®C = B由A©5 = A5 + A5 = CnJMB(AB + AB) = BC B* AB + AB = 5C艮"万=BC AB = BC将以上两式相加得配+ BC = A(B + B)即B©C=A同理可MA © C = B3.4 设Y ,= Z…, (0, 4,8, 12), %=£,“(1,4, 7,9, 10),试求下列逻辑函数:(1) A =匕+匕(2)L2 =匕•匕(3)L} =Y X・K解:(1)Lj = Kj + Y2A=匕+匕= £〃?(0,4,8,12) + £〃?(l,4,7,9,10)= £〃?(0,l,4,7,8,9,10,12)(2)L2 =Y t»Y2右=约•匕= £m(0,4,8,12)・£m(l,4,7,9,10)= £m(4)(3)L} =Y X・KA=K况=£m(0,4,8,12)・却1,4,7,9,10)= £〃?(0,8,12)3.5已知Y,=riM (0,2, 4, 6), 丫亓日心(1, 3, 5, 7),试求下列逻辑函数:(1) A =匕+七(2)L2 =匕・*(3)£3 =工•匕(4)L4=1T«K解:匕=f[M(0,2,4,6)= £m(0,2,4,6)K = f[M(l,3,5,7)= £〃?(1,3,5,7)(1)Lj = Kj + Y2A=匕+匕=E=0(2)L2 =匕•匕= X+Y;= £m(0,2,4,6) + £m(l,3,5,7)=0(3)L3=K•匕♦ X •七=K・M= £〃?(0,2,4,6)・£〃?(l,3,5,7)= £m(0,2,4,6)(4)L4=Y[»Y^乙4="= £m(0,2,4,6)・£m(l,3,5,7)3.6试写出图P3. 6所示电路的逻辑函数表达式。
数字逻辑第3章答案
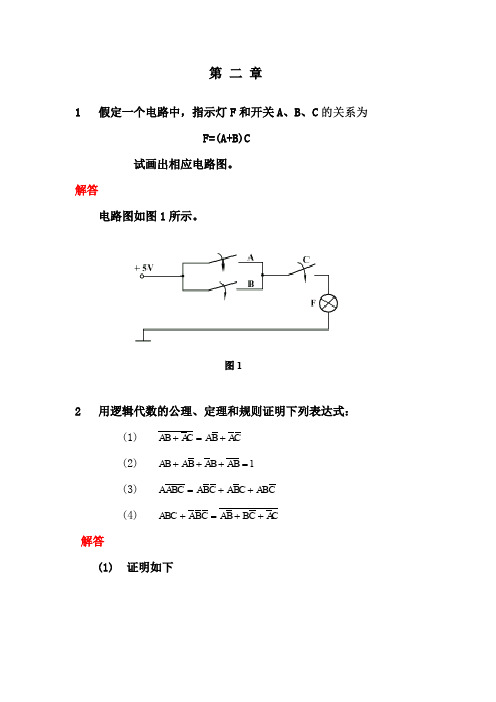
F, A B[(C D)E G]
5 (1) 如果已知 X + Y 和 X + Z 的逻辑值相同,那么 Y 和 Z 的逻
辑值一定相同。正确吗?为什么? (2) 如果已知 XY 和 XZ 的逻辑值相同,那么那么 Y 和 Z 的逻辑值
一定相同。正确吗?为什么? (3)如果已知 X + Y 和 X + Z 的逻辑值相同,且 XY 和 XZ 的逻辑
(1) F(A, B,C, D) BD AD CD CD ACD ABD
(2) F(A, B,C, D) (AB AB) C (AB AB) C
解答
G(A, B,C, D) AB BC AC (A B C) ABC
(1) 当 b a 时,令 a=1,b=0 能得到最简“与-或”表达式: F BC CD ACD (3 项)
(2) 当 a=1,b=1 时,能得到最简的“与-或”表达式:
F BC CD AC (3 项)
11 用列表法化简逻辑函数
F(A, B,C, D) m(0,2,3,5,7,8,10,11,13,15)
10
0
0
01 0 0 1 1
1
1
10 0 0 1 1
1
1
11 0 1 0 1
0
0
4 求下列函数的反函数和对偶函数: (1) F AB AB
(2) F A B A C C DE E
(3) F (A B)(C DAC)
(4) F A B CD E G
值相同,那么 Y = Z。正确吗?为什么? (4) 如果已知 X+Y 和 X·Y 的逻辑值相同,那么 X 和 Y 的逻辑值
第三章 逻辑代数基础 作业题(参考答案)

第三章逻辑代数基础(Basis of Logic Algebra)1.知识要点逻辑代数(Logic Algebra)得公理、定理及其在逻辑代数化简时得作用;逻辑函数得表达形式及相互转换;最小项(Minterm)与最大项(Maxterm)得基本概念与性质;利用卡诺图(Karnaugh Maps)化简逻辑函数得方法。
重点:1.逻辑代数得公理(Axioms)、定理(Theorems),正负逻辑(Positive Logic, Negative Logic)得概念与对偶关系(Duality Theorems)、反演关系(plement Theorems)、香农展开定理,及其在逻辑代数化简时得作用;2.逻辑函数得表达形式:积之与与与之积标准型、真值表(Truth Table)、卡诺图(Karnaugh Maps)、最小逻辑表达式之间得关系及相互转换;3.最小项(Minterm)与最大项(Maxterm)得基本概念与性质;4.利用卡诺图化简逻辑函数得方法。
难点:利用卡诺图对逻辑函数进行化简与运算得方法(1)正逻辑(Positive Logic)、负逻辑(Negative Logic)得概念以及两者之间得关系。
数字电路中用电压得高低表示逻辑值1与0,将代数中低电压(一般为参考地0V)附近得信号称为低电平,将代数中高电压(一般为电源电压)附近得信号称为高电平。
以高电平表示1,低电平表示0,实现得逻辑关系称为正逻辑(Positive Logic),相反,以高电平表示0,低电平表示1,实现得逻辑关系称为负逻辑(Negative Logic),两者之间得逻辑关系为对偶关系。
(2)逻辑函数得标准表达式积之与标准形式(又称为标准与、最小项与式):每个与项都就是最小项得与或表达式。
与之积标准形式(又称为标准积、最大项积式):每个或项都就是最大项得或与表达式。
逻辑函数得表达形式具有多样性,但标准形式就是唯一得,它们与真值表之间有严格得对应关系。
数字逻辑课后答案 第三章

第三章 时序逻辑1.写出触发器的次态方程,并根据已给波形画出输出 Q 的波形。
解:2. 说明由RS 触发器组成的防抖动电路的工作原理,画出对应输入输出波形解:3. 已知JK 信号如图,请画出负边沿JK 触发器的输出波形(设触发器的初态为0)1)(1=+++=+c b a Qa cb Q nn4. 写出下图所示个触发器次态方程,指出CP 脉冲到来时,触发器置“1”的条件。
解:(1),若使触发器置“1”,则A 、B 取值相异。
(2),若使触发器置“1”,则A 、B 、C 、D 取值为奇数个1。
5.写出各触发器的次态方程,并按所给的CP 信号,画出各触发器的输出波形(设初态为0)解:6. 设计实现8位数据的串行→并行转换器。
B A B A D +=DC B A K J ⊕⊕⊕==Q AQ B Q D Q C Q E Q F Q7. 分析下图所示同步计数电路解:先写出激励方程,然后求得状态方程状态图如下:该计数器是五进制计数器,可以自启动。
8. 作出状态转移表和状态图,确定其输出序列。
解:求得状态方程如下故输出序列为:000119. 用D 触发器构成按循环码(000→001→011→111→101→100→000)规律工作的六进制同步计数器解:先列出真值表,然后求得激励方程PS NS 输出N0 0 0 0 0 1 00 0 1 0 1 1 0 0 1 1 1 1 1 0 1 1 1 1 0 1 0 1 0 1 1 0 0 0 1 0 0 0 0 0 1化简得:逻辑电路图如下:n Q 2n Q 1n Q 012+n Q 11+n Q 10+n Q n n n nn n n n n n nnQ Q Q Q Q Q Q Q Q Q Q Q Z 121002*********+==+==+++nnn nnn nnnn QQ Q D QQ Q D QQ Q Q D 121211121122+====+==+++10. 用D 触发器设计3位二进制加法计数器,并画出波形图。
代数第三章习题解答

习题三习题解答 (A)1.用消元法解以下线性方程组.(1)⎪⎪⎩⎪⎪⎨⎧-=-+=+-=+--=-+3102332362382321321321321x x x x x x x x x x x x .(2)⎪⎩⎪⎨⎧=+-+-=--++=+---84342222222543215432154321x x x x x x x x x x x x x x x .(3)⎪⎩⎪⎨⎧-=--+=-+=--+55631236232343213214321x x x x x x x x x x x . (4)⎪⎪⎩⎪⎪⎨⎧-=-+-+=+-+-=+-+-=+-+-137824633422322254321543215432154321x x x x x x x x x x x x x x x x x x x x .(5)⎪⎪⎩⎪⎪⎨⎧=-+-+=-++-=-+-=--+0744420436240203543215432143215421x x x x x x x x x x x x x x x x x x .(6)⎪⎪⎩⎪⎪⎨⎧=--=+-=--=+-05220430320321321321321x x x x x x x x x x x x .解:(1) ⎪⎪⎪⎪⎪⎭⎫⎝⎛----→⎪⎪⎪⎪⎪⎭⎫⎝⎛----=614409175061440382131023311236213821A⎪⎪⎪⎪⎪⎭⎫⎝⎛---→⎪⎪⎪⎪⎪⎭⎫⎝⎛---→00003100120103001000031001201027021, 所以原方程组的解为31-=x ,122-=x 33-=x .(2) ⎪⎪⎪⎭⎫⎝⎛-----→⎪⎪⎪⎭⎫ ⎝⎛-------=252450052450222121814113412212222121A ⎪⎪⎪⎭⎫ ⎝⎛----→200000052450222121, 所以原方程组无解.(3) ⎪⎪⎪⎭⎫ ⎝⎛-----→⎪⎪⎪⎭⎫ ⎝⎛------=8440062100312315563112036231231A ⎪⎪⎪⎭⎫ ⎝⎛-→410002010030031, 所以原方程组的全部解为⎪⎪⎩⎪⎪⎨⎧=-==-=42334321x x c x cx 〔c 为任意常数〕.(4)⎪⎪⎪⎪⎪⎭⎫⎝⎛---------→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---------=131111782463211122342231131111782463342231211122A⎪⎪⎪⎪⎪⎭⎫⎝⎛→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------→000000457100226010102001000000457100231110342231, 所以原方程组的全部解为⎪⎪⎪⎩⎪⎪⎪⎨⎧==--=--=-=25142132121157426221c x c x c c x c c x c x (21,c c 为任意常数)..(5) ⎪⎪⎪⎪⎪⎭⎫⎝⎛------→⎪⎪⎪⎪⎪⎭⎫⎝⎛--------=05102200015660012220013011074242043624001211013011A ⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----→00000003110000650110067011, 所以原方程组的全部解为⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧===+=+-=252413212211316567c x c x c x c c x c c x (21,c c 为任意常数).(6) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------=700120310111522413132111A ⎪⎪⎪⎪⎪⎭⎫⎝⎛→⎪⎪⎪⎪⎪⎭⎫⎝⎛-→000100010001000100310111, 所以原方程组的解为⎪⎩⎪⎨⎧===000321x x x .2.当k 为何值时,齐次线性方程组 有非零解,并求出非零解.解:⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛--=0120253012101202530374k k A⎪⎪⎪⎭⎫ ⎝⎛+---→023*********k ⎪⎪⎪⎭⎫ ⎝⎛---→010*********k , 当01=-k ,即1=k 时,原方程组有非零解,当1=k 时,继续对上述行阶梯形矩阵施以初等行变换⎪⎪⎪⎭⎫ ⎝⎛-→000001100101,由此得⎩⎨⎧=-=3231x x x x ,令自由未知量c x =3,那么原方程组的非零解为⎪⎩⎪⎨⎧===c x c x c x 321〔c 为任意常数〕.3.当k 为何值时,线性方程组有唯一解?无解?有无穷多解?并在有无穷多解的情况下,求出它的解.解:)1(3)1(3112132-=++-+k k k kk k kk ,(1)当0≠k 且1≠k 时,所以原方程组有唯一解; (2)当0=k 时,⎪⎪⎪⎭⎫ ⎝⎛-→300001100213, 所以原方程组有无解;当1=k 时,⎪⎪⎪⎭⎫ ⎝⎛----→321032101101⎪⎪⎪⎭⎫ ⎝⎛--→000032101101, 由此得⎩⎨⎧+-=-=3231231x x x x ,令自由未知量c x =3,那么原方程组的全部解为⎪⎩⎪⎨⎧=+-=-=c x c x c x 321231〔c 为任意常数〕. 4.向量)2,0,2,3(1-=α,)2,2,1,6(2--=α,)2,3,4,1(3-=α,且向量β满足βααβαβ-=+--321)(4)(2,求向量β.解:由题有32142αααβ---=,所以 )2,3,4,1()2,2,1,6(4)2,0,2,3(2-------=β )10,5,12,17(--=.5.把β表示为其余向量的线性组合.(1))7,4,3(-=β,)1,0,1(1-=α,)1,1,1(2=α,)2,1,0(3-=α. (2))2,1,1(--=β,)1,1,1(1=α,)4,3,1(2---=α,)2,1,1(3-=α.解:(1)对矩阵),,,(321TT T T βααα施以初等行变换⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛→310010102001310041103011, 所以32132αααβ++=.(2)对矩阵),,,(321TT T T βααα施以所以,对应的线性方程组有无穷解,令 0,1,2321===k k k ,β表示向量321,,ααα的线性组合为32102αααβ++=.6.设有向量⎪⎪⎪⎭⎫ ⎝⎛+=1111λα,⎪⎪⎪⎭⎫ ⎝⎛+=1112λα,⎪⎪⎪⎭⎫ ⎝⎛+=λα1113,⎪⎪⎪⎭⎫ ⎝⎛=20λλβ.试问当λ为何值时,(1) β可由321,,ααα线性表示,且表达式唯一. (2) β可由321,,ααα线性表示,但表达式不唯一.(3) β不能由321,,ααα线性表示. 解:设βααα=++332211k k k ,因此有 其系数行列式=321,,ααα)3(1111111112+=+++λλλλλ,(1) 当30-≠λ≠λ且时,方程组有唯一解,此时,β可由321,,ααα唯一地线性表示.(2) 当0=λ时,方程组有无穷多个解,此时,β可由321,,ααα线性表示 ,但表达式不唯一.(3) 当3-=λ.时,上述方程组的增广阵⎪⎪⎪⎭⎫ ⎝⎛---→⎪⎪⎪⎭⎫ ⎝⎛---=6000123309211921131210112A ,由于3)(,2)(==A r A r ,因此,上述方程组无解,故β不能由321,,ααα线性表示 .7.判断以下向量组是线性相关,还是线性无关?(1) )3,2,1(1-=α,)5,0,2(2=α,)5,4,2(3---=α. (2) )1,3,2,1(1-=α,)2,3,1,1(2--=α,)1,0,1,2(3=α.解:(1) ⎪⎪⎪⎭⎫ ⎝⎛---→⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎪⎪⎭⎫ ⎝⎛=180140321542502321321αααA ⎪⎪⎪⎭⎫⎝⎛---→100140321, 于是3)(=A r ,所以向量组321,,ααα线性无关.(2) ⎪⎪⎪⎭⎫ ⎝⎛-----→⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛=363036301321101223111321321αααA⎪⎪⎪⎭⎫ ⎝⎛---→000036301321, 于是32)(<=A r ,所以向量组321,,ααα线性相关.8.设21,αα线性无关,βαβα++21,线性相关,试将β由21,αα线 性表示.解:因为βαβα++21,线性相关,所以存在不全为零的数21,k k ,使0)()(2211=+++βαβαk k ,即221121)(ααβk k k k --=+,因为21,αα线性无关,21k k +不为零,否那么,假设021=+k k ,必有02211=+ααk k ,于是021==k k ,这与21,k k 不全为零矛盾,所以 22121211ααβk k k k k k +-+-=,)0(21≠+k k9.设21,αα线性相关,21,ββ也线性相关,问2211,βαβα++是否一定线性相关?举例说明.解:否.例如⎪⎪⎭⎫ ⎝⎛=011α,⎪⎪⎭⎫ ⎝⎛=022α,⎪⎪⎭⎫ ⎝⎛=201β,⎪⎪⎭⎫⎝⎛=302β,于是⎪⎪⎭⎫ ⎝⎛=+2111βα,⎪⎪⎭⎫⎝⎛=+3222βα,而21,αα线性相关,21,ββ也线性相关,但2211,βαβα++线性无关.10.向量组)1,2,(1-=k α,)0,,2(2k -=α,)1,1,1(3-=α,求k 为何值时,向量组321,,ααα线性相关?线性无关?解:由题有)2)(1(1110212321k k k k +-=---=ααα,当2-≠k 且1≠k 时, 线性无关;当2-=k 或1=k 时, 线性相关.11.向量组s ααα,,,21 线性无关,试证:向量组1α,s ααααα++++ 2121,,也线性无关.证明:设有数s k k k ,,,21 ,使得0)()(232121=++++++++s s s s k k k k k k k ααα ,即 0)()(2121211=+++++++s s k k k αααααα , 由于向量组s ααα,,,21 线性无关,所以⎪⎪⎩⎪⎪⎨⎧==++=+++0003221s ss k k k k k k k ,解这个方程组得021====s k k k ,由此可知,向量组1α,s ααααα++++ 2121,,也线性无关.12.向量组321,,βββ由321,,ααα线性表示为3211αααβ+-=,3212αααβ-+=,3213αααβ++-=,(1)试把向量组321,,ααα由321,,βββ线性表示; (2)这两个向量组是否等价?解:(1)将向量组321,,ααα由321,,βββ线性表示的关系式写成矩阵形式为⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛321321111111111αααβββ, 于是⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛-3213211321210212121002121111111111ββββββααα, 所以向量组321,,ααα由321,,βββ线性表示的关系是为2112121ββα+=,3222121ββα+=,3132121ββα+=. (2)由(1)知,向量组321,,ααα与321,,βββ能相互线性表示,所以这两个向量组等价.13.设n 维向量组),0,,0,0,1(1 =α,),0,,0,1,1(2 =α1,1,1(=n α)1,, ,证明:n ααα,,,21 与n 维根本单位向量组n εεε,,,21 等价.证明:向量组n ααα,,,21 可由n 维根本单位向量组n εεε,,,21 线性表示,即11εα=,,,212 εεα+=,n n εεεα+++= 21.n 维根本单位向量组n εεε,,,21 可由向量组n ααα,,,21 线性表示,即11αε=,,,122 ααε-=1--=n n n ααε.向量组n ααα,,,21 与n 维根本单位向量组n εεε,,,21 能相互线性表示,所以这两个向量组等价.14.设向量组)1(,,,21>s s ααα 中,O ≠1α,并且i α不能由121,,,-i ααα 线性表示),,3,2(s i =,证明:s ααα,,,21 线性无关.证明:设存在数s k k k ,,,21 ,使得02211=+++s s k k k ααα .对于s k k k ,,,21 ,从右往左考虑,设i k 是第一个不为零的数,即0≠i k ,0,,01==+s i k k ,而O ≠1α,所以1≠i ,从而02211=+++i i k k k ααα ,即)(1112211--+++-=i i ii k k k k αααα , i α能由121,,,-i ααα 线性表示,与题设矛盾,因此,021====s k k k ,因此s ααα,,,21 线性无关.15.设向量组)2(,,,21≥r r ααα 线性无关,作以下线性组合 r k ααβ111+=,,,222 r k ααβ+=r r r r k ααβ111---+=,证明:121,,,-r βββ 也线性无关.证明:设存在数s t t t ,,,21 ,使得0112211=+++--r r t t t βββ ,即0)()()(111222111=++++++---r r r r r r k t k t k t αααααα ,于是0)(112211112211=+++++++----r r r r r k t k t k t t t t αααα ,由题设,向量组)2(,,,21≥r r ααα 线性无关,所以0112211121=+++====---r r r k t k t k t t t t ,121,,,-r βββ 也线性无关.16.证明:n 维向量组n ααα,,,21 线性无关的充分必要条件是任一n 维向量都可由n ααα,,,21 线性表示.证明:必要性 对于任一n 维向量β,向量组βααα,,,,21n 线性相关,从而存在不全为零的数k k k k n ,,,,21 使得02211=++++βαααk k k k n n ,其中0≠k ,那么n k k k ,,,21 不全为零,且02211=+++n n k k k ααα ,这与n ααα,,,21 线性无关矛盾.因为0≠k ,所以β可被n ααα,,,21 线性表示.充分性 因为任一n 维向量均可被n ααα,,,21 线性表示,所以n 维根本单位向量组n εεε,,,21 可由n ααα,,,21 线性表示,而,,,21 ααn α又可由n εεε,,,21 线性表示,所以n r r n n ==),,,(),,,(2121εεεααα ,从而n ααα,,,21 线性无关.17.设向量组s ααα,,,21 的秩为r )(s r <,求证:s ααα,,,21 中任意r 个线性无关的向量都是该向量组的一个极大线性无关组.证明:设向量组r i i i ααα,,,21 是向量组s ααα,,,21 中的线性无关的局部组,因为r r s =),,,(21ααα ,所以对于任一向量)1(s i i ≤≤α,向量组i i i i r αααα,,,,21 必线性相关。
逻辑代数基础试题及答案

逻辑代数基础试题及答案1. 逻辑代数中,与运算的符号是什么?答案:与运算的符号是“∧”。
2. 逻辑代数中,或运算的符号是什么?答案:或运算的符号是“∨”。
3. 逻辑代数中,非运算的符号是什么?答案:非运算的符号是“¬”。
4. 逻辑代数中,异或运算的符号是什么?答案:异或运算的符号是“⊕”。
5. 逻辑代数中,同或运算的符号是什么?答案:同或运算的符号是“≡”。
6. 逻辑代数中,如何表示变量A和变量B的与运算?答案:变量A和变量B的与运算表示为“A∧B”。
7. 逻辑代数中,如何表示变量A和变量B的或运算?答案:变量A和变量B的或运算表示为“A∨B”。
8. 逻辑代数中,如何表示变量A的非运算?答案:变量A的非运算表示为“¬A”。
9. 逻辑代数中,如何表示变量A和变量B的异或运算?答案:变量A和变量B的异或运算表示为“A⊕B”。
10. 逻辑代数中,如何表示变量A和变量B的同或运算?答案:变量A和变量B的同或运算表示为“A≡B”。
11. 在逻辑代数中,德摩根定律是什么?答案:德摩根定律包括两个部分,即(¬A)∨(¬B) = ¬(A∧B)和 (¬A)∧(¬B) = ¬(A∨B)。
12. 逻辑代数中,如何证明A∧(A∨B) = A?答案:根据分配律,A∧(A∨B) = (A∧A)∨(A∧B)。
由于A∧A = A,所以表达式简化为A∨(A∧B)。
由于A∨A = A,最终表达式简化为A。
13. 逻辑代数中,如何证明A∨(¬A∧B) = A∨B?答案:根据分配律,A∨(¬A∧B) = (A∨¬A)∧(A∨B)。
由于A∨¬ A = 1(真),表达式简化为1∧(A∨B)。
由于任何变量与1的与运算结果都是该变量本身,最终表达式简化为A∨B。
14. 逻辑代数中,如何证明A∧(¬A∨B) = ¬A∨B?答案:根据分配律,A∧(¬A∨B) = (A∧¬A)∨(A∧B)。
线性代数第一三四章练习题参考答案

第一章练习题参考答案一、填空题.1.-6d;2. 12;3. 23231414()()a a b b a a b b --;4. 1(1)(1)n n ---;5. -10;6. 0;7.-888;8. 4;-6.9. 132531445213253241541325344251,,a a a a a a a a a a a a a a a . 二、计算题. 1. 14().j k k j D x x ≤<≤=∏-2. 117!(2)27D =-+++.3. (1)(2)2121(1)(1)2n n n n n D x x x ---+=- ;4. 34560;5. 11[1]()nni i i i a x a x a==+⋅∏--∑.6.11024x +.7. 3(2)x x + 三、3(1)2n n -第三章练习参考答案 一、选择题1. C ;2. C ;3. C;4.C. 二、填空题1. (1)m nab -; 2.100122010345⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦; 3. 2123n --; 4. 108; 5. 2132-⎡⎤⎢⎥-⎣⎦; 6. 0; 7. 301050103⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦;8. 12; 9. 1100BA B A--⎡⎤⎢⎥⎣⎦; 10. 3E ;11. 3A E +; 12. 25A ;13. 88000880008808⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦; 14. 12.三、计算与证明题 1. 600006006060031⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦; 2. 02100000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦; 3. (1) T CA , (2) 101214122--⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦; 4. 2a =-; 5. 12345B A A E -=++; 6. -16; 7. 001010100B -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦; 8. 见课堂笔记; 9. 111212132122222331323233114411441144b b b b b b b b b b b b ⎡⎤-+⎢⎥⎢⎥⎢⎥-+⎢⎥⎢⎥⎢⎥-+⎢⎥⎣⎦. 10. 22211212513--⎡⎤⎢⎥-⎢⎥⎢⎥--⎣⎦. 11. 略. 第四章练习参考答案一、选择题1. C ;2. D ;3. B;4.D. 二、填空题1. (1,2,0,4)(0,3,3,10)T T t -+--, 其中t 为任意实数;2. 12,αα; 2;3. 3-;4.122113311441233224423443,,,,,E E E E E E E E E E E E ------; dimV=6;(2,3,1,4,2,2)T--; 5. 极大无关组为12,αα; 3124122,23αααααα=-+=-+;6. 12(1,0,1,1)(1,1,0,1)(1,3,1,0),T T Tk k α=-+-+-- 其中 12,k k 是任意数;7.141113M ⎡⎤=⎢⎥⎣⎦, 15(,)33TX =-. 三、计算与证明题1.(1) 当1b =时, 极大无关组为124,,ααα, (2) 当1b =时, 4α不能由12,αα线性表示, 3α能由12,αα线性表示(3122ααα=-+).2. (1) 5λ≠时,123,,ααα是基,21311222131222M λλλ⎡⎤⎢⎥-+⎢⎥⎢⎥=--⎢⎥⎢⎥+⎢⎥--⎣⎦; (2)ξ在基123,,βββ下的坐标为 (1,0,1)T;(3)所有非零向量为 (3,3,2)T k -. 3. (1) 只要证123,,0ααα≠ ,(2) 1232,0),1,1),2,1,5)TTTβββ==-=-;(3)M ⎤⎥⎥⎢⎥=⎢⎥⎢⎥⎢⎢⎣; (4)坐标为10)T β=.4. 1)通解为0112233X k k k ξηηη=+++, 其中021(,,0,0,0)33T ξ=-,1(5,2,3,0,0)Tη=,2(1,0,0,1,0)Tη=-,3(1,2,0,0,3)Tη=-, 123,,k k k 为任意数.2)解向量的极大无关组是0010203,,,.ξξηξηξη+++5. 1)过渡矩阵111100010010010M ⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥-⎣⎦; 2)α在基I 下的坐标为(1,1,1,1)TX =,α在基II 下的坐标为(4,1,1,1)TX =---; 3)(1,1,1,1)Tk β=,k 为任意常数.6. 15,5a b ==, 3121322βαα=+;7. 因为1V 的零元素00000⎡⎤=⎢⎥⎣⎦不在1V 中,所以1V 不是V 的子空间;而2V 是V 的子空间(主要验证运算封闭),2V 的基是2111010,,;dim 3.001001V -⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦6-10. 证明略。
第三章逻辑代数基础作业题(参考答案)

第三章逻辑代数基础(Basis of Logic Algebra)1.知识要点逻辑代数(Logic Algebra)的公理、定理及其在逻辑代数化简时的作用;逻辑函数的表达形式及相互转换;最小项(Minterm)和最大项(Maxterm)的基本概念和性质;利用卡诺图(Karnaugh Maps)化简逻辑函数的方法。
重点:1.逻辑代数的公理(Axioms)、定理(Theorems),正负逻辑(Positive Logic, Negative Logic)的概念与对偶关系(Duality Theorems)、反演关系(Complement Theorems)、香农展开定理,及其在逻辑代数化简时的作用;2.逻辑函数的表达形式:积之和与和之积标准型、真值表(Truth Table)、卡诺图(Karnaugh Maps)、最小逻辑表达式之间的关系及相互转换;3.最小项(Minterm)和最大项(Maxterm)的基本概念和性质;4.利用卡诺图化简逻辑函数的方法。
难点:利用卡诺图对逻辑函数进行化简与运算的方法(1)正逻辑(Positive Logic)、负逻辑(Negative Logic)的概念以及两者之间的关系。
数字电路中用电压的高低表示逻辑值1和0,将代数中低电压(一般为参考地0V)附近的信号称为低电平,将代数中高电压(一般为电源电压)附近的信号称为高电平。
以高电平表示1,低电平表示0,实现的逻辑关系称为正逻辑(Positive Logic),相反,以高电平表示0,低电平表示1,实现的逻辑关系称为负逻辑(Negative Logic),两者之间的逻辑关系为对偶关系。
(2)逻辑函数的标准表达式积之和标准形式(又称为标准和、最小项和式):每个与项都是最小项的与或表达式。
和之积标准形式(又称为标准积、最大项积式):每个或项都是最大项的或与表达式。
逻辑函数的表达形式具有多样性,但标准形式是唯一的,它们和真值表之间有严格的对应关系。
逻辑代数基础习题解答

分析电路中可能出现的竞争与冒险现象,采取相应措施进行消除或 抑制。
时序逻辑电路分析与设计
分析时序逻辑电路
了解时序逻辑电路的基本概念和组成,包括触发器、寄存器、计数器等。根据给定的电路图,分 析电路的工作原理和功能。
设计时序逻辑电路
根据实际需求,确定输入与输出之间的逻辑关系以及电路的状态转换关系。选择合适的触发器类 型,设计状态转换表和状态转换图,并进行电路连接。
备考策略指导
明确考试要求
了解考试形式和评分标准,明确备考方向和重 点。
制定复习计划
根据考试要求和自身情况,制定合理的复习计 划,并按照计划有序进行复习。
多做模拟试题
通过做模拟试题来检验自己的学习成果,找出自己的不足之处,有针对性地进 行弥补。
考试技巧点拨
仔细审题
在考试时,认真阅读题目,理解题意和要求 ,避免因为误解题意而导致失分。
题目1:逻辑代数中,基本的逻辑运算包括哪些?
02
A. 与、或、非
03
B. 与、或、异或
选择题解析
C. 与、非、同或 D. 或、非、异或 答案:A. 与、或、非
选择题解析
• 题目2:在逻辑代数中,下列哪个公式是正 确的?
选择题解析
C. A + A'B = A + B
B. A(A + B) = AB
表示方法
逻辑函数可以用多种方法表示,如真值表、逻辑表达式、卡诺图等。其中,真值表是列出所有输入组合及对应输 出的表格;逻辑表达式是用逻辑运算符和逻辑变量表示的式子;卡诺图是一种图形化表示方法,用于简化逻辑函 数。
02 逻辑代数化简方法
公式化简法
利用基本公式进行化简
逻辑代数基础练习题

数字电子技术
逻辑代数基础
单项选择题
26、和函数 F = AB + BC 不相等的表达式为
( )。
A AB BC
√
B AB BC
×
C ( A B)(B C) ×
D ABBC ×
分析提示
将各答案变换成与或式,再和给定函数式对比: AB BC AB BC A B BC A B AB BC AB BC AB BC (A B)(B C) AB AC BC AB BC ( A B)(B C) AB AC BC AB BC
)。
参考答案
1,2,3,4,5,6
分析提示
将给定的函数式作如下变换: F ( A, B,C) AB BC AC AB(C C) ( A A)BC A(B B)C ABC ABC ABC ABC ABC ABC m (1,2,3,4,5,6) 或列出给定函数式的真值表,再由真值表写出最小项表达式。
A B B C A B B C (A B)(B C) AB BC
第 12 页
数字电子技术
逻辑代数基础
单项选择题
29、图示电路均为TTL门,多余输入端接错的是
( )。
A√B
&
A AB
AB×
&
B 5V A B C
A+B× ≥1
≥1
&
A B D AB
AB+ CD
数字电子技术自测练习
逻辑代数基础
单项选择题 填空题
第1页
数字电子技术
逻辑代数基础
单项选择题
西工大逻辑代数基础作业答案

西工大逻辑代数基础作业答案
1.在式子n-3、a2b、m+s≤2、x、﹣ah、s=ab中代数式的个数有() [单选题] * A.6个
B.5个
C.4个(正确答案)
D.3个
2.下列代数式书写正确的是() [单选题] *
A.a4
B.m÷n
C.x(b+c)(正确答案)
3.代数式的意义是() [单选题] *
A.x除以y加3
B.y加3除x
C.y与3的和除以x
D.x除以y与3的和所得的商(正确答案)
4.若x表示某件物品的原价,则代数式(1+10%)x表示的意义是() [单选题] * A.该物品打九折后的价格
B.该物品价格上涨10%后的售价(正确答案)
C.该物品价格下降10%后的售价
D.该物品价格上涨10%时上涨的价格
5. 购买2个单价为a元的面包和5瓶单价为b元的饮料,所需钱数为() [单选题] *
A.(2a+b)元
B.3(a+b)元
C.(5a+2b)元
D.(2a+5b)元(正确答案)。
数字逻辑设计基础 何建新 高胜东 主编第3章 逻辑代数基础习题答案

第3章 逻辑代数基础3.3用逻辑代数的基本公式和定律将下列逻辑函数式化简为最简与-或表达式。
(3) AC +AD +BC +BD +BC E=+AD +BC +BD =+D +BC=+D +BCY A B A B A B A B A B =+() (7) ()()Y A B C D AC D AC A D =++++()C D A B A AC DC D AC DC D C D+++=+==+ =3.5根据反演规则求出下列逻辑函数的反函数。
(2) Y A B CD CD AB =++++ 解:()+()Y A B C D C D A B =++ (4) AB+A B A B AB Y AB =⋅++()解:[A +B (A+B)+(A +B A+B ()Y A B =⋅⋅⋅+())()]3.6 根据对偶规则,求出下列逻辑函数的对偶式。
(1) C A D B C A Y ++=)(解:'[()][]Y A C BD A C =++⋅+ (4) AC B A B A B A Y ++⋅+= 解:'[()()]()Y AB A B A B A C =++⋅+⋅+[题3-7] 将下列逻辑函数表示成“最小项之和”形式及“最大项之积”形式(1)(,,)(1,3,6,7)(0,2,4,5)F A B C AB AC BC m M =++==∑∏ [题3-8] 用卡诺图化简将下列逻辑函数为最简与或表示式:(3)D C B A D C B BD AD B A Y ++++=由逻辑函数式作卡诺图,得最简与-或表达式 Y B C B D A B=++ (8)∑∑+=)151413320()12119861()(,,,,,,,,,,,,,d m D C B A F解: Y AC BD BC D =++(10)⎩⎨⎧=++++=0AC BCD DC C B AD C A CD B A Y解:(,,,)Y A B C D D A B =+。
逻辑代数基础试题

逻辑代数基础一、选择题1. 以下代码中为相邻两个码字之间只有一位码有差异的是 。
A . 8421BCD 码B . 自然二进制码C . 余三码D . 格雷码2. 一位十六进制数可以用 位二进制数来表示。
A . 1B . 2C . 4D . 163. 十进制数25用8421BCD 码表示为 。
A .10 101B .0010 0101C .100101D .101014. 当逻辑函数有n 个变量时,共有 个变量取值组合?A. nB. 2nC. n 2D. 2n5. 逻辑函数的表示方法中具有唯一性的是 。
A .真值表 B.表达式 C.逻辑图 D.卡诺图6. 逻辑函数F=)(B A A ⊕⊕ = 。
A.BB.AC.B A ⊕D. B A ⊕7. A+BC= 。
A .A+B B.A+C C.(A+B)(A+C) D.B+C8. 在何种输入情况下,“与非”运算的结果是逻辑0。
A.全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是19. 在何种输入情况下,“或非”运算的结果是逻辑0。
A.全部输入是0 B.全部输入是1 C.任一输入为0,其他输入为1 D.任一输入为110. 与十进制数(53.5)10等值的数或代码为 。
A .(0101 0011.0101)8421BCDB .(35.8)16C .(110101.1)2D .(65.4)811. 与八进制数(47.3)8等值的数为 。
A. (100111.011)2B.(27.6)16C.(27.3 )16D. (100111.11)212.与模拟电路相比,数字电路主要的优点有 。
A.容易设计B.通用性强C.保密性好D.抗干扰能力强13.以下表达式中符合逻辑运算法则的是 。
A.C·C=C2B.1+1=10C.0<1D.A+1=114.逻辑变量的取值1和0可以表示: 。
A.开关的闭合、断开B.电位的高、低C.真与假D.电流的有、无二、判断题(正确打√,错误的打×)1.8421码1001比0001大。
数字逻辑第三章习题答案

A B C
Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7
&
G
3.21 F = X⊕Y⊕Z X 0 0 1 1 3.22 ⑴
74138 Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y X & F Z Z A B Y C0 C1 C2 C3 74153 F
74153
Y 0 1 0 1
F Z Z Z Z
74LS283
S3 S2 S1 S0
Y2Y4Y2Y1
3.29 ⑴ 当B=1时 F = C+C 静态 险象 静态1险象 时 静态1险象 当A=1,C=0 时 F = B+B 静态 险象 化简F 可消除险象。 化简 = B + AC 可消除险象。 静态1险象 ⑵ 当 B=C=D=1时 F = A+A 静态 险象 时 静态1险象 当 A=C=0 时 F = B+B 静态 险象 静态1险象 当 A=D=1,B=0 时 F = C+C 静态 险象 F = AB + BC + ACD + AC + BCD + ABD 可消除险象。 可消除险象。 3.30 ⑴ F=AB+CD+BCD+ACD ⑶ F=BD+BD+ABC+ACD
+5V
AGTB AGTB AEQB AEQB ALTB ALTB A0 B0 74LS85 A1 B1 A2 B2 A3 B3
X>Y X=Y X<Y
••• •••
••• •••
+5V
X12 Y12 X13 Y13 X14 Y14 X15 Y15
3.26 ⑸ 2421码→8421码 码 码 A = 0:+ 0000 A = 1:- 0110(+ 1010) A B C D
数字电路与逻辑统计答案第三章

第1页共8页 宁夏大学校址: 宁夏银川西夏区贺兰山西路 489 号 联系电话:0951-2077800
邮政编码:750021
宁夏大学物理电气信息学院 3.1.4 将下列各式转换成与-或形式: (a) A⊕ B ⊕ A⊕ D (b) A + B + C + D + C + D + A + D (c) AC ⋅ BDBC ⋅ AB
3.1.8 利用或非门实现下列函数: (a) L = AB + AC (b) L = ABCD + ABCD + ABCD + ABCD + ABCD + ABCD + ABCD
3.2.1 将下列函数展开为最小项表达式: (a) L = A(B + C)
第2页共8页 宁夏大学校址: 宁夏银川西夏区贺兰山西路 489 号 联系电话:0951-2077800
3.2.3 已知逻辑函数 L = AB + BC + C A ,试用真值表、卡诺图和逻辑图(与 非-与非)表示。
3.3.1 写出如图题3.3.1所示电路对应的真值表。 3.3.2 试分析图题3.3.2所示逻辑电路的功能。
第3页共8页 宁夏大学校址: 宁夏银川西夏区贺兰山西路 489 号 联系电话:0951-2077800
( ) (c) A + ABC + ACD + C + D E = A + CD + E
数字电路与逻辑设计
3.1.3 用代数法化简下列各式: (a) AB(BC + A) (c) ABC(B + C) (e) AB + AB + AB + AB (g)( A + B + C)( A + B + C) (i) AB + ( A + B) (k) ABCD + ABD + BCD + ABCD + BC (m) AB + ABC + A(B + AB)
数字电子电路与逻辑 刘可文主编 第三章 逻辑代数基础 答案

习 题3题3.1写出下述逻辑表达的真值表。
(1)L=C B D B C A ++⋅, (2)L=B C D A C B ++, (3)L= B A C B C A ++⋅, (4)L=C B A C B A C B A ++, (5)L= B A +, (6)L=D B C B A CD B ++ (7)L= BC A C AB C AB ++, (8)L= C A C A +, (9)L= BC A C AB C AB ++, (10)L= B A C B C A ++。
解:各个小题所对应的逻辑表达式的真值表如表3.1(1)、(2)、(3)、(4)、(5)、(6)、(7)、(8)、(9)、(10)所示。
D B A C B A CD B 表3.1 (7)L=表3.1 (2) L=B C D A C B ++的真值表(1)A ⊙0=A , (2)0A ⊕=A , (3)A ⊙1=A , (4),A 1A =⊕ (5)0A A =⊕,(6)1A A =⊕, (7)A ⊙A=1, (8)A ⊙A =0,(9))A B (C )C A (B C )B A (⊕⊕=⊕⊕=⊕⊕, (10))B C ()AC (C )B A (⊕=⊕,(11)A ⊙(B ⊙C)= B ⊙(A ⊙C), (12)A +(B ⊙C)=(AB ⊙AC)。
解:题3.2(1~12)的各个等式的真值表如表3.2(1)、(2)、(3)、(4)、(5)、(6)、(7)、(8)、(9)、(10)、(11)、(12)所示。
从表3.2(1)、(2)、(3)、(4)、(5)、(6)、(7)、(8)、(9)、(10)、(11)、(12)所示真值表的对应关系,可以证明命题各式成立。
表3.1 (8)L= C B A C B A +的真值表表3.1 (9) L=BC A C AB C AB ++的真值表表3.1 (10) L=B AC B C A ++的真值表表3.2 (1)真值表表3.2 (2)真值表 表3.2 (3)真值表 表3.2 (5)真值表 表3.2 (6)真值表表3.2 (4)真值表表3.2 (9) L=的真值表题3.3逻辑式A ⊕B ⊕C 的对偶式是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章逻辑代数基础(Basis of Logic Algebra)1.知识要点逻辑代数(Logic Algebra)的公理、定理及其在逻辑代数化简时的作用;逻辑函数的表达形式及相互转换;最小项(Minterm)和最大项(Maxterm)的基本概念和性质;利用卡诺图(Karnaugh Maps)化简逻辑函数的方法。
重点:1.逻辑代数的公理(Axioms)、定理(Theorems),正负逻辑(Positive Logic, Negative Logic)的概念与对偶关系(Duality Theorems)、反演关系(Complement Theorems)、香农展开定理,及其在逻辑代数化简时的作用;2.逻辑函数的表达形式:积之和与和之积标准型、真值表(Truth Table)、卡诺图(Karnaugh Maps)、最小逻辑表达式之间的关系及相互转换;3.最小项(Minterm)和最大项(Maxterm)的基本概念和性质;4.利用卡诺图化简逻辑函数的方法。
难点:利用卡诺图对逻辑函数进行化简与运算的方法(1)正逻辑(Positive Logic)、负逻辑(Negative Logic)的概念以及两者之间的关系。
数字电路中用电压的高低表示逻辑值1和0,将代数中低电压(一般为参考地0V)附近的信号称为低电平,将代数中高电压(一般为电源电压)附近的信号称为高电平。
以高电平表示1,低电平表示0,实现的逻辑关系称为正逻辑(Positive Logic),相反,以高电平表示0,低电平表示1,实现的逻辑关系称为负逻辑(Negative Logic),两者之间的逻辑关系为对偶关系。
(2)逻辑函数的标准表达式积之和标准形式(又称为标准和、最小项和式):每个与项都是最小项的与或表达式。
和之积标准形式(又称为标准积、最大项积式):每个或项都是最大项的或与表达式。
逻辑函数的表达形式具有多样性,但标准形式是唯一的,它们和真值表之间有严格的对应关系。
由真值表得到标准和的具体方法是:找出真值表中函数值为1的变量取值组合,每一组变量组合对应一个最小项(变量值为1的对应原变量,变量值为0的对应反变量),将这些最小项相或,即得到标准和表达式。
由真值表得到标准积的具体方法是:找出真值表中函数值为0的变量取值组合,每一组变量组合对应一个最大项(变量值为1的对应反变量,变量值为0的对应原变量),将这些最大项相与,即得到标准积表达式。
每个真值表所对应的标准和与标准积表达方式是唯一的。
(3)利用卡诺图化简逻辑函数卡诺图是真值表的图形表示,利用卡诺图对逻辑函数进行化简的原理是反复使用公式AB+AB′=A,对应到卡诺图上,即为相邻的小方格可以合并。
通常:2个相邻的方格可以合并,并可消去1个变量;4个相邻的方格可以合并,并可消去2个变量;8个相邻的方格可以合并,并可消去3个变量……在相邻方格合并的过程中,通常采用画圈的方法进行标记。
利用卡诺图化简,圈1的结果是得到最简和的表达式,圈0的结果是得到最简积的表达式。
利用卡诺图化简的步骤(以最简和为例):①填卡诺图;②找出全部质主蕴含项;③找到奇异1单元,圈出对应的质主蕴含项;④若未圈完所有1方格,则从剩余的主蕴含项中找出最简的;⑤写出各圈所对应的与项表达式(取值发生变化的变量不写,取值无变化的变量保留,取值为0写反变量,取值为1写原变量)。
⑥将所得到的与项相或,即为化简结果。
化简的原则是:圈1不圈0,1至少圈1次,圈数越少越好,圈越大越好。
(4)利用卡诺图对逻辑函数进行运算利用卡诺图可以完成逻辑函数的逻辑加(或)、逻辑乘(与)、反演(非)、异或等运算。
进行这些运算时,要求参加运算的两个卡诺图具有相同的维数(即变量数相同)。
①卡诺图相加两函数做逻辑加(或)运算时,只需将卡诺图中编号相同的各相应方格中的0、1按逻辑加的规则相或,而得到的卡诺图应包含每个相加卡诺图所出现的全部1项。
②卡诺图相乘两函数做逻辑乘(与)运算时,只需将卡诺图中编号相同的各相应方格中的0、1按逻辑乘的规则相与,所得到的卡诺图中的1方格,是参加相乘的卡诺图中都包含的1格。
③反演卡诺图的反演(非),是将函数F的卡诺图中各个为1的方格变换为0,将各个为0的方格变换为1。
④卡诺图异或两函数做异或运算,只需将卡诺图中编号相同的各相应方格中的0、1按异或运算的规则进行运算,所得到的卡诺图中的1方格,是进行异或运算的卡诺图中取值不同的方格。
2.ExercisesProve theorems (X+Y)(X+Z) = X+Y·Z using perfect induction.If X = 0, Left = (0+Y)(0+Z) = Y·Z Right = 0+ Y·Z = Y·Z ∴ Left = RightIf X = 1, Left = (1+Y)(1+Z) = 1·1 = 1Right = 1+ Y·Z = 1∴ Left = RightAccording to DeMorgan’s theorem, the complement of WX+YZ is W′+X′Y′+Z′. Yet both functions are 1 for WXYZ= 1110. How can both a function and its complement be 1 for the same input combination What’s wrong hereThe mistake is that the original operation priority has been changed.The complement of WX+YZ should be (W′+X′)(Y′+Z′)Use the theorems of switching algebra to simplify each of the following logic functions:(1) F = WXYZ(WXYZ′+WX′YZ+W′XYZ+WXY′Z)(2) F = AB+ABC′D+ABDE′+ A′BC′E+A′B′C′E(3) F = MRP+ QO′R′+MN+ONM+QPMO′(1) F = W·X·Y·Z·(W·X·Y·Z'+W·X'·Y·Z+W'·X·Y·Z+W·X·Y'·Z)= W·X·Y·Z·W·X·Y·Z'+ W·X·Y·Z·W·X'·Y·Z+ W·X·Y·Z·W'·X·Y·Z+ W·X·Y·Z·W·X·Y'·Z= 0(2) F = A·B·(1+C'·D+D·E') + A'·C'·E·(B+B') = A·B + A'·C'·E(3) F = M·R·P + Q·O'·R' + M·N + Q·P·M·O' = M·P·R + Q·O'·R' + M·P·Q·O' + M·N = M·P·R + Q·O'·R' + M·NWrite the truth table for each of the following logic functions:(1) F = AB′+B′C+CD′+CA′(2) F = (A′+B+C′)(A′+B′+D)(B+C+D′)(A+B+C+D)(3) F = AB+AB′C′+A′BC(4) F = XY′+YZ+Z′X(1)0101001101011111000110011101011011111000110101110111110(2)A B C D F00000000100010100111010010101101101011111000110010101001011011000110111110011111(3)A B C F00000010010001111001101011011111(4)X Y Z F00000010010001111001101111011111Write the canonical sum and product for each of the following logic functions:(1) FX,Y (1,2)∑(2) F =A,B(0,1,2)∏(3) F =A,B,C,D (1,2,5,6)∑(4) F = A′B+B′C+A(1) F = ∑X,Y (1,2) = X'·Y+X·Y' (标准和)= ∏X,Y(0,3) = (X+Y)·(X'+Y') (标准积)(2) F = ∏A,B (0,1,2) = (A+B)·(A+B')·(A'+B) (标准积)= ∑A,B (3) = A·B (标准和)(3) F = ∑A,B,C,D (1,2,5,6) = A'·B'·C'·D + A'·B'·C·D' + A'·B·C'·D + A'·B·C·D' (标准和)= ∏A,B,C,D (0,3,4,7,8,9,10,11,12,13,14,15)= (A+B+C+D)·(A+B+C'+D')·(A+B'+C+D)·(A+B'+C'+D')·(A'+B+C+D)·(A'+B+C+D')·(A'+B+C'+D)(A'+B+C'+D')·(A'+B'+C+D)·(A'+B'+C+D')·(A'+B'+C'+D)·(A'+B'+C'+D') (标准积)(4) F = A'·B+B'·C+A = A'·B·(C+C')+(A+A')·B'·C+A·(B+B')·(C+C')= A'·B·C+A'·B·C'+A·B'·C+A'·B'·C+A·B·C+A·B·C'+A·B'·C+A·B'·C'= A'·B·C+A'·B·C'+A·B'·C+A'·B'C+A·B·C+A·B·C'+A·B'C' (标准和)F = A'·B+B'·C+A = A+B+C (标准积)If the canonical sum for an n -input logic function is also a minimal sum, how many literals are in each product term of the sum Might there be any other minimal sums in this case若某函数的标准和也是最小和,说明其卡诺图中的1都不相邻,无法合并。
