必修一函数的图像专题

合集下载

2019高考数学《函数的图像》题型专题汇编

2019高考数学《函数的图像》题型专题汇编题型一作函数的图象1、分别画出下列函数的图象：(1)y ＝|lg(x －1)|； (2)y ＝2x ＋1－1； (3)y ＝x 2－|x |－2； (4)y ＝2x －1x －1.解 (1)首先作出y ＝lg x 的图象，然后将其向右平移1个单位，得到y ＝lg(x －1)的图象，再把所得图象在x 轴下方的部分翻折到x 轴上方，即得所求函数y ＝|lg(x －1)|的图象，如图①所示(实线部分)．(2)将y ＝2x 的图象向左平移1个单位，得到y ＝2x ＋1的图象，再将所得图象向下平移1个单位，得到y ＝2x＋1－1的图象，如图②所示．(3)y ＝x 2－|x |－2＝⎩⎪⎨⎪⎧x 2－x －2，x ≥0，x 2＋x －2，x <0，其图象如图③所示．(4)∵y ＝2＋1x －1，故函数的图象可由y ＝1x 的图象向右平移1个单位，再向上平移2个单位得到，如图④所示．题型二函数图象的辨识1、函数y ＝x 2ln|x ||x |的图象大致是( )答案 D解析从题设解析式中可以看出函数是偶函数，x ≠0，且当x >0时，y ＝x ln x ，y ′＝1＋ln x ，可知函数在区间⎝⎛⎭⎫0，1e 上单调递减，在区间⎝⎛⎭⎫1e ，＋∞上单调递增．由此可知应选D.2、设函数f (x )＝2x ，则如图所示的函数图象对应的函数解析式是( )A ．y ＝f (|x |)B ．y ＝－|f (x )|C ．y ＝－f (－|x |)D ．y ＝f (－|x |) 答案 C解析题图中是函数y ＝－2－|x |的图象，即函数y ＝－f (－|x |)的图象，故选C. 3、函数f (x )＝1＋log 2x 与g (x )＝⎝⎛⎭⎫12x在同一直角坐标系下的图象大致是( )答案 B解析因为函数g (x )＝⎝⎛⎭⎫12x 为减函数，且其图象必过点(0,1)，故排除A ，D.因为f (x )＝1＋log 2x 的图象是由y ＝log 2x 的图象上移1个单位得到的，所以f (x )为增函数，且图象必过点(1,1)，故可排除C ，故选B. 4、函数f (x )＝⎝⎛⎭⎫21＋e x －1·sin x 的图象的大致形状为( )答案 A解析 ∵f (x )＝⎝ ⎛⎭⎪⎫21＋e x －1·sin x ，∴f (－x )＝⎝ ⎛⎭⎪⎫21＋e －x －1·sin(－x ) ＝－⎝ ⎛⎭⎪⎫2e x1＋e x －1sin x ＝⎝ ⎛⎭⎪⎫21＋e x －1·sin x ＝f (x )，且f (x )的定义域为R ， ∴函数f (x )为偶函数，故排除C ，D ；当x ＝2时，f (2)＝⎝ ⎛⎭⎪⎫21＋e 2－1·sin 2<0，故排除B ，只有A 符合．5、若函数f (x )＝(ax 2＋bx )e x 的图象如图所示，则实数a ，b 的值可能为( )A ．a ＝1，b ＝2B ．a ＝1，b ＝－2C ．a ＝－1，b ＝2D ．a ＝－1，b ＝－2解析：选B.令f (x )＝0，则(ax 2＋bx )e x ＝0，解得x ＝0或x ＝－b a ，由图象可知，－b a ＞1，又当x ＞－ba 时，f (x )＞0，故a ＞0，结合选项知a ＝1，b ＝－2满足题意，故选B.6、如图，有四个平面图形分别是三角形、平行四边形、直角梯形、圆．垂直于x 轴的直线l ：x ＝t (0≤t ≤a )经过原点O 向右平行移动，l 在移动过程中扫过平面图形的面积为y (图中阴影部分)，若函数y ＝f (t )的大致图象如图所示，那么平面图形的形状不可能是( )解析：选C.由y ＝f (t )的图象可知面积递增的速度先快后慢，对于选项C ，后半程是匀速递增，所以平面图形的形状不可能是C.7、函数f (x )＝|x |＋ax2(其中a ∈R )的图象不可能是( )解析：选C.当a ＝0时，函数f (x )＝|x |＋ax 2＝|x |，函数的图象可以是B ；当a ＝1时，函数f (x )＝|x |＋a x 2＝|x |＋1x2，函数的图象可以是A ；当a ＝－1时，函数f (x )＝|x |＋a x 2 ＝|x |－1x 2，x >0时，|x |－1x 2＝0只有一个实数根x ＝1，函数的图象可以是D ；所以函数的图象不可能是C.故选C.8、已知f (x )＝⎩⎨⎧－2x ，－1≤x ≤0，x ，0＜x ≤1，则下列函数的图象错误的是( )解析：选D.在坐标平面内画出函数y ＝f (x )的图象，将函数y ＝f (x )的图象向右平移1个单位长度，得到函数y ＝f (x －1)的图象，因此A 正确；作函数y ＝f (x )的图象关于y 轴的对称图形，得到y ＝f (－x )的图象，因此B 正确；y ＝f (x )在[－1，1]上的值域是[0，2]，因此y ＝|f (x )|的图象与y ＝f (x )的图象重合，C 正确；y ＝f (|x |)的定义域是[－1，1]，且是偶函数，当0≤x ≤1时，y ＝f (|x |)＝x ，这部分的图象不是一条线段，因此选项D 不正确．故选D.9、如图，长方形ABCD 的边AB ＝2，BC ＝1，O 是AB 的中点，点P 沿着边BC ，CD 与DA 运动，记∠BOP ＝x .将动点P 到A ，B 两点距离之和表示为x 的函数f (x )，则y ＝f (x )的图象大致为( )答案 B解析当x ∈⎣⎡⎦⎤0，π4时，f (x )＝tan x ＋4＋tan 2x ，图象不会是直线段，从而排除A ，C ；当x ∈⎣⎡⎦⎤π4，3π4时，f ⎝⎛⎭⎫π4＝f ⎝⎛⎭⎫3π4＝1＋5，f ⎝⎛⎭⎫π2＝2 2.∵22<1＋5， ∴f ⎝⎛⎭⎫π2<f ⎝⎛⎭⎫π4＝f ⎝⎛⎭⎫3π4，从而排除D ，故选B.10、已知函数f (x )的图象如图所示，则f (x )的解析式可以是( )A ．f (x )＝ln|x |xB ．f (x )＝e xx C ．f (x )＝1x 2－1 D ．f (x )＝x －1x答案 A解析由函数图象可知，函数f (x )为奇函数，应排除B ，C.若函数为f (x )＝x －1x ，则x →＋∞时，f (x )→＋∞，排除D ，故选A.11、函数f (x )＝e x －e －xx 2的图象大致为( )答案 B解析 ∵y ＝e x －e －x 是奇函数，y ＝x 2是偶函数，∴f (x )＝e x －e －xx 2是奇函数，图象关于原点对称，排除A 选项．当x ＝1时，f (1)＝e －e －11＝e －1e >0，排除D 选项．又e>2，∴1e <12，∴e －1e >32，排除C 选项．故选B.12、已知定义在区间[0,4]上的函数y ＝f (x )的图象如图所示，则y ＝－f (2－x )的图象为( )答案 D解析方法一先作出函数y ＝f (x )的图象关于y 轴的对称图象，得到y ＝f (－x )的图象；然后将y ＝f (－x )的图象向右平移2个单位，得到y ＝f (2－x )的图象；再作y ＝f (2－x )的图象关于x 轴的对称图象，得到y ＝－f (2－x )的图象．故选D.方法二先作出函数y ＝f (x )的图象关于原点的对称图象，得到y ＝－f (－x )的图象；然后将y ＝－f (－x )的图象向右平移2个单位，得到y ＝－f (2－x )的图象．故选D. 方法三当x ＝0时，y ＝－f (2－0)＝－f (2)＝－4.故选D.题型三函数图象的应用命题点1 研究函数的性质1、已知函数f (x )＝x |x |－2x ，则下列结论正确的是( ) A ．f (x )是偶函数，单调递增区间是(0，＋∞) B ．f (x )是偶函数，单调递减区间是(－∞，1) C ．f (x )是奇函数，单调递减区间是(－1,1) D ．f (x )是奇函数，单调递增区间是(－∞，0) 答案 C解析将函数f (x )＝x |x |－2x ，去掉绝对值，得f (x )＝⎩⎪⎨⎪⎧x 2－2x ，x ≥0，－x 2－2x ，x <0，画出函数f (x )的图象，如图，观察图象可知，函数f (x )的图象关于原点对称，故函数f (x )为奇函数，且在(－1,1)上单调递减．2、已知函数f (x )＝|log 3x |，实数m ，n 满足0<m <n ，且f (m )＝f (n )，若f (x )在[m 2，n ]上的最大值为2，则nm ＝________. 答案 9解析作出函数f (x )＝|log 3x |的图象，观察可知0<m <1<n 且mn ＝1.若f (x )在[m 2，n ]上的最大值为2，从图象分析应有f (m 2)＝2， ∴log 3m 2＝－2，∴m 2＝19.从而m ＝13，n ＝3，故nm＝9.3、若函数f (x )＝⎩⎪⎨⎪⎧ax ＋b ，x <－1，ln （x ＋a ），x ≥－1的图象如图所示，则f (－3)等于___解析：由图象可得a (－1)＋b ＝3，ln(－1＋a )＝0，所以a ＝2，b ＝5，所以f (x )＝⎩⎪⎨⎪⎧2x ＋5，x <－1，ln （x ＋2），x ≥－1，故f (－3)＝2×(－3)＋5＝－1.答案：－14、已知f (x )＝2x －1，g (x )＝1－x 2，规定：当|f (x )|≥g (x )时，h (x )＝|f (x )|；当|f (x )|<g (x )时，h (x )＝－g (x )，则h (x )( )A ．有最小值－1，最大值1B ．有最大值1，无最小值C ．有最小值－1，无最大值D ．有最大值－1，无最小值答案 C解析画出y ＝|f (x )|＝|2x －1|与y ＝g (x )＝1－x 2的图象，它们交于A ，B 两点．由“规定”，在A ，B 两侧，|f (x )|≥g (x )，故h (x )＝|f (x )|；在A ，B 之间，|f (x )|<g (x )，故h (x )＝－g (x )．综上可知，y ＝h (x )的图象是图中的实线部分，因此h (x )有最小值－1，无最大值．5、已知函数f (x )＝⎩⎪⎨⎪⎧|x |，x ≤m ，x 2－2mx ＋4m ，x >m ，其中m >0.若存在实数b ，使得关于x 的方程f (x )＝b 有三个不同的根，则m 的取值范围是____________．答案 (3，＋∞)解析在同一坐标系中，作y ＝f (x )与y ＝b 的图象．当x >m 时，x 2－2mx ＋4m ＝(x －m )2＋4m －m 2，所以要使方程f (x )＝b 有三个不同的根，则有4m －m 2<m ，即m 2－3m >0.又m >0，解得m >3.6、不等式3sin ⎝⎛⎭⎫π2x －12log x <0的整数解的个数为________．答案 2解析不等式3sin ⎝⎛⎭⎫π2x －12log x <0，即3sin ⎝⎛⎭⎫π2x <12log x .设f (x )＝3sin ⎝⎛⎭⎫π2x ，g (x )＝12log x ，在同一坐标系中分别作出函数f (x )与g (x )的图象，由图象可知，当x 为整数3或7时，有f (x )<g (x )，所以不等式3sin ⎝⎛⎭⎫π2x －12log x <0的整数解的个数为2.7、已知函数f (x )＝⎩⎪⎨⎪⎧sin πx ，0≤x ≤1，log 2 020x ，x >1，若实数a ，b ，c 互不相等，且f (a )＝f (b )＝f (c )，则a ＋b ＋c 的取值范围是__________．答案 (2,2 021)解析函数f (x )＝⎩⎪⎨⎪⎧sin πx ，0≤x ≤1，log 2 020x ，x >1的图象如图所示，不妨令a <b <c ，由正弦曲线的对称性可知a ＋b ＝1，而1<c <2 020，所以2<a ＋b ＋c <2 021.8、已知点A (1，0)，点B 在曲线G ：y ＝ln x 上，若线段AB 与曲线M ：y ＝1x 相交且交点恰为线段AB 的中点，则称B 为曲线G 关于曲线M 的一个关联点．那么曲线G 关于曲线M 的关联点的个数为________．解析：设B (x 0，ln x 0)，x 0＞0，线段AB 的中点为C ，则C ⎝⎛⎭⎪⎫x 0＋12，ln x 02，又点C 在曲线M 上，故ln x 02＝2x 0＋1，即ln x 0＝4x 0＋1.此方程根的个数可以看作函数y ＝ln x 与y ＝4x ＋1的图象的交点个数．画出图象(如图)，可知两个函数的图象只有1个交点．答案：19、已知y ＝f (x )是定义在R 上的偶函数，当x ≥0时，f (x )＝x 2－2x . (1)求当x ＜0时，f (x )的解析式；(2)作出函数f (x )的图象，并指出其单调区间； (3)求f (x )在[－2，5]上的最小值，最大值．解：(1)设x ＜0，则－x ＞0，因为x ＞0时，f (x )＝x 2－2x .所以f (－x )＝(－x )2－2·(－x )＝x 2＋2x .因为y ＝f (x )是R 上的偶函数，所以f (x )＝f (－x )＝x 2＋2x . (2)函数f (x )的图象如图所示：由图可得：函数f (x )的单调递增区间为(－1，0)和(1，＋∞)；单调递减区间为(－∞，－1)和(0，1)． (3)由(2)中函数图象可得：在[－2，5]上，当x ＝±1时，取最小值－1，当x ＝5时，取最大值15. 10、已知函数f (x )＝x |m －x |(x ∈R )，且f (4)＝0. (1)求实数m 的值； (2)作出函数f (x )的图象；(3)根据图象指出f (x )的单调递减区间；(4)若方程f (x )＝a 只有一个实数根，求a 的取值范围．解：(1)因为f (4)＝0，所以4|m －4|＝0，即m ＝4.(2)f (x )＝x |x －4|＝⎩⎪⎨⎪⎧x （x －4）＝（x －2）2－4，x ≥4，－x （x －4）＝－（x －2）2＋4，x <4，f (x )的图象如图所示．(3)f (x )的单调递减区间是[2，4]．(4)从f (x )的图象可知，当a >4或a <0时，f (x )的图象与直线y ＝a 只有一个交点，方程f (x )＝a 只有一个实数根，即a 的取值范围是(－∞，0)∪(4，＋∞)．命题点2 解不等式1、函数f (x )是定义在[－4,4]上的偶函数，其在[0,4]上的图象如图所示，那么不等式f (x )cos x<0的解集为________________．答案 ⎝⎛⎭⎫－π2，－1∪⎝⎛⎭⎫1，π2 解析当x ∈⎝⎛⎭⎫0，π2时，y ＝cos x >0.当x ∈⎝⎛⎭⎫π2，4时，y ＝cos x <0. 结合y ＝f (x )，x ∈[0,4]上的图象知，当1<x <π2时，f (x )cos x <0.又函数y ＝f (x )cos x 为偶函数，所以在[－4,0]上，f (x )cos x <0的解集为⎝⎛⎭⎫－π2，－1，所以f (x )cos x<0的解集为⎝⎛⎭⎫－π2，－1∪⎝⎛⎭⎫1，π2. 2、定义在R 上的奇函数f (x )，满足f ⎝⎛⎭⎫－12＝0，且在(0，＋∞)上单调递减，则xf (x )＞0的解集为________．解析：因为函数f (x )是奇函数，在(0，＋∞)上单调递减，且f ⎝⎛⎭⎫－12＝0，所以f ⎝⎛⎭⎫12＝0，且在区间(－∞，0)上单调递减，因为当x ＜0，若－12＜x ＜0时，f (x )＜0，此时xf (x )＞0，当x ＞0，若0＜x ＜12时，f (x )＞0，此时xf (x )＞0，综上xf (x )＞0的解集为⎝⎛⎭⎫－12，0∪⎝⎛⎭⎫0，12. 答案：⎝⎛⎭⎫－12，0∪⎝⎛⎭⎫0，12 命题点3 求参数的取值范围1、已知函数()12log ,020x x x f x x >⎧⎪⎨⎪≤⎩，＝，，若关于x 的方程f (x )＝k 有两个不等的实数根，则实数k 的取值范围是________．答案 (0,1]解析作出函数y ＝f (x )与y ＝k 的图象，如图所示，由图可知k ∈(0,1]．2、已知函数f (x )＝|x －2|＋1，g (x )＝kx .若方程f (x )＝g (x )有两个不相等的实根，则实数k 的取值范围是__________．答案 ⎝⎛⎭⎫12，1解析先作出函数f (x )＝|x －2|＋1的图象，如图所示，当直线g (x )＝kx 与直线AB 平行时斜率为1，当直线g (x )＝kx 过A 点时斜率为12，故f (x )＝g (x )有两个不相等的实根时，k 的取值范围为⎝⎛⎭⎫12，1.3、设函数f (x )＝|x ＋a |，g (x )＝x －1，对于任意的x ∈R ，不等式f (x )≥g (x )恒成立，则实数a 的取值范围是__________．答案 [－1，＋∞)解析如图作出函数f (x )＝|x ＋a |与g (x )＝x －1的图象，观察图象可知，当且仅当－a ≤1，即a ≥－1时，不等式f (x )≥g (x )恒成立，因此a 的取值范围是[－1，＋∞)．4、给定min{a ，b }＝⎩⎪⎨⎪⎧a ，a ≤b ，b ，b ＜a ，已知函数f (x )＝min{x ，x 2－4x ＋4}＋4，若动直线y ＝m 与函数y ＝f (x )的图象有3个交点，则实数m 的取值范围为________．解析：函数f (x )＝min{x ，x 2－4x ＋4}＋4的图象如图所示，由于直线y ＝m 与函数y ＝f (x )的图象有3个交点，数形结合可得m 的取值范围为(4，5)．答案：(4，5)5、直线y ＝k (x ＋3)＋5(k ≠0)与曲线y ＝5x ＋17x ＋3的两个交点坐标分别为A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＋y 1＋y 2＝________．解析：因为y ＝5x ＋17x ＋3＝2x ＋3＋5，其图象关于点(－3，5)对称．又直线y ＝k (x ＋3)＋5过点(－3，5)，如图所示．所以A ，B 关于点(－3，5)对称，所以x 1＋x 2＝2×(－3)＝－6，y 1＋y 2＝2×5＝10. 所以x 1＋x 2＋y 1＋y 2＝4.答案：46、函数f (x )的图象与函数h (x )＝x ＋1x ＋2的图象关于点A (0，1)对称．(1)求f (x )的解析式；(2)若g (x )＝f (x )＋ax，且g (x )在区间(0，2]上为减函数，求实数a 的取值范围．解：(1)设f (x )图象上任一点P (x ，y )(x ≠0)，则点P 关于(0，1)点的对称点P ′(－x ，2－y )在h (x )的图象上，即2－y ＝－x －1x ＋2，即y ＝f (x )＝x ＋1x(x ≠0)．(2)g (x )＝f (x )＋ax ＝x ＋a ＋1x ，g ′(x )＝1－a ＋1x2.因为g (x )在(0，2]上为减函数，所以1－a ＋1x 2≤0在(0，2]上恒成立，即a ＋1≥x 2在(0，2]上恒成立，所以a ＋1≥4，即a ≥3，故实数a 的取值范围是[3，＋∞)．《函数的图像》课后作业1、y ＝2|x |sin 2x 的图象可能是( )答案 D解析由y ＝2|x |sin 2x 知函数的定义域为R ，令f (x )＝2|x |sin 2x ，则f (－x )＝2|－x |sin(－2x )＝－2|x |sin 2x .∵f (x )＝－f (－x )，∴f (x )为奇函数．∴f (x )的图象关于原点对称，故排除A ，B. 令f (x )＝2|x |sin 2x ＝0，解得x ＝k π2(k ∈Z )，∴当k ＝1时，x ＝π2，故排除C.故选D.2、如图，不规则四边形ABCD 中，AB 和CD 是线段，AD 和BC 是圆弧，直线l ⊥AB 交AB 于E ，当l 从左至右移动(与线段AB 有公共点)时，把四边形ABCD 分成两部分，设AE ＝x ，左侧部分的面积为y ，则y 关于x 的图象大致是( )答案 C解析当l 从左至右移动时，一开始面积的增加速度越来越快，过了D 点后面积保持匀速增加，图象呈直线变化，过了C 点后面积的增加速度又逐渐减慢．故选C.3、已知函数f (x )＝log a x (0<a <1)，则函数y ＝f (|x |＋1)的图象大致为( )答案 A解析方法一先作出函数f (x )＝log a x (0<a <1)的图象，当x >0时，y ＝f (|x |＋1)＝f (x ＋1)，其图象由函数f (x )的图象向左平移1个单位得到，又函数y ＝f (|x |＋1)为偶函数，所以再将函数y ＝f (x ＋1)(x >0)的图象关于y 轴对称翻折到y 轴左边，得到x <0时的图象，故选A. 方法二因为|x |＋1≥1,0<a <1，所以f (|x |＋1)＝log a (|x |＋1)≤0，故选A.4、函数f (x )＝⎩⎪⎨⎪⎧ax ＋b ，x <－1，ln (x ＋a )，x ≥－1 的图象如图所示，则f (－3)等于( )A ．－12B ．－54C ．－1D ．－2答案 C解析由图象可得－a ＋b ＝3，ln(－1＋a )＝0，得a ＝2，b ＝5，∴f (x )＝⎩⎪⎨⎪⎧2x ＋5，x <－1，ln (x ＋2)，x ≥－1，故f (－3)＝2×(－3)＋5＝－1，故选C.5、函数f (x )的图象向右平移1个单位，所得图象与曲线y ＝e x 关于y 轴对称，则f (x )的解析式为( ) A ．f (x )＝e x ＋1B ．f (x )＝e x －1C ．f (x )＝e－x ＋1D ．f (x )＝e－x －1答案 D解析与y ＝e x 的图象关于y 轴对称的函数为y ＝e －x .依题意，f (x )的图象向右平移一个单位，得y ＝e －x 的图象．∴f (x )的图象由y ＝e －x 的图象向左平移一个单位得到． ∴f (x )＝e －(x ＋1)＝e －x －1.6、已知函数f (x )的定义域为R ，且f (x )＝⎩⎪⎨⎪⎧2－x －1，x ≤0，f (x －1)，x >0，若方程f (x )＝x ＋a 有两个不同实根，则实数a的取值范围为( ) A ．(－∞，1) B ．(－∞，1] C ．(0,1) D ．(－∞，＋∞)答案 A解析当x ≤0时，f (x )＝2－x －1，当0<x ≤1时，－1<x －1≤0，f (x )＝f (x －1)＝2－(x －1)－1.类推有f (x )＝f (x －1)＝22－x －1，x ∈(1,2]，…，也就是说，x >0的部分是将x ∈(－1,0]的部分周期性向右平移1个单位得到的，其部分图象如图所示．若方程f (x )＝x ＋a 有两个不同的实数根，则函数f (x )的图象与直线y ＝x ＋a 有两个不同交点，故a <1，即a 的取值范围是(－∞，1)．7、设函数y ＝f (x ＋1)是定义在(－∞，0)∪(0，＋∞)上的偶函数，在区间(－∞，0)上是减函数，且图象过点(1,0)，则不等式(x －1)f (x )≤0的解集为______________．答案 {x |x ≤0或1<x ≤2}解析画出f (x )的大致图象如图所示．不等式(x －1)f (x )≤0可化为⎩⎨⎧ x >1，f (x )≤0或⎩⎨⎧x <1，f (x )≥0.由图可知符合条件的解集为{x |x ≤0或1<x ≤2}． 8、设函数y ＝f (x )的图象与y ＝2x －a的图象关于直线y ＝－x 对称，且f (－2)＋f (－4)＝1，则实数a ＝________.答案－2解析由函数y ＝f (x )的图象与y ＝2x －a 的图象关于直线y ＝－x 对称，可得f (x )＝－a －log 2(－x )，由f (－2)＋f (－4)＝1，可得－a －log 22－a －log 24＝1，解得a ＝－2.9、已知f (x )是以2为周期的偶函数，当x ∈[0,1]时，f (x )＝x ，且在[－1,3]内，关于x 的方程f (x )＝kx ＋k ＋1(k ∈R ，k ≠－1)有四个实数根，则k 的取值范围是__________．答案 ⎝⎛⎭⎫－13，0 解析由题意作出f (x )在[－1,3]上的示意图如图所示，记y ＝k (x ＋1)＋1，∴函数y ＝k (x ＋1)＋1的图象过定点A (－1,1)．记B (2,0)，由图象知，方程有四个实数根，即函数f (x )与y ＝kx ＋k ＋1的图象有四个交点，故k AB <k <0，k AB ＝0－12－(－1)＝－13，∴－13<k <0.10、给定min{a ，b }＝⎩⎪⎨⎪⎧a ，a ≤b ，b ，b <a ，已知函数f (x )＝min{x ，x 2－4x ＋4}＋4，若动直线y ＝m 与函数y ＝f (x )的图象有3个交点，则实数m 的取值范围为__________．答案 (4,5)解析作出函数f (x )的图象，函数f (x )＝min{x ，x 2－4x ＋4}＋4的图象如图所示，由于直线y ＝m 与函数y ＝f (x )的图象有3个交点，数形结合可得m 的取值范围为(4,5)．11、数f (x )＝⎩⎪⎨⎪⎧log 2(1－x )＋1，－1≤x <0，x 3－3x ＋2，0≤x ≤a 的值域为[0,2]，则实数a 的取值范围是_____答案 [1，3]解析先作出函数f (x )＝log 2(1－x )＋1，－1≤x <0的图象，再研究f (x )＝x 3－3x ＋2,0≤x ≤a 的图象．令f ′(x )＝3x 2－3＝0，得x ＝1(x ＝－1舍去)，由f ′(x )>0，得x >1，由f ′(x )<0，得0<x <1.又f (0)＝f (3)＝2，f (1)＝0.所以1≤a ≤ 3.12已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋2x －1，x ≥0，x 2－2x －1，x <0，则对任意x 1，x 2∈R ，若0<|x 1|<|x 2|，下列不等式成立的是( )A ．f (x 1)＋f (x 2)<0B ．f (x 1)＋f (x 2)>0C ．f (x 1)－f (x 2)>0D ．f (x 1)－f (x 2)<0 答案 D解析函数f (x )的图象如图实线部分所示，且f (－x )＝f (x )，从而函数f (x )是偶函数且在[0，＋∞)上是增函数，又0<|x 1|<|x 2|，∴f (x 2)>f (x 1)，即f (x 1)－f (x 2)<0.13、函数f (x )＝x|x －1|，g (x )＝1＋x ＋|x |2，若f (x )<g (x )，则实数x 的取值范围是____________．答案 ⎝ ⎛⎭⎪⎫－∞，－1＋52∪⎝ ⎛⎭⎪⎫1＋52，＋∞解析 f (x )＝⎩⎪⎨⎪⎧1＋1x －1，x >1，－1＋11－x ，x <1，g (x )＝⎩⎪⎨⎪⎧1＋x ，x ≥0，1，x <0，作出两函数的图象如图所示．当0≤x <1时，由－1＋11－x ＝x ＋1，解得x ＝5－12；当x >1时，由1＋1x －1＝x ＋1，解得x ＝5＋12.结合图象可知，满足f (x )<g (x )的x 的取值范围是⎝ ⎛⎭⎪⎫－∞，5－12∪⎝ ⎛⎭⎪⎫1＋52，＋∞. 14、函数f (x )＝⎩⎪⎨⎪⎧(x －1)2，0≤x ≤2，14x －12，2<x ≤6.若在该函数的定义域[0,6]上存在互异的3个数x 1，x 2，x 3，使得f (x 1)x 1＝f (x 2)x 2＝f (x 3)x 3＝k ，则实数k 的取值范围是__________．答案 ⎝⎛⎦⎤0，16解析由题意知，直线y ＝kx 与函数y ＝f (x )的图象至少有3个公共点．函数y ＝f (x )，x ∈[0,6]的图象如图所示，由图知k 的取值范围是⎝⎛⎦⎤0，16.15、已知函数f (x )＝2x ，x ∈R .(1)当实数m 取何值时，方程|f (x )－2|＝m 有一个解？两个解？ (2)若不等式f 2(x )＋f (x )－m >0在R 上恒成立，求实数m 的取值范围．解 (1)令F (x )＝|f (x )－2|＝|2x －2|， G (x )＝m ，画出F (x )的图象如图所示．由图象可知，当m ＝0或m ≥2时，函数F (x )与G (x )的图象只有一个交点，原方程有一个实数解；当0<m <2时，函数F (x )与G (x )的图象有两个交点，原方程有两个实数解．(2)令f (x )＝t (t >0)，H (t )＝t 2＋t ，t >0，因为H (t )＝⎝⎛⎭⎫t ＋122－14在区间(0，＋∞)上是增函数，所以H (t )>H (0)＝0.因此要使t 2＋t >m 在区间(0，＋∞)上恒成立，应有m ≤0，即所求m 的取值范围为(－∞，0]．16、数()2131log 1,x x x f x x x ⎧≤⎪⎨>⎪⎩－＋，，＝，g (x )＝|x －k |＋|x －2|，若对任意的x 1，x 2∈R ，都有f (x 1)≤g (x 2)成立，求实数k 的取值范围．解对任意的x 1，x 2∈R ，都有f (x 1)≤g (x 2)成立，即f (x )max ≤g (x )min .观察f (x )＝2131log 1,x x x x x ⎧≤⎪⎨>⎪⎩－＋，，，的图象可知，当x ＝12时，函数f (x )max ＝14.因为g (x )＝|x －k |＋|x －2|≥|x －k －(x －2)|＝|k －2|，所以g (x )min ＝|k －2|，所以|k －2|≥14，解得k ≤74或k ≥94.故实数k 的取值范围是⎝⎛⎦⎤－∞，74∪⎣⎡⎭⎫94，＋∞.。

2023年新高考数学大一轮复习专题11 函数的图象(解析版)

专题11 函数的图象【考点预测】一、掌握基本初等函数的图像（1）一次函数；（2）二次函数；（3）反比例函数；（4）指数函数；（5）对数函数；（6）三角函数. 二、函数图像作法 1.直接画①确定定义域；②化简解析式；③考察性质：奇偶性（或其他对称性）、单调性、周期性、凹凸性；④特殊点、极值点、与横/纵坐标交点；⑤特殊线（对称轴、渐近线等）.2.图像的变换（1）平移变换①函数()(0)y f x a a =+>的图像是把函数()y f x =的图像沿x 轴向左平移a 个单位得到的； ②函数()(0)y f x a a =->的图像是把函数()y f x =的图像沿x 轴向右平移a 个单位得到的； ③函数()(0)y f x a a =+>的图像是把函数()y f x =的图像沿y 轴向上平移a 个单位得到的； ④函数()(0)y f x a a =+>的图像是把函数()y f x =的图像沿y 轴向下平移a 个单位得到的；（2）对称变换①函数()y f x =与函数()y f x =-的图像关于y 轴对称；函数()y f x =与函数()y f x =-的图像关于x 轴对称；函数()y f x =与函数()y f x =--的图像关于坐标原点(0,0)对称； ②若函数()f x 的图像关于直线x a =对称，则对定义域内的任意x 都有()()f a x f a x -=+或()(2)f x f a x =-（实质上是图像上关于直线x a =对称的两点连线的中点横坐标为a ，即()()2a x a x a -++=为常数）；若函数()f x 的图像关于点(,)a b 对称，则对定义域内的任意x 都有()2(2)()2()f x b f a x f a x b f a x =---=-+或③()y f x =的图像是将函数()f x 的图像保留x 轴上方的部分不变，将x 轴下方的部分关于x 轴对称翻折上来得到的（如图（a ）和图（b ））所示④()y f x =的图像是将函数()f x 的图像只保留y 轴右边的部分不变，并将右边的图像关于y 轴对称得到函数()y f x =左边的图像即函数()y f x =是一个偶函数（如图（c ）所示）.注：()f x 的图像先保留()f x 原来在x 轴上方的图像，做出x 轴下方的图像关于x 轴对称图形，然后擦去x 轴下方的图像得到；而()f x 的图像是先保留()f x 在y 轴右方的图像，擦去y 轴左方的图像，然后做出y 轴右方的图像关于y 轴的对称图形得到.这两变换又叫翻折变换.⑤函数1()y fx -=与()y f x =的图像关于y x =对称.（3）伸缩变换①()(0)y Af x A =>的图像，可将()y f x =的图像上的每一点的纵坐标伸长(1)A >或缩短(01)A <<到原来的A 倍得到.②()(0)y f x ωω=>的图像，可将()y f x =的图像上的每一点的横坐标伸长(01)ω<<或缩短(1)ω>到原来的1ω倍得到. 【方法技巧与总结】(1)若)()(x m f x m f -=+恒成立，则)(x f y =的图像关于直线m x =对称.(2)设函数)(x f y =定义在实数集上，则函数)(m x f y -=与)(x m f y -=)0(>m 的图象关于直线m x =对称.(3)若)()(x b f x a f -=+，对任意∈x R 恒成立，则)(x f y =的图象关于直线2ba x +=对称.(4)函数)(x a f y +=与函数)(x b f y -=的图象关于直线2ba x +=对称. (5)函数)(x f y =与函数)2(x a f y -=的图象关于直线a x =对称. (6)函数)(x f y =与函数)2(2x a f b y --=的图象关于点)(b a ，中心对称. (7)函数平移遵循自变量“左加右减”，函数值“上加下减”.【题型归纳目录】题型一：由解析式选图（识图）题型二：由图象选表达式题型三：表达式含参数的图象问题题型四：函数图象应用题题型五：函数图像的综合应用【典例例题】题型一：由解析式选图（识图）例1．（2022·浙江·赫威斯育才高中模拟预测）函数2()sin 12xf x x =++的图象可能是（） A ． B ．C ．D ．【答案】D 【解析】【分析】通过判断()f x 不是奇函数，排除A ，B ，又因为302f π⎛⎫<⎪⎝⎭，排除C ，即可得出答案. 【详解】因为2()sin 12x f x x =++的定义域为R ，又因为()()222sin()sin 1221xx x f x x x f x -⋅-=-+=-+≠-++，所以()f x 不是奇函数，排除A ，B. 33223322sin()10221212f ππππ⎛⎫=+=-+< ⎪⎝⎭++，所以排除C.故选：D.例2．（2022·陕西·汉台中学模拟预测（理））函数2ln x y x=的图象大致是（）A ．B ．C ．D ．【答案】C 【解析】【分析】根据函数的定义域与奇偶性，排除A 、B 选项；结合导数求得函数在(1,)+∞上的单调性，排除D 选项，即可求解. 【详解】由题意，函数()2ln x f x x =的定义域为(,1)(1,0)(0,1)(1,)-∞--+∞，关于原点对称，且满足()()22()ln ln x x f x f x x x--===-，所以函数()f x 为偶函数，其图象关于y 轴对称，排除B 选项；当1x >时，可得()2ln x f x x =，则()()()222ln (2ln 1)ln ln x x x x x f x x x --'==，当x ∈时，()0f x '<，()f x 单调递减；排除A 选项当)x ∈+∞时，()0f x '>，()f x 单调递增，所以排除D 选项，选项C 符合. 故选：C.例3．（2022·天津·二模）函数sin exx xy =的图象大致为（）A ．B ．C ．D ．【答案】D 【解析】【分析】分析函数sin exx xy =的奇偶性及其在()0,π上的函数值符号，结合排除法可得出合适的选项. 【详解】令()sin e x x xf x =，该函数的定义域为R ，()()()sin sin e ex xx x x x f x f x ----===，所以，函数sin exx xy =为偶函数，排除AB 选项，当0πx <<时，sin 0x >，则sin 0exx xy =>，排除C 选项. 故选：D.例4．（2022·全国·模拟预测）已知函数())lnsin f x x x =⋅则函数()f x 的大致图象为（）A ．B ．C ．D ．【答案】A【分析】先利用函数的奇偶性排除部分选项，再根据()0,x π∈时，函数值的正负判断. 【详解】易知函数)lny x =为奇函数，sin y x =也是奇函数，则函数())ln sin f x x x =⋅为偶函数，故排除选项B ，C ；因为)lnln y x ⎛⎫==，当0x >1x >恒成立，所以ln 0⎛⎫<恒成立，且当()0,x π∈时，sin 0x >，所以当()0,x π∈时，()0f x <，故选项A 正确，选项D 错误，故选：A ．例5．（2022·全国·模拟预测）函数()22e xx xf x -=的图象大致是( )A ．B ．C ．D ．【答案】B 【解析】【分析】根据f (x )的零点和x →+∞时函数值变化情况即可判断求解．【详解】由()0f x =得0x =或2，故排除选项A ；当x →+∞时，函数值无限靠近x 轴，但与x 轴不相交，只有选项B 满足．例6．（2022·河北·模拟预测）函数4cos3()cos (ππ)33xf x x x =---≤≤的部分图象大致为（） A ． B ．C ．D ．【答案】A 【解析】【分析】利用函数的奇偶性和代入特殊值即可求解. 【详解】由已知条件得函数()f x 的定义域关于原点对称， ∵()()cos 34()cos 33x f x x --=---()4cos3cos 33x x f x -=-=， ∴()f x 为偶函数，函数的图象关于y 轴对称，则排除选项B 、C , 又∵4cos3π(π)cos π33f =--4181333=++=， ∴排除选项D ，故选：A .【方法技巧与总结】利用函数的性质（如定义域、值域、奇偶性、单调性、周期性、特殊点等）排除错误选项，从而筛选出正确答案题型二：由图象选表达式例7．（2022·全国·模拟预测）已知y 关于x 的函数图象如图所示，则实数x ，y 满足的关系式可以为（）A ．311log 0x y --=B ．321xx y-=C ．120x y --=D ．ln 1x y =-【答案】A 【解析】【分析】将311log 0x y --=化为11133x x y ---⎛⎫== ⎪⎝⎭，结合图像变换，可判断A;取特殊值验证，可判断B;作出函数12x y -=的图象，可判断C;根据函数ln 1y x =+的性质，可判断D.【详解】由311log 0x y --=，得31log 1x y=-，所以3log 1y x -=-，即3log 1y x =--，化为指数式，得11133x x y ---⎛⎫== ⎪⎝⎭，其图象是将函数1,01333,0xxx x y x ⎧⎛⎫≥⎪⎛⎫⎪==⎨⎝⎭⎪⎝⎭⎪<⎩的图象向右平移1个单位长度得到的，即为题中所给图象，所以选项A 正确；对于选项B ，取1x =-，则由()31121y---=，得21y =>，与已知图象不符，所以选项B 错误；由120x y --=，得12x y -=，其图象是将函数2xy =的图象向右平移1个单位长度得到的，如图：与题中所给的图象不符，所以选项C 错误；由ln 1x y =-，得ln 1y x =+，该函数为偶函数，图象关于y 轴对称，显然与题中图象不符，所以选项D 错误，故选：A.例8．（2022·江西赣州·二模（理））已知函数()f x 的图象的一部分如下左图，则如下右图的函数图象所对应的函数解析式（）A ．(21)y f x =-B ．412x y f -⎛⎫= ⎪⎝⎭C ．(12)y f x =-D ．142x y f -⎛⎫= ⎪⎝⎭【答案】C 【解析】【分析】分三步进行图像变换①关于y 轴对称②向右平移1个单位③纵坐标不变，横坐标变为原来的一半【详解】12()()(1)(12)x xx x x xy f x y f x y f x y f x →-→-→=→=-→=-→=-①②③①关于y 轴对称②向右平移1个单位③纵坐标不变，横坐标变为原来的一半故选：C.例9．（2022·浙江·模拟预测）已知函数()f x 的大致图象如图所示，则函数()y f x =的解析式可以是（）A ．()()2211--=xxex y eB ．()21sin -=xxex y eC ．()()2211-+=xxex y eD ．()21cos -=xxex y e【答案】B【解析】【分析】根据函数图象，可知函数为偶函数，排除A ，D ，根据C 项函数没有零点，排除C 项，最终选出正确结果. 【详解】根据函数图象，可知函数为偶函数，排除A ，D ；对于C ，当0x >时，22110,2-+>≥x xe x e x ，函数显然不存在零点，排除C ．故选：B ．例10．（2022·全国·模拟预测）已知函数()f x 的部分图象如图所示，则()f x 的解析式可能为( )A ．()sin πf x x x =B ．()()1πsin f x x x =-C ．()()sin π1f x x x =+D ．()()1cos πf x x x =-【答案】B 【解析】【分析】根据已知图象的对称性，结合AC 的奇偶性可排除AC ，根据已知图象f (0)=0可排除D ，从而正确可得B 为正确选项．【详解】对于A ，()()()sin πsin πf x x x x x f x -=--==，故()sin πf x x x =为偶函数，图象应该关于y 轴对称，与已知图象不符；对于C ，()()sin ππf x x x =+sin πx x =-也为偶函数，故排除AC ；对于D ，()01f =-，与已知图象不符，故排除D ．对于B ，()()()()()()221sin 2(1)sin π1sin ππf x x x x x x x f x -=---=--=-=，故f (x )关于x =1对称，f (0)=0，均与已知图象符合，故B 正确．故选：B ．例11．（2022·河北沧州·模拟预测）下列图象对应的函数解析式正确的是（）A ．()cos f x x x =B ．()sin f x x x =C ．()sin cos f x x x x =+D ．()cos sin f x x x x =+【答案】D 【解析】【分析】由图可知，函数()f x 的图象关于原点中心对称，所以函数()f x 为奇函数，且()02f π>，对选项B 、C ：由函数()f x 为偶函数即可判断，对选项A ：函数()f x 为奇函数，但()cos 0222f πππ==即可判断；对选项D ：函数()f x 为奇函数，且()cos sin 102222f ππππ=+=>即可判断.【详解】解：由图可知，函数()f x 的图象关于原点中心对称，所以函数()f x 为奇函数，且()02f π>，对A ：因为()()()cos cos ()f x x x x x f x -=--=-=-，所以函数()f x 为奇函数，但()cos 0222f πππ==，故选项A 错误；对B ：因为()()()sin sin ()f x x x x x f x -=--==，所以函数()f x 为偶函数，故选项B 错误；对C ：因为()()()()sin cos sin cos ()f x x x x x x x f x -=--+-=+=，所以函数()f x 为偶函数，故选项C 错误；对D ：因为()()()()cos sin cos sin ()f x x x x x x x f x -=--+-=--=-，所以函数()f x 为奇函数，且()cos sin 102222f ππππ=+=>，符合题意，故选项D 正确. 故选：D.例12．（2022·浙江绍兴·模拟预测）已知函数()sin f x x =，()e e x x g x -=+，下图可能是下列哪个函数的图象（）A ．()()2f x g x +-B ．()()2f x g x -+C ．()()⋅f x g xD ．()()f xg x【答案】D 【解析】【分析】根据图象体现的函数性质，结合每个选项中函数的性质，即可判断和选择. 【详解】由图可知，图象对应函数为奇函数，且()011f <<；显然,A B 对应的函数都不是奇函数，故排除；对C ：()()()sin e e x xy f x g x x -=⋅=⋅+，其为奇函数，且当1x =时，11sin1e e 1e 2⎛⎫⋅+>⨯> ⎪⎝⎭，故错误；对D ：y =()()f xg x sin e e x xx-=+，其为奇函数，且当1x =时，sin110112e e<<<+，故正确. 故选：D .【方法技巧与总结】1.从定义域值域判断图像位置；2.从奇偶性判断对称性；3.从周期性判断循环往复；4.从单调性判断变化趋势；5.从特征点排除错误选项．题型三：表达式含参数的图象问题（多选题）例13．（2022·全国·高三专题练习）函数()()2,,R ax bf x a b c x c+=∈+的图象可能为（） A ． B ．C ．D ．【答案】ABD 【解析】【分析】讨论0,0,0a b c >=>、0,0,0a b c <=<、0,0,0a b c =><、0,0,0a b c =<<四种情况下，()f x 的奇偶性、单调性及函数值的正负性判断函数图象的可能性. 【详解】当0,0a b ≠=时，22()()()ax axf x f x x c x c--==-=--++；当0,0a c >>时，()f x 定义域为R 且为奇函数，在(0,)+∞上()0f x >，在上递增，在)+∞上递减，A 可能；当0,0a c <<时，()f x 定义域为{|x x ≠且为奇函数，在上()0f x >且递增，在)+∞上()0f x <且递增，B 可能；当0,0,0a b c =≠<时，22()()()b bf x f x x c x c-===-++且定义域为{|x x ≠，此时()f x 为偶函数，若0b >时，在(上()0f x <(注意(0)0f <)，在(,)-∞+∞上()0f x >，则C 不可能；若0b <时，在(上()0f x >，在(,)-∞+∞上()0f x <，则D 可能；故选：ABD（多选题）例14．（2022·福建·莆田二中高三开学考试）函数2||()x f x x a=+的大致图象可能是（）A ．B ．C ．D ．【答案】AC 【解析】【分析】先判断函数的奇偶性，可排除D 选项，然后对a 的取值进行分类讨论，比如0a =，可判断A 可能，再对a 分大于零和小于零的情况讨论，结合求导数判断函数单调性，即可判断B,C 是否可能. 【详解】因为2||()x f x x a=+为定义域上的偶函数，图象关于y 轴对称，所以D 不可能.由于()f x 为定义域上的偶函数，只需考虑,()0x ∈+∞的情况即可. ①当0a =时，函数2||11()||x f x x x x===，所以A 可能； ②当0a >时，2()xf x x a =+，()222()a x f x x a '-=+，所以()f x 在单调递增，在)+∞单调递减，所以C 可能； ③当0a <时，2()x f x x a =+，()222()0a x f x x a -'=<+，所以()f x 在单调递减，在)+∞单调递减，所以B 不可能；故选:AC.（多选题）例15．（2021·河北省唐县第一中学高一阶段练习）已知()2xf x x a=-的图像可能是（）A ．B ．C ．D ．【答案】ABC 【解析】【分析】根据a 的取值分类讨论函数f (x )的单调性、奇偶性、值域，据此判断图像即可. 【详解】若a ＝0，则f (x )＝1x，图像为C ；若a ＞0，则f (x )定义域为{x |x ，f (0)＝0，f (－x )＝－f (x )，f (x )为奇函数，x ∈(－∞，时，f (x )＜0，x ∈(0)时，f (x )＞0，x ∈(0，f (x )＜0，x ∈＋∞)时，f (x )＞0，又x ≠0时，f (x )＝1a x x-，函数y ＝x －ax 在(－∞，0)和(0，＋∞)均单调递增，∴f (x )在(－∞，(0)，(0，∞)均单调递减，综上f (x )图像如A 选项所示；若a ＜0，则f (x )定义域为R ，f (x )为奇函数，f (0)＝0，当x ＞0时，f (x )＞0，当x ＜0时，f (x )＜0，当x ≠0时，f (x )＝1a x x-+，函数y ＝x ＋ax-时双勾函数，x ∈((),时，y 均单调递减，x ∈)(,,+∞-∞时，y 均单调递增，∴f (x )在((),单调递增，在)(,,+∞-∞单调递减，结合以上性质，可知B 图像符合.故选：ABC.（多选题）例16．（2022·湖北武汉·高一期末）设0a >，函数21axx y e ++=的图象可能是（）A ．B ．C ．D ．【答案】BD 【解析】令()21,0g x ax x a =++>，得到抛物线的开口向上，对称轴的方程为12x a=-，再根据0,0∆=∆<和0∆>三种情形分类讨论，结合复合函数的单调性，即可求解. 【详解】由题意，函数21axx y e ++=，令()21,0g x ax x a =++>，可得抛物线的开口向上，对称轴的方程为102x a=-<，当140a ∆=-=时，即14a =时，可得()21104g x x x =++≥，此时函数()y g x =在1(,]2a -∞-单调递减，在1[,)2a-+∞上单调递增，且(2)0g -= 可得21axx y e ++=在1(,]2a -∞-递减，在1[,)2a -+∞上递增，且(2)1g e -=；当140a ∆=-<时，即14a >时，可得()0g x >，此时函数()y g x =在1(,]2a -∞-单调递减，在1[,)2a-+∞上单调递增，由复合函数的单调性，可得21ax x y e ++=在1(,]2a -∞-递减，在1[,)2a-+∞上递增，且1y >，此时选项B 符合题意；当当140a ∆=->时，即104a <<时，此时函数()21g x ax x =++有两个零点，不妨设另个零点分别为12,x x 且1212x x a<-<，此时函数()y g x =在1(,]2a -∞-单调递减，在1[,)2a-+∞上单调递增，可得()y g x =在121(,],[,]2x x a-∞-递减，在121[,],[,)2x x a -+∞上递增，且12()()0g x g x ==，则21axx y e ++=在121(,],[,]2x x a-∞-递减，在121[,],[,)2x x a -+∞上递增，且12()()1g x g x e e ==，此时选项D 符合题意.综上可得，函数的图象可能是选项BD. 故选：BD.（多选题）例17．（2022·广东东莞·高一期末）已知函数()af x x x=+()a R ∈，则其图像可能为（） A ． B ．C ．D ．【答案】BC 【解析】【分析】按照0a =，0a >，0a <讨论a 的取值范围，利用排除法解决. 【详解】 0a =，()(0)af x x x x x=+=≠，定义域需要挖去一个点，不是完整的直线，A 选项错误；0a <时，y x =在(,0),(0,)-∞+∞上递增，ay x=也在(,0),(0,)-∞+∞递增，两个增函数相加还是增函数，即()f x 在(,0),(0,)-∞+∞上递增，故D 选项错误，C 选项正确.；0a >时，由对勾函数的性质可知B 选项正确. 故选：BC.（多选题）例18．（2021·山西省长治市第二中学校高一阶段练习）在同一直角坐标系中，函数()()()10,1,x f x a a a g x a x =->≠=-且的图象可能是（）A ．B ．C ．D ．【答案】AC 【解析】【分析】根据给定条件对a 值进行分类讨论函数()f x 的单调性及0一侧的函数值，再结合()g x a x =-图象与y 轴交点位置即可判断作答. 【详解】依题意，当1a >时，函数()g x a x =-图象与y 轴交点在点(0,1)上方，排除B ，C ，而()1,011,0x xxa x f x a a x ⎧-≥=-=⎨-<⎩，因此，()f x 在(,0)-∞上递减，且x <0时，0<f (x )<1，D 不满足，A 满足；当01a <<时，函数()g x a x =-图象与y 轴交点在原点上方，点(0,1)下方，排除A ，D ，而()1,011,0x xxa x f x a a x ⎧-<=-=⎨-≥⎩，因此，f (x )在(0,)+∞上递增，且x >0时，0<f (x )<1，B 不满足，C 满足，所以给定函数的图象可能是AC. 故选：AC（多选题）例19．（2021·河北·高三阶段练习）函数()211ax f x x +=+的大致图象可能是（） A ． B ．C ．D ．【答案】ABD 【解析】【分析】对a 的取值进行分类讨论，利用导数对函数的单调性进行分析即可判断函数的大致图象. 【详解】当0a =时，()01f =，令21y x =+，易知，其在(),0-∞上为减函数，()0,∞+上为增函数，所以()211f x x =+在(),0-∞上为增函数，在()0,∞+上为减函数，故D 正确；当0a <时，()01f =，()()2'2221ax x afx x--+=+，令22y ax x a =--+，当0x <且0x →时，0y <，当0x >且0x →时，0y <，所以()'0f x <，故A 正确；当0a >时，()01f =，()()2'2221ax x afx x--+=+，令22y ax x a =--+，当0x <且0x →时，0y >，当0x >且0x →时，0y >，所以()'0f x >，故B 正确；综上，()f x 的图象不可能为C. 故选：ABD.（多选题）例20．（2022·全国·高三专题练习）已知()x x f x e ke -=+（k 为常数），那么函数()f x 的图象不可能是（）A ．B ．C ．D ．【答案】AD【解析】【分析】根据选项，四个图象可知备选函数都具有奇偶性．当1k =时，()x x f x e e -=+为偶函数，当1k =-时，()x x f x e e -=-为奇函数，再根据单调性进行分析得出答案．【详解】由选项的四个图象可知，备选函数都具有奇偶性．当1k =时，()x x f x e e -=+为偶函数，当0x ≥时，1x t e =≥且单调递增，而1y t t=+在1) [,t ∈+∞上单调递增，故函数()x x f x e e -=+在0) [,x ∈+∞上单调递增，故选项C 正确，D 错误；当1k =-时，()x x f x e e -=-为奇函数，当0x ≥时，1x t e =≥且单调递增，而1y t t=-在1) [,t ∈+∞上单调递减，故函数()x x f x e e -=-在0) [,x ∈+∞上单调递减，故选项B 正确，A 错误. 故选:AD ．【方法技巧与总结】根据函数的解析式识别函数的图象，其中解答中熟记指数幂的运算性质，二次函数的图象与性质，以及复合函数的单调性的判定方法是解答的关键，着重考查分析问题和解答问题的能力，以及分类讨论思想的应用.题型四：函数图象应用题例21．（2022·全国·高三专题练习）如图，正△ABC 的边长为2，点D 为边AB 的中点，点P 沿着边AC ，CB 运动到点B ，记∠ADP ＝x ．函数f （x ）＝|PB |2﹣|P A |2，则y ＝f （x ）的图象大致为（）A ．B ．C ．D ．【答案】A 【解析】【分析】根据题意，结合图形，分析区间（0，2π）和（2π，π）上f （x ）的符号，再分析f （x ）的对称性，排除BCD ，即可得答案．【详解】根据题意，f （x ）＝|PB |2﹣|P A |2，∠ADP ＝x ．在区间（0，2π）上，P 在边AC 上，|PB |＞|P A |，则f （x ）＞0，排除C ；在区间（2π，π）上，P 在边BC 上，|PB |＜|P A |，则f （x ）＜0，排除B ，又由当x 1+x 2＝π时，有f （x 1）＝﹣f （x 2），f （x ）的图象关于点（2π，0）对称，排除D ，故选：A例22．（2022·全国·高三专题练习）匀速地向一底面朝上的圆锥形容器注水，则该容器盛水的高度h 关于注水时间t 的函数图象大致是（）A ．B ．C ．D ．【答案】A 【解析】【分析】设出圆锥底面圆半径r ，高H ，利用圆锥与其轴垂直的截面性质，建立起盛水的高度h 与注水时间t 的函数关系式即可判断得解. 【详解】设圆锥PO 底面圆半径r ，高H ，注水时间为t 时水面与轴PO 交于点O '，水面半径AO x '=，此时水面高度PO h '=，如图：由垂直于圆锥轴的截面性质知，x h r H =，即r x h H =⋅，则注入水的体积为2223211()333r r V x h h h h H H πππ==⋅⋅=⋅，令水匀速注入的速度为v ，则注水时间为t 时的水的体积为V vt =，于是得22332233r H vt h vt h h H r ππ⋅=⇒=⇒=而,,r H v 是常数，所以盛水的高度h 与注水时间t 的函数关系式是h =203r H t v π≤≤，23103h t -'=>，函数图象是曲线且是上升的，随t 值的增加，函数h 值增加的幅度减小，即图象是先陡再缓， A 选项的图象与其图象大致一样，B ，C ，D 三个选项与其图象都不同. 故选：A例23．（2022·四川泸州·模拟预测（文））如图，一高为H 且装满水的鱼缸，其底部装有一排水小孔，当小孔打开时，水从孔中匀速流出，水流完所用时间为.T 若鱼缸水深为h 时，水流出所用时间为t ，则函数()h f t =的图象大致是( )A ．B ．C ．D ．【答案】B 【解析】【分析】根据时间和h 的对应关系分别进行排除即可．【详解】函数()h f t =是关于t 的减函数，故排除C ，D ，则一开始，h 随着时间的变化，而变化变慢，超过一半时，h 随着时间的变化，而变化变快，故对应的图象为B ，故选B ．【点睛】本题主要考查函数与图象的应用，结合函数的变化规律是解决本题的关键．例24．（2021·山东济南·高三阶段练习）如图，公园里有一处扇形花坛，小明同学从A 点出发，沿花坛外侧的小路顺时针方向匀速走了一圈(路线为AB BO OA →→)，则小明到O 点的直线距离y 与他从A 点出发后运动的时间t 之间的函数图象大致是（）A ．B ．C．D．【答案】D【解析】根据距离随与时间的增长的变化增减情况即可判定.【详解】小明沿AB走时，与О点的直线距离保持不变，沿BO走时，随时间增加与点О的距离越来越小，沿OA走时，随时间增加与点О的距离越来越大.故选：D.例25．（2021·江苏·常州市西夏墅中学高三开学考试）如图，△AOD是一直角边长为1的等腰直角三角形，平面图形OBD是四分之一圆的扇形，点P在线段AB上，PQ⊥AB，且PQ交AD或交弧DB于点Q，设AP ＝x(0<x<2)，图中阴影部分表示的平面图形APQ(或APQD)的面积为y，则函数y＝f(x)的大致图像是A．B．C．D．【答案】A【解析】【分析】分两段，当P点在AO之间时，当P点在OB之间时，再由二次函数的性质及增长趋势可知．【详解】当P 点在AO 之间时，f （x ）12=x 2（0＜x ≤1），排除B,D 当P 点在OB 之间时，y 随x 的增大而增大且增加速度原来越慢，故只有A 正确故选A ．【点睛】本题主要考查了函数图像的识别的性质，考查分类讨论思想及排除法应用，属于基础题．【方法技巧与总结】思路点睛：函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置． (2)从函数的单调性，判断图象的变化趋势； (3)从函数的奇偶性，判断图象的对称性； (4)从函数的特征点，排除不合要求的图象.题型五：函数图像的综合应用例26．（2022·四川·宜宾市教科所三模（理））定义在R 上的偶函数()f x 满足()()2f x f x =-，且当[]0,1x ∈时，()e 1xf x =-，若关于x 的方程()()()10f x m x m =+>恰有5个解，则m 的取值范围为（）A ．e 1e 1,65--⎛⎫⎪⎝⎭ B ．e 1e 1,64--⎛⎫⎪⎝⎭ C ．e 1e 1,86--⎛⎫⎪⎝⎭ D ．()0,e 1-【答案】B 【解析】【分析】由题可知函数()y f x =与直线()1y m x =+有5个交点，利用数形结合即得. 【详解】∵()()2f x f x =-，∴函数()f x 关于直线1x =对称，又()f x 为定义在R 上的偶函数，故函数()f x 关于直线0x =对称，作出函数()y f x =与直线()1y m x =+的图象，要使关于x 的方程()()()10f x m x m =+>恰有5个解，则函数()y f x =与直线()1y m x =+有5个交点，∴6e 14e 1m m >-⎧⎨<-⎩，即e 1e 164m --<<. 故选：B.例27．（2022·北京丰台·一模）已知函数()32,,3,x x a f x x x x a -<⎧=⎨-≥⎩无最小值，则a 的取值范围是（）A ．(,1]-∞-B ．(,1)-∞-C ．[1,)+∞D ．(1,)+∞【答案】D 【解析】【分析】利用导数研究函数的性质，作出函数函数33y x x =-与直线2y x =-的图象，利用数形结合即得. 【详解】对于函数33y x x =-，可得()()233311y x x x '=-=+-，由0y '>，得1x <-或1x >，由0y '<，得11x -<<，∴函数33y x x =-在(),1-∞-上单调递增，在()1,1-上单调递减，在()1,+∞上单调递增， ∴函数33y x x =-在1x =-时有极大值2，在1x =时有极小值2-，作出函数33y x x =-与直线2y x =-的图象，由图可知，当1a ≤时，函数()f x 有最小值12f ，当1a >时，函数()f x 没有最小值.故选：D.例28．（2022·全国·高三专题练习）已知函数()2ln ,0,43,0x x f x x x x >⎧=⎨---≤⎩若函数()()21y f x mf x =++⎡⎤⎣⎦有6个零点，则m 的取值范围是（） A ．102,3⎛⎫- ⎪⎝⎭B ．102,3⎛⎤- ⎥⎝⎦C ．102,3⎛⎫⎪⎝⎭D ．102,3⎛⎤ ⎥⎝⎦【答案】D 【解析】【分析】利用数形结合可得210t mt ++=在[)3,1-上有两个不同的实数根，然后利用二次函数的性质即得. 【详解】设()t f x =，则()21y g t t mt ==++，作出函数()f x 的大致图象，如图所示，则函数()()21y f x mf x =++⎡⎤⎣⎦有6个零点等价于()0g t =在[)3,1-上有两个不同的实数根，则()()24039310,1110,31,2m g m g m m ⎧->⎪-=-+≥⎪⎪⎨=++>⎪⎪-<-<⎪⎩解得1023m <≤.故选：D. 【点睛】关键点点睛：本题的关键是利用数形结合，把问题转化为方程210t mt ++=在[)3,1-上有两个不同的实数根，即二次方程根的分布问题，利用二次函数的性质即解.例29．（2022·甘肃省武威第一中学模拟预测（文））已知函数()221xf x =--，则关于x 的方程()()20f x mf x n ++=有7个不同实数解，则实数,m n 满足（） A ．0m >且0n > B ．0m <且0n > C ．01m <<且0n = D ．10m -<<且0n =【答案】C 【解析】【分析】令()u f x =，利用换元法可得20u mu n ++=，由一元二次方程的定义知该方程至多有两个实根1u 、2u ，作出函数()f x 的图象，结合题意和图象可得10u =、2u m =-，进而得出结果. 【详解】令()u f x =，作出函数()u f x =的图象如下图所示：由于方程20u mu n ++=至多两个实根，设为1u u =和2u u =，由图象可知，直线1u u =与函数()u f x =图象的交点个数可能为0､2､3､4，由于关于x 的方程()()20f x mf x n ++=有7个不同实数解，则关于u 的二次方程20u mu n ++=的一根为10u =，则0n =，则方程20u mu +=的另一根为2u m =-，直线2u u =与函数()u f x =图象的交点个数必为4，则10m -<-<，解得01m <<. 所以01m <<且0n =. 故选：C.例30.（2022·天津市滨海新区塘沽第一中学模拟预测）已知函数21244,1(),1x x x x f x e x x -⎧-+>=⎨+≤⎩，若不等式1()||022mf x x --<的解集为∅，则实数m 的取值范围为（） A ．1,52ln 34⎡⎤-⎢⎥⎣⎦B ．1,53ln 33⎡⎤-⎢⎥⎣⎦C ．1,62ln 34⎡⎤-⎢⎥⎣⎦D ．1,63ln 32⎡⎤-⎢⎥⎣⎦【答案】D 【解析】【分析】由不等式1()||022mf x x --<的解集为∅，等价于()|2|f x x m ≥-在R 上恒成立.根据相切找临界位置，结合函数的单调性以及图像特征，即可求解. 【详解】不等式1()||022mf x x --<的解集为∅,等价于()|2|f x x m ≥-在R 上恒成立. 当1x >时,2()=244,f x x x -+此时()f x 在1x >上单调递增,当11,()=,x x f x e x -≤+则1()=-1,x f x e -'+当<1x 时,0()<f x ',故()f x 在<1x 上单调递减.当2-y x m =与2()=244f x x x -+相切时,设切点为()00,x y ,所以00()4-4=2f x x '=,解得032x =,35()22f =,此时切线方程为35y=2x-+22⎛⎫ ⎪⎝⎭,该切线与x 轴的交点为1,04A ⎛⎫⎪⎝⎭,同理可得当-2+y x m =与1()=x f x e x -+相切时,切线与x 轴的交点为33-ln 3,02B ⎛⎫⎪⎝⎭,又因为=|2|y x m -与x 轴的交点为,02mC ⎛⎫⎪⎝⎭要使()|2|f x x m ≥-在R 上恒成立,则点C 在,A B 之间移动即可.故133-ln 3422m ≤≤,解得16-3ln 32m ≤≤故选:D例31．（2022·安徽·巢湖市第一中学高三期中（理））已知函数()11,11ln ,1x f x x x x ⎧-<⎪=-⎨⎪≥⎩，若函数()()()1g x f x k x =--有4个零点，则实数k 的取值范围为_______________. 【答案】1(0,)4【解析】【分析】转化求()11,11ln ,1x f x x x x ⎧-<⎪=-⎨⎪≥⎩的图像与()1y k x =-图像交点，求出直线与1()11f x x =--相切时的k ，进而得到有4个交点时k 的范围即可【详解】因为()()()1g x f x k x =--有4个零点，所以方程()()1f x k x =-有4个实数根，画出()11,11ln ,1x f x x x x ⎧-<⎪=-⎨⎪≥⎩的图像，以及()1y k x =-，则两函数的图象有4个公共点．其中直线()1y k x =-经过定点(1,0)，斜率为k当直线与()f x 相切时，联立111(1)y x y k x ⎧=-⎪-⎨⎪=-⎩，22(12)40k k ∆=--=，可求出14k =，由图可知，当104x <<时，方程()()1f x k x =-有4个交点，故k 的取值范围为1(0,)4故答案为1(0,)4.【点睛】方法点睛：根据函数零点个数求参数取值范围的注意点：（1）结合题意构造合适的函数，将函数零点问题转化成两函数图象公共点个数的问题处理；（2）在同一坐标系中正确画出两函数的图象，借助图象的直观性进行求解；（3）求解中要注意两函数图象的相对位置，同时也要注意图中的特殊点，如本题中直线(1)y k x =-经过定点(1,0)等．例32．（2022·贵州遵义·高三开学考试（文））已知函数()3112,21ln ,2x m x f x x x m x ⎧--<⎪⎪=⎨⎪-≥⎪⎩恰有3个零点，则m 的取值范围是________．【答案】1ln 2,(0,1)3e 8⎛⎤--⎥⎝⎦【解析】【分析】设函数()3112,21ln ,2x x g x x x x ⎧-<⎪⎪=⎨⎪≥⎪⎩，根据题意转化为函数()g x 与直线y m =的图象有3个公共点，利用导数求得函数()g x 的极值，画出函数()g x 的图象，结合图象，即可求解. 【详解】设函数()3112,21ln ,2x x g x x x x ⎧-<⎪⎪=⎨⎪≥⎪⎩，根据题意函数()f x 恰有3个零点，即为函数()g x 的图象与直线y m =有3个公共点，当12x ≥时，可得2()(3ln 1)g x x x '=+，令()0g x '=，得131e 2x -=>，当131[,e )2x -∈时，函数()g x 单调递减；当13(e ,)x -∈+∞时，函数()g x 单调递增，所以当13e x -=时，函数()g x 取得极小值，极小值为131e 3e g -⎛⎫=- ⎪⎝⎭，又由11()ln 2028g =-<，作出()g x 的图象，如图所示，由图可知，实数m 的取值范围是1ln 2,(0,1)3e 8⎛⎤-- ⎥⎝⎦．故答案为：1ln 2,(0,1)3e 8⎛⎤-- ⎥⎝⎦．例33．（2022·全国·高三专题练习）已知函数f （x ）＝244,01,43,1x x x x x -<≤⎧⎨-+>⎩和函数g （x ）＝2log x ，则函数h （x ）＝f （x ）－g （x ）的零点个数是________．【答案】3 【解析】【分析】函数零点个数可转化为()y g x =与()y f x =图象交点的个数问题，作出图象，数形结合即可求解. 【详解】在同一直角坐标系中，作出()y g x =与()y f x =的图象如图，由()()()0h x f x g x =-=可得，()()f x g x =，即函数的零点为(),()y f x y g x ==图象交点的横坐标，由图知()y f x =与()y g x =的图象有3个交点，即()h x 有3个零点．故答案为：3例34．（2022·全国·高三专题练习（理））如图，在等边三角形ABC 中， AB =6.动点P 从点A 出发，沿着此三角形三边逆时针运动回到A 点，记P 运动的路程为x ，点P 到此三角形中心O 距离的平方为f (x )，给出下列三个结论：①函数f (x )的最大值为12；②函数f (x )的图象的对称轴方程为x =9； ③关于x 的方程()3f x kx =+最多有5个实数根. 其中，所有正确结论的序号是____. 【答案】①② 【解析】写出P 分别在,,AB BC CA 上运动时的函数解析式2()f x OP =，利用分段函数图象可解. 【详解】P 分别在AB 上运动时的函数解析式22()3(3),(06)f x OP x x ==+-≤≤， P 分别在BC 上运动时的函数解析式22()3(9),(612)f x OP x x ==+-≤≤， P 分别在CA 上运动时的函数解析式22()3(15),(1218)f x OP x x ==+-≤≤，22223(3),(06)()||3(9),(612)3(15),(1218)x x f x OP x x x x ⎧+-≤≤⎪==+-≤≤⎨⎪+-≤≤⎩，由图象可得，方程()3f x kx =+最多有6个实数根故正确的是①②. 故答案为：①② 【点睛】利用函数图象可以解决很多与函数有关的问题，如利用函数的图象解决函数性质问题，函数的零点、方程根的问题，有关不等式的问题等.解决上述问题的关键是根据题意画出相应函数的图象，利用数形结合思想求解.【方法技巧与总结】1.利用函数图像判断方程解的个数.由题设条件作出所研究对象的图像，利用图像的直观性得到方程解。

高中函数图像大全

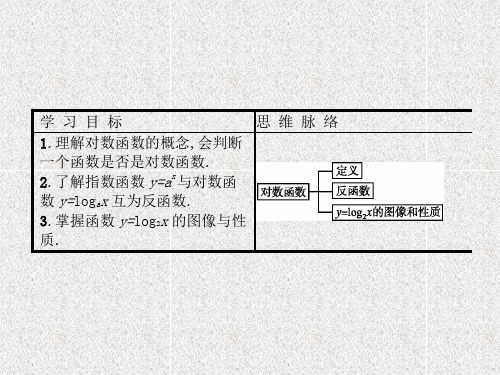
高中必考函数大全指数函数概念：一般地，函数y=a^x（a＞0，且a≠1）叫做指数函数，其中x是自变量，函数的定义域是R。

注意：⒈指数函数对外形要求严格，前系数要为1，否则不能为指数函数。

⒉指数函数的定义仅是形式定义。

指数函数的图像与性质：规律：1. 当两个指数函数中的a互为倒数时，两个函数关于y轴对称，但这两个函数都不具有奇偶性。

2.当a＞1时，底数越大，图像上升的越快，在y轴的右侧，图像越靠近y轴；当0＜a＜1时，底数越小，图像下降的越快，在y轴的左侧，图像越靠近y轴。

在y轴右边“底大图高”；在y轴左边“底大图低”。

3.四字口诀：“大增小减”。

即：当a＞1时，图像在R上是增函数；当0＜a＜1时，图像在R上是减函数。

4. 指数函数既不是奇函数也不是偶函数。

比较幂式大小的方法：1.当底数相同时，则利用指数函数的单调性进行比较；2.当底数中含有字母时要注意分类讨论；3.当底数不同，指数也不同时，则需要引入中间量进行比较；4.对多个数进行比较，可用0或1作为中间量进行比较底数的平移：在指数上加上一个数，图像会向左平移；减去一个数，图像会向右平移。

在f(X)后加上一个数，图像会向上平移；减去一个数，图像会向下平移。

对数函数1.对数函数的概念由于指数函数y=a x在定义域(-∞，+∞)上是单调函数，所以它存在反函数，我们把指数函数y=a x(a＞0，a≠1)的反函数称为对数函数，并记为y=log a x(a＞0，a≠1).因为指数函数y=a x的定义域为(-∞，+∞)，值域为(0，+∞)，所以对数函数y=log a x的定义域为(0，+∞)，值域为(-∞，+∞).2.对数函数的图像与性质对数函数与指数函数互为反函数，因此它们的图像对称于直线y=x. 据此即可以画出对数函数的图像，并推知它的性质.为了研究对数函数y=log a x(a＞0，a≠1)的性质，我们在同一直角坐标系中作出函数y=log 2x ，y=log 10x ，y=log 10x,y=log 21x,y=log 101x 的草图由草图，再结合指数函数的图像和性质，可以归纳、分析出对数函数y=log a x(a ＞0，a ≠1)的图像的特征和性质.见下表. 图象 a ＞1a ＜1性 (1)x ＞0(2)当x=1时，y=0质(3)当x＞1时，y＞00＜x＜1时，y＜0 (3)当x＞1时，y＜0 0＜x＜1时，y＞0(4)在(0，+∞)上是增函数(4)在(0，+∞)上是减函数补充性质设y1=log a x y2=log b x其中a＞1，b＞1(或0＜a＜1 0＜b＜1)当x＞1时“底大图低”即若a＞b则y1＞y2当0＜x＜1时“底大图高”即若a＞b，则y1＞y2比较对数大小的常用方法有：(1)若底数为同一常数，则可由对数函数的单调性直接进行判断.(2)若底数为同一字母，则按对数函数的单调性对底数进行分类讨论.(3)若底数不同、真数相同，则可用换底公式化为同底再进行比较.(4)若底数、真数都不相同，则常借助1、0、-1等中间量进行比较.3.指数函数与对数函数对比名称指数函数对数函数一般形式y=a x(a＞0，a≠1) y=log a x(a＞0，a≠1)定义域(-∞，+∞) (0，+∞)值域(0，+∞) (-∞，+∞)函数值变化情况当a＞1时，⎪⎩⎪⎨⎧<<==>>)0(1)0(1)0(1xxxa x当0＜a＜1时，⎪⎩⎪⎨⎧<>==><)0(1)0(1)0(1xxxa x当a＞1时⎪⎩⎪⎨⎧<<==>>)1(0)1(0)1(0logxxxxa当0＜a＜1时，⎪⎩⎪⎨⎧<>==><)1(0)1(0)1(0logxxxxa单调性当a＞1时，a x是增函数；当0＜a＜1时，a x是减函数. 当a＞1时，log a x是增函数；当0＜a＜1时，log a x是减函数.图像y=a x的图像与y=log a x的图像关于直线y=x对称.幂函数幂函数的图像与性质幂函数ny x=随着n的不同，定义域、值域都会发生变化，可以采取按性质和图像分类记忆的方法．熟练掌握ny x=，当112,1,,,323n=±±±的图像和性质，列表如下．从中可以归纳出以下结论：①它们都过点()1,1，除原点外，任何幂函数图像与坐标轴都不相交，任何幂函数图像都不过第四象限．② 11,,1,2,332a =时，幂函数图像过原点且在[)0,+∞上是增函数．③ 1,1,22a =---时，幂函数图像不过原点且在()0,+∞上是减函数．④ 任何两个幂函数最多有三个公共点．n y x =奇函数偶函数非奇非偶函数1n >01n <<0n <定义域 R R R奇偶性奇奇奇非奇非奇OxyOxyOxyOxyOxyOx yOxyOxyOxy偶在第Ⅰ象限的增减性在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递减幂函数y x α=（x ∈R ，α是常数）的图像在第一象限的分布规律是：①所有幂函数y x α=（x ∈R ，α是常数）的图像都过点)1,1(； ②当21,3,2,1=α时函数y x α=的图像都过原点)0,0(；③当1=α时，y x α=的的图像在第一象限是第一象限的平分线（如2c ）；④当3,2=α时，y x α=的的图像在第一象限是“凹型”曲线（如1c ）⑤当21=α时，y x α=的的图像在第一象限是“凸型”曲线（如3c ）⑥当1-=α时，y x α=的的图像不过原点)0,0(，且在第一象限是“下滑”曲线（如4c ）当0>α时，幂函数y x α=有下列性质：（1）图象都通过点)1,1(),0,0(；（2）在第一象限内都是增函数；（3）在第一象限内，1>α时，图象是向下凸的；10<<α时，图象是向上凸的；（4）在第一象限内，过点)1,1(后，图象向右上方无限伸展。

高一必修1-函数图象的变换ppt课件.ppt

如:y=f(x)±h的图象可由y=f(x)的图象 _向__上__（__下__）__平__移__h_个__单__位__而得到.
练习：将直线y=2x+1向左平移5个单位，
得到的函数为__y_=_2_x+_1_1_______
左右平移时，发生变化的仅是x本身，如果x的系数不是1时，需要把系数提出来，再进行变换.
(6)y=f(|x|)的图象:可先作出y=f(x)当x≥0 时的图象,再利用_偶__函__数__的__图__象__关__于__y_轴__对__称, 作出y=f(x)(x≤0)的图象.
函数y=|log2x|的图象是( A )
解析
f
(x)
|
lo g2
x
|
lo g2
lo
g1
2
x, x x,0
1, x
课前练习：
当a>2时,函数 y ax和y (a 1)x2 的图象只可能是( )
y
y
y
y
0
x
A
0
x
B
0x
C
0x
D
知识回顾：基本初等函数及图象（大致图象）
函数一次函数 y=kx+b
图象
二次函数
y=ax2+bx+ c
指数函数 y=ax
对数函数 y=logax
知识回顾：
下列二次函数的图象，是由抛物线y=x2通过怎样的平移变换得到的？
y f 1(x) 与y=f(x)的图象关于直线y=x对称.
设奇函数 f(x) 的定义域为[-5, 5], 若当x∈[0, 5]时, f(x)的图象如右图所
示. 则不等式 f(x)<0 的解集
是 (-2, 0)∪(2, 5]

高中数学 14种函数图像和性质知识解析新人教A版必修1

高中数学14种函数图像和性质知识解析新人教A版必修1高中数学 14种函数图像和性质知识解析新人教A版必修1高中不得不掌握的函数图像与常用性质高中常用函数有14种，它们是:1.正比例函数；2.反比例函数；3.根式函数；4一次函数；5.二次函数；6双勾函数.；7..双抛函数；8.指数函数；9对数函数；10.三角函数；11分段函数.；12.绝对值函数；13.超越函数；14.抽象函数。

而函数的性质常见的有：1.定义域；2.值域；3.单调性；4.奇偶性；5.周期性；6.对称性；7.有界性；8.反函数；9.连续性.高中都是从函数解析式入手画出函数图像，再利用函数图像研究其性质，下面我们就函数的图像和性质做归纳总结。

1.正比例函数解析式图像定义域：值域：单调性：奇偶性：反函数：2.反比例函数解析式图像性质定义域：值域：单调性：奇偶性：反函数：对称性：定义域：值域：单调性：对称性：3根式函数解析式图像定义域：值域：单调性：奇偶性：反函数：4一次函数解析式图像定义域：值域：1 性质性质性质用心爱心专心单调性：反函数：5二次函数解析式图像定义域：值域：单调性：对称性：定义域：值域：单调性：对称性：6.双勾函数解析式图像定义域：值域：单调性：奇偶性：对称性：定义域：值域：单调性：奇偶性：对称性：7.双抛函数解析式图像定义域：值域：单调性：奇偶性：对称性：定义域：性质性质性质用心爱心专心值域：单调性：奇偶性：对称性：8.指数函数解析式图像定义域：值域：单调性：9.对数函数解析式图像定义域：值域：单调性：10.三角函数解析式图像单调性：周期性：奇偶性：有界性：对称性：定义域：值域：单调性：周期性：奇偶性：有界性：对称性：定义域：值域：单调性：周期性：奇偶性：有界性：对称性：定义域：值域：单调性：周期性：奇偶性：有界性：对称性：11.分段函数分段函数是在其定义域的不同子集上，分别用几个不同的式子来表示对应关系的函数，它是一类较特殊的函数。

高中数学必修一：函数的图象 PPT课件图文

<0 可化为fxx<0，即 xf(x)<0，f(x)的大致图象如图所示．所以 xf(x)<0 的解集为(－1,0)∪(0,1)．答案：D
返回 3．若不等式(x－1)2<logax(a>0，且a≠1)在x∈(1,2)内恒成立，
则实数a的取值范围为
()
A．(1,2]
B. 22，1
π 4
＝f
34π ＝1＋
5 ，f
π 2
＝2
2 .∵2
2
<1＋
5，∴f
π 2<f
π4＝f
34π，从而排除D，故选B.
答案：B
5.如图，不规则四边形ABCD中，AB和CD是线
返回
段，AD和BC是圆弧，直线l⊥AB交AB于E，
当l从左至右移动(与线段AB有公共点)时，把
返回
课堂考点突破
练透基点，研通难点，备考不留死角
返回
考点一函数图象的识辨 [考什么·怎么考]
作为函数关系的一种重要表示方法，函数图象的识辨是每年高考的热点内容，题型多为选择题，难度适中，得分较易.
考法(一) 根据函数解析式或图象识辨函数图象
返回
1．函数f(x)＝1＋log2x与g(x)＝
C．(1， 2) D．( 2，2)
解析：要使当x∈(1,2)时，不等式(x－1)2<logax
恒成立，只需函数y＝(x－1)2在(1,2)上的图象
在y＝logax的图象的下方即可．当0<a<1时，显然不成立；当a>1时，如图，要使x∈(1,2)时，y
＝(x－1)2的图象在y＝logax的图象的下方，只需(2－1)2 ≤loga2，即loga2≥1，解得1<a≤2，故实数a的取值范围是 (1,2]．故选A. 答案：A

人教A版数学必修一5、函数的图像.docx

函数的图像一、考点分解1、熟记常见基本初等函数图像①y=kx+b(k ≠0)) ②y=xk (k ≠0) ③y=ax 2++bx+c (a ≠0) ④y=a x (a>0,a ≠1) ⑤y=log a x (a>0,a ≠1)2、会通过平移变换及对称变换作函数的图像。

3、掌握数形结合的数学思想方法，能利用函数图像解决有关问题。

二、作图例1：作下列函数的图像：(1)y=1-x(x Z ∈) (2)y=2x 2-4x-3(0<x<3) (3)y=⎪⎩⎪⎨⎧≥<<)1()10(1x x x x (4)y=1+x x(5)y=432-+x x (6)y=2x(7)y=2log 21-x (8)y=x 2-2x -1知识要点归纳（1）画函数图像不仅要注意函数的解析式还应该注意函数的________________（2）列表描点是画函数图像的基本方法。

但通过平移变换及对称变换作函数的图像是函数作图的主要方法① 平移变换y=f(x)移移__________0________0<>h h y=f(x-h)y=f(x)移移___________0_________0<>k k y=f(x)+k ② 对称变换y=f(x)对称轴关于x y=_____________ y=f(x)对称轴关于y y=________ y=f(x)对称关于直线a x =y=_____________ y=f(x)对称关于原点y=______________ ③ 翻折变换 y=f(x)对称的图像并作其关于图像去掉图像保留_______________,_________y=f(x ) y=f(x)翻折上去将图像保留_________________y=)(x f 三、用图-------利用数形结合的数学思想方法处理问题题型一、运用数形结合求字母的取值范围例1：不等式12-++x x >a 恒成立,求实数a 的取值范围练习1：已知a ∈R 讨论关于x 的方程a x x =+-862的实数解的个数2：当m 为怎样的实数时,方程x 2-4x +5=m 有四个不相等的实数根题型二、利用数形结合求最值例2、已知函数y=x 21-上任意一点M(x,y) ，求 (1) (x-1)2+(y-1)2的取值范围 (2)求11++x y 的取值范围练习：1、已知直线y=x+m 与函数y=x 21-的图像有两个不同交点,则m 的取值范围是____________2、求函数y=12+-x x x ]2,3[--∈的值域题型三、利用数形结合解不等式例3、解不等式x x ->-2112练习：解不等式 122≥-x x题型四、由抽象函数性质构建函数图象研究抽象函数例4：定义在R 上的函数y fx =-∞()()在，2上为增函数，且函数y f x =+()2为偶函数则（）A.f f ()()-<13B.f f ()()03>C.f f ()()-=-13D.f f ()()23<练习：若函数)(x f 是定义在R 上的偶函数，在]0,(-∞上是减函数,且0)2(=f ，则使得0)(<x f 的x 的取值范围（）A.)2,(-∞B.),2(+∞C.),2()2,(+∞--∞D.（－2，2）题型五、图像的对称原理及应用（1） Y=f(x)的图像关于直线x=a 对称⇔f(a+x)=f(a-x) 或 f(x)=f(2a-x)（2） Y=f(x)的图像关于点(a,b)对称⇔f(a+x)+f(a-x)=2b 或 f(x)+f(2a-x)=2b（3） Y=f(x)与y=g(x)的图像关于直线x=a 对称⇔f(x)=g(2a-x)或 f(a+x)=g(a-x)（4） Y=f(x)与y=g(x)的图像关于点(a,b)对称⇔f(a+x)+g(a-x)=2b 或f(x)+g(2a-x)=2b例5、函数y=f(x)对任意x ∈R 都有f(3+x)=f(3-x)且f(x)=0的所有实数根之和为24。

高一数学必修一函数图像知识点总结

03
通过大量的练习和实践，提高对复杂函数图像的识别能力和分
析水平。
观看
REPORTING
复合函数性质
复合函数具有“同增异减”的性质，即内外函数的单调性相同时，复合函数为增函数；内外函数的单调性不同时，复合函数为减函数。
分段函数表达式及性质
分段函数定义
在自变量的不同取值范围内，用不同的解析式来表示一个函数，这样的函数叫做分段函数。
分段函数性质
分段函数的定义域是各段定义域的并集；分段函数的值域是各段值域的并集；分段函数在定义域的不同子集上，具有不同的对应关系。
坐标平面
由x轴和y轴组成的平面称为坐标平面，其中x轴和y轴的交点称为原点，坐标为(0,0)。
函数图像绘制方法
01
02
03
列表法
列出函数自变量与函数值的对应表，然后在坐标系中描出各点，最后用平滑的曲线连接各点。
解析法
根据函数解析式，直接利用函数的性质绘制出函数的图像。
图象变换法
通过对基本初等函数的图像进行平移、伸缩、对称等变换，得到所求函数的图像。
PART 02
一次函数图像知识点
一次函数表达式及性质
一次函数表达式
y = kx + b (k ≠ 0)
性质
当 k > 0 时，函数图像为增函数；当 k < 0 时，函数图像为减函数。
一次函数图像特征
直线性
一次函数的图像是一条直线。
斜率
直线的斜率等于一次函数表达式中的 k 值。
截距
直线在 y 轴上的截距等于一次函数表达式中的 b 值。
PART 05
三角函数图像知识点
三角函数基本概念及性质

函数图像专题PPT课件图文

答案 B
2．(2011·福州质检)函数y＝log2|x|的图象大致是( ) 答案 C 解析函数y＝log2|x|为偶函数，作出x>0时y＝log2x的图象，图象关于y轴对称，应选C.
答案 A
4．(08·山东)设函数f(x)＝|x＋1|＋|x－a|的图象关于直线x＝1对称，则a的值为( ) A．3 B．2 C．1 D．－1 答案 A 解析 ∵函数f(x)图象关于直线x＝1对称，∴f(1＋x)＝f(1－x)，∴f(2)＝f(0)．即3＋|2－a|＝1＋|a|，用代入法知选A.
思考题1 将函数y＝lg(x＋1)的图象沿x轴对折，再向右平移一个单位，所得图象的解析式为________．【答案】 y＝－lgx
题型二知式选图或知图选式问题例2 (2011·合肥模拟)函数f(x)＝loga|x|＋1(0<a<1)的图象大致为( )
【解析】首先分析奇偶性，知函数为偶函)＝1，∴选A.
1.函数图象的三种变换 (1)平移变换：y＝f(x)的图象向左平移a(a>0)个单位，得到y＝f(x＋a)的图象；y＝f(x－b)(b>0)的图象可由y＝f(x)的图象向右平移b个单位而得到；y＝f(x)的图象向下平移b(b>0)个单位，得到y＝f(x)－b的图象；y＝f(x)＋b(b>0)的图象可由y＝f(x)的图象向上平移b个单位而得到．总之，对于平移变换，记忆口诀为：左加右减上加下减．
【答案】 C
题型三函数图象的对称性例3 (1)已知f(x)＝ln(1－x)，函数g(x)的图象与f(x)的图象关于点(1,0)对称，则g(x)的解析式为________________． (2)设函数y＝f(x)的定义域为实数集R，则函数y＝f(x－1)与y＝f(1－x)的图像关于( ) A．直线y＝0对称 B．直线x＝0对称 C．直线y＝1对称 D．直线x＝1对称

高数数学必修一《5.4.1正弦函数、余弦函数的图像》教学课件

过两直线y＝1和y＝－1所夹的范围．
其中正确的个数是(
)
A．0
B．1
C．2
D．3
答案：D
题型 2 利用“五点法”作三角函数的图象
【问题探究2】在确定正弦函数的图象形状时，应抓住哪些关键点？
π
2
3π
2
提示：(0，0)，( ，1)，(π，0)，( ，－1)，(2π，0)
例2 用“五点法”作出下列函数的图象：
)
(2)函数y＝cos
1
2
x，x∈[0，2π]的图象与直线y＝－的交点有________
2
个．
1
2
解析：作出y＝cos x，x∈[0，2π]与y＝－的图象(图略)，由图象可知，函数y＝cos x，x∈[0，2π]的图象与
1
直线y＝－2有两个交点．
ቤተ መጻሕፍቲ ባይዱ
随堂练习
5π
1.已知点( ，m)在余弦曲线上，则m＝(
____________
________
正(余)弦函数的图象叫做正(余)弦曲线，是一条“波浪
起伏”的连续光滑曲线
【即时练习】
1．观察正弦函数y＝sin x，x∈R的图象，下列说法错误的是(
A．过原点
B．与y＝cos x的图象形状相同，只是位置不同
C．与x轴有无数个交点
D．关于y轴对称
答案：D
解析：观察题图可得，正弦函数y＝sin x，x∈R的图象不关于y轴对称．故选D.
B．介于直线y＝1与直线y＝－1之间
C．关于x轴对称
D．与y轴仅有一个交点
答案：ABD
微点拨❶
(1)作正弦函数、余弦函数图象时，函数自变量的取值要用弧度制，
以保证自变量的取值与函数值都为实数．

数学人教A版必修第一册5.4.1正弦函数、余弦函数的图象课件

点( ，�� )，将这些点用光滑的曲线连接起来，可得的比较精确的函数 =
， ∈ [，]的图象.
知识梳理
探究二：根据函数 = ， ∈ [，]的图象，你能想象函数 = ， ∈
的图象吗？
由诱导公式一可知，函数 = ， ∈ [, ( + )]， ∈ 且 ≠ 的图象

−
− −
−

− −

− −

知识梳理
探究三：在确定正弦函数的图象形状时，应抓住哪些关键点？
【提示】
视察图，在函数 = ， x∈［0,2π］的图象上，
以下五个点： 0，0 ，

，1
2
，，0 ，
3
，1
2
， 2，0

= ， ∈ 的图

象向左平移个单位长度而得到.所以，将正弦函数的图象向左平移个单位长度，
就得到余弦函数的图象，如图所示：
知识梳理

− −

−

−
−
− −

−

余弦函数 = ， ∈ 的图象叫做余弦曲线.它是与正弦曲线具有相同形状
若把轴上从0到2这一段分成12等份，使

的值分别为0，，，， … ，2，

它们所对应的角的终边与单位圆的交点将圆周12等分，再按上述画点( , )

高一上学期函数专题：函数的图像(含答案解析)

高一上学期函数专题：函数的图像学校:___________姓名：___________班级：___________考号：___________一、单选题 1．函数241xy x =+的图象大致为（） A ． B ．C ．D ．2．函数y =x cos x +sin x 在区间[–π，π]的图象大致为（）A ．B ．C ．D ．3．如图下面的四个容器高度都相同，将水从容器顶部一个孔中以相同的速度注入其中，注满为止．用下面对应的图象显示该容器中水面的高度h 和时间t 之间的关系，其中不正确的有（）A．1个B．2个C．3个D．4个4．如图所示，单位圆上一定点A与坐标原点重合．若单位圆从原点出发沿x轴正向滚动一周，则A点形成的轨迹为（）A．B．C．D．5．设函数()f x 的定义域为R ，满足(1) 2 ()f x f x +=，且当(0,1]x ∈时，()(1)f x x x =-.若对任意(,]x m ∈-∞，都有8()9f x ≥-，则m 的取值范围是A ．9,4⎛⎤-∞ ⎥⎝⎦B ．7,3⎛⎤-∞ ⎥⎝⎦C ．5,2⎛⎤-∞ ⎥⎝⎦D ．8,3⎛⎤-∞ ⎥⎝⎦6．已知定义在()(),00,-∞⋃+∞上的奇函数()f x 在(),0-∞上单调递增，且满足()12f -=-，则关于x 的不等式()2sin f x x xπ<+的解集为（）． A ．()(),11,-∞-+∞B ．()()1,01,-⋃+∞C ．()(),10,1-∞-⋃D ．()()1,00,1-7．已知定义在R 上的函数()[)[)222,0,12,1,0x x f x x x ⎧+∈⎪=⎨-∈-⎪⎩，且()()2f x f x +=,若方程()20f x kx --=有三个不相等的实数根，则实数k 的取值范围是A ．1,13⎛⎫⎪⎝⎭B ．11,34⎛⎫-- ⎪⎝⎭C ．111,,133⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭D ．1111,,3443⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭8．已知定义在R 上的奇函数，满足(2)()0f x f x -+=，当(]0,1x ∈时，2()log f x x =-，若函数()()()sin π=-F x f x x ，在区间[]1-，m 上有10个零点，则m 的取值范围是（）A ．[)3.54，B ．(]3.5,4C ．(]5,5.5D ．[)55.5，9．函数()218x f x +⎛⎫= ⎪⎝⎭的部分图象大致为A ．B ．C ．D ．10．设函数21,2()5,2x x f x x x ⎧-⎪=⎨-+>⎪⎩，若互不相等的实数,,a b c 满足()()()f a f b f c ==，则222a b c ++的取值范围是（） A ．(16,32) B ．(18,34) C ．(17,35) D ．(6,7)二、多选题11．已知直线2y x =-+分别与函数x y e =和ln y x =的图象交于点()()1122,,,A x y B x y ，则下列结论正确的是 A ．122x x += B ．122x x e e e +>C ．1221ln ln 0x x x x +<D ．12x x >三、填空题12．设方程24x x +=的根为m ，方程2log 4x x +=的根为n ，则m n +=________；参考答案1．A 【分析】由题意首先确定函数的奇偶性，然后考查函数在特殊点的函数值排除错误选项即可确定函数的图象. 【详解】由函数的解析式可得：()()241xf x f x x --==-+，则函数()f x 为奇函数，其图象关于坐标原点对称，选项CD 错误；当1x =时，42011y ==>+，选项B 错误. 故选：A. 【点睛】函数图象的识辨可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势．(3)从函数的奇偶性，判断图象的对称性．(4)从函数的特征点，排除不合要求的图象．利用上述方法排除、筛选选项． 2．A 【分析】首先确定函数的奇偶性，然后结合函数在x π=处的函数值排除错误选项即可确定函数的图象. 【详解】因为()cos sin f x x x x =+，则()()cos sin f x x x x f x -=--=-，即题中所给的函数为奇函数，函数图象关于坐标原点对称，据此可知选项CD 错误；且x π=时，cos sin 0y ππππ=+=-<，据此可知选项B 错误. 故选：A. 【点睛】函数图象的识辨可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势．(3)从函数的奇偶性，判断图象的对称性．(4)从函数的特征点，排除不合要求的图象．利用上述方法排除、3．A 【分析】结合几何体的结构和题意知，容器的底面积越大水的高度变化慢、反之变化的快，再由图象越平缓就是变化越慢、图象陡就是变化快来判断．【详解】A 、因正方体的底面积是定值，故水面高度的增加是均匀的，即图象是直线型的，故A 不对；B 、因几何体下面窄上面宽，且相同的时间内注入的水量相同，所以下面的高度增加的快，上面增加的慢，即图象应越来越平缓，故B 正确；C 、球是个对称的几何体，下半球因下面窄上面宽，所以水的高度增加的越来越慢；上半球恰相反，所以水的高度增加的越来越快，则图象先平缓再变陡；故C 正确；D 、图中几何体两头宽、中间窄，所以水的高度增加的越来越慢后再越来越慢快，则图象先平缓再变陡，故D 正确．故选A ．【点睛】本题考查了数形结合思想，对于此题没有必要求容器中水面的高度h 和时间t 之间的函数解析式，因此可结合几何体和图象作定性分析，即充分利用数形结合思想． 4．A 【分析】分析当单位圆向x 轴正向滚动π个单位长度时A 的纵坐标，由此判断出A 点形成的轨迹. 【详解】如图所示，记,,B C D 为圆上的三个四等分圆周的点，由题意可知：圆是逆时针滚动的，因为圆的周长为2π，所以2AB BC CD AD π====，且圆上点的纵坐标最大值为2，当圆逆时针滚动π单位长度时，此时,A C 的相对位置互换，所以A 的纵坐标为2，排除BCD ，故选：A.关键点点睛：解答本题的关键是通过特殊位置（向右滚动π个单位长度）分析对应A 点的纵坐标，通过排除法判断出轨迹. 5．B 【分析】本题为选择压轴题，考查函数平移伸缩，恒成立问题，需准确求出函数每一段解析式，分析出临界点位置，精准运算得到解决．【详解】(0,1]x ∈时，()=(1)f x x x -，(+1)= ()f x 2f x ，()2(1)f x f x ∴=-，即()f x 右移1个单位，图像变为原来的2倍．如图所示：当23x <≤时，()=4(2)=4(2)(3)f x f x x x ---，令84(2)(3)9x x --=-，整理得：2945560x x -+=，1278(37)(38)0,,33x x x x ∴--=∴==（舍），(,]x m ∴∈-∞时，8()9f x ≥-成立，即73m ≤，7,3m ⎛⎤∴∈-∞ ⎥⎝⎦，故选B ．【点睛】易错警示：图像解析式求解过程容易求反，画错示意图，画成向左侧扩大到2倍，导致题目出错，需加深对抽象函数表达式的理解，平时应加强这方面练习，提高抽象概括、数学建模能力． 6．C 【分析】令()()2g x f x x=-，利用奇偶性定义可知()g x 为奇函数，并可确定()g x 在(),0-∞，()0,∞+上单调递增，由()10g -=知()10g =，结合55sin 22g π⎛⎫< ⎪⎝⎭不成立可确定()g x 与sin y x =π大致图象，由图象可确定解集. 【详解】()f x 为()(),00,-∞⋃+∞上的奇函数，()()f x f x ∴-=-，令()()2g x f x x =-，则()()()()22g x f x f x g x x x-=-+=-+=-，()g x ∴为()(),00,-∞⋃+∞上奇函数；()f x 在(),0-∞上单调递增，2y x=-在(),0-∞上单调递增，()g x ∴在(),0-∞上单调递增，由奇函数性质知：()g x 在()0,∞+上单调递增；()12f -=-，()()1120g f ∴-=-+=，则()10g =，又()()51122f f f ⎛⎫>=--= ⎪⎝⎭，当52x =时，2459sin sin525x x ππ+=+=， ∴当52x =时，()2sin f x x x π<+不成立，即55sin 22g π⎛⎫< ⎪⎝⎭不成立，由此可在坐标系中画出()g x 与sin y x =π大致图象如下图所示：由图象可知：当()(),10,1x ∈-∞-时，()sin g x x π<，即当()(),10,1x ∈-∞-时，()2sin f x x xπ<+. 故选：C. 【点睛】关键点点睛：本题考查函数不等式的求解，解题关键是能够通过构造函数的方式，结合奇偶性和单调性的知识确定函数的大致图象，利用数形结合的方式求得结果.7．C 【分析】由()()2f x f x +=可得函数周期为2，结合函数在[]1,1-上的解析式，利用周期作出()f x 的函数图象,根据()y f x =和2y kx =+图象交点个数判断k 的范围. 【详解】方程()20f x kx --=有三个不相等的实数根，等价于()y f x =和2y kx =+图象有三个不同交点，因为()()2f x f x +=,所以()f x 的周期为2，由函数()[)[)222,0,12,1,0x x f x x x ⎧+∈⎪=⎨-∈-⎪⎩，利用周期性作出()f x 的函数图象，如图所示: 不妨设0,k >当直线2y kx =+过()()3,1,1,1--时，k 的值分别为13与1，由图可知，113k <<时直线2y kx =+与()f x 的图象有三个交点，113k ∴<<时, 方程()20f x kx --=有三个不相等的实数根, 同理,若0k <,可得113k -<<-时，方程()20f x kx --=有三个不相等的实数根,所以实数k 的取值范围是111,,133⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，故选C.【点睛】本题主要考查函数的周期与函数图象的应用，考查了函数零点与方程根的关系，同时考查了转化思想与数形结合思想的应用，属于难题. 函数零点的几种等价形式：函数()()y f x g x =-的零点⇔函数()()y f x g x =-在x 轴的交点⇔方程()()0f x g x -=的根⇔函数()y f x =与()y g x =的交点.8．A 【分析】由()()20f x f x -+=得出函数()y f x =的图象关于点()1,0成中心对称以及函数()y f x =的周期为2，由函数()y f x =为奇函数得出()00f =，并由周期性得出()2f = ()40f =，然后作出函数()y f x =与函数()sin y x π=的图象，列举前10个交点的横坐标，结合第11个交点的横坐标得出实数m 的取值范围．【详解】由()()20f x f x -+=可知函数()y f x =的图象关于点()1,0成中心对称，且()()()2f x f x f x -=-=-，所以，()()2f x f x +=，所以，函数()y f x =的周期为2，由于函数()y f x =为奇函数，则()00f =，则()()240f f ==，作出函数()y f x =与函数()sin y x π=的图象如下图所示：211log 122f ⎛⎫=-= ⎪⎝⎭，则11122f f ⎛⎫⎛⎫-=-=- ⎪ ⎪⎝⎭⎝⎭，于是得出7311222f f f ⎛⎫⎛⎫⎛⎫==-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，51122f f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，由图象可知，函数()y f x =与函数()sin y x π=在区间[]1,m -上从左到右10个交点的横坐标分别为1-、12-、0、12、1、32、2、52、3、72，第11个交点的横坐标为4，因此，实数m 的取值范围是[)3.5,4，故选A ．【点睛】本题考查方程的根与函数的零点个数问题，一般这类问题转化为两个函数图象的交点个数问题，在画函数的图象时，要注意函数的奇偶性、对称性、周期性对函数图象的影响，属于难题．9．B【分析】根据函数的定义域以及单调性求解.【详解】由题意得，()f x 的定义域为R ，排除C,D ；当2x ≥-时，()218x f x +⎛⎫= ⎪⎝⎭，∵1018<<，∴()f x 在[)2,-+∞上单调递减，排除A ，故选B.【点睛】本题考查了已知函数表达式，识别函数图象，涉及了函数的定义域以及指数函数的单调性；从函数的定义域可以判断函数图象的“左右”位置，以及是否有断点；单调性可以判断函数的变化趋势.10．B【分析】画出函数()f x 的图象，不妨令a b c <<，则222a b +=．结合图象可得45c <<，从而可得结果．【详解】画出函数()f x 的图象如图所示．不妨令a b c <<，则1221a b -=-，则222a b +=．结合图象可得45c <<，故16232c <<．∴1822234a b c <++<．故选：B ．【点睛】数形结合是根据数量与图形之间的对应关系，通过数与形的相互转化来解决数学问题的一种重要思想方法，.函数图象是函数的一种表达形式，它形象地揭示了函数的性质，为研究函数的数量关系提供了“形”的直观性．归纳起来，图象的应用常见的命题探究角度有：1、确定方程根的个数；2、求参数的取值范围；3、求不等式的解集；4、研究函数性质． 11．ABC【分析】根据互为反函数的性质可得()()1122,,,A x y B x y 的中点坐标为()1,1，从而可判断A ；利用基本不等式可判断B 、D ；利用零点存在性定理以及对数的运算性质可判断C.【详解】函数x y e =与ln y x =互为反函数，则x y e =与ln y x =的图象关于y x =对称，将2y x =-+与y x =联立，则1,1x y ==，由直线2y x =-+分别与函数x y e =和ln y x =的图象交于点()()1122,,,A x y B x y ，作出函数图像：则()()1122,,,A x y B x y 的中点坐标为()1,1，对于A ，由1212x x +=，解得122x x +=，故A 正确；对于B，122x x e e e ≥=+=，因为12x x ≠，即等号不成立，所以122x x e e e +>，故B 正确；对于C ，将2y x =-+与x y e =联立可得2x x e -+=，即20x e x +-=，设()2x f x e x =+-，且函数为单调递增函数，()010210f =+-=-<，112211320222f e e ⎛⎫=+-=-> ⎪⎝⎭，故函数的零点在10,2⎛⎫ ⎪⎝⎭上，即1102x <<，由122x x +=，则212x <<， 122112211ln ln ln ln x x x x x x x x +=- ()1222122ln ln ln 0x x x x x x x <-=-<，故C 正确；对于D，由12x x +≥，解得121x x ≤，由于12x x ≠，则121x x <，故D 错误；故选：ABC【点睛】本题考查了互为反函数的性质、基本不等式的应用、零点存在性定理以及对数的运算性质，考查了数形结合的思想，属于难题.12．4【详解】由题意，方程24x x +=的根为m ，方程2log 4x x +=的根为n ，24m m ∴+=……①，24n log n += …… ②由①得24m m =-，24m log m ∴=-（）令4t m =- ，代入上式得24t log t -=24t log t ∴+= 与②式比较得t n =于是44m n m n -=∴+= 故答案为4．【点睛】本题主要考查方程的根，即为相应函数图象交点的横坐标，解题的关键是利用设而不求的思想，充分利用题设条件得到m n +的值.。

新人教A版必修一对数函数的概念对数函数图像和性质课件(22张)

;
(2)下列函数中,是对数函数的是
.(填序号)
①y=log4x;②y=log2(3x);③y=logx2;④y=log3(x-1);⑤y=log2x2;
1
⑥y= 2 log3x.
探究一
探究二
探究三
易错辨析
解析:(1)设 f(x)=logax(a>0,且 a≠1),
1
依题意有 loga4=-1,故 a=4,
探究三
易错辨析
对于含有偶次根式中被开方式为对数式时,要注意被开方的代数
式为非负,还要顾及对数式中本身的真数大于0这一隐含信息,错解
中显然忘记了真数大于0这一隐含条件.
1
2
3
4
5
6
1.下列函数中,是对数函数的是(
A.y=log2x-1
B.y=logx3x
C.y= log 1 x
D.y=3log5x
2
探究一
探究二
探究三
易错辨析
变式训练2函数f(x)=3x(0<x≤2)的反函数的定义域为(
A.(0,+∞)
B.(1,9]
C.(0,1)
D.[9,+∞)
解析:∵ 0<x≤2,∴1<3x≤9,
即函数f(x)的值域为(1,9].
故函数f(x)的反函数的定义域为(1,9].
答案:B
)
探究一
探究二
探究三
易错辨析
C.
2
D.x2
解析:由题意,知 f(x)=logax.∵f(x)的图像过点(√,a),
1
∴a=loga√.∴a=2.∴f(x)=log 1 x.故选 B.
2
答案:B
函数y=logax(a>0,且a≠1)的反函数是y=ax(a>0,且a≠1);函数

(完整word版)高中数学必修一三角函数图像性质总结(精华版)

•正弦、余弦、正切函数图象和性质函数正弦函数y =sinx,x运R余弦函数y=cosx, x^R正切函数y = tanx, xHkr +上2有界性有界有界无界疋义域(^□0, +Xi)r 兀i2 x | x式k兀+—, Z ,I 2 J值域[-1,1]当X =3 +2kjl(k 乏Z)时，y max =〔2■JT当x =_二+2kir(k ^Z)时，2『min =-〔3,1]当X=2k H(k€Z)时，y max =1当x =兀+2k n(k€Z)时，『min = -1(^aC, ^C)周期性是周期函数，最小正周期T=2兀是周期函数，最小正周期T =2兀T =兀奇偶性奇函数，图象关于原点对称偶函数，图象关于y轴对称奇函数，图象关于原点对称单调性在［一生+2k兀，壬+2小］,(k € z)2 2上是单调增函数在［壬+2kn,竺+2阪］,(k乏Z)2 2上是单调减函数在［兀+2kir,2兀+2kn:］, (k 乏Z)上是单调增函数在［2k%兀+2kn］, (k^Z)上是单调减函数”H 兀在(_一+k兀，一+k兀),(k^ Z) 2 2上是单调增函数对称轴1Tx =k 兀+ = ,(k E Z)2x =kir, (k w Z)对称中心(也,0) (MZ)(k兀+ 匹,0) (k^Z)2k兀(三,0) (HZ)正弦函数、余弦函数、正切函数的图像三角函数的性质1定义域与值域 2、奇偶性(1) 基本函数的奇偶性奇函数：y = sinx , y = tanx ；偶函数：y = cosx.(2),型三角函数的奇偶性(i) g ( x )=—二匚(x € R )g (x )为偶函数二T ■-匚「•匚O 虫血(曲+®)二虫sm (-蕊+©(XE R) n 迪欧刚片Q (応R) 8$少二 Oo®=fc?r+—优eZ)由此得同理，=虫迎(的物仃E 去)为奇函数sin = 0(p — k7l(k € Z).(丘).；'：.■. - ■ J .：!■, ■ /.'■■■.'■.I宀'-■■ : - ■■- - /'为偶函数---::1 ；：—上:-■■- - -；1 为奇函数 (圧 2) 2 .3、周期性1)基本公式(i)基本三角函数的周期 y = sinx , y = cosx 的周期为：•'； ; y = tanx , y = cotx的周期为匚.(ii)「V 」型三角函数的周期2JTy= 4$in(眾x+卩)+kj=i4coK 驱+©+上开y 二虫 tan (临+仍 +匕丁二 Acot(@z+g) + 上的周期为|少| . (2) 认知y=ta nxyiy；y=cotx II 丿 /f f / y1 /I112■ z n -2oJ2! , n 212x-JI2o恥312-込：—1 r [ ii f I\tI 1 1 i2 2-1y=cosx(i) 讨型函数的周期开尸恤in(处+©卩屮cos(曲+创的周期为0| ；7T》=|血购(亦+ ©卜=|乂嗽(倾+釧的周期为0 .(ii) 一：“」的周期严|加1伽+©+斗尸血o$伽+©+貝的周期为青；71尸|伽血+ ©+丽二血0t伽+© +上|的周期为0 .均同它们不加绝对值时的周期相同，即对+ 的解析式施加绝对值后，该函数的周期不变•注意这一点与(i)的区别•(ii) 若函数为「川型两位函数之和，则探求周期适于“最小公倍数法”.(iii) 探求其它“杂”三角函数的周期，基本策略是试验一一猜想一一证明(3)特殊情形研究7T(i) y = tanx —cotx的最小正周期为］;(ii) '的最小正周期为］;(iii) y = sin 4X + cos4x的最小正周期为 _ .由此领悟“最小公倍数法”的适用类型，以防施错对象.4、单调性(1)基本三角函数的单调区间(族)依从三角函数图象识证“三部曲”：①选周期：在原点附近选取那个包含全部锐角，单调区间完整，并且最好关于原点对称的一个周期；②写特解：在所选周期内写出函数的增区间(或减区间)；③获通解：在②中所得特解区间两端加上有关函数的最小正周期的整数倍，即得这一函数的增区间族(或减区间族)循着上述三部曲，便可得出课本中规范的三角函数的单调区间族.揭示：上述“三部曲”也适合于寻求简单三角不等式的解集或探求三角函数的定义域•(2)R 型三角函数的单调区间此类三角函数单调区间的寻求“三部曲”为①换元、分解：令u—二，将所给函数分解为内、外两层：y二f （u）, u… ；②套用公式：根据对复合函数单调性的认知，确定出f （u）的单调性，而后利用（1）中公式写出关于u的不等式；③还原、结论：将u=J「二代入②中u的不等式，解出x的取值范围，并用集合或区间形成结论•正弦、余弦、正切、余切函数的图象的性质：/y =s inx y =cosx y =ta nx y =cotxy = Asin®x+申)(A、⑷ > 0)定义域R R- 1 _x|x E R且x #冗岂兀k亡Z卩{x|x^R 且x^k jL k^z}R值域[_1,+1][_1,+1]R RL A, A】周期性2兀2兀312H看奇偶性奇函数偶函数奇函数奇函数当甲式0,非奇非偶当® =0,奇函数单调性n:[——+2kTi,2-+2^I]2上为增函数；TT[—+2kir,23兀丄—■ +2kn]2上为减函数( "Z )［（2k—1兀.2kn］上为增函数［2k 兀,（2k +1 対上为减函数（"Z ）+k ii,匹+k n〕1 2 2丿上为增函数（"Z ）(5, (k+1^ )上为减函数(k^Z ) 1[上■上兀 22kn:------- Q2( A)(A),12kn: +— n 一申2( A)（八丿_ 0 」二为增函数；2kn十匹一护(A),O2k兀+^3兀一半2 ( 八)（一八）. ⑷一二为减函数注意：①y =-sinx与y =sinx的单调性正好相反；y =-cosx与y =cosx的单调性也同样相反一般地，若y =f（x）在［a,b］上递增（减），则y=-f（x）在［a,b］上递减（增）②y =sin x与y =COSX的周期是二.③y =sin（灼x+巧或y=cos®x+®）（⑷芒0 ）的周期T =吾.y=tan x的周期为2兀（T=2L—T=2TT，如图，翻折无效）•2抄厂JT④y =sin（，x •「）的对称轴方程是- （k • Z ），对称中心（k二,0 ） ; y住x ）的对称轴方程是x=k二（Z），对称中心（k-）；y =a x :）的对称中心（—,0）.k 2 ,02原点对称> y - _cos( _2x) - _cos2xy =cos2x⑤当tan : tan 1 =1, : - -k (k Z)；ta n : tan 一- _1, ： - 一- k (k Z).2 2⑥y =cosx与y =sin i x 2k二是同一函数，而y=(.x・)是偶函数，贝UI 2 丿1y =( x ：T)二sin( x k - ) = cos( x).⑦函数yy=tanx为增函数，同样也是错误的］.⑧定义域关于原点对称是f （x）具有奇偶性的必要不充分条件.（奇偶性的两个条件：一是定义域关于原点对称（奇偶都要），二是满足奇偶性条件，偶函数：f（「x）=f（x），奇函数：f（_x）--f（x））奇偶性的单调性：奇同偶反.例如：y=tanx是奇函数，y =tan（x --）是非奇非偶.（定义域不3关于原点对称）奇函数特有性质：若x的定义域，则f （x）一定有f（o）=o. （O^x的定义域，贝U无此性质）⑨y =sinx不是周期函数；y = sin x为周期函数（T ★）;y .cosx是周期函数（如图）；y = cos x为周期函数（T二二）；y=cos2x』的周期为兀（如图），并非所有周期函数都有最小正周期, 2y、 /一：、X *例如：y =f (x) =5 =f (x k),k R.⑩ y =a cos* 亠bsin - - a2b2sin(x 亠门)cos =b有a2b2y .、形如y =Asin（「x •的函数:11、几个物理量：A—振幅；f二1—频率（周期的倒数）；「X •「一相位；‘一初相；2、函数y = Asin（）表达式的确定：A由最值确定；• •由周期确定；:由图象上的特殊点确定,如f（x）= Asgx +申"“妙＞0宀的图象如图所示,则 f (x)(答:f (x)二2sin^ x3.函数y 二Asin(・x ) B (其中 A 0, ，0)最大值是A最小正周期T十|y= cos|x| 图象yy=| cos2x+1/21图象Q JT频率是f ，相位是，初相是：;其图象的对称轴是直线•■x W：=k （k・Z），凡2兀2是该图象与直线y=B 的交点都是该图象的对称中心 4、研究函数y =Asin （「x •「）性质的方法：类比于研究y =sin x 的性质，只需将y = Asin （ • x J 中的看成y =si n x 中的x ，但在求y = A si n （・・x •「）的单调区间时，要特别注意 A 和• ‘的符号，通过诱导公式先将•’化正。

新教材人教版B版必修一函数的图象课件(53张)

()
(2)(2019·宁波九校模拟)已知函数 f(x)＝x－ln1x－1，则 y＝f(x) 的图象大致为( )
【解析】 (1)设 f(x)＝2|x|sin 2x，其定义域关于坐标原点对称，又 f(－x)＝2|－x|·sin(－2x)＝－f(x)，所以 y＝f(x)是奇函数，故排除选项 A，B；令 f(x)＝0，所以 sin 2x＝0，所以 2x＝kπ(k∈Z)，所以 x＝k2π(k∈Z)，故排除选项 C.故选 D. (2)由于 f(e)＝e－1 2＞0，排除 D.由于 f(1e)＝e＞0，排除 B.由于 f(e2)＝e2－1 3＜f(e)，故函数在(1，＋∞)为减函数，排除 C，所以选 A. 【答案】 (1)D (2)A
②y＝f(x) 0＜a＞a＜1，1，纵纵坐坐标标伸缩长短为为原原来来的的a倍a倍，，横横坐坐标标不不变变→ y＝_a_f_(x_)____．
判断正误(正确的打“√”，错误的打“×”) (1)当 x∈(0，＋∞)时，函数 y＝|f(x)|与 y＝f(|x|)的图象相同．( × ) (2)函数 y＝af(x)与 y＝f(ax)(a>0 且 a≠1)的图象相同．( × ) (3)函数 y＝f(x)与 y＝－f(x)的图象关于原点对称．( × ) (4)若函数 y＝f(x)满足 f(1＋x)＝f(1－x)，则函数 f(x)的图象关于直线 x＝1 对称．( √ ) (5)将函数 y＝f(－x)的图象向右平移 1 个单位得到函数 y＝f(－ x－1)的图象．( × )
(3)作 y＝log2|x|的图象，再将图象向右平移一个单位，如图，即得到 y＝log2|x－1|的图象．
函数图象的识别
(高频考点)
函数图象的识别是每年高考的重点，题型为选择题，难度适

高一数学人教版必修一函数的奇偶性 PPT课件图文

猜想： f(x)f(x)
x ..3.2 1 0 1 2 3..
... f (x) x2
941
0
14
9..
偶函数的定义
一般地，如果对函数 f (x) 的定义域内任意一个 x, 都有f (x) f (x)，那么函数 f (x)就叫偶函数 .
类比&探究
f(1)f(1) f(2)f(2) f(3)f(3)
1.3.2函数的奇偶性
必修1（人教版）
故宫
女子跳水10米跳台决赛，正反跳映衬对称美
数学&生活
生活中的对称美引入我们的数学领域中，它又是怎样的情况呢？
请同学们观察下列函数图形，说出他们各有怎样的对称性？
问题与思考
以上函数图像有什么共同特征呢？哈哈，我来回答
以上函数图像都关于y轴对称
把图像关于y轴对称函数称为偶函数
问题与思考
以上函数图像有什么共同特征呢？
以上函数图像都关于原点对称
把图像关于原点对称函数称为奇函数
根据下列函数图象,判断其奇偶性.
y
y
o
奇函数
x
o
x 偶函数
y
b
oLeabharlann x 偶函数yo
x 奇函数
观察 & 发现
f(1)1f(1)
f(2)4f(2)
f( 3)9f(3) ……
2.两个性质:
一个函数为奇函数它的图象关于原点对称。一个函数为偶函数它的图象关于y 轴对称。
3. 判断函数奇偶性的方法和步骤
我来总结
判断函数的奇偶性，注意定义域优先
1.
课堂小结
f ( x )是函数f (x)的图像对函数 f (x)的定义

高一数学函数图像专题(含详解)

高一数学函数图像专题(含详解)一、函数的概念函数是一种数学关系，它将一个集合中的每个元素映射到另一个集合中的唯一元素。

在数学中，我们用函数来描述数量之间的关系。

二、函数图像的绘制为了更好地理解函数的性质和规律，我们可以通过绘制函数图像来进行观察和分析。

绘制函数图像时，我们需要确定函数的定义域和值域，并选取一些代表性的输入值，计算出对应的输出值，然后将这些点连接起来，即可得到函数图像。

三、常见函数图像1.直线函数图像：直线函数的图像通常是一条直线，可以通过确定直线的斜率和截距来确定。

2.平方函数图像：平方函数的图像是一条抛物线，开口的方向由平方项的系数决定，开口向上为正，开口向下为负。

3.正弦函数图像：正弦函数的图像是一条波浪形曲线，表现周期性的特点。

4.指数函数图像：指数函数的图像呈现出递增或递减的趋势，斜率随着自变量的增大而增大或减小。

5.对数函数图像：对数函数的图像通常是一条曲线，呈现出随着自变量的增大，函数值增长趋缓的特点。

四、函数图像的性质1.奇偶性：函数图像关于原点对称的称为奇函数，图像关于y轴对称的称为偶函数。

2.单调性：函数图像上的点随着自变量的增大或减小而具有递增或递减的趋势。

3.零点与极值点：函数图像与x轴相交的点称为零点，图像上的极值点包括最大值和最小值。

五、总结函数图像是研究函数性质和规律的重要工具。

通过绘制函数图像，我们可以直观地了解函数的特点，并进行更深入的分析和推理。

在研究函数图像时，需要注意函数的定义域、值域以及一些常见函数的特点和性质。

这对于理解和应用函数概念都非常重要。

以上是关于高一数学函数图像专题的详细解释和内容总结，希望对你有所帮助。