材料力学第一章轴向拉伸和压缩资料重点
(材料力学)第一章轴向拉伸和压缩

24
根据Saint-Venant原理:
25
7. 应力集中(Stress Concentration):
由于截面尺寸急剧变化而引起的局部应力增大的现象。
·应力集中因数
K max m
26
不同性质的材料对应力集中的敏感程度不同
1.脆性材料
σmax 达到强度极限,此位置开裂,所 以脆性材料构件对应力集中很敏感。
轴力图如右图 N
2P + –
3P
BC
PB
PC
N3
C
PC N4
5P
+
P
D PD D PD D PD
x
11
[例2] 图示杆长为L,受轴线方向均布力 q 作用,方向如图,试画
出杆的轴力图。 q
解:x 坐标向右为正,坐标原点在 自由端。
L
取左侧x 段为对象,内力N(x)为:
O x
N – qL
N(x)maxqL
2.塑性材料
应力集中对塑性材料在静载作用下的强度影响不 大,因为σmax 达到屈服极限,应力不再增加,未达 到屈服极限区域可继续承担加大的载荷,应力分布 趋于平均。
在静载荷情况下,不需考虑应力集中的影响;但 在交变应力情况下,必须考虑应力集中对塑性材料 的影响。
况、安全重要性、计算模型等等
16
依强度准则可进行三种强度计算:
①校核强度:
m ax
②设计截面尺寸:
Amin
Nmax
[ ]
③许可载荷:
N ma xA ;
Pf(Ni)
17
[例4] 已知三铰屋架如图,承受竖向均布载荷,载荷的分布 集度为:q =4.2kN/m,屋架中的钢拉杆直径 d =16 mm,许用
《材料力学》第1章知识点+课后思考题

第一章绪论第一节材料力学的任务与研究对象一、材料力学的任务1.研究构件的强度、刚度和稳定度载荷:物体所受的主动外力约束力:物体所受的被动外力强度:指构件抵抗破坏的能力刚度:指构件抵抗变形的能力稳定性:指构件保持其原有平衡状态的能力2.研究材料的力学性能二、材料力学的研究对象根据几何形状以及各个方向上尺寸的差异,弹性体大致可以分为杆、板、壳、体四大类。
1.杆:一个方向的尺寸远大于其他两个方向的尺寸的弹性体。
轴线:杆的各截面形心的连线称为杆的轴线;轴线为直线的杆称为直杆;轴线为曲线的杆称为曲杆。
按各截面面积相等与否,杆又分为等截面杆和变截面杆。
2.板:一个方向的尺寸远小于其他两个方向的尺寸,且各处曲率均为零,这种弹性体称为板3.壳:一个方向的尺寸远小于其他两个方向的尺寸,且至少有一个方向的曲率不为零,这种弹性体称为板4.体:三个方向上具有相同量级的尺寸,这种弹性体称为体。
第二节变形固体的基本假设一、变形固体的变形1.变形固体:材料力学研究的构件在外力作用下会产生变形,制造构件的材料称为变形固体。
(所谓变形,是指在外力作用下构建几何形状和尺寸的改变。
)2.变形弹性变形:作用在变形固体上的外力去掉后可以消失的变形。
塑性变形:作用在变形固体上的外力去掉后不可以消失的变形。
又称残余变形。
二、基本假设材料力学在研究变形固体时,为了建立简化模型,忽略了对研究主体影响不大的次要原因,保留了主体的基本性质,对变形固体做出几个假设:连续均匀性假设认为物体在其整个体积内毫无间隙地充满物质,各点处的力学性质是完全相同的。
各向同性假设任何物体沿各个方向的力学性质是相同的小变形假设认为研究的构件几何形状和尺寸的该变量与原始尺寸相比是非常小的。
第三节 构件的外力与杆件变形的基本形式一、构件的外力及其分类1.按照外力在构件表面的分布情况:度,可将其简化为一点分布范围远小于杆的长集中力:一范围的力连续分布在构件表面某分布力: 二、杆件变形的基本形式杆件在各种不同的外力作用方式下将发生各种各样的变形,但基本变形有四种:轴向拉伸或压缩、剪切、扭转和弯曲。
(完整版)材料力学各章重点内容总结

材料力学各章重点内容总结第一章 绪论一、材料力学中工程构件应满足的3方面要求是:强度要求、刚度要求和稳定性要求。
二、强度要求是指构件应有足够的抵抗破坏的能力;刚度要求是指构件应有足够的抵抗变形的能力;稳定性要求是指构件应有足够的保持原有平衡形态的能力。
三、材料力学中对可变形固体进行的3个的基本假设是:连续性假设、均匀性假设和各向同性假设。
第二章 轴向拉压一、轴力图:注意要标明轴力的大小、单位和正负号。
二、轴力正负号的规定:拉伸时的轴力为正,压缩时的轴力为负。
注意此规定只适用于轴力,轴力是内力,不适用于外力。
三、轴向拉压时横截面上正应力的计算公式:N F Aσ= 注意正应力有正负号,拉伸时的正应力为正,压缩时的正应力为负。
四、斜截面上的正应力及切应力的计算公式:2cos ασσα=,sin 22αστα=注意角度α是指斜截面与横截面的夹角。
五、轴向拉压时横截面上正应力的强度条件[],maxmax N F A σσ=≤六、利用正应力强度条件可解决的三种问题:1.强度校核[],maxmax N F A σσ=≤一定要有结论 2.设计截面[],maxN F A σ≥ 3.确定许可荷载[],max N F A σ≤七、线应变l l ε∆=没有量纲、泊松比'εμε=没有量纲且只与材料有关、 胡克定律的两种表达形式:E σε=,N F l l EA∆= 注意当杆件伸长时l ∆为正,缩短时l ∆为负。
八、低碳钢的轴向拉伸实验:会画过程的应力-应变曲线,知道四个阶段及相应的四个极限应力:弹性阶段(比例极限p σ,弹性极限e σ)、屈服阶段(屈服极限s σ)、强化阶段(强度极限b σ)和局部变形阶段。
会画低碳钢轴向压缩、铸铁轴向拉伸和压缩时的应力-应变曲线。
九、衡量材料塑性的两个指标:伸长率1100l l lδ-︒=⨯︒及断面收缩率1100A A Aϕ-︒=⨯︒,工程上把5δ︒≥︒的材料称为塑性材料。
十、卸载定律及冷作硬化:课本第23页。
材料力学 -轴向拉伸和压缩PPT课件

第二章
轴向拉伸和压缩
最新课件
1
第二章 轴向拉伸和压缩
§2 — 1 概述 §2 — 2 轴力 轴力图
目 §2 — 3 拉(压)杆截面上的应力
§2 — 4 拉(压)杆的变形 胡克定律 泊松比
录 §2 — 5 材料在拉伸与压缩时的力学性质
§2 — 6 拉(压)杆的强度计算 §2 — 7 拉(压)杆超静定问题 §2 — 8 连接件的实用计算
§ 2-3拉(压)杆截面上的应力
σ FN A
AB
——FN 为轴力, A 为杆的横截面面积
F
F
3、圣维南原理
说明:杆端集中力作用点附近区域内的应力分布比较复杂,并 非均匀分布,上式只能计算该区域内横截面上的平均应力,而 不是应力的真实情况;且应力分布规律及其计算公式与外力作 用方式有关,其研究已经超出N材料力学范围。
p
MA
➢应力的正、负号约定:正应力 以拉应力
为正,压应力为负;切应力 以使所作用的微段绕其内部任
意点有顺时针方向转动趋势者为正,反之为负。
➢应力的单位:帕斯卡 (pa)、兆帕(Mpa)、吉帕(Gpa) 1帕=1牛顿 / 米2 ( N/m2 ) 1MPa =1N/mm2 = 106 Pa 1GPa = 109 Pa 注意:1、在谈到应力时,必须指明应力所在的平面及点的位置; 2、没有特别说明的情况下,提最到新应课件力一般指正应力和切应力2。0
m
F
F
m
最新课件
6
§2-2 轴力、轴力图
截开 在求内力的截面 mm处, F
假想地将杆截为两部分
分离
留下左段为分离体
F
m
m m
F FN
材料力学——2拉伸和压缩

反面看:危险,或 失效(丧失正常工作能力) (1)塑性屈服 (2)脆性断裂
28
• 正面考虑 —— 应力 为了—— 安全,或不失效
( u — Ultimate, n — 安全因数 Safety factor)
(1)塑性 n =1.5 - 2.5 (2)脆性 n = 2 - 3.5 • 轴向拉伸或压缩时的强度条件 ——
截面法(截、取、代、平) 轴力 FN(Normal) 1.轴 力
Fx 0
得
FN P 0 FN P
5
•轴力的符号
由变形决定——拉伸时,为正 压缩时,为负
注意: • 1)外力不能沿作用线移动——力的可传性不
成立 变形体,不是刚体
6
2. 轴 力 图
• 纵轴表示轴力大小的图(横轴为截面位 置) 例2-1 求轴力,并作轴力图
哪个杆先破坏?
§2-2 拉 ( 压 ) 杆 的 应 力
杆件1 —— 轴力 = 1N, 截面积 = 0.1 cm2 杆件2 —— 轴力 = 100N, 截面积 = 100 cm2
哪个杆工作“累”?
不能只看轴力,要看单位面积上的力—— 应力 • 怎样求出应力?
思路——应力是内力延伸出的概念,应当由 内力 应力
材料力学
Mechanics of Materials
1
2
§2-1 概念及实例
• 轴向拉伸——轴力作用下,杆件伸长 (简称拉伸)
• 轴向压缩——轴力作用下,杆件缩短 (简称压缩)
3
拉、压的特点:
• 1.两端受力——沿轴线,大小相等,方向相反
• 2. 变形—— 沿轴线的伸长或缩短
材料力学 -轴向拉伸和压缩

材料力学 - 轴向拉伸和压缩材料力学是研究材料性质和行为的学科,包括弹性、塑性、疲劳、断裂等方面。
在材料力学中,轴向拉伸和压缩是重要的力学测试方法。
轴向拉伸测试轴向拉伸测试是材料测试中最常用的测试方法之一。
该测试方法涉及将试验样品拉伸至破裂点,并测量在拉伸过程中的应力和应变。
在这种测试中,试验样品的截面积比长度更重要,因为应力是由试样的横截面积决定的。
实验过程首先,通过切割样品制备试样。
样品应该是长条状,尺寸应该足够大,能够容纳拉伸机的夹具和测量设备。
然后将样品置于拉伸机上,将试样夹具固定在机器的上部,并将另一个夹具固定在机器的下部。
然后将机器调整到适当的测试条件,比如设置测试速度、卸载条件等。
开始拉伸后,由于拉伸过程会导致不均匀应变,需要使用应变计进行应变测量。
最后,测试结果应该包括应力 - 应变曲线和破坏点。
结果解释轴向拉伸测试的结果由两种性质构成:杨氏模量和屈服强度。
杨氏模量衡量材料的弹性变形特性,而屈服强度则衡量材料开始塑性变形的能力。
在拉伸试验中,将出现线性区域,在该区域,样品的杨氏模量可由应力-应变曲线的斜率计算。
当样品的应变超过线性区域后,就会进入塑性区域,此时材料会表现出不可逆的形变特性。
轴向压缩测试轴向压缩测试是一种用于测量材料在压缩负载下的应变和应力的测试方法。
在这种测试中,材料试件放置在压力夹具之间,并受到垂直于试件轴向的载荷。
压缩测试与轴向拉伸测试非常相似,但它们的结果不同。
由于材料的差异,它们所能承受的压缩力和拉伸力也会存在一定的不同。
实验过程样品制备和夹具的选择与轴向拉伸测试类似,但是在拉伸试验机与压缩机之间存在差异。
进行轴向压缩测试时,需要将夹具安装在垂直于轴向的方向上,并将试件放置在夹具内。
与轴向拉伸测试相同,需要记录测试过程中的应变和应力变化。
结果解释与轴向拉伸测试一样,轴向压缩测试的结果也由杨氏模量和屈服强度构成。
杨氏模量是指在材料的弹性变形区域中,材料的应力与应变的比例系数。
第一章 轴向拉伸和压缩1 材料力学

T Qz
z
My N x 主矢
N 轴力; Qy, Qz 剪力;
T 扭矩; My, Mz 弯矩 。
2020/11/11
9
截面法的步骤 1 沿截面假想地截开,留下一部分作为研究对
象,弃去另一部分;
2 用作用于截面上的内力代替弃去部分对留下部
分的作用;
3
对留下部分,列平衡方程求出内力。
2020/11/11
2020/11/11
18
为了得到正应力分布规律,先研究杆件变形。
ac
杆的变形 F
a'
c'
F
变形后a' b',c' d'
b'
d'
(1) 仍为直线;
bd
(2) 仍互相平行且垂直于轴线;
平面假设
变形前为平面的横截面,变形后仍保持为平面,
而2020且/11/11仍垂直于轴线。
19
平面假设 F
ac
a'
c'
下面建立变形与力之间的关系
应变
l
2020/11/11
l
23
2. 横向变形 横向变形量
bb1b
横向应变 b
试验证明
b
当应力不超过比例极限时,有:
泊松比或横向变形系数。
上式也可写成:
2020/11/11
24
在弹性范围内,有变形 x 与外力 F 成正比的弹性定律
Fkx
它是由英国力学家胡克(Robert Hooke, 1635-1703) 于1678年发现的,实际上早于他1500年前,东汉的经学 家和教育家郑玄(公元127-200)就已经发现
AB段:
天津大学工程力学材料力学第一章-轴向拉伸与压缩

34
由上述结果可见,砖柱的最大 工作应力在柱的下段,其值为 1.1MPa ,是压应力。最大工作应 力所在的截面称为危险截面。 危险截面
工程力 学
35
例2- 3 图(a)所示构架的BC杆为直径 d=20mm 的 钢 杆 , AB 杆 的 横 截 面 积 为 540mm2,已知p=2KN, 试求AB杆和BC杆 横截面上的应力。 C (a) A P
P
P
圣文南原理:“ 力作用于杆端方式不同, 只会使与杆端距离不大于杆的 横向尺寸的范围内受影响。” 应力集中现象
工程力 学
30
例2-2 一横截 面为正方形的砖柱 分上、下两段,其 受力情况,各段长 度横截面尺寸如图 (a) 所 示 , 已 知 P=50KN, 试求构件 的最大工作应力。
A I P P B II C
2
τ0 = 0 τπ = 0
2
工程力 学
44
§ §2-4 2-4 拉 拉( (压 压) )杆的变形,胡克定律 杆的变形,胡克定律 1、轴向变形,胡克定律
l1 (a) P l (b) P l1 P b1
工程力 学
45
b1 P b
轴向变形: ΔL=L1−L =变形后的长度−变形前的长度
PL Δl ∝ A
Stress & Strain: Axial Loading
工程力 学
28
• 集中压力会引起力作用点附近很大的应 力分布。 • 从力作用点后相对较短的距离后应力和 应变分布变的趋向均匀。
text, p. 104
Stress & Strain: Axial Loading
工程力 学
29
P A
P A
σ
材料力学——第一章 轴向拉伸和压缩

形象表示轴力随截面的变化情况,发现危险面;
材料力学
例题1-1 已知F1=10kN;F2=20kN; F3=35kN;F4=25kN;试画 出图示杆件的轴力图。 1 B 2 C 3 D A 解:1、计算各段的轴力。
F1 F1 F1
FN kN
1 F2
2
F3 3
F4
AB段 BC段
FN1 FN2
F
F
F
F
d变) 拉伸ε'<0、 压缩ε’>0 ;
'
d
d
材料力学
2、泊松比 实验证明:
称为泊松比;
注意
(1)由于ε、ε‘总是同时发生,永远反号, 且均由
(2)
s 产生,
故有
=-
‘
0 FN 1 F1 10kN
x x
F
0 FN 2 F2 F1
FN 2 F1 F2
F2
FN3
10
CD段
F4
25
10 20 10kN Fx 0
FN 3 F4 25kN
2、绘制轴力图。
10
x
材料力学
画轴力图步骤
1、分析外力的个数及其作用点; 2、利用外力的作用点将杆件分段; 3、截面法求任意两个力的作用点之间的轴力; 4、做轴力图; 5、轴力为正的画在水平轴的上方,表示该段杆件发生 拉伸变形
材料力学
例题1-3 起吊钢索如图所示,截面积分别为 A2 4 cm2, A1 3 cm2,
l1 l 2 50 m, P 12 kN, 0.028 N/cm3,
试绘制轴力图,并求
高职材料力学1—轴向拉伸与压缩

1.1 轴向拉伸与压缩的概念与实例
力学模型如图
F
F
轴向拉伸, 对应的力称为拉力。
F
F
轴向压缩, 对应的力称为压力。
1.2 轴向拉伸或压缩时的内力
1.2.1 内力及轴力 内力指由外力作用所引起的、物体内相邻部分之间 分布内力系的合成(附加内力)。
要求截面上的内力,一般采用截面法,其基本步骤 如下:
的正应力为:
d2
s1
FN1 A1
4 2.0104
0.0202
6.37 107 Pa
63.7
MPa
同理,得 BC 段内任一横截面 2-2 上的正应力为:
s2
FN2 A2
4 (3.0104 )
0.0302
4.24107 Pa
42.4 MPa
是压应力
1.4 轴向拉伸或压缩时的变形
直杆在轴向拉力作用下,将引起轴向尺寸的增大和 横向尺寸的缩小。反之,在轴向压力作用下,将引 起轴向的缩短和横向的增大。
1.3 横截面上的应力 结论
F
F
(1)各纤维的伸长相同, 所以它们所受的力也相同。
(2)平面假设:变形前为平面的横截面,变形后仍保 持为平面且仍垂直于轴线。
1.3 横截面上的应力
推导公式 由结论可知, 在横截面上作用着均匀分布的正应力。
F
}s
FN
s FN
(2.1)
A
式中, FN为轴力, A 为杆的横截面面积。s的符号与轴
横向增大,所以'和的符号是相反的。'和的关
系可以写成
说明P18:表1-1.
例 图所示杆系由两根钢杆1和2组成。已知杆端铰接,两杆与
铅垂线均成=30º的角度,长度均为l=2 m,直径均为d=25
工程力学(材料力学)1_3轴向拉伸与压缩

BC
D
PB PC N3 C
PC N4
5P +
–
PD D
PD D
PD
P
x
P8-9 例题
A 3F
1
2
B
C
F
2F
1
2
1
2
3F
F
1
2
3.应力
应力的表示:
(1)平均应力
(A上平均内力集度)
p平均
ΔP ΔA
P
M
A
(2)实际应力 (M点内力集度)
lim p
ΔP dP
ΔA0 ΔA dA
应力分解
垂直于截面的应力称为“正应力” (Normal Stress);
平杆BC为2杆)用截面法取节点B为研究对象
Fx 0 Fy 0
N1 cos 45 N2 0 N1sin 45 P 0
N1 28.3kN (拉力) N2 20kN (压力)
45° B C
p
N1
y
N2 45° B x
P
(2)计算各杆件的应力
1
N1 A1
28.3103 202 106
轴力的正负规定: N 与外法线同向,为正轴力(拉力); N
N与外法线反向,为负轴力(压力)。 N
轴力图—— N (x) 的图象表示。
N N>0 N
N<0
意 (1)轴力与截面位置的变化关系,较直观;
义
(2)最大轴力的数值及其所在面的位置,即危险截面位
置,为强度计算提供依据。 N
P
+
x
例1 图示杆的A、B、C、D点分别作用着大小为5P、8P、4P、 1P 的力,方向如图,试画出杆的轴力图。
第1章(轴向拉伸与压缩)重要知识点总结(材料力学)
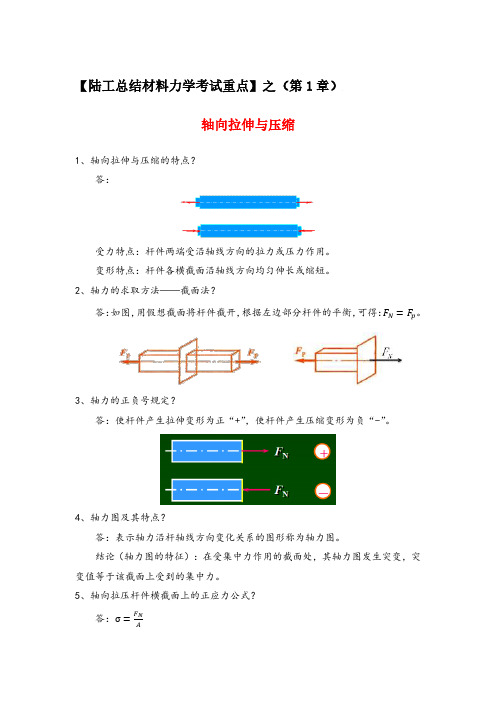
【陆工总结材料力学考试重点】之(第1章)轴向拉伸与压缩1、轴向拉伸与压缩的特点?答:受力特点:杆件两端受沿轴线方向的拉力或压力作用。
变形特点:杆件各横截面沿轴线方向均匀伸长或缩短。
2、轴力的求取方法——截面法?答:如图,用假想截面将杆件截开,根据左边部分杆件的平衡,可得:F N=F p。
3、轴力的正负号规定?答:使杆件产生拉伸变形为正“+”,使杆件产生压缩变形为负“-”。
4、轴力图及其特点?答:表示轴力沿杆轴线方向变化关系的图形称为轴力图。
结论(轴力图的特征):在受集中力作用的截面处,其轴力图发生突变,突变值等于该截面上受到的集中力。
5、轴向拉压杆件横截面上的正应力公式?答:σ=F NA正应力的正负号规定:拉应力为正,压应力为负。
6、轴向拉压杆件的强度条件?答:对于杆件来说,当材料一定时,其许用正应力[σ](即杆件能够正常工作时横截面上任何一点所允许的最大正应力)为一常数,故为保证轴向拉压杆件的强度安全,就必须使杆件横截面上的最大正应力σmax满足:σmax≤[σ]7、应力集中现象及应用?答:如图A处,因有切口、开槽、螺纹等,使横截面面积A剧烈变小,而轴力F N=F不变,而σ=F NA,故发生应力局部增大现象,称为应力集中。
8、拉压变形与胡克定律?答:如图,设杆件原长为l,横截面尺寸为b×h,在轴向载荷F的作用下产生拉伸变形。
绝对变形量:∆l=±F N lEA(拉伸取“+”,压缩取“-”)相对变形量(正应变,也称线应变):=∆ll又:σ=F NA ,则:=∆ll=F N lEAl=F NEA=E即:σ=(胡克定律)由图可知,当杆件伸长(或缩短时),横截面尺寸相应就会变细(或变粗)。
=∆ll称为轴向线应变,而==称为横向正应变,且=。
式中:为泊松比,其值一般小于0.5。
9、材料拉伸、压缩时的力学性能?答:(1)低碳钢拉伸时的力学性能低碳钢拉伸时的σ关系曲线低碳钢拉伸过程可分为四个阶段:1)弹性阶段(OB段)B点对应的应力σ称为弹性极限。
材料力学复习笔记上课讲义

材料力学(一)轴向拉伸与压缩【内容提要】材料力学主要研究构件在外力作用下的变形、受力与破坏、失效的规律。
为设计既安全可靠又经济合理的构件,提供有关强度、刚度与稳定性分析的基本理论与方法。
【重点、难点】重点考察基本概念,掌握截面法求轴力、作轴力图的方法,截面上应力的计算。
【内容讲解】一、基本概念强度——构件在外力作用下,抵抗破坏的能力,以保证在规定的使用条件下,不会发生意外的断裂或显著塑性变形。
刚度——构件在外力作用下,抵抗变形的能力,以保证在规定的使用条件下不会产生过分的变形。
稳定性——构件在外力作用下,保持原有平衡形式的能力,以保证在规定的使用条件下,不会产生失稳现象。
杆件——一个方向的尺寸远大于其它两个方向的尺寸的构件,称为杆件或简称杆。
根据轴线与横截面的特征,杆件可分为直杆与曲杆,等截面杆与变截面杆。
二、材料力学的基本假设工程实际中的构件所用的材料多种多样,为便于理论分析,根据它们的主要性质对其作如下假设。
(一)连续性假设——假设在构件所占有的空间内均毫无空隙地充满了物质,即认为是密实的。
这样,构件内的一些几何量,力学量(如应力、位移)均可用坐标的连续函数表示,并可采用无限小的数学分析方法。
(二)均匀性假设——很设材料的力学性能与其在构件中的位置无关。
按此假设通过试样所测得的材料性能,可用于构件内的任何部位(包括单元体)。
(三)各向同性假设——沿各个方向均具有相同力学性能。
具有该性质的材料,称为各向同性材料。
综上所述,在材料力学中,一般将实际材料构件,看作是连续、均匀和各向同性的可变形固体。
三、外力内力与截面法(一)外力对于所研究的对象来说,其它构件和物体作用于其上的力均为外力,例如载荷与约束力。
外力可分为:表面力与体积力;分布力与集中力;静载荷与动载荷等。
当构件(杆件)承受一般载荷作用时,可将载荷向三个坐标平面(三个平面均通过杆的轴线,其中两个平面为形心主惯性平面)内分解,使之变为两个平面载荷和一个扭转力偶作用情况。
工程力学材料力学第一章

直杆、杆的截面无突变、截面到载荷作用点有一定 的距离。
直杆轴向拉伸或压缩时斜截面上的应力 k
设有一等直杆受拉力P作用。 P 求:斜截面k-k上的应力。 解:采用截面法 由平衡方程:Pα=P P P k P
α α
k Pα k
Pα 则: pα = Aα
Aα:斜截面面积;Pα:斜截面上内力。
A 由几何关系: α = cos Aα
σ 0 ( 45°斜截面上剪应力达到最大 ) |τ 当α = ± 45°时, α |max =
目 录
公式的应用条件: 公式的应用条件: 直杆、杆的截面无突变、 的距离。 直杆、杆的截面无突变、截面到载荷作用点有一定 的距离。 圣维南( 原理: 圣维南 Saint-Venant)原理: 原理 离开载荷作用处一定距离, 离开载荷作用处一定距离,应力分布与大小不受外载荷作 用方式的影响。 用方式的影响。 应力集中( 应力集中(Stress Concentration): ): 在截面尺寸突变处,应力急剧变大。 在截面尺寸突变处,应力急剧变大。
工程构件,大多数情形下,内力并非均匀分布,集度的定 义不仅准确而且重要,因为“破坏”或“失效”往往从内力集 度最大处开始。 2. 应力的表示: 应力的表示: ① 平均应力: 平均应力: ∆P M ∆A
ΔP pM = ΔA
全应力(总应力): ② 全应力(总应力):
p = lim
∆A → 0
∆P dP = ∆ A dA
目 录
目 录
目 录
例题
图示结构,已知斜杆AB长2m,横截面面积为 图示结构,已知斜杆AB长2m,横截面面积为 AB 水平杆AC的横截面面积为250mm AC的横截面面积为 200mm2。水平杆AC的横截面面积为250mm2。材料的 弹性摸量E=200GPa 载荷F=10kN 试求节点A E=200GPa。 F=10kN。 弹性摸量E=200GPa。载荷F=10kN。试求节点A的位 移。 计算各杆件的轴力。(设斜杆为1 。(设斜杆为 解:1、计算各杆件的轴力。(设斜杆为1杆,水 平杆为2 用截面法取节点A 平杆为2杆)用截面法取节点A为研究对象
材料力学(1)

1-1 工程实际中的轴向拉伸和 压缩问题
F F
工程实际中,有很多发生轴向 拉伸和压缩变形的构件。 如联接钢板的螺栓(图 a ), 在钢板反力作用下,沿其轴 向发生伸长(图c),称为轴 向拉伸; 托架的撑杆CD(图a),在 外力的作用下,沿其轴向发 生缩短(图b),称为轴向压 缩。 产生轴向拉伸(或压缩)变 形的杆件, 简称为拉(压) 杆。
I
50kN 150kN
II
100kN
I 50kN I II FN2 100kN II FN2= −100kN FN1 FN1=50kN
I 50kN FN
II
+ −
100kN
| FN |max=100kN
1-3 轴向拉伸和压缩时的应力
应力的概念
确定了杆的内力后,还不能解决杆件的强度问题。 经验告诉我们,材料相同,直径不等的两根直杆, 在相 同的拉力F作用下, 内力相等。当力F增大时,直径小的杆 必先断,这是由于内力仅代表内力系的总和,而不能表明截 面上各点受力的强弱程度, 直径小的杆因截面积小,截面上 各点受力大,因此先断。 所以, 需引入表示截面上某点受力强弱程度的量——应 表示截面上某点受力强弱程度的量—— 表示截面上某点受力强弱程度的量——应 力,作为判断杆件强度是否足够的量。 (内力集度) 内力集度)
2 截面法
轴力
截面法: 用假想的截面将杆件截为两部分,任取杆 截面法 :
件的一部分为研究对象,利用静力平衡方程求内力 的方法称为截面法。
m F1 F2 m (a) F1 F2
m m m
F3
FN
∑Fx=0 FN-F1+F2=0
F3
FN = F1 − F2
工程力学材料力学第四版习题答案解析

工程力学材料力学(北京科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解:(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。
解:σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3:试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN,吊杆的尺寸如图b所示。
解:下端螺孔截面:σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面:σ2=2P S =8.72MPa 上端双螺孔截面:σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4:一桅杆起重机如图所示,起重杆AB为一钢管,其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。
已知起重量P=2000N,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5:图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127ACACCBCBPMPaSPMPaSσσ====ACACACLNLEA EAσε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:QNllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
材料力学第一章

解: 1.建立如图坐标系
2.计算1-1截面的内力
1
F 0
x
2
F 2F FN 2 0 FN 2 F 10kN
3F 2F
4.计算3-3截面的内力
3
FN1
F=10kN
x
FN3
3
F=10kN
x
F 0
x
1
F FN1 0
FN1 F 10kN
F 0
x
F 2F 3F FN 3 0 FN 3 2F 20kN
注意!
b
d
c
e
1. 服从胡克定律:oa段
f
b
e P
a
s
E E tan
2. 两个强度指标
o
d g
f h
s — 屈服极限 b — 强度极限
A0 A1 100% 断面收缩率 A0
3. 两个塑性指标
断后伸长率
l1 l0 100% l0
bt
o
σbt—拉伸强度极限(约为140MPa)。它是
衡量脆性材料(铸铁)拉伸的唯一强度指标。
四、材料在压缩时的力学性能
1.低碳钢的压缩
p — 比例极限 e — 弹性极限 S — 屈服极限 E --- 弹性摸量
拉伸与压缩在屈服 阶段以前完全相同。
2. 脆性材料的压缩
1)铸铁 脆性材料的抗拉与抗压 性质不完全相同 压缩时的强度极限远大 于拉伸时的强度极限
计算步骤:
1、截开 2、代替 3、平衡
轴向拉伸或压缩变形
§1-2 变形固体力学的基本概念
一、应力
第1章拉伸与压缩 材料力学讲诉

= 截面以右外力之和(右指为正) 2019/3/9
截面上 下亦然
10
《 材 料 力 学 》—— 李章政
三、 轴力图
轴力图的概念
• 轴力N一般是截面位置x的函数N=N(x) • 轴力N 随x的变化曲线,称为轴力图
作轴力图的目的
• 直观了解轴力变化情况 N • 判断危险截面 (kN)
轴力随截面位置 变化的图形
3. 应力的单位
基本单位:N/m2=Pa 常用单位:kN/m2=kPa 1kPa=103Pa
2019/3/9
s
帕 千帕
P
n
MN/m2=MPa 兆帕
GN/m2=GPa 吉帕 1MPa=106Pa=1N/mm2 1GPa=109Pa=103N/mm2
7
《 材 料 力 学 》—— 李章政
1.2 轴力与轴力图
F
微元面积上的平均应力 点的应力
F sm A
A P
n
F dF s lim A 0 A dA
2019/3/9
应力s 的方向就是内力F 的方向
6
《 材 料 力 学 》—— 李章政
2. 应力的分量
• 应力沿截面法线方向的分量,称为法向应力 (normal stress)或正应力,用 表 示 • 应力平行于截面的分量,称为切向应力、切 应力(shear stress)或 剪应力,用 表 示
例1.2 作图示杆件的轴力图。 解
杆件分三段,自左至右分别为第1段,第2段, 第 3段
N1 15 kN
N 2 25 15 10 kN
15kN 25kN 10kN 20kN
N3 20 kN
N 10kN
20kN x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m
m
P
k
p
m
p
N A
N
A / cos
cos
p cos cos2
p
s in
sin cos
2
sin 2
13
四、应力集中的概念 拉压杆横截面的应力并不完全是均匀分布的,当横截面
上有孔或槽时,在截面曲率突变处的应力要比其它处的应力 大得多,这种现象称为应力集中。
P
P
P
P
P 14
五、拉压杆的强度条件 拉压杆在正常情况下不发生破坏的条件是:拉压杆的
⑵等轴力杆(N=常数):
max
N Am in
⑶变截面变轴力杆:分别计算各危险截面的应力,取其
最大者进行强度校核。
16
⒉ 确定截面尺寸
A
N
⒊ 确定容许荷载
首先确定容许轴力
N A
再根据轴力与荷载的平衡关系计算容许荷载。
17
[例1—4] 已知A1=200mm2,A2=500mm2 ,A3=600mm2 ,
11
解:
A1 A2 60kN 20kN
A B CD
轴力图
20kN ⊕
-○
40kN
AB
N AB A1
40103 2000
20MPa
BC
N BC A2
40103 1000
40MPa
CD
NCD A2
20103 1000
20MPa
12
三、斜截面的应力
m
NP
P P
P
m m
N
p A A
A——斜截面面积
许应力[]1=150MPa; AC为方形截面木杆,边长l=100mm, 容许应力[]2=4.5MPa。求容许荷载[P]。
2.0m
1.5m B
C NAB NAC
解: N AB 1 A1
A
N AC 2 A2
取结点A。
Y 0;
4N 5
AC
P
0
P
P
4 5
N
AC
A
X 0;
3
N 5
AC
N AB
0
P
P
4 3
N AB
19
1.5m
B
A
NAB
A
2.0m
NAC
P
C
P
单考虑AB杆:
P
4 3
N AB
4 3
1
A1
4 3
1
4
d
2
150106 162 106 40.212kN
3
单考虑AC杆:
P
4 5
N AC
4 5
2
A2
4 5
2 l 2
4 4.5106 1002 106 36kN
5
∴[P] = 36kN
30kN
⊕
第二段, X 0
N2 60 80 0
N1
Ⅰ
Ⅱ
N2 20kN
60kN
80kN
N2
第三段, X 0
Ⅱ
N3
Ⅲ 30kN
N3 30 0
N3 30kN
Ⅲ
6
[例1—2]长为l ,重为W 的均质杆,上端固定,下端受一轴
向拉力P 作用,画该杆的轴力图。
轴力图 解:
N
P+W X 0; N P x 0
⊕ N P x PW x
l
x
P
x 0; N Nmin P
P
P
x l; N Nmax P W
7
[练习1]画图示杆的轴力图。
3kN 2kN 2kN
10kN 4kN 8kN
AB
CD
3kN
6kN
⊕
轴力图
1⊕kN
⊕
○ - 轴力图
1kN
○-
4kN 8kN
8
§1–2 拉压杆的应力及强度条件
一、应力的概念
10
二、横截面的正应力
拉压杆横截面上只有正应力而无剪应力,忽略应力集中
的影响,横截面上的正应力可视作均匀分布的,于是有
N
A
正应力正负的规定与轴力相同,以拉为正,以压为负。
[例1—3]已知A1=2000mm2,A2=1000mm2,求图示杆各段横 截面上的正应力。
A1
A2 60kN 20kN
AB
CD
第一章 轴向拉伸和压缩
§1–1 拉压杆的内力 ·轴力与轴力图 §1–2 拉压杆的应力及强度条件 §1-3 拉压杆的变形 虎克定律 §1-4 材料在拉伸和压缩时的力学性质 §1-5 拉压超静定问题
2
§1–1 拉压杆的内力 ·轴力与轴力图
杆件在轴向荷载作用下,将发生轴向拉伸或压缩。
拉伸 P
P
压缩 P
[]=12MPa,试校核该杆的强度。
2kN 2kN 9kN
A1
A2
A3
4kN
2k⊕N
⊕
- ○
5kN
解:
1
N1 A1
2000 200
10MPa
2
N2 A2
4000 500
8MPa
3
Na
max 1 10MPa 12MPa
∴ 此杆安全。
18
[例1—5]图示支架中,AB为圆截面钢杆,直径d=16mm,容
截面上一点分布内力的集度称为该点的应力。
P
pm A
P
Pm称为A面积上的平均应力。
k
lim p
P
A0 A
A
P 称为截面上k 点的应力。
9
将应力p分解为与截面垂直 和平行的两个分量,与截面垂直 p
的分量称为正应力,用表示之,
k
A
与截面平行的分量称为剪应力,
用表示之。
应力的单位为:
1Pa 1N / m2 1kPa 103 Pa 1kN / m2 1MPa 106 Pa 106 N / m2 1N / mm2 1GPa 109 Pa 103 MPa
最大工作应力(横截面的最大正应力)不超过材料的容许 应力。
max
N A
其中[]为材料的容许应力,其值为
jx
n
其中jx为材料破坏时的应力,称为极限应力,由实验测得; n 为安全系数。
15
根据强度条件可进行下述三种工程计算。
⒈ 强度校核
max
N A
⑴等截面杆(A=常数):
max
Nmax A
P
3
一、拉压杆的内力——轴力
m
P
P
m
P
N
X 0; N P 0, N P
拉压杆横截面的内力沿杆的轴线,故称为轴力。轴力以 拉为正,以压为负。
4
二、轴力图 一般情况,拉压杆各截面的的轴力是不同的,表示拉压
杆各截面的的轴力的图象称为轴力图。 轴力图的画法步骤如下: ⒈ 画一条与杆的轴线平行且与杆等长的直线作基线; ⒉ 将杆分段,凡集中力作用点处均应取作分段点; ⒊ 用截面法,通过平衡方程求出每段杆的轴力;画受
20
[练习2]图示结构中,已知P=2kN,杆CD的截面面积
A=80mm2,容许应力[]=160MPa,试校核杆CD的强度并
计算容许荷载。
D
N
A 30 C
B
A 30 C
B
a
a
P XA YA
P
解:
1
mA 0;
N a P 2a 0 2
N 4P 8kN
N 8000 100MPa ∴ CD 杆安全
力图时,截面轴力一定按正的规定来画。 ⒋ 按大小比例和正负号,将各段杆的轴力画在基线两
侧,并在图上表出数值和正负号。 5
[例1—1]画图示杆的轴力图。
60kN
Ⅰ
Ⅱ
80kN
Ⅲ 50kN
Ⅰ
Ⅱ
Ⅲ
60kN
解:
30kN
第一段, X 0
N1 60 0
N1 60kN
⊕ 轴力图
Ⅰ 60kN
○ - 20kN
