第2讲 简便运算(一)
第二课时 运算定律及简便运算

125÷(50÷8)
=3.25÷(2.5×4) =125÷50×8
350÷(35×2) =350÷35÷2
=3.25÷10
=2.5×8
=10÷2
=0.325
=20
=5
差错类型及归纳
类型1 添括号后运算符号的错误使用。 【例1】计算:493-255-145 错解:493-255-145 =493-(255-145) =493-110 =383
104×0.25 =(100+4)×0.25 =100×0.25+4×0.25
=25+1
=26
125÷(50÷8) =125÷50×8
=125×8÷50
=1000÷50
=20
72×101-72 =72×(101-1) =72×100 =7200
69×32+67×69+69 =69×(32+67+1) =69×100 =6900
3. 在○填上“>”“<”或“=”。
(87-87)÷3○= (105-105)÷3
50+<4×5○(50+4)×
750÷15-10○< 750÷(15-10) 69+65÷5○> 69-65÷5
4. 一套校服,上衣每件35元,裤子每条25元,某班订
购了40套校服,需要( 2400 )元。
5.学校新采购了50套课桌椅(1张课桌和1把椅子是1套),
凡 事都 是多棱 镜, 不同 的角 度会
凡 事都是 多棱 镜, 不同 的角度 会看 到不 同的 结果 。若 能把一 些事 看淡 了, 就会 有个好 心境 ,若 把很 多事 看开 了 ,就会 有个 好心 情。 让聚散 离合 犹如 月缺 月圆那 样寻 常, 让得失 利弊 犹如花 开花 谢那 样自然 ,不 计较, 也不 刻意执 着;让 生命 中各 种的喜 怒哀 乐,就 像风 儿一 样,来 了, 不管是 清风 拂面 ,还是 寒风 凛冽, 都报 以自 然 的微笑 ,坦然 的接 受命 运的馈 赠, 把是非 曲折 ,都 当作是 人生 的
小学奥数举一反三六年级A版

- 1 -第1讲 定义新运算一、知识要点定义新运算是指运用某种特殊符号来表示特定的意义,从而解答某些算式的一种运算。
解答定义新运算,关键是要正确地理解新定义的算式含义,然后严格按照新定义的计算程序,将数值代入,转化为常规的四则运算算式进行计算。
定义新运算是一种人为的、临时性的运算形式,它使用的是一些特殊的运算符号,如:*、△、⊙等,这是与四则运算中的“+、-、×、÷”不同的。
新定义的算式中有括号的,要先算括号里面的。
但它在没有转化前,是不适合于各种运算定律的。
二、精讲精练【例题1】假设a*b=(a+b)+(a-b),求13*5和13*(5*4)。
【思路导航】这题的新运算被定义为:a*b 等于a 和b 两数之和加上两数之差。
这里的“*”就代表一种新运算。
在定义新运算中同样规定了要先算小括号里的。
因此,在13*(5*4)中,就要先算小括号里的(5*4)。
练习1:1.将新运算“*”定义为:a*b=(a+b)×(a-b).。
求27*9。
2.设a*b=a2+2b ,那么求10*6和5*(2*8)。
3.设a*b=3a -b ×1/2,求(25*12)*(10*5)。
【例题2】设p 、q 是两个数,规定:p △q=4×q-(p+q)÷2。
求3△(4△6)。
【思路导航】根据定义先算4△6。
在这里“△”是新的运算符号。
练习2:1.设p 、q 是两个数,规定p △q =4×q -(p+q )÷2,求5△(6△4)。
2.设p 、q 是两个数,规定p △q =p2+(p -q )×2。
求30△(5△3)。
3.设M 、N 是两个数,规定M*N =M/N+N/M ,求10*20-1/4。
【例题3】如果1*5=1+11+111+1111+11111,2*4=2+22+222+2222,3*3=3+33+333,4*2=4+44,那么7*4=________;210*2=________。
小学奥数举一反三(六年级)上

小学奥数举一反三(六年级)上一、知识要点定义新运算是指运用某种特殊符号来表示特定的意义’从而解答某些算式的一种运算。
解答定义新运算’关键是要正确地理解新定义的算式含义’然后严格按照新定义的计算程序’将数值代入’转化为常规的四则运算算式进行计算。
定义新运算是一种人为的、临时性的运算形式’它使用的是一些特殊的运算符号’如;*、△、⊙等’这是与四则运算中的“+、-、×、÷”不同的。
新定义的算式中有括号的’要先算括号里面的。
但它在没有转化前’是不适合于各种运算定律的。
二、精讲精练[例题1]假设a*b=(a+b)+(a-b)’求13*5和13*[5*4]。
[思路导航]这题的新运算被定义为;a*b 等于a 和b 两数之和加上两数之差。
这里的“*”就代表一种新运算。
在定义新运算中同样规定了要先算小括号里的。
因此’在13*[5*4]中’就要先算小括号里的[5*4]。
练习1;1’将新运算“*”定义为;a*b=(a+b)×(a-b)’。
求27*9。
2’设a*b=a2+2b ’那么求10*6和5*[2*8]。
3’设a*b=3a -b ×1/2’求[25*12]*[10*5]。
[例题2]设p 、q 是两个数’规定;p △q=4×q-(p+q)÷2。
求3△(4△6)。
[思路导航]根据定义先算4△6。
在这里“△”是新的运算符号。
练习2;1.设p 、q 是两个数’规定p △q =4×q -[p+q]÷2’求5△[6△4]。
2.设p 、q 是两个数’规定p △q =p2+[p -q]×2。
求30△[5△3]。
3.设M 、N 是两个数’规定M*N =M/N+N/M ’求10*20-1/4。
[例题3]如果1*5=1+11+111+1111+11111’2*4=2+22+222+2222’3*3=3+33+333’4*2=4+44’那么7*4=________;210*2=________。
小学四年级运算定律:简便计算讲义

(1)除法的性质1:一个数连续除以两个数等于这个数除以这两个数的乘积,用字母表示 为a÷b÷c=a÷(b×c)
(2)除法性质2:两个数的和或差除以一个数,等于两个数分别除以这个数再求和或差, 字母表示为:(a±b)÷c=a÷c±b÷c
(3)除法的性质3:被除数和除数同时扩大或算小相同的倍数商不变。
乘除法的简便运算中利用“25×4=100”和“125×8=1000”是经常用到的凑整方法。
类型二、除法的性质 例3.计算
104×24×69)÷(23×12×13)
答案:
104×24×69)÷(23×12×13)
=104×24×69÷23÷12÷13=(104÷23)×(24÷12)×(69÷13)=8×2×3 =48
解析:
乘除法中的添括号法则: 添加括号时括号前若是乘号, 则括号中的符号不改变, 若括号 前是除号,则括号中改变符号,乘号变为除号,除号变为乘号 如:13×25×4=13×(25×4),100÷25÷4=100÷(25×4)
例6.简便计算
6300÷54×6
答案:
6300÷54×6
=6300÷(54÷6) =6300÷9 =700
解析:
一个数除以几个数的乘积, 等于这个数依次除以这几个数, 此题先利用除法的这一性质 去括号,逆用此性质添括号即可,添括号过程中利用交换律“带符号搬家”
例4.计算
2500÷4÷25(两种方法进行简便运算)
答案:
例5.计算
1400÷25
答案:
1400÷25 =14×100÷25 =14×(100÷25)=14×4 =56
运算定律 第
【知识梳理】
1.加减法中常用的简便算法
(1)加法运算律的应用: 在计算过程中可以通过交换律或结合律将能“凑整” 的数先凑整,
五年级下册数学一课一练 第2讲 简便计算 沪教版(含答案)
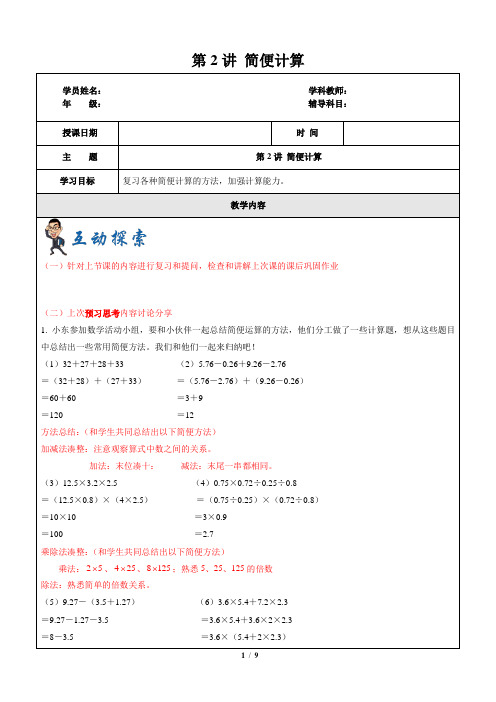
第2讲 简便计算 学员姓名: 学科教师:年 级: 辅导科目:授课日期时 间主 题第2讲 简便计算 学习目标 复习各种简便计算的方法,加强计算能力。
教学内容(一)针对上节课的内容进行复习和提问,检查和讲解上次课的课后巩固作业(二)上次预习思考内容讨论分享1. 小东参加数学活动小组,要和小伙伴一起总结简便运算的方法,他们分工做了一些计算题,想从这些题目中总结出一些常用简便方法。
我们和他们一起来归纳吧!(1)32+27+28+33 (2)5.76-0.26+9.26-2.76=(32+28)+(27+33) =(5.76-2.76)+(9.26-0.26)=60+60 =3+9=120 =12方法总结:(和学生共同总结出以下简便方法)加减法凑整:注意观察算式中数之间的关系。
加法:末位凑十: 减法:末尾一串都相同。
(3)12.5×3.2×2.5 (4)0.75×0.72÷0.25÷0.8=(12.5×0.8)×(4×2.5) =(0.75÷0.25)×(0.72÷0.8)=10×10 =3×0.9=100 =2.7乘除法凑整:(和学生共同总结出以下简便方法)乘法:25⨯、425⨯、8125⨯;熟悉5、25、125的倍数除法:熟悉简单的倍数关系。
(5)9.27-(3.5+1.27) (6)3.6×5.4+7.2×2.3=9.27-1.27-3.5 =3.6×5.4+3.6×2×2.3=8-3.5 =3.6×(5.4+2×2.3)=4.5 =3.6×10=36四则运算简算:(和学生共同总结出以下简便方法)添/脱括号:注意是否可以添/脱,注意变号。
乘法分配律与提取公因数:注意观察算式中相同或有倍数关系的部分。
(完整)小学六年级奥数简便运算(含答案),推荐文档

简便运算(一)一、知识要点根据算式的结构和数的特征. 灵活运用运算法则、定律、性质和某些公式.可以把一些较复杂的四则混合运算化繁为简. 化难为易。
二、精讲精练【例题 1】计算 4.75-9.63+ (8.25-1.37 )【思路导航】先去掉小括号 . 使 4.75 和 8.25 相加凑整 . 再运用减法的性质:a-b-c = a -( b+c). 使运算过程简便。
所以原式= 4.75+8.25 -9.63 -1.37=13-( 9.63+1.37 )=13-11=2练习 1:计算下面各题。
1. 6.73 - 2 又 8/17+ (3.27 -1 又 9/17 )2.7 又 5/9 -(3.8+1 又 5/9 )- 1 又 1/53.14.15 -( 7 又 7/8 - 6 又 17/20 )- 2.1254.13 又 7/13 -( 4 又 1/4+3 又 7/13 )- 0.75【例题 2】计算 333387 又 1/2 ×79+790× 66661 又 1/4【思路导航】可把分数化成小数后 . 利用积的变化规律和乘法分配律使计算简便。
所以:原式= 333387.5 × 79+790×66661.25=33338.75 ×790+790× 66661.25=( 33338.75+66661.25 )× 790=100000× 790=79000000练习 2:计算下面各题:1.3.5 ×1 又 1/4+125% +1 又 1/2 ÷4/52.975 ×0.25+9 又 3/4 ×76-9.753.9 又 2/5 ×425+4.25÷1/604.0.9999 ×0.7+0.1111 ×2.7【例题 3】计算: 36× 1.09+1.2 ×67.3【思路导航】此题表面看没有什么简便算法. 仔细观察数的特征后可知:36 =1.2 ×30。
小学六年级奥数举一反三

小学六年级奥数举一反三一、知识要点定义新运算是指运用某种特殊符号来表示特定的意义’从而解答某些算式的一种运算。
解答定义新运算’关键是要正确地理解新定义的算式含义’然后严格按照新定义的计算程序’将数值代入’转化为常规的四则运算算式进行计算。
定义新运算是一种人为的、临时性的运算形式’它使用的是一些特殊的运算符号’如;某、△、⊙等’这是与四则运算中的“+、-、某、÷”不同。
新定义的算式中有括号的’要先算括号里面的。
但它在没有转化前’是不适合于各种运算定律的。
二、精讲精练[例题1]假设a某b=(a+b)+(a-b)’求13某5和13某[5某4]。
[思路导航]这题新运算被定义为;a某b等于a和b两数之和加上两数之差。
这里“某”就代表一种新运算。
在定义新运算中同样规定了要先算小括号里的。
因此’在13某[5某4]中’就要先算小括号里的[5某4]。
练习1;1’将新运算“某”定义为;a某b=(a+b)某(a-b)’。
求27某9。
2’设a某b=a2+2b’那么求10某6和5某[2某8]。
3’设a某b=3a-b某1/2’求[25某12]某[10某5]。
[例题2]设p、q是两个数’规定;p△q=4某q-(p+q)÷2。
求3△(4△6)。
[思路导航]根据定义先算4△6。
在这里“△”是新的运算符号。
练习2;1.设p、q是两个数’规定p△q=4某q-[p+q]÷2’求5△[6△4]。
2.设p、q是两个数’规定p△q=p2+[p-q]某2。
求30△[5△3]。
3.设M、N是两个数’规定M某N=M/N+N/M’求10某20-1/4。
[例题3]如果1某5=1+11+111+1111+11111’2某4=2+22+222+2222’2/263某3=3+33+333’4某2=4+44’那么7某4=________;210某2=________。
[思路导航]经过观察’可以发现本题的新运算“某”被定义为。
因此练习3;1.如果1某5=1+11+111+1111+11111’2某4=2+22+222+2222’3某3=3+33+333’……那么4某4=________。
小学数学简便运算

第一讲 简便运算以前我们学过,为了使一些题计算简便/快捷,常常采用“凑整”的方法。
这讲除了进一步学习这方面内容之外,还要用这种思想来学习加、减混合及减法的一些简便计算。
【例1】计算:(1)46+270+30 (2)610+270+190分析:(1)题中270和30能凑成整百数,所以先把它们的和算出来。
(2)题中610+190=800能凑成整百数,所以把它们的和算出来。
解: (1) 46+270+30 (2) 610+270+190 =46+(270+30) =(610+190)+270 =46+300 = 800+270=346 = 1070【例2】计算:(1)290+350-150 (2)320-60+180分析:(1)题中350-150=200,能得到一个整百数,所以先算出它们的差。
(2)题中320+180能凑成整百数,所以先算出它们的和。
解: (1) 290+350-150 (2) 320-60+180=290+(350-150) =(320+180)-60 =290+200 = 500-60=490 = 440【例3】计算:45+280+55-80分析:题中45+55=100能凑成整百数,280-80=200也能得到整百数。
因此先分别计算。
解: 45+280+55-80=(45+55)+(280-80) = 100+200 = 300【例4】计算:537-45-55 分析:题中45+55=100(整百数),我们就可以先把45和55相加,再从537里减去它们的和,其结果不变。
解: 537-45-55=537-(45+55) =537-100 =437【例5】计算:372-(72+89)分析:这道题是把减法性质反过来用,就是把减去这两个数的和变成连减,其结果不变。
解: 372-(72+89)=372-72-89=300-89=211【例6】计算:568-98-97分析:这道题中,98与97都接近100,我们就可以先把它们看作100减去,这样,对于98来说,多减了2,对于97来说,多减了3,因此在计算结果的最后,还要再加上2和3两个数。
小学数学简便计算精品PPT课件

简便运算的解题步骤
归纳为三步曲:
验 变 一看 二
三
一看,就是看题目的特征
做题前要求学生先由总体到部 分,由运算符号到参加运算的数的 特点进行全面观察。结合学过的有 关知识,寻找简便计算的方法。
如: 54×101之类的题目,其题目特征就是一 个数乘接近整百、整千的数,就可以指 导学生将算式转化成一个数乘整百整千 数与多余数的和或差,然后再利用乘法 分配律进行计算。有些题目,简便运算 的步骤隐藏在运算过程中,因此,每完 成一步运算都要认真观察,从而发现简 算条件,进行简便运算。
(2)加法结合律:三个数相加,先把前两个数 相加或者先把后两个数相加,和不变。
用字母表示:(a+b)+c=a+(b+c)
乘法运算定律
(1)乘法交换律:交换两个因数的位置,积不变。 用字母表示:a×b=b×a
(2)乘法结合律:三个数相乘,先乘前两个数或者先 乘后两个数,积不变。 用字母表示:(a×b)×c=a×(b×c)
1、 3.2×12.5×25 2、 1.25×88+3.6×0.25 3、 765×64×0.5×2.5×0.125
3、巧变除为乘
也就是说,把除法变成乘法,例如:除以 可以变成乘4。
1、7÷0.25+3÷0.125
2、6.4×480×33.3÷3.2÷120÷66.6
五、裂项法
裂项法是指将分数算式中的项进行拆分,使拆分后 的项可前后抵消,这种拆项计算称为裂项法。常见的裂 项方法是将数字分拆成两个或多个数字单位的和或差。 遇到裂项的计算题时,要仔细的观察每项的分子和分母, 找出每项分子分母之间具有的相同的关系,找出共有部 分。
小学奥数(六年级)举一反三

小学奥数举一反三(六年级)1-20第1讲定义新运算一、知识要点定义新运算是指运用某种特殊符号来表示特定的意义,从而解答某些算式的一种运算。
解答定义新运算,关键是要正确地理解新定义的算式含义,然后严格按照新定义的计算程序,将数值代入,转化为常规的四则运算算式进行计算。
定义新运算是一种人为的、临时性的运算形式,它使用的是一些特殊的运算符号,如:*、△、⊙等,这是与四则运算中的“+、-、×、÷”不同的。
新定义的算式中有括号的,要先算括号里面的。
但它在没有转化前,是不适合于各种运算定律的。
二、精讲精练【例题1】假设a*b=(a+b)+(a-b),求13*5和13*(5*4)。
【思路导航】这题的新运算被定义为:a*b等于a和b两数之和加上两数之差。
这里的“*”就代表一种新运算。
在定义新运算中同样规定了要先算小括号里的。
因此,在13*(5*4)中,就要先算小括号里的(5*4)。
练习1:1.将新运算“*”定义为:a*b=(a+b)×(a-b).。
求27*9。
2.设a*b=a2+2b,那么求10*6和5*(2*8)。
3.设a*b=3a-b×1/2,求(25*12)*(10*5)。
【例题2】设p、q是两个数,规定:p△q=4×q-(p+q)÷2。
求3△(4△6)。
【思路导航】根据定义先算4△6。
在这里“△”是新的运算符号。
练习2:1.设p、q是两个数,规定p△q=4×q-(p+q)÷2,求5△(6△4)。
2.设p、q是两个数,规定p△q=p2+(p-q)×2。
求30△(5△3)。
3.设M、N是两个数,规定M*N=M/N+N/M,求10*20-1/4。
【例题3】如果1*5=1+11+111+1111+11111,2*4=2+22+222+2222,3*3=3+33+333,4*2=4+44,那么7*4=________;210*2=________。
第1、2讲 简便运算

第1讲简便运算(一)一、知识要点在进行分数运算时,除了牢记运算定律、性质外,还要仔细审题,仔细观察运算符号和数字特点,合理地把参加运算的数拆开或者合并进行重新组合,使其变成符合运算定律的模式,以便于口算,从而简化运算。
二、精讲精练【例题1】计算:(1)4445×37 (2) 27×1526练习1用简便方法计算下面各题:1. 1415×8 2.225×1263. 35×11364. 73×7475——5. 19971998×1999【例题2】计算:73115×18练习2计算下面各题:1. 64117×192. 22120×1213. 17×57164. 4113×34+5114×45——【例题3】计算:15×27+35×41练习3计算下面各题:1. 14×39+34×27 2.16×35+56×173. 18×5+58×5+18×10【例题4】计算:56×113+59×213+518×613计算下面各题:1.117×49+517×192.17×34+37×16+67×1123.59×791617+50×19+19×5174.715×38+115×716+115×312【例题5】计算:(1)166120÷41(2) 1998÷19981998 1999计算下面各题:1. 5425 ÷172. 238÷2382382393. 163113 ÷41139第2讲 简便运算(二)一、知识要点前面我们介绍了运用定律和性质以及数的特点进行巧算和简算的一些方法,下面再向同学们介绍怎样用拆分法(也叫裂项法、拆项法)进行分数的简便运算。
分数简便计算(一)教学设计

分数简便计算(一)教学设计课题名称:简便运算(一)学习目标:根据算式的结构和数的特征,灵活运用运算法则、定律、性质和某些公式,可以把一些较复杂 的四则混合运算化繁为简,化难为易。
教学过程: A 、 知识回顾:(1)64×125 (2)293×4×25 (3)75×16+84×75(4)325-165-135 (5)101×99 (6)7500÷25÷4(7)145+785+255+15 (8)25×8×4×125 (9)98×25B 、例题精讲:例题1计算4.75-9.63+(8.25-1.37) 原式=4.75+8.25-9.63-1.37 =13-(9.63+1.37) =13-11 =2 练习1计算下面各题。
1. 6.73-2 817 +(3.27-1 917 ) 2. 759 -(3.8+1 59 )-115例题2:计算33338712 ×79+790×6666114原式=333387.5×79+790×66661.25 =(33338.75+66661.25)×790 =100000×790 =79000000练习2计算下面各题:1. 3.5×114 +1.25+112 ÷452. 975×0.25+934 ×76-9.753. 925 ×425+4.25÷160 4. 0.9999×0.7+0.1111×2.7例题3:计算:36×1.09+1.2×67.3原式=1.2×30×1.09+1.2×67.3 =1.2×(32.7+67.3) =1.2×100 =120练习 3 计算:1. 45×2.08+1.5×37.6 2. 52×11.1+2.6×778例题4计算81.5×15.8+81.5×51.8+67.6×18.5 原式=81.5×(15.8+51.8)+67.6×18.5 =81.5×67.6+67.6×18.5 =(81.5+18.5)×67.6 =100×67.6=6760 练习453.5×35.3+53.5×43.2+78.5×46.52. 235×12.1+235×42.2-135×54.3C 、课堂小结:简便计算方法:1、遇到连加想加法的交换率和结合律。
简便运算

第2讲简便运算(1)一、基础所谓简算,就是利用我们学过的运算法则和运算性质以及运算技巧,来解决一些用常规方法在短时间内无法实现的运算问题。
简便运算中常用的技巧有拆凑,拆是指把一个数拆成的两部分中含有一个整十、整百、整千或者有利于简算的数,凑是指把几个数凑成整十、整百、整千……的数,或者把题目中的数进行适当的变化,运用运算定律或性质再进行简算。
让我们先回忆一下基本的运算法则和性质:乘法结合律:a×b×c=a×(b×c)=(a×c)×b乘法分配律:a×(b+c)=a×b+a×c a×(b-c)=a×b-a×c二、典型例题例1. (1)9999×7778+3333×6666 (2)765×64×0.5×2.5×0.125分析(一):通过观察发现这道题中9999是3333的3倍,因此我们可以把3333和6666分解后重组,即3333×3×2222=9999×2222 这样再利用乘法分配律进行简算。
解(一): 原式=9999×7778+3333×3×2222=9999×7778+9999×2222=(7778+2222)×9999=99990000分析(二):我们知道0.5×2,2.5×4,0.125×8均可得到整数或整十数,从而使问题得以简化,故可将64分解成2×4×8,再运用乘法交换律、结合律等进行计算。
解(二):原式=765×(2×4×8)×0.5×2.5×0.125=765×(2×0.5)×(4×2.5)×(8×0.125)=765×1×10×1=7650例2.399.6×9-1998×0.8分析:这道题我们仔细观察两个积的因数之间的关系,可以发现减数的因数1998是被减数因数399.6的5倍,因此我们根据积不变的规律将399.6×9改写成(399.6×5)×(9÷5),即1998×1.8,这样再根据乘法分配律进行简算。
人教版升五年级暑假讲义第2讲:运算定律(一)--加减(含答案)

运算定律(一)--加减____________________________________________________________________________________________________________________________________________________________________1本探索、理解并掌握加法交换率、加法结合律及减法的性质,能运用运算定律进行一些简便运算。
2.根据学生的具体情况,选择算法的意识与能力,发展思维的灵活性。
3.使学生感受数学与现实生活的联系,能用所学知识解决简单的实际问题。
1.加法的交换律:交换两个加数的位置,和不变。
字母公式:a+b=b+a2.加法的结合律:先加前两个数,或者先加后两个数,和不变。
字母公式:(a+b)+c=a+(b+c)3.减法的性质:①一个数同时减去两个数等于这个数减去另外两个数的和。
字母表示:a-b-c=a-(b+c)②一个数减去另一个数的同时加上一个数等于这个数减去另外两个数的差。
字母表示:a-b+c=a-(b-c)题目类型一:加法的交换律例题1.填空。
387+425=()+ 387 525+()=137+ 525300+600=()+()()+65=()+35甲数+乙数=()+()偶数+()=奇数+()答案:387+425=( 425 )+ 387 525+( 137 )=137+ 525300+600=( 600 )+( 300 )( 35 )+65=( 65 )+35甲数+乙数=(乙数)+(甲数)偶数+(奇数)=奇数+(偶数)练习1.连线。
56+68 150+75+25150+25+75 50+BB+50 68+56A+B+100 A+100+B答案:56+68 150+75+25 150+25+75 50+BB+50 68+56A+B+100 A+100+B例题2.简便计算下面各题。
简便计算(一)

平时所学公式或运算性质总结: 加法交换律:a+b=b+a (两个以上加数同样适用) 加法结合律:(a+b)+c=a+(b+c) (不要局限于三个加数) 加减法性质:1、连续的加法,可随意的交换位置, 随意的加括号或去括号。 2、连续的减法,后面的减数可随意的交换 位置。 3、加减法在一块时,也可交换位置,但交 换位置时,连同前面的运算符号一同交换。 加减法添加括号:括号前面是加号,括号里面不变号, 括号前面是减号,括号里面要变号。 a+b-c=a+(b-c) a-b+c=a-(b-c) a-b-c=a-(b+c) 加减法去括号:括号前面是加号,去括号时不变号, 括号前面是减号,去括号时要变号。
例1. (1)36+38+64 (2)124+568+876+432 (3)56+45 (4)539+67-139
(1)36+38+64 =36+64+38
=100+38 =138
(2)124+568+876+432 =( 124+876) + (568+432) =1000+1000 =2000
练习
(1)1742-(742-125) (2)2983-3755+1755 =1742-742+125 =2983-(3755-1755) =1000+125 =2983-2000 =1125 =983 (3)2536-(558+536) =2536-558-536 =2536-536-558 =2000-558 =1442 (4)989-271-529 =989-(271+529) =989-800 =189
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2讲 简便运算(一)
一、知识要点
根据算式的结构和数的特征,灵活运用运算法则、定律、性质和某些公式,可以把一些较复杂的四则混合运算化繁为简,化难为易。
二、精讲精练
【例题1】计算4.75-9.63+(8.25-1.37)
练习1:计算下面各题。
1、6.73-17
82
+(3.27-1791)
学习奥数的优点
1、激发学生对数学学习的兴趣,更容易让学生体验成功,树立自信。
2、训练学生良好的数学思维习惯和思维品质。
要使经过奥数训练的学生,思维更敏捷,考虑问题比别人更深层次。
3、锻炼学生优良的意志品质。
可以培养持之以恒的耐心和克服困难的信心, 以及战胜难题的勇气。
可以养成坚韧不拔的毅力
4、获得扎实的数学基本功,发挥创新精神和创造力的最大空间。
2、957-(3.8+9
51)-511
3、14.15-(877-20
176)-2.125
【例题2】计算21333387×79+790×4
16666
练习2:计算下面各题:
1、 3.5×411+125%+211÷5
4
2、975×0.25+4
39×76-9.75
3、529×425+4.25÷60
1
【例题3】计算:36×1.09+1.2×67.3
练习3:计算:
1、 45×2.08+1.5×37.6
2、 52×11.1+2.6×778
3、 48×1.08+1.2×56.8
【例题4】计算:533×5
225+37.9×526
练习4:
计算下面各题:
1、6.8×16.8+19.3×3.2
2、
138137139 +137×138
1 3、4.4×57.8+45.3×5.6
【例题5】计算81.5×15.8+81.5×51.8+67.6×18.5
练习5:
1、53.5×35.3+53.5×43.2+78.5×46.5
2、235×12.1++235×42.2-135×54.3
三、课后作业
1、13713-(414+1373)-0.75
2、 0.9999×0.7+0.1111×2.7
3、 72×2.09-1.8×73.6
4.3.75×735-3/8×5730+16.2×62.5。
