结构力学考研 三铰拱例题精讲
合集下载
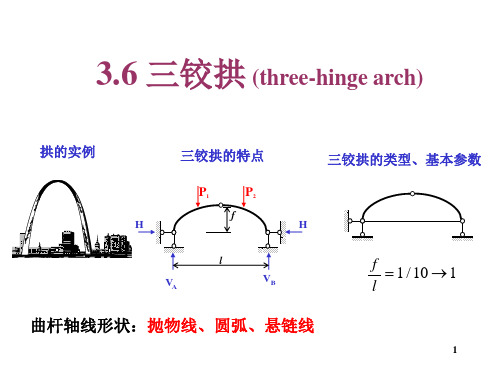
结构力学5三铰拱
Q
M
N
R
e
拱截面一般承受三种内力：M、Q、N。 若用合力 R 代替截面所有内力，则其偏心距为e = M/N， 显然我们可以求出各个截面的合力大小、方向和作用点。
P1
作用线
P2
G
rD k2 C D
P3
H
F
A
（1）确定各截面合力的 大小和方向： 数解 RA RB
绘力多边形
k1
k3
B
射线
RA
大小和方向 o
特征方程为：
2
2
H
0
x
H
H
H
y C1e
C2 e
x
H H qc y a , 代入原方程， a 设其特解 q y x A ch x B sh x c H H qc x 0 , y 0 A 设 x 0, y 0 B 0 q y c ch x 1 悬链线 H
这表明拱在法向均布荷载作用下处于无弯矩状态时，截面的轴力为一常数。
y0
q dS 2 N sin
d 0 2 N qR
q Rd N d 0RFra bibliotekN q
因N为一常数，q也为一常数，所以任一点的曲率半径R也是常数，即拱轴为园弧。
例3、设三铰拱上承受填土荷载，填土表面为一水平面，试求拱的合理轴线，设 填土的容重为，拱所受的分布荷载为 [解]由拱截面弯矩计算式
M2 M2 Hy2 11 3 2 3 15 . 7.5 3
15 . kN m
tg 2 4 f 2x 1 l l
M
N
R
e
拱截面一般承受三种内力：M、Q、N。 若用合力 R 代替截面所有内力，则其偏心距为e = M/N， 显然我们可以求出各个截面的合力大小、方向和作用点。
P1
作用线
P2
G
rD k2 C D
P3
H
F
A
（1）确定各截面合力的 大小和方向： 数解 RA RB
绘力多边形
k1
k3
B
射线
RA
大小和方向 o
特征方程为：
2
2
H
0
x
H
H
H
y C1e
C2 e
x
H H qc y a , 代入原方程， a 设其特解 q y x A ch x B sh x c H H qc x 0 , y 0 A 设 x 0, y 0 B 0 q y c ch x 1 悬链线 H
这表明拱在法向均布荷载作用下处于无弯矩状态时，截面的轴力为一常数。
y0
q dS 2 N sin
d 0 2 N qR
q Rd N d 0RFra bibliotekN q
因N为一常数，q也为一常数，所以任一点的曲率半径R也是常数，即拱轴为园弧。
例3、设三铰拱上承受填土荷载，填土表面为一水平面，试求拱的合理轴线，设 填土的容重为，拱所受的分布荷载为 [解]由拱截面弯矩计算式
M2 M2 Hy2 11 3 2 3 15 . 7.5 3
15 . kN m
tg 2 4 f 2x 1 l l
结构力学-3.6 三铰拱.ppt
7.5 0.832 9.015kN
kN
9
N图
13.300 10.958 9.015 7.749 7.500 7.433 1.421 6.796 3.325 11.235 11.665 11.700
0.600 0.354 0.003 0.472 1.000
3.331 1.060 0.600
Q图 kN
对于三铰拱，竖向荷载作用下任意截面上弯矩计算公式为：
M M Hy
它是由两项组成，第一项是简支梁的弯矩，而后一项与拱轴形状有关。
令
M M Hy 0
yx M x
H
在竖向荷载作用下，三铰拱的合理轴线的纵标值与简支梁
的弯矩纵标值成比例。
10
例1 设三铰拱承受沿水平方向均匀分布的竖向荷载，求其合理轴线。
qc+.f
qc q qc y
yx
f y*
d2y dx2
1 H
d 2M dx2
对简支梁来说，
d2M dx 2
qx
而 qx qc y,
d2y dx 2
1 H
qc
y
即 y y qc , 特征方程为：
HH
2 0
H
H
x
x
y C1e H C2e H
y
ex shx chx ex chx shx
q
y
C
q
A l/2
f
Bx
A
ql x
l/2
2
B
ql 2
[解] 由式 yx M x 先列出简支梁的弯矩方程
H
M x q xl x
2
拱的推力为：
H
M
C
ql 2
f 8f
kN
9
N图
13.300 10.958 9.015 7.749 7.500 7.433 1.421 6.796 3.325 11.235 11.665 11.700
0.600 0.354 0.003 0.472 1.000
3.331 1.060 0.600
Q图 kN
对于三铰拱，竖向荷载作用下任意截面上弯矩计算公式为：
M M Hy
它是由两项组成，第一项是简支梁的弯矩，而后一项与拱轴形状有关。
令
M M Hy 0
yx M x
H
在竖向荷载作用下，三铰拱的合理轴线的纵标值与简支梁
的弯矩纵标值成比例。
10
例1 设三铰拱承受沿水平方向均匀分布的竖向荷载，求其合理轴线。
qc+.f
qc q qc y
yx
f y*
d2y dx2
1 H
d 2M dx2
对简支梁来说，
d2M dx 2
qx
而 qx qc y,
d2y dx 2
1 H
qc
y
即 y y qc , 特征方程为：
HH
2 0
H
H
x
x
y C1e H C2e H
y
ex shx chx ex chx shx
q
y
C
q
A l/2
f
Bx
A
ql x
l/2
2
B
ql 2
[解] 由式 yx M x 先列出简支梁的弯矩方程
H
M x q xl x
2
拱的推力为：
H
M
C
ql 2
f 8f
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第4章 静定拱【圣才出品】
第4章 静定拱4.1 复习笔记【知识框架】【重点难点归纳】一、拱的基本概念及特点 ★★表4-1-1 拱的基本概念及特点表4-1-2 有拉杆和无拉杆三铰拱的区别与联系二、三铰拱的计算 ★★★★★1．支座反力的计算（见表4-1-3）表4-1-3 支座反力的计算2．内力的计算（见表4-1-4）表4-1-4 三铰拱的内力计算三、三铰拱的合理拱轴线（见表4-1-5） ★★★表4-1-5 三铰拱的合理拱轴线4.2 课后习题详解复习思考题1．拱的受力情况和内力计算与梁和刚架有何异同？答：（1）拱与梁的受力情况和内力计算的区别①约束反力方面，拱在竖向荷载作用下会产生水平反力（推力），而梁在竖向荷载作用下不会产生水平反力（推力）；②内力分布方面，由于水平推力的存在，拱的弯矩常比跨度、荷载相同的梁的弯矩小得多，使得拱截面上的应力分布较为均匀；③内力分析方法方面，若只有竖向荷载时，梁只需进行简单的整体分析即可求解，而拱由于水平力的存在，需要整体分析与局部分析相结合。
（2）拱与刚架的受力情况和内力计算的异同①内力分析方法方面，拱与刚架的受力情况和内力计算的特点和所应用方法基本一致，例如三铰刚架也属于拱式结构；②拱的轴线是曲线，刚架杆的轴线是直线，在应用平衡条件计算内力时，拱仍然取投2．在非竖向荷载作用下怎样计算三铰拱的反力和内力？能否使用式（4-1）和（4-2）？答：（1）对于三铰拱承受非竖向荷载的情况，可将非竖向荷载分解为水平荷载和竖向荷载。
（2）仍然可以应用式（4-1）和（4-2），将水平反力加上非竖向荷载水平方向上的分量一起代入公式中进行求解。
(4-1)o AV AV o BV BV o c H F F F F M F f ⎫⎪=⎪⎪=⎬⎪⎪=⎪⎭cos sin (4-2)sin cos o H o S S H o N S H M M F y F F F F F F ϕϕϕϕ⎫=-⎪⎪=-⎬⎪=+⎪⎭3．什么是合理拱轴线？试绘出图4-2-1各荷载作用下三铰拱的合理拱轴线形状。
工程力学：三铰拱的内力计算
三铰拱的内力计算
➢ 三铰拱的反力和内力计算
支座反力
y FP1
C FP2
取整体，由
FHA A
MB 0
FVA
FVA
FPibi l
FV0A
yk f
a1 a2
l/2
yJ b1
l/2
B FHB x
b2 FVB
MA 0
FVB
FPi ai l
FV0B
FP1 A
K
FV0A
FP2
C
B
J
FV0B
代梁（相应简支梁）
FND (FVA FP1) sin FH cos (FV0A FP1) sin FH cos FQ0D sin FH cos
内力计算
小结：
1）由于推力 的存在，拱的弯矩比梁的要小。 2）三铰拱的内力值不但与荷载及三个铰的位置 有关，而且与各铰间拱轴线的形状有关。
C D
三铰拱 FHA A
FVA
相应简支梁
AD
C
FV0A
约 FVA FV0A
束 FVB FV0B
内
反 力
FH
M
0 C
f
力
B FHB
FVB B
FV0B
➢ 三铰拱的合理轴线
在给定荷载作用下，三铰拱任一截面弯矩为零， 只承受轴力，这样的轴线就称为合理拱轴。
在竖向荷载作用下三铰拱任一截面弯矩为
M M 0 FH y
令 M 0 得到 y M 0
FVA A
FV0A
FVA FV0A
FVB FV0B
FH
M
0 C
f
C B FHB
FVB
C
B
FV0B
➢ 三铰拱的反力和内力计算
支座反力
y FP1
C FP2
取整体，由
FHA A
MB 0
FVA
FVA
FPibi l
FV0A
yk f
a1 a2
l/2
yJ b1
l/2
B FHB x
b2 FVB
MA 0
FVB
FPi ai l
FV0B
FP1 A
K
FV0A
FP2
C
B
J
FV0B
代梁（相应简支梁）
FND (FVA FP1) sin FH cos (FV0A FP1) sin FH cos FQ0D sin FH cos
内力计算
小结：
1）由于推力 的存在，拱的弯矩比梁的要小。 2）三铰拱的内力值不但与荷载及三个铰的位置 有关，而且与各铰间拱轴线的形状有关。
C D
三铰拱 FHA A
FVA
相应简支梁
AD
C
FV0A
约 FVA FV0A
束 FVB FV0B
内
反 力
FH
M
0 C
f
力
B FHB
FVB B
FV0B
➢ 三铰拱的合理轴线
在给定荷载作用下，三铰拱任一截面弯矩为零， 只承受轴力，这样的轴线就称为合理拱轴。
在竖向荷载作用下三铰拱任一截面弯矩为
M M 0 FH y
令 M 0 得到 y M 0
FVA A
FV0A
FVA FV0A
FVB FV0B
FH
M
0 C
f
C B FHB
FVB
C
B
FV0B
结构力学 三铰拱
4 4 yk 2 4(16 4) 3m 求MK 16 MK 0 MK 12.5 4 10 3 20kN.m(下拉)
求MJ
yJ 3m
M
J
0
M J 7.5 4 10 3 30 30 0
3. 求FQ、FN的计算公式
拱轴任意截面D切线与水平线夹角为φ。 相应代梁中， F 设为正方向。
FP1=15kN K FHA A yk 4m
l/2
C f=4m
MC 0
FVA
4m
l l FVA FHA f FP1 0 2 4 0 MC 1 l l FHA ( FVA FP1 ) () f 2 4 f
0 上式中，M C 为代梁C截面弯矩。
M FHB () f
0 ND右 QD右 sin D H cosD 12 0.555 10.5 0.832 15.4kN
重复上述步骤，可求出各等分截面的内力，作出内力图。
三、三较拱的合理轴线
在给定荷载作用下，三铰拱任一截面弯 矩为零的轴线就线为合理拱轴。 三铰拱任一截面弯矩为 M M FH y
超静定拱
拉杆拱 静定拱
拱顶
C
拱轴线 拱高 f
B
拱趾
A
起拱线 跨度 l
f l
f
高跨比
l 通常 f l 在1-1/10之间变化，f 的值对内力有 很大影响。
工程实例
拱桥 （无铰拱）
超静定拱
世界上最古老的铸铁拱桥（英国科尔布鲁克代尔桥)
万县长江大桥：世界上跨度最大的混凝土拱桥
二、三铰拱的计算
A 12.5kN K左 Fº ＝12.5kN QK左 A 12.5kN
三铰拱
M
O
0 FN ( FN d FN ) 0
可得 d FN 0 合理拱轴线方程为
FN q
FN =常数
d 2 qd 0
沿s-s 写出投影方程为
2 FN sin sin d 2
圆弧线
因 d 极小
d 2
返 章
M
0
FH
合理拱轴线方程
例4-2 试求图a所示对称三铰拱在图示荷载作用下的合理拱轴 线。
解：相应简支梁（图b）的弯矩方程为
M
0
1 2
qx ( l x )
0
三铰拱的推力为
FH
0
MC f
4f l
2
ql
2
8f
合理拱轴线方程为
y
M
FH
x (l x )
北京建筑工程学院
三铰拱合理拱轴线形状的确定
三铰拱
14kN m
A
50kN
B
C
75.5kN 58.5kN
175.5 201
M图(kNm)
与三铰拱相应弯矩相比，要大 很多。
北京建筑工程学院
结构力学教研室
三铰拱
计算图（a）斜拱的支反力 时为避免解联立方程，可将反力
分解如图（b）。
由平衡条件可得 （a
F AV F
0 AV
, F BV F
0
FS F AV F1
0 0
轴力以压力为正
北京建筑工程学院
结构力学教研室
三铰拱
三铰拱的内力不但与荷载及三个铰的位置有关，而 且与拱轴线的形状有关。 由于水平推力的存在，拱的弯矩比相应简支梁的弯矩要 小。 三铰拱在竖向荷载作用下轴向受压。
3山东建筑结构力学三铰拱
2P/ 3
2P/ 2
2P/ 2 P/ 2 P / 3
P/3
P/2
P/2
P/2
2P/ 2 P / 3
P/2
P/2 P/6 P/3
P/3 P/2 P/6
作业
• 3-19a
迪拜 最长拱桥
重庆朝天门
三铰拱
拱 <arch>
1.拱的定义 这是拱结构吗?
杆一轴线、为概曲线
在 用竖 下向不述荷产载生作水
拱的合理轴线 在固定荷载作用下,使拱处于无弯矩状态的轴线称为合理轴 线.由上述可知,按照压力曲线设计的拱轴线就是合理轴线. 从结构优化设计观点出发,寻找合理轴线即拱结构的优化选型.
对拱结构而言,任意截面上弯矩计算式子为：
MM Hy
它是由两项组成,第一项是简支梁的弯矩,而后一项与拱 轴形状有关.令 MMH y0
YA0
a2
b2 YB0
q=2kN .m
P=8kN
例 1、三铰拱及其所受荷载如
y
34
5
图所示拱的轴线为抛物线方程
2 1
2
y2
0
6 7 8
f=4m
4f y l2
xlx
计算反力并绘
x
A
7.5kN
x2=3m 6m
VA 11kN
B
3m
制内力图.
H 7.5kN
〔1〕计算支座反力
6m
VB 9kN
V AV A 26 1 9 28311kN
yqc
ch
x1
悬链线
H
作业
• 3-21
B
YB0
YB=YB0
YA=YA0
XA=XB =H
哈工大·结构力学(32学时) 课件 3.2-三铰拱
抛物线
例 ：试求图示抛物线 y 4 fx(l x) / l 2 三铰拱距左支座5m的截面内力
解：一、先求支座反力 1、取整体为分离体
m (F ) 0
B
FAy 20m 200kN.m 20 10 15kN.m 0
整理可得
FAy 160kN
2、取AC为分离体
m (F ) 0
0
合理拱轴线
合理拱轴线：拱在给定荷载作用下只产生
轴力的拱轴线被称为 与该荷载对应的合理 拱轴线，当拱轴线为合理拱轴线时,拱截面 上只受压力（弯矩和剪力均为零）
作业：
3-7;3-9
小结：
以结点作为平衡对象，结点承受汇交力系 作用。
按与“组成顺序相反”的原则，逐次建立 各结点的平衡方程，则桁架各结点未知内 力数目一定不超过独立平衡方程数。
由结点平衡方程可求得桁架各杆内力。
在用结点法进行计算时，注意以下三点，可 使计算过程得到简化。
1. 对称性的利用 如果结构的杆件轴线对某轴（空间桁架为某 面）对称，结构的支座也对同一条轴对称的静 定结构，则该结构称为对称结构 （symmetrical structure）。 对称结构在对称或反对称的荷载作用下，结 构的内力和变形（也称为反应）必然对称或反 对称，这称为对称性（symmetry）。
n m 1 3 A 2.5FP FP 4 n2m FP FP B FP FP 6m
6 5m
2.5FP
截面单杆
FN1 =-3.75FP FN2 =3.33FP FN4=0.65FP
截面法取出的隔离体，不管其 上有几个轴力，如果某杆的轴力可以通过列一 个平衡方程求得，则此杆称为截面单杆。可能 的截面单杆通常有相交型和平行型两种形式。
例 ：试求图示抛物线 y 4 fx(l x) / l 2 三铰拱距左支座5m的截面内力
解：一、先求支座反力 1、取整体为分离体
m (F ) 0
B
FAy 20m 200kN.m 20 10 15kN.m 0
整理可得
FAy 160kN
2、取AC为分离体
m (F ) 0
0
合理拱轴线
合理拱轴线：拱在给定荷载作用下只产生
轴力的拱轴线被称为 与该荷载对应的合理 拱轴线，当拱轴线为合理拱轴线时,拱截面 上只受压力（弯矩和剪力均为零）
作业：
3-7;3-9
小结：
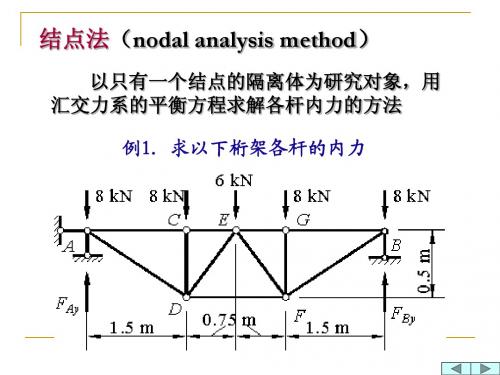
以结点作为平衡对象，结点承受汇交力系 作用。
按与“组成顺序相反”的原则，逐次建立 各结点的平衡方程，则桁架各结点未知内 力数目一定不超过独立平衡方程数。
由结点平衡方程可求得桁架各杆内力。
在用结点法进行计算时，注意以下三点，可 使计算过程得到简化。
1. 对称性的利用 如果结构的杆件轴线对某轴（空间桁架为某 面）对称，结构的支座也对同一条轴对称的静 定结构，则该结构称为对称结构 （symmetrical structure）。 对称结构在对称或反对称的荷载作用下，结 构的内力和变形（也称为反应）必然对称或反 对称，这称为对称性（symmetry）。
n m 1 3 A 2.5FP FP 4 n2m FP FP B FP FP 6m
6 5m
2.5FP
截面单杆
FN1 =-3.75FP FN2 =3.33FP FN4=0.65FP
截面法取出的隔离体，不管其 上有几个轴力，如果某杆的轴力可以通过列一 个平衡方程求得，则此杆称为截面单杆。可能 的截面单杆通常有相交型和平行型两种形式。