河南地区中考数学23题汇总
2024年河南中考数学试题

2024年河南省中考数学试题及答案一、选择题(每题4分,共40分)1. 下列选项中,既是有理数又是无理数的是()A. √2B. -3C. 1.414D. 0.333…答案:B2. 如果一个数列的前三项分别是1,3,5,那么它的第10项是()A. 18B. 20C. 22D. 24答案:B3. 下列函数中,奇函数是()A. y = x²B. y = x³C. y = |x|D. y = 2x答案:B4. 在三角形ABC中,a=3,b=4,C=60°,那么三角形ABC的面积是()A. 3√3B. 4√3C. 6D. 8答案:A5. 下列关于x的不等式中,有解的是()A. x² < 0B. x² > 0C. x² = 0D. x² ≠ 0答案:B6. 一个二次函数的图像开口向上,且顶点坐标为(-1,-4),那么该二次函数的一般形式是()A. y = (x + 1)² - 4B. y = (x - 1)² + 4C. y = (x + 1)² + 4D. y = (x - 1)² - 4答案:A7. 下列关于x的方程中,有实数解的是()A. x² + 1 = 0B. x² - 1 = 0C. x² + 2 = 0D. x² - 2 = 0答案:B8. 下列关于x的不等式组中,有解的是()A.\[\begin{cases}x < 2 \\x > 3\end{cases} \]B.\[\begin{cases} x \leq 1 \\ x \geq 2\end{cases} \]C.\[\begin{cases} x \geq 1 \\ x \leq 2\end{cases} \]D.\[\begin{cases}x > 2 \\x < 3\end{cases}\]答案:C9. 一个正方体的表面积是54cm²,那么它的体积是()A. 27cm³B. 36cm³C. 54cm³D. 72cm³答案:A10. 下列关于三角形ABC的说法中,正确的是()A. 如果a² + b² = c²,那么三角形ABC是直角三角形B. 如果a² + b² > c²,那么三角形ABC是锐角三角形C. 如果a² + b² < c²,那么三角形ABC是钝角三角形D. 如果a² - b² = c²,那么三角形ABC是直角三角形答案:A二、填空题(每题4分,共40分)11. 如果一个数列的前三项分别是2,4,6,那么它的第n项是_________。
2024年河南省中考数学试卷正式版含答案解析

绝密★启用前2024年河南省中考数学试卷学校:___________姓名:___________班级:___________考号:___________注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)一、选择题:本题共10小题,每小题3分,共30分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,数轴上点P表示的数是( )A. −1B. 0C. 1D. 22.据统计,2023年我国人工智能核心产业规模达5784亿元.数据“5784亿”用科学记数法表示为( )A. 5784×108B. 5.784×1010C. 5.784×1011D. 0.5784×10123.如图,乙地在甲地的北偏东50°方向上,则∠1的度数为( )A. 60°B. 50°C. 40°D. 30°4.信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶的包装盒,它的主视图为( )A.B.C.D.5.下列不等式中,与−x>1组成的不等式组无解的是( )A. x>2B. x<0C. x<−2D. x>−36.如图,在▱ABCD中,对角线AC,BD相交于点O,点E为OC的中点,EF//AB 交BC于点F.若AB=4,则EF的长为( )A. 12B. 1 C. 43D. 27.计算(a·a···a⏟a个)3的结果是( )A. a5B. a6C. a a+3D. a3a8.豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片如图所示,它们除正面外完全相同.把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )A. 19B. 16C. 15D. 13⏜的中点,连接BD,CD.以点D为圆心,BD的长为半径在⊙O内画弧,则阴影部分的面积为( )A. 8π3B. 4πC. 16π3D. 16π10.把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患.数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流I与使用电器的总功率P的函数图象(如图1),插线板电源线产生的热量Q与I的函数图象(如图2).下列结论中错误的是( )A. 当P=440W时,I=2AB. Q随I的增大而增大C. I每增加1A,Q的增加量相同D. P越大,插线板电源线产生的热量Q越多第II卷(非选择题)二、填空题:本题共5小题,每小题3分,共15分。
2024年河南中考数学试题及答案

2024年河南中考数学试题及答案注意事项:1.本试卷共6页,三个大题,满分120分,考试时间100分钟。
2.本试卷上不要答题,请按答题卡上注意事项的要求,直接把答案填写在答题卡上。
答在试卷上的答案无效。
一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的)1. 如图,数轴上点P 表示的数是( )A. 1-B. 0C. 1D. 22. 据统计,2023年我国人工智能核心产业规模达5784亿元,数据“5784亿”用科学记数法表示为()A. 8578410⨯ B. 105.78410⨯ C. 115.78410⨯ D. 120.578410⨯3. 如图,乙地在甲地的北偏东50︒方向上,则∠1的度数为( )A. 60︒B. 50︒C. 40︒D. 30︒4. 信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶的包装盒,它的主视图为( )A. B.C D.5. 下列不等式中,与1x ->组成不等式组无解的是().的A 2x > B. 0x < C. <2x D. 3x >-6. 如图,在ABCD 中,对角线AC ,BD 相交于点O ,点E 为OC 的中点,EF AB ∥交BC 于点F .若4AB =,则EF 的长为( )A. 12B. 1C. 43D. 27. 计算3···a a a a ⎛⎫ ⎪ ⎪⎝⎭个的结果是( )A. 5a B. 6a C. 3a a + D. 3aa 8. 豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片如图所示,它们除正面外完全相同.把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )A. 19 B. 16 C. 15 D. 139. 如图,O是边长为ABC 的外接圆,点D 是 BC的中点,连接BD ,CD .以点D 为圆心,BD 的长为半径在O 内画弧,则阴影部分的面积为( )A. 8π3 B. 4π C. 16π3 D. 16π10. 把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐.患.数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流I 与使用电器的总功率P 的函数图象(如图1),插线板电源线产生的热量Q 与I 的函数图象(如图2).下列结论中错误的是( )A. 当440W P =时,2A I =B. Q 随I 的增大而增大C. I 每增加1A ,Q 的增加量相同D. P 越大,插线板电源线产生的热量Q 越多二、填空题(每小题3分,共15分)11. 请写出2m 的一个同类项:_______.12. 2024年3月是第8个全国近视防控宣传教育月,其主题是“有效减少近视发生,共同守护光明未来”.某校组织各班围绕这个主题开展板报宣传活动,并对各班的宣传板报进行评分,得分情况如图,则得分的众数为___________分.13. 若关于x 的方程2102x x c -+=有两个相等的实数根,则c 的值为___________.14. 如图,在平面直角坐标系中,正方形ABCD 的边AB 在x 轴上,点A 的坐标为()20-,,点E 在边CD 上.将BCE 沿BE 折叠,点C 落在点F 处.若点F 的坐标为()06,,则点E 的坐标为___________.15. 如图,在Rt ABC △中,90ACB ∠=︒,3CA CB ==,线段CD 绕点C 在平面内旋转,过点B 作AD 的垂线,交射线AD 于点E .若1CD =,则AE 的最大值为_________,最小值为_________.三、解答题(本大题共8个小题,共75分)16. (1(01-;(2)化简:231124a a a +⎛⎫+÷ ⎪--⎝⎭.17. 为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下.技术统计表队员平均每场得分平均每场篮板平均每场失误甲26.582乙26103根据以上信息,回答下列问题.(1)这六场比赛中,得分更稳定的队员是_________(填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为________分.(2)请从得分方面分析:这六场比赛中,甲、乙两名队员谁表现更好.(3)规定“综合得分”为:平均每场得分×1+平均每场篮板×1.5+平均每场失误()1⨯-,且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.的18. 如图,矩形ABCD 的四个顶点都在格点(网格线的交点)上,对角线AC ,BD 相交于点E ,反比例函数()0k y x x=>的图象经过点A .(1)求这个反比例函数的表达式.(2)请先描出这个反比例函数图象上不同于点A 的三个格点,再画出反比例函数的图象.(3)将矩形ABCD 向左平移,当点E 落在这个反比例函数的图象上时,平移的距离为________.19. 如图,在Rt ABC △中,CD 是斜边AB 上的中线,∥B E D C 交AC 的延长线于点E .(1)请用无刻度的直尺和圆规作ECM ∠,使ECM A ∠=∠,且射线CM 交BE 于点F (保留作图痕迹,不写作法).(2)证明(1)中得到的四边形CDBF 是菱形20. 如图1,塑像AB 在底座BC 上,点D 是人眼所在的位置.当点B 高于人的水平视线DE 时,由远及近看塑像,会在某处感觉看到的塑像最大,此时视角最大.数学家研究发现:当经过A ,B 两点的圆与水平视线DE 相切时(如图2),在切点P 处感觉看到的塑像最大,此时APB 为最大视角.(1)请仅就图2的情形证明APB ADB ∠>∠.(2)经测量,最大视角APB 为30︒,在点P 处看塑像顶部点A 的仰角APE ∠为60︒,点P 到塑像的水平距离PH 为6m .求塑像AB 的高(结果精确到0.1m 1.73≈).21. 为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了A ,B 两种食品作为午餐.这两种食品每包质量均为50g ,营养成分表如下.(1)若要从这两种食品中摄入4600kJ 热量和70g 蛋白质,应选用A ,B 两种食品各多少包?(2)运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共7包,要使每份午餐中的蛋白质含量不低于90g ,且热量最低,应如何选用这两种食品?22. 从地面竖直向上发射的物体离地面的高度()m h 满足关系式205h t v t =-+,其中()s t 是物体运动的时间,()0m /s v 是物体被发射时的速度.社团活动时,科学小组在实验楼前从地面竖直向上发射小球.(1)小球被发射后_________s 时离地面的高度最大(用含0v 的式子表示).(2)若小球离地面的最大高度为20m ,求小球被发射时的速度.(3)按(2)中的速度发射小球,小球离地面的高度有两次与实验楼的高度相同.小明说:“这两次间隔的时间为3s .”已知实验楼高15m ,请判断他的说法是否正确,并说明理由.23. 综合与实践在学习特殊四边形的过程中,我们积累了一定的研究经验,请运用已有经验,对“邻等对补四边形”进行研究定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.(1)操作判断用分别含有30︒和45︒角的直角三角形纸板拼出如图1所示的4个四边形,其中是邻等对补四边形的有________(填序号).(2)性质探究根据定义可得出邻等对补四边形的边、角的性质.下面研究与对角线相关的性质.如图2,四边形ABCD 是邻等对补四边形,AB AD =,AC 是它的一条对角线.①写出图中相等的角,并说明理由;②若BC m =,DC n =,2BCD θ∠=,求AC 的长(用含m ,n ,θ的式子表示).(3)拓展应用如图3,在Rt ABC △中,90B Ð=°,3AB =,4BC =,分别在边BC ,AC 上取点M ,N ,使四边形ABMN 是邻等对补四边形.当该邻等对补四边形仅有一组邻边相等时,请直接写出BN 的长.2024年河南省普通高中招生考试试卷数学注意事项:1.本试卷共6页,三个大题,满分120分,考试时间100分钟。
题型-河南近几年中考数学第23题(全部整合)
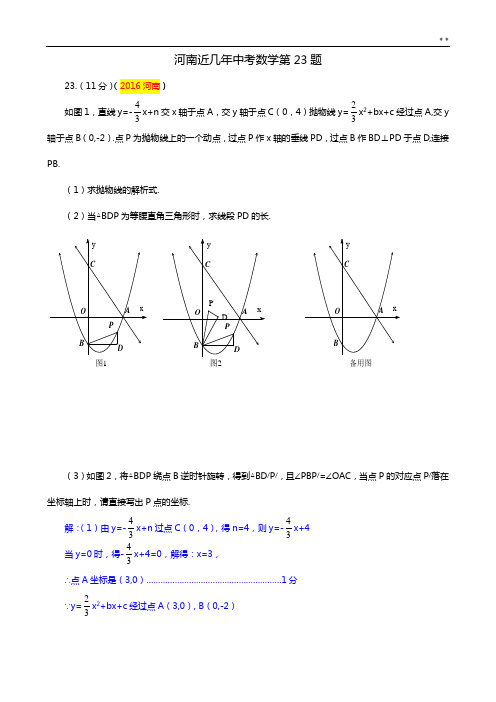
河南近几年中考数学第23题23.(11分)(2016河南)如图1,直线y=-43x+n交x轴于点A,交y轴于点C(0,4)抛物线y=23x2+bx+c经过点A,交y轴于点B(0,-2).点P为抛物线上的一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB.(1)求抛物线的解析式.(2)当△BDP为等腰直角三角形时,求线段PD的长.(3)如图2,将△BDP绕点B逆时针旋转,得到△BD/P/,且∠PBP/=∠OAC,当点P的对应点P/落在坐标轴上时,请直接写出P点的坐标.解:(1)由y=-43x+n过点C(0,4),得n=4,则y=-43x+4当y=0时,得-43x+4=0,解得:x=3,∴点A坐标是(3,0)…………………………………………………1分∵y=23x2+bx+c经过点A(3,0), B(0,-2)图1备用图∴22033b+c32c⎧=⨯+⎪⎨⎪-=⎩,解得:4b3c2⎧=-⎪⎨⎪=-⎩∴抛物线的解析式是23x2-43x-2……………………………………………3分(2)∵点P的横坐标为m,∴P(m,23m2-43m-2),D(m,-2)…………4分若△BDP为等腰直角三角形时,则PD=BD;①当点P在直线BD上方时,PD=23m2-43m-2+2=23m2-43m,(ⅰ)若P在y轴左侧,则m<0,BD=-m;∴2 3m2-43m=-m,解得:m=12或m=0(舍去)…………………………………5分(ⅱ)若P在y轴右侧,则m>0,BD=m;∴2 3m2-43m=m,解得:m=72或m=0(舍去)…………………………………6分②当点P在直线BD下方时,PD=-2-(23m2-43m-2) =-23m2+43m,则m>0,BD=m;∴-23m2+43m=m,解得:m=12或m=0(舍去)……………………………7分综上:m=72或m=12。
即当△BDP为等腰直角三角形时,PD的长为72或12。
2024年河南省中考数学真题试卷及答案
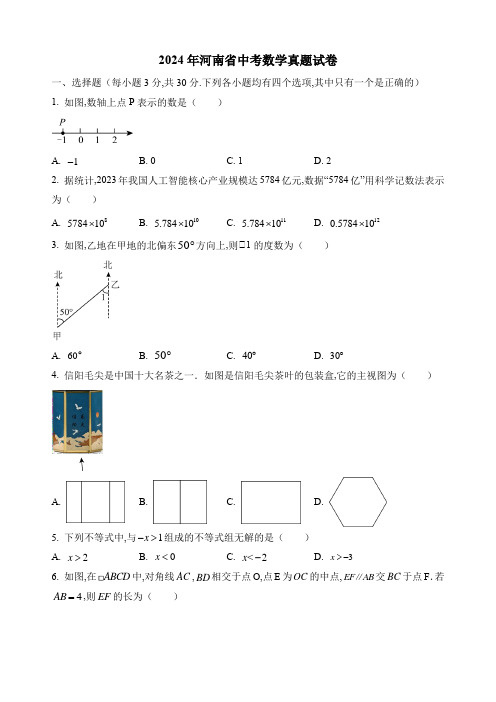
2024年河南省中考数学真题试卷一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的) 1. 如图,数轴上点P 表示的数是( )A. 1-B. 0C. 1D. 22. 据统计,2023年我国人工智能核心产业规模达5784亿元,数据“5784亿”用科学记数法表示为( )A. 8578410⨯B. 105.78410⨯C. 115.78410⨯D. 120.578410⨯ 3. 如图,乙地在甲地的北偏东50︒方向上,则∠1的度数为( )A. 60︒B. 50︒C. 40︒D. 30︒4. 信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶的包装盒,它的主视图为( )A. B. C. D. 5. 下列不等式中,与1x ->组成的不等式组无解的是( )A. 2x >B. 0x <C. <2x -D. 3x >-6. 如图,在ABCD 中,对角线AC ,BD 相交于点O,点E 为OC 的中点,EF AB ∥交BC 于点F .若4AB =,则EF 的长为( )A. 12 B. 1 C. 43 D. 27. 计算3()a a a a a ⋅⋅⋅个的结果是( )A. 5aB. 6aC. 3a a +D. 3a a 8. 豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片如图所示,它们除正面外完全相同.把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )A. 19B. 16C. 15D. 139. 如图,O 是边长为ABC 的外接圆,点D 是BC 的中点,连接BD ,CD .以点D 为圆心,BD 的长为半径在O 内画弧,则阴影部分的面积为( )A. 8π3B. 4πC. 16π3D. 16π10. 把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患.数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流I 与使用电器的总功率P 的函数图象(如图1),插线板电源线产生的热量Q 与I 的函数图象(如图2).下列结论中错误的是( )A. 当440W P =时,2A I =B. Q 随I 的增大而增大C. I 每增加1A,Q 的增加量相同D. P 越大,插线板电源线产生的热量Q 越多二、填空题(每小题3分,共15分) 11. 请写出2m 的一个同类项:_______.12. 2024年3月是第8个全国近视防控宣传教育月,其主题是“有效减少近视发生,共同守护光明未来”.某校组织各班围绕这个主题开展板报宣传活动,并对各班的宣传板报进行评分,得分情况如图,则得分的众数为___________分.13. 若关于x 的方程2102x x c -+=有两个相等的实数根,则c 的值为___________. 14. 如图,在平面直角坐标系中,正方形ABCD 的边AB 在x 轴上,点A 的坐标为()20-,,点E 在边CD 上.将BCE 沿BE 折叠,点C 落在点F 处.若点F 的坐标为()06,,则点E 的坐标为___________.15. 如图,在Rt ABC △中,90ACB ∠=︒,3CA CB ==,线段CD 绕点C 在平面内旋转,过点B 作AD 的垂线,交射线AD 于点E .若1CD =,则AE 的最大值为_________,最小值为_________.三、解答题(本大题共8个小题,共75分)16. (1)计算(01 (2)化简:231124a a a +⎛⎫+÷ ⎪--⎝⎭. 17. 为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下.技术统计表根据以上信息,回答下列问题.(1)这六场比赛中,得分更稳定的队员是_________(填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为________分.(2)请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.(3)规定“综合得分”为:平均每场得分×1+平均每场篮板×1.5+平均每场失误()1⨯-,且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好. 18. 如图,矩形ABCD 的四个顶点都在格点(网格线的交点)上,对角线AC ,BD 相交于点E,反比例函数()0k y x x=>的图象经过点A .(1)求这个反比例函数的表达式.(2)请先描出这个反比例函数图象上不同于点A 的三个格点,再画出反比例函数的图象. (3)将矩形ABCD 向左平移,当点E 落在这个反比例函数的图象上时,平移的距离为________.19. 如图,在Rt ABC △中,CD 是斜边AB 上的中线,∥BE DC 交AC 的延长线于点E .(1)请用无刻度的直尺和圆规作ECM ∠,使ECM A ∠=∠,且射线CM 交BE 于点F (保留作图痕迹,不写作法).(2)证明(1)中得到的四边形CDBF 是菱形20. 如图1,塑像AB 在底座BC 上,点D 是人眼所在的位置.当点B 高于人的水平视线DE 时,由远及近看塑像,会在某处感觉看到的塑像最大,此时视角最大.数学家研究发现:当经过A,B 两点的圆与水平视线DE 相切时(如图2),在切点P 处感觉看到的塑像最大,此时APB ∠为最大视角.图1 图2(1)请仅就图2的情形证明APB ADB ∠>∠.(2)经测量,最大视角APB ∠为30︒,在点P 处看塑像顶部点A 的仰角APE ∠为60︒,点P 到塑像的水平距离PH 为6m .求塑像AB 的高(结果精确到0.1m .参考数据 1.73≈). 21. 为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了A,B 两种食品作为午餐.这两种食品每包质量均为50g ,营养成分表如下.(1)若要从这两种食品中摄入4600kJ 热量和70g 蛋白质,应选用A,B 两种食品各多少包? (2)运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共7包,要使每份午餐中的蛋白质含量不低于90g ,且热量最低,应如何选用这两种食品? 22. 从地面竖直向上发射的物体离地面的高度()m h 满足关系式205h t v t =-+,其中()s t 是物体运动的时间,()0m /s v 是物体被发射时的速度.社团活动时,科学小组在实验楼前从地面竖直向上发射小球.(1)小球被发射后_________s 时离地面的高度最大(用含0v 的式子表示).(2)若小球离地面的最大高度为20m ,求小球被发射时的速度.(3)按(2)中的速度发射小球,小球离地面的高度有两次与实验楼的高度相同.小明说:“这两次间隔的时间为3s .”已知实验楼高15m ,请判断他的说法是否正确,并说明理由. 23. 综合与实践在学习特殊四边形的过程中,我们积累了一定的研究经验,请运用已有经验,对“邻等对补四边形”进行研究定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.(1)操作判断用分别含有30︒和45︒角的直角三角形纸板拼出如图1所示的4个四边形,其中是邻等对补四边形的有________(填序号).(2)性质探究根据定义可得出邻等对补四边形的边、角的性质.下面研究与对角线相关的性质. 如图2,四边形ABCD 是邻等对补四边形,AB AD =,AC 是它的一条对角线.∠写出图中相等的角,并说明理由∠若BC m =,DC n =,2BCD θ∠=,求AC 的长(用含m,n,θ的式子表示).(3)拓展应用如图3,在Rt ABC △中,90B ,3AB =,4BC =,分别在边BC ,AC 上取点M,N,使四边形ABMN 是邻等对补四边形.当该邻等对补四边形仅有一组邻边相等时,请直接写出BN 的长.2024年河南省中考数学真题试卷答案一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的) 1. 【答案】A2. 【答案】C3. 【答案】B4. 【答案】A5. 【答案】A6. 【答案】B7. 【答案】D8. 【答案】D9. 【答案】C10. 【答案】C【解析】解∠根据图1知:当440W P =时,2A I =,故选项A 正确,但不符合题意 根据图2知:Q 随I 的增大而增大,故选项B 正确,但不符合题意根据图2知:Q 随I 的增大而增大,但前小半段增加的幅度小,后面增加的幅度大,故选项C 错误,符合题意根据图1知:I 随P 的增大而增大,又Q 随I 的增大而增大,则P 越大,插线板电源线产生的热量Q 越多,故选项D 正确,但不符合题意故选:C .二、填空题(每小题3分,共15分)11. 【答案】m (答案不唯一)12. 【答案】913. 【答案】1214. 【答案】()3,1015.【答案】 ∠. 1 ∠. 1【解析】解:∠90ACB ∠=︒,3CA CB == ∠190452BAC ABC ∠=∠=⨯︒=︒∠线段CD 绕点C 在平面内旋转,1CD =∠点D 在以点C 为圆心,1为半径的圆上∠BE AE ⊥∠90AEB ∠=︒∠点E 在以AB 为直径的圆上在Rt ABE △中,cos AE AB BAE =⋅∠∠AB 为定值∠当cos BAE ∠最大时,AE 最大,cos BAE ∠最小时,AE 最小 ∠当AE 与C 相切于点D,且点D 在ABC 内部时,BAE ∠最小,AE 最大,连接CD ,CE ,如图所示:则CD AE ⊥∠90ADE CDE ∠=∠=︒∠AD ==∠AC AC =∠45CED ABC ==︒∠∠∠90CDE ∠=︒∠CDE 为等腰直角三角形∠1DE CD ==∠1AE AD DE =+=+即AE 的最大值为1当AE 与C 相切于点D,且点D 在ABC 外部时,BAE ∠最大,AE 最小,连接CD ,CE ,如图所示:则CD AE ⊥∠90CDE ∠=︒∠AD ==∠四边形ABCE 为圆内接四边形 ∠180135CEA ABC =︒-=︒∠∠∠18045CED CEA =︒-=︒∠∠∠90CDE ∠=︒∠CDE 为等腰直角三角形∠1DE CD ==∠1AE AD DE =-=-即AE 的最小值为1故答案为:1;1.三、解答题(本大题共8个小题,共75分) 16. 【答案】(1)9(2)2a +17. 【答案】(1)甲 29(2)甲 (3)乙队员表现更好 18. 【答案】(1)6y x= (2)见解析 (3)92【小问1详解】解:反比例函数k y x =的图象经过点()3,2A ∠23k = ∠6k = ∠这个反比例函数的表达式为6y x =【小问2详解】解:当1x =时,6y =当2x =时,3y =当6x =时,1y =∠反比例函数6y x=的图象经过()1,6,()2,3,()6,1 画图如下:【小问3详解】解:∠()6,4E 向左平移后,E 在反比例函数的图象上∠平移后点E 对应点的纵坐标为4当4y =时,64x=解得32x = ∠平移距离为39622-=.故答案为:92.19. 【答案】(1)见解析(2)见解析【小问1详解】解:如图【小问2详解】证明:∠ECM A∠=∠∠CM AB∥∠∥BE DC∠四边形CDBF是平行四边形∠在Rt ABC△中,CD是斜边AB上的中线∠12 CD BD AB ==∠平行四边形CDBF是菱形.20. 【答案】(1)见解析(2)塑像AB的高约为6.9m 【小问1详解】证明:如图,连接BM.则AMB APB∠=∠.∠AMB ADB∠>∠∠APB ADB ∠>∠.【小问2详解】解:在Rt AHP 中,60APH ∠=︒,6PH =. ∠tan AH APH PH∠=∠tan 606AH PH =⋅︒==∠30APB ∠=︒∠603030BPH APH APB ∠=∠-∠=︒-︒=︒.在Rt BHP △中,tan BH BPH PH ∠=∠tan 306BH PH =⋅︒==∠()4 1.73 6.9m AB AH BH =-==≈⨯≈.答:塑像AB 的高约为6.9m .21. 【答案】(1)选用A 种食品4包,B 种食品2包(2)选用A 种食品3包,B 种食品4包【小问1详解】解:设选用A 种食品x 包,B 种食品y 包根据题意,得7009004600,101570.x y x y +=⎧⎨+=⎩解方程组,得4,2.x y =⎧⎨=⎩答:选用A 种食品4包,B 种食品2包.【小问2详解】解:设选用A 种食品a 包,则选用B 种食品()7-a 包根据题意,得()1015790a a +-≥.∠3a ≤.设总热量为kJ w ,则()70090072006300w a a a =+-=-+.∠2000-<∠w 随a 的增大而减小.∠当3a =时,w 最小.∠7734a -=-=.答:选用A 种食品3包,B 种食品4包.22. 【答案】(1)010v (2)()20m /s(3)小明的说法不正确,理由见解析【小问1详解】解:205h t v t =-+220051020v v t ⎛⎫=--+ ⎪⎝⎭ ∠当010v t =时,h 最大 故答案为:010v 【小问2详解】解:根据题意,得 当010v t =时,20h = ∠20005201010v v v ⎛⎫-⨯+⨯= ⎪⎝⎭∠()020m /s v =(负值舍去)【小问3详解】解:小明的说法不正确.理由如下:由(2),得2520h t t =-+当15h =时,215520t t =-+解方程,得11t =,23t =∠两次间隔的时间为312s -=∠小明的说法不正确.23. 【答案】(1)∠∠ (2)∠ACD ACB ∠=∠.理由见解析;∠2cos m n θ+(3)5或7 【小问1详解】解:观察图知,图∠和图∠中不存在对角互补,图2和图4中存在对角互补且邻边相等 故图∠和图∠中四边形是邻等对补四边形故答案为:∠∠【小问2详解】解:∠ACD ACB ∠=∠,理由:延长CB 至点E,使BE DC =,连接AE∠四边形ABCD 是邻等对补四边形∠180ABC D ∠+∠=︒∠180ABC ABE ∠+∠=︒∠ABE D ∠=∠∠AB AD =∠()SAS ABE ADC ≌∠E ACD ∠=∠,AE AC =∠E ACB ∠=∠∠ACD ACB ∠=∠∠过A 作AF EC ⊥于F∠AE AC = ∠()()1112222m n CF CE BC BE BC DC +==+=+= ∠2BCD θ∠=∠ACD ACB θ∠=∠=在Rt AFC △中,cos CF θAC= ∠cos 2cos CF m n AC θθ+== 【小问3详解】解:∠90B ,3AB =,4BC =∠5AC∠四边形ABMN 是邻等对补四边形 ∠180ANM B ∠+∠=︒∠90ANM =︒当AB BM =时,如图,连接AM ,过N 作NH BC ⊥于H∠22218AM AB BM =+=在Rt AMN 中222218MN AM AN AN =-=- 在Rt CMN 中()()22222435MN CM CN AN =-=--- ∠()()22218435AN AN -=--- 解得 4.2AN = ∠45CN = ∠90NHC ABC ∠=∠=︒,C C ∠=∠ ∠NHC ABC ∽534∠1225NH =,1625CH = ∠8425BH =∠BN ==当AN AB =时,如图,连接AM∠AM AM =∠Rt Rt ABM ANM ≌ ∠BM NM =,故不符合题意,舍去 当AN MN =时,连接AM ,过N 作NH BC ⊥于H∠90MNC ABC ∠=∠=︒,C C ∠=∠ ∠CMN CAB ∽△△ ∠CN MN BC AB =,即543CN CN -= 解得207CN =∠90NHC ABC ∠=∠=︒,C C ∠=∠ ∠NHC ABC ∽534∠127NH =,167CH = ∠127BH =∠BN ==当BM MN =时,如图,连接AM∠AM AM =∠Rt Rt ABM ANM ≌ ∠AN AB =,故不符合题意,舍去综上,BN 的长为5或7.。
题型:河南近几年中学考试数学第23题(新颖)

近几年中考数学第23题23.(11分)(2016)如图1,直线y=-43x+n交x轴于点A,交y轴于点C(0,4)抛物线y=23x2+bx+c经过点A,交y轴于点B(0,-2).点P为抛物线上的一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB.(1)求抛物线的解析式.(2)当△BDP为等腰直角三角形时,求线段PD的长.(3)如图2,将△BDP绕点B逆时针旋转,得到△BD/P/,且∠PBP/=∠OAC,当点P的对应点P/落在坐标轴上时,请直接写出P点的坐标.解:(1)由y=-43x+n过点C(0,4),得n=4,则y=-43x+4当y=0时,得-43x+4=0,解得:x=3,∴点A坐标是(3,0)…………………………………………………1分∵y=23x2+bx+c经过点A(3,0), B(0,-2)图1备用图∴22033b+c32c⎧=⨯+⎪⎨⎪-=⎩,解得:4b3c2⎧=-⎪⎨⎪=-⎩∴抛物线的解析式是23x2-43x-2……………………………………………3分(2)∵点P的横坐标为m,∴P(m,23m2-43m-2),D(m,-2)…………4分若△BDP为等腰直角三角形时,则PD=BD;①当点P在直线BD上方时,PD=23m2-43m-2+2=23m2-43m,(ⅰ)若P在y轴左侧,则m<0,BD=-m;∴23m2-43m=-m,解得:m=12或m=0(舍去)…………………………………5分(ⅱ)若P在y轴右侧,则m>0,BD=m;∴23m2-43m=m,解得:m=72或m=0(舍去)…………………………………6分②当点P在直线BD下方时,PD=-2-(23m2-43m-2) =-23m2+43m,则m>0,BD=m;∴-23m2+43m=m,解得:m=12或m=0(舍去)……………………………7分综上:m=72或m=12。
即当△BDP为等腰直角三角形时, PD的长为72或12。
2021河南中招数学23题

23.(10分)下面是某数学兴趣小组探究用不同方法作一个角 的平分线的讨论片段,请仔细阅读,并完成相应的任务。
小明:如图1,(1)分别在射线OA ,OB 上截取OC=OD ,OE=OF (C, E 不重合);(2)分别作线段CE ,DF 的垂直平分线l[1,]l[2],交点为P ,垂足分别为G ,H ;(3)作射线OP ,射线OP 即为∠AOB 的角平分线.简述理由如下:由作图知,∠PGO=∠PHO=90°, OG=0H,OP=OP,所以Rt △PGO ≅Rt △PHO,则射线OP 是∠AOB 的平分线。
小军:我认为小明的作图方法很有创意,但是太麻烦了,可以改进如下,如图2,(1)分别在OA,OB 上截取OC=OD ,OE=OF (点C,E 不重合)(2)连接DE ,CF ,交点为P ;(3)作射线OP ,射线OP 即为∠AOB 的平分线,…… 任务:(1)小明得出Rt △PGO ≅Rt △PHO 的依据是______(填序号) ①SSS ②SAS ③AAS ④ASA ⑤HL (2)小军作图得到的射线OP 是∠AOB 的角平分线吗?请判 断并说明理由(3)如图3,已知∠AOB=60°,点E ,F 分别在射线OA ,OB 上,且OE=OF=√3+1.点C ,D 分别为射线OA ,OB 上的动点.且OC=OD ,连接DE ,CF ,交点为P. 当∠CPE=30°时,直接写出OC 的长。
图2OB图1解:(1)⑤(2)射线OP 是∠AOB 的平分线,理由如下: 解法一:连接EF 在△EOD 与△FOC 中 OD=OC ∠EOD=∠FOC OE=OF∴△EOD ≅△FOC(SAS) ∴∠OED=∠OFC ∵OE=OF ∴∠OEF=∠OFE ∴∠PEF=∠PFE ∴PE=PF ∵OE=OF图3BO图4BO∴OP 垂直平分EF ∴∠EOP=∠FOP∴OP 是∠AOB 的角平分线。
2023年河南省中考数学真题(解析版)

2023年河南省普通高中招生考试试卷数学一、选择题1. 下列各数中,最小的数是( )A. -lB. 0C. 1D. 【答案】A【解析】【分析】根据实数的大小比较法则,比较即可解答.【详解】解:∵101-<<<,∴最小的数是-1.故选:A【点睛】本题考查实数的大小比较,负数都小于0,正数都大于0,正数大于一切负数,两个负数,其绝对值大的反而小.2. 北宋时期的汝官窑天蓝釉刻花鹅颈瓶是河南博物院九大镇院之宝之一,具有极高的历史价值、文化价值.如图所示,关于它的三视图,下列说法正确的是( )A. 主视图与左视图相同B. 主视图与俯视图相同C. 左视图与俯视图相同D. 三种视图都相同【答案】A【解析】【分析】直接利用已知几何体分别得出三视图进而分析得出答案.【详解】解:这个花鹅颈瓶的主视图与左视图相同,俯视图与主视图和左视图不相同.故选:A .【点睛】此题主要考查了简单几何体的三视图,掌握三视图的概念是解题关键.3. 2022年河南省出版的4.59亿册图书,为贯彻落实党的二十大关于深化全民阅读活动的重要精神,建设学习型社会提供了丰富的图书资源.数据“4.59亿”用科学记数法表示为( )A. 74.5910´B. 845.910´C. 84.5910´D. 90.45910´【答案】C【解析】【分析】将一个数表示为10n a ´的形式,其中110a £<,n 为整数,这种记数方法叫做科学记数法,据此即可得出答案.【详解】解:4.59亿8459000000 4.9510==´.故选:C .【点睛】本题主要考查了用科学记数法表示较大的数,掌握形式为10n a ´,其中110a £<,确定a与n 的值是解题的关键.4. 如图,直线AB ,CD 相交于点O ,若180∠=︒,230∠=︒,则AOE ∠的度数为( )A. 30︒B. 50︒C. 60︒D. 80︒【答案】B【解析】【分析】根据对顶角相等可得180AOD ∠=∠=︒,再根据角和差关系可得答案.【详解】解:∵180∠=︒,∴180AOD ∠=∠=︒,∵230∠=︒,∴2803050AOE AOD ∠=∠-∠=︒-︒=︒,故选:B【点睛】本题主要考查了对顶角的性质,解题的关键是掌握对顶角相等.5. 化简11a a a -+的结果是( )A 0 B. 1 C. a D. 2a -【答案】B【解析】的.【分析】根据同母的分式加法法则进行计算即可.【详解】解:11111a a a a a a a--++===,故选:B .【点睛】本题考查同分母的分式加法,熟练掌握运算法则是解决问题的关键.6. 如图,点A ,B ,C 在O e 上,若55C ∠=︒,则AOB ∠的度数为( )A. 95︒B. 100︒C. 105︒D. 110︒【答案】D【解析】【分析】直接根据圆周角定理即可得.【详解】解:∵55C ∠=︒,∴由圆周角定理得:2110AOB C ==︒∠∠,故选:D .【点睛】本题考查了圆周角定理,熟练掌握圆周角定理是解题关键.7. 关于x 的一元二次方程280x mx +-=的根的情况是( )A. 有两个不相等的实数根B. 有两个相等的实数根C. 只有一个实数根D. 没有实数根【答案】A【解析】【分析】对于20(0)ax bx c a ++=¹,当0D >, 方程有两个不相等的实根,当Δ0=, 方程有两个相等的实根,Δ0<, 方程没有实根,根据原理作答即可.【详解】解:∵280x mx +-=,∴()2248320m m D =-´-=+>,所以原方程有两个不相等的实数根,故选:A .【点睛】本题考查了一元二次方程根的判别式,熟练掌握一元二次方程根的判别式是解题关键.8. 为落实教育部办公厅、中共中央宣传部办公厅关于《第41批向全国中小学生推荐优秀影片片目》的通知精神,某校七、八年级分别从如图所示的三部影片中随机选择一部组织本年级学生观看,则这两个年级选择的影片相同的概率为( )A. 12 B. 13 C. 16 D. 19【答案】B【解析】【分析】先画树状图,再根据概率公式计算即可.【详解】设三部影片依次为A 、B 、C ,根据题意,画树状图如下:故相同的概率为3193=.故选B .【点睛】本题考查了画树状图法计算概率,熟练掌握画树状图法是解题的关键.9. 二次函数2y ax bx =+的图象如图所示,则一次函数y x b =+的图象一定不经过( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】D【解析】【分析】根据二次函数图象的开口方向、对称轴判断出a 、b 的正负情况,再由一次函数的性质解答.【详解】解:由图象开口向下可知a<0,由对称轴b x 02a=->,得0b >.∴一次函数y x b =+的图象经过第一、二、三象限,不经过第四象限.故选:D .【点睛】本题考查二次函数图象和一次函数图象的性质,解答本题的关键是求出a 、b 的正负情况,要掌握它们的性质才能灵活解题,此题难度不大.10. 如图1,点P 从等边三角形ABC 的顶点A 出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B .设点P 运动的路程为x ,PB y PC=,图2是点P 运动时y 随x 变化的关系图象,则等边三角形ABC 的边长为( )A. 6B. 3C.D. 【答案】A【解析】【分析】如图,令点P 从顶点A 出发,沿直线运动到三角形内部一点O ,再从点O 沿直线运动到顶点B .结合图象可知,当点P 在AO 上运动时,PB PC =,AO =30BAO CAO ∠=∠=︒,当点P 在OB 上运动时,可知点P 到达点B 时的路程为AO OB ==O 作OD AB ^,解直角三角形可得cos303AD AO =×︒=,进而可求得等边三角形ABC 的边长.【详解】解:如图,令点P 从顶点A 出发,沿直线运动到三角形内部一点O ,再从点O 沿直线运动到顶点B .结合图象可知,当点P 在AO 上运动时,1PB PC=,∴PB PC =,AO =又∵ABC V 为等边三角形,∴60BAC ∠=︒,AB AC =,∴()SSS APB APC △≌△,∴BAO CAO ∠=∠,∴30BAO CAO ∠=∠=︒,当点P 在OB 上运动时,可知点P 到达点B 时的路程为∴OB =AO OB ==,∴30BAO ABO ∠=∠=︒,过点O 作OD AB ^,∴AD BD =,则cos303AD AO =×︒=,∴6AB AD BD =+=,即:等边三角形ABC 的边长为6,故选:A .【点睛】本题考查了动点问题的函数图象,解决本题的关键是综合利用图象和图形给出的条件.二、填空题11. 某校计划给每个年级配发n 套劳动工具,则3个年级共需配发______套劳动工具.【答案】3n【解析】【分析】根据总共配发的数量=年级数量´每个年级配发的套数,列代数式.【详解】解:由题意得:3个年级共需配发得套劳动工具总数为:3n 套,故答案为:3n .【点睛】本题考查了列代数式,解答本题的关键是读懂题意,找出合适的等量关系,列代数式.12. 方程组35,37x y x y +=ìí+=î的解为______.【答案】12x y =ìí=î【解析】【分析】利用加减消元法求解即可.【详解】解:3537x y x y +=ìí+=î①②由3´-①②得,88x =,解得1x =,把1x =代入①中得315y ´+=,解得2y =,故原方程组的解是12x y =ìí=î,故答案为:12x y =ìí=î.【点睛】本题主要考查了二元一次方程组的解法,解二元一次方程组的常用解法:代入消元法和加减消元法,观察题目选择合适的方法是解题关键.13. 某林木良种繁育试验基地为全面掌握“无絮杨”品种苗的生长规律,定期对培育的1000棵该品种苗进行抽测.如图是某次随机抽测该品种苗的高度x (cm )的统计图,则此时该基地高度不低于300cm 的“无絮杨”品种苗约有______棵.【答案】280【解析】【分析】利用1000棵乘以样本中不低于300cm 的百分比即可求解.【详解】解:该基地高度不低于300cm 的“无絮杨”品种苗所占百分比为10%18%28%+=,则不低于300cm 的“无絮杨”品种苗约为:100028%280´=棵,故答案为:280.【点睛】本题考查用样本估计总体,明确题意,结合扇形统计图中百分比是解决问题的关键.14. 如图,PA 与O e 相切于点A ,PO 交O e 于点B ,点C 在PA 上,且CB CA =.若5OA =,12PA =,则CA 的长为______.【答案】103【解析】【分析】连接OC ,证明OAC OBC V V ≌,设CB CA x ==,则12PC PA CA x =-=-,再证明PAO PBC V V ∽,列出比例式计算即可.【详解】如图,连接OC ,∵PA 与O e 相切于点A ,∴90OAC ∠=︒;∵OA OB CA CB OC OC =ìï=íï=î,∴OAC OBC V V ≌,∴90OAC OBC ∠=∠=︒,∴90PAO PBC ∠=∠=︒,∵P P ∠=∠,∴PAO PBC V V ∽,∴PO AO PC BC=,∵5OA =,12PA =,∴13PO ==,设CB CA x ==,则12PC PA CA x =-=-,∴13512x x=-,解得103x =,故CA 的长为103,故答案为:103.【点睛】本题考查了切线的性质,三角形全等的判定和性质,勾股定理,三角形相似的判断和性质,熟练掌握性质是解题的关键.15. 矩形ABCD 中,M 为对角线BD 的中点,点N 在边AD 上,且1AN AB ==.当以点D ,M ,N 为顶点的三角形是直角三角形时,AD 的长为______.【答案】21【解析】分析】分两种情况:当90MND ∠=︒时和当90NMD ∠=︒时,分别进行讨论求解即可.【详解】解:当90MND ∠=︒时,∵四边形ABCD 矩形,∴90A ∠=︒,则∥MN AB ,由平行线分线段成比例可得:AN BM ND MD =,又∵M 为对角线BD 的中点,∴BM MD =,∴1AN BM ND MD==,即:1ND AN ==,【∴2AD AN ND =+=,当90NMD ∠=︒时,∵M 为对角线BD 的中点,90NMD ∠=︒∴MN 为BD 的垂直平分线,∴BN ND =,∵四边形ABCD 矩形,1AN AB ==∴90A ∠=︒,则BN ==∴BN ND ==∴1AD AN ND =+=,综上,AD 的长为21,故答案为:21+.【点睛】本题考查矩形的性质,平行线分线段成比例,垂直平分线的判定及性质等,画出草图进行分类讨论是解决问题的关键.三、解答题16. (1)计算:135---+;(2)化简:()()224x y x x y ---.【答案】(1)15;24y 【解析】【分析】(1)先求绝对值和算术平方根,再进行加减计算即可;(2)先利用完全平方公式去括号,再合并同类项即可.【详解】(1)解:原式1=335-+15=;(2)解:原式222444x xy y x xy=-+-+24y =.【点睛】本题考查实数的混合运算、多项式乘多项式的混合运算,熟练掌握完全平方公式是解题的关键.17. 蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:a .配送速度得分(满分10分):甲:6 6 7 7 7 8 9 9 9 10乙:6 7 7 8 8 8 8 9 9 10b .服务质量得分统计图(满分10分):c .配送速度和服务质量得分统计表:配送速度得分服务质量得分项目统计量快递公司平均数中位数平均数方差甲78m 72s 甲乙8872s乙根据以上信息,回答下列问题:(1)表格中的m =______;2s 甲______2s 乙(填“>”“=”或“<”).(2)综合上表中的统计量,你认为小丽应选择哪家公司?请说明理由.(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息(列出一条即可)?【答案】(1)7.5;<.(2)甲公司,理由见解析(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)【解析】【分析】(1)根据中位数和方差概念求解即可;(2)通过比较平均数,中位数和方差求解即可;(3)根据题意求解即可.【小问1详解】由题意可得,787.52m +==,()()()()22222137748726757110s éù=´´-+´-+´-+-=ëû甲()()()()()()()222222221478721072679725777 4.210s éù=´-+-+´-+´-+-+´-+-=ëû乙,∴22s s <甲乙,故答案为:7.5;<;【小问2详解】∵配送速度得分甲和乙的得分相差不大,服务质量得分甲和乙的平均数相同,但是甲的方差明显小于乙的方差,∴甲更稳定,∴小丽应选择甲公司;【小问3详解】还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)【点睛】本题考查中位数、平均数、方差的定义,掌握中位数、平均数、方差的定义是解题的关键.18. 如图,ABC V 中,点D 在边AC 上,且AD AB =.(1)请用无刻度的直尺和圆规作出A ∠的平分线(保留作图痕迹,不写作法).(2)若(1)中所作的角平分线与边BC 交于点E ,连接DE .求证:DE BE =.【答案】(1)见解析(2)见解析【解析】【分析】(1)利用角平分线的作图步骤作图即可;的(2)证明()SAS BAE DAE △≌△,即可得到结论.【小问1详解】解:如图所示,即为所求,【小问2详解】证明:∵AE 平分BAC ∠,∴BAE DAE ∠=∠,∵AB AD =,AE AE =,∴()SAS BAE DAE △≌△,∴DE BE =.【点睛】此题考查了角平分线的作图、全等三角形的判定和性质等知识,熟练掌握角平分线的作图和全等三角形的判定是解题的关键.19. 小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数k y x =图象上的点)A 和点B 为顶点,分别作菱形AOCD 和菱形OBEF ,点D ,E 在x 轴上,以点O 为圆心,OA 长为半径作 AC ,连接BF .(1)求k 的值;(2)求扇形AOC 的半径及圆心角的度数;(3)请直接写出图中阴影部分面积之和.【答案】(1(2)半径为2,圆心角为60︒(3)23p -【解析】【分析】(1)将)A 代入k y x=中即可求解;(2)利用勾股定理求解边长,再利用三角函数求出AOD ∠的度数,最后结合菱形的性质求解;(3)先计算出AOCD S =菱形,再计算出扇形的面积,根据菱形的性质及结合k 的几何意义可求出FBO S =V 【小问1详解】解:将)A 代入k y x=中,得1=,解得:k =【小问2详解】解:Q 过点A 作OD 的垂线,垂足为G ,如下图:)A Q ,1,AG OG \==,2OA \==,\半径为2;12AG OA =Q ,∴1sin 2AG AOG OG ∠==,30AOG \∠=︒,由菱形的性质知:30AOG COG ∠=∠=︒,60AOC \∠=︒,\扇形AOC 的圆心角的度数:60︒;【小问3详解】解:2OD OG ==Q ,1AOCD S AG OD \=´=´=菱形221122663AOC S r p p p =´=´´=Q 扇形,如下图:由菱形OBEF 知,FHO BHO S S =V V ,2BHO k S ==V Q2FBO S \==V ,2233FBO AOCD AOC S S S S p p \=+-=+=V 阴影部分面积菱形扇形.【点睛】本题考查了反比例函数及k 的几何意义,菱形的性质、勾股定理、圆心角,解题的关键是掌握k 的几何意义.20. 综合实践活动中,某小组用木板自制了一个测高仪测量树高,测高仪ABCD 为正方形,30cm AB =,顶点A 处挂了一个铅锤M .如图是测量树高的示意图,测高仪上的点D ,A 与树顶E 在一条直线上,铅垂线AM 交BC 于点H .经测量,点A 距地面1.8m ,到树EG 的距离11m AF =,20cm BH =.求树EG 的高度(结果精确到0.1m ).【答案】树EG 的高度为9.1m 【解析】【分析】由题意可知,90BAE MAF BAD ∠=∠=∠=︒, 1.8m FG =,易知EAF BAH ∠=∠,可得2tan tan 3EF EAF BAH AF ∠==∠=,进而求得22m 3EF =,利用EG EF FG =+即可求解.【详解】解:由题意可知,90BAE MAF BAD ∠=∠=∠=︒, 1.8m FG =,则90EAF BAF BAF BAH ∠+∠=∠+∠=︒,∴EAF BAH ∠=∠,∵30cm AB =,20cm BH =,则2tan 3BH BAH AB ∠==,∴2tan tan 3EF EAF BAH AF ∠==∠=,∵11m AF =,则2113EF =,∴22m 3EF =,∴22 1.89.1m 3EG EF FG =+=+»,答:树EG 的高度为9.1m .【点睛】本题考查解直角三角形的应用,得到EAF BAH ∠=∠是解决问题的关键.21. 某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种.活动一:所购商品按原价打八折;活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80元,需付款220元;所购商品原价为770元,可减160元,需付款610元)(1)购买一件原价为450元的健身器材时,选择哪种活动更合算?请说明理由.(2)购买一件原价在500元以下的健身器材时,若选择活动一和选择活动二的付款金额相等,求一件这种健身器材的原价.(3)购买一件原价在900元以下的健身器材时,原价在什么范围内,选择活动二比选择活动一更合算?设一件这种健身器材的原价为a 元,请直接写出a 的取值范围.【答案】(1)活动一更合算(2)400元 (3)当300400a £<或600800a £<时,活动二更合算【解析】【分析】(1)分别计算出两个活动需要付款价格,进行比较即可;(2)设这种健身器材的原价是x 元,根据“选择活动一和选择活动二的付款金额相等”列方程求解即可;(3)由题意得活动一所需付款为0.8a 元,活动二当0300a <<时,所需付款为a 元,当300600a £<时,所需付款为()80a -元,当600900a £<时,所需付款为()160a -元,然后根据题意列出不等式即可求解.【小问1详解】解:购买一件原价为450元的健身器材时,活动一需付款:4500.8360´=元,活动二需付款:45080370-=元,∴活动一更合算;【小问2详解】设这种健身器材的原价是x 元,则0.880x x =-,解得400x =,答:这种健身器材的原价是400元,【小问3详解】这种健身器材的原价为a 元,则活动一所需付款为:0.8a 元,活动二当0300a <<时,所需付款为:a 元,当300600a £<时,所需付款为:()80a -元,当600900a £<时,所需付款为:()160a -元,①当0300a <<时,0.8a a >,此时无论a 为何值,都是活动一更合算,不符合题意,②当300600a £<时,800.8a a -<,解得300400a £<,即:当300400a £<时,活动二更合算,③当600900a £<时,1600.8a a -<,解得600800a £<,即:当600800a £<时,活动二更合算,综上:当300400a £<或600800a £<时,活动二更合算.【点睛】此题考查了一元一次方程及一元一次不等式的应用,解答本题的关键是仔细审题,注意分类讨论的应用.22. 小林同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析.如图,在平面直角坐标系中,点A ,C 在x 轴上,球网AB 与y 轴的水平距离3m OA =,2m CA =,击球点P 在y 轴上.若选择扣球,羽毛球的飞行高度()m y 与水平距离()m x 近似满足一次函数关系0.4 2.8y x =-+;若选择吊球,羽毛球的飞行高度()m y 与水平距离()m x 近似满足二次函数关系()21 3.2y a x =-+.(1)求点P 的坐标和a 的值.(2)小林分析发现,上面两种击球方式均能使球过网.要使球的落地点到C 点的距离更近,请通过计算判断应选择哪种击球方式.【答案】(1)()0,2.8P ,0.4a =-,(2)选择吊球,使球的落地点到C 点的距离更近【解析】【分析】(1)在一次函数上0.4 2.8y x =-+,令0x =,可求得()0,2.8P ,再代入()21 3.2y a x =-+即可求得a 的值;(2)由题意可知5m OC =,令0y =,分别求得0.4 2.80x -+=,()20.41 3.20x --+=,即可求得落地点到O 点的距离,即可判断谁更近.【小问1详解】解:在一次函数0.4 2.8y x =-+,令0x =时, 2.8y =,∴()0,2.8P ,将()0,2.8P 代入()21 3.2y a x =-+中,可得: 3.2 2.8a +=,解得:0.4a =-;【小问2详解】∵3m OA =,2m CA =,∴5m OC =,选择扣球,则令0y =,即:0.4 2.80x -+=,解得:7x =,即:落地点距离点O 距离为7m ,∴落地点到C 点的距离为752m -=,选择吊球,则令0y =,即:()20.41 3.20x --+=,解得:1x =±+(负值舍去),即:落地点距离点O 距离为()1m +,∴落地点到C 点的距离为()(514m -=-,∵42-<,∴选择吊球,使球的落地点到C 点的距离更近.【点睛】本题考查二次函数与一次函数的应用,理解题意,求得函数解析式是解决问题的关键.23. 李老师善于通过合适的主题整合教学内容,帮助同学们用整体的、联系的、发展的眼光看问题,形成科学的思维习惯.下面是李老师在“图形的变化”主题下设计的问题,请你解答.(1)观察发现:如图1,在平面直角坐标系中,过点()4,0M 的直线l y P 轴,作ABC V 关于y 轴对称的图形111A B C △,再分别作111A B C △关于x 轴和直线l 对称的图形222A B C △和333A B C △,则222A B C △可以看作是ABC V 绕点O 顺时针旋转得到的,旋转角的度数为______;333A B C △可以看作是ABC V 向右平移得到的,平移距离为______个单位长度.(2)探究迁移:如图2,ABCD Y 中,()090BAD a a ∠=︒<<︒,P 为直线AB 下方一点,作点P 关于直线AB 的对称点1P ,再分别作点1P 关于直线AD 和直线CD 的对称点2P 和3P ,连接AP ,2AP ,请仅就图2的情形解决以下问题:①若2PAP b ∠=,请判断b 与a 的数量关系,并说明理由;②若AD m =,求P ,3P 两点间的距离.(3)拓展应用:在(2)的条件下,若60a =︒,AD =,15PAB ∠=︒,连接23P P .当23P P 与ABCD Y 的边平行时,请直接写出AP 的长.【答案】(1)180︒,8.(2)①2b a =,理由见解析;②2sin m a(3)或【解析】【分析】(1)观察图形可得222A B C △与ABC V 关于O 点中心对称,根据轴对称的性质可得即可求得平移距离;(2)①连接1AP ,由对称性可得,112PAB P AB P AD P AD ∠=∠∠=∠,,进而可得22PAP BAD ∠=∠,即可得出结论;②连接113,PP PP 分别交,AB CD 于,E F 两点,过点D 作DG AB ^,交AB 于点G ,由对称性可知:113PE PE PF P F ==,且113PP AB PP CD ^^,,得出32PP EF =,证明四边形EFDG 是矩形,则DG EF =,在Rt DAG △中,根据sin DG DAG DA∠=,即可求解;(3)分23P P AD ∥,23P P CD ∥,两种情况讨论,设AP x =,则12AP AP x ==,先求得1PP x =,勾股定理求得13PP ,进而表示出3PP ,根据由(2)②可得32sin PP AD a =,可得36PP =,进而建立方程,即可求解.【小问1详解】(1)∵ABC V 关于y 轴对称的图形111A B C △,111A B C △与222A B C △关于x 轴对称,∴222A B C △与ABC V 关于O 点中心对称,则222A B C △可以看作是ABC V 绕点O 顺时针旋转得到的,旋转角的度数为180︒∵()1,1A -,∴12AA =,∵()4,0M ,13,A A 关于直线4x =对称,∴131248A A AA +=´=,即38AA =,333A B C △可以看作是ABC V 向右平移得到的,平移距离为8个单位长度.故答案为:180︒,8.【小问2详解】①2b a =,理由如下,连接1AP ,由对称性可得,112PAB P AB P AD P AD ∠=∠∠=∠,,2112PAP PAB P AB P AD P AD∠=∠+∠+∠+∠1122P AB P AD=∠+∠()112P AB P AD =∠+∠2BAD=∠∴2b a =,②连接113,PP PP 分别交,AB CD 于,E F 两点,过点D 作DG AB ^,交AB 于点G ,由对称性可知:113PE PE PF P F ==,且113PP AB PP CD ^^,,∵四边形ABCD 为平行四边形,∴AB CD∥∴13P P P ,,三点共线,∴311311222PP PE PE PF P F PE PF EF =+++=+=,∵113,,PP AB PP CD DG AB ^^^,∴1190PFD PEG DGE ∠=∠=∠=︒,∴四边形EFDG 是矩形,∴DG EF =,在Rt DAG △中,DAG a ∠=,AD m=∵sin DG DAG DA∠=,∴sin sin DG AD DAG m a =×∠=,∴3222sin PP EF DG m a===【小问3详解】解:设AP x =,则12AP AP x ==,依题意,12PP AD ^,当23P P AD ∥时,如图所示,过点P 作1PQ AP ^于点Q ,∴12390PP P ∠=︒∵15PAB ∠=︒,60a =︒,∴1320P PAP AB ∠=︒∠=,1245DAP DAP ∠=∠=︒∴2190P AP ∠=︒,则12PP =,在1APP V 中,()111180752APP PAP ∠=︒-∠=︒,∴213180457560P PP ∠=︒-︒-︒=︒,则13230PP P ∠=︒,∴13212PP P P ==在Rt APQ △中,30PAQ ∠=︒,则1122PQ AP x ==,AQ x ==,在1Rt PQP V 中,11PQ AP AQ x x =-=,1PP x ====,∴3113PP PP PP x x =+=+=由(2)②可得32sin PP AD a =,∵AD =∴326PP =´=6x =,解得:x =;如图所示,若23P P DC ∥,则13290PP P ∠=︒,∵21360P PP ∠=︒,则32130P P P ∠=︒,则131212PP PP x ==,∵1PP x =,3PP x x x =+=,∵36PP =,6=,解得:x =,综上所述,AP 的长为或【点睛】本题考查了轴对称的性质,旋转的性质,平行四边形的性质,解直角三角形,熟练掌握轴对称的性质是解题的关键.。
2024河南中招数学试卷试题

选择题下列数中,是无理数的是:A. 3/5B. √4C. π(正确答案)D. -2在平面直角坐标系中,点A(3, -4)关于x轴对称的点的坐标是:A. (-3, 4)B. (3, 4)(正确答案)C. (-3, -4)D. (4, -3)已知三角形ABC的三边长为a, b, c,且满足a2 + b2 = c2 + 2ab,则三角形ABC是:A. 直角三角形B. 等腰三角形C. 等边三角形D. 等腰直角三角形(正确答案)函数y = 2x - 1与y = -x + 4的交点坐标是:A. (1, 3)B. (3, 1)C. (-1, 5)(正确答案)D. (5, -1)下列不等式组中,解集为x > 2的是:A. {x | x > 1, x < 3}B. {x | x ≥ 2, x ≤ 4}C. {x | x > 2, x < 5}(正确答案)D. {x | x ≥ 1, x < 2}若关于x的一元二次方程x2 - kx + k - 2 = 0有两个相等的实数根,则k的值为:A. 1B. 2C. 3D. 4(正确答案)在平行四边形ABCD中,AB = 5,AD = 8,且∠BAD的平分线AE交BC于点E,则BE的长为:A. 2B. 3(正确答案)C. 4D. 5下列函数中,图像经过原点的是:A. y = x + 1B. y = x2 - 1C. y = 1/xD. y = 2x(正确答案)已知圆O的半径为5cm,圆心O到直线l的距离为4cm,则直线l与圆O的位置关系是:A. 相离B. 相切C. 相交(正确答案)D. 无法确定。
2023年河南中考数学试题

2023年河南中考数学试题数学试题一:1. 解方程(1)已知方程2x + 5 = 9,求x的值。
解:将方程改写为2x = 9 - 5,得2x = 4。
两边同时除以2,得x = 2。
2. 计算(1)计算2的平方加3的立方的值。
解:2的平方为2 × 2 = 4,3的立方为3 × 3 × 3 = 27。
所以,2的平方加3的立方的值为4 + 27 = 31。
3. 几何题(1)如图所示,三角形ABC中,∠ABC = 90°,BC = 8 cm,AC = 10 cm。
已知底边BC等于8 cm,底边上的高BD等于6 cm。
求三角形的面积。
解:三角形的面积可以由底边和高的乘积的一半得出。
根据题意,三角形ABC的底边BC等于8 cm,高BD等于6 cm。
所以,三角形的面积为(8 × 6) ÷ 2 = 24 cm²。
数学试题二:1. 解方程组(1)解方程组⎧ 2x + y = 5⎨ x - y = 1解:将第一个方程改写为y = 5 - 2x,代入第二个方程,得x - (5 - 2x) = 1。
整理得3x - 5 = 1,再移到等号左边,得3x = 6。
最后,两边同时除以3,得x = 2。
代入第一个方程,得到2(2) + y = 5,解得y = 1。
所以,方程组的解是x = 2,y = 1。
2. 数列(1)定义数列{an}如下:a1 = 2,an = an-1 + 3(n ≥ 2)。
求该数列的前5项。
解:根据递推公式an = an-1 + 3,可以依次计算出数列的前5项:a1 = 2a2 = a1 + 3 = 2 + 3 = 5a3 = a2 + 3 = 5 + 3 = 8a4 = a3 + 3 = 8 + 3 = 11a5 = a4 + 3 = 11 + 3 = 14所以,数列的前5项分别为2、5、8、11、14。
数学试题三:1. 几何题(1)如图所示,正方形ABCD的边长为10 cm。
2023年河南中考数学试题及答案

2023年河南中考数学试题及答案第一部分:选择题(共20题,每题2分,共40分)1. 设函数 f(x) = 3x - 5,求 f(2) 的值。
A. 1B. 3C. 4D. 7答案:B2. 若 x = -2 是方程 3x + k = 7 的解,求常数 k 的值。
A. -1B. 1C. 3D. 5答案:D3. 已知平行四边形 ABCD 中,AB = 3cm,BC = 4cm,点 E、F分别是 AB、BC 的中点,则平行四边形 EFGH 的周长等于多少?A. 14cmB. 16cmC. 18cmD. 20cm答案:C...第二部分:填空题(共10题,每题4分,共40分)11. 已知 a + 2b = 5,b + 3c = 6,求 a + c 的值。
答案:212. 一辆车从 A 地出发,经过 240km,到达 B 地,再经过320km,返回 A 地。
若该车每小时的速度不变,则车的来回总用时为多少小时?答案:1613. 化简下列分式:$\frac{{2x(x + 1)}}{{(x - 1)^2}}$答案:$\frac{{2(x + 1)}}{{x - 1}}$...第三部分:计算题(共5题,每题10分,共50分)21. 计算下列各数的最小公倍数:8,12,18答案:7222. 计算 $\frac{3}{4} + \frac{5}{6}$ 的值。
答案:$\frac{19}{12}$23. ......第四部分:证明题(共2题,每题25分,共50分)31. 已知任意数 a 和 b,则 $(a+b)^2 = a^2 + 2ab + b^2$。
请证明该等式。
答案:证明略。
32. ......。
河南数学中招试题及答案

河南数学中招试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是方程\(2x - 5 = 11\)的解?A. \(x = 4\)B. \(x = 6\)C. \(x = 8\)D. \(x = 10\)2. 一个数的平方根是4,那么这个数是:A. 8B. 16C. -8D. -163. 圆的直径是14,那么它的半径是:A. 7B. 14C. 28D. 214. 一个三角形的三个内角分别是45°、45°和90°,这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不存在5. 函数\(y = 3x + 2\)的图象与x轴的交点坐标是:A. (-2/3, 0)B. (2/3, 0)C. (-2, 0)D. (2, 0)6. 下列哪个选项是不等式\(2x - 3 > 5\)的解集?A. \(x > 4\)B. \(x < 4\)C. \(x > 1\)D. \(x < 1\)7. 一个数的立方是-27,那么这个数是:A. 3B. -3C. 9D. -98. 一个等腰三角形的两边长分别是5和5,底边长是8,那么这个三角形的面积是:A. 12B. 20C. 24D. 309. 函数\(y = x^2 - 4x + 4\)的最小值是:A. 0B. 1C. 4D. 1610. 一个长方体的长、宽、高分别是2、3和4,那么它的体积是:A. 24B. 32C. 48D. 64二、填空题(每题4分,共20分)1. 一个数的相反数是-5,那么这个数是____。
2. 一个数的绝对值是7,那么这个数可以是____或____。
3. 一个三角形的周长是30,其中两边长分别是8和15,那么第三边长是____。
4. 一个圆的半径是5,那么它的面积是____。
5. 函数\(y = 2x - 3\)与y轴的交点坐标是____。
三、解答题(每题10分,共50分)1. 解方程:\(3x + 5 = 14\)。
2023年河南省中考数学真题(解析)

2023年河南省普通高中招生考试试卷数学一、选择题1.【答案】A【解析】解:∵101-<<<,∴最小的数是-1.故选:A2.【答案】A【解析】解:这个花鹅颈瓶的主视图与左视图相同,俯视图与主视图和左视图不相同.故选:A .3.【答案】C【解析】解:4.59亿8459000000 4.9510==⨯.故选:C .4.【答案】B【解析】解:∵180∠=︒,∴180AOD ∠=∠=︒,∵230∠=︒,∴2803050AOE AOD ∠=∠-∠=︒-︒=︒,故选:B5.【答案】B 【解析】解:11111a a a a a a a--++===,故选:B .6.【答案】D【解析】解:∵55C ∠=︒,∴由圆周角定理得:2110AOB C ==︒∠∠,故选:D .7.【答案】A【解析】解:∵280x mx +-=,∴()2248320m m ∆=-⨯-=+>,所以原方程有两个不相等的实数根,故选:A .8.【答案】B【解析】设三部影片依次为A 、B 、C ,根据题意,画树状图如下:故相同的概率为3193=.故选B .9.【答案】D 【解析】解:由图象开口向下可知a<0,由对称轴b x 02a=->,得0b >.∴一次函数y x b =+的图象经过第一、二、三象限,不经过第四象限.故选:D .10.【答案】A【解析】解:如图,令点P 从顶点A 出发,沿直线运动到三角形内部一点O ,再从点O 沿直线运动到顶点B .结合图象可知,当点P 在AO 上运动时,1PB PC=,∴PB PC =,AO =又∵ABC 为等边三角形,∴60BAC ∠=︒,AB AC =,∴()SSS APB APC △≌△,∴BAO CAO ∠=∠,∴30BAO CAO ∠=∠=︒,当点P 在OB 上运动时,可知点P 到达点B时的路程为∴OB =,即AO OB ==∴30BAO ABO ∠=∠=︒,过点O 作OD AB ⊥,∴AD BD =,则cos303AD AO =⋅︒=,∴6AB AD BD =+=,即:等边三角形ABC 的边长为6,故选:A .二、填空题11.【答案】3n【解析】解:由题意得:3个年级共需配发得套劳动工具总数为:3n 套,故答案为:3n .12.【答案】12x y =⎧⎨=⎩【解析】解:3537x y x y +=⎧⎨+=⎩①②由3⨯-①②得,88x =,解得1x =,把1x =代入①中得315y ⨯+=,解得2y =,故原方程组的解是12x y =⎧⎨=⎩,故答案为:12x y =⎧⎨=⎩.13.【答案】280【解析】解:该基地高度不低于300cm 的“无絮杨”品种苗所占百分比为10%18%28%+=,则不低于300cm 的“无絮杨”品种苗约为:100028%280⨯=棵,故答案为:280.14.【答案】103【解析】如图,连接OC ,∵PA 与O 相切于点A ,∴90OAC ∠=︒;∵OA OB CA CB OC OC =⎧⎪=⎨⎪=⎩,∴OAC OBC ≌,∴90OAC OBC ∠=∠=︒,∴90PAO PBC ∠=∠=︒,∵P P ∠=∠,∴PAO PBC ∽,∴PO AO PC BC=,∵5OA =,12PA =,∴13PO ==,设CB CA x ==,则12PC PA CA x =-=-,∴13512x x=-,解得103x =,故CA 的长为103,故答案为:103.15.【答案】21+【解析】解:当90MND ∠=︒时,∵四边形ABCD 矩形,∴90A ∠=︒,则∥MN AB ,由平行线分线段成比例可得:AN BM ND MD =,又∵M 为对角线BD 的中点,∴BMMD =,∴1AN BM ND MD==,即:1ND AN ==,∴2AD AN ND =+=,当90NMD ∠=︒时,∵M 为对角线BD 的中点,90NMD ∠=︒∴MN 为BD 的垂直平分线,∴BN ND =,∵四边形ABCD 矩形,1AN AB ==∴90A ∠=︒,则BN ==∴BN ND ==∴1AD AN ND =+=,综上,AD 的长为21,故答案为:21+.三、解答题16.【答案】(1)15;24y 【解析】(1)解:原式1=335-+15=;(2)解:原式222444x xy y x xy=-+-+24y =.17.【答案】(1)7.5;<(2)甲公司,理由见解析(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)【解析】(1)由题意可得,787.52m +==,()()()()22222137748726757110s ⎡⎤=⨯⨯-+⨯-+⨯-+-=⎣⎦甲()()()()()()()222222221478721072679725777 4.210s ⎡⎤=⨯-+-+⨯-+⨯-+-+⨯-+-=⎣⎦乙,∴22s s <甲乙,故答案为:7.5;<;(2)∵配送速度得分甲和乙的得分相差不大,服务质量得分甲和乙的平均数相同,但是甲的方差明显小于乙的方差,∴甲更稳定,∴小丽应选择甲公司;(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)18.【答案】(1)见解析(2)见解析【解析】(1)解:如图所示,即为所求,(2)证明:∵AE 平分BAC ∠,∴BAE DAE ∠=∠,∵AB AD =,AE AE =,∴()SAS BAE DAE △≌△,∴DE BE =.19.【答案】(13(2)半径为2,圆心角为60︒(3)2333π-【解析】(1)解:将)3,1A 代入k y x=中,得13=,解得:3k =(2)解: 过点A 作OD 的垂线,垂足为G ,如下图:)3,1A ,1,3AG OG ∴==,22(3)12OA ∴=+=,∴半径为2;12AG OA = ,∴1sin 2AG AOG OG ∠==,30AOG ∴∠=︒,由菱形的性质知:30AOG COG ∠=∠=︒,60AOC ∴∠=︒,∴扇形AOC 的圆心角的度数:60︒;(3)解:2OD OG == ,1AOCD S AG OD ∴=⨯=⨯菱形221122663AOC S r πππ=⨯=⨯⨯= 扇形,如下图:由菱形OBEF 知,FHO BHO S S = ,322BHO kS == ,322FBO S ∴=⨯= ,2233FBO AOCD AOC S S S S ππ∴=+-=+= 阴影部分面积菱形扇形.20.【答案】树EG 的高度为9.1m【解析】解:由题意可知,90BAE MAF BAD ∠=∠=∠=︒, 1.8m FG =,则90EAF BAF BAF BAH ∠+∠=∠+∠=︒,∴EAF BAH ∠=∠,∵30cm AB =,20cm BH =,则2tan 3BH BAH AB ∠==,∴2tan tan 3EF EAF BAH AF ∠==∠=,∵11m AF =,则2113EF =,∴22m 3EF =,∴22 1.89.1m 3EG EF FG =+=+≈,答:树EG 的高度为9.1m .21.【答案】(1)活动一更合算(2)400元(3)当300400a ≤<或600800a ≤<时,活动二更合算【解析】(1)解:购买一件原价为450元的健身器材时,活动一需付款:4500.8360⨯=元,活动二需付款:45080370-=元,∴活动一更合算;(2)设这种健身器材的原价是x 元,则0.880x x =-,解得400x =,答:这种健身器材的原价是400元,(3)这种健身器材的原价为a 元,则活动一所需付款为:0.8a 元,活动二当0300a <<时,所需付款为:a 元,当300600a ≤<时,所需付款为:()80a -元,当600900a ≤<时,所需付款为:()160a -元,①当0300a <<时,0.8a a >,此时无论a 为何值,都是活动一更合算,不符合题意,②当300600a ≤<时,800.8a a -<,解得300400a ≤<,即:当300400a ≤<时,活动二更合算,③当600900a ≤<时,1600.8a a -<,解得600800a ≤<,即:当600800a ≤<时,活动二更合算,综上:当300400a ≤<或600800a ≤<时,活动二更合算.22.【答案】(1)()0,2.8P ,0.4a =-,(2)选择吊球,使球的落地点到C 点的距离更近【解析】(1)解:在一次函数0.4 2.8y x =-+,令0x =时, 2.8y =,∴()0,2.8P ,将()0,2.8P 代入()21 3.2y a x =-+中,可得: 3.2 2.8a +=,解得:0.4a =-;(2)∵3m OA =,2m CA =,∴5m OC =,选择扣球,则令0y =,即:0.4 2.80x -+=,解得:7x =,即:落地点距离点O 距离为7m ,∴落地点到C 点的距离为752m -=,选择吊球,则令0y =,即:()20.41 3.20x --+=,解得:1x =±(负值舍去),即:落地点距离点O 距离为()1m +,∴落地点到C 点的距离为()(514m -=-,∵42-<,∴选择吊球,使球的落地点到C 点的距离更近.23.【答案】(1)180︒,8.(2)①2βα=,理由见解析;②2sin m α(3)或【解析】(1)(1)∵ABC 关于y 轴对称的图形111A B C △,111A B C △与222A B C △关于x 轴对称,∴222A B C △与ABC 关于O 点中心对称,则222A B C △可以看作是ABC 绕点O 顺时针旋转得到的,旋转角的度数为180︒∵()1,1A -,∴12AA =,∵()4,0M ,13,A A 关于直线4x =对称,∴131248A A AA +=⨯=,即38AA =,333A B C △可以看作是ABC 向右平移得到的,平移距离为8个单位长度.故答案为:180︒,8.(2)①2βα=,理由如下,连接1AP ,由对称性可得,112PAB P AB P AD P AD ∠=∠∠=∠,,2112PAP PAB P AB P AD P AD ∠=∠+∠+∠+∠1122P AB P AD=∠+∠()112P AB P AD =∠+∠2BAD=∠∴2βα=,②连接113,PP PP 分别交,AB CD 于,E F 两点,过点D 作DG AB ⊥,交AB 于点G ,由对称性可知:113PE PE PF P F ==,且113PP AB PP CD ⊥⊥,,∵四边形ABCD 为平行四边形,∴AB CD∥∴13P P P ,,三点共线,∴311311222PP PE PE PF P F PE PF EF =+++=+=,∵113,,PP AB PP CD DG AB ⊥⊥⊥,∴1190PFD PEG DGE ∠=∠=∠=︒,∴四边形EFDG 是矩形,∴DG EF =,在Rt DAG △中,DAG α∠=,AD m =∵sin DG DAG DA∠=,∴sin sin DG AD DAG m α=⋅∠=,∴3222sin PP EF DG m α===(3)解:设AP x =,则12AP AP x ==,依题意,12PP AD ⊥,当23P P AD ∥时,如图所示,过点P 作1PQ AP ⊥于点Q ,∴12390PP P ∠=︒∵15PAB ∠=︒,60α=︒,∴1320P PAP AB ∠=︒∠=,1245DAP DAP ∠=∠=︒∴2190P AP ∠=︒,则122PP x =,在1APP 中,()111180752APP PAP ∠=︒-∠=︒,∴213180457560P PP ∠=︒-︒-︒=︒,则13230PP P ∠=︒,∴1321222PP P P ==在Rt APQ △中,30PAQ ∠=︒,则1122PQ AP x ==,2232AQ AP PQ x =-=,在1Rt PQP 中,1132PQ AP AQ x x =-=-,222211316223222PP PQ PQ x x x x ⎛⎫⎛⎫=+=-+-= ⎪ ⎪ ⎪⎝⎭⎝⎭,∴3113626322222PP PP PP x x x +=+=+=由(2)②可得32sin PP AD α=,∵23AD =∴332362PP =⨯=∴63262x +=,解得:326x =;如图所示,若23P P DC ∥,则13290PP P ∠=︒,∵21360P PP ∠=︒,则32130P P P ∠=︒,则13121222PP PP x ==,∵1622PP x =,36226222PP x x x =+=,∵36PP =,∴662x =,解得:x =,综上所述,AP 的长为或.。
河南中招数学试题及答案

河南中招数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是正确的等式?A. \(2x + 3 = 5x - 1\)B. \(3x - 2 = 2x + 3\)C. \(4x + 5 = 9x - 7\)D. \(5x + 6 = 10x - 2\)答案:B2. 计算下列哪个选项的结果为正数?A. \(-3 \times (-2)\)B. \(-4 \div 2\)C. \(-5 + (-6)\)D. \(-7 - 8\)答案:A3. 哪个选项表示的是一个锐角?A. \(30^\circ\)B. \(90^\circ\)C. \(120^\circ\)D. \(180^\circ\)答案:A4. 下列哪个图形的面积是最大的?A. 边长为3的正方形B. 半径为2的圆C. 长为4,宽为2的矩形D. 底为5,高为3的三角形答案:B5. 哪个选项是二次方程 \(x^2 - 5x + 6 = 0\) 的解?A. \(x = 2\)B. \(x = 3\)C. \(x = 6\)D. \(x = 9\)答案:A6. 下列哪个选项是不等式 \(2x - 3 > 5\) 的解?A. \(x > 4\)B. \(x < 4\)C. \(x > 2\)D. \(x < 2\)答案:A7. 哪个选项是函数 \(y = 2x + 3\) 的图像?A. 一条通过原点的直线B. 一条斜率为2的直线C. 一条斜率为-2的直线D. 一条与y轴交于点(0,3)的直线答案:D8. 哪个选项是等腰三角形的内角和?A. \(90^\circ\)B. \(180^\circ\)C. \(360^\circ\)D. \(540^\circ\)答案:B9. 下列哪个选项是正比例函数?A. \(y = 3x + 2\)B. \(y = \frac{1}{x}\)C. \(y = 5x\)D. \(y = x^2\)答案:C10. 哪个选项是反比例函数?A. \(y = 3x\)B. \(y = \frac{1}{x}\)C. \(y = x^2\)D. \(y = 2x + 3\)答案:B二、填空题(每题3分,共15分)11. 计算 \(\sqrt{25}\) 的结果是 ________。
河南省中考数学第23题压轴题(2010-2020)
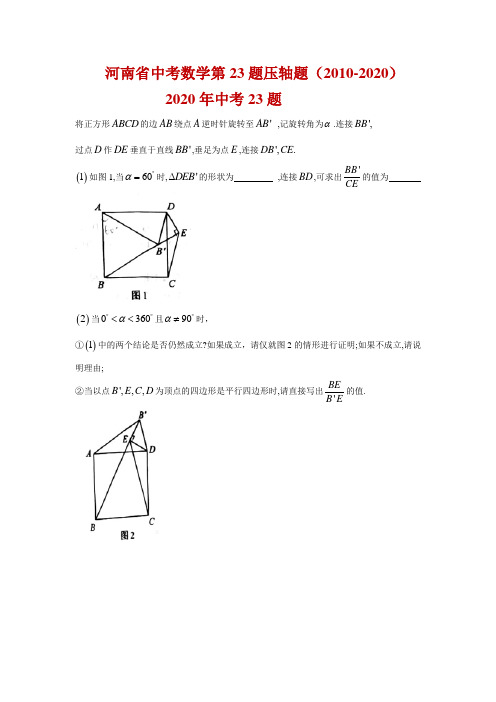
河南省中考数学第23题压轴题(2010-2020)2020年中考23题将正方形ABCD 的边AB 绕点A 逆时针旋转至'AB ,记旋转角为α.连接',BB 过点D 作DE 垂直于直线'BB ,垂足为点E ,连接',.DB CE()1如图1,当60α︒=时,'DEB ∆的形状为 ,连接BD ,可求出'BB CE的值为()2当0360α︒︒<<且90α︒≠时,①()1中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;②当以点',,,B E C D 为顶点的四边形是平行四边形时,请直接写出'BEB E的值.2019年中考23题如图,抛物线212y ax x c =++交x 轴于A ,B 两点,交y 轴于点C .直线122y x =--经过点A ,C . (1)求抛物线的解析式.()()()()22141241202162,00,42,00,42212-+=∴⎪⎩⎪⎨⎧-==∴⎩⎨⎧-==--↓→----→--=x x y c a c c a C A C A x y 抛物线(2)点P 是抛物线上一动点,过点P 作x 轴的垂线,交直线AC 于点M ,设点P 的横坐标为m .①当△PCM 是直角三角形时,求点P 的坐标;21P AC C C P y C P PC M y PM 的垂线交抛物线于点作处的作图方法是:过点点轴的平行线交抛物线于作处的作图方法是:过点处都可能是直角处不可能是直角轴,∥直角三角形的存在性:∴()()()10,62222141222212,22214122,0221222P x y x x y x y x y P x x C CP CP AC ∴⎪⎩⎪⎨⎧-=-+=-=--=--∴-+=--②作点B 关于点C 的对称点B′,则平面内存在直线l ,使点M ,B ,B′到该直线的距离都相等.当点P 在y 轴右侧的抛物线上,且与点B 不重合时,请直接写出直线l :y =kx +b 的解析式.(k ,b 可用含m 的式子表示)的中位线所在的直线这一问就是求△M BB 12018年中考23题如图,抛物线y =ax 2+6x +c 交x 轴于A ,B 两点,交y 轴于点C .直线y =x -5经过点B ,C .(1)求抛物线的解析式. ()()()()565,00,55,00,552-+-=→--→-=x x y C B C B x y 抛物线 (2)过点A 的直线交直线BC 于点M .①(两定两动)当AM ⊥BC 时,过抛物线上一动点P (不与点B ,C 重合),作直线AM 的平行线交直线BC 于点Q ,若以点A ,M ,P ,Q 为顶点的四边形是平行四边形,求点P 的横坐标;32118,P P AP PBC AP A BC P A BC AM AMPQ PQAM 个单位,就得到直线向下平移将交抛物线于点∥作过点直线的距离相等到∥∴⊥=∴ ()⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛+,2415,2415,4321P P P②连接AC ,当直线AM 与直线BC 的夹角等于∠ACB 的2倍时,请直接写出点M 的坐标.()()⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-====-+=+===67,623,617,6136223,6213621323222522212122221212M M CM CM m m m AM DM AD BC BD AD2017年中考23题如图,直线23y x c =-+与x 轴交于点A (3,0),与y 轴交于点B ,抛物线243y x bx c =-++经过点A ,B .(1)求点B 的坐标和抛物线的解析式;()()()2310342,00,32,02322++-=→→+-=→x x y B A B x y A 抛物线(2)M (m ,0)为x 轴上一动点,过点M 且垂直于x 轴的直线与直线AB 及抛物线分别交于点P ,N .①点M 在线段OA 上运动,若以B ,P ,N 为顶点的三角形与△APM 相似,求点M 的坐标;⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛∴⊥2,25,,811,,2211N N AB B B N N x B N N B P AB BP y x PN 的垂线交抛物线于点作处直角:过点点轴的平行线交抛物线于作处直角:过点处有直角处不能有直角上,在直线轴轴,即平行于M,N,P 三点的横坐标一样②点M 在x 轴上自由运动,若三个点M ,P ,N 中恰有一点是其它两点所连线段的中点(三点重合除外),则称M ,P ,N 三点为“共谐点”.请直接写出使得M ,P ,N 三点成为“共谐点”的m 的值.()()()()023223103432310342232:2232223103410,231034,232,2222=+-+++-⎪⎭⎫⎝⎛++-=+-⎪⎭⎫ ⎝⎛+-=++-⎪⎭⎫⎝⎛++-⎪⎭⎫⎝⎛+-m m m M m m m N m m m P m M m m m N m m P 是中点:是中点是中点:2016年中考23题如图1,直线43y x n =-+交x 轴于点A ,交y 轴于点C (0,4).抛物线223y x bx c=++经过点A ,交y 轴于点B (0,-2).点P 为抛物线上一个动点,过点P 作x 轴的垂线PD ,过点B 作BD ⊥PD 于点D ,连接PB ,设点P 的横坐标为m .(1)求抛物线的解析式;234322--=x x y (2)当△BDP 为等腰直角三角形时,求线段PD 的长;()()1271,27343234323432,2,2,023432,2222或或==∴=∴-=-=-∴=-==--⎪⎭⎫⎝⎛--PD BD m m m m m m m PDBD m m PD m BD m D B m m m P(2)如图2,将△BDP 绕点B 逆时针旋转,得到△BD ′P ′,且旋转角∠PBP ′=∠OAC ,当点P 的对应点P ′落在坐标轴上时,请直接写出点P 的坐标.()()mm PD m BD m D B m m m P 3432,2,2,023432,22-==--⎪⎭⎫⎝⎛-- 52543432532211==+⎪⎭⎫ ⎝⎛-==+m m m m OB I D HD ()()mm PD m BD m D B m m m P 3432,2,2,023432,22-==--⎪⎭⎫⎝⎛-- 8255334325422==⎪⎭⎫ ⎝⎛-=m m m m BIH P()()mm PD m BD m D B m m m P 3432,2,2,023432,22-=-=--⎪⎭⎫⎝⎛-- ()525434325325453223333-==--⎪⎭⎫ ⎝⎛-=-=-m m m m ID D P HI HD图2DD'P'CO y ABxP2015年中考23题如图,边长为8的正方形OABC 的两边在坐标轴上,以点C 为顶点的抛物线经过点A ,点P 是抛物线上点A ,C 间的一个动点(含端点),过点P 作PF ⊥BC 于点F .点D ,E 的坐标分别为(0,6),(-4,0),连接PD ,PE ,DE .(1)请直接写出抛物线的解析式.8812+-=x y(2)小明探究点P 的位置发现:当点P 与点A 或点C 重合时,PD 与PF的差为定值.进而猜想:对于任意一点P ,PD 与PF 的差为定值.请你判断该猜想是否正确,并说明理由.()猜想正确22812812816881,881,0,818,881,2222222222222=-∴+=∴⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛-+=+=-+-==⎪⎭⎫ ⎝⎛+-=⎪⎭⎫⎝⎛+-PF PD m PD m m m DH PH PD m DH m PH m H m PF m F m m P(3)小明进一步探究得出结论:若将“使△PDE 的面积为整数”的点P 记作“好点”,则存在多个“好点”,且使△PDE 的周长最小的点P 也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE 的周长最小时“好点”的坐标.()081364143412142238122381623,881,62322222≤≤-++-=+--=⨯⨯⎪⎭⎫⎝⎛+--=+--=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+-+=m m m m m m S m m PM m m M m m P x y PED DE △个点中周长最小的点在这时,有两个点但是面积是个面积整数共有,到面积从11121013,12,11,910,8,7,6,5,41342014年中考23题如图,抛物线2y x bx c =-++与x 轴交于A (-1,0),B (5,0)两点,直线334y x =-+与y 轴交于点C ,与x 轴交于点D .点P 是x 轴上方的抛物线上一动点,过点P作PF ⊥x 轴于点F ,交直线CD 于点E .设点P 的横坐标为m .(1)求抛物线的解析式;542++-=x x y (2)若PE =5EF ,求m 的值;()()2691,2343524193432419510,,343,54,222+=∴+-=++-+-=++-=-⎪⎭⎫⎝⎛+-++-m m m m m EF m m PE m m F m m E m m m P ()()269134352419204213205234434352419222+=∴⎪⎭⎫⎝⎛+--=++-==--=+-⎪⎭⎫ ⎝⎛+-=++-m m m m m m m m m m m m(3)若点E'是点E 关于直线PC 的对称点,是否存在点P ,使点E'落在y 轴上?若存在,请直接写出相应的点P 的坐标;若不存在,请说明理由.P 点在y 轴和直线CD 的角平分线上()4,21433524194335343,,3,0241922-=∴=++-∴=⎪⎭⎫⎝⎛+-++-==m m m m mCE m m E C m m PE CE PE()()()()5,113,3112,1135432323215,414324411舍掉,超过了知:互相垂直根据邻补角的角平分线)知由(+--∴⎩⎨⎧++-=+-=+-=+=P P x x y x y x y x y P CP CP CP2013年中考23题如图,抛物线y =-x 2+bx +c 与直线221+=x y 交于C ,D 两点,其中点C 在y 轴上,点D 的坐标为)273(,.点P 是y 轴右侧的抛物线上一动点,过点P 作PE ⊥x轴于点E ,交CD 于点F .(1)求抛物线的解析式.()25.32,02++-=x x y C(2)(两定两动)若点P 的横坐标为m ,当m 为何值时,以O ,C ,P ,F 为顶点的四边形是平行四边形?请说明理由.()()2173,2,1232325.0,25.3,222-=∴=+-∴=+-=+++-m m m CO PF OC m m PF m m F m m m P ∥(3)若存在点P ,使∠PCF =45°,请直接写出....相应的点P 的坐标.由此可知P应该有两个点212532525221111=∴=+-∴=∴==∴==∴m m m m m F P m CF FG CG G P FG G P FG P CFH ∵∽△△()⎪⎭⎫ ⎝⎛∴=∴⎪⎪⎩⎪⎪⎨⎧++-=+-=+-=+=⎪⎭⎫⎝⎛1813,6236232272312312327,211221221P x x x y x y x y x y P CP CP CP 得到互相垂直由于邻补角的角平分线得到知由2012年中考23题如图,在平面直角坐标系中,直线112y x =+与抛物线23y ax bx =+-交于A ,B 两点,点A 在x 轴上,点B 的纵坐标为3.点P 是直线AB 下方的抛物线上一动点(不与点A ,B 重合),过点P 做x 轴的垂线交直线AB 于点C ,作PD ⊥AB 于点D .(1)求a ,b 及sin ACP ∠的值;()()()()3212121,213,40,23,40,21212--=-==→--→+=x x y b a B A B A x y 抛物线55252sin sin 51,2)1,0==∠=∠=∴==AEO ACP AE EO AO E E y AB 为(,则点轴交于点与设直线(2)设点P 的横坐标为m .①用含m 的代数式表示线段PD 的长,并求出线段PD 长的最大值;PC PD PC PD AE AO EAO DPC AE EO AO 55255252cos cos 51,2=∴====∠=∠=∴== 5594121552,12121421552421121,,32121,222=⎪⎭⎫ ⎝⎛++-=⎪⎭⎫ ⎝⎛-⨯-=⎪⎭⎫⎝⎛++-=∴++-=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛--为最大时,当PD m m m PD m m PC m m C m m m P②(铅锤法求面积)连接PB ,线段PC 把△PDB 分成两个三角形,是否存在合适的m 的值,使这两个三角形的面积之比为9:10?若存在,直接写出m 的值;若不存在,说明理由.以PC 为底,面积之比,也就是底之比,⎪⎭⎫⎝⎛++-==⎪⎭⎫ ⎝⎛++-∴∠==∠-===4215251421552sin sin 491010922m m DF m m DF EAO PD DF DPC mBG BG DF BG DF 或 932,2591052109525244215242152491010922==+=+∴+=-⎪⎭⎫ ⎝⎛++-=⎪⎭⎫ ⎝⎛++-=-===m m m m m m m BG DF m m DF mBG BG DF BG DF 或或2011年中考23题如图,在平面直角坐标系中,直线3342y x =-与抛物线214y x bx c =-++交于A ,B 两点,点A 在x 轴上,点B 的横坐标为-8.(1)求该抛物线的解析式.2543412+--=x x y(2)点P 是直线AB 上方的抛物线上一动点(不与点A ,B 重合),过点P 作x 轴的垂线,垂足为C ,交直线AB 于点D ,作PE ⊥AB 于点E . ①设△PDE 的周长为l ,点P 的横坐标为x ,求l 关于x 的函数关系式,并求出l 的最大值;⎪⎭⎫ ⎝⎛+--==+--=⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛+--42341512512423412343,254341,222x x PD l x x PD x x D x x x P 15341223-最大为最大时,当l l x -=⎪⎭⎫ ⎝⎛--= ②连接PA ,以PA 为边作图示一侧的正方形APFG .随着点P 的运动,正方形的大小、位置也随之改变.当顶点F 或G 恰好落在y 轴上时,直接写出对应的点P 的坐标.双垂直全等的横纵坐标一样即P PMPC =22的纵坐标是即P OA PC ==⎪⎪⎭⎫⎝⎛+-+-⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛+-2897,2897,2,2173,2,2173P2010年中考23题在平面直角坐标系中,已知抛物线经过A (-4,0)B (0,-4)C (2,0)(1)求抛物线的解析式4212-+=x x y(2)(面积的铅锤法)若点M 为第三象限内抛物线上一个动点,点M 的横坐标为m ,△AMB 的面积为S ,求S 关于m 的函数关系式,并求出S 的最大值()()42124-42142212214,4421,2222时面积最大,最大为当△-=--=--=⨯⨯⎪⎭⎫⎝⎛--=+=----=⎪⎭⎫ ⎝⎛-+m mm m m S mm MD m m D x y m m m M ABM B A(3)(两定两动,考虑OB 是边和对角线)若点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P,Q,B,O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标()4,522,52244221,421,422---+-==-+=-⎪⎭⎫ ⎝⎛-+==m m m PQ m m Q m m m P PQ OB PQ OB 时∥当()()()4442104,0,0,0,421,22=∴⎪⎩⎪⎨⎧-=--+=+∴--⎪⎭⎫ ⎝⎛-+n n m m n m B O n n Q m m m P OB 是对角线时当。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008-2013年河南省中考数学第23题汇总(2008年)23.(12分)如图,直线y=434+-x 和x 轴、y 轴的交点分别为B ,C 。
点A 的坐标是(-2,0)(1) 试说明△ABC 是等腰三角形;(2) 动点M 从点A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度,当其中一个动点到达终点时,它们都停止运动,设点运动t 秒时,△MON 的面积为s 。
① 求s 与t 的函数关系式;② 当点M 在线段OB 上运动时,是否存在s=4的情形?若存在,求出对应的t 值;若不存在,说明理由;③ 在运动过程中,当△MON 为直角三角形时,求t 的值。
(2009年)23.(11分)如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (4,0)、C (8,0)、D (8,8).抛物线y=ax 2+bx 过A 、C 两点.(1)直接写出点A 的坐标,并求出抛物线的解析式;(2)动点P 从点A 出发.沿线段AB 向终点B 运动,同时点Q 从点C 出发,沿线段CD 向终点D 运动.速度均为每秒1个单位长度,运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E①过点E 作EF ⊥AD 于点F ,交抛物线于点G.当t 为何值时,线段EG 最长?②连接EQ .在点P 、Q 运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值.(2010年)23.(11分)在平面直角坐标系中,已知抛物线经过A )0,4(-,B )4,0(-,C )0,2(三点.(1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值.(3)若点P 是抛物线上的动点,点Q 是直线x y -=上的动点,判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.(2011年)23. (11分)如图,在平面直角坐标系中,直线3342y x =-与抛物线214y x bx c =-++交于A 、B 两点,点A 在x 轴上,点B 的横坐标为-8.(1)求该抛物线的解析式; (2)点P 是直线AB 上方..的抛物线上一动点(不与点A 、B 重合),过点P 作x 轴的垂线,垂足为C ,交直线AB 于点D ,作PE ⊥AB 于点E .①设△PDE 的周长为l ,点P 的横坐标为x ,求l 关于x 的函数关系式,并求出l 的最大值;②连接P A ,以P A 为边作图示一侧的正方形APFG .随着点P 的运动,正方形的大小、位置也随之改变.当顶点F 或G 恰好落在y 轴上时,直接写出对应的点P 的坐标.2012(2013年)23.(11分)如图,抛物线2y x bx c =-++与直线122y x =+交于C 、D 两点,其中点C 在y 轴上,点D 的坐标为(3,72),点P 是y 轴右侧的抛物线上的一动点,过点P 作PE ⊥x 轴于点E ,交CD 于点F 。
(1)求抛物线的解析式;(2)若点P 的横坐标为m ,当m 为何值时, 以O 、C 、P 、F 为顶点的四边形是平形四边形? 请说明理由.(3)若存在点P ,使∠PCF=45°,请直接写... 出.相应的点P 的坐标. 答案 2008年解:(1)将y=0代入y=434+-x ,得到x=3,∴点B 的坐标为(3,0); 将x=0,代入y=434+-x ,得到y=4, ∴点C 的坐标为(0,4) …………2分 在Rt △OBC 中,∵OC =4,OB =3,∴BC =5。
又A (-2,0),∴AB =5,∴AB =BC ,∴△ABC 是等腰三角形。
………………4分 (2)∵AB=BC=5,故点M 、N 同时开始运动,同时停止运动。
过点N 作ND ⊥x 轴于D , 则ND =NB ●sin ∠OBC =t 54, ① 当0<t <2时(如图甲)OM =2-t,∴s=ND OM •21=t t 54)2(21•- =t t 54522+- ……………………7分当2<t ≤5时(如图乙),OM =t -2,∴s=ND OM •21=t t 54)2(21•- =t t 54522- …………………………8分 (注:若将t 的取值范围分别写为0≤t ≤2和2≤t ≤5,不扣分) ② 存在s =4的情形。
当s =4时,t t 54522-=4 解得t 1=1+11, t 2=1-11秒。
…………………………10分 ③ 当MN ⊥x 轴时,△MON 为直角三角形,MB =NB ●COS ∠MBN =t 53,又MB =5-t.∴t 53=5-t, ∴t=825 ………………11分 当点M ,N 分别运动到点B ,C 时,△MON 为直角三角形,t=5. 故△MON 为直角三角形时,t=825秒或t =5秒 …………12分 2009年23.(1)点A 的坐标为(4,8) …………………1分 将A (4,8)、C (8,0)两点坐标分别代入y=ax 2+bx8=16a +4b得0=64a +8b解 得a =-12,b =4 ∴抛物线的解析式为:y =-12x 2+4x …………………3分(2)①在Rt △APE 和Rt △ABC 中,tan ∠PAE =PE AP =BC AB ,即PE AP =48∴PE =12AP =12t .PB=8-t .∴点E的坐标为(4+12t ,8-t ).∴点G 的纵坐标为:-12(4+12t )2+4(4+12t )=-18t 2+8. …………………5分∴EG=-18t 2+8-(8-t )=-18t 2+t .∵-18<0,∴当t =4时,线段EG 最长为2. …………………7分②共有三个时刻. …………………8分t 1=163, t 2=4013,t 3. …………………11分2010年2011年23.(1)对于3342y x =-,当y =0,x =2.当x =-8时,y =-152. ∴A 点坐标为(2,0),B 点坐标为15(8,).2--…………………………………………1分由抛物线214y x bx c =-++经过A 、B 两点,得012,15168.2b c b c =-++⎧⎪⎨-=--+⎪⎩ 解得235135..42442b c y x x =-=∴=--+,…………………………………………3分 (2)①设直线3342y x =-与y 轴交于点M当x =0时,y =32-. ∴OM =32.∵点A 的坐标为(2,0),∴OA =2.∴AM 225.2OA OM +=……………………4分∵OM :OA :AM =3∶4:5.由题意得,∠PDE =∠OMA ,∠AOM =∠PED =90°,∴△AOM ~△PED .∴DE :PE :PD =3∶4:5.…………………………………………………………………5分 ∵点P 是直线AB 上方的抛物线上一动点, ∴PD =y P -y D213533()()44242x x x =--+--=213444x x --+.………………………………………………………………………6分∴21213(4)542l x x =--+231848.555x x =--+…………………………………………………………………7分23(3)15.315.5l x x l ∴=-++∴=-=最大时,……………………………………8分②满足题意的点P 有三个,分别是122),2),P P3P ……………………………………………………………11分 【解法提示】当点G 落在y 轴上时,由△ACP ≌△GOA 得PC =AO =2,即21352442x x --+=,解得32x -±=,所以1233(2),(,2).22P P ---当点F 落在y 轴上时,同法可得377()22P -+-+,4P (舍去). 2012年2013年 23.(11分)(1)∵直线122y x =+经过C ,∴C 点坐标为(0,2) ∵抛物线2y x bx c =-++经过C (0,2)和D (3,72)∴227332c b c =⎧⎪⎨=++⎪⎩,∴272c b =⎧⎪⎨=⎪⎩,∴抛物线的解析式为2722y x x =-++ (2)∵P 点横坐标为m ,∴P (m ,2722m m -++),F (m ,122m +) ∵PF ∥CO ,∴ 当PF=CO 时,以O 、C 、P 、F 为定点的四边形为平行四边形 ①当03m <<时,22712(2)322PF m m m m m =-++-+=-+ ∴232m m -+=,解得:11m =,22m =, 即当12m =或时,OCPF 为平行四边形.②当3m ≥时,2217(2)(2)322PF m m m m m =+--++=- ∴232m m -=,解得:1317m +=,2317m -=(舍去) 即当3172m +=时,四边形OCPF 为平行四边形. (3)点P 的坐标为(12,72)或(236,1318) ①当03m <<时,点P 在CD 上方且∠PCF=45°, 作PM ⊥CD 于M ,CN ⊥PF 于N ,则: △PMF ∽△CNF ,从而212PM CN mMF FN m ===,∴PM=CM=2CF ,∴5555=52CN =52m 又∵PF=23m m -+,∴2532m m m -+=, 解得:112m =,20m =(舍去),∴P 的坐标为(12,72) ②当3m >时,点P 在CD 下方且∠FCP=45°,作PM ⊥CD 于M ,CN ⊥PF 于N ,则: △PMF ∽△CNF ,从而212MP CN mFM FN m===,∴5FP ∵∠MCP=45°,∴CM=MP=55FP ,∴FC=FM+MC=355FP^.又∵FC=2=2m , ∴有52FP m =,56FP m = 又∵2217(2)(2)322FP m m m m m =+--++=-,∴2536m m m =- 解得:1236m =,20m =(舍去)∴P 的坐标为(236,1318)。
