第二节 菲涅耳衍射(圆孔和圆屏)
§5-10-11圆孔和圆屏的菲涅耳衍射§7-1偏振光和自然光

则:
~ ~ E1 En n为奇数 2 2 ~ E ~ ~ E n 1 E1 ~ E n n为偶数 2 2
§5-10圆孔和圆屏的菲涅耳衍射
~ 当n足够大时, En ~ ~ 2 2 故 ~ E1 En
~ E n 1
~ En
E
2
2
当n为奇数时取“+”号,n为偶数时取“- ” 号 ~ ~ ~ ~ E E 当n不很大时(即孔径不大时) ~ E1 E n E n为奇数 2 2 可以认为 ~
§5-10圆孔和圆屏的菲涅耳衍射
此为处理次波相干迭加的一种简化方法,菲
涅耳衍射公式要求对波前作无限分割,半波 带法则用较粗糙的分割来代替,从而使菲涅 耳衍射公式化为有限项求和,此方法虽不够 精确,但可较方便地得出衍射图样的某些定 Z +3λ/2 性特征,故为人们所喜用。 如图所示,平面波垂直入射孔径 c Z 为了决定波面在点产生的复振幅 ∑ M k 的大小,以这样的方法来作图: 3 j 以为中心,以
§5-10圆孔和圆屏的菲涅耳衍射
作业:5.32、5.33、5.34、 5.35 、 5.36、5.37
第七章: 光的偏振与晶体光学基础
第七章:光的偏振与晶体光学基础
电磁波是一种矢量波,大量的干涉和衍射 问题可以用标量近似处理。
然而本章所要讨论的偏振和双折射。却是 矢量波所特有的现象。不能再按标量处理。 历史上,双折射的发现。曾经是光的横波 (矢量波)特性的一个有力佐证。
1 n 1
故
E
第二章光的衍射

用振动矢量叠加法
K为奇数
K为偶数
说明:
1.圆孔中露出半波带数目(k不是很大)
K为奇数,
A
=
1 2
(a1
+
ak
)
≈
a1
P为亮点
K为偶数,
A
=
1 2
(a1
− ak )
≈
0
P为暗点
∞ 2.k
无障碍物(自由传播)
ak → 0
AP
=
a1 2
IP
=
a12 4
三. 计算露出半波带数目k
Rh2k = rk2 − (r0 + h)2 = rk2 − r02 − 2r0h − h2 ≈ rk2 − r02 − 2r0h
把每一个半波带进一步划分,分割为m个更窄的环 带!如何来分析?
2、观察点P不在轴线上时,振幅如何计算?
§2.3 、菲涅耳衍射(圆孔和圆屏)
一. 圆孔衍射 圆孔衍射的特点
(1)、Ak 取决于 k ,当 λ, R, Rhk一定时,k 取决于 r0 ,
即P的点位置 ⎩⎨⎧rr00小大,,kk大小
k 偶数时轴上点是暗点,奇数时是亮点。
6)、缺点:(1)f ′ 与 λ 有关,色差很大。激光
的出现使波片的应用成为可能;
(2)除
f′
外,尚有1 3f Nhomakorabea′,
1 5
f
′L
多个焦距的存
在,对给定物点,波片可给出多个象点。
菲涅耳直边衍射的矢量分析:
四、直线传播和衍射的关系
即使是直线传播,也要按惠——菲原理的方式进行,此 原理主要指同一波面上所有点所发次波在某一给定观察点 的相干迭加。衍射现象是光的波动特性最基本的表现,直 线传播不过是衍射现象的极限表现而已。
菲涅尔圆孔衍射和圆屏衍射修正版课件

象的基本原理和特点。
02
重点与难点解析
课程重点讲解了衍射现象的数学模型和物理机制,以及如何通过实验手
段观察和验证衍射现象。同时,对于学习过程中的难点和疑点,课程提
供了详细的解析和解答。
03
课程特色与亮点
本课程采用理论与实践相结合的方式,既注重理论推导,又强调实验操
作。通过修正版课件,学习者可以更加直观地理解衍射现象,提高学习
圆屏衍射模型
圆屏衍射模型通常采用菲涅尔-基尔霍夫衍射积分 公式,该公式描述了光波通过圆孔或圆屏后在远 场产生的衍射强度分布。
圆屏衍射模型需要考虑光源、圆孔或圆屏、接收 屏幕等多个因素,通过积分公式计算出衍射光强 的分布情况。
衍射公式推 导
菲涅尔-基尔霍夫衍射积分公式是圆屏衍射模型的核心公式,其推导过程涉及到波动光学的基本 原理和数学运算。
更新与完善课程内容
随着科学技术的不断发展,菲涅尔圆孔衍射和圆屏衍射的相关研究也在不断深入。为了使 课程内容更加前沿和有深度,未来课程需要对内容进行定期更新和完善,以反映最新的研 究进展和成果。
清晰度
通过增加图解和实例分析,使知识 点更加清晰易懂。
实用性
修正后的课件更贴近实际,有助于 学生将理论知识与实验观察相结合。
课程实践与实验
实验设备与材料
光源
激光器或单色光源
菲涅尔圆孔
若干个不同直径的圆孔
圆屏
不同半径的圆屏
屏幕
用于接收衍射图像的白色 屏幕
测量工具
尺子、测角仪等
实验步骤与操作
1. 准备实验设备
效果。
对未来课程的展望
增加应用案例分析
在未来的课程中,可以增加更多关于菲涅尔圆孔衍射和圆屏衍射在实际应用中的案例分析, 使学习者更好地理解这两种衍射现象的应用价值。
菲涅耳圆孔和圆屏衍射 33菲涅耳圆孔和圆屏衍射

a1 E P0 2
光强为第一个半波带产生的光强的 一半,光强不受圆孔大小的影响。 与几何光学结论一致。几何光学是 波动光学的极限。
P0 的光强是不存在衍 4)圆孔很小,如只包含一个半波带,则 圆孔很小,如只包含一个半波带,则P0 4倍!典型的衍射效应。 射屏时的4 射屏时的
菲涅耳衍射 二、圆屏的 圆屏的菲涅耳衍射
rj z j z 2 2
2
j jz 1 4z
1 2
Aj 1 cos aj C zj 2
由于 z
∴
rj
jz
Aj rj2 rj21 z
即近似地各半波带面积相等 则
a1 a2 a3
菲涅耳波带片不仅给惠更斯-菲涅耳原理提供了使
人信服的论据,而且在微波、红外和紫外线、X射线的 成像技术方面开辟了新的方向,并在近代全息照相术 等方面也获得了重要的应用。
P0点产生的复振幅叠加 P0 的复振幅 = ∑上所有半波带发出的子波在 上在P0点产生的复振幅:
Aj 1 cos aj C zj 2 Aj :半波带面积;
z j :半波带到P0点平均距离
C:比例常数
下面来比较 a1, a 2 , a 3 各振幅的大小
点光源通过圆屏时也将发生衍射现象。光波传播 时被圆屏遮了k个半波带。于是从第k+1个半波带 开始,所有其余的波带所发的子波都能到达P点。 不管圆屏的大小和位置怎样,圆屏几何影子的中心永远有光。 但圆屏的面积较小时,被遮蔽的带的数目k就少,因而 ak 1 就 大,到达P点的光就强。
如果圆屏足够小,只遮住中心带的一小部分,则光看起来可 完全绕过它,圆屏影子中心有亮点。
a1 a2 a3
菲涅耳圆孔和圆屏衍射ok

05
06
4. 使用测量工具测量衍射图案的直径、形 状等参数。
实验结果与分析
结果
通过实验可以观察到菲涅耳圆孔衍射图案的变化,如中央亮斑的直径变化、衍射 条纹的形状和数量等。
分析
通过对实验结果的分析,可以了解光波的波动性质和衍射规律,验证光的波动理 论。
04
菲涅耳圆孔和圆屏衍射的 应用
在光学领域的应用
菲涅耳圆孔和圆屏衍 射
目录
• 引言 • 菲涅耳圆孔衍射 • 菲涅耳圆屏衍射 • 菲涅耳圆孔和圆屏衍射的应用 • 结论
01
引言
衍射现象简介
衍射是光波遇到障碍物时,偏离 直线方向传播的现象。
衍射现象是光的波动性的一种表 现,与光的干涉现象密切相关。
衍射可以分为菲涅耳衍射和夫琅 禾费衍射,其中菲涅耳衍射是指 光波遇到边缘或狭缝时发生的衍
05
结论
对菲涅耳圆孔和圆屏衍射的总结
01
菲涅耳圆孔衍射
当光波通过一个小的圆形孔洞时,会在孔洞的周围产生衍射现象。衍射
光斑的形状和大小取决于孔洞的大小和波长。随着孔洞的增大,光斑的
直径也会增大,但形状保持圆形。
02
菲涅耳圆屏衍射
当光波遇到一个大的圆形障碍物时,同样会产生衍射现象。与菲涅耳圆
孔衍射不同的是,菲涅耳圆屏衍射的光斑形状为椭圆形,且长轴方向与
障碍物的法线方向一致。
03
应用领域
菲涅耳圆孔和圆屏衍射在光学、物理、工程等领域有着广泛的应用。例
如,在光学仪器制造、光通信、光学检测等领域,人们常常需要理解和
掌深入研究其他形状的衍射现象
除了圆形孔洞和障碍物外,还有许多其他形状的物体也会产生衍射现象。未来研究可以进 一步探索这些形状的衍射规律和特性,以丰富和完善衍射理论。
2019年大学光学经典课件L10圆孔衍射和圆屏衍射.ppt

____
0
光强为自由传播时的两倍
4、菲涅耳波带片
1)定义:将偶数个或奇数个半波带遮挡住,
就形成菲涅耳波带片。
2)例题:
波带片的孔径内有20个半波带,遮挡偶数个 半波带,求轴上场点P0处的光强? 解:
A ' A1 A3 A5 A19 10 A1 20 A0
I ' A' 400 A0 400I 0
sin sin ikr0 , E (0, 0) E 0 ab E ( P) E 0 e sin 2 sin 2 I ( P) I 0 ( ) ( ) 其中:I (ab) 2 0
ˆ ( x cos ' y cos ' ) r r r0 OQ r 0 1 ' , 2 ' 2 2
r ( x sin 1 y sin 2 )
i E ( P) r0
E (Q)e
光 源 衍 射 屏
衍 射 图 样
不同宽度的单缝衍射图样
单缝衍射
2.单缝衍射光强分布
L a sin
2
a sin
1)用矢量图解法计算光强分布
(1)分割成 m个窄波带 再求出每一个窄带的复振幅
E1 ( P ) A( P )e
E 2 (P ) A( P )e
AB R 2
a sin =2
B
D ____ sin 故: A AB AB
A
A0
0 时,
sin
1
A0 AB
sin
菲涅尔圆孔衍射和圆屏衍射(修正版)讲义34页PPT

▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
34
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
菲涅尔圆孔衍射和圆屏衍射(修正版) 讲义
16、人民应该为法律而战斗,就像为 了城墙 而战斗 一样。 ——赫 拉克利 特 17、人类对于不公正的行为加以指责 ,并非 因为他 们愿意 做出这 种行为 ,而是 惟恐自 己会成 为这种 行为的 牺牲者 。—— 柏拉图 18、制定法律法令,就是为了不让强 者做什 么事都 横行霸 道。— —奥维 德 19、法律是社会的习惯和思想的结晶 。—— 托·伍·威尔逊 20、人们嘴上挂着的法律,其真实含 义是财 富。— —爱献 生
8菲涅耳圆孔和圆屏衍射ok

S
R
bn
b
2
p
zs
zp
2 nb 2bh r (b h) ; rn b n 2 nb 2 2 2 2 h R (R h) rn (b h) 2( R b) 2 1 1 n R b
只让奇(偶)序数半波带透过
(1)n1 An ( p0 )
一块波带片的孔径内20个半波带,透奇挡偶,轴上场点 的强度是自由传播时的多少倍 ??
A A1 A3 A5
A19 10 A1 20 A
自由传播时的振 幅是第一个半波 带振幅的一半
点光源S发出的光经过菲涅耳波带片可在适当的位置P 形成很强的亮点
E1 ( p0 ) A1 ( p0 )ei1 E2 ( p0 ) A2 ( p0 )ei (1 )
E3 ( p0 ) A3 ( p0 )e
i (1 2 )
轴上 p0点的复振幅
E ( p0 )
k 1
n
Ek ( p0 )
A1 ( p0 ) A2 ( p0 ) A3 ( p0 ) (1)n 1 An ( p0 )
A1
边缘与中心光程差为/4 相位差为/2
C
B
振动曲线应取OB一段
A
O
AOB 2 A
光强为自由传播时的两倍
利用该振动曲线图可以较方便的求出任何半径的圆孔 和圆屏在轴上产生的振幅和光强
(a) b=0.5m
(b) b=1.0m
(c) b=1.5m
(d) b=2.0m
(e) b=2.5m
正方形孔的菲涅耳衍射仿真图样(不同观察平面上)
第二章 光的衍射 第二节 菲涅尔衍射课件

③. 圆孔半径固定:
2 A a I A 2 4A I 1 1 1
④. 圆孔足够大:
Rhk R、r0
ak 0 2 a1 Ak 2
几何光学
二、圆屏衍射 1.装置: 2.结果:P点永远是亮点 3.分析:
A ak 1 ak 2 ak 3 ak 4
Jason Ren Physics
小
一、圆孔衍射
结
Jason Ren Physics
) Rhk 2 ( R 1 r 1 k ( 0 ) R R r0 r0
a k 1 2
第 二 章 光 的 衍 射
二、圆屏衍射
A ak 1 ak 2 ak 3 ak 4
三、菲涅耳波带片
1 1 1 2 Rhk R r0 ( ) k
4.讨论:
a k 1 2
第 二 章 光 的 衍 射
a k 1 const 圆屏几何中心永远是亮的; ①. 2
②. 屏中有亮点,没有其他影子; ③. 圆屏使光源成实像;
三、菲涅耳波带片
Jason Ren Physics
a2 k 1 奇数 1.波带片:合振幅:Ak a1 a3 a5 k
Jason Ren Physics
h r0
第 二 章 光 的 衍 射
rk r0 (k / 2)
2 2 2 2 r rk2 r02 k [r ( k / 2 )] r k / 4 0 0 0
k
r0
Rhk 2 k r0 2r0h
2 2 2 2 22 2 2 2 r 2 r h h r ( r h ) R R h 2 Rh R2 R ( R h ) 00 0 k hk
第二节菲涅耳衍射(圆孔和圆屏)详解

−
r0 kλr0
(R + r0 )
=
kλr0 (1 −
r0 (R +
) r0 )
=
k
r0 R R + r0
λ
k = ρ 2 (R + r0 ) = ρ 2 ( 1 + 1 )
λr0 R
λ r0 R
• 如果用平行光照射圆孔, R → ∞则
ρ k = kλr0
• P点合振幅的大小取决于露出的带数k,而当波长及圆孔的位置和大小 都给定时,k取决于观察点P的位置,k为奇数相对应的那些点,合振 幅Ak较大,与k为偶数相对应的那些P点,Ak较小。这个结果很容易 用实验来证实。
图2-7
• 我们讨论一下点光源发出的光通过圆屏边缘时的衍射现象。0为点光 源,光路上有一不透明的圆屏,现在先讨论P点的振幅。设圆屏遮蔽 了开始的k个带。于是从第k+1个带开始,所有其余的带发的次波都能 到达P点。把所有这些带的次波叠加起来,可得P点的合振幅为:
A = a k +1 2
• 即不论圆屏的大小和位置怎样,圆屏几何影子的中心永远有光。不过
实了菲涅耳的理论的正确性。
三、菲涅耳波带片
根据以上的讨论,可以看到圆屏的作用能使点光源造成实象,可以设
想它和一块汇聚透镜相当。另一方面,从菲涅耳半波带的特征来看,
对于通过波带中心而与波带面垂直的轴上一点来说,圆孔露出半波带
的数目k可为奇数或偶数。如果设想制造这样一种屏,使它对于所考
查的点只让奇数半波带或只让偶数半波带透光。这样在考查点处振动
a 圆屏的面积越小时,被遮蔽的带的数目就越小,因而 k+1就越大,到
达P点的光就越强。变更圆屏和光源之间或圆屏和P之间的距离时,k 也将因之改变,因而也将影响P点的光强。
第二章光的衍射(菲涅耳圆孔衍射)PPT课件
.
1
光学 §2.2 菲涅耳半波带 菲涅耳衍射
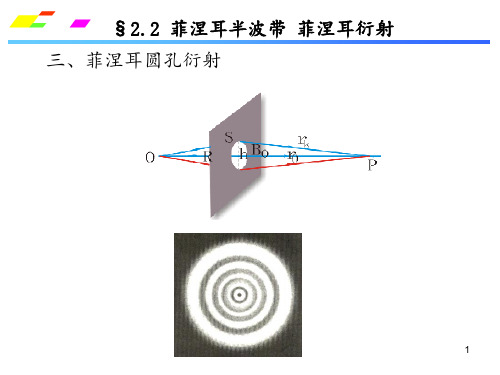
将一束光(例激光)投射在一个圆孔上,并在距孔1m -2m处放置一接收屏,可观察衍射图样。
根据前面的讨论,对圆孔后光强起作用的半波带数 量有k个。
Ak 12a1ak
Ak 12a1ak
O
R
Bk
Rh
k rk
置,我们可以看到,光 屏的中心点会有时明时
O
暗地变化。
l R
sB k
k
Rh
B
h
0
rk
r0
P
.
6
k Rh2 ( 1 1 )
r0 R
R
2 h
Rh
Rh Rh
Rh
.
7
• P点的合振幅的大小取决于露出的波带数, 而波 带数又取决于圆孔的位置和半径.改变圆孔的 位置和半径,给定P点的光强也将发生变化.
• 如果对于P点露出的波带数为整数,为奇数相对 应的那些点,合振幅较大;偶数相对应的那些 点,合振幅较小.
• 如果带数不是整数,那么合振幅介乎上述最大 值和最小值之间.
• 结论:当置于P处的屏沿着圆孔的对称轴线移动 时,将看合振幅到屏上的光强不断地变化.
.
8
四、菲涅耳圆屏衍射
当点光源发出的光通过圆屏(盘)衍射时,由于圆屏不 透明,被圆屏挡住部分的波面(也即有k个半波带发 出的次波不起作用)对轴线上p点的光强将没有贡献。
• 光传播 次波叠加 衍射
• 无论光是直线传播还是具有明显的衍射现 象,都遵循惠更斯----菲涅尔原理。
.
15
例题:一块波带片的孔径内有20个半波带,其中第1、 3、5、…、19等10个奇数带露出。第2、4、6、…、20 等10个偶数带遮蔽,试分析轴上场点的光强是自由传 播时光强的多少倍?
菲涅耳衍射圆孔圆屏

点光源入射衍射屏,自由光场按几何光学 原理成象,除象点之外,处处振动为零。
~ U0 ( P) 0
~ ~ U a (P) U b (P)
I a ( P) I b ( P)
细丝与狭缝的衍射花样,除零级中央主 极大外,处处相同。
1.4 衍射现象的分类
1 Fresnel衍射(近场衍射)
障碍物(孔隙)距光源和光屏的距离都是有限的,或 其中之一是有限的。
菲涅耳—基尔霍夫衍射积分公式
1 ik 2 (1 cos k )e n k 1 (1 cos k ) A (1) 2 k 1 ~ i0 S k A KUe rk
~ i 0 S k KUe rk
~ k 1 (1 cos k ) U ( P) A (1) 2 k 1
可见,相邻波带次波的位相相反,且k越大的波带, 振幅越小 。
n 1 1 1 1 1 ~ k 1 U ( P) (1) Ak A1 ( A1 A2 A3 ) ( A3 A4 A5 ) 2 2 2 2 2 k 1
1 [ A1 ( 1) n 1 An ] 2
球冠面积
d
R
dr / 2
M
S 2Rh
rk 1
k
S
rk r0 b
R D h B0
dS 2R sin d
2
2R 2 (1 cos )
P
2 2 2
drk / 2
dS S k
R ( R r0 ) rk cos ΔSMP中 2R( R r0 ) rk sin d drk R( R r0 )
2
2 Rh
kr0 h 2( R r0 )
菲涅耳衍射圆孔和圆屏

圆孔的多缝衍射
描述
当光通过多个小的圆孔时, 每个孔都会产生衍射现象, 多个衍射光波相互叠加形 成多缝衍射。
衍射模式
多缝衍射呈现为多个明暗 相间的条纹,条纹的形状 和数量取决于圆孔的排列 和间距。
影响因素
圆孔的数量、排列方式、 光的波长和观察的距离都 会影响多缝衍射的强度和 模式。
圆孔衍射的应用
光学仪器校准
当光线通过菲涅耳衍射圆孔时,会在屏幕 上形成多个同心圆环的衍射光斑,这是由 于光的波动性质导致的。
光强分布
圆屏衍射
衍射光斑的光强分布呈现中间强、四周弱 的特点,这是因为光在衍射过程中能量分 散到了各个方向。
当光线照射在圆屏上时,同样会产生衍射 现象,形成类似的衍射光斑和光强分据波长与障碍物尺寸的关系, 衍射可分为菲涅耳衍射和夫琅禾 费衍射。
衍射公式
菲涅耳衍射公式
描述了波长、孔径、角度等因素与衍射强度分布之间的关系 。
夫琅禾费衍射公式
描述了波长、距离、角度等因素与衍射强度分布之间的关系 。
衍射的分类
菲涅耳衍射
当波长与障碍物尺寸相近或更小时, 衍射现象表现为菲涅耳衍射。
菲涅耳衍射圆孔和圆屏的理论分 析表明,衍射现象与波长、孔径 大小、观察角度等因素密切相关。
通过实验验证,我们发现菲涅耳 衍射圆孔和圆屏的衍射模式与理 论预测一致,为进一步研究提供
了可靠依据。
本研究还发现,衍射模式受到光 源特性和环境因素的影响,这为 实际应用中提高成像质量和降低
噪声提供了指导。
研究展望
未来研究可以进一步探讨菲涅耳衍射圆孔和圆屏在不同条 件下的表现,例如在不同波长范围、不同观察角度、不同 孔径大小以及不同环境因素下的衍射特性。
结合现代光学技术和计算机模拟方法,可以更深入地理解 菲涅耳衍射的物理机制,并探索其在光学成像、光谱分析、 信息处理等领域的应用前景。
圆孔和圆屏的菲涅耳衍射圆孔的菲涅...

3.6衍射光栅衍射光栅:能对入射光波的振幅或相位,或者两者同时产生空间周期性调制的光学元件。
*一种应用非常广泛、非常重要的光学元件,主要用作分光(从远红外到真空紫外)元件,还可用于长度和角度的精密测量、以及调制元件;*工作基础:夫朗禾费多缝衍射效应。
光栅的分类:按工作方式分类:–透射光栅–反射光栅按对入射光的调制作用分类:–振幅光栅–相位光栅3.6.1 光栅的分光性能1. 光栅方程多缝衍射中干涉主极大条件sin d m θλ=d ϕθ为缝间距,称为, 为入射角,光常数 栅为衍射角衍射光与入射光同侧取正,异侧取负号↑斜入射衍射极大条件 (s 0,1,2, in sin )d m m ϕθλ±=±±="----光栅方程2. 性能参数(1) 色散本领3.6.1 光栅的分光性能将不同波长的同级主极大光分开的程度,通常用角色散和线色散表示。
A.角色散d θ/d λ。
•波长相差10-10 m 的两条谱线分开的角距离称为角色散。
•由光栅方程对波长取微分求得θλθcos d md d =此值愈大,角色散愈大,表示不同波长的光被分得愈开。
* 光栅的角色散与光谱级次m 成正比,级次愈高,角色散就愈大;与光栅刻痕密度1/d 成正比,刻痕密度愈大(光栅常数d 愈小),角色散愈大。
B.线色散dl/d λ在聚焦物镜的焦平面上,单位波长差的两条谱线分开的距离称为线色散。
cos dld mf f d d d θλλθ==长焦物镜可以使不同波长的光被分得更开。
* 光栅的刻痕密度1/d 很大(光栅常数d 很小),故光栅的色散本领很大。
* 若在θ不大的位置记录光栅光谱,cos θ几乎不随θ变化,则色散是均匀的,这种光谱称为匀排光谱,对于光谱仪的波长标定来说,十分方便。
3.6.1 光栅的分光性能(2) 色分辨本领* 由于衍射,每一条谱线都具有一定宽度。
当两谱线靠得较近时,尽管主极大分开了,它们还可能因彼此部分重叠而分辨不出是两条谱线。
光学 菲涅耳衍射

sin u u
B'
dx
θ
b
x
B
θ
P0
P F
三、光强分布特点
sin 2 u 由 I P = I 0 2 可知 : 不同的θ对应着不同的观察点 也对应着不同的光强值 , . u dI P d sin 2 u 2 sin u (u cos u sin u ) = 0 时, I P取得极值,即 : 2 = =0 当: 3 u du du u πb ① λ sin θ 0 = 0 u0 = 0 sin u = 0 uk = kπ πb sin θ = kπ ② 时取得极值. k λ tgu = u ③
决定,在居间位置,光强介于最大值和最小值之间。对线光源,整个花样 为平行于缝、并以中央条纹为中心、对称展开的明暗相间的直线状条纹。 2 2、各级亮条纹(最大值)光强不等。中央亮条纹强度最强;其余亮 条纹 (次最大)光强远小于中央条纹,并随级数的增大而很快减小。
λ
P0
3、条纹宽度—角宽度θ
亮条纹宽度—相邻暗条纹间的间隔。
L2
MD N
dx
θ
b
x
B
θ
P0
P
dE 0 =
A0 dx cos ω t b
F
由惠—菲原理可知: BB‘上所有窄带发出的次波在屏上叠加,就形成了衍射花样。 现取一束与原入射方向成θ角(称为衍射角)的光束,并作辅助平面BD垂直于衍 射方向,则BD面上任一点到P点的光程相等。
∴ M , B 两点沿 θ 方向到 P 点的光程差 δ = M N = x sin θ 又 : N 点的振动表达式为 A dx 复数式为 : dE = 0 e b dE = A0 dx 2π x sin θ ω t cos b λ ~ A0 dx i , 复振幅 d E = e b
菲涅尔圆孔衍射和圆屏衍射PPT课件
14
(3)处理步骤
1) 将半波带分割成 m个更窄的小环带
2) 写出每个小环带在P0点的复振幅
U%1(P0 ) A(P0 )ei0 U% 2 (P0 ) A(P0 )ei(0 m) U%3 (P0 ) A(P0 )ei(0 2 /m)
A( P0 ) An1 An2 A
1 2
[
An1
(
1 )
A
]
1 2
An1
1 A(P0 ) 2 An1
I A2 (P0 )
9
(6)讨论:
1)圆孔衍射中心场点P0处的总振幅近似为:
A(P0 ) A1 A2 A3 (1)(n1) An
则:dr l / 2
k Rl 是一个常量
由菲涅耳原理可知:
Ak
k(k )
Rl
Rb
rk
Ak
R
k( k(k )
b
k
)
k rk
Ak仅随 k(k ) 变化,随k的增加缓慢减小,最后
趋近于零。即:
A1 A2 A3 Ak1 Ak2 A 0
邻露出波带间相差一个波长的光程差。 (3)波带片具有面积大、轻便、
可折叠等透镜不具备的………….
U% m (P0 ) A(P0 )ei(0 )
15
3)画出矢量图
注意: 矢量图是正多边形, 一个完整半波带首尾矢量的
位相差是
4)连接首尾矢量,得到合成矢
量,则半波带在P0点产生的光
强为:
I (P0 ) A2
m M Am
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图2-8
四、直线传播和衍射的关系
• 上一章讨论光的干涉现象时,仅注意到两束或多束相干光光波整束的 叠加,没有考略到每一光束中波面上所有各点发出的次波的叠加。当 时实际上是假定每束光是直线传播的。
• 按照惠—菲原理的方式进行。所以,衍射现象是光的波动 特性最基本的表现。光的直线传播不过是衍射现象的极限 表现而已。这样,通过惠—菲原理的解释,进一步揭示了 光的直线传播和衍射现象的内在联系。
五、
0
菲涅耳直边衍射
• 迈干涉仪用λ = 5893 A的钠黄光观察,视场中心为亮点,此 外还能看到10个亮环。今移动一臂中的反射镜,发现有10 个亮环向中心收缩而消失,即中心级次减小10,此时视场 中除中央亮点外还剩5个亮环,求开始中央干涉级,移动 后最外干涉级。
图2-9
图2-10
1 1 1 + = R r0 ρ k2 ( ) kλ
• 和一般的汇聚透镜一样,波带片也有它的焦距,透镜的焦距就是发光 点在无限远时的象距。 ρ k2 f ′ =r 0 = 令 R→∞ ,得
kλ
即
1 1 1 + = R r0 f′
和薄透镜的物象公式完全相似。
•
波带片的焦距取决于波带片通光孔的半径 ρ k 、k 和 λ 。由于波带片的 ,LL 焦聚和光波波长有密切的关系,色差大。由于波带片尚有 f ′ 3, f ′ 5焦 距存在,波带片成象的情况与透镜成象的情况也有所不同。对于给定 的物点,对应于不同的焦距,波带片可以给出多个象点。
根据以上的讨论,可以看到圆屏的作用能使点光源造成实象,可以设 想它和一块汇聚透镜相当。另一方面,从菲涅耳半波带的特征来看, 对于通过波带中心而与波带面垂直的轴上一点来说,圆孔露出半波带 的数目k可为奇数或偶数。如果设想制造这样一种屏,使它对于所考 查的点只让奇数半波带或只让偶数半波带透光。这样在考查点处振动 的振幅为
a
•
如果圆屏足够小,只遮住中心带的一小部分,则光看起来可完全绕过 它,除了圆屏影子中心有亮点外没有其它影子。这个初看起来似乎是 荒谬的结论,是泊松于1818年在巴黎科学院研究菲涅耳的论文时把它 当作菲涅耳论点谬误的证据提出来的。但阿喇果做了相应的实验,证 实了菲涅耳的理论的正确性。
三、菲涅耳波带片
• 还有关系
kλ ⎤ kλ 2 2 + ( )⎥ − r0 = kλr0 + ( ) ≈ kλr0 2 ⎦ 2
2
(2)
ρ k2 = R 2 − ( R − h) 2 = rk2 − (r0 + h) 2
2 Rh − h 2 = rk2 − r02 − 2r0 h − h 2 rk2 − r02 h= 2 ( R + r0 )
•
如果圆孔的半径具有一定的大小,观察点P的位置仅使波面上露出第 一个带,则 A1=a1 与没有光阑时比较,振幅是二倍,光强则增加到四倍。所以光在通过 圆孔以后到达任一点时的光强,不能够单独由光源到该点的距离来决 定,还取决于圆孔的位置及大小,只当圆孔足够大,使 a k 小到可以略 去不计时,才和光的直线传播概念所推得的结果一致。 2 • 所有这些讨论都假定0是理想的点光源,但实际的光源都有一定的大 小,光源的每点各自产生它自己的衍射花样,它们是不相干的,光源 的线度应小到使光源上某些点所产生的亮条纹不致落到另外一些点所 产生的暗条纹上去。否则由于不相干叠加,衍射花样就会完全模糊了, 通常情况不会产生衍射花样,正是由于这个缘故。
Ak = a1 + a 3 + a 5 + a 7 + a 9 = 5a1
• •
这是不用光阑时振幅的10倍,光强则为100倍。如果以偶数个波带代 替,上述结果也成立。 由于波带片能使点光源成一实象,故它有类似于透镜成象的功用,其 物距R和象距r 0 所遵从的关系和透镜的物象公式相仿。
ρ2 1 1 k= ( + ) λ r0 R
将(2)和(3)代入(1)
(3)
ρ 2 = ρ k2 = kλr0 −
r0 kλr0 r0 rR = kλr0 (1 − )=k 0 λ R + r0 ( R + r0 ) ( R + r0 )
ρ 2 ( R + r0 ) ρ 2 1 1 k= = ( + ) λr0 R λ r0 R
•
如果用平行光照射圆孔, R → ∞ 则
二、圆屏衍射
图2-7
•
我们讨论一下点光源发出的光通过圆屏边缘时的衍射现象。0为点光 源,光路上有一不透明的圆屏,现在先讨论P点的振幅。设圆屏遮蔽 了开始的k个带。于是从第k+1个带开始,所有其余的带发的次波都能 到达P点。把所有这些带的次波叠加起来,可得P点的合振幅为:
a k +1 A= 2
• 即不论圆屏的大小和位置怎样,圆屏几何影子的中心永远有光。不过 圆屏的面积越小时,被达P点的光就越强。变更圆屏和光源之间或圆屏和P之间的距离时,k 也将因之改变,因而也将影响P点的光强。
第二节 菲涅耳衍射(圆孔和圆屏)
一、圆孔衍射
将一束光投射在一个小圆孔上,在距孔1~2m处放置一块毛玻璃屏, 观察小圆孔的衍射花样。
图2-6
ρ k2 = rk2 − (r0 + h) 2 = rk2 − r02 − 2r0 h − h 2
≈ r − r − 2r0 h
2 k 2 0
(1)
⎡ rk2 − r02 = ⎢ r0 ⎣
Ak = Ak =
∑a ∑a
k k
2 k +1
2k
•
•
这样做成的光学元件叫做菲涅耳波带片。各菲涅耳半波带的半径正比 于序数k的平方根,所以波带片可按如下方法制作,先在绘图纸上画 出半径正比于序数k的平方根的一组同心圆,把相间的波带涂黑,然 后用照相机拍射在底片上,该底片即为波带片。还可做成长条形、方 形波带片。 如果某一点波带片对考查点露出前5个奇数半波带,则考查点的振幅 为
ρ k = kλr0
• P点合振幅的大小取决于露出的带数k,而当波长及圆孔的位置和大小 都给定时,k取决于观察点P的位置,k为奇数相对应的那些点,合振 幅Ak较大,与k为偶数相对应的那些P点,Ak较小。这个结果很容易 用实验来证实。 • 如果不用光阑,相当于圆孔的半径为无限大, ak为无限小,此时P点的 a1 合振幅为 A ∞ = ,即没有遮蔽的整个波面对 P点的作用等于一个波带 2 在该点的作用的一半,因为波带的面积非常小。如:λ=5000Å, 1 3 2 mm γ R= 0=1m。第一个波带的面积约为 4 ,半径约为 2 mm 。所以没有遮 避的整个波面的光能的传播,几乎可以看作沿OP直线进行,这也是一 般把光视作直线传播的缘由。P点离开光源越远,a愈小,光强愈弱。 在此情况下屏沿着对称轴线前进时,不发生上述某些点较强某些点较 弱的现象。
