因式分解及其应用(中考)
初中数学因式分解常见的6种方法和7种应用

因式分解的六种方法及其应用因式分解的常用方法有:(1)提公因式法;(2)公式法;(3)提公因式法与公式法的综合运用.在对一个多项式因式分解时,首先应考虑提公因式法,然后考虑公式法.对于某些多项式,如果从整体上不能利用上述方法因式分解,还要考虑对其进行分组、拆项、换元等.方法一提公因式法题型1 公因式是单项式的因式分解1.若多项式-12x2y3+16x3y2+4x2y2的一个因式是-4x2y2,则另一个因式是()A.3y+4x-1 B.3y-4x-1C.3y-4x+1 D.3y-4x【解析】B2.分解因式:2mx-6my=__________.【解析】2m(x-3y)3.把下列各式分解因式:(1)2x2-xy;(2)-4m4n+16m3n-28m2n.【解析】(1)原式=x(2x-y).(2)原式=-4m2n(m2-4m+7).题型2公因式是多项式的因式分解4.把下列各式分解因式:(1)a(b-c)+c-b;(2)15b(2a-b)2+25(b-2a)2.【解析】(1)原式=a(b-c)-(b-c)=(b-c)(a-1).(2)原式=15b(2a-b)2+25(2a-b)2=5(2a-b)2(3b+5).方法二公式法题型1直接用公式法5.把下列各式分解因式:(1)-16+x4y4;(2)(x2+y2)2-4x2y2;(3)(x2+6x)2+18(x2+6x)+81.【解析】(1)原式=x4y4-16=(x2y2+4)(x2y2-4)=(x2y2+4)(xy+2)(xy-2).(2)原式=(x 2+y 2+2xy )(x 2+y 2-2xy )=(x +y )2(x -y )2.(3)原式=(x 2+6x +9)2=[(x +3)2]2=(x +3)4.题型2 先提再套法6.把下列各式分解因式:(1)(x -1)+b 2(1-x );(2)-3x 7+24x 5-48x 3.【解析】(1)原式=(x -1)-b 2(x -1)=(x -1)(1-b 2)=(x -1)(1+b )(1-b ).(2)原式=-3x 3(x 4-8x 2+16)=-3x 3(x 2-4)2=-3x 3(x +2)2(x -2)2.题型3 先局部再整体法7.分解因式:(x +3)(x +4)+(x 2-9).【解析】原式=(x +3)(x +4)+(x +3)·(x -3)=(x +3)[(x +4)+(x -3)]=(x +3)(2x +1). 题型4 先展开再分解法8.把下列各式分解因式:(1)x (x +4)+4;(2)4x (y -x )-y 2.【解析】(1)原式=x 2+4x +4=(x +2)2.(2)原式=4xy -4x 2-y 2=-(4x 2-4xy +y 2)=-(2x -y )2.方法三 分组分解法9.把下列各式分解因式:(1)m 2-mn +mx -nx ;(2)4-x 2+2xy -y 2.【解析】(1)原式=(m 2-mn )+(mx -nx )=m (m -n )+x (m -n )=(m -n )(m +x ).(2)原式=4-(x 2-2xy +y 2)=22-(x -y )2=(2+x -y )(2-x +y ).方法四 拆、添项法10.分解因式:x 4+14. 【解析】原式=x 4+x 2+14-x 2=⎝⎛⎭⎫x 2+122-x 2=⎝⎛⎭⎫x 2+x +12(x 2-x +12). 方法五 整体法题型1 “提”整体11.分解因式:a (x +y -z )-b (z -x -y )-c (x -z +y ).【解析】原式=a (x +y -z )+b (x +y -z )-c (x +y -z )=(x +y -z )(a +b -c ).题型2 “当”整体12.分解因式:(x+y)2-4(x+y-1).【解析】原式=(x+y)2-4(x+y)+4=(x+y-2)2.题型3“拆”整体13.分解因式:ab(c2+d2)+cd(a2+b2).【解析】原式=abc2+abd2+cda2+cdb2=(abc2+cda2)+(abd2+cdb2)=ac(bc+ad)+bd(ad+bc)=(bc+ad)(ac+bd).题型4“凑”整体14.分解因式:x2-y2-4x+6y-5.【解析】原式=(x2-4x+4)-(y2-6y+9)=(x-2)2-(y-3)2=(x+y-5)(x-y+1).方法六换元法15.分解因式:(1)(a2+2a-2)(a2+2a+4)+9;(2)(b2-b+1)(b2-b+3)+1.【解析】(1)设a2+2a=m,则原式=(m-2)(m+4)+9=m2+4m-2m-8+9=m2+2m+1=(m+1)2=(a2+2a+1)2=(a+1)4.(2)设b2-b=n,则原式=(n+1)(n+3)+1=n2+3n+n+3+1=n2+4n+4=(n+2)2=(b2-b+2)2.因式分解的7种应用因式分解是整式的恒等变换的一种重要变形,它与整式的乘法是两个互逆的过程,是代数恒等变形的重要手段,在有理数计算、式子的化简求值、几何等方面起着重要作用.应用一用于简便计算1.利用简便方法计算:23×2.718+59×2.718+18×2.718.【解析】23×2.718+59×2.718+18×2.718=(23+59+18)×2.718=100×2.718=271.8.2.计算:2 0162-4 034×2 016+2 0172.【解析】2 0162-4 034×2 016+2 0172=2 0162-2×2 016×2 017+2 0172=(2 016-2 017)2=1.应用二用于化简求值3.已知x-2y=3,x2-2xy+4y2=11.求下列各式的值:(1)xy;(2)x2y-2xy2.【解析】(1)∵x-2y=3,∴x2-4xy+4y2=9,∴(x2-2xy+4y2)-(x2-4xy+4y2)=11-9,即2xy=2,∴xy=1.(2)x2y-2xy2=xy(x-2y)=1×3=3.应用三用于判断整除4.随便写出一个十位数字与个位数字不相等两位数,把它的十位数字与个位数字对调得到另一个两位数,并用较大两位数减去较小的两位数,所得的差一定能被9整除吗?为什么?【解析】所得的差一定能被9整除.理由如下:不妨设该两位数个位上的数字是b,十位上的数字是a,且a>b,b不为0,则这个两位数是10a+b,将十位数字与个位数字对调后的数是10b+a,则这两个两位数中,较大的数减较小的数的差是(10a+b)-(10b+a)=9a-9b=9(a-b),所以所得的差一定能被9整除.应用四用于判断三角形的形状5.已知a,b,c是△ABC的三边长,且满足a2+b2+c2-ab-bc-ac=0,判断△ABC形状.【解析】∵a2+b2+c2-ab-bc-ac=0,∴2a2+2b2+2c2-2ab-2bc-2ac=0.即a2-2ab+b2+b2-2bc+c2+a2-2ac+c2=0.∴(a-b)2+(b-c)2+(a-c)2=0.又∵(a-b)2≥0,(b-c)2≥0,(a-c)2≥0,∴a-b=0,b-c=0,a-c=0,即a=b=c,∴△ABC为等边三角形.应用五用于比较大小6.已知A=a+2,B=a2+a-7,其中a>2,试比较A与B的大小.【解析】B-A=a2+a-7-a-2=a2-9=(a+3)(a-3).因为a>2,所以a+3>0,从而当2<a<3时,a-3<0,所以A>B;当a=3时,a-3=0,所以A=B;当a>3时,a-3>0,所以A<B.应用六 用于解方程(组)7.已知大正方形的周长比小正方形的周长多96 cm ,大正方形的面积比小正方形的面积多960 cm 2.请你求这两个正方形的边长.【解析】设大正方形和小正方形的边长分别为x cm ,y cm ,根据题意,得⎩⎪⎨⎪⎧4x -4y =96,①x 2-y 2=960,② 由①得x -y =24,③;由②得(x +y )(x -y )=960,④把③代入④得x +y =40,⑤;由③⑤得方程组⎩⎪⎨⎪⎧x -y =24,x +y =40,,解得⎩⎪⎨⎪⎧x =32,y =8. 故大正方形的边长为32 cm ,小正方形的边长为8 cm.应用七 用于探究规律8.观察下列各式:12+(1×2)2+22=9=32,22+(2×3)2+32=49=72,32+(3×4)2+42=169=132,…. 你发现了什么规律?请用含有字母n (n 为正整数)的等式表示出来,并说明理由.【解析】规律:n 2+[n (n +1)]2+(n +1)2=[n (n +1)+1]2.理由如下:n 2+[n (n +1)]2+(n +1)2=[n (n +1)]2+2n 2+2n +1=[n (n +1)]2+2n (n +1)+1=[n (n +1)+1]2.。
中考数学“因式分解”典例及巩固训练

中考数学“因式分解”典例及巩固训练(1)一、典型例题例1、(2017•广东省)分解因式:a 2+a = .解:答案为a (a+1)例2、(2019•黄冈市)分解因式3x 2﹣27y 2= . 解:原式=3(x 2﹣9y 2)=3(x +3y )(x ﹣3y ),故答案为:3(x +3y )(x ﹣3y )例3、因式分解:221222x xy y ++. 解:22221122(44)22x xy y x xy y ++=++21(2)2x y =+.二、巩固训练1.下列等式从左到右的变形,属于因式分解的是( )A .x 2+2x ﹣1=(x ﹣1)2B .(a +b )(a ﹣b )=a 2﹣b 2C .x 2+4x +4=(x +2)2D .ax 2﹣a =a (x 2﹣1)2.下列多项式可以用平方差公式分解因式的是( )A .224x y +B .224x y -+C .224x y --D .324x y -3. 下列各式中,能用完全平方公式分解的个数为( )①21025x x -+:②2441a a +-;③221x x --;④214m m -+-;⑤42144x x -+ A .1个 B .2个 C .3个 D .4个4.如果代数式2425x kx ++能够分解成2(25)x -的形式,那么k 的值是( )A .10B .20-C .10±D .20±5. 分解因式:(1)a 2b ﹣abc = .(2)3a (x ﹣y )﹣5b (y ﹣x )= .6.分解因式:4a 2﹣4a +1= .7.分解因式:2a 2﹣4a +2= .8.(2017•广州市)分解因式:xy 2﹣9x = .9.分解因式:x 6﹣x 2y 4= .10.(2018•黄冈市)因式分解:x 3﹣9x = .11.(2018•葫芦岛市)分解因式:2a 3﹣8a = .12.因式分解: (1)2218x -; (2)224129a ab b -+; (3)3221218x x x -+;13.(2019·河池市)分解因式:2(1)2(5)x x -+-.14.分解因式:4224816x x y y -+.15.分解因式:(1)22()+x y x y -- ; (2)22()()a x y b x y ---; (3)229()()m n m n +--.★★★★1.阅读下列材料:在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.下面是小涵同学用换元法对多项式22(41)(47)9x x x x -+-++进行因式分解的过程. 解:设24x x y -=原式(1)(7)9y y =+++(第一步)2816y y =++(第二步)2(4)y =+(第三步)22(44)x x =-+(第四步)请根据上述材料回答下列问题:(1)小涵同学的解法中,第二步到第三步运用了因式分解的 ;A .提取公因式法B .平方差公式法C .完全平方公式法(2)老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果: ;(3)请你用换元法对多项式22(2)(22)1x x x x ++++进行因式分解.2.【阅读材料】对于二次三项式222a ab b ++可以直接分解为2()a b +的形式,但对于二次三项式2228a ab b +-,就不能直接用公式了,我们可以在二次三项式2228a ab b +-中先加上一项2b ,使其成为完全平方式,再减去2b 这项,(这里也可把28b -拆成2b +与29b -的和),使整个式子的值不变.于是有:2228a ab b +-222228a ab b b b =+-+-2222(2)8a ab b b b =++--22()9a b b =+-[()3][()3]a b b a b b =+++-(4)(2)a b a b =+-我们把像这样将二次三项式分解因式的方法叫做添(拆)项法.【应用材料】(1)上式中添(拆)项后先把完全平方式组合在一起,然后用 法实现分解因式.(2)请你根据材料中提供的因式分解的方法,将下面的多项式分解因式:①268m m ++;②4224a a b b ++★★★★★1.数形结合是解决数学问题的重要思想方法,借助图形可以对很多数学问题进行直观推导和解释.如图1,有足够多的A 类、C 类正方形卡片和B 类长方形卡片.用若干张A 类、B 类、C 类卡片可以拼出如图2的长方形,通过计算面积可以解释因式分解:2223(2)()a ab b a b a b ++=++.(1)如图3,用1张A 类正方形卡片、4张B 类长方形卡片、3张C 类正方形卡片,可以拼出以下长方形,根据它的面积来解释的因式分解为 ;(2)若解释因式分解2234()(3)a ab b a b a b ++=++,需取A 类、B 类、C 类卡片若干张(三种卡片都要取到),拼成一个长方形,请画出相应的图形;(3)若取A 类、B 类、C 类卡片若干张(三种卡片都要取到),拼成一个长方形,使其面题1图积为22++,则m的值为,将此多项式分解因式5a mab b为.巩固训练参考答案1.C2.B3. B4.B5. (1) ab (a ﹣c) . (2)(3a+5b )(x ﹣y ) .6.(2a ﹣1)2.7.2(a ﹣1)2.8.x (y +3)(y ﹣3).9. x 2(x 2+y 2)(x +y )(x ﹣y ) .10.x (x +3)(x ﹣3).11.2a (a +2)(a -2).12.解:(1);(2);(3)原式.13.解:原式.14.解:原式.15.解:(1)原式=;(2)原式;(3)原式.★★★★1.解:(1)故选:;2218x -22(9)x =-2(3)(3)x x =+-224129a ab b -+22(2)12(3)a ab b =-+2(23)a b =-222(69)2(3)x x x x x =-+=-221210x x x =-++-29x =-(3)(3)x x =+-22(4)x y =-22(2)(2)(2)x y x y x y =+-+22())(x y x y ---)[2(1])(x y x y =---)(22(1)x y x y =---22()()x y a b =--()()()x y a b a b =-+-22[3()]()m n m n =+--(33)(33)m n m n m n m n =++-+-+4(2)(2)m n m n =++C(2),设,原式,,,,;故答案为:;(3)设,原式,,,,.2.解:(1)上式中添(拆项后先把完全平方式组合在一起,然后用公式法实现分解因式. 故答案为:公式;(2)①;②.22(41)(47)9x x x x -+-++24x x y -=(1)(7)9y y =+++2816y y =++2(4)y =+22(44)x x =-+4(2)x =-4(2)x -22x x y +=(2)1y y =++221y y =++2(1)y =+22(21)x x =++4(1)x =+)268m m ++2691m m =++-22(3)1m =+-(31)(31)m m =+++-(4)(2)m m =++4224a a b b ++4224222a a b b a b =++-2222()()a b ab =+-2222()()a b ab a b ab =+++-★★★★★1.解:(1)由图可得,,故答案为:;(2)如右图所示;(3)由题意可得,,,故答案为:6,.2243()(3)a ab b a b a b ++=++2243()(3)a ab b a b a b ++=++6m =2256(5)()a ab b a b a b ++=++(5)()a b a b ++中考数学“因式分解”典例及巩固训练(2)一、典型例题例1、因式分解:222a ab b ac bc ++++.解:原式22(2)()a ab b ac bc =++++2()()a b c a b =+++()()a b a b c =+++例2、用十字相乘法进行因式分解:232x x ++.解:原式(1)(2)x x =++.例3、在实数范围内进行分解因式:35x x -.解:原式2(5)x x =-(x x x =+-.二、巩固训练1.用分组分解法进行因式分解:(1)2221x y xy +--; (2)3223x x y xy y +--.2.(2017•百色市)阅读理解:用“十字相乘法”分解因式2x 2﹣x ﹣3的方法.(1)二次项系数2=1×2;(2)常数项﹣3=﹣1×3=1×(﹣3),验算:“交叉相乘之和”; 题2图1×3+2×(﹣1)=1 1×(﹣1)+2×3=5 1×(﹣3)+2×1=﹣1 1×1+2×(﹣3)=﹣5(3)发现第③个“交叉相乘之和”的结果1×(﹣3)+2×1=﹣1,等于一次项系数﹣1. 即:(x +1)(2x ﹣3)=2x 2﹣3x +2x ﹣3=2x 2﹣x ﹣3,则2x 2﹣x ﹣3=(x +1)(2x ﹣3).像这样,通过十字交叉线帮助,把二次三项式分解因式的方法,叫做十字相乘法.仿照以上方法,分解因式:3x 2+5x ﹣12= .3.用十字相乘法分解因式:(1)x 2+2x ﹣3= .(2)x 2﹣4x +3= .(3)22x x +-= .(4)2215a a --= .(5)4x 2+12x ﹣7= .4.选择恰当的方法进行分解因式:(1)26x x --; (2)2363a a -+; (3)226a ab b --;(4)29(2)(2)a x y y x -+-; (5)2222a b a b --+;(6)34x x -;5.分解因式:(1)22430y y --; (2)224414a b b +--.6.在实数范围内将下列各式分解因式:(1)22363ax axy ay -+; (2)35x x -.7.在实数范围内分解因式:(1)9a 44b - 4; (2)x 22- 3+;(3)x 5﹣4x .★★★★1.阅读下面的问题,然后回答,分解因式:223x x +-,解:原式22113x x =++--2(21)4x x =++-2(1)4x =+-(12)(12)x x =+++- (3)(1)x x =+-上述因式分解的方法称为配方法.请体会配方法的特点,用配方法分解因式: (1)243x x -+; (2)24127x x +-.2.在实数范围内分解因式221x x --.3.因式分解是数学解题的一种重要工具,掌握不同因式分解的方法对数学解题有着重要的意义.我们常见的因式分解方法有:提公因式法、公式法、分组分解法、十字相乘法等.在此,介绍一种方法叫“试根法”例:32331x x x -+-,当1x =时,整式的值为0,所以,多项式有因式(1)x -,设322331(1)(1)x x x x x ax -+-=-++,展开后可得2a =-,所以3223331(1)(21)(1)x x x x x x x -+-=--+=-根据上述引例,请你分解因式:(1)2231x x -+; (2)32331x x x +++.★★★★★1.请看下面的问题:把44x +分解因式.分析:这个二项式既无公因式可提,也不能直接利用公式,怎么办呢?19世纪的法国数学家苏菲·热门抓住了该式只有两项,而且属于平方和222()2x +的形式,要使用公式就必须添一项24x ,随即将此项24x 减去,即可得:4422222222224444(2)4(2)(2)(22)(22)x x x x x x x x x x x x +=++-=+-=+-=++-+人们为了纪念苏菲·热门给出这一解法,就把它叫做“热门定理”. 请你依照苏菲·热门的做法,将下列各式因式分解. (1)444x y +;(2)2222x ax b ab ---. 2.【阅读与思考】整式乘法与因式分解是方向相反的变形.如何把二次三项式2ax bx c ++进行因式分解呢?我们已经知道,2211221212211212122112()()()a x c a x c a a x a c x a c x c c a a x a c a c x c c ++=+++=+++.反过来,就得到:2121221121122()()()a a x a c a c x c c a x c a x c +++=++.我们发现,二次项的系数a 分解成12a a ,常数项c 分解成12c c ,并且把1a ,2a ,1c ,2c ,如图①所示摆放,按对角线交叉相乘再相加,就得到1221a c a c +,如果1221a c a c +的值正好等于2ax bx c ++的一次项系数b ,那么2ax bx c ++就可以分解为1122()()a x c a x c ++,其中1a ,1c 位于图的上一行,2a ,2c 位于下一行.像这种借助画十字交叉图分解系数,从而帮助我们把二次三项式分解因式的方法,通常叫做“十字相乘法”. 例如,将式子26x x --分解因式的具体步骤为:首先把二次项的系数1分解为两个因数的积,即111=⨯,把常数项6-也分解为两个因数的积,即62(3)-=⨯-;然后把1,1,2,3-按图②所示的摆放,按对角线交叉相乘再相加的方法,得到1(3)121⨯-+⨯=-,恰好等于一次项的系数1-,于是26x x --就可以分解为(2)(3)x x +-.题2图请同学们认真观察和思考,尝试在图③的虚线方框内填入适当的数,并用“十字相乘法” 分解因式:26x x +-= (3)(2)x x +- .【理解与应用】请你仔细体会上述方法并尝试对下面两个二次三项式进行分解因式:(1)2257x x +- ;(2)22672x xy y -+= . 【探究与拓展】对于形如22ax bxy cy dx ey f +++++的关于x ,y 的二元二次多项式也可以用“十字相乘法”来分解,如图④,将a 分解成mn 乘积作为一列,c 分解成pq 乘积作为第二列,f 分解成jk乘积作为第三列,如果mq np b +=,pk qj e +=,mk nj d +=,即第1,2列、第2,3列和第1,3列都满足十字相乘规则,则原式()()mx py j nx qy k =++++,请你认真阅读上述材料并尝试挑战下列问题:(1)分解因式2235294x xy y x y +-++-= .(2)若关于x ,y 的二元二次式22718524x xy y x my +--+-可以分解成两个一次因式的积,求m 的值.(3)已知x ,y 为整数,且满足2232231x xy y x y ++++=-,请写出一组符合题意的x ,y 的值.巩固训练参考答案1.解:(1).解:(2)原式. 2.(x +3)(3x ﹣4). 3.(1)(x +3)(x -1) . (2)(x ﹣1)(x ﹣3) . (3) . (4) . (5)(2x +7)(2x ﹣1) .4.解:(1)原式. (2)原式; (3)原式; (4)原式.(5)原式. (6)原式; 5..解:(1)原式 ;(2)原式.6.解:(1)原式;2221x y xy +--2()1x y =--(1)(1)x y x y =-+--3223222()()()()()()x x y xy y x x y y x y x y x y =+-+=+-+=+-(2)(1)x x +-(5)(3)a a -+(2)(3)x x =+-23(21)a a =-+23(1)a =-(3)(2)a b a b =-+29(2)(2)a x y x y =---2(2)(91)x y a =--(2)(31)(31)x y a a =-+-()()2()()(2)a b a b a b a b a b =+---=-+-2(4)(2)(2)x x x x x =-=+-22(215)y y =--2(5)(3)y y =-+224(144)a b b =--+224(12)a b =--(221)(221)a b a b =+--+223(2)a x xy y =-+23()a x y =-(2)原式,.7.解:(1)原式; (2)原式.(3)原式=★★★★1.解:(1)(2)2.解:.3.解:(1)当时,整式的值为0,所以,多项式有因式, 于是; (2)当时,整式的值为0,多项式中有因式,2(5)x x =-(x x x =222222(32)(32)(32)a b a b a b =+-=++2(x =2(2)(x x x x +243x x -+24443x x =-+-+2(2)1x =--(21)(21)x x =-+--(1)(3)x x =--24127x x +-2412997x x =++--2(23)16x =+-(234)(234)x x =+++-(27)(21)x x =+-221x x --22111x x =-+--2(1)2x =--(11x x =---1x =(1)x -2231(1)(21)x x x x -+=--1x =-∴32331x x x +++(1)x +于是可设,,, ,,.★★★★★1.解:(1)原式; (2)原式. 2.解:【阅读与思考】分解因式:; 故答案为:; 【理解与应用】(1); (2);故答案为:(1);(2); 【探究与拓展】(1)分解因式; 故答案为:(2)∵关于,的二元二次式可以分解成两个一次因式的积, 存在其中,,;而,,或,故的值为43或;(3),为整数,且满足,可以是,(答案不唯一).32232331(1)()(1)()x x x x x mx n x m x n m x n +++=+++=++++-13m ∴+=3n m +=2m ∴=1n =3223331(1)(21)(1)x x x x x x x ∴+++=+++=+442222222222222444(2)4(22)(22)x y x y x y x y x y x y xy x y xy =++-=+-=+++-22222222()()()(2)x ax a a b ab x a a b x b x a b =-+---=--+=+--26(3)(2)x x x x +-=+-(3)(2)x x +-2257(1)(27)x x x x +-=-+22672(1)(27)x xy y x x -+=-+(1)(27)x x -+(1)(27)x x -+2235294(21)(34)x xy y x y x y x y +-++-=+--+(21)(34)x y x y +--+x y 22718524x xy y x my +--+-∴111⨯=9(2)18⨯-=-(8)324-⨯=-71(2)19=⨯-+⨯51(8)13-=⨯-+⨯271643m ∴=+=72678m =--=-m 78-x y 2232231x xy y x y ++++=-1x =-0y =。
中考数学专题-因式分解及其应用

第13讲 因式分解及其应用考点·方法·破译1.因式分解的定义:把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式;2.因式分解的基本方法有提公因式法、运用公式法、分组分解法等;3.因式分解的基本原则:有公因式先提出公因式、分解必须进行到每一个多项式都不能再分解为止;4.竞赛中常出现的因式分解问题,常用到换元法、主元法、拆项添项阿、配方法和待定系数法等方法、另外形如2x px q ++的多项式,当p =a +b ,q =ab 时可分解为(x +a )(x +b )的形式;5.利用因式分解求代数式的值与求某些特殊方程的解经典·考题·赏析【例1】⑴若229x kxy y ++是完全平方式,则k =______________⑵若225x xy ky -+是完全平方式,则k =______________【解法指导】形如222a ab b ±+的形式的式子,叫做完全平方式.其特点如下:⑴有三项;⑵有两项是平方和的形式;⑶还有一项是乘积的2倍,符号自由.解:⑴22229(3)x kxy y x kxy y ++=++是完全平方式,∴6kxy xy =± ∴6k =±; ⑵22225522y x xy ky x x ky -+=-⋅⋅+是完全平方式,∴225()2ky y = ∴254k = 【变式题组】01.若22199m kmn n -+是一个完全平方式,则k =________02.若22610340x y x y +-++=,求x 、y 的值03.若2222410a a b ab b +-++=,求a 、b 的值04.(四川省初二联赛试题)已知a 、b 、c 满足22|24||2|22a b a c ac -+++=+,求a b c -+的值【例2】⑴(北京)把3222x x y xy -+分解因式,结果正确的是( )A .()()x x y x y +-B .22(2)x x xy y -+C .2()x x y +D .2()x x y -⑵(杭州)在实数范围内分解因式44x -=____________⑶(安徽)因式分解2221a b b ---=_______________【解法指导】分解因式的一般步骤为:一提,二套,三分组,四变形解:⑴3222222(2)()x x y xy x x xy y x x y -+=-+=-⑵42224(2)(2)(2)(x x x x x x -=+-=+⑶22222221(21)(1)(1)(1)a b b a b b a b a b a b ---=-++=-+=++--【变式题组】⑴3223223612x y x y x y -+⑵2222(1)2a x ax +-⑶222045a bx bxy -⑷2249()16()a b b a --+⑸222(5)8(5)16a a -+-+【例3】要使二次三项式25x x p -+在实数范围内能进行因式分解,那么整数P 的取值可能有( )A .2个B .4个C .6个D .无数多个【解法指导】由2()()()x a b x ab x a x b +++=++可知,在整数范围内分解因式25x x p -+,p 为(5)n n -的积为整数,∴p 有无数多个,因而选D【变式题组】⑴已知212x ax +-能分解成两个整系数的一次因式的乘积,则符合条件的整数a 的个数是( )A .2个B .4个C .6个D .8个⑵在1~100间,若存在整数n ,使2x x n +-能分解为两个整系数的一次因式的乘积,则这样的n 有__个【例4】分解因式:⑴221112x x -+⑵22244x y z yz --+⑶22(52)(53)12x x x x ++++-⑷226136x xy y x y +-++-【解法指导】解:⑴ ∴221112(23)(4)x x x x -+=--⑵222244x y z y --+222(44)x y yz z =--+22(2)x y z =--(2)(2)x y z x y z =+--+ ⑶设2525x x ++=,则原式可变为2(1)1212(3)(4)t t t t t t +-=+-=-+∴原式=22(523)(524)x x x x ++-+++ 2 1 -3 -422(51)(56)x x x x =+-++2(51)(2)(3)x x x x =+-++⑷226136x xy y x y +-++-22(6)(13)6x xy y x y =+-++-(2)(3)(13)6x y x y x y =-+++-(23)(32)x y x y =-++-【变式题组】01.分解因式:⑴2224912x y z yz --- ⑵224443x x y y --+-⑶236ab a b --+ ⑷(1)(2)(3)(4)1x x x x +++++⑸261910y y -+【例5】⑴(上海竞赛试题)求方程64970xy x y +--=的整数解;⑵(希望杯)设x 、y 为正整数,且224960x y y ++-=,求xy 的值【解法指导】⑴结合方程的特点对其因式分解,将不定方程转化为方程组求解; ⑵将等式左边适当变形后进行配方,利用x 、y 为正整数的特点,结合不等式求解. 解:⑴64970xy x y +--=,(64)(96)1xy x y +-+=,2(32)3(32)1x y y +-+=,∴(23)(32)1x y -+=,∵x 、y 都是整数 ∴{{(23)1(23)1(32)1(32)1x x y y -=-=-+=+=-或 ∴{21113x x y y =⎧⎪=⎨=-=-⎪⎩(舍去)或,∴方程的整数解为{11x y ==-, ⑵224960x y y ++-=,2244100y y x ++=-,22(2)100y x +=-,∵21000x -≥∴2100x ≤ ∵x 为正整数,∴x =1,2,…,10 ,又∵2(2)y +是平方数,∴x =6或8当x =6时2(2)y +=64,y =6,当x =8时2(2)y +=36,y =4,∴xy =36或32【变式题组】01.设x 、y 是正整数,并且222132y x =-,则代数式222x xy y x y+-+的值是___________ 02.(第二届宗沪杯)已知a 、b 为整数,则满足a +b +ab =2008的有序数组(a ,b )共有__________03.(北京初二年级竞赛试题)将2009表示成两个整数的平方差的形式,则不同的表示方法有( )A .16种B .14种C .12种D .10种04.方程332232x y x y xy -+-=的正整数解的个数为( )A .0个B .1个C .2个D .不少于3个05.一个正整数,如果加上100是一个完全平方数:如果加上168则是另外一个完全平方数,求这个正整数.【例6】已知k 、a 都是正整数,2004k +a 、2004(k +1)+a 都是完全平方数⑴请问这样的有序正整数(k 、a )共有多少组?⑵试指出a 的最小值,并说明理由.解:⑴22004k a m +=① 22004(1)k a n ++=②,这里m 、n 都是正整数,则222004n m -= 故()()2004223167n m n m +-==⨯⨯⨯注意到,m n +、n m -奇偶性相同,则{{100233426n m n m n m n m +=+=-=-=或,解得{{500164502170m m n n ====或, 当n =502,m =500时,由①得2004k +a =250000,所以2004(124)1504a k =-+③由于k 、a 都是正整数,故k 可以取值1,2,3,…,124,相应得满足要求的正整数数组(k 、a )共124组当n =170,m =164时,由①得2004k +a =26896所以2004(13)844a k =-+④由于k 、a 都是正整数,故k 可以取值1,2,3,…,13,相应得满足要求的正整数数组(k 、a )共13组从而,满足要求的正整数组(k 、a )共有124+13=137(组)⑵满足式③的最小正整数a 的值为1504,满足式④的最小正整数a 的值为844,所以,所求的a 的最小值为844【变式题组】01.(北京竞赛)已知a 是正整数,且22004a a +是一个正整数的平方,求a 的最大值02.设x 、y 都是整数,y y 的最大值演练巩固 反馈提高01.如果分解因式281(9)(3)(3)n x x x x -=++-,那么n 的值为( )A .2B .4C .6D .8 02.若多项式22(3)(3)x pxy qy x y x y ++=-+,则p 、q 的值依次为() A .12-,9- B .6,9- C .9-,9- D .0,9-03.下列各式分解因式正确的是( )A .291(91)(91)x x x -=+-B .4221(1)(1)a a a -=+-C .2281(9)(9)a b a b a b --=--+D .32()()()a ab a a b a b -+=-+-04.多项式()()()()x y z x y z y z x z x y +--+-+---的公因式是( )A .x y z +-B .x y z -+C .y z x +-D .不存在05.22()4()4m n m m n m+-++分解因式的结果是()A.2()m n+B.2(2)m n+C.2()m n-D.2(2)m n-06.若218x ax++能分解成两个因式的积,则整数a的取值可能有()A.4个B.6个C.8个D.无数个07.已知224250a b a b++-+=,则a ba b+-的值为()A.3 B.13C.3-D.13-08.分解因式:2(2)(4)4x x x+++-=__________________09.分解因式:22423a b a b-+++=__________________10.分解因式:33222x y x y xy-+=___________________11.已知5a b+=,4ab=-,那么22223a b a b ab++的值等于____________ 12.分解因式:2242x y x y-++=_______________13.分解因式:2()6()9a b b a---+=_________________14.分解因式:222(41)16a a+-=___________________15.已知20m n+=,则332()4m mn m n n+++的值为_____________ 16.求证:791381279--能被45整除17.已知9621-可被在60到70之间的两个整数整除,求这两个整数培优升级 奥赛检测01.(四川省初二数学联赛试题)使得381n +为完全平方数的正整数n 的值为( )A .2B .3C .4D .502.(四川省初二数学联赛试题)设m 、n 是自然数,并且219980n n m --=,则m +n 的最小值是( )A .100B .102C .200D .不能确定03.(四川省初二数学联赛试题)满足方程32326527991x x x y y y ++=+++的正整数对(x ,y )有( )A .0对B .1对C .3对D .无数对04.(全国初中数学竞赛试题)方程323652x x x y y ++=-+的整数解(x ,y )的个数是()A .0B .1C .3D .无穷多05.(四川省初二数学试题)已知42(1)M p p q =+,其中p 、q 为质数,且满足29q p -=,则M=()A .2009B .2005C .2003D .200006.(仙桃竞赛试题)不定方程2()7x y xy +=+的所有整数解为_________________07.已知多项式2223286x xy y x y +--+-可以分解为(2)(2)x y m x y n ++-+的形式,那么3211m n +-的值是______08.对于一个正整数n ,如果能找到a 、b ,使得n =a +b +ab ,则称n 为一个“好数”,例如:3=1+1+1×1,3就是一个好数,在1~20这20个正整数中,好数有_______个 09.一个正整数a 恰好等于另一个正整数b 的平方,则称正整数a 为完全平方数,如2648=,64就是一个完全平方数;若22222992299229932993a =+⨯+,求证a 是一个完全平方数10.已知实数a 、b 、x 、y 满足2a b x y +=+=,5ax by +=,求2222()()a b xy ab x y +++的值11.若a 为自然数,则4239a a -+是质数还是合数?请你说明理由12.正数a 、b 、c 满足3ab a b bc b c ca c a ++=++=++=,求(1)(1)(1)a b c +++的值13.某校在向“希望工程”捐款活动中,甲班有m 个男生和11个女生的捐款总数与乙班的9个男生和n 个女生的捐款总数相等,都是(mn +9m +11n +145)元,已知每人的捐款数相同,且都是整数,求每人的捐款数。
初中数学因式分解的12种方法

因式分解常用12种方法及应用【因式分解的12种方法】把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式因式分解。
因式分解的方法多种多样,现总结如下:1.提公因法如果一个多项式的各项都含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式。
例1.分解因式x3-2x2-x(2003淮安市中考题)x3-2x2-x=x(x2-2x-1)2.应用公式法由于分解因式与整式乘法有着互逆的关系,如果把乘法公式反过来,那么就可以用来把某些多项式分解因式。
@初中生家长例2.分解因式a2+4ab+4b2(2003南通市中考题)解:a2+4ab+4b2=(a+2b)23.分组分解法要把多项式am+an+bm+bn分解因式,可以先把它前两项分成一组,并提出公因式a,把它后两项分成一组,并提出公因式b,从而得到a(m+n)+b(m+n),又可以提出公因式m+n,从而得到(a+b)(m+n)例3.分解因式m2+5n-mn-5m解:m2+5n-mn-5m=m2-5m-mn+5n@初中生家长=(m2-5m)+(-mn+5n)=m(m-5)-n(m-5)=(m-5)(m-n)4.十字相乘法对于mx2+px+q形式的多项式,如果a×b=m,c×d=q且ac+bd=p,则多项式可因式分解为(ax+d)(bx+c)例4.分解因式7x2-19x-6分析:1×7=7,2×(-3)=-61×2+7×(-3)=-19解:7x2-19x-6=(7x+2)(x-3)5.配方法对于那些不能利用公式法的多项式,有的可以利用将其配成一个完全平方式,然后再利用平方差公式,就能将其因式分解。
@初中生家长例5.分解因式x2+6x-40解x2+6x-40=x2+6x+(9)-(9)-40=(x+3)2-(7)2=[(x+3)+7][(x+3)–7]=(x+10)(x-4)6.拆、添项法可以把多项式拆成若干部分,再用进行因式分解。
初三数学因式分解的应用教案

初三数学因式分解的应用教案【】初三数学因式分解的运用教案教案让先生学会运用因式分解停止复杂的多项式除法并且学会运用因式分解解复杂的方程。
教学目的1、会运用因式分解停止复杂的多项式除法。
2、会运用因式分解解复杂的方程。
二、教学重点与难点教学重点:因式分解在多项式除法和解方程两方面的运用。
教学难点:运用因式分解解方程触及较多的推理进程。
三、教学进程〔一〕引入新课1、知识回忆(1) 因式分解的几种方法: ①提取公因式法: ma+mb=m(a+b) ②运用平方差公式: = (a+b) (a-b)③运用完全平方公式:a 2ab+b =(ab) (2) 课前热身:①分解因式:(x +4) y - 16x y〔二〕师生互动,讲授新课1、运用因式分解停止多项式除法例1 计算: (1) (2ab -8a b) (4a-b)(2)(4x -9) (3-2x)解:(1) (2ab -8a b)(4a-b) =-2ab(4a-b) (4a-b) =-2ab (2) (4x -9) (3-2x) =(2x+3)(2x-3) [-(2x-3)] =-(2x+3) =-2x-3 一个小效果 :这里的x能等于3/2吗 ?为什么?想一想:那么(4x -9) (3-2x) 呢?练习:课本P162课内练习12、协作学习想一想:假设 ( )( )=0 ,那么这两个括号内应填入怎样的数或代数式子才可以满足条件呢? (让先生自己思索、相互之间讨论!)理想上,假定AB=0 ,那么有下面的结论:(1)A 和B同时都为零,即A=0,且B=0(2)A和B中有一个为零,即A=0,或B=0试一试:你能运用下面的结论解方程(2x+1)(3x-2)=0 吗?3、运用因式分解解复杂的方程例2 解以下方程: (1) 2x +x=0 (2) (2x-1) =(x+2) 解:x(x+1)=0 解:(2x-1) -(x+2) =0那么x=0,或2x+1=0 (3x+1)(x-3)=0原方程的根是x1=0,x2= 那么3x+1=0,或x-3=0 原方程的根是x1= ,x2=3注:只含有一个未知数的方程的解也叫做根,当方程的根多于一个时,常用带足标的字母表示,比如:x1 ,x2等练习:课本P162课内练习2做一做!关于方程:x+2=(x+2) ,你是如何解该方程的,方程左右两边能同时除以(x+2)吗?为什么?教员总结:运用因式分解解方程的基本步骤(1)假设方程的左边是零,那么把左边分解因式,转化为解假定干个一元一次方程;(2)假设方程的两边都不是零,那么应该先移项,把方程的左边化为零以后再停止解方程;遇到方程两边有公因式,异样需求先停止移项使左边化为零,切忌两边同时除以公因式!4、知识延伸解方程:(x +4) -16x =0解:将原方程左边分解因式,得 (x +4) -(4x) =0(x +4+4x)(x +4-4x)=0(x +4x+4)(x -4x+4)=0 (x+2) (x-2) =0接着继续解方程,5、练一练① a、b、c为三角形的三边,试判别 a -2ab+b -c 大于零?小于零?等于零?解: a -2ab+b -c =(a-b) -c=(a-b+c)(a-b-c)∵ a、b、c为三角形的三边 a+c ﹥b a﹤b+c a-b+c﹥0 a-b-c ﹤0即:(a-b+c)(a-b-c) ﹤0 ,因此 a -2ab+b -c 小于零。
因式分解的基本性质及应用

因式分解的基本性质及应用因式分解是将一个多项式分解成较简单的乘积形式的过程。
因素分解的基本性质和应用包括以下几个方面:1. 唯一性:一个多项式的因式分解不是唯一的,但是当我们考虑整数多项式时,因式分解是唯一的。
这是因为整数多项式的因子只能是整数常数或次数为1的一次多项式,而这些多项式已经是不可再分解的。
2. 分解定理:分解定理表明,如果一个多项式P(x)在x=a处取值为0,则P(x)可以被x-a整除。
这意味着x-a是P(x)的一个因子,或者等价地说,P(x)可以分解成(x-a)乘以另一个多项式Q(x)。
3. 公因式提取:公因式提取是一种将多项式的各项提取出一个公因子的方法。
例如,在多项式2x^3+4x^2中,可以提取出2x^2,然后得到2x^2(x+2)。
这个方法在简化多项式计算、化简分式等方面非常有效。
4. 因式分解定理:因式分解定理表明,一个多项式P(x)可以分解成多个一次或者二次的因子。
这个定理对于计算多项式的根和化简复杂的多项式表达式非常有用。
5. 最大公因式:最大公因式是多个多项式的最高次的公因式。
最大公因式的求解可以通过因式分解的方法进行。
最大公因式在多项式的约分、分式的化简等方面扮演着重要的角色。
6. 应用方面:因式分解在数学和物理等方面有着广泛的应用。
在数学中,因式分解可以用于求解多项式方程的根,化简复杂的表达式,计算多项式的导函数等。
在物理中,因式分解可以用于分解物体的运动方程,分析物理过程等。
除此之外,因式分解还有其他的一些应用。
例如在数论中,因式分解可以用于分析质数和合数的性质,判断一个数的因子等。
在代数几何中,因式分解可以用于分析曲线的结构和性质。
在概率论中,因式分解可以用于计算事件的概率等。
因式分解是数学中一个非常重要和基础的概念,在数学和其他学科中都有着广泛而重要的应用。
2023年中考数学高频考点训练——因式分解的应用
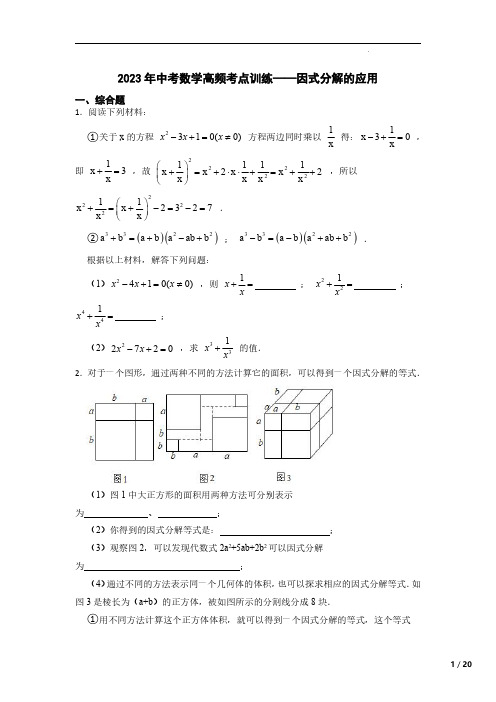
2023年中考数学高频考点训练——因式分解的应用一、综合题1.阅读下列材料:①关于x 的方程2310(0)x x x -+=≠方程两边同时乘以1x 得:1x 30x -+=,即1x 3x +=,故222221111x x 2x x 2x x x x ⎛⎫+=+⋅⋅+=++ ⎪⎝⎭,所以222211x x 2327x x ⎛⎫+=+-=-= ⎪⎝⎭.②()()3322a b a b a ab b +=+-+;()()3322a b a b a ab b -=-++.根据以上材料,解答下列问题:(1)2410(0)x x x -+=≠,则1x x +=;221x x +=;441x x +=;(2)22720x x -+=,求331x x +的值.2.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个因式分解的等式.(1)图1中大正方形的面积用两种方法可分别表示为、;(2)你得到的因式分解等式是:;(3)观察图2,可以发现代数式2a 2+5ab+2b 2可以因式分解为;(4)通过不同的方法表示同一个几何体的体积,也可以探求相应的因式分解等式.如图3是棱长为(a+b )的正方体,被如图所示的分割线分成8块.①用不同方法计算这个正方体体积,就可以得到一个因式分解的等式,这个等式是:;②已知a+b =5,ab =2,利用上面的规律求a 3+b 3的值.3.如图,将一张矩形纸板按照图中虚线裁剪成九块,其中有两块是边长都为m 的大正方形,两块是边长都为n 的小正方形,五块是长为m ,宽为n 的全等小矩形,且m>n ,(以上长度单位:cm)(1)观察图形,可以发现代数式2m 2+5mn +2n 2可以因式分解为;(2)若每块小矩形的面积为10cm 2,四个正方形的面积和为58cm 2,试求图中所有裁剪线(虚线部分)长之和.4.仔细阅读下面的例题:例题:已知二次三项式25x x m ++有一个因式是2x +,求另一个因式及m 的值.解:设另一个因式为x n +,得25(2)()x x m x x n ++=++,则225(2)2x x m x n x n ++=+++,25n ∴+=,2m n =,解得3n =,6m =,∴另一个因式为3x +,m 的值为6.依照以上方法解答下列问题:(1)若二次三项式254x x -+可分解为(1)()x x a -+,则a =;(2)若二次三项式226x bx +-可分解为(23)(2)x x +-,则b =;(3)已知二次三项式229x x k +-有一个因式是21x -,求另一个因式以及k 的值.5.解答下列问题:(1)一正方形的面积是()22690,0a ab b a b ++>>,则表示该正方形的边长的代数式是.(2)求证:当n 为正整数时,()()222121n n +--能被8整除.6.回答下列问题:(1)填空:22211(x x x x +=+-21(x x =-+;(2)填空:若15a a +=,则221a a +=;(3)若2310a a -+=,0a ≠,求221a a +的值.7.已知8x y +=,6xy =.求:(1)22x y xy +的值;(2)22x y +的值.8.解下列各题:(1)分解因式:()()263a b a b -+-;(2)利用因式分解简便计算:224959909595-⨯+.9.下面是多项式x 3+y 3因式分解的部分过程,.解:原式=x 3+x 2y ﹣x 2y +y 3(第一步)=(x 3+x 2y )﹣(x 2y ﹣y 3)(第二步)=x 2(x +y )﹣y (x 2﹣y 2)(第三步)=x 2(x +y )﹣y (x +y )(x ﹣y )(第四步)=.阅读以上解题过程,解答下列问题:(1)在上述的因式分解过程中,用到因式分解的方法有.(至少写出两种方法)(2)在横线继续完成对本题的因式分解.(3)请你尝试用以上方法对多项式8x 3﹣1进行因式分解.10.已知4a b +=,2225a b +=.求下列各式的值.(1)ab ;(2)32231a a b ab b ++++.11.阅读图中的材料:利用分组分解法解决下面的问题:(1)分解因式:x 2﹣2xy+y 2﹣4;(2)已知△ABC 的三边长a ,b ,c 满足a 2﹣ab ﹣ac+bc =0,判断△ABC 的形状并说明理由.12.已知x+y=3,xy=54,求下列各式的值:(1)(x 2-2)(y 2-2);(2)x 2y-xy 2.13.我们常利用数形结合思想探索整式乘法的一些法则和公式.类似地,我们可以借助一个棱长为a 的大正方体进行以下探索:(1)在大正方体一角截去一个棱长为()b b a <的小正方体,如图1所示,则得到的几何体的体积为;(2)将图1中的几何体分割成三个长方体①、②、③,如图2所示,∵BC a =,AB a b =-,CF b =,∴长方体①的体积为()ab a b -.类似地,长方体②的体积为,长方体③的体积为;(结果不需要化简)(3)将表示长方体①、②、③的体积相加,并将得到的多项式分解因式的结果为;(4)用不同的方法表示图1中几何体的体积,可以得到的等式为.(5)已知4a b -=,2ab =,求33a b -的值.14.n 是正整数.(1)请用n 表示两个连续的奇数为、.(2)这两个连续奇数的平方差是8的倍数吗?给出理由.15.请认真观察图形,解答下列问题:(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);(2)由(1),你能得到怎样的等量关系?请用等式表示;(3)如果图中的a ,()b a b >满足2253a b +=,14ab =,求:①a b +的值;②44a b -的值.16.若一个数能表示成某个整数的平方的形式,则称这个数为完全平方数,完全平方数是非负数.例如:0=02,1=12,4=22,9=32,16=42,25=52,36=62,121=112….(1)若28+210+2n 是完全平方数,求n 的值.(2)若一个正整数,它加上61是一个完全平方数,当减去11是另一个完全平方数,写出所有符合的正整数.17.阅读:因为(x+3)(x-2)=x 2+x-6,说明x 2+x-6有一个因式是x-2;当因式x-2=0,那么多项式x 2+x-6的值也为0,利用上面的结果求解:(1)多项式A 有一个因式为x+m (m 为常数),当x=,A=0;(2)长方形的长和宽都是整式,其中一条边长为x-2,面积为x 2+kx-14,求k 的值;(3)若有一个长方体容器的长为(x+2),宽为(x-1),体积为4x 3+ax 2-7x+b ,试求a ,b 的值.18.阅读下列因式分解的过程,再回答所提出的问题.2(1)(1)(1)(1)[1x x x x x x x +++++=+++23(1)](1)(1)(1).x x x x x +=++=+(1)上述分解因式的方法是,共应用了次(2)若分解2(1)(1)(1)x x x x x +++++++ 2001(1)x x +,则需应用上述方法次.结果是.(3)分解因式:2(1)(1)(1)x x x x x +++++++ (1)(n x x n +为正整数).19.我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图A 可以用来解释2222()a ab b a b ++=+,实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.(1)图B 可以解释的代数恒等式是;(2)现有足够多的正方形和矩形卡片,如图C :①若要拼出一个面积为(3a+b )(a+2b )的矩形,则需要1号卡片张,2号卡片张,3号卡片张;②试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形,使该矩形的面积为6a 2+7ab+2b 2,并利用你画的图形面积对6a 2+7ab+2b 2进行因式分解.20.对任意一个四位正整数数m ,若其千位与百位上的数字之和为9,十位与个位上的数字之和也为9,那么称m 为“重九数”,如:1827、3663.将“重九数”m 的千位数字与十位数字对调,百位数字与个位数字对调,得到一个新的四位正整数数n ,如:m =2718,则n =1827,记D (m ,n )=m+n.(1)请写出两个四位“重九数”:,.(2)求证:对于任意一个四位“重九数”m ,其D (m ,n )可被101整除.(3)对于任意一个四位“重九数”m ,记f (m ,n )=D(m,n)101,当f (m ,n )是一个完全平方数时,且满足m >n ,求满足条件的m 的值.21.如图①是由边长为a 的大正方形纸片剪去一个边长为b 的小正方形后余下的图形.我们把纸片剪开后,拼成一个长方形(如图②).(1)探究:上述操作能验证的等式的序号是.①a 2+ab =a (a+b )②a 2-2ab +b 2=(a -b )2③a 2-b 2=(a +b )(a -b )(2)应用:利用你从(1)中选出的等式,完成下列各题:①已知4x 2-9y 2=12,2x +3y =4,求2x -3y 的值;②计算22222111111-1-1-1-1-2345100⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⨯⨯⨯⨯⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭22.如图,将一张大长方形纸板按图中虚线裁剪成9块,其中有2块是边长为a 厘米的大正方形,2块是边长都为b 厘米的小正方形,5块是长为a 厘米,宽为b 厘米的相同的小长方形,且a >b .(1)观察图形,可以发现代数式2a 2+5ab +2b 2可以因式分解为.(2)若图中阴影部分的面积为242平方厘米,大长方形纸板的周长为78厘米,求图中空白部分的面积.答案解析部分1.【答案】(1)4;14;194(2)解:∵22720x x -+=,∴172x x +=,2221141()24x x x x +=+-=,3232111741259(1)(1)248x x x x x x +=+-+=⨯-=.【解析】【解答】解:(1)∵2410x x -+=,∴14x x +=,222111()216214x x x x x x +=+-⋅=-=,4222422111()2194x x x x x x +=+-⋅=;故答案为:4;14;194;【分析】(1)模仿例题利用完全平方公式即可求解;(2)模仿例题利用完全平方公式和立方和公式即可求解。
因式分解的应用与探究(含答案)-

因式分解的应用与探究【温馨提示】《分解因式》一章中,我们主要学习了分解因式的概念、会用两种方法分解因式,即提公因式法、平方差公式和完全平方公式(直接用公式不超过两次)进行因式分解(指数是正整数)。
具体要求有:1、经历探索分解因式方法的过程,体会数学知识之间的整体(整式乘法与因式分解)联系。
2、了解因式分解的意义,会用提公因式法、平方差公式和完全平方公式(直接用公式不超过两次)进行因式分解(指数是正整数)。
3、通过乘法公式:(a +b )(a -b )=a 2-b 2,(a ±b )2=a 2±2ab +b 2的逆向变形,进一步发展观察、归纳、类比、概括等能力,发展有条理思考及语言表达能力。
在中考中,除了考查对一个整式进行分解因式等常规题型外,因式分解作为一种重要的解题方法和工具,经常出现于各种题型中,以下几种就值得引起注意。
★ 范例精讲例1【构造求值型】【山西04】已知x +y =1,那么221122x xy y ++的值为 ;分析:通过已知条件,不能分别求出x 、y 的值,所以要考虑把所求式进行变形,构造出x +y 的整体形式,即221122x xy y ++=12(x 2+2xy +y 2)=12(x +y )2=12.在此过程中,我们先提取公因式12,再用完全平方公式对原式进行因式分解,产生x +y 的整体形式,最后将x +y =1代入求出最终结果.例2【构造求值型】已知x 2+2x +y 2+6y +10=0,求xy 的值. 答:xy =3例3【构造求值型】已知:a =10000,b =9999,求a 2+b 2-2ab -6a +6b +9的值。
解:a 2+b 2-2ab -6a +6b +9=(a -b )2-2×(a -b )×3+32=(a -b -3)2=4例4【构造求值型】【广西桂林04】计算:=+--⋅⋅⋅---20191832222222 ;分析:为了便于观察,我们将原式“倒过来”,即 原式=22222223181920+--⋅⋅⋅--- =2222)12(2231819+--⋅⋅⋅---=22222231819+--⋅⋅⋅-- =222)12(22318+--⋅⋅⋅-- =22222318+--⋅⋅⋅- =……=22+2=4+2=6此题的解题过程中,巧妙地用到了提公因式法进行分解因式,使结构特点明朗化,规律凸现出来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
x 1 x 1
8.(2017·宿迁)先化简,再求值:
x
x 1
x 1 x2 1
,其中 x 2 .
9.(2013•宿迁)先化简,再求值:
1
x
1
1
x
2
4x x2 1
4
,其中
x=3.
课堂小结
通过本节课的学习,你有那些收获? 先想一想,再与大家交流.
课后作业
完成学案上的“巩固练习”.
因 2.运用公式法:
式 分
(1)平方差公式: a2-b2=(a+b)(a-b); (2)完全平方公式:
解 a2±2ab+b2=(a±b)2.
的 3.十字相乘法:
方 x2+(p+q)x+pq=(x+p)(x+q)
法
注意点
确定好公因式是解 题的关键.
要熟记公式的特点, 两项式时考虑平方差 公式,三项式时考虑 完全平方公式化.
一、因式分解
巩固练习 快速抢答:
1.(2017·常德)下列各式由左到右的变形中,属 于分解因式的是( C ) A.a(m+n)=am+an B.a2-b2-c2=(a-b)(a+b)-c2 C.10x2-5x=5x(2x-1) D.x2-16+6x=(x+4)(x-4)+6x
一、因式分解
巩固练习 快速抢答: 2.(2016·淮安)分解因式:m2-4= (m+2)(m-2) . 3.(2017·苏州)因式分解:4a2-4a+1= (2a-1)2 . 4.(2016·宿迁)因式分解:2a2-8=2(a+2)(a-2) . 5.(2017·南京玄武区模拟)分解因式:
变式提高
(2016·苏州)先化简,再求值:
x2 x2
2x 1 x
1
x
2 1
,其中 x
3.
四、因式分解与方程
例6解方程: (1)x2+2x=0; (2)(2015·宿迁)解方程:x2+2x=3.
思考:分解因式:x2+2x-3= (x+3)(x-1) .
四、因式分解与方程
则△ABC的形状是( A ) A.等腰三角形 B.等边三角形 C.锐角三角形 D.不确定
课堂检测
1.(2015·常州)分解因式: 2x2 2y2 =
.
2.(2017·南通通州区模拟)因式分解: a2b b3
.
3.(2016·南京)分解因式 2ab c 3b c的结果是
2018中考专题复习
因式分解及其应用
宿迁市近五年中考命题规律
考点
2013 2014 2015 2016 2017
因式分解 题号
11 9
(概念与方法 )
分值
33
因式分解 题号
9
11
与求值 分值
3
3
因式分解 题号 20
10 18
与分式 分值 8
36
因式分解 题号 27
18
25
与方程 分值 2
ห้องสมุดไป่ตู้
3
2
共计 分值 10 3 6 6 11
.
4.(2017·盐城亭湖区模拟)若 a 2b 2 ,则6 3a 6b 的值为
.
5.(2018·模拟)若 x2-2x-3=(x+p)(x+q)(p>q),则 p=
,q=
.
6.(2016·扬州)当 a=2016 时,分式 a2 4 的值是
.
a2
7.(2016·宿迁)计算:x2 x
这个是课后的内容, 不做硬性的要求,熟 练运用在高中学习就 会轻松许多.一定要 熟记公式的特点.
核心考点解读
知识点
因 式 一“提”; 分 二“套”; 解 三“查”. 的 步 骤
注意点
一“提”:提取公因式; 二“套”:套用公式; 三“查”:检查结果—— ①整式积的形成,②每一 个因式要分解到不能再分 解为止.
一、因式分解
例1 (2013河北中考)下列等式从左到右的变形, 属于因式分解的是( D ) A.a(x-y)=ax-ay B.x2+2x+1=x(x+2)+1 C.(x+1)(x+3)=x2+4x+3 D.x3-x=x(x+1)(x-1)
一、因式分解
例 2 分解因式: (1)(2017·淮安)分解因式: ab b2 b(a-b) . (2)(2017·扬州)因式分解:3x2 27 3(x+3)(x-3). (3)(2017·无锡)分解因式:3a2 6a 3 3(a-1)2 .
核心考点解读
知识点
注意点
因 式
就是把一个多项式化 为几个整式的乘积的
因式分解是将一个多项 式化成几个整式积的形
分 形式.
式的恒等变形,若结果
解 因式分解与整式乘法 不是积的形式,则不是
的 是互逆运算. 概
因式分解,还要注意分 解要彻底.
念
核心考点解读
知识点
1.提取公因式法:
ma+mb+mc=m(a+b+c)
例7 已知a,b,c为△ABC的三条边的长,且满 足:b2+2ab=c2+2ac,回答下列问题: (1)试判断△ABC属于哪一类三角形; (2)若a=4,b=3,则△ABC的周长为 10 .
四、因式分解与方程
巩固练习 1.方程t2+5t+6=0的解为 t1=﹣2, t2=﹣3 .
2.已知a、b是△ABC的两边,且a2+b2=2ab,
a-b=2,则a2b-ab2的值是 6 . 2.(2017·宿迁)若 a-b=2,则代数式
5+2a-2b的值为 9 . 3.(2015·苏州)若a-2b=3,则 9-2a+4b的值
为 3.
三、因式分解与分式
例
5(2016·徐州)计算:
x2 1 x 1
x
2
x2
2x x
1
.
三、因式分解与分式
2x2+4x+2= 2(x+1)2 .
二、因式分解与求值
例3(2017·徐州)已知a+b=10,a-b=8,则 a2-b2= 80 .
例4(2016·淮安)已知a-b=2,则代数式 2a-2b-3的值是( A )
A.1 B.2 C.5 D.7
二、因式分解与求值
巩固练习 快速抢答: 1.(2014•宿迁)已知实数a,b满足ab=3,
