工程力学第十二章全解
12第12章动能定理

d ( 1 mv 2 ) = δW 2
动能定理的微分形式
积分, 将上式沿路径 M 1M 2 积分,可得
1 1 2 2 mv2 − mv1 = W12 动能定理的积分形式 2 2
18
2.质点系的动能定理 . 对质点系中的一质点 M i : d ( 1 mi vi 2 ) = δWi 2 对整个质点系, 对整个质点系,有:
1 1 − ). r2 r1
(ϕ =ϕ 2 −ϕ 1 )
∴ W12 =
ϕ2 ϕ1
∫
r M z ( F ) dϕ
ϕ2
作用于转动刚体上力的功等于力矩的功。 作用于转动刚体上力的功等于力矩的功。
如果作用力偶, 如果作用力偶,M , 且力 W12 = 偶的作用面垂直转轴
注意:功的符号的确定。 注意:功的符号的确定。
2.定轴转动刚体 T = ∑ mi vi 2 = (∑ mi ri 2 )ω 2 = 1 J zω 2 .
2
2 3.平面运动刚体 T = 1 M vC + 1 J Cω 2 . 2 2 1 T = J Pω 2 (P为速度瞬心)
1 2
1 2
2
1 = ( J C + Md 2 )ω 2 2 1 1 1 1 2 2 2 2 2 = J Cω + M (d ω ) = J Cω + M vC 2 2 2 2
r r r δW = Fs ⋅ drc = Fs ⋅ vC dt = 0. r r drc = vC ⋅ dt = 0,
(3) 滚动摩擦阻力偶 M 的功
r vo
A F s
10
s 若M = 常量则 W12 = − Mϕ = − M R
FN
五.质点系内力的功 r r r r r r r r δ W = F ⋅ drA + F '⋅drB = F ⋅ drA − F ⋅ drB
工程力学 第12章 强度理论 习题及解析

工程力学(工程静力学与材料力学)习题与解答第12章 强度理论12-1 对于建立材料在一般应力状态下的失效判据与设计准则,试选择如下合适的论述。
(A )逐一进行试验,确定极限应力;(B )无需进行试验,只需关于失效原因的假说;(C )需要进行某些试验,无需关于失效原因的假说; (D )假设失效的共同原因,根据简单试验结果。
知识点:建立强度理论的主要思路 难度:一般 解答:正确答案是 D 。
12-2 对于图示的应力状态(y x σσ>)若为脆性材料,试分析失效可能发生在: (A )平行于x 轴的平面; (B )平行于z 轴的平面;(C )平行于Oyz 坐标面的平面; (D )平行于Oxy 坐标面的平面。
知识点:脆性材料、脆性断裂、断裂原因 难度:难 解答:正确答案是 C 。
12-3 对于图示的应力状态,若x y σσ=,且为韧性材料,试根据最大切应力准则,失效可能发生在: (A )平行于y 轴、其法线与x 轴的夹角为45°的平面,或平行于x 轴、其法线与y 轴的夹角为45°的平面内;(B )仅为平行于y 轴、法线与z 轴的夹角为45°的平面; (C )仅为平行于z 轴、其法线与x 轴的夹角为45°的平面; (D )仅为平行于x 轴、其法线与y 轴的夹角为45°的平面。
知识点:韧性材料、塑性屈服、屈服原因 难度:难 解答:正确答案是 A 。
12-4 铸铁处于图示应力状态下,试分析最容易失效的是: (A )仅图c ; (B )图a 和图b ; (C )图a 、b 和图c ; (D )图a 、b 、c 和图d 。
知识点:脆性材料、脆性断裂、断裂准则 难度:一般 解答:正确答案是 C 。
12-5低碳钢处于图示应力状态下,若根据最大切应力准则, 试分析最容易失效的是: (A )仅图d ; (B )仅图c ; (C )图c 和图d ; (D )图a 、b 和图d 。
工程力学第12章答案
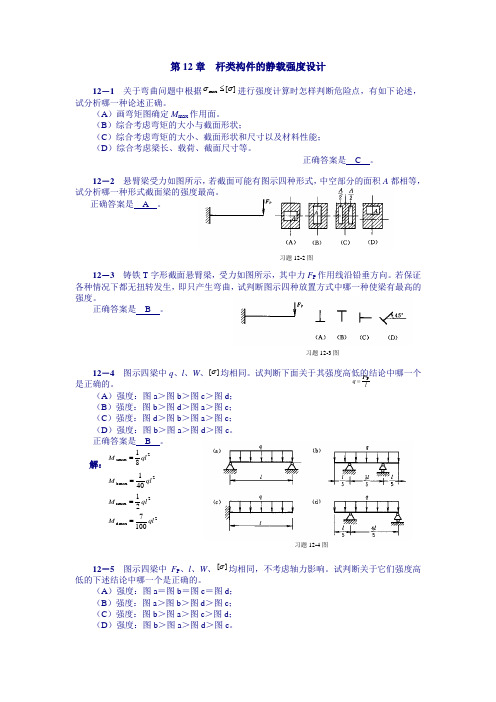
习题12-3图 习题12-2图习题12-4图 第12章 杆类构件的静载强度设计12-1 关于弯曲问题中根据][max σσ≤进行强度计算时怎样判断危险点,有如下论述,试分析哪一种论述正确。
(A )画弯矩图确定M max 作用面。
(B )综合考虑弯矩的大小与截面形状;(C )综合考虑弯矩的大小、截面形状和尺寸以及材料性能; (D )综合考虑梁长、载荷、截面尺寸等。
正确答案是 C 。
12-2 悬臂梁受力如图所示,若截面可能有图示四种形式,中空部分的面积A 都相等,试分析哪一种形式截面梁的强度最高。
正确答案是 A 。
12-3 铸铁T 字形截面悬臂梁,受力如图所示,其中力F P 作用线沿铅垂方向。
若保证各种情况下都无扭转发生,即只产生弯曲,试判断图示四种放置方式中哪一种使梁有最高的强度。
正确答案是 B 。
12-4 图示四梁中q 、l 、W 、][σ均相同。
试判断下面关于其强度高低的结论中哪一个是正确的。
(A )强度:图a >图b >图c >图d ; (B )强度:图b >图d >图a >图c ; (C )强度:图d >图b >图a >图c ; (D )强度:图b >图a >图d >图c 。
正确答案是 B 。
解:2amax 81ql M =2bmax 401ql M =2cmax 21ql M = 2dmax 1007ql M =12-5 图示四梁中F P 、l 、W 、][σ均相同,不考虑轴力影响。
试判断关于它们强度高低的下述结论中哪一个是正确的。
(A )强度:图a =图b =图c =图d ; (B )强度:图a >图b >图d >图c ; (C )强度:图b >图a >图c >图d ; (D )强度:图b >图a >图d >图c 。
l q PF=3231ABM )(o M(a)习题12-5题习题12-6题32l M P /F 31(d-1)lM P /F 21AB(c-1)lM P /F 10351BA 10351 (b-1) l M P /F 41AB 41 (a-1) 正确答案是 B 。
理论力学基础 动量矩定理3

平 面
二、分清各构件的运动情况(平移、转动、平面运动、 静止)
运 动
三、各构件的运动情况之间的关系
微 (平移:速度、加速度)(转动:角速度、角加速度)
分
方 (平面运动:质心速度和加速度、角速度、角加速度)
程
四、根据运动情况运用各类方程
鞍山科技大学机械工程与自动化学院工程力学系
理论力学
第十二章 动量矩定理
Fi(e)
F1
D
运 动 微 分 方 程
d
dt
JC
JC
m
d
2
rC
dt 2
F (e)
i
C
M C (Fi(e) )
x′
O
x
刚体平面运动微分方程
JC
d 2
dt 2
M C (Fi(e) )
鞍山科技大学机械工程与自动化学院工程力学系
理论力学
第十二章 动量矩定理
例题十五 如图所示,有一轮子,轴的直径为
例题十九 如图所示,板的质量为m1,受水平力
F作用,沿水平面运动,板与平面间的动摩擦因数
第 六 节
为f。在板上放一质量为m2的均质实心圆柱,此圆 柱对板只滚不滑。求板的加速度。(习题12-18)
平
C
面 运
动
微
分
方 程
F2′ FN′ 2
F
C
ar m2g
aC
a
F
FN2 F2
F1
m1g
FN1
鞍山科技大学机械工程与自动化学院工程力学系
mg
鞍山科技大学机械工程与自动化学院工程力学系
第十二章:动量矩定理

周期 T = 2π J O
mga
§12-4 刚体对轴的转动惯量
n
Jz
=
∑
i −1
m
i
ri
2
单位:kg·m2
1. 简单形状物体的转动惯量计算
(1)均质细直杆对一端的转动惯量
∫ J z =
l 0
ρl x2dx
=
ρll3
3
由 m = ρll ,得
Jz
=
1 ml 2 3
(2)均质薄圆环对中心轴的转动惯量
与 zC 轴之间的距离。
即:刚体对于任一轴的转动惯量,等于刚体对 于通过质心并与该轴平行的轴的转动惯量,加 上刚体的质量与两轴间距离平方的乘积.
证明: J zC = ∑ mi (x12 + y12 )
Jz =∑mi r2 =∑mi (x2 +y2)
= ∑ mi[x12 + ( y1 + d )2 ]
=
1 ml 2 3
则
J zC
=
Jz
−
m( l )2 2
=
ml 2 12
要求记住三个转动惯量
(1) 均质圆盘对盘心轴的
转动惯量 mR2
2
(2) 均质细直杆对一端的
转动惯量 ml 2
3
(3) 均质细直杆对中心轴
的转动惯量 ml 2
12
§12-5 质点系相对于质心的动量矩定理
1.对质心的动量矩
∑ ∑ r
=
r LC
r LO
=
rrC
× mvrC
+
r LC
=
r M
O
(
mvrC
)
+
工程力学习题 及最终答案

第一章第二章第三章绪论思考题1) 现代力学有哪些重要的特征?2) 力是物体间的相互作用。
按其是否直接接触如何分类?试举例说明。
3) 工程静力学的基本研究内容和主线是什么?4) 试述工程力学研究问题的一般方法。
第二章刚体静力学基本概念与理论习题2-1 求图中作用在托架上的合力F R。
12030200N习题2-1图页脚内容页脚内容2-2 已知F 1=7kN ,F 2=5kN, 求图中作用在耳环上的合力F R 。
2-3 求图中汇交力系的合力F R 。
2-4 求图中力F 2的大小和其方向角。
使 a )合力F R =1.5kN, 方向沿x 轴。
b)合力为零。
2-5 二力作用如图,F 1=500N 。
为提起木桩,欲使垂直向上的合力为F R =750N ,且F 2力尽量小,试求力F 2的大小和角。
245601习题2-2图(b)xy4530F 1=30NF 2=20NF3=40N A xy4560F 1=600NF 2=700NF 3=500NA 习题2-3图(a )x70F 2F 1=1.25kN A习题2-4图30F 1=500NAF 2页脚内容2-6 画出图中各物体的受力图。
(b)B (a )A (c)(d)DACDB页脚内容2-7 画出图中各物体的受力图。
2-8 试计算图中各种情况下F 力对o 点之矩。
习题2-6图(d)习题2-7图(a )C DB DABCBABC页脚内容2-9 求图中力系的合力F R 及其作用位置。
习题2-8图P (d)PF( a )F 3M =6kN m F 3F 2页脚内容2-10 求图中作用在梁上的分布载荷的合力F R 及其作用位置。
( a )q 1=600N/mq=4kN/m( b )q A =3kN/m习题2-9图( c ) F 4F 3页脚内容2-11 图示悬臂梁AB 上作用着分布载荷,q 1=400N/m ,q 2=900N/m, 若欲使作用在梁上的合力为零,求尺寸a 、b 的大小。
工程力学 第2版 第12章 动荷应力和交变应力

影响构件持久极限的主要因素 构件外形的影响 构件截面尺寸的影响 构件表面加工质量的影响
a
Kd 1 g
j max
Kd
12.1.2 构件受冲击时的动荷应力 当具有一定速度的运动物体碰到静止的构件时,物体 和构件间会产生很大的作用力,这种现象称为冲击。如汽 锤锻造工件、落锤打桩、金属冲压加工、铆钉枪铆接、高
速转动的传动轴制动等,都是冲击的一些工程实例。
d max Kd j max [ ]
综合考虑以上三种主要因素,则在对称循环下构件的持久极限表示为
0 1
K
1
或
0 1
K
1
目前在机械设计中,通常将疲劳强度设计准则写成比较安全因数的形式
构件在对称循环弯曲或拉压时
n n
n
0 1
[ 1 ]
n
0 1
max
通 常 把 由 最 大 应 力 max 变 到 最 小 应 力 min , 再 由 最 小 应 力 min变回到最大应力max的过程,称之为一个应力循环。把 一个应力循环中最小应力与最大应力之比值称为循环特性, 用r表示,即
r min max
常见的交变应力循环有 对称循环,
循环特性r = -1。
第12章 动荷应力与交变应力
12.1 动荷应力 10.2 交变应力
12.1 动荷应力
如果作用在构件上的载荷随时间有显著的变化,或在载荷作
用下构件上各点有显著的加速度,这种载荷即称为动载荷。
《工程力学》最新备课课件:第十二章-静定结构的内力计算

0.086 ql2 l
q
x 0.172l
1 ql2 8
1 ql2 0.125ql2 8
与简支梁相比:弯矩较小而且均匀. 从分析过程看:附属部分上若无外力,其上也无内力。
二、静定平面刚架的内力计算
刚架的杆件主要是以弯曲变形为主的,是以梁和柱组成的 具有刚结点的结构。刚架的变形特点在于:它的刚结点处 各杆不能发生相对转动,因而各杆之间的夹角始终保持不 变。
最新版
《工程力学》
备课课件 第十二章:静定结构的内力计算
一、多跨静定梁的内力计算
静定结构几何特性:无多余约束的几何不变体系 静力特征:仅由静力平衡条件可求全部反力内力
1.单跨静定梁
(1)梁支反力 (2)截面法求指定截面内力 (3)作内力图的基本方法 (4)弯矩、剪力、荷载集度之间的微分关系 (5)叠加法作弯矩图
➢画层叠图,即将多跨静定梁拆成单跨梁; ➢计算各单跨梁的约束力:
按层叠图依次画出各单跨梁的受力图,注意基 础部分受到由附属部分传来的反作用力; ➢结合区段叠加绘制整个多跨静定梁的内力图
例1: 作内力图
ql
q
AB
C
l l 2l
4l
ql
D EF 2l l l
ql
q
1 ql
2
ql ql
ql
1 ql 2
ql
1/2qa2
↓↓↓↓↓↓↓↓↓↓↓↓↓↓
C
MB=0.5qa2+2aXB-aYB=0 (2q) a
解方程(1)和(2)可得
a
1/2qa2
XB=0.5qa YB=1.5qa
A
3) 再由整体平衡
qa/X2 A
X=0 解得:XA=0.5qa
(完整版)工程力学课后详细答案

(完整版)⼯程⼒学课后详细答案第⼀章静⼒学的基本概念受⼒图第⼆章平⾯汇交⼒系2-1解:由解析法,23cos 80RX F X P P N θ==+=∑12sin 140RY F Y P P N θ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos 2944RYR RF F P F '∠==o v v2-2解:即求此⼒系的合⼒,沿OB 建⽴x 坐标,由解析法,有123cos45cos453RX F X P P P KN ==++=∑o o13sin 45sin 450RY F Y P P ==-=∑o o故:223R RX RY F F F KN=+= ⽅向沿OB 。
2-3 解:所有杆件均为⼆⼒杆件,受⼒沿直杆轴线。
(a )由平衡⽅程有:0X =∑sin 300AC AB F F -=o0Y =∑cos300AC F W -=o0.577AB F W=(拉⼒)1.155AC F W=(压⼒)(b )由平衡⽅程有:0X =∑ cos 700AC AB F F -=o0Y =∑sin 700AB F W -=o1.064AB F W=(拉⼒)0.364AC F W=(压⼒)(c )由平衡⽅程有:0X =∑cos 60cos300AC AB F F -=o o0Y =∑sin 30sin 600AB AC F F W +-=o o 0.5AB F W= (拉⼒)0.866AC F W=(压⼒)(d )由平衡⽅程有:0X =∑sin 30sin 300AB AC F F -=o o0Y =∑cos30cos300AB AC F F W +-=o o0.577AB F W= (拉⼒)0.577AC F W= (拉⼒)2-4 解:(a )受⼒分析如图所⽰:由x =∑ 22cos 45042RA F P -=+o15.8RA F KN∴=由0Y =∑22sin 45042RA RB F F P +-=+o7.1RB F KN∴=(b)解:受⼒分析如图所⽰:由x =∑cos 45cos 45010RA RB F F P ? --=o o0Y =∑sin 45sin 45010RA RB F F P ?+-=o o联⽴上⼆式,得:22.410RA RB F KN F KN==2-5解:⼏何法:系统受⼒如图所⽰三⼒汇交于点D ,其封闭的⼒三⾓形如图⽰所以:5RA F KN= (压⼒)5RB F KN=(与X 轴正向夹150度)2-6解:受⼒如图所⽰:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-?=--2-7解:受⼒分析如图所⽰,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=o o0Y =∑sin 45sin 450CBRA F F '-=o o联⽴后,解得:0.707RA F P=0.707RB F P=由⼆⼒平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为⼆⼒杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ?--=o o0Y =∑sin 30sin 600AB AC F F W +-=o o联⽴上⼆式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反⼒全为拉⼒,以D ,B 点分别列平衡⽅程(1)取D 点,列平衡⽅程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡⽅程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联⽴上⼆式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα=+取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '=Q 故有:22cos 1cos 2sin cos 2sin NH P P F ααααα??=+= ?2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=o o0Y =∑cos 75cos 750AB AD F F P +-=o o联⽴后可得: 2cos 75AD AB PF F ==o取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=o ocos5cos80NDAD F F '=?oo由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND ADP F F F KN '∴===?=o o o o o2-12解:整体受⼒交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=o0Y =∑sin sin 300RA F P α-=o联⽴上⼆式得:2.92RA F KN=1.33DC F KN=(压⼒)列C 点平衡x =∑405DC AC F F -?=0Y =∑ 305BC AC F F +?=联⽴上⼆式得: 1.67AC F KN=(拉⼒)1.0BC F KN=-(压⼒)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联⽴⽅程后解得: 5RD F Q =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=o0Y =∑sin 450RB RA F F P --=o且RE REF F '=联⽴上⾯各式得: 22RA FQ =2RB F Q P=+(3)取BCE 部分。
工程力学(上)电子教案第十二章重点教材

第十二章 动量矩定理第一、二节 质点和质点系的动量矩 动量矩定理教学时数:2学时教学目标:1、 对动量矩的概念有清晰的理解2、 熟练的计算质点系的动量矩教学重点:质点系的动量矩 质点系的动量矩定理教学难点:质点系的动量矩定理 教学方法:板书+PowerPoint教学步骤: 一、引言由静力学力系简化理论知:平面任意力系向任一简化中心简化可得一力和一力偶,此力等于平面力系的主矢,此力偶等于平面力系对简化中心的主矩。
由刚体平面运动理论知:刚体的平面运动可以分解为随同基点的平动和相对基点的转动。
若将简化中心和基点取在质心上,则动量定理(质心运动定理)描述了刚体随同质心的运动的变化和外力系主矢的关系。
它揭示了物体机械运动规律的一个侧面。
刚体相对质心的转动的运动变化与外力系对质心的主矩的关系将有本章的动量矩定理给出。
它揭示了物体机械运动规律的另一个侧面。
二、质点和质点系的动量矩 1、质点的动量矩设质点M 某瞬时的动量为v m ,质点相对固定点O 的矢径为r,如图。
质点M 的动量对于点O 的矩,定义为质点对于点O 的动量矩,即()v m r v m M L O O ⨯==()v m M O垂直于△OMA ,大小等于△OMA 面积的二倍,方向由右手法则确定。
类似于力对点之矩和力对轴之矩的关系,质点对固定坐标轴的动量矩等于质点对坐标原点的动量矩在相应坐标轴上的投影,即 ()d mv v m M L xy Z z ==质点对固定轴的动量矩是代数量,其正负号可由右手法则来确定。
动量矩是瞬时量。
在国际单位制中,动量矩的单位是s m kg /2⋅ 2、质点系的动量矩(1)质点系对固定点的动量矩设质点系由n 个质点组成,其中第i 个质点的质量为i m ,速度为i v ,到O 点的矢径为i r,则质点系对O 点的动量矩(动量系对点的主矩)为:()∑∑⨯==i i i i i O O v m r v m M L即:质点系对任一固定点O 的动量矩定义为质点系中各质点对固定点动量矩的矢量和。
工程力学第12章PPT教案学习

思第考35题页1/共2-456图页
12-6 一压杆如图所示。在计算其临界力Fcr时,如考虑在yz平面内失稳,应该 用哪一根轴的惯性矩I和惯性半径i来计算?
第3思6页考/共题4162页-6图
12-7 图中所示各压杆的材料和截面尺寸均相同,试问哪种情况承受的压力最大 ? 哪种情况承受的压力最小?
第31页/共46页
2. 选用合理的截面形状 压杆的截面形状对临界力的数值有很大的影响,在一定的截面面积下,应设法 增大截面的惯性矩,从而增大惯性半径, 减小压杆的柔度,起到提高压杆稳定性的 作用。为此,应尽量使截面的材料远离中性轴。例如,空心圆管要比截面面积相同的 实心圆杆合理。另外,当压杆两端各方向具有相同的支承条件时,它的失稳总是发 生在抗弯刚度最小的纵向平面。 为了充分发挥压杆抗失稳的能力,不仅要选用惯性 矩大的截面, 而且还应选用具有Imax=Imin的截面,使压杆在各个方向的稳定性相等 。
稳定安全系数都大于强度安全系数。例如:对于钢材,取nst=2.8~3.0;对于铸铁, 取nst=5.0~5.5;对于木材,取nst =2.8~3.2。基于如上压杆稳定设计要求,在工 程上常采用安全系数法。采用安全系数法时,
nst [nst ]
第24页/共46页
(12-8)
式中,[n]st为规定的稳定安全系数,在静载荷作用下, 它略高于强度安全系 数。nst为工作稳定安全系数,可由下式确定:
cr a b 589 3.82 75 303MPa
于是可得临界力
Fcr
cr
A
303
3.14
4
40
2
381KN
第29页/共46页
(2) 校核压杆的稳定性。
nst
清华出版社工程力学答案-第12章 简单的静不定问题

4. 联立求解 将(a) 、 (b) 、 (c)三式联立,求得:
F1 =
(16 + 2 ) l
2 Eδ
2 EAδ
, F2 =
1
(16 + 2 ) l
4 EAδ
1
据此求得二杆横截面上的正应力分别为:
F1杆 = F2杆 =
(16 + 2 ) l
4 Eδ
=
2 × 200 ×109 × 1. 5 × 10−3
1
(16 + 2 ) ×1.5
= 16.2 MPa
(16 + 2 ) l
=
4 × 200 × 109 ×1. 5 ×10−345.9 MPa
12-7 两端固定的阶梯杆如图所示。已知 AC 段和 BD 段的横截面面积为 A,CD 段的 横截面面积为 2A。杆材料的弹性模量 E=210GPa,线膨胀系数α =12×10-6 /oC。试求:当温 度升高 30°C 后,该杆各段横截面内的应力。
将式(2)代入式(1) ,得到 4 x − 2b = 3b − 2 x 由此解得
=
σi
(2)
x=
5 b 6
12-4 在图示结构中,假设梁 AC 为钢杆,杆 1,2,3 的横截面面积相等,材料相同。 试求:三杆的轴力。 解:设三杆轴力分别为 FN1、FN2、FN3,方向如图 b 所示。由于假设 3 杆缩短,1、2 杆 伸长,故应将 FN3 设为压力,而 FN1、FN2 设均为拉力。
A
(a) 固定端
圆管
m
B
M=ml
实心圆轴 l 刚性圆盘 M=ml m
A
(b)
圆管
B
MB 管
MB B管 管 MB B轴 轴 圆管 实心圆轴 刚性圆盘
第十二章 工程力学之组合变形

二、叠加原理 杆在组合变形下的应力和变形分析,一般可利用叠加原理。
叠加原理: 实践证明,在小变形和材料服从虎克定律的前提下, 杆在几个载荷共同作用下所产生的应力和变形,等于每个载荷 单独作用下所产生的应力和变形的总和。 当杆在外力作用下发生几种基本变形时,只要将载荷简化为一 系列发生基本变形的相当载荷,分别计算杆在各个基本变形下 所产生的应力和变形,然后进行叠加,就得到杆在组合变形下 的应力和变形。 另外,在组合变形情况下,一般不考虑弯曲剪应力。
(2)根部截面的内力分析
作轴的扭矩图和弯矩图如图12-6(c)所示。
根部截面上的扭矩 T m 120 N m
弯矩
M Pl 3Fl 3 960 0.12 346 N m
(3)应力分析
根部截面在弯曲、扭转基本变形下的应力分布如图12-6(d) 所示
由此可见,A点既有正应力,也有剪应力,B点只有剪应力
max N M 5.9 115 120.9MPa
最大应力几乎等于许用应力,故可安全工作。
例12-2:图12-5(a)所示为一钻床,在零件上钻孔时,钻床的 立柱受到的压力为P=15kN。已知钻床的立柱由铸铁制成,许用 拉应力,[σ拉]=35MPa,e=400mm试计算立柱所需的直径d。 解: (1)内力分析,判断变形 形式 用截面法求立柱横截面上 的内力,如图12-5(b)所 示,横截面上的内力有两 个,轴力FN和弯矩M,且 有
可见, Tx和Fcx使AC产生轴向压缩,而Ty、P和Fcy产生弯曲变 形,所以AC杆实际发生的是轴向压缩与弯曲的组合变形。 (2)作内力图,找出危险截面 AC梁的轴力图和弯矩图如图12-4(b)所示。
从图中可以看出,在梁的中间截面上有最大弯矩,而轴力在各 个截面上是相同的,所以,梁的中间截面是危险截面。
疲劳破坏及其断口特征.ppt

有缺陷怎么办? 有裂纹是否发生破坏?
研究含缺陷材料的强度 --断裂 Fracture
缺陷从何而来? 裂纹如何萌生?
材料固有或使用中萌生、扩展 --疲劳与断裂
多次载荷作用下如何破坏? 构件能用多长 研究多次使用载荷作用下 时间?(寿命) 裂纹如何萌生、扩展。 --疲劳 Fatigue & Fracture
1954年1月, 英国慧星(Comet)号喷气客机坠入地中 海(机身舱门拐角处开裂);
3
1967年12月15日,美国西弗吉尼亚的 Point Pleasant桥倒塌, 46人死亡;
1980年3月27日,英国北海油田Kielland 号钻井 平台倾复;127人落水只救起 89人;
主要原因是由缺陷或裂纹导致的断裂。
破坏是局部损伤累积的结 破坏是瞬间发生的。
剩余的47%,有待于进一步基础研究的突破。
如裂纹起始、扩展的进一步基础研究;高强度、 高韧性、无缺陷材料的研究等。
7
疲劳断裂引起的空难达每年100次以 上国际民航组织 (ICAO)发表的
“涉及金属疲劳断裂的重大飞机失事调查”指出: 80年代以来,由金属疲劳断裂引起的机毁人亡
重大事故,平均每年100次。(不包括中、苏) Int. J. Fatigue, Vol.6, No.1, 1984
已知任意二 个量,其余 即可导出。
应力比或循环特性参数 R=Smin/Smax
11
应力比R反映了载荷的循环特性。如
S R=-1
S R=0
S R=1
0
t
Smax=-Smin 对称循环
0 Smin=0 t 脉冲循环
0
t
Smax=Smin
静载
设计:用Smax,Smin;直观; 试验:用Sm,Sa; 便于加载; 分析:用Sa,R;突出主要控制参量, 便于分类讨论。
工程力学第12章2-讲义修改稿

扭转时的变形大小表现为两个横截面之间的相对转角 (扭转角)的大小。
(1) 相邻为 dx 的两个横截面之间的相对扭转角为
(12.1)
d
T
dx
GIp
(12.14)
d
(12.1)
T
dx GIp
(2) 距离为 l 的两个横截面之间的相对扭转角为
d l T dx
l
0 GIp
圆轴扭转时的破坏为屈服或断裂,通过扭转破坏试验可以
确定各种材料屈服或断裂时的 s或 b,统称为扭转极限应
力 u。
u
(12.18)
n
为了保证圆轴扭转时的强度,应要求轴内各横截面上的最大 切应力
max
(12.7)
(
T
Wp
)max
圆轴扭转的强度条件 (12.19)
5
圆轴扭转的强度计算
受扭过程中,线性弹性;屈服 (出现纵、横向滑移线);试件
s
沿横截面破断(被剪段)。
O
3
(2) 脆性材料(铸铁)的扭转试验
受扭过程中,变形很小,没有线 b
弹性和塑性阶段,只有强度极
限 b,最终与轴线约成 45倾角
的螺旋面上破断(拉断)。
O
4
§12.4 圆轴扭转时的强度与刚度计算
圆轴扭转的强度准则
6
圆轴扭转的刚度准则
工程实际中,大部分的轴类构件还对扭转变形有严格的限制。 例如:某些机床轴的扭转角过大会降低加工精度。 因此,轴类构件常需进行刚度计算。
轴的刚度条件是限制单位长度的扭转角在某个范围内
(12.3)
T
180
GIp
(12.20)
单位换算的需要
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E E
M
y
r
这表明,直梁的横截面上的正应力
沿垂直于中性轴的方向按线性规律变化
(3)静力学关系━━ 应力与内力。
梁的横截面上与正应力相应的法 向内力元素dA(图d )不可能组成轴 力( FN A d A 0 ),也不可能组成对 (d) 于与中性轴垂直的y 轴(弯曲平面内的
只是绕垂直于弯曲平面(纵向平面)的某一轴转动,转动后
的横截面与梁弯曲后的轴线保持正交。
此假设已为弹性力学的理论分析结果所证实。
〈3〉纵向线应变在横截面范围内的变化规律 图c为由相距d x的两横截面取出的梁段在梁弯曲后的情况, 两个原来平行的横截面绕中性轴相对转动了角d。梁的横截
面上距中性轴 z为任意距离 y 处的纵向线应变由图c可知为
第十二章 弯曲应力
§12-1 梁弯曲时的正应力 §12-2 惯性矩的计算 §12-3 梁弯曲时的强度计算 §12-4 梁弯曲时的切应力 §12-5 提高弯曲强度的措施
M
FQ
梁横截面上 与弯矩M对应, 与剪力F对应。
F
FQ
M
C F
C
M
F
A
12-1 梁弯曲时的正应力
一、弯曲分类
轴)的内力偶矩( M y AzdA 0 ),只
能组成对于中性轴 z 的内力偶矩,即
M z y d A M
A
将 E
r 代入上述三个静力学条件,有
y
FN d A
A
E
r
E
A
yd A
ESz
r
0
(a)
M y z d A
A
r
E
A
yz d A
B1B B1 B y d AB1 O1O2 dx
若中性层的半径为r(如图c),则有 (c)
dx r d
y
r
即梁在纯弯曲时,其横截面上任一点处的纵向线应变 与该点至中性轴的距离 y 成正比。 (2)物理关系━━力与变形(应力、应变) 梁的材料在线弹性范围内工作(胡克定律),且拉、 压弹性模量相同时,有
纯弯曲理论的推广
工程中实际的梁大多发生横力弯曲,此时梁的横截面 由于切应力的存在而发生翘曲(warping)。此外,横向力还 使各纵向线之间发生挤压(bearing)。因此,对于梁在纯弯曲 时所作的平面假设和纵向线之间无挤压的假设实际上都不
再成立。但弹性力学的分析结果表明,受满布荷载的矩形
截面简支梁,当其跨长与截面高度之比 l 大于5时,梁的
纯弯曲 (pure bending) ━━ 梁或梁上的某段内各横截面上
无剪力而只有弯矩,横截面上只有与弯矩对应的正应力。
横力弯曲 (bending by transverse force) ━━ 梁横截面上既 有弯矩又有剪力;相应的,横截面既有正应力又有切应力。
二、 纯弯曲时的正应力
计算公式的推导
横截面的转动使梁凹入一侧的纵向线缩短,凸出一侧 的纵向线伸长,从而根据变形的连续性可知,中间必有一
层纵向线只弯曲而无长度改变的中性层 (图f),而中性层与
横截面的交线就是梁弯曲时横截面绕着它转动的轴━━ 中性轴 (neutral axis)。
(f)
推论(假设):
平面假设
梁在纯弯曲时,其原来的横截面仍保持为平面,
h
跨中横截面上按纯弯曲理论算得的最大正应力其误差不超
过1%,故在工程应用中就将纯弯曲时的正应力计算公式用
于横力弯曲情况.
b o z d o
d2
yc,max
h
z
yt,max
O z y
y (a)
y (b)
b
(c)
中性轴 z 为横截面对称轴的梁 (图a,b) 其横截面上最大拉应
力和最大压应力的值相等;中性轴 z 不是横截面对称轴的梁 (图c) ,其横截面上的最大拉应力和最大压应力的值不相等。
E r
M z y d A
A
E
r
A
y dA
2
EI z
r
M
(c)
由式(c)可知,直梁纯弯曲时中性层的曲率为
M r EI z
上式中的EIz称为梁的抗弯刚度(对Z轴)。显然,由 于纯弯曲时,梁的横截面上的弯矩M 不随截面位置变化,
1
所以纯弯曲梁段轴线为一段圆弧。
将上式代入得出的式子 E 公式:
r 即得弯曲正应力计算
y
My Iz
My Iz
应用此式时,如果如图中那样取 y 轴向下为正的坐标系来定义式中 y 的正 负,则在弯矩 M 按以前的规定确定其正
负的情况下,所得正应力的正负自动表
示拉应力或压应力。但实际应用中往往 直接根据横截面上弯矩的转向及求正应 力之点在中性轴的哪一侧来判别弯曲正 应力为拉应力还是压应力;在此情况下 可以把式中的 y 看作求应力的点离中性 轴 z 的距离。
A
E
r
E
A
yz d A
y dA
2
EI yz
r
EI z
0
M
(b) (c)
M z y d A
A
r
A
r
由于式(a),(b)中的 不可能等于零,因而该两式要求: 1. 横截面对于中性轴 z 的静矩等于零,A y d A 0 ;显 然这是要求中性轴 z 通过横截面的形心; 2. 横截面对于 y 轴和 z 轴的惯性积等于零, A yz d A 0 ; 在对称弯曲情况下,y 轴为横截面的对称轴,因而这一条件自 动满足。
I yz yz d A
A
为截面对于y轴和z轴的惯性积,其单位
为m4。
I z y 2 d A 为截面对于z轴的惯性矩(moment of inerita A
of an area)或二次轴矩,其单位为m4。
FN d A
A
E
r
A
yd A
ESz
r
0
(a)
M y z d A
(1) 几何关系━━变形与应变
观察在竖直平面内发生纯弯曲的梁,研梁的侧面上相邻横向线mm和nn间的
纵向直线段aa和bb,在梁弯曲后成为弧线,靠近梁的顶面
的线段aa缩短,而靠近梁的底面的线段bb则伸长; <2>. 相邻横向线mm和nn,在梁弯曲后仍为直线,只是 相对旋转了一个角度,且与弧线aa和bb保持正交。
y2 d A
EI yz
r
EI z
0
M
(b) (c)
M z y d A
A
r
A
r
以上三式中的Sz,Iyz,Iz都是只与截面的形状和尺寸相
关的几何量,属于截面的几何性质,而
其中
S z y d A 为截面对于z轴的静矩(static moment of an A
area)或一次矩(形心计算公式),其单位为m3。
