习题答案 (1)分析
材料分析测试习题及答案1

1.计算0.071 nm (MoK α)和0.154 nm (CuK α)的X 射线的振动频率和能量。
解:由公式max 0hceU h νλ==得 将题目中数据带入= = =892.998100.15410-⨯⨯= = == = 考虑相对论效应,220/1cv m m -=,结果会有小许不同。
2.计算当管电压为50 kv 时,电子在与靶碰撞时的速度与动能以及所发射的连续谱的短波限和光子的最大动能。
解:已知U=50kV ,电子的质量为m0 =9.1×10-31kg ,光速为c=2.998×108m/s ,电子电量e=1.602×10-19C ,普朗克常数:h=6.626×10-34J.s电子从阴极飞出到达靶的过程中所获得的总动能为E=eU=1.602×10-19C ×50kv=8.01×10-15J由于所以电子与靶碰撞时的速度为=1.32×108m/s所发射连续谱的短波限=12400/U=0.248Å 辐射出来的光子的最大动能为= = 8.01×10-15J3.分析下列荧光辐射产生的可能性,为什么? (1)用CuK α X 射线激发CuK α荧光辐射; (2)用CuK β X 射线激发CuK α荧光辐射; (3)用CuK α X 射线激发CuL α荧光辐射。
解:(网上参考答案)根据经典原子模型,原子内的电子分布在一系列量子化的壳层上,在稳定状态下,每个壳层有一定数量的电子,他们有一定的能量。
最内层能量最低,向外能量依次增加。
根据能量关系,M 、K 层之间的能量差大于L 、K 成之间的能量差,K 、L 层之间的能量差大于M 、L 层能量差。
由于释放的特征谱线的能量等于壳层间的能量差,所以 K β的能量大于 K α的能量,K α能量大于L α的能量,即 。
因此在不考虑能量损失的情况下: CuK α能激发CuK α荧光辐射;(能量相同) CuK β能激发CuK α荧光辐射; (K β>K α)cνλ=0M ν892.998100.07110-⨯⨯1814.2310s -⨯Cu ν1811.9510s -⨯O M eU 34186.62610 4.2310-⨯⨯⨯152.810J -⨯Cu eU 34186.62610 1.9510-⨯⨯⨯151.2910J-⨯2012E mv =12002E v m ⎛⎫= ⎪⎝⎭0λ0E 00hc h νλ=CuKα能激发CuLα荧光辐射;(Kα>Lα)解:假设E K为K壳层的能量,E L为L壳层的能量,E M为M壳层的能量,CuKαX射线的能量为E K-E L,CuKβX射线的能量为E K-E M,CuKα荧光辐射的能量为E K-E L,CuLα荧光辐射的能量为E L-E M,(1)不可能,用CuKαX射线激发CuKα荧光辐射,需要E K的能量;(2)不可能,用CuKβX射线激发CuKα荧光辐射,需要E K的能量;(3)有可能,用CuKαX射线激发CuLα荧光辐射,需要E L的能量,具体能不能还要比较E K-E L 和E L的大小。
(2021年整理)分析化学课堂上练习题答案1

(完整)分析化学课堂上练习题答案1编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)分析化学课堂上练习题答案1)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)分析化学课堂上练习题答案1的全部内容。
第十六章色谱概论一、选择题1.在色谱过程中,从总体上看,组分在流动相中停留的时间为:()。
A. t0 B。
t R C. t′R D。
k2.衡量色谱柱的柱效应使用( )。
A 保留值 B。
分离度 C.板高 D。
峰面积3.衡量色谱柱效能的参数为()。
A. 分离度B. 容量因子C. 塔板数D。
分配系数4.下列哪种色谱方法的流动相,对色谱选择性无影响?( ).A.液-固吸附色谱 B.液—液分配色谱 C.空间排阻色谱 D.离子交换色谱5.在气-液色谱中,为了改变色谱柱的选择性,主要可进行如下哪种(些)操作?( )。
A.改变固定相的种类B.改变载气的种类和流速C.改变色谱柱的柱温D.(A)和(C)1. A;2. C ;3.C ;4.C ;5.D二、判断题1.色谱柱越长,单位长度所包含的理论塔板数(片/米)就越多。
()2.在其他实验条件相同的情况下,色谱柱越长,色谱峰越宽。
( )3.从总体上看,各种组分在流动相中停留的时间都等于死时间。
( )4.组分被载气完全带出色谱柱所消耗的载气体积为保留体积。
()5.某一组分的分配比 k=1/3,表明该组分的移动速度是流动相速度的 3倍。
( )1.×;2.√;3.√;4.×;5.×第十七章气相色谱法一、选择题1.在气相色谱法中其他条件均不改变,柱长增加一倍则将发生().A.物质对的分离度增大,但半峰宽不变 B.理论塔板高度增加C.分离度和半峰宽都增大至倍 D.每米所含塔板数增大2.在GC法中对某一组分来说,一定的柱长下,与组分的保留时间无关的是()A.保留比B.分配系数 C.扩散速度 D.分配比3.在一根 1 米长的柱上测得两组峰的分离度为 0。
极谱与库仑分析法答案(1)

答案-极谱分析法习题一.选择题:1. (1121)极谱波形成的根本原因为( (4) )(1) 滴汞表面的不断更新(2) 溶液中的被测物质向电极表面扩散(3) 电化学极化的存在(4) 电极表面附近产生浓差极化2. (1510)极谱波出现平台是由于( (2) )(1)电化学极化使电流上不去(2)浓差极化使电流受扩散控制(3)离子还原后, 电极周围的电场发生了变化(4)汞滴落下, 将电荷带走了3. 1111直流极谱法中将滴汞电极和饱和甘汞电极浸入试液中组成电解电池,两个电极的性质应为( (3) )(1) 两个电极都是极化电极(2) 两个电极都是去极化电极(3) 滴汞电极是极化电极,饱和甘汞电极是去极化电极(4) 滴汞电极是去极化电极,饱和甘汞电极是极化电极4. 1112在极谱分析中,在底液中加入配合剂后,金属离子则以配合物形式存在,随着配合剂浓度增加,半波电位变化的方式为( (2))(1) 向更正的方向移动(2) 向更负的方向移动(3) 不改变(4) 决定于配合剂的性质,可能向正,可能向负移动5.1118极谱催化波的形成过程如下:O + n e-→R (电极反应)↑_________↓R + Z =O (化学反应)其产生机理是( (1) )(1) O 催化Z 的还原(2) O 催化R 的氧化(3) Z 催化O 的还原(4) Z 催化R 的氧化6. (1150)在极谱分析中与极限扩散电流呈正比关系的是( (2) )(1) 汞柱高度平方(2) 汞柱高度平方根(3) 汞柱高度的一半(4) 汞柱高度7.1592在极谱分析中常用汞电极为指示电极, 但氢离子不干扰分析测定, 是利用了(1)(1) 在汞上氢有很大的超电位(2) 在汞上氢没有超电位(3) 氢离子难以得到电子(4) 氢的还原电位较其它金属大8. (1601)在单扫描极谱图上, 某二价离子的还原波的峰电位为-0.89V, 它的半波电位应是( (2) ) (1) -0.86V (2) -0.88V (3) -0.90V (4) -0.92V9. (1925)阳极溶出伏安法的预电解过程是((1) )(1)恒电位电解(2)恒电流电解(3)控制时间电解(4)控制电流和时间10. (1494)极谱分析中, 在底液中加入表面活性剂, 其目的是为了消除( (3) ) (1)迁移电流;(2)光电电流;(3)极谱极大;(4)残余电流11. (1501)在电化学分析中溶液不能进行搅拌的方法是( (3) ) (1)电解分析法;(2)库仑分析法;(3)极谱分析法;(4)离子选择电极电位分析法12.(1548)库仑分析的理论基础是( (2) ) (1)电解方程式;(2)法拉第定律;(3)能斯特方程式;(4)菲克定律13. (1550)控制电位库仑分析的先决条件是( (1) )(1)100%电流效率(2)100%滴定效率(3)控制电极电位(4)控制电流密度14. (1165)在恒电流库仑滴定中采用大于45V 的高压直流电源是为了((3) )(1) 克服过电位(2) 保证100% 的电流效率(3) 保持电流恒定(4) 保持工作电极电位恒定15.(1549)以镍电极为阴极电解NiSO4溶液, 阴极产物是( (4) ) (1)H2 (2)O2 (3)H2O (4)Ni16. (1915)控制电位电解分析法常用的工作电极(3)(1) 碳电极;(2) 饱和甘汞电极(3) Pt网电极和汞阴极;(4) Pt丝电极和滴汞电极17 (1934)实际分解电压,包括(4)(1)反电动势;(2)超电压;(3)反电动势加超电压;(4)反电动势、超电压和IR降二、填空题( 共5题13分)1. (2939)在极谱分析中使用大面积汞池电极或大面积饱和甘汞电极, 使用大面积电极的原因是____防止它的表面发生浓差极化__, 使该电极的电极电位_______保持稳定。
合工大材料现代分析测试方法习题答案(1)

第一章1. X 射线学有几个分支?每个分支的研究对象是什么?2. 分析下列荧光辐射产生的可能性,为什么?(1)用CuK αX 射线激发CuK α荧光辐射;(2)用CuK βX 射线激发CuK α荧光辐射;(3)用CuK αX 射线激发CuL α荧光辐射。
3. 什么叫“相干散射”、“非相干散射”、“荧光辐射”、“吸收限”、“俄歇效应”、“发射谱”、“吸收谱”?4. X 射线的本质是什么?它与可见光、紫外线等电磁波的主要区别何在?用哪些物理量描述它?5. 产生X 射线需具备什么条件?6. Ⅹ射线具有波粒二象性,其微粒性和波动性分别表现在哪些现象中?7. 计算当管电压为50 kv 时,电子在与靶碰撞时的速度与动能以及所发射的连续谱的短波限和光子的最大动能。
8. 特征X 射线与荧光X 射线的产生机理有何异同?某物质的K 系荧光X 射线波长是否等于它的K 系特征X 射线波长?9. 连续谱是怎样产生的?其短波限V eV hc 301024.1⨯==λ与某物质的吸收限kk k V eV hc 31024.1⨯==λ有何不同(V 和V K 以kv 为单位)? 10. Ⅹ射线与物质有哪些相互作用?规律如何?对x 射线分析有何影响?反冲电子、光电子和俄歇电子有何不同?11. 试计算当管压为50kv 时,Ⅹ射线管中电子击靶时的速度和动能,以及所发射的连续谱的短波限和光子的最大能量是多少?12.为什么会出现吸收限?K吸收限为什么只有一个而L吸收限有三个?当激发X系荧光Ⅹ射线时,能否伴生L系?当L系激发时能否伴生K系?13.已知钼的λKα=0.71Å,铁的λKα=1.93Å及钴的λKα=1.79Å,试求光子的频率和能量。
试计算钼的K激发电压,已知钼的λK=0.619Å。
已知钴的K激发电压V K=7.71kv,试求其λK。
14.X射线实验室用防护铅屏厚度通常至少为lmm,试计算这种铅屏对CuKα、MoKα辐射的透射系数各为多少?15.如果用1mm厚的铅作防护屏,试求Cr Kα和Mo Kα的穿透系数。
财务分析练习题及答案1
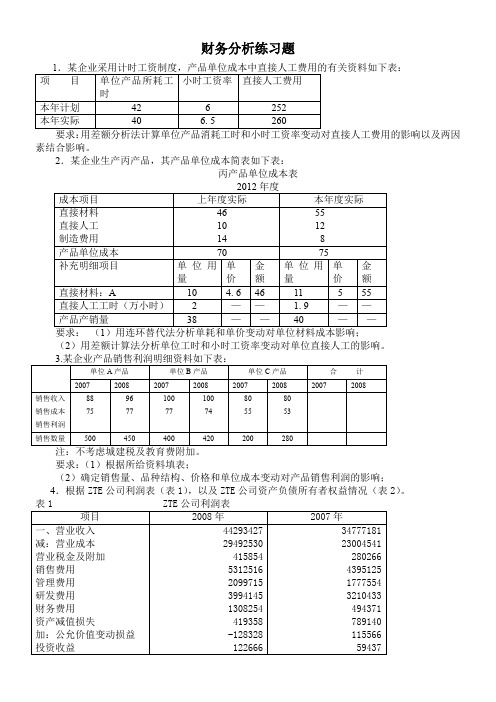
财务分析练习题素结合影响。
2.某企业生产丙产品,其产品单位成本简表如下表:丙产品单位成本表(2)用差额计算法分析单位工时和小时工资率变动对单位直接人工的影响。
要求:(1)根据所给资料填表;(2)确定销售量、品种结构、价格和单位成本变动对产品销售利润的影响;4.根据ZTE公司利润表(表1),以及ZTE公司资产负债所有者权益情况(表2)。
(2)对企业利润结构进行分析;(3)评价企业经营成果完成情况。
2、(1)计算反映资产经营盈利能力和资本经营盈利能力的指标;(2)分析总资产报酬率变动的原因;(3)评价企业盈利能力状况。
2、(1)计算反映资产经营盈利能力和资本经营盈利能力的指标;(2)分析总资产报酬率变动的原因;(3)评价企业盈利能力状况。
5、某产品是等级品,其有关资料如下:根据商上表资料确定等级品质量变动和价格变动对利润的影响。
分析要求:(1)计算销售费用构成率;(2)计算百元销售收入销售费用;(3)评价企业销售费用情况。
(2)计算该公司本期销售收入;(3)计算该公司本期流动资产平均余额和流动资产周转率。
8.某企业上年产品销售收入为6624万元,全部资产平均余额为2760万元,流动资产占全部资产的比重为40%;本年产品销售收入为7350万元,全部资产平均余额为2940万元,流动资产占全部资产的比重为45%。
根据以上资料,对全部资产周转率变动的原因进行分析。
9.某企业上年流动资金平均占用额为150000元,本年为180000元,产品销售收入上年为300000元,本年为450000元。
产品销售成本上年为210000元,本年为360000元。
要求:(1)计算本年和上年流动资产周转率;(2)分析全部流动资产周转率变动的原因;(3)计算由于加速流动资产周转节约的流动资金。
10.某企业上年存货平均占用额为150000元,流动资产平均占用额为300000元;本年存货平均占用额为180000元,流动资产平均占用额为450000元;产品销售成本上年为210000元,本年为360000元。
财务管理 企业盈利能力分析习题及答案[1]
![财务管理 企业盈利能力分析习题及答案[1]](https://img.taocdn.com/s3/m/d63e133f55270722192ef761.png)
四、计算题 1.收入利润率和成本利润率分析 某公司2001年度、2002年度有关经营成果资料如下表: 利润表(1)根据上述资料,计算2001、2002两个年度的收入利润率指标及其变动情况。
(2)根据上述资料,计算2001、2002两个年度的成本利润率指标及其变动情况。
2.资本经营能力分析 根据某公司2001、2002两个年度的资产负债表、利润表及其附表资料以及会计报表附注,给出以下分析数据: 五、业务题 1.股份公司盈利能力分析某公司2001年度、2002年度有关资料如下表:(1)根据所给资料计算该公司2002年度每股收益、普通股权益报酬率、股利发放率和价格与收益比率等指标。
(2)用差额分析法对普通股权益报酬率进行分析。
2.成本利润率分析 要求:(1)根据所给资料填表;(2)确定品种结构、价格、单位成本变动对销售成本利润率的影响;(3)对企业商品经营盈利能力进行评价。
六、典型案例 2002年底A 公司拥有B 公司20%有表决权资本的控制权,2003年A 公司有意对B 公司继续投资。
A 公司认为B 公司的盈利能力比财务状况、营运能力更重要,他们希望通过投资获得更多的利润。
因此,A 公司搜集了B 公司的有关资料。
资料1: 利润表资料2: 资料3:年度的投资决策。
(1)计算反映资产经营盈利能力和资本经营盈利能力的指标;(2)采用因素分析法分析总资产报酬率变动的原因;(3)评价企业盈利能力状况。
三、判断题 1.错误。
资产经营盈利能力分析主要对全部资产报酬率指标进行分析和评价。
2.错误。
对企业盈利能力的分析主要指对利润率的分析。
3.错误。
从经济学角度看,资本的内涵与我们通常所说的资产的内涵是基本相同的,它侧重于揭示企业所拥有的经济资源,而不考虑这些资源的来源特征。
4.错误。
在负债利息率和资本构成等条件不变的情况下,总资产报酬率越高,净资产收益率就越高。
5.正确。
6.正确。
7.错误。
资产经营的基本内涵是合理配置与使用资产,以一定的资产投入,取得尽可能多的收益。
2022年小学数学二年级下册第六单元经典练习题(答案解析)(1)

一、选择题1.每条船限乘6人,32人去划船,至少需要租()条船。
A. 5B. 6C. 7B解析: B【解析】【解答】32÷6=5(条)......2(人);5+1=6(条)。
故答案为:B。
【分析】人数÷每条船限乘人数=船坐满的条数+余下人数;船坐满的条数+1=至少需要租船条数。
2.□÷○=4……6,○中的数最小是()。
A. 6B. 7C. 4B解析: B【解析】【解答】□÷○=4……6,○中的数最小是7。
故答案为:B。
【分析】在有余数的除法里,余数必须比除数小,据此解答。
3.余数是2的算式是()。
A. 15÷7B. 18÷4C. 16÷3B解析: B【解析】【解答】A:15÷7=2……1;B:18÷4=4……2;C:16÷3=5……1。
故答案为:B。
【分析】两位数除以一位数商是一位数,根据乘法口诀直接试商,用被除数减去商和除数的积确定余数,余数一定要比除数小。
4.循环小数5.678678.…的小数部分的第十位上的数字是()。
A. 6B. 7C. 8A解析: A【解析】【解答】解:10÷3=3……1,所以第十位上的数字是6。
故答案为:A。
【分析】循环小数5.678678.…从小数部分第一位开始就循环,循环节是65.一辆小车最限坐5人;现有带队老师5人,比赛学生8人,一起参加十一月份的县运会,需要派()辆小车才够用。
(老师是司机)A. 2B. 3C. 4B解析: B【解析】【解答】解:(5+8)÷5=2……3,2+1=3,所以需要派3辆小车才够用。
故答案为:B。
【分析】这是一道有余数的除法计算,用参加县运会的人数除以一辆小车限坐的人数,因为这些人都要去,所以需要派小车的辆出就是把计算得出的商加1即可。
6.□84÷52,要使商是两位数,方框里可以填()。
A. 0~9B. 1~4C. 5~9C解析: C【解析】【解答】□84÷52,要使商是两位数,方框里可以填5-9。
新初中数学数据分析技巧及练习题附答案(1)

新初中数学数据分析技巧及练习题附答案(1)一、选择题1.样本数据3,a,4,b,8的平均数是5,众数是3,则这组数据的中位数是()A.2 B.3 C.4 D.8【答案】C【解析】【分析】+=,由众数是3知a、b中一个数据为3、另一个数据为先根据平均数为5得出a b107,再根据中位数的定义求解可得.【详解】解:Q数据3,a,4,b,8的平均数是5,+=,3a4b825∴++++=,即a b10又众数是3,∴、b中一个数据为3、另一个数据为7,a则数据从小到大为3、3、4、7、8,∴这组数据的中位数为4,故选C.【点睛】此题考查了平均数、众数和中位数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,众数是一组数据中出现次数最多的数.2.如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是()A.平均数是6B.中位数是6.5C.众数是7D.平均每周锻炼超过6小时的人数占该班人数的一半【答案】A【解析】【分析】根据中位数、众数和平均数的概念分别求得这组数据的中位数、众数和平均数,由图可知锻炼时间超过6小时的有20+5=25人.即可判断四个选项的正确与否.【详解】A、平均数为150×(5×7+18×6+20×7+5×8)=6.46,故本选项错误,符合题意;B、∵一共有50个数据,∴按从小到大排列,第25,26个数据的平均值是中位数,∴中位数是6.5,故此选项正确,不合题意;C、因为7出现了20次,出现的次数最多,所以众数为:7,故此选项正确,不合题意;D、由图可知锻炼时间超过6小时的有20+5=25人,故平均每周锻炼超过6小时的人占总数的一半,故此选项正确,不合题意;故选A.【点睛】此题考查了中位数、众数和平均数的概念等知识,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会错误地将这组数据最中间的那个数当作中位数.3.对于一组统计数据:1,1,4,1,3,下列说法中错误的是()A.中位数是1 B.众数是1C.平均数是1.5 D.方差是1.6【答案】C【解析】【分析】将数据从小到大排列,再根据中位数、众数、平均数及方差的定义依次计算可得答案.【详解】解:将数据重新排列为:1、1、1、3、4,则这组数据的中位数1,A选项正确;众数是1,B选项正确;平均数为111345++++=2,C选项错误;方差为15×[(1﹣2)2×3+(3﹣2)2+(4﹣2)2]=1.6,D选项正确;故选:C.【点睛】本题主要考查中位数、众数、平均数及方差,解题的关键是掌握中位数、众数、平均数及方差的定义与计算公式.4.在学校的体育训练中,小杰投掷实心球的7次成绩如统计图所示,则这7次成绩的中位数和平均数分别是()A.9.7m,9.9m B.9.7m,9.8m C.9.8m,9.7m D.9.8m,9.9m 【答案】B【解析】【分析】将这7个数据从小到大排序后处在第4位的数是中位数,利用算术平均数的计算公式进行计算即可.【详解】把这7个数据从小到大排列处于第4位的数是9.7m,因此中位数是9.7m,平均数为:(9.59.69.79.79.810.110.2)79.8++++++÷=m,故选:B.【点睛】考查中位数、算术平均数的计算方法,将一组数据从小到大排列后处在中间位置的一个数或两个数的平均数就是这组数据的中位数,平均数则是反映一组数据的集中水平.5.有甲、乙两种糖果,原价分别为每千克a元和b元.根据调查,将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合,取得了较好的销售效果.现在糖果价格有了调整:甲种糖果单价下降15%,乙种糖果单价上涨20%,但按原比例混合的糖果单价恰好不变,则xy等于()A.34abB.43abC.34baD.43ba【答案】D【解析】【分析】根据已知条件表示出价格变化前后两种糖果的平均价格,进而得出等式求出即可.【详解】解:∵甲、乙两种糖果,原价分别为每千克a元和b元,两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合,∴两种糖果的平均价格为:ax byx y++,∵甲种糖果单价下降15%,乙种糖果单价上涨20%,∴两种糖果的平均价格为:1520(1)(1)100100a x b y x y-•+++,∵按原比例混合的糖果单价恰好不变,∴ax by x y++=1520(1)(1)100100a x b y x y-•+++,整理,得 15ax =20by ∴43x b y a=, 故选:D . 【点睛】本题考查了加权平均数,解决本题的关键是表示出价格变化前后两种糖果的平均价格.6.某青年排球队12名队员的年龄情况如下:则12名队员的年龄( ) A .众数是20岁,中位数是19岁 B .众数是19岁,中位数是19岁 C .众数是19岁,中位数是20.5岁 D .众数是19岁,中位数是20岁【答案】D 【解析】 【分析】中位数是指将统计总体当中的各个变量值按大小顺序排列起来,形成一个数列,处于变量数列中间位置的变量值就称为中位数 ;众数是指在统计分布上具有明显集中趋势点的数值,代表数据的一般水平(众数可以不存在或多于一个). 【详解】解:在这一组数据中19岁是出现次数最多的,故众数是19岁;将这组数据从小到大的顺序排列后,处于中间位置的数是20岁,那么由中位数的定义可知,这组数据中的中位数是20岁.故选:D. 【点睛】理解中位数和众数的定义是解题的关键.7.某班40名同学一周参加体育锻炼时间统计如表所示:那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是()A.17,8.5 B.17,9 C.8,9 D.8,8.5【答案】D【解析】【分析】根据中位数、众数的概念分别求得这组数据的中位数、众数.【详解】解:众数是一组数据中出现次数最多的数,即8;由统计表可知,处于20,21两个数的平均数就是中位数,∴这组数据的中位数为898.5 2+=;故选:D.【点睛】考查了中位数、众数的概念.本题为统计题,考查众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.8.某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差239s=.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是()A.平均分不变,方差变大B.平均分不变,方差变小C.平均分和方差都不变D.平均分和方差都改变【答案】B【解析】【分析】根据平均数,方差的定义计算即可.【详解】解:∵小亮的成绩和其他39人的平均数相同,都是90分,∴该班40人的测试成绩的平均分为90分,方差变小,故选:B.【点睛】本题考查方差,算术平均数等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.9.已知一组数据:6,2,8,x,7,它们的平均数是6.则这组数据的中位数是()A.7 B.6 C.5 D.4【答案】A【解析】分析:首先根据平均数为6求出x的值,然后根据中位数的概念求解.详解:由题意得:6+2+8+x+7=6×5,解得:x=7,这组数据按照从小到大的顺序排列为:2,6,7,7,8,则中位数为7.故选A.点睛:本题考查了中位数和平均数的知识,将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数;平均数是指在一组数据中所有数据之和再除以数据的个数.10.某校在中国学生核心素养知识竞赛中,通过激烈角逐,甲、乙、丙、丁四名同学胜出,他们的成绩如表:如果要选出一个成绩较好且状态稳定的同学去参加市级比赛,应选()A.丁B.丙C.乙D.甲【答案】B【解析】【分析】先比较平均数得到甲和丙成绩较好,然后比较方差得到丙的状态稳定,即可决定选丙去参赛.【详解】∵甲、丙的平均数比乙、丁大,∴甲和丙成绩较好,∵丙的方差比甲的小,∴丙的成绩比较稳定,∴丙的成绩较好且状态稳定,应选的是丙,故选:B.【点睛】本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差;方差是反映一组数据的波动大小的一个量,方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.也考查了平均数的意义.11.数据2、5、6、0、6、1、8的中位数是( ) A .8 B .6C .5D .0【答案】C 【解析】 【分析】将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数. 【详解】将数据从小到大排列为:0,1,2,5,6,6,8 ∵这组数据的个数是奇数 ∴最中间的那个数是中位数 即中位数为5 故选C . 【点睛】此题考查了平均数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.12.甲、乙两位运动员在相同条件下各射击10次,成绩如下: 甲:9,10,8,5,7,8,10,8,8,7; 乙:5,7,8,7,8,9,7,9,10,10.根据上述信息,下列结论错误的是( ) A .甲、乙的众数分别是8,7 B .甲、乙的中位数分别是8,8 C .乙的成绩比较稳定 D .甲、乙的平均数分别是8,8【答案】C 【解析】 【分析】分别根据众数,平均数,中位数和方差的概念以及计算方法计算出结果,然后进行判断. 【详解】在甲的10次射击成绩中8环出现次数最多,有4次,故众数是8,而乙的10次射击成绩中7环出现次数最多,故众数是7,因此选项A 说法正确,不符合题意;甲的10次射击成绩按大小顺序排列为:5,7,7,8,8,8,8,9,10,10,故其中位数为:8+8=82; 乙的10次射击成绩按大小顺序排列为:5,7,7,7,8,8,9,9,10,10,故其中位数为:8+8=82,所以甲、乙的中位数分别是8,8,故选项B 说法正确,不符合题意; 甲的平均数为:5+72+84+9+102=810⨯⨯⨯;乙的平均数:5+73+82+92+102=810⨯⨯⨯⨯,所以,甲、乙的平均数分别是8,8,故选项D 不符合题意;甲组数据的方差为:2222221=[(58)2(78)4(88)(98)2(108)]10S -+⨯-+⨯-+-+⨯-甲=2; 乙组数据的方差为:2222221=[(58)3(78)2(88)2(98)2(108)]10S -+⨯-+⨯-+⨯-+⨯-乙=2.2;所以甲乙两组数据的方差不相等,甲的成绩更稳定,故选项C 符合题意. 故选:C. 【点睛】本题考查了平均数、中位数、众数和方差的定义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.13.某中学为了了解同学们平均每月阅读课外书籍的情况,在某年级随机抽查了20名同学,结果如下表所示: 平均每月阅读本数 4 5 6 7 8 人数26543这些同学平均每月阅读课外书籍本数的中位数和众数为( ) A .5,5 B .6,6C .5,6D .6,5【答案】D 【解析】 【分析】根据中位数和众数的定义分别进行解答即可. 【详解】把这组数据从小到大排列中间的两个数都是6,则这组数据的中位数是6; 5出现了6次,出现的次数最多,则众数是5. 故选D . 【点睛】此题考查了中位数和众数,将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数;众数是一组数据中出现次数最多的数.14.某兴趣小组为了解我市气温变化情况,记录了今年月份连续6天的最低气温(单位:℃):7,4,2,1,2,2----,关于这组数据,下列结论不正确的是( ) A .平均数是B .中位数是C .众数是D .方差是【答案】D【分析】一组数据中出现次数最多的数据叫做这组数据的众数.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数.一般地设n个数据,x1,x2,…x n的平均数为,则方差S2= [(x1﹣)2+(x2﹣)2+…+(x n﹣)2].【详解】解:有题意可得,这组数据的众数为-2,中位数为-2,平均数为-2,方差是9故选D.15.某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:该店主决定本周进货时,增加一些41码的衬衫,影响该店主决策的统计量是( )A.平均数B.方差C.中位数D.众数【答案】D【解析】【分析】平均数、中位数、众数是描述一组数据集中程度的统计量;方差、标准差是描述一组数据离散程度的统计量.销量大的尺码就是这组数据的众数.【详解】由于众数是数据中出现次数最多的数,故影响该店主决策的统计量是众数.故选D.【点睛】此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.16.下列说法正确的是()A.了解全国中学生最喜爱哪位歌手,适合全面调查.B.甲乙两种麦种,连续3年的平均亩产量相同,它们的方差为:S甲2=5,S乙2=0.5,则甲麦种产量比较稳.C.某次朗读比赛中预设半数晋级,某同学想知道自己是否晋级,除知道自己的成绩外,还需要知道平均成绩.D.一组数据:3,2,5,5,4,6的众数是5.【答案】D【解析】根据数据整理与分析中的抽样调查,方差,中位数,众数的定义和求法即可判断. 【详解】A 、了解全国中学生最喜爱的歌手情况时,调查对象是全国中学生,人数太多,应选用 抽样调查的调查方式,故本选项错误;B 、甲乙两种麦种连续3年的平均亩产量的方差为:25S =甲,20.5S =乙,因方差越小越稳定,则乙麦种产量比较稳,故本选项错误;C 、某次朗读比赛中预设半数晋级,某同学想知道自己是否晋级,除知道自己的成绩外,还需要知道这次成绩的中位数,故本选项错误;D 、.一组数据:3,2,5,5,4,6的众数是5,故本选项正确;. 故选D . 【点睛】本题考查了数据整理与分析中的抽样调查,方差,中位数,众数,明确这些知识点的概念和求解方法是解题关键.17.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:则这些运动员成绩的中位数、众数分别为( ) A .1.70,1.75 B .1.70,1.70C .1.65,1.75D .1.65,1.70【答案】A 【解析】分析:找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.详解:共15名学生,中位数落在第8名学生处,第8名学生的跳高成绩为1.70m ,故中位数为1.70;跳高成绩为1.75m 的人数最多,故跳高成绩的众数为1.75; 故选A .点睛:本题为统计题,考查众数与中位数的意义.众数是一组数据中出现次数最多的数.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.18.甲、乙两班举行电脑汉字输入比赛,参赛学生每分输入汉字的个数统计结果如下表: 班级参加人数中位数方差平均数某同学分析上表后得到如下结论:①甲、乙两班学生平均成绩相同;为优秀)②乙班优秀的人数多于甲班优秀的人数(每分输入汉字个数150③甲班成绩的波动比乙班大.上述结论中正确的是()A.①②③B.①②C.①③D.②③【答案】A【解析】【分析】平均水平的判断主要分析平均数;优秀人数的判断从中位数不同可以得到;波动大小比较方差的大小.【详解】从表中可知,平均字数都是135,①正确;甲班的中位数是149,乙班的中位数是151,比甲的多,而平均数都要为135,说明乙的优秀人数多于甲班的,②正确;甲班的方差大于乙班的,又说明甲班的波动情况大,所以③也正确.①②③都正确.故选:A.【点睛】此题考查平均数,中位数,方差的意义.解题关键在于掌握平均数表示一组数据的平均程度.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.19.为了迎接2022年的冬奥会,中小学都积极开展冰上运动,小乙和小丁进行500米短道速滑比赛,他们的五次成绩(单位:秒)如表所示:设两人的五次成绩的平均数依次为x乙,x丁,成绩的方差一次为2S乙,2S丁,则下列判断中正确的是()A .22,x x S S =<乙丁乙丁 B .22,x x S S =>乙丁乙丁 C .22,x x S S >>乙丁乙丁D .22,x x S S <<乙丁乙丁【答案】B 【解析】 【分析】根据平均数的计算公式先求出甲和乙的平均数,再根据方差的意义即可得出答案. 【详解】x 乙45635552605++++==55,则215S =⨯乙 [(45﹣55)2+(63﹣55)2+(55﹣55)2+(52﹣55)2+(60﹣55)2]=39.6, x 丁51535856575++++==55,则215S =⨯丁 [(51﹣55)2+(53﹣55)2+(58﹣55)2+(56﹣55)2+(57﹣55)2]=6.8, 所以x 乙x =丁,22S S >乙丁,故选:B . 【点睛】本题考查方差的定义与意义:一般地设n 个数据,x 1,x 2,…x n 的平均数为x ,则方差S 2=1n[(x 1-x )2+(x 2-x )2+…+(x n -x )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.20.在创建平安校园活动中,九年级一班举行了一次“安全知识竞赛”活动,第一小组6名同学的成绩(单位:分)分别是:87,91,93,87,97,96,下列关于这组数据说正确的是( ) A .中位数是90 B .平均数是90C .众数是87D .极差是9【答案】C 【解析】 【分析】根据中位数、平均数、众数、极差的概念求解. 【详解】解:这组数据按照从小到大的顺序排列为:87,87,91,93,96,97, 则中位数是(91+93)÷2=92, 平均数是(87+87+91+93+96+97)÷6=9156, 众数是87, 极差是97﹣87=10.故选C.【点睛】本题考查了中位数、平均数、众数、极差的知识,掌握各知识点的概念是解答本题的关键.。
分析化学练习题和答案[1]
![分析化学练习题和答案[1]](https://img.taocdn.com/s3/m/cb1458e9f605cc1755270722192e453610665b8a.png)
分析化学练习题和答案[1]分析化学综合练习题答案⼀.误差、有效数字、数据处理、滴定基础和实验常识1、测定某样品中A 物质的平均含量是25.13%,相对标准偏差为0.15%。
在测定报告中表达 W A %=25.13%±0.15%2、分析化学中常⽤误差 / 准确度表⽰分析结果的好与差。
3、指出标定下列标准溶液时常选⽤的基准物质:NaOH :邻苯⼆甲酸氢钾; EDTA : CaCO 3 / ZnO / Zn ; HCl :硼砂 / Na 2CO 3 ; AgNO 3: NaCl ; KMnO 4:Na 2C 2O 4 ; Fe 2+: K 2Cr 2O 7 。
4、化学计量点是:滴定剂与待测物按化学反应式完全反应的点。
滴定误差是:化学计量点与滴定终点不⼀致造成的误差。
滴定终点:指⽰剂变⾊的点。
5、写出H 2P 2O 72-的共轭酸 H 3P 2O 7- 和共轭碱 HP 2O 73- 。
反应NH 3·H 2O→NH 4++OH -中的酸是 H 2O ;碱是 NH 3·H 2O 。
6 pH -V H + ( O H - ) 变化。
(⾦属离⼦浓度)pM -V ED T A 变化。
(溶液的电极电位)φ-V O X ( R e d ) 变化。
7、已知C(HNO 3)=0.1000mol/L ,该溶液对CaO 的滴定度为:(M CaO = 56g/mol )(A) 0.005600 g /mL/mL ;(C) 0.0112 g /mL ; (D) 0.0028 g /mL 。
① CaO → Ca(OH)2;② 2HNO 3 + Ca(OH)2 → Ca(NO 3) 2 + 2H 2O③ )/(../mL g 00280001000256100001000M C 21T CaO HNO CaOHNO 33=??=??= 8、已知K 2Cr 2O 7标准溶液浓度为0.01683 mol/L ,该溶液对Fe 2O 3的滴定度为 0.008063 g /mL 。
算法设计与分析(第2版)-王红梅-胡明-习题答案(1)

算法设计与分析(第2版)-王红梅-胡明-习题答案习题11. 图论诞生于七桥问题。
出生于瑞士的伟大数学家欧拉(Leonhard Euler ,1707—1783)提出并解决了该问题。
七桥问题是这样描述的:一个人是否能在一次步行中穿越哥尼斯堡(现在叫加里宁格勒,在波罗的海南岸)城中全部的七座桥后回到起点,且每座桥只经过一次,图 1.7是这条河以及河上的两个岛和七座桥的草图。
请将该问题的数据模型抽象出来,并判断此问题是否有解。
七桥问题属于一笔画问题。
输入:一个起点输出:相同的点1, 一次步行2, 经过七座桥,且每次只经历过一次3, 回到起点该问题无解:能一笔画的图形只有两类:一类是所有的点都是偶点。
另一类是只有二个奇点的图形。
2.在欧几里德提出的欧几里德算法中(即最初的欧几里德算法)用的不是除法而是减法。
请用伪代码描述这个版本的欧几里德算法1.r=m-n2.循环直到r=02.1 m=n图1.7 七桥问题2.2 n=r2.3 r=m-n3 输出m3.设计算法求数组中相差最小的两个元素(称为最接近数)的差。
要求分别给出伪代码和C++描述。
//采用分治法//对数组先进行快速排序//在依次比较相邻的差#include <iostream>using namespace std;int partions(int b[],int low,int high){int prvotkey=b[low];b[0]=b[low];while (low<high){while (low<high&&b[high]>=prvotkey)--high;b[low]=b[high];while (low<high&&b[low]<=prvotkey)++low;b[high]=b[low];}b[low]=b[0];return low;}void qsort(int l[],int low,int high){int prvotloc;if(low<high){prvotloc=partions(l,low,high); //将第一次排序的结果作为枢轴qsort(l,low,prvotloc-1); //递归调用排序由low 到prvotloc-1qsort(l,prvotloc+1,high); //递归调用排序由 prvotloc+1到 high}}void quicksort(int l[],int n){qsort(l,1,n); //第一个作为枢轴,从第一个排到第n个}int main(){int a[11]={0,2,32,43,23,45,36,57,14,27,39};int value=0;//将最小差的值赋值给valuefor (int b=1;b<11;b++)cout<<a[b]<<' ';cout<<endl;quicksort(a,11);for(int i=0;i!=9;++i){if( (a[i+1]-a[i])<=(a[i+2]-a[i+1]) )value=a[i+1]-a[i];elsevalue=a[i+2]-a[i+1];}cout<<value<<endl;return 0;}4.设数组a[n]中的元素均不相等,设计算法找出a[n]中一个既不是最大也不是最小的元素,并说明最坏情况下的比较次数。
大学物理习题答案解析第一章

第一章 质点运动学1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v ,t 至(t +Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ|r |),平均速度为v ,平均速率为v .(1) 根据上述情况,则必有( ) (A) |Δr |= Δs = Δr(B) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d s ≠ d r (C) |Δr |≠ Δr ≠ Δs ,当Δt →0 时有|d r |= d r ≠ d s (D) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d r = d s (2) 根据上述情况,则必有( )(A) |v |= v ,|v |= v (B) |v |≠v ,|v |≠ v (C) |v |= v ,|v |≠ v (D) |v |≠v ,|v |= v分析与解 (1) 质点在t 至(t +Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs =PP′, 位移大小|Δr |=PP ′,而Δr =|r |-|r |表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′无限趋近P 点,则有|d r |=d s ,但却不等于d r .故选(B).(2) 由于|Δr |≠Δs ,故tst ΔΔΔΔ≠r ,即|v |≠v . 但由于|d r |=d s ,故tst d d d d =r ,即|v |=v .由此可见,应选(C). 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即(1)t r d d ; (2)t d d r ; (3)t s d d ; (4)22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x .下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确 (C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解trd d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量;td d r表示速度矢量;在自然坐标系中速度大小可用公式t s d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解.故选(D).1 -3 质点作曲线运动,r 表示位置矢量, v 表示速度,a 表示加速度,s 表示路程, a t表示切向加速度.对下列表达式,即(1)d v /d t =a ;(2)d r /d t =v ;(3)d s /d t =v ;(4)d v /d t |=a t. 下述判断正确的是( )(A) 只有(1)、(4)是对的 (B) 只有(2)、(4)是对的 (C) 只有(2)是对的 (D) 只有(3)是对的分析与解td d v表示切向加速度a t,它表示速度大小随时间的变化率,是加速度矢量沿速度方向的一个分量,起改变速度大小的作用;t r d d 在极坐标系中表示径向速率v r (如题1 -2 所述);tsd d 在自然坐标系中表示质点的速率v ;而td d v表示加速度的大小而不是切向加速度a t.因此只有(3) 式表达是正确的.故选(D).1 -4 一个质点在做圆周运动时,则有( ) (A) 切向加速度一定改变,法向加速度也改变 (B) 切向加速度可能不变,法向加速度一定改变 (C) 切向加速度可能不变,法向加速度不变 (D) 切向加速度一定改变,法向加速度不变分析与解 加速度的切向分量a t起改变速度大小的作用,而法向分量a n 起改变速度方向的作用.质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的.至于a t是否改变,则要视质点的速率情况而定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时, a t为一不为零的恒量,当a t改变时,质点则作一般的变速率圆周运动.由此可见,应选(B).*1 -5 如图所示,湖中有一小船,有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动.设该人以匀速率v 0 收绳,绳不伸长且湖水静止,小船的速率为v ,则小船作( )(A) 匀加速运动,θcos 0v v =(B) 匀减速运动,θcos 0v v = (C) 变加速运动,θcos 0v v =(D) 变减速运动,θcos 0v v = (E) 匀速直线运动,0v v =分析与解 本题关键是先求得小船速度表达式,进而判断运动性质.为此建立如图所示坐标系,设定滑轮距水面高度为h,t 时刻定滑轮距小船的绳长为l ,则小船的运动方程为22h l x -=,其中绳长l随时间t 而变化.小船速度22d d d d h l t llt x -==v ,式中t l d d 表示绳长l 随时间的变化率,其大小即为v 0,代入整理后为θlh l cos /0220v v v =-=,方向沿x 轴负向.由速度表达式,可判断小船作变加速运动.故选(C).讨论 有人会将绳子速率v 0按x 、y 两个方向分解,则小船速度θcos 0v v =,这样做对吗? 1 -6 已知质点沿x 轴作直线运动,其运动方程为32262t t x -+=,式中x 的单位为m,t 的单位为 s .求:(1) 质点在运动开始后4.0 s 内的位移的大小; (2) 质点在该时间内所通过的路程;(3) t =4 s 时质点的速度和加速度.分析 位移和路程是两个完全不同的概念.只有当质点作直线运动且运动方向不改变时,位移的大小才会与路程相等.质点在t 时间内的位移Δx 的大小可直接由运动方程得到:0Δx x x t -=,而在求路程时,就必须注意到质点在运动过程中可能改变运动方向,此时,位移的大小和路程就不同了.为此,需根据0d d =tx来确定其运动方向改变的时刻t p ,求出0~t p 和t p ~t 内的位移大小Δx 1 、Δx 2 ,则t 时间内的路程21x x s ∆+∆=,如图所示,至于t =4.0 s 时质点速度和加速度可用tx d d 和22d d t x两式计算.解 (1) 质点在4.0 s 内位移的大小m 32Δ04-=-=x x x(2) 由 0d d =tx得知质点的换向时刻为s 2=p t (t =0不合题意)则m 0.8Δ021=-=x x xm 40Δ242-=-=x x x所以,质点在4.0 s 时间间隔内的路程为m 48ΔΔ21=+=x x s(3) t =4.0 s 时1s0.4s m 48d d -=⋅-==t t xv2s0.422m.s 36d d -=-==t t x a1 -7 一质点沿x 轴方向作直线运动,其速度与时间的关系如图(a)所示.设t =0 时,x =0.试根据已知的v -t 图,画出a -t 图以及x -t 图.分析 根据加速度的定义可知,在直线运动中v -t 曲线的斜率为加速度的大小(图中AB 、CD 段斜率为定值,即匀变速直线运动;而线段BC 的斜率为0,加速度为零,即匀速直线运动).加速度为恒量,在a -t 图上是平行于t 轴的直线,由v -t 图中求出各段的斜率,即可作出a -t 图线.又由速度的定义可知,x -t 曲线的斜率为速度的大小.因此,匀速直线运动所对应的x -t 图应是一直线,而匀变速直线运动所对应的x –t 图为t 的二次曲线.根据各段时间内的运动方程x =x (t ),求出不同时刻t 的位置x ,采用描数据点的方法,可作出x -t 图.解 将曲线分为AB 、BC 、CD 三个过程,它们对应的加速度值分别为2s m 20-⋅=--=AB AB AB t t a v v (匀加速直线运动)0=BC a (匀速直线运动)2s m 10-⋅-=--=CD CD CD t t a v v (匀减速直线运动)根据上述结果即可作出质点的a -t 图[图(B)].在匀变速直线运动中,有2021t t x x ++=v由此,可计算在0~2s和4~6s时间间隔内各时刻的位置分别为用描数据点的作图方法,由表中数据可作0~2s和4~6s时间内的x -t 图.在2~4s时间内, 质点是作1s m 20-⋅=v 的匀速直线运动, 其x -t 图是斜率k =20的一段直线[图(c)].1 -8 已知质点的运动方程为j i r )2(22t t -+=,式中r 的单位为m,t 的单位为s.求: (1) 质点的运动轨迹;(2) t =0 及t =2s时,质点的位矢;(3) 由t =0 到t =2s内质点的位移Δr 和径向增量Δr ;*(4) 2 s 内质点所走过的路程s .分析 质点的轨迹方程为y =f (x ),可由运动方程的两个分量式x (t )和y (t )中消去t 即可得到.对于r 、Δr 、Δr 、Δs 来说,物理含义不同,可根据其定义计算.其中对s 的求解用到积分方法,先在轨迹上任取一段微元d s ,则22)d ()d (d y x s +=,最后用⎰=s s d 积分求s.解 (1) 由x (t )和y (t )中消去t 后得质点轨迹方程为2412x y -= 这是一个抛物线方程,轨迹如图(a)所示.(2) 将t =0s和t =2s分别代入运动方程,可得相应位矢分别为j r 20= , j i r 242-=图(a)中的P 、Q 两点,即为t =0s和t =2s时质点所在位置. (3) 由位移表达式,得j i j i r r r 24)()(Δ020212-=-+-=-=y y x x其中位移大小m 66.5)(Δ)(ΔΔ22=+=y x r而径向增量m 47.2ΔΔ2020222202=+-+=-==y x y x r r r r*(4) 如图(B)所示,所求Δs 即为图中PQ 段长度,先在其间任意处取AB 微元d s ,则22)d ()d (d y x s +=,由轨道方程可得x x y d 21d -=,代入d s ,则2s内路程为m 91.5d 4d 42=+==⎰⎰x x s s Q P1 -9 质点的运动方程为23010t t x +-= 22015t t y -=式中x ,y 的单位为m,t 的单位为s.试求:(1) 初速度的大小和方向;(2) 加速度的大小和方向.分析 由运动方程的分量式可分别求出速度、加速度的分量,再由运动合成算出速度和加速度的大小和方向.解 (1) 速度的分量式为t t xx 6010d d +-==v t ty y 4015d d -==v当t =0 时, v o x =-10 m·s-1 , v o y =15 m·s-1 ,则初速度大小为120200s m 0.18-⋅=+=y x v v v设v o 与x 轴的夹角为α,则23tan 00-==xy αv vα=123°41′(2) 加速度的分量式为2s m 60d d -⋅==ta xx v , 2s m 40d d -⋅-==t a y y v则加速度的大小为222s m 1.72-⋅=+=y x a a a设a 与x 轴的夹角为β,则32tan -==x ya a β β=-33°41′(或326°19′)1 -10 一升降机以加速度1.22 m·s-2上升,当上升速度为2.44 m·s-1时,有一螺丝自升降机的天花板上松脱,天花板与升降机的底面相距2.74 m .计算:(1)螺丝从天花板落到底面所需要的时间;(2)螺丝相对升降机外固定柱子的下降距离.分析 在升降机与螺丝之间有相对运动的情况下,一种处理方法是取地面为参考系,分别讨论升降机竖直向上的匀加速度运动和初速不为零的螺丝的自由落体运动,列出这两种运动在同一坐标系中的运动方程y 1 =y 1(t )和y 2 =y 2(t ),并考虑它们相遇,即位矢相同这一条件,问题即可解;另一种方法是取升降机(或螺丝)为参考系,这时,螺丝(或升降机)相对它作匀加速运动,但是,此加速度应该是相对加速度.升降机厢的高度就是螺丝(或升降机)运动的路程.解1 (1) 以地面为参考系,取如图所示的坐标系,升降机与螺丝的运动方程分别为20121at t y +=v20221gt t h y -+=v当螺丝落至底面时,有y 1 =y 2 ,即20202121gt t h at t -+=+v vs 705.02=+=ag ht (2) 螺丝相对升降机外固定柱子下降的距离为m 716.021202=+-=-=gt t y h d v解2 (1)以升降机为参考系,此时,螺丝相对它的加速度大小a ′=g +a ,螺丝落至底面时,有2)(210t a g h +-=s 705.02=+=ag ht (2) 由于升降机在t 时间内上升的高度为2021at t h +='v则 m 716.0='-=h h d1 -11 一质点P 沿半径R =3.0 m 的圆周作匀速率运动,运动一周所需时间为20.0s,设t =0 时,质点位于O 点.按(a )图中所示Oxy 坐标系,求(1) 质点P 在任意时刻的位矢;(2)5s时的速度和加速度.分析 该题属于运动学的第一类问题,即已知运动方程r =r (t )求质点运动的一切信息(如位置矢量、位移、速度、加速度).在确定运动方程时,若取以点(0,3)为原点的O′x′y′坐标系,并采用参数方程x′=x′(t )和y′=y′(t )来表示圆周运动是比较方便的.然后,运用坐标变换x =x 0 +x ′和y =y 0 +y ′,将所得参数方程转换至Oxy 坐标系中,即得Oxy 坐标系中质点P 在任意时刻的位矢.采用对运动方程求导的方法可得速度和加速度.解 (1) 如图(B)所示,在O′x′y′坐标系中,因t Tθπ2=,则质点P 的参数方程为t T R x π2sin=', t T R y π2cos -='坐标变换后,在O x y 坐标系中有t TR x x π2sin='=, R t TR y y y +-=+'=π2cos0 则质点P 的位矢方程为j i r ⎪⎭⎫ ⎝⎛+-+=R t T R t T R π2cos π2sinj i )]π1.0(cos 1[3)π1.0(sin 3t t -+=(2) 5s时的速度和加速度分别为j j i r )s m π3.0(π2sin π2π2cos π2d d 1-⋅=+==t TT R t T T R t vi j i r a )s m π03.0(π2cos )π2(π2sin )π2(d d 222222-⋅-=+-==t TT R t T T R t 1 -12 地面上垂直竖立一高20.0 m 的旗杆,已知正午时分太阳在旗杆的正上方,求在下午2∶00 时,杆顶在地面上的影子的速度的大小.在何时刻杆影伸展至20.0 m ?分析 为求杆顶在地面上影子速度的大小,必须建立影长与时间的函数关系,即影子端点的位矢方程.根据几何关系,影长可通过太阳光线对地转动的角速度求得.由于运动的相对性,太阳光线对地转动的角速度也就是地球自转的角速度.这样,影子端点的位矢方程和速度均可求得.解 设太阳光线对地转动的角速度为ω,从正午时分开始计时,则杆的影长为s =h tg ωt ,下午2∶00 时,杆顶在地面上影子的速度大小为132s m 1094.1cos d d --⋅⨯===tωωh t s v 当杆长等于影长时,即s =h ,则s 606034πarctan 1⨯⨯===ωh s ωt 即为下午3∶00 时.1 -13 质点沿直线运动,加速度a =4 -t2 ,式中a 的单位为m·s-2 ,t 的单位为s.如果当t =3s时,x =9 m,v =2 m·s-1 ,求质点的运动方程.分析 本题属于运动学第二类问题,即已知加速度求速度和运动方程,必须在给定条件下用积分方法解决.由t a d d v =和tx d d =v 可得t a d d =v 和t x d d v =.如a =a (t )或v =v (t ),则可两边直接积分.如果a 或v 不是时间t 的显函数,则应经过诸如分离变量或变量代换等数学操作后再做积分.解 由分析知,应有⎰⎰=tt a 0d d 0vv v得 03314v v +-=t t (1)由⎰⎰=txx t x 0d d 0v得 00421212x t t t x ++-=v (2) 将t =3s时,x =9 m,v =2 m·s-1代入(1) (2)得v 0=-1 m·s-1,x 0=0.75 m .于是可得质点运动方程为75.0121242+-=t t x 1 -14 一石子从空中由静止下落,由于空气阻力,石子并非作自由落体运动,现测得其加速度a =A -B v ,式中A 、B 为正恒量,求石子下落的速度和运动方程.分析 本题亦属于运动学第二类问题,与上题不同之处在于加速度是速度v 的函数,因此,需将式d v =a (v )d t 分离变量为t a d )(d =v v后再两边积分. 解 选取石子下落方向为y 轴正向,下落起点为坐标原点.(1) 由题意知 v vB A ta -==d d (1) 用分离变量法把式(1)改写为t B A d d =-vv(2)将式(2)两边积分并考虑初始条件,有⎰⎰=-t t B A 0d d d 0v vvvv得石子速度 )1(Bt e BA--=v 由此可知当,t →∞时,BA→v 为一常量,通常称为极限速度或收尾速度. (2) 再由)1(d d Bt e BAt y --==v 并考虑初始条件有 t e BA y t Bt y d )1(d 00⎰⎰--= 得石子运动方程)1(2-+=-Bt e BAt B A y 1 -15 一质点具有恒定加速度a =6i +4j ,式中a 的单位为m·s-2 .在t =0时,其速度为零,位置矢量r 0 =10 m i .求:(1) 在任意时刻的速度和位置矢量;(2) 质点在Oxy 平面上的轨迹方程,并画出轨迹的示意图.分析 与上两题不同处在于质点作平面曲线运动,根据叠加原理,求解时需根据加速度的两个分量a x 和a y 分别积分,从而得到运动方程r 的两个分量式x (t )和y (t ).由于本题中质点加速度为恒矢量,故两次积分后所得运动方程为固定形式,即20021t a t x x x x ++=v 和20021t a t y y y y ++=v ,两个分运动均为匀变速直线运动.读者不妨自己验证一下.解 由加速度定义式,根据初始条件t 0 =0时v 0 =0,积分可得⎰⎰⎰+==ttt t 0)d 46(d d j i a vvj i t t 46+=v又由td d r=v 及初始条件t =0 时,r 0=(10 m)i ,积分可得 ⎰⎰⎰+==tt r r t t t t 0)d 46(d d 0j i r vj i r 222)310(t t ++=由上述结果可得质点运动方程的分量式,即x =10+3t 2y =2t 2消去参数t ,可得运动的轨迹方程3y =2x -20 m 这是一个直线方程.直线斜率32tan d d ===αx y k ,α=33°41′.轨迹如图所示. 1 -16 一质点在半径为R 的圆周上以恒定的速率运动,质点由位置A 运动到位置B,OA 和OB 所对的圆心角为Δθ.(1) 试证位置A 和B 之间的平均加速度为)Δ(/)Δcos 1(22θR θa v -=;(2) 当Δθ分别等于90°、30°、10°和1°时,平均加速度各为多少? 并对结果加以讨论.分析 瞬时加速度和平均加速度的物理含义不同,它们分别表示为t d d v =a 和tΔΔv =a .在匀速率圆周运动中,它们的大小分别为Ra n 2v =,t a ΔΔv = ,式中|Δv |可由图(B)中的几何关系得到,而Δt 可由转过的角度Δθ 求出.由计算结果能清楚地看到两者之间的关系,即瞬时加速度是平均加速度在Δt →0 时的极限值. 解 (1) 由图(b)可看到Δv =v 2 -v 1 ,故θΔcos 2Δ212221v v v v -+=v)Δcos 1(2θ-=v而vv θR s t ΔΔΔ==所以θR θt a Δ)cos Δ1(2ΔΔ2v -==v (2) 将Δθ=90°,30°,10°,1°分别代入上式,得R a 219003.0v ≈,Ra 229886.0v ≈ R a 239987.0v ≈,Ra 24000.1v ≈ 以上结果表明,当Δθ→0 时,匀速率圆周运动的平均加速度趋近于一极限值,该值即为法向加速度R2v . 1 -17 质点在Oxy 平面内运动,其运动方程为r =2.0t i +(19.0 -2.0t 2 )j ,式中r 的单位为m,t 的单位为s .求:(1)质点的轨迹方程;(2) 在t 1=1.0s 到t 2 =2.0s 时间内的平均速度;(3) t 1 =1.0s时的速度及切向和法向加速度;(4) t =1.0s 时质点所在处轨道的曲率半径ρ.分析 根据运动方程可直接写出其分量式x =x (t )和y =y (t ),从中消去参数t ,即得质点的轨迹方程.平均速度是反映质点在一段时间内位置的变化率,即t ΔΔr =v ,它与时间间隔Δt 的大小有关,当Δt →0 时,平均速度的极限即瞬时速度td d r =v .切向和法向加速度是指在自然坐标下的分矢量a t 和a n ,前者只反映质点在切线方向速度大小的变化率,即t t te a d d v =,后者只反映质点速度方向的变化,它可由总加速度a 和a t 得到.在求得t 1 时刻质点的速度和法向加速度的大小后,可由公式ρa n 2v =求ρ.解 (1) 由参数方程x =2.0t , y =19.0-2.0t 2消去t 得质点的轨迹方程:y =19.0 -0.50x 2(2) 在t 1 =1.00s 到t 2 =2.0s时间内的平均速度j i r r 0.60.2ΔΔ1212-=--==t t t r v (3) 质点在任意时刻的速度和加速度分别为j i j i j i t ty t x t y x 0.40.2d d d d )(-=+=+=v v v j j i a 222220.4d d d d )(-⋅-=+=s m ty t x t 则t 1 =1.00s时的速度v (t )|t =1s=2.0i -4.0j切向和法向加速度分别为t t y x t t t tt e e e a 222s 1s m 58.3)(d d d d -=⋅=+==v v v n n t n a a e e a 222s m 79.1-⋅=-=(4) t =1.0s质点的速度大小为122s m 47.4-⋅=+=y x v v v 则m 17.112==na ρv 1 -18 飞机以100 m·s-1 的速度沿水平直线飞行,在离地面高为100 m 时,驾驶员要把物品空投到前方某一地面目标处,问:(1) 此时目标在飞机正下方位置的前面多远? (2) 投放物品时,驾驶员看目标的视线和水平线成何角度?(3) 物品投出2.0s后,它的法向加速度和切向加速度各为多少?分析 物品空投后作平抛运动.忽略空气阻力的条件下,由运动独立性原理知,物品在空中沿水平方向作匀速直线运动,在竖直方向作自由落体运动.到达地面目标时,两方向上运动时间是相同的.因此,分别列出其运动方程,运用时间相等的条件,即可求解.此外,平抛物体在运动过程中只存在竖直向下的重力加速度.为求特定时刻t 时物体的切向加速度和法向加速度,只需求出该时刻它们与重力加速度之间的夹角α或β.由图可知,在特定时刻t ,物体的切向加速度和水平线之间的夹角α,可由此时刻的两速度分量v x 、v y 求出,这样,也就可将重力加速度g 的切向和法向分量求得.解 (1) 取如图所示的坐标,物品下落时在水平和竖直方向的运动方程分别为x =v t , y =1/2 gt 2飞机水平飞行速度v =100 m·s -1 ,飞机离地面的高度y =100 m,由上述两式可得目标在飞机正下方前的距离m 4522==gy x v(2) 视线和水平线的夹角为 o 5.12arctan==x y θ (3) 在任意时刻物品的速度与水平轴的夹角为vv v gt αx yarctan arctan == 取自然坐标,物品在抛出2s 时,重力加速度的切向分量与法向分量分别为2s m 88.1arctan sin sin -⋅=⎪⎭⎫ ⎝⎛==v gt g αg a t 2s m 62.9arctan cos cos -⋅=⎪⎭⎫ ⎝⎛==v gt g αg a n 1 -19 如图(a)所示,一小型迫击炮架设在一斜坡的底端O 处,已知斜坡倾角为α,炮身与斜坡的夹角为β,炮弹的出口速度为v 0,忽略空气阻力.求:(1)炮弹落地点P 与点O 的距离OP ;(2) 欲使炮弹能垂直击中坡面.证明α和β必须满足αβtan 21tan =并与v 0 无关. 分析 这是一个斜上抛运动,看似简单,但针对题目所问,如不能灵活运用叠加原理,建立一个恰当的坐标系,将运动分解的话,求解起来并不容易.现建立如图(a)所示坐标系,则炮弹在x 和y 两个方向的分运动均为匀减速直线运动,其初速度分别为v 0cos β和v 0sin β,其加速度分别为g sin α和gcos α.在此坐标系中炮弹落地时,应有y =0,则x =OP .如欲使炮弹垂直击中坡面,则应满足v x =0,直接列出有关运动方程和速度方程,即可求解.由于本题中加速度g 为恒矢量.故第一问也可由运动方程的矢量式计算,即20g 21t t +=v r ,做出炮弹落地时的矢量图[如图(B)所示],由图中所示几何关系也可求得OP (即图中的r 矢量).(1)解1 由分析知,炮弹在图(a)所示坐标系中两个分运动方程为αgt βt x sin 21cos 20-=v (1) αgt βt y cos 21sin 20-=v (2) 令y =0 求得时间t 后再代入式(1)得)cos(cos sin 2)sin sin cos (cos cos sin 2220220βααg ββαβααg βx OP +=-==v v 解2 做出炮弹的运动矢量图,如图(b)所示,并利用正弦定理,有βgt αt βαsin 212πsin 2πsin 20=⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛--v r 从中消去t 后也可得到同样结果.(2) 由分析知,如炮弹垂直击中坡面应满足y =0 和v x =0,则0sin cos 0=-=αgt βx v v (3)由(2)(3)两式消去t 后得αβsin 21tan = 由此可知.只要角α和β满足上式,炮弹就能垂直击中坡面,而与v 0 的大小无关.讨论 如将炮弹的运动按水平和竖直两个方向分解,求解本题将会比较困难,有兴趣读者不妨自己体验一下.1 -20 一直立的雨伞,张开后其边缘圆周的半径为R ,离地面的高度为h ,(1) 当伞绕伞柄以匀角速ω旋转时,求证水滴沿边缘飞出后落在地面上半径为g ωh R r /212+=的圆周上;(2) 读者能否由此定性构想一种草坪上或农田灌溉用的旋转式洒水器的方案?分析 选定伞边缘O 处的雨滴为研究对象,当伞以角速度ω旋转时,雨滴将以速度v 沿切线方向飞出,并作平抛运动.建立如图(a)所示坐标系,列出雨滴的运动方程并考虑图中所示几何关系,即可求证.由此可以想像如果让水从一个旋转的有很多小孔的喷头中飞出,从不同小孔中飞出的水滴将会落在半径不同的圆周上,为保证均匀喷洒对喷头上小孔的分布还要给予精心的考虑.解 (1) 如图(a)所示坐标系中,雨滴落地的运动方程为t ωR t x ==v (1)h gt y ==221 (2) 由式(1)(2)可得 g h ωR x 2222= 由图(a)所示几何关系得雨滴落地处圆周的半径为22221ωgh R R x r +=+= (2) 常用草坪喷水器采用如图(b)所示的球面喷头(θ0 =45°)其上有大量小孔.喷头旋转时,水滴以初速度v 0 从各个小孔中喷出,并作斜上抛运动,通常喷头表面基本上与草坪处在同一水平面上.则以φ角喷射的水柱射程为gR 2sin 0v = 为使喷头周围的草坪能被均匀喷洒,喷头上的小孔数不但很多,而且还不能均匀分布,这是喷头设计中的一个关键问题.1 -21 一足球运动员在正对球门前25.0 m 处以20.0 m·s-1 的初速率罚任意球,已知球门高为3.44 m .若要在垂直于球门的竖直平面内将足球直接踢进球门,问他应在与地面成什么角度的范围内踢出足球? (足球可视为质点)分析 被踢出后的足球,在空中作斜抛运动,其轨迹方程可由质点在竖直平面内的运动方程得到.由于水平距离x 已知,球门高度又限定了在y 方向的范围,故只需将x 、y 值代入即可求出.解 取图示坐标系Oxy ,由运动方程θt x cos v =, 221sin gt θt y -=v 消去t 得轨迹方程 222)tan 1(2tan x θg θx y +-=v以x =25.0 m,v =20.0 m·s-1 及3.44 m≥y ≥0 代入后,可解得71.11°≥θ1 ≥69.92°27.92°≥θ2 ≥18.89°如何理解上述角度的范围?在初速一定的条件下,球击中球门底线或球门上缘都将对应有两个不同的投射倾角(如图所示).如果以θ>71.11°或θ <18.89°踢出足球,都将因射程不足而不能直接射入球门;由于球门高度的限制,θ 角也并非能取71.11°与18.89°之间的任何值.当倾角取值为27.92°<θ <69.92°时,踢出的足球将越过门缘而离去,这时球也不能射入球门.因此可取的角度范围只能是解中的结果.1 -22 一质点沿半径为R 的圆周按规律2021bt t s -=v 运动,v 0 、b 都是常量.(1) 求t 时刻质点的总加速度;(2) t 为何值时总加速度在数值上等于b ?(3) 当加速度达到b 时,质点已沿圆周运行了多少圈?分析 在自然坐标中,s 表示圆周上从某一点开始的曲线坐标.由给定的运动方程s =s (t ),对时间t 求一阶、二阶导数,即是沿曲线运动的速度v 和加速度的切向分量a t,而加速度的法向分量为a n =v 2 /R .这样,总加速度为a =a te t+a n e n .至于质点在t 时间内通过的路程,即为曲线坐标的改变量Δs =s t -s 0.因圆周长为2πR,质点所转过的圈数自然可求得.解 (1) 质点作圆周运动的速率为bt ts -==0d d v v其加速度的切向分量和法向分量分别为b t s a t -==22d d , Rbt R a n 202)(-==v v 故加速度的大小为R )(402222bt b a a a a t tn -+=+=v 其方向与切线之间的夹角为⎥⎦⎤⎢⎣⎡--==Rb bt a a θt n 20)(arctan arctan v (2) 要使|a |=b ,由b bt b R R=-+4022)(1v 可得 bt 0v = (3) 从t =0 开始到t =v 0 /b 时,质点经过的路程为b s s s t 2200v =-= 因此质点运行的圈数为bRR s n π4π220v == 1 -23 一半径为0.50 m 的飞轮在启动时的短时间内,其角速度与时间的平方成正比.在t =2.0s 时测得轮缘一点的速度值为4.0 m·s-1.求:(1) 该轮在t′=0.5s的角速度,轮缘一点的切向加速度和总加速度;(2)该点在2.0s内所转过的角度.分析 首先应该确定角速度的函数关系ω=kt 2.依据角量与线量的关系由特定时刻的速度值可得相应的角速度,从而求出式中的比例系数k ,ω=ω(t )确定后,注意到运动的角量描述与线量描述的相应关系,由运动学中两类问题求解的方法(微分法和积分法),即可得到特定时刻的角加速度、切向加速度和角位移.解 因ωR =v ,由题意ω∝t 2 得比例系数322s rad 2-⋅===Rtt ωk v 所以 22)(t t ωω== 则t ′=0.5s 时的角速度、角加速度和切向加速度分别为12s rad 5.02-⋅='=t ω2s rad 0.24d d -⋅='==t tωα 2s m 0.1-⋅==R αa t总加速度n t t n R ωR αe e a a a 2+=+= ()()2222s m 01.1-⋅=+=R ωR αa在2.0s内该点所转过的角度rad 33.532d 2d 203202200====-⎰⎰t t t t ωθθ 1 -24 一质点在半径为0.10 m 的圆周上运动,其角位置为342t θ+=,式中θ 的单位为rad,t 的单位为s.(1) 求在t =2.0s时质点的法向加速度和切向加速度.(2) 当切向加速度的大小恰等于总加速度大小的一半时,θ 值为多少?(3) t 为多少时,法向加速度和切向加速度的值相等?分析 掌握角量与线量、角位移方程与位矢方程的对应关系,应用运动学求解的方法即可得到. 解 (1) 由于342t θ+=,则角速度212d d t tθω==.在t =2 s 时,法向加速度和切向加速度的数值分别为 22s 2s m 30.2-=⋅==ωr a t n 2s 2s m 80.4d d -=⋅==t ωr a t t(2) 当22212/t n t a a a a +==时,有223n t a a =,即 ()()422212243t r rt = 得 3213=t此时刻的角位置为 rad 15.3423=+=t θ(3) 要使t n a a =,则有()()422212243t r rt = t =0.55s1 -25 一无风的下雨天,一列火车以v 1=20.0 m·s-1 的速度匀速前进,在车内的旅客看见玻璃窗外的雨滴和垂线成75°角下降.求雨滴下落的速度v2 .(设下降的雨滴作匀速运动)分析 这是一个相对运动的问题.设雨滴为研究对象,地面为静止参考系S,火车为动参考系S′.v 1 为S′相对S 的速度,v 2 为雨滴相对S的速度,利用相对运动速度的关系即可解.解 以地面为参考系,火车相对地面运动的速度为v 1 ,雨滴相对地面竖直下落的速度为v 2 ,旅客看到雨滴下落的速度v 2′为相对速度,它们之间的关系为1'22v v v += (如图所示),于是可得 1o 12s m 36.575tan -⋅==v v 1 -26 如图(a)所示,一汽车在雨中沿直线行驶,其速率为v 1 ,下落雨滴的速度方向偏于竖直方向之前θ 角,速率为v 2′,若车后有一长方形物体,问车速v 1为多大时,此物体正好不会被雨水淋湿?分析 这也是一个相对运动的问题.可视雨点为研究对象,地面为静参考系S,汽车为动参考系S′.如图(a)所示,要使物体不被淋湿,在车上观察雨点下落的方向(即雨点相对于汽车的运动速度v 2′的方向)应满足hlαarctan ≥.再由相对速度的矢量关系122v v v -=',即可求出所需车速v 1.解 由122v v v -='[图(b)],有θθαcos sin arctan221v v v -= 而要使hlαarctan ≥,则 hl θθ≥-cos sin 221v v v ⎪⎭⎫ ⎝⎛+≥θh θl sin cos 21v v 1 -27 一人能在静水中以1.10 m·s-1 的速度划船前进.今欲横渡一宽为1.00 ×103 m 、水流速度为0.55 m·s-1 的大河.(1) 他若要从出发点横渡该河而到达正对岸的一点,那么应如何确定划行方向? 到达正对岸需多少时间? (2)如果希望用最短的时间过河,应如何确定划行方向? 船到达对岸的位置在什么地方?分析 船到达对岸所需时间是由船相对于岸的速度v 决定的.由于水流速度u 的存在, v 与船在静水中划行的速度v ′之间有v =u +v ′(如图所示).若要使船到达正对岸,则必须使v 沿正对岸方向;在划速一定的条件下,若要用最短时间过河,则必须使v 有极大值.解 (1) 由v =u +v ′可知v '=u αarcsin ,则船到达正对岸所需时间为。
宏观经济学第1章习题及答案分析

13章宏观经济问题与理论争论一、名词解释:宏观经济学失业率经济增长经济周期卢卡斯楔奥肯缺口通货膨胀通货膨胀率汇率萨伊定律凯恩斯革命二、判断题(正确的标“T”,错误的标“F”)1.经济学根据研究的方法不同,可以划分为微观经济学与宏观经济学。
()2.微观经济学的中心理论是价格理论,宏观经济学的中心理论是国民收入决定理论。
()3.宏观经济学是在微观经济学基础上发展起来的,是作为微观经济学补充的经济学理论。
()4.在1936年以凯恩斯发表《通论》之前,经济学上并不存在宏观经济理论。
()5.经济增长理论是宏观经济学的中心理论。
()6.宏观经济学研究的主要经济问题是经济增长和国际收支问题。
()7.一国的经济增长总是呈现出波动性。
()8.宏观经济学研究考察国民经济作为整体的功能。
()9.“看不见的手”指的是市场机制。
();“看得见的手”指政府对经济的宏观调控。
()10.宏观经济学采取总量分析的方法。
()11.宏观经济状况影响和制约着微观经济个体的行为。
()12.经济增长是指一国一定时期内总产出的增长。
()13.经济增长意味着一国将来有更多的商品和服务供人们消费14.一国稀缺资源中最容易被闲置的是劳动力资源。
()15.劳动力就是一国在一定年龄范围内成年人的总数。
()16.失业率是失业数量占就业数量的比率。
()17.一个社会总会存在失业。
()18.充分就业意味着人人都有工作。
()19.如果汽油或计算机的价格上升了,经济就一定经历着通货膨胀。
()20.如果平均物价水平上升一倍,那么,货币的价值就下降了一半。
()21.经济学家一致认为,物价上升就是通货膨胀。
()22.充分就业与稳定物价是一致的,只要达到了其中的一项,也就实现了另一项。
()23.采取降低失业的政策,很可能会导致物价水平的上升。
()24.政府所追求的宏观经济目标是:高速而稳定的经济增长;低失业;低通货膨胀;避免国际收支赤字和汇率的过度波动。
()25.宏观经济学家一致认为,只要政府积极地干预经济,就能实现宏观经济目标。
《定量分析简明教程》习题一参考答案

一、 选择题1、用同一NaOH 滴定相同浓度和体积的两种弱一元酸,则a K Θ较大的弱一元酸(B ) A 消耗NaOH 多;B 突跃范围大;C 计量点pH 较低;D 指示剂变色不敏锐。
2、滴定分析要求相对误差±0.1%,万分之一的分析天平绝对误差为±0.0001g ,则一般至少称取试样质量为(B )A0.1g ;B0.2g ;C0.3g ;D0.4g.3、以HCl 溶液滴定某碱样,滴定管的初读数为0.25±0.01ml ,终读数为32.25±0.01ml ,则用去HCl 溶液的准确体积为(D )A32.0ml ;B32.00ml ;C32.00±0.01ml ;D32.00±0.02ml 。
4、指示剂的变色范围越窄,则(A )A 滴定越准确;B 选择指示剂越多;C 变色敏锐;D 滴定越不准确。
5、溶液pH 降低,EDTA 的配位能力会(B ) A 升高;B 降低;C 不变;D 无法确定。
6、用KMnO 4法测定Ca 2+离子,所采用的滴定方式是(B )法 A 直接滴定法;B 间接滴定法;C 返滴定法;D 置换滴定法。
7、不同波长的电磁波,具有不同的能量,其波长与能量的关系为(B ) A 波长愈长,能量愈大;B 波长愈长,能量愈小;C 波长无能量无关。
8、在酸性条件下,莫尔法测Cl -,其测定结果(B ) A 偏低;B 偏高;C 正好;D 无法确定。
9、下列有关配体酸效应叙述正确的是(B ) A 酸效应系数越大,配合物稳定性越大;B 酸效应系数越小,配合物稳定性越大;CpH 越高,酸效应系数越大。
10、酸性介质中,用草酸钠标定高锰酸钾溶液,滴入高锰酸钾的速度为(B ) A 同酸碱滴定一样,快速进行;B 开始几滴要慢,以后逐渐加快; C 始终缓慢;D 开始快,然后逐渐加快,最后稍慢。
11、酸碱滴定中,选择指示剂可不考虑的因素是(D )ApH 突跃范围;B 要求的误差范围;C 指示剂的变色范围;D 指示剂的结构。
2023年一级造价师之工程造价案例分析(交通)练习题(一)及答案

2023年一级造价师之工程造价案例分析(交通)练习题(一)及答案大题(共10题)一、某施工单位与某建设单位按照《公路工程标准施工招标文件》(2018年版)签订了一高速公路项目的施工合同。
双方合同规定:工期为302天,施工日期为2018年3月1日至12月27日。
工程实施过程中,在同一个关键工作面上发生了下列事件,并经专业监理工程师审查,情况属实。
事件1:由于不能及时提供场地,施工方于2018年3月4日才进场开始作业,延期开工造成的实际损失3万元。
事件2:土方开挖工程,开挖时遇到了难以预料的暴雨天气,实际持续时间延长了12天,直接经济损失10万元。
事件3:建设单位负责设备的采购,甲施工单位经建设单位同意后将安装工作专业分包给具备相应条件的乙施工单位。
乙施工单位完成设备安装后,单机无负荷试车没有通过,经分析是设备本身出现问题。
经设备制造单位修理,第二次试车合格。
由此发生的设备拆除、修理、重新安装和重新试车的各项费用分别为2万元、5万元、3万元和1万元,安装工作实际持续时间延长了14天。
事件4:为了确保工程质量,施工单位对路基工作增加一次检验,增加费用2万元,路基工作持续时间增加2天。
、如果甲施工单位就工程中发生的1~4项事件提出索赔要求,试问工期和费用能否成立?说明理由。
、对1~4项事件工期索赔各是多少天?总工期索赔多少天?、计算1~4项事件费用索赔总额?、乙施工单位承接对应的安装工作专业分包应该满足哪些条件?【答案】1.事件1:工期和费用索赔成立。
因为不能及时提供场地属建设单位责任,延误的时间将导致工期延长。
事件2:工期索赔成立。
费用索赔不成立。
因为不可抗力造成的费用损失双方各自承担,造成工期延误的可以索赔工期。
事件3:工期和费用索赔成立。
因为建设单位负责设备的采购,因设备本身出现问题造成的费用损失应由建设单位承担,延误的时间将导致工期延长。
事件4:工期和费用索赔不成立。
因为保证工程质量的检验费用已包含在合同价中,施工方额外增加的检验费用应自己承担,增加的工作时间也不能顺延。
复习题一答案分析_课后习题答案

计算机网络技术复习题一选择题.1、计算机网络发展史上具有典型代表意义的网络是()A.SAGE B.ARPANET C.NSFNET D.Internet答案:B解析:SAGE是第一代计算机网络(面向终端的计算机网络)的典型代表。
ARPANET是第二代计算机网络(计算机-计算机互联网络)的典型代表,ARPANET对网络的发展具有重大意义,意义见书上。
NSFNET是美国国家科学基金会NSF(National Science Foundation)建立的美国国家科学基金网,于1990年6月彻底取代了ARPAnet而成为Internet的主干网。
Internet是国际上最大的网络,又叫做国际互联网,任何个人、组织、机构只要遵循TCP/IP协议,便能方便接入。
2、在计算机通信网络中,误码率一般要低于()A.10-4B.10-6 C.10-8D.10-9答案:B解析:在计算机网络中,一般要求误码率低于10-6,电话线模拟通信系统的误码率为10-4~10-5;光纤通信系统的误码率为10-9以下。
3、计算机网络按照覆盖范围可分为()、城域网和广域网。
答案:A4、网络协议的三要素分别是语义、语法和()。
答:B解析:语法是指规定了数据单元结构和格式.语义是指各字段的含义。
时序是指通信双方操作的执行顺序和规则。
5、一个单位在一座大楼内的一个计算机网络系统,属于()。
答:A6、以下不是数字通信系统的优点?()A.抗干扰强,适合长距离传输B.方便加密、解密C.方便存储D.需要带宽小答:D解析:与模拟信号相比,数字信号占用带宽大。
7、以太网中采用的同步技术是()A.异步传输传输答:C解析:异步传输:以单个字符为单位进行传输,每个字符前后加1位或1位半“起始位”、“停止位”,字符与字符之间的时间间隔可不固定,即不对时。
适用于低速、不可靠数据传输,如键盘输入数据、电话拨号通信,计算机串口通信等。
面向字符的同步传输:以字符块为传输单位,字符块中的每位要对时,每块前后加若干位“前同步码”和“后同步码”,“前同步码”和“后同步码”采用特殊的字符标识。
紫外光谱分析法习题答案(1)

紫外光谱分析法习题班级姓名分数一、选择题( 共85题170分)1. 2 分(1010)在紫外-可见光度分析中极性溶剂会使被测物吸收峰((3) )(1) 消失(2) 精细结构更明显(3) 位移(4) 分裂9. 2 分(1101)双光束分光光度计与单光束分光光度计相比,其突出优点是( (4) )(1) 可以扩大波长的应用范围(2) 可以采用快速响应的检测系统(3) 可以抵消吸收池所带来的误差(4) 可以抵消因光源的变化而产生的误差14. 2 分(1217)许多化合物的吸收曲线表明,它们的最大吸收常常位于200─400nm 之间,对这一光谱区应选用的光源为( (1) )(1) 氘灯或氢灯(2) 能斯特灯(3) 钨灯(4) 空心阴极灯灯16. 2 分(1232)助色团对谱带的影响是使谱带( (1) )(1)波长变长(2)波长变短(3)波长不变(4)谱带蓝移19. 2 分(1300)指出下列哪种是紫外-可见分光光度计常用的光源?((4) )(1) 硅碳棒(2) 激光器(3) 空心阴极灯(4) 卤钨灯20. 2 分(1301)指出下列哪种不是紫外-可见分光光度计使用的检测器?( (1) )(1) 热电偶(2) 光电倍增管(3) 光电池(4) 光电管28. 2 分(1324)紫外-可见吸收光谱主要决定于((2) )(1) 分子的振动、转动能级的跃迁(2) 分子的电子结构(3) 原子的电子结构(4) 原子的外层电子能级间跃迁38. 2 分(1343)基于发射原理的分析方法是( (2) )(1) 光电比色法(2) 荧光光度法(3) 紫外及可见分光光度法(4) 红外光谱法39. 2 分(1344)基于吸收原理的分析方法是( (4) )(1) 原子荧光光谱法(2) 分子荧光光度法(3) 光电直读光谱法(4) 紫外及可见分光光度法40. 2 分(1346)在紫外-可见分光光度计中, 强度大且光谱区域广的光源是( (3) )(1) 钨灯(2) 氢灯(3) 氙灯(4) 汞灯43. 2 分(1367)物质的紫外-可见吸收光谱的产生是由于( (3) )(1) 分子的振动(2) 分子的转动(3) 原子核外层电子的跃迁(4) 原子核内层电子的跃迁46. 1 分(1374)阶跃线荧光的波长((1) )(1)大于所吸收的辐射的波长(2)小于所吸收的辐射的波长(3)等于所吸收的辐射的波长(4)正比于所吸收的辐射的波长60. 2 分(1764)比较下列化合物的UV-VIS吸收波长的位置(λmax )((4) )(C)CH 3O CH 3OC(b)COOHOCl(a)O(1) a>b>c (2) c>b>a (3)b>a>c (4)c>a>b 62. 2 分 (1766)在紫外-可见光谱区有吸收的化合物是 ((4) ) (1) CH 3-CH=CH-CH 3 (2) CH 3-CH 2OH(3) CH 2=CH-CH 2-CH=CH 2(4) CH 2=CH-CH=CH-CH 3 64. 2 分 (1768)双波长分光光度计和单波长分光光度计的主要区别是 ((2) ) (1)光源的个数 (2)单色器的个数 (3)吸收池的个数(4)单色器和吸收池的个数 71. 2 分 (1775)下列哪种方法可用于测定合金中皮克数量级(10-12)的铋? ((2) ) (1)分光光度法 (2)中子活化 (3)极谱法 (4)电位滴定法 74. 2 分 (1778)在分光光度法中,运用朗伯-比尔定律进行定量分析采用的入射光为((2) ) (1)白光 (2)单色光 (3)可见光 (4)紫外光 76. 2 分 (1780)分子运动包括有电子相对原子核的运动(E 电子)、核间相对位移的振动(E 振动) 和转动(E 转动)这三种运动的能量大小顺序为 ((3) ) (1) E 振动>E 转动>E 电子 (2) E 转动>E 电子>E 振动 (3) E 电子>E 振动>E 转动 (4) E 电子>E 转动>E 振动二、填空题( 共15题57分)3. 5 分(2319)在紫外-可见吸收光谱中, 一般电子能级跃迁类型为:(1)______________跃迁, 对应________________光谱区(2)______________跃迁, 对应________________光谱区(3)______________跃迁, 对应________________光谱区(4)______________跃迁, 对应________________光谱区2319[答] 1. σ─>σ*, 真空紫外;2. n─>σ*, 远紫外;3. π─>π*, 紫外;4. n─>π*, 近紫外, 可见.89. 5 分(2024)可见-紫外、原子吸收的定量分析吸收光谱法都可应用一个相同的_____________________定律, 亦称为___________ 。
仪器分析课后习题答案1

课后习题答案第一章:绪论1.解释下列名词:(1)仪器分析和化学分析;(2)标准曲线与线性范围;(3)灵敏度、精密度、准确度和检出限。
答:(1)仪器分析和化学分析:以物质的物理性质和物理化学性质(光、电、热、磁等)为基础的分析方法,这类方法一般需要特殊的仪器,又称为仪器分析法;化学分析是以物质化学反应为基础的分析方法。
(2)标准曲线与线性范围:标准曲线是被测物质的浓度或含量与仪器响应信号的关系曲线;标准曲线的直线部分所对应的被测物质浓度(或含量)的范围称为该方法的线性范围。
(3)灵敏度、精密度、准确度和检出限:物质单位浓度或单位质量的变化引起响应信号值变化的程度,称为方法的灵敏度;精密度是指使用同一方法,对同一试样进行多次测定所得测定结果的一致程度;试样含量的测定值与试样含量的真实值(或标准值)相符合的程度称为准确度;某一方法在给定的置信水平上可以检出被测物质的最小浓度或最小质量,称为这种方法对该物质的检出限。
第三章光学分析法导论1.解释下列名词:(1)原子光谱和分子光谱;(2)原子发射光谱和原子吸收光谱;(3)统计权重和简并度;(4)分子振动光谱和分子转动光谱;(5)禁戒跃迁和亚稳态;(6)光谱项和光谱支项;(7)分子荧光、磷光和化学发光;(8)拉曼光谱。
答:(1)由原子的外层电子能级跃迁产生的光谱称为原子光谱;由分子的各能级跃迁产生的光谱称为分子光谱。
(2)当原子受到外界能量(如热能、电能等)的作用时,激发到较高能级上处于激发态。
但激发态的原子很不稳定,一般约在10-8s内返回到基态或较低能态而发射出的特征谱线形成的光谱称为原子发射光谱;当基态原子蒸气选择性地吸收一定频率的光辐射后跃迁到较高能态,这种选择性地吸收产生的原子特征的光谱称为原子吸收光谱。
(3)由能级简并引起的概率权重称为统计权重;在磁场作用下,同一光谱支项会分裂成2J+1个不同的支能级,2J+1称为能级的简并度。
(4)由分子在振动能级间跃迁产生的光谱称为分子振动光谱;由分子在不同的转动能级间跃迁产生的光谱称为分子转动光谱。
需求分析习题一、二(答案)

习题1一、单项选择题1、软件生产中产生需求问题的最大原因在于对应用软件的(C)理解不透彻或应用不坚决。
(A)复杂性(B)目的性(C)模拟性(D)正确性2、需求分析的目的是保证需求的(B)。
(A)目的性和一致性(B)完整性和一致性(C)正确性和目的性(D)完整性和目的性3\现实世界中的(B)构成了问题解决的基本范围,称为该问题的问题域。
(A)属性和状态(B)实体和状态(C)实体和操作(D)状态和操作4、比较容易发现的涉众称为初始涉众,又称为(B),通常包括客户、管理者和相关的投资者。
(A)关键涉众(B)涉众基线(C)普通涉众(D)一般涉众5、按照使用方式进行分类,原型可分为:演示原型、(D)、试验原型和引示系统原型。
(A)非操作原型(B)系列首发原型(C)选定特征原型(D)严格意义上的原型二、填空题1、传统的需求分析方法都是从设计领域转入分析领域的。
2、需求工程是所有需求处理活动的总和,它收集信息、分析问题、整合观点、记录需求并验证其正确性,最终反映软件被应用后与其环境互动形成的期望效应。
3、软件需求开发用来确定系统需求中应该由软件满足的部分,将其映射为软件行为,产生软件需求规格说明。
三、简答题1、简述需求工程的主要任务。
答:需求工程有以下三个主要任务:①需求工程必须说明软件系统将被应用的环境及其目标,说明用来达成这些目标的软件功能,还要说明在设计和实现这些功能时上下文环境对软件完成任务所用方式、方法所施加的限制和约束,也即要同时说明软件需要“做什么”和“为什么”需要做。
②需求工程必须将目标、功能和约束反映到软件系统中,映射为可行的软件行为,并对软件行为进行准确的规格说明。
需求规格说明是需求工程最为重要的成果,是项目规划、设计、测试、用户手册编写等很多后继软件开发阶段的工作基础。
③现实世界是不断变化的世界,因此需求工程还需要妥善处理目标、功能和约束随着时间的演化情况。
同时,为了节省开支和进行需求规格说明的重用,需求工程还需要对目标、功能和约束在软件产品族中的演化和分布情况进行综合考虑与处理。
算法设计与分析习题答案1

算法设计与分析习题答案1算法设计与分析习题答案1习题1 1. 图论诞生于七桥问题。
出生于瑞士的伟大数学家欧拉提出并解决了该问题。
七桥问题是这样描述的:北区一个人是否能在一次步行中穿越哥尼斯堡城中全部岛区的七座桥后回到起点,且每座桥只经过一次,南区图是这条河以及河上的两个岛和七座桥的图七桥问题草图。
请将该问题的数据模型抽象出来,并判断此问题是否有解。
七桥问题属于一笔画问题。
输入:一个起点输出:相同的点1,一次步行2,经过七座桥,且每次只经历过一次3,回到起点该问题无解:能一笔画的图形只有两类:一类是所有的点都是偶点。
另一类是只有二个奇点的图形。
2.在欧几里德提出的欧几里德算法中用的不是除法而是减法。
请用伪代码描述这个版本的欧几里德算法=m-n 2.循环直到r=0 m=n n=r r=m-n 3 输出m 3.设计算法求数组中相差最小的两个元素的差。
要求分别给出伪代码和C++描述。
//采用分治法//对数组先进行快速排序//在依次比较相邻的差#include using namespace std; int partions(int b,int low,int high) { int prvotkey=b[low]; b[0]=b[low]; while (low while (low=prvotkey)--high; b[low]=b[high]; while (low b[high]=b[low]; } b[low]=b[0]; return low; } void qsort(int l,int low,int high) { int prvotloc; if(low prvotloc=partions(l,low,high);//将第一次排序的结果作为枢轴qsort(l,low,prvotloc-1); //递归调用排序low 到prvotloc-1 qsort(l,prvotloc+1,high); //递归调用排序prvotloc+1到high } } void quicksort(int l,int n) { qsort(l,1,n); // 第一个作为枢轴,从第一个排到第n个} int main() { int a[11]={0,2,32,43,23,45,36,57,14,27,39};int value=0;//将最小差的值赋值给value for (int b=1;b quicksort(a,11); for(int i=0;i!=9;++i) { if( (a[i+1]-a[i]) value=a[i+2]-a[i+1]; } cout return 0; } 4.设数组a[n]中的元素均不相等,设计算法找出a[n]中一个既不是最大也不是最小的元素,并说明最坏情况下的比较次数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.已知一算术表达式的中缀形式为A+B*C-D/E,后缀形式为ABC*+DE/-,其前缀形式为()。
A.-A+B*C/DE B.-A+B*CD/E C.-+*ABC/DE D.-+A*BC/DE参考答案:D3.一棵完全二叉树上有1001个结点,其中叶子结点的个数是()。
A.250 B.500 C.254 D.505 E.以上答案都不对参考答案:E8.在一棵三元树中度为3的结点数为2个,度为2的结点数为1个,度为1的结点数为2个,则度为0的结点数为()个。
A.4 B.5 C.6D.7参考答案:C10.具有10个叶结点的二叉树中有()个度为2的结点。
A.8 B.9C.10 D.11参考答案:B53.由3个结点可以构造出()种不同的二叉树。
A.2 B.3 C.4 D.5参考答案:D47.引入二叉线索树的目的是()。
A.加快查找结点的前驱或后继的速度B.为了能在二叉树中方便的进行插入与删除C.为了能方便的找到双亲D.使二叉树的遍历结果唯一19.将如下由三棵树组成的森林转换为二叉树。
参考答案:HGDACJIBFEMPONKOL反过来,将一个二叉树转化成森林或树?(注意:转化成森林的结果和转化成树的结果不一样)21.设某二叉树的前序遍历序列为ABCDEFGGI ,中序遍历序列为BCAEDGHFI ,试画出该二叉树。
参考答案:27.设二叉树T 的存储结构如下:1 2 3 4 5 6 7 8 9 10Lchild 0 0 2 3 7 5 8 0 10 1 Data JH F D B A C E G I Rchild0 094其中Lchild 、Rchild 分别为结点的左、右孩子指针域,Data 为结点的数据域,若根指针T 的值为6,试:(1)画出二叉树的逻辑结构;(2)写出按前序、中序、后序遍历该二叉树所得到的结点序列;(3)画出二叉树的后序线索树。
参考答案:前序序列:ABCEDFHGIJ 中序序列:ECBHFDJIGA 后序序列:ECHFJIGDBA31.假定用于通讯的电文仅有8个字母C1,C2,…,C8组成,各个字母在电文中出现的频率分别为5,25,3,6,10,11,36,4,试为这8个字母设计哈夫曼编码树。
参考答案:A ID BE C HF G各字母编码如下:c1:0110 c2:10 c3:0010 c4:0111 c5:000 c6:010 c7:11 c8:0011 注意虽然哈夫曼树的带权路径长度是唯一的,但形态不唯一。
33.设T 是一棵二叉树,除叶子结点外,其它结点的度皆为2,若T 中有6个叶结点,试问:(1)树T 的最大深度和最小可能深度分别是多少?(2)树T 中共有多少非叶结点?(3)若叶结点的权值分别为1、2、3、4、5、6,请构造一棵哈曼夫树,并计算该哈曼夫树的带权路径长度wpl 。
参考答案:(1)最大深度6,最小深度4; (2)非叶结点数5;(3)哈夫曼树见下图,其带权路径长度wpl=51。
34.一棵深度为H的满k叉树有如下性质:第H层上的结点都是叶子结点,其余各层上每个结点都有k棵非空子树。
若按层次顺序从1开始对全部结点编号,问:(1)第i层上有多少个结点?(2)编号为p的结点的第i个孩子结点(若存在)的编号是多少?(3)编号为p的结点的双亲结点(若存在)的编号是多少? 参考答案: (1)1-i k个(2)(1+(p-1)*k)+i (3)⎥⎦⎥⎢⎣⎢-+k k p 2(p≠1) 】2.给出算法将二叉树表示的表达式二叉树按中缀表达式输出,并加上相应的括号。
参考答案:本题是将符号算术表达式用二叉树表示的逆问题,即将二叉树表示的表达式还原成原表达式。
二叉树的中序遍历序列与原算术表达式基本相同,差别仅在于二叉树表示中消除了括号。
将中序序列加上括号就恢复原貌。
当根结点运算符优先级高于左子树(或右子树)根结点运算符时,就需要加括号。
int Precede(char optr1, char optr2)// 比较运算符级别高低,optr1级别高于optr2时返回1,相等时返回0,低于时返回-1 {switch(optr1){case‘+’:case‘-’:if(optr2==‘+’||optr2==‘-’)return(0);else return(-1);case‘*’:case‘/’:if(optr1==‘*’||optr2==‘/’)return(0);else return(1);}}void InorderExp (BiTree bt)//输出二叉树表示的算术表达式,设二叉树的数据域是运算符或变量名{int bracket;if(bt){if(bt->lchild!=null){bracket=Precede(bt->data,bt->lchild->data)//比较双亲与左子女运算符优先级if(bracket==1) printf(‘(’);InorderExp(bt->lchild); //输出左子女表示的算术表达式if(bracket==1)printf(‘)’); //加上右括号}printf(bt->data); //输出根结点if(bt->rchild!=null) //输出右子树表示的算术表达式{bracket=Precede(bt->data,bt->rchild->data)if (bracket==1)printf(“(”); //右子女级别低,加括号InorderExp (bt->rchild);if(bracket==1)printf(“)”);} }}//结束Inorder Exp4.有n个结点的完全二叉树存放在一维数组A[1..n]中,试据此建立一棵用二叉链表表示的二叉树,根由tree指向。
参考答案:方法一:BiTree Creat(ElemType A[],int i)//n个结点的完全二叉树存于一维数组A中,本算法据此建立以二叉链表表示的完全二叉树{BiTree tree;if (i<=n){tree=(BiTree)malloc(sizeof(BiNode)); tree->data=A[i];if(2*i>n) tree->lchild=null;else tree->lchild=Creat(A,2*i);if(2*i+1>n) tree->rchild=null;else tree->rchild=Creat(A,2*i+1); } return (tree); }//Creat初始调用时i=1。
图的部分习题答案5.n个结点的完全有向图含有边的数目()。
A.n*n B.n(n+1)C.n/2 D.n*(n-1)参考答案:D15.设图如右所示,,在下面的5个序列中,符合深度优先遍历的序列有()个。
a eb d fc a c fde b a e df c b a e f d c b a e f d b cA.5个B.4个C.3个D.2个参考答案:D21.已知有向图G=(V,E),其中V={V1,V2,V3,V4,V5,V6,V7},E={<V1,V2>,<V1,V3>,<V1,V4>,<V2,V5>, <V3,V5>,<V3,V6>,<V4,V6>,<V5,V7>,<V6,V7>},G的拓扑序列是()。
A.V1,V3,V4,V6,V2,V5,V7B.V1,V3,V2,V6,V4,V5,V7C.V1,V3,V4,V5,V2,V6,V7D.V1,V2,V5,V3,V4,V6,V7参考答案:A24.在有向图G的拓扑序列中,若顶点Vi在顶点Vj之前,则下列情形不可能出现的是()。
A.G中有弧<Vi,Vj> B.G中有一条从Vi到Vj的路径C.G中没有弧<Vi,Vj> D.G中有一条从Vj到Vi的路径参考答案:D26.关键路径是事件结点网络中()。
A.从源点到汇点的最长路径B.从源点到汇点的最短路径C.最长回路D.最短回路参考答案:A37.设有无向网如下,写出其邻接矩阵,并在此基础上按普里姆算法求最小生成树。
参考答案:邻接矩阵: ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞6456252363794567555553955434 最小生成树:38.试写出对如下有向无环图进行拓扑排序可能得到的所有拓扑序列。
参考答案:每次输出一个入度为0的顶点。
abcdefg、abcdfeg、abcfdeg。
39.设有向网如下,用弗洛伊德算法求图中各对顶点间的最短路径。
参考答案:35.设有AOE网如下,试求关键路径。
参考答案:关键路径1:v1→v2→v5→v7关键路径2:v1→v3→v6→v732.下图是带权的有向图G的邻接表表示法,求:(1)以结点V1出发深度遍历图G所得的结点序列;(2)以结点V1出发广度遍历图G所得的结点序列;(3)从结点V1到结点V8的最短路径;(4)从结点V1到结点V8的关键路径。
参考答案:(1)V1,V2,V3,V8,V5,V7,V4,V6;(2)V1,V2,V4,V6,V3,V5,V7,V8;(3)V1到V8最短路径56,路径为V1----V2----V5----V7----V8;(4)V1到V8的关键路径是V1----V6----V5----V3----V8,长97。
29.试利用Dijkstra算法求下图中从顶点a到其他个顶点间的最短路径,写出执行算法过程中各步的状态。
参考答案:顶点a到顶点b,c,d,e,f,g间的最短路径分别是15,2,11,10,6,13。
34.对图示的AOE网络,计算各活动弧的e(a i)和l(a i)的函数值,各事件(顶点)的ve(Vj)和vl (Vj)的函数值,列出各条关键路径。
7.有向图的邻接表存储如下,要求:(1)画出其邻接矩阵存储;(2)写出图的所有强连通分量;(3)写出顶点a到顶点i的全部简单路径。
参考答案:(1)略。
(注:邻接矩阵下标按字母升序:abcdefghi)(2)强连通分量:(a),(d),(h),(b,e,i,f,c,g)(3)顶点a到顶点i的简单路径:(a->b->e->i),(a->c->g->i),(a->c->b->e->i)。
数组20.设有一个10阶的对称矩阵A,采用压缩存储方式,以行序为主存储,a11为第一元素,其存储地址为1,每个元素占一个地址空间,则a85的地址为()。
