广东专插本(高等数学)模拟试卷55(题后含答案及解析)

合集下载

2020年广东专插本全真模拟大联考-高等数学【试卷】

B． lim x2 +1 x→0 x
D． lim x sin 1
x→0
x
A． (1,1)
B． (1, −3)
C． (0, 0)
D． (2,8)
∫ 3. 已知 F (x) 是 f (x) 的一个原函数，则 f (e−x )e−xdx =
A． F (ex ) + C
B． F (e−x ) + C
C． −F (ex ) + C
6.
已知
lim
x→∞
x+a x − 2a
x
=
8 ，则 a
=
.
7. 曲线 y = xe−x 的拐点是
.
x3
∫ 8. 设 f (x) 连续，且 f (t)dt = x ，则 f (27) = 0
.
1
9. 已知 y = e2x 是微分方程 y′′ + ay′ + 2 y = 0 的一个解，则 a =
0
y
2
1− y2
∫ ∫ C． 2 dy
f (x, y)dx
0
0
∞
n
∑ ∑ 5. 若级数 un 收敛，记 Sn = ui ，则
n=1
i =1
A．
lim
n→∞
Sn
存在
C．
lim
n→∞
Sn
可能不存在
2
1− x2
∫ ∫ D． 2 dx
f (x, y)dy
0
x
B．
lim
n→∞
Sn
=
0
D．{Sn} 题，每小题 3 分，共 15 分）
广东省 2020 年普通高等学校本科插班生招生考试

广东专插本(高等数学)模拟试卷54(题后含答案及解析)

广东专插本（高等数学）模拟试卷54(题后含答案及解析) 题型有：1. 选择题 2. 填空题 4. 解答题 5. 综合题选择题在每小题给出的四个选项中，只有一项是符合要求的。

1．设函f(χ)＝( ) A．－1B．0C．1D．不存在正确答案：D解析：极限不存在，本题应选D．2．设函数f(χ)＝lnsinχ，则df(χ)＝( )A．B．－cotχdχC．cotχdχD．tanχdχ正确答案：C解析：d(lnsinχ)＝cosχdχ＝cotχdχ，故应选C．3．f′(χ2)＝(χ＞0)，则f(χ)＝( )A．2χ＋CB．2＋CC．χ2＋CD．＋C正确答案：B解析：令t＝χ2则χ＝，f′(χ)＝(χ＞0)，f(χ)＝∫f′(χ)dχ＝＋C，故应选B．4．如果使函数f(χ)＝在点χ＝0处连续，应将其在点χ＝0处的函数值补充定义为( )A．0B．2C．－1D．1正确答案：D解析：若f(χ)在χ＝0处连续需补充定义f(0)＝1，故本题选D．5．设pn＝，qn＝，n＝1，2，…，则下列命题中正确的是( )A．若an条件收敛，则Pn与qn都收敛B．若an绝对收敛，则Pn与qn都收敛C．若an条件收敛，则Pn与qn的敛散性都不定D．若an绝对收敛，则Pn与qn的敛散性都不定正确答案：B解析：an绝对收敛都收敛，an条件收敛都发散，一个收敛，一个发散an发散，故本题选B．填空题6．设＝6，则a＝_______．正确答案：－1解析：＝6，则(1＋0)(1＋2.0)(1＋3.0)＋a＝0，a＝－1．7．已知曲线y＝χ2＋χ－2上点M处的切线平行于直线y－5χ－1，则点M的坐标为_______．正确答案：(2，4)解析：y′＝2χ＋1＝5，则χ＝2，故M点坐标为(2，4)．8．已知f(χ)＝χ2＋cosχ＋∫01f(χ)dχ，则f(χ)＝_______．正确答案：χ＋cosχ＋＋sin1解析：令f(χ)＝χ2＋cosχ＋C，则f(χ)＝χ2＋cosχ＋(χ2＋cosχ＋C)dχ，f(χ)＝即C＝，C＝＋sin1，故f(χ)＝χ＋cosχ＋＋sin1．9．微分方程y?－y′＝0的通解为_______．正确答案：y＝C1＋C2eχ解析：微分方程的特征方程为λ2－λ＝0，则特征根为λ1＝0，λ2＝1，故微分方程的通解为y＝C1＋C2eχ(C1，C2为任意常数)．10．若函数f(χ)＝在χ＝0处连续，则a＝_______．正确答案：6解析：即＝3，故a＝6．解答题解答时应写出推理、演算步骤。

2020年广东省专插本考试《高等数学》真题+答案

广东省2020年普通高等学校本科插班生招生考试《高等数学》试题本试卷共2⻚，20⻚题，满分100分。

考试时间120一、单项选择题(本大题共5小题，每小题3分，共15分。

每小题只有一个符合题目要求)1.设lim x→0[cos x −f(x)]=1, 则下列等式正确的是（）A.lim x→0f(x)=1 B.lim x→0f(x)cos x =1C.lim x→0f(x)=−1 D.lim x→0[f(x)+cos x ]=12.函数f(x)=2x 3−3x 2的极小值点为（） A.x =−1 B.x =0 C.x =1 D.x =23.已知3x 是函数f(x)的一个原函数，则f(x)=（） A.3x B.3x ln 3 C.x3xD.3x ln 34.设平⻚区域D ={(x,y )|x 2+y 2≤1，y ≥0},则∬(x 2+y 2)4dσD（） A.π10 B.π9 C.π5 D.2π95.设级数∑a n ∞n=1 满⻚0≤a n ≤15n ，则下列级数发散的是（）A.∑3a n ∞n=1B. ∑a n ∞n=1+3C.∑(a n ∞n=1+√n23) D.∑(a n ∞n=1−√n3) 二、填空题。

6.若函数f(x)={(1+a )x 2， x ≤1a (x −2)3+3, x >1 在x=1处连续，则常数a= . 7.曲线x 22+y 2=3在点（2，−1）处的切线方程为y= . 8.微分方程 y n +3y ’−4y =0的通解为y= .9.设二元函数f (x,y )在点(0,0)的某个邻域内有定义,且当x ≠0时，f(x,0)−f(0,0)x=3x +2，则f ’x (0,0)= 。

10.设函数f(x)在(−∞，+∞)内可导，且满足f(x)=f ‘(x)，f(0)=m ,如果∫f(x)e xdx =81−1,则m=____________。

三、计算题。

11.求极限limx→0∫tarctantdtx0x 312.已知y 是x的函数，且y ′=ln √x +√ln x +2ln 2，求d 2y dx 2|x =e13.求不定积分∫(cos x −x sin x 2)dx14.设函数f(x)={x 31+x 2, x ≤1x, x >1，求定积分∫f(x +2)dx 0−315.求二元函数z =3xy 2+x 2y的全微分dz ，并求ð2zðxðy16.计算∬ydσD ，其中D 是由直线y =x,y =−2与y =0,y =2x 围成的有界闭区域。

广东省2017年普通高等学校本科插班生招生考试试题与详细解答

广东省 2017 年普通高等学校本科插班生招生考试《高等数学》（公共课）试题和详细解答
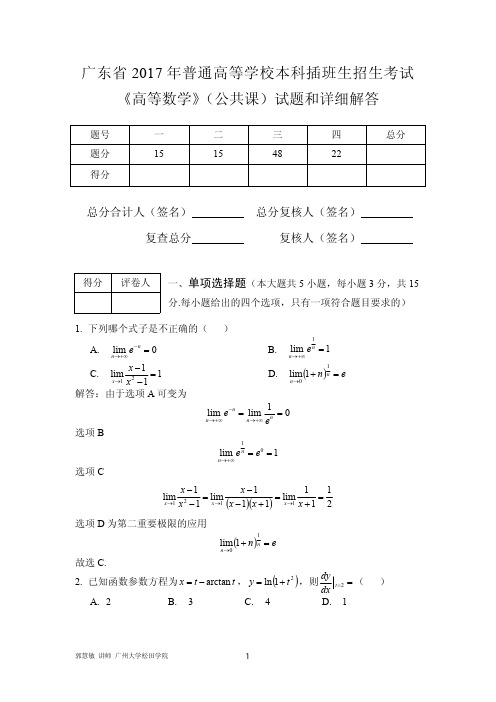
题号
一
二
三
四
总分
题分
15
15
48
22
得分
总分合计人（签名）复查总分
总分复核人（签名）复核人（签名）
得分评卷人一、单项选择题（本大题共 5 小题，每小题 3 分，共 15
分.每小题给出的四个选项，只有一项符合题目要求的）
n
选项 C
lim
x1
x 1 x2 1

lim
x1
x
x 1
1x 1

lim
x1
x
1 1

1 2
选项 D 为第二重要极限的应用
lim1

n
1 n

e
n0
故选 C.
2.
已知函数参数方程为 x t arctan t ， y ln 1 t 2
，则 dy dx
8
5. 已知 1 dx 1x2 f x, y dy ，转换成极坐标的形式（）
1
0
A.
2
d
1 f r cos , r sin dr
0
0
B.

0
d
1 0
f
r
cos
,
r
sin

rdr
C.
2
d
1 f r cos , r sin rdr
1. 下列哪个式子是不正确的（）
A. lim en 0 n
1
B. lim e n 1 n
C.
lim
x1
x 1 x2 1

广东省2010~2020年专插本考试《高等数学》真题及答案

广东省2010年普通高校本科插班生招生考试《高等数学》试题一、单项选择题（本大题共5小题,每小题3分，共15分）1．设函数()y f x =的定义域为(,)-∞+∞，则函数1[()()]2y f x f x =--在其定义域上是（）A ．偶函数B ．奇函数C ．周期函数D ．有界函数2．0x =是函数1,0()0,0x e x f x x ⎧⎪<=⎨≥⎪⎩的（）A ．连续点B ．第一类可去间断点C ．第一类跳跃间断点D ．第二类间断点3．当0x →时，下列无穷小量中，与x 等价的是（）A ．1cos x-B ．211x +-C ．2ln(1)x x ++D ．21x e -4．若函数()f x 在区间[,]a b 上连续，则下列结论中正确的是（）A ．在区间(,)a b 内至少存在一点ξ，使得()0f ξ=B ．在区间(,)a b 内至少存在一点ξ，使得()0f ξ'=C ．在区间(,)a b 内至少存在一点ξ，使得()()()()f b f a f b a ξ-'=-D ．在区间(,)a b 内至少存在一点ξ，使得()()()b af x dx f b a ξ=-⎰5．设22(,)f x y xy x y xy +=+-，则(,)f x y y∂∂=（）A ．2y x-B ．-1C ．2x y-D ．-3二、填空题（本大题共5小题，每小题3分，共15分）6．设a ，b 为常数，若2lim()21x ax bx x →∞+=+，则a b +=.7．圆²²x y x y =+＋在0,0()点处的切线方程是.8．由曲线1y x=是和直线1x =，2x =及0y =围成的平面图形绕x 轴旋转一周所构成的几何体的体积V =.9．微分方程5140y y y '--'='的通解是y =.10．设平面区域22{(,)|1}D x y x y =+≤D={x ，y ）x ²+y'≤1}，则二重积分222()Dx y d σ+=⎰⎰.三、计算题（本大题共8小题，每小题6分，共48分）11．计算22ln sin lim(2)x xx ππ→-.12．设函数22sin sin 2,0()0,0x x x f x xx ⎧+≠⎪=⎨⎪=⎩，用导数定义计算(0)f '.13．已知点1,1()是曲线12xy ae bx =+的拐点，求常数a ，b 的值.14．计算不定积分cos 1cos xdx x -⎰.15．计算不定积分ln 51x e dx -⎰.16．求微分方程sin dy yx dx x+=的通解.17．已知隐函数(,)z f x y =由方程231x xy z -+=所确定，求z x ∂∂和z y∂∂.18．计算二重积分2Dxydxdy ⎰⎰，其中D 是由抛物线²1y x =+和直线2y x =及0x =围成的区域.四、综合题（本大题共2小题，第19小题10分，第20小题12分，共22分）19.求函数0Φ()(1)xx t t dt =-⎰的单调增减区间和极值。

2015年广东专插本(高等数学)真题试卷(题后含答案及解析)精选全文完整版

精选全文完整版2015年广东专插本（高等数学）真题试卷(题后含答案及解析) 题型有：1. 选择题 2. 填空题 4. 解答题 5. 综合题选择题在每小题给出的四个选项中，只有一项是符合要求的。

1．若当χ→0时，kχ＋2χ2＋3χ3与χ是等价无穷小，则常数k＝( ) A．0B．1C．2D．3正确答案：B解析：＝k＝1，故本题选B．2．已知函数f(χ)在χ0处有二阶导数，且f′(χ0)＝0，f?(χ0)＝1，则下列结论正确的是( )A．χ0为f(χ)的极小值点B．χ0为f(χ)的极大值点C．χ0不是f(χ)的极值点D．(χ0，f(χ0))是曲线y＝f(χ)的拐点正确答案：A解析：由f(χ)在χ0处有二阶导数，f?(χ0)＝1＞0且f′(χ)＝0，则χ0为f(χ)的极小值点．3．设F(χ)是f(χ)的一个原函数，C为任意实数，则∫f(2χ)dχ＝( ) A．F(χ)＋CB．F(2χ)＋CC．F(2χ)＋CD．2F(2χ)＋C正确答案：C解析：∫f(2χ)dχ＝∫(2χ)d(2χ)＝F(2χ)＋C，故本题选C．4．若函数f(χ)＝＋kχ在区间[0，1]上满足罗尔(Rolle)定理的条件，则常数k＝( )A．－1B．0C．1D．2正确答案：C解析：由f(χ)在[0，1]上满足罗尔定理知，f(0)＝f(1)，即1＝k，故本题选C．5．下列级数中，收敛的是( )A．B．C．D．正确答案：D解析：级数为公比小于1的几何级数，是收敛的；级数为p＞1的p-级数，也是收敛的，故级数是收敛的．填空题6．曲线y＝(1－)χ的水平渐进线为y＝_______．正确答案：e-5解析：＝e-5，则y＝e-5为曲线的一条水平渐近线．7．设函数y＝f(χ)由参数方程所确定，则＝_______．正确答案：2解析：8．广义积分＝_______．正确答案：解析：9．微分方程y′－χy＝0满足初始条件y｜χ＝0＝1的特解为y＝_______．正确答案：解析：对微分方程分离变量为χdχ，则ln｜y｜＝χ2＋C，C为任意常数．即y＝，又y｜χ＝0＝1，故C＝0，特解为y＝．10．设函数f(χ)＝log2χ(χ＞0)，则＝_______．正确答案：解析：解答题解答时应写出推理、演算步骤。

广东省2020年普通高等学校本科插班生招生考试真题、详细答案及考点详解

广东省2020年普通高等学校本科插班生招生考试高等数学真题、详细答案及考点详解一、单项选择题（本大题共5小题，每小题3分，共15分.每小题只有一个选项符合题目要求）1.设()[]1cos lim 0=-→x f x x ，则下列等式正确的是间断点是（）A.()1lim 0=→x f x B.()1cos lim 0=→x x f x C.()1lim 0-=→x f x D.()[]1cos lim 0=+→x x f x 解答：根据初等函数的连续性，可得()[]()()()0lim 1lim 0cos lim cos lim cos lim 0=⇒=-=-=-→→→→→x f x f x f x x f x x x x x x 因此()()1cos lim ,0cos lim 0=+=→→x x f x x f x x 故选D.本题考试内容：初等函数的连续性；考试要求：会利用函数的连续性求极限.2.函数()2332x x x f -=的极小值是（）A.1-=xB.0=xC.1=x D.2=x 解答：对函数进行一阶导数求导，可得()()16662-=-='x x x x x f 令()()⇒=-=-='016662x x x x x f 10==x x 或而()612-=''x x f 因此()060<-=''f ，即x =0为极大值点()066121>=-=''f ，即x =1为极小值点从而极小值为()1321-=-=f ，故选A.本题考试内容：函数极值与极值点；考试要求：理解函数极值的概念，掌握求函数的极值、最值的方法，并会应用函数极值的方法求解应用题.3.已知x 3是函数()x f 的一个原函数，则()=x f （）A.x 3B.3ln 3xC.13-x x D.3ln 3x 解答：根据原函数的定义，可知()()()3ln 33x x x f x f =⇒='故选B.本题考试内容：原函数与不定积分的定义；考试要求：理解原函数与不定积分的概念及其关系.4.设平面区域(){}0,1|,22≥≤+=y y x y x D ，则()=+⎰⎰σd y x D422（）A.10π B.9πC.5πD.92π解答：使用极坐标计算二重积分，由于平面区域如下图所示令⎩⎨⎧==θθsin cos r y r x ，其中⎩⎨⎧≤≤≤≤πθ010r ，因此()()10sin cos 1904222210422ππθθθσπ==⋅+=+⎰⎰⎰⎰⎰dr r d r r r dr d y xD故选A.本题考试内容：极坐标系下二重积分的计算；考试要求：掌握直角坐标系与极坐标系下二重积分的计算.5.设级数∑∞=1n n a 满足nn a 510≤≤，则下列级数发散的是（）A.∑∞=13n naB.∑∞=+13n n aC.∑∞=⎪⎪⎭⎫ ⎝⎛+1321n n n a D.∑∞=⎪⎪⎭⎫⎝⎛-131n n n a 解答：根据正项级数的比较审敛法，由于n n a 510≤≤，由于∑∞=151n n 收敛，因此∑∞=1n na 收敛，再根据级数的性质，可以对下列选项进行判断A 选项：∑∑∞=∞==1133n n n n a a ，因此根据级数的性质可知，∑∞=13n n a 收敛；B 选项：321113a a a a a n n n n ---=∑∑∞=∞=+，因此，级数增加（减去）有限项，不改变敛散性，因此∑∞=+13n n a 收敛；C 选项：∑∑∑∑∑∞=∞=∞=∞=∞=+=+=⎪⎪⎭⎫ ⎝⎛+13211321132111n n n n n n n n n a n a n a ，其中∑∞=1321n n 为p -级数（132<=p ），故∑∞=1321n n 发散，而∑∞=1n n a 收敛，因此根据级数收敛的性质可知∑∞=⎪⎪⎭⎫ ⎝⎛+1321n n n a 发散；D 选项：∑∑∑∑∑∞=∞=∞=∞=∞=+=+=⎪⎪⎭⎫ ⎝⎛+123113113111n n n n n n n n n a n a n a ，其中∑∞=1231n n 为p -级数（123>=p ），故∑∞=1231n n 收敛，而∑∞=1n n a 收敛，因此根据级数收敛的性质可知∑∞=⎪⎪⎭⎫ ⎝⎛+1321n n n a 收敛，故选D.本题考试内容：收敛级数的基本性质；考试要求：掌握几何级数（等比级数）、调和级数、p -级数的敛散性；理解收敛级数的基本性质.二、填空题（本大题共5小题，每小题3分，共15分）6.若函数()()()⎪⎩⎪⎨⎧>+-≤+=1,321,132x x a x x a x f 在1=x 处连续，则常数=a .解答：根据函数极限的充分必要条件可知，()()()Ax f x f A x f x x x ==⇔=+→-→→111lim lim lim 而()()a x a x f x x +=+=-→-→11lim lim 211，()()332lim lim 311+-=+-=+→+→a x a x f x x 因此()().131lim lim 11=⇒+-=+⇒=+→-→a a a x f x f x x 本题考试内容：函数在一点连续的充分必要条件；考试要求：掌握判断函数（分段函数）在一点处连续的方法.7.曲线3222=+y x 在()1,2-点处的切线方程为=y .解答：隐函数求导，因此()122|20212=--='⇒-='⇒='⋅+-，y y x y y y x 从而切线方法为()().3211-=⇒-⋅=--x y x y 本题考试内容：求导方法：函数的四则运算求导方法、隐函数的求导法；考试要求：熟练掌握隐函数的求导方法.8.微分方程043=-'+''y y y 的通解为=y .解答：特征方程为()()0140432=-+⇒=-+r r r r 故1,421=-=r r 故通解为.241x x e C e C y +=-本题考试内容：二阶常系数线性齐次微分方程；考试要求：会求二阶常系数线性齐次微分方程的通解和特解.9.设二元函数()y x f ,在点()0,0的某个领域有定义，且当0≠x 时，()()230,00,+=-x xf x f ，则()='0,0x f .解答：根据偏导数的定义，()()()230,00,0,+=-='x x f x f x f x 因此().20,0='x f 本题考试内容：多元函数的定义；考试要求：理解一阶偏导数和全微分的概念.10.设函数()x f 在()+∞∞-,内可导且满足()()x f x f '=，()m f =0，如果()811=⎰-dx e x f x ，则=m .解答：使用分离变量法，可得：()()()()()()()()⎰⎰=⇒=⇒=⇒'=dx x df x f dx x f x df x f dx x df x f x f 1因此()()Cx e x f C x x f +=⇒+=ln 由于()m f =0，因此()m C m e f C ln 0=⇒==从而()xmx me ex f ==+ln ，将此式子代入()811=⎰-dx e x f x，可得().482888111111=⇒=⇒=⇒=⇒=⎰⎰⎰---m m dx m dx e me dx e x f x xx本题考试内容：可分离变量的微分方程；考试要求：会求可分离变量的微分方程.三、计算题（本大题共8小题，每小题6分，共48分）11.求极限xdt t t xx ⎰→0arctan lim.解：使用洛必达法则00arctan 01arctan limarctan lim=⋅==→→⎰xx xdt t t x xx 本题考试内容：洛必达法则和变上限的定积分；考试要求：熟练掌握应用洛必达法则求未定式极限的方法以及掌握变上限定积分求导数的方法.12.已知y 是x 的函数，且2ln 2ln ln ++='x x y ，求.|22e x dxyd =解：使用复合函数求导法，可得x x x xx x x y ln 212101ln 21211+=+⋅+⋅=''则.1ln 2121|22ee e e dx y d e x =+==本题考试内容：求导方法——复合函数的求导法；考试要求：熟练掌握复合函数求导方法.13.求不定积分().sin 2cos 2⎰-dx x x x 解：根据不定积分的性质，可得()dxx x dx x dx x x x ⎰⎰⎰-=-22sin 2cos sin 2cos 其中12sin 2122cos 212cos C x x xd xdx +==⎰⎰22222cos 21sin 21sin C x dx x dx x x +-==⎰⎰因此()C x x dx x x x +-=-⎰22cos 212sin 21sin 2cos （其中21C C C +=）.本题考试内容：基本积分公式、换元积分法——第一换元法（凑微分法）；考试要求：熟练掌握不定积分的基本积分公式、熟练掌握不定积分的第一换元法.14.设函数()⎪⎩⎪⎨⎧>≤+=1,1,123x x x x x x f ，求定积分().203dx x f ⎰-+解：令2+=x t ，从而2-=t x ，dt dx =，当3-=x 时，1-=t ；当0=x 时，2=t ，从而原式可变为()().23|210122122111232103=+=++==+⎰⎰⎰⎰---t dt t dt t t dt t f dx x f 本题考试内容：定积分的性质、定积分的计算——换元积分法；考试要求：掌握定积分的基本性质以及掌握定积分的换元法.15.求二元函数y x xy z 223+=的全微分dz ，并求.2yx z∂∂∂解：y x y x z 232+=∂∂，226yx xy y z -=∂∂，因此dyy x xy dx y x y dz ⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫ ⎝⎛+=222623.2662222yxy y x xy x y x z -=⎪⎪⎭⎫ ⎝⎛-∂∂=∂∂∂本题考试内容：全微分以及高阶偏导数；考试要求：掌握二元函数一阶偏导数与二阶偏导数的求法，掌握二元函数全微分的求法.16.计算σd y D⎰⎰，其中D 是由直线x y =，2-=x y 与0=y ，2=y 围成的有界区域.解：x则有界区域可写为Y-型区域⎩⎨⎧+≤≤≤≤220y x y y 因此原二重积分可变为().4|2|202222220=====⎰⎰⎰⎰⎰⎰++y ydy dy x y dx y dy d y y yy yDσ本题考试内容：直角坐标系下二重积分的计算；考试要求：掌握直角坐标系下二重积分的计算方法.17.求微分方程22sec yxdx dy =，满足初始条件1|0==x y 的特解.解：使用分离变量法，可得⎰⎰=⇒=⇒=xdx dy y xdx dy y yx dx dy 222222sec sec sec 因此C x y +=tan 313将1|0==x y 代入上式，可得310tan 131=⇒+=⨯C C 从而可得微分方程特解为.1tan 331tan 3133+=⇒+=x y x y 本题考试内容：可分离变量方程；考试要求：会求分离变量微分方程的通解和特解.18.判断级数∑∞=12!2n n n n 的收敛性.解：由于∑∞=12!2n n n n 为正项级数，()()()()()1021lim !2!121lim !2!121lim lim 22122121<=+=++=++=∞→+∞→+∞→+∞→n n n n n n n n n n a a n n n n n n n nn n 因此根据比值判别法可知：∑∞=12!2n n n n 收敛.本题考试内容：常数项级数审敛法；考试要求：掌握正项级数的比值审敛法.四、综合题（本大题共2小题，第19小题10分，第20小题12分，共22分）19.设有界平面图形G 由曲线ax e y =和直线0==x e y ，围成，其中a ＞0，若G 的面积等于1（1）求a 的值；（2）求G 绕y 轴旋转一周而成的旋转体体积V .解：（1）由题设可得平面图形G ，如下图所示因此aa a e a e e e a a e e a ex dx e e S a a a ax a ax1111|1011010=+-=⎪⎪⎭⎫ ⎝⎛--⋅=⎪⎭⎫ ⎝⎛-=-=⋅⎰又因为平面G 的面积为1，因此.111=⇒==a aS ye1/ax（2）要求G 绕y 轴旋转一周，因此根据公式可得()()().2|21|ln 2ln 21ln 2|ln ln 11111121212-=--=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⋅-⋅-=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⋅⋅-⋅===⎰⎰⎰⎰⎰e y e e dy y y y y e dy y e dy y y y y y dy y dy x V ee eee ee ey πππππππ本题考试内容：定积分的应用——平面图形的面积、旋转体的体积；考试要求：掌握直角坐标系下用定积分计算平面图形的面积以及平面图形绕坐标轴旋转所生的旋转体体积的方法.20.设函数()bxeax f +=1，其中b a ,为常数，且0≠ab （1）判别()x f 在区间()+∞∞-,内单调性；（2）求曲线()x f y =的拐点；（3）求曲线()x f y =的水平渐近线方程.解：（1）函数()bxeax f +=1定义域为()+∞∞-,，而()()211bxbx bx e abe e a x f +-='⎪⎭⎫⎝⎛+='因此，当0>ab 时，函数()bxeax f +=1定义域为()+∞∞-,单调递减；当0<ab 时，函数()bxeax f +=1定义域为()+∞∞-,单调递增.（2）由于()()()()()()()324222*********bx bx bx bx bx bx bx bx bx bx e e e ab e e e ab e e ab e abe x f +--=++++-='⎪⎪⎭⎫ ⎝⎛+-=''令()()()01132=+--=''bx bxbx e e e ab x f ，且0≠ab ，可得0010=⇒=⇒=-x e e ebx bx显然()x f ''在x =0左右两端异号，因此把x =0代入原式，可得()2100ae af =+=因此，拐点为⎪⎭⎫⎝⎛2,0a .（3）当0>b 时，()01limlim =+=+∞→+∞→bx x x e a x f ，()a e ax f bx x x =+=-∞→-∞→1lim lim ；当0<b 时，()a e a x f bx x x =+=+∞→+∞→1lim lim ，()01lim lim =+=-∞→-∞→bx x x e ax f ，因此水平渐近线为0==y a y 和.本题考试内容：函数单调性的判定法、曲线的凹凸性、拐点以及函数曲线的水平渐近线：掌握利用导数判定函数单调性的方法，会判定曲线的凹凸性、会求曲线的拐点以及会求曲线的水平渐近线.。

广东省2022年专升本《高等数学》真题解析精选全文完整版

广东省2022年普通高等学校专升本招生考试高等数学本试卷共20小题，满分100分。

考试时间120分钟。

一、单项选择题（本大题共5小题，每小题3分，共15分，每小题只有一项符合题目要求）1.若函数1,1(),1x x f x a x +≠⎧=⎨=⎩，1x =在处连续，则常数a =（）A.-1B.0C.1D.22.1lim(13)xx x →-=（）A.3e - B.13e-C.1D.3e 3.1lim 0n n x n u u ∞→==∑是级数收敛的（）A.充分条件B.必要条件1C.充要条件D.即非充也非公必要条件得分阅卷人4.2+1()()1f x f x dx x∞=⎰已知是函数的一个原函数，则（）A.2B.1C.-1D.-25.xf (x 2+y 2)dy 化为极坐标形成的二次积分，则 I =（）110I dx =⎰⎰将二次积分 A.2sec ()400d f p dp πθθ⎰⎰ B.2c ()40cs d pf p dp πθθ⎰⎰B.2sec 2()04d f p dp πθθπ⎰⎰ D.2csc 2()04d pf p dp πθθπ⎰⎰二、填空题（本大题共5小题，每小题3分，共15分）6.若0→x 时，无穷小量x 2与x x m 32+等价，则常数m =7.2225,log t x t t dy dx y t=⎧=-=⎨=⎩设则8.椭圆13422=+y x 所围成的图形绕x 轴旋转一周而成的旋转体体积为9.微分方程2'=-y ex的通解是10.ln (,)(,)ye e Z xe e dz==函数在点处的全微分得分阅卷人三、计算题（本大题共8小题，每小题6分，共48分）12.2212=tan ,x d yy arc x dx=设求13.设函数21sin ,00,0x x x x ⎧≠⎪⎨⎪=⎩，利用导数定义(0)f '.14.求不定积分2.得分阅卷人15.已知tan ln cos xdx x C=-+⎰，求定积分24sec x xdx π⎰.16.2(,)2z z z Z f x y Z x y e y x y∂∂==--∂∂设是由方程所确定的隐函数，计算.17.cos ,sin (0)0,2Dxd D y x x y πσ=≤≤=⎰⎰计算二重积分其中是曲线和曲线2x π=围成的有界闭区域。

(word完整版)广东专插本2001-2011年高等数学历年题集(2011年10月更新)

高等数学历年试题集(含标准答案)5、计算二重积分(),Dx y dxdy +⎰⎰其中D 为2,2x y x y ==及2xy =所围成(0)x >。

6、求一阶线性微分方程423(cos )2x xy yx e x x -=+-的通解。

四、应用题（本题8分）设有椭圆22221x y a b+= （1）用定积分计算要椭圆绕x 轴旋转所产生的旋转体体积。

（2）求内接于该随圆而平行于坐标轴的最大矩形面积。

20、试求函数xy ze =在点（2，3）处的全微分。

四、应用题（每小题8分，共24分）21、三个点A 、B 、C 不在同一直线上，60ABC∠=o 。

汽车以80千米/小时的速度由A 向B 行驶，同时火车以50千米/小时的速度由B 向C 行驶。

如果AB=200千米，试求运动开始几小时后汽车与火车间的距离为最小？ 22、试计算由抛物线2y x =与直线23y x =-所围成的图形的面积。

23、设有边长为2a 的在方形薄板。

如果薄板材料的度和到对解线线交点的距离平方成正比，且在它的角上的密度为l ，试求这个正方形薄板的质量。

2004年专升本插班考试《高等数学》试题一、填空题（每小题4分，共20分） 1、函数211x xy --=的定义域是。

2、=+→x x xx 52tan 30lim 。

3、若=-=dxdyx x e y x 则),cos (sin 。

4、若函数⎰+--=x dt t t t x f 02112)(,=)21(f 则。

5、设23,32a i j k b i j k c i j =-+=-+=-r r r r r r r r r r r和,()()a b b c +⨯+=r r r r则。

二、单项选择题（每小题4分，共20分） 6、若⎰=+=I dx x I 则,231（）（A ）C x ++23ln 21 （B ）()C x ++23ln 21（C ）C x ++23ln （D ）()C x ++23ln 7、设)2ln(),(xyx y x f +=,=），f y 01('则( ) （A ）0, （B ）1, (C)2, (D)21 8、曲线2,,1===x x y x y 所围成的图形面积为S ，则S=（）（A ）dx x x )1(21-⎰ （B ）dx xx )1(21-⎰（C ）dx y dx y )2()12(2121-+-⎰⎰（D ）dx x dx x)2()12(2121-+-⎰⎰9、函数项级数∑∞=-1)2(n nx n的收敛区间是（）（A ）1x > （B ）1x < （C ）13x x <>及（D ）13x << 10、⎰⎰=12),(xx dy y x f dx I 变换积分分次序后有I=（）（A ）210(,)x x dx f x y dy ⎰⎰ （B ）⎰⎰10),(yydx y x f dx（C ）⎰⎰102),(yy dx y x f dx （D ）⎰⎰yydx y x f dx 1),(三、简单计算题（每题9分，共36分）11、求极限x x x e x x 30sin )2()2(lim ++-→12、求由方程0sin 21=+-y y x 所确定的隐函数y 的二阶导数22dx y d 。

广东专插本(高等数学)模拟试卷45(题后含答案及解析)

广东专插本（高等数学）模拟试卷45(题后含答案及解析)题型有：1. 选择题 2. 填空题 4. 解答题 5. 综合题选择题在每小题给出的四个选项中，只有一项是符合要求的。

1．当χ→0时，下列无穷小量中与等价的是( ) A．χB．2χC．χ2D．2χ2正确答案：A解析：故应选A．2．函数y＝sinχ－χ在区间[0，π]上的最大值是( )A．B．0C．－πD．π正确答案：B解析：y′＝cosχ－1≤0，故y在[0，π]上单调递减，故最大值为y(0)＝0，故应选B．3．若∫f(χ)dχ＝F(χ)＋C，则∫e-χf(e－χ)dχ( )A．e-χ)＋F(e－χ)＋CB．e－χ－F(e－χ)＋CC．F(e-χ)＋CD．－F(e-χ)＋C正确答案：D解析：∫e-χf(e-χ)dχ＝－∫f(-χ)d(e-χ)＝－F(e-χ)＋C，故应选D．4．曲线y＝在χ＝1处的切线方程是( )A．3y－2χ＝5B．－3y＋2χ＝5C．3y＋2χ＝－5D．3y＋2χ＝5正确答案：D解析：，则切线方程为y－1＝－(χ－1)，整理得3y＋2χ＝5，故应选D．5．下列无穷级数中，发散的是( )A．B．C．D．正确答案：D解析：＝1，因为p级数发散，则发散，故应选D．填空题6．f(χ)＝χeχ，则f(n)(χ)的极小值点为_______．正确答案：χ＝－(n＋1)解析：f′(χ)＝eχ＋χeχ＝(1＋χ)eχ，f?(χ)＝eχ(1＋χ)eχ＝(2＋χ)eχ，…，f(n)＝(n＋χ)e2χ，f(n)(χ)＝(n＋1＋χ)eχ，令f(n+1)(χ)＝0，得χ＝－(n＋1)，当χ＞－(n＋1)时，f(n+1)(χ)＞0；当χ＜－(n＋1)时，f(n+1)(χ)＜0，故f(n)(χ)在χ＝－(n＋1)处取得极小值．7．函数f(χ)＝在χ＝0处是_______间断点．正确答案：第一类可去间断点解析：＝1故χ＝0是f(χ)的第一类可去间断点．8．＝_______．正确答案：0解析：令f(χ)＝，则f(－χ)＝＝－f(χ)，故f(χ)为奇函数，所以dχ＝0．9．交换二次积分I＝∫-11dy f(χ，y)dχ的积分次序，则I＝_______．正确答案：解析：二次积分区域为((χ，y)－1≤y≤1，0≤χ≤1－y2)，如图所示：又可表示为{(χ，y)｜0≤χ≤1，)，即I＝10．方程y?－4y′＋3y＝0满足初始条件y｜χ＝0＝6，y′｜χ＝0＝10的特解是_______．正确答案：y＝4χ＋2e3χ解析：方程对应的特征方程为r2－4r＋3＝0，即r1＝1，r2＝3，故方程的通解为y＝C1eχ＋C2e3χ，y′＝C1eχ＋3C2e3χ，代入初始条件得解得C1＝4，C2＝2，故所求特解为y＝4eχ＋2e3χ．解答题解答时应写出推理、演算步骤。

广东专插本(高等数学)模拟试卷50(题后含答案及解析)

广东专插本（高等数学）模拟试卷50(题后含答案及解析) 题型有：1. 选择题 2. 填空题 4. 解答题 5. 综合题选择题在每小题给出的四个选项中，只有一项是符合要求的。

1．y＝＋lg(χ＋2)的定义域为( )A．(－2，＋∞)B．(1，＋∞)C．(－2，－1]∪[1，＋∞)D．(－2，－1)正确答案：C解析：由题有即－2＜χ≤－1或χ≥1，故选C．2．若f′(χ0)＝－3，则＝( ) A．－3B．－6C．－9D．－12正确答案：D解析：故选D．3．设∫f(χ)dχ＝χ2＋C，则∫χf(1－χ2)dχ＝( )A．－2(1－χ2)2＋CB．2(1－χ2)2＋CC．－(1－χ2)2＋CD．(1－χ2)2＋C正确答案：C解析：∫χf(1－χ2)dχ＝－∫f(1－χ2)d(1－χ2)＝－(1－χ2)2＋C，故选C．4．设f(χ，y)在点(χ0，y0)处偏导数存在，＝( )A．f′χ(χ0，y0)B．f′y(2χ0，y0)C．2f′χ(χ0，y0)D．f′χ(χ0，y0)正确答案：C解析：故选C．5．如果＝ρ(un＞0，n＝1，2，…)，则级数un的收敛条件是( )A．ρ＞1B．ρ≥1C．ρ＜1D．ρ≤1正确答案：C解析：由比值判别法可知：当un＞0时，若所以级数un的收敛条件是ρ＜1，故选C．填空题6．函数f(χ)＝的极值为_______．正确答案：f(0)＝1解析：f′(χ)＝2χ，令f′(χ)＝0得χ＝0，χ＜0，f′(χ)＜0；χ＞0，f′(χ)＞0，所以χ＝0为f(χ)的极小值点，f(0)＝1．7．已知f(χ)＝χ2lnχ，χ＝h(t)满足条件h(0)＝3，h′(0)＝7，则f[h(t)]｜t＝0＝_______．正确答案：7(6ln3＋3)解析：f′(χ)＝2χlnχ＋χ，f[h(t)]｜t＝0＝f′[h(t)].h′(t)｜t＝0＝f′(3).7＝7(6ln3＋3)．8．设f(χ)在[a，b]上满足f(χ)＞0，f′(χ)＜0，f?(χ)＞0，令S1＝∫abf(χ)d χ，S2＝f(b)(b－a)，S3＝[f(b)＋f(a)](b－a)，则S1，S2，S3的大小顺序为_______．正确答案：S2＜S1＜S3解析：由已知条件，f(χ)在[a，b]递减，且是凹的，∴0＜f(b)＜[f(b)＋f(a)]，∴S2＜S3．又S1表示的是χ＝a，χ＝b，y＝f(χ)与χ轴围成曲边梯形的面积，S2表示的是χ＝a，χ＝b，y＝f(b)与χ轴所围成矩形的面积，S3表示的是χ＝a，χ＝b y＝f(χ)在χ＝a和χ＝b两个端点连线，这三条直线所围成梯形的面积，∴S2＜S1＜S3．9．通解为y＝C1cos2χ＋C2sin2χ(C1，C2为任意常数)的二阶线性常系数齐次微分方程为_______．正确答案：y?＋4y＝0解析：由微分方程的通解为y＝C1cos2χ＋C2sin2χ知特征根为λ＝±2i，则特征方程为λ2＋4＝0，故微分方程为y?＋4y＝0．10．设f(χ，y)＝2χ＋arcsin，则fχ(2，1)＝_______．正确答案：解析：解答题解答时应写出推理、演算步骤。

广东省普通高校本科插班生招生考试(数学真题答案)

2分
( ,1)
— 下降
-1 0 极小
（-1，1） + 上升
1 0 极大
(1, )
— 下降
f ' ( x) f ( x)
可知极小值 f ( 1)
1 e
4分
极大值 f (1)
1 e
5分
，内只有一个（2）因 f ( x ) 在[0，2]上连续，由（1）知 f ( x ) 在（0，2）内可导，且在（0，2）驻点 x 1 （极大值点），因 f (0) 0, f (1)
2 ln( 1 x ) 1 x 0 2
5分
ln x 13、解： y ' (arctan x 1 2 x 1
'

' 1 2 x 1 x 2 1 ln x 1 x2 1 x 2 1 x 1 x2 1 2x ln x 2x 1 x ln x 2 x2 1 2 32 2 2 2 2 x 1 x 1 2x x 1 x x 1
0 0

4分
6分
由题意有 f ( ) f (0) 5, f ( ) 2, 所以f (0) 3
2006 年广东省普通高校本科插班生招生考试
《高等数学》试题答案及评分参考
一、单项选择题（本大题共 5 小题，每小题 3 分，共 15 分） 1、D 2、B 3、B 4、A 5、C 二、填空题（本大题共 5 小题，每个空 3 分，共 15 分） 6、8 7、x+2y-3=0 8、4 9、
6分
17、解：由两条曲线 y cos x, y sin x 及两条直线 x 0, x （要画出草图，不画图不扣分），依题意，旋转体的体积为

2024广东专插本考试高等数学试题

2024广东专插本考试高等数学试题2024广东专插本考试高等数学试题一、选择题1、下列函数中，在区间(0,1)内为增函数的是： A. y = ln(x + 1) B. y = e^(-x) C. y = sinx D. y = cosx2、设{an}为等比数列，a1 = 2，公比为q，则a2 等于： A. 2q B. qC. 1/qD. q^23、下列图形中，面积为S的平行四边形的个数是： A. 1 B. 2 C. 3D. 4二、填空题 4. 已知向量a = (1, -2)，向量b = (3, -4)，则向量a 与向量b 的夹角为__________。

5. 设函数f(x) = x^3 - 6x^2 + 9x - 3，则f(-2) = __________。

6. 若矩阵A = [1, 2; 3, 4]，则|A| = __________。

三、解答题 7. 求函数y = sinx + cosx + sinxcosx + 1的最大值与最小值。

8. 求下列微分方程的通解：dy/dx = y/(x + 1)，其中y(0) = 1。

9. 在等差数列{an}中，已知a1 = 1，S100 = 100a10，求{an}的前n项和Sn的公式。

四、应用题 10. 某公司生产一种产品，每年需投入固定成本40万元，此外每生产100件产品还需增加投资2万元。

设总收入为R(x)万元，x为年产量，产品以每百件为单位出售，售价为47万元/百件。

若当年产量不足300件时，可全部售出；若当年产量超过300件，则只能销售75%。

试求该公司的年度总收入R(x)的表达式。

五、选做题 11. 在极坐标系中，已知两点A、B的极坐标分别为(3, π/6)、(4, π/3)，求△AOB的面积S。

12. 已知函数f(x)在[0,1]上连续，且f(0) = f(1) = 0。

试求证：存在一点ξ∈[0,1]，使得f(ξ) = -ξ。

六、附加题 13. 求证：在正整数中，n^3 - n一定是6的倍数。

广东专插本(高等数学)模拟试卷56(题后含答案及解析)

广东专插本（高等数学）模拟试卷56(题后含答案及解析)题型有：1. 选择题 2. 填空题 4. 解答题 5. 综合题选择题在每小题给出的四个选项中，只有一项是符合要求的。

1．设f(χ)＝∫01－cosχsint2dt，g(χ)＝，则当χ→0时，g(χ)是g(χ)的( )A．低阶无穷小B．高阶无穷小C．等价无穷小D．同阶但不等价无穷小正确答案：B解析：2．设＝－1，则在χ＝a处( )A．f(χ)的导数存在，且f′(a)≠0B．f(χ)取得极大值C．f(χ)取得极小值D．f(χ)的导数不存在正确答案：B解析：由极限的保号性知，在χ＝a的去心邻域内有＜0，从而f(χ)＜f(a)，即f(χ)在χ＝a处取极大值．故选B．3．设f(χ)是连续函数，且∫f(χ)dχ＝F(χ)＋C，则下列各式正确的是( )A．∫f(χ2)χdχ＝F(χ2)＋CB．∫(3χ＋2)dχ＝F(3χ＋2)＋CC．∫f(eχ)eχdχ＝F(eχ)＋CD．∫f(ln2χ)＝F(ln2χ)＋C正确答案：C解析：∫f(eχ)eχdχ＝∫(eχ)d(eχ)＝(eχ)＋C．故选C．4．下列函数在给定区间满足罗尔定理条件的有( )A．y＝sin2χ，[0，]B．y＝｜χ｜，[－1，1]C．y＝cos3χ，[0，π]D．y＝，[－2，2]正确答案：A解析：B选项中，函数在χ＝0处不可导；C选项中，y(0)≠y(3π)；D选项中，函数在χ＝1处不可导；A选项中，函数在[0，]上连续，在(0，)可导，y(0)＝y()，符合罗尔定理条件，故本题选A．5．如果级数un收敛，则它的和是( )A．u1＋u2＋…＋unB．C．D．以上都不是正确答案：C解析：令Sn＝uk，若级数un收敛，则极限Sn存在，即级数uk的和uk存在，故应选C．填空题6．曲线y＝－2的水平渐近线是_______，铅垂渐近线是_______．正确答案：y＝－2，χ＝0解析：＝－2，则y＝－2是曲线的一条水平渐近线．＝∞，则χ＝0是曲线的一条铅垂渐近线．7．已知eχ＋y2＝1，则_______．正确答案：解析：方程两边同时对χ求导eχ＋2y＝0，则．8．广义积分∫0＋∞dχ＝1，其中k为常数，则忌_______．正确答案：解析：所给问题为计算广义积分的反问题，由于因此，应有＝1，故k＝．9．微分方程χy′－y＝0满足条件y｜χ＝1＝2的特解为_______．正确答案：y＝2χ解析：χ－y＝0，即，解得y＝Cχ，又y｜χ＝1＝C＝2，即微分方程的特解为y＝2χ．10．设函数f(χ)在χ＝χ0处可微，且f′(χ0)≠0，则当｜△χ｜很小时，f(χ0＋△χ)≈_______．正确答案：f(χ0)＋f′(χ0)△χ解析：当｜△χ｜很小时，有f′(χ0)≈知f(χ0＋△χ)≈f(χ0)＋△χf′(χ0)．解答题解答时应写出推理、演算步骤。

(完整版)《高等数学》专插本-2019年历年试卷(最新整理)

D．点 x 1 是 f (x) 的极大值点
3. 已知 f (x)dx x2 C, 其中 C 为任意常数，则 f (x2 )dx
A． x5 C
B． x4 C
C． 1 x4 C 2
D． 2 x3 C 3
4．级数 2 (1)n
n1
3n
A． 2 3
C．
4
B． 1 1
D．
2
5．已知 D {(x, y) | 4 x2 y2 9}，则
B． f (x)dx 2x tan x C
g(x)
C． f [g(x)]dx tan(2x ) C
[ f (x) g(x)]dx tan x 2x C
4．下列级数收敛的是
1
A． en n1
C．
2 n1 ( 3n
1 n3 )
D．
3 n
B． ( ) n1 2
D．
n1
(
2 3
x
g(x) 在 (0, ) 单调递减即 g(b) g(a) 即 ba ab 成立
，
即 20182019 20192018
广东省 2018 年普通高等学校本科插班生招生考试
高等数学
一、单项选择题（本在题共 5 小题，每小题 3 分，共 15 分。每小题只有一个选项符合题目要求）
1．
lim
x0
z
xy 1 y2
,
，求
z y
,
2z yx
17．求 1 x d ，其中 D 是由直线 y x 和 y 1, y 2 及 x 0 所围成的闭区域
D
y
n
18．判定设级数
的收敛性
n1 | sin n | 2
四、综合题（大题共 2 小题，第 19 小题 12 分，第 20 小题 10 分，共 22 分）

广东插本考试题库及答案

广东插本考试题库及答案一、单项选择题（每题2分，共20分）1. 广东插本考试的全称是什么？A. 广东省本科插班生考试B. 广东省专科升本科考试C. 广东省本科直升考试D. 广东省专科插班生考试答案：A2. 广东插本考试的报名流程包括哪些步骤？A. 网上报名、现场确认、缴费B. 现场报名、网上报名、缴费C. 网上报名、缴费、现场确认D. 现场报名、缴费、网上报名答案：C3. 广东插本考试的考试科目通常包括哪些？A. 语文、数学、英语B. 政治、历史、地理C. 语文、数学、英语、政治D. 数学、物理、化学答案：C4. 广东插本考试的合格分数线是如何确定的？A. 由各高校自行划定B. 由广东省教育考试院统一划定C. 由各专业自行划定D. 由各市教育考试院统一划定答案：B5. 广东插本考试的录取原则是什么？A. 先到先得B. 择优录取C. 按地区分配D. 按专业分配答案：B二、多项选择题（每题3分，共15分）6. 广东插本考试的报名资格包括哪些？A. 具有广东省户籍的专科毕业生B. 在广东省就读的专科毕业生C. 具有广东省户籍的专科在校生D. 在广东省就读的专科在校生答案：A、B7. 广东插本考试的考试时间通常安排在什么时候？A. 每年的1月份B. 每年的3月份C. 每年的5月份D. 每年的9月份答案：B、C8. 广东插本考试的考试形式包括哪些？A. 笔试B. 面试C. 机试D. 实践操作答案：A、B、C9. 广东插本考试的报名费用通常包括哪些？A. 考试费B. 材料费C. 报名费D. 培训费答案：A、C10. 广东插本考试的考试内容通常涉及哪些方面？A. 专业知识B. 公共基础课C. 综合素质D. 英语水平测试答案：A、B、C三、判断题（每题1分，共10分）11. 广东插本考试的报名通常在每年的10月份进行。

（对/错）答案：错12. 广东插本考试的考试科目中不包括英语。

（对/错）答案：错13. 广东插本考试的合格分数线每年都是固定的。

《高等数学》专插本2005-2019年历年试卷

广东省2019年普通高等学校本科插班生招生考试高等数学一、单项选择题（本在题共小题，每小题分，共分。

每小题只有一个选项符合题目要求）．函数22()2x xf x x x -=+-的间断点是．2x =- 和0x = ．2x =- 和1x = ．1x =- 和2x = ．0x = 和1x =．设函数1,0()2,0cos ,0x x f x x x x +<⎧⎪==⎨⎪>⎩，则0lim ()x f x → ．等于1 ．等于2 ．等于1 或2 ．不存在已知()tan ,()2xf x dx x Cg x dx C =+=+⎰⎰C 为任意常数，则下列等式正确的是．[()()]2tan x f x g x dx x C +=+⎰ ．()2tan ()x f x dx x C g x -=++⎰．[()]tan(2)x f g x dx C =+⎰．[()()]tan 2x f x g x dx x C +=++⎰．下列级数收敛的是．11nn e ∞=∑ ．13()2nn ∞=∑．3121()3n n n ∞=-∑ ．121()3n n n ∞=⎡⎤+⎢⎥⎣⎦∑．．已知函数 ()bf x ax x =+在点1x =-处取得极大值，则常数,a b 应满足条件．0,0a b b -=< ．0,0a b b -=>．0,0a b b +=< ．0,0a b b +=> 二、填空题（本大题共小题，每小题分，共分）．曲线33arctan x t ty t ⎧=+⎨=⎩，则0t =的对应点处切线方程为y =．微分方程0ydx xdy +=满足初始条件的1|2x y ==特解为y = ．若二元函数(,)z f x y =的全微分sin cos ,xxdz e ydx e ydy =+ 则2zy x∂=∂∂ ．设平面区域{(,)|0,01}D x y y x x =≤≤≤≤，则Dxdxdy =⎰⎰．已知1()sin(1)tf x dx t t tπ=>⎰，则1()f x dx +∞=⎰三、计算题（本大题共小题，每小题分，共分）．求20sin 1lim x x e x x →--．设(0)21x x y x x =>+，求dydx．求不定积分221xdx x ++⎰．计算定积分012-⎰．设xyzx z e-=，求z x ∂∂和z y∂∂ ．计算二重积分22ln()Dx y d σ+⎰⎰，其中平面区域22{(,)|14}D x y x y =≤+≤ ．已知级数1n n a ∞=∑和1n n b ∞=∑满足0,n n a b ≤≤且414(1),321n n b n b n n ++=+- 判定级数1nn a ∞=∑的收敛性．设函数()f x 满足(),xdf x x de-=求曲线()y f x =的凹凸区间四、综合题（大题共小题，第小题分，第小题分，共分）．已知函数()x ϕ满足0()1()()xxx x t t dt x t dt ϕϕϕ=+++⎰⎰（）求()x ϕ；（）求由曲线 ()y x ϕ=和0,2x x π==及0y =围成的平面图形绕x 轴旋转而成的立体的体积．设函数()ln(1)(1)ln f x x x x x =+-+ （）证明：()f x 在区间(0,)+∞内单调减少；（）比较数值20192018与20182019的大小，并说明理由；年广东省普通高校本科插班生招生考试《高等数学》参考答案及评分标准一、单项选择题（本大题共小题，每小题分，共分）二、填空题（本大题共小题，每个空分，共分）13x2x cos xe y 13π 三、计算题（本大题共小题，每小题分，共分）原式00cos sin 1limlim 222x x x x e x e x x →→-+=== 解：21ln ln ln(21)12ln 1212(ln 1)2121xx x y x y x x x y x y x dy x x dx x x =+∴=-+'∴=+-+∴=+-++解：22222211112(1)12112arctan ln(1)2x dxx dx d x x xx x C++=++++=+++⎰⎰⎰,t =则211,22x t dx tdt =-=20121021420153011,,2211()221()2111()253115t x t dx tdt t t tdtt t dtt t -==-==-=-=-=-⎰⎰⎰解：设(,,)xyzf x y z x z e=--(,,)1(,,)(,,)11,11xyz x xyz y xyzz xyz xyz xyz xyzf x y z yze f x y z xze f x y z xye z yze z xze x xye y xye ∴=-=-=--∂-∂∴==-∂+∂+解：由题意得12,0r θπ≤≤≤≤222020ln()3(4ln 2)23(4ln 2)|2(8ln 23)Dx y d d ππσθθπ∴+==-=-=-⎰⎰⎰ 解：由题意得414(1),321n n b n b n n ++=+-414(1)1lim lim 1,3213n x x nb n b n n +→∞→∞+∴==<+- 由比值判别法可知1nn b∞=∑收敛0,n n a b ≤≤由比较判别法可知1n n a ∞=∑也收敛．解()()()()(1)xx x x df x x de df x xde f x xe f x e x ----=∴='∴=-''∴=-()f x ∴的凹区间为(1,)+∞，凸区间为(,1)-∞（）由题意得0()1()()()1()xxx x x t dt x x t dt ϕϕϕϕϕ'=++-=+⎰⎰()()()()0x x x x ϕϕϕϕ''∴=-''∴+=特征方程210r +=，解得r i=±通解为()cos sin x x x Cϕ=++(0)1,0()cos sin C x x xϕϕ=∴=∴=+由题意得2202022(cos sin )(1sin 2)1(cos 2)22x V x x dx x dx x x ππππππππ=+=+=-=+⎰⎰证明（）()ln(1)(1)ln 1()ln(1)ln 111ln(1)ln ()1f x x x x x x x f x x x x x x x x x=+-++'∴=+-+-+=+--++ 证明11ln(1)ln ()01x x x x +--+<+即可即证11ln(1)ln ()1x x x x+-<++令()ln g x x =()ln g x x =在(0,)+∞连续可导，由拉格朗日中值定理得ln(1)ln 1ln(1)ln ()1x x x x g x x x ξ+-'+-===+-且1x x ξ<<+ 111101x x x xξξ<<+∴<<<+11ln(1)ln ()1x x x x ∴+-<++成立11ln(1)ln ()01x x x x∴+--+<+()f x ∴在(0,)+∞单调递减（）设2019,2018a b ==则201820192019,2018b a a b ==比较,a b b a 即可，假设a bb a>即ln ln a b b a >即ln ln b ab a >设ln (),x g x x =则21ln ()xg x x -'=()g x 在(0,)+∞单调递减即()()g b g a ∴>，即a b b a >成立即2019201820182019>广东省年普通高等学校本科插班生招生考试高等数学一、单项选择题（本在题共小题，每小题分，共分。