六年级奥数几何图形汇总
六年级奥数平面几何部分

平面几何部分教学目标:1. 熟练掌握五大面积模型 2. 掌握五大面积模型的各种变形 知识点拨一、等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如右图12::S S a b =③夹在一组平行线之间的等积变形,如右图ACDBCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCBA图⑴ 图⑵三、蝴蝶定理ba S 2S 1DCBA S 4S 3S 2S 1O DCBA A BCDO ba S 3S 2S 1S 4任意四边形中的比例关系(“蝴蝶定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.梯形中比例关系(“梯形蝴蝶定理”): ①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +. 四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形. 五、燕尾定理在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=.OFE DCBA上述定理给出了一个新的转化面积比与线段比的手段,因为ABO∆的形状很象燕子∆和ACO的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.典型例题【例 1】如图,正方形ABCD的边长为6,AE=,CF=2.长方形EFGH的面积为.【巩固】如图所示,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形的宽为几厘米【例 2】长方形ABCD的面积为362cm,E、F、G为各边中点,H为AD边上任意一点,问阴影部分面积是多少E【巩固】在边长为6厘米的正方形ABCD内任取一点P,将正方形的一组对边二等分,另一组对边三等分,分别与P点连接,求阴影部分面积.【例 3】如图所示,长方形ABCD内的阴影部分的面积之和为70,8AD=,四AB=,15边形EFGO的面积为.AB【巩固】如图,长方形ABCD的面积是36,E是AD的三等分点,2=,则阴影部分AE ED的面积为.B【例 4】已知ABC为等边三角形,面积为400,D、E、F分别为三边的中点,已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形HBC)B【例 5】如图,已知5EF=,6FG=,线段AB将图形分成两部分,DE=,15CD=,7左边部分面积是38,右边部分面积是65,那么三角形ADG的面积是.GFE DC BA【例 6】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBA【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少EDCBA【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍乙甲E DCBA【例 7】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBA【例 8】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EF【例 9】 如图所示的四边形的面积等于多少DC131213131212【例 10】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC ∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【例 11】 如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.【例 12】 如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米FEABDC【例 13】 如图,三角形ABC 的面积是1,E 是AC 的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于 .FED CBA【巩固】如图,长方形ABCD 的面积是2平方厘米,2EC DE =,F 是DG 的中点.阴影部分的面积是多少平方厘米x xABFGE D CBA【例 14】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍.ABCDO【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =B【例 15】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE△的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGFEDCBA【例 16】 如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.ABCDEF G【例 17】 如图,正方形ABCD 面积为3平方厘米,M 是AD 边上的中点.求图中阴影部分的面积.CBA【巩固】在下图的正方形ABCD中,E是BC边的中点,AE与BD相交于F点,三角形BEF 的面积为1平方厘米,那么正方形ABCD面积是平方厘米.AB CDEF【例 18】已知ABCD是平行四边形,:3:2BC CE ,三角形ODE的面积为6平方厘米.则阴影部分的面积是平方厘米.B【巩固】右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是平方厘米.B【巩固】右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.B【例 19】 如图,长方形ABCD 被CE 、DF 分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为___________平方厘米.?852O A BCD EF【例 20】 如图,ABC ∆是等腰直角三角形,DEFG 是正方形,线段AB 与CD 相交于K 点.已知正方形DEFG 的面积48,:1:3AK KB =,则BKD ∆的面积是多少B【例 21】 下图中,四边形ABCD 都是边长为1的正方形,E 、F 、G 、H 分别是AB ,BC ,CD ,DA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数mn,那么,()m n +的值等于 .BEE【例 22】 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==,则::ADEDEGF FGCB S S S =△四边形四边形 .EGF A D CB【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.A ED CB【巩固】如图, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD DF FM MP PB ====,则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形 .【例 23】 如图,已知正方形ABCD 的边长为4,F 是BC 边的中点,E 是DC 边上的点,且:1:3DE EC =,AF 与BE 相交于点G ,求ABG S △Q E GNMF PADCBGFAEDCB【例 24】 如图所示,已知平行四边形ABCD 的面积是1,E 、F 是AB 、AD 的中点, BF交EC 于M ,求BMG ∆的面积.MHGF E DCBA【例 25】 如图,ABCD 为正方形,1cm AM NB DE FC ====且2cm MN =,请问四边形PQRS 的面积为多少CA【例 26】 如右图,三角形ABC 中,:4:9BD DC =,:4:3CE EA =,求:AF FB .O F EDCBA【巩固】如右图,三角形ABC 中,:3:4BD DC =,:5:6AE CE =,求:AF FB .O F EDCBA【巩固】如右图,三角形ABC 中,:2:3BD DC =,:5:4EA CE =,求:AF FB .O F EDCBA【例 27】 如右图,三角形ABC 中,:::3:2AF FB BD DC CE AE ===,且三角形ABC 的面积是1,则三角形ABE 的面积为______,三角形AGE 的面积为________,三角形GHI 的面积为______.I HGFEDCBA【巩固】 如右图,三角形ABC 中,:::3:2AF FB BD DC CE AE ===,且三角形GHI 的面积是1,求三角形ABC 的面积.IH G FEDCBA【巩固】如图,ABC ∆中2BD DA =,2CE EB =,2AF FC =,那么ABC ∆的面积是阴影三角形面积的 倍.B【巩固】如图在ABC △中,12DC EA FB DB EC FA ===,求GHI ABC △的面积△的面积的值. IHG FEDCBA【例 28】 如图,三角形ABC 的面积是1,BD DE EC ==,CF FG GA ==,三角形ABC 被分成9部分,请写出这9部分的面积各是多少GFE D CBA【巩固】如图,ABC ∆的面积为1,点D 、E 是BC 边的三等分点,点F 、G 是AC 边的三等分点,那么四边形JKIH 的面积是多少K JI HABC D EF G【例 29】 右图,ABC △中,G 是AC 的中点,D 、E 、F 是BC 边上的四等分点,AD 与BG 交于M ,AF 与BG 交于N ,已知ABM △的面积比四边形FCGN 的面积大7.2平方厘米,则ABC △的面积是多少平方厘米N M GA BCD EF【例 30】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求阴影部分面积.GCB【例 31】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求中心六边形面积.GCBA课后练习:练习1. 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA练习2. 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A练习3. 正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是 平方厘米.H GFEDC BA练习4. 如图,已知4cm AB AE ==,BC DC =,90BAE BCD ∠=∠=︒,10cm AC =,则S ABC ACE CDE S S ∆∆∆++= 2cm .DCEBA练习5. 如图,正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是_____平方厘米.ED练习6. 如图,ABC ∆中,点D 是边AC 的中点,点E 、F 是边BC 的三等分点,若ABC∆的面积为1,那么四边形CDMF 的面积是_________.FABCDE MN练习7. 如右图,三角形ABC 中,:::4:3AF FB BD DC CE AE ===,且三角形ABC 的面积是74,求角形GHI 的面积.IH G FEDCBA备选【备选1】 按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为2cm 和4cm ,乙三角形两条直角边分别为3cm 和6cm ,求图中阴影部分的面积.【备选2】 如图所示,矩形ABCD 的面积为36平方厘米,四边形PMON 的面积是3平方厘米,则阴影部分的面积是 平方厘米.【备选3】 如图,已知3BD DC =,2EC AE =,BE 与CD 相交于点O ,则ABC △被分成的4部分面积各占ABC △ 面积的几分之几OE DCBA【备选4】 如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少A BCDEF【备选5】 如图,:2:3BD DC =,:5:3AE CE =,则:AF BF =GF EDCBA【备选6】 如图在ABC △中,13DC EA FB DB EC FA ===,求GHI ABC △的面积△的面积的值. IHG FEDCBA。
六年级奥数平面几何常用技巧

平面几何常用技巧【加油站】常有正多边形:正三正方形正五边正六正八边形正十边形正十二角形形边形边形图形内角和每个内角【加油站】正十二边形的做法:一、做正六边形二、以正六边形每边为边长向外做六个正方形三、依次连接正方形外面的十二个极点。
则所构成的是正十二边形。
【例 1】(★★★)125 平方厘米,那么【例 2】(★★★)1 厘米,空白部分是等边以下列图,正八边形中的阴影部分面积是以下列图,一个正十二边形的边长是正八边形的面积是多少?三角形,一共有 12 个.请算出阴影部分的面积.1cm1【例 3】(★★★★)如右图,正十二边形和中心白色的正六边形的边长均为 12,图中阴影部分的面积 _________。
【例 5】(★★★★)如图,三角形 ABC 是等腰直角三角形, P 是三角形外的一点,其中 AP = 10 厘米,∠BPC =90°,求四边形 ABPC 的面积.QDBCP 【例 4】(★★★)依照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为 2 和 4,乙三角形两条直角边分别为 3 和 6,求图中阴影部分的面积.甲43乙6【例 6】(★★★)以下列图的四边形 ABCD 中,∠A=∠C=45°∠ABC=105 °, AB= CD =10 厘米,连接对角线,∠ABD =30°.求四边形 ABCD 的面积.CDA2【例 7】 (★★)6 厘米,小正方形边长是 4 厘米,两块阴【例 8】(★★★)华杯赛复赛试题10 厘米, 则阴影部分的面积为多少如图,大正方形边长是右图中的正方形的边长为影的面积差是多少?平方厘米?【本讲总结】一、特别图形的性质二、割补法、差不变:化不可以求为可求三、平移、旋转、对称:动向几何——改变地址不改变形状重点例题:例 3、例 4、例 5 、例 6、例 83。
六年级奥数专题训练-几何.风筝模型和梯形蝴蝶定理(A级).学生版

知识框架板块一 风筝模型:(又叫任意四边形模型)S 4S 3S 2S 1O DCBA ①1243::S S S S 或者1324S S S S ②1243::AO OC S S S S 风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO baS 3S 2S 1S 4①2213::S S a b②221324::::::S S S S a b ab ab ;③S 的对应份数为 2a b .梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)风筝模型和梯形蝴蝶定理例题精讲图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形【例 1】的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?76EDCB A76如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,【巩固】△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?OCDBA如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC【例 2】的面积;⑵:AG GC?CB在△ABC 中DC BD =2:1, EC AE =1:3,求OE OB=?【巩固】如图相邻两个格点间的距离是1,则图中阴影三角形的面积为 .【例 3】A如图,每个小方格的边长都是1,求三角形ABC 的面积.【巩固】A B如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依【例 4】次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGF EDC BA如右上图,已知BO=2DO ,CO=5AO ,阴影部分的面积和是11平方厘米,求四边形ABCD 的面积。
六年级下册奥数知识点梳理:几何图形
二 几何图形
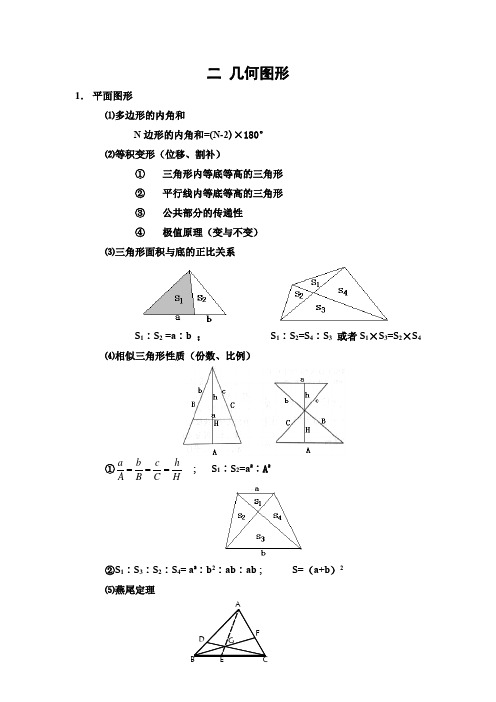
1. 平面图形
⑴多边形的内角和
N 边形的内角和=(N -2)×180°
⑵等积变形(位移、割补)
①
三角形内等底等高的三角形 ②
平行线内等底等高的三角形 ③
公共部分的传递性 ④ 极值原理(变与不变)
⑶三角形面积与底的正比关系
S 1︰S 2 =a ︰b ; S 1︰S 2=S 4︰S 3 或者S 1×S 3=S 2×S 4 ⑷相似三角形性质(份数、比例)
①a b c h A B C H === ; S 1︰S 2=a 2︰A 2
②S 1︰S 3︰S 2︰S 4= a 2︰b 2︰ab ︰ab ; S=(a+b )2 ⑸燕尾定理
S△ABG:S△AGC=S△BGE:S△GEC=BE:EC;
S△BGA:S△BGC=S△AGF:S△GFC=AF:FC;
S△AGC:S△BCG=S△ADG:S△DGB=AD:DB;
⑹差不变原理
知5-2=3,则圆点比方点多3。
⑺隐含条件的等价代换
例如弦图中长短边长的关系。
⑻组合图形的思考方法
①化整为零
②先补后去
③正反结合
2.立体图形
⑴规则立体图形的表面积和体积公式
⑵不规则立体图形的表面积
整体观照法
⑶体积的等积变形
①水中浸放物体:V升水=V物
②测啤酒瓶容积:V=V空气+V水
⑷三视图与展开图
最短线路与展开图形状问题
⑸染色问题
几面染色的块数与“芯”、棱长、顶点、面数的关系。
六年级奥数专题—几何五大模型—鸟头模型学习与巩固

几何五大模型——鸟头模型一 两点都在边上:鸟头定理:(现出“鸟头模型”。
然后按一下出现一个鸟头,勾勒出鸟头的轮廓,出现如图的鸟头几何模型。
最后真实的鸟头隐去,只留下几何模型。
最后按一下,出公式。
)△ADE △ABC S AD ×AE=S AB ×ACED C B A二 一点在边上,一点在边的延长线上:△CDE△ABC S CD ×CE =S BC ×AC例 1 如图,AD=DB ,AE=EF=FC ,已知阴影部分面积为5平方厘米,△ ABC的面积是平方厘米.例2 (1)如图在△ABC中,D、E分别是AB,AC上的点,且AD:AB=2:5, AE:AC=4:7,△ABC的面积是16平方厘米,求△ABC的面积。
(2)如图在△ABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△ADE的面积是12平方厘米,求△ABC的面积。
例3 已知△DEF的面积为12平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC的面积。
例4 三角形ABC 面积为1,AB 边延长一倍到D ,BC 延长2倍到E ,CA 延长3倍到F ,问三角形DEF 的面积为多少?FEDC BA例5 长方形ABCD 面积为120,EF 为AD 上的三等分点,G 、H 、I 为DC 上的四等分点,阴影面积是多大?例6 如图,过平行四边形ABCD内的一点P作边AD、BC的平行线EF、GH,若PBD 的面积为8平方分米,求平行四边形PHCF的面积比平行四边形PGAE的面积大多少平方分米?作业:1. 如下左图,在ABC △中,D 、E 分别是BC 、AB 的三等分点,且ABC △的面积是54,求CDE △的面积。
2. 如图,长方形ABCD 的面积是1,M 是AD 边的中点,N 在AB 边上,且12AN BN.那么,阴影部分的面积等于 .AB CD M N 图13. 如图以ABC △的三边分别向外做三个正方形ABIH 、ACFG 、BCED ,连接HG 、EF 、BID ,又得到三个三角形,已知六边形DEFGHI 的面积是77平方厘米,三个正方形的面积分别是9、16、36平方厘米,则三角形ABC 的面积是多少?I HGFED CB A4. 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积。
苏教版六年级下册奥数几何图形专题

9.42-8=1.42cm2
答:两个阴影部分的面积相差1.42平方厘米。
练一练
【例题12】(48中)如图,一个三角形的三个顶点分别为三个 半径为3厘米的圆的圆心,则图中阴影部分的面积是多少?
阴影面积=半圆面积 3.14×3²÷2=14.13cm2
答:两个阴影部分的面积相差14.13平方厘米。
逢3必过
练一练
【例题11】如图A与B是两个圆(只有四分之一)的圆心。那么,
两个阴影部分的面积相差多少平方厘米?(单位:厘米)
1
差不变模型 ②-①=(②+③)-(①+③) 2
3.14×4²÷4=12.56cm2
③
2A 2 B
3.14×2²÷4=3.14cm2
2×4=8cm2
12.56-3.14=9.42cm2
小学数学 六年级
欢 迎 同 学 们
几何综合
优 翼
1、公式法:基本图形的面积求解公式 2、概念法:根据基本图形的基本概念进行判断并求解 3、加减法: 相加求整,相减求部分。 4、分割法:将整体分割成若干个规则的多边形 5、割补法:将一部分割补到图形中的另一个地方组成较规则 的图形进行求解。
6、等量代换法:如果图中有和所求部分面积相等的图形,可 以通过先求该图形的面积间接求出所要求部分的面积。 7、重组法:将所求部分打乱重新组合。 8、倍比法:通过边长之间的倍数关系求解面积之间的倍数关 系。 9、差不变法:A-B=(A+C)-(B+C) 10、整体法:在求解过程中没必要一定求出某一个具体的量, 只需要知道某一个计算过程的整体也是可以求出面积的。
倍比法 S△BCD=1cm2
S△DBE=1×(2+1)=3cm2
小学奥数几何图形大全

小学奥数几何图形大全小学奥数:几何图形大全几何图形综合1.如图,四边形是直角梯形.其中12(厘米),8(厘米),15(厘米),且△,四边形,△的面积相等.阴影△的面积是多少平方厘米?2.如图,长方形的面积是96平方厘米,E 是边上靠近D 点的三等分点,F 是边上靠近C 点的四等分点.阴影部分的面积是多少平方厘米?3.如图,把一个正方形的两边分别增加3和5厘米,米(阴影部分).原正方形的面积为多少平方厘米?4.如图,把一个正方形的相邻两边分别减少2厘米和446平方厘米(阴影部分).原正方形的面积为多少平方厘米?5.如图,在△中,的长度是的四分之三,的长度是的三分之二.请问:△的面积是△面积的几分之几?6.如图,在△中,3,3,那么△的面积是△的多少倍?7.如图,某公园的外轮廓是四边形,被对角线、分成四个部分.△的面积是3平方千米,△的面积是2平方千米,△的面积是1平方千米,如果公园由大小为6.9平方千米的陆地和一块人工湖组成,那么人工湖的面积是多少平方千米?8.如图,在梯形中,长9厘米,长15厘米,E DF B CA D EA B C E A D A D O小学奥数:几何图形大全长12厘米,那么长多少厘米?9.如图,有8个半径为1厘米的小圆,用它们圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心.如果圆周率π取3.14,那么花瓣图形的周长和面积分别是多少?10.图中甲区域比乙区域的面积大57其中直角三角形竖直的直角边的长度是多少?(π取3.14)11.如图,在3×3的方格表中,分别以A 、E 为圆心,3、2为半径,画出圆心角都是90o的两段圆弧.图中阴影部分的面积是多少? (π取3.14).(π取13.下图是一个直角边长为3厘米、4厘米的直角三角形.将该三角形一任意一条边所在直线为轴进行旋转,求所得立体图形的表面积和体积.14.如图,已知正方形的边长为4厘米,求阴影部分的面积.15.斜边长为10厘米的等腰直角三角形的面积是多少?● ●●● ●●● ● ●● ● ●● ● ●a b c def h g16.右图中两个完全相同的三角形重叠在一起,则阴影部分的面积是多少?17.求图中四边形的面积.18.图中八条边的长度正好分别是1,2,3,4,5,6,7,8厘米. 已知2厘米,4厘米,5厘米,求图形的面积.19.如图所示,∠1+∠2+∠3+∠4+∠5+∠6等于多少度?20.如图,一个边长为1米的正方形被分成4平方米、0.4平方米、0.2平方米、0.1平方米. 已知图中的阴影部分是正方形,那么它的面积是多少平方米?21.如图所示,三角形中,与平行,且5:2,求及.22.如图,间相互重叠.已知露在外面的部分中,红色的面积是20,黄色的面积是14,绿色的面积是10.那么,23.如图所示,已知△的面积为1平方厘米,D 、E 分别B A D 12 3 4 5 6 绿是、边的中点.求三角形的面积.24.在如图所示的正方形中,A 、B 、C 分别是、、的中点.请问:△的面积是△面积的几倍?25.如图,四边形是平行四边形,面积为72平方厘米,E 、F 分别为边、的中点,请问:阴影部分的面积为多少平方厘米?26.如图,△中,2,F 是的中点,△的面积为1,那么阴影部分的面积多少?27.如图,△中,、相交于点O ,△、△、△的面积分别为1、2、3,那么四边形的面积多少?28.图中有半径分别为5厘米、4厘米、3厘米的三个圆,A 部分(即两小圆重叠部分)的面积与阴影部分的面积相比,哪个大?大多少?29.如图,图中最大的长方形面积是27,最小的长方形面积是5面积.30.阅读理解:(1)阅读:勾股定理是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”,中国是发现和研究勾股定理最古老的国家之一。
六年级奥数几何图形汇总

六年级奥数几何图形汇总(总12页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--几何部分题型大汇总1.2.3.如下图,两个相同的直角三角形重叠在一起,求阴影部分的面积是多少4.四个相同的长方形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x、y表示长方形的长和宽,则小长方形的长为______,宽为______。
5.第4题图第5题6.三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABCD的长和宽分别为6、4厘米,DF长多少厘米?7.8.6.如图中三角形ABC被分成了甲(阴影部分)、乙两部分,BD=DC=4,BE=2,EA=4,那么甲部分的面积是乙部分面积的几倍?7.如图,正方形ABCD的面积为3平方厘米,M是AD边上的中点,求阴影部分面积8.有红黄蓝三块大小一样的正方形纸片,放在一个底面为正方形的盒内,它们之间互相叠合.已知露在外面的部分中,红色面积是20.黄色面积是14,绿色面积为10,求正方形盒底的面积。
9.如图,梯形ABCD的上底AD长为3厘米,下底BC长为9厘米.三角形ABO的面积为12平方厘米,则梯形ABCD的面积为多少?10.已知如图大正方形的边长是5厘米,小正方形的边长是3厘米,求阴影部分的面积11.如图,三角形ABC的面积为1,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为多少?12.如图,一块长方形的布料ABCD,被剪成大小相等的甲、乙、丙、丁四块,其中甲块布料的长与宽的比为a:b=3:2,那么丁块布料的长与宽的比是______.13.如图一块长方形铁皮,利用图中的阴影部分刚好能做成一个圆柱形油桶(接头处忽略不计).求油桶的容积?14.直角三角形ABC的三条边分别是5cm, 3cm和4cm,将它的直角边AC对折到斜边AB上,使AC 与AD重合,如下图,则图中阴影部分(未重叠部分)的面积是多少平方厘米15.如图,已知直角三角形的面积是12平方厘米,求阴影部分面积.16.半径20厘米圆的外面和里面各有一个正方形,外面正方形的面积是多少,里面正方形的面积是多少?第16题第18题18.19.如下图,三角形ABC是等腰直角三角形,一直角边长为4厘米,求阴影部分的面积20.已知下图平行四边形的面积是36平方厘米,求图中阴影部分面积.要求写出计算过。
六年级奥数几何图形汇总

几何部分题型大汇总1.-饨万秫醸懿分狐何长方臥护三个帼驰鼬擁詡分的郦2.⑦如右图”在长方形A BCD中「丹是正方形f已知二1%如「GC二九m ’则长方形卫弘刀的周长垦多厘米?知右图,在氏方^ADCD^ t山・G丿是工方腿,已知AA・10cf GC^7nn t则反方形丄此册周士磔附?3•如下图,两个相同的直角三角形重叠在一起,求阴影部分的面积是多少?4.四个相同的长方形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x、y表示长方形的长和宽,贝y小丄宽为长方形的长为第4题图5.三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABCD勺长和宽分别为6、4厘米,DF长多少厘米?6•如图中三角形ABC被分成了甲(阴影部分)、乙两部分,BD=DC= 4,BE=2,EA=4,那么甲部分的面积是乙部分面积的几倍?7.如图,正方形ABCD的面积为3平方厘米,M是AD边上的中点,求阴影部分面积?8.有红黄蓝三块大小一样的正方形纸片,放在一个底面为正方形的盒,它们之间互相叠合.已知露在外面的部分中,红色面积是20. 黄色面积是14,绿色面积为10,求正方形盒底的面积。
9•如图,梯形ABCD的上底AD长为3厘米,下底BC长为9厘米•三角形ABO的面积为12平方厘米,则梯形ABCD的面积为多少?10.已知如图大正方形的边长是5厘米,小正方形的边长是3厘米,求阴影部分的面积?11.如图,三角形ABC的面积为1, BD : DC=2 : 1 , E是AC的中点, AD与BE相交于点P,那么四边形PDCE的面积为多少?B DC12.如图,一块长方形的布料ABCD,被剪成大小相等的甲、乙、丙、丁四块,其中甲块布料的长与宽的比为a:b=3 : 2,那么丁块布料的长与宽的比是_______ • 13.如图一块长方形铁皮,利用图中的阴影部分刚好能做成一个圆柱形油桶(接头处忽略不计).求油桶的容积?14.直角三角形ABC的三条边分别是5cm, 3cm和4cm,将它的直角边AC 对折到斜边AB上,使AC与AD重合,如下图,则图中阴影部分(未重叠部分)的面积是多少平方厘米?15.如图,已知直角三角形的面积是12平方厘米,求阴影部分面积.16.半径20厘米圆的外面和里面各有一个正方形,外面正方形的面积是多少,里面正方形的面积是多少?第16题第18题八炯罡由两衽罚腕来斯边卅别対耿和僱栄.硼謡盼匸角恤C)的酿是平方鳏・18.蛆大斯聊觸聽分是-个正?<嫌方蹦瞅是si19. 如下图,三角形ABC是等腰直角三角形,一直角边长为4厘米,求阴影部分的面积?20. 已知下图平行四边形的面积是36平方厘米,求图中阴影部分面积要求写出计算过。
小学奥数几何六大模型及例题06165

例题5 如图,已知三角形ABC面积为1,延长AB至D,使BD=AB,延长BC至E,使CE=2BC,延 长CA至F,使AF=3AC,求三角形DEF的面积。
例题6 如图1,正六边形的面积为6,那么阴影部分的面积是多少?历史ⅱ岳麓版第13课交Fra bibliotek与通讯 的变化资料
精品课件欢迎使用
[自读教材·填要点]
若干个三角形,所以三角形是最基本图形,等积变形里主要研究的 是三角形面积变换。
三角形面积=底×高÷2 决定三角形面积的大小,取决于底和高这两个量。 等底等高:如果两个三角形等底等高,则这两个三角形面积相同 (如图1);(典型的夹在一组平行线间的,两个三角形若同底,则 面积相同) 同底看高:如果两个三角形等底,但高不等,则面积比等于高的 比(如图2); 同高看底:如果两个三角形等高,但底不等,则面积比等于底的 比(如图3)。
()
A.江南制造总局的汽车
B.洋人发明的火车
C.轮船招商局的轮船
D.福州船政局的军舰
[解析] 由材料信息“19世纪七十年代,由江苏沿江居民 到上海”可判断最有可能是轮船招商局的轮船。
[答案] C
[题组冲关]
1.中国近代史上首次打破列强垄断局面的交通行业是 ( )
A.公路运输
B.铁路运输
C.轮船运输
2.特点 (1)近代中国交通业逐渐开始近代化的进程,铁路、水运和 航空都获得了一定程度的发展。 (2)近代中国交通业受到西方列强的控制和操纵。 (3)地域之间的发展不平衡。 3.影响 (1)积极影响:促进了经济发展,改变了人们的出行方式, 一定程度上转变了人们的思想观念;加强了中国与世界各地的 联系,丰富了人们的生活。 (2)消极影响:有利于西方列强的政治侵略和经济掠夺。
小学奥数几何图形知识

小学奥数几何图形知识小学奥数几何立体图形知识:1、特征六个面都是长方形(有时有两个相对的面是正方形)。
相对的面面积相等,12条棱相对的4条棱长度相等。
有8个顶点。
相交于一个顶点的三条棱的长度分别叫做长、宽、高。
两个面相交的边叫做棱。
三条棱相交的点叫做顶点。
把长方体放在桌面上,最多只能看到三个面。
长方体或者正方体6个面的总面积,叫做它的外表积。
2、计算公式s=2(ab+ah+bh)V=shV=abh1、特征六个面都是正方形;六个面的面积相等;12条棱,棱长都相等;有8个顶点;正方体可以看作特殊的长方体。
2、计算公式S表=6a2v=a31、圆柱的认识圆柱的上下两个面叫做底面。
圆柱有一个曲面叫做侧面。
圆柱两个底面之间的间隔叫做高。
2、计算公式s侧=chs表=s侧+s底×2v=sh/31、圆锥的认识圆锥的底面是个圆,圆锥的侧面是个曲面。
从圆锥的顶点到底面圆心的间隔是圆锥的高。
测量圆锥的高:先把圆锥的底面放平,用一块平板水平地放在圆锥的顶点上面,竖直地量出平板和底面之间的间隔。
把圆锥的侧面展开得到一个扇形。
2、计算公式v=sh/31、认识球的外表是一个曲面,这个曲面叫做球面。
球和圆类似,也有一个球心,用O表示。
从球心到球面上任意一点的线段叫做球的半径,用r表示,每条半径都相等。
通过球心并且两端都在球面上的线段,叫做球的直径,用d表示,每条直径都相等,直径的长度等于半径的2倍,即d=2r。
2、计算公式d=2r。
六年级奥数专项精品讲义及常考易错题汇编-几何图形问题十二大专题汇编含详解

六年级奥数专项精品讲义及常考易错题汇编-几何图形问题-等积变形(位移、割补)【知识点归纳】等积变形的主要方法是:1.三角形内等底等高的三角形2.平行线内等底等高的三角形3.公共部分的传递性4.极值原理(变与不变)【经典题型】例1:求如图的体积.(π取3.14)分析:此题上面是斜面,可以把一个和它完全一样的图形拼成一个高是20+15=35厘米,底面直径是4厘米的圆柱体,所以此图的体积是圆柱体积的12;利用圆柱体的体积公式计算出体积即可.解:3.14×(4÷2)2×(15+20)×,=3.14×4×35×,=219.8;答:体积是219.8;故答案为:219.8.点评:此题主要根据圆柱体的体积公式解决问题,解题的关键是把两个完全一样的图形拼成一个圆柱体,此图的体积是圆柱体积的.例2:如图所示:一块长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路.求小路的占地面积?分析:无论这曲折小路如何再曲折,都可以将曲折小路分成两类,一类是竖的,一类是横的,可以把竖的往左拼,横的往上拼,如下图则小路面积不难算出,竖的部分14×2,横的部分20×2,计算重叠2×2,则小路面积为(20+14)×2-2×2=64(平方米).解:小路面积为:(20+14)×2-2×2=64(平方米),答:小路的占地面积64平方米.点评:利用等积变形、平移知识把曲折的小路拉直,就变成规则的图形包括三部分竖的长方形,横的长方形和重叠的小正方形,进而解答.一.选择题1.如图,长方形的面积与圆的面积相等,已知阴影部分的面积是84.78cm2,圆的周长是()cm.A.18.84 B.75.36 C.37.682.以下是四位同学运用转化的策略将左边的图形转化成右边的图形解决问题,其中做对的有()位.A.1 B.2 C.3 D.4二.填空题3.有一种饮料瓶的容积是50立方厘米,瓶身呈圆柱形(不包括瓶颈).现在瓶中装有一些饮料,正放时饮料高度为20厘米,倒放时空余部分的高度为5厘米.瓶内现有饮料立方厘米.4.如图,外侧大正方形的边长是10厘米,图中阴影部分的面积是27.5平方厘米,那么圆内的大正方形面积是小正方形面积的倍.5.将一底面半径为2分米的圆柱的底面平均分成若干个扇形,截开拼成一个和它等底等高的长方体后,表面积增加16平方分米,圆柱的体积是.6.在如图的长方形内,有四对正方形(标号相同的两个正方形为一对),每一对是相同的正方形,那么中间这个小正方形(阴影部分)的面积为.7.如图,E,F,G,H是边长为2的正方形ABCD各边的中点,则图中阴影部分的面积等于.8.如图,三个大小相同的正方形重叠地放在一个大的正方形ABCD内,已知能看见的部分Ⅰ、Ⅱ、Ⅲ的面积分别是64平方厘米、38平方厘米、34平方厘米.那么正方形ABCD的边长是厘米.9.下图是一个正方体木块.M是AB的中点,N是AD的中点.用一把锋利的锯,过M、N、G三个点将木块锯成两块,使截面是平的,这个截面是边形.10.如图所示,一种饮料瓶,容积是200ml,瓶身是圆柱形.将该瓶正放时饮料高20cm,倒放时余部分高5cm,瓶内的饮料是ml.三.操作题11.把下列图形改成平行四边形四.解答题12.如图,正方形ABCD的边长为10厘米,E,F,G,H分别为正方形四边上的中点,求阴影部分的面积是多少平方厘米.13.看图求阴影部分的面积.(1)求出图(1)中阴影部分的面积.(2)分析上面各图形之间的关系,看一看、想一想、找一找图(4)中阴影部分的面积是.14.如图所示的多边形是由一个三角形和三个长方形组成的.已知三个长方形的面积分别是12平方厘米、4平方厘米和6平方厘米.三角形面积是多少平方厘米?15.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为多少平方厘米?16.给一个直角楼梯铺地毯,如图所示(图中阴影处不铺),至少需要多少平方米的地毯?(单位:米)17.求小路的占地面积.如图所示:一块长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路.18.一个圆锥形沙堆,底面积是3.6平方米,高1.2米.把这堆沙装在长2米、宽1.5米的沙坑里,可以装多高?19.如图所示,用一张斜边长为17厘米的红色直角三角形纸片,一张斜边长为29厘米的黄色直角三角形纸片,一张蓝色的正方形纸片,拼成一个直角三角形.红、黄两张三角形纸片面积之和是多少?20.雨哗哗地不停地下着.如果在雨地放一个如图1那样的长方体的容器(单位:厘米),雨水将它灌满要用1小时.雨水灌满图2容器各需多长时间?21.把一个底面直径是4厘米的圆柱底面分成许多相等的扇形,然后沿着直径切开,拼成一个和它体积相等的长方体,这个长方体的表面积比原来圆柱的表面积增加了20平方厘米,这个长方体的体积是多少立方厘米?22.求如图的体积.(π取3.14)23.求如图的体积.(π取3.14)24.给一个直角楼梯铺地毯,如图(图中阴影处不铺)情根据图中的数据,算一算,至少需要多少平方米地毯?(单位:米)25.用20个大小相同的小正方可以组成一个十字图形.把这个十字图形分割为4个部分,是的它们的形状和大小都一样(分割线须沿着图内的虚线),方法有很多,如图例所示,请你再画出与范例不同的两种分割方法.26.如图,O是半圆的圆心,AC=BC,CD=DB,AB=12厘米,求阴影部分的面积.27.如图,直角梯形ABCD中,AB=12,BC=8,CD=9,且三角形AED、三角形FCD和四边形EBFD 的面积相等,求三角形DEF的面积.六年级奥数专项精品讲义及常考易错题汇编-几何图形问题-等积变形(位移、割补)参考答案一.选择题1.解:84.78÷÷5.14=113.04÷3.14=36(cm2);6×6=36(cm2),8.14×6×2=37.68(cm).答:圆的周长是37.68cm.答案:C.2.解:(1)如图,,因为阴影部分A的面积等于空白部分B的面积,所以涂色部分的面积可以转化为圆的面积,所以涂色部分的面积占整个图形面积的,所以(1)正确.(2)如图,,因为△ABC的面积可以转化为△CDE的面积,△AFG的面积可以转化为△EFH的面积,所以涂色部分的面积可以转化为10个小方格的面积,所以涂色部分的面积占整个图形面积的,即,所以(2)不正确.(3)如图,,因为阴影部分A的面积等于空白部分B的面积,所以涂色部分的面积转化为一个正方形的面积,所以涂色部分的面积占整个图形面积的,所以(3)正确.(4)因为该图形的周长转化为直径是7cm的半圆的周长和直径是4cm的圆的周长的和,而不是转化为直径是4cm的半圆的周长和一条7cm的直径的长度之和,所以(4)不正确.综上,可得做对的有2位:(1)(3).答案:B.二.填空题3.解:50×[20÷(20+5)]=50×=40(立方厘米)答案:40立方厘米.4.解:由分析可知:总阴影部分的面积=大正方形的面积四分之一+圆内小正方形的面积四分之一=27.5(平方厘米),大正方形的面积四分之一:10×10×=25(平方厘米),所以圆内小正方形的面积四分之一:27.5﹣25=2.8(平方厘米),则圆内小正方形的面积=2.5×8=10(平方厘米),圆内大正方形的面积:(10÷2)×(10÷2)÷7×4=5×6×2=50(平方厘米),圆内的大正方形面积是小正方形面积的:50÷10=5(倍);答案:7.5.解:3.14×2=4.28(分米),16÷2÷2=7(分米),6.28×2×3=50.24(立方分米);答:圆柱的体积是50.24立方分米.答案:50.24立方分米.6.解:长方形的宽,是“一”与“二”两个正方形的边长之和,长方形的长,是“一”,则长﹣宽=30﹣22=8;宽又是两个“三”正方形与中间小正方形的边长之和,因此中间小正方形边长=22﹣8×4=6.所以中间小正方形面积=6×4=36.答:中间这个小正方形(阴影部分)的面积为36.答案:36.7.解:根据题干分析可得:2×2×=2,答:阴影部分的面积是5.答案:2.8.解:如上图图所示:设出其中两条边分别为a,b:则将图Ⅱ所在的小正方形向左移动到最左边,图Ⅱ减少的面积等于图Ⅲ增加的面积,图Ⅱ面积+图Ⅲ面积=38+34=72(平方厘米),因为大正方形ABCD的边长=小正方形的边长+a=小正方形的边长+b,所以a=b,所以将图Ⅱ所在的小正方形向左移动到最左边后,图Ⅱ的面积等于图Ⅲ的面积,即8a=8b=72÷7=36(平方厘米),则a=b=36÷8=4.2(厘米),则大正方形ABCD的边长为:8+4.8=12.5(厘米).答:正方形ABCD的边长是12.5厘米.答案:12.4.9.解:如图过M、N、G三个点将木块锯成两块、左、右、前、后五个面相交,所以得到的截面是五边形;答案:五边形.10.解:200×[20÷(20+5)]=200×=160(ml).答:瓶内的饮料是160ml.答案:160.三.操作题11.解:根据题干分析可得:四.解答题12.解:将原图割补为下图:.;答:阴影部分的面积是20平方厘米.13.解:(1)正方形边长:2×2=2(cm);阴影部分的面积:4×4﹣8.14×22,=16﹣12.56,=8.44(cm2);(2)把第一幅图横竖分割成4等份,可组拼成后3个图形,所以第四幅图中阴影部分的面积仍是3.44cm2;答案:7.44cm2.14.解:如图,设三角形面积为x平方厘米,则2x:12=6:84×2x=12×78x=728x÷6=72÷8x=9答:三角形面积是8平方厘米.15.解:如图,,阴影部分A的面积等于空白部分B的面积,阴影部分C的面积等于空白部分D的面积,所以阴影部分的面积和等于正方形面积的一半,4×4÷7=8(平方厘米)答:图中阴影部分的面积为8平方厘米.16.解:(2.5+5.2)×2=3.7×2=11.5(平方米),答:至少需要11.4平方米的地毯.17.解:小路面积为:(20+14)×2﹣2×4=64(平方米),答:小路的占地面积64平方米.18.解:3.6×2.2×÷(2×1.6),=1.44÷3,=8.48(米);答:可以装0.48米高.19.解:根据题干分析可得:29×17÷2=246.5(平方厘米),答:这两个直角三角形的面积和是246.5平方厘米.答案:246.5平方厘米.20.解:图①所示的容积中,容积:接水面积=(30×20×10):(30×20)=6000:600=10:1;图②所示的容器中,容积:接水面积=(20×10×10+10×10×10):(10×10)=3000:100=30:1;图③所示的容器中,容积:接水面积=(20×10×10+10×10×10):(20×10)=3000:200=15:2;答:雨水灌满图2的容器需3小时、雨水灌满图4的容器需1.5小时.21.解:20÷2=10(平方厘米),4×2.14÷2=6.28(厘米),10×8.28=62.8(立方厘米);答:这个长方体的体积是62.8立方厘米.22.解:3.14×(4÷2)2×(15+20)×,=3.14×4×35×,=219.8;答:体积是219.3;答案:219.8.23.解:3.14×(4÷2)2×(8+12)÷7=3.14×4×20÷5=125.6(立方厘米);答:它的体积是125.6立方厘米.24.解:(2.5+8)×2=5.8×2=11(平方米),答:至少需要11平方米地毯.25.解:根据题干分析可将这个图形分割如下:26.解:S阴=S扇形COB=×2.14×,=2.14×9,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.27.解:(1)根据题干可得,梯形ABCD的面积为:(9+12)×8÷6,=21×8÷2,=84,所以三角形AED、三角形FCD和四边形EBFD的面积分别为:84÷5=28,(2)在直角梯形BECD中,BE=28×2×2÷6﹣9=14﹣9=4,(3)在直角三角形FCD中,FC=28×2÷9=,所以BF=8﹣=,所以直角三角形BEF的面积为:2×=,故三角形DEF的面积为:28﹣=,答:三角形DEF的面积为.六年级奥数专项精品讲义及常考易错题汇编-几何图形问题-立体图形的表面积和体积【知识点归纳】立体图形表面积公式:1.圆柱体:表面积:2πR2+2πRh 体积:πR2h (R为圆柱体上下底圆半径,h为圆柱体高)2.圆锥体:体积:πR2h (r为圆锥体低圆半径,h为其高)3.长方体:表面积=(长×宽+长×高+宽×高)×24.球:表面积=4πR2.一.选择题1.3个棱长都是10厘米的正方体堆放在墙角处,露在外面的面积是()平方厘米.A.1800B.700C.900D.8002.彤彤用18个棱长1cm的正方体摆出如图所示模型,若从模型的三个不同的位置上拿走2个正方体后,可分别得到图(A)、(B)、(C).在图(A)、(B)、(C)中表面积比图甲小的是( )A.B.C.3.如图是一个长3米、宽与高都是2米的长方体.将它挖掉一个棱长1米的小正方体,它的表面积()A.比原来大B.比原来小C.不变D.无法确定4.甲图和乙图占空间的大小关系是甲()乙.A.>B.<C.=D.无法比较5.如图图形的体积是()厘米3.A.100B.267C.240)cm.6.如图是由31cm的小正方体搭成的,它的体积是(3A.10B.9C.67.如图是一个长3厘米、宽与高都是2厘米的长方体.将它挖掉一个棱长1厘米的小正方体,它的表面积()A.比原来大B.比原来小C.不变8.将棱长为1厘米的小正方体按如图方式摆方在地上,露在外面的面积是()平方厘米.A.18B.21C.24D.27二.填空题9.如图是由同样大小的小方块堆积起来的,每个小方块的棱长是1分米,这堆小方块露在外面的面积是.10.有5个棱长为40厘米的正方体放在墙角处.有个面露在外面.露在外面的面积共有平方厘米?11.将4个棱长都是1cm的正方体堆在墙角,体积是3cm.cm,露在外面的面积是212.如果如图中每个小正方体的棱长都是1厘米,这个物体的体积是立方厘米,表面积是平方厘米。
小升初六年级奥数——几何(平面图形)

⼩升初六年级奥数——⼏何(平⾯图形)⼀、分数百分数问题,⽐和⽐例这是六年级的重点内容,在历年各个学校测试中所占⽐例⾮常⾼,重点应该掌握好以下内容:对单位1的正确理解,知道甲⽐⼄多百分之⼏和⼄⽐甲少百分之⼏的区别;求单位1的正确⽅法,⽤具体的量去除以对应的分率,找到对应关系是重点;分数⽐和整数⽐的转化,了解正⽐和反⽐关系;通过对“份数”的理解结合⽐例解决和倍(按⽐例分配)和差倍问题;⼆、⾏程问题应⽤题⾥最重要的内容,因为综合考察了学⽣⽐例,⽅程的运⽤以及分析复杂问题的能⼒,所以常常作为压轴题出现,重点应该掌握以下内容:路程速度时间三个量之间的⽐例关系,即当路程⼀定时,速度与时间成反⽐;速度⼀定时,路程与时间成正⽐;时间⼀定时,速度与路程成正⽐。
特别需要强调的是在很多题⽬中⼀定要先去找到这个“⼀定”的量;当三个量均不相等时,学会通过其中两个量的⽐例关系求第三个量的⽐;学会⽤⽐例的⽅法分析解决⼀般的⾏程问题;有了以上基础,进⼀步加强多次相遇追及问题及⽕车过桥流⽔⾏船等特殊⾏程问题的理解,重点是学会如何去分析⼀个复杂的题⽬,⽽不是⼀味的做题;三、⼏何问题⼏何问题是各个学校考察的重点内容,分为平⾯⼏何和⽴体⼏何两⼤块,具体的平⾯⼏何⾥分为直线形问题和圆与扇形;⽴体⼏何⾥分为表⾯积和体积两⼤部分内容。
学⽣应重点掌握以下内容:等积变换及⾯积中⽐例的应⽤;与圆和扇形的周长⾯积相关的⼏何问题,处理不规则图形问题的相关⽅法;⽴体图形⾯积:染⾊问题、切⾯问题、投影法、切挖问题;⽴体图形体积:简单体积求解、体积变换、浸泡问题;四、数论问题常考内容,⽽且可以应⽤于策略问题,数字谜问题,计算问题等其他专题中,相当重要,应重点掌握以下内容:掌握被特殊整数整除的性质,如数字和能被9整除的整数⼀定是9的倍数等;最好了解其中的道理,因为这个⽅法可以⽤在许多题⽬中,包括⼀些数字谜问题;掌握约数倍数的性质,会⽤分解质因数法,短除法,辗转相除法求两个数的最⼤公因数和最⼩公倍数;学会求约数个数的⽅法,为了提⾼灵活运⽤的能⼒,需了解这个⽅法的原理;了解同余的概念,学会把余数问题转化成整除问题,下⾯的这个性质是⾮常有⽤的:两个数被第三个数去除,如果所得的余数相同,那么这两个数的差就能被这个数整除;能够解决求⼀个多位数除以⼀个较⼩的⾃然数所得的余数问题,例如求1011121314 (9)899除以11的余数,以及求20082008除以13的余数这类问题;五、计算问题计算问题通常在前⼏个题⽬中出现概率较⾼,主要考察两个⽅⾯,⼀个是基本的四则运算能⼒,同时,⼀些速算巧算及裂项换元等技巧也经常成为考察的重点。
小学六年级奥数--立体几何综合

学科培优 数学立体几何综合学生姓名 授课日期 教师姓名授课时长知识定位本讲复习已经学过的立体图形的相关知识和解题技巧,主要有:长方体、立方体、圆柱、圆锥的体积及表面积求解,立体几何计数及多面体顶点与棱以及表面的关系。
重难点在于:1.不规则立体图形的表面积或体积求解2.多面体的顶点与棱数计数 3.体积的等量代换主要的考点:1.规则立体图形的表面积(侧面积)与体积计算2.不规则立体图形的表面积与体积计算 3.染色问题4.立体图形的三视图与展开图知识梳理主要知识点 立体几何⑴规则立体图形的表面积和体积公式长方体:体积:长宽高 表面积:(长宽+宽高+长高) 立方体:体积:棱长的立方 表面积:棱长的平方6 圆柱: 体积:2r h π 侧面积:2rh π 圆锥: 体积:213r h π⑵不规则立体图形的表面积整体观照法⑶体积的等积变形①水中浸放物体:V 升水=V 物 ②测啤酒瓶容积:V=V 空气+V 水⑷三视图与展开图最短线路与展开图形状问题⑸染色问题几面染色的块数与“芯”、棱长、顶点、面数的关系。
例题精讲【试题来源】【题目】一个长方体的表面积是33.66平方分米,其中一个面的长是2.3分米,宽是2.1分米,它的体积是_____立方分米.【试题来源】 【题目】右图是一个棱长为2厘米的正方体,在正方体上面的正中向下挖一个棱长为1厘米的正方形小洞;接着在小洞的底面正中再挖一个棱长为21厘米的小洞;第三个小洞的挖法与前两个相同,棱长为41厘米.那么最后得到的立体图形的表面积是 平方厘米【试题来源】【题目】把一个长25厘米,宽10厘米,高4厘米的长方体木块锯成若干个大小相等的正方体,然后拼成一个大的正方体.这个大正方体的表面积是_____平方厘米。
【试题来源】【题目】右图是3层没有缝隙的小立方块组成的.如果它的外表面(包括底面)全都被涂成红色,那么把它们再分开成一个个小立方块时,有多少个小立方块恰有三面是红色的?【试题来源】【题目】一个正方体木块,棱长是15.从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体.这个木块剩下部分的表面积最少是( ).【试题来源】【题目】把一根长2.4米的长方体木料锯成5段(如图),表面积比原来增加了96平方厘米.这根木料原来的体积是_____立方厘米.【试题来源】【题目】用棱长是1厘米的立方体拼成右图所示的立体图形.求这个立体图形的表面积.【试题来源】【题目】把1个棱长是3厘米的正方体分割成若干个小的正方体,这些小正方体的棱长必须是整厘米数.如果这些小正方体的体积不要求都相等,那么最少可分割成个小正方体.【试题来源】【题目】用10块长7厘米,宽5厘米,高3厘米的长方体积木堆成一个长方体,这个长方体的表面积最小是多少?【试题来源】【题目】一个盛有水的圆柱形容器,底面内半径为5厘米,深20厘米,水深15厘米.今将一个底面半径为2厘米,高为17厘米的铁圆柱垂直放人容器中.求这时容器的水深是多少厘米?【试题来源】【题目】有甲、乙两只圆柱形玻璃杯,其内直径依次是10厘米、20厘米,杯中盛有适量的水.甲杯中沉没着一铁块,当取出此铁块后,甲杯中的水位下降了2厘米;然后将铁块沉没于乙杯,且乙杯中的水未外溢.问:这时乙杯中的水位上升了多少厘米?【试题来源】【题目】将高都是1米,底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体.求这个物体的表面积.【试题来源】【题目】这里有一个圆柱和一个圆锥(下图),它们的高和底面直径都标在图上,单位是厘米.请回答:圆锥体积与圆柱体积的比是多少?【试题来源】【题目】一个长、宽、高分别为21厘米、15厘米、12厘米的长方体.现从它的上面尽可能大的切下一个正方体.然后从剩余的部分再尽可能大的切下一个正方体.最后再从第二次剩余的部分尽可能大的切下一个正方体.剩下的体积是平方厘米.【试题来源】【题目】一个圆柱形玻璃杯内盛有水,水面高2.5厘米,玻璃杯内侧的底面积是72平方厘米.在这个杯中放进棱长6厘米的正方体铁块后,水面没有淹没铁块.这时水面高多少厘米?【试题来源】【题目】图1是下面的表面展开图①甲正方体;②乙正方体;③丙正方体;④甲正方体或丙正方体.【试题来源】【题目】如图,剪一块硬纸片可以做成一个多面体的纸模型(沿虚线折,沿实线粘).这个多面体的面数、顶点数和棱数的总和是多少?【试题来源】【题目】下面是一辆汽车模型纸工平面展开图,中轴线上面的一半标出了尺寸.将该图剪下折叠粘合(相同字母标记处粘合在一起)做成汽车模型的体积为V .请回答:①403<v<445②473<V<500,哪一个正确,为什么?【试题来源】【题目】现有一张长40厘米、宽20厘米的长方形铁皮,请你用它做一只深是5厘米的长方体无盖铁皮盒(焊接处及铁皮厚度不计,容积越大越好),你做出的铁皮盒容积是多少立方厘米?【试题来源】【题目】如图,在一个立方体的两对侧面的中心各打通一个长方体的洞在上下侧面的中心打通一个圆柱形的洞,已知立方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下侧面的洞口是直径为4厘米的圆,求该立方体的表面积和体积(取 =3.14).【试题来源】【题目】用大小相等的无色透明玻璃小正方体和红色玻璃小正方体拼成一个大正方体ABCD —1A 1B 1C 1D (如图),大正方体内的对角线A 1C ,B 1D ,C 1A ,D 1B 所穿的小正方体都是红色玻璃小正方体,其它部分都是无色透明玻璃小正方体,小红正方体共用了401个,问:无色透明小正方体用了多少个?习题演练【试题来源】【题目】一个长方体的各条棱长的和是48厘米,并且它的长是宽的2倍,高与宽相等,那么这个长方体的体积是______ 立方厘米【试题来源】【题目】右图是一个表面被涂上红色的棱长为lO厘米的正方体木块,如果把它沿虚线切成8个正方体,这些小正方体中没有被涂上红色的所有表面的面积和是_____平方厘米【试题来源】【题目】张大爷去年用长2米、宽1米的长方形苇席围成容积最大的圆柱形粮囤.今年改用了长3米、宽2米的长方形苇席围成容积最大的圆柱形粮囤.问:今年粮囤的容积是去年粮囤容积的多少倍?【试题来源】【题目】把一个大长方体木块表面上涂满红色后,分割成若干个同样大小的小长方体,其中只有两个面涂上红色的小长方体恰好是12块.那么至少要把这个大长方体分割成个小长方体.【试题来源】【题目】六个立方体A、B、C、D、E、F的可见部分如下图,下边是其中一个立体的侧面展开图,那么它是立方体____的侧面展开图.2。
经典小学奥数题型(几何图形)

小学奥数平面几何五种模型(等积,鸟头,蝶形,相似,共边)目标:熟练掌握五大面积模型等积,鸟头,蝶形,相似(含金字塔模型和沙漏模型),共边(含燕尾模型和风筝模型), 掌握五大面积模型的各种变形 知识点拨一、等积模型①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比;如右图12::S S a b =③夹在一组平行线之间的等积变形,如右图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比. 二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCBA图⑴ 图⑵三、蝶形定理任意四边形中的比例关系(“蝶形定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++b a S 2S 1DC BA S 4S 3S 2S 1O DCBA蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.梯形中比例关系(“梯形蝶形定理”): ①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AF ABACBCAG===;②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下: ⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形. 五、共边定理(燕尾模型和风筝模型)在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=.上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径. 典型例题【例 1】如图,正方形ABCD 的边长为6,AE =1.5,CF =2.长方形EFGH 的面积A BCD O ba S 3S 2S 1S 4O FED C BA为 .【解析】 连接DE ,DF ,则长方形EFGH 的面积是三角形DEF 面积的二倍.三角形DEF 的面积等于正方形的面积减去三个三角形的面积,66 1.562262 4.54216.5DEF S =⨯-⨯÷-⨯÷-⨯÷=△,所以长方形EFGH 面积为33.【巩固】如图所示,正方形ABCD 的边长为8厘米,长方形EBGF 的长BG 为10厘米,那么长方形的宽为几厘米?【解析】 本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形).三角形面积等于与它等底等高的平行四边形面积的一半. 证明:连接AG .(我们通过ABG △把这两个长方形和正方形联系在一起).∵在正方形ABCD 中,G 12AB S AB AB =⨯⨯△边上的高, ∴12ABG ABCDS S=△(三角形面积等于与它等底等高的平行四边形面积的一半)同理,12ABG EFGB S S =△.∴正方形ABCD 与长方形EFGB 面积相等. 长方形的宽8810 6.4=⨯÷=(厘米).【例 2】长方形ABCD 的面积为362cm ,E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影部分面积是多少?E_H_G_ F_E_D_C_B_ A _A_B_C_D_E_ F_G_H_ A _ B_ G_ C _ E _ F_ D_ A _ B_ G_ C_ E_ F_ D【解析】 解法一:寻找可利用的条件,连接BH 、HC ,如下图:E可得:12EHB AHB S S ∆∆=、12FHB CHB S S ∆∆=、12DHG DHCS S ∆∆=,而36ABCD AHB CHB CHD S S S S ∆∆∆=++=即11()361822EHB BHF DHG AHB CHB CHDS S S S S S ∆∆∆∆∆∆++=++=⨯=; 而EHB BHF DHG EBFS S S S S ∆∆∆∆++=+阴影,11111()()36 4.522228EBF S BE BF AB BC ∆=⨯⨯=⨯⨯⨯⨯=⨯=.所以阴影部分的面积是:1818 4.513.5EBF S S ∆=-=-=阴影解法二:特殊点法.找H 的特殊点,把H 点与D 点重合,那么图形就可变成右图:GE (H )这样阴影部分的面积就是DEF ∆的面积,根据鸟头定理,则有:11111113636363613.52222222ABCD AED BEF CFD S S S S S ∆∆∆=---=-⨯⨯-⨯⨯⨯-⨯⨯=阴影.【巩固】在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与P 点连接,求阴影部分面积.【解析】 (法1)特殊点法.由于P 是正方形内部任意一点,可采用特殊点法,假设P 点与A 点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的14和16,所以阴影部分的面积为2116()1546⨯+=平方厘米.(法2)连接PA 、PC .由于PAD ∆与PBC ∆的面积之和等于正方形ABCD 面积的一半,所以上、下两个阴影三角形的面积之和等于正方形ABCD 面积的14,同理可知左、右两个阴影三角形的面积之和等于正方形ABCD 面积的16,所以阴影部分的面积为2116()1546⨯+=平方厘米.【例 3】如图所示,长方形ABCD 内的阴影部分的面积之和为70,8AB =,15AD =,四边形EFGO 的面积为 .B【解析】 利用图形中的包含关系可以先求出三角形AOE 、DOG 和四边形EFGO 的面积之和,以及三角形AOE 和DOG 的面积之和,进而求出四边形EFGO 的面积.由于长方形ABCD 的面积为158120⨯=,所以三角形BOC 的面积为1120304⨯=,所以三角形AOE 和DOG 的面积之和为312070204⨯-=;又三角形AOE 、DOG 和四边形EFGO 的面积之和为111203024⎛⎫⨯-= ⎪⎝⎭,所以四边形EFGO 的面积为302010-=. 另解:从整体上来看,四边形EFGO 的面积=三角形AFC 面积+三角形BFD 面积-白色部分的面积,而三角形AFC 面积+三角形BFD 面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部分的面积,即1207050-=,所以四边形的面积为605010-=.【巩固】如图,长方形ABCD 的面积是36,E 是AD 的三等分点,2AE ED =,则阴影部分的面积为 .ABB【解析】 如图,连接OE .根据蝶形定理,1:::1:12COE CDE CAE CDE ON ND S S S S ∆∆∆∆===,所以12OEN OED S S ∆∆=;1:::1:42BOE BAE BDE BAE OM MA S S S S ∆∆∆∆===,所以15OEM OEA S S ∆∆=.又11334OEDABCD S S ∆=⨯=矩形,26OEA OED S S ∆∆==,所以阴影部分面积为:1136 2.725⨯+⨯=.【例 4】已知ABC 为等边三角形,面积为400,D 、E 、F 分别为三边的中点,已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形HBC)B【解析】 因为D 、E 、F 分别为三边的中点,所以DE 、DF 、EF 是三角形ABC 的中位线,也就与对应的边平行,根据面积比例模型,三角形ABN 和三角形AMC 的面积都等于三角形ABC 的一半,即为200.根据图形的容斥关系,有ABC ABN AMC AMHN S S S S S ∆∆∆-=+-丙,即400 200200AMHN S S -=+-丙,所以AMHN S S =丙. 又ADF AMHN S S S S S ∆+=++乙甲阴影,所以1143400434ADF S S S S S ∆=++-=-⨯=乙甲丙阴影.【例 5】如图,已知5CD =,7DE =,15EF =,6FG =,线段AB 将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG 的面积是 .GFE DC BAABC DE FG【解析】 连接AF ,BD .根据题意可知,571527CF =++=;715628DG =++=;所以,1527BE CBF F S S ∆∆=,1227BE CBF C S S ∆∆=,2128AEG ADG S S ∆∆=,728AED ADG S S ∆∆=, 于是:2115652827ADG CBFS S ∆∆+=;712382827ADG CBF S S ∆∆+=; 可得40ADG S ∆=.故三角形ADG 的面积是40.【例 6】如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE的面积等于1,那么三角形ABC 的面积是多少?EDCBAABCD E【解析】 连接BE .∵3EC AE =∴3ABC ABE S S = 又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷,∴1515ABC ADE S S ==.【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E DCBAABCDE甲乙【解析】 连接AD .∵3BE =,6AE =∴3AB BE =,3ABD BDE S S = 又∵4BD DC ==,∴2ABC ABD S S =,∴6ABC BDE S S =,5S S =乙甲.【例 7】如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =, :3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBAEDCB A【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△, 所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例 8】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGAB CD EF【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABCFBES AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△. 所以213618ABCDEFGHS S ==.【例 9】如图所示的四边形的面积等于多少?DCB13131212【解析】 题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积.我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点O 逆时针旋转,使长为13的两条边重合,此时三角形OAB 将旋转到三角形OCD 的位置.这样,通过旋转后所得到的新图形是一个边长为12的正方形,且这个正方形的面积就是原来四边形的面积. 因此,原来四边形的面积为1212144⨯=.(也可以用勾股定理)【例 10】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC ∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【解析】 如图,将OAB ∆沿着O 点顺时针旋转90︒,到达OCF ∆的位置.由于90ABC ∠=︒,90AOC ∠=︒,所以180OAB OCB ∠+∠=︒.而OCF OAB ∠=∠, 所以180OCF OCB ∠+∠=︒,那么B 、C 、F 三点在一条直线上.由于OB OF =,90BOF AOC ∠=∠=︒,所以BOF ∆是等腰直角三角形,且斜边BF为538+=,所以它的面积为218164⨯=.根据面积比例模型,OBC ∆的面积为516108⨯=.【例 11】 如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.【解析】 如图,连接DE ,以A 点为中心,将ADE ∆顺时针旋转90︒到ABF ∆的位置.那么90EAF EAB BAF EAB DAE ∠=∠+∠=∠+∠=︒,而AEB ∠也是90︒,所以四边形AFBE 是直角梯形,且3AF AE ==, 所以梯形AFBE 的面积为:()1353122+⨯⨯=(2cm ). 又因为ABE ∆是直角三角形,根据勾股定理,222223534AB AE BE =+=+=,所以21172ABD S AB ∆==(2cm ). 那么()17125BDE ABD ABE ADE ABD AFBE S S S S S S ∆∆∆∆∆=-+=-=-=(2cm ), 所以1 2.52OBE BDE S S ∆∆==(2cm ).【例 12】 如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米?FEABDCGFEABDC【解析】 如图,我们将BCD ∆平移使得CD 与AF 重合,将DEF ∆平移使得ED 与AB 重合,这样EF 、BC 都重合到图中的AG 了.这样就组成了一个长方形BGFD ,它的面积与原六边形的面积相等,显然长方形BGFD 的面积为2418432⨯=平方厘米,所以六边形ABCDEF 的面积为432平方厘米.【例 13】 如图,三角形ABC 的面积是1,E 是AC 的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于 .FED CBA33321F E DC BAABCDEF【解析】 方法一:连接CF ,根据燕尾定理,12ABF ACF S BD S DC ==△△,1ABF CBF S AE S EC ==△△, 设1BDF S =△份,则2DCF S =△份,3ABF S =△份,3AEF EFC S S ==△△份,如图所标所以551212DCEF ABC S S ==△ 方法二:连接DE ,由题目条件可得到1133ABD ABCS S ==△△, 11212233ADE ADC ABC S S S ==⨯=△△△,所以11ABD ADES BF FE S ==△△, 111111122323212DEFDEB BEC ABC S S S S =⨯=⨯⨯=⨯⨯⨯=△△△△, 而211323CDE ABCS S =⨯⨯=△△.所以则四边形DFEC 的面积等于512. 【巩固】如图,长方形ABCD 的面积是2平方厘米,2EC DE =,F 是DG 的中点.阴影部分的面积是多少平方厘米?y B CD EGE D CBAEDB A 【解析】 设1DEFS =△份,则根据燕尾定理其他面积如图所示551212BCD S S ==△阴影平方厘米.【例 14】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍.ABCDOH GA BCD O【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形.看到题目中给出条件:1:3ABD BCD S S =,这可以向模型一蝶形定理靠拢,于是得出一种解法.又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得到第二种解法,但是第二种解法需要一个中介来改造这个”不良四边形”,于是可以作AH 垂直BD 于H ,CG 垂直BD 于G ,面积比转化为高之比.再应用结论:三角形高相同,则面积之比等于底边之比,得出结果.请老师注意比较两种解法,使学生体会到蝶形定理的优势,从而主观上愿意掌握并使用蝶形定理解决问题.解法一:∵::1:3ABD BDC AO OC S S ∆∆==,∴236OC =⨯=,∴:6:32:1OC OD ==. 解法二:作AH BD ⊥于H ,CG BD ⊥于G . ∵13ABDBCD S S ∆∆=,∴13AH CG =,∴13AOD DOC S S ∆∆=, ∴13AO CO =,∴236OC =⨯=,∴:6:32:1OC OD ==.【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知, 求:⑴三角形BGC 的面积;⑵:AG GC =?B【解析】 ⑴根据蝶形定理,123BGCS⨯=⨯,那么6BGCS=;⑵根据蝶形定理,()():12:361:3AG GC =++=.【例 15】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE△的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGF EDCBA【解析】 ⑴根据题意可知,BCD △的面积为244616+++=,那么BCO △和CDO ∆的面积都是1628÷=,所以OCF △的面积为844-=; ⑵由于BCO △的面积为8,BOE △的面积为6,所以OCE △的面积为862-=, 根据蝶形定理,::2:41:2COE COF EG FG S S ∆∆===,所以::1:2GCE GCF S S EG FG ∆∆==,那么11221233GCE CEF S S ∆∆==⨯=+.【例 16】 如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.ABCDEF GABCD EF G【解析】 连接AE ,FE .因为:2:3BE EC =,:1:2DF FC =,所以3111()53210DEFABCD ABCD S S S =⨯⨯=长方形长方形. 因为12AED ABCD SS =长方形,11::5:1210AG GF ==,所以510AGD GDF S S ==平方厘米,所以12AFD S =平方厘米.因为16AFDABCD S S =长方形,所以长方形ABCD 的面积是72平方厘米.【例 17】 如图,正方形ABCD 面积为3平方厘米,M 是AD 边上的中点.求图中阴影部分的面积.CBA【解析】 因为M 是AD 边上的中点,所以:1:2AM BC =,根据梯形蝶形定理可以知道22:::1:12:12:21:2:2:4AMG ABG MCG BCG S S S S =⨯⨯=△△△△()(),设1AGM S =△份,则123MCD S =+=△ 份,所以正方形的面积为1224312++++=份,224S =+=阴影份,所以:1:3S S =阴影正方形,所以1S =阴影平方厘米.【巩固】在下图的正方形ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF 的面积为1平方厘米,那么正方形ABCD 面积是 平方厘米.A BCDEF【解析】 连接DE ,根据题意可知:1:2BE AD =,根据蝶形定理得2129S =+=梯形()(平方厘米),3ECD S =△(平方厘米),那么12ABCDS=(平方厘米).【例 18】 已知ABCD 是平行四边形,:3:2BC CE =,三角形ODE 的面积为6平方厘米.则阴影部分的面积是 平方厘米.BB【解析】 连接AC .由于ABCD 是平行四边形,:3:2BC CE =,所以:2:3CE AD =,根据梯形蝶形定理,22:::2:23:23:34:6:6:9COE AOC DOE AOD S S S S =⨯⨯=,所以6AOC S =(平方厘米),9AOD S =(平方厘米),又6915ABC ACD S S ==+=(平方厘米),阴影部分面积为61521+=(平方厘米).【巩固】右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.BB【分析】 连接AE .由于AD 与BC 是平行的,所以AECD 也是梯形,那么OCD OAE S S ∆∆=.根据蝶形定理,4936OCD OAE OCE OAD S S S S ∆∆∆∆⨯=⨯=⨯=,故236OCD S ∆=, 所以6OCD S ∆=(平方厘米).【巩固】右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.BB【解析】 连接AE .由于AD 与BC 是平行的,所以AECD 也是梯形,那么OCD OAE S S ∆∆=.根据蝶形定理,2816OCD OAE OCE OAD S S S S ∆∆∆∆⨯=⨯=⨯=,故216OCD S ∆=,所以4OCD S ∆=(平方厘米).另解:在平行四边形ABED 中,()111681222ADE ABEDS S∆==⨯+=(平方厘米), 所以1284AOE ADE AOD S S S ∆∆∆=-=-=(平方厘米),根据蝶形定理,阴影部分的面积为8244⨯÷=(平方厘米).【例 19】 如图,长方形ABCD 被CE 、DF 分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为___________平方厘米.?852O A BCDEF?852O A BC DEF【解析】 连接DE 、CF .四边形EDCF 为梯形,所以EOD FOC S S ∆=,又根据蝶形定理,EOD FOC EOF COD S S S S ∆∆∆∆⋅=⋅,所以2816EOD FOC EOF COD S S S S ∆∆∆∆⋅=⋅=⨯=,所以4EOD S ∆=(平方厘米),4812ECD S ∆=+=(平方厘米).那么长方形ABCD 的面积为12224⨯=平方厘米,四边形OFBC 的面积为245289---=(平方厘米).【例 20】 如图,ABC ∆是等腰直角三角形,DEFG 是正方形,线段AB 与CD 相交于K点.已知正方形DEFG 的面积48,:1:3AK KB =,则BKD ∆的面积是多少?BB【解析】 由于DEFG 是正方形,所以DA 与BC 平行,那么四边形ADBC 是梯形.在梯形ADBC 中,BDK ∆和ACK ∆的面积是相等的.而:1:3AK KB =,所以ACK ∆的面积是ABC ∆面积的11134=+,那么BDK ∆的面积也是ABC ∆面积的14.由于ABC ∆是等腰直角三角形,如果过A 作BC 的垂线,M 为垂足,那么M 是BC 的中点,而且AM DE =,可见ABM ∆和ACM ∆的面积都等于正方形DEFG 面积的一半,所以ABC ∆的面积与正方形DEFG 的面积相等,为48. 那么BDK ∆的面积为148124⨯=.【例 21】 下图中,四边形ABCD 都是边长为1的正方形,E 、F 、G 、H 分别是AB ,BC ,CD ,DA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数m n,那么,()m n +的值等于 .E【解析】 左、右两个图中的阴影部分都是不规则图形,不方便直接求面积,观察发现两个图中的空白部分面积都比较好求,所以可以先求出空白部分的面积,再求阴影部分的面积.如下图所示,在左图中连接EG .设AG 与DE 的交点为M .左图中AEGD 为长方形,可知AMD ∆的面积为长方形AEGD 面积的14,所以三角形AMD 的面积为21111248⨯⨯=.又左图中四个空白三角形的面积是相等的,所以左图中阴影部分的面积为111482-⨯=.BEE如上图所示,在右图中连接AC 、EF .设AF 、EC 的交点为N . 可知EF ∥AC 且2AC EF =.那么三角形BEF 的面积为三角形ABC 面积的14,所以三角形BEF 的面积为21111248⨯⨯=,梯形AEFC 的面积为113288-=.在梯形AEFC 中,由于:1:2EF AC =,根据梯形蝶形定理,其四部分的面积比为:221:12:12:21:2:2:4⨯⨯=,所以三角形EFN 的面积为3118122424⨯=+++,那么四边形BENF 的面积为1118246+=.而右图中四个空白四边形的面积是相等的,所以右图中阴影部分的面积为111463-⨯=.那么左图中阴影部分面积与右图中阴影部分面积之比为11:3:223=,即32m n =, 那么325m n +=+=.【例 22】 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==,则::ADE DEGF FGCB S S S =△四边形四边形 .EGF A D CB【解析】 设1ADE S =△份,根据面积比等于相似比的平方,所以22::1:4ADE AFG S S AD AF ==△△,22::1:9ADE ABC S S AD AB ==△△, 因此4AFG S =△份,9ABC S =△份,进而有3DEGF S =四边形份,5FGCB S =四边形份,所以::1:3:5ADE DEGF FGCB S S S =△四边形四边形【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.A ED CB【解析】 由金字塔模型得:::2:5AD AB AE AC DE BC ===,所以42510AC =÷⨯=【巩固】如图, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD DF FM MP PB ====,则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形 . 【解析】 设1ADE S =△份,22::1:4ADE AFG S S AD AF ==△△,因此Q E GNMF P AD CB4AFG S =△份,进而有3DEGF S =四边形份,同理有5FGNM S =四边形份,7MNQP S =四边形份,9PQCB S =四边形份.所以有::::1:3:5:7:9ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形【例 23】 如图,已知正方形ABCD 的边长为4,F 是BC 边的中点,E 是DC 边上的点,且:1:3DE EC =,AF 与BE 相交于点G ,求ABG S △GFAEDBM GFAEDCBGFAEDCB【解析】 方法一:连接AE ,延长AF ,DC 两条线交于点M ,构造出两个沙漏,所以有::1:1AB CM BF FC ==,因此4CM =,根据题意有3CE =,再根据另一个沙漏有::4:7GB GE AB EM ==,所以4432(442)471111ABG ABE S S ==⨯⨯÷=+△△. 方法二:连接,AE EF,分别求4224ABF S =⨯÷=△,4441232247AEFS =⨯-⨯÷-⨯÷-=△,根据蝶形定理::4:7ABF AEF S S BG GE ==△△,所以4432(442)471111ABG ABE S S ==⨯⨯÷=+△△.【例 24】 如图所示,已知平行四边形ABCD 的面积是1,E 、F 是AB 、AD 的中点,BF 交EC 于M ,求BMG ∆的面积.MHGF E D CBAA【解析】 解法一:由题意可得,E 、F是AB、AD的中点,得//EF BD,而::1:2FD BC FH HC ==,::1:2EB CD BG GD ==所以::2:3CH CF GH EF ==,并得G 、H 是BD 的三等分点,所以BG GH =,所以::2:3BG EF BM MF ==,所以25BM BF =,11112224BFDABD ABCDS S S ∆∆==⨯=;又因为13BG BD =,所以1212113535430BMG BFD S S ∆∆=⨯⨯=⨯⨯=. 解法二:延长CE 交DA 于I ,如右图,可得,::1:1AI BC AE EB ==,从而可以确定M 的点的位置, ::2:3BM MF BC IF ==,25BM BF =,13BG BD =(鸟头定理),可得2121115353430BMG BDF ABCDS S S ∆∆=⨯=⨯⨯=【例 25】 如图,ABCD 为正方形,1cm AM NB DE FC ====且2cm MN =,请问四边形PQRS 的面积为多少?CACA 【解析】 (法1)由//AB CD ,有MP PC MNDC=,所以2PC PM =,又MQ MB QC EC =,所以12MQ QC MC ==,所以111236PQ MC MC MC =-=,所以SPQR S 占AMCF S 的16,所以121(112)63SPQR S =⨯⨯++=2(cm ).(法2)如图,连结AE ,则14482ABE S ∆=⨯⨯=(2cm ),而RB ER AB EF =,所以2RB AB EF EF ==,22168333ABR ABE S S ∆∆==⨯=(2cm ). 而1134322MBQ ANS S S ∆∆==⨯⨯⨯=(2cm ),因为MN MP DC PC=,所以13MP MC =,则11424233MNP S ∆=⨯⨯⨯=(2cm ),阴影部分面积等于164233333ABR ANS MBQ MNP S S S S ∆∆∆∆--+=--+=(2cm ).【例 26】 如右图,三角形ABC 中,:4:9BD DC =,:4:3CE EA =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::4:912:27AOB AOC S S BD CD ===△△::3:412:16AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:27:16:AOC BOC S S AF FB ==△△【点评】本题关键是把AOB △的面积统一,这种找最小公倍数的方法,在我们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达到解奥数题四两拨千斤的巨大力量!【巩固】如右图,三角形ABC 中,:3:4BD DC =,:5:6AE CE =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::3:415:20AOB AOC S S BD CD ===△△::5:615:18AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:20:1810:9:AOC BOC S S AF FB ===△△【巩固】如右图,三角形ABC 中,:2:3BD DC =,:5:4EA CE =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::2:310:15AOB AOC S S BD CD ===△△::5:410:8AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:15:8:AOC BOC S S AF FB ==△△【点评】本题关键是把AOB △的面积统一,这种找最小公倍数的方法,在我们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达到解奥数题四两拨千斤的巨大力量!【例 27】 如右图,三角形ABC 中,:::3:2AF FB BD DC CE AE ===,且三角形ABC 的面积是1,则三角形ABE 的面积为______,三角形AGE 的面积为________,三角形GHI 的面积为______.I HGFEDCBAI H G FEDCBA【分析】 连接AH 、BI 、CG .由于:3:2CE AE =,所以25AE AC =,故2255ABE ABC S S ∆∆==;根据燕尾定理,::2:3ACG ABG S S CD BD ∆∆==,::3:2BCG ABG S S CE EA ∆∆==,所以::4:6:9ACG ABG BCG S S S ∆∆∆=,则419ACG S ∆=,919BCG S ∆=; 那么2248551995AGE AGC S S ∆∆==⨯=; 同样分析可得919ACH S ∆=,则::4:9ACG ACH EG EH S S ∆∆==,::4:19ACG ACB EG EB S S ∆∆==,所以::4:5:10EG GH HB =,同样分析可得::10:5:4AG GI ID =, 所以5521101055BIE BAE S S ∆∆==⨯=,55111919519GHI BIE S S ∆∆==⨯=.【巩固】 如右图,三角形ABC 中,:::3:2AF FB BD DC CE AE ===,且三角形GHI 的面积是1,求三角形ABC 的面积.IH G FEDCBAIH G FEDCBA【解析】 连接BG ,AGC S △=6份根据燕尾定理,::3:26:4AGC BGC S S AF FB ===△△,::3:29:6ABG AGC S S BD DC ===△△ 得4BGC S =△(份),9ABG S =△(份),则19ABC S =△(份),因此619AGCABCS S =△△, 同理连接AI 、CH 得619ABHABCS S =△△,619BIC ABC S S =△△,所以1966611919GHI ABC S S ---==△△三角形GHI 的面积是1,所以三角形ABC 的面积是19【巩固】如图,ABC ∆中2BD DA =,2CE EB =,2AF FC =,那么ABC ∆的面积是阴影三角形面积的 倍.BCB【分析】 如图,连接AI .根据燕尾定理,::2:1BCI ACIS S BD AD ∆∆==,::1:2BCI ABI S S CF AF ∆∆==,所以,::1:2:4ACI BCI ABI S S S ∆∆∆=,那么,221247BCI ABC ABC S S S ∆∆∆==++.同理可知ACG ∆和ABH ∆的面积也都等于ABC ∆面积的27,所以阴影三角形的面积等于ABC ∆面积的211377-⨯=,所以ABC ∆的面积是阴影三角形面积的7倍.【巩固】如图在ABC △中,12DC EA FB DBECFA===,求GHI ABC △的面积△的面积的值.IHG FEDCBAIHG FEDCB A【解析】 连接BG ,设BGC S △=1份,根据燕尾定理::2:1AGC BGC S S AF FB ==△△,::2:1ABG AGC S S BD DC ==△△,得2AGC S =△(份),4ABG S =△(份),则7ABC S =△(份),因此27AGC ABC S S =△△,同理连接AI 、CH 得27ABH ABC S S =△△,27BIC ABC S S =△△,所以7222177GHI ABC S S ---==△△ 【点评】如果任意一个三角形各边被分成的比是相同的,那么在同样的位置上的图形,虽然形状千变万化,但面积是相等的,这在这讲里面很多题目都是用“同理得到”的,即再重复一次解题思路,因此我们有对称法作辅助线.【例 28】 如图,三角形ABC 的面积是1,BD DE EC ==,CF FG GA ==,三角形ABC 被分成9部分,请写出这9部分的面积各是多少?GFE D CBAN MQPGF EDCBA【解析】 设BG 与AD 交于点P ,BG 与AE 交于点Q ,BF 与AD 交于点M ,BF 与AE 交于点N .连接CP ,CQ ,CM ,CN .根据燕尾定理,::1:2ABP CBP S S AG GC ==△△,::1:2ABP ACP S S BD CD ==△△,设1ABP S =△(份),则1225ABC S =++=△(份),所以15ABP S =△ 同理可得,27ABQ S =△,12ABN S =△,而13ABG S =△,所以2137535APQ S =-=△,1213721AQG S =-=△.同理,335BPMS =△121BDM S =△,所以1239273570PQMN S =--=四边形,13953357042MNEDS =--=四边形,1151321426NFCE S =--=四边形,1115321642GFNQ S =--=四边形【巩固】如图,ABC ∆的面积为1,点D 、E 是BC 边的三等分点,点F 、G 是AC 边的三等分点,那么四边形JKIH 的面积是多少?K J IHABC D EF GKJI HABCD EFG【解析】 连接CK 、CI 、CJ.根据燕尾定理,::1:2ACK ABK S S CD BD ∆∆==,::1:2ABK CBK S S AG CG ∆∆==, 所以::1:2:4ACK ABK CBK S S S ∆∆∆=,那么111247ACK S ∆==++,11321AGK ACK S S ∆∆==. 类似分析可得215AGI S ∆=. 又::2:1ABJ CBJ S S AF CF ∆∆==,::2:1ABJ ACJ S S BD CD ∆∆==,可得14ACJ S ∆=. 那么,111742184CGKJS =-=. 根据对称性,可知四边形CEHJ 的面积也为1784,那么四边形JKIH 周围的图形的面积之和为172161228415370CGKJ AGI ABES S S ∆∆⨯++=⨯++=,所以四边形JKIH 的面积为61917070-=.【例 29】 右图,ABC △中,G 是AC 的中点,D 、E 、F是BC 边上的四等分点,AD 与BG 交于M ,AF 与BG 交于N ,已知ABM △的面积比四边形FCGN 的面积大7.2平方厘米,则ABC △的面积是多少平方厘米?N M GA BCD EFNMGA BC D EF【解析】 连接CM 、CN .根据燕尾定理,::1:1ABM CBMS S AG GC ==△△,::1:3ABM ACM S S BD CD ==△△,所以15ABM ABC S S =△△;再根据燕尾定理,::1:1ABN CBN S S AG GC ==△△,所以::4:3ABN FBN CBN FBN S S S S ==△△△△,所以:4:3AN NF =,那么1422437ANGAFCS S =⨯=+△△,所以2515177428FCGN AFC ABC ABC S S S S ⎛⎫=-=⨯= ⎪⎝⎭△△△.根据题意,有157.2528ABC ABC S S -=△△,可得336ABC S =△(平方厘米)【例 30】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA的三等分点,求阴影部分面积.GC BACB【解析】 三角形在开会,那么就好好利用三角形中最好用的比例和燕尾定理吧!令BI 与CD 的交点为M ,AF 与CD 的交点为N ,BI 与AF 的交点为P ,BI 与CE 的交点为Q ,连接AM 、BN 、CP⑴求ADMI S 四边形:在ABC △中,根据燕尾定理,::1:2ABM CBM S S AI CI ==△△::1:2ACM CBM S S AD BD ==△△设1ABM S =△(份),则2CBM S =△(份),1ACM S =△(份),4ABC S =△(份),所以14ABMACM ABC S S S ==△△△,所以11312ADM ABM ABC S S S ==△△△,112AIM ABC S S =△△,所以111()12126ABC ABC ADMI S S S =+=△△四边形,同理可得另外两个顶点的四边形面积也分别是ABC △面积的16⑵求DNPQE S 五边形:在ABC △中,根据燕尾定理::1:2ABN ACN S S BF CF ==△△::1:2ACN BCN S S AD BD ==△△,所以111133721ADN ABN ABC ABC S S S S ==⨯=△△△△,同理121BEQ ABC S S =△△在ABC △中,根据燕尾定理::1:2ABP ACP S S BF CF ==△△,::1:2ABP CBP S S AI CI ==△△ 所以15ABP ABCS S =△△,所以1111152121105ABP ADN BEPABC ABC DNPQE S S S S S S ⎛⎫=--=--= ⎪⎝⎭△△△△△五边形 同理另外两个五边形面积是ABC△面积的11105,所以11113133610570S =-⨯-⨯=阴影【例 31】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA的三等分点,求中心六边形面积.GCBAGCBA【解析】 设深黑色六个三角形的顶点分别为N 、R 、P 、S 、M 、Q ,连接CR在ABC △中根据燕尾定理,::.2:1ABR ACR S S BG CG ==△△, ::1:2ABR CBR S S AI CI ==△△所以27ABR ABC S S =△△,同理27ACS ABC S S =△△,27CQB ABC S S =△△所以222117777RQS S =---=△,同理17MNP S =△根据容斥原理,和上题结果11131777010S =+-=六边形课后练习: 练习1. 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA【解析】 :():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEFS =△份,244497DEF S =---=△份,恰好是7平方厘米,所以24ABC S =△平方厘米练习2. 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB AAB CDEFGH【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米练习3. 正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是 平方厘米.H GFEDCBAM H GFEDCBA【解析】 欲求四边形BGHF 的面积须求出EBG ∆和CHF ∆的面积.由题意可得到:::1:2EG GC EB CD ==,所以可得:13EBG BCE S S ∆∆=将AB 、DF 延长交于M 点,可得::::1:1BM DC MF FD BF FC ===,而1::():3:22EH HC EM CD AB AB CD ==+=,得25CH CE =,而12CF BC =,所以121255CHF BCE BCE S S S ∆∆∆=⨯=11112030224BCES AB BC ∆=⨯⨯=⨯=117730141515EBC EBC EBC EBC BGHF S S S S S ∆∆∆∆=--==⨯=四边形. EF ,确定H 的位置(也就是:FH HD ),练习4. 如图,已知4cmAB AE ==,BC DC=,90BAE BCD ∠=∠=︒,10cmAC =,则S ABC ACE CDE S S ∆∆∆++= 2cm .DCEBABCA'C'EDA【解析】 将三角形ABC 绕A 点和C 点分别顺时针和逆时针旋转90,构成三角形'AEC 和'A DC ,再连接''A C ,显然'AC AC ⊥,'AC A C ⊥,''AC A C AC ==,所以''ACA C 是正方形.三角形'AEC 和三角形'A DC 关于正方形的中心O 中心对称,在中心对称图形''ACA C 中有如下等量关系: ''AEC A DC S S ∆∆=;''AEC A DC S S ∆∆=;'CED C DE S S ∆∆=.所以2'''11101050cm 22ABC ACE CDE AEC ACE CDE ACA C S S S S SS S ∆∆∆∆∆∆++=++==⨯⨯=.练习5. 如图,正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是_____平方厘米.EDED【解析】 连接BH ,根据沙漏模型得:1:2BG GD =,设1BHC S =△份,根据燕尾定理2CHD S =△份,2BHD S =△份,因此122)210S =++⨯=正方形(份,127236BFHG S =+=,所以712010146BFHG S =÷⨯=(平方厘米).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9.如图,梯形ABCD的上底AD长为3厘米,下底BC长为9厘米.三角形ABO的面积为12平方厘米,则梯形ABCD的面积为多少?
六年级奥数几何图形汇总
———————————————————————————————— 作者:
———————————————————————————————— 日期:
ﻩ
几何部分题型大汇总
1.
2.
3.如下图,两个相同的直角三角形重叠在一起,求阴影部分的面积是多少?
4.四个相同的长方形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x、y表示长方形的长和宽,则小长方形的长为______,宽为______。
27.如图,在长为10米,宽为8米的长方形空地中,沿平行于长方形各边方向分割出三个能完全重合的小长方形作为生物兴趣小组的实验基地.求每个小长方形的面积?
28.如图所示,并排放着两个正方形,大正方形的边长为5,小正方形的边长为3,求三角形BEF的面积是多少?
29.己知正方形甲边长为5cm,正方形乙的边长为4cm,那么图中阴影部分面积是多少?
18. + +Байду номын сангаас+ -------+ +
19.规定 , ,求 等于多少?
20.定义 ,已知 ,求 是几?
21.规定 ,且 ,求
解方程。
(1) 51-4.5=(51-10X)×3(2) 3X-2×(10-X)=15
(3) (1-X)÷3=2-X(4) X÷25+X÷5=X-19
(5)如果1*2=1+2,2*3=2+3+4,4*3=4+5+6,那么6*5=()。
10.已知如图大正方形的边长是5厘米,小正方形的边长是3厘米,求阴影部分的面积?
11.如图,三角形ABC的面积为1,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为多少?
12.如图,一块长方形的布料ABCD,被剪成大小相等的甲、乙、丙、丁四块,其中甲块布料的长与宽的比为a:b=3:2,那么丁块布料的长与宽的比是______.
13.如图一块长方形铁皮,利用图中的阴影部分刚好能做成一个圆柱形油桶(接头处忽略不计).求油桶的容积?
14.直角三角形ABC的三条边分别是5cm, 3cm和4cm,将它的直角边AC对折到斜边AB上,使AC与AD重合,如下图,则图中阴影部分(未重叠部分)的面积是多少平方厘米?
15.如图,已知直角三角形的面积是12平方厘米,求阴影部分面积.
16.半径20厘米圆的外面和里面各有一个正方形,外面正方形的面积是多少,里面正方形的面积是多少?
第16题 第18题
18.
19.如下图,三角形ABC是等腰直角三角形,一直角边长为4厘米,求阴影部分的面积?
20.已知下图平行四边形的面积是36平方厘米,求图中阴影部分面积.要求写出计算过。
21.已知,正方形的边长为8厘米,求图中阴影部分的周长和面积?
25.如图是一回形图,其回形通道的宽和OB的长均为,回形线与射线OA交于点A1,A2,A3.若从O点到A1点的回形线为第圈(长为),从A1点到A2点的回形线为第圈,依此类推.则第圈的长为_______.
26.如右图,abc中ae=2eb,d为bc的中点,三角形acd的面积是6平方厘米,求阴影部分面积
计算题题型大汇总
1、 2、
3、 4、
5. 6.
7. 8. 9.
10、若 ,求 的值。11、若 ,且 ,
求
12.10÷10 +24 ÷1213. × +5.2× +1÷
14.974×74+974+974×2515.6.8×6.8+4 ×6.8-6.8
16.99999×77778+33333×6666617. × +11.2× +9÷
22.如图是边长为8厘米的正方形,求阴影部分的周长与面积?
23.图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米那么阴影部分的总面积是多少平方厘米?ﻫ
24.如下图所示.在一个等腰直角三角形中.去掉一个小三角形,使余下部分为一个等腰梯形(阴影部分),这个等腰梯形的面积是______平方厘米.ﻫ
第4题图 第5题
5.三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABCD的长和宽分别为6、4厘米,DF长多少厘米?
6.如图中三角形ABC被分成了甲(阴影部分)、乙两部分,BD=DC=4,BE=2,EA=4,那么甲部分的面积是乙部分面积的几倍?
7.如图,正方形ABCD的面积为3平方厘米,M是AD边上的中点,求阴影部分面积?
