人教版九年级数学第27章达标卷(附答案)

合集下载

人教版九年级下册数学第二十七章测试卷带答案

人教版九年级下册数学第二十七章测试题一、单选题1．已知△ABC与△A1B1C1相似，且相似比为1：3，则△ABC与△A1B1C1的面积比为（）A．1：1B．1：3C．1：6D．1：92．如图，在△ABC中，点D是边AB上的一点，∠ADC＝∠ACB，AD＝2，BD＝6，则边AC的长为（）A．2B．4C．6D．83．两个相似三角形的对应边的比是2∶3,周长之和是20,那么这两个三角形的周长分别为A．8和12B．9和11C．7和13D．8和154．已知：如图，△ABC的面积为12，点D、E分别是边AB、AC的中点，则四边形BCED 的面积为()A．9B．4C．6D．4.85．位似图形的位似中心可以在()A．原图形外B．原图形内C．原图形上D．以上三种可能都有6．已知△ABC∽△A1B1C1，且∠A＝60°，∠B＝95°，则∠C1的度数为()A．60°B．95°C．25°D．15°7．如图，在△ABC中，DE∥BC，DE分别与AB，AC相交于点D，E，若AD=4，DB=2，则DE：BC的值为（）A．23B．12C．34D．358．要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm ，6cm 和9cm ，另一个三角形的最短边长为2.5cm ，则它的最长边为（）A ．3cm B ．4cm C ．4.5cm D ．5cm9．《孙子算经》是中国古代重要的数学著作，成书于约一千五百年前，其中有首歌谣：今有竿不知其长，量得影长一丈五尺，立一标杆，长一尺五寸，影长五寸，问竿长几何？意即：有一根竹竿不知道有多长，量出它在太阳下的影子长一丈五尺，同时立一根一尺五寸的小标杆，它的影长五寸（提示：1丈=10尺，1尺=10寸），则竹竿的长为（）A ．五丈B ．四丈五尺C ．一丈D ．五尺10．如图，点A 在线段BD 上，在BD 的同侧作等腰Rt ABC ∆和等腰Rt ADE ∆，CD 与BE 、AE 分别交于点P 、M .对于下列结论：①BAE CAD ∆∆ ；②MP MD MA ME ⋅=⋅；③22CB CP CM =⋅.其中正确的是（）A ．①②③B ．①C ．①②D ．②③11．如图，在平行四边形ABCD 中，点E 在边DC 上，DE ：EC=3：1，连接AE 交BD 于点F ，则△DEF 的面积与△BAF 的面积之比为（）A ．3：4B ．9：16C ．9：1D ．3：1二、填空题12．如图，在矩形ABCD 中，E 是边AB 的中点，连接DE 交对角线AC 于点F ，若4AB =，3AD =，则CF 的长为________．13．两三角形的相似比是2：3，则其面积之比是__________．14．.若4a =56b c =，且a －b ＋c ＝10，则a ＋b －c 的值为_________.15．学校门口的栏杆如图所示，栏杆从水平位置BD 绕O 点旋转到AC 位置，已知AB ⊥BD ，CD ⊥BD ，垂足分别为B ，D ，AO=4m ，AB=1.6m ，CO=1m ，则栏杆C 端应下降的垂直距离CD 为__________.16．已知534a b c ==，则222a b c a b c ++++＝____.17．在比例尺为1：6000000的海南地图上，量得海口与三亚的距离约为3.7厘米，则海口与三亚的实际距离约为_____千米．18．如图，正方形ABCD 中，E ，F 分别在边AD ，CD 上，AF ，BE 相交于点G ，若AE=3ED ，DF=CF ，则AG:GF 的值是_______.19．已知△ABC ∽△DEF ，相似比为2，且△ABC 的面积为16，则△DEF 的面积为___.20．如图，四边形ABCD 中，AD ∥BC ，∠ABC=90°，AB=5，BC=10，连接AC 、BD ，以BD 为直径的圆交AC 于点E ．若DE=3，则AD 的长为________.21．如图，在△ABC 中，E ，F 分别为AB ，AC 的中点，则△AEF 与△ABC 的面积之比为__________．22．如图，平行于BC的直线DE把△ABC分成面积相等的两部分，则BDAD的值为_____．三、解答题23．已知矩形ABCD中，AD=3，AB=1.若EF把矩形分成两个小的矩形，如图所示，其中矩形ABEF与矩形ABCD相似.求AF∶AD的值.24．如图．利用标杆BE测量建筑物的高度．已知标杆BE高1.2m，测得AB=1.6m．BC=12.4m．则建筑物CD的高是多大？25．如图所示，在正方形ABCD中，G为CD边中点，连接AG并延长，交BC边的延长线于E点，对角线BD交AG于F点．已知FG=2，求线段AE的长度.26．已知：如图，正方形ABCD中，P是边BC上一点，BE⊥AP，DF⊥AP，垂足分别是点E、F．（1）求证：EF=AE﹣BE；（2）连接BF，如果AFBF=DFAD．求证：EF=EP．27．如图，在正方形ABCD中，E是AB上一点，连接DE．过点A作AF⊥DE，垂足为F，⊙O经过点C、D、F，与AD相交于点G．（1）求证：△AFG∽△DFC；（2）若正方形ABCD的边长为4，AE＝1，求⊙O的半径．参考答案1．D【详解】分析：利用相似三角形面积之比等于相似比的平方，求出即可．详解：已知△ABC与△A1B1C1相似，且相似比为1：3，则△ABC与△A1B1C1的面积比为1：9，故选D．点睛：此题考查了相似三角形的性质，熟练掌握相似三角形的性质是解本题的关键．2．B【分析】证明△ADC∽△ACB，根据相似三角形的性质可推导得出AC2=AD•AB，由此即可解决问题.【详解】∵∠A=∠A，∠ADC=∠ACB，∴△ADC∽△ACB，∴AC AD AB AC，∴AC2=AD•AB=2×8=16，∵AC>0，∴AC=4，故选B.【点睛】本题考查相似三角形的判定和性质、解题的关键是正确寻找相似三角形解决问题.3．A【解析】【分析】根据相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比等于相似比得到两个相似三角形的周长的比为2∶3,设这两个三角形的周长分别为2x,3x,则2x+3x=20,然后解方程求出x后计算2x和3x即可.【详解】∵两个相似三角形对应边的比2∶3,∴两个相似三角形的周长的比为2∶3,设这两个三角形的周长分别为2x,3x,则2x+3x=20,解得x=4,∴2x=8,3x=12,即两个三角形的周长分别8和12.故选A.【点睛】本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等;相似三角形(多边形)的周长的比等于相似比;相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比也等于相似比.4．A 【解析】【分析】根据三角形的中位线得出DE=12BC，DE∥BC，推出△ADE∽△ABC，再求出△ABC和△ADE的面积比，进而可求出梯形DBCE的面积．【详解】∵点D、E分别是AB、AC边的中点，∴DE是三角形的中位线，∴DE=12BC，DE∥BC，∴△ADE∽△ABC，∴S△ADE：S△ABC=1：4，∵△ABC的面积为12cm2，∴△ADE的面积为3cm2，∴梯形DBCE的面积=12-3=9cm2，故选A．【点睛】本题考查了三角形的中位线和相似三角形的性质和判定的应用，解此题的关键是求出△ABC 和△ADE的面积比，题型较好，但是一道比较容易出错的题目．5．D【分析】由位似图形的位似中心可以在：原图形外，原图形内，原图形的边上，即可求得答案．【详解】解：位似图形的位似中心可以在：原图形外，原图形内，原图形的边上．故选D．【点睛】此题考查位似图形的性质．解题关键是注意位似图形的位似中心可以在平面内的任何位置．6．C【解析】【分析】先由三角形内角和定理求出∠C 的度数，再根据相似三角形的对应角相等得出∠C 1=∠C【详解】△ABC 中，∵∠A =60°，∠B =95°，∴∠C =180°−∠A −∠B =25°，∵△ABC ∽△A 1B 1C 1∴∠C 1=∠C =25°.故选C.【点睛】本题考查了相似三角形的性质，熟练掌握性质是解题的关键.7．A【分析】根据相似的性质，得到对应边成比例，代值求解即可.【详解】∵DE ∥BC ，∴△ADE ∽△ABC ，42.63DE AD AD BC AB AD DB ∴====+故选A.【点睛】：根据平行于三角形一边的直线和其他两边相交，所截得的三角形与原三角形相似，再根据相似三角形的对应边成比例解则可．8．C【详解】【分析】根据相似三角形三边对应成比例进行求解即可得.【详解】设另一个三角形的最长边为xcm ，由题意得5：2.5=9：x ，解得：x=4.5，故选C.【点睛】本题考查了相似三角形的性质，熟知相似三角形对应边成比例是解题的关键.9．B【分析】根据同一时刻物高与影长成正比可得出结论．【详解】设竹竿的长度为x尺，∵竹竿的影长=一丈五尺=15尺，标杆长=一尺五寸=1.5尺，影长五寸=0.5尺，∴1.5 150.5 x，解得x=45（尺），故选B．【点睛】本题考查了相似三角形的应用举例，熟知同一时刻物高与影长成正比是解答此题的关键．10．A【详解】分析：（1）由等腰Rt△ABC和等腰Rt△ADE三边份数关系可证；（2）通过等积式倒推可知，证明△PAM∽△EMD即可；（3）2CB2转化为AC2，证明△ACP∽△MCA，问题可证．详解：由已知：，AE∴AC AD AB AE＝∵∠BAC=∠EAD ∴∠BAE=∠CAD ∴△BAE∽△CAD 所以①正确∵△BAE∽△CAD ∴∠BEA=∠CDA ∵∠PME=∠AMD ∴△PME∽△AMD∴MP ME MA MD＝∴MP•MD=MA•ME 所以②正确∵∠BEA=∠CDA∠PME=∠AMD∴P 、E 、D 、A 四点共圆∴∠APD=∠EAD=90°∵∠CAE=180°-∠BAC-∠EAD=90°∴△CAP ∽△CMA∴AC 2=CP•CM∵AB∴2CB 2=CP•CM所以③正确故选A ．点睛：本题考查了相似三角形的性质和判断．在等积式和比例式的证明中应注意应用倒推的方法寻找相似三角形进行证明，进而得到答案．11．B【分析】可证明△DFE ∽△BFA ，根据相似三角形的面积之比等于相似比的平方即可得出答案．【详解】∵四边形ABCD 为平行四边形，∴DC ∥AB ，∴△DFE ∽△BFA ，∵DE ：EC=3：1，∴DE ：DC=3：4，∴DE ：AB=3：4，∴S △DFE ：S △BFA =9：16．故选B ．12．103【详解】分析：根据勾股定理求出5AC =，根据AB ∥CD ，得到12AF AE CF CD ==，即可求出CF 的长.详解：∵四边形ABCD 是矩形，∴4AB CD ==，AB ∥CD ，90ADC ∠=︒，在Rt ADC 中，90ADC ∠=︒，∴5AC =，∵E 是AB 中点，∴1122AE AB CD ==，∵AB ∥CD ，∴12AF AE CF CD ==，∴21033CF AC ==．故答案为103.点睛：考查矩形的性质，勾股定理，相似三角形的性质及判定，熟练掌握相似三角形的判定方法和性质是解题的关键.13．4:9【分析】根据相似三角形的面积比等于相似比的平方计算即可．【详解】∵两三角形的相似比是2：3，∴其面积之比是4：9．故答案为4：9．【点睛】本题考查了相似三角形的性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．14．6【解析】【分析】设a =4k ,b =5k ,c =6k ,代入a －b ＋c ＝10求出k 的值，从而可求出a ,b ,c 的值，再把求得的a ,b ,c 的值代入a ＋b －c 计算即可.【详解】设a =4k ,b =5k ,c =6k ,代入a －b ＋c ＝10，得4k －5k ＋6k ＝10，解之得k =2，∴a =8,b =10,c =12,∴a ＋b －c =8+10-12=6.故答案为：6.本题考查了比例的性质及见比设参的数学思想，通过设参数k 求出a ,b ,c 的值是解答本题的关键.15．0.4m【分析】先证明△OAB ∽△OCD ，再根据相似三角形的对应边成比例列方程求解即可.【详解】∵AB ⊥BD ，CD ⊥BD ，∴∠ABO =∠CDO .∵∠AOB =∠COD ,∴△OAB ∽△OCD ，∴AO :CO =AB :CD ,∴4:1=1.6:CD ,∴CD =0.4.故答案为0.4.【点睛】本题主要考查了相似三角形的应用，正确地把实际问题转化为相似三角形问题，利用相似三角形的判定与性质解决是解题的关键．16．57【解析】【分析】根据已知比例关系，用未知量k 分别表示出a 、b 和c 的值，代入原式中，化简即可得到结果【详解】设534a b c ===k ∴a=5k ，b=3k ，c=4k ∴222a b c a b c ++++=5641038k k k k k k ++++=1521k k =57故答案为：57本题考查了比例的性质，熟练掌握性质是解题的关键.17．222【分析】知道比例尺，带入数值计算，化单位为千米即可.【详解】比例尺为1:6000000,图上距离3.7厘米则实际距离为3.76000000cm222km⨯=故答案为222【点睛】此题重点考察学生对比例尺的应用能力，理解比例尺的单位换算是解题的关键.18．6：5【分析】作FN∥AD,交AB与N，设DE=a，则AE=3a，利用平行线分线段成比例定理解决问题即可.【详解】作FN∥AD,交AB与N，∵四边形ABCD是正方形，∴AB∥CD,∴FN∥AD,∴四边形ANFD是平行四边形，∵∠D=90°，∴四边形ANFD是矩形.设DE=a，则AE=3a，AD=AB=CD=FN=4a,AN=DF=2a,∵AN=BN,MN∥AE,∴BM=ME,∴MN=3 2 a,∴FM=5 2 a,∵AE∥FM,∴36552AG AE aGF FM a===.故答案为6:5.【点睛】本题考查了正方形的性质、平行线分线段成比例定理、三角形中位线等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题.19．4【解析】【分析】根据相似三角形面积的比等于相似比的平方求解即可.【详解】∵△ABC∽△DEF，相似比为2，∴△ABC与△DEF面积的比是4，∵△ABC的面积为16，∴△DEF的面积为16÷4=4.故答案为：4.【点睛】本题考查了相似三角形的性质，如果两个三角形相似，那么它们的对应角相等，对应边的比，对应高的比，对应中线的比，对应角平分线的比，对应周长的比都等于相似比；它们对应面积的比等于相似比的平方.20．【解析】【分析】先证明△ADF∽△CAB，利用相似三角形的性质可得AD=.再证明△DEF∽△DBA，利用相似三角形的性质可得DE DFDB DA=，据此可求出DF的值，进而求出AD的值.【详解】如图所示，过点D 作DF ⊥AC 于点F ，则∠AFD =∠CBA =90°.∵AD ∥BC ，∴∠DAF =∠ACB ，∴△ADF ∽△CAB ，∴DF :AB =AD :CA 。

人教版九年级下册数学第二十七章测试卷有答案

人教版九年级下册数学第二十七章测试题一、单选题1．已知13ba=，则a ba-的值为（）A．2B．12C．32D．232．下列四条线段能成比例线段的是（）A．1，1，2，3B．1，2，3，4C．2，2，3，3D．2，3，4，5 3．下列说法正确的是（）A．每条线段有且仅有一个黄金分割点B．黄金分割点分一条线段为两条线段，其中较长的线段约是这条线段的0.618倍C．若点C把线段AB黄金分割，则AC2＝AB•BCD．以上说法都不对4．如图，在ABC中，点D、E分别在边AB、AC上，联结DE，如果AD：BD2=：3，那么下列条件中能判断DE//BC的是()A．AE3EC2=B．CE3AC5=C．DE2BC5=D．AB5BD3=5．观察下列各组图形，其中不相似的是（）A．B．C．D．6．制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是（）A．360元B．720元C．1080元D．2160元7．已知△ABC∽△A1B2C2，如果∠A＝40°，那么∠A1等于（）A．40°B．80°C．140°D．20°8．如图，如果BAD CAE ∠=∠，那么添加下列一个条件后，仍不能确定ABC 和ADE 相似的是（）．A ．B D ∠=∠B ．C AED ∠=∠C ．AB DEAD BC=D ．AB ACAD AE=9．如图，△ABC 中，∠C ＝90°，AD 平分∠CAB ，交BC 于点D ，DE ⊥AB 于点E ，若CDDE 的长为（）A ．2B ．3CD ．10．如图．利用标杆BE 测量建筑物的高度．已知标杆BE 高1.2m ，测得AB ＝1.6m ．BC ＝12.4m ．则建筑物CD 的高是（）A ．9.3mB ．10.5mC ．12.4mD ．14m二、填空题11．如图在Rt △ABC 中，∠A ＝90°，斜边上的高AD 交BC 于D ，若BD ＝9，CD ＝4，则AD 的长度等于_____．12．如图，在平面直角坐标系中，已知A （1.5，0），D （4.5，0），△ABC 与△DEF 位似，原点O 是位似中心．若DE ＝7.5，则AB ＝_____．13．若x yy＝43，则xy＝_____14．如图，直线l1、l2、…、l6是一组等距离的平行线，过直线l1上的点A作两条射线m、n，射线m与直线l3、l6分别相交于B、C，射线n与直线l3、l6分别相交于点D、E．若BD＝1，则CE的长为_____．15．在比例尺为1：100的地图上，量得甲、乙两点的距离为25cm，甲、乙两点的实际距离为______m．16．如图，线段AE、BD交于点C，如果AC＝9，CE＝4，BC＝CD＝6，DE＝3，那么AB ＝_____．17．如图，△ABC中，EF∥BC，S△AEF：S四边形BEFC＝1：2，则EF：BC＝_____．18．如图，∠A＝∠B＝90°，AB＝7，AD＝2，BC＝3，在边AB上取点P，使得△PAD与△PBC相似，则满足条件的AP长_____．三、解答题19．已知234x y z==，且2x+3y ﹣z ＝18，求4x+y ﹣3z 的值．20．如图所示，在线段AB 上有C 、D 两点，已知AB ＝7，AC ＝1，且线段CD 是线段AC 和BD 的比例中项，求线段CD 的长．21．如图，AD 是△ABC 的中线，E 是AD 上一点，且AE ：ED ＝2：3，CE 延长∠AB 于F ，若AF ＝3cm ，求AB 的长．22．如图，在△ABC 中，D 为AC 边上一点，∠DBC ＝∠A ．（1）求证：△BDC ∽△ABC ；（2）若BC ＝4，AC ＝8，求CD 的长．23．已知：如图，在△ABC 中，AB ＝AC ，点E 、F 在边BC 上，∠EAF ＝∠B ．求证：BF•CE ＝AB 2．24．如图，在△ABC 中，BC =3，D 为AC 延长线上一点，AC =3CD ，过点D 作DH ∥AB ，交BC 的延长线于点H ，求CH 的长．25．如图，△OAB的顶点坐标分别为O（0，0）、A（3，2）、B（2，0），将这三个顶点的坐标同时扩大到原来的2倍，得到对应点D、E、F．(1)在图中画出△DEF；(2)点E是否在直线OA上？为什么？(3)△OAB与△DEF______位似图形（填“是”或“不是”）26．如图，△ABC是等边三角形，点D，E分别在BC，AC上，且BD＝CE，AD与BE相交于点F，(1)证明：△ABD≌△BCE；(2)证明：△ABE∽△FAE；(3)若AF＝7，DF＝1，求BD的长．参考答案1．D【分析】根据比例的性质得出3b=a，求出a-b=2b，即可得出答案．【详解】∵ba＝13∴3b=a∴3233 a b b ba b--==故答案为D.【点睛】本题考查的知识点是比例的性质，解题关键是找出a与b的等量关系.2．C【详解】分析：根据成比例线段的定义进行分析判断即可.详解：A选项中，因为1：1≠2：3，所以A中的四条线段不是成比例线段；B选项中，因为1：2≠3：4，所以B中的四条线段不是成比例线段；C选项中，因为2：2=3：3，所以C中的四条线段是成比例线段；D选项中，因为2：3≠3：4，所以D中的四条线段不是成比例线段.故选C.点睛：熟记成比例线段的定义：“若四条线段a、b、c、d满足a：b=c：d，我们就说线段a、b、c、d是成比例线段”是解答本题的关键.3．B【分析】根据黄金分割的定义分别进行解答即可．【详解】A．每条线段有两个黄金分割点，故本选项错误；B．黄金分割点分一条线段为两条线段，其中较长的线段约是这条线段的0.618倍，正确；C．若点C把线段AB黄金分割，则AC2＝AB•BC，不正确，有可能BC2＝AB•AC．故选B．【点睛】本题考查了黄金分割，熟练掌握黄金分割的定义是解题的关键．4．B【分析】先求出比例式，再根据相似三角形的判定得出△ADE∽△ABC，由相似推出∠ADE=∠B，再由平行线的判定得出即可．【详解】解：只有选项B正确，理由是：∵AD：BD=2：3，∴25 ADAB=，∵35 CEAC=，∴25 AEAC=，∴25 AD AEAB AC==，∵∠DAE=∠BAC，∴△ADE∽△ABC，∴∠ADE=∠B，∴DE∥BC，根据选项A、C、D的条件都不能推出DE∥BC，故选B．【点睛】本题考查了相似三角形的判定，能熟练转移比例线段得三角形相似是解此题的关键．5．A【分析】根据相似图形的定义，结合图形，对选项一一分析，排除错误答案．【详解】解：A、形状不相同，大小不同，不符合相似定义，故符合题意；B、形状相同，但大小不同，符合相似定义，故不符合题意；C、形状相同，但大小不同，符合相似定义，故不符合题意；D、形状相同，但大小不同，符合相似定义，故不符合题意；故选A．【点睛】本题考查的是相似形的识别，关键要联系图形，根据相似图形的定义得出．6．C【分析】根据题意求出长方形广告牌每平方米的成本，根据相似多边形的性质求出扩大后长方形广告牌的面积，计算即可．【详解】3m×2m=6m2，∴长方形广告牌的成本是120÷6=20元/m2，将此广告牌的四边都扩大为原来的3倍，则面积扩大为原来的9倍，∴扩大后长方形广告牌的面积=9×6=54m2，∴扩大后长方形广告牌的成本是54×20=1080元，故选C．【点睛】本题考查的是相似多边形的性质，掌握相似多边形的面积比等于相似比的平方是解题的关键．7．A【解析】【分析】根据相似三角形对应角相等解答．【详解】∵△ABC∽△A1B1C1，∠A=40°∴∠A1=∠A=40°．故答案为A．【点睛】本题考查的知识点是相似三角形对应角相等的性质，解题关键是熟记性质．8．C 【分析】由BAD CAE ∠=∠结合图形可得∠DAE=∠CAB ，所以再需一对对应角相等或或夹这个角的两边对应成比例即可．【详解】∵BAD CAE ∠=∠，∴DAE BAC ∠=∠，∴A ，B 可由两角对应相等的三角形相似，判定ABC ∽ADE ，D 可据一角对应相等夹边成比例判定ABC ∽ADE ．选项C 中不是夹这两个角的边，所以不能判定相似．故选：C ．【点睛】此题考查相似三角形的判定．其关键是先看已知什么条件，结合已知的条件，再据相似的判定方法找所缺条件．9．C 【解析】【分析】分析题目已知条件，可利用角平分线的性质进行解答.【详解】∵AD 平分∠CAB 交BC 于点D ，∠C ＝90°，DE ⊥AB∴故选C ．【点睛】本题考查的知识点是角平分线上的点到两边的距离相等，解题关键是熟记定理.10．B 【分析】先证明∴△ABE ∽△ACD ，则利用相似三角形的性质得 1.6 1.21.612.4CD=+，然后利用比例性质求出CD 即可．【详解】解：∵EB ∥CD ，∴△ABE∽△ACD，∴AB BEAC CD=，即1.6 1.21.612.4CD=+，∴CD=10.5（米）．故选B．【点睛】考查了相似三角形的应用：借助标杆或直尺测量物体的高度．利用杆或直尺测量物体的高度就是利用杆或直尺的高（长）作为三角形的边，利用视点和盲区的知识构建相似三角形，用相似三角形对应边的比相等的性质求物体的高度．11．6【解析】【分析】证明△BDA∽△ADC，然后根据相似三角形的对应边成比例即可得出结论．【详解】∵∠BAC=90°，∴∠B+∠C=90°．∵AD⊥BC，∴∠B+∠BAD=90°，∴∠BAD=∠C．∵∠ADB=∠ADC=90°，∴△BDA∽△ADC，∴BD：DA=AD：DC，∴AD2＝BD•CD，则AD2＝9×4＝36，∴AD＝6．故答案为6．【点睛】本题考查了相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解题的关键．12．2.5．【分析】利用以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k得到位似比为13，然后根据相似的性质计算AB的长．【详解】解：∵A（1.5，0），D（4.5，0），∴OAOD=1.54.5=13，∵△ABC与△DEF位似，原点O是位似中心，∴ABDE=OAOD=13,∴AB=13DE=13×7.5=2.5．故答案为2.5．【点睛】本题考查了位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k．13．1 3【解析】【分析】根据比例的性质得出3(x+y)=4y，解得y=3x，即可得出答案．【详解】∵x yy+＝43∴3(x+y)=4y ∴y=3x∴133 x xy x==故答案为：1 3 .【点睛】本题考查的知识点是比例的性质，解题关键是找出x与y的等量关系.14．5 2【解析】【分析】根据相似三角形对应边成比例即可解.【详解】∵BD∥CE，∴∠ABD=∠ACE，∠ADB=∠AEC，∴△ABD∽△ACE，根据相似三角形对应边成比例可得：25 BD ABCE AC==，∵BD=1，∴CE=5 2 .故本题正确答案为5 2 .【点睛】本题考查的知识点是平行线和相似三角形的判定与性质，解题关键是熟记相似三角形对应边成比例.15．25【分析】依据“实际距离=图上距离÷比例尺”，代入数据即可求解．【详解】解：25÷1 100=25×100=2500（厘米）=25米，故答案为25．【点睛】此题主要考查图上距离、实际距离和比例尺的关系，解答时要注意单位的换算．16．9 2【解析】【分析】根据两边对应成比例且夹角相等，证得两三角形相似，再根据相似三角形的对应边的比相等即可求解．【详解】∵32 BC ACCE CD==，又∵∠ACB=∠DCE，∴△ABC∽△DEC；∴32 ABDE=，∴3393222 AB DE==⨯=．故答案为：9 2 .【点睛】本题考查了相似三角形的判定与性质，解题关键是熟练运用熟记相似三角形对应边成比例. .17【解析】【分析】根据已知可得到△AEF∽△ABC，根据相似三角形的面积之比等于边之比的平方不难求解．【详解】∵EF∥BC∴△AEF∽△ABC∵S△AEF：S四边形BEFC＝1：2∴S△AEF：S△ABC=1：3∴由相似三角形的面积之比等于边之比的平方得EF：BC故答案为：3.【点睛】本题考查的知识点是相似三角形的判定与性质，解题的关键是熟练的掌握相似三角形的判定与性质.18．2.8或1或6【分析】设AP=x，则有PB=AB-AP=7-x，分两种情况考虑：三角形PDA与三角形CPB相似；三角形PDA与三角形PCB相似，分别求出x的值，即可确定出P的个数．【详解】设AP=x，则有PB=AB−AP=7−x，当△PDA∽△CPB时,DA PB=AP BC,即27-x=x3，解得：x=1或x=6，当△PDA∽△PCB时,AD AP=BC PB,即2x=37-x，解得：x=145.故答案为x=1或x=6或2.8.【点睛】本题考查的知识点是相似三角形的判定，解题的关键是熟练的掌握相似三角形的判定.19．x=4，y=6，z=8.【分析】设234x y z==＝k ，由2x+3y-z=18列出含k 的等式，解出k ，x ，y ，z ，再代入所求即可.【详解】解：设234xy z==＝k ，可得：x ＝2k ，y ＝3k ，z ＝4k ，把x ＝2k ，y ＝3k ，z ＝4k 代入2x+3y ﹣z ＝18中，可得：4k+9k ﹣4k ＝18，解得：k ＝2，所以x ＝4，y ＝6，z ＝8，把x ＝4，y ＝6，z ＝8代入4x+y ﹣3z ＝16+6﹣24＝﹣2．【点睛】本题考查的知识点是比例的性质，解题的关键是熟练的掌握比例的性质.20．2.【分析】由线段CD 是线段AC 和BD 的比例中项，列出CD 2＝AC•BD ，带值解得.【详解】解：∵AB ＝7，AC ＝1，∴BD ＝AB ﹣AC ﹣CD ＝6﹣CD ，∵线段CD 是线段AC 和BD 的比例中项，∴CD 2＝AC•BD ，即CD 2＝1×（6﹣CD ），解得：CD ＝2．【点睛】本题考查的知识点是比例线段，解题的关键是熟练的掌握比例线段.【分析】作DH∥CF交AB于H，根据平行线分线段成比例定理列出比例式，计算即可．【详解】作DH∥CF交AB于H，则FHHB＝CDDB＝1，AFFH＝23AEED=，∴FH＝HB，3FH＝23，解得，FH＝BH=4.5，∴AH＝AF+FH＝7.5，∴AB＝AH+HB＝12．【点睛】本题考查的是平行线分线段成比例定理，灵活运用定理，找准对应关系是解题的关键．22．（1）证明见解析；（2）CD＝2．【解析】【分析】（1）根据相似三角形的判定得出即可；（2）根据相似得出比例式，代入求出即可．【详解】解：（1）∵∠DBC＝∠A，∠BCD＝∠ACB，∴△BDC∽△ABC；（2）∵△BDC∽△ABC，∴BC DC AC BC=，∵BC＝4，AC＝8，∴CD＝2．【点睛】本题考查的知识点是相似三角形的判定与性质，解题的关键是熟练的掌握相似三角形的判定23．证明见解析.【解析】【分析】利用两角对应成比例可得△ABF∽△ECA，对应边成比例可得相应的比例式，整理可得所求的乘积式．【详解】证明：∵∠AEC＝∠B+∠BAE＝∠EAF+∠BAE＝∠BAF，又∵AB＝AC，∴∠B＝∠C，∴△ABF∽△ECA，∴AB：CE＝BF：AC，∴BF•EC＝AB•AC＝AB2．【点睛】本题考查的知识点是相似三角形的判定与性质,等腰三角形的性质，解题的关键是熟练的掌握相似三角形的判定与性质,等腰三角形的性质.24．CH=1．【分析】根据相似三角形的判定得出两三角形相似，得出比例式，代入求出即可.【详解】解：∵DH∥AB，∴△ABC∽△DHC，∴BC AC CH DC，∵BC=3，AC=3CD，∴CH=1．【点睛】考查了平行线的性质，相似三角形的性质和判定，解直角三角形的应用，能求出△ABC∽△DHC是解此题的关键．25．（1）见解析；（2）点E在直线OA上；（3）是.（1）根据题意将各点坐标扩大2倍得出答案；（2）求出直线OA的解析式，进而判断E点是否在直线上；（3）利用位似图形的定义得出△OAB与△DEF的关系．【详解】解：（1）如图所示：△DEF，即为所求；（2）点E在直线OA上，理由：设直线OA的解析式为：y＝kx，将A（3，2）代入得：2＝3k，解得：k＝23，故直线OA的解析式为：y＝23x，当x＝6时，y＝23×6＝4，故点E在直线OA上；（3）△OAB与△DEF是位似图形．故答案为是．【点睛】本题考查的知识点是作图-位似变换，解题的关键是熟练的掌握作图-位似变换. 26．（1）证明见解析；（2）证明见解析；（3）BD＝．【分析】（1）根据等边三角形的性质，利用SAS证得△ABD≌△BCE；（2）由△ABD≌△BCE得∠BAD=∠CBE，又∠ABC=∠BAC，可证∠ABE=∠EAF，又∠AEF=∠BEA，由此可以证明△AEF∽△BEA；（3）由△ABD≌△BCE得：∠BAD=∠FBD，又∠BDF=∠ADB，由此可以证明△BDF∽△ADB，然后可以得到AD BD=BC DF，即BD2=AD•DF=（AF+DF）•DF．【详解】解：（1）∵△ABC是等边三角形，∴AB ＝BC ，∠ABD ＝∠BCE ，在△ABD 与△BCE 中∵ABC=BAC=C BD=CE AB BC =⎧⎪∠∠∠⎨⎪⎩，∴△ABD ≌△BCE （SAS ）；（2）由（1）得：∠BAD ＝∠CBE ，又∵∠ABC ＝∠BAC ，∴∠ABE ＝∠EAF ，又∵∠AEF ＝∠BEA ，∴△AEF ∽△BEA ；（3）∵∠BAD ＝∠CBE ，∠BDA ＝∠FDB ，∴△ABD ∽△BDF ，∴=AD BD BC DF，∴BD 2＝AD•DF ＝（AF+DF ）•DF ＝8，∴BD ＝．【点睛】本题考查的知识点是相似三角形的判定与性质,全等三角形的判定,等边三角形的性质，解题的关键是熟练的掌握相似三角形的判定与性质,全等三角形的判定,等边三角形的性质.。

人教版初3数学9年级下册第27章(相似)达标检测卷(含解析)

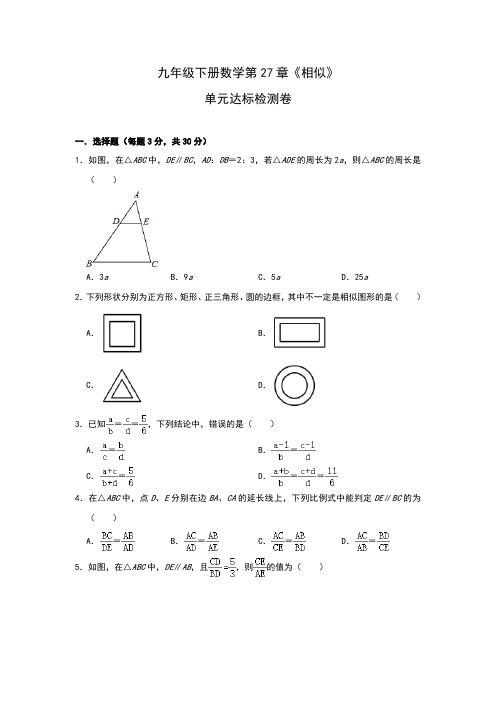
九年级下册数学第27章《相似》单元达标检测卷一．选择题（每题3分，共30分）1．如图，在△ABC中，DE∥BC，AD：DB＝2：3，若△ADE的周长为2a，则△ABC的周长是（）A．3a B．9a C．5a D．25a2．下列形状分别为正方形、矩形、正三角形、圆的边框，其中不一定是相似图形的是（）A．B．C．D．3．已知＝＝，下列结论中，错误的是（）A．＝B．＝C．＝D．＝＝4．在△ABC中，点D、E分别在边BA、CA的延长线上，下列比例式中能判定DE∥BC的为（）A．＝B．＝C．＝D．＝5．如图，在△ABC中，DE∥AB，且，则的值为（）A．B．C．D．6．如图，在平行四边形ABCD中，E为CD上一点，DE：EC＝2：3，连接AE、BD，且AE、BD 交于点F，则DF：BF等于（）A．2：5B．2：3C．3：5D．3：27．如图，以点O为位似中心，把△ABC中放大到原来的2倍得到△A'B'C'．以下说法中错误的是（）A．△ABC∽△A'B'C'B．点C，O，C'三点在同一条直线上C．AO：AA'＝1：2D．AB∥A'B'8．如图，有一块三角形余料ABC，它的面积为36cm2，边BC＝12cm，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB，AC上，则加工成的正方形零件的边长为（）cm．A．8B．6C．4D．39．如图，在菱形ABCD中，AB＝6，∠DAB＝60°，AE分别交BC、BD于点E、F，CE＝2，连CF，以下结论：①△ABF≌△CBF；②点E到AB的距离是；③△ADF与△EBF的面积比为3：2，④△ABF的面积为，其中一定成立的有（）个．A．2B．3C．1D．410．如图，正方形ABCD的边长为6，点E是BC的中点，连接AE与对角线BD交于点G，连接CG并延长，交AB于点F，连接DE交CF于点H，连接AH．以下结论：①∠DEC＝∠AEB；②CF⊥DE；③AF＝BF；④＝，其中正确结论的个数是（）A．1B．2C．3D．4二．填空题（每题4分，共20分）11．已知点P是线段AB的黄金分割点，那么AP：AB的值等于．12．如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，CD⊥AB，垂足为D，E为BC的中点，AE与CD交于点F，则DF的长为．13．在△ABC中，AB＝AC，点D在直线BC上，DC＝3DB，点E为AB边的中点，连接AD，射线CE交AD于点M，则的值为．14．如图，在直角坐标系中，正方形ABCD的边BC在x轴上，其中点A的坐标为（1，2），正方形EFGH的边FG在x轴上，且H的坐标为（9，4），则正方形ABCD与正方形EFGH 的位似中心的坐标是．15．如图，在平面直角坐标系中，矩形OABC的两边OA、OC分别在x轴和y轴上，且OA＝2，OC＝1．在第一象限内，将矩形OABC以原点O为位似中心放大为原来的2倍，得到矩形OA1B1C1，再将矩形OA1B1C1以原点O为位似中心放大2倍，得到矩形OA2B2C2…，以此类推，得到的矩形OA n B n∁n的对角线交点的坐标为．三．解答题（每题10分，共50分）16．如图，点D是等腰Rt△ABC的斜边AB上的一点，AB＝3BD，AF⊥CD于点F交BC于点E．（1）求证：E是BC的中点；（2）求AF：CF的值；（3）求DF：CF的值．17．如图，在平行四边形ABCD中，过点A作AE⊥BE，垂足为E，连接DE，F为线段DE上一点，且∠AFE＝∠B．（1）求证：△ADF∽△DEC；（2）若AB＝8，AD＝6，AF＝4，求tan∠DEC．18．如图是一把落地的遮阳伞的侧面示意图，伞柄CD垂直于水平地面GQ，当点P与点A重合时，伞收紧；当点P由点A向点B移动时，伞慢慢撑开；当点P与点B重合时，伞完全张开．已知遮阳伞的高度CD是220厘米，在它撑开的过程中，总有PM＝PN＝CM＝CN＝50厘米，CE＝CF＝120厘米，BC＝20厘米．（1）当∠CPN＝53°，求BP的长？（2）如图，当伞完全张开时，求点E到地面GQ的距离．（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.3）19．如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△OAB和△OA1B1（顶点是网格线的交点）．点A、B坐标为（﹣1，0），（﹣1，2）．（1）观察图形填空：△OA1B1是由△OAB绕点顺时针旋转度得到的；（2）把（12）中的图形作为一个新的”基本图形“，将新的基本图形绕O点顺时针旋转180°度，请作出旋转后的图形，其中，A、B、A1、B1的对应点分别为A2、B2、A3、B3．依次连接B、B1、B2、B3，则四边形BB1B2B3的形状为；（3）以O点为位似中心，位似比为1：2（原图与新图对应边的比为1：2），作出四边形BB1B2B3的位似图形．20．如图，在矩形ABCD中，AB＝12cm，BC＝6cm，点P沿AB边从点A开始向点B以2cm/s 的速度移动，点Q沿DA边从点D开始向点A以1cm/s的速度移动，如果P、Q同时出发，用t（s）表示运动时间（0≤t≤6）．（1）分别用含有t的代数式表示AP和AQ．（2）当t为何值时，以Q、A、P为顶点的三角形与△ABC相似？参考答案一．选择题1．解：∵DE∥BC，∴△ADE∽△ABC，∴＝＝，∴C△ABC＝×2a＝5a，故选：C．2．解：A、两图形形状相同，是相似图形，不符合题意；B、两图形形状不同，不是相似图形，符合题意；C、两图形形状相同，是相似图形，不符合题意；D、两图形形状相同，是相似图形，不符合题意；故选：B．3．解：∵＝＝，∴，，，所以ACD正确，B错误．故选：B．4．解：如图：A、当时，不能判定DE∥BC，不符合题意；B、当时，不能判定DE∥BC，不符合题意；C、当，能判定DE∥BC，符合题意；D、当时，能判定DE∥BC，而当时，不能判定DE∥BC，不符合题意；故选：C．5．解：∵DE∥AB，∴，故选：D．6．解：∵四边形ABCD为平行四边形，∴AB∥CD，且AB＝CD．∵DE：EC＝2：3，∴＝＝＝．∵AB∥CD，∴△DEF∽△BAF，∴＝＝．故选：A．7．解：∵点O为位似中心，把△ABC中放大到原来的2倍得到△A'B'C'，∴△ABC∽△A'B'C'，OA：OA′＝1：2，AB∥A′B′，CC′经过点O．故选：C．8．解：作BC边上的高AM交EF于点N，∵面积为36cm2，边BC＝12cm，∴AM＝6cm，设正方形的边长为xmm，则EF＝FP＝NM＝x，∴AN＝AM﹣MN＝6﹣x，∵EF∥BC，∴△AEF∽△ABC，∴，即，解得x＝4．故选：C．9．解：∵四边形ABCD是菱形，∴AB＝BC＝6，∵∠DAB＝60°，∴AB＝AD＝DB，∠ABD＝∠DBC＝60°，在△ABF与△CBF中，，∴△ABF≌△CBF（SAS），故①正确；如图：过点E作EG⊥AB，过点F作MH⊥CD，MH⊥AB，∵CE＝2，BC＝6，∠ABC＝120°，∴BE＝6﹣2＝4，∵EG⊥AB，∴EG＝2，故②正确；∵AD∥BE，∴△ADF∽△EBF，∴，故③错误；∵△ADF∽△EBF，∴，∵BD＝6，∴BF＝，∴FH＝BF•sin∠FBH＝，∴，故④正确；故选：B．10．解：∵四边形ABCD是边长为6的正方形，点E是BC的中点，∴AB＝AD＝BC＝CD＝6，BE＝CE＝3，∠DCE＝∠ABE＝90°，∠ABD＝∠CBD＝45°，∴△ABE≌△DCE（SAS）∴∠DEC＝∠AEB，∠BAE＝∠CDE，DE＝AE，故①正确，∵AB＝BC，∠ABG＝∠CBG，BG＝BG，∴△ABG≌△CBG（SAS）∴∠BAE＝∠BCF，∴∠BCF＝∠CDE，且∠CDE+∠CED＝90°，∴∠BCF+∠CED＝90°，∴∠CHE＝90°，∴CF⊥DE，故②正确，∵∠CDE＝∠BCF，DC＝BC，∠DCE＝∠CBF＝90°，∴△DCE≌△CBF（ASA），∴CE＝BF，∵CE＝BC＝AB，∴BF＝AB，∴AF＝FB，故③正确，∵DC＝6，CE＝3，∴DE＝＝＝3，∵S△DCE＝×CD×CE＝×DE×CH，∴CH＝，∵∠CHE＝∠CBF，∠BCF＝∠ECH，∴△ECH∽△FCB，∴＝，∴CF＝＝3，∴HF＝CF﹣CH＝，∴＝，故④正确，故选：D．二．填空题（共5小题）11．解：当点P是线段AB的黄金分割点AP＞PB时，＝，即＝，∴AP2+AP•AB﹣AB2＝0，解得，AP1＝AB（舍去），AP2＝AB，∴AP：AB＝，当点P是线段AB的黄金分割点AP＜PB时，AP：AB＝，故答案为：或．12．解：如图，过点F作FH⊥AC于H．在Rt△ABC中，∵∠ACB＝90°，AC＝3，BC＝4，∴AB＝＝＝5，∵CD⊥AB，∴S△ABC＝•AC•BC＝•AB•CD，∴CD＝，AD＝＝＝，∵FH∥EC，∴＝，∵EC＝EB＝2，∴＝，设FH＝2k，AH＝3k，CH＝3﹣3k，∵tan∠FCH＝＝，∴＝，∴k＝，∴FH＝，CH＝3﹣＝，∴CF＝＝＝，∴DF＝﹣＝，故答案为．13．解：当D点在B点右侧时，如图：过D作DN∥EC，交AB于点N，则∠DNB＝∠CEB，∠BDN＝∠BCE，∴△DBN∽△CBE，∴，∵DC＝3DB，∴，∵E为AB的中点，∴AE＝BE，∴，∵DN∥EC，∴∠AEM＝∠AND，∠AME＝∠ADN，∴△AEM∽△AND，∴，∴，∴；当D点在B点左侧时，如图：过D作DN∥EC，交AB的延长线于点N，则∠DNB＝∠CEB，∠BDN＝∠BCE，∴△DBN∽△CBE，∴，∵DC＝3DB，∴，∴，∵E为AB的中点，∴AE＝BE，∵DN∥EC，∴∠AEM＝∠AND，∠AME＝∠ADN，∴△AEM∽△AND，∴，∴，∴．故答案为或．14．解：连接HD并延长交x轴于点P，则点P为位似中心，∵四边形ABCD为正方形，点A的坐标为（1，2），∴点D的坐标为（3，2），∵DC∥HG，∴△PCD∽△PGH，∴＝，即＝，解得，OP＝3，∴正方形ABCD与正方形EFGH的位似中心的坐标是（﹣3，0），连接CE、DF交于点P，由题意得C（3，0），E（5，4），D（3，2），F（5，0），求出直线DF解析式为：y＝﹣x+5，直线CE解析式为：y＝2x﹣6，，解得，，直线DF，CE的交点P为（，），所以正方形ABCD与正方形EFGH的位似中心的坐标是（，），故答案为：（﹣3，0）或（，）．15．解：∵在第一象限内，将矩形AOCB以原点O为位似中心放大为原来的2倍，∴矩形A1OC1B1与矩形AOCB是位似图形，点B与点B1是对应点，∵OA＝2，OC＝1．∵点B的坐标为（2，1），∴点B1的坐标为（2×2，1×2），∵将矩形A1OC1B1以原点O为位似中心放大2倍，得到矩形A2OC2B2…，∴B2（2×2×2，1×2×2），以此类推，B n（2n+1，2n），矩形OA n B n∁n的对角线交点为B n﹣1，即（2n，2n﹣1），故答案为：（2n，2n﹣1）．三．解答题（共5小题）16．（1）证明：作BP⊥BC交CD的延长线于P，如图1，∵∠ACB＝90°，∴AC∥BP，∴＝，∵AB＝3BD，∴AD＝2BD，∴AC＝2BP，而AC＝BC，∴BC＝2BP，∵AF⊥CD，∴∠CAF+∠ACF＝90°，而∠ACF+∠ECF＝90°，∴∠CAF＝∠ECF，在△ACE和△CBP中，，∴△ACE≌△CBP，∴CE＝BP，∴BC＝2CE，∴E是BC的中点；（2）解：∵∠CAF＝∠ECF，∴Rt△ACF∽△CEF，∴＝，而BC＝AC＝2CE，∴＝2；（3）解：作DH∥AE交BC于H，如图2，∴＝＝，∴EH＝BE，∵EF∥DH，∴＝＝＝．17．（1）证明：∵平行四边形ABCD中，AB∥CD，AD∥BC，∴∠B+∠DCE＝180°，∠ADF＝∠CED，∵∠B＝∠AFE，∠AFD+∠AFE＝180°，∴∠AFD＝∠DCE，∴△ADF∽△DEC；（2）解：∵四边形ABCD为平行四边形，∴CD＝AB，AD∥BC，∴AE⊥AD，∵△ADF∽△DEC，∴＝，即＝，∴DE＝12，∵在RT△ADE中，AE2＝DE2﹣AD2，∴AE＝6，∴tan∠DEC＝tan∠ADE＝＝＝．18．解：（1）如图1中，连接MN交CD于H．∵CM＝MP＝NC＝NP＝50cm，∴四边形PMCN是菱形，∴CP⊥NM，CH＝PH，∴PH＝PN•cos53°≈30（cm），∴PC＝2PH＝60cm，∴PB＝PC﹣BC＝40cm．（2）如图2中，连接MN交CD于J，连接EF交CD于H．∵四边形CMBN是菱形，∴CJ＝JB＝10cm，∵MJ∥EH，∴△CMJ∽△CEH，∴＝，∴＝，∴CH＝24，∴HD＝CD﹣CH＝220﹣24＝196cm，∴当伞完全张开时，求点E到地面GQ的距离＝HD＝196cm．19．解：（1）△OA1B1是由△OAB绕O点顺时针旋转90度得到的；（2）如图1，四边形BB1B2B3的为所作，它是正方形；（3）如图2，四边形CDEF为所作；故答案为O，90，正方形．20．解：（1）AP＝2t，AQ＝6﹣t，（2）∵∠QAP＝∠ABC＝90°，∴当＝时，△AQP∽△BCA，即＝，解得t＝3；当＝时，△AQP∽△BAC，即＝，解得t＝．答：当t s或3s时，以Q、A、P为顶点的三角形与△ABC相似．。

人教版九年级数学下册--第二十七章达标测试卷--(附解析答案)

第二十七章达标测试卷时间：100分钟满分：120分一、选择题(每题3分，共30分)1．在下列各组线段中，不成比例的是()A．a＝3，b＝6，c＝2，d＝4 B．a＝1，b＝2，c＝2，d＝4C．a＝4，b＝6，c＝5，d＝10 D．a＝1，b＝2，c＝6，d＝ 32．已知△ABC与△DEF相似，且相似比为1∶4，则△ABC与△DEF的面积比为()A．1∶2 B．1∶3 C．1∶4 D．1∶16 3．如图，l1∥l2∥l3，直线a，b与l1，l2，l3分别相交于点A，B，C和点D，E，F，若ABBC＝23，DE＝6，则EF的长是()A．8 B．9 C．10 D．12(第3题) (第4题) (第5题)4．如图，在△ABC中，点D，E分别在边AB，AC上，下列条件中不能判断△ABC ∽△AED的是()A．∠AED＝∠B B．∠ADE＝∠CC. ADAE＝ACAB D.ADAB＝DEBC5．如图，在平行四边形ABCD中，EF∥AB交AD于点E，交DB于点F，DE∶EA＝3∶4，EF＝3，则CD的长为()A．4 B．7 C．3 D．12 6．下列说法：①有一个角等于30°的两个等腰三角形相似；②有一个角等于120°的两个等腰三角形相似；③相似三角形一定不是全等三角形；④相似三角形对应角平分线的长度比等于面积比．其中正确的个数是()A．1 B．2 C．3 D．4 7．下列四个三角形，与图中的三角形相似的是()(第7题)8．如图，在平面直角坐标系中，点E(－4，2)，F(－1，－1)，以O为位似中心，将△EFO缩小为原来的12，则点E的对应点E′的坐标为()A．(2，－1)或(－2，1) B．(8，－4)或(－8，4) C．(2，－1) D．(8，－4)(第8题) (第9题) (第10题)9．为了测量校园水平地面上一棵不可攀的树的高度，学校数学兴趣小组做了如下探索：根据光的反射定律，利用一面镜子和一根皮尺，设计如图所示的测量方案：把一面很小的镜子水平放置在离树底(点B)8.4 m的点E处，然后沿着直线BE走到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE＝3.2 m，观察者眼高CD＝1.6 m，则树(AB)的高度约为()A．4.2 m B．4.8 m C．6.4 m D．16.8 m10．如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，分析下列四个结论：①△AEF∽△CAB；②CF＝2AF；③DF＝DC；④CDAD＝2，其中正确的结论有()A．4个B．3个C．2个D．1个二、填空题(每题3分，共24分)11．已知△ABC∽△A′B′C′，且其相似比是34，△ABC的周长是27 cm，则△A′B′C′的周长为________cm.12．如果xy＝25，那么y－xy＋x＝________.13．两个多边形相似，面积的比是1∶4，一个多边形的周长为16，则另一个多边形的周长为________．14．如图，锐角三角形ABC的边AB，AC上的高线CE，BF相交于点D，请写出图中的两对相似三角形：____________________________(用相似符号连接)．(第14题) (第15题) (第16题)15．如图，请添加一个条件，使△ADB∽△ABC，你添加的条件是______________．16．如图，在平行四边形ABCD中，点E在BC边上，且CE BC＝23，AC 与DE相交于点F.若S△AFD＝9，则S△EFC＝________.17．如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为34，∠OCD＝90°，∠AOB＝60°，若点B的坐标是(6，0)，则点C的坐标是__________．(第17题) (第18题)18．如图，将边长为6 cm的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在点Q处，EQ与BC交于点G，则△EBG的周长是________cm.三、解答题(19题12分，24题14分，其余每题10分，共66分)19．如图，△ABC在方格纸(小正方形的边长均为1)中．(1)请在方格纸上建立平面直角坐标系，使A(3，4)，C(7，3)，并求出点B的坐标；(2)以原点O为位似中心，相似比为2，在第一象限内将△ABC放大，画出放大后的位似图形△A′B′C′；(3)计算△A′B′C′的面积S.(第19题)20．如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，E，D分别是BC，AC上的点，且∠AED＝45°.(1)求证△ABE∽△ECD；(2)若AB＝4，BE＝2，求CD的长．(第20题)21．如图，九(1)班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度CD＝3 m，标杆与旗杆的水平距离BD＝15 m，人的眼睛与地面的高度EF ＝1.6 m，人与标杆CD的水平距离DF＝2 m，求旗杆AB的高度．(第21题)22．如图，在△ABC中，AB＝10 cm，BC＝20 cm，点P从点A开始沿AB边以2 cm/s的速度向点B移动，点Q从点B开始沿BC边以4 cm/s的速度向点C 移动．如果点P，Q分别从A，B同时出发，问经过多久，△PBQ与△ABC 相似？(第22题)23．如图，已知AB是⊙O的直径，弦CD⊥AB，垂足为H.(1)求证AH·AB＝AC2；(2)过点A的直线与弦CD(不含端点)相交于点E，与⊙O相交于点F，求证AE·AF＝AC2.(第23题)24．如图①，在Rt△ABC中，∠B＝90°，BC＝2AB＝8，点D，E分别是边BC，AC的中点，连接DE.将△EDC绕点C按顺时针方向旋转，记旋转角为α.(1)问题发现①当α＝0°时，AEBD＝________；②当α＝180°时，AEBD＝________．(2)拓展研究试判断：当0°≤α<360°时，AEBD 的大小有无变化？请仅就图②的情况给出证明． (3)问题解决当△EDC 旋转至A ，D ，E 三点共线时，直接写出线段BD 的长．(第24题)答案一、1．C2．D3．B4．D5．B6．A7．B8．A9．A点拨：如图，过点E作EF⊥BD，则∠1＝∠2.∵∠DEF＝∠BEF＝90°，∴∠DEC＝∠AEB.∵CD⊥BD，AB⊥BD，∴∠CDE＝∠ABE＝90°，∴△CDE∽△ABE，∴DEBE＝CDAB.∵DE＝3.2，CD＝1.6，EB＝8.4，∴3.28.4＝1.6AB，解得AB＝4.2(m)．(第9题)10．B点拨：如图，过点D作DM∥BE交AC于点N，交BC于点M.∵四边形ABCD是矩形，∴AD∥BC，∠ABC＝90°，AD＝BC.∴∠EAC＝∠ACB，∵BE⊥AC，∴∠ABC＝∠AFE＝90°，∴△AEF∽△CAB，故①正确．∵AD∥BC，∴△AEF∽△CBF，∴AEBC＝AFCF.∵AE＝12AD＝12BC，∴AFCF＝12，∴CF＝2AF，故②正确．∵DE∥BM，BE∥DM，∴四边形BMDE是平行四边形，∴BM＝DE＝12BC，∴BM＝CM，∴CN＝NF.∵BE⊥AC，DM∥BE，∴DN⊥CF，∴DF＝DC，故③正确．设AD＝a，AB＝b，易知△BAE∽△ADC，则BAAD＝AEDC，即ba＝a2b，∴ba＝22.∴CDAD＝ba＝22，故④错误．故选B.(第10题)二、11．3612．3 713．8或32点拨：∵面积的比是1∶4，∴相似比为1∶2.(1)若周长为16的多边形是较大的多边形，则另一多边形的周长为16÷2＝8；(2)若周长为16的多边形是较小的多边形，则另一多边形的周长为16×2＝32.故另一多边形的周长为8或32.14．△ABF∽△ACE，△BDE∽△CDF(答案不唯一)15．∠ABD＝∠C(答案不唯一)16.417．(2，23)点拨：如图，过点C作CF⊥OB于点F.(第17题)∵∠OCD＝90°，∠AOB＝60°，∴∠CDO＝30°，∠OCF＝30°.∵△OAB与△OCD是以点O为位似中心的位似图形，相似比为34，点B的坐标是(6，0)，∴D(8，0)，则DO＝8，故OC＝4.∴FO＝2，CF＝CO·cos 30°＝4×32＝2 3.∴点C的坐标是(2，23)．18．12点拨：由折叠的性质，得DF＝EF，设EF＝x，则AF＝6－x.∵点E是AB的中点，∴AE＝BE＝12×6＝3.在Rt△AEF中，由勾股定理，得AE2＋AF2＝EF2，即32＋(6－x)2＝x2，解得x＝154(cm)，∴AF＝6－154＝94.∵∠FEG＝∠D＝90°，∴∠AEF＋∠BEG＝90°，∵∠AEF＋∠AFE＝90°，∴∠AFE＝∠BEG.又∵∠A＝∠B＝90°，∴△AEF∽△BGE，∴BEAF＝BGAE＝EG EF，即394＝BG3＝EG154，解得BG＝4(cm)，EG＝5(cm)．∴△EBG的周长为3＋4＋5＝12(cm)．三、19.解：(1)建立平面直角坐标系如图所示．点B的坐标为(3，2)．(2)如图所示．(第19题)(3)△A′B′C′的面积S为12×4×8＝16.20．(1)证明：在Rt△ABC中，∠BAC＝90°，AB＝AC，∴∠B＝∠C＝45°.∵∠AEC＝∠B＋∠BAE＝∠AED＋∠CED，∠AED＝45°，∴∠BAE＝∠CED.∴△ABE∽△ECD.(2)解：在Rt△ABC中，∠BAC＝90°，AB＝AC＝4，∴BC＝4 2.∵BE＝2，∴EC＝3 2.∵△ABE∽△ECD，∴ABEC＝BECD，即432＝2CD，∴CD＝3 2.21．解：作EH⊥AB，垂足为H，交CD于点G.∵CD⊥FB，AB⊥FB，∴CD∥AB.∴△CGE∽△AHE.∴CGAH＝EGEH，即CD－EFAH＝FDFD＋BD，∴3－1.6AH＝22＋15，解得AH＝11.9(m)．∴AB＝AH＋HB＝AH＋EF＝11.9＋1.6＝13.5(m)．答：旗杆AB的高度为13.5 m.22．解：设经过时间t，△PB Q与△ABC相似．由题意得AP ＝2t ，B Q ＝4t ，BP ＝10－2t . 当△PB Q ∽△ABC 时，有BP AB ＝BQBC ，即10－2t 10＝4t20，解得t ＝2.5(s )；当△Q BP ∽△ABC 时，有BP BC ＝BQAB ，即10－2t 20＝4t10，解得t ＝1(s)．综上所述，经过2.5 s 或1 s ，△Q BP 和△ABC 相似．23．证明：(1)连接BC .∵AB 为⊙O 的直径，AB ⊥CD ， ∴AC ︵＝AD ︵. ∴∠ACD ＝∠ABC .又∠CAH ＝∠BAC ，∴△ACH ∽△ABC . ∴AH AC ＝AC AB . ∴AH ·AB ＝AC 2. (2)连接CF .∵AC ︵＝AD ︵，∴∠ACE ＝∠F . 又∠CAF ＝∠EAC ，∴△ACE∽△AFC.∴ACAF＝AEAC.∴AE·AF＝AC2.24．解：(1)①52②52(2)无变化．证明：在题图①中，∵DE是△ABC的中位线，∴DE∥AB.∴CECA＝CDCB，∠EDC＝∠B＝90°.在题图②中，∵△EDC在旋转过程中形状、大小不变，∴CECA＝CDCB仍然成立．又∵∠ACE＝∠BCD＝α，∴△CEA∽△CDB.∴AEBD＝ACBC.在Rt△ABC中，AC＝AB2＋BC2＝42＋82＝45，∴AC BC＝458＝52.∴AEBD＝52，即AEBD的大小不变．(3) BD＝45或125 5.。

人教版九年级数学册第二十七章测试卷(附答案)

初中数学人教版九年级下学期第二十七章测试卷一、单选题（共9题；共18分）1.如图，l1∥l2∥l3，AC、DF交于点O，则下列比例中成立的是（）A. B. C. D.2.如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，且DE∥BC，EF∥AB．若AD=2BD，则的值为( )A. B. C. D.3.若= ，则的值为( )A. 1·B.C.D.4.如图，在中，，，为边上的一点，且．若的面积为，则的面积为（）A. B. C. D.5.如图，在ABCD中，点E在对角线BD上，EM∥AD，交AB于点M，EN∥AB，交AD于点N，则下列式子一定正确的是( ）．A. B. C. D.6.如图，在科Rt△ABC中，∠ACB=90°，AC=6，BC=12，点D在边BC上，点E在线段AD上，EF⊥AC于点F，EG⊥EF交AB于点G，若EF=EG，则CD的长为（）A. 3.6B. 4C. 4.8D. 57.下列命题是真命题的是（）A. 如果两个三角形相似，相似比为4:9，那么这两个三角形的周长比为2:3；B. 如果两个三角形相似，相似比为4:9，那么这两个三角形的周长比为4:9；C. 如果两个三角形相似，相似比为4:9，那么这两个三角形的面积比为2:3；D. 如果两个三角形相似，相似比为4:9，那么这两个三角形的面积比为4:9.8.如图，为估算某河的宽度，在河对岸边选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上。

若测得BE=20m，EC=10m，CD=20m，则河的宽度AB等于（）A. 60mB. 40mC. 30mD. 20m9.如图，在矩形ABCD中，E，F分别是AD，AB边上的点，连接CE，DF，他们相交于点G，延长CE交BA 的延长线于点H，则图中的相似三角形共有( )A. 5对B. 4对C. 3对D. 2对二、填空题（共3题；共5分）10.小明想测量一棵树的高度，他发现树的影子恰好落在地面和一躲墙上，如图，此时测得地面上的影长为8米，墙上的影长为4米．同一时刻，一根长为1米且垂直于地面放置的标杆在地面上的影长为2米，则树的高度为________。

人教版九年级数学下册第27章相似单元达标训练试题(含答案)

人教版九年级数学下册第27章相似单元达标训练一．选择题1．下面给出了一些关于相似的命题，其中真命题有( )(1)菱形都相似；(2)等腰直角三角形都相似；(3)正方形都相似；(4)矩形都相似；(5)正六边形都相似．A．1个 B．2个 C．3个 D．4个2．图K－9－2中的四个三角形与图K－9－1中的三角形相似的是( )图K－9－1图K－9－23．下列关于位似图形的表述：①相似图形一定是位似图形，位似图形一定是相似图形；②位似图形一定有位似中心；③如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么这两个图形是位似图形；④位似图形上任意两点到位似中心的距离之比等于相似比．其中正确的序号是( )A．②③ B．①②C．③④ D．②③④4．五边形ABCDE相似于五边形A′B′C′D′E′，若对应边AB与A′B′的长分别为50厘米和40厘米，则五边形A′B′C′D′E′与五边形ABCDE的相似比是( ) A．5∶4 B．4∶5 C．5∶2 5 D．25∶55. 如图，在△ABC中，AD是中线，BC＝8，∠B＝∠DAC，则线段AC的长为( )A．4 B．4 2 C．6 D．4 36．某学习小组在讨论“变化的鱼”时，知道大鱼与小鱼是位似图形，如图，则小鱼上的点(a，b)对应大鱼上的点( )A．(－2a，－2b) B．(－a，－2b)C．(－2b，－2a) D．(－2a，－b)7．图K－6－4中与图K－6－3相似的图形是( )图K－6－3图K－6－48．如图K－10－6，已知矩形ABCD的顶点A，D分别落在x轴、y轴上，OD＝2OA＝6，AD∶AB＝3∶1，则点C的坐标是( )图K－10－6A．(2，7) B．(3，7) C．(3，8) D．(4，8)9．如图K－14－4所示，△A′B′C′是△ABC以点O为位似中心经过位似变换得到的，若△A′B′C′的面积与△ABC的面积比是4∶9，则OB′∶OB为( )图K－14－4A．2∶3 B．3∶2C．4∶5 D．4∶910．观察图K－6－1中各组图形，其中相似的图形有( )图K －6－1A ．3组B ．4组C ．5组D ．6组二、填空题11．如图K －15－4，△ABO 三个顶点的坐标分别为A(2，4)，B(6，0)，O(0，0)，以原点O 为位似中心，把这个三角形缩小为原来的12，可以得到△A′B′O，已知点B′的坐标是(3，0)，则点A′的坐标是________．图K －15－412．如图K －9－5，D 是△ABC 内的一点，连接BD 并延长到点E ，连接AD ，AE ，若AD AB＝DE BC ＝AEAC，且∠CAE ＝29°，则∠BAD ＝________°.图K －9－513．如图K －7－2，已知在矩形ABCD 中，AB ＝1，在BC 上取一点E ，沿AE 将△ABE 向上折叠，使点B 落在AD 上的点F 处．若四边形FDCE 与矩形ABCD 相似，则AD ＝________．图K －7－214．在平面直角坐标系中，点C ，D 的坐标分别为C(2，3)，D(1，0)．现以原点为位似中心，将线段CD 放大得到线段AB ，若点D 的对应点B 在x 轴上且OB ＝2，则点C 的对应点A 的坐标为__________．15.如图K －11－8，Rt △AOB 的一条直角边OB 在x 轴上，双曲线y ＝kx(x >0)经过斜边OA 的中点C ，与另一条直角边交于点D .若S △OCD ＝9，则S △OBD 的值为________．图K －11－816.放大镜下的图形和原来的图形________相似图形；哈哈镜中的图形和原来的图形________相似图形．(填“是”或“不是”)三、解答题17．如图K －6－6是用相似图形设计的图案．图K －6－6(1)想一想：各个图案的基本图形是什么？(2)做一做：自己设计几个漂亮有趣的图案(至少两个)．18．如图K －11－11所示，在▱ABCD 中，E 是CD 延长线上的一点，BE 与AD 交于点F ，DE ＝12CD .(1)求证：△ABF ∽△CEB ；(2)若△DEF 的面积为2，求▱ABCD 的面积．图K －11－1119．如图K －14－11，矩形ABCD 与矩形AB ′C ′D ′是位似图形，点A 为位似中心，已知矩形ABCD 的周长为24，BB ′＝4，DD ′＝2，求AB ，AD 的长．图K －14－1120．如图K－12－8是一个常见铁夹的侧面示意图，OA，OB表示铁夹的两个面，C是轴，CD⊥OA于点D，已知DA＝15 mm，DO＝24 mm，DC＝10 mm，我们知道铁夹的侧面是轴对称图形，请求出A，B两点间的距离．图K－12－821. 如图K－7－4是学校内的一矩形花坛，四周修筑的小路中相对的两条小路的宽均相等．已知AB＝20米，AD＝30米，试问当小路的宽x与y的比值为多少时，能使小路四周所围成的矩形A′B′C′D′与矩形ABCD相似？(A′B′与AB是对应边)图K－7－422．如图K－12－9 所示，小明想测量电线杆AB的高度，发现电线杆的影子恰好落在土坡的坡面CD和地面BC上，量得CD＝4米，BC＝10米，CD与地面成30°的角，且此时测得1米高的标杆的影长为2米，求电线杆的高度(精确到0.1米)．图K－12－9参考答案一、选择题1．下面给出了一些关于相似的命题，其中真命题有( C )(1)菱形都相似；(2)等腰直角三角形都相似；(3)正方形都相似；(4)矩形都相似；(5)正六边形都相似．A．1个 B．2个 C．3个 D．4个2．图K－9－2中的四个三角形与图K－9－1中的三角形相似的是( B )图K－9－1图K－9－23．下列关于位似图形的表述：①相似图形一定是位似图形，位似图形一定是相似图形；②位似图形一定有位似中心；③如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么这两个图形是位似图形；④位似图形上任意两点到位似中心的距离之比等于相似比．其中正确的序号是( A )A．②③ B．①②C．③④ D．②③④4．五边形ABCDE相似于五边形A′B′C′D′E′，若对应边AB与A′B′的长分别为50厘米和40厘米，则五边形A′B′C′D′E′与五边形ABCDE的相似比是( B ) A．5∶4 B．4∶5 C．5∶2 5 D．25∶55. 如图，在△ABC中，AD是中线，BC＝8，∠B＝∠DAC，则线段AC的长为( B )A．4 B．4 2 C．6 D．4 36．某学习小组在讨论“变化的鱼”时，知道大鱼与小鱼是位似图形，如图，则小鱼上的点(a，b)对应大鱼上的点( A )A．(－2a，－2b) B．(－a，－2b)C．(－2b，－2a) D．(－2a，－b)7．图K－6－4中与图K－6－3相似的图形是( D )图K－6－3图K －6－48．如图K －10－6，已知矩形ABCD 的顶点A ，D 分别落在x 轴、y 轴上，OD ＝2OA ＝6，AD ∶AB ＝3∶1，则点C 的坐标是( A )图K －10－6A ．(2，7)B ．(3，7)C ．(3，8)D ．(4，8)9．如图K －14－4所示，△A ′B ′C ′是△ABC 以点O 为位似中心经过位似变换得到的，若△A ′B ′C ′的面积与△ABC 的面积比是4∶9，则OB ′∶OB 为( A )图K －14－4A ．2∶3B ．3∶2C ．4∶5D ．4∶910．观察图K －6－1中各组图形，其中相似的图形有( B )图K －6－1A ．3组B ．4组C ．5组D ．6组二、填空题11．如图K －15－4，△ABO 三个顶点的坐标分别为A(2，4)，B(6，0)，O(0，0)，以原点O 为位似中心，把这个三角形缩小为原来的12，可以得到△A′B′O，已知点B′的坐标是(3，0)，则点A′的坐标是________．图K －15－4[答案] (1，2)12．如图K －9－5，D 是△ABC 内的一点，连接BD 并延长到点E ，连接AD ，AE ，若AD AB＝DE BC ＝AEAC，且∠CAE ＝29°，则∠BAD ＝________°.图K －9－5[答案] 2913．如图K －7－2，已知在矩形ABCD 中，AB ＝1，在BC 上取一点E ，沿AE 将△ABE 向上折叠，使点B 落在AD 上的点F 处．若四边形FDCE 与矩形ABCD 相似，则AD ＝________．图K －7－2[答案].5＋1214．在平面直角坐标系中，点C ，D 的坐标分别为C(2，3)，D(1，0)．现以原点为位似中心，将线段CD 放大得到线段AB ，若点D 的对应点B 在x 轴上且OB ＝2，则点C 的对应点A 的坐标为__________．[答案] (4，6)或(－4，－6)15.如图K －11－8，Rt △AOB 的一条直角边OB 在x 轴上，双曲线y ＝kx(x >0)经过斜边OA 的中点C ，与另一条直角边交于点D .若S △OCD ＝9，则S △OBD 的值为________．图K －11－8[答案] 616.放大镜下的图形和原来的图形________相似图形；哈哈镜中的图形和原来的图形________相似图形．(填“是”或“不是”)[答案] 是不是三、解答题17．如图K －6－6是用相似图形设计的图案．图K －6－6(1)想一想：各个图案的基本图形是什么？(2)做一做：自己设计几个漂亮有趣的图案(至少两个)．解：(1)各个图案的基本图形分别是直角三角形、正方形、正五边形． (2)答案不唯一，只要是用相似图形做的，都符合要求．如图：18．如图K －11－11所示，在▱ABCD 中，E 是CD 延长线上的一点，BE 与AD 交于点F ，DE ＝12CD .(1)求证：△ABF ∽△CEB ；(2)若△DEF 的面积为2，求▱ABCD 的面积．图K －11－11[解析] (1)由平行四边形的对角相等，对边平行，证得△ABF ∽△CEB ；(2)由△DEF ∽△CEB ，△DEF ∽△ABF ，根据相似三角形的面积比等于相似比的平方可以求出△ABF 和△BCE 的面积，从而▱ABCD 的面积可求．解：(1)证明：∵四边形ABCD 是平行四边形， ∴∠A ＝∠C ，AB ∥CD ， ∴∠ABF ＝∠CEB ， ∴△ABF ∽△CEB.(2)∵四边形ABCD 是平行四边形， ∴AD ∥BC ，AB 綊CD ，∴△DEF ∽△CEB ，△DEF ∽△ABF.∵DE ＝12CD ，∴EC ＝3DE ，∴S △DEF S △CEB ＝(DE EC )2＝19，S △DEF S △ABF ＝(DE AB )2＝14. ∵S △DEF ＝2，∴S △CEB ＝18，S △ABF ＝8,∴S 四边形BCDF ＝S △CEB －S △DEF ＝16，∴S ▱ABCD ＝S 四边形BCDF ＋S △ABF ＝16＋8＝24.19．如图K －14－11，矩形ABCD 与矩形AB ′C ′D ′是位似图形，点A 为位似中心，已知矩形ABCD 的周长为24，BB ′＝4，DD ′＝2，求AB ，AD 的长．图K －14－11解：∵矩形ABCD 的周长为24， ∴AB ＋AD ＝12.设AB ＝x ，则AD ＝12－x ，AB′＝x ＋4，AD′＝14－x. ∵矩形ABCD 与矩形AB′C′D′是位似图形， ∴AB AB′＝AD AD′，即x x ＋4＝12－x 14－x，解得x ＝8，∴AB ＝8，AD ＝12－8＝4.20．如图K －12－8是一个常见铁夹的侧面示意图，OA ，OB 表示铁夹的两个面，C 是轴，CD ⊥OA 于点D ，已知DA ＝15 mm ，DO ＝24 mm ，DC ＝10 mm ，我们知道铁夹的侧面是轴对称图形，请求出A ，B 两点间的距离．图K －12－8解：如图，连接AB ，同时连接OC 并延长交AB 于点E ，∵铁夹的侧面是轴对称图形，故OE 是对称轴，∴OE ⊥AB ，AE ＝BE. ∵∠COD ＝∠AOE ，∠CDO ＝∠AEO ＝90°，∴Rt △OCD ∽Rt △OAE ，∴OC OA ＝CDAE ，而OC ＝OD 2＋DC 2＝242＋102＝26，∴2624＋15＝10AE ，∴AE ＝39×1026＝15，∴AB ＝2AE ＝30(mm)．答：A ，B 两点间的距离为30 mm.21. 如图K －7－4是学校内的一矩形花坛，四周修筑的小路中相对的两条小路的宽均相等．已知AB ＝20米，AD ＝30米，试问当小路的宽x 与y 的比值为多少时，能使小路四周所围成的矩形A ′B ′C ′D ′与矩形ABCD 相似？(A ′B ′与AB 是对应边) 图K －7－4[解析] 若矩形A′B′C′D′与矩形ABCD 相似，由相似多边形的性质可知，这两个矩形的对应边成比例，即可求出相似比，再由相似比求出x 与y 的比值．解：由题意可知，矩形A′B′C′D′与矩形ABCD 相似(A′B′与AB 是对应边)，则应有AB A′B′＝BC B′C′，即2020＋2y ＝3030＋2x ，从而有20(30＋2x)＝30(20＋2y)，解得x y ＝32.22．如图K －12－9 所示，小明想测量电线杆AB 的高度，发现电线杆的影子恰好落在土坡的坡面CD 和地面BC 上，量得CD ＝4米，BC ＝10米，CD 与地面成30°的角，且此时测得1米高的标杆的影长为2米，求电线杆的高度(精确到0.1米)．图K －12－9解：如图所示，过点D 作DF ⊥BC 交BC 的延长线于点F ，延长AD 交BC 的延长线于点E.∵∠DCF ＝30°，∴DF ＝12CD ＝2米，CF ＝CD 2－DF 2＝2 3 米．根据已知条件，1米高的标杆的影长为2米，可求得EF ＝2DF ＝4米，∴BE ＝(14＋2 3)米．∵DF ⊥BE ，AB ⊥BE ，∴△DFE ∽△ABE ，∴DF AB ＝EF BE，∴2AB ＝4BE， ∴AB ＝12BE ＝7＋3≈8.7(米)．即电线杆的高度约为8.7米．1、只要朝着一个方向奋斗，一切都会变得得心应手。

2023年人教版九年级数学下册第27章《相似》复习检测卷(一)附答案解析

2023年九年级数学下册第27章《相似》复习检测卷（一）考试范围：§27.1图形的相似~27.2相似三角形的判定满分：120分一、选择题(每小题3分，共30分)1.将△ABC 的每条边都扩大3倍得到△DEF ，其中点A 、B 、C 的对应点分别是D 、E 、F ，则∠D 与∠A 的关系为（）A .∠D ＝∠AB .∠D ＝3∠AC .∠D ＝6∠AD .∠D ＝9∠A2.如图，在△ABC 中，∠A ＝78°，AB ＝4，AC ＝6，将△ABC 沿图中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）3.如图，已知直线a ∥b ∥c ，直线m 、n 与a 、b 、c 分别交于点A 、C 、E ，B 、D 、F ，AC ＝8，CE ＝12，BD ＝6，则DF 的长为（）A .4B .5C .9D .74.如图，在△ABC 中，D 、E 分别为AB 、AC 边上的点，DE ∥BC ，F 为BC 边上一点，连接AF交DE 于点G ，则下列结论中一定正确的是（）A .AD AEAB CE=B .AC AEGF BD=C .BD CEAD AE=D .AG ACAF CE=5.如图，在正方形网格上有两个三角形，且△ABC 和△DEF 相似，则∠BAC 的度数为（）A .135°B .125°C .115°D .105°6.如图，△ACP ∽△ABC ，若∠A ＝100°，∠ACP ＝20°，则∠ACB 的度数是（）A .80°B .60°C .50°D .30°7.如图，在□ABCD 中，EF ∥AB ，DE ∶EA ＝2∶3，EF ＝4，则CD 的长为（）A .6B .8C .9D .108.要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为5cm 、6cm 和9cm ，另一个三角形的最短边长为2.5cm ，则它的最长边为（）A .3cmB .4cmC .4.5cmD .5cm9.如图，在矩形ABCD 中，AB ＝a ，AD ＝3，按照图中的方式将它分成完全相同的三个矩形，如果每一个小矩形都与矩形ABCD 相似，则a 的值为（）第5题第3题第4题第6题第7题第9题第10题A .22B .23C .33D .3210.如图，正方形ABCD 的边长为4，E 是BC 边上一点，过点E 作EF ⊥AE 交CD 边于点F ，则CF 的最大值是（）A .0.5B .1C .1.5D .2二、填空题(每小题3分，共18分)11.如图，添加一个条件__________________，使△ADE ∽△ACB .12.如图，在□ABCD 中，E 是AD 的中点，EC 交对角线BD 于点F ，则BF ∶FD 的值为_________.13.如图，在△ABC 中，DE ∥BC ，若AD ＝1，BD ＝3，BC ＝8，则DE 的长为________.14.已知654a b c==，且a ＋b －2c ＝6，则a 的值为_______.15.如图，在Rt △OAC 中，O 为坐标原点，直角顶点C 在x 轴的正半轴上，反比例函数ky x=(k ＞0)在第一象限的图象经过OA 的中点B ，交AC 于点D ，连接OD ，若△OCD ∽△ACO ，则直线OA 的解析式为_______.16.如图，直线l 1∥l 2∥l 3，直线l 1与l 2之间的距离为2，直线l 2与l 3之间的距离为1，等边△ABC 的三个顶点分别在直线l 1、l 2、l 3上，则等边三角形的边长是______.三、解答题(共8题，共72分)17.(8分)如图，四边形ABCD ∽四边形A 'B 'C 'D '，∠BCD ＝125°，分别求x 、y 、α的值.18.(8分)如图，在矩形ABCD 中，点E 、F 分别在BC 、CD 上，AE ⊥BF 于点M ，若BC ＝2AB ，探究AE 与BF 的数量关系，并证明你的结论.第10题第11题第16题第12题第13题第15题19.(8分)如图，在四边形ABCD中，AC平分∠BAD，∠ADC＝∠ACB＝90°.(1)求证：AC2＝AB·AD；(2)若BC＝3，AB＝5，求CD的长.20.(8分)如图，在矩形ABCD中，E是AD上一点，连接BE.(1)请用尺规在BE上求作一点P，使得△PCB∽△ABE(不写作法，保留作图痕迹)；(2)若AE＝3，AB＝4，BC＝6，求EP的长.21.(8分)如图，在△ABC中，AB＝2，BC＝4，D为BC边上一点，BD＝1.(1)求证：△ABD∽△CBA；(2)作DE∥AB交AC于点E，请直接写出另一个与△ABD相似的三角形，并求出DE的长.22.(10分)在△ABC中，AB＝6，AC＝8，点D、E分别在AB、AC上，连接DE，设BD＝x(0＜x＜6)，CE＝y(0＜y＜8).(1)当x＝2，y＝5时，求证：△AED∽△ABC；(2)若△ADE和△ABC相似，求y与x的函数表达式.23.(10分)如图，在△ABC中，∠ABC＝90°，D是斜边AC的中点，连接DB.过点A作AE⊥BD于点F，交BC于点E.(1)求证：EB2＝EF・EA；(2)若AB＝4，CE＝3BE，求AE的长.24.(12分)(1)【问题背景】如图1，D是等边△ABC中AB边上的点，以CD为边在CD的上方作等边△CDE，连接AE，求证：BD＝AE；(2)【尝试应用】如图2，D是Rt△ABC中AB边上的一点，∠B＝90°，∠BAC＝30°，以CD为边在CD的上方作Rt△CDE，使∠CDE＝90°，∠CED＝30°，连接AE，请探究BD与AE的数量关系，并说明理由；(3)【拓展创新】如图3，在Rt△ABC中，∠ABC＝90°，点D在AB边上，以CD为边在CD的上方作Rt△CDE，使∠CDE＝90°，43DE ABCD BC==，DE交AC于F，若AD＝3BD，求AFDF的值.《相似》阶段检测卷(一)考试范围：§27.1图形的相似~27.2相似三角形的判定满分：120分一、选择题(每小题3分，共30分)1.将△ABC 的每条边都扩大3倍得到△DEF ，其中点A 、B 、C 的对应点分别是D 、E 、F ，则∠D 与∠A 的关系为（）A .∠D ＝∠AB .∠D ＝3∠AC .∠D ＝6∠A D .∠D ＝9∠A【答案】A .详解：依题意，△ABC 与△DEF 的三边成比例，∴△ABC ∽△DEF ，∴∠A ＝∠D ，故选A .2.如图，在△ABC 中，∠A ＝78°，AB ＝4，AC ＝6，将△ABC 沿图中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）【答案】C .详解：由两个角分别相等的两个三角形相似，知选项A 和B 中的阴影三角形与原三角形相似，选项D 中，阴影三角形的∠A 的两边分别为4－1＝3，6－4＝2，∵4623=，∠A ＝∠A ，∴选项D 中的阴影三角形与原三角形相似.而选项C 中，不能保证∠B 的两边成比例，故选C .3.如图，已知直线a ∥b ∥c ，直线m 、n 与a 、b 、c 分别交于点A 、C 、E ，B 、D 、F ，AC ＝8，CE ＝12，BD ＝6，则DF 的长为（）A .4B .5C .9D .7【答案】C .详解：∵a ∥b ∥c ，∴AC BD CE DF =，即8612DF=，解得DF ＝9，故选C . 4.如图，在△ABC 中，D 、E 分别为AB 、AC 边上的点，DE ∥BC ，F 为BC 边上一点，连接AF 交DE 于点G ，则下列结论中一定正确的是（）A .AD AEAB CE=B .AC AEGF BD=C .BD CEAD AE=D .AG ACAF CE=【答案】C .详解：∵DE ∥BC ，∴BD CE AD AE =，故C 对；AD AEAB AC=，故A 错；AG AE ADAF AC AB==，故D 错；选项B 中的4条线段不成比例，故D 错.故选C .5.如图，在正方形网格上有两个三角形，且△ABC 和△DEF 相似，则∠BAC 的度数为（）A .135°B .125°C .115°D .105°【答案】A .详解：∵△ABC 和△DEF 相似，观察角的大小，∠BAC ＝∠DEF ＝90°＋45°＝135°，故选A . 6.如图，△ACP ∽△ABC ，若∠A ＝100°，∠ACP ＝20°，则∠ACB 的度数是（）A .80°B .60°C .50°D .30°【答案】B .详解：在△ACP 中，∵∠A ＝100°，∠ACP ＝20°，∴∠APC ＝60°.∵△ACP ∽△ABC ，∴∠ACB ＝∠APC ＝60°，故选B .7.如图，在□ABCD 中，EF ∥AB ，DE ∶EA ＝2∶3，EF ＝4，则CD 的长为（）A .6B .8C .9D .10【答案】D .详解：∵EF ∥AB ，∴EF DEAB DA=，∵DE ∶EA ＝2∶3，EF ＝4，∴4223AB =+，∴AB ＝10，则CD ＝AB ＝10，故选D .8.要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为5cm 、6cm 和9cm ，另一个三角形的最短边长为2.5cm ，则它的最长边为（）A .3cmB .4cmC .4.5cmD .5cm【答案】C .详解：设所求的最长边为xcm ，则592.5x=，解得x ＝4.5，故选C .9.如图，在矩形ABCD 中，AB ＝a ，AD ＝3，按照图中的方式将它分成完全相同的三个矩形，如果每一个小矩形都与矩形ABCD 相似，则a 的值为（）A .B .C .D .【答案】C .详解：小矩形的边边分别为13a 和3，∵小矩形与矩形ABCD 相似，∴13a ∶3＝3∶a ，解得a ＝±(舍去负值)，∴a ＝C .10.如图，正方形ABCD 的边长为4，E 是BC 边上一点，过点E 作EF ⊥AE交CD 边于点F ，则CF 的最大值是（）A .0.5B .1C .1.5D .2【答案】B .详解：∵∠B ＝∠C ＝90°，AE ⊥EF ，可证△ABE ∽△ECF ，∴AB BECE CF=，设BE ＝x ，则CE ＝4－x ，∴44x x CF =-，∴CF ＝14x (4－x )＝－14(x －2)2＋1，当x ＝2时，CF 取得最大值1，故选B .二、填空题(每小题3分，共18分)11.如图，添加一个条件__________________，使△ADE ∽△ACB .【答案】答案不唯一，可以填下列中的一个：∠ADE ＝∠C ，∠AED ＝∠B ，AD AEAC AB=.12.如图，在□ABCD 中，E 是AD 的中点，EC 交对角线BD 于点F ，则BF ∶FD的值为_________.【答案】2.详解：∵四边形ABCD 为平行四边形，∴BC ＝AD ，BC ∥AD .∵E 为AD 的中点，∴BC ＝AD ＝2DE ，由AD ∥BC ，得△BCF ∽DEF ，∴BF ∶FD ＝BC ∶DE ＝2.13.如图，在△ABC 中，DE ∥BC ，若AD ＝1，BD ＝3，BC ＝8，则DE 的长为________.【答案】2.详解：∵DE ∥BC ，∴AD DE AB BC =，即1138DE=+，∴DE ＝2.14.已知654a b c==，且a ＋b －2c ＝6，则a 的值为_______.【答案】12.详解：∵654a b c==，故可设a ＝6x ，b ＝5x ，c ＝4x ，代入a ＋b －2c ＝6，得：6x ＋5x －2(4x )＝6，解得x ＝2，∴a ＝6x ＝12.15.如图，在Rt △OAC 中，O 为坐标原点，直角顶点C 在x 轴的正半轴上，反比例函数ky x=(k ＞0)在第一象限的图象经过OA 的中点B ，交AC 于点D ，连接OD ，若△OCD ∽△ACO ，则直线OA 的解析式为_______.【答案】y ＝2x .详解：设B (t ，k t )，则直线OA 的解析式为y ＝2ktx .∵B 为OA 的中点，∴A (2t ，2k t )，∴D (2t ，2k t )，OC ＝2t ，CD ＝2k t ，CA ＝2kt.∵△OCD ∽△ACO ，∴OC CD AC OC =，∴OC 2＝AC ·CD ，∴4t 2＝2k t ·2k t，∴k 2＝4t 4，∵k ＞0，∴k ＝2t 2，∴直线OA 的解析式为y ＝2x .16.如图，直线l 1∥l 2∥l 3，直线l 1与l 2之间的距离为2，直线l 2与l 3之间的距离为1，等边△ABC 的三个顶点分别在直线l 1、l 2、l 3上，则等边三角形的边长是______.【答案】2213.F详解：过C 作CE ⊥AC 交AB 的延长线于D ，过C 作CF ⊥l 1于F ，交l 3于H ，过E 作ED ⊥FC 交延长线于D ，∵∠AFC ＝∠ACE＝∠CDE ＝90°，∴△ACF ∽△CED ，∴DE CD CECF AF AC==，∵△ABC 为等边△，∴CE ，AB ＝BC ＝BE ，则CD AF .依题意，FH ＝FC ＋CH ＝2＋1＝3，由AB ＝BE ，l 1∥l 3∥ED ，得DH ＝FH ＝3，CD ＝4，∴AF CD AC .三、解答题(共8题，共72分)17.(8分)如图，四边形ABCD ∽四边形A 'B 'C 'D '，∠BCD ＝125°，分别求x 、y 、α的值.【答案】∵四边形ABCD ∽四边形A 'B 'C 'D '，∴∠C ′＝∠C ＝125°，∴∠α＝360°－80°－75°－125°＝80°，且AD AB BC A D A B B C ==''''''，即45316x y==，解得x ＝20，y ＝12.答：x ＝20，y ＝12，α＝80°.18.(8分)如图，在矩形ABCD 中，点E 、F 分别在BC 、CD 上，AE ⊥BF 于点M ，若BC ，探究AE 与BF 的数量关系，并证明你的结论.【答案】BF AE ，理由如下：∵四边形ABCD 是矩形，∴∠ABC ＝∠C ，∵AE ⊥BF ，∴∠AMB ＝∠BAM ＋∠ABM ＝90°，又∵∠ABM ＋∠CBF ＝90°，∴∠BAM ＝∠CBF ，∴△ABE ∽△BCF ，∴AE AB BF BC ==，∴BF AE .19.(8分)如图，在四边形ABCD 中，AC 平分∠BAD ，∠ADC ＝∠ACB ＝90°.(1)求证：AC 2＝AB ·AD ；(2)若BC ＝3，AB ＝5，求CD 的长.【答案】(1)∵AC 平分∠BAD ，∴∠DAC ＝∠CAB .∵∠ADC ＝∠ACB ＝90°，∴△ADC ∽△ACB ，∴AD ACAC AB=，∴AC 2＝AB ·AD .(2)在Rt △ABC 中，∵BC ＝3，AB ＝5，由勾股定理，得AC ＝4.∵AC 2＝AB ·AD ，∴42＝5AD ，∴AD ＝165.在Rt △ADC 中，CD 125.20.(8分)如图，在矩形ABCD 中，E 是AD 上一点，连接BE .(1)请用尺规在BE 上求作一点P ，使得△PCB ∽△ABE(不写作法，保留作图痕迹)；(2)若AE ＝3，AB ＝4，BC ＝6，求EP 的长.【答案】(1)如图所示；(2)由勾股定理，得BE 5，由△PCB ∽△ABE ，得BP BC AE BE =，即635BP =，∴BP ＝185，∴EP ＝BE －BP ＝5－185＝75.21.(8分)如图，在△ABC 中，AB ＝2，BC ＝4，D 为BC 边上一点，BD ＝1.(1)求证：△ABD ∽△CBA ；(2)作DE ∥AB 交AC 于点E ，请直接写出另一个与△ABD 相似的三角形，并求出DE 的长.【答案】(1)∵AB ＝2，BC ＝4，BD ＝1，∴AB BDBC AB=，又∠ABD ＝∠CBA ，∴△ABD ∽△CBA .(2)如图，∵DE ∥AB ，∴△CDE ∽△CBA ，∵△ABD ∽△CBA ，∴△CDE ∽△ABD ，∴DE CD BD AB =，即4112DE -=，∴DE ＝1.5.22.(10分)在△ABC 中，AB ＝6，AC ＝8，点D 、E 分别在AB 、AC 上，连接DE ，设BD ＝x (0＜x ＜6)，CE ＝y (0＜y ＜8).(1)当x ＝2，y ＝5时，求证：△AED ∽△ABC ；(2)若△ADE 和△ABC 相似，求y 与x 的函数表达式.【答案】(1)∵AB ＝6，BD ＝x ＝2，∴AD ＝4.∵AC ＝8，CE ＝y ＝5，∴AE ＝3.∴AD AEAC AB=.又∵∠EAD ＝∠BAC ，∴△AED ∽△ABC .(2)分两种情况，1°当△ADE ∽△ABC 时，AD AE AB AC =，则6868x y --=，∴y ＝43x (0＜x ＜6).2°当△ADE ∽△ACB 时，AD AE AC AB =，则6886x y --=，∴y ＝34x ＋72(0＜x ＜6).23.(10分)如图，在△ABC 中，∠ABC ＝90°，D 是斜边AC 的中点，连接DB .过点A 作AE ⊥BD 于点F ，交BC 于点E .(1)求证：EB 2＝EF ・EA ；(2)若AB ＝4，CE ＝3BE ，求AE 的长.【答案】(1)∵AE ⊥BD ，∴∠BFE ＝90°＝∠ABC .又∵∠BEF ＝∠AEB ，∴△EBF ∽△EAB ，∴BE EFAE BE=，∴EB 2＝EF ・EA .(2)在Rt △ABC 中，∵D 为斜边AC 的中点，∴BD ＝CD ，∴∠DBC ＝∠C .由(1)，得△EBF∽△EAB，∴∠EBF＝∠EAB，∴∠C＝∠EAB.又∠ABE＝∠CBA，∴△BAE∽△BCA，∴AB BEBC AB=，∴AB2＝BE·BC.∵AB＝4，CE＝3BE，∴BC＝4BE，42＝BE(4BE)，∴BE＝2.∴AE＝.24.(12分)(1)【问题背景】如图1，D是等边△ABC中AB边上的点，以CD为边在CD的上方作等边△CDE，连接AE，求证：BD＝AE；(2)【尝试应用】如图2，D是Rt△ABC中AB边上的一点，∠B＝90°，∠BAC＝30°，以CD为边在CD的上方作Rt△CDE，使∠CDE＝90°，∠CED＝30°，连接AE，请探究BD与AE的数量关系，并说明理由；(3)【拓展创新】如图3，在Rt△ABC中，∠ABC＝90°，点D在AB边上，以CD为边在CD的上方作Rt△CDE，使∠CDE＝90°，43DE ABCD BC==，DE交AC于F，若AD＝3BD，求AFDF的值.【答案】(1)∵△ABC与△CDE均为等边三角形，∴BC＝AC，CD＝CE，∠ACB＝∠DCE＝60°，∴∠BCD＝∠ACE，∴△BCD≌△ACE，∴BD＝AE.(2)AE＝2BD，理由如下：∵∠BAC＝∠DEC＝30°，∠B＝∠EDC＝90°，∴△ABC∽△EDC，∴BC AC CD CE=.由条件得∠ACB＝∠DCE，AC＝2BC，∴∠BCD＝∠ACE，∴△BCD∽△ACE，∴12BD BCAE AC==，∴AE＝2BD.(3)由(2)得，△BCD∽△ACE，∴AE ACBD BC=，∵43DE ABCD BC==，∴53ACBC=，∴53AE ACBD BC==设BD＝a，则AD＝3BD＝3a，AB＝4a，BC＝3a，CDa，AE＝53BD＝53a.∵△AFE∽△DFC ，∴53aAF AEDF CD=.。

第27章相似三角形应用举例达标训练2022-2023学年人教版九年级数学下册

人教版九年级数学下册27.2.3 相似三角形应用举例达标训练一、单选题1．如图，阳光从教室的窗户射入室内，窗户框AB 在地面上的影子长DE ＝1.8m ，窗户下沿到地面的距离BC＝1m ，EC ＝1.2m ，那么窗户的高AB 为（）A ．1.5mB ．1.6mC ．1.86mD ．2.16m2．某班某同学要测量学校升旗的旗杆高度，在同一时刻，量得某一同学的身高是1.5m ，影长是1m ，旗杆的影长是8m ，则旗杆的高度是（） A ．12mB ．11mC ．10mD ．9m3．如图，王华晚上由路灯A 下的B 处走到C 处时，测得影子CD 的长为1 m ，继续往前走3 m 到达E 处时，测得影子EF 的长为2 m.已知王华的身高是1.5 m ，那么路灯A 的高度AB 等于( )A ．4.5 mB ．6 mC ．7.2 mD ．8 m4．如图，身高为1.6m 的某学生想测量一棵大树的高度，她沿着树影BA 由B 到A 走去，当走到C 点时，她的影子顶端正好与树的影子顶端重合，测得BC=3.2m ，CA=0.8m ，则树的高度为（）A ．4.8mB ．6.4mC ．8mD ．10m5．如图，小明晚上由路灯A 下的点B 处走到点C 处时，测得自身影子CD 的长为1米，他继续往前走3米到达点E 处（即CE=3米），测得自己影子EF 的长为2米，已知小明的身高是1.5米，那么路灯A 的高度AB 是（）A ．4.5米B ．6米C ．7.2米D ．8米6．如图所示的梯形梯子，AA′∥EE′，AB=BC=CD=DE ，A′B′=B′C′=C′D′=D′E′，AA′=60cm ，EE′=80cm ．则BB′的长为（）A ．0.65mB ．0.675mC ．0.725mD ．0.75m7．现有一个测试距离为5m 的视力表（如图），根据这个视力表，小华想制作一个测试距离为3m 的视力表，则图中的ab的值为（）A ．32B ．23C ．35D ．538．如图，A 、B 两点被池塘隔开，在AB 外任选一点C ，连接AC，BC分别取其三等分点M，N ，量得MN=38m ．则AB 的长是（）A ．76mB ．104mC ．114mD ．152m二、填空题9．图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面AB=cm10．小明在离路灯底部6m 处测得自己的影子长为1.2m ，小明的身高为1.6m ，那么路灯的高度为m .11．如图，AB 是斜靠在墙角的长梯，梯角B 距墙0.8m ，长梯上一点D 距墙0.7m ，BD 长0.55m ，则梯子的长度是 m ．12．如图，某风景区在建设规划过程中，需要测量两岸码头A 、B 之间的距离．设计人员在O 点设桩，取OA 、OB 的三等分点C 、D ，测得CD=25m ，则AB= ．13．为测量操场上悬挂国旗的旗杆的高度，设计的测量方案如图所示：标杆高度CD=3m ，标杆与旗杆的水平距离BD=15 m ，人的眼睛与地面的高度EF=1.6m ，人与标杆CD 的水平距离DF=2m ，E 、C 、A 三点共线，则旗杆AB 的高度为米．14．如图；课外活动小组测量学校旗杆的高度．如图，在地面上C 处放一小镜子，当镜子离旗杆AB 底端6米，小明站在离镜子3米的E 处，恰好能看到镜子中旗杆的顶端，测得小明眼睛D 离地面1.5米，则旗杆AB 的高度约是米．三、解答题15．如图，要测量河岸相对的两点A 、B 的距离，先从点B 出发与AB 成90°角方向，向前走50m 到C 处立一根标杆，然后方向不变继续朝前走10m 到D 处，在D 处转90°沿DE 方向再走17m ，这时A 、C 、E 在同一直线上．问A 、B 间的距离约为多少？16．如图，某人在点A 处测量树高，点A 到树的距离AD 为21米，将一长为2米的标杆BE 在与点A 相距3米的点B 处垂直立于地面，此时，观察视线恰好经过标杆顶点E及树的顶点C，求树CD的高．17．又到了一年中的春游季节．某班学生利用周末去参观“三军会师纪念塔”．下面是两位同学的一段对话：甲：我站在此处看塔顶仰角为60°；乙：我站在此处看塔顶仰角为30°；甲：我们的身高都是1.6m ；乙：我们相距36m ．请你根据两位同学的对话，计算纪念塔的高度．（精确到1米）18．如图，已知∥ABC 的面积S ∥ABC =1.在图（1）中，若11112AA BB CC AB BC CA ===，则11114A B C S =；在图（2）中，若22213AA BB CC AB BC CA ===，则22213A B C S =；在图（3）中，若33314AA BB CC AB BC CA ===，则333716A B C S =；按此规律，若44415AA BB CC AB BC CA ===，则444A B C S = 若88819AA BB CC AB BC CA ===，则888A B C S = . 19．如图，在直角梯形ABCD 中，AD∥BC ，∥A=90°，BD∥CD ，垂足为D ．（1）若AD=9，BC=16，求BD 的长；（2）求证：AB 2•BC=CD 2•AD ．答案解析部分1．【答案】A【解析】【解答】∵BE∥AD，∴∥BCE∥∥ACD，∴CB CEAC CD=，即CB CEAB BC DE EC=++，∵BC=1，DE=1.8，EC=1.2∴1 1.21 1.8 1.2 AB=++∴1.2AB=1.8，∴AB=1.5m．故答案为：A．【分析】先证明∥BCE∥∥ACD，再利用相似三角形的性质可得CB CEAC CD=，即CB CEAB BC DE EC=++，再将数据代入计算可得1 1.21 1.8 1.2AB=++，最后求出AB的长即可。

人教版数学九下第二十七章综合达标训练卷(A卷)及答案解析

箭头缩小到原来的１,得到的图形是(２)．时间:４５分钟满分:１００分题序一二三总分结分人核分人得分一、选择题(每题３分,共２４分),()１．若相似△A B C与△D E F的相似比为１∶３则△A B C与△D E F的面积比为．A．１∶３B．１∶９C．３∶１D．１∶３２．将图中的(第２题)３．如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A、C、E、B、D、F,A C＝４,C E＝６,B D ＝３,则B F＝()．A．７B．７．５C．８D．８．５(第３题) (第４题)４．已知如图(１)、(２)中各有两个三角形,其边长和角的度数已在图上标注,图(２)中A C、B D交于O点,对于各图中的两个三角形而言,下列说法正确的是()．A．都相似,B．都不相似C．只有(１)相似D．只有(２)相似５．已知矩形A B C D中A B＝１,在B C上取一点E,沿A E将△A B E向上折叠,使B点落在A D 上的F点,若四边形E F D C与矩形A B C D相似,则A D＝()．A．５－１B．５＋１C．３D．２(第５题) (第７题) (第８题)６．一个铝质三角形框架三条边长分别为２４c m,３０c m,３６c m,要做一个与它相似的铝质三角形第二七章综合达标训练卷相似框架,现有长为２７c m,４５c m的两根铝材,要求以其中的一根为一边,从另一根上截下两段(允许有余料)作为另外两边,则截法有()．A.０种B．１种C．２种D．３种７．如图,在R t△A B C中,∠A C B＝９０°,∠A＝３０°,C D⊥A B于点D,则△B C D与△A B C的周长之比为()．A．１∶２B．１∶３C．１∶４D．１∶５８．如图,在菱形A B C D中,对角线A C、B D相交于点O,M、N分别是边A B、A D的中点,连接O M、O N、M N,则下列叙述正确的是()．A．△A O M和△A O N都是等边三角形B.四边形M B O N和四边形M O D N都是菱形C.四边形AMON 与四边形A B C D是位似图形D.四边形M B C O和四边形N D C O都是等腰梯形二、填空题(每题３分,共２４分)９．在比例尺为１∶２００的地图上,测得A、B两地间的图上距离为４．５c m,则A、B两地间的实际距离为m．１０．如图,点D、E分别在A B、A C上,且∠A B C＝∠A E D．若D E＝４,A E＝５,B C＝８,则A B的长为．(第１０题)(第１１题)１１．如图,正方形A B C D的两边B C、A B分别在平面直角坐标系内的x 轴、y 轴的正半轴上,正方形A′B′C′D′与正方形A B C D是以A C的中点O′为中心的位似图形,已知A C＝３２,若点A′的坐标为(１,２),则正方形A′B′C′D′与正方形A B C D的相似比是．１２．如图,锐角三角形A B C的边AB、A C上的高线C E和B F相交于点D ,请写出图中的两对相似三角形:．(用相似符号连接)(第１２题)(第１３题)(第１２题)１３．如图,∠A B D＝∠C,A B＝５,A D＝３．５,则A C＝．１４．如图是重叠的两个直角三角形．将其中一个直角三角形沿B C方向平移得到△D E F．如果A B＝８c m,B E＝４c m,DH＝３c m,那么图中阴影部分的面积为c m２．１５．如图是一山谷的横断面示意图,宽A A′为１５m,用曲尺(两直尺相交成直角)从山谷两侧测量出O A＝１m,O B＝３m,O′A′＝０．５m,O′B′＝３m(点A、O、O′、A′在同一条水平线上),则该山谷的深h为m．(第１５题)(第１６题)１６．如图,∠D A B＝∠C A E,请你再补充一个条件,使得△A B C∽△A D E．三、解答题(第１７、１８题每题７分,第１９、２０题每题８分,第２１题１０分,第２２题１２分,共５２分) １７．如图,在平行四边形A B C D中,A D＝１０厘米,C D＝６厘米,E为A D上一点,且B E＝B C,C E＝C D,求D E的长．(第１７题)１８．如图,☉O是△A B C的外接圆,圆心O在A B上,过点B作☉O的切线交A C的延长线于点D．(１)求证:△A B C∽△B D C;(２)若A C＝８,B C＝６,求△B D C的面积．(第１８题)１９．如图,在６×８网格图中,每个小正方形边长均为１,点O和△A B C的顶点均为小正方形的顶点．(１)以O为位似中心,在网络图中作△A′B′C′,使△A′B′C′和△A B C位似,且位似比为１∶２;(２)连接(１)中的A A′,求四边形A A′C′C的周长．(结果保留根号)(第１９题)２０．如图,在梯形A B C D中,A D∥B C,∠D C B＝９０°,E是A D的中点,点P是边B C上的动点(不与点B重合),E P与B D相交于点O;(１)当点P在边B C上运动时,求证:△B O P∽△D O E;(２)设(１)中的相似比为k,若A D∶B C＝２∶３．请探究:当k为下列三种情况时,四边形ABPE 是什么四边形?①当k＝１时,是;②当k＝２时,是;③当k＝３时,是．并证明k＝２时的结论．(第２０题)２１．如图,在边长为１的小正方形组成的网格中,△A B C和△D E F的顶点都在格点上,P１、P２、P３、P４、P５是△D E F边上的５个格点,请按要求完成下列各题:(１)试证明三角形△A B C为直角三角形;(２)判断△A B C和△D E F是否相似,并说明理由;(３)画一个三角形,它的三个顶点为P１、P２、P３、P４、P５中的３个格点并且与△A B C相似．(要求:用尺规作图,保留痕迹,不写作法与证明)(第２１题)２２．如图,E是矩形A B C D的边B C上一点,E F⊥A E,E F分别交A C、C D于点M、F,B G⊥A C,垂足为G,B G交A E于点H．(１)求证:△A B E∽△E C F;(２)找出与△A B H相似的三角形,并证明．(第２２题)９７ , CD DE B C CD１第二十七章综合达标训练卷(A卷) ．B ２．A ３．B ４．A ５．B ６．B ７．A ８．C ．９１０．１０１１．１∶３１２．△B D E ∽ △C D F ,△A B F ∽ △A C E１３．５０１４．２６１５．３０１６．∠D ＝ ∠B 或∠A E D ＝ ∠C１７．∵ △B C E 与△C D E 均为等腰三角形角∠D E C ＝ ∠B C E ,∴ △B C E ∽ △C D E∴ BC ＝CE , ,且两个底 ∴ １０＝６ , ６ D E ( ) ∴ D E ＝３．６厘米．１８．(１)∵ A B 是圆O 的直径,∴ ∠A C B ＝９０°．∵ BD 是圆O 的切线,∴ ∠A B D ＝９０°, , ,∵ ∠A ＋∠A B C ＝９０° ∠A B C ＋ ∠C B D ＝９０° ∴ ∠A ＝ ∠C B D ． , ∵ ∠A C B ＝ ∠D C B ＝９０° ∴ △A B C ∽ △B D C ; (２)∵ △A B C ∽ △B D C , ∴AC ＝BC ,∵ A C ＝８,B C ＝６, ∴ CD ＝９．∴ S ２１ B CC D ＝１ ×６× ９＝２７． △B D C＝２１９．(１)如图所示: ２２２DE∴ ∥(第１９题)２２．(１)∵ 四边形A B C D 是矩形,∴ ∠A B E ＝ ∠E C F ＝９０°, ∴ ∠A E B ＋ ∠B A E ＝９０°．∵ A E ⊥E F ,即∠A E B ＋ ∠F E C ＝９０°．∴ ∠B A E ＝ ∠C E F ,∴ △A B E ∽ △E C F ; (２)△A B H ∽ △E C M ． (２)A A ′＝C C ′＝２．证明:∵ B G ⊥A C , , 在 R t △O A ′C ′中,O A ′＝O C ′＝２,得A ′C ′＝２２;∴ ∠A B G ＋ ∠B A G ＝９０°∵ ∠E C F ＝９０°, ,同理可得AC ＝４２．所以,四边形A A ′C ′C 的周长为４＋６２．２０．(１)∵ A D ∥B C ,∴ ∠OBP ＝ ∠ODE ．在△BOP 和△DOE 中, ∠O B P ＝ ∠O D E ,∠B O P ＝ ∠D O E ,∴ △BO P ∽ △D O E(有两个角对应相等的两三角形相似);(２)①平行四边形 ②直角梯形 ③等腰梯形 ∵ k ＝２时,B P ＝２, ∴ B P ＝２D E ＝A D ．又 A D ∶B C ＝２∶３, ∴ BC ＝３AD ,∴ ∠E C M ＋ ∠M C F ＝９０° 又 ∠BAG ＝ ∠MCF , ∴ ∠ABH ＝ ∠ECM ,由(１)知,∠B AH ＝ ∠C E M , ∴ △ABH ∽ △ECM ．２PC ＝BC ＝３AD －AD ＝１AD ＝ED ．－B P ２２∵ ED ∥P C ,∴ 四边形PCDE 是平行四边形．∵ ∠D C B ＝９０°, ∴ 四边形PCDE 是矩形．∴ ∠E P B ＝９０°． , , 又在直角梯形 ABCD 中 AD ∥BC AB 与DC 不平行,, ,AE B P A B 与E P 不平行四边形 A B P E 是直角梯形．２１．(１)由勾股定理,得A B ＝２５,A C ＝５,B C ＝５,显然有A B ２＋A C ２＝B C２, 根据勾股定理的逆定理得△A B C 为直角三角形; (２)△A B C 和△D E F 相似．由勾股定理,得A B ＝２５,A C ＝５,B C ＝５,D E ＝４２,D F ＝２２,E F ＝２１０．∵ AB ＝AC ＝BC ＝５ , DE DF EF ２２ ∴ △A B C ∽ △D E F ; (３)如图:△P ２P ４P ５．(第２１题)。

人教版九年级下册数学第二十七章测试卷有答案

人教版九年级下册数学第二十七章测试题一、单选题1．制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是（）A．360元B．720元C．1080元D．2160元2．若xy＝23，则下列各式不成立的是（）A．x yy+＝53B．y xy-＝13C．2xy＝13D．11xy++＝343．如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，若BD=2AD，则（）A．12ADAB=B．12AEEC=C．12ADEC=D．12DEBC=4．下列各组图形中不一定相似的是()A．各有一个角是45°的两个等腰三角形B．各有一个角是60°的两个等腰三角形C．各有一个角是105°的两个等腰三角形D．两个等腰直角三角形5．如图，在正方形ABCD中，点E，F分别在BC，CD上，且∠EAF=45°，将△ABE绕点A顺时针旋转90°，使点E落在点E'处，则下列判断不正确的是（）A．△AEE′是等腰直角三角形B．AF垂直平分EE'C．△E′EC∽△AFD D．△AE′F是等腰三角形6．下列图形中不是位似图形的是A．B．C．D．7．已知△ABC中，AB=AC，∠A=36°，以点A为位似中心把△ABC的各边放大2倍后得到△AB′C′，则∠B的对应角∠B′的度数为（）A．36°B．54°C．72°D．144°8．若四条线段a,b,c,d成比例,且a=3cm,b=2cm,c=9cm,则线段d的长为()A．4cm B．5cmC．6cm D．8cm9．如图，在△ABC中，DE∥BC，∠ADE=∠EFC，AD:BD=5:3，CF=6，则DE的长为（）A．6B．8C．10D．1210．下列3个图形中是位似图形的有()A．1个B．2个C．3个D．0个11．在△ABC和△DEF中，AB=AC，DE=DF，根据下列条件，能判断△ABC和△DEF相似的是（）A．AB ACDE DF=B．AB BCDE EF=C．∠A=∠E D．∠B=∠D12．如图，在等边△ABC中，D为AC边上的一点，连接BD，M为BD上一点，且∠AMD=60°，AM交BC于E．当M为BD中点时，CDAD的值为（）A ．23B C D ．35二、填空题13．在比例尺为1：6000000的海南地图上，量得海口与三亚的距离约为3.7厘米，则海口与三亚的实际距离约为_____千米．14．若k ＝2a b c-＝b 2c a -＝2c a b -，且a ＋b ＋c≠0，则k ＝______.15．若△ABC ∽△A 1B 1C 1，AB ＝2，A 1B 1＝3；则△A 1B 1C 1与△ABC 的相似比为_____.16．如图，有三个三角形，其中相似的是___________.17．如图，四边形ABCD 与四边形EFGH 相似，位似中心点是O ，35OE OA =，则FG BC =__.18．如图，已知矩形OABC 与矩形ODEF 是位似图形，P 是位似中心，若点B 的坐标为()2,4，点E 的坐标为()1,2-，则点P 的坐标为______．19．在△ABC 中，MN ∥BC 分别交AB ，AC 于点M ，N ；若AM=1，MB=2，BC=3，则MN 的长为_____．三、解答题20．若+2+5==346a b c ，且2a －b ＋3c ＝21.试求a ∶b ∶c.21．已知四边形ABCD 和A 1B 1C 1D 1中，1111111135AB BC CD AD A B B C C D A D ====，且周长之差为12cm ，两个四边形的周长分别是多少？22．如图，梯形ABCD 中，AB CD ∥，点F 在BC 上，连DF 与AB 的延长线交于点G ．（1）求证：CDF BGF ∽；（2）当点F 是BC 的中点时，过F 作EF CD ∥交AD 于点E ，若6cm 4cm AB EF ==，，求CD的长．23．如图，四边形ABCD 中，AB AC AD ==，AC 平分BAD ∠，点P 是AC 延长线上一点，且PD AD ⊥.（1）证明：BDC PDC ∠=∠；（2）若AC 与BD 相交于点E ，1,:2:3AB CE CP ==，求AE 的长.24．如图，在矩形ABCD 中，对角线AC 、BD 相交于点O ，过点O 作OE ⊥BC 于E 点，连接DE 交OC 于F 点，作FG ⊥BC 于G 点，则△ABC 与△FGC 是位似图形吗？若是，请说出位似中心，并求出相似比；若不是，请说明理由．25．如图，△ABC、△DEP是两个全等的等腰直角三角形，∠BAC=∠PDE=90°．（1）若将△DEP的顶点P放在BC上（如图1），PD、PE分别与AC、AB相交于点F、G．求证：△PBG∽△FCP；（2）若使△DEP的顶点P与顶点A重合（如图2），PD、PE与BC相交于点F、G．试问△PBG与△FCP还相似吗？为什么？参考答案1．C【分析】根据题意求出长方形广告牌每平方米的成本，根据相似多边形的性质求出扩大后长方形广告牌的面积，计算即可．【详解】3m×2m=6m2，∴长方形广告牌的成本是120÷6=20元/m2，将此广告牌的四边都扩大为原来的3倍，则面积扩大为原来的9倍，∴扩大后长方形广告牌的面积=9×6=54m2，∴扩大后长方形广告牌的成本是54×20=1080元，故选C．【点睛】本题考查的是相似多边形的性质，掌握相似多边形的面积比等于相似比的平方是解题的关键．2．D【分析】根据比例设x＝2k，y＝3k，然后代入比例式对各选项分析判断利用排除法求解．【详解】：∵23 xy=，∴设x＝2k，y＝3k，A.23533x y k ky k++==，正确，故本选项错误；B.32133y x k ky k--==，正确，故本选项错误；C.212233x ky k==⋅，正确，故本选项错误；D.12131314x ky k++=≠++，故本选项正确．故选D．【点睛】本题考查了比例的性质，利用“设k法”表示出x、y求解更加简便．3．B【详解】∵DE∥BC，∴△ADE∽△ABC，∴AD AE DE AB AC BC==，∵BD=2AD，∴13ADAB=，31DEBC=，12AEEC=，故选B4．B【分析】判定三角形相似的方法：①有两个对应角相等的三角形相似；②有两个对应边的比相等，且其夹角相等，则两个三角形相似；③三组对应边的比相等，则两个三角形相似．【详解】解：A、由已知我们可以得到这是两个正三角形，从而可以根据三组对应边的比相等的两个三角形相似判定这两个三角形相似；B、不正确，因为没有指明这个45°的角是顶角还是底角，则无法判定其相似；C、正确，已知一个角为105°，则我们可以判定其为顶角，这样我们就可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似判定这两个三角形相似；D、正确，因为是等腰直角三角形，则我们可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定这两个三角形相似．故选B．【点睛】本题考查学生对常用的相似三角形的判定方法的掌握情况，解题关键是熟练掌握相似三角形的判定方法．5．D【详解】试题分析：因为将△ABE绕点A顺时针旋转90°，使点E落在点E'处，∴AE′=AE，∠E′AE=90°，∴△AEE′是等腰直角三角形，故A正确；∵将△ABE绕点A顺时针旋转90°，使点E落在点E'处，∴∠E′AD=∠BAE，∵四边形ABCD是正方形，∴∠DAB=90°，∵∠EAF=45°，∴∠BAE+∠DAF=45°，∴∠E′AD+∠FAD=45°，∴∠E′AF=∠EAF，∵AE′=AE，∴AF垂直平分EE'，故B正确；∵AF⊥E′E，∠ADF=90°，∴∠FE′E+∠AFD=∠AFD+∠DAF，∴∠FE′E=∠DAF，∴△E′EC∽△AFD，故C正确；∵AD⊥E′F，但∠E′AD不一定等于∠DAE′，∴△AE′F不一定是等腰三角形，故D错误；故选D．考点：旋转的性质；线段垂直平分线的性质；等腰三角形的判定；等腰直角三角形；正方形的性质；相似三角形的判定．6．C【分析】对应顶点的连线相交于一点的两个相似多边形叫位似图形．【详解】根据位似图形的概念，A、B、D三个图形中的两个图形都是位似图形；C中的两个图形不符合位似图形的概念，对应顶点不能相交于一点，故不是位似图形．故选C．【点睛】此题主要考查了位似图形，注意位似与相似既有联系又有区别，相似仅要求两个图形形状完全相同；而位似是在相似的基础上要求对应点的连线相交于一点．7．C【分析】以点A为位似中心，把△ABC放大2倍后得△AB′C′，则这两个三角形一定相似，则∠B′等于∠B，根据等腰三角形的性质可以求出∠B．【详解】解：∵AB=AC，∠A=36°∴∠B=∠C=72°又∵△ABC∽△AB′C′∴∠B′=∠B=72°．故选C．【点睛】本题考查对位似概念的理解以及等腰三角形的性质，要明确位似是相似的特例是解题关键．8．C【解析】【分析】根据比例线段的定义，即可列出方程求解．【详解】根据题意得：a：b=c：d，即3：2=9：d，解得d=6cm，故选：C．【点睛】本题考查了比例线段的定义，注意a、b、c、d是成比例线段，要理解各个字母的顺序．9．C【分析】由DE//BC可得出53AD AEBD EC==，∠AED＝∠C，结合∠ADE＝∠EFC可得出△ADE∽△EFC，根据相似三角形的性质可得出53AE DEEC FC==，再根据CF＝6,即可求出DE的长度．【详解】解：∵DE//BC，∴53AD AEBD EC==，∠AED＝∠C．又∵∠ADE＝∠EFC，∴△ADE∽△EFC，∴53 AE DEEC FC==，∵CF＝6，∴5 63 DE=，∴DE＝10．故选C【点睛】本题考查了相似三角形的判定与性质、平行线分线段成比例定理，根据平行线分线段成比例定理和相似三角形的性质列出比例式是解题的关键．10．B【详解】由位似图形的定义：“如果两个图形不仅是相似图形，而且每组对应点的连线交于一点，对应边互相平行或在一条直线上，那么这两个图形叫做位似图形”分析可知，上面3个图形中，第1个和第3个图形是位似图形，第2个图形不是位似图形，即3个图形中位似图形有2个.故选B.11．B【详解】在△ABC 和△DEF 中，∵AB DE =BC EF =AC DF，∴△ABC ∽△DEF ，故选B.12．B【分析】作DK ∥BC ，交AE 于K ．首先证明BE=DK=CD ，CE=AD ，设BE=CD=DK=a ，AD=EC=b ，由DK ∥EC ，可得DK AD EC AC =，推出a b b a b =+，即a 2+ab-b 2=0，可得（a b ）2+（a b ）-1=0，求出a b即可解决问题．【详解】作DK ∥BC ，交AE 于K．∵△ABC 是等边三角形，∴AB=CB=AC ，∠ABC=∠C=60°，∵∠AMD=60°=∠ABM+∠BAM ，∵∠ABM+∠CBD=60°，∴∠BAE=∠CBD ，在△ABE 和△BCD 中，BAE CBD ABE C AB BC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABE ≌△BCD ，∴BE=CD ，CE=AD ，∵BM=DM ，∠DMK=∠BME ，∠KDM=∠EBM ，∴△MBE ≌△MDK ，∴BE=DK=CD ，设BE=CD=DK=a ，AD=EC=b ，∵DK∥EC，∴DK AD EC AC=，∴a bb a b =+，∴a2+ab-b2=0，∴（ab）2+（ab）-1=0，∴ab，∴CD aAD b==，故选B．【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、平行线分线段成比例定理、一元二次方程等知识，解题的关键是学会添加常用辅助线，学会用方程的思想思考问题，本题体现了数形结合的思想13．222【分析】知道比例尺，带入数值计算，化单位为千米即可.【详解】比例尺为1:6000000,图上距离3.7厘米则实际距离为3.76000000cm222km⨯=故答案为222【点睛】此题重点考察学生对比例尺的应用能力，理解比例尺的单位换算是解题的关键.14．-1【分析】根据等比性质可以直接得到答案，注意通分即可.【详解】等比性质()2221a b ca b b c c ac a b a b c-++---====-++(a＋b＋c≠0)故答案为-1【点睛】此题重点考察学生对等比性质的理解，会化简是解题的关键.15．3∶2【解析】【分析】根据相似三角形的性质：相似三角形的对应角相等，对应边成比例，且比例就是相似比.题目中已知△ABC∽△A1B1C1，且对应边的长分别为AB＝2，A1B1＝3，组成比例即可求出相似比.【详解】根据相似三角形的性质，可得△A1B1C1与△ABC的相似比为A1B1∶AB=3∶2.故答案为：3∶2.【点睛】本题考查相似三角形的性质.16．①与②【分析】先分别计算三个三角形的第三个角做对比，再根据相似三角形的性质即可求出【详解】第一个图：第三个角为:180°-68°-61°=51°∴此三角形三个角分别为：51°，61°，68°第二个图：第三个角为:180°-68°-51°=61°∴此三角形三个角分别为：51°，61°，68°第三个图：第三个角为:180°-68°-49°=63°∴此三角形三个角分别为：49°，63°，68°根据两角对应相等，两个三角形相似.期中相似的是:①和②.故答案为:①和②.【点睛】本题考查了相似三角形的性质，熟练掌握性质是解题的关键.17．3 5【详解】解：如图所示：∵四边形ABCD与四边形EFGH位似，∴△OEF∽△OAB，△OFG∽△OBC，∴35 OE OFOA OB==，∴35 FG OFBC OB==．故答案为3 518．()2,0-【详解】分析：由矩形OABC中，点B的坐标为（2，4），可求得点C的坐标，又由矩形OABC与矩形ODEF是位似图形，P是位似中心，点C的对应点点E的坐标为（-1，2），即可求得其位似比，继而求得答案．详解：∵四边形OABC是矩形，点B的坐标为（2，4），∴OC=AB=4，OA=2，∴点C的坐标为：（0，4），∵矩形OABC与矩形ODEF是位似图形，P是位似中心，点E的坐标为（-1，2），∴位似比为：2，∴OP：AP=OD：AB=1：2，设OP=x，则1x22x=+，解得：x=2，∴OP=2，即点P的坐标为：（-2，0）．点睛：此题考查了位似变换的性质，难度中等．注意求得矩形OABC与矩形ODEF的位似比是解此题的关键．19．1【详解】∵MN∥BC，∴△AMN∽△ABC，∴，即，∴MN=1.故答案为1.20．4∶8∶7.【详解】试题分析：首先设等式为m ，然后分别将a 、b 、c 用含m 的代数式来进行表示，根据2a-b+3c=21求出m 的值，从而得出a 、b 、c 的值，最后求出比值．试题解析：令＝＝＝m ，则a ＋2=3m ，b=4m ，c ＋5=6m ，∴a=3m －2，b=4m ，c=6m －5，∵2a －b ＋3c=21，∴2(3m －2)－4m ＋3(6m －5)=21，即20m=40，解得m=2，∴a=3m －2=4，b=4m=8，c=6m －5=7，∴a ∶b ∶c=4∶8∶7.21．两个四边形的周长分别为18cm 和30cm.【解析】【分析】根据四边形周长比等于相似比和已知条件设其中一个周长，就可以求出周长.【详解】设四边形ABCD 和四边形A 1B 1C 1D 1的周长分别为C 1和C 2，∵1111111135AB BC CD AD A B B C C D A D ====，，∴12C C ＝35∴C 1＝35C 2∵C 2－C 1＝12∴C 2－35C 2＝12∴C 2＝30∴C 1＝18故两个四边形的周长分别为18cm 和30cm.【点睛】此题重点考察学生对相似比的应用，掌握四边形周长比等于相似比是解题的关键.22．（1）证明见解析；（2）2cm 【分析】（1）根据梯形的性质，利用平行线的性质得到CDF FGB DCF GBF ∠=∠∠=∠，，然后由相似三角形的判定得到结论；（2）根据点F 是BC 的中点，可得△CDF ≌△BGF ，进而根据全等三角形的性质得到CD=BG ，然后由中位线的性质求解即可.【详解】（1）证明：∵梯形ABCD ，AB CD ，∴CDF FGB DCF GBF ∠=∠∠=∠，，∴CDF BGF ∽．（2）由（1）CDF BGF ∽，又F 是BC 的中点，BF FC=∴CDF BGF ≌，∴DF FG CD BG==，又∵EF CD ，AB CD ，∴EF AG ，得2EF BG AB BG ==+．∴22462BG EF AB =-=⨯-=，∴2cm CD BG ==．【点睛】此题主要考查了相似三角形的性质与判定，全等三角形的性质与判定及中位线的性质，比较复杂，关键是灵活利用平行线的性质解题.23．（1）详见解析；（2）23AE =【分析】（1）直接利用等腰三角形的性质结合互余的定义得出∠BDC=∠PDC ；（2）首先过点C 作CM ⊥PD 于点M ，进而得出△CPM ∽△APD ，求出EC 的长即可得出答案．【详解】解：（1）：∵AB AD =，AC 平分BAD ∠，∴AC BD ⊥，∴90ACD BDC ∠+∠=︒，∵AC AD =，∴ACD ADC ∠=∠，∴90ADC BDC ∠+∠=︒，∴BDC PDC ∠=∠；（2）过点C 作CM PD ⊥于点M ，∵BDC PDC ∠=∠，∴CE CM =，∵90,CMP ADP P P ∠=∠=︒∠=∠，∴CPM APD ∆∆∽，∴CM PC AD PA=，设CM CE x ==，∵:2:3CE CP =，∴32PC x =，∵1AB AD AC ===，∴323112x x x =+，解得：13x =，∴12133AE =-=.【点睛】此题主要考查了相似三角形的判定与性质以及等腰三角形的性质等知识，正确得出△CPM ∽△APD 是解题关键．24．△ABC 与△FGC 是位似图形，位似中心是点C ，△ABC 与△FGC 的相似比为3∶1.【分析】利用位似图形的性质得出位似中心，进而利用平行线分线段成比例定理求出即可;【详解】△ABC 与△FGC 是位似图形，位似中心是点C.因为在矩形ABCD 中，AD ∥BC ，所以∠FAD ＝∠FCE ，∠FDA ＝∠FEC ，所以△AFD∽△CFE，所以CF CE AF AD=因为AD＝BC，所以CF CE AF CB=因为∠ABC＝90°，OE⊥BC，所以OE∥AB.因为OA＝OC，所以CE＝12 BC，所以CFAF＝12所以CFAC＝13.即△ABC与△FGC的相似比为3∶1.【点睛】此题主要考查了位似图形的性质以及平行线分线段成比例定理,利用未知数表示各线段长是解题关键.25．（1）证明见解析（2）△PBG与△FCP相似【详解】试题分析：（1）已知△ABC、△DEP是两个全等的等腰直角三角形，即可得∠B=∠C=∠DPE=45°，∠BPG+∠CPF=135°；在△BPG中，∠B=45°，∠BPG+∠BGP=135°，由此可得∠BGP=∠CPF，再由∠B=∠C，根据两角对应相等的两个三角形相似即可得△PBG∽△FCP；（2）△PBG与△FCP相似，由△ABC、△DEP是两个全等的等腰直角三角形，可得∠B=∠C=∠DPE=45°，又因∠BGP=∠C+∠CPG=45°+∠CAG，∠CPF=∠FPG+∠CAG=45°+∠CAG，所以∠AGP=∠CPF，再由∠B=∠C，根据两角对应相等的两个三角形相似即可得△PBG∽△FCP．试题解析：（1）证明：如图1，∵△ABC、△DEP是两个全等的等腰直角三角形，∴∠B=∠C=∠DPE=45°，∴∠BPG+∠CPF=135°，在△BPG中，∵∠B=45°，∴∠BPG+∠BGP=135°，∴∠BGP=∠CPF，∵∠B=∠C，∴△PBG∽△FCP；（2）△PBG与△FCP相似．理由如下：如图2，∵△ABC、△DEP是两个全等的等腰直角三角形，∴∠B=∠C=∠DPE=45°，∵∠BGP=∠C+∠CPG=45°+∠CAG，∠CPF=∠FPG+∠CAG=45°+∠CAG，∴∠AGP=∠CPF，∵∠B=∠C，∴△PBG∽△FCP．。

人教版数学九年级下学期第27章《相似》测试卷含答案

人教版数学九年级下学期第27章《相似》测试卷（测试时间：120分钟满分：120分）一、选择题（每小题3分，共30分）1．已知：线段a、b，且,则下列说法错误的是( )A．a＝2cm，b＝3cm B．a＝2k，b＝3k(k≠0)C．3a＝2b D．2．下列命题正确的是（）A．有一个角对应相等的平行四边形都相似B．对应边成比例的两个平行四边形相似C．有一个角对应相等的两个等腰梯形相似D．有一个角对应相等的菱形是相似多边形3．如果（其中顶点、、依次与顶点、、对应），那么下列等式中不一定成立的是（）A．B．∠B=∠E C．D．4．在比例尺为1∶8 000的某学校地图上，矩形运动场的图上尺寸是1 cm×2 cm，那么矩形运动场的实际尺寸应为( )A．80 m×160 m B．8 m×16 m C．800 m×160 m D．80 m×800 m5．如图，在平面直角坐标系中，已知点，，以原点为位似中心，相似比为，把缩小，则点的对应点的坐标是（）A．(-1, 2)B．(-9, 18)C．(-9, 18)或(9, -18) D．(-1, 2)或(1, -2)6．如图，点O是△ABC内任一点，点D，E，F分别为OA，OB，OC的中点，则图中相似三角形有( ) A．1对B．2对C．3对D．4对7．已知：如图，在中，，则下列等式成立的是（）A ．B ．C ．D ．8．如图，在平行四边形中，是上的一点，直线与的延长线交于点，并与交于点，下列式子中错误的是（）A ．B ．C ．D ．9．如图，在中，是边上一点，连接，给出下列条件：①；②；③；④．其中单独能够判定的个数是（）A ． 1个B ． 2个C ． 3个D ． 4个 10．点是线段的黄金分割点，且，下列命题：，中正确的有（）A ． 1个B ． 2个C ． 3个D ． 4个二、填空题（每小题3分，共30分） 11．如图，在△ABC 中，DE ∥BC ，23AD DB =，则DEBC = ．12．如图，直角三角形ABC 中，︒=∠90ACB ，10=AB ， 6=BC ，在线段AB 上取一点D ，作AB DF ⊥交AC 于点F .现将ADF ∆沿DF 折叠，使点A 落在线段DB 上，对应点记为H ；AD 的中点E 的对应点记为G. 若GFH ∆∽GBF ∆，则AD =______ ____.13．如图，等边ABC △的边长为3，P 为BC 上一点，且1BP =，D 为AC 上一点，若60APD ∠=°，则CD 的长为 .14．如图，D 、E 分别是△ABC 的边AB 、BC 上的点，且DE ∥AC ，AE 、CD 相交于点O ，若S △DOE ：S △COA =1：25，则S △BDE 与S △CDE 的比=___________．15．如图，以点O 为位似中心，将五边形ABCDE 放大后得到五边形A′B′C′D′E′，已知OA=10cm ，OA′=20cm，则五边形ABCDE 的周长与五边形A′B′C′D′E′的周长的比值是．16．把一个矩形剪去一个正方形，若剩下的矩形与原矩形相似，则原矩形的长边与短边之比为 17．如图，菱形ABCD 的边长为1，直线l 过点C ，交AB 的延长线于M ，交AD 的延长线于N ，则AM1+AN1= ．18．如图，在菱形ABCD 中，E 是BC 边上的点，AE 交BD 于点F ，若EC=2BE ，则BFFD的值是．19．已知女排赛场球网的高度是2.24米，某排球运动员在一次扣球时，球恰好擦网而过，落在对方场地距离球网4米的位置上，此时该运动员距离球网1.5米，假设此次排球的运行路线是直线，则该运动员击球的高度是米．2.244 1.520．如图，在矩形ABCD中，AB=2，AD=，在边CD上有一点E，使EB平分∠AEC．若P为BC 边上一点，且BP=2CP，连接EP并延长交AB的延长线于F．给出以下五个结论：①点B平分线段AF；②PF=DE；③∠BEF=∠FEC；④S矩形ABCD=4S△BPF ；⑤△AEB是正三角形．其中正确结论的序号是．三、解答题（共60分）21．（本题6分）如图，在△ABC中，D是AB上一点，且∠ACD=∠B，已知AD=8cm，BD=4cm，求AC的长．22．（本题6分）如图，在边长为1 的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）和格点O，按要求画出格点△A1B1C1和格点△A2B2C2．（1）将△ABC绕O点顺时针旋转90°，得到△A1B1C1；（2）以A1为一个顶点，在网格内画格点△A1B2C2，使得△A1B1C1∽△A1B2C2，且相似比为1：2．23．（本题6分）如图，Rt△ABC中，∠C=90°，AB=14，AC=7，D是BC上一点，BD=8，DE⊥AB，垂足为E，求线段DE的长．24．（本题8分）如图，在Rt△ABC中，∠C=90°，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．（1）求证：△BDE∽△BAC；（2）已知AC=6，BC=8，求线段AD的长度．25．（本题7分）为了测量校园水平地面上一棵树的高度，数学兴趣小组利用一根标杆、皮尺，设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上，此同学眼睛距地面1.6米，标杆高为3.2米，且BC=2米，CD=6米，求树ED的高．26．（本题8分）如图，正方形A1A2B1C1，A2A3B2C2，…A n a n+1B n C n，如图位置依次摆放，已知点C1，C2，C3…，C n在直线y=x上，点A1的坐标为（1，0）．（1）写出正方形A1A2B1C1，A2A3B2C2，…A n a n+1B n C n，的位似中心坐标；（2）正方形A4A3B4C4四个顶点的坐标．27．（本题8分）如图，在△ABC中，BE平分∠ABC交AC于点E，过点E作ED∥BC交AB于点D．（1）求证：AE•BC=BD•A C；（2）如果S△ADE=3，S△BDE=2，DE=6，求BC的长．28．（本题11分） (1)、问题：如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°．求证：AD·BC=AP·BP．(2)、探究：如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．(3)、应用：请利用（1）（2）获得的经验解决问题：如图3，在△ABD中，AB=6，AD=BD=5．点P以每秒1个单位长度的速度，由点A 出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当DC的长与△ABD底边上的高相等时，求t的值．答案（测试时间：120分钟满分：120分）一、选择题（每小题3分，共30分）1．已知：线段a、b，且,则下列说法错误的是( )A．a＝2cm，b＝3cm B．a＝2k，b＝3k(k≠0)C．3a＝2b D．【答案】A【解析】选项A，两条线段的比，没有长度单位，它与所采用的长度单位无关，选项A错误；选项B，，根据等比性质，a=2k，b=3k（k≠0），选项B正确；选项C，，根据比例的基本性质可得3a=2b，选项C正确；选项D，，根据比例的基本性质可得a=b，选项D正确．故选A．2．下列命题正确的是（）A．有一个角对应相等的平行四边形都相似B．对应边成比例的两个平行四边形相似C．有一个角对应相等的两个等腰梯形相似D．有一个角对应相等的菱形是相似多边形【答案】D3．如果（其中顶点、、依次与顶点、、对应），那么下列等式中不一定成立的是（）A．B．∠B=∠E C．D．【答案】C【解析】△ABC∽△DEF，故：A．∠A＝∠D正确，故本选项错误；B．∠B=∠E正确，故本选项错误；C．AB＝DE不一定成立，故本选项正确；D．正确，故本选项错误．故选C．4．在比例尺为1∶8 000的某学校地图上，矩形运动场的图上尺寸是1 cm×2 cm，那么矩形运动场的实际尺寸应为( )A．80 m×160 m B．8 m×16 m C．800 m×160 m D．80 m×800 m【答案】A解得y=16000（cm）=160（m）∴矩形运动场的实际尺寸是80m×160m.故选A.5．如图，在平面直角坐标系中，已知点，，以原点为位似中心，相似比为，把缩小，则点的对应点的坐标是（）A．(-1, 2)B．(-9, 18)C．(-9, 18)或(9, -18) D．(-1, 2)或(1, -2)【答案】D6．如图，点O是△ABC内任一点，点D，E，F分别为OA，OB，OC的中点，则图中相似三角形有( )A．1对B．2对C．3对D．4对【答案】D【解析】因为点D,E,F分别为OA,OB,OC的中点,所以DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,所以DE//AB,DF//AC,EF//BC,所以△DOE∽△AOD,△DOF∽△AOC,△EOF∽△BOC,因为DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,所以,,所以，所以△DEF∽△ABC,因此有四对相似三角形,故选D.7．已知：如图，在中，，则下列等式成立的是（）A．B．C．D．【答案】C8．如图，在平行四边形中，是上的一点，直线与的延长线交于点，并与交于点，下列式子中错误的是（）A．B．C．D．【答案】D【解析】∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BE，∵CG∥AE，∴四边形AGCF是平行四边形，△BCG∽△BEA，△CEF∽△BEA，∴，，CF=AG，∴DF=BG，，∴选项A、B正确；∵AD∥BE，∴，∴，∴选项C正确，D不正确；故选D．9．如图，在中，是边上一点，连接，给出下列条件：①；②；③；④．其中单独能够判定的个数是（）A．1个B．2个C．3个D．4个【答案】B10．点是线段的黄金分割点，且，下列命题：，中正确的有（）A．1个B．2个C．3个D．4个【答案】B二、填空题（每小题3分，共30分） 11．如图，在△ABC 中，DE ∥BC ，23AD DB =，则DEBC = ．【答案】25【解析】根据AD:DB=2:3可得：AD:AB=2:5，∵DE ∥BC ，∴△ADE ∽△ABC ，∴25DE AD BC AB . 12．如图，直角三角形ABC 中，︒=∠90ACB ，10=AB ， 6=BC ，在线段AB 上取一点D ，作AB DF ⊥交AC 于点F .现将ADF ∆沿DF 折叠，使点A 落在线段DB 上，对应点记为H ；AD 的中点E 的对应点记为G. 若GFH ∆∽GBF ∆，则AD =______ ____.【答案】3.2 【解析】利用勾股定理列式求出AC=8，设AD=2x ，得到AE=DE=DE 1=A 1E 1=x ，然后求出BE 1=10-3x ，再利用相似三角形对应边成比例列式求出DF=32x ，然后利用勾股定理列式求出E 1F=132x ，然后根据相似三角形对应边成比例列式求解得到x=85，从而可得AD 的长为2×85=165=3.2． 13．如图，等边ABC △的边长为3，P 为BC 上一点，且1BP =，D 为AC 上一点，若60APD ∠=°，则CD的长为 .【答案】23．14．如图，D、E分别是△ABC的边AB、BC上的点，且DE∥A C，AE、CD相交于点O，若S△DO E：S△COA=1：25，则S△BDE与S△CDE的比=___________．【答案】1：4【解析】根据S△DOE：S△COA=1：25可得：DE:AC=1:5，则BE：BC=1:4，即BE:CE=1:4，△BDE和△CDE是登高三角形，则S△BDE：S△CDE=BE:EC=1:4.15．如图，以点O为位似中心，将五边形ABCDE放大后得到五边形A′B′C′D′E′，已知OA=10cm，OA′=20cm，则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是．【答案】1：2【解析】由五边形ABCDE与五边形A′B′C′D′E′位似，可得五边形ABCDE∽五边形A′B′C′D′E′，又由OA=10cm，OA′=20cm，即可求得其相似比为1:2，根据相似多边形的周长的比等于其相似比，即可求得答案为五边形ABCDE 的周长与五边形A′B′C′D′E′的周长的比为：OA ：OA′=1：2．16．把一个矩形剪去一个正方形，若剩下的矩形与原矩形相似，则原矩形的长边与短边之比为【答案】152【解析】设原矩形的长为x ，宽为y ，则剩下的矩形的长为y ，宽为(x －y)，根据矩形相似可求出比值. 17．如图，菱形ABCD 的边长为1，直线l 过点C ，交AB 的延长线于M ，交AD 的延长线于N ，则AM1+AN1= ．【答案】1．18．如图，在菱形ABCD 中，E 是BC 边上的点，AE 交BD 于点F ，若EC=2BE ，则BFFD的值是．【答案】13【解析】根据菱形的性质得出AD=BC ，AD ∥BC ，求出AD=3BE ，根据相似三角形的判定得出△AFD ∽△EFB ，根据相似得出比例式BF BE DF AD =，代入求出即可求得结果为13． 19．已知女排赛场球网的高度是2.24米，某排球运动员在一次扣球时，球恰好擦网而过，落在对方场地距离球网4米的位置上，此时该运动员距离球网1.5米，假设此次排球的运行路线是直线，则该运动员击球的高度是米．41.52.24【答案】3.08 【解析】根据三角形相似的性质可得：x24.25.144=+，则x=3.08 20．如图，在矩形ABCD 中，AB=2，AD=，在边CD 上有一点E ，使EB 平分∠AEC．若P 为BC 边上一点，且BP=2CP ，连接EP 并延长交AB 的延长线于F ．给出以下五个结论： ①点B 平分线段AF ；②PF=DE ；③∠BEF=∠FEC；④S 矩形ABCD =4S △BPF ；⑤△AEB 是正三角形．其中正确结论的序号是．【答案】①②③⑤在Rt△BPF 中，BF=2，由勾股定理可求得PF=22BF BP +=22343⎛⎫+ ⎪ ⎪⎝⎭=433，∵DE=1，∴PF=433DE ，故②正确；在Rt△BCE 中，EC=1，BC=3，由勾股定理可求得BE=2，∴BE=BF，∴∠BEF=∠F，又∵AB∥CD，∴∠FEC=∠F，∴∠BEF=∠FEC，故③正确；∵AB=2，AD=3，∴S 矩形ABCD =AB×AD=2×3=23，∵BF=2，BP=433，∴S △BPF =12BF×BP=12×2×433=433， ∴4S △BPF =1633，∴S 矩形ABCD =≠4S △BPF ，故④不正确；由上可知AB=AE=BE=2，∴△AEB 为正三角形，故⑤正确；综上可知正确的结论为：①②③⑤．故答案为：①②③⑤．三、解答题（共60分）21．（本题6分）如图，在△ABC 中，D 是AB 上一点，且∠ACD=∠B，已知AD=8cm ，BD=4cm ，求AC 的长．【答案】4622．（本题6分）如图，在边长为1 的小正方形组成的网格中，给出了格点△ABC （顶点是网格线的交点）和格点O ，按要求画出格点△A 1B 1C 1和格点△A 2B 2C 2．（1）将△ABC 绕O 点顺时针旋转90°，得到△A 1B 1C 1；（2）以A 1为一个顶点，在网格内画格点△A 1B 2C 2，使得△A 1B 1C 1∽△A 1B 2C 2，且相似比为1：2．【答案】（1）图形见解析；（2）图形见解析.【解析】（1）如图所示：△A1B1C1，即为所求；（2）如图所示：△A1B2C2，即为所求．23．（本题6分）如图，Rt△ABC中，∠C=90°，AB=14，AC=7，D是BC上一点，BD=8，DE⊥AB，垂足为E，求线段DE的长．【答案】4．【解析】∵DE⊥AB，∴∠BED=90°，又∠C=90°，∴∠BED=∠C．又∠B=∠B，∴△BED∽△BCA，∴BD DEAB AC，∴DE=BD ACAB⋅=8714⨯=4．24．（本题8分）如图，在Rt△ABC中，∠C=90°，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．（1）求证：△BDE∽△BAC；（2）已知AC=6，BC=8，求线段AD的长度．【答案】(1)证明见解析；(2) AD=3525．（本题7分）为了测量校园水平地面上一棵树的高度，数学兴趣小组利用一根标杆、皮尺，设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上，此同学眼睛距地面1.6米，标杆高为3.2米，且BC=2米，CD=6米，求树ED的高．【答案】8米【解析】如图，过A作AH垂直ED，垂足为H，交线段FC与G,由题知，FG//EH, △AFG∽△AEH，FG AG EH AH=又因为AG=BC=2,AH=BD=2+6=8,FG=FC-GC=3.2 -1.6=1.6，所以1.628EH=，EH=6.4，∴ED=EH+HD=6.4+1.6=8 树ED的高为8米26．（本题8分）如图，正方形A1A2B1C1，A2A3B2C2，…A n a n+1B n C n，如图位置依次摆放，已知点C1，C2，C3…，C n在直线y=x上，点A1的坐标为（1，0）．（1）写出正方形A1A2B1C1，A2A3B2C2，…A n a n+1B n C n，的位似中心坐标；（2）正方形A4A3B4C4四个顶点的坐标．【答案】（1）（0，0）；（2）A4（8，0），A5（16，0），B4（16，8），C4（8，8）．27．（本题8分）如图，在△ABC中，BE平分∠ABC交AC于点E，过点E作ED∥BC交AB于点D．（1）求证：AE•BC=BD•AC；（2）如果S△ADE=3，S△BDE=2，DE=6，求BC的长．【答案】(1)证明见解析；(2) BC=10.28．（本题11分） (1)、问题：如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°．求证：AD·BC=AP·BP．(2)、探究：如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．(3)、应用：请利用（1）（2）获得的经验解决问题：如图3，在△ABD中，AB=6，AD=BD=5．点P以每秒1个单位长度的速度，由点A 出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当DC的长与△ABD底边上的高相等时，求t的值．【答案】(1)证明见解析；(2)证明见解析；(3) t=1秒或5秒.【解析】(1)、如图1 ∵∠DPC=∠A=∠B=90°，∴∠ADP+∠APD=90°，∠BPC+∠APD=90°，∴∠ADP =∠BPC ∴△ADP∽△BPC．∴ADBP=APBC.即AD·BC=AP·BP．(2)结论AD·BC=AP·BP 仍成立．理由：如图2，∵∠BPD=∠DPC+∠BPC，又∵∠BPD=∠A+∠ADP，∴∠DPC+∠BPC =∠A+∠ADP，∵∠DPC =∠A=θ，∴∠BPC =∠ADP ，又∵∠A=∠B=θ，∴△ADP∽△BPC，∴ADBP=APBC.，∴AD·BC=AP·BP．(3)如图3，过点D作DE⊥AB于点E，∵AD=BD=5，AB=6，∴AE=BE=3，由勾股定理得DE=4，∴DC=DE=4，∴BC=5-4=1，又∵AD=BD，∴∠A=∠B，由已知，∠DPC =∠A，∴∠DPC =∠A=∠B，由（1）、（2）可得：AD·BC=AP·BP，又AP=t，BP=6-t，∴t（6-t）=5×1，解得t1=1，t2=5，∴t的值为1秒或5秒．。

人教版九年级下册数学第二十七章测试卷附答案

人教版九年级下册数学第二十七章测试题一、单选题1．如图，下列条件不能判定△ADB∽△ABC的是（）A．∠ABD=∠ACB B．∠ADB=∠ABCC．AB2=AD•AC D．AD AB AB BC2．如图，已知点P是边长为5的正方形ABCD内一点，且PB＝3，BF⊥BP于B，若在射线BF上找一点M，使以点B，M，C为顶点的三角形与△ABP相似，BM的值为（）A．3B．253C．3或253D．3或53．如图，AD∥BE∥CF，直线m，n与这三条平行线分别交于点A，B，C和点D，E，F，已知AB＝5，BC＝10，DE＝4，则EF的长为（）A．12B．9C．8D．44．如图，A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点，如果△RPQ∽△ABC，那么点R应是甲、乙、丙、丁四点中的（）A ．甲B ．乙C ．丙D ．丁5．如图，已知∠ABC ＝90°，BD ⊥AC 于D ，AB ＝4，AC ＝10，则AD ＝（）A ．85B ．2C 10D ．16．若b a =25，则a b a b -+的值为（）A ．14B ．37C ．35D ．757．如图，在ABC 中，点P 在边AB 上，则在下列四个条件中：：ACP B ∠∠=①；APC ACB ∠∠=②；2AC AP AB =⋅③；AB CP AP CB ⋅=⋅④，能满足APC 与ACB 相似的条件是（）A ．①②④B ．①③④C ．②③④D ．①②③8．如图，DE ∥FG ∥BC ，若DB=4FB ，则EG 与GC 的关系是（）A ．EG=4GCB ．EG=3GC C ．EG=52GCD ．EG=2GC9．如图，在正方形网格上有两个相似三角形△ABC 和△DEF ，则∠BAC 的度数为（）A．105°B．115°C．125°D．135°10．如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条边DF＝50cm，EF＝30cm，测得边DF离地面的高度AC＝1.5m，CD＝20m，则树高AB为（）A．12m B．13.5m C．15m D．16.5m二、填空题11．在同一时刻，一杆高为2m，影长为1.2m，某塔的影长为18m，则塔高为_____m．12．若两个相似三角形的周长比是4:9，则对应中线的比是________．13．方格纸中每个小正方形的边长都是单位1，△OAB在平面直角坐标系中的位置如图所示．解答问题：（1）请按要求对△ABO作如下变换：①将△OAB向下平移2个单位，再向左平移3个单位得到△O1A1B1；②以点O为位似中心，位似比为2：1，将△ABC在位似中心的异侧进行放大得到△OA2B2．（2）写出点A1，A2的坐标：_______，________；（3）△OA2B2的面积为_______．14．如图，用长3m、4m、5m的三根木棒正好搭成一个Rt△ABC，AC＝3，∠C＝90°，用一束垂直于AB的平行光线照上去，AC、BC在AB的影长分别为AD、DB，则AD＝_____，BD＝_____．15．一个4米高的电线杆的影长是6米，它临近的一个建筑物的影长是36米．则这个建筑的高度是_____m．16．两个相似三角形的面积比为1：9，则它们的周长比为_____．17．如图，四边形ABCD与四边形EFGH位似，其位似中心为点O，且43OEEA=，则FGBC=______．18．上午某一时刻,身高1.7米的小刚在地面上的影长为3.4米,则影长26米的旗轩高度为___________米三、解答题19．如图，已知AD∥BE∥CF，它们依次交直线l1、l2于点A、B、C和点D、E、F．（1）如果AB＝6，BC＝8，DF＝7，求EF的长；（2）如果AB：AC＝2：5，EF＝9，求DF的长．20．已知：平行四边形ABCD，E是BA延长线上一点，CE与AD、BD交于G、F．求证：2CF GF EF=⋅．21．已知：如图，D是AC上一点，BE∥AC，BE＝AD，AE分别交BD、BC于点F、G，且∠1＝∠2．（1）填空：图中与△BEF全等的三角形是______，与△BEF相似的三角形是_____（不再添加任何辅助线）；（2）对（1）中的两个结论选择其中一个给予证明．22．如图，AC是▱ABCD的对角线，在AD边上取一点F，连接BF交AC于点E，并延长BF交CD的延长线于点G．（1）若∠ABF＝∠ACF，求证：CE2＝EF•EG；（2）若DG＝DC，BE＝6，求EF的长．23．求证：相似三角形对应边上的中线之比等于相似比．（要求：先画出图形，再根据图形写出已知、求证和证明过程）24．已知如图，E为平行四边形ABCD的边AB的延长线上的一点，DE分别交AC、BC于G、F，试说明：DG是GE、GF的比例中项．25．如图，△ABC与△ADE中，∠C＝∠E，∠1＝∠2；（1）证明：△ABC∽△ADE．（2）请你再添加一个条件，使△ABC≌△ADE．你补充的条件为：．26．探究：如图①，在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥m于点D，CE⊥m于点E，求证：△ABD≌△CAE．应用：如图②，在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC ＝∠BAC，求证：DE＝BD+CE．参考答案1．D【分析】根据有两个角对应相等的三角形相似，以及根据两边对应成比例且夹角相等的两个三角形相似，分别判断得出即可．【详解】解：A、∵∠ABD=∠ACB，∠A=∠A，∴△ABC∽△ADB，故此选项不合题意；B、∵∠ADB=∠ABC，∠A=∠A，∴△ABC∽△ADB，故此选项不合题意；C、∵AB2=AD•AC，∴AC ABAB AD，∠A=∠A，△ABC∽△ADB，故此选项不合题意；D、ADAB=ABBC不能判定△ADB∽△ABC，故此选项符合题意．故选D．【点睛】点评：本题考查了相似三角形的判定，利用了有两个角对应相等的三角形相似，两边对应成比例且夹角相等的两个三角形相似．2．C【分析】由于∠ABC=∠PBF=90°，同时减去∠PBC后可得到∠ABP=∠CBF，若以点B，M，C为顶点的三角形与△ABP相似，那么必有：AB：PB=BC：BM或AB：BP=BM：BC，可据此求得BM的值．【详解】∵四边形ABCD是正方形，∴∠ABC=90°，AB=BC=5；又∵∠PBF=90°，∴∠ABP=∠CBF=90°-∠CBP；若以点B，M，C为顶点的三角形与△ABP相似，则：①AB BMPB BC=，即535BM=，解得BM=253；②AB BCBP BM=，即553BM=，解得BM=3；故选C．【点睛】本题考查的知识点是相似三角形的判定和性质，解题关键是应注意相似三角形的对应顶点不明确时，要分类讨论，不要漏解．3．C【解析】试题解析：∵AD∥BE∥CF，∴AB DEBC EF=，即5410EF=，解得，EF=8，故选C．4．B【详解】∵△RPQ∽△ABC，∴RPQ PQABC BC∆=∆的高的高，即633RPQ∆=的高，∴△RPQ的高为6．故点R应是甲、乙、丙、丁四点中的乙处．故选B．5．A【解析】【分析】根据射影定理每一条直角边是这条直角边在斜边上的射影和斜边的比例中项即可得出BC的长．【详解】根据射影定理得：AB 2=AD•AC ，∴AD=168105=．故选A ．【点睛】本题考查射影定理的知识，属于基础题，注意掌握每一条直角边是这条直角边在斜边上的射影和斜边的比例中项．6．B【分析】根据比例设b=2k ，a=3k ，然后代入比例式计算即可得解．【详解】解:∵b a =25∴设b=2k,a=5k,则a b a b -+=5252k k k k -+=37故选B【点睛】本题考查比例的基本性质，解题关键是熟练掌握性质.7．D【分析】根据相似三角形的判定定理，结合图中已知条件进行判断.【详解】当ACP B ∠∠=，A A ∠∠= ，所以APC ∽ACB ,故条件①能判定相似，符合题意；当APC ACB ∠∠=，A A ∠∠= ，所以APC ∽ACB ，故条件②能判定相似，符合题意；当2AC AP AB =⋅，即AC ：AB AP =：AC ，因为A A∠=∠所以APC ∽ACB ，故条件③能判定相似，符合题意；当AB CP AP CB ⋅=⋅，即PC ：BC AP =：AB ，而PAC CAB ∠∠=，所以条件④不能判断APC 和ACB 相似，不符合题意；①②③能判定相似，故选D ．【点睛】本题考查相似三角形的判定，熟练掌握判定定理是解题的关键.8．B【详解】分析：根据平行线分线段成比例定理即可得到答案．详解：∵DE ∥FG ∥BC ，DB=4FB ，∴31EG DF GC FB ＝＝=3．故选B ．点睛：此题主要考查平行线分线段成比例定理的理解及运用．根据平行线分线段成比例定理解答是解题的关键．9．D【分析】根据相似三角形的对应角相等即可得出．【详解】∵△ABC ∽△EDF ，∴∠BAC ＝∠DEF ，又∵∠DEF ＝90°+45°＝135°，∴∠BAC ＝135°，故选：D ．【点睛】本题考查相似三角形的性质，解题的关键是找到对应角10．D【分析】利用直角三角形DEF 和直角三角形BCD 相似求得BC 的长后加上小明同学的身高即可求得树高AB．【详解】∵∠DEF=∠BCD=90°，∠D=∠D，∴△DEF∽△DCB，∴BC DC EF DE=，∵DF=50cm=0.5m，EF=30cm=0.3m，AC=1.5m，CD=20m，∴由勾股定理求得DE=40cm，∴20 0.30.4 BC=，∴BC=15米，∴AB=AC+BC=1.5+15=16.5（米）．故答案为16.5m．【点睛】本题考查了相似三角形的应用，解题的关键是从实际问题中整理出相似三角形的模型．11．30．【解析】试题分析：设塔高为xm,根据题意可得，解得x=30．考点：投影．12．4:9【分析】相似三角形的面积之比等于相似比的平方．【详解】解：两个相似三角形的周长比是4:9，∴两个相似三角形的相似比是4:9，∴两个相似三角形对应中线的比是4:9，故答案为4:9．13．（1）①图见解析；②图见解析；（2）（0，﹣1），（﹣6，﹣2）；（3）10．【解析】试题分析：（1）根据平移的方向和距离作出△O1A1B1；根据位似中心的位置以及位似比的大小作出△OA2B2；（2）根据三角形的位置得出点A1，A2的坐标即可；（3）根据△OA2B2的位置，运用割补法求得△OA2B2的面积即可．试题解析：（1）①如图所示，△O1A1B1即为所求；②如图所示，△OA2B2即为所求；（2）由图可得，点A1，A2的坐标分别为（0，﹣1），（﹣6，﹣2）；（3）若以x轴为分割线，则△OA2B2的面积为：12×5×（2+2）=10．考点：作图-位似变换；作图-平移变换．14．95165【分析】由射影定理得到AC2=AD⋅AB,BC2=BD⋅AB,把相关线段的长度代入计算即可.【详解】解：依题意知，AC＝3cm，AB＝5cm，BC＝4cm，∠C＝90°．∵CD⊥AB，∴AC2＝AD•AB，BC2＝BD•AB，则9＝5AD，16＝5BD，所以AD＝95，BD＝165．故答案是：95；165．【点睛】本题考查了射影定理:①直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项.②每一条直角边是这条直角边在斜边上的射影和斜边的比例中项. 15．24米．【分析】先设建筑物的高为h米，再根据同一时刻物高与影长成正比列出关系式求出h的值即可．【详解】设建筑物的高为h米，由题意可得：则4：6=h：36，解得：h=24（米）．故答案为24米．【点睛】本题考查的是相似三角形的应用，熟知同一时刻物高与影长成正比是解答此题的关键．16．1：3【详解】已知两个相似三角形的面积比为1：9，相似三角形的面积的比等于相似比的平方，周长的比等于相似比，由此可得这两个三角形的周长比为1：3，故答案为1：3.17．4 7【分析】利用位似图形的性质结合位似比等于相似比得出答案．【详解】四边形ABCD与四边形EFGH位似，其位似中心为点O，且OE4 EA3=，OE4 OA7∴=，则FG OE4 BC OA7==，故答案为4 7．【点睛】本题考查了位似的性质，熟练掌握位似的性质是解题的关键.18．13【分析】影子是光的直线传播形成的,物体、影子与光线组成一直角三角形;利用数学知识(相似三角形的边与边之间对应成比例)计算.【详解】解：由题意，根据光的直线传播，根据相似三角形对应边成比例；由题意可知：=身高旗杆高影长旗杆影长即：1.7=3.426旗杆高∴旗杆高＝13m ．故答案为13．【点睛】本题考查了相似三角形的知识,解题的关键是正确的构造直角三角形.19．（1）EF ＝4；（2）DF ＝15．【分析】（1）根据三条平行线截两条直线，所得的对应线段成比例可得AB DE BC EF=，再由AB=6，BC=8，DF=7即可求出EF 的长；（2）根据三条平行线截两条直线，所得的对应线段成比例可得AB DE BC EF =，再由AB ：AC ＝2：5，EF=9，即可求出EF 的长.．【详解】解：（1）∵AD ∥BE ∥CF ，∴AB DE BC EF =，即678EF EF -=，解得：EF ＝4；（2）∵AD ∥BE ∥CF ，∴AB DE AC DF =，即295DF DF-=，解得；DF ＝15．【点睛】本题考查的知识点是平行线分线段成比例的知识，解题关键是掌握三条平行线截两条直线，所得的对应线段成比例．20．详见解析【分析】由平行四边形对边互相平行，可得平行线分线段成比例，得出比例式进行等比代换即可得证.【详解】解：∵四边形ABCD 是平行四边形，∴AD BC ∥，AB CD ∥．∴GF DF CF BF =，CF DF EF BF =∴GF CF CF EF=，即2CF GF EF =⋅．【点睛】本题考查证明线段乘积关系，由平行线分线段成比例得到比例式是解决本题的关键.21．（1）△BEF ≌△DAF ；△BEF ∽△GBF ；（2）证明见解析.【解析】【分析】（1）结合图形，根据全等三角形的判定即可得解；根据相似三角形的判定，结合图形找出与△BEF 能够有两组对应角相等的三角形即可；（2）根据两直线平行，内错角相等可得∠1=∠E ，然后利用“角角边”证明△BEF 和△DAF 全等；根据∠1=∠2可得∠2=∠E ，又∠E 为公共角，可以证明△BEF 和△GBF 相似．【详解】（1）解：△BEF ≌△DAF ，△BEF ∽△GBF ；（2）证明：∵BE ∥AC ，∴∠1＝∠E ，在△BEF 和△DAF 中，∵()1E BFE ADF BE AD ⎧∠=∠⎪∠=∠⎨⎪=⎩对顶角相等，∴△BEF ≌△DAF （AAS ）；∵BE ∥AC ，∴∠1＝∠E ，∵∠1＝∠2，∴∠2＝∠E，又∵∠F为公共角，∴△BEF∽△GBF．【点睛】本题考查的知识点是相似三角形的判定，全等三角形的判定，熟练掌握三角形全等的判定方法，相似三角形的判定方法，解题关键是并准确识图找出相关的条件．22．（1）证明见解析；（2）3.【分析】（1）依据等量代换得到∠ECF=∠G，依据∠CEF=∠CEG，可得△ECF∽△EGC，进而得出CE FEGE CE=，即CE2=EF•EG；（2）依据AB=CD=DG，可得AB：CG=1：2，依据AB∥CG，即可得出EG=12，BG=18，再根据AB∥DG，可得192BF BG==，进而得到EF=BF-BE=9-6=3．【详解】解：（1）∵AB∥CG，∴∠ABF＝∠G，又∵∠ABF＝∠ACF，∴∠ECF＝∠G，又∵∠CEF＝∠CEG，∴△ECF∽△EGC，∴CE FEGE CE=，即CE2＝EF•EG；（2）∵平行四边形ABCD中，AB＝CD，又∵DG＝DC，∴AB＝CD＝DG，∴AB：CG＝1：2，∵AB∥CG，∴12 AB BECG GE==，即612 GE=，∴EG＝12，BG＝18，∵AB ∥DG ，∴1BF AB GF DG==，∴BF ＝12BG ＝9，∴EF ＝BF ﹣BE ＝9﹣6＝3．【点睛】本题考查的知识点是相似三角形的判定与性质，平行四边形的性质，解题关键是熟练掌握平行四边形的判定方法与性质．23．证明见解析.【分析】先根据题意画出图形，写出已知，求证，再证明即可．【详解】已知，如图，△ABC ∽△A'B'C'，''''''A B B C A C AB BC AC===k ，D 是AB 的中点，D'是A'B'的中点，求证：''C D k CD =.证明：∵D 是AB 的中点，D'是A'B'的中点，∴AD ＝12AB ，A'D'＝12A'B'，∴1''''''212A B A D A B AD AB AB ==，∵△ABC ∽△A'B'C'，∴''''A B A C AB AC =，∠A'＝∠A ，∵A''''D A C AD AC=，∠A'＝∠A ，∴△A'C'D'∽△ACD，∴''''C D A CCD AC＝k．【点睛】本题考查的知识点是相似三角形的性质，解题关键是注意文字叙述性命题的证明格式. 24．答案见解析【分析】根据平行四边形两条对边平行,得到两对相似三角形,写出对应边成比例,得到两个比例式中各有两条线段的比相等,根据等量代换得到比例式,再转化成乘积式,即可得出答案.【详解】解：∵四边形ABCD是平行四边形，∴DC∥AE，∴DG CG= GE AG∵AD∥BC，∴GF CG= DG AG∴DG GF= GE DG∴DG2＝GE•GF，∴DG是GE、GF的比例中项．【点睛】此题考查了平行线分线段成比例,用到的知识点是平行四边形的性质、平行线分线段成比例定理,用到两次等量代换是本题的关键.25．(1)证明见解析；(2)见解析.【分析】(1)由∠1=∠2,证出∠BAC=∠DAE.再由∠C=∠E,即可得出结论;(2)由AAS证明△ABC≌△ADE即可.【详解】(1)∵∠1=∠2，∴∠1+∠DAC=∠2+∠DAC，∴∠BAC=∠DAE．∵∠C=∠E，∴△ABC∽△ADE．(2)补充的条件为：AB=AD（答案不唯一）；理由如下：由(1)得：∠BAC=∠DAE，在△ABC和△ADE中，BAC DAEC EAB AD∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABC≌△ADE；故答案为AB=AD（答案不唯一）．【点睛】本题主要考查全等三角形的判定及相似三角形的判定.26．证明见解析【分析】(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90o,而∠BAC=90o,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA.则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;(2)利用∠BDA=∠BAC=α,则∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α,得出∠CAE=∠ABD,进而得出△ADB≌△CEA即可得出答案.【详解】证明：（1）∵BD⊥直线m，CE⊥直线m，∴∠BDA＝∠CEA＝90°，∵∠BAC＝90°∴∠BAD+∠CAE＝90°，∵∠BAD+∠ABD＝90°，∴∠CAE＝∠ABD，∵在△ADB和△CEA 中，∴△ADB≌△CEA（AAS）；（2）设∠BDA＝∠BAC＝α，∴∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α，∴∠CAE＝∠ABD，∵在△ADB和△CEA中，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE．【点睛】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”,“SAS”,“ASA”,“AAS”;本题得出∠CAE=∠ABD证三角形全等是解题关键.。

人教版九年级数学下册第二十七章达标测试卷含答案

人教版九年级数学下册第二十七章达标测试卷一、选择题(每题2分，共20分)1．观察下列每组图形，是相似图形的是()2．下列四组线段中，不成比例的是()A．3，9，2，6 B．1，3，2， 6C．1，2，3，9 D．1，2，4，83．若两个相似多边形周长的比为15，则它们的相似比为() A．125 B．1 5 C．1 2.5 D．1 54．如图，l1∥l2∥l3，ABBC＝53，DF＝24，则EF的长为()A．8 B．9 C．12 D．15(第4题)(第7题)5.在平面直角坐标系中，已知点A(－4，2)，B(－6，－4)，以原点O为位似中心，把△ABO缩小，相似比为12，则点A的对应点A′的坐标是()A．(－2，1) B．(－8，4)C．(－8，4)或(8，－4) D．(－2，1)或(2，－1)6．在△ABC中，∠B＝100°，BC＝5，AB＝7，将△ABC沿虚线剪开，剪下的阴影三角形与原三角形不相似的是()7．一种燕尾夹如图①所示，图②是在闭合状态时的示意图，图③是在打开状态时的示意图(数据如图，单位均为mm)，从图②闭合状态到图③打开状态，则点B，D之间的距离减少了()A．25 mm B．20 mmC．15 mm D．8 mm8．如图，在平行四边形ABCD中，如果CM＝2DM，AM与BD相交于点N，那么△DMN与平行四边形ABCD的面积之比为()A．1：24 B．1：15C．1：12 D．1：99.如图，在正方形ABCD中，AB＝6，AE＝13AB，点F在AD上运动(不与A，D重合)，过点F作FG⊥EF交CD于点G，则DG的最大值为()A．4.5 B．4 C．3.5 D．310．如图，在△ABC中，∠ACB＝90°，角平分线BE与中线CD交于点F，若AC＝16，BC＝12，则EFBF的值为()A.5－12 B.38 C.13 D.925二、填空题(每题3分，共18分)11．已知3x－5y＝0，则xy＝________．12．如图所示，某超市在一楼至二楼之间装有电梯，天花板与地面平行．张强扛着箱子(人与箱子的总高度约为2.2 m)乘电梯刚好安全通过，请你根据图中数据回答，两层楼之间的高约为________m.13．如图所示的网格是正方形网格，A，B，C，D，E是网格线的交点，那么△ADE 的面积与△ABC的面积的比是________．(第13题)(第15题)(第16题)14.某同学的眼睛到黑板的距离是6 m，课本上的文字大小为0.4 cm×0.35 cm.要使这名同学看黑板上的字时，与他看相距30 cm的课本上的字的感觉相同，老师在黑板上写的文字大小应约为________(答案请按同一形式书写)．15．如图，已知正方形ABCD的边长为6 2，E是边CD上的中点，对角线BD 上有一动点F，当△ABF与△DEF相似时，BF的值为________．16．如图，在平面直角坐标系中，△OAC的顶点A在反比例函数y＝kx的图象上，点C在x轴上，边AC交反比例函数图象于点B，若S△BOC＝2，且AB＝2BC，则k的值为________．三、解答题(17题6分，18～21题每题8分，22，23题每题10分，24，25题每题12分，共82分)17．(6分)计算：(1)已知2x＝53，求x.(2)已知y2＝2y－x3(y≠0)，求xy的值．18．(8分)如图，在△ABC中，DE∥BC.(1)若AD＝2 cm，DB＝3 cm，AE＝1 cm，求EC的长；(2)若AB＝5 cm，AD＝2 cm，AC＝4 cm，求EC的长．19．(8分)如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A(0，3)，B(3，4)，C(2，2)．(1)画出△ABC向下平移4个单位长度得到的△A1B1C1；(2)画出△A1B1C1绕着点A1按顺时针方向旋转90°得到的△A1B2C2，C2的坐标为________；(3)以点B为位似中心，在给出的网格内画出△A3BC3，使△A3BC3与△ABC位似，且相似比为2 1.20.(8分)如图，点C是线段AB的黄金分割点，即BCAC＝ACAB，若S1表示以CA为一边的正方形的面积，S2表示长为AB，宽为CB的矩形的面积，求S1与S2的大小关系．21．(8分)如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC于点D，点O是AC边上一点，连接BO交AD于F，OE⊥OB交BC边于点E.求证：△ABF∽△COE.22．(10分)小红家的阳台上放置了一个晒衣架，如图是晒衣架的侧面示意图，立杆AB，CD相交于点O，B，D两点在地面上，经测量得到AB＝CD＝136 cm，OA＝OC＝51 cm，OE＝OF＝34 cm，现将晒衣架完全稳固张开，扣链EF成一条线段．(1)连接AC.求证：AC∥EF；(2)若EF＝32 cm，求利用夹子垂挂在晒衣架上的连衣裙总长度小于多少时，连衣裙才不会拖在地面上．23．(10分)如图，在平面直角坐标系xOy中，平行四边形OABC的顶点A在x轴的正半轴上，点D(4，3)在对角线OB上，且ODOB＝13.反比例函数y＝kx(k>0，x>0)的图象经过C，D两点，直线CD交x轴于点E.(1)求k的值；(2)求△ODE的面积．24．(12分)有一种工具叫磨，最初叫硙，用人力或畜力可使它转动．如图是从石磨中抽象出来的模型，在Rt △ABC 中，∠ACB ＝90°，在AB 上取点D ，以AD 为直径作⊙O ，切直线BC 于点E ，连接DE ，AE .(1)求证：△ADE ∽△AEC ；(2)若⊙O 的半径为5，AC ＝8，求S △BDE .25．(12分)如图，在△ABC 中，∠BAC ＝90°，AB ＝AC ，点D 为射线BA 上的一点，连接CD ，将线段CD 绕点C 顺时针旋转90°得到线段CE ，连接DE ，DE 所在直线与射线CA 交于点F ，且EF ＝3DF .(1)若点D 在线段BA 上．①求证：∠ADF ＝∠BCD ；②求ADAC 的值． (2)连接AE ，BE ，若AE ＝，直接写出BE 的长．答案一、1.C 2.C 3.B 4.B 5.D 6.D7.A8.A9.A10．B点拨：作EH⊥AB于H，延长CD到M，使DM＝CD，连接BM，如图．∵∠ACB＝90°，AC＝16，BC＝12，∴AB＝AC2＋BC2＝20，∵BE平分∠ABC，∴EH＝EC，∵△ABC的面积＝△ABE的面积＋△BCE的面积，∴12AC·BC＝12AB·EH＋12BC·CE，∴16×12＝20CE＋12CE，∴CE＝6，∵AD＝BD，∠ADC＝∠BDM，DM＝DC，∴△BDM≌△ADC(SAS)，∴BM＝AC＝16，∠M＝∠ECF，∴CE∥MB，∴易知△CEF∽△MBF，∴EFBF＝CEMB＝616＝38.二、11.5312.5.513.1 414．8 cm×7 cm15.6或816．3点拨：过点B作BD⊥CO于点D，过点A作AE⊥CO于点E，如图，∴BD∥AE，∴△BCD∽△ACE，∴BCAC＝BDAE，∵AB＝2BC，∴BCAC＝BDAE＝13.设B ⎝ ⎛⎭⎪⎫m ，k m ，∴BD ＝－k m ，∴AE ＝3BD ＝－3km ，当y ＝3k m 时，x ＝m 3，即点A ⎝ ⎛⎭⎪⎫m 3，3k m .∵S △BOC ＝2，AB ＝2BC ， ∴易得S △AOB ＝4，∴易得S 梯形ABDE ＝S △AOB ＋S △BOD －S △AOE ＝S △AOB ＝4， ∴12⎝ ⎛⎭⎪⎫－k m －3k m ⎝ ⎛⎭⎪⎫m 3－m ＝4，解得k ＝3.三、17.解：(1)∵2x ＝53，∴5x ＝6.∴x ＝65.(2)∵y 2＝2y －x3，∴3y ＝2(2y －x )．∴3y ＝4y －2x .∴3y －4y ＝－2x .∴－y ＝－2x .∴x y ＝12. 18．解：(1)∵DE ∥BC ，∴AE EC ＝AD DB ，∴1EC ＝23，∴EC ＝32 cm.(2)∵DE ∥BC ，∴AD AB ＝AE AC ，即25＝AE4.∴AE ＝85 cm ，∴EC ＝AC －AE ＝4－85＝125(cm)． 19．解：(1)如图，△A 1B 1C 1即为所求．(2)如图，△A 1B 2C 2即为所求． (－1，－3) (3)如图，△A 3BC 3即为所求．20．解：∵点C是线段AB的黄金分割点，即BCAC＝ACAB，∴AC2＝AB·BC，∵S1＝AC2，S2＝AB·BC，∴S1＝S2.21．证明：∵OE⊥OB，∠BAC＝90°，∴∠BOA＋∠COE＝90°，∠BOA＋∠ABF＝90°，∴∠ABF＝∠COE.∵AD⊥BC，∴∠DAC＋∠C＝90°，∵∠BAC＝90°，∴∠BAF＋∠DAC＝90°，∴∠BAF＝∠C.∴△ABF∽△COE.22．(1)证明：∵立杆AB，CD相交于点O，∴∠AOC＝∠EOF.又∵OAOE＝OCOF＝5134＝32，∴△AOC∽△EOF，∴∠A＝∠OEF，∴AC∥EF.(2)解：过点A作AM⊥BD于点M，过点O作ON⊥EF于点N. ∵OE＝OF＝34 cm，∴△OEF是等腰三角形．∴∠OEF＝12(180°－∠EOF)．∵ON⊥EF，EF＝32 cm，∴ON是边EF上的中线，∴EN＝16 cm.在Rt△OEN中，根据勾股定理可得ON＝OE2－EN2＝342－162＝30(cm)．∵ON⊥EF，AM⊥BD，∴∠ONE ＝∠AMB ＝90°.∵OA ＝OC ，AB ＝CD ，∴OB ＝OD ，∴∠OBD ＝12(180°－∠BOD )，∴∠OBD ＝∠OEF ，∴易知△EON ∽△BAM ， ∴OE AB ＝ON AM ，即34136＝30AM ，解得AM ＝120 cm.答：利用夹子垂挂在晒衣架上的连衣裙总长度小于120 cm 时，连衣裙才不会拖在地面上．23．解：(1)∵反比例函数y ＝k x (k >0，x >0)的图象经过点D (4，3)，∴k ＝4×3＝12.(2)分别过点D ，B 作x 轴的垂线DF ，BG ，垂足分别为F ，G ，如图．易得DF ∥BG ，∴△ODF ∽△OBG ，∴OD OB ＝DF BG ，∵OD OB ＝13，DF ＝3，∴BG ＝9，∴点C 的纵坐标为9，∵点C 在反比例函数y ＝12x (x >0)的图象上，∴C ⎝ ⎛⎭⎪⎫43，9. 设直线CD 的解析式为y ＝ax ＋b ，则⎩⎪⎨⎪⎧4a ＋b ＝3，43a ＋b ＝9，解得⎩⎪⎨⎪⎧a ＝－94，b ＝12，∴直线CD 的解析式为y ＝－94x ＋12，令y ＝0，－94x ＋12＝0，解得x ＝163，∴E ⎝ ⎛⎭⎪⎫163，0，∴OE ＝163， ∴S △ODE ＝12DF ·OE ＝12×3×163＝8.24．(1)证明：连接OE ，如图．∵BC 是⊙O 的切线，∴OE ⊥BC ，∴∠OEC ＝90°，∴∠AEC ＋∠AEO ＝90°，∵AD 为直径，∴∠AED ＝90°，∴∠AEO ＋OED ＝90°，∴∠AEC ＝∠OED ，∵OD ＝OE ，∴∠OED ＝∠ODE ，∴∠AEC ＝∠ODE ，∵∠C ＝∠AED ＝90°，∴△ADE ∽△AEC .(2)解：由(1)知，△ADE ∽△AEC ，∴AD AE ＝AE AC ，∵AD ＝2×5＝10，AC ＝8，∴10AE ＝AE 8，∴AE ＝4 5(负值舍去)．∴DE ＝AD 2－AE 2＝102－（4 5）2＝2 5，CE ＝AE 2－AC 2＝（4 5）2－82＝4，∴S △ADE ＝12DE ·AE ＝12×2 5×4 5＝20， S △ACE ＝12AC ·CE ＝12×8×4＝16.∵∠OEB ＝∠C ＝90°，∠EBO ＝∠CBA ，∴△BEO ∽△BCA ，∴OB AB ＝OE AC ，∴BD ＋5BD ＋10＝58，∴BD ＝103， ∴AB ＝BD ＋AD ＝103＋10＝403，∴BC ＝AB 2－AC 2＝⎝ ⎛⎭⎪⎫4032－82＝323， ∴S △ABC ＝12AC ·BC ＝12×8×323＝1283，∴S △BDE ＝S △ABC －S △ACE －S △AED ＝1283－16－20＝203.25．(1)①证明：∵∠BAC ＝90°，AB ＝AC ，∴∠ACB ＝∠ABC ＝180°－∠BAC 2＝45°. ∵由旋转得∠DCE ＝90°，CD ＝CE ，∴∠CDE ＝∠CED ＝180°－∠DCE 2＝45°， ∴∠ABC ＝∠CDE ＝45°.∵∠ADF ＋∠CDE ＋∠BDC ＝180°，∠BCD ＋∠ABC ＋∠BDC ＝180°. ∴∠ADF ＝∠BCD .②解：过E 作EH ⊥AC 于点H ，如图．∵EH ⊥AC ，∴∠EHA ＝∠BAC ＝90°.∵∠AFD ＝∠EFH ，∴△AFD ∽△HFE ，∴AD EH ＝DF EF .∵EF ＝3DF ，∴EH ＝3AD .∵∠DCE ＝∠BAC ＝90°，∴∠ACD ＋∠ADC ＝90°，∠ACD ＋∠ECH ＝90°.∴∠ADC ＝∠ECH .∵∠EHC ＝∠DAC ＝90°，DC ＝CE ，∴△CAD ≌△EHC ，∴AC ＝EH ，∴AC ＝3AD ，∴AD AC ＝13.(2)解：265或2 10.。

人教版九年级数学下册第二十七章检测卷(含答案)

第二十七章检测卷时间：120分钟满分：150分题号一二三四五六七八总分得分一、选择题(本大题共10小题，每小题4分，满分40分) 1．观察下列每组图形，相似图形是( )2．已知a b ＝23，那么aa ＋b 的值为( )A.13B.25C.35D.343．已知△ABC ∽△DEF ，且AB ∶DE ＝1∶2，则△ABC 的面积与△DEF 的面积之比为( )A ．1∶2B ．1∶4C ．2∶1D ．4∶1第4题图第5题图第6题图第7题图4．如图，在△ABC 中，DE ∥BC ，AD AB ＝13，BC ＝12，则DE 的长是( )A ．3B ．4C ．5D ．65．如图，在6×6的正方形网格中，连接两格点A ，B ，线段AB 与网格线的交点为M ，N ，则AM ∶MN ∶NB 为( )A ．3∶5∶4B ．1∶3∶2C ．1∶4∶2D ．3∶6∶56．如图，线段AB 两个端点的坐标分别为A (4，4)，B (6，2)，以原点O 为位似中心，在第一象限内将线段AB 缩小为原来的12后得到线段CD ，则端点C 和D 的坐标分别为( )A ．(2，2)，(3，2)B ．(2，4)，(3，1)C ．(2，2)，(3，1)D ．(3，1)，(2，2)7．如图，四边形ABCD 是平行四边形，点E 在BA 的延长线上，点F 在BC 的延长线上，连接EF ，分别交AD ，CD 于点G ，H ，则下列结论错误的是( )A.EA BE ＝EG EFB.EG GH ＝AG GDC.AB AE ＝BC CFD.FH EH ＝CF AD8．“今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学《九章算术》中的“井深几何”问题，它的题意可以由图获得，则井深为( )A ．1.25尺B ．57.5尺C ．6.25尺D ．56.5尺第 8题图第9题图第10题图9．如图，在正方形ABCD 中，M 为BC 上一点，ME ⊥AM ，ME 交AD 的延长线于点E .若AB ＝12，BM ＝5，则DE 的长为( )A ．18 B.1095 C.965 D.25310．如图，在锐角△ABC 中，BC ＝6，S △ABC ＝12，两动点M ，N 分别在边AB ，AC 上滑动，且MN ∥BC ，MP ⊥BC ，NQ ⊥BC ，得矩形MPQN .设MN 的长为x ，矩形MPQN 的面积为y ，则y 关于x 的函数图象大致形状是( )二、填空题(本大题共4小题，每小题5分，满分20分)11．比例尺为1∶4000000的地图上，两城市间的图上距离为3cm ，则这两城市间的实际距离为________km.12．如图，已知点B ，E ，C ，F 在同一条直线上，∠A ＝∠D ，要使△ABC ∽△DEF ，还需添加一个条件，你添加的条件是____________(只需写一个条件，不添加辅助线和字母)．第12题图第14题图13．将一个矩形沿着一条对称轴翻折，如果所得到的矩形与这个矩形相似，那么我们就将这样的矩形定义为“白银矩形”．事实上，“白银矩形”在日常生活中随处可见，如：我们常见的A4纸就是一个“白银矩形”．请根据上述信息求A4纸的较长边与较短边的比值，这个比值是________．14．将三角形纸片(△ABC)按如图折叠，使点C落在AB边上的点D处，折痕为EF.已知AB＝AC＝3，BC＝4，若以点B，D，F为顶点的三角形与△ABC相似，那么CF的长是__________．三、(本大题共2小题，每小题8分，满分16分)15．如图，四边形ABCD∽四边形A′B′C′D′，求x，y的值和α的大小．16．如图，在△ABC中，D是AB上一点，且∠ACD＝∠B，已知AD＝8cm，BD＝4cm，求AC的长．四、(本大题共2小题，每小题8分，满分16分)17．如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(－2，1)，B(－1，4)，C(－3，2)．(1)画出△ABC关于点B成中心对称的图形△A1BC1；(2)以原点O为位似中心，相似比为1∶2，在y轴的左侧，画出△ABC放大后的图形△A2B2C2，并直接写出点C2的坐标.18．如图，AB 是半圆O 的直径，点C 在圆弧上，D 是AC ︵的中点，OD 与AC 相交于点E .求证：△ABC ∽△COE .五、(本大题共2小题，每小题10分，满分20分)19．如图，在△ABC 中，AB ＝AC ＝8，BC ＝6，点D 为BC 上一点，BD ＝2.过点D 作射线DE 交AC 于点E ，使∠ADE ＝∠B .求线段CE 的长度．20．如图，在▱ABCD 中，E 是CD 的延长线上一点，连接BE 交AD 于点F ，且AF ＝2FD . (1)求证：△ABF ∽△CEB ；(2)若△CEB 的面积为9，求▱ABCD 的面积．六、(本题满分12分) 21．如图，△ABC 和△CEF 均为等腰直角三角形，E 在△ABC 内，∠CAE ＋∠CBE ＝90°，连接BF .(1)求证：△CAE ∽△CBF ；(2)若BE ＝1，AE ＝2，求CE 的长．七、(本题满分12分)22．已知正方形ABCD ，点E 在边CD 上，点F 在线段BE 的延长线上，连接FC ，且∠FCE ＝∠CBE .(1)如图①，当点E 为CD 边的中点时，求证：CF ＝2EF ；(2)如图②，当点F 位于线段AD 的延长线上时，求证：EF BE ＝DEDF.八、(本题满分14分)23．如图①，P 为△ABC 所在平面上一点，且∠APB ＝∠BPC ＝∠CP A ＝120°，则点P 叫作△ABC 的费马点．(1)如果点P 为锐角△ABC 的费马点，且∠ABC ＝60°. ①求证： △ABP ∽△BCP ；②若P A ＝3，PC ＝4，求PB 的长；(2)如图②，已知锐角△ABC ，分别以AB ，AC 为边向外作正△ABE 和正△ACD ，CE 和BD 相交于点P ，连接AP .①求∠CPD 的度数；②求证：点P 为△ABC 的费马点．参考答案与解析1．D 2.B 3.B 4.B 5.B 6.C 7.C 8.B 9.B10．B 解析：如图，过点A 作AD ⊥BC 于点D ，交MN 于点E .∵在锐角△ABC 中，BC ＝6，S △ABC ＝12，∴AD ·BC 2＝AD ×62＝12，解得AD ＝4.由MN ∥BC ，MP ⊥BC ，NQ ⊥BC ，AD ⊥BC ，易得四边形MPDE 为矩形，∴MP ＝ED .∵MN ∥BC ，∴△AMN ∽△ABC ，∴AEAD ＝MN BC ，即AE 4＝x 6，解得AE ＝2x 3，∴ED ＝AD －AE ＝4－2x 3，∴MP ＝4－2x3，∴矩形MPQN 的面积y ＝MN ·MP ＝x ⎝⎛⎭⎫4－2x 3＝－23x 2＋4x ＝－23(x －3)2＋6，∴y 关于x 的函数是二次函数，其函数图象的顶点坐标是(3，6)．故选B.11．12012．∠B ＝∠DEC (答案不唯一)13. 2 14.127或2 解析：由折叠可得DF ＝CF .设DF ＝CF ＝x ，则BF ＝BC －CF ＝4－x .以点B ，D ，F 为顶点的三角形与△ABC 相似，分两种情况：①若∠BFD ＝∠C ，则DF AC ＝BF BC ，即x 3＝4－x4，解得x ＝127；②若∠BFD ＝∠A ，则FD AC ＝BF BA ，即x 3＝4－x 3，解得x ＝2.综上所述，CF 的长为127或2.15．解：∵四边形ABCD ∽四边形A ′B ′C ′D ′，∴x 8＝y 11＝96，∠C ＝α，∠D ＝∠D ′＝140°，(4分)∴x ＝12，y ＝332，α＝∠C ＝360°－∠A －∠B －∠D ＝360°－62°－75°－140°＝83°.(8分)16．解：∵∠ACD ＝∠B ，∠A ＝∠A ，∴△ACD ∽△ABC ，∴AC AB ＝ADAC .(4分)∵AD ＝8cm ，BD ＝4cm ，∴AB ＝12cm ，(6分)∴AC ＝8×12＝46(cm)．(8分)17．解：(1)△A 1BC 1如图所示．(4分)(2)△A 2B 2C 2如图所示，点C 2的坐标为(－6，4)．(8分)18．证明：∵AB 为半圆O 的直径，∴∠BCA ＝90°.∵D 是AC ︵的中点，∴OE ⊥AC ，∴∠OEC ＝90°＝∠BCA .(4分)∵OA ＝OC ，∴∠BAC ＝∠OCE ，∴△ABC ∽△COE .(8分)19．解：∵AB ＝AC ，∴∠B ＝∠C .∵∠ADC ＝∠B ＋∠BAD ，∠ADC ＝∠ADE ＋∠CDE ，而∠ADE ＝∠B ，∴∠BAD ＝∠CDE ，∴△ABD ∽△DCE ，(5分)∴AB DC ＝BDCE .∵AB ＝8，BC ＝6，BD ＝2，∴DC ＝BC －BD ＝4，∴84＝2CE，∴CE ＝1.(10分)20．(1)证明：∵四边形ABCD 是平行四边形，∴∠A ＝∠C ，AB ∥CD ，∴∠ABF ＝∠E ，∴△ABF ∽△CEB .(4分)(2)解：∵AF ＝2FD ，∴AD ＝3FD .∵四边形ABCD 是平行四边形，∴AB ∥CD ，AD ∥BC ，AD ＝BC ，∴△ABF ∽△DEF ，△CEB ∽△DEF ，∴S △ABF ∶S △DEF ＝AF 2∶FD 2＝4，S △CEB ∶S △DEF ＝BC 2∶FD 2＝AD 2∶FD 2＝9.又∵△CEB 的面积为9，∴△DEF 的面积为1，△ABF 的面积为4，∴▱ABCD 的面积为9－1＋4＝12.(10分)21．(1)证明：∵△ABC 和△CEF 均为等腰直角三角形，∴AC BC ＝CECF ＝2，∠ACB ＝∠ECF＝45°.(3分)∵∠ACB ＝∠ACE ＋∠BCE ，∠ECF ＝∠BCF ＋∠BCE ，∴∠ACE ＝∠BCF ，∴△CAE ∽△CBF .(6分)(2)解：由(1)可知△CAE ∽△CBF ，∴∠CAE ＝∠CBF ，AE BF ＝AC BC ＝ 2.又∵AE ＝2，∴2BF ＝2，∴BF ＝ 2.(9分)∵∠CAE ＋∠CBE ＝90°，∴∠CBF ＋∠CBE ＝90°，∴∠EBF ＝90°，∴EF 2＝BE 2＋BF 2＝12＋(2)2＝3，∴EF ＝3，∴CE ＝2EF ＝ 6.(12分)22．证明：(1)∵四边形ABCD 是正方形，∴CD ＝BC .∵点E 为CD 边的中点，∴CE ＝12CD ＝12BC .(2分)∵∠FCE ＝∠CBE ，∠F ＝∠F ，∴△FCE ∽△FBC ，∴EF CF ＝CE BC .又∵CE ＝12BC ，∴EF CF ＝12，∴CF ＝2EF .(6分) (2)∵四边形ABCD 是正方形，∴DE ∥AB ，AD ∥BC ，AD ＝CD ，∴EF BE ＝DF AD ，∴EF BE ＝DFCD.(8分)∵AF ∥BC ，∴∠DFE ＝∠CBE .∵∠FCE ＝∠CBE ，∴∠DFE ＝∠FCE .又∵∠FDE ＝∠CDF ，∴△FDE ∽△CDF ，∴DE DF ＝DF CD ，∴EF BE ＝DEDF.(12分)23．(1)①证明：∵∠P AB ＋∠PBA ＝180°－∠APB ＝60°，∠PBC ＋∠PBA ＝∠ABC ＝60°，∴∠P AB ＝∠PBC .又∵∠APB ＝∠BPC ＝120°，∴△ABP ∽△BCP .(4分)②解：由①可知△ABP ∽△BCP ，∴P A PB ＝PBPC，∴PB 2＝P A ·PC ＝12，∴PB ＝2 3.(6分) (2)①解：如图，∵△ABE 和△ACD 是正三角形，∴AE ＝AB ，AC ＝AD ，∠EAB ＝∠5＝60°.∵∠EAC ＝∠EAB ＋∠BAC ，∠BAD ＝∠BAC ＋∠5，∴∠EAC ＝∠BAD ，∴△ACE ≌△ADB ，∴∠1＝∠2.∵∠3＝∠4，∴∠CPD ＝∠5＝60°.(10分)②证明：由①可知∠1＝∠2，∠3＝∠4，∴△ADF ∽△PCF ，∴AF ∶PF ＝DF ∶CF ，∴AF ∶DF ＝PF ∶CF .∵∠AFP ＝∠CFD ，∴△AFP ∽△DFC ，∴∠APF ＝∠ACD ＝60°.由①可知∠CPD ＝60°，∴∠APC ＝∠CPD ＋∠APF ＝120°，∠BPC ＝180°－∠CPD ＝120°，∴∠APB ＝360°－∠BPC －∠APC ＝120°，∴点P 为△ABC 的费马点．(14分)。

人教版初3数学9年级下册第27章(相似)单元达标测试(含解析)

人教版九年级数学下册《第27章相似》单元达标测试（附答案）一．选择题（共10小题，满分40分）1．已知，则等于（）A．B．C．2D．32．如图，用图中的数据不能组成的比例是（）A．2：4＝1.5：3B．3：1.5＝4：2C．2：3＝1.5：4D．1.5：2＝3：4 3．点P是长度为1的线段上的黄金分割点，则较短线段的长度为（）A．B．C．D．4．将一个四边形放在2倍的放大镜下，则下列说法不正确的是（）A．四边形的边长扩大为原来的2倍B．四边形的各角扩大为原来的2倍C．四边形的周长扩大为原来的2倍D．四边形的面积扩大为原来的4倍5．如图，在△ABC中，AD∥BC，点E在AB边上，EF∥BC，交AC边于点F，DE交AC 边于点G，则下列结论中错误的是（）A．B．C．D．6．已知点P是线段AB的黄金分割点，AP＞BP．记以AP为一边的正方形面积为S1，以BP、AB为邻边矩形的面积为S2，则（）A．S1＞S2B．S1＝S2C．S1＜S2D．S1、S2大小不能确定7．如图，AD是△ABC的中线，点E在AD上，AD＝4DE，连接BE并延长交AC于点F，则AF：FC的值是（）A．3：2B．4：3C．2：1D．2：38．如图，点D、E分别在△ABC的边AB、AC上，且AB＝9，AC＝6，AD＝3，若使△ADE 与△ABC相似，则AE的长为（）A．2B．C．2或D．3或9．如图是用卡钳测量容器内径的示意图，现量得卡钳上A，D两个端点之间的距离为10cm，＝＝，则容器的内径是（）A．5cm B．10cm C．15cm D．20cm10．如图，在直角坐标系中，有一等腰直角三角形OBA，∠OAB＝90°，直角边OA在x轴正半轴上，且OA＝1，将Rt△OBA绕原点O顺时针旋转90°，同时扩大边长的1倍，得到等腰直角三角形OB1A1（即A1O＝2AO）．同理，将Rt△OB1A1顺时针旋转90°，同时扩大边长1倍，得到等腰直角三角形OB2A2……依此规律，得到等腰直角三角形OB2019A2019，则点B2019的坐标为（）A．（﹣22019，22019）B．（22019，﹣22019）C．（﹣22018，22018）D．（22018，﹣22018）二．填空题（共6小题，满分24分）11．如图L4，L5被一组平行线L1，L2，L3所截，显然三条平行线不是等距的，若＝，则为．12．如图，矩形EFGO的两边在坐标轴上，点O为平面直角坐标系的原点，以y轴上的某一点为位似中心，作位似图形ABCD，且点B，F的坐标分别为（﹣4，4），（2，1），则位似中心的坐标为．13．两个相似三角形的最短边长分别为5cm和3cm，它们的周长之差为12cm，那么较大三角形的周长为 cm．14．如图，矩形ABCD中，AB＝2，BC＝4，剪去一个矩形ABEF后，余下的矩形EFDC∽矩形BCDA，则EC的长为．15．如图，在矩形ABCD中，AD＝2，CD＝1，连接AC，以对角线AC为边，按逆时针方向作矩形ABCD的相似矩形AB1C1C，再连接AC1，以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1，…，按此规律继续下去，则矩形AB4C4C3的面积为．16．如图，△ABC的顶点在1×3的正方形网格的格点上，在图中画出一个与△ABC相似但不全等的△DEF（△DEF的顶点在格点上），则△DEF的三边长分别是．三．解答题（共8小题，满分56分）17．已知如图，Rt△ABC中，∠C＝90°，CD是斜边上的高，求证：CD2＝AD•BD．18．如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（﹣2，1），B（﹣1，4），C（﹣3，2）（1）画出△ABC关于点B中心对称的△A1BC1，并直接写出点C1的坐标．（2）以原点O为位似中心，位似比为2：1，在y轴的左侧画出△ABC放大后的△A2B2C2，并直接写出点C2的坐标．19．如图，在△ABC中，CD⊥AB，DE⊥AC，DF⊥BC，垂足分别为D，E，F．（1）求证：CE•CA＝CF•CB；（2）EF交CD于点O，求证：△COE∽△FOD；20．如图，△ABC与△ADE中，∠ACB＝∠AED＝90°，连接BD、CE，∠EAC＝∠DAB．（1）求证：△ABC∽△ADE；（2）求证：△BAD∽△CAE；（3）已知BC＝4，AC＝3，AE＝．将△AED绕点A旋转，当点E落在线段CD上时，求BD的长．21．如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFMN的一边MN在边BC 上，顶点E、F分别在AB、AC上，其中BC＝24cm，高AD＝12cm．（1）求证：△AEF∽△ABC：（2）求正方形EFMN的边长．22．为了估计河的宽度，勘测人员在河的对岸选定一个目标点A，在近岸分别取点B、D、E、C，使点A、B、D在一条直线上，且AD⊥DE，点A、C、E也在一条直线上，且DE∥BC．经测量BC＝24米，BD＝12米，DE＝40米，求河的宽度AB为多少米？23．已知在平行四边形ABCD中，过点D作DE⊥BC于点E，且AD＝DE．连接AC交DE 于点F，作DG⊥AC于点G．（1）如图1，若，AF＝，求DG的长；（2）如图2，作EM⊥AC于点M，连接DM，求证：AM﹣EM＝2DG．24．如图，矩形ABCD中，E是BC上一点，点F是点E关于点C的对称点，过点F作对角线BD的平行线，交DC的延长线于点H，连接HE并延长与矩形的边AB、对角线BD 于点N、M．（1）试判定△BME的形状，并说明理由．（2）若BE＝2EC，连接DE，当△MED为直角三角形时，求AB：BC的值．参考答案一．选择题（共10小题，满分40分）1．解：∵，∴y＝2x，∴＝＝．故选：A．2．解：A、2：4＝1：2＝1.5：3，能组成比例，错误；B、3：1.5＝2：1＝4：2，能组成比例，错误；C、2：3≠1.5：4；不能组成比例，正确；D、1.5：2＝3：4，能组成比例，错误；故选：C．3．解：较短线段的长度＝1﹣×1＝，故选：C．4．解：放大前后的多边形按照比例放大与缩小，因此它们是相似多边形，放大后的倍数就是相似比，∴选项：A，C，D正确，故选：B．5．解：∵EF∥BC∴，∴答案A正确；根据合比性质，则有即：，∴答案D正确；又∵AD∥EF∴，∴答案B正确；而，∴答案C错误．故选：C．6．解：根据黄金分割的概念得：AP：AB＝PB：AP，即AP2＝PB•AB，则S1：S2＝AP2：（PB•AB）＝1，即S1＝S2．故选：B．7．解：过点D作DG∥AC，与BF交于点G．∵AD＝4DE，∴AE＝3DE，∵AD是△ABC的中线，∴，∴，即AF＝3DG∴，即FC＝2DG，∴AF：FC＝3DG：2DG＝3：2．故选：A．8．解：①若∠AED对应∠B时，＝，即＝，解得AE＝；②当∠ADE对应∠B时，＝，即＝，解得AE＝2．故选：C．9．解：如图，连接AD，BC，∵，∠AOD＝∠BOC，∴△AOD∽△BOC，∴＝＝，又AD＝10cm，∴BC＝2AD＝20cm．故选：D．10．解：∵△AOB是等腰直角三角形，OA＝1，∴AB＝OA＝1，∴B（1，1），将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1，且A1O＝2AO，再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2，且A2O＝2A1O…，依此规律，∴每4次循环一周，B1（2，﹣2），B2（﹣4，﹣4），B3（﹣8，8），B4（16，16），∵2019÷4＝502…3，∴点B2019与B3同在一个象限内，∵﹣4＝﹣22，8＝23，16＝24，∴点B2019（﹣22019，22019）．故选：A．二．填空题（共6小题，满分24分）11．解：∵L1∥L2∥L3，∴＝，∴＝，故答案为：．12．解：如图，连接BF交y轴于P，∵四边形ABCD和四边形EFGO是矩形，点B，F的坐标分别为（﹣4，4），（2，1），∴点C的坐标为（0，4），点G的坐标为（0，1），∴CG＝3，∵BC∥GF，∴＝＝，∴GP＝1，PC＝2，∴点P的坐标为（0，2），故答案为：（0，2）．13．解：∵两个相似三角形的最短边分别是5cm和3cm，∴两个三角形的相似比为5：3，设大三角形的周长为5x，则小三角形的周长为3x，由题意得，5x﹣3x＝12，解得，x＝6，则5x＝30，故答案为：30．14．解：∵四边形ABCD是矩形，∴AB＝CD＝2，AD＝BC＝4，∵四边形EFDC是矩形，∴EF＝CD＝2，CE＝DF，∵余下的矩形EFDC∽矩形BCDA，∴，即＝，∴CE＝1，故答案为：1．15．解：∵四边形ABCD是矩形，∴AD⊥DC，∴AC＝＝＝，∵按逆时针方向作矩形ABCD的相似矩形AB1C1C，∴矩形AB1C1C的边长和矩形ABCD的边长的比为：2∴矩形AB1C1C的面积和矩形ABCD的面积的比5：4，∵矩形ABCD的面积＝2×1＝2，∴矩形AB1C1C的面积＝，依此类推，矩形AB2C2C1的面积和矩形AB1C1C的面积的比5：4∴矩形AB2C2C1的面积＝∴矩形AB3C3C2的面积＝，按此规律第4个矩形的面积为，故答案为：．16．解：如图所示：△ABC∽△DEF，DE＝，ED＝2，EF＝．故答案为：，2，．三．解答题（共8小题，满分56分）17．证明：∵CD是斜边AB上的高．∴∠ADC＝∠CDB＝90°，又∵在Rt△ABC中，∠C＝90°，∴∠ACD+∠BCD＝90°∴∠A+∠ACD＝90°，∴∠A＝∠BCD，∴△ACD∽△CBD，∴，∴CD2＝AD•BD．18．解：（1）△A1BC1如图所示，点C1的坐标（1，6）．（2）△A2B2C2如图所示，点C2的坐标（﹣6，4）．19．证明：（1）∵∠CED＝∠CDA＝90°，∠ECD＝∠DCA，∴△CED∽△CDA，∴，即CD2＝CE•CA，∵∠CFD＝∠CDB＝90°，∠FCD＝∠DCB，∴△CDF∽△CBD，∴，即CD2＝CB•CF，则CA•CE＝CB•CF；（2）∵∠CED＝∠CFD＝90°，∴C，E，D，F四点共圆，∴∠FED＝∠FCD，∠DEC＝∠DFC，∴△COE∽△FOD，20．证明：（1）∵∠EAC＝∠DAB，∴∠CAB＝∠EAD，∵∠ACB＝∠AED＝90°，∴△ABC∽△ADE；（2）由（1）知△ABC∽△ADE，∴，∵∠EAC＝∠BAD，∴△BAD∽△CAE；（3）∵∠ACB＝90°，BC＝4，AC＝3，∴AB＝＝＝5，∵△ABC∽△ADE，∴，∴AD＝＝，如图，将△AED绕点A旋转，当点E落在线段CD上时，∠AEC＝∠ADB＝90°，∴BD＝．21．（1）证明：∵四边形EFMN是正方形，∴EF∥BC，∴∠AEF＝∠B，∠AFE＝∠C，∴△AEF∽△ABC．（2）解：设正方形EFMN的边长为x．∵△AEF∽△ABC，AD⊥BC，∴＝，∴＝，∴x＝8，∴正方形的边长为8cm．22．解：设宽度AB为x米，∵DE∥BC，∴△ABC∽△ADE，∴＝，又∵BC＝24，BD＝12，DE＝40，∴＝，解得x＝18，答：河的宽度为18米．23．（1）解：设EF＝x，DF＝2x，则DE＝EF+DF＝3x＝AD在Rt△ADF中，AD2+DF2＝AF2，，∵x＞0，∴x＝1，∴EF＝1，DF＝2，AD＝3，∴由三角形面积公式得：S△ADF＝＝，即；（2）证明：过D点作DK⊥DM交AC于点K，∵∠1+∠KDF＝90°，∠2+∠KDF＝90°，∴∠1＝∠2，∵∠3+∠4＝90°，∠5+∠EFM＝90°，又∵∠4＝∠EFM，∴∠3＝∠5，在△ADK和△EDM中，∴△ADK≌△EDM（ASA），∴DK＝DM，AK＝EM，∴△MDK为等腰直角三角形，∵DG⊥AC，∴MK＝2DG，∴AM﹣EM＝AM﹣AK＝MK＝2DG．24．解：（1）△BME是等腰三角形，理由如下：由题意可知EC＝FC，CH⊥EF，所以∠F＝∠HEC．∵FH∥BD，∴∠F＝∠MBF．∴∠HEC＝∠MBF．又∠HEC＝∠MEB，∴∠MEB＝∠MBE．∴MB＝ME．∴△MBE是等腰三角形；（2）①当∠DME＝90°时，如图1，∵MB＝ME，即∠MEB＝∠MBE，∴∠DBC＝45°．∴∠DBC＝∠BDC，∴BC＝DC．∴AB：BC＝DC：BC＝1；②当∠DEM＝90°时，如图2，过点M作MG⊥BC于G点，∵∠MEB+∠DEC＝90°，∠DEC+∠EDC＝90°，∠EDC＝∠MEB＝∠MBE．由（1）得MB＝ME，又MG⊥BC，∴BE＝2GE＝2GB，又BE＝2EC，∴EG＝EC，则△MGE≌△HCE（ASA）∴ME＝HE．又DE⊥MH，∴∠MDE＝∠EDC．∴∠DBE＝∠EDC＝∠BDE＝30°．∴AB：BC＝DC：BC＝tan∠DBC＝tan30°＝．综上所述AB：BC＝1或。

人教版九年级下册数学第二十七章测试卷及答案

人教版九年级下册数学第二十七章测试题一、单选题1．如图，在△ABC中，DE∥BC分别交AB，AC于点D，E，若23ADDB=，则下列说法不正确的是()A．AD AEAB AC=B．23AEEC=C．23DEBC=D．421ADEDBCESS=四边形2．在平行四边形ABCD中，点E是边AD上一点，且AE=2ED，EC交对角线BD于点F，则EFFC等于（）A．13B．12C．23D．323．如图，有一块三角形余料ABC，BC＝120mm，高线AD＝80mm，要把它加工成一个矩形零件，使矩形的一边在BC上，点P，M分别在AB，AC上，若满足PM：PQ＝3：2，则PM的长为()A．60mm B．16013mm C．20mm D．24013mm4．如图，在△ABC中，AB＝6，AC＝8，BC＝10，D是△ABC内部或BC边上的一个动点(与B、C不重合)，以D为顶点作△DEF，使△DEF∽△ABC(相似比k＞1)，EF∥BC．两三角形重叠部分是四边形AGDH，当四边形AGDH的面积最大时，最大值是多少？()A．12B．11.52C．13D．25．已知线段AB的长为4，点P是线段AB的黄金分割点(AP＞BP)，则PA的长为() A．52B．6﹣2√5C．512D．4﹣56．如图，在△ABC中，点D、E、F分别在边AB、AC、BC上，DE∥BC，DF∥AC，若△ADE与四边形DBCE的面积相等，则△DBF与△ADE的面积之比为()A．12B．14C21D．27．如图，正方形OABC的边长为8，点P在AB上，CP交OB于点Q．若S△BPQ＝19OQC S，则OQ长为()A．6B．2C．1623D．1638．在△ABC中，点D在边BC上，联结AD，下列说法错误的是（）A．如果∠BAC＝90°，AB2＝BD•BC，那么AD⊥BCB．如果AD⊥BC，AD2＝BD•CD，那么∠BAC＝90°C．如果AD⊥BC，AB2＝BD•BC，那么∠BAC＝90°D．如果∠BAC＝90°，AD2＝BD•CD，那么AD⊥BC9．如图，在△ABC中，点O是∠ABC和∠ACB两个内角平分线的交点，过点O作EF∥BC 分别交AB，AC于点E，F，已知△ABC的周长为8，BC＝x，△AEF的周长为y，则表示y与x的函数图象大致是（）A．B．C．D．10．如图，已知△ABO与△DCO位似，且△ABO与△DCO的面积之比为1：4，点B的坐标为(﹣3，2)，则点C的坐标为()A．(3，﹣2)B．(6，﹣4)C．(4，﹣6)D．(6，4)11．在比例尺是1：8000的南京市城区地图上，太平南路的长度约为25cm，它的实际长度约为()A．320cm B．320m C．2000cm D．2000m12．△DEF和△ABC是位似图形，点O是位似中心，点D，E，F分别是OA，OB，OC的中点，若△DEF的面积是2，则△ABC的面积是()A．2B．4C．6D．8二、填空题13．如图，△ABC 中，D 、E 分别是AB 、AC 上的点（DE 不平行BC ），若使△ADE 与△ABC 相似，则需要添加_____即可（只需添加一个条件）．14．如图，已知△ABC 和△ADE 都是等边三角形，点D 在边BC 上，且BD ＝4，CD ＝2，那么AF ＝_____．15．如图，矩形ABCD 中，AB ＝2，BC ＝4，剪去一个矩形ABEF 后，余下的矩形EFDC ∽矩形BCDA ，则FC 的长为_____．16．若23a b =，则2a ba +＝_____．17．如图，平行四边形ABCD 中，点E 是AD 边上一点，连结EC 、BD 交于点F ，若AE ：ED ＝5：4记△DFE 的面积为S 1，△BCF 的面积为S 2，△DCF 的面积为S 3，则DF ：BF ＝_____，S 1：S 2：S 3＝_____．18．如图，在四边形ABCD 中，AD ∥BC ∥EF ，EF 分别与AB ，AC ，CD 相交于点E ，M ，F ，若EM ：BC ＝2：5，则FC ：CD 的值是_____．19．如图，已知△ABC ，AB=6，AC=5，D 是边AB 的中点，E 是边AC 上一点，∠ADE=∠C ，∠BAC 的平分线分别交DE 、BC 于点F 、G ，那么AFAG的值为__________．三、解答题20．如图，在△ABC 中，AB ＝AC ，D 是边BC 的中点，DE ⊥AC ，垂足为点E ．(1)求证：DE •CD ＝AD •CE ；(2)设F 为DE 的中点，连接AF 、BE ，求证：AF •BC ＝AD •BE．21．如图，已知菱形ABCD ，点E 是AB 的中点，AF ⊥BC 于点F ，联结EF 、ED 、DF ，DE 交AF 于点G ，且AE 2＝EG •ED ．(1)求证：DE ⊥EF ；(2)求证：BC 2＝2DF •BF．22．如图，在ABC 中，D 、E 分别是边AB 、AC 上的点，// DE BC ，点F 在线段DE 上，过点F 作//FG AB 、//FH AC 分别交BC 于点G 、H ，如果::2:4:3BG GH HC ．求ADEFGHS S △△的值．23．如图，△ABC的面积为12，BC与BC边上的高AD之比为3：2，矩形EFGH的边EF 在BC上，点H，G分别在边AB、AC上，且HG＝2GF．(1)求AD的长；(2)求矩形EFGH的面积．24．如图，四边形ABGH，四边形BCFG，四边形CDEF都是正方形．请在图中找出与△HBC相似的三角形，并说明它们相似的理由．25．如图，在△ABC中，点D为边BC上一点，且AD＝AB，AE⊥BC，垂足为点E．过点D作DF∥AB，交边AC于点F，连接EF，EF2＝12BD•EC．(1)求证：△EDF∽△EFC；(2)如果14EDFADCSS，求证：AB＝BD．参考答案1．C 【分析】根据题意可以得到△ADE ∽△ABC ，然后根据题目中的条件即可推出选项中的说法是否正确，从而可以解答本题．【详解】∵DE ∥BC ，∴△ADE ∽△ABC ，∴AD AE AB AC =，AE AD EC DB ==23，DE BC==AD AB =25，ADE ABC S S ∆∆=（AD AB ）2=425，∴ADE DBCE S S ∆四边形=421，故A 、B 、D 选项正确，C 选项错误，故选C ．【点睛】本题考查相似三角形的判定与性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用相似三角形的性质解答问题．2．A 【详解】试题分析：如图，∵四边形ABCD 为平行四边形，∴ED ∥BC ，BC=AD ，∴△DEF ∽△BCF ，∴EF DEFC CB =，设ED=k ，则AE=2k ，BC=3k ，∴EF FC =3k k =13，故选A ．考点：1．相似三角形的判定与性质；2．平行四边形的性质．3．A【分析】利用相似三角形的性质构建方程即可解决问题．【详解】如图，设AD交PN于点K，∵PM：PQ=3：2，∴可以假设MP=3k，PQ=2k，∵四边形PQNM是矩形，∴PM∥BC，∴△APM∽△ABC，∵AD⊥BC，BC∥PM，∴AD⊥PN，∴PM AK BC AD=，∴3802 12080k k-=，解得k=20mm，∴PM=3k=60mm，故选A．【点睛】本题考查相似三角形的应用，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．4．A【分析】先判断面积最大时点D的位置，由△BGD∽△BAC，找出AH=8-43GA，得到S矩形AGDH=-43AG2+8AG，确定极值，AG=3时，面积最大，于是得到结论．【详解】∵AB2+AC2=100=BC2，∴∠BAC=90°，∵△DEF∽△ABC，∴∠EDF=∠BAC=90°，如图1延长ED交BC于M，延长FD交BC于N，∵△DEF∽△ABC，∴∠B=∠E，∵EF∥BC，∴∠E=∠EMC，∴∠B=∠EMC，∴AB∥DE，同理：DF∥AC，∴四边形AGDH为平行四边形，∵∠EDF=90°，∴四边形AGDH为矩形，∵GA⊥AC，∴四边形AGDH为正方形，当点D在△ABC内部时，四边形AGDH的面积不可能最大，如图2，点D在内部时（N在△ABC内部或BC边上），延长GD至N，过N作NM⊥AC于M，∴矩形GNMA面积大于矩形AGDH，∴点D在△ABC内部时，四边形AGDH的面积不可能最大，只有点D在BC边上时，面积才有可能最大，如图3，点D在BC上，∵△DEF∽△ABC，∴∠F=∠C，∵EF∥BC．∴∠F=∠BDG，∴∠BDG=∠C，∴DG∥AC，∴△BGD∽△BAC，∴BG GD AB AC=，∴AB AG AH AB AC-=，∴668AG AH -=，∴AH=8-43 GA，S矩形AGDH=AG×AH=AG×（8-43AG）=-43AG2+8AG，当AG=-842()3⨯-=3时，S矩形AGDH最大，S矩形AGDH最大=12．故选A．【点睛】此题主要考查了相似三角形的性质和判定，平行四边形，矩形，极值的确定，勾股定理的逆定理，解本题的关键是作出辅助线，5．A【分析】利用黄金分割的定义得到PA=12AB ，然后把AB=4代入计算即可．【详解】∵点P 是线段AB 的黄金分割点（AP ＞BP ），∴12AB=12．故选A ．【点睛】本题考查了黄金分割：把线段AB 分成两条线段AC 和BC （AC ＞BC ），且使AC 是AB 和BC 的比例中项（即AB ：AC=AC ：BC ），叫做把线段AB 黄金分割，点C 叫做线段AB 的黄金分割点．其中，并且线段AB 的黄金分割点有两个．6．D【分析】根据矩形的性质得到DE=CF ，根据相似三角形的性质得到ADE ABC S S =（DE BC ）2=12，求得DE BC=2，设k ，BC=2k ，得到k ，根据相似三角形的性质即可得到结论．【详解】∵DE ∥BC ，DF ∥AC ，∴四边形DFCE 是平行四边形，∴DE=CF ，∵△ADE 与四边形DBCE 的面积相等，∴ADE ABC S S =12，∵DE ∥BC ，∴△ADE ∽△ABC ，∴ADE ABC S S =（DE BC ）2=12，∴DE BC=2，设k ，BC=2k ，∴，∵DF ∥AC ，∴△BDF ∽△BAC ，∴△DBF ∽△ADE ，∴BDF ADE S S =（BF DE ）2=2⎛⎫⎪⎪⎭=)2故选D ．【点睛】本题考查了相似三角形的判定和性质，矩形的性质，熟练掌握相似三角形的判定和性质是解题的关键．7．B【分析】根据正方形的性质得到AB ∥OC ，推出△PBQ ∽△COQ ，根据相似三角形的性质得到OC=3PB ，求得PB=83，于是得到结论．【详解】∵四边形ABCO 是正方形，∴AB ∥OC ，∴△PBQ ∽△COQ ，∴BPQOQC S S =（PB OC）2=19，∴OC=3PB ，∵OC=8，∴PB=83，∵BQ OQ =PB OC =13，∴OQ=34故选B ．【点睛】本题考查相似三角形的判定和性质、正方形的性质、平行线分线段成比例定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．8．D根据相似三角形的判定定理证明相应的三角形相似，根据相似三角形的性质判断即可．【详解】如图：A、∵AB2=BD•BC，∴AB BC BD AB=，又∠B=∠B，∴△BAD∽△BCA，∴∠BDA=∠BAC=90°，即AD⊥BC，故A选项说法正确，不符合题意；B、∵AD2=BD•CD，∴AD CD BD AD=，又∠ADC=∠BDA=90°，∴△ADC∽△BDA，∴∠BAD=∠C，∵∠DAC+∠C=90°，∴∠DAC+∠BAD=90°，∴∠BAC=90°，故B选项说法正确，不符合题意；C、∵AB2=BD•BC，∴AB BC BD AB=，又∠B=∠B，∴△BAD∽△BCA，∴∠BAC=∠BDA=90°，即AD⊥BC，故C选项说法正确，不符合题意；D、如果∠BAC=90°，AD2=BD•CD，那么AD与BC不一定垂直，故D选项错误，不符合题意；故选D．本题考查的是相似三角形的判定和性质，掌握相似三角形的判定定理和性质定理是解题的关键．9．A【分析】根据角平分线和平行证明△EBO和△OFC是等腰三角形,再由周长关系得ｙ＝８－ｘ,即可解题.【详解】解：∵点O是∠ABC和∠ACB两个内角平分线的交点,EF∥BC,∴∠OBC＝∠EOB,∠OBC＝∠EBO,∴△EBO是等腰三角形,同理,△OFC是等腰三角形,即BE＝EO,CF＝OF,∴△AEF的周长y＝AE＋EF＋AF＝AB＋AC,∵△ABC的周长为8,BC=x,∴y＝8－x,即x是关于y的一次函数,图像是递减的直线,故选A【点睛】本题考查了一次函数的实际应用,中等难度,证明等腰三角形,找到函数关系是解题关键. 10．B【分析】利用位似是特殊的相似，若两个图形△ABC和△A′B′C′以原点为位似中心，相似比是k，△ABC上一点的坐标是（x，y），则在△A′B′C′中，它的对应点的坐标是（kx，ky）或（-kx，ky）．【详解】∵△ABO与△DCO位似，且△ABO与△DCO的面积之比为1：4，∴△ABO与△DCO为1：2，∵点B的坐标为（-3，2），∴点C的坐标为（6，-4），故选B．【点睛】此题主要考查了位似变换的性质，正确理解位似与相似的关系，记忆关于原点位似的两个图形对应点坐标之间的关系是解题的关键．11．D【分析】首先设它的实际长度是xcm ，然后根据比例尺的定义，即可得方程：1:800025:x =，解此方程即可求得答案，注意统一单位.【详解】设它的实际长度是xcm ，根据题意得：1:800025:x =，解得：200000x =，2000002000cm m =，∴它的实际长度为2000m .故选D .【点睛】此题考查了比例线段.此题难度不大，解题的关键是理解题意，根据比例尺的定义列方程，注意统一单位.12．D【分析】先根据三角形中位线的性质得到DE=12AB ，从而得到相似比，再利用位似的性质得到△DEF ∽△ABC ，然后根据相似三角形的面积比是相似比的平方求解即可．【详解】∵点D ，E 分别是OA ，OB 的中点，∴DE=12AB ，∵△DEF 和△ABC 是位似图形，点O 是位似中心，∴△DEF ∽△ABC ，∴DEF ABC S S ∆∆=14，∴△ABC 的面积=2×4=8故选D ．【点睛】本题考查了位似变换：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．13．∠ADE＝∠C【分析】根据相似三角形判定定理：两个角相等的三角形相似；夹角相等，对应边成比例的两个三角形相似，即可解题．【详解】∵∠A是公共角，如果∠ADE=∠C，∴△ADE∽△ABC，故答案为∠ADE=∠C．【点睛】本题主要考查相似三角形的判定，掌握相似三角形的判定方法是解题的关键，即①有两组角对应相等的三角形相似，②三边对应成比例的两个三角形相似，③两组边对应成比例且夹角相等的两个三角形相似．14．143【分析】根据三角形的角性质定理、相似三角形的性质进行求解.【详解】∵△ABC和△ADE都是等边三角形，∴∠B=∠ADE=∠C=60°，∵∠B+∠BAD=∠ADF+∠FDC,∴∠BAD=∠FDC,∴△ABD∽△FDC，∴DC FC AB BD=,∵BD=4,CD=2，且△ABC是等边三角形，∴AB=BC=BD+DC=6,∴2=6 DC FCAB BD=，∴FC=4 3 ,AF=AC-FC=14 3 .【点睛】本题主要考查的是三角形的角性质定理、相似三角形的性质，熟练掌握是本题的解题关键. 15【分析】根据相似多边形的性质得CD CEAD AB=，即242CE=，然后利用比例性质求出CE，再利用勾股定理计算FC即可．【详解】∵四边形ABCD是矩形，∴AB=CD=2，AD=BC=4，∵四边形EFCD是矩形，∴EF=CD=2，CF=DE，∵余下的矩形EFCD∽矩形BCDA，∴CD CEAD AB=，即242CE=，∴CE=1，∴FC的长【点睛】本题考查了相似多边形的性质：如果两个多边形的对应角相等，对应边的比相等，则这两个多边形是相似多边形；相似多边形对应边的比叫做相似比．16．4【分析】设a b k23==，则a=2k，b=3k，再代入式子中即可求得结果.【详解】设a b k23==，则a=2k，b=3k，a 2b a+=2k 6k 2k +=8k 2k =4故答案为4【点睛】此题考查了比例的基本性质，熟练掌握性质是解答此题的关键.17．4：916：81：36．【分析】由AE ：ED=5：4，得到DE ：AD=4：9，根据平行四边形的性质得到AD ∥BC ，AD=BC ，根据相似三角形的性质即可得到结论．【详解】∵AE ：ED=5：4，∴DE ：AD=4：9，∵四边形ABCD 是平行四边形，∴AD ∥BC ，AD=BC ，∴△DEF ∽△BCF ，∴49DE DF BC BF ==，∴12S S =（49）2=1681，23S S =94，∴S 1：S 2：S 3=16：81：36，故答案为4：9，16：81：36．【点睛】本题考查了相似三角形的判定和性质，平行四边形的性质，熟练掌握相似三角形的判定和性质是解题的关键．18．35【分析】首先得出△AEM ∽△ABC ，△CFM ∽△CDA ，进而利用相似三角形的性质求出即可．【详解】∵AD ∥BC ∥EF ，∴△AEM ∽△ABC ，△CFM ∽△CDA ，∵EM ：BC=2：5，∴25 AM EMAC BC==，设AM=2x，则AC=5x，故MC=3x，∴35 CM CFAC CD==，故答案为3 5．【点睛】此题主要考查了相似三角形的判定与性质，得出25AMAC=是解题关键．19．3 5【分析】由题中所给条件证明△ADF~△ACG，可求出AFAG的值.【详解】解：在△ADF和△ACG中，AB=6，AC=5，D是边AB的中点AG是∠BAC的平分线，∴∠DAF=∠CAG∠ADE＝∠C∴△ADF~△ACG∴35 AF AD AG AC==.故答案为3 5 .【点睛】本题考查了相似三角形的判定和性质，难度适中，需熟练掌握.20．(1)证明见解析；(2)证明见解析.【分析】（1）由AB=AC，D是边BC的中点，利用等腰三角形的性质可得出∠ADC=90°，由同角的余角相等可得出∠ADE=∠DCE，结合∠AED=∠DEC=90°可证出△AED∽△DEC，再利用相似三角形的性质可证出DE•CD=AD•CE；（2）利用等腰三角形的性质及中点的定义可得出CD=12BC，DE=2DF，结合DE•CD=AD•CE可得出CE BCDF AD=，结合∠BCE=∠ADF可证出△BCE∽△ADF，再利用相似三角形的性质可证出AF•BC=AD•BE．【详解】(1)∵AB＝AC，D是边BC的中点，∴AD⊥BC，∴∠ADC＝90°，∴∠ADE+∠CDE＝90°．∵DE⊥AC，∴∠CED＝90°，∴∠CDE+∠DCE＝90°，∴∠ADE＝∠DCE．又∵∠AED＝∠DEC＝90°，∴△AED∽△DEC，∴DE CE AD CD=，∴DE•CD＝AD•CE；(2)∵AB＝AC，∴BD＝CD＝12 BC，∵F为DE的中点，∴DE＝2DF．∵DE•CD＝AD•CE，∴2DF•12BC＝AD•CE，∴CE BC DF AD=，又∵∠BCE＝∠ADF，∴△BCE∽△ADF，∴BC BE AD AF=，∴AF•BC＝AD•BE．【点睛】本题考查了相似三角形的判定与性质、等腰三角形的性质以及余角，解题的关键是：（1）利用相似三角形的判定定理证出△AED∽△DEC；（2）利用相似三角形的判定定理证出△BCE∽△ADF．21．(1)证明见解析；(2)证明见解析.【分析】（1）根据直角三角形的性质得到AE=FE，根据相似三角形的性质得到∠EAG=∠ADG，求得∠DAG=∠FEG，根据菱形的性质得到AD∥BC，求得∠DAG=∠AFB=90°，于是得到结论；（2）由AE=EF，AE2=EG•ED，得到FE2=EG•ED，推出△FEG∽△DEF，根据相似三角形的性质得到∠EFG=∠EDF，根据相似三角形的判定和性质即可得到结论．【详解】(1)∵AF⊥BC于点F，∴∠AFB＝90°，∵点E是AB的中点，∴AE＝FE，∴∠EAF＝∠AFE，∵AE2＝EG•ED，∴AE DE EG AE，∵∠AEG＝∠DEA，∴△AEG∽△DEA，∴∠EAG＝∠ADG，∵∠AGD＝∠FGE，∴∠DAG＝∠FEG，∵四边形ABCD是菱形，∴AD∥BC，∴∠DAG＝∠AFB＝90°，∴∠FEG＝90°，∴DE⊥EF；(2)∵AE＝EF，AE2＝EG•ED，∴FE2＝EG•ED，∴EF EG DE EF=，∵∠FEG ＝∠DEF ，∴△FEG ∽△DEF ，∴∠EFG ＝∠EDF ，∴∠BAF ＝∠EDF ，∵∠DEF ＝∠AFB ＝90°，∴△ABF ∽△DFE ，∴AB BF DF EF=，∵四边形ACBD 是菱形，∴AB ＝BC ，∵∠AFB ＝90°，∵点E 是AB 的中点，∴FE ＝12AB ＝12BC ，∴BC DF ＝12BF BC ，∴BC 2＝2DF•BF ．【点睛】本题考查了相似三角形的判定和性质，菱形的性质，直角三角形的性质，正确的识别图形是解题的关键．22．2516ADE FGH S S ∆=△．【分析】设BG=2k ，GH=4k ，HC=3k ，根据平行四边形的性质可得DF=BG=2k ，EF=HC=3k ，可得DE=5k ，根据△ADE ∽△FGH 可得22516ADE FGH S DE SGH == （）．【详解】解：∵DE BC ‖，∴ADE B∠=∠∴FG AB ‖，∴FGH B∠=∠∴ADE FGH∠=∠同理：AED FHG∠=∠∴ADE FGH∽△△∴2ADE FGH S DE S GH ⎛⎫= ⎪⎝⎭△△∵DE BC ‖，FGAB ‖，∴DF BG =同理：FE HC=∵::2:4:3BG GH HC =，∴设2BG k =，4GH k =，3HC k=∴2DF k =，3FE k =，∴5DE k=∴2525416ADE FGH S k S k ∆⎛⎫== ⎪⎝⎭△【点睛】此题考查相似三角形的判定和性质，平行四边形判定和性质，熟练掌握相似三角形的性质是解题的关键．23．(1)AD ＝4；(2)矩形EFGH 的面积28849．【分析】（1）设BC=3x ，根据三角形的面积公式列式计算即可；（2）设GF=y ，根据矩形的性质得到HG ∥BC ，得到△AHG ∽△ABC ，根据相似三角形的性质列出比例式，计算即可．【详解】(1)设BC ＝3x ，则AD ＝2x ，∵△ABC 的面积为12，∴12×3x×2x ＝12，解得，x 1＝2，x 2＝﹣2(舍去)，则AD 的长＝2x ＝4；(2)设GF ＝y ，则HG ＝2y ，∵四边形EFGH 为矩形，∴HG ∥BC ，∴△AHG ∽△ABC ，∴HG AM BC AD =，即2464y y -=，解得，y ＝127，HG ＝2y ＝247，则矩形EFGH 的面积＝127×247＝28849．【点睛】本题考查的是相似三角形的判定和性质，矩形的性质，掌握相似三角形的判定定理和性质定理是解题的关键．24．△DBH ∽△HBC ，理由见解析.【分析】根据正方形的性质得到∠A=90°，设AB=x ，则AH=BC=CD=x ，推出BH BD BC BH=，由∠HBC=∠HBC ，即可得到结论．【详解】△DBH ∽△HBC ，理由：∵四边形ABGH ，四边形BCFG ，四边形CDEF 都是正方形，∴A ，B ，C ，D 在一条直线上，∠A ＝90°，设AB ＝x ，则AH ＝BC ＝CD ＝x ，∴BHx ，BD ＝2x ，∴BH BD BC BH =，∵∠HBC ＝∠HBC ，∴△DBH ∽△HBC ．【点睛】此题主要考查了相似三角形的判定方法：如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似；需注意的是所有的全等三角形都相似．25．(1)证明见解析；(2)证明见解析.【分析】（1）利用两边成比例夹角相等两个三角形相似即可证明；（2）由△EDF ∽△ADC ，推出EDF ADC S S =（ED AD ）2=14，推出ED AD =12，即ED=12AD ，由此即可解决问题.【详解】(1)∵AB ＝AD ，AE ⊥BC ，∴BE ＝ED ＝12DB ，∵EF 2＝12•BD•EC ，∴EF 2＝ED•EC ，即得EF EC ＝ED EF，又∵∠FED ＝∠CEF ，∴△EDF ∽△EFC ；(2)∵AB ＝AD ，∴∠B ＝∠ADB ，又∵DF ∥AB ，∴∠FDC ＝∠B ，∴∠ADB ＝∠FDC ，∴∠ADB+∠ADF ＝∠FDC+∠ADF ，即得∠EDF ＝∠ADC ，∵△EDF ∽△EFC ，∴∠EFD ＝∠C ，∴△EDF ∽△ADC ，∴EDF ADC S S ＝(ED AD )2＝14，∴ED AD ＝12，即ED ＝12AD ，又∵ED ＝BE ＝12BD ，∴BD ＝AD ，∴AB ＝BD ．【点睛】本题考查等腰三角形的性质，相似三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．。

人教版九年级下册数学第二十七章测试卷含答案

人教版九年级下册数学第二十七章测试题一、单选题1．若△ABC∽△A΄B΄C΄，∠A=40°，∠B=110°，则∠C΄=（）. A．40°B．110°C．70°D．30°2．已知：a、b是不等于0的实数，2a=3b，那么下列等式中正确的是（）A．23ab=B．32ab=C．43a bb+=D．53a bb+=3．下列4组条件中，能判定△ABC∽△DEF的是（）A．AB=5，BC=4，∠A=45°；DE=10，EF=8，∠D=45°B．∠A=45°，∠B=55°；∠D=45°，∠F=75°C．BC=4，AC=6，AB=9；DE=18，EF=8，DF=12D．AB=6，BC=5，∠B=40°；DE=5，EF=4，∠E=40°4．如图，点D在△ABC的边AC上，要判断△ADB与△ABC相似，添加一个条件，不正确的是（）A．∠ABD=∠C B．∠ADB=∠ABC C．AB CBBD CD=D．AD ABAB AC=5．如果x：（x+y）=3：5，那么x yx-的值是（）A．13B．12C．23D．326．如果两个相似三角形对应边之比是1：4，那么它们的对应中线之比是（）A．1：2B．1：4C．1：8D．1：167．如图，在△ABC中，D、E分别是AB、AC的点，且DE∥BC，如果AD=2cm，DB=1cm，DE=1.6cm，则BC=（）A ．0.8cmB ．2cmC ．2.4cmD ．3.2cm8．将两个长为a cm ，宽为b cm 的矩形铁片加工成一个长为c cm ，宽为d cm 的矩形铁片，有人就a ，b ，c ，d 的关系写出了如下四个等式，但是有一个写错了，它是()A ．=2a d c bB ．=2a d c bC ．2=a d c bD ．2a c d b=9．如图，已知AD 为△ABC 的角平分线，DE∥AB 交AC 于E ，如果AE EC =35，那么ACAB等于（）A ．35B ．53C ．85D ．3210．如图，小明在地面上放了一个平面镜，选择合适的位置，刚好在平面镜中看到旗杆的顶部，此时小明与平面镜的水平距离为2m ，旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m ，则旗杆的高度为(单位：m)A ．163B ．9C ．12D ．643二、填空题11．如图，在△ABC 中，D 、E 分别为AB 、AC 上的点，若DE ∥BC ，AD AB =13，则AD DE AEAB BC AC++++=______．12．如图，△ABC中，A、B两个顶点在x轴的上方，点C的坐标是（﹣1，0）．以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C，并把△ABC的边长放大到原来的2倍．设B′的坐标是（3，﹣1），则点B的坐标是________．13．在△ABC中，AB=5，AC=4，BC=3，D是边AB上的一点，E是边AC上的一点（D，E均与端点不重合），如果△CDE与△ABC相似，那么CE=________14．在平面直角坐标系中，△ABC的坐标分别是A（﹣1，2），B（﹣2，0），C（﹣1，1），若以原点O为位似中心，将△ABC放大到原来的4倍得到△△A′B′C′，那么落在第四象限的A′的坐标是_____．15．有一块三角形的草地，它的一条边长为25m．在图纸上，这条边的长为5cm，其他两条边的长都为4cm，则其他两边的实际长度都是_________m．16．如图，在△ABC中，D、E分别为边AB、AC上的点．ADAC=AEAB，点F为BC边上一点，添加一个条件：________，可以使得△FDB与△ADE相似．（只需写出一个）17．已知等腰直角三角形ABC中，∠C=90°，AC=BC=4，点D在直线AC上，且CD=2，连接BD，作BD的垂直平分线交三角形的两边于E、F，则EF的长为________．18．如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE，BE 分别交于点G、H．有下列结论：①FD=FE；②AH=2CD；③22；④S=2S．其中正确结论的序号是_____．（把你认为正确结论的序号都填上）19．如图，△DEF是由△ABC经过位似变换得到的，点O是位似中心，ODDA=23，则△DEF与△ABC的面积比是______．三、解答题20．已知：如图，△ABC∽△ADE，∠A=45°，∠C=40°．求：∠ADE的度数．21．如图，在△ABC和△CDE中，∠B=∠D=90°，C为线段BD上一点，且AC⊥CE，证明：△ABC∽△CDE．22．如图，在正方形ABCD中，E、F分别是边AD、CD上的点，AE=ED，DF=14DC，求证：△ABE∽△DEF．23．如图，点C 、D 在线段AB 上，PCD 是等边三角形，且ACP PDB ∽，求APB ∠的度数．24．已知AD ⊥BC ，BE=CE ，∠ABC=2∠C ，BF 为∠B 的平分线．求证：AB=2DE ．25．如图，在正方形ABCD 中，E 、F 分别是边AD 、CD 上的点，AE ED =，14DF DC =，连接EF 并延长交BC 的延长线于点G ．（1）求证：ABE △∽DEF ；（2）若正方形的边长为4，求BG 的长．26．（提出问题）（1）如图1，在等边△ABC 中，点M 是BC 上的任意一点（不含端点B 、C ），连结AM ，以AM 为边作等边△AMN ，连结CN ．求证：∠ABC=∠ACN ．（类比探究）（2）如图2，在等边△ABC 中，点M 是BC 延长线上的任意一点（不含端点C ），其它条件不变，（1）中结论∠ABC=∠ACN 还成立吗？请说明理由．（拓展延伸）（3）如图3，在等腰△ABC 中，BA=BC ，点M 是BC 上的任意一点（不含端点B 、C ），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC 与∠ACN的数量关系，并说明理由．参考答案1．D【详解】解：因为⊿ABC∽⊿，所以所以在三角形⊿中，∠=180°-40°-110°=30°故答案为D2．B【详解】∵2a=3b，∴32ab=，∴52a bb+=，∴A、C、D选项错误，B选项正确，故选B.3．C【分析】根据已知条件推出证三角形相似的条件，根据相似三角形的判定判断即可．【详解】A.ABDE=BCEF=12夹角是∠B和∠E，两角不一定相等，故本选项错误；B.应符合∠A=∠D=45°，∠B 和∠E 相等才能证两三角形相似，故本选项错误；C.根据BC EF =AB DE =AC DF =12得到两三角形相似，故本选项正确；D.∠B=∠E=40°，但夹此角的两边不成比例，故本选项错误；故选C ．【点睛】本题考查了对相似三角形的判定的理解和掌握，能熟练地运用相似三角形的判定定理进行判断是解题的关键．4．C 【分析】由∠A 是公共角，利用有两角对应相等的三角形相似，即可得A 与B 正确；又由两组对应边的比相等且夹角对应相等的两个三角形相似，即可得D 正确，继而求得答案，注意排除法在解选择题中的应用．【详解】∵∠A 是公共角，∴当∠ABD=∠C 或∠ADB=∠ABC 时，△ADB ∽△ABC （有两角对应相等的三角形相似），故A 与B 正确，不符合题意要求；当AB ：AD=AC ：AB 时，△ADB ∽△ABC （两组对应边的比相等且夹角对应相等的两个三角形相似），故D 正确，不符合题意要求；AB ：BD=CB ：AC 时，∠A 不是夹角，故不能判定△ADB 与△ABC 相似，故C 错误，符合题意要求，故选C ．5．A 【详解】试题解析：设3x k =，则2y k =，则321.33x y k k x k --==故选A ．6．B 【分析】利用相似三角形的相似比，对应高、中线、角平分线的比，都等于相似比来解答．【详解】∵两个相似三角形对应边之比是1：4，又∵相似三角形的对应高、中线、角平分线的比等于相似比，∴它们的对应中线之比为1：4．故选B ．【点睛】本题考查相似三角形的相似比问题，须熟练掌握：①相似三角形的对应高、角平分线、中线的比等于相似比；②相似三角形的周长比等于相似比；③相似三角形的面积比等于相似比的平方．7．C 【分析】由平行线分线段成比例可得AD DEAB BC=，把线段代入可求得BC ．【详解】∵AD=2cm ，DB=1cm ，∴AB=AD+DB=3cm ，∵DE ∥BC ，∴AD DE AB BC =,即2 1.6=3BC，解得：BC=2.4．故选C ．【点睛】本题考查了平行线分线段成比例，掌握平行线分线段所得线段对应成比例是解题的关键．8．B 【详解】【分析】由面积关系得2ab=dc ，再写成比例式即可.【详解】将两个小矩形拼成一个大矩形，由面积关系可知：2ab=dc,即=2a d c b ，或2=a dc b 或2a cd b=，故选项A,C,D 正确.故选B【点睛】本题考核知识点：比例式.解题关键点：由面积关系列出比例式.9．B 【详解】解：∵DE ∥AB ，∴∠ADE ＝∠BAD ，∵AD 为△ABC 的角平分线，∴∠BAD ＝∠EAD ，∴∠EAD ＝∠ADE ，∴AE ＝DE ，∵AE 3EC 5=，∴EC 5DE 3=，∵DE ∥AB ，∴△CDE ∽△CBA ，∴DE AB ECAC =，∴5AB 3EC A DE C ==．故选B ．10．C 【详解】分析：根据题意容易得到△CDE ∽△AEB ，再根据相似三角形的性质解答即可．详解：如图：∵根据入射角与反射角相等可知,∠CED=∠AEB,故Rt △CDE ∽Rt △AEB ，∴=CD DE AB BE，即1.52=16AB ，解得AB=12m.故选C.点睛：本题考查相似三角形性质的应用，解题的关键是找出相似三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题.11．1 3．【详解】解：∵DE∥BC，∴△ADE∽△ABC，∴ADAB=AD DE AEAB BC AC++++=13．故答案为13．12．（﹣3，）．【详解】试题分析：作BD⊥x轴于D，B′D′⊥x轴于D′，根据相似三角形的性质求出CD，BD的长，得到点B的坐标．解：作BD⊥x轴于D，B′D′⊥x轴于D′，∵点C的坐标是（﹣1，0），B′的坐标是（3，﹣1），∴CD′=4，B′D′=1，由题意得，△ABC∽A′B′C，相似比为1：2，∴==，∴CD=2，BD=，∴点B的坐标是（﹣3，）．故答案为（﹣3，）．考点：位似变换；坐标与图形性质．13．2，258，3625【分析】先利用勾股定理的逆定理得到△ABC为直角三角形，∠ACB=90°，再分类讨论：当△ABC∽△CDE，如图1，则∠CED=∠ACB=90°，∠DCE=∠A，所以CE=AE，根据等腰三角形得CE=12AC=2；当△ABC∽△DCE，如图2，则∠CED=∠ACB=90°，∠DCE=∠B，接着证明CD⊥AB，利用面积法可计算出CD=125，利用相似比可计算出CE=3625；当△ABC∽△CED，如图3，∠CDE=∠ACB=90°，∠DCE=∠A，证明CD为斜边上的中线，则CD=DA=DB=12AB=52，然后利用相似比可计算出CE=258，综上所述，CE的长为2，258，3625．【详解】∵AB=5，AC=4，BC=3，∴AC2+BC2=AB2，∴△ABC为直角三角形，∠ACB=90°，当△ABC∽△CDE，如图1，则∠CED=∠ACB=90°，∠DCE=∠A，∴△ADC为等腰三角形，∴CE=AE，∴CE=12AC=2；当△ABC∽△DCE，如图2，则∠CED=∠ACB=90°，∠DCE=∠B，而∠BCD+∠DCE=90°，∴∠B+∠BCD=90°，∴CD⊥AB，∴CD=·BC ACAB=125，∵△ABC∽△DCE，∴AB：CD=BC：CE，即5：125=3：CE，∴CE=36 25；当△ABC∽△CED，如图3，∠CDE=∠ACB=90°，∠DCE=∠A，∴DC=DA，∵∠A+∠B=90°，∠DCE+∠BCD=90°，∴∠B+∠BCD=90°，∴DB=DC，∴CD=DA=DB=12AB=52，∵△ABC∽△CED，∴CE：AB=CD：AC，即CE：5=52：4，∴CE=25 8，综上所述，CE的长为2，258，3625．故答案为2，258，3625．【点睛】本题考查了相似三角形的性质：相似三角形的对应角相等，对应边的比相等；相似三角形（多边形）的周长的比等于相似比；相似三角形的对应线段（对应中线、对应角平分线、对应边上的高）的比也等于相似比；相似三角形的面积的比等于相似比的平方．也考查了分类讨论的思想.14．（4，﹣8）．【详解】试题分析：根据位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k，即可得出A′的坐标．解：∵A（﹣1，2），以原点O为位似中心，将△ABC放大到原来的4倍得到△A′B′C′，∴落在第四象限的A′的坐标是：（4，﹣8）．故答案为（4，﹣8）．考点：位似变换；坐标与图形性质．15．20【详解】试题分析：首先求出相似比，然后进行计算.25m=2500cm，相似比为：2500:5=500:1，则其余两边的长度为：4×500=2000cm=20m.考点：相似的应用16．DF∥AC或∠BFD=∠A【分析】根据题意，已知对应边成比例，添加DF∥AC或∠BFD=∠A，都可证△FBD∽△AED.【详解】DF∥AC，或∠BFD=∠A．理由：∵∠A=∠A，AD AE AC AB，∴△ADE∽△ACB，∴①当DF∥AC时，△BDF∽△BAC，∴△BDF∽△EAD．②当∠BFD=∠A时，∵∠B=∠AED，∴△FBD∽△AED．故答案为DF∥AC或∠BFD=∠A．【点睛】本题考查相似三角形的判定和性质．平行线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．17【分析】如图，作辅助线；首先证明DE ＝BE （设为μ），DF ＝BF （设为γ）；运用勾股定理分别求出BE 、BF 、BD 的长度；借助三角形的面积公式，列出关于EF 的等式，求出EF 即可解决问题．【详解】如图，过点D 作DG ⊥AE 于点G ；∵∠C ＝90°，AC ＝BC ＝4，∴AB ==A ＝45°；∵∠ADG ＝90°﹣45°＝45°，∴∠A ＝∠ADG ，AG ＝DG （设为λ），由勾股定理得：λ2+λ2＝AD 2，而AD ＝AC ﹣2＝2，λ=BG ＝．由勾股定理得：BD ＝∵EF ⊥BD ，且平分BD ，∴DE ＝BE （设为μ），DF ＝BF （设为γ），∴GE ＝μ，CF ＝4﹣γ；在△DGE 中，由勾股定理得：222μμ+=（），解得：μ3=；在△DCF 中，同理可求：γ＝2.5；∵S 四边形BEDF ＝S △BED +S △BFD ，12BEDF S BD EF =⋅四边形，∴111222BE DG BF DC BD EF ⋅+⋅=⋅，解得：EF 6=．故答案为6．【点睛】本题考查了勾股定理、等腰三角形的性质、线段垂直平分线的性质等几何知识点及其应用问题；牢固掌握勾股定理、等腰三角形的性质、线段垂直平分线的性质等几何知识点是灵活解题的基础和关键．18．①②③【详解】分析：仔细审题，首先根据直角三角形斜边上的中线性质得出FD =12AB ，再证明△ABE 是等腰直角三角形，进而可得FE=12AB，据此不难判断①是否正确；根据已有信息易得∠ABC=∠C，进而可得出AB=AC，由等腰三角形的性质得出BC=2CD，∠BAD=∠CAD=∠CBE，由ASA证明△AEH≌△BEC，再结合全等三角形的性质判断②是否正确；对于③，可通过证明△ABD～△BCE，得出BC：AB=BE：AD，即BC·AD=AB·BE，再由等腰直角三角形的性质和三角形的面积得出结论；对于④，由F是AB的中点，BD=CD进行判断即可.详解：∵在△ABC中，AD和BE是高，∴∠ADB=∠AEB=∠CEB=90°，∵点F是AB的中点，∴FD=AB，∵∠ABE=45°，∴△ABE是等腰直角三角形，∴AE=BE，∵点F是AB的中点，∴FE=AB，∴FD=FE，①正确；∵∠CBE=∠BAD，∠CBE+∠C=90°，∠BAD+∠ABC=90°，∴∠ABC=∠C，∴AB=AC，∵AD⊥BC，∴BC=2CD，∠BAD=∠CAD=∠CBE，在△AEH和△BEC中，∵∠AEH=∠CEB,AE=BE,∠EAH=∠CBE，∴△AEH≌△BEC（ASA），∴AH=BC=2CD，②正确；∵∠BAD=∠CBE，∠ADB=∠CEB，∴△ABD～△BCE，∴，即BC·AD=AB·BE，∵AE2=AB·AE=AB·BE，BC·AD=AC·BE=AB·BE，∴BC·AD2；③正确；∵F是AB的中点，BD=CD，∴S△ABC=2S△ABD=4S△ADF．④错误；故答案为①②③．点睛：本题考查了相似三角形的判定与性质、全等三角形的判定与性质、直角三角形斜边上的中线的性质、等腰三角形的判定与性质；本题综合性强，有一定难度，证明三角形相似和三角形全等是解决问题的关键.19．4：25【分析】本题考查解直角三角形的应用，解题的关键是理解题意，属于中考常考题型．【详解】解：∵△DEF是由△ABC经过位似变换得到的，∴△DEF∽△ABC，∵23= OD DA，∴25ODOA=，即△DEF与△ABC的相似比为25，∴△DEF与△ABC的面积比是4：25，故答案为4：25．【点睛】本题考查的是位似变换的概念、相似三角形的性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．20．∠ADE=95°【分析】由△ABC∽△ADE，∠C=40°，根据相似三角形的对应角相等，即可求得∠AED的度数，又由三角形的内角和等于180°，即可求得∠ADE的度数．【详解】∵△ABC∽△ADE，∠C=40°，∴∠AED=∠C=40°．在△ADE中，∵∠AED+∠ADE+∠A=180°，∠A=45°即40°+∠ADE+45°=180°，∴∠ADE=95°．【点睛】此题考查了相似三角形的性质与三角形内角定理．题目比较简单，注意相似三角形的对应角相等．21．证明见解析.【分析】证出∠A=∠ECD，再由∠B=∠D=90°，即可得出△ABC∽△CDE．【详解】∵∠B=90°，∴∠A+∠ACB=90°，∵C为线段BD上一点，且AC⊥CE，∴∠ACB+∠ECD=90°，∴∠A=∠ECD，∵∠B=∠D=90°，∴△ABC∽△CDE．考点：相似三角形的判定．22．见解析【分析】由正方形的性质得出∠A=∠D=90°，AB=AD=CD=BC，证出AE DFAB DE=，即可得出结论．【详解】∵ABCD为正方形，∴AD=AB=DC=BC，∠A=∠D=90°，∵AE=ED，∴12 AEAB=，∵DF=14DC ，∴12DF DE =，∴AE DF AB DE=，又∠A=∠D=90°，∴△ABE ∽△DEF ．考点：相似三角形的判定．23．120°．【详解】试题分析：根据等边三角形的性质得到∠PCD=60°，根据相似三角形的判定定理证明△ACP ∽△ABP ，根据相似三角形的性质得到答案．解：∵△PCD 是等边三角形，∴∠PCD=60°，∴∠ACP=120°，∵△ACP ∽△PDB ，∴∠APC=∠B ，又∠A=∠A ，∴△ACP ∽△ABP ，∴∠APB=∠ACP=120°．考点：相似三角形的性质．24．证明见解析.【详解】试题分析：连接EF ．根据角平分线的性质知AF ：FC=DE ：EC ，由平行线分线段成比例知AF ：FC=DE ：EC ，由这两个比例式和已知条件“BE=CE”知2·2DE AB EC DE EC==，即AB=2DE ．试题解析:连接EF ．∵∠ABC=2∠C ，BF 为∠B 的平分线，∴∠FBC=∠C=12∠ABC ，∴BF=CF ；又∵BE=CE ，∴EF ⊥BC ；∵AD ⊥BC ，∴EF ∥AD ，∴AF ：FC=DE ：EC ；而AB ：BC=AF ：FC ，∴AB ：BC=DE ：EC ，∴2·2DE AB EC DE EC ==，即AB=2DE ．考点:1.平行线分线段成比例；2.角平分线的性质；3.等腰三角形的判定与性质.25．（1）见详解；（2）10BG =【分析】（1）由题意易得11,22AE DF DE AB ==，∠D=∠A=90°，则有AE DF AB DE =，进而问题可证；（2）由题意易得△DEF ∽△CGF ，DE=2，则有13DE DF CG CF ==，进而可得CG=6，然后问题可求解．【详解】（1）证明：∵四边形ABCD 是正方形，∴∠D=∠A=90°，AD=DC=AB ，∵AE ED =，14DF DC =，∴111,222AE AD AB DF DE ===，∴12AE DF AB DE ==，∴△ABE ∽△DEF ；（2）解：∵四边形ABCD 是正方形，且边长为4，∴AD ∥BG ，BC=AD=4，∴△DEF ∽△CGF ，∵14DF DC=，∴13 DE DFCG CF==，∵AE ED=，∴ED=2，∴CG=6，∴BG=BC+CG=10．【点睛】本题主要考查正方形的性质及相似三角形的性质与判定，熟练掌握正方形的性质及相似三角形的性质与判定是解题的关键．26．见解析【分析】（1）利用SAS可证明△BAM≌△CAN，继而得出结论．（2）也可以通过证明△BAM≌△CAN，得出结论，和（1）的思路完全一样．（3）首先得出∠BAC=∠MAN，从而判定△ABC∽△AMN，得到AB ACAM AN=，根据∠BAM=∠BAC﹣∠MAC，∠CAN=∠MAN﹣∠MAC，得到∠BAM=∠CAN，从而判定△BAM∽△CAN，得出结论．【详解】解：（1）证明：∵△ABC、△AMN是等边三角形，∴AB=AC，AM=AN，∠BAC=∠MAN=60°．∴∠BAM=∠CAN．∵在△BAM和△CAN中，AB AC {BAM CAN AM AN=∠=∠=，∴△BAM≌△CAN（SAS）．∴∠ABC=∠ACN．（2）结论∠ABC=∠ACN仍成立．理由如下：∵△ABC、△AMN是等边三角形，∴AB=AC，AM=AN，∠BAC=∠MAN=60°．∴∠BAM=∠CAN．∵在△BAM和△CAN中，AB AC {BAM CAN AM AN=∠=∠=，∴△BAM≌△CAN（SAS）．∴∠ABC=∠ACN．（3）∠ABC=∠ACN．理由如下：∵BA=BC，MA=MN，顶角∠ABC=∠AMN，∴底角∠BAC=∠MAN．∴△ABC∽△AMN．∴AB AC AM AN=．又∵∠BAM=∠BAC﹣∠MAC，∠CAN=∠MAN﹣∠MAC，∴∠BAM=∠CAN.∴△BAM∽△CAN．∴∠ABC=∠ACN．21。

人教版九年级数学下册第二十七章达标检测卷含答案

人教版九年级数学下册第二十七章达标检测卷一、选择题(每小题3分，共30分)1．下列图形中，属于相似图形的是()2．下列各组线段中，是成比例线段的是()A．1，2，3，4 B．3，6，9，18C．1，2，2，6 D．1，2，4，3 23．已知△ABC∽△DEF，若∠A＝40°，∠E＝80°，则∠F的度数为() A．30°B．60°C．70°D．80°4．如图，l1∥l2∥l3，BC＝1，DEEF＝32，则AB的长为()A．4 B．2 C.32 D.23(第4题) (第5题)5．如图，△ABC与△DEF是位似图形，点O为位似中心，已知BO：OE＝2：1，则△ABC与△DEF的面积比是()A．2：1 B．3：1 C．4：1 D．5：16．如图，在△ABC中，点D，E分别在边AB，AC上，下列条件不能判定△ADE 与△ACB相似的是()A．∠AED＝∠B B.ADAC＝AEABC．AD·BC＝DE·AC D．DE∥BC(第6题) (第7题)7．如图，在Rt△ABC中，∠CAB＝90°，AD⊥CB，两两相似的三角形对数为()A ．2B ．3C ．4D ．58．如图，小正方形的边长均为1，则下列三角形(阴影部分)与△ABC 相似的是( )(第8题) (第9题)9．如图，为测量河的宽度，在河对岸选定一个目标点A ，在近岸取点B ，C ，D ，使得AB ⊥BC ，CD ⊥BC ，点E 在BC 上，并且点A ，E ，D 在同一条直线上．若测得BE ＝15 m ，EC ＝9 m ，CD ＝16 m ，则河的宽度AB 为( ) A ．35 m B.653 m C.803 m D.503 m10．如图，在△ABC 中，AB ＝6，BC ＝5，点D ，E 分别在BC ，AC 上，CD ＝2BD ，CE ＝2AE ，BE 交AD 于点F ，则△AFE 面积的最大值是( ) A ．2 B ．3 C ．4 D ．5(第10题) (第12题) (第13题)二、填空题(每小题3分，共15分) 11．如果x y ＝25，那么y －x y ＋x＝________．12．如图，在▱ABCD 中，E 是BC 边上的点，连接AE 交BD 于点F , 若EC ＝2BE,EF ＝2，则AE ＝________．13．如图，有一组平行横格线，相邻横格线间的距离都相等，已知点A ，B ，C ，D ，O 都在横格线上，且线段AD ，BC 交于点O ，则AB CD 等于________． 14．在平面直角坐标系中，点C ，D 的坐标分别为(2，3)，(1，0)，现以原点为位似中心，将线段CD 放大得到线段AB ，若点D 的对应点B 在x 轴上且OB ＝2，则点C 的对应点A 的坐标为__________．15．如图，n 个边长为1的相邻正方形的一边均在同一直线上，点P 1，P 2，P 3，…，P n 分别为边B 1B 2，B 2B 3，B 3B 4，…，B n B n ＋1的中点，△B 1C 1P 1的面积为S 1，△B 2C 2P 2的面积为S 2，…，△B n C n P n 的面积为S n .(1)S 1＝________；(2)S n ＝________(用含n 的式子表示)．三、解答题(一)(每小题8分，共24分)16．若a 3＝b 5＝c7，且3a ＋2b －4c ＝9，求a ＋b ＋c 的值．17．如图，△ABC 在方格纸(小正方形的边长均为1)中．(1)请在方格纸上建立平面直角坐标系，使点A 的坐标为(3，4)，点C 的坐标为(7，3)，并写出点B 的坐标；(2)以(1)中所建立的坐标系的原点O 为位似中心，相似比为21，在第一象限内将△ABC 放大，画出放大后的位似图形△A ′B ′C ′； (3)计算△A ′B ′C ′的面积S .18．如图，在Rt △ABC 中，∠BAC ＝90°，AB ＝AC ，E ，D 分别是BC ，AC 上的点，且∠AED＝45°.(1)求证：△ABE∽△ECD；(2)若AB＝4，BE＝2，求CD的长．四、解答题(二)(每小题9分，共27分)19．如图，小强在地面E处放一个平面镜，刚好能从平面镜中看到教学楼的顶端B，此时EA＝25米，CE＝2.5米．已知眼睛距离地面的高度DC＝1.6米，请计算出教学楼AB的高度．20．如图，CD是Rt△ABC斜边AB上的高，E为CB的中点，ED的延长线交CA的延长线于点F.求证：AC·CF＝CB·DF.21．如图，在梯形ABCD中，AD∥BC, AB⊥BC，∠AEB＝∠ADC.(1)求证：△ADE∽△DBC；(2)连接EC，若CD2＝AD·BC，求证：∠DCE＝∠ADB.五、解答题(三)(每小题12分，共24分)22．如图，BC是⊙O的一条弦，过点O作OM⊥BC于点M，延长MO交⊙O于点A，连接AB，AC，∠ABC的平分线交AM于点D，交⊙O于点F，并与过点A的⊙O的切线交于点G.(1)求证：AB＝AG；(2)连接AF，若AB＝10，BC＝12，求AF的长．23．如图，在△ABC中，BA＝BC＝20 cm，AC＝30 cm，点P从点A出发，沿AB 以每秒4 cm的速度向点B运动；同时点Q从点C出发，沿CA以每秒3 cm 的速度向点A运动，当其中一个动点停止，另一个动点也停止运动，设运动时间为x秒．(1)当x为何值时，PQ∥BC；(2)是否存在某一时刻，使△APQ与△CQB相似？若存在，求出此时AP的长；若不存在，请说明理由．答案一、1.D 2.B 3.B 4.C 5.C 6.C 7.B 8.B 9.C 10．A 点拨：连接DE ，过点D 作DH ⊥AB 于点H ，如图．∵CD ＝2BD ，CE ＝2AE ，∴CD BD ＝CEAE ＝2，∴DE ∥AB ， ∴△CDE ∽△CBA ，△DEF ∽△ABF ，∴DE BA ＝CD CB ，DF AF ＝DE AB .易知CD CB ＝23，∴DF AF ＝DE AB ＝23， ∴S △BDF S △ABF ＝23，∴S △BDF S △ABD ＝25， ∵DE ∥AB ，∴S △ABE ＝S △ABD ， ∴S △ABE －S △ABF ＝S △ABD －S △ABF ， ∴S △AEF ＝S △BDF ＝25S △ABD .∵AB ＝6，是定值，∴当DH 最大时，△ABD 的面积最大，∵DH ≤BD ，易知BD ＝13BC ＝53，∴当DH ＝53时，△ABD 的面积最大，最大值为12×53×6＝5，∴△AFE 面积的最大值是25×5＝2.二、11.37 12.8 13.2∶3 14.(4，6)或(－4，－6)15．(1)14 (2)14（2n －1）三、16.解：设a 3＝b 5＝c7＝k (k ≠0)，则a ＝3k ，b ＝5k ，c ＝7k ，代入3a ＋2b －4c ＝9，得9k ＋10k －28k ＝9，解得k ＝－1， ∴a ＋b ＋c ＝15k ＝－15.17．解：(1)建立平面直角坐标系如图所示．点B的坐标为(3，2)．(2)△A′B′C′如图所示．(3)△A′B′C′的面积S为12×4×8＝16.18．(1)证明：在Rt△ABC中，∠BAC＝90°，AB＝AC，∴∠B＝∠C＝45°.∵∠AEC＝∠B＋∠BAE＝∠AED＋∠CED，∠AED＝45°，∴∠BAE＝∠CED，∴△ABE∽△ECD.(2)解：在Rt△ABC中，∠BAC＝90°，AB＝AC＝4，∴BC＝4 2.∵BE＝2，∴EC＝3 2.∵△ABE∽△ECD，∴ABEC＝BECD，即43 2＝2CD，解得CD＝3 2.四、19.解：根据题意得∠AEB＝∠CED，∠BAE＝∠DCE＝90°，∴△AEB∽△CDE，∴ABCD＝AECE，即AB1.6＝252.5，解得AB＝16米．答：教学楼AB的高度为16米．20．证明：∵CD是Rt△ABC斜边AB上的高，E为CB的中点，∴CE＝EB＝DE，∴∠B＝∠BDE＝∠FDA.∵∠B＋∠CAB＝90°，∠FCD＋∠CAB＝90°，∴∠B＝∠FCD，∴∠FDA＝∠FCD.又∵∠F＝∠F，∴△FDA∽△FCD，∴DFCF＝ADDC.∵∠ADC＝∠CDB＝90°，∠ACD＝∠B，∴△ACD ∽△CBD ，∴AD CD ＝AC CB ，∴DF CF ＝ACCB ，即AC ·CF ＝CB ·DF . 21．证明：(1)∵AD ∥BC ，∴∠ADE ＝∠DBC ，∠ADC ＋∠C ＝180°， ∵∠AEB ＝∠ADC ，∠AEB ＋∠AED ＝180°， ∴∠AED ＝∠C ，∴△ADE ∽△DBC . (2)由(1)得△ADE ∽△DBC ， ∴AD DB ＝DEBC，∴DB ·DE ＝AD ·BC ， ∵CD 2＝AD ·BC ，∴CD 2＝DB ·DE ，∴CD BD ＝DEDC . 又∵∠CDE ＝∠BDC ，∴△CDE ∽△BDC ， ∴∠DCE ＝∠DBC ，∵∠ADB ＝∠DBC ，∴∠DCE ＝∠ADB .五、22. (1)证明：∵BG 平分∠ABC ，∴∠ABG ＝∠CBG ，∵AG 是⊙O 的切线，∴AG ⊥AM ，∵AM ⊥BC ，∴AG ∥BC ，∴∠G ＝∠CBG ，∴∠G ＝∠ABG ， ∴AB ＝AG .(2)解：设AC 与BG 交于点N ，由(1)知AG ＝AB ＝10. ∵OM ⊥BC ，∴AB ︵＝AC ︵，∴∠C ＝∠ABC ，AC ＝AB ＝10， ∵AG ∥BC ，∴∠GAN ＝∠C ，∴∠ABC ＝∠GAN ，∵∠GAN ＝∠GAF ＋∠F AN ，∠ABC ＝∠FBC ＋∠ABG ，∠F AN ＝∠FBC ， ∴∠GAF ＝∠ABG .由(1)知∠G ＝∠ABG ， ∴∠GAF ＝∠G ，∴AF ＝GF . ∵AG ∥BC ，∴△GAN ∽△BCN ，∴AN CN ＝NG BN ＝GA BC ＝1012＝56，∴易得CN ＝6011，设NG ＝5x ，AF ＝GF ＝y (x >0，y >0)，则BN ＝6x ， ∴BG ＝11x ，∵∠ABF ＝∠NBC ，∠AFB ＝∠C ， ∴△ABF ∽△NBC ，∴AB BN ＝AF NC ＝BFBC ，∴106x ＝y 6011＝11x －y 12，解得x ＝8 511，y ＝5 52，∴AF ＝5 52.23．解：(1)由题意知，AP ＝4x cm ，CQ ＝3x cm.若PQ ∥BC ，则△APQ ∽△ABC ，∴AP AB ＝AQAC ，即4x 20＝30－3x 30，解得x ＝103， ∵⎩⎨⎧0<4x ≤20，0<3x ≤30，∴0<x ≤5， ∴x ＝103符合题意，即当x ＝103时，PQ ∥BC . (2)存在．∵AB ＝BC ，∴∠A ＝∠C ，分以下两种情况：①当△APQ ∽△CQB 时，AP CQ ＝AQCB ，即4x 3x ＝30－3x 20，解得x 1＝109，x 2＝0(舍去)．经检验，x ＝109是上述方程的解．∴当AP ＝409cm 时，△APQ ∽△CQB ；②当△APQ ∽△CBQ 时，AP CB ＝AQCQ ，即4x 20＝30－3x3x ，解得x 3＝5，x 4＝－10(舍去)．经检验，x ＝5是上述方程的解． ∴当AP ＝20 cm 时，△APQ ∽△CBQ .综上所述，当AP 的长为409cm 或20 cm 时，△APQ 与△CQB 相似．。

人教版九年级数学第27章达标卷(附答案)

人教版九年级下册数学第二十七章测试卷带答案

人教版九年级下册数学第二十七章测试卷有答案

人教版初3数学9年级下册 第27章(相似)达标检测卷(含解析)

人教版九年级数学下册--第二十七章达标测试卷--(附解析答案)

人教版九年级数学册 第二十七章测试卷(附答案)

人教版九年级数学下册第27章相似单元达标训练试题(含答案)

2023年人教版九年级数学下册第27章《相似》复习检测卷(一)附答案解析

第27章 相似三角形应用举例 达标训练2022-2023学年人教版九年级数学下册

人教版数学九下第二十七章综合达标训练卷(A卷)及答案解析

人教版九年级下册数学第二十七章测试卷有答案

人教版数学九年级下学期第27章《相似》测试卷含答案

人教版九年级下册数学第二十七章测试卷附答案

人教版九年级数学下册第二十七章达标测试卷含答案

人教版九年级数学下册第二十七章检测卷(含答案)

人教版初3数学9年级下册 第27章(相似)单元达标测试(含解析)

人教版九年级下册数学第二十七章测试卷及答案

人教版九年级下册数学第二十七章测试卷含答案

人教版九年级数学下册第二十七章达标检测卷含答案

人教版初3数学9年级下册第27章(相似)达标检测卷(含解析)

人教版九年级数学册第二十七章测试卷(附答案)

第27章相似三角形应用举例达标训练2022-2023学年人教版九年级数学下册

人教版初3数学9年级下册第27章(相似)单元达标测试(含解析)