北师大版公式法2PPT课件

合集下载

公式法PPT课件(北师大版)

2
2 92 − 4 2
4 −4 +16
3. 已知 + 2 = 3， 2 -4 2 =-15,求 − 2，，的值.
同学们，再见！
课题：公式法——平方差公式
复习引入
问题：什么叫因式分解?
把一个多项式化成几个整式的积的情势，这样的变
形叫做因式分解.
问题：我们已学过哪一种分解因式的方法?
提公因式法
复习引入
问题：整式乘法中的平方差公式是什么？
平方差公式：
(a+b)(a－b)=a2－b2
整式乘法
(a+b)(a－b) =a2－b2
a2－b2 =(a+b)(a－b)
－ =( + )( − )
公式左边：1.多项式有两项；
2.这两项异号；
3.两项是平方差.
公式右边：两个数的和与两个数的差的乘积的情势。
练习：判断下列各式能否用平方差公式因式分解？
(1)
m 81
2
(2) 1 16b 2
√
=2 − 92
√
=12 − (4)2
×
不能转化为平方差情势
3.两项是平方差.
注：公式中的字母a，b可以代表数、字母，也可以代
表一个式子；分解因式时要把式子看作一个整体.
（整体思想）
归纳总结
۞2.利用平方差公式分解因式的步骤：
（1）若多项式中有公因式，应先提取公因式；
（2）剩余因式若有两项、异号，两项是平方差，
则用平方差公式继续分解因式；
۞3.分解因式一定要分解到每个因式都不能再分
=( + 1)( − 1)
先考虑能否用提取公因式法，再考虑能否用平方差公式

北师大版2.3公式法解一元二次方程PPT课件第二课时

2014年8月18日星期一6时56分36秒
3
学习是件很愉快的事
公式法
程为一般形式;
例1、用公式法解方程 5x2-4x-12=0 1.变形:化已知方解: a 5, b 4, c 12
b 4ac 4 4 5 (12) 256 0.
2 2
a=1，b=-2 b2-4ac=(-2 ∴x= x1 = x 2 =
2014年8月18日星期一6时56分36秒
6
二，思考题：m取什么值时，方程
2 2 x +(2m+1)x+m -4=0
有两个相等的实数解
2014年8月18日星期一6时56分36秒 7
三，想一想：
关于x的一元二次方程ax2+bx+c=0 (a≠0)。当a，b，c 满足什么条件时，方程的两根为互为相反数？
一元二次方程解：
x1 b
ax 2 bx c 0 a 0 的解为：
b 2 4ac b b 2 4ac , x2 2a 2a
x1 x2
b b 2 4ac b b 2 4ac 2a 2a
b b 2a 2a
2014年8月18日星期一6时56分36秒
2014年8月18日星期一6时56分36秒 10
五，根据题意，列出方程： 1.《九章算术》“勾股”章中有一题:“今有户高多于广六尺八寸 ,两相去适一丈.问户高,广各几何.” 大意是说:已知长方形门的高比宽多6尺8寸,门的对角线长1丈, 那么门的高和宽各是多少? 解：设门的高为 x 尺，根据题意得 2 10 x x 2 x 6.8 102.
2014年8月18日星期一6时56分36秒

初中数学《完全平方公式》优秀课件北师大版2

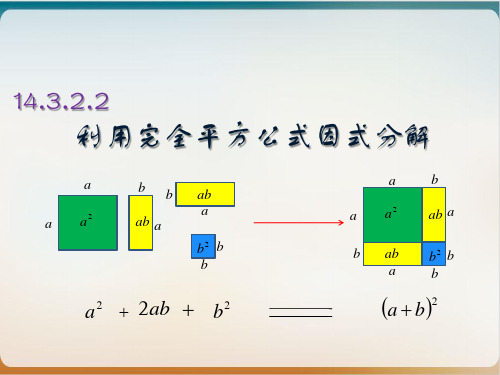
a2 2• a •bb2
(1)、解：16x2 24x 9
方法：当一个式子满足完全
(4x)2 2 4x 3 32
平方式的所有特征时，可直接分解因式。结果为这两平
4x 32
方项底数和或差的平方，是
和是差看中间项的符号
分析：- x2 4xy 4 y2 - x2 2 • x • 2 y 2 y2
• 学习重点：
运用完全平方公式分解因式．
学习难点：综合运用提公因式和公式法分解
因式
复习引入
问题一：大家还记得什么是因式分解吗?
因式分解就是将一个多项式化成几个整式的积的形式
即：和
积
问题二：我们已经学习了分解因式的哪
些方法？
1、提公因式法 2、公式法
平方差公式 a2 b2 a ba b
即：两个数的平方差等于这两个数的和与差的积
方法：若式子有整体满足完全平方式可直接进行因式分解，需注意中间项的符号
练习2 将下列多项式分解因式：
1 25a3 ax2 10a2x
2 12x3 12x2 2 y 1- 3x2y -12
答案：
1 a5a x2
a b2 b a2
2 - 3x2 y 1 2x2
或 - 32x 2 y 12
你对因式分解的方法有什么新的发现？请尝试概括你的发现.
把整式的乘法公式——完全平方公式倒过来就得到因式分解的完全平方公式：
a2 2ab+b2 =（a b）2
首2 2 首尾尾2 首尾2
即两个数的平方和加上（或减去）这两个数的积的2倍，等于这两个数的和（或差）的平方
1、在下面括号ቤተ መጻሕፍቲ ባይዱ填空
14.3.2.2 利用完全平方公式因式分解

用公式法求解一元二次方程课件北师大版数学九年级上册

程ax2＋bx＋ Δ=b2－4ac=0 方程有两个相等的实数根
c=0
Δ=b2－4ac<0 方程没有实数根
知2－讲
特别说明：(1)由Δ=b2－4ac 的符号可判定ax2＋bx＋c=
0(a ≠ 0)的根的情况. 反之，由ax2＋bx＋c= 0(a ≠ 0)的根的
情况也可得到Δ=b2－4ac 的符号.
(2)一元二次方程有实数根(或有两个实数根)包括有两
2k－1=0 的根的情况为(
A. 有两个相等的实数根
B. 没有实数根
C. 有两个不等的实数根
D. 无法判断
)
知2－练
思路导引：
解：∵ a=1，b=－2(k＋1)，c=－k2＋2k－1，
∴ Δ =b2－4ac=［－2(k＋1)］2－4×1×(－k2＋2k－
1)=8＋8k2>0.
当方程中的a，b，c含有字母时，求出
第二章一元二次方程
3 用公式法求解一元二次方程
1 课时讲授用公式法解一元二次方程
一元二次方程根的判别式
2 课时流程
逐点
导讲练
课堂
小结
作业
提升
知识点 1 用公式法解一元二次方程
知1－讲
1. 求根公式：对于一元二次方程ax2＋bx＋c= 0(a ≠ 0)，当
b2－4ac
≥ 0 时，它的根是x =
知1－练
(3)x2－2x＋3=0.
解：这里a=1，b=－2，c=3 .
∵ b2 －4ac=(－2)2 －4×1×3=－8<0，
∴方程无实数根.
知1－练
知1－练
1-1. 用公式法解下列方程：
(1)y2－2y－2=0；
解：这里 a＝1，b＝－2，c＝－2.

《公式法》因式分解PPT课件(第2课时)

B. + −
C. − +
D. − + +
D
）
课堂检测
基础巩固题
3.如果x2-6x+N是一个完全平方式,那么N是(
A . 11
B. 9
C. -11
)
B
D. -9
4.如果x2-mx+16是一个完全平方式,那么m的值为________.
±8
课堂检测
∴＋＋＝(＋) ＝112＝121.
连接中考

（2020•眉山）已知 + = − − ，则 −
. 4

的值为

解析：由 +
得
+

= − − ，
− + + = ，

即 − + + + + = ，
∵ − = , = ，
∴原式=2.
巩固练习
变式训练
已知－＋－＋＝，求＋＋的值．
解：∵x2－4x＋y2－10y＋29＝0，
∴(－)＋(－)＝.
∵(－) ≥ ，(－) ≥ ，
∴－＝，－＝，∴＝，＝，
是.
巩固练习
变式训练
将前面例题的（2）（3）（4）变为完全平方式？
（2） + ²;
+ ² + ；
（3） + − ；
+ + ；
（4） + + .
+ + .
探究新知
知识点 2
用完全平方公式因式分解

九年级数学上册第二章一元二次方程2.3用公式法求解一元二次方程第2课时课件新版北师大版

• 一、释疑难 • 对课堂上老师讲到的内容自己想不通卡壳的问题，应该在课堂上标出来，下课时，在老师还未离开教室的时候，要主动请老师讲解清楚。如果老师已
经离开教室，也可以向同学请教，及时消除疑难问题。做到当堂知识，当堂解决。 • 二、补笔记 • 上课时，如果有些东西没有记下来，不要因为惦记着漏了的笔记而影响记下面的内容，可以在笔记本上留下一定的空间。下课后，再从头到尾阅读一
第二课时
一块矩形菜地的面积是120 m2,如果它的长减少2 m,那么菜地就变成正方形,则原菜地的长是 12 m.
12345
1.把一个小球以20 m/s的速度竖直向上抛出,它在空中的高度h(m)
与运动时间t(s)满足关系式h=20t-5t2,当h=20时,小球的运动时间为
()
A.20 s
B.2 s
解:设垂直于墙的一边长为x m,得 x(58-2x)=200. 解得x1=25,x2=4. 则平行于墙的另一边长为8 m或50 m. 答:矩形的长为25 m,宽为8 m或矩形的长为50 m,宽为4 m.
关闭
答案
编后语
• 常常可见到这样的同学，他们在下课前几分钟就开始看表、收拾课本文具，下课铃一响，就迫不及待地“逃离”教室。实际上，每节课刚下课时的几分钟是我们对上课内容查漏补缺的好时机。善于学习的同学往往懂得抓好课后的“黄金两分钟”。那么，课后的“黄金时间”可以用来做什么呢？
遍自己写的笔记，既可以起到复习的作用，又可以检查笔记中的遗漏和错误。遗漏之处要补全，错别字要纠正，过于潦草的字要写清楚。同时，将自己对讲课内容的理解、自己的收获和感想，用自己的话写在笔记本的空白处。这样，可以使笔记变的更加完整、充实。 • 三、课后“静思2分钟”大有学问 • 我们还要注意课后的及时思考。利用课间休息时间，在心中快速把刚才上课时刚讲过的一些关键思路理一遍，把老师讲解的题目从题意到解答整个过程详细审视一遍，这样，不仅可以加深知识的理解和记忆，还可以轻而易举地掌握一些关键的解题技巧。所以，2分钟的课后静思等于同一学科知识的课后复习30分钟。

新北师大版九年级数学上册《用公式法求解一元二次方程》优质课课件(共18张PPT)

解：(1)设该项绿化工程原计划每天完成 x m2，根据题意
46 000－22 000 46 000－22 000
得：
x
－
1.5x
＝4，解得 x＝2 000，经
检验，x＝2 000 是原方程的解，答：该绿化项目原计划每天完

成 2 000 平方米 (2)设人行道的宽度为 x 米，根据题意得，(20
－3x)(8－2x)＝56，解得 x1＝2 或 x2＝236(不合题意，舍去)．答：人行道的宽为 2 米
2.3 用公式法求解一元二次方程
1．对于一元二次方程 ax2＋bx＋c＝0(a≠0)，当 b2－4ac≥0 时，－b± b2－4ac
它的根 x＝
2a
，我们把这个式子称为一元二次方程的
求根公式，用求根公式解一元二次方程称为公式法．
2．对于一元二次方程ax2＋bx＋c＝0(a≠0)，当b2－4ac>0时，
－1＋ 5
－1－ 5
则方程(x＋2)*5＝0 的解为x1＝ 2 ，x2＝ 2
．
15．用公式法解方程：
(1)7x2－6x＝5
3＋2 11
3－2 11
解：x1＝ 7 ，x2＝ 7
(2)x(2x－4)＝5－8x
－2＋ 14
－2－ 14
解：x1＝ 2 ，x2＝ 2
16．解方程 2x2＋4 3x＝2 2.有一位同学解答如下：这里 a＝ 2，b＝4 3，c＝2 2，∴b2－4ac＝(4 3)2－4× 2
(2)x2－2 3x＋3＝0 解：∵Δ＝12－4×3＝0，∴x1＝x2＝ 3
知识点二：根的判别式 6．下列关于x的方程有实数根的是( D ) A．x2＋1＝0 B．x2＋x＋1＝0 C．x2－x＋1＝0 D．x2－x－1＝0 7．(2014·宁波)已知命题“关于x的一元二次方程x2＋bx＋1 ＝0，当b<0时，必有实数解”，能说说这个命题是假命题的反例是( A ) A．b＝－1 B．b＝2 C．b＝－2 D．b＝0

新北师大版数学九年级上册课件：用公式法求解一元二次方程(第2课时)

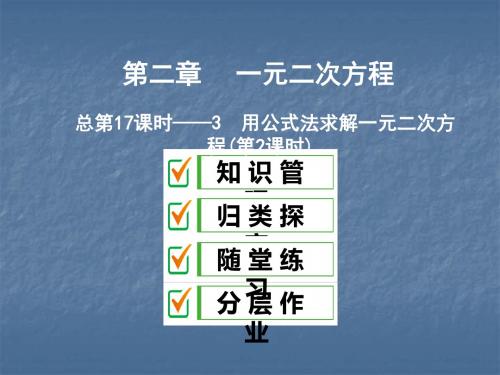
3.如图175，利用一面墙(墙的长度不超过45 m)，用80 m 长的篱笆围一个矩形场地．
图175
(1)怎样围才能使矩形场地的面积为750 m2? (2)能否使所围矩形场地的面积为810 m2，为什么？
【解析】围成的矩形场地只有三面篱笆，设长为x， 1 则宽为 (80－x)，然后根据面积公式列方程即可． 2
① 图172
②
同学们都认为小华的方案是正确的，但对小芳方案是否符合条件有不同意见，你认为小芳的方案符合条件吗？若不符合，请用方程的方法说明理由．
解：不符合．设小路宽度均为x m，根据题意，得 1 (16－2x)(12－2x)＝ ×16×12， 2 解这个方程，得x1＝2，x2＝12. 但x2＝12不符合题意，应舍去，∴x＝2. ∴小芳的方案不符合条件，小路的宽度均为2 m.
(2)如答图，作AI⊥CD，HJ⊥EF，垂足分别为I，J.
例题答图
∵AB∥CD，∠1＝60° ， ∴∠ADI＝60° ， ∵BC∥AD， ∴四边形ADCB为平行四边形． ∴BC＝AD. 由(1)得x＝2， ∴BC＝HE＝2＝AD，在Rt△ADI中，AI＝ 3.
∵∠HEJ＝60° ，∴HJ＝ 3. ∴小颖的设计方案中四块绿地的总面积＝52×48－52×2－48×2＋( 3 )2＝2 299 m2.
1．在一块正方形钢板上截去3 cm宽的矩形钢条，剩下的面积是54 cm2，则原来这块钢板的面积是 81 cm2.
随堂练习
【解析】设正方形钢板边长为x cm，依题意得 x(x－3)＝54，解这个方程，并舍去负值得x＝9，故原来这块钢板面积为92＝81 cm2.
2．在宽为15 m，长为25 m的矩形地面上铺540 m2的草坪，并留出如图1所示的宽度相同的通道，设通道宽为x m，列方程得 (25－x)(15－x)＝540 .

432公式法第2课时-广东省河源市正德中学北师大版八年级数学下册课件(共18张PPT)

2.多项式x2－mxy＋9y2能用完全平方公式分解,则m的
值是( )
A.3 B. 6
C.±3
D.±6
3.已知代数式－a2＋2a－——无论a取任何值,它的值
一定是( )
A.正数 B.非正数 C.负数 D.非负数
4．把下列式子因式分解： (1)x2＋14x＋49;
(2)(x＋y)2＋6(x＋y)＋9；
（3）2019×20132-2013×4028×2019+2019×20142
3.已知ab＝2,a－b＝3,求a3b－2a2b2＋ab3的值.
【课堂小结】本节课我们主要学习了哪些知识?
课堂检测
1.计算1252－50×125＋252的结果为( )
A.100 B.150 C.10 000 D.22 500
因式分解：
(1)3x3－ 6x2y＋3xy2； (2)4x2y－4xy2－x3.
归纳：分解因式要注意以下问题：首先提取公因式,然后考虑运用分式法,看能否用平方差公式或完全平方公式分解因式.分解因式要使每一个因式都不能再分解为止.
交流研讨、展示表现
1.小明同学利用完全平方公式对下列式子进行
因式分解，你认为正确的是(
第4章因式分解
§4.3公式法（第2课时）
学习目标
河源市正德中学
1.理解完全平方公式,弄清完全平方公式的形式和特点. 2.掌握运用完全平方公式分解因式的方法,能正确运用完全平方公式把多项式分解因式.
(一)、温故知新计算：(a＋b)2＝ (a－b)2＝ (x－3)2＝ (y＋1)2＝
；；； .
（5）9－6(m－n)＋( )2 （6） a2－b2＋2ab
归纳：能运用完全平方公式分解因式的条件： ①多项式是三项式； ②两项可化为两个数(或整式)的平方； ③另一项为这两个数(或整式)积的2 倍.

北师大版数学九年级上册用公式法求解一元二次方程课件(共25张)

解：（1）∵关于x的一元二次方程x2-（2m+1）x+m （m+1）=0． ∴△=（2m+1）2-4m（m+1）=1＞0， ∴方程总有两个不相等的实数根；（2）∵x=0是此方程的一个根， ∴把x=0代入方程中得到m（m+1）=0， ∴m=0或m=-1， ∵（2m-1）2+（3+m）（3-m）+7m-5=4m2-4m+1+9m2+7m-5=3m2+3m+5，把m=0代入3m2+3m+5得：3m2+3m+5=5；把m=-1代入3m2+3m+5得：3m2+3m+5=3×1-3+5=5．
0(a≠0)没有实数根．
练习
参考答案:
1.用公式法解下列方程.
1). 2x2-4x－1＝0； 2). 5+2＝3x2 ； 3). (x-2)(3x-5) =1;
2.一个直角三角形三边的长为三个连续偶数,求这个三角形的三边长.
B
A
C
课堂练习
1．下列一元二次方程中，有两个不相等的实数根的方程是( A )
x2＝
1－ 2
5
x2＝1－
6 2
.
探究新知
知识模块一探索一元二次方程的求根公式 (一)自主探究
1.你能用配方法解方程 ax2+bx+c=0(a≠0) 吗?
解: 移项，得 ax2 bx c，
方程两边都除以a x2 b x c ，
a
a
配方，得
x2
b a
x
b 2a
2
c a
b 2a
2
.

9年级数学北师大版上册课件第2章《用公式法求解一元二次方程》

新知导入
一元二次方程的一般形式是：
ax2＋bx＋c = 0(a≠0)
【思考】如果使用配方法解出一元二次方程一般形式的根，那么这个根是不是可以普遍适用呢？
新知讲解
你能用配方法解方程ax2+bx+c=0 (a≠0)吗？
方程的两边同除以a，得
移项，得x2
+
b a
x
=___-__ca______
x2 +b x+ c =0 aa
配方法：
x2-2x+3=0 x2-2x=-3
x2-2x+1=-3+1 （x-1）2=-2 ∵不论x为何值，（x-1）2都不能为负数，∴此方程无解。
公式法：解：已知a=1，b=-2，c=3. ∵b2-4ac=(-2)2-4×1×3
=-8<0
你能发现什么？
新知讲解
对于一元二次方程ax2+bx+c=0(a≠0)，当b2-4ac<0时，它的根的情况是怎样的？
∵b2-4ac=(-4)2-4×4×1=0
∴ x = -（- 4）± 0 = 1 24 2
即x1=x2=
1 2
新知讲解
公式法解方程的步骤
1.变形:化已知方程为一般形式;
2.确定系数:用a,b,c写出各项系数; 3.计算: b2-4ac的值; 4.判断:若b2-4ac ≥0，则利用求根公式求出;
若b2-4ac<0，则方程没有实数根.
根，即
x1＝－b＋ 2ba2－4ac，x2＝－b－ 2ba2－4ac；
(2)当Δ＝b2－4ac＝0时，一元二次方程ax2＋bx＋c＝0(a≠0)有两个相等实数根，
即
x1＝x2＝－2ba；

北师大版九年级数学上册用公式法求解一元二次方程第2课时课件

(1)若此时花圃的面积刚好为45 m2，求此时花圃的长 BC 和宽 AB ；解：(1)设花圃的宽 AB 为 x 米，则长 BC 为(22－3 x ＋2)米. 根据题意，可得(22－3 x ＋2) x ＝45，解得 x1＝3， x2＝5，当 AB ＝3时， BC ＝15＞14，不符合题意，舍去；当 AB ＝5时， BC ＝9，满足题意. 答：花圃的长 BC 为9米，宽 AB 为5米.
123
第2课时公式法的实际应用
知识梳理课时学业质量评价
3. 如图，用长为22米的篱笆，一面利用墙(墙的最大可用长度为14米)，围成中间隔有一道篱笆的长方形花圃 ABCD ，为了方便出入，在建造篱笆花圃时，在 BC 上用其他材料做了宽为1米的两扇小门.
123
第2课时公式法的实际应用
知识梳理课时学业质量评价
⁠
第2课时公式法的实际应用
知识梳理课时学业质量评价
1. 用一条长40 cm的绳子围成一个面积为64 cm2的矩形.设矩形的长为
x cm，则可列方程为( B )
A. x (20＋ x )＝64
B. x (20－ x )＝64
C. x (40＋ x )＝64
D. x (40－ x )＝64
123
第2课时公式法的实际应用
图3
当堂训练
解：根据题意，得 (16-x)(12-x)=12 ×16×12 ，
或
16
x＋（12－
x
）
x=
1 2
×16×12
，
或12
x＋（16－
x
）
x=
1 2
×16×12
，
或
16
x＋12
x-x2=

北师大版《公式法》ppt公开课课件2

③4a-2b+c<0；
且对称轴为直线x=3，所以x＜3时，y的值随x的（3）因为抛物线y= （x-3）2-3开口向上，且对称轴为直线x=3，所以x＜3时，y的值随x的值增大而减小.
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出下列结论：①abc>0；
值增大而减小. ③4a-2b+c<0；
用公式法求抛物线y=x2+x+1的顶点坐标. （）
ax2+bx+c=0有两个不相等
（2）请指出抛物线y=a（x-h）2+k的开口方向、对称轴和顶点坐标.
解：（1）设直线AB对应的函数表达式为y=kx+b，把A，B两点坐标代入，得b=3，3k+b=0，解得b=3，k=-1.
解：因为对称轴是直线x=-1,所以
（抛例物3线）y=下x列2-6是x+抛5物可线以y由=-抛2x物2-线3xy+=1x的2经大过致怎图样象的是平移得到？
m=-1
B.
已用知公二式次法函求数抛物y=线axy2=+xb2x++xc+（1的a≠顶0）点的坐图标象. 如图所示，给出下列结论：①abc>0；
（已1知）将△抛A物O线C的y=面a（积x；-h）2+k先向左平移2个单位长度，再向上平移3个单位长度得到抛物线y= （x-1）2.
解：y＝x2-6x+5=（x-3）2-4，由抛物线y＝x2先向右平移3个单位长度，再向下平移4个单位长度得到.
二级能力提升练
13. 当m= -2 时，抛物线y=（m-1）
+9的开
口向下，对称轴是 y轴（或直线x=0） .在对