静电场中的电介质
合集下载
静电场中的电介质

r0
在国际单位制中,ε的单位为法拉每米(F·m–1)。
3.电介质的击穿
如果外电场足够大,电介质分子就会摆脱分子的束缚成为 自由电子,电介质的绝缘性被破坏而成为导体,这个过程称为 电介质的击穿,这个外电场的场强称为击穿场强。下表所示为 几种电介质的相对电容率和击穿场强。
1.3 电介质中的高斯定理
1.2 电介质的极化
电介质的极化是指在外电场作用下电介质表面产生极化电 荷的现象。其中,极化电荷又称束缚电荷,是指在外电场中, 均匀介质内部各处仍成电中性,但在介质表面出现的不能离开 电介质到其他带电体,也不能在电介质内部自由移动的电荷。
1.电介质极化的机理
由于组成电介质的分子结构不同,所以在外电场中极化 的微观机理也有所不同。对于无极分子,在外电场E0的作用 下,正、负电荷的中心被电场力拉开,使得正、负电荷中心 产生相对位移(这种极化称为位移极化),形成电偶极子。
由于受到外电场E0的作用,这些电偶极子的电偶极矩P 的方向将转向与外电场E0的方向一致。这样,在垂直E0方向 的介质两端表面就会出现正负电荷,如下图所示。
无外点场时,无极分子 正负电荷中心重合
外电场作用下,正负电荷 中心分离,形成电偶极子
电介质在垂直于外电场的 两端表面出现极化电荷
对于有极分子,无外电场时,虽然每个分子都有一定的电 偶极矩,但由于分子作无规则的热运动,所以各电偶极子的电 偶极矩的取向是杂乱无章的,对外不呈现出电性,如左图所示 但有外电场E0时,每个分子都受到一个力偶矩的作用。在此力 偶矩的作用下,有极分子的电偶极矩方向将转向与外电场基本 一致的方向,这种极化称为转向极化,其结果是电介质的两端 出现等量异号的电荷,如中图和右图所示。
物理学
静电场中的电介质
在国际单位制中,ε的单位为法拉每米(F·m–1)。
3.电介质的击穿
如果外电场足够大,电介质分子就会摆脱分子的束缚成为 自由电子,电介质的绝缘性被破坏而成为导体,这个过程称为 电介质的击穿,这个外电场的场强称为击穿场强。下表所示为 几种电介质的相对电容率和击穿场强。
1.3 电介质中的高斯定理
1.2 电介质的极化
电介质的极化是指在外电场作用下电介质表面产生极化电 荷的现象。其中,极化电荷又称束缚电荷,是指在外电场中, 均匀介质内部各处仍成电中性,但在介质表面出现的不能离开 电介质到其他带电体,也不能在电介质内部自由移动的电荷。
1.电介质极化的机理
由于组成电介质的分子结构不同,所以在外电场中极化 的微观机理也有所不同。对于无极分子,在外电场E0的作用 下,正、负电荷的中心被电场力拉开,使得正、负电荷中心 产生相对位移(这种极化称为位移极化),形成电偶极子。
由于受到外电场E0的作用,这些电偶极子的电偶极矩P 的方向将转向与外电场E0的方向一致。这样,在垂直E0方向 的介质两端表面就会出现正负电荷,如下图所示。
无外点场时,无极分子 正负电荷中心重合
外电场作用下,正负电荷 中心分离,形成电偶极子
电介质在垂直于外电场的 两端表面出现极化电荷
对于有极分子,无外电场时,虽然每个分子都有一定的电 偶极矩,但由于分子作无规则的热运动,所以各电偶极子的电 偶极矩的取向是杂乱无章的,对外不呈现出电性,如左图所示 但有外电场E0时,每个分子都受到一个力偶矩的作用。在此力 偶矩的作用下,有极分子的电偶极矩方向将转向与外电场基本 一致的方向,这种极化称为转向极化,其结果是电介质的两端 出现等量异号的电荷,如中图和右图所示。
物理学
静电场中的电介质
23. 静电场中的电介质

1 E dS 0S1 S2
S
P dS P dS PS2 S 2
S S2
0
1 1 E dS 0 S1
S
S
0 E P dS q0
0
0
四、电极化强度与极化电荷的关系 在均匀介质中, 极化电荷只出现在介质表面 或两种介质的分界面上。 设一均匀电介质薄片(S、l)置于电场(E) 中,表面将出现极化电荷。
p ql p ql P P V Sl 一般情形: P e P cos P n n
的q’为多少?
介质被均匀极化,介质内无净极化电荷。
介质内的场强: E E0 E
极化电荷产生的附加电场 实验表明: 对于各向同性的电介质,在E0不太大的 情况下,有:
P ( r 1) 0 E
上式表明P,E的简单比例关系,将比例系数写 成稍复杂的形式,是为了以后相对更重要的式子 表达方便。
en为薄片表面外法向单位矢量
例:
n
θ - - - - - + + + + +
- - - - - - + + + + +P +
P
思考:将介质从中分开,能否分离正、负
极化电荷?
§7-9 有电介质时的高斯定理 电位移
1 真空中的高斯定理: E dS qi
S
0
1 介质中的高斯定理: E dS
极化面电荷: P ·en
介质内表面(r =R1)处:
( r 1) q0 er P 0 ( r 1) E 2 4r r
1 P r R
大学物理 电介质

电介质的种类和状态的不同而不同
χ = εr − 1 电极化率
令 ε r = (1 + χ e ) 为相对介电常量(相对电容率)
ε = ε 0ε r ~电介质的电容率
5
四、极化电荷与自由电荷的关系
E
=
E0
−
E'=
E0 εr
E'=
εr − 1 εr
E0
d
σ'=
εr − εr
1
σ
0
Q' =
εr − εr
即 D⇒ E ⇒ P ⇒σ′ ⇒q′
9
物理意义
E
单位试验电荷 的受力
单位体积内的 P 电偶极矩的矢
量和 无物理意义, D 只有一个数学 上的定义 D = ε0E + P
= ε 0ε r E
特点
真空中关于电场的讨论都 适用于电介质:高斯定律、 电势的定义、环路定理等
各向同性均匀电介质中
P = ε0χe E ,表面束缚电荷 σ ′ = P ⋅ n ,电介质中P ≠ 0
D = (1+ χ )ε0E
ε r = (1 + χ )
ε = ε rε 0
相对电容率或相对介电常量
电容率或介电常量
D=ε0ε r E = εE
•注意: D 是辅助矢量,描写电场性质的物理量仍为 E ,V
对于真空 χ e = 0 ε r = 1 ε = ε 0 则 D = ε 0 E
3、有电介质时的高斯定理的应用
在垂直于电场方向的两个表面上,将产生极化电荷。
4.极化电荷
在外电场中,均匀介质内部各处仍呈电中性,但在介质表 面要出现电荷,这种电荷不能离开电介质到其它带电体,也不 能在电介质内部自由移动。我们称它为束缚电荷或极化电荷。 它不象导体中的自由电荷能用传导方法将其引走。
χ = εr − 1 电极化率
令 ε r = (1 + χ e ) 为相对介电常量(相对电容率)
ε = ε 0ε r ~电介质的电容率
5
四、极化电荷与自由电荷的关系
E
=
E0
−
E'=
E0 εr
E'=
εr − 1 εr
E0
d
σ'=
εr − εr
1
σ
0
Q' =
εr − εr
即 D⇒ E ⇒ P ⇒σ′ ⇒q′
9
物理意义
E
单位试验电荷 的受力
单位体积内的 P 电偶极矩的矢
量和 无物理意义, D 只有一个数学 上的定义 D = ε0E + P
= ε 0ε r E
特点
真空中关于电场的讨论都 适用于电介质:高斯定律、 电势的定义、环路定理等
各向同性均匀电介质中
P = ε0χe E ,表面束缚电荷 σ ′ = P ⋅ n ,电介质中P ≠ 0
D = (1+ χ )ε0E
ε r = (1 + χ )
ε = ε rε 0
相对电容率或相对介电常量
电容率或介电常量
D=ε0ε r E = εE
•注意: D 是辅助矢量,描写电场性质的物理量仍为 E ,V
对于真空 χ e = 0 ε r = 1 ε = ε 0 则 D = ε 0 E
3、有电介质时的高斯定理的应用
在垂直于电场方向的两个表面上,将产生极化电荷。
4.极化电荷
在外电场中,均匀介质内部各处仍呈电中性,但在介质表 面要出现电荷,这种电荷不能离开电介质到其它带电体,也不 能在电介质内部自由移动。我们称它为束缚电荷或极化电荷。 它不象导体中的自由电荷能用传导方法将其引走。
静电场中的电介质

由定义
C 与 d S 0 有关
S
C ; d C
插入介质
0S q C u A uB d
C
0 r S
d
C
(2)球形电容器 已知
设+q、-q 场强分布: E 电势差:
RB
RA RB
q
r q
B A
RA
q 4 0 r 2
q q
RB
1 1 u A uB dr ( ) 2 4 0 RA RB R A 4 0 r
f
pe
pe
3;
+ E + 外 + + + +
在外电场中有极分子的固有电 矩要受到一个力矩作用,电矩方 向趋于外电场方向。但由于热运 动的存在,不会完全一致。
有极分子的取向极化!
+ E + 外 + + + +
+
两端面出现极化电荷层
电介质被极化的宏观效果
①外电场越强,极化电荷越多; ②电介质不均匀,则不仅在电介质表面会出现极 化电荷,在电介质内部也会出现极化电荷; ③对均匀电介质,在其内部任一小区域内,正负 电荷数量仍然相等,因而仍然表现出电中性。
二、电极化强度和极化电荷
单位体积内分子电偶极矩的矢量和 P
1、电极化强度(矢量)
pi
V
物理意义:描述了电介质极化强弱,反映了电介质 内分子电偶极矩排列的有序或无序程度。
在各向同性的电介质中,P 0 E
称为电介质的电极化率,它取决于电介质的性质。
2、极化电荷和自由电荷 极化电荷
E E0
++++++ r + ------- C
C 与 d S 0 有关
S
C ; d C
插入介质
0S q C u A uB d
C
0 r S
d
C
(2)球形电容器 已知
设+q、-q 场强分布: E 电势差:
RB
RA RB
q
r q
B A
RA
q 4 0 r 2
q q
RB
1 1 u A uB dr ( ) 2 4 0 RA RB R A 4 0 r
f
pe
pe
3;
+ E + 外 + + + +
在外电场中有极分子的固有电 矩要受到一个力矩作用,电矩方 向趋于外电场方向。但由于热运 动的存在,不会完全一致。
有极分子的取向极化!
+ E + 外 + + + +
+
两端面出现极化电荷层
电介质被极化的宏观效果
①外电场越强,极化电荷越多; ②电介质不均匀,则不仅在电介质表面会出现极 化电荷,在电介质内部也会出现极化电荷; ③对均匀电介质,在其内部任一小区域内,正负 电荷数量仍然相等,因而仍然表现出电中性。
二、电极化强度和极化电荷
单位体积内分子电偶极矩的矢量和 P
1、电极化强度(矢量)
pi
V
物理意义:描述了电介质极化强弱,反映了电介质 内分子电偶极矩排列的有序或无序程度。
在各向同性的电介质中,P 0 E
称为电介质的电极化率,它取决于电介质的性质。
2、极化电荷和自由电荷 极化电荷
E E0
++++++ r + ------- C
第10章 静电场中的电介质

R2
解:1.场的分布 R1
r <R 0
导体内部
E1 ? 0
P? 0
?0
?r1
?r2
R0
? ? R0< r< R1
?r1 内
? E2 ?
Q
4??0?r1r 2
r^
? P2 ?
?0
?r1 ? 1
Q
4??0?r1r 2
^r
R1< r< R2
?r2 内
? E3
?
Q
4??0?r2r 2
^r
? P3 ?
?0
??r
分子中的正负电荷束缚的很紧,介质内部 几乎没有自由电荷。
电介质对电场的影响
实验表明 ,当在真空电场中放入电介质时 ,电场将 会发生变化 .
例: 在已达到静电平衡的两平行带电金属板引 入电介质
?Q
? Q 相对介电常数 ? Q
?Q
U ? U0 /?r ,?r ? 1 E ? E0 / ?r
10.2 电介质及其极化
极化电荷带负电
电极化强度通过任意封闭曲面的通量:
??
?SP ?d S ? ?SP cos? d S ? ?S? ??d S
??
? ? P S
?d
S
?
? qi?
(S内)
例1. 平行板电容器自由电荷面密度为 ó0
? 充满相对介电常数为 r 的均匀各向同
性线性电介质 , 求:板内的电场强度。
解:介质将均匀极化 ,其表面出现束缚电荷
-+
Eo
? p
+
F
F
-
Eo
?
外电场: E0
?
(大学物理ppt)第 4 章 静电场中的电介质

第 4 章
静电场中的电介质
一、电介质对电场的影响 二、电介质的极化 三、电极化强度
四、极化电荷
五、D 的高斯定律
六、电容器和它的电容
七、电容器的能量
一、电介质对电场的影响
电介质也即绝缘体
特点是分子中正负电荷束缚得很紧,内
部几乎没有自由电荷,不导电,但在电场中会
受到电场的影响,反过来也会影响原有电场的
P
pi
V
P np
其中 n 表示电介质单位体积内的分子数。
三、电极化强度
2. 电极化强度与电场的关系
对 各向同性 的电介质,当电场不太强时, 试验表明:
P 0 ( r 1) E 0 E
其中 r 1 叫做电介质的电极化率。
四、极化电荷
1. 面束缚电荷
在介质中取一斜柱,长为 l ,则穿过 dS 面 的总正电荷为
dq qndV qnldScos
而 故 p ql, np P dq PcosdS
-q
e n
l
dS +q
面束缚电荷密度 dq P cos P e n dS
E
四、极化电荷
2. 体束缚电荷
穿过 dS面的总正电荷为 PcosdS P dS dqout 穿过整个封闭面 S 向外的 电荷应为 d qout P dS qout
S S
-q
e n
l
S
dS +q
E
留在封闭面 S 内的体束缚电荷应为 q in - q out P dS
二、电介质的极化 在电介质内部的宏观微小的区域内,正负电
静电场中的电介质
一、电介质对电场的影响 二、电介质的极化 三、电极化强度
四、极化电荷
五、D 的高斯定律
六、电容器和它的电容
七、电容器的能量
一、电介质对电场的影响
电介质也即绝缘体
特点是分子中正负电荷束缚得很紧,内
部几乎没有自由电荷,不导电,但在电场中会
受到电场的影响,反过来也会影响原有电场的
P
pi
V
P np
其中 n 表示电介质单位体积内的分子数。
三、电极化强度
2. 电极化强度与电场的关系
对 各向同性 的电介质,当电场不太强时, 试验表明:
P 0 ( r 1) E 0 E
其中 r 1 叫做电介质的电极化率。
四、极化电荷
1. 面束缚电荷
在介质中取一斜柱,长为 l ,则穿过 dS 面 的总正电荷为
dq qndV qnldScos
而 故 p ql, np P dq PcosdS
-q
e n
l
dS +q
面束缚电荷密度 dq P cos P e n dS
E
四、极化电荷
2. 体束缚电荷
穿过 dS面的总正电荷为 PcosdS P dS dqout 穿过整个封闭面 S 向外的 电荷应为 d qout P dS qout
S S
-q
e n
l
S
dS +q
E
留在封闭面 S 内的体束缚电荷应为 q in - q out P dS
二、电介质的极化 在电介质内部的宏观微小的区域内,正负电
大学物理 4.7 静电场中的电介质
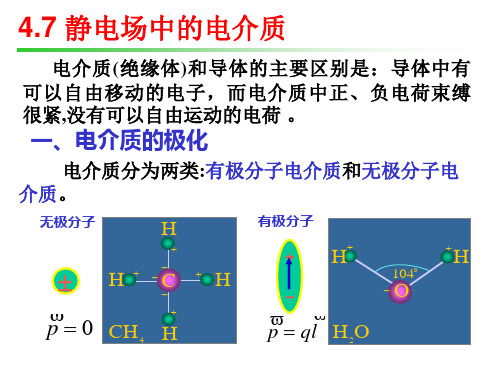
4.7 静电场中的电介质
电介质 ( 绝缘体 ) 和导体的主要区别是:导体中有 可以自由移动的电子,而电介质中正、负电荷束缚 很紧,没有可以自由运动的电荷 。
一、电介质的极化
电介质分为两类:有极分子电介质和无极分子电 介质。
无极分子
H
有极分子
H
C
+
H
H
1040
H
p 0 CH
σ '
E ' E
0
实验ቤተ መጻሕፍቲ ባይዱ明:
E E0 E' E0
σ '
E
一、有介质时的高斯定理
1.极化强度
体积V中分子 电矩的矢量和 i P V 体积V
p ei
实验证明,对于各向同性的电介质:
2
r1
Q0
(r R0 )
( R0 r R1 ) ( R1 r R2 ) ( R2 r )
E D
1
例题
如图金属球半径为R1 、带电量+Q;均匀、各 向同性介质层外半径R2 、相对介电常数 r ;
求: D、E、U
R1
分布 解(1)对称性分析确定E、D沿矢径方向 (2)大小
束缚电荷´
束缚电荷´
(分子) 取向极化
结果:无论是有极分子电介质还是无极分子电介质,
在外电场的作用下,电介质表面附近的电荷会越过介 质表面而在均匀电介质的表面上出现一层束缚(极化) 电荷。这种现象称为电介质的极化。
电介质 ( 绝缘体 ) 和导体的主要区别是:导体中有 可以自由移动的电子,而电介质中正、负电荷束缚 很紧,没有可以自由运动的电荷 。
一、电介质的极化
电介质分为两类:有极分子电介质和无极分子电 介质。
无极分子
H
有极分子
H
C
+
H
H
1040
H
p 0 CH
σ '
E ' E
0
实验ቤተ መጻሕፍቲ ባይዱ明:
E E0 E' E0
σ '
E
一、有介质时的高斯定理
1.极化强度
体积V中分子 电矩的矢量和 i P V 体积V
p ei
实验证明,对于各向同性的电介质:
2
r1
Q0
(r R0 )
( R0 r R1 ) ( R1 r R2 ) ( R2 r )
E D
1
例题
如图金属球半径为R1 、带电量+Q;均匀、各 向同性介质层外半径R2 、相对介电常数 r ;
求: D、E、U
R1
分布 解(1)对称性分析确定E、D沿矢径方向 (2)大小
束缚电荷´
束缚电荷´
(分子) 取向极化
结果:无论是有极分子电介质还是无极分子电介质,
在外电场的作用下,电介质表面附近的电荷会越过介 质表面而在均匀电介质的表面上出现一层束缚(极化) 电荷。这种现象称为电介质的极化。
静电场中电介质(共10张PPT)

自由电荷Q0和介质均呈球对称分
O--
-q
= 讨论: (1) 平板电容器(±Q)中充有均匀介质( r ),求 D与 的关系;
(1)电介质内正负电荷处于束缚状态, 在外电场作用下,束缚电荷只作微观的相对位移
H 自由电荷Q0和介质均呈球对+称分
布, 故 也为球对称分布
+
H+
+q
H O 布, 故 也为球对称分布
2、有极分子的取向极化
有极分子在外场中发生偏转而 产生的极化称为取向极化。
F
- + Eo
+
F
- p Eo
第六页,共10页。
三、静电场中的电介质
小结: (1)电介质极化现象∶在外电场作用下,介质表面 产生极化(束缚)电荷的现象。 (2)不论是有极分子还是无极分子的极化,微观 机理虽然不相同,但在宏观上表现相同。
在外电场的作用下,介质表面产生电荷的2现象称为电介质的极化。
(3)电介质内的电场强度。
(2)、无极分子: + + + + +
-----------
分子的正、负电荷中心在无外场时重
及
与各种因素均有关
合。不存在固有分子电偶极矩。 在外电场的作用下,介质表面产生电荷的现象称为电介质的极化。
+++++++++++
静电场中电介质
第一页,共10页。
电介质对电场的影响
B
+ + + + +
在平板电容器之间插 入一块介质板
E0
-- ---
实验发现:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Er
R3
, U r
q1 q2
R2
曲线
E
q1 q1 R1
1 2 3 4
A
B
U
o R1 R2 R3
r
r
<2>若将球与球壳用导线连接,情况如何?
qA qB内 0 ; qB外 q1 q2
R3
R2 R1
1 2 3 4
q2 q1
E1 E 2 E 3 0 q1 q2 E4 2 40 r4
2 3 4
B
R3
R2
q1 q2
R1
<1> qA q1 qB内 q1 qB外 q1 q2
q1 q1
1 2 3 4
A
B
E1 0 E3 0
E2
4 r
q1
2 0 2
q1 q2 E4 4 0 r42
q1 q1 q1 q2 1 q1 q2 U1 ( ) ; U3 40 R1 R2 R3 40 R3 1 q1 q1 q1 q2 U2 ( ) ; 40 r2 R2 R3 1 1 q1 q2 U4 40 r4
P
pi V
设 分子数密度:n
极化后每个分子的偶极矩: q1 L
P nq1 L
实验规律
P 0 E
空间矢量 函数
介质 总场 极化率
E E0 E
P 0 E
作如图斜圆柱
' q1 dq + + dS q
χ:由介质的性质决定,与E无关。在各
电介质中的高斯定理:
s
D dS
q
s内
0
电位移矢量通过静电场中任意封闭曲面的通量 等于曲面内自由电荷的代数和
电介质中的高斯定理:
注意:
D dS q0
s s内
' q , q 电位移矢量 D 0 E P : 与 均有关 0 s D dS : 穿过闭合曲面的 D 通量仅与 q0 有关.
充介质前
0
300V
0 E 0
D 0
0
5 0 3 1 0 3
D
100 V
1
5 0 3
1 D2 0 3 0 E1 E 2 3 0
4 0 3
充介质后
pi 0
i
出现束缚电荷(面电荷、体电荷)
实例:均匀介质球在均匀外场中的极化
非均匀场, 在介质球内 与外场反向。
在介质球外可能 与外场同向或反 向。在介质球内 削弱外场。
3. 金属导体和电介质比较
金属导体
特征 模型 电介质(绝缘体)
有大量的 自由电子 “电子气” 静电感应
基本无自由电子,正负电荷 只能在分子范围内相对运动
1. 导体内无净电荷(ρ=0),电荷只分布于导体表面.
s
S'
实心导体
s
q S
q
空腔、腔内无电荷 空腔、腔内有电荷
2. 导体表面电荷面密度与表面紧邻处场强成正比.
E n
0
3. 孤立导体σ与表面曲率有关 .
• 有导体存在时的 E , U 分布
求解思路:
静电平衡条件 电荷守恒定律 导体上的 电荷分布
r
20
d
0 U 0 E0 d d 300V 0
充介质后:
0 U0 U E1d d 100V 3 0 3
P1n P1cos P1 0 E1 0 4 ( r 1 ) 0 0 3 0 3
' 1
比较
' P dS dq q内
s
P dS q内
s s
极化强度通过某封闭曲面的通量等于曲面内 极化电荷代数和的负值
二. 电介质中的电场 1. 介质中的高斯定理
静电场高斯定理
1 1 E dS q内
s
自由电荷
0
0
由高斯定理
s
D1 dS
D1
( S 内)
q
0
D1S 10 S
D1 10 ; E1
0 r
10
S
S
S
20
1
'
'
S
D1 10 ; E1
0 r
D2
D1
1 10
r
20
d
同理
D2 20 ; E2
s内
特例: 真空——特别介质
'
q 0 , P 0 , D 0E P 0E
回到
1 E dS
s
0 ( S内 )
q
0
2. 如何求解介质中电场?
' 总场 = 外场 + 极化电荷附加电场 E E 0 E
E0 P q ( , )
0
电量不变:
又: 解得
S S 10 20 0 S 2 2 E1d E2d U
10
5 D1 0 3
1 E1 E 2 0 3 0
20
1 D2 0 3
10
n
P
已知充介质前:
S 20
1
'
'
1 10
解: 〈1〉画出未接地前的电荷分布图.
+
+ + -
+
+
R
-
q -
o d q
+
+
+
腔内壁非均匀分布的负电荷 对外效应等效于:
q
在与 q 同位置处置 q .
+ + - q -
+
〈2〉外壳接地后电荷分布如何变化?
+
+ +
R
-
q -
o d q
+
+
U壳 U地 Uq U内壁 U外壁 0
( q
s内
0
q )
'
1
0
( q0 P dS )
s内 s
极化电荷
( 0 E P ) dS q0
s s内
自由电荷
( 0 E P ) dS q0
s s内
自由电荷
定义:电位移矢量
D 0E P
1 r
介质的相对电容率
式中
D 0 r E E
真空电容率
0 : 0 r :
介质电容率
E
D
D
0 r
' q , q ( 2) 0 分别具有某些对称性 才能选取到恰当高斯面使 D dS 积分能求出.
s
步骤: 对称性分析,选高斯面.
计算 E , U 分布
( 方法同前 )
练习: 若 A 带电 q1 , B 带电 〈1〉图中1,2,3,4 各区域的
q2 ,求: E 和 U 分布,
并画出 E r 和
U r 曲线.
〈2〉若将球与球壳用导线连接,情况如何?
〈3〉若将外球壳接地,情况如何?
R3
R2 R1
q2 q1 1 A
2. 介质中的高斯定理, D矢量.
3. 求解电介质中的的电场.
§ 9.7
静电场中的电介质
一. 电介质的极化及其描述 1.电介质的分类
H
e
+ 无极 - 分子
H
+
pi 0
H
H
+ 有极
c
H 无极分子
电介质
物质结构 中存在着 正负电荷
104
-
pi 0
分子
o
H 有极分子
电介质
2.极化现象
H
H H
H
c
+ + + 无外场
i
+ + + -
-
pi
+ + -
E0
+ +
+ - + E
pi 0
i
无极分子 电介质
pi 0
pi 0
外场中(位移极化)
pi 0
出现束缚电荷和附加电场 E总 E 0 E 0
q1 - q1
B
A
q1 q1 U1 ( ) 4 0 R1 R2 q1 q1 U2 ( ) 4 0 r2 R2 U3 0 U4 0 1
1
[例三] 内半径为 R 的导体球壳原来不带电,在腔 内离球心距离为 d ( d R )处,固定一电量 q的 点电荷,用导线将球壳接地后再撤去地线,求球心 处电势.
不一定与表面垂直
H
104
pi
+
o
H
-
F
pi
-
+
E0
F
E
有极分子 电介质
无外场 pi 0 pi 0
i
外场中(转向极化) pi 0 pi 0
i
出现束缚电荷和附加电场
位移极化和转向极化微观机制不同,宏观效果相同。
统一描述
上讲回顾: 静电场中的导体
