第九章影响线及其应用资料
影响线的应用

1§9-7 影响线的应用9 利用影响线求固定荷载作用下的某量值大小9 确定移动荷载的最不利位置利用影响线计算量值绘制影响线时,考虑的是单位荷载FP=1 的作用。
当若干具体荷载作用于结构时,可根据叠 加原理,利用影响线计算出该内力所受的总影 响,即产生的该内力总值称之为影响量。
2(1)一组集中荷载作用下的影响FP1 FP2 FP3 FPn3y1y2 y3 ynS影响线由FP1产生的S 值等于 FP1 ⋅ y1 由FP2产生的S 值等于 FP2 ⋅ y2 FP1、FP2、…、FPn共同作用下S 的数值为:S = FP1 ⋅ y1 + FP 2 ⋅ y2 + FP 3 ⋅ y3 L FPn ⋅ yn简化计算当若干个荷载作用在影响线某一段直线的 范围内时,可用它们的合力来代替。
FR F FP1 FP2 FP i Pn4αy1 xiy2y yiynS影响线S = FP1 ⋅ y1 + FP 2 ⋅ y2 + FP 3 ⋅ y3 Λ FP n ⋅ yn= ∑ FP i ⋅ yi = ∑ FP i ( xi ⋅ tgR α ) = tg α ∑ FP i xiS=F ⋅y(2)均布荷载作用下的影响q a x qdx b dx y S影响线5在均布荷载作用段上,将微段dx上的荷载qdx看 作一个集中荷载,则它引起的S 的量值为qdx · y。
在ab段均布荷载产生的S 的值为:b b bS = qAa aS =∫ qdx ⋅ y = q ∫ y ⋅ dx = q ∫ dA = qAa6工程中常见的荷载有集中荷载和均布荷载FP1 FP2 q FP3yi 和 A 是代数量y3⊕ y2\nA \ y 1m由叠加原理S = ∑ FP i yi + ∑ q j A ji =1 j =1例:利用影响线求图示梁K截面的弯矩100kN7K100kN 50kN/m↓↓↓↓↓↓ ↓↓↓↓↓↓↓↓↓ ↓↓↓↓↓↓↓↓↓ ↓↓↓↓↓↓30kN/m30kN.m6m3m 3m 3m 4 6 5 46m A1 26m A23m A3 1I.L.MK (m)MK=P1y1+ P2y2 +q1A1+q2(A2- A3)+mtgθ=100×4+100×5+50 × 18+30× 6-30 × 1.5 -30×1/3 =1925kN.m中—活载(普通活载)8车头煤水车车箱中—活载(普通活载)9使用中一活载时,可由图式中任意截取,但不得 变更轴距。
第九章 影响线

1
F
F=1
x
ห้องสมุดไป่ตู้
A
B
FAy
l
图9.3
FAy
l
l
x
(0≤x≤l)
1
F
F
x
A
B
l FBy
FBy的影响线方程: FBy
x
(0≤x≤l)
l
二、剪力的影响线
现在绘制简支梁[图9.4]截面C上剪力FSC的影响线。
仍取A点为坐标原点。
1
b/l
F=1 x
F=F1SC
A
C
B
a
a/l
b
l
FAy
FBy
1
图9.4
当当荷荷载载F=F=1在1在截截面面C以C以右左((CBA段C段))移移动动时时,,取取截截面面C的
左C边右为边研为究隔对离象体,,由由平平衡衡方方程程∑∑YY==00,,得得
FSCFSC FAy FBly l x(xl(a<0≤xx≤<l)a )
由图9.4(b)可见,FSC的影响线分为AC和CB两段, 且两段直线相互平行。FSC的影响线在C点出现突变, 说明当F=1由左侧越过C点移到右侧时,截面C上 的剪力FSC将发生突变。当F=1正好作用于点C时, FSC的影响线无意义。
三、弯矩的影响线
绘制简支梁[图9.4(a)]截面C上弯矩MC的影响线
也应分段考虑。
b
a
ab/l
F=1x F=1
A
C
B
a
b
l
FAy
图9.4
FBy
当当荷荷载载FF==11作作用用于于ACCB段段时时,,取取截截面面CC的的右左边边为为隔研
影响线自编.ppt
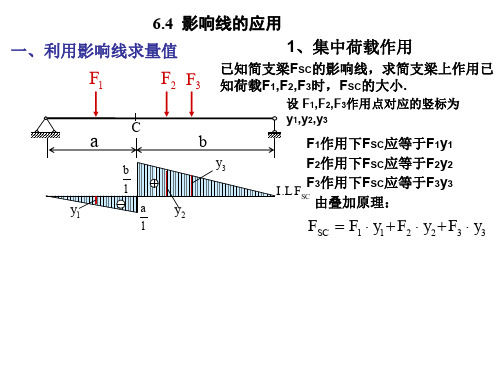
1)车道荷载:由均布荷载和集中荷载组成
a.计ห้องสมุดไป่ตู้图示
Fk qk
b.公路-I级车道荷载:均布荷载标准值为qk=10.5kN/m,集中荷载标准值Fk 按以下规定取值:桥涵计算跨径或等于5m时,Fk=180kN;大于50m时, Fk=360kN;5m~50m时,Fk值采用直线内插求得。 计算剪力效应时,上述集中荷载标准值应乘以1.2的系数。
用试算的方法确定最不利荷载位置。
4、确定最不利荷载位置的步骤:
1)选一个荷载置于影响线的某个顶点; 2)利用判别式,看是否变号;
3)求出每个临界位置对应的S值; 4)比较各S值,得出最大值。
例1:设有一跨度为12m的简支吊车梁,同时承受两台吊车轮压作用, F1=F2=F3=F4=20kN,如图(a),试求跨中截面C的最大弯矩。
则: S FR1 y1 FR2 y2 FR3 y3
设荷载发生一位移∆x,则S将有 一变量∆S,y1、y2、y3变量为 ∆y1、 ∆y2 、∆y3有:
F1 FR1 F2
F3F4 FR2 F5 F6 FR3F7
S S FR1( y1 y1)
FR2 ( y2 y2 ) FR3( y3 y3) y1
其余详见《公路工程技术标准》JTGB01-2003
二、最不利荷载位置
如果荷载移到某一个位置,使某一指定内力达到最大值(+、-), 则此荷载所在位置称为最不利位置。
我们可以利用影响线来确定最不利位置,对比较简单的情况可以直观 地判断最不利位置。
1、可动均布荷载
由 S q
当q大小一定时,要使S取正的最大值,显然只需要q布满对 应于影响线正号面积的范围。
FSC F1 y1 F2 y2 F3 y3
影响线的应用

通过影响线分析,可以评估反应器在不同操作条 件下的稳定性,为化工生产的安全和效率提供保 障。
储罐载荷分析
在储罐设计中,影响线可用于分析储罐在不同液 位和温度条件下的载荷分布,优化储罐的结构设 计。
05
影响线应用的优缺点
优点
预测结构响应
影响线可以用于预测结构在不同载荷下的响应,如位移、应变和应力 等。
无法考虑非线性效应 对于一些非线性结构,如某些复 合材料或超材料,影响线可能无 法准确预测其响应。
06
影响线未来的发展趋势
技术发展
人工智能与机器学习
随着人工智能和机器学习技术的不断进步,影响线分析将更加智能化,能够处理更复杂 的数据和模型,提高预测精度和效率。
大数据与云计算
大数据和云计算技术将为影响线分析提供更强大的数据处理能力和存储能力,实现实时 分析和数据共享。
未来挑战与机遇
数据安全与隐私保护
随着数据应用的广泛,数据安全和隐私保护将成为影 响线分析的重要挑战。
跨学科融合
影响线分析需要与其他学科领域进行融合,以解决更 复杂的问题。
国际化合作
随着全球性问题日益突出,国际化合作将成为影响线 分析的重要机遇。
感谢您的观看
THANKS
结构健康监测
在建筑结构健康监测中,影响线可 用于评估结构的性能变化,及时发 现潜在的安全隐患。
机械行业
机械设计
振动分析
在机械设计中,影响线可用于分析机 械零件的受力分布,优化零件结构和 设计参数。
影响线可用于分析机械设备的振动特 性,优化设备的动态性能和稳定性。
疲劳寿命评估
通过影响线分析,可评估机械零件的 疲劳寿命,提高机械设备的可靠性和 安全性。
《影响线的应用》课件

考虑影响线的约束条件,如材 料强度、结构稳定性等
优化影响线的形状和位置,以 实现最优设计效果
确定影响线的类型和范围 分析影响线的特点和规律 制定优化方案和策略 实施优化措施和调整 评估优化效果和反馈 持续优化和改进
优化效果:提高 了影响线的准确 性和稳定性
优化方法:采用 了先进的优化算 法和模型
感谢您的观看
汇报人:
影响线在桥梁设计中的应用
影响线在桥梁施工中的应用
影响线在桥梁监测中的应用
影响线在桥梁维护中的应用
影响线在房屋 建筑中的应用: 确定建筑物的 稳定性和承载
能力
影响线在房屋 建筑中的作用: 预测建筑物的 变形和破坏情
况
影响线在房屋 建筑中的计算 方法:采用有 限元法、边界 元法等数值计
算方法
影响线在房屋 建筑中的实际 应用:用于设 计、施工、维 护等各个阶段
确定影响线的起 点和终点
确定影响线的方 向和长度
绘制影响线的形 状和轮廓
标注影响线的名 称和参数
影响线是表示结构中某一点受力状态的线 影响线是结构力学中的重要概念,用于分析结构受力情况 影响线图可以帮助我们更好地理解结构的受力情况 影响线图可以帮助我们更好地理解结构的变形情况
影响线在工程中的 应用
数值积分法:通过数值积分求解影响线方程 解析法:通过解析解求解影响线方程 数值模拟法:通过数值模拟求解影响线方程 实验法:通过实验测量求解影响线方程
影响线的优化设计
提高影响线的准确性
降低影响线的计算复杂度
提高影响线的稳定性
优化影响线的可视化效果
确定影响线的类型和范围
采用合适的优化算法,如遗传 算法、模拟退火算法等
影响线的应用
影响线的应用

2. 移动集中荷载
① 单个移动荷载:当只有一个荷载 P 作用时,只要将力 P 移动到该 最值 S 影响线的最大纵标处(即 ymax ) 即可得量值 S 的最大值。
② 一组移动荷载:汽车、吊车等轮压荷载是由一组间距不变的移动集
中荷载组成,根据式 (12-8),可求得 S Pi yi 的最大值,相应的荷载位置
建筑力学
【例12-3】 求图12-15a 所示简支梁 C 截面的最大弯矩。已知简支梁承 受汽车荷载 ,各荷载为汽车轮压。
解:首先作出 MC 的影响线 如图12-15b 所示。车队集中荷 载( P = 100 kN ) 数值最大并且 靠近移动荷载的合力,故取其 为临界荷载。考虑车队左行、 右行时荷载的序列不同,因此 荷载的分布有两种情况。
即是量值 S 的最不利荷载位置。
由此推断:产生最不利荷载位置时,必有一个集中荷载作用于影响 线的顶点处。通常将这一位于影响线顶点的集中荷载称为临界荷载,其 常为荷载密度集中数值最大并且靠近移动荷载的合力的移动荷载。可用 试算法或判别法确定最不利荷载位置,当荷载不太复杂时常用试算法, 即将各移动荷载依次移到影响线的顶点位置上,分别求出量值 S 的大小, 其中产生最大量值 Smax 的荷载位置就是最不利荷载位置。
可利用前面所学方法进行校核。
图 12-13
1.2 确定最不利荷载位置 确定某一量值发生最大或最小值时,移动荷载的位置即为最不利荷载 位置。在活荷载作用下,结构上的某一量值一般都随着位置的变化而变化。 在结构设计时,必须求出各量值的最大值(包括最大正值和最大负值,最 大负值也称最小值),只要所求最值的最不利荷载位置确定,则其最大值 不难求得,下面对常见的情况进行讨论。
② 求出力 P 作用点和均布荷载所对
结构力学 影响线及其应用
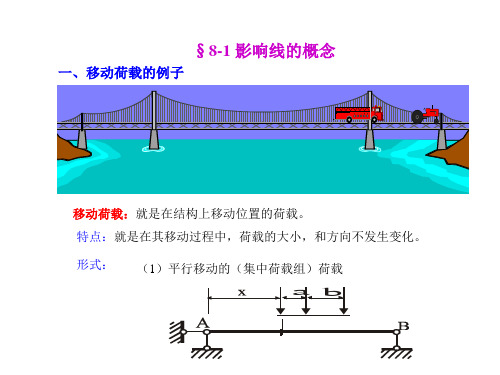
曲线即得内力包络图。
例:绘制简支梁在两台吊车作用下的弯矩包络图和剪力包络图。
P1
A
3.5m
P2 P3
1.5
3.5m
P4
P1 P2 P3 P4 82kN
B
RA
0 1.2 2.4
215
12m 6.0
RB
12m
弯矩包络图(kN· m)
366
465
559 94.3
65.0
574 41.7
25.3
f
b
4
A C D
E P=1
F
B
l=6a
4a/3 +
(a)
+ (b)
M C .IL
N 5 .IL
a
§8-3 用机动法做影响线
用机动法作静定结构内力(反力)影响线的理论基础是刚体系虚功原理。
机动法作内力(反力)影响线步骤如下:
1、去除与所求量值相应的约束,并代以正向的约束力。 2、使所得体系沿约束力的正方向发生相应的单位位移, 由此得到的P =1作用点的位移图即为该量值的影响线。 3、基线以上的竖标取正号,以下取负号。
只有当一个荷载通过影响线 顶点时,S`才有可能变号 令PK通过影响线顶点时,使S`变号,且使S取得极大值。 即:PK位于影响线顶点时;S`=0 左移荷载时:S`>0 右移荷载时:S`<0 用式子表示:
P1 P 2 PK PK 1 PN h 0 a b P1 P 2 PK 1 PK PK 1 PN h 0 a b
同理可以判定P4不是PK
MK max 1610 kN .m
影响线及其应用

FQC F1 y1 F2 y2 F3 y3 Fi yi
i 1
3
图9-12
一般情况下,结构在一组平行荷载F1、F2、 F3、...、Fn共同作用下某量值S的计算式为 n
i 1
S F1 y1 F2 y 2 Fn y n Fi yi
(9-1)
二、均布荷载
第二节 用静力法绘制单跨静定梁影响线
用静力法作单跨静定梁支座反力及内力的影响线,其方法是: 1、先选取坐标系,将单位荷载布置在梁的任意x位置。 2、根据静力平衡方程建立所研究量值与x之间的影响线方程; 3、再由影响线方程绘制量值影响线。 一、支座反力的影响线 图9-2a所示为一简支梁AB,当单位竖向荷载F=1在梁上移动时,试讨论支座反力 FAy、FBy的变化规律。 取A点为支座原点,建立xAy坐标系,将移动荷载F=1暂固定在x位置,由平衡方 程可求出支座反力 lx lx FAy F (0≤x≤l) l l x x (0≤x≤l) F F
下面介绍一种解析法,以求最大弯矩值。在移动荷载作 用下确定最大弯矩,需要知道绝对最大弯矩发生的位置 和发生绝对最大弯矩的最不利荷载位置,即有两个因素 影响简支梁的绝对最大弯矩。由于梁的弯矩图的顶点总 是集中荷载作用处,可以断定Mmax必发生在某集中荷载 作用下,计算时,可在移动荷载中假定某一荷载为临界 荷载Fk,可用求弯矩极值的方法确定产生相对最大 弯矩的截面位置。
则有
S x Fi tan i
i 1
n
图9-10
一、移动集中荷载
3、由前分析可知,使S称为极大值临界位置,必须满足如下 条件:荷载自临界位置向右或向左移动时,△S值均应减 少或为零,即 由此可得:使S值为极大值时应满足 荷载稍向右移 ΣFitanαi≤0 (9-4) 荷载稍向左移 ΣFitanαi ≥0 同理:使S值为极小值时应满足 荷载稍向右移 ΣFitanαi ≥0 (9-5) 荷载稍向左移 ΣFitanαi ≤0 上述二式称为临界荷载位置的判别式。
结构力学BⅡ 08影响线的概念

1第九章 影响线及其应用移动荷载与影响线的概念2目的:解决移动荷载作用下结构的内力计算问题。
内容:1)在移动荷载作用下结构内力变化规律和范围;2)确定内力的最大值及相应的荷载位置——最不利荷载位置。
方法:在各种荷载中抽象出单位荷载(FP =1)。
利用平衡条件建立影响线方程:FP=1xFP=1FR B=x lFP=x (0l≤x≤l)lx = l , l , 3l , l4 24y1FRB = 0.25, 0.5, 0.75, 10.25 0.5FRB的影响线(I . L)-Influence LineFP1y20.75 FP23FR B1.0影响线的应用例:FRB = FP1 ⋅ y1 + FP2 ⋅ y2lFR B定义:当单位荷载(FP=1)在结构上移动时,表示结构某一量值变化规律的图线,称为该量值的影响线。
定义:当单位荷载(FP=1)在结构上移动时,表示结构某一量 4 值变化规律的图线,称为该量值的影响线。
FP=1FP=1DFRBy=FRB1+yDxFRB影响线影响线基线5在绘影响线时,反映FP=1的作用范围, 垂直于FP=1的直线称为基线。
通常规定其量值为正值的竖标画在基线的上 方,反之,画在基线的下方,影响线要标明符号。
I . L. FRB1基线无论是研究结构在移动荷载作用下的内力变化规律或最 6 不利荷载位置,内力影响线都是最基本的工具。
影响线有两种画法;静力法和机动法。
xAF RA1FP=1 l静力法作静定梁的影响线B (1)FRA∑MB = 0FFRA ⋅l −1⋅(l − x) = 0RBFR A=l− lx,(0 ≤ x ≤ l)I.L.FRA (2)FRB∑MA =01FR B=x lP=x l(0≤x≤l)I.L.FRB作简支梁C截面的弯矩影响线、剪力影响线 7FP=1AxCBabl正负号规定:支反力以向上为正;弯矩以梁的下侧纤 维受拉为正;剪力以沿截面产生顺时针转动方向为正FP=1Ax FAy aMC MCBFQC FQC b FBy作I . L . MCxFP=1Ca lbMC C FQCb当FP=1在C之左移动 8由 ∑MC = 0,MC = FRB ⋅ b = x ⋅ b (0 ≤ x ≤ a) lB左直线方程 FRB当FP=1在C之右移动 9xFP=1Cal由 ∑ MC = 0,AFRA aCMCFQC.MC = FRA ⋅ a = l − x ⋅a (a ≤ x ≤ l) l右直线方程绘出I . L . MC左直线方程10FP=1aClMC = FRB ⋅ b = x ⋅b l (0 ≤ x ≤ a)右直线方程MC = FRA ⋅ aaab/l左直线b右直线+= l − x ⋅a l(a ≤ x ≤ l)I . L . MC简支梁C截面的剪力影响线11xFP=1Ca当FP=1在C之左移动由 ∑ Fy = 0,lMC C FQCFQC=−FRB=−x lB(0 ≤ x ≤ a)FRB 左直线方程当FP=1在C之右移动 12xFP=1C由 ∑ Fy = 0 ,a lA FRAC MC FQCFQC=FRA=l− lx(a ≤ x ≤ l)右直线方程绘出I . L . FQCFP=1aCl13左直线方程FQC=−FRB=−x l(0 ≤ x ≤ a)1 左直线I . L . FQC右直线方程b/l右直线+ -FQC=FRA=l− lx(a ≤ x ≤ l)a/l1内力影响线与内力图的比较14FP=1FPA lBabbll1FPbalabalI . L . FQC1bI . L . MClFP aFQlMFPab影响线内力图 l荷载大小 荷载性质FP=1 移动实际 固定横座标表示荷载位置表示截面位置纵座标 表示某一截面内力变化规律 表示全部截面内力分布规律悬臂梁的影响线15求MC 、FQC 、 MA、FQA的影响线FP=1悬臂梁MC 、FQC的影响线16FP=1当FP=1在AC段移动时:左直线MC = 0 FQC = 0当FP=1在CB段移动时:MCxFP=1x右直线FQC MC =- x FQC = 1悬臂梁MC 、FQC的影响线171左直线-+右直线I . L . MC bI . L . FQC悬臂梁MA 、FQA的影响线18-I . L . MA l1+I . L . FQA。
第9章 影响线及其应用

第一节影响线概念一般工程结构除了承受恒载外,还将受到活载的作用。
吊车梁要承受吊车荷载(图9-1),桥梁要承受汽车、火车荷载等。
在进行结构设计时,需要算出结构在恒载和活载共同作用下各量值的最大值。
就需要研究活载作用下结构各量值的变化规律,以便找出它们的最大值。
图9-1结构在活载作用下的计算,从原理上讲与前述静力计算无异,只是荷载位置不是固定的。
显然,要求出活载作用下某一量值的最大值,必须先确定产生这种最大值的荷载位置。
这一荷载位置称为该量值的最不利荷载位置。
在寻求最不利荷载位置时,由于结构上各量值的变化规律并不相同,因此只能逐一考虑。
例如:(图9-2a)所示的简支梁,当有一汽车自左向右移动时,各截面的内力和支座反力等都将随荷载的移动而变化(图9-2b)。
其中,左支座反力FAy是逐渐减小的;相反,右支座反力FBy 的变化却是逐渐增大的。
可见FAy和FBy的变化规律是不同的,因而它们的最不利荷载位置也是不同的。
图9-2在实际工程中,活载又可分为移动活载和可动活载两类。
汽车荷载吊车荷载都属移动荷载,而人群、风、雪等活载则属可动活荷载。
=1移动为了清晰和直观起见,最好把量值随FP而变化的规律用函数图形表示出来,这种图形称为影响线。
它的定义如下:当一个方向不变的单位荷载沿一结构移动时,表示某指定截面的某一量值变化规律的函数图形,称为该量值的影响线。
图9-3a 所示的简支梁,其支座A 的反力F Ay 的影响线(图9-3b)的竖标分别表示F P =1作用于A 、C 、…、B 各点时,反力F Ay 的大小。
显然,F Ay 的影响线只能表示F P =1在梁上移动时F Ay 的变化规律。
如果要表示F By 或其它量值的变化规律,则需另行作出F By 的影响线或其它相应量值的影 、 、 、 B Ay C Ay A Ay F F F F P =14l 4l 4l 4l F Ay F By E A B C D 1=A Ay F 43=C Ay F 21=D Ay F 41=E Ay F 0=B AyF F Ay 影响线(a)(b)图9-3影响线是研究活载作用下结构计算的基本工具。
影响线

0 0 , FQ 为代梁相应截面的剪力。借助代梁内力影响线同样可求桁架的轴力影响线。 FNy = ±FQ
,其中 h 为桁架高,M 0 为代梁弯矩。桁架斜杆轴力的竖向分量可表示为
*利用机动法绘制移动荷载在单位移动力偶 m=1 作用下的影响线: STEP1.撤去与 Z 相应的约束,代以正向未知力 Z,使结构成为具有一个自由度的机构; STEP2.给体系以刚体运动的虚位移,使沿 Z 正方向产生单位位移δZ = 1。形成虚位移图及荷载行走线的δP 图。 � (x) = −δP (x)。由δP 图画出影响线。 STEP3.根据刚体系虚位移原理,得Z 此处δP 是与广义单位力相应的虚位移,与竖向单位力FP = 1相应的δP 图是指荷载行走线的竖向位移图,与单位移动力 偶 m=1 相应的δP 图是指力偶行走线的角位移图(即位移图的斜率)。 注:静定结构在移动的单位力偶作用下内力和反力影响线在各段内影响系数为常数。这是因为力偶在一个几何不变体 系(视作刚片)内部任意移动不会改变该体系静定的外部约束力,而静定结构正是由这种体系所组成。 (3)使用机动法作影响线时的注意事项: 1°保留未被撤除的约束及其作用; 2°准确掌握机构运动的几何特征,例如滑动铰两侧的杆件必须保持平行; 3°δP 图是沿单位荷载方向的虚位移分量图。遇到斜梁或者间接荷载时要特别注意。例如荷载作用于短梁并通过结点传 到主梁时,δP 图不是主梁的虚位移图,而是相应短梁(即荷载作用点)的虚位移图。
dyi − 集中力偶Mi 作用点处影响线切线的斜率,正负按切线斜率的正负确定。 dxi
Ai − 均布荷载qi 分布范围内影响线面积的代数和,q(x)以向下为正, A 以在 x 轴上方为正;
yi − 与集中力FPi 相应的影响线的竖标,FP 以向下为正, yi 以在 x 轴上方为正; [ x1 , x2 ] − 与qi (x)相应的杆段;
lv_9渐进法及超静定结构影响线解析

第九章 渐进法及 超静定结构影响线
2019年4月6日4时45分 By Lvyanping 1
9-1 渐近法概述
1、结构力学的渐近法
不建立方程式,直接逼近真实受力状态。
力学建立方程,数学渐近解
本章讲解第二种方法,其突出的优点是每一步都有明确 的物理意义。
2、不建立方程组的渐近解法有:
传递
50 50 → 25 16.7 ← 33.3 7.2 ← 14.3 10.7 → 5.4 -3.6 - 3.6 → 1.8 -2.7 ← -5.4 1.3 ← 2.6 1.9 → 1 - 0.6 → -0.3 0.5 -0.5 ← 0.3 100 100 40.3
计算单刚结点无侧移结构的解是精确的。
2019年4月6日4时45分 By Lvyanping 8
例1. 作图示连续梁弯矩图。 167.2
(1)固定B结点 MAB=
M图(kN· m) 115.7 200kN 60 20kN/m MBA= 150 kN m 2 90 20 6 300 90kN m MBC= EI EI C B 8 A 150 -90 -150 MB= MBA+ MBC= 60 kN m 3m 6m 3m (2)放松B,即加-60分配 + -60 设i =EI/l 计算转动刚度: 0.571 0.429 SBA=4i SBC=3i A -17.2 4i -34.3 B -25.7 0 C 分配系数: BA 4i 3i 0.571 0.571 A -150 -17.2 -167.2 0.429 150 B -90 -34.3 -25.7 115.7 -115.7 C 分配力矩: 0 0
分配传递 -20.8 -4.2
教09-影响线及应用

第九章影响线及应用§9-1 影响线的概念在以前各章中,我们讨论了结构在恒载作用下的计算。
这类荷载不仅在大小和方向上不变,而且它们的作用点在结构上的位置也固定不动,故结构的反力和各截面的内力是不变的。
但是,一般工程结构除了承受恒载外,还将受到移动荷载的作用,例如桥梁要承受火车,汽车等荷载,工业厂房中的吊车梁要承受吊车荷载(图9-1,a、b)。
这些荷载的作用点在结构上是不断移动的,因而结构的反力和各截面的内力也将随荷载位置的移动而变化。
图9-1图9-1,c为吊车梁的计算简图,P表示吊车最大轮压。
作用于吊车梁的这些轮压就构成了一个平行移动的荷载系统(移动荷载),它们的特点是:当吊车移动时,各轮压的大小、方向以及轮压间的距离均保持不变。
现考察一下该移动荷载对结构的影响。
当吊车自左向右移动时,左支座反力R A将逐渐减小,而右支座反力R B则不断增大。
相应地,梁上各截面的弯矩和剪力也将随荷载位置的移动而变化。
本章的主要内容,就是要研究结构上各量值(反力、内力等)随荷载移动而变化的规律。
由于结构上各量值变化情况各不相同,因此在研究移动荷载对结构的影响时,对各个反力和内力的变化情况只能逐一来考虑。
在进行结构设计时,必须求出各个量值的最大值。
显然,要求出某一量值的最大值,就必须先确定产生这种最大值的荷载位置。
这一荷载位置称为该量值的最不利荷载位置。
在实际工程中所遇到的移动荷载通常是间距不变的平行荷载或均布荷载。
为简便起见,我们先研究一个竖向集中荷载P=1在结构上移动时所产生的影响,然后根据叠加原理再进一步研究各种移动荷载对结构产生的影响。
在研究单位移动荷(P=1)所产生的影响时,常把所考虑的某一量值随荷载位置移动而变化的规律用图形表示出来,这种图形称为该量值的影响线。
现以荷载P=1在简支梁上移动时(图9-2,a )对支座反力R A 的影响为例,说明影响线的概念。
要知道单位荷载在梁上移动时R A 的变化情况,可把P=1依次作用于梁上各个位置,并逐一算出相应的R A 值,然后用图形表示出R A 的变化规律。
影响线及影响面

第9章影响线及影响面§9.1绪论结构承受移动荷载(方向、大小不变,仅作用位置变化的荷载)作用时,其反力、内力以及位移等量值均随荷载作用位置的变化而变化。
对于线弹性结构,由于叠加原理成立,只要研究在最简单的单位移动荷载的作用下,结构的反力、内力或位移的变化规律即可。
结构反力(或内力、位移)随荷载作用位置变化的函数关系式,被称为反力(或内力、位移)影响系数方程,对应的函数图形则称为反力(或内力、位移)影响线(英文Influence Line,缩写为IL)。
正确的影响线应具有正确的外形、必要的控制点纵坐标(竖标)值和正负号。
由于内力图(如梁的弯矩图)也是内力方程(表达内力与截面位置的函数关系)所对应的图形,初学者容易与内力影响线混淆(如图9.1.1)。
应明确,内力图是反映在实际固定荷载下所有截面内力的分布规律,横坐标是截面位置,纵坐标是该截面的内力值,其量纲是力的量纲;而影响线只表达在单位移动荷载下某一关心截面内力的变化规律,横坐标是外力移动作用的位置,纵坐标是关心截面关心内力值,其量纲是内力量纲与移动荷载量纲之比。
静定结构反力和内力影响线为直线形或折线形,位移影响线则为曲线形,从而超静定结构各类影响线(除静定部分和间接荷载作用外)均为曲线形。
影响线的用途很广,凡设计各种桥梁、吊车梁等一切由活荷载作用的结构都要应用它。
影响线可用于确定移动荷载作用下结构的最不利荷载位置及其对应的最大量值,也用来计算简支梁的绝对最大弯矩、绘制包络图。
此外,影响线还可用以求结构某一截面在复杂的固定荷载作用下的内力、位移等量值。
但受叠加原理限制,只能近似考虑非线性的Ⅱ阶效应。
随着大型复杂桥梁的设计建造,使得结构分析不能仅采用单纯的梁单元模型,而必须分析二维的内力影响面。
影响线和影响面的分析可以采用静力法,但更多地采用机动法,在实际工程中机动法比静力法方便且效率高。
图9.1.1 简支梁内力图与影响线§9.2 静力法与机动法绘制影响线有两种基本方法:静力法和机动法。
长沙理工大学结构力学考试题库及详细答案(适合本科期末和考研)影响线
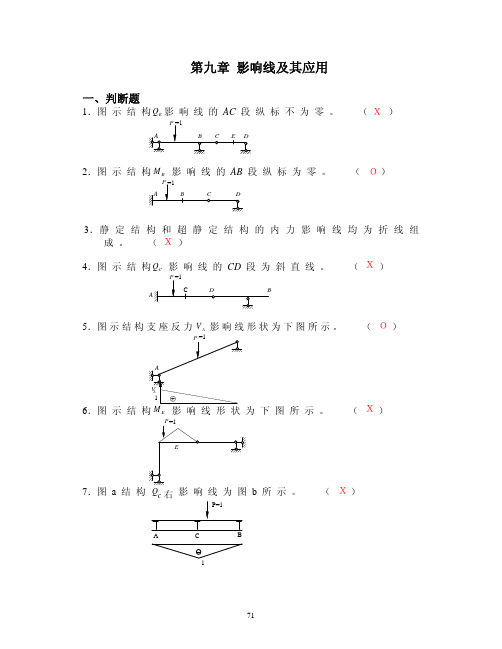
第九章 影响线及其应用一、判断题1.图 示 结 构影 响 线 的 AC 段 纵 标 不 为 零 。
( )Q E2.图 示 结 构 影 响 线 的 AB 段 纵 标 为 零 。
( )M B3.静 定 结 构 和 超 静 定 结 构 的 内 力 影 响 线 均 为 折 线 组成 。
( )4.图 示 结 构 影 响 线 的 CD 段 为 斜 直 线 。
( )Q C5.图 示 结 构 支 座 反 力 V 影 响 线 形 状 为 下 图 所 示 。
( )A 6.图 示 结 构 影 响 线 形 状 为 下 图 所 示 。
( )M E7.图 a 结 构右所示 。
( )c Q A C 1XOXXOXX二、选择题8.图 示 结 构 影 响 线 ( P = 1 在 BE 移 动 ) BC 、CD 段 纵 标为 :( )c Q A. BC 、CD 均 不 为 零 ; B. BC 、CD 均 为 零 ;C. BC 为 零, CD 不 为 零 ;D. BC 不 为 零,CD 为 零 。
9.图 示 结 构 影 响 线 ,其 中 ACD 部 分 为 :( )Q C A. AC 不 为 零 ,CD 为 斜 线 ; B. AC 为 零 ,CD 为 水 平 线 ; C. AC 为 零 ,CD 为 斜 线 ; D. AC 为 零 ,CD 为 零 。
10.单 位 荷 载 作 用 在 简 支 结 间 梁 上 , 通 过 结 点 传 递 的 主梁 影 响 线 , 在 各 结 点 之 间 ( ):A. 部 分 为 直 线 , 部 分 为 曲 线 ;B. 均 为 曲 线 ;C. 均 为 直 线 ;D. 竖 标 为 零 。
11.图 示 结 构 ,M 影 响 线 (下 侧 受 拉 为 正)D 处 的 纵 标 为 :( )A A . 0 ;B . l ;C . - l ; D. -2.236l /2 。
CBCC22l/212.图示结构影响线(P = 1在BE移动,右侧受拉为正)B、D 两点纵标(单位m)为:()MAA.4 ,4 ;B. B.-4 , -4 ;C.0 , -4;D.D. 0 , 4。
第九章 影响线

结构力学
第9章 影响线
结构力学
第9章 影响线
§8-1 概述 计算超静定结构,不论采用力法或位移法,均要组成和解算 典型方程,当未知量较多时,其工作量非常大。为了寻求较简捷 的计算方法,自上世纪三十年代以来,又陆续出现了各种渐进法 ,力矩分配法就是其一。 渐进法的共同特点是,避免了组成和解算典型方程,而以逐 次渐进的方法来计算杆端弯矩,其结果的精度随计算轮次的增加 而提高,最后收敛于精确解。 这些方法的概念生动形象,每轮计算的程序均相同,易于掌 握,适合手算,并可不经过计算结点位移而直接求得杆端弯矩。 在结构设计中被广泛采用。 力矩分配法为克罗斯(H.Cross)于1930年提出,这一方法对连续 梁和无结点线位移刚架的计算尤为方便。
KA
杆端 分配系数
3i 4i = = 0.429 EI=C = = 0.571 ∑ KI = 1 4i + 3i l 4i + 3i 3、固端弯矩(查表) C=0 C =1 2 KA 4、分配、传递 AK KA KA
0.571 0.429 0.125 0 0 0
0.250
S KA + S KB
S KA + S KB
+
B
mK
A K态
F A M AK M KA K M KB M BK B
A M AK
F
固定状态
F FRKF M KA K
F
放松状态(转动状态)
mK = - FRKF
A M AK
C
B M KA K
D
M KB
F
M BK
F
M KB
D
M BK
C
固端弯矩
F F 固定状态下杆端弯矩 KI 杆:M IK、M KI
影响线---1-1

k1
由上式可见:
11
——在X1=1作用下,k点处的相对转角,
X 1 与 P 1 成正比,上式
即为影响线方程。
P1
是恒正常数。 ——在X1=1作用下,FP 点处的竖向位移;
因此,在 X 1 1 作用下, 基本结构产生的绕曲线
由于单位力可以在梁上任意移动, 因此它是整个梁的绕度,是变量。
即为 X
P=1
A
B
CK D E
F
a
a
+
-
1
-
MK影响线
+
QB左影响线
1
+ RF影响线
多跨静定梁任一反力或内力影响线的 一般作法:
①当P=1在量值本身所在的梁段上移动时, 量值的影响线与相应单跨静定梁的相同。
②当P=1在对于量值所在部分来说是基本部 分的梁段上移动时,量值影响线的竖标为零。
③当P=1在对于量值所在部分来说是附属部 分的梁段上移动时,量值影响线为直线。
MB(x)
P1(x) 11
计算P1的公式:
yx
xl x
6EIl
M
A
2l
x
MB l
x
(力矩分配
计
算
1
:
1
影响线方程:
EI
MB(x)
P1(x) 11
结 论:
机动法作影响线的 依据为虚位移原理
静定结构的反力、内力影响线 都是由直线所组成;静定结构 的位移,以及超静定结构的各 种量值的影响线一般为曲线。
影响线的轮廓线。
1
▲比拟关系法作影响线步骤归纳如下:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P33
一、前言
P4
一、移动载荷和影响线的概念。
一、固定荷载:
其荷载大小、方向和作用位置都保持不变的荷载。 已知荷载,就可求出内力图(剪力、弯矩和轴力图)。 最大应力的截面位置和数值---一目了然。
P5
一、移动载荷和影响线的概念。
二. 移动荷载
即结构所承受的荷载作用点在结构 上是移动的。桥梁上承受火车、汽 车和走动的人群等荷载。其荷载大 小和作用方向都保持不变,但作用 位置却不断变化的荷载。
简支梁的影响线
1.反力影响线。
x
FP 1
K
2.剪力影响线。
3.弯矩影响线。
简支梁的影响线
1.反力FRA的影响线。
由静力平衡条件 MB 0
FRAl FP( l x ) 0
FP 1,
FRA
(
l
l
x
)
1
x l
0 x l x=0 x=l
FRA=1 FRA=0
P8
x
FP 1
K
简支梁的影响线
C
B
RA
MC 0 aRA M A M C 0
a xl
a xl
M C aRA M A a x
x=a
x=l
MA RA
VC M C
MC 0
MA=0
VC =a-l
悬臂梁的影响线
(1) 0 x a
MC 0
x=0
x=a
MC=0
MC =0
P24
x FP 1
MA
Aa
C
B
RA
(2) a x l
l
M C aRA M A a x M C a
C
B
x=a
x=l
X
MA=0
MC=-(l-a)
(l a )
悬臂梁的影响线
x FP 1
MA
Aa
C
B
RA
+1
X
RA
a
C
l
B
P25
l
B
a
C
MA
FRB
x l
x=0
x=a
VK =0
VK =-a/l
P10 K
0 xa VK K
Fy 0
简支梁的影响线
3.K截面的剪力影响线。
剪力的正负号规定与 材料力学相同。
Fy 0 FRA Vk 0
x
a x l Vk FRA 1 l
x=a VK =(b/l)
x=l VK =0
P11
x
FP 1
K
a xl
P14
x
FP 1
K
a xl
x=a MK =ab/l
x=l MK =0
A
K MK
MK 0
简支梁的影响线
(1) 0 x a
Mk
bFRB
b
x l
x=0
x=a
MK=0
Mk=ab/l
(2) a x l
Mk
aFRA
a( 1
x l
)
x=a
x=l
MK =ab/l MK =0
P15
x
FP 1
K
MK
+1
X
RA=1 RA=1
RA
a
C
l
B
P18
悬臂梁的影响线
例题9-1求悬臂梁支承反
MA
x FP 1
力影响线RA、MA、Vc、Mc。
由静力平衡条件 MA 0
Aa
C
B
RA
M A FP( x ) 0
FP 1, M A x
MA
l
B
0 x l x=0 x=l
a
C
MA=0 MA=-l
l
X
悬臂梁的影响线
三、影响线
单位移动荷载作用下, 结构上的某特定点反力、 内力和位移等物理量将 随着荷载位置的移动而 变化。
V (Shear) Diagram
X
M
v
X
P66
二、9.1 静力法作影响线。
P7
二、静力法作静定梁的影响线。
绘制影响线的基本方法有两种:静力法和机动法。
静力法: 应用静力平衡条件,求出某量值与荷 载FP=1位置x之间的函数关系式(即影响线方 程)。一般规定,量值为正值时,影响线竖标 绘在基线上方,负值时绘在基线下方。
a
ab / l
X Kb
简支梁的影响线
x
FP 1
K
P16
VK
a
b/l
X
b
a/ l
MK
a
ab / l
X Kb
P17
悬臂梁的影响线
例题9-1求悬臂梁支承反
MA
x FP 1
力影响线RA、MA、Vc、Mc。
由静力平衡条件 Fy 0
Aa
C
B
RA
RA FP 0
FP 1, RA 1
0 x l x=0 x=l
P1
第九章影响线及其应用
土木工程与建筑学院
教师:钟瑜隆
2013年11月4日
1
P2
课程内容
一、前言移动载荷和影响线的概念。 二、9.1 静力法作影响线。 三、9.2 机动法作影响线。 四、9.3 间接荷载下的影响线。 五、9.4 桁架的影响线。 六、9.5 影响线的应用。 七、9.6 超静定结构的影响线。
2.反力FRB的影响线。
同理:静力平衡条件 M A 0
FRBl FP( x ) 0
FP 1,
FRB
x l
0 x l x=0 x=l
FRB=0 FRB=1
P9
x
FP 1
K
简支梁的影响线
3.K截面的剪力影响线。
剪力的正负号规定与 材料力学相同。
Fy 0 FRB Vk 0
0 xa
Vk
x=a VC=1
x=l VC =1
P20
x
FP 1
MA
Aa
C
B
RA
a xl
MA RA
VC
Fy 0
悬臂梁的影响线
(1) 0 x a
VC 0
x=0
x=a
VC =0
VC =0
(2) a x l
VC RA 1
x=a VC=1
x=l VC =1
P21
x FP 1
MA
Aa
C
B
RA
+1
VCAA源自K VKFy 0简支梁的影响线
(1) 0 x a
Vk
FRB
x l
x=0
x=a
VK =0
VK =-a/l
(2) a x l
x Vk FRA 1 l
x=a
x=l
VK=(b/l)
VK =0
P12
x
FP 1
K
VK
a
b/l
X
b
a / l
简支梁的影响线
4.K截面的弯矩影响线。
弯矩的正负号规定与 材料力学相同。
P13 K
MK 0 M K FRB( b ) 0
0 xa
Mk
bFRb
b
x l
x=0
x=a
MK=0
Mk=ab/l
0 xa
MK K
MK 0
简支梁的影响线
4.K截面的弯矩影响线。
弯矩的正负号规定与 材料力学相同。
MK 0 FRA( a ) M k 0
a xl
Mk
aFRA
a( 1
x l
)
a
C
B
悬臂梁的影响线
4.C截面的弯矩影响线。
弯矩的正负号规定与 材料力学相同。
MC 0 MC 0
0 xa
x=0 MC=0
x=a MC =0
P22
x FP 1
MA
Aa
C
B
RA
0 xa
MC
MC 0
悬臂梁的影响线
MA
4.C截面的弯矩影响线。
P23
x
FP 1
弯矩的正负号规定与 材料力学相同。
Aa
4.C截面的剪力影响线。
剪力的正负号规定与 材料力学相同。
Fy 0 VC 0
0 xa
x=0 VC=0
x=a VC =0
P19
x FP 1
MA
Aa
C
B
RA
0 xa
VC
Fy 0
悬臂梁的影响线
4.C截面的剪力影响线。
剪力的正负号规定与 材料力学相同。
Fy 0 RA VC 0
a x l VC RA 1
