薄壁筒的内压的应力计算
第二章内压薄壁圆筒应力分析2精品

a
σm
b a=2b a
σθ
b 1 a 1.4
b
a
椭球
σθ b a=2b
a
椭球
3.2.3、受气体内压的椭球壳(椭圆形封头)
1)椭球壳上各点应力是不相等的,与点的位置(x,y)有关。
在壳体顶点处(x=0,y=b):
m
pa ( a)
2 b
经向应力与环向应力相等,均为拉应力。
在壳体赤道处(x=a,y=0 ):
pD
2
p(Di ) 2
2 508 63.5MPa 28
p
(2)上半封头(半球形)
m
pD
4
2508 31.75MPa 48
Di
(3)下半封头(椭圆,a/b=2)最大应
力出现在顶点:
8/21/2019m
pa ( a)
2 b
2508/ 2 2 63.5MPa 28
m
pR2
2
PD
4
m P R1 R2
PR2
PD
2
3.2.1、受气体内压的圆筒形壳体
推论:①环向应力是经 向应力的2倍,所以环 向承受应力更大,环向 上就要少削弱面积,故 开设椭圆孔时,椭圆孔 之短轴平行于向体轴线, 如图
②
m
PD
4
P
4 /
D
,
锥形壳体内最大薄膜应力是同直径同壁厚圆筒形壳 体的薄膜应力的1/cos a 倍。
锥形壳体的环向应力是经向应力的两倍。
内压薄壁容器的应力

受气体内压旳碟形壳(蝶形封头)
如图所示,是一种受内压旳
碟形封头。它由三部分经线曲率
b
p
b
不同旳壳体所构成:
a
b-b段是半径为R旳球壳;a-c段
M
j
a
c
c
是中径为D旳圆筒;a-b段是连接
r
j0
球顶与圆筒旳摺边,它是过渡半
径为r1旳圆弧。
所以,应分别用薄膜理论求
O D
出各段壳体中旳应力sm和 sq 。
2.基本假设:
(1)小位移假设。壳体受压变形,各 点位移都远不大于壁厚。简化计算。
(2)直法线假设。沿厚度各点法向位 移均相同,即厚度不变。
(3)不挤压假设。沿壁厚各层纤维互 不挤压,即法向应力为零。
11
3.1.3 经向应力计算——区域平衡方程
12
Dd
d
作用在该部分上旳外力(内压)在Z轴方向上旳合力为:
32
sm
p
2d b
sq
p
2d b
a4 x2 (a2 b2 )
a4
x2
(a2
b2
)[2
a4
a4 x2 (a2
b2
] )
应力分布分析:
x=0 ,即椭球壳旳顶点处
sm
sq
pa ( a )
2d b
※两向应力相等,均为拉应力。
x=a, 即椭球壳旳边沿处,
sm
pa
2d
sq
pa
2d
(2
a2 b2
)
※sq 是a/b旳函数。即受椭球壳旳构造影响。
b
2
)]
1 2
31
椭球壳应力计算公式:
sm
化工设备设计基础第7章内压薄壁容器的应力分析

c
1
os
σ
pD 2S
1
cos
五、受气体内压的碟形封头
❖ 碟形封头由三部分经线曲率不同的 壳体组成: ▪ b-b段是半径为R的球壳; ▪ a-c段是半径为r的圆筒; ▪ a-b段是联接球顶与圆筒的摺边, 是过渡半径为r1的圆弧段。
❖ 1. 球顶部分
m
pD 4S
❖ 2. 圆筒部分
m
pD 4S
pD 2S
二、内压圆筒的应力计算公式
1.轴向应力σm的计算公式
介质压力在轴向的合力Pz为:
pz 4Di2p4D2p
圆筒形截面上内力为应力的合
力Nz:
Nz DSm
由平衡条件 Fz 0 得:Pz-Nz=0
→ 4D2pDSm
m
pD 4S
【提示】在计算作用于封头上的总压力Pz时,严格地讲,应采用筒体
内径,但为了使公式简化,此处近似地采用平均直径D。
m
pR2 2S
三、环向应力计算-微体平衡方程
❖ 1.微元体的取法
❖ 三对曲面截取微元体: ▪ 一是壳体的内外表面; ▪ 二是两个相邻的、通过壳体轴线的经线平面; ▪ 三是两个相邻的、与壳体正交的圆锥面。
三、环向应力计算-微体平衡方程
❖ 2.微元体的受力分析
▪ 微单元体的上下面:经向应力σm ;
▪ 内表面:内压p作用;
❖ ⑷ 标准椭圆封头(a/b=2)
❖ 中心位置x=0处:
❖ 赤道位置x=a处:
m
pa 2S
m
pa 2S
pa S
四、受气体内压的锥形壳体
❖ 1.第一曲率半径和第二曲率半径
❖ R1= ,R2=r/cosα
❖ 2.锥壳的薄膜应力公式
薄壁圆筒强度计算公式

薄壁圆筒强度计算公式压力容器相关知识一、压力容器的概念同时满足以下三个条件的为压力容器,否则为常压容器。
1、最高工作压力P :×104Pa ≤P ≤×106Pa ,不包括液体静压力;2、容积V ≥25L ,且P ×V ≥1960×104L Pa;3、介质:为气体,液化气体或最高工作温度高于标准沸点的液体。
二、强度计算公式1、受内压的薄壁圆筒当K=~,压力容器筒体可按薄壁圆筒进行强度计算,认为筒体为二向应力状态,且各受力面应力均匀分布,径向应力σr =0,环向应力σt =PD/4s ,σz = PD/2s ,最大主应力σ1=PD/2s ,根据第一强度理论,筒体壁厚理论计算公式,δ理=PPD -σ][2 考虑实际因素,δ=P PD φ-σ][2+C 式中,δ—圆筒的壁厚(包括壁厚附加量),㎜;D —圆筒内径,㎜;P —设计压力,㎜;[σ] —材料的许用拉应力,值为σs /n ,MPa ;φ—焊缝系数,~;C —壁厚附加量,㎜。
2、受内压P 的厚壁圆筒①K >,压力容器筒体按厚壁容器进行强度计算,筒体处于三向应力状态,且各受力面应力非均匀分布(轴向应力除外)。
径向应力σr =--1(222a b Pa 22rb )环向应力σθ=+-1(222a b Pa 22rb )轴向应力σz =222a b Pa - 式中,a —筒体内半径,㎜;b —筒体外半径,㎜;②承受内压的厚壁圆筒应力最大的危险点在内壁,内壁处三个主应力分别为:σ1=σθ=P K K 1122-+ σ2=σz =P K 112-σ3=σr =-P第一强度理论推导处如下设计公式σ1=P K K 1122-+≤[σ] 由第三强度理论推导出如下设计公式σ1-σ3=P K K 1122-+≤[σ] 由第四强度理论推导出如下设计公式:P K K 132-≤[σ] 式中,K =a/b3、受外压P 的厚壁圆筒径向应力σr =---1(222a b Pb 22ra )环向应力σθ=-+-1(222ab Pb 22ra ) 4、一般形状回转壳体的应力计算经向应力σz =sP 22ρ 环向应力 sP t z =+21ρσρσ 式中,P —内压力,MPa ;ρ1—所求应力点回转体曲面的第一主曲率半径,㎜;(纬)ρ2—所求应力点回转体曲面的第一主曲率半径,㎜;(经)s —壳体壁厚,㎜。
第7章_内压薄壁容器的应力

二、经向应力计算公式-区域平衡方程
❖ 2.静力分析
❖
作用在分离体上外力在轴向的合力Pz为:
pz
4
D2
p
❖ 截面上应力的合力在Z轴上的投影Nz为: Nz m DS sin
❖
平衡条件 Fz 0 得:Pz-Nz=0,即:
4
D2 p
- mDSsin
0
力Nz:
Nz DS m
由平衡条件 Fz 0 得:Pz-Nz=0
→
4
D2
p
DS
m
m
pD 4S
【提示】在计算作用于封头上的总压力Pz时,严格地讲,应采用筒体
内径,但为了使公式简化,此处近似地采用平均直径D。
二、内压圆筒的应力计算公式
2.环向应力σθ的计算公式
分离体的取法:用一通过圆筒轴线的纵截面B-B将圆筒剖开,移走上半
3.内压薄壁圆筒的应力特点在工程中的应用
⑴在圆筒上开设椭圆形孔时,应使椭圆孔之短轴平行于筒体 的轴线,以尽量减小纵截面的削弱程度,从而使环向应力增 加少一些。 ⑵筒体承受内压时,筒壁内的应力与壁厚S成反比,与中径D 成正比。
第二节 回转壳体的薄膜理论
一、基本概念与基本假设 二、经向应力计算公式-区域平衡方程式 三、环向应力计算公式-微体平衡方程式 四、轴对称回转壳体薄膜理论的应用范围
第七章 内压薄壁容器的应力分析
❖ 第一节 ❖ 第二节 ❖ 第三节 ❖ 第四节
内压薄壁圆筒的应力分析 回转壳体的应力分析-薄膜应力理论 薄膜理论的应用 内压圆筒边缘应力的概念
第一节 内压薄壁圆筒的应力分析
一、薄壁容器及其应力特点 二、内压圆筒的应力计算公式
一、薄壁容器及其应力特点
1.薄壁容器与厚壁容器
化工设备机械基础:第三章 内压薄壁容器的应力分析

上一内容 下一内容 回主目录
返回
2020/12/14
第二节 薄膜理论的应用
代入微体平衡方程式及区域平衡方程式并求解得:
m
PD
4
,
PD
4
推论:对相同的内压,球壳的环向应力要比同直径、 同厚度的圆筒壳的环向应力小一半,这是球壳显著的 优点。
三、受气体内压的椭球壳(椭圆形封头)
上一内容 下一内容 回主目录
(一)壳体理论的基本概念 壳体在外载荷作用下,
要引起壳体的弯曲,这种变 形由壳体内的弯曲和中间面 上的拉或压应力共同承担, 求出这些内力或内力矩的理 论称为一般壳体理论或有力 矩理论,比较复杂;
上一内容 下一内容 回主目录
返回
2020/12/14
第一节 薄膜应力理论
但是,对于壳体很薄,壳体具有连续的几何曲面,所 受外载荷连续,边界支承是自由的,壳体内的弯曲应 力与中间面的拉或压应力相比,可以忽略不计, 认为壳体的外载荷只是由中间面的应力来平衡,这种 处理方法,称为薄膜理论或无力矩理论。 1、有力矩理论 2、无力矩理论(应用无力矩理论,要假定壳体完全弹 性,材料具有连续性、均匀性各各向同性,此外,对 于薄壁壳体,通常采用以下三点假设使问题简化) 1)小位移假设 2)直法线假设 3)不挤压假设
上一内容 下一内容 回主目录
返回
2020/12/14
第二节 薄膜理论的应用
一、受气体内压的圆筒形壳体
R1
R2
r
D 2
上一内容 下一内容 回主目录
返回
2020/12/14
第二节 薄膜理论的应用
由区域平衡方程式
m
pR2
2
PD
4
代入微体平衡方程式
内压薄壁圆筒容器讲解

pD
≤[σ]tφ
2
实际应用中还必须考虑以下几种情况:
(2)容器内径
内径Di,受力分析中的D是中面直径,D换算成 Di的形式,可得:
D Di
故有: p(Di ) ≤[σ]tφ 2
实际应用中还必须考虑以下几种情况:
(3)计算压力pc
确定筒体厚度的压力为计算压力pc
pc (Di ) t
(二)内压薄壁圆筒容器的强度条件与壁厚计算
按第一强度理论(最大主应力理论),
应使筒体上的最大应力小于或等于圆筒材 料在设计温度下的许用应力[σ]t。对于内压 圆筒,筒体上最大应力为环向应力σt,即:
t
pD
2
≤[σ]t
实际应用中还必须考虑以下几种情况:
(1)焊缝系数
筒体多由钢板卷焊而成,焊缝可能隐含 缺陷,使焊缝及其附近金属的强度低于钢 板本体强度。考虑这种影响引入焊接接头 系数φ:
2
所以内压薄壁圆筒体的计算厚度δ为:
pc Di
2[ ]t
pc
实际应用中还必须考虑以下几种情况:
(4)腐蚀裕量、钢板负偏差与壁厚
考虑到介质或周围大气对筒壁的腐蚀作用,在
确定钢板所需厚度时,还应在计算厚度基础上,加
上腐蚀裕量c2,得设计壁厚
d
C2
pc Di
2[ 差,将设计厚度加上厚度
职业教育应用化工技术专业教学资源库《化工设备认知与制图》课程
内压薄壁圆筒容器
吉林工业职业技术学院
内压薄壁圆筒容器
(一)内压薄壁圆筒容器的应力
设介质压力p,中间直径D,壁厚为δ。
变形分析:在内压力作用下,直径将会变大,长度 也会增长。 受力分析:经向拉力和环向拉力
(一)内压薄壁圆筒容器的应力
《化工机械基础》第3章 内压薄壁容器的应力
3.1.2 基本概念与基本假设
1. 基本概念
• 回转壳体
——由直线或平 面曲线绕其同 平面内的固定 轴旋转3600而 成的壳体。
4
几个典型回转壳体
5
轴对称——指壳体的几何形状、约束条件和
所受外力都对称于回转轴。
与壳体内外表面等距离的曲面
母线:
6
法线:
经线:
纬线(平形圆):
7
8
2.基本假设:
1
薄膜理论与有矩理论概念:
计算壳壁应力有如下理论: (1)无矩理论,即薄膜理论。 假定壳壁如同薄膜一样,只承 受拉应力和压应力,完全不能承 受弯矩和弯曲应力。壳壁内的应 力即为薄膜应力。
2
(2)有矩理论。壳壁内存在除拉应力或压 应力外,还存在弯曲应力。 在工程实际中,理想的薄壁壳体是不 存在的,因为即使壳壁很薄,壳体中还 会或多或少地存在一些弯曲应力,所以 无矩理论有其近似性和局限性。由于弯 曲应力一般很小,如略去不计,其误差 仍在工程计算的允许范围内,而计算方 法大大简化,所以工程计算中常采用无 矩理论。
D
摺边部分
R 2 r1
2 sin
- r1
32
③ 碟形壳的应力分布
1.b点和c点的R1,R2如何变化? 2.碟形壳与圆筒壳连接点处应力状态如何?
33
3.3 内压容器边缘应力简介
3.3.1 边缘应力概念
压力容器边缘——指“不连续处”,主要是几何不连续及载荷(支 撑)不连续处,以及温度不连续,材料不连续等处。 例如:几何不连续处:
)
pa
※两向应力相等,均为拉应力。
x=a, 即椭球壳的边缘处,
2S pa 2S (2 a b
2 2
第三章内压薄壁容器应力分析
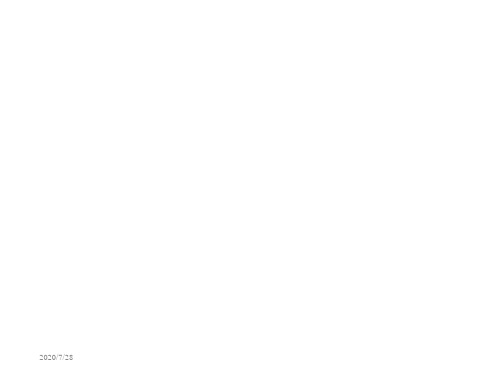
根据力平衡条件:
(πD2p)/4=σmπDδ·sinθ
根据D=2R2sinθ代入上式
σm=pR2/2δ
2020/7/28
σm
σm
M
D
δ
σm
R2 O
P σm θ
M
θ
D
第一节 回转壳体的应力分析
三、经向应力的计算公式—区域平衡
例题3:求三个截面处的经向应力。
解:M点
M
向上的力因内压引起:F=(πD2p)/4 O N
向下的力为应力集中力F=σm·πDδ
根据力平衡条件及D=2R2
H
(πD2p)/4=σm·πDδ
σm=pD/4δ =pR2/2δ
M点、N点、H点情况相同。
直 径 D壁 厚 δ
P
M O
N
H x
为简化分析过程,忽略壳体重量:看某一位置是否具有应力作 用,可以通过观察该位置在该方向上是否起到约束作用。
2020/7/28
纬线
平行圆
2020/7/28
第一节 回转壳体的应力分析
二、概念和基本假设 (一)概念 8、第一曲率半径R1:过该点的经线在该点的曲率半径。
第一曲率半径
M
2020/7/28
O M
M O
N
第一节 回转壳体的应力分析
二、概念和基本假设 (一)概念 例题1:求圆筒,圆锥,圆球上A、B、C点的第一曲率半径。
2020/7/28
第一节 回转壳体的应力分析
一、薄壁容器及其应力的特点
(一)薄壁容器:δ/Dimax<0.1;K=D0/Dimax<1.2
2020/7/28
第一节 回转壳体的应力分析
第二章 内压薄壁圆筒应力分析2
3.2 薄膜理论的应用
3.2.2、受气体内压的球形壳体
2018/10/11
3.2.2、受气体内压的球形壳体
D R1 R2 , 2
pD m 4
2018/10/11
3.2.2、受气体内压的球形壳体
①在直径与内压相同的情况下,球壳内的应力 仅是圆筒形壳体环向应力的一半,即球形壳 体的厚度仅需圆筒容器厚度的一半。 ②当容器容积相同时,球表面积最小,故大型 贮罐制成球形较为经济。
标准椭圆形封头内的最大薄膜应力与同直径、同厚度的 圆筒形壳体的最大薄膜应力相等。 2018/10/11
pa
3.2 薄膜理论的应用
3.2.4 圆锥形壳体中的薄膜应力
圆锥形壳体的使用场合:容器的锥形封头,塔体之间 的变径段,储槽顶盖等。
2018/10/11
3.2.4 圆锥形壳体中的薄膜应力
m
精品课件!
2018/10/11
精品课件!
2018/10/11
3.2
薄膜理论的应用
2018/10/11
锥形壳体的环向应力是经向应力的两倍。
锥形壳体的应力,随半锥角a的增大而增大,设计 时,a角要合适,不宜太大。
2018/10/11
3.2.4 圆锥形壳体中的薄膜应力
四种壳体(圆筒、球、椭球、锥形)的最大薄膜应 力:
max
pD K 2
圆筒形壳体和标准椭球形壳体:K=1 球形壳体:K=0.5 圆锥形壳体:K=1/cosa
pD 1 4 co s pD 1 2 co s
D
p p
δ:圆锥形壳体的壁厚,mm α:半锥角 D:讨论点所在处的锥形壳体中间面直径,mm
2018/10/11
内压薄壁圆筒应力分析

❖ 二、回转壳体的无力矩理论 ❖ 1、有力矩理论:壳体在外载荷作用下,要引起壳体
的弯曲,这种变形由壳体内的弯曲和中间面上的拉 或压应力共同承担,求出这些内力或内力矩的理论 称为一般壳体理论或有力矩理论,比较复杂;
2020/7/10
2、 无力矩理论:对于壳体很薄,壳体具有连续的几 何曲面,所受外载荷连续,边界支承是自由的,壳 体内的弯曲应力与中间面的拉或压应力相比,小到 可以忽略不计,认为壳体的外载荷只是由中间面的 应力来平衡,这种处理方法,称为薄膜理论或无力 矩理论。
P
θ R2 M
δ
向下的力因内压引起: F=(πD2P)/4
向上的力为应力集中力在竖 直方向的分力为:
F=σm·πDδ·sinθ
根据力平衡条件:
(πD2p)/4=σmπDδ·sinθ
根据D=2R2sinθ代入上式
σm=pR2/2δ
σm
σm
M
D
δ
σm R2
O
P σm θ
M
θ
D
五、环向应力的计算公式—微体平衡 已求得经向应力σm=pR2/2δ,求环向应力,取小微分体,如 图所示。
K2
σ dθ 2 σ θ
2 R2
dθ 2 P
m
dl2
σθ
小结:薄膜理论的适用条件 薄壁无力矩应力状态的存在,必须满足:
壳体是轴对称的,即几何形状、材料、载荷的对称性与连续 性,同时需要保证壳体应具有自由边缘。
1、壳转壳体曲面在几何上是轴对称,壳体厚度无突变; 曲率半径是连续变化的,材料是各向同性的,且物理性能( 主要是E和μ)应当是相同的;
回转壳体:以回转曲面为中间面的壳体
轴对称:我们把几何形状、所受外力、约束 条件都对称于回转轴的问题称为轴对称问题 。
内压薄壁容器的应力理论

矩形房间
适用于相对简单的结构,如 矩形房间,美术馆大厅等。
球形温室
适用于各种历史上已经建成 的球形建筑,如巴黎的拉丁 区地下停车场。
应力对薄壁容器的影响
1 测量和检测
2 应对压力波动
对薄壁容器进行应力检测,就可以定期 了解它的强度、稳定性和寿命等数据。
理解应力对薄壁容器的影响,可更好地 利用压实性,降低波动压力,并将其转 换为向设计用的方向施加压力,降低应 力的大小,提高容器的使用寿命。
总结
容器形变
应用应力理论可以避免薄壁容器的变形。
应力计算
运用适当的应力计算方法是保证薄壳结构完整性的核心。
应力影响
掌握应力对薄壁容器的影响,可以更好地利用压实性,降低压力波动,提高其使用寿命。
应力的传递和计算方法
圆筒形
直径方向的应力和周向的 应力不同,对应不同的计 算式,计算方便,适用性 广。
球形
球形内部承受的压力均等, 直接应用高中物理学中的 公式即可,简单有效。
其他形式
最常见的如球筒形容器, 非常复杂的容器需要结合 实践经验进行计算。
应力理论的适用范围
轴对称的薄壳结构
适用于任何几何形状的旋转 体,其表面轮廓相同,沿其 轴线对称。
实际工程中的应用案例
1
内燃机汽缸
是绝大多数机械装置的基础部件,应用广泛,如乘用车、船舶、小型飞机等机器 中都有它的身影。
2
地下储油罐
是油品市场之一,为了保护存储的石油、化工品等流体不泄漏,需要采用薄壳结 构的容器。
3
卫星外壳
是航天器中最复杂、最高科技含量的部分之一,具有优良的结构材料、结构组合 方式,耐热、隔热性能强。
内压薄壁容器的应力理论
内压薄壁圆筒应力分析
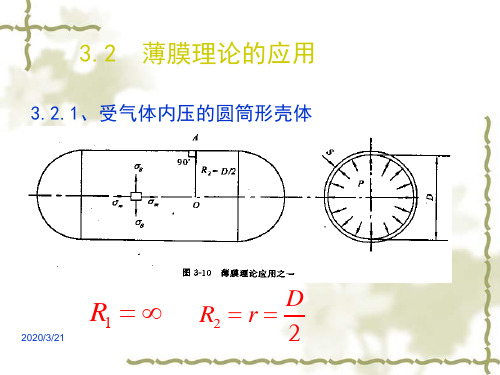
x :椭球壳上任意点距椭球壳中心轴的距离mm。
2020/3/21
O
x2 y2 1 a2 b2
3.2.3、受气体内压的椭球壳(椭圆形封头)
pa
2
σm
b a=b
a pa
pa
2
2
σθ
b a=b
a
pa
2020/3/21 圆球 2
σm
b 1 a 1.4
b
a
σm
b a=2b a
σθ
b 1 a 1.4
2020/3/21
3.2.4 圆锥形壳体中的薄膜应力
最大薄膜应力在锥形壳体大端,在锥顶处, 应力为零。
锥形壳体内最大薄膜应力是同直径同壁厚圆筒形壳 体的薄膜应力的1/cos a 倍。
锥形壳体的环向应力是经向应力的两倍。
锥形壳体的应力,随半锥角a的增大而增大,设计 时,a角要合适,不宜太大。
2020/3/21
②
m
PD
4
P
4 /
D
,
PD
2
P,
2 / D
所以应力与S/D成反比,不能只看壁厚大小 。
2020/3/21
3.2 薄膜理论的应用
3.2.2、受气体内压的球形壳体
2020/3/21
2
,
m
pD
4
2020/3/21
3.2.2、受气体内压的球形壳体
①在直径与内压相同的情况下,球壳内的应力 仅是圆筒形壳体环向应力的一半,即球形壳 体的厚度仅需圆筒容器厚度的一半。
pa
b a=2b a
σθ
pa
3.2.3、受气体内压的椭球壳(椭圆形封头)
pa
σm
b a=2b a pa 2
轴对称载荷作用下薄壁圆筒的内力计算

轴对称载荷作用下薄壁圆筒的内力计算下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!在工程力学中,薄壁圆筒是一种常见的结构形式,在受到轴对称载荷作用时,其内力计算是一个重要的问题。
第三章-内压薄壁容器设计
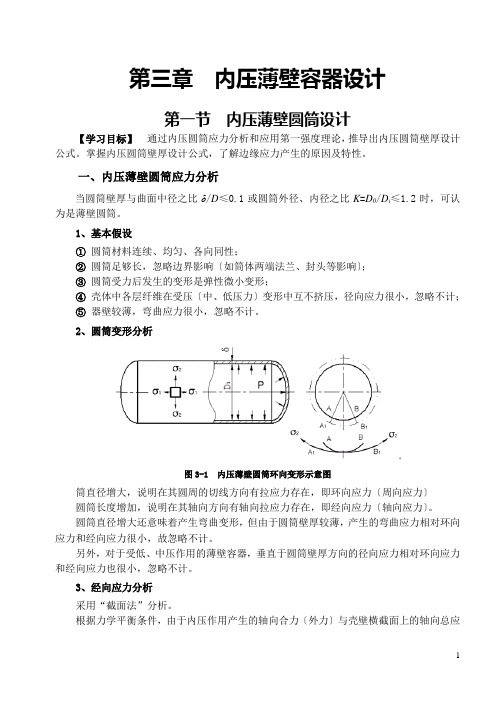
第三章内压薄壁容器设计第一节内压薄壁圆筒设计【学习目标】通过内压圆筒应力分析和应用第一强度理论,推导出内压圆筒壁厚设计公式。
掌握内压圆筒壁厚设计公式,了解边缘应力产生的原因及特性。
一、内压薄壁圆筒应力分析当圆筒壁厚与曲面中径之比δ/D≤0.1或圆筒外径、内径之比K=D0/D i≤1.2时,可认为是薄壁圆筒。
1、基本假设①圆筒材料连续、均匀、各向同性;②圆筒足够长,忽略边界影响〔如筒体两端法兰、封头等影响〕;③圆筒受力后发生的变形是弹性微小变形;④壳体中各层纤维在受压〔中、低压力〕变形中互不挤压,径向应力很小,忽略不计;⑤器壁较薄,弯曲应力很小,忽略不计。
2、圆筒变形分析图3-1 内压薄壁圆筒环向变形示意图筒直径增大,说明在其圆周的切线方向有拉应力存在,即环向应力〔周向应力〕圆筒长度增加,说明在其轴向方向有轴向拉应力存在,即经向应力〔轴向应力〕。
圆筒直径增大还意味着产生弯曲变形,但由于圆筒壁厚较薄,产生的弯曲应力相对环向应力和经向应力很小,故忽略不计。
另外,对于受低、中压作用的薄壁容器,垂直于圆筒壁厚方向的径向应力相对环向应力和经向应力也很小,忽略不计。
3、经向应力分析采用“截面法”分析。
根据力学平衡条件,由于内压作用产生的轴向合力〔外力〕与壳壁横截面上的轴向总应力〔内力〕相等,即:124δσππD p D =由此可得经向应力: δσ41pD=图3-2 圆筒体横向截面受力分析4、环向应力分析 采用“截面法”分析。
图3-3 圆筒体纵向截面受力分析根据力学平衡条件,由于内压作用产生的环向合力〔外力〕与壳壁纵向截面上的环向总应力〔内力〕相等,即:22δσL LDp = 〔3-3〕由此可得环向应力: δσ22pD= 〔3-4〕 5、结论通过以上分析可以得到结论:122σσ=,即环向应力是经向应力的2倍。
因此,对于圆筒形内压容器,纵向焊接接头要比环向焊接接头危险程度高。
在圆筒体上开设椭圆形人孔或手孔时,应当将短轴设计在纵向,长轴设计在环向,以减少开孔对壳体强度的影响。
第三章 内压薄壁容器及封头的强度设计

锥体曲线上任意一点A处的曲率半径:
R1
,
R2
r
cos
由式(3-1)、(3-2)得任意点A处的经向应力 m 和环向应力 :
m
pr 2S
g1
cos
(3-8)
pr g 1
S cos
(3-9)
最大应力出现在r=D/2,即锥底处:
m
pDg 1
4S cos
pDg 1
2S cos
D R2 r
αα A
HW(3/15) 一、名词解释: 薄壁容器、回转壳体、经线、薄膜理论、第一曲率半径、区域平衡方程式 法线、无力矩理论、第二曲率半径、微体平衡方程式
椭球壳主要是椭圆形封头。承受内压p作用的椭圆形封头,其长、短 半径分别为a,b,壳体壁厚为S。
σm
y
A(x,y)
根据壳体椭圆曲线的曲线方程式:
x2 y2 1 a2 b2
σm
x
b
R1
a R2
x
求得壳体上任意点A(x,y)处的曲率半径:
R1
1 a4b
a4
x2
a2 b2
3/2
R2
1 b
a4
x2
Nmn
2 m Sdl2 gsin
d1
2
微小单元体经向应力分析 σθ
环向应N力 nσθ在法2线方S向dl上1 g的si分n量dN2θ2n:
dθ2
dl2
n
p
n
R2
σθ
微小单元体纬向应力分析
根据法线方向上的平衡条件:
Fn Nmn Nn 0
pgdl1gdl2
2
m
Sdl2
gsin
d1
2
2
薄壁筒的内压的应力计算
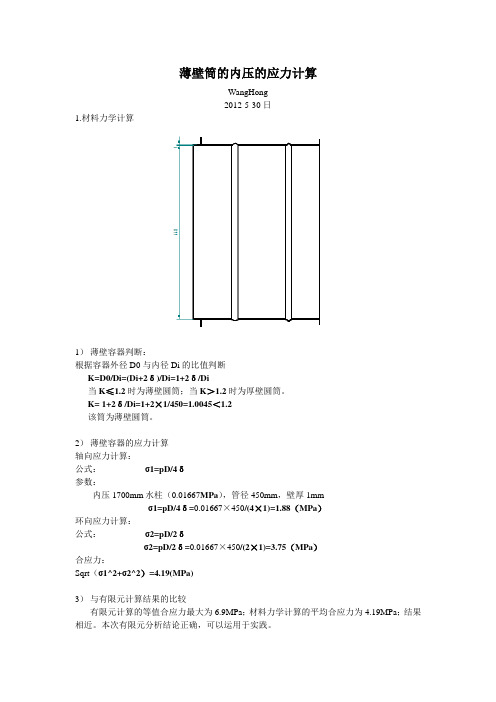
K=1+2δ/Di=1+2×1/450=1.0045<1.2
该筒为薄壁圆筒。
2)薄壁容器的应力计算
轴向应力计算:
公式:σ1=pD/4δ
参数:
内压1700mm水柱(0.01667MPa),管径450mm,壁厚1mm
σ1=pD/4δ=0.01667×450/(4×1)=1.88(MPa)
环向应力计算:Βιβλιοθήκη 公式:σ2=pD/2δσ2=pD/2δ=0.01667×450/(2×1)=3.75(MPa)
合应力:
Sqrt(σ1^2+σ2^2)=4.19(MPa)
3)与有限元计算结果的比较
有限元计算的等值合应力最大为6.9MPa;材料力学计算的平均合应力为4.19MPa;结果
相近。本次有限元分析结论正确,可以运用于实践。
薄壁筒应力计算公式应力计算正应力计算公式弯矩计算应力剪应力计算公式ansys热应力计算土的自重应力计算接触应力计算切应力计算公式
薄壁筒的内压的应力计算
WangHong
2012-5-30日
1.材料力学计算
1)薄壁容器判断:
根据容器外径D0与内径Di的比值判断
K=D0/Di=(Di+2δ)/Di=1+2δ/Di
