巴特沃斯低通滤波器设计
二阶巴特沃斯滤波器电路设计

二阶巴特沃斯滤波器电路设计
二阶巴特沃斯滤波器可以通过使用电容器和电感器来实现。
下面是一个常见的二阶巴特沃斯低通滤波器的电路设计:
1. 选择合适的电容和电感。
根据要求的截止频率和阻带衰减率选择合适的电容和电感。
截止频率是滤波器开始衰减的频率,阻带衰减率是滤波器在截止频率之上的衰减量。
2. 设计RC网络。
使用一个电阻和一个电容构建一个RC网络。
这个网络是滤
波器的一部分,用于控制截止频率。
3. 设计RL网络。
使用一个电阻和一个电感构建一个RL网络。
这个网络也是
滤波器的一部分,用于增加滤波器的阻带衰减率。
4. 连接RC和RL网络。
将RC网络和RL网络连接起来,形成一个二阶巴特沃斯低
通滤波器。
5. 使用操作放大器。
如果需要,可以使用操作放大器来增强滤波器的增益和带宽。
6. 测试及调整。
连接信号源和输出设备,对滤波器进行测试,并根据需要调
整电路参数。
需要注意的是,这只是一个基本的二阶巴特沃斯滤波器电路设计步骤的概述。
具体的设计取决于所需的截止频率、阻带衰减率和其他特定需求。
巴特沃斯低通滤波器法

巴特沃斯低通滤波器法
巴特沃斯低通滤波器是一种常用的频率域滤波器,用于将高频信号从输入信号中滤除。
它是基于巴特沃斯函数设计的,具有平坦的幅频响应和最小的相位延迟。
巴特沃斯低通滤波器的设计方法如下:
1. 确定滤波器的通带截止频率和阻带截止频率。
通带是指允许信号通过的频率范围,阻带是指需要被滤除的频率范围。
2. 根据所需的通带和阻带性能,选择滤波器的阶数。
阶数越高,滤波器性能越好,但计算复杂度也越高。
3. 根据选择的通带和阻带截止频率,使用巴特沃斯低通滤波器的设计公式计算滤波器的系数。
4. 将计算得到的滤波器系数应用于输入信号进行滤波操作。
巴特沃斯低通滤波器的设计公式和计算方法是比较复杂的,一般需要使用专门的滤波器设计软件或者数学计算工具进行计算。
设计得到的滤波器可以通过软件实现,或者通过硬件电路进行实现。
LC低通滤波器设计(巴特沃斯低通滤波器归一化)讲解

C1 1.84776F C2 0.76537F
1NEW
0.76537 K 0.76537 4 12.29μH 5 M 2.512 10
L2NEW
1.84776 K 1.84776 4 29.42μH 5 M 2.512 10
待设计LPF的电容参数为 :
(1 2 )Hz
特征阻抗变换K 4 4 1 四阶Butterworth低通滤波器的电感电容参 数
2018/10/24
只因准备不足,才导致失败
7
四阶Butterworth低通滤波器的归一化LPF基 准滤波器的参数,设 L1 0.76537H L2 1.84776H 得:L
1.84776 1.84776 C1NEW 1.84 μF 5 M K 4 2.512 10 0.76537 0.76537 C2NEW 0.76μF 5 M K 4 2.512 10
2018/10/24 只因准备不足,才导致失败 8
电感采用无损磁芯及细包漆线绕制而成,其 电感值可用数字电桥测量仪器测量得到。
2018/10/24
只因准备不足,才导致失败
1
对滤波器截止角频率的变换是通过先求出待 设计滤波器截止角频率与基准角频率的比值 M,再用这个M去除滤波器中的所有元件值 来计算所需参数,其计算公式如下:
待设计滤波器的截止频 率 M 基准滤波器的截止频率
C (base) Cm(new) M
2018/10/24
5. 低通滤波器设计
1)归一化LPF设计方法 归一化低通滤波器设计数据,指的是特征阻 1 抗为 1 且截止频率为 0.159Hz 的基准 低通滤波器的数据。 2 在设计巴特沃思型的归一化LPF的情况下, 以巴特沃思的归一化LPF设计数据为基准滤 波器,将它的截止频率和特征阻抗变换为待 设计滤波器的相应值。
巴特沃斯低通滤波器课程设计

电路基础课程设计巴特沃斯低通滤波器设计目标:通带边界频率ωc=4396rad/s (f c=700Hz);通带最大衰减αmax=3dB;阻带边界频率ωs=26376rad/s(f s=4200Hz); 阻带最小衰减αmin=30dB;1.设计步骤⑴设计电压转移函数①将给定的电压衰减技术指标进行频率归一化选取归一化角频率ωr=ωc,这样通带边界频率Ωc=ωc/ ωr=1,阻带边界频率Ωs=ωs/ ωr=ωs/ωc。
②根据归一化的技术指标求出电压转移函数巴特沃斯低通滤波器的阶数n=Log(100.1αmin−1) 2Log(Ωs)带入数据求得n=1.93 取整得n=2由a k=2sin(2k−1)π2n,b k=1和H(s)=U out(s)U in(s)=∏A ks2+a k s+b kn2k=1可得到电压转移函数H(s)=U out(s)U in(s)=1s2+√2s+1将转移函数进行反归一化,即另s=sωc 得到实际转移函数H(s)=U out(s)U in(s)=1s243962+√2s4396+1⑵转移函数的实现选取下图作为实现转移函数的具体电路:列节点方程求解转移函数节点1 U1(1R1+1R2+s∗C1)−1R1U in−1R2−s∗C1∗U2=0节点2 (1R2+s∗C2)U2−1R2U1=0又有U out=U3解得H(s)=U outU in=11+(R2+R2)s∗C2+C1C2R1R2s2对比解得的电压转移函数和推得的电压转移函数里各项的系数并且令R1= R2,C1=1μF,可以得到C1=11000000F=1μFR1=250000√21099Ω=321.705ΩR2=250000√21099Ω==321.705ΩC2=12000000F=0.5μF因实验室没有0.5μF的电容因此取C2=0.47μF2.计算机仿真⑴软件环境:Multisim 10⑵电路图:⑶仿真结果:①700Hz下的波形图②4200Hz下的波形图③波特图◎700Hz下衰减2.673dB◎4200Hz下衰减30.491dB3.实验室实际操作因实验室没有0.5μF的电容和321.705Ω的电阻,因此取C2=0.47μFR1=R2=330Ω实际连电路时,选取集成电路块的第1、2、3引脚分别作为放大器的输出端、负端和正端,第4和11引脚作为供电端,C2一端连接电压源的接地线。
巴特沃斯低通滤波器的设计精编资料

巴特沃斯低通滤波器的设计巴特沃斯低通滤波器的设计1、巴特沃斯滤波器的介绍巴特沃斯低通滤波器的幅度平方函数定义为2221|()|1NH j C λλ=+其中C 为一常数参数,N 为滤波器阶数,λ为归一化低通截止频率,/p λ=ΩΩ。
式中N 为整数,是滤波器的阶次。
巴特沃斯低通滤波器在通带内具有最大平坦的振幅特性,这就是说,N 阶低通滤波器在0Ω=处幅度平方函数的前2N-1阶导数等于零,在阻带内的逼近是单调变化的。
巴特沃斯低通滤波器的振幅特性如图a 所示。
滤波器的特性完全由其阶数N 决定。
当N 增加时,滤波器的特性曲线变得更陡峭,这时虽然由a 式决定了在p Ω=Ω处的幅度函数总是衰减3dB ,但是它们将在通带的更大范围内接近于1,在阻带内更迅速的接近于零,因而振幅特性更接近于理想的矩形频率特性。
滤波器的振幅特性对参数N 的依赖关系如图a 所示。
设归一化巴特沃斯低通滤波器的归一化频率为λ,归一化传递函数为()H p ,其中p j λ=,则可得:2221()1(1)N Np jH j C pλλ==+-p 图a 巴特沃斯低通滤波器的振幅特性由于221()()()1()a a jsNcH s H s AsjΩ=--=Ω=+Ω所以巴特沃斯滤波器属于全极点滤波器。
2、常用设计巴特沃斯低通滤波器指标pλ:通带截止频率;pα:通带衰减,单位:dB;sλ:阻带起始频率;sα:阻带衰减,单位:dB。
说明:(1)衰减在这里以分贝(dB)为单位;即222110lg10lg1()NCH jαλλ⎡⎤==+⎣⎦(2)当3dBα=时p CΩ=Ω为通常意义上的截止频率。
(3)在滤波器设计中常选用归一化的频率/Cλ=ΩΩ,即1,p sp sp pλλΩΩ===ΩΩ图b 为巴特沃斯低通滤波器指标3、设计巴特沃斯低通滤波器的方法如下:(1)计算归一化频率1p p pλΩ==Ω,ss pλΩ=Ω。
(2) 根据设计要求按照210101pC α=-和lg lg saN λ=其中a =特沃斯滤波器的参数C 和阶次N ;注意当3p dB α=时 C=1。
巴特沃斯低通滤波器

带最小衰减α =30dB,按照以上技术指标设计巴特沃斯低通滤波器。 0.1a s
1a p
1a s
2.4
0242 4.25, 2.4
2.4 10 1 2 f lg 0.0242 lg 0.0242 NN 2 4.25, 55 lgf 2.4 4.25, N N s sp lg 2.4 2.4 2 f p
H( a s)
N c
(s s
k 0
N 1
k
)
7 j 3
• 例如N=3, 通过下式可以计算出6个极点 5 2 4 j j j j s 3 c 3 s 2 c 3 s 0 c 3 s1 c
s 4 c
j2
s 5 c
要求
f i g u r e ; p l o t ( Q , H a s ) ; a x i s ( [ 0 5]);xlabel('f(kHz)'),ylabel('20lg(abs(H_{a}(j{\Omega})))(dB)');
3 0
- 7 0
• • • • •
L=length(Ha); Yt=Xt(1:L).*Ha; figure;plot(Q,abs(Yt));axis([0 60 0 150]); yt=ifft(Yt); figure;plot(Q,yt);
• 模拟低通滤波器的设计指标 • 构造一个逼近设计指标的传输函数Ha(s) • Butterworth(巴特沃斯)低通逼近
模拟低通滤波器的设计指标及逼近方法(续)
• 模拟低通滤波器的设计指标有αp, Ωp,αs和Ωs。 • Ωp;通带截止频率 • Ωs:阻带截止频率
c 2巴特沃斯低通滤波器的设计方法

2.数字滤波器的技术指标
我们通常用的数字滤波器一般属于选频滤波器。假设数字滤 波器的传输函数H(ejω)用下式表示:
H (e j ) H (e j ) e j ()
通带纹波幅度 阻带纹波幅度 通带截止频率 3dB通带截止频率 阻带截止频率
数字低通滤波器的技术要求
5
通带内和阻带内允许的衰减一般用dB数表示,通带内允许的
脉冲响应不变法 阶跃响应不变法 双线性变换法
Desired IIR
7
5.2 模拟滤波器的设计
模拟滤波器的理论和设计方法已发展得相当成熟, 且有若干典型的模拟滤波器供我们选择,如巴特沃斯 (Butterworth)滤波器、切比雪夫(Chebyshev)滤波器、椭 圆(Elliptic)滤波器、贝塞尔(Bessel)滤波器等,这些滤 波器都有严格的设计公式、现成的曲线和图表供设计 人员使用。
输函数
Ha ( p) N 1 1
( p pk )
(5.2.12)
k 0
15
式中,pk为归一化极点,用下式表示:
pk
sk c
最大衰减用ap表示,阻带内允许的最小衰减用as表示,ap和as分别 定义为:
H (e j0 ) ap 20 lg H (e jp ) dB
H (e j0 ) as 20 lg H (e js ) dB
(5.1.3) (5.1.4)
如将|H(ej0)|归一化为1,(5.1.3)和(5.1.4)式则表示成:
11
2.巴特沃斯低通滤波器的设计方法
幅度平方函数:
Ha(
j) 2
1 (
1
)2N
c
(5.2.6) 两个参数:N, Ωc
设计一个巴特沃斯模拟低通滤波器

1. 设计一个巴特沃斯模拟低通滤波器,要求通带截止频率为Hz f p 25=,通带最大衰减dB a p 3=,阻带起始频率Hz f s 50=,阻带最小衰减dB a s 25=。
解:根据已知条件确定巴特沃斯低通滤波器的阶数N :053.01010202520===--sa s δ()()2355.46021.05502.22lg 21053.01lg lg211lg 22==⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-≥p s s ΩΩδN取N =5。
低通滤波器3dB 截止频率为)/(157502s rad πf πΩΩp p c ====则五阶巴特沃斯滤波器的传输函数为:1021.010719.110095.110326.510048.111236.3236.4236.4236.31)(2436495112345++⨯+⨯+⨯+⨯=+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=----s s s s s Ωs Ωs Ωs Ωs Ωs s H c c c c c2. 设计一个切比雪夫模拟低通滤波器,要求通带截止频率为kHz f p 3=,通带最大衰减dB a p 2.0=,阻带起始频率kHz f s 12=,阻带最小衰减dB a s 50=。
解:由()2.01lg 20-=-p δ,求得9772.0101202.0==--p δ。
则2171.019772.011)1(122=-=--=p δε 由50lg 20-=s δ,求得0032.0102050==-s δ,则23.31610032.011122=-=-=s δδ 所需滤波器的阶数为:()()()()8604.30634.29770.7312arccos 2171.0/23.316arccos arccos arccos ===≥h h ΩΩh εδh N p s取N =4。
则该模拟低通滤波器的幅度表示为:⎪⎭⎫ ⎝⎛⨯⨯+=⎪⎪⎭⎫⎝⎛+=32422210322171.01111)(πΩC ΩΩC εΩj H pNa归一化的系统函数表示为:∏∏==--=-⋅=Nk k Nk k N a p p p p εp H 111)(7368.11)(21)(其中极点k p 为:0715.14438.01j p +-=,4438.00715.12j p +-=,4438.00715.13j p --=,0715.14438.01j p --=将)(p H a 去归一化,求得实际滤波器的系统函数)(s H a()()()8428426414107790.4100394.4107791.4106731.1102687.77368.1)()(⨯+⨯+⨯+⨯+⨯=-==∏==s s s s p Ωs Ωp H s H k k p pΩsp a a p3. 设计一个巴特沃斯模拟高通滤波器,要求通带截止频率为kHz f p 20=,通带最大衰减dB a p 3=,阻带起始频率kHz f s 10=,阻带最小衰减dB a s 15=。
数字信号处理巴特沃斯滤波器设计

数字信号处理巴特沃斯滤波器设计数字信号处理在当今科技领域中扮演着至关重要的角色,滤波器作为数字信号处理领域中的重要组成部分,广泛应用于信号去噪、信号增强、信号分析等方面。
巴特沃斯滤波器作为数字信号处理领域中的一种重要类型,具有平滑的频率响应曲线和较陡的截止特性,被广泛应用于语音处理、图像处理、生物医学信号处理等领域。
本文将介绍数字信号处理中巴特沃斯滤波器的设计原理和方法。
在数字信号处理中,滤波器是一种通过对信号进行处理来实现滤除或增强某些频率成分的系统。
巴特沃斯滤波器是一种典型的低通滤波器,其特点是在通频带范围内频率响应平坦,截止频率处有较 steependifferentiation,可有效滤除非所需频率信号。
要设计一个巴特沃斯滤波器,首先需要确定滤波器的截止频率和阶数。
巴特沃斯滤波器的阶数决定了滤波器的频率选择性能,在实际应用中可根据信号处理的要求进行选择。
一般来说,阶数越高,滤波器的截止特性越陡,但相应的频率选择性能也会增强。
确定好阶数后,接下来需要进行巴特沃斯滤波器的参数计算,包括极点位置和幅频特性。
根据巴特沃斯滤波器的传递函数形式,可以通过公式计算各个极点的位置,并绘制出滤波器的幅频特性曲线。
设计完巴特沃斯滤波器的参数后,接下来是实现滤波器的数字化。
数字巴特沃斯滤波器一般通过模拟滤波器的模拟频率响应和数字频率响应之间的变换来实现。
常用的数字化方法包括脉冲响应不变法和双线性变换法,通过这些方法可以将模拟滤波器的参数转换为数字滤波器的参数,实现数字滤波器的设计。
在实际应用中,巴特沃斯滤波器的设计需要根据具体的信号处理要求和系统性能来选择合适的截止频率和阶数,确保滤波器设计的稳定性和性能。
同时,在设计过程中需要考虑到滤波器的实现复杂性和计算成本,选择合适的设计方法和参数计算技术,以实现滤波器设计的有效性和可靠性。
综上所述,巴特沃斯滤波器作为数字信号处理领域中的重要组成部分,在信号处理、通信系统、生物医学等领域中有着广泛的应用前景。
巴特沃斯低通滤波器设计

巴特沃斯低通滤波器一、设计要求(1)设计一巴特沃斯数字低通滤波器,在0.3π通带频率范围内,通带幅度波动小于1dB ,在0.5π~πrad 阻带频率范围内,阻带衰减大于12dB 。
二.设计过程巴特沃斯双线性变换法(1)数字指数:p w =0.3π,s w =0.5π,(2)求p Ω,s Ω利用频率预畸变公式得:p Ω=2T tan 2p w =2T tan 320π=1.019⨯1Ts Ω=2T tan 2s w =2T tan 4π=2T (3)确定滤波器阶数sp λ=s p ΩΩ=211.019TT ⨯=1.963 sp k≈0.132 N=—lg lg sp sp k λ=—lg 0.132lg1.963≈3.0023 N=4 (4)确定系统函数G(p)= 43212.613 3.4142 2.61311p p p p ++++ c Ω=p Ω()10.12101p a N --=1.019⨯1T⨯()10.1124101-⨯⨯-=1.2065T P=11211c s z s T z ---=Ω+=1c Ω⨯2T ⨯1111z z ---+=11211.20651z z ---+ H(z)=G(p)=12341234146434.1675441.3465432.542711.06234 1.69864z z z z z z z z--------++++-+-+三.软件仿真(1)将分子分母带入Matlab 验证b=[1 4 6 4 1];a=[34.16754 -41.34654 32.5427 -11.06234 1.69864];[H,w]=freqz(b,a,1000);plot(w,20*log10(abs(H)/max(H)),'-');grid;xlabel('frequency');ylabel('magnitude');-250-200-150-100frequency m a g n i t u d e图(a )频率——幅度衰减图0.3π≈0.940.9250.930.9350.940.9450.950.955frequency m a g n i t u d e图(b)0.5π≈1.57frequency m a g n i t u d e图(c)(2)用Matlab 直接仿真出低通滤波器wp=2*tan(0.3*pi/2)*1000;ws=2*tan(0.5*pi/2)*1000;ap=1;as=12;[n,wn]=buttord(wp,ws,ap,as,'s');[b,a]=butter(n,wn,'s');[bn,an]=bilinear(b,a,1000);[H,w]=freqz(bn,an);plot(w,abs(H),'-');grid;xlabel('frequency');ylabel('magnitude');legend('双线性变化法');figure(2);plot(w,20*log10(abs(H)/max(H)),'-');grid;00.51 1.522.533.5frequency m a g n i t u d e0.3π≈0.94图(d)0.5π≈1.57图(e)四.分析将计算得出的低通滤波器系统函数H(z)的分子分母各项系数用Matlab验证,得图(a)幅频关系图。
巴特沃斯低通滤波电路设计

巴特沃斯低通滤波电路设计:
巴特沃斯低通滤波电路的设计主要包括以下几个步骤:
1.确定系统函数的极点:巴特沃斯滤波器的极点位于Z平面的单位圆上,因此可以通
过选取适当的滤波器阶数和电气参数,使得滤波器的极点位于单位圆上。
2.设计传递函数:根据滤波器的性能要求,如通带增益、阻带增益、过渡带宽度等,
设计出传递函数。
巴特沃斯滤波器的传递函数具有固定的形式,可以通过选取电气参数来调整其性能。
3.实现电路结构:将设计好的传递函数转换为实际电路结构。
根据不同的电路形式,
可以选择不同的电路元件和结构,如运算放大器、RC电路等。
4.参数调整:对电路中的元件参数进行适当调整,以保证滤波器的性能符合设计要求。
参数调整是滤波器设计中非常关键的一步,需要通过实验和仿真反复验证和调整。
5.测试和验证:对设计好的滤波器进行测试和验证,包括频率响应、相位响应、群延
迟等性能指标的测试。
如果测试结果不符合设计要求,需要对电路或参数进行调整。
八阶巴特沃斯低通滤波器的设计方法

八阶巴特沃斯低通滤波器的设计方法设计八阶巴特沃斯低通滤波器可以通过以下步骤进行:
1. 确定滤波器的规格:首先确定滤波器的截止频率和通带衰减。
截止频率是指滤波器开始降低信号幅度的频率,通带衰减是指滤波器在通带内允许的最大幅度变化。
2. 计算极点位置:使用巴特沃斯滤波器的公式可以计算出滤波器极点的位置。
对于八阶低通滤波器,共有四对共轭极点。
这些极点会决定滤波器的频率响应。
3. 进行归一化:对于滤波器的极点位置,需要对其进行归一化处理,将其转换为标准低通滤波器的情况。
4. 进行极点频率转换:通过将归一化后的极点位置转换为实际的截止频率,即可得到实际滤波器的极点位置。
5. 构造传递函数:使用极点位置构造滤波器的传递函数,可以表示为巴特沃斯多项式的形式。
6. 计算滤波器系数:通过将传递函数展开并与标准低通滤波器的传递函数进行比较,可以计算滤波器的系数。
7. 实施滤波器:将计算得到的滤波器系数应用于数字滤波器的差分方程中,从而实现滤波器的效果。
需要注意的是,设计巴特沃斯滤波器需要一定的信号处理和滤波器设计知识。
如果不熟悉滤波器设计或数字信号处理的相关概念,建议咨询专业的工程师或使用现成的滤波器设计软件来完成滤波器设计任务。
巴特沃斯低通滤波器公式 巴特沃斯低通滤波器设计原理

巴特沃斯低通滤波器公式巴特沃斯低通滤波器设计原理
巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示:其中, = 滤波器的阶数= 截止频率= 振幅下降为-3分贝时的频率=通频带边缘频率在通频带边缘的数值。
关于“巴特沃斯低通滤波器公式巴特沃斯低通滤波器设计原理”的详细说明。
1.巴特沃斯低通滤波器公式
巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示:
其中, = 滤波器的阶数= 截止频率= 振幅下降为-3分贝时的频率=通频带边缘频率在通频带边缘的数值。
2.巴特沃斯低通滤波器设计原理
巴特沃斯型低通滤波器在现代设计方法设计的滤波器中,是最为有名的滤波器,由于它设计简单,性能方面又没有明显的缺点,又因它对构成滤波器的元件Q值较低,因而易于制作且达到设计性能,因而得到了广泛应用。
其中,巴特沃斯滤波器的特点是通频带的频率响应曲线最平滑。
滤波器的截止频率的变换是通过先求出待设计滤波器的截止频率与基准滤波器的截止频率的比值M,再用这个M去除滤波器中的所有元件值来实现的,其计算公式如下:M=待设计滤波器的截止频率/基准滤波器的截止频率。
滤波器的特征阻抗的变换是通过先求出待设计滤波器的特征阻抗与基准滤波器的特征阻抗的比值K,再用这个K去乘基准滤波器中的所有电感元件值和用这个K去除基准滤波器中的
所有电容元件值来实现的。
巴特沃斯滤波器设计
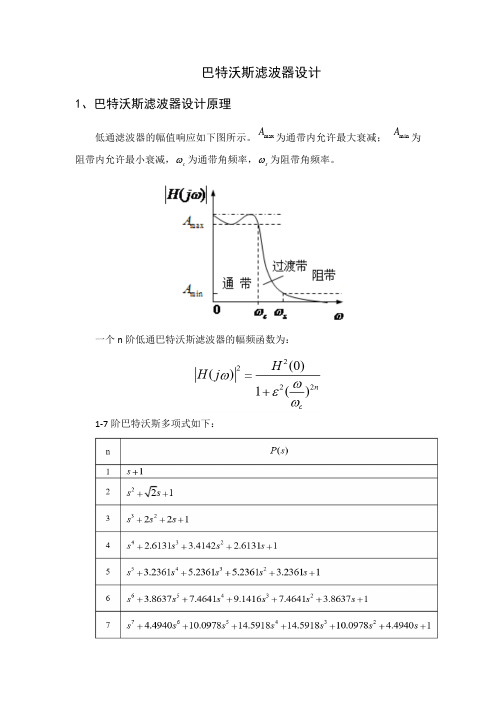
巴特沃斯滤波器设计1、巴特沃斯滤波器设计原理低通滤波器的幅值响应如下图所示。
maxA 为通带内允许最大衰减;minA 为阻带内允许最小衰减,c ω为通带角频率,s ω为阻带角频率。
一个n 阶低通巴特沃斯滤波器的幅频函数为:1-7阶巴特沃斯多项式如下:常数ε的作用是调整通带内允许的最大衰减,使其可小于3dB。
逼近过程中,A 需要确定的参数为ε和巴特沃斯多项式的阶数n,其中,通带内允许最大衰减maxA。
首先,推导确定了ε的大小;阶数n的大小取决于阻带内允许的最小衰减minε。
习惯上,多用衰减(分贝数)表示幅频特性。
因此,巴特沃斯低通响应为:ωω时,产生通带内最大衰减,即当=c解上式,可得:ωω时,产生阻带内最小衰减当=s上式可写为:对上式求解,可得:把 的表达式带入,可得:例子:用matlab 重复以上计算过程:wp=90*pi; ws=150*pi; Rp=3; Rs=10;N_true=(10^(Rp/10)-1)/(10^(Rs/10)-1);%真数 Num_Base=wp/ws;%底数N=ceil(log10(N_true)/log10(Num_Base)/2); wc=ws/((10^(Rs/10)-1)^(1/(2*N)));附加:Matlab 计算对数的时候,没有以a 为底b 的对数的函数,因此需要通过lgblog lg b a a改为以10为底的对数或者自然对数进行计算。
来源:https:///view/06e71fc5c67da26925c52cc58bd63186bceb92ca.html2、matlab 的巴特沃斯滤波器设计matlab 中提供了函数进行巴特沃斯滤波器设计同样对应上边的例子,通带90πHz ,通带最大衰减3dB ,阻带150πHz ,阻带最小衰减10 dB 。
Matlab 计算方法如下:229010lg 1315010lg 110nc nc πωπω⎧⎡⎤⎛⎫⎪⎢⎥+= ⎪⎪⎢⎥⎝⎭⎪⎣⎦⎨⎡⎤⎪⎛⎫⎢⎥+=⎪⎪⎢⎥⎝⎭⎪⎣⎦⎩20.32901010.995261501019nc nc πωπω⎧⎛⎫⎪=-= ⎪⎪⎝⎭⎨⎛⎫⎪=-= ⎪⎪⎝⎭⎩两式相除有:2290150900.99526/0.110581509nncc πππωωπ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ 整理得:()20.60.11058n=因此,0.110580.61log 2.15532n ==取3n =,带入215010lg 110n c πω⎡⎤⎛⎫⎢⎥+= ⎪⎢⎥⎝⎭⎣⎦,即21509nc πω⎛⎫= ⎪⎝⎭计算得:1/6150326.7388/9c rad s πω== 3n =,查表得对应的巴特沃斯滤波器,并去归一化:7323232711 3.488210221653.5 2.135 3.488210221c c c s s s s s s s s s ωωω⨯==++++++⨯⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭Matlab 代码如下: wp=90*pi; ws=150*pi; Rp=3; Rs=10;[N,wc]=buttord(wp,ws,Rp,Rs,'s');[B,A]=butter(N,wc,'s');f=1:300;w=2*pi*f;H=freqs(B,A,w);figure(1)plot(f,20*log10(abs(H)));grid on,xlabel('频率(Hz)'),ylabel('幅度(dB)')title('巴特沃斯模拟滤波器')设计滤波器幅值响应如下:3、pscad和matlab关于滤波器的配合设计的滤波器的系数经常很大,连续的滤波器在pscad中用s的传递函数实现,pscad中该元件系数有限制要在-810之间,实际的滤波器不满足该条件。
巴特沃斯低通滤波器设计

L1'
2
600 1.304 104
0.7654H
5.61mH
C2
1 c RS
C2'
2
1 1.304 104
600
1.8478F
0.038uF
L3
RS c
L'3
2
600 1.304 104
1.8478H
13.53mH
C4
1 c RS
C4'
2
1 1.304 104
600
0.7654F
0.016uF
设计实现电路
巴特沃斯低通滤波器迅速设计总结
一:根据滤波器性
能指标(通带内旳
最大衰减 c ,阻带
内旳最小衰减 s ,
截至频率 c ,阻带
起始频率 s )利用
公式
N
lg
1
s2
-1
2 lg s / c
求巴特沃斯低通滤波 器旳阶次N。
二:根据阶次N和考尔 型电路
RS' 1
L1' 0.7654
L'3 1.8478
一般情况下,电路是在匹配情况下工作,所以取
信源内阻 Rs 和负载电阻 RL 相等。
此时满足
Ha ( j0)
RL RS RL
1 2
根据反射系数公式
(s)
(
s)=1- 4RS RL
s' s
H
a
s
H
a
-s
j
达林顿电路构造
Rs 源电阻 RL 负载电阻
RS
I1
Es
V1
1
2
LC
I2
无损
巴特沃斯阶跃阻抗低通滤波器设计

巴特沃斯阶跃阻抗低通滤波器设计引言巴特沃斯阶跃阻抗低通滤波器是一种常用于信号处理和电子电路设计中的滤波器类型。
它的设计原理是通过调整滤波器的阶数和截止频率,来实现对输入信号的频率成分进行筛选和衰减。
本文将详细介绍巴特沃斯阶跃阻抗低通滤波器的设计方法及其在实际应用中的一些注意事项。
巴特沃斯阶跃阻抗低通滤波器概述巴特沃斯阶跃阻抗低通滤波器是一种I IR(无无限冲激响应)滤波器,具有平坦的通带、陡峭的衰减特性以及相对较低的群延迟。
它广泛应用于音频处理、通信系统等领域。
巴特沃斯滤波器的设计步骤1.确定滤波器的阶数(n):阶数决定了滤波器的衰减程度和复杂度,一般取偶数值。
2.确定滤波器的截止频率(f c):截止频率即信号通过滤波器时频率衰减到原来的1/√2,是决定滤波器频率特性的关键参数。
3.计算滤波器的极点位置:根据巴特沃斯滤波器的特性方程,计算极点位置。
4.标准化滤波器:对计算得到的极点位置进行标准化处理,使得滤波器的截止频率为1。
巴特沃斯滤波器设计实例以下是一个以设计一个4阶巴特沃斯阶跃阻抗低通滤波器为例的设计过程。
步骤1:确定滤波器的阶数我们选择设计一个4阶的巴特沃斯阶跃阻抗低通滤波器。
步骤2:确定滤波器的截止频率假设我们需要将信号的截止频率设置在1k H z。
步骤3:计算滤波器的极点位置根据巴特沃斯滤波器的特性方程,我们可以计算出滤波器的极点位置。
对于一个4阶的巴特沃斯低通滤波器,其极点位置可以通过下式计算得到:p_k=-s in h(π*fc)*s in(π*(2k-1)/(2n)),k=1,2,...,n式中,f c是截止频率,n是滤波器阶数。
步骤4:标准化滤波器标准化滤波器是将计算得到的极点位置通过变换使得滤波器的截止频率为1。
标准化后的滤波器的特性方程为:H(s)=1/((s+p1)(s+p2)...(s+pn))巴特沃斯滤波器的应用注意事项-在实际设计中,应根据需要调整滤波器的阶数和截止频率,以满足对信号的频率特性要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
s
'
L3 R S s
' '
得到实际电感和电容值
' 7 ' 6 ' 5 ' 4 ' 3 ' 2 '
设计步骤
一:求巴特沃斯阶数N 二:求系统函数(可以省略) H
a
(s)
三:归一化电路的实现
备注:(1,根据连除法得到;2,直接根据阶次查表得到)
四:实际电路的实现,即去归一化
三:归一化电路的实现
由于N阶巴特沃斯滤波器的分母多项式是霍尔为
茨多项式,并且 H ( s ) 全部传输零点在 s= 处,因 而可以用达林顿电路结构实现。 一般情况下,电路是在匹配情况下工作,所以取 信源内阻 R 和负载电阻 R 相等。 R 1 H ( j0) 此时满足 R R 2 根据反射系数公式
C
L
' 2
C
' 3
L
' 4
C
' 5
L6
'
C7
'
设计步骤
一:求巴特沃斯阶数N 二:求系统函数(可以省略) H
a
(s)
三:归一化电路的实现
备注:(1,根据连除法得到;2,直接根据阶次查表得到)
四:实际电路的实现,即去归一化
四:实际电路的实现,即解归一化
因
Z 11 ( s ) RS
'
L1 s
3 .4 4 3
或者利用公式:
N
取整后得阶数:N=4, 按其设计的滤波器,通 带实际特性优于给定之 指标。
设计步骤
一:求巴特沃斯阶数N 二:求系统函数(可以省略) H
a
(s)
三:归一化电路的实现
备注:(1,根据连除法得到;2,直接根据阶次查表得到)
四:实际电路的实现,即去归一化
二:求系统函数 H
a
s
L
L
a
S
L
( s ) ( s ) =1-
4 RS RL
H a s H a -s
s
'
s j
达林顿电路结构
Rs
RL
源电阻 负载电阻
1
2
L C 无损 网络
RS
I1
V1
I2
RL
Es
V0
Z 11 ( s )
1
'
2
'
滤波器插在负载电阻
RL
和内阻
Rs
之间
三:归一化电路的实现
特性曲线图
H
a
( jΩ )
1 N=2 1 2 N=4 N=8
解得:
N
1 lg 15 1 0 20
-1
2 4
o
c
2 2 1 0 2 lg 4 2 1 .30 4 1 0
1 lg 2 -1 s 2 lg s / c
2 .6 1 3 1( s ) 3 .41 4 2 ( s ) 2 .6 1 3 1( s ) 1
' 3 ' 2 '
应用T型电路,连续除法可以得到(此处根据连除法)
Z 11 ( s ) RS
'
0 .7 6 5 4 s
'
1 1 .8 4 7 8 s
'
1 1 .8 4 7 8 s
c
s
'
( s ) 2 . 6 1 3 1 ( s ) 3 . 41 4 2 ( s ) 2 . 6 1 3 1 ( s ) 1
' 4 ' 3
代入上式得系统函数
H a (s) 4 .5 0 6 1 0
4 5 3 10 2 19 15 19
( s ) 3 .2 3 6 1( s ) 5 .2 3 6 1( s ) 5 .2 3 6 1( s ) 3 .2 3 6 1( s ) 1
a
(s)
三:归一化电路的实现
备注:(1,根据连除法得到;2,直接根据阶次查表得到)
四:实际电路的实现,即去归一化
一:求巴特沃斯阶数N
-15dB 对应
s =1 0
15 20
巴特沃斯滤波器是最基本
的逼近函数形式之一。它 的幅频特性模平方为
1 2 | H a ( j ) | 2N 1 c
'
BN (s ) (s )
' '
N N
BN (s ) (s )
' '
和
Z
' 11
(s ) RS
'
BN (s ) (s )
' '
N N
BN (s ) (s )
' '
卡尔 型电路)
第一种实现电路: 根据式
Z 11 ( s ) RS
'
BN (s ) (s )
' '
N N
BN (s ) (s )
'
N '
BN (s )
用达林顿电路实现时,策动点阻抗函数:
Z 11 ( s ) R S
'
1 (s )
'
1 (s )
'
RS
BN (s ) (s )
' '
N N
BN (s ) (s )
'
'
上式表示具有巴特沃斯滤波器特性的电路有两种可能的 综合形式:
Z 11 ( s ) R S
' ' ' 4 ' 3 ' 2 '
则可以推出
Z 11 ( s ) RS
'
B4 (s ) (s )
' '
4 4
B4 (s ) (s )
' '
2 ( s ) 2 .6 1 3 1( s ) 3 .41 4 2 ( s ) 2 .6 1 3 1( s ) 1
' 4 ' 3 ' 2 '
' 3 ' 2 '
第三步
' 2
0 .7 6 5 4 s 1
'
1 .8 4 7 8 s
'
'
1 .4 1 4 2 ( s ) 1 .8 4 7 7 s 1 0 .7 6 5 4 s 1
'
1 .4 1 4 2 ( s ) 1 .8 4 7 7 s
' 2
'
1
第四步
0 .7 6 5 4 s 1
查看巴特沃斯滤波器多项
a
(s)
当N=4时,巴特沃斯多项
式表
N 1 2 3 4 5 6 7
BN (s ) aN (s ) aN 1 (s ) ....... a1s a
' ' N ' ' N 1
式 B (s ) ,可得到归一化 的系统函数
' N
s
' 2
'
1
2s 1
2
H a ( j)
-3dB
-15dB
o
c
s
根据上式由此联立方程
1 | H a ( j s ) | s 2N s 1 c 4 c = 2 1 .3 0 4 1 0 ra d /s
根据巴特沃斯滤波器幅频
' 2
第二步
' 3 ' 2
1 .8 4 7 8 s
'
'
2 .6 1 3 1( s ) 3 .41 4 2 ( s ) 2 .6 1 3 1( s ) 1 1 .4 1 4 2 ( s ) 1 .8 4 7 7 s 1
' 2 '
2 .6 1 3 1( s ) 3 .41 4 2 ( s ) 1 .8 4 7 8( s )
'
H a (s )
'
1 B N (s )
'
1 ( s ) 2 .6 1 3 1( s ) 3 .41 4 2 ( s ) 2 .6 1 3 1( s ) 1
' 4 ' 3 ' 2 '
(s )
' 3
( s ) 2( s ) 2 s 1
' 2 '
将
' 2 '
s
'
'
1 C4s 1
' '
RS 1
'
L1 0 .7 6 5 4
'
L 3 1 .8 4 7 8
可以实现电 路
C 4 0 .7 6 5 4
'
ES
C 2 1 .8 4 7 8
'
RL RS
1
此处也可以查询巴特沃斯低通原型滤波器归一化元件值表 也可以得到
N 1 2 3 4 5 6 7 N
' 5 ' 4 ' 3 ' 2 '
s 2 .1 4 1 0 s 2 .2 9 2 1 0 s 1 .4 3 7 1 0 s 4 .5 0 6 1 0
