第5章基团贡献法及其应用
基团贡献方法UNIFAC估算局部组成模型NRTLWILSONUNIQUAC的二元参数
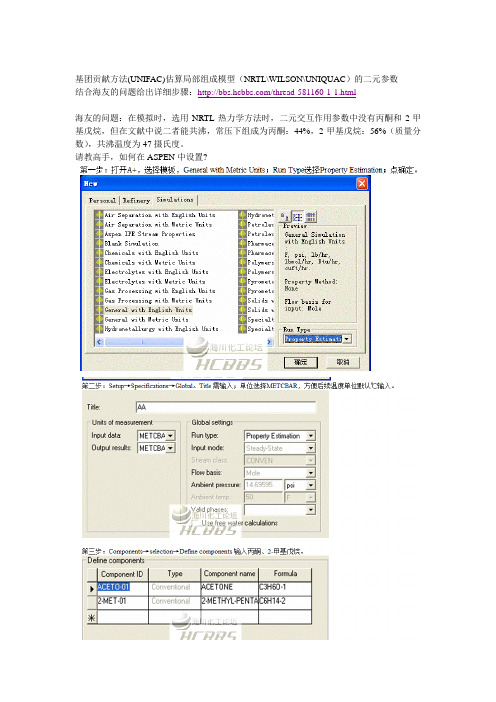
基团贡献方法(UNIFAC)估算局部组成模型(NRTL\WILSON\UNIQUAC)的二元参数结合海友的问题给出详细步骤:/thread-581160-1-1.html海友的问题:在模拟时,选用NRTL热力学方法时,二元交互作用参数中没有丙酮和2-甲基戊烷,但在文献中说二者能共沸,常压下组成为丙酮:44%,2-甲基戊烷:56%(质量分数),共沸温度为47摄氏度。
请教高手,如何在ASPEN中设置?问题:1. 在第五步中的Method为什么选Unif-DMD,而没有选其他的方法,比如UNIF-LBY、UNIF-R4等,这些方法有什么本质上的区别吗UNIFAC-DMD,LBY等没有本质区别,只是修正模型不同而已。
你找我发的那个A+10说明书看下,有详细介绍是什么修正。
2. 如果我不想使用Aspen自带的unifac基团交互参数,而是用自己的unifac基团交互参数(基团参数rq仍旧采用软件自带的),来进行楼主帖子中这样的估算,如何操作?另外,除了上面的问题外,还有一问,那就是如果我自己定义了Aspen中没有的新基团(有时候想把一个物质自己来进行拆分),而且通过别的途径得到了新基团的基团参数RQ以及所需要的相关基团交互参数,那么在这种情况下,在Aspen中怎么样来定义新基团,然后进行楼主帖子中的估算操作呢?还请楼主解答。
今天研究了一下,你的这两个问题应该都可以解决:1、当你选择UNIFAC方法的时候,A+默认使用数据库中参数,但也可以修改。
你只需要在parameters→unifac group binary→GMUFB-1中输入参数即可。
但这前提是你在components中有定义unifac groups,否则gmufb-1是灰色。
2、a+ components的UNIFAC group支持定义新的基团。
号码可以自己定义。
关键是你能定义官能团(方法有很多,bondi、unifac等等),这一步在分子结构中实现,并可以求的q、r的值。
计算环烷烃沸点的新方法——基团键贡献法

计算环烷烃沸点的新方法——基团键贡献法2∞2第22卷第3期.194~199有机化学Chine~Joamalof(…0…v0l22.2∞2I3.J94~199研究简报?计算环烷烃沸点的新方法——基团键贡献法王克强,王捷冯瑞英(.洛阳师范学院化学系洛阳471022)(许昌职业技术学院许昌461000)洛阳市第一高级中学洛阳471002)摘要根据分子中基团的特性和连接性.发展了一种直接根据分子结构信息计算环烷烃沸点的新方法基团键贡献法,该方法既考虑分子中基团的特性,又考虑基团之问的连接性(化学键),具有基团贡献法和化学键贡献法的特点对256种环烷烃沸点的计算结果表明,计算值与宴验值的一致性令人满意,平均误差071啦.关键词结构性能关系,基团键,基团键贡献法,沸点,烷烃GroupBondContribution'__.?.___-——ANewMethodforCalculating BomngPointsofCycloalkanesW ANG,Ke-QiangwA№,Jie.FENG,Rui—Yiag(mofChoTaist~,Normalc.,h~/ang471022)(~XuchangI.'ocatiormlTerhnical0f,461000)('.增sHigh&hodNoJ,4~002) AbslractOilcharacteristicsandconnectivi~,ofthegroupsinmolecules.groupbondscanbea ppliedtocharacterizemolecularstructure.Groupbondscontaininformationofgrouppropertyandco nnectivityinmoleculcs.Groupbonds,obtaineddirectlyfr(1堋molecularstructure,COIlbeusedtocNcuhWthepropertiesofmolecules.Anewmethod,thegroupbondcontributionmeth~,WItSdevelopedtocalculatetb eboilingpoints0fcycloalkmmsfrommolecularstructurelrhecalculatndresultsshowedthatthecaleutatedb oilingpointsof cycloalkaneswereingoodagreementwiththeexperimentaldata,withilloanrelativedeviatio nbeing0.71%for256cyeloalkanes(includingmonoeycloalkanesandpolyeycloalkmaes)egroupbondcontri butionmethodhasadvantagesoverthegroupcontributionmethodKeywordsatrueture-prepet~-relationship,groupbond,groupbendcontributhmmethod.bo ilingpoints,CVC】0日Ikane有机化台物结构性能定量关系的研究,是化学中'个十分活跃的研究领域.多年来,国内外许多研究者作了大量研究的工作,发展了许多根据分子结构预测化合物性能的方法.在有机化台物性能的预测方法中,应用较广的是基团贡献法和化学键贡献法,由于这些方法对同分异构体的区分能力相对较差,预测精度不够理想,作者之?4—6根据分子结构的特点,将基团贡献法和化学键贡献法结合在一起,发展了一种预测化合物性能的新方法一基团键贡献法,该方法具有基团贡献法和化学键贡献法的特点.可有效地预测化合物的性能.在有机化合物结构性能研究中,环状化台物的研究相对较为E-nHn:~'3558101@sdauO00t.~3558IOI@37InelRemlwdApril28,2001;re~sedSeptetnber17,2001;~ptedOctober22.ⅫNo3王克强等:计算:烷烃沸点的新方法摹囝键贡献法困难,无论是基团贡献法.还是化学键贡献法,都需要刘同的环进行修正,拓扑方法也需要对环状化台物分别处理.例如在环烷烃的研究中,拓扑方法对链烷烃和环烷烃的研究是分成陌类进行的,Estrade【提出计算环烷烃拓扑指数的方法.Schultz对单环烷烃的沸点与分子结构之间的关系作了研究,取得了较好的结果.本文用基团键贡献法发展一种计算环皖烃沸点的方法.对环烷烃沸点的计算结果表明.计算值与实验值的一致性令人满意1基本原理和方法结构决定性能是化学中的一条基本规律.化合物的性能不仅与分子中原子的种类和数El有关,而日更与原子的连接性有关根据前文的研究结果町知,分子结构可用基团键进行表征.显然,分子中基团的种类不同,基团键就不同;分子中基团的连接性不同,基团键也不同为简化起见,我们暂不考虑分子中环的大小,将环烷烃分子中的基团分为烷烃基团和环烷烃基团两大类,据此确定分子中基团键的数日对于烷烃,分子中有4种基团:分子中存在着1O种基团键.对于环烷烃,分子中有7种基团c其中包括烷烃分子的3种基团).其中三种新的基团为:为简化起,我们将环烷烃基团与烷烃基团之问形成的基团键作为烷烃基团键处理,仅考虑环烷烃基团之间形成的新基团键.同时根据环的大小进行适,的修正.环烷烃分子中有3种新基团,根据排列组台原理可以确定环烷烃分子中存在着C{+C;=6种新的基团键.表1列出了烷烃和环烷烃分子中存在的16种基团键,其中前l0种(C~C139)为烷烃基团键,后6种(GB『1_~GB』)为环烷烃基团键.分子中基团键的种类和数日可以直接根据分子结构确定,也可以根据分子结构的邻接矩阵和染色矩阵计算得到,具体计算方法见前文6.环烷烃与烷烃的主要差别在于前者分子中存在着环状结构,我们分两步计算环烷烃的沸点.第一步暂不考虑环烷烃与烷烃的差别,将环烷烃摹团烷烃基团处理,计算得到环烷烃沸点的近似值rlI(烷烃);第二步考虑环烷烃与烷烃的差别,计算环烷烃基团和环对沸点的影响,计算沸点的修JE量△r¨1这样即可计算得到环烷烃的沸点:(环烷烃)=Tb(烷烃J+AT1.(1)因此,只要根据分子结构计算,(烷烃)和△,即可得到环烷烃的沸点r(环烷烃).自先.我们探讨烷烃沸点T(烷烃)的计算.沸点是与分子结构密切相关的物理量,分了结构不同,沸点就不同既然分子结构可用基团键表征,那么,沸电必然为基团键的函数,因此.,(烷烃)满足:rlIc烷烃)=fl(GB)].显然,从理论上确定这函数是相当困难的,我们用数学方法进行近似处理我们发现,烷烃的沸点r(烷烃)随着分子巾碳原子数(碳原子数"与基团键之间存在着定量关系[TJ)的增加而增大,烷烃同分异构体之问的沸差异可用基团键定量描述,即碳原子数反映烷烃沸点的体变化趋势,基团键则从细节上反映r分子结构差异对沸点的影响.对烷烃沸点的拟台结果表明,沸点随着分子中碳原子的增加而增大,随着基团键的变化而改变,且烷烃的沸点1(烷烃)/n与基团键数n(GB)的线性函数和n(GB)/n显着相关,因此.我们选择的函数为b(烷烃)/=144.723+∑(+/)n(GB)…(2)式中为分子中的碳原子数,12.(GB,)为基团键GB. 的数目,日和C是与基团键特性有关的常数(基团键参数).表l列出了本文用753种烷烃沸点数据J 拟合得到基团键参数.其次,我们探讨环对沸点的影响.环烷烃中环对沸点的影响△r与环的大小及环上取代基的位置有关,前者对沸点的影响可根据环的人小进j修正, 后者对沸点的影响可根据环烷烃的基团键修正我们发现,环对△.的影响不仪与环的大小和数日有关,而且与分子中的碳原子数有关,在环的数目和大小一定的条件下,环的影响随着碳原子数的增加而增大;环烷烃基团键对沸点的影响同样与基团键的数目和分子中的碳原于数有关,且基团键的影响随着分子中碳原子数的增加而减小因此,我们选择的△函数为:l96有机化学V ol22.2002Bj)e-O.frS~c/n+哺㈥Tal~~靴2ParametersB.雌ofth团e式中(GBj)为环烷烃基团键GBj的数目,日是与基团键特性有关的常数(基团键参数),为环的数目.A为环的修正量.表2列出了本文用256种环烷烃沸点数据[拟合得到基团键参数和环修正量.表3列出了确定基团键参数所用的基团键数目. 表1计算Tb(烷烃)的基团键参数日和l'al~e1ParametemBi,Cofthegroupbondsforcalculating (alkane)2计算结果及讨论应用表2提供的基团键参数日,,c和环修正量△,可直接根据分子结构计算环烷烃的沸点.值得指出的是,在确定分子中环的大小和数目时,应注意各环应尽可能独立,不能存在环包含环的情况,即以取小环为主,所取的大环不能包含小环.例如,四环[2, 2,I,02一,os,]庚烷(图1)分子中的环为:1个四元环,2个三元环,1个五元环;三环r5,2,1,o2]癸烷分子中有3个五元环计算沸点的基本方法是:第一ringsforcalculatingATb下标C表示环烷烃基团之间形成的基团键表3确定基团键参数所用基团键的数目NTalde3Numberofthegroupbondstrsedincorre]atingthe paratt~etem丑andC代码Ⅳ代码Ⅳ代码Ⅳ代码N代码GB112492187G355GB】0737GB"9lGB2l5l91337G252GBl_494GB】d14G璐l015G57027GB】246GB】51由于G玮仅存在于乙烷中.其基团键的数目为H川H2圈1P耳环[2,2.1,o2~,os:庚烷和--~[5.2.1,0=]癸烷Figure1Quadrlcyclo[2.2,1.~,.]heptmr~andlricyclo[52,1.02,]deeane步暂不考虑环烷烃与烷烃的差别,将环烷烃基团作为烷烃基团处理,根据分子结构确定分子中基团键的种类,数目,代人式(2)计算(烷烃);第二步考虑环烷烃与烷烃的差别,根据分子中环烷烃基团之03王克强等:计算环烷烃沸点的新方法一基团键贡献法197 间形成的基团键及环的大小和数曰,代人式(3)计算△Th,将计算得到的I(烷烃)和△I代人式(1)即呵计算得到环烷烃的沸点.例如四环一2,2,l,.",03']庚烷,"=7,第一步,将环烷烃基团作为烷烃基团处理,分子中有2种基团键:n(G)=2,n(GB7)=8,代人式(2)得到Th(烷烃)=3O4.24K;第2步,考虑环烷烃基团的与烷烃基团的差别.环烷烃基团之间形成2种基团键:n(GB】1):2,n(GB】3)=8,分子中有1个四元环,2个三元环和1个五元环,代人式(3)可得△=82.5lK,代人式(1)得(环烷烃)=(烷烃)+△】,=386.75K;对于三环[5,2,1,02,]癸烷,,fr=10,第一步,将环烷烃基团作为烷烃基团处理,分子中有3种基团键:n(G)=3,(G)=6,n(GB7)=3,代人式(2)得到Th(烷烃)=339,05K;第2步.考虑环烷烃基团的与烷烃基团的羞别,环烷烃基团之间形成3种基团键:n(GB)=3,n(GB】1)=6,n(GBl)=3,分子中有3个五元环,代人式(3)可得△Tb=120.41K,代人式(1)得I(环烷烃)=(烷烃)+△TI=45946K.为确定本文方法的可靠程度和适用范围,我们对环烷烃(包括环丙烷到环二十烷)进行计算,并与实验值I进行比较.限于篇幅,表4列出了部分环烷烃沸点的计算结果,全体256种环烷烃的计算结果绘于图2.表4部分环烷烃沸点it-算值(ca1.)和实验值Tb(exl~)的比较Table4CⅥ)aI1s0nofthec~leulatedboilingpointTbmt}Iexperime.t.1dataofsoⅡcyclOalka~es环烷烃Tk,(exp)Th(ca1)E1%环烷烃(唧)Tb(eat)£/%甲基环丙烷27388271.88—0.73戊基环烷4768247587—0201一顺一2-二甲基环丙烷31018310.81020辛基环己烷5367553303—0.69异丙基环丙烷154340.57272十一烷基环己烷58635581.60—0.811一甲基一反2-£基环丙烷331.8133714161十四烷基环己烷6281562366—071 1顺一2一反一3三甲基环丙烷332.853H430.48十七烷基环己烷664.1566o58—054己基环丁烷34:375344.300.16=十烷基环己烷6951569332—0261一反一2-二甲基环丁烷33315337.30l24二十三烷基环己烷72215722.560.06秫-1'1AIA1nm+"1…AA…丙基环戊烷己基环戊烷壬基环戊烷十二烷基环戊烷五烷基环戊烷十八烷基环戊烷=十一烷基环1萱烷二四烷基环戊烷=十七烷基环戊烷三}烷基环戊烷三十三烷基环戊烷三十六烷基环戊烷己摹环戊烷】一反_2'二甲基环戊烷丙基环戊烷l一甲基一顺一2一乙基环戊烷】一甲基一反一3一乙基环戊烷1一』匝一2一顺一3一三甲基环戊烷l一顺一2顺一4-i甲基环戊烷丁基环戊烷特丁基戊烷1一甲基一反一2一丙基环戊烷41)4.1O476055351558435626.15662.1569'3157201574515767】57s7.15805.1537662 365024O4.10 401.20 39425 39615390.15 429754l800419.5241)447O.09 473】8—0.60 529.82一1.00 5_77.91—1.10 61952—106 65601—093 68834—069 717.】9—041 743.09—028 7054.5—009 787610068o6阻0.21 377.86033 37083】59 404.47009 39856—0.66 394.980l9 39150一l17 38793—0.57429.03—0.17422.5811O422.55072=十九烷基环己烷三十=烷基环己烷三十五烷基环己烷甲基环己烷1一顺一2一=甲基环己烷1一反一3-二甲基环己烷l雨基环己烷1甲基一顺2-乙基环己烷l一甲基一反一3一己基环己烷1,1,2一三甲基环己烷】一顺0丽一3一三甲基环已烷1一顺2一顺4三甲基环己烷l一反2一反4三甲基环己烷二环己甲烷1,】一二环己丁烷l_l一二环己庚烷1.1一二环己癸烷1.1一二环己十三烷】,】一二环己十六烷环千烷环十二烷环十五烷68.15788l5妍15374084O2939760 42987 42925424】5 418.35426l54211541437525.95 566.12605l564.O15 670.15 697.15 451555l2l5559】5772O58 794080758】3.640.8O 37806106 39953—084 39596—041 43】350.34 424.87一1.o2 421.63一O59 4】575—062 4l779一】96 414.55一1.57 414.5500452489一O205690305l608.9l0.62643.42O516736】()527002】04444896—0.57510.75—02755537一O68l98有机化学V o1.22,2g02续表环烷烃TbE/%环烷烃To7E/%(exp)(ca1)(exp.)(ca1)1一甲基一1一异而基环戊烷42l1542319048环十八烷5981560246()721一甲基一顺一3一异丙基环戊烷4151541717049联环庚烷56415565870311圳2一二己基环戊烷4267l42315~083环戊基环己烷4882548244—119I一反一3一二乙基环戊烷423154199l~0762,4,6-三甲基二环[3,1.1]庚烷4426543597—15】l一顺一2一二甲基一1一乙基环戊烷41715417740142一甲基二环[2,2.2]辛烷43l15435541O21一顺一2一一甲基一反一3一乙基环戊烷418.15416.07~050二环[2.1.O]戊烷318.653155l一0981一顺一2一二甲基一顺4乙基环戊烷420.1541284~17,4环『1n]_丁辟1'11钔一n11一顺一3一_I甲基一反一2一乙基环戊烷410.15416.07I44四环[2,2.I,.03]庚烷381.15386.75I.471一顺一3一二甲基反4乙基环戊烷410.15412.84065顺一一环[3.3,0]辛烷410.15412300.521.1,2,2_四甲基环戊烷496.15405.27~0.22反.=环[3,3.O]辛烷405.15412301.76 1.1-顺一2_顺一4一四甲基环戊烷403.15403.720.142一甲基二环l2,2,2辛烷43115435541.o21,1一顺一3一顺一4一四甲基环戊烷496.154.9O.89~I.313二环4,2.0一辛烷4091540892-一0.嘶1,2,2-反一3一四甲基环虎烷4l1.15409.79~0.33二环4.1,0.庚烷3896538017—2.43I一顺一2一反一3一婀4四甲基环戊烷4O415408.991.20三环:5,2,l,02癸烷4661545946—1.44I一反2一反一3一顺4四甲基环戊烷4O4154O8991.20螺[2.2]戊烷3131530746一12己基环己烷4O493406.5904l顺一六氢茚44O1543886—0.29表中环烷烃是用计算机选取的,方法是:对256种环烷烃编号为No1~256,选取No. 2,N05.8,….约占总数的三分之一!II2环烷烃沸点计算值Tb(c)与实验值(.xp)的比较Figure2(_^】m90nofthecalctrlatedboihngI~intTh(ca1)htheexperimentaldatars(e~p)ofcycl0alkane对256环烷烃的计算结果表明,无论是对含有一个环的简单环烷烃,还是对含有多个环的复杂环烷烃,沸点的计算值与实验值".]的一致性令人满意,计算结果的平均绝对误差3.29K,平均相对误差0.71%在计算的256种环烷烃中,计算误差小于0.5%的106种,计算误差在0.5%~l0%之问的90种,计算误差1.0%一1.5%之间的38种,计算误差1.5%~2.0%之间的l2种,计算误差2.0%~2.5%之间的6种,计算误差2.5%~3.0%之间的2种.计算误差大于3.0%的2种,最大计算误差3.13%.显然,绝大多数化合物的计算误差在l0%以内.文献上应用较广的计算烷烃沸的方法是Jobaek方法",该方法对上述256种烷烃计算结果的平均绝对误差46.89K,平均相对误差7.1】%.显然,与Joback方法相比,基团键贡献法将计算精度提高了一个数量级.因此,基团键贡献法具有适用范围,..,计算结果可靠的特点.此外,基团键贡献法是根据分子中基团的特性和连接性发展的,易丁实现计算机程序化设计,我们开发了相应的计算机程序,只需输A少量分子结构参数即可计算得到沸点预测值3结论本文根据分子中基团的特性和连接性,发展了一种根据计算环烷烃沸点的新方法——基团键贡献法,该方法既考虑了分子中基团的特性,又考虑了基团的连接性,同时具有基团贡献法和化学键贡献法的特点,对环烷烃(包括单环和多环烷烃)的计算结果表明,沸点计算值与实验值的一致性令人满意.No3王克强等:计算环烷烃沸点的新方法一基团键贡献法l99 1Reid,R.C;Prausrdtz,J.M;Poling,BE.Properties‰andt/qt,i&,4thEd.,McGraw-HillBook Company.NewY0rk.1987.2Xu,ZH;Mao,Z.X.;Wang,LS;Pang,YLHandbo&Chemi*'alProperey"EstimationMeth,~,Huaxue Got~,gyeChiCle.Bing,I99l(inCtfine~)(许志宏.毛卓雄,王乐珊,鹿瑶琳译,亿学性质估算方法手册,化学工业出版社,北京,1991.)3Wang,K.Q;Hu.YChin,.忡Ctwm.1997,17,230(inChinese)(王克强.胡英,有机化学,1997.t7.230.)4Wang,KQJ~.jiHngHuax,w1996,13.182 (inChisese)(土克强.计算机与应用化学,1996,17,182.)5Gutman,I;Estrade,E.JChemComputSci1996.36.5416schuhz.HP:Schultz1993.33,2407Wang,K.Q.Ch/nJChit~se)PjCheml《0唧nOrgCtwm.1999,19,304(in(于克强,有机化学,1997,19,304)8:~ericanPetroleumhmfituteResearchProject44,Seleaed pⅡofl#opertyofH)~warbonsandRelatedCom~unds1lrmo[hIacResearchCenterdtheAmericanPetroleum hrstitute,Texas,1,Tablea9Weast,RCCRCHandbookChen~tO,andm.66thFA.CRCPress.h,e..Horida,l986,04210Dean,J.Ahinge'HandbookofChemic-.13thEd. McGraw-HillBookCompany,NewY ork.1赠5.PP.7~82. 】lMa,PS踊uHuagong肛^u卧咖S,%uce,Huaxue Gon~,eChubami~e,l~ijing,1993(inChinese).(马肺生,石油化工数据手册,化学工业出版社,北京, 1993,(Y0104281LI,L.T:F,YY)。
UNIFAC基团贡献法研究及应用进展_魏静

于气液平衡、液液平衡、固FAC 基团贡献法的研究进展
1.1.1 相互作用参数 anmk 的修正
Nagata 和 Ohta [10]针 对
中的
anmk 研究发现,anmk 是随温度变化的函数,而不是 常数,因此提出了 anm(k T)的关联式:
1.1.2 晶格配位数 Z 的修正 Skjolld- JΦrgense 等[11]研究(3)式 中晶格配
DOI:10.13840/21-1457/tq.2008.06.001
第 37 卷第 6 期 2008 年12 月
当代化工 Contemporary Chemical Industry
Vo1.37,No.6 December,2008
UNIFAC 基团贡献法研究及应用进展*
魏 静,解新安,丁年平,刘华敏
此模型的推算精度可满足工程需要,平均相 对偏差在 10%左右。缺点是发表的参数太少,适 用的温度范围过窄,除基团 CH2 与 COH 之间有 15,30,45 和 55℃的参数外,其余均只有 25℃的 参数,大大限制了它的应用。
(9) 式中:K—缔合常数;
Δho—组分氢键生成焓; xB,φB—溶液中组分的摩尔分率和容积分率。
化热:
,再 由 式(13)得 到 纯
组分蒸汽压。
(3)典型气液平衡预测
预测典型的气液平衡体系是 UNIFAC 模型
的主要功能。最初它只用于预测 300~425 K、中
低压范围内非电解质溶液体系的汽液平衡,并且
可预测的体系范围也有限,所提供的参数也较
少。经过多年的修正和补充,UNIFAG 模型的参
数已发展到了 50 个主基团,下属 108 个亚基团,
位数 Z 发现,晶格配位数 Z 是温度的函数,而不 是恒为 10,即:
北京化工大学高等化热大作业-基团贡献法

浅谈基团贡献法引言不久前,我前往导师XXX的办公室,与他沟通交流学业上的问题。
谈话间,王老师提及的一种建立自由基聚合反应过程机理模型的方法──链节分析法[1],引起了我极大的兴趣。
这一方法可以对复杂的聚合反应过程进行准确的动态模拟,解决了以往须同时求解无限多个微分方程才能模拟聚合过程的难题。
通过这篇文献[1]我得知,对于高分子聚合物体系的热力学性质的处理,一直是建立聚合反应机理模型的难题之一。
此法[1]不再把组成和链长不同的无穷多的聚合物大分子作为组分,而是将流程模拟系统的组分中出现的C、E、A·、R·等基本单元,参考其相应的单体物性,从而得到大分子聚合物的各种热力学性质。
高分子的绝大部分热力学性质如密度ρ、比热容C p、焓H、摩尔体积V b、各种临界参数都能利用Joback基团贡献法,由基本单元的物性计算得到。
联想到化热课堂上与基团贡献法有关的似乎只有UNIFAC模型,因此我想对物性估算法中的基团贡献法展开讨论,描述各种不同的方法并加以简单的评价。
这便是本题目的来源。
第1章临界参数估算方法不论是通过自己对化工热力学的学习,还是通过对文献的查阅,都不难得出这样的结论:对纯物质而言,临界参数是最重要的物性参数之一。
其实,在所有的PVT关系中,无论是对应状态法还是状态方程法都与临界数据有关。
对应状态法已成为应用热力学的最基本法则[2],借助于对应状态法,物质的几乎所有的热力学参数和大量的传递参数可被预测,而对应状态法的使用又强烈地依赖于临界数据。
此外,涉及到临界现象的高压操作,如超临界萃取和石油钻井[2],也与临界参数密切相关。
总而言之,临界数据是化工设计和计算中不可缺少的重要数据。
临界参数如此重要,前人自然少不了花费巨大精力对其进行收集、整理和评定,但据我了解,所收集的临界数据大多局限于稳定物质的临界数据。
虽然近几年对不稳定物质临界参数测定方法的研究在开展着,并且也测定了一些不稳定物质的临界参数,但大部分的不稳定物质仍由于测定难度大而缺乏实测的临界数据。
基团贡献法预测含极性基团离子液体对气体的溶解选择性对气体的溶解选择性

关键 词 :离 子 液 体 ;溶 解 ;极 性 基 团 ;基 团贡 献 法
DOI 0 3 6 /.s n 0 3 — 1 7 2 1 1 . 0 :1 . 9 9 jis . 4 8 1 5 . 01 . 0 0 2
中 国分 类 号 :TQ 0 3 1 1 .
文献 标 志码 : A
文 章编 号 :O 3 —1 5 ( 0 1 1 一2 8 一O 4 8 17 2 1 ) O 64 7
De e m i a i n o a e e tv t f s l t o n RTI t l r t r n to f g s s l c i iy o o u i n i Ls wih po a g o p b r u o r b to e h d r u y g o p c nt i u i n m t o
W U a Y nhu 。 YU hi u i S k n, D UAN ng h o, LiTo g i Yo c a n m ng
( p rme to Ch mity ,To g i ie st De a t n f e sr n J v riy,S a g a 0 0 2,C ia Un h n h i2 0 9 hn )
基于正规溶液理论根据文献发表的常规咪唑盐离子液体对不同气体的溶解度数据结合基团贡献法预测了常压下co2ch4n2co在含氰基醚键等极性基团的咪唑盐离子液体中的亨利系数进而得到不同气体在该类离子液体中的溶解选择性
第 6 2卷
第 1 期 O
化
工 学
报
Vo1 6 N o 0 .2 .1 Oc o r 2 t be 01 1
预测烷烃折光指数的新方法—基团键贡献法

题目:预测烷烃折光指数的新方法—基团键贡献法近年来,随着石油化工领域的发展,对于烷烃等化合物的性质预测和评估变得愈发重要。
其中,烷烃折光指数是描述烷烃分子中碳氢键性质的重要参数之一。
传统的预测方法主要依赖于分子结构的拓扑指纹或者理论计算,然而这些方法在预测精度和适用范围上存在一定的局限性。
本文将探讨一种新的方法——基团键贡献法,来预测烷烃折光指数,并分析其在实际应用中的优势和局限性。
1. 烷烃折光指数简介烷烃是一类碳氢化合物,其分子中主要由碳氢键构成。
折光指数是介质中传播光线速度与真空中光线速度的比值,它与分子的极性和结构有关。
在石油化工领域,烷烃折光指数的准确预测对于原油质量评估和燃料性能优化具有重要意义。
2. 标准方法与问题传统的预测方法主要包括量子化学计算、分子对接模拟和拓扑指纹分析。
然而,这些方法在预测大量烷烃混合物的折光指数时存在计算复杂度高、精度不够等问题,难以满足工程实际需求。
3. 基团键贡献法原理基团键贡献法是将烷烃分子中的每一个碳氢键看作一个基团,通过统计每种基团对折光指数的影响,建立基于基团键的预测模型。
该方法通过实验数据验证和拟合,实现了对烷烃折光指数的准确预测。
4. 优势和应用相比于传统方法,基团键贡献法在预测速度和精度上都有较大优势。
该方法适用于各类烷烃混合物的折光指数预测,具有较好的通用性和适用范围。
在石油化工工程中,该方法可以为原料选择、生产过程优化等方面提供重要的理论指导。
5. 局限性和展望然而,基团键贡献法也存在一些局限性,例如在一些特殊结构或者多环烃方面的适用性仍有待验证。
未来的研究可以进一步优化基团键贡献法的模型,并且结合机器学习和人工智能等技术,拓展其在预测烷烃性质中的应用。
总结回顾本文探讨了基团键贡献法在预测烷烃折光指数中的应用,指出了该方法相对于传统方法的优势和局限性。
在石油化工领域,基团键贡献法有望成为一种有效的烷烃性质预测方法,并为相关工程应用提供重要的理论支持。
化工热力学

i
0
对二元系统:
x1d ln γ1 x2 d ln γ 2 0
用途: 由已知组分的活度系数计算未知组分的活度系数。
4-9-2 不对称超额性质
定义:真实溶液与理想稀溶液的摩尔性质之差
若M=G:
M
G G
is*
E
M M
is*
is
G
E*
xi (G i Gi ) xi RT ln γ* i
is fi
其中上标 is " 理想稀溶液 "
2 溶质的计算:Herry规则
H i , solvent xi
H i , solvent 溶质i在溶剂中的 Herry 常数
4-8
活度系数及其归一化
•
根据参考态不同活度系数分为:
1 对称归一化的活度系数 2 不对称归一化的活度系数
4-8-1对称归一化的活度系数
4-10-4 NRTL方程和Uniquac方程
为了改进Wilson方程,出现了许多修正的Wilson方
程,有代表性的有NRTL和Uniquac方程。
优点: 1.二者和Wilson一样,能进行多元系统的计算。 2.能用于液相分层系统,因此可用于L-L平衡计算。
1.NRTL方程:
ln i
x j jiG ji
2 3 4 ln γ1 2 x2 3 x2 4 x2
其中 2 , 3 , 4 仅是T的函数,求:在同T下溶质组分 的活度系数模型。 解: ∵在低P下,对液体的影响不大,故可按 等T、P处理。由G-D的简化式: 有 x d ln γ 0
i
i
x1d ln γ1 x2 d ln γ 2 0
基团贡献法及其应用讲解

5.2.2 分子性质与基团元贡献值的关联
分子性质的值与基团元贡献值之间的关联有下列的一些形式:
(1)直接加和法 就是分子性质值直接由各基团的贡献值以及各
种修正项直接加和而得,即 A niai
i
式中A代表分子的某一性质;ni为i基团的数目;ai为i基团的元贡献或 某种修正项。
(2)函数式法 这种关联法将分子的性质A作为某些参数B,
参照基团所在分子的主体结构及其特点将同一基团再加细分 :如: OH基团,在醇与酚中表现出不一样的性质
按照分子的立体构型划定基团 :顺反结构基团
在划分基团时往往把有共轭效应的基团分开:如1,3丁二烯中的C-C键 比没有共轭分子中的C-C键要短一些
同系物的第一化合物常被当作一个基团单独列出:如甲酸与羧基相连 的是氢原子,而醋酸与羧基相连的是碳原子
5.2.3 基团贡献法中的修正项
分子内构型强烈的影响分子性质的值,而采用纯粹由基团 性质的元贡献值加和,往往不能充分反映分子构型的差异 对分子性质影响的大小。除按基团加和外,常常还要加上 一些修正项,这些修正项常见的有:
1)环式构型修正
如环丙烷、环丁烷、环戊烷、环己烷与环庚烷比较: n<6 的环烃每个-CH2-具有不同的燃烧热,n6以后的环烃每个CH2-具有正常和相同的燃烧热。因此估算环状结构的化合 物的性质时常有修正项,尤其是碳数少的环。
同一种键在各种化合物中不但基本保持一定长度,而且,在典型的
键中A-B的距离可以很准确的表示为A-A及B-B距离的算术平均值
(A和B均代表原子,d代表距离)
d AB
1 2
(d
A
A
dBB )
例如(硅晶体中),由此求得
dCC 1.54A,dSiSi 2.34A
应用基团键贡献法计算炔烃的密度

第33卷第4期河南师范大学学报(自然科学版)Vol.33 No.4 2005年11月Journal of Henan Normal Uniuersity(Natural Science)Nou.2005 文章编号:1000-2367(2005)04-0098-04应用基团键贡献法计算炔烃的密度*王捷(许昌职业技术学院,河南许昌461000)摘要:根据分子中基团的特性和连接性,将基团贡献法和拓扑方法结合在一起,发展了一种计算炔烃密度的新方法———基团键贡献法,该方法具有基团贡献法适用范围广和拓扑方法计算结果准确可靠的特点.对85种炔烃密度的计算结果表明,计算值与实验值的一致性令人满意.关键词:结构性能关系;分子结构;基团键;基团键贡献法;密度;炔烃中图分类号:0621.2 文献标识码:A结构性能关系的研究,是化学中一个十分活跃的研究领域,近年来,拓扑学的发展及其向化学领域的渗透为结构性能关系的深入研究提供了一种有力的工具[1].多年来,国内外许多研究者作了大量研究的工作,发展了许多根据分子结构预测化合物性能的方法[2~3],其中应用最广的是基团贡献法.基团贡献法是根据分子中的基团计算分子性能的方法,该方法具有适用范围广的特点,但对同分异构体的区分能力较差,计算结果难以令人满意.拓扑方法是近年来发展起来的方法,该方法根据分子中原子或基团的连接性计算分子的性能,对同分异构体有良好的区分能力,计算结果可靠,但适用范围相对较小.显然,基团贡献法的不足之处主要是未考虑分子中基团之间的连接性,拓扑方法的不足之处是未考虑分子中基团的特性,本文在前文[4~6]工作的基础上,根据分子中基团的特性和连接性,将基团贡献法和拓扑方法结合在一起,发展了一种普适的计算有机化合物性能的新方法———基团键贡献法.作为系列工作之一,本文探讨炔烃的密度与分子结构之间的定量关系,发展一种计算炔烃密度的方法.对炔烃密度的计算结果表明,计算值与实验值的一致性令人满意.!"基本原理和方法结构决定性能是化学中的一条基本规律.化合物的性能不仅与分子中基团的种类和数目有关,而且更与基团之间的连接性有关.根据文献已发表[6]的研究结果,分子中基团的特性和连接性可用基团键表征,基团键指两个基团之间成的化学键,基团键的重点是考虑化学键所连接的基团,因此基团键既包括基团的特性信息,又包括基团的连接性信息.分子中基团键的数目,可根据邻接矩阵和顶点矩阵用数学方法计算或根据分子结构确定.显然,分子中基团的种类不同,基团键就不同;分子中基团的连接性不同,基团键也不-”、同.因此,基团键能够有效地区分化合物的同分异构体.对于炔烃,分子中存在着6种基团:“CH3 -”、“>CH-”、“>C<”、“CH E”、“-C E”,前4种为烷烃基团,后2种为炔烃基团.对于烷烃的“-CH24种基团,根据排列组合原理,可确定烷烃基团之间形成的10种基团键[6];炔烃中的2种基团之间可形成3种基团键,烷烃基团与炔烃基团之间可形成4种基团键,故炔烃分子中存在着17种基团键(包括烷烃分子中已有的10种基团键[6]).炔烃基团形成的基团键见表1.密度是与分子结构密切相关的物理量,分子结构不同,密度就不同.既然分子结构可用基团键表征,那*收稿日期:2004-11-16基金项目:河南省教育厅自然科学研究计划项目(2004601086)作者简介:王捷(1959-),男,河南临颍人,许昌职业技术学院副教授,主要从事有机化学研究工作.么,密度d 必然为基团键GB i 的函数.考虑到不同基团键对密度的影响程度不同及当基团键无限增加时密度值趋于有限值的事实,为得到一个普遍适用于各种化合物的密度计算公式,本文采用和烷烃密度相同的的数学计算公式[6]d =2i c i n (GB i )/2iw i n (GB i )(1)式中n (GB i )为基团键GB i 的数目,c i 和w i 是与基团键特性有关的常数(基团键贡献值).由于炔烃基团键中包括烷烃基团键,且烷烃基团键的贡献值已经确定[6],因此只需确定炔烃基团键的贡献值即可.表1列出了本文用计算机拟合得到的炔烃基团键的贡献值c i 和w i .表1 炔烃基团键对密度的贡献值c i 和w i代码基团键c i wi代码基团键c i wiGB 1CH 3-CH 2- 1.3569 2.5234GB 9l l --ll -C C 0.3696-1.2692GB 2CH 3-CH <1.19232.0640GB 10CH E CH ——————GB 3CH 3-ll-C 1.1101 1.8206GB 11CH E C - 1.1708 3.6512GB 4-CH 2-CH 2-0.8632 1.0000GB 12-C E C -0.7392 4.1307GB 5-CH 2-CH <0.69860.4354GB 13E C -CH 3 1.29480.3338GB 6-CH 2-ll-C 0.61640.0890GB 14E C -CH 2-0.8012-0.9995GB 7>CH -CH <0.5341-0.2492GB 15E C -CH <0.6336-1.4660GB 8-ll->CH C 0.4519-0.7035GB 16E -l l-C C 0.5544-1.5736注:由于基团键GB 10仅存在于乙炔中,乙炔在293.15K 、101.325kpa 条件下不能以液体稳定存在,故表中无GB 10的贡献值.!"计算结果及讨论式(1)揭示了炔烃的分子结构与密度之间的定量关系,应用式(1)和表1提供的基团键贡献值,可根据分子结构计算炔烃的密度.计算炔烃密度的基本方法是:首先由分子结构确定基团键的种类和数目,然后代入式(1)计算即可,例如,2-己炔CH 3-C E C -CH 2-CH 2-CH 3,其分子中的基团键为:n (GB 1)=1,n (GB 4)=1,n (GB 11)=1,n (GB 12)=1,n (GB 13)=1,将基团键代入式(1)可计算得到2-己炔的密度d =0.7324(Mg ·m -3).为确定式(1)的可靠程度和适用范围,我们用式(1)计算C 5到C 40炔烃的密度,并与实验值[7]比较,结果列于表1.表2 部分炔烃密度d (Mg ·m -3)计算值d (caI )与实验值d (exp )的比较NO 炔烃d (exp )d (caI )E 1E 2/%NO炔烃d (exp )d (caI )E 1E 2/%11-丁炔0.65000.6432-0.0068-1.04123,3-二甲基-1-丁炔0.66780.67050.00270.4022-丁炔0.69100.69380.00280.40131-庚炔0.73280.7240-0.0088-1.2131-戊炔0.69010.6789-0.0112-1.63142-庚炔0.74800.7409-0.0071-0.9542-戊炔0.71070.7000-0.0107-1.50153-庚炔0.73810.7237-0.0144-1.9653-甲基-1-丁炔0.66600.6640-0.0020-0.30163-甲基-1-己炔0.71850.72110.00260.3661-己炔0.71550.7045-0.0110-1.53174-甲基-1-己炔0.73270.7298-0.0029-0.4072-己炔0.73130.7234-0.0079-1.08185-甲基-1-己炔0.72740.7204-0.0070-0.9683-己炔0.72270.7042-0.0185-2.56194-甲基-2-己炔0.73860.7378-0.0008-0.1093-甲基-1-戊炔0.70370.7013-0.0024-0.34205-甲基-2-己炔0.73780.7372-0.0006-0.08104-甲基-1-戊炔0.70450.7006-0.0039-0.55212-甲基-3-己炔0.72490.7116-0.0133-1.83114-甲基-2-戊炔0.71570.7094-0.0063-0.89223-乙基-1-戊炔0.72710.73040.00330.4699第4期 王 捷等:应用基团键贡献法计算炔烃的密度00l河南师范大学学报(自然科学版)2005年(续表2)NO炔烃!(exp)!(caI)"l"2/%NO炔烃!(exp)!(caI)"l"2/% 233,3-二甲基-l-戊炔0.70770.7l030.00260.3755l-三十六炔0.82920.83260.00340.4l 243,4-二甲基-l-戊炔0.72360.728l0.00450.6256l-三十七炔0.82990.83340.00350.42 254,4-二甲基-l-戊炔0.7l420.72l50.0073l.0257l-三十八炔0.83050.834l0.00360.44 264,4-二甲基-2-戊炔0.7l760.7086-0.0090-l.2658l-三十九炔0.83l l0.83490.00380.4527l-辛炔0.74680.739l-0.0077-l.0359l-四十炔0.83l70.83560.00390.4628l-壬炔0.75790.75l3-0.0066-0.87602-辛炔0.75940.7545-0.0049-0.6529l-癸炔0.76700.76l3-0.0057-0.746l2-壬炔0.76860.7654-0.0032-0.4230l-十一炔0.77460.7697-0.0049-0.63622-癸炔0.77630.7743-0.0020-0.263l l-十二炔0.78090.7768-0.004l-0.52632-十一炔0.78260.78l7-0.0009-0.l232l-十三炔0.78640.7829-0.0035-0.45642-十二炔0.78800.7880-0.0000-0.0033l-十四炔0.79l00.7882-0.0028-0.36652-十三炔0.79270.79340.00070.0834l-十五炔0.795l0.7928-0.0023-0.29662-十四炔0.79670.79800.00l30.l635l-十六炔0.79870.7969-0.00l8-0.22672-十五炔0.80030.802l0.00l80.2236l-十七炔0.80l80.8006-0.00l2-0.l5682-十六炔0.80340.80570.00230.2837l-十八炔0.80500.8038-0.00l2-0.l4692-十七炔0.80620.80890.00270.3338l-十九炔0.80750.8068-0.0007-0.09702-十八炔0.80870.8ll70.00300.3839l-二十炔0.80980.8094-0.0004-0.047l2-十九炔0.8ll00.8l430.00330.4l40l-二十一炔0.8ll80.8ll90.000l0.0l722-二十炔0.8l300.8l660.00360.454l l-二十二炔0.8l370.8l4l0.00040.05733-辛炔0.75220.7389-0.0l33-l.7742l-二十三炔0.8l540.8l6l0.00070.09743-壬炔0.75970.75l l-0.0086-l.l343l-二十四炔0.8l700.8l800.00l00.l2753-癸炔0.76580.76l l-0.0047-0.6l44l-二十五炔0.8l840.8l970.00l30.l6763-十一炔0.77l30.7695-0.00l8-0.2345l-二十六炔0.8l980.82l30.00l50.l8773-十二炔0.77620.77660.00040.0546l-二十七炔0.82l00.82280.00l80.22783-十三炔0.78070.78270.00200.2647l-二十八炔0.82220.82420.00200.24793-十四炔0.78470.78800.00330.4248l-二十九炔0.82330.82550.00220.26803-十五炔0.78840.79270.00430.5449l-三十炔0.82430.82670.00240.298l3-十六炔0.79l70.79680.005l0.6450l-三十一炔0.82530.82780.00250.3l823-十七炔0.79470.80040.00570.725l l-三十二炔0.82620.82890.00270.33833-十八炔0.79750.80370.00620.7852l-三十三炔0.82700.82990.00290.35843-十九炔0.80000.80660.00660.8353l-三十四炔0.82780.83080.00300.37853-二十炔0.80230.80930.00700.8754l-三十五炔0.82850.83l70.00320.39注:表中E l和E2分别表示密度计算结果的相对误差和绝对误差.对85种炔烃的计算结果表明,密度的式(l)计算值与实验值[7]的一致性令人满意,平均绝对误差0.0042(Mg·m-3),平均相对误差0.56%,其中计算误差小于l.0%的炔烃7l种,计算误差在l.0%~ 2.0%之间的炔烃l3种,计算误差大于2.0%的炔烃l种,最大计算误差2.56%.显然,大部分炔烃密度的计算误差在l%以内.因此,式(l)具有适用范围广、计算结果可靠的特点.这一事实也说明,拓扑方法与基团贡献法的结合,可以更有效地预测分子的性能.作为进一步推广,我们用该方法计算了烷基苯、脂肪醚、脂肪酸等化合物的密度,均获得了较理想的结果,有关这方面的工作将另文报道.此外,本文方法是根据分子中基团连接性发展的,易于实现计算机程序化设计,我们开发了相应的计算机程序,只需输入少量分子结构参数即可计算得到密度预测值.3 结 论本文根据分子中基团的特性和连接性,发展了一种根据分子结构计算炔烃密度的方法,该方法将基团贡献法和拓扑方法结合在一起,具有基团贡献法适用范围广和拓扑方法计算结果可靠的特点.对85种炔烃的计算结果表明,密度计算值与实验值的一致性令人满意,计算精度优于基团贡献法.参 考 文 献[1] 王化云,江元生.应用拓扑指数预测化学性质[J ].化学通报,1992,(11):6-11.[2] Reid R C ,Prausnitz J M ,PoIing B E.Properties of Gases and Liguids ,4th edition [M ].New York :McGraw-HiII Book Com-pany ,1987:1-80.[3] [美]W J 莱曼,W F 雷尔,D H 罗布拉森著.许志宏,毛卓雄,王乐珊,庞瑶琳译.化学性质估算方法手册[M ].北京:化学工业出版社,1991:455-794.[4] 王克强,胡英.硫醇和硫醚的分子结构与折光指数之间关系的拓扑化学研究[J ].有机化学,1997,17(3):230-233.[5] 王克强.计算环烷烃沸点的新方法———基团键贡献法[J ].有机化学,2002,22(3):194-199.[6] 王克强.预测烷烃密度的新方法———基团键贡献法[J ].有机化学,1999,19(3):304-308.[7] American PetroIeum Institute Research Project 44.SeIected VaIues of Property of Hydrocarbons and ReIated Compounds [M ].Texas :Thermodynamic Research Center and the American PetroIeum Institute ,1972.TabIe 4b.Calculating the Density of Alkyne Using theGroup Bond Contribution MethodWANG Jie(Xuchang VocationaI TechnicaI CoIIege ,Xuchang 461000,China )Abstract :Based on characteristics and connectivity of the groups in moIecuIes ,the group contribution method and topoIogicaImethod was combined together ,a new method was deveIoped which can be used to caIcuIate the density of aIkyne from moIecuIar struc-ture.The caIcuIated resuIts showed that the caIcuIated density of aIkyne were in good agreement with the experimentaI data ,and the mean reIative deviation was 0.56%for 85aIkynes ,and had advantages over the group contribution method.Key words :structure property reIationship ;moIecuIar structure ;group bond ;group bond contribution method ;density ;aIkyne101第4期 王 捷等:应用基团键贡献法计算炔烃的密度。
基团贡献法及其应用

5.1.2 分子内原子的作用距离
✓有机化合物分子中直接相连两个原子之间的作用多为共价键,共价 键的键长多数在1至2Å之间 ✓分子内以形成化学键的相邻两原子的相互作用最为强烈 ✓诱导效应 ✓共轭效应 ✓空间效应
总目录
本章目录
上页
下页
5.1.3 结构单元的选择与加和性规则的近似程度
加和性规则是一种近似规则,其近似的程度取决于我们所 选择的结构单元精细程度
子中的手征性碳原子数。
对CӨp和HӨf,则不必作对映异构体修正。
总目录
本章目录
上页
下页
5.3 基团贡献法估算纯组分的基本性质
5.3.1 纯物质临界性质估算
临界性质包括临界温度(Tc)、临界压力(Pc)、临界体 积(Vc)等。在各种临界参数估算法中,比较通用而又可 靠的是基团加和法。
1)Joback法
4)邻位修正
由于邻位的两个基团(或原子)较接近,基团之间便产 生排斥作用,这是不相邻基团所没有的,这种相互作用不能 忽略,而基团贡献参数又无法反映它的存在,故需另加设邻 位修正。
总目录
本章目录
上页
下页
5)对称性修正 用键贡献法和基团贡献法估算理想气体熵SӨ时,通常
必须作分子对称性的修正。 ▪对称数为定义是:分子刚性转动时,分子内相同原子 (或基团)出现独立互换的总次数(不得反转)。为便于 计算,通常把分解为外和内,即: =外. 内 ▪计算分子的对称数一些规律 CP
键中A-B的距离可以很准确的表示为A-A及B-B距离的算术平均值
(A和B均代表原子,d代表距离)
d AB
1 2
(d
A
A
dBB )
例如(硅晶体中),由此求得
dCC 1.54A,dSiSi 2.34A
一种基于基团贡献法的气体GWP计算方法

一种基于基团贡献法的气体GWP计算方法张聪;陈庆国;林林;邱睿【期刊名称】《绝缘材料》【年(卷),期】2018(51)10【摘要】为了对潜在SF_6替代气体进行筛选,采用基团贡献法计算含有碳碳不饱和键、氢元素等官能团的气体与大气中OH自由基的反应速度。
利用气体与OH自由基的反应速度算出气体的大气寿命,并使用密度泛函理论(DFT)在原子和分子层面上计算出气体的辐射效率(RE),然后结合气体的大气寿命与RE值计算出气体的全球变暖潜能值(GWP)。
结果表明:使用基团贡献法计算气体的大气寿命相比传统的过渡态法具有计算速度快、计算成本低以及精度高等优点,将计算结果与实验结果进行对比,证明基于基团贡献法可以准确地计算大气寿命,使用DFT方法可以计算出气体的RE值,然后结合气体的RE值和大气寿命可以准确地计算出气体的GWP值。
【总页数】5页(P78-82)【关键词】SF_6替代气体;基团贡献法;气体辐射效率;大气寿命;GWP【作者】张聪;陈庆国;林林;邱睿【作者单位】哈尔滨理工大学【正文语种】中文【中图分类】TM213【相关文献】1.一种适用于推算气态乙烷系氟里昂粘度的基团贡献法 [J], 吕萍;刘志刚2.基团贡献法预测离子液体性质及酸性气体溶解度 [J], 刘雅茹;刘宝友3.基团贡献法预测含极性基团离子液体对气体的溶解选择性 [J], 伍艳辉;于世昆;段永超;李佟茗4.基于高阶基团贡献法与COSMO-SAC模型的溶剂设计方法 [J], 唐坤;刘奇磊;张磊;刘琳琳;都健;孟庆伟5.基于基团贡献法的制冷工质GWP计算探讨 [J], 安青松;马一太;田华因版权原因,仅展示原文概要,查看原文内容请购买。
化工热力学基团贡献法

配 位 数 Z 取 为
ln γ
R i
( = ∑ν ki ) (ln Γk − ln Γk( i ) ) k
N
(i ) Γk是基团 的活度系数 是基团k的活度系数 的活度系数; Γk 是在纯溶剂 中基团k的活度系数; 是在纯溶剂i中基团 的活度系数 中基团 的活度系数;
纯组分i中基团 的活度系数 纯组分 中基团k的活度系数 中基团
Tc = 181.728 × ln
( ∑ n ∆T + ∑ n ∆T )
i bi j bj
( ∑ n ∆T + ∑ n ∆T )
i ci j cj
pc = 0.13705 + 0.1 0.100220 + ∑ ni ∆pci + ∑ n j ∆pcj
Vc = −4.350 + ln
(
)
−2
( ∑ n ∆V + ∑ n ∆V )
基团法发展和分类
早期的基团法很简单,基团划分“粗糙”,所划基团很少。 早期的基团法很简单,基团划分“粗糙” 所划基团很少。 20世纪中叶,用基团法估算标准生产焓及临界性质时,划分 世纪中叶,用基团法估算标准生产焓及临界性质时, 世纪中叶 的基团较多较细。 的基团较多较细。 早期的基团法中,不考虑各种基团间的交互作用。 早期的基团法中,不考虑各种基团间的交互作用。从20世纪 世纪 40年代起,开始修正临近基团的影响。 年代起, 年代起 开始修正临近基团的影响。 基团法从估算固定温度点开始,经过发展, 基团法从估算固定温度点开始,经过发展,目前基团法已经 提出了温度关联式,用于各种温度下。 提出了温度关联式,用于各种温度下。 开始基团法仅用于纯物质的物性估算, 开始基团法仅用于纯物质的物性估算,目前已用于汽液平衡 估算,并用于多种相平衡估算中, 估算,并用于多种相平衡估算中,成为唯一的估算相平衡的 方法。 方法。
《物性估算原理及计算机计算》 第5章基团贡献法及其应用

5.1 分子性质的加和性 5.2 基团贡献法 5.3 基团贡献法估算纯组分的基本性质 5.4 基团法计算纯物质的蒸汽压和汽化热 5.5 基团贡献法估算理想气体的标准生成热、标准熵和比热容 5.6 基团贡献法估算饱和液体密度和液体比热容 5.7 基团贡献法估算流体的传递性质 5.8 基团贡献法估算表面张力 5.9 基团贡献法计算机编程示例
总目录
本章目录
上页
下页
5.2 基团贡献法
5.2.1 基团的划分
按功能团划分基团,这是基团划分的最基本依据,因为每种功能团 往往表现出有其独特的物理化学性质,即使在不同类型的分子中也是如 此,在同系物分子中规律性尤其明显。这正好与划分结构单元的目的相 符合,而功能团之所以具有独特的物理化学性质,正是由于它所具有的 是特定原子间的特定相互作用。除了按功能团划分基团外,还从下面几 个方面加以细分:
对称性修正只对估算标准熵SӨ和标准生成只有焓GӨf才需 要修正。对于CӨp和HӨf等则不必要
总目录
本章目录
上页
下页
6)对映异构体修正
若分子中含有手征性碳原子(不对称碳原子),则分子有 对映异构体 .
若分子中含有手征性碳原子,在估算熵值时要增加一个
Rln的修正项。其中R是通用气体常数,=2m,而m是分
表5-4列出了若干以碳原子为中心的键角。可以看出:饱和碳化物 中,不但不同的分子中同一种键角(HCH, CCC, CCCl)基本相等,而且 这些以饱和碳原子为中心,以不同的键构成的键角都近于110。
5.1.2 分子内原子的作用距离
有机化合物分子中直接相连两个原子之间的作用多为共价键,共价 键的键长多数在1至2Å之间 分子内以形成化学键的相邻两原子的相互作用最为强烈 诱导效应 共轭效应 空间效应
基团贡献法预测离子液体性质及酸性气体溶解度

基团贡献法预测离子液体性质及酸性气体溶解度刘雅茹;刘宝友【摘要】基团贡献法是预测化合物物化性质的有效方法,被广泛应用于纯物质及混合体系的物性估算.介绍了基团贡献法对离子液体的密度、黏度、电导率及对CO2和SO2气体吸收的预测.分析表明,通过建立基团贡献法的参数模型,可以定向设计离子液体,推动离子液体在气体吸收方面的工业化应用.对基团贡献法主要优势进行总结,对ILs吸收气体的工业化应用进行了展望.【期刊名称】《河北工业科技》【年(卷),期】2015(032)002【总页数】5页(P161-165)【关键词】大气污染防治工程;基团贡献法;离子液体;预测;性质【作者】刘雅茹;刘宝友【作者单位】河北科技大学环境科学与工程学院,河北石家庄 050018;河北省污染防治生物技术实验室,河北石家庄050018;河北科技大学环境科学与工程学院,河北石家庄 050018;河北省污染防治生物技术实验室,河北石家庄050018【正文语种】中文【中图分类】X511刘雅茹,刘宝友.基团贡献法预测离子液体性质及酸性气体溶解度[J].河北工业科技,2015,32(2):161-165.LIU Yaru,LIU Baoyou.Group contribution method for prediction of ionicliquids properties and flue gas absorption[J].Hebei Journal of Industrial Science and Technology,2015,32(2):161-165.离子液体(ILs)作为一种新型绿色溶剂,已在能源、环境、材料等领域中展现出广阔的应用前景[1]。
但ILs的种类繁多,性质多种多样,而工业应用过程中需要完整的数据资料,完全依赖实验测定性质既不可能也没必要。
因此,开发合适的预测模型估算ILs的热物理性质显得极为迫切。
基团贡献法是预测化合物物化性质的有效方法,被广泛应用于纯物质及混合体系的物性估算。
基团贡献法及其应用

5.1.2 分子内原子的作用距离
分子许多性质之所以具有加和性,与分子内原子的相互作用的特点 有关,分子内的原子间相互作用属于短程作用( 1至3Å ),有机化合 物分子中直接相连两个原子之间的作用多为共价键,共价键的键长多 数在1至2Å之间,最长C-I为2.1 Å,最短O-H为0.096 Å,所以分子内 以形成化学键的相邻原子间的相互作用最为强烈。 分子内以形成化学键的相邻两原子的相互作用最为强烈
5.2 基团贡献法 5.2.1 基团的划分
按功能团划分基团,这是基团划分的最基本依据,因为每种功能团 往往表现出有其独特的物理化学性质,即使在不同类型的分子中也是如 此,在同系物分子中规律性尤其明显。这正好与划分结构单元的目的相 符合,而功能团之所以具有独特的物理化学性质,正是由于它所具有的 是特定原子间的特定相互作用。除了按功能团划分基团外,还从下面几 个方面加以细分。(功能团划分依据) 参照基团所在分子的主体结构及其特点将同一基团再加细分 :如: OH基团,在醇与酚中表现出不一样的性质 按照分子的立体构型划定基团 :顺反结构基团 在划分基团时往往把有共轭效应的基团分开:如1,3丁二烯中的C-C键 比没有共轭分子中的C-C键要短一些 同系物的第一化合物常被当作一个基团单独列出:如甲酸与羧基相连 的是氢原子,而醋酸与羧基相连的是碳原子
5.3.2 纯物质正常沸点的估算 正常沸点的实验数据相当丰富,可靠性也高,许多文献中, 有大量实验数据,但仍然有一些物质的Tb值有待估算。正 常沸点较难估算,虽然提出了一些Tb的估算方法,但有实 用价值的只有基团贡献法。
1)Joback法
式中Tb的单位是K,基团贡献值△Tbi见表5-10,通过438种 有机物的数据检验,式(5-15)的平均误差为3.6%。 2)C-G法
估算有机物正常沸点的基团贡献法的研究进展

中 图分 类 号 :6 1 1 0 2 . 文 献 标 识 码 : A 文 章 编 号 :0 8—0 1 2 1 ) 5— 0 4一O l0 2 x(0 2 0 0 3 3
Ree rh Pr g eso o p—c nrb t nM eh d o t t gNo ma sa c o r s fGr u — o tiui to sfrEs ncCo o n s in on fOr a i mp u d i
p icpe ,a v na e n i d a tg s p l ain rn e fJ b e to r ils d a tg sa d ds v na e ,a pi t a g s o o a k meh d,C — G meh d n a c o to ,Xu —
W e t o , o i o r u o tiu i n me h d,ee n s a d b n s h i e e c ft e e meh d n meh d p s i n g o p c n r t t o t b o lme t n o d .T e d f r n e o s t o s f h
第5章基团贡献法及其应用

5)对称性修正 用键贡献法和基团贡献法估算理想气体熵SӨ时,通常必 须作分子对称性的修正。
对称数为定义是:分子刚性转动时,分子内相同原子 (或基团)出现独立互换的总次数(不得反转)。为便于 计算,通常把分解为外和内,即: =外. 内 计算分子的对称数一些规律 CP
对称性修正只对估算标准熵SӨ和标准生成只有焓GӨf才需 要修正。对于CӨp和HӨf等则不必要
在划分基团时往往把有共轭效应的基团分开
同系物的第一化合物常被当作一个基团单独列出
总目录
本章目录
上页
下页
5.2.2 分子性质与基团元贡献值的关联 分子性质的值与基团元贡献值之间的关联有下列的一些形式: 就是分子性质值直接由各基团的贡献值以及各 种修正项直接加和而得,即
(1)直i为i基团的数目;ai为i基团的元贡献或 某种修正项。
n a
i i
这种关联法将分子的性质A作为某些参数B, C,….等等的函数,而B,C,….各基团的元贡献加和而得, 即: B nb
(2)函数式法
A f ( B, C , )
i
i i
C
n c
i
i i
其中bi和ci分别代表i基团对B和C的元贡献值。
总目录
本章目录
上页
下页
(3)统计力学模型法 溶液的活度系数。
总目录
本章目录
上页
下页
5.4.2 纯物质的汽化热的估算 1) 基团对应状态法(CSGC)
Li等基于CSGC法,提出从正常沸点汽化热ΔHVb求取ΔHV的方法,即 CSGC-HW1法,其基本关系式与Watson公式类似:
1 Tr* H V H Vb 1 T br
式中, Tr T / Tc
基于基团贡献法和分子动力学预测聚间苯二甲酰对苯二胺的玻璃化转变温度

Vol.40高等学校化学学报No.12019年1月㊀㊀㊀㊀㊀㊀CHEMICALJOURNALOFCHINESEUNIVERSITIES㊀㊀㊀㊀㊀㊀180 186㊀㊀doi:10.7503/cjcu20180344基于基团贡献法和分子动力学预测聚间苯二甲酰对苯二胺的玻璃化转变温度吴红枚,李惠婷,李永成,王宏青,王㊀孟(南华大学化学化工学院高分子材料与工程系,衡阳421001)摘要㊀采用基团贡献法(GC)和分子动力学法(MD)模拟了聚间苯二甲酰间苯二胺纤维(MPDI)和聚对苯二甲酰对苯二胺(PPTA)的玻璃化转变温度,并与实验值进行了对比.结果表明,使用基团贡献法和分子动力学法测得的MPDI和PPTA的玻璃化转变温度与实验值接近,说明基团贡献法和分子动力学法可以用来预测芳香族聚酰胺的玻璃化转变温度.在此基础上,采用GC和MD预测了聚间苯二甲酰对苯二胺(PPIA)的玻璃化转变温度.在MD模拟中,对密度㊁比体积㊁回转半径和非键相互作用随温度的变化规律进行了分析.结果表明,自由体积理论能较好地解释PPIA的玻璃化转变现象,其中非键相互作用随温度的变化是玻璃化转变的本质原因.PPIA的玻璃化转变温度介于MPDI和PPTA之间,有望成为综合性能介于两者之间的另一种高性能聚酰胺.关键词㊀基团贡献法;分子动力学模拟;玻璃化转变温度;聚间苯二甲酰对苯二胺中图分类号㊀O631㊀㊀㊀㊀文献标志码㊀A㊀㊀㊀㊀收稿日期:2018⁃05⁃04.网络出版日期:2018⁃11⁃15.基金项目:国家自然科学基金(批准号:21104031)和南华大学研究生科学基金(批准号:2018KYY046)资助.联系人简介:吴红枚,女,博士,副教授,主要从事功能高分子方面的研究.E⁃mail:wuhongmei2016@163.com绝大部分高分子材料都属于非晶态聚合物,玻璃化转变温度(Tg)是描述非晶态聚合物最重要的一个特征温度[1],它决定着这类材料的使用性能;对于结晶性高聚物而言,其非晶区的玻璃化转变温度也是非常重要的热参数[2].如果能够从聚合物的化学结构预测其玻璃化转变温度,对选择和设计新材料具有非常重要的意义.近年来,使用计算机进行分子模拟成为一种趋势,这可以大大缩短新材料的研发周期[3].迄今为止,用于预测聚合物的Tg的计算机模拟方法有基团贡献(GC)法和分子动力学模拟(MD).Han等[4]通过对一系列无定形高分子材料进行分子动力学模拟,得到聚合物的体积与温度关系,计算出无规聚丙烯(PP)㊁聚丁二烯(PBD)和聚苯乙烯(PS)等的Tg,并对比了所得聚合物的Tg与实验值的关系,发现其Tg比实验值高;Boudouris等[5]利用基团贡献法预测一系列聚合物的Tg,发现预测值和实验值非常吻合;Wang等[6]采用动力学模拟方法研究了高结晶的聚对苯二甲酸乙二醇酯(PET)及掺杂纳米硅的复合材料的Tg,结果表明PET中掺杂纳米硅可以影响PET的Tg,掺杂的纳米硅可以增加聚合物链的流动性能,减少体系的自由体积和能量,从而降低PET的Tg,而加入羟基化的硅会使纳米硅与高分子之间内部缠结,降低分子之间的流动性能,使PET的Tg升高.目前,用计算机模拟方法预测聚酰胺的Tg报道较少,Cousin等[7]通过分子动力学和基团贡献法对半结晶聚苯二甲酰胺(PPA)进行了表征,将理论计算的Tg与实验测定的结果进行对比,研究表明不论是基团贡献法还是动力学方法,结果都与实验数据具有良好的一致性.全芳香族聚酰胺的Tg的计算机模拟至今未有报道.全芳香族聚酰胺[8]在聚酰胺家族中占有极其重要的地位,这类聚酰胺性能卓越,常被用于高性能纤维等领域.目前已商业化的芳香族聚酰胺有聚间苯二甲酰间苯二胺(MPDI)和聚对苯二甲酰对苯二胺(PPTA)[9,10]及由此发展出的共聚型品种.开发新的全芳香族聚酰胺是一个重要的研究领域,而使用计算机模拟技术可以提前预测其性能,帮助研究人员深入认识其规律,缩短研发周期.本文采用基团贡献法和分子动力学方法模拟了聚间苯二甲酰间苯二胺(MPDI)和聚对苯二甲酰对苯二胺(PPTA)的Tg,通过与文献值[8,11,12]进行对比,验证采用基团贡献法和分子动力学方法预测全芳香族聚酰胺Tg的可行性,在此基础上,使用基团贡献法和分子动力学方法预测聚间苯二甲酰对苯二胺(PPIA)的Tg,分析引起其玻璃化转变的本质原因,这有利于深入探索PPIA的玻璃化转变现象及对应的分子运动规律.1㊀模拟方法1.1㊀模型建立基团贡献法[13]主要使用MaterialsStudio(MS)软件中的Synthia模块.首先建立MPDI和PPTA的重Fig.1㊀ChemicalstructuresofMPDIandPPTA复结构单元(其结构式如图1所示),在Forcite模块中进行几何优化,再用Synthia模块进行计算,温度设置为300K,MPDI和PPTA的分子量都设置为952 95200,即聚合度为4 400,从计算的数据中获得高分子的Tg与分子质量.分子动力学模拟方法主要参考了Pant等[14 16]的工作,主要涵盖以下步骤(具体的参数设定则根据体系的不同各异):(1)建立聚合物重复单元并优化结构;(2)构建聚合物的单链结构并优化模型;(3)建立无定形结构(Amorphouscell);(4)退火(Anneal);(5)分子动力学(NVT,NPT);(6)性能参数(Analysis).使用MaterialsStudio软件中的Dynamics模块进行模拟.首先,建立MPDI和PPTA的结构单元,考虑到聚合物的分子量对其玻璃化温度有很大的影响,在MD模拟过程中,建模时应充分考虑聚合度的合理设定使模型具有代表性,参考了GC法的分子量与Tg的关系曲线,分别构造聚合度为100的MPDI和聚合度为100的PPTA的单链模型,并对所建模型进行结构优化,步数为20000步,力场选用COMPASS力场[17 23],范德华力使用Atom⁃based方法,静电作用使用Group⁃based方法,其中Quality选择Ultra⁃fine,非键截断半径取1 85nm,样条宽度为0 1nm,缓冲宽度为0 05nm.Algorithm选择SmartFig.2㊀AmorphouscellconstructionforaMPDI对聚合物单链的电荷和能量进行平衡优化.Smart运算作为一种有效使系统达到平衡的运算方法,综合了Steepestdescent,ABNR和Quasi⁃Nowton3种运算.优化完成后,使用Amorphouscell模块建立密度为0 6g/cm3的MPDI单链无定形单胞模型和密度为0 4g/cm3的PPTA单链无定形单胞模型(图2),并对所建的模型进行20000步的结构优化(模拟参数同上).初始建模密度选择0 6g/cm3的MPDI和0 4g/cm3的PPTA的原因是为了避免在建模过程中密度设置过高导致分子链太过拥挤而相互缠结,进而导致体系能量过高而无法建立单胞模型.使用Forcite模块中的Anneal进行退火动力学模拟,为了得到真实可靠的聚合物结构,选择在0 0001GPa,300K下运行1000ps的NPT退火分子动力学模拟,共进行20个循环温度,温度梯度为25K,每个循环从300K升温到1000K再降温到300K的退火处理,退火的目的是为了消除由于在建模过程中产生的局部不合理的结构,为下一步动力学模拟提供合理的构象.分子动力学模拟选择Nose⁃Hoover控温,这种控温并不能改变系统平衡,但可以有效维持系统的平衡,这个设置描述原子运动更为真实,并且可以调整聚合物分子链的构象.压力的控制采用181㊀No.1㊀吴红枚等:基于基团贡献法和分子动力学预测聚间苯二甲酰对苯二胺的玻璃化转变温度Berendsen控压.第1步进行NVT系综动力学模拟,时间为100ps,使高分子链进一步松弛;第2步进行时间为200ps的NPT系综的动力学模拟,系统达到平衡,得到系统平衡时的密度并分析㊁采集数据.分子动力学模拟初始阶段温度设为700K,每个阶段实验完成以后温度将依次降低20K,并且上一阶段(较高温度)的动力学最终平衡构象作为下一阶段(较低温度)分子动力学模拟的初始构象,直到实验温度下降到440K为止,实验温度范围为700 440K,共进行14组实验,从建模到动力学模拟结束的总模拟时间为6 6ns,体系达到平衡.1.2㊀方法验证使用基团贡献法测得聚合度为100时MPDI和PPTA的Tg趋于平衡,此时对应的Tg分别为524 5K和583 8K.使用分子动力学模拟,当系统到达平衡后分别用密度⁃温度法㊁比体积⁃温度法㊁回转半径⁃温度法和能量⁃温度法分析可得到聚合物的玻璃化转变温度.模拟结果与实验值列于表1.Table1㊀TgofMPDIandPPTAfromdifferentmethodsMethodTg(MPDI)/KTg(PPTA)/KExperimentvalue545.2 548.2600 618.2GC524.5583.8MD(Density⁃Temperature)565.2616.5MD(Specificvolume⁃Temperature)566.9616.3MD(Radiusofgyration⁃Temperature)571.3615.8MD(Non⁃bondenergy⁃Temperature)567.4617.4㊀㊀表1结果表明,基团贡献法模拟所得的Tg较实验值低,而分子动力学模拟所得的Tg较实验值高.MPDI和PPTA实验所测的真实Tg介于基团贡献法和分子动力学法模拟值之间.通过对比2种模拟方法及实验所得Tg的数值,发现基团贡献法和MD模拟计算得到的聚合物的Tg与实验数据接近,这说明2种模拟方法均可以用来模拟真实状态下MPDI和PPTA的Tg,表明使用基团贡献法和分子动力学预测全芳香性的聚酰胺Tg具有合理性.2㊀结果与讨论聚间苯二甲酰对苯二胺(PPIA)是一种全新的聚酰胺[24].从结构上看,PPIA的结构兼具MPDI和PPTA的特点,有可能发展成为高性能芳香族聚合物中的新品种.本文通过基团贡献法和分子动力学模拟预测该聚合物的Tg,这有利于深入探索PPIA的玻璃化转变现象及对应的分子运动规律,对PPIA的潜在应用具有指导意义.2.1㊀基团贡献法基团贡献法是使用定量结构⁃性能关系来预测聚合物性质的方法,通过Synthia模块计算不同聚合度(DP)的PPIA的Tg,计算结果使用Origin软件作图,得到PPIA的Tg与聚合度的关系如图3所示.Fig.3㊀Tgvs.degreeofpolymerization(DP)chartforPPIAat300K从图3可以看出,聚合物的Tg随着聚合度的增加而增加,当聚合度达到某个值时,Tg达到了一个平台区,不再发生显著变化.由图3可见,当聚合度达到100时,PPIA的Tg已经非常接近平台区的数值,此时对应的Tg为554 4K.考虑到在进行分子动力学模拟时,计算时间与体系中的原子数目有关.原子数目增加,模拟时间将大大增加,并且原子数目越多,模拟体系就越复杂,建立无定形结构模型越困难,因此在后续的分子动力学模拟中,选取聚合度为100的PPIA作为分子动力学模拟的模型.2.2㊀分子动力学模拟2.2.1㊀平衡的判定㊀分子动力学模拟体系的平衡需要足够的模拟时间,只有模拟体系达到平衡才能获281高等学校化学学报㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Vol.40㊀得可靠有效的模拟数据.判定分子动力学模拟达到平衡的条件[25,26]主要有以下两方面:首先温度需处于平衡状态,要求温度在平衡值上下波动,其波动的标准偏差应该小于10K;其次能量也需处于平衡状态,要求能量沿平衡值上下波动或者恒定.图4为PPIA在500K和200ps的NPT系综状态下温度与能量的平衡图,可见,PPIA的分子动力学模拟体系已经达到平衡.Fig.4㊀Temperature(A)andenergyfluctuationproperties(B)vs.simulationtimeofPPIA(500K,200psNPT)2.2.2㊀PPIA的密度与温度之间的关系㊀通过分子动力学模拟得到PPIA的密度⁃温度关系(图5).由图5可以看出,Tg将260K的温差范围分成2个温度区间,这2个温度区间内的密度与温度呈线性变化,根据2个温度区间的数据进行线性拟合,可得到2条斜率不同直线,2条直线的交点对应的温度即为PPIA的Tg,为593 6K.这种玻璃化转变可以用 等自由体积理论 [27,28]来说明.高分子的体积可以分成2个部分:一部分为占有体积,即为分子与原子自身体积;另一部分被称为自由体积,也就是分子间的空隙体积.自由体积是以大小不一的 空穴 分散在高分子中,因此这为链段运动提供了足够的转动空间,从而分子链可以通过转动和位移来调整构象.自由体积理论认为,处于Tg时,自由体积为链段运动提供空间,是正好处于链段可以运动或者运动被冻结这2种状态之间的临界值.Fig.5㊀Densityvs.temperaturechartforanMDsimulationofPPIAFig.6㊀Specificvolumevs.temperaturechartforanMDsimulationofPPIA2.2.3㊀PPIA的比体积与温度之间的关系㊀通过MD模拟得到PPIA的比体积⁃温度关系(图6).2个温度区间内的比体积与温度呈线性变化,经线性拟合得到2条直线的交点,对应的温度即是PPIA的玻璃化转变温度(594 1K).这种玻璃化转变同样可以用 等自由体积理论 来解释.2.2.4㊀PPIA的回转半径与温度之间的关系㊀聚合物是通过小分子聚合而成的,因此聚合物单键仍能内旋转,而正因为这种内旋转导致聚合物拥有许多不同的构象.众所周知,分子不停地进行热运动,而这种热运动可以使分子的构象发生改变,由于构象发生了改变,聚合物分子尺寸也会发生相应的改变.在高分子中,通常使用均方回转半径来表征分子尺寸.由于均方回转半径的大小可以用来表征聚合物分子链柔顺性的大小,而聚合物的玻璃化转变又和链的柔顺性有直接关系[25].因此,通过分子动力学模拟,对不同温度下PPIA的回转半径和温度进行了分析(图7).由图7可见,PPIA的回转半径随温度的升高而升高.随着温度升高,聚合物的自由体积和分子所占据的体积都会发生膨胀,因此分子间距离将会逐渐增大,从而导致回转半径也会增大.通过线性拟合PPIA的回转半径与温度图,可以得到PPIA的Tg为592 2K.分析结果说明,通过回转半径与温度381㊀No.1㊀吴红枚等:基于基团贡献法和分子动力学预测聚间苯二甲酰对苯二胺的玻璃化转变温度Fig.7㊀Radiusofgyrationvs.temperaturechartforanMDsimulationofPPIA变化关系可以预测PPIA的Tg.2.2.5㊀PPIA的力场能量与温度之间的关系㊀在分子力学原理中,通常力场的总能量可以简单地分成3项[26],公式为Etotal=Evalence+Enon⁃bond+Ecrossterm,其中,Etotal为力场的总能量;Evalence为成键相互作用能;Enon⁃bond为非成键相互作用能;Ecrossterm为交叉形式的能量.对于成键相互作用能又可以分为键伸缩能㊁键角弯曲能和扭转能等;非成键相互作用能也可以分为范德华作用能和库仑作用能.对PPIA的键能㊁键角能㊁扭转能与非键作用能与温度作图,研究力场各能量与Tg的关系,结果示于图8.Fig.8㊀Plotsofenergycomponentsvs.temperaturechartforanMDsimulationofPPIA由图8可看出,PPIA的键能㊁键角能和扭转能都随温度的升高线性上升,能量与温度的关系图中没有拐点,由此可知键能㊁键角能和扭转能在玻璃化转变时不会发生突变,不是玻璃化转变的主要因素.而PPIA的非键能与温度关系图中出现一个拐点,不管在拐点之上还是在拐点之下,随着温度降低,非键能都直线下降,但是处于拐点之下的直线斜率较小,这个拐点即是PPIA的Tg,为594 3K.非键能在玻璃化转变出现一个拐点的现象可以认为,非键能可能处于Tg以下时受到限制,对于PPIA来说,这也是出现玻璃化转变的根本原因.㊀Table2㊀TgofPPIAfromdifferentmethodsMethodTg/KGC554.4MD(Density⁃Temperature)593.6MD(Specificvolume⁃Temperature)594.1MD(Radiusofgyration⁃Temperature)592.2MD(Non⁃bondenergy⁃Temperature)594.32.3㊀不同方法测得PPIA的玻璃化转变温度PPIA的Tg的模拟结果列于表2.可以看到,在分子动力学模拟中,密度⁃温度法㊁比体积⁃温度法㊁回转半径⁃温度法和非键能量⁃温度法测得的PPIA的Tg的差值都不大,基团贡献法得到的PPIA的Tg比分子动力学的5种方法所得值要低40K左右.基团贡献法是利用定量结构性能关系来预测聚合物的Tg,可能是没有考虑这2种聚合物结晶的缘故;MD建立的聚合物链长模型是单分散性,而真实情况下聚合物链长是多分散性,由于链长的多分散性导致低分子链作为高分子量的增塑剂,从而降低高分子481高等学校化学学报㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Vol.40㊀的Tg;其次,加热/冷却的速率和时间尺度也是影响Tg的重要因素,通常DSC测试样品的冷却速度是10K/min,而模拟时,两步的温差范围是20K,两步的时间却为1 3ns,温度快速变化导致材料的变硬,从而使Tg升高.不管是基团贡献法,还是分子动力学模拟,所测得的Tg均大于500K,对比表1和表2可见,PPIA的Tg值介于MPDI和PPTA的Tg值之间,能量项中引起PPIA玻璃化转变的原因同样是非键能随温度的变化.可以合理地推断PPIA的热性能可能介于MPDI和PPTA之间,若能纺制成纤维,极可能发展成介于MPDI和PPTA之间的高性能聚酰胺.3㊀结㊀㊀论采用基团贡献法和分子动力学预测了聚间苯二甲酰对苯二胺的Tg.基团贡献法测得PPIA的Tg值为554 4K,分子动力学模拟经密度⁃温度法㊁比体积⁃温度法㊁回转半径⁃温度法㊁非键能量⁃温度法测得的Tg值分别为593 6,594 1,592 2和594 3K,表明引起PPIA玻璃化转变的本质原因是非键能项随温度的变化.PPIA的Tg介于MPDI和PPTA的Tg之间,有希望发展成为一种性能介于MPDI和PPTA之间的新品种芳香族聚酰胺.基团贡献法和分子动力学模拟可以很好地预测芳香族聚芳酰胺的Tg,有助于深入认识芳香族聚芳酰胺的玻璃化转变现象及其分子运动规律,对研究芳香族聚芳酰胺的性质具有参考价值.感谢东华大学材料科学与工程学院提供的MaterialsStudio软件.参㊀考㊀文㊀献[1]㊀ZhangR.,HeX.R.,YuH.,PolymerMaterialsScience&Engineering,2015,31(4),186 190(张睿,何显儒,余慧.高分子材料科学与工程,2015,31(4),186 190)[2]㊀DiegoJ.A.,CanadasJ.,MudarraM.,BelanaJ.,Polymer,2000,40(40),5355 5363[3]㊀RoeR.J.,MDSimulationStudyofGlassTransitionandShortTimeDynamicsinPolymerLiquids.In:AtomisticModelingofPhysicalProperties,Ed.:MonnerieL.,SuterU.W.,Springer⁃Verlag,BerlinHeidelberg,1994,116(1),415 426[4]㊀HanJ.,GeeR.H.,BoydR.H.,Macromolecules,1994,27(26),7781 7784[5]㊀BoudourisD.,ConstantinouL.,PanayiotouC.,FluidPhaseEquilibria,2000,167(1),1 19[6]㊀WangY.H.,WangW.H.,ZhangZ.Q.,XuL.C.,LiP.,EuropeanPolymerJournal,2016,75,36 45[7]㊀CousinT.,GalyJ.,DupuyJ.,Polymer,2012,53(15),3203 3210[8]㊀GarcíaJ.M.,GarcíaF.C.,SernaF.,PeñaJ.L.D.L.,ProgressinPolymerScience,2010,35(5),623 686[9]㊀KakidaH.,ChataniY.,TadokoroH.,JournalofPolymerSciencePolymerPhysicsEdition,1976,14(3),427 435[10]㊀NortholtM.G.,vanAartsenJ.J.,JournalofPolymerSciencePartCPolymerLetters,1973,11(11),333 337[11]㊀BiceranoJ.,EncyclopediaofPolymerScienceandTechnology,2006,655 678[12]㊀YangZ.,StudyonThePolycondensationandSpinningProcessofPoly(p⁃phenyleneterephthalamide)Copolymer,DonghuaUniversity,Shanghai,2006(杨拯.聚对苯二甲酰对苯二胺(PPTA)及其共聚物的聚合及纺丝工艺研究,上海:东华大学,2006)[13]㊀VanKrevelenD.W.,HoftyzerP.,JournalofAppliedPolymerScience,1969,13(13),871 881[14]㊀PantP.V.K.,HanJ.,SmithG.D.,BoydR.H.,JournalofChemicalPhysics,1993,99(1),597 604[15]㊀Abu⁃SharkhB.F.,Computational&TheoreticalPolymerScience,2001,11(1),29 34[16]㊀SarangapaniR.,ReddyS.T.,SikderA.K.,JournalofMolecularGraphics&Modelling,2015,57,114[17]㊀RigbyD.,SunH.,EichingerB.E.,PolymerInternational,2015,44(3),311 330[18]㊀SunH.,JournalofPhysicalChemistryB,1998,102(38),7338 7364[19]㊀SacristanJ.,MijangosC.,Macromolecules,2010,43(17),7357 7367[20]㊀GeeR.H.,AndL.E.F.,CookR.C.,Macromolecules,2001,34(9),3050 3059[21]㊀AhmadiA.,FreireJ.J.,Polymer,2009,50(20),4973 4978[22]㊀ChangK.S.,HuangY.H.,LeeK.R.,TungK.L.,JournalofMembraneScience,2010,354(1),93 100[23]㊀FermegliaM.,FerroneM.,PriclS.,FluidPhaseEquilibria,2003,212(1/2),315 329[24]㊀DingY.,WuH.M.,WangM.,LiangZ.H.,LiY.C.,JournalofShandongChemicalIndustry,2016,45(11),74 77(丁勇,吴红枚,王孟,梁振辉,李永成.山东化工,2016,45(11),74 77)581㊀No.1㊀吴红枚等:基于基团贡献法和分子动力学预测聚间苯二甲酰对苯二胺的玻璃化转变温度681高等学校化学学报㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Vol.40㊀[25]㊀FuY.Z.,LiuY.Q.,ZhangL.Y.,LanY.H.,JournalofMolecularScience,2009,25(1),1 4(付一政,刘亚青,张丽燕,兰艳花.分子科学学报,2009,25(1),1 4)[26]㊀FuY.Z.,LiuY.Q.,LanY.H.,PolymerMaterialsScience&Engineering,2009,25(10),53 56(付一政,刘亚青,兰艳花.高分子材料科学与工程,2009,25(10),53 56)[27]㊀WhiteR.P.,LipsonJ.E.G.,Macromolecules,2016,49(11),3987 4007[28]㊀WhiteR.P.,LipsonJ.E.G.,ACSMacro.Letters,2015,4(5),588 592UsingGroupContributionMethodandMolecularDynamicstoPredicttheGlassTransitionTemperatureofPoly(p⁃phenyleneisophthalamide)†WUHongmei∗,LIHuiting,LIYongcheng,WANGHongqing,WANGMeng(DepartmentofPolymerScienceandEngineering,CollegeofChemistryandChemicalEngineering,UniversityofSouthChina,Hengyang421001,China)Abstract㊀Aramidfibersmainlyincludewhollyaromaticpolyamideandheterocyclicaromaticpolyamide,whilethewhollyaromaticpolyamides(aramids)areconsideredtobehigh⁃performanceorganicmaterialsduetotheiroutstandingthermalandmechanicalproperties.Theirhigh⁃performancesarisefromtheiraromaticstruc⁃tureandamidelinkages.Thebetterknowncommercialaramids,poly(p⁃phenyleneterephthalamide)(PPTA)andpoly(m⁃phenyleneisophthalamide)(MPDI),areusedinadvancedtechnologiesandhavebeentrans⁃formedintohigh⁃strengthandflame⁃retardantfibersandcoatings,withapplicationsintheaerospaceandarma⁃mentindustry.Poly(p⁃phenyleneisophthalamide)(PPIA),anewaromaticpolyamide,hasnotyetbeencommercializedandtherearefewreportsaboutitscomprehensiveperformanceuntilnowadays.Inthispaper,GroupContribution(GC)methodandmoleculardynamics(MD)simulationwereusedtosimulatetheglasstransitiontemperatures(Tg)ofMPDIandPPTA.ThenanalysisandcomparisonsoftheglasstransitiontemperaturesbyGCmethodandMDsimulationwiththeirexperimentalvaluesarepresented.TheresultsshowthattheglasstransitiontemperaturemeasuredbyGCmethodandMDsimulationisveryclosetotheexperimen⁃talvalue,andthatthechangeofthedensity,specificvolume,radiusofgyrationandenergyalongwithtemperaturecancha⁃racterizetheglasstransitiontemperature.Thenthesetwomethodswereexploitedtosimu⁃latetheTgofPPIA.Thechangeofthedensity,specificvolume,radiusofgyrationandenergyinteractionsalongwithtemperaturewereanalyzedintheMDsimulation.TheresultsshowthatthefreevolumetheorycanexplaintheglasstransitionphenomenonofPPIA,andthechangeofthenon⁃bondenergyinteractionswithtemperatureistheessentialreason.TheseresultsindicatesthatPPIAhasthepotentialtobecomeanotherhighperformancepolyamidewithitsTglyingbetweenthoseofbothMPDIandPPTA.ItisofgreatsignificancetoemphasizeonthesynthesisofPPIAwithsufficientlyhighmolecularweight.Ingeneral,thegroupcontributionmethodandmoleculardynamicssimulationcanpredicttheTgofaromaticpolyamidesucessfully,andtheycancontributetoadeeperunderstandingontheglasstransitionphenomenonofaromaticpolyamidesandthemolecularmotionbehind.Keywords㊀Groupcontributionmethod;Moleculardynamicssimulation;Glasstransitiontemperature;Poly(p⁃phenyleneisophthalamide)(Ed.:W,Z)†SupportedbytheNationalNaturalScienceFoundationofChina(No.21104031)andtheGraduateScienceFoundationinUniversityofSouthChina,China(No.2018KYY046).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.1.2 分子内原子的作用距离
有机化合物分子中直接相连两个原子之间的作用多为共价键,共价 键的键长多数在1至2Å之间
分子内以形成化学键的相邻两原子的相互作用最为强烈 诱导效应 共轭效应 空间效应
总目录
本章目录
上页
下页
5.1.3 结构单元的选择与加和性规则的近似程度 加和性规则是一种近似规则,其近似的程度取决于我们所 选择的结构单元精细程度 总的来说,分子内原子的相互作用考虑得越精细,由此而 建立起来的加和性规则也就越精确,由此而得的计算结果 也就越符合实际。 基团贡献法是工程上估算物性所常用的方法之一。
Vc 4.350 ( ni Vci n j Vcj )
式中临界性质的单位与Joback法相同,但基团的贡献分一级基团贡献 和二级基团贡献,其中△Tci、△Pci、△Vci是一级基团贡献值,见表5-12, △Tcj、△Pcj、△Vcj是二级基团贡献值,见表5-13。
总目录
本章目录
式中Tm的单位是K,△Tmi是基团贡献值,见表5-10。本法的 平均误差为11%。 2) C-G法
Tm 122 ni Tmi
Tm 102.425ln( ni Tmi n j Tmj )
式中,Tm的单位是K,△Tmi是一级基团贡献值,见表5-12, △Tmj是二级基团贡献值,见表5-13。 总目录 本章目录 上页 下页
ln Tb Pc 0.046672 0.285250 ( ni Pci ) 2 ni Pci 0.050511
6.038530 Vc 28.89746 14.75246 ni Vci ni Vci 总目录 本章目录
上页
下页
本方法使用单位及式中各参数的意义与Joback法相同,各种基团的 △Tci、△Pci、△Vci值列于表5-11之中。
总目录
本章目录
上页
下页
2)顺反式构型修正 如果基团贡献值是以其中一种构型为基准(通常选反 式),则另一种构型便要做修正。 3)扭歪作用修正 分子中有歪曲作用对时,也就有歪曲作用能存在,然而 基团加和法中的基团贡献参数中却无法反映歪曲作用能的存 在。因此一些估算生成焓的键贡献法或基团贡献法设立了歪 曲作用修正项,而给出的基团参数则对应于对位交叉的最稳 定构型。 4)邻位修正 由于邻位的两个基团(或原子)较接近,基团之间便产 生排斥作用,这是不相邻基团所没有的,这种相互作用不能 忽略,而基团贡献参数又无法反映它的存在,故需另加设邻 位修正。 总目录 本章目录 上页 下页
第 5 章 基团贡献法及其应用
5.1 分子性质的加和性
5.2 基团贡献法
5.3 基团贡献法估算纯组分的基本性质 5.4 基团法计算纯物质的蒸汽压和汽化热 5.5 基团贡献法估算理想气体的标准生成热、标准熵和比热容 5.6 基团贡献法估算饱和液体密度和液体比热容
5.7 基团贡献法估算流体的传递性质
5.8 基团贡献法估算表面张力
总目录
本章目录
上页
下页
5.2 基团贡献法 5.2.1 基团的划分
按功能团划分基团,这是基团划分的最基本依据,因为每种功能团 往往表现出有其独特的物理化学性质,即使在不同类型的分子中也是如 此,在同系物分子中规律性尤其明显。这正好与划分结构单元的目的相 符合,而功能团之所以具有独特的物理化学性质,正是由于它所具有的 是特定原子间的特定相互作用。除了按功能团划分基团外,还从下面几 个方面加以细分: 参照基团所在分子的主体结构及其特点将同一基团再加细分 按照分子的立体构型划定基团
3)C-G法
1994年提出的Constantinous-Gani法(简称C-G法),该法不需要常沸 点温度Tb ,基团的影响分成一级基团 ,二级基团,精度明显提高。C-G法 估算公式为:
Tc 181.728ln( ni Tci n j Tcj )
Pc 1.3705 (0.100220 ni Pci n j Pcj ) 2
5.9 基团贡献法计算机编程示例
总目录
5.1 分子性质的加和性
除了对应状态法外,物性估算中常用的另一方法是基因贡献法,基因 贡献法是建立在分子性质具有加和性的基础之上的
5.1.1 分子中的键长与键角
键长: 大量的实验数据表明,同一种键在不同的分子中键长基本上是
个常数,表5-1中列出不同的分子中C-C键键长的数值。 同一种键在各种化合物中不但基本保持一定长度,而且,在典型的 键中A-B的距离可以很准确的表示为A-A及B-B距离的算术平均值 (A和B均代表原子,d代表距离)
Tb 198 ni Tbi
Tb 204.359ln( ni Tbi n j Tbj )
式中,Tb的单位是K,△Tbi是一级基团贡献值,见表5-12, △Tbj是二级基团贡献值,见表5-13。 总目录 本章目录 上页 下页
5.3.3 纯物质熔点的估算 纯物质熔点Tm(或凝固点Tf)的数据也比较充分。同沸 点一样,熔点Tm或Tf的估算也是困难的,误差也较大。下面 介绍两个比较好的估算方法。 1)Joback法
* r
B 36Q
C 42Q c
D Q
其中虚拟临界参数采用基团贡献法计算:
总目录
本章目录
上页
下页
Tb T AT BT ni T i CT ( ni T i) 2 DT ( ni T i ) 3
* c
1.01325ln Tb P AP BP ni P i C P ( ni P i ) 2 DP ( ni P i ) 3
在划分基团时往往把有共轭效应的基团分开
同系物的第一化合物常被当作一个基团单独列出
总目录
本章目录
上页
下页
5.2.2 分子性质与基团元贡献值的关联 分子性质的值与基团元贡献值之间的关联有下列的一些形式: 就是分子性质值直接由各基团的贡献值以及各 种修正项直接加和而得,即
(1)直接加和法
A
i 式中A代表分子的某一性质;ni为i基团的数目;ai为i基团的元贡献或 某种修正项。
* c
上式中 Tc*和 Pc* 的单位分别是K和bar,常数AT、BT、CT、DT、 AP、BP、CP、DP的值见表5-14,基团贡献值见表5-15; CSGC-PRV法采用Vetere改进的Riedel方程,其主要关联式与 CSGC-PR法相同,但计算虚拟临界参数时需将酸类、醇类和 酚类单独处理(见表5-14),且参数Q采用下列关联式进行计算:
总目录
本章目录
上页
下页
Q K (a c )
* ln( P ) * c / 1.01325 K B1 C1Tbr * 1 Tbr
aK b ln(Pc* / 1.01325 ) c * 0.0838 b ln Tbr
式中常数B1、C1和a见表5-14。本法的平均误差为0.73%。
总目录
本章目录
上页
下页
5.4.2 纯物质的汽化热的估算 1) 基团对应状态法(CSGC)
Li等基于CSGC法,提出从正常沸点汽化热ΔHVb求取ΔHV的方法,即 CSGC-HW1法,其基本关系式与Watson公式类似:
1 Tr* H V H Vb 1 T br
式中, Tr T / Tc
总目录
本章目录
上页
下页
6)对映异构体修正
若分子中含有手征性碳原子(不对称碳原子),则分子有 对映异构体 .
若分子中含有手征性碳原子,在估算熵值时要增加一个 Rln的修正项。其中R是通用气体常数,=2m,而m是分 子中的手征性碳原子数。 对CӨp和HӨf,则不必作对映异构体修正。
总目录
本章目录
5.3.4 基团贡献法估算纯组分的基本性质实例 〔例5-1〕估算乙苯的临界参数。文献值为Tc=617.10K, Pc=36.07bar,Vc=374cm3.mol-1。已知乙苯的Tb=409.3K, M=106.168。
〔例5-2〕估算异戊硫醇的正常沸点,文献值为393K
〔例5-3〕估算2-溴丁烷的熔点,文献值为161K
上页
下页
5.3 基团贡献法估算纯组分的基本性质
5.3.1 纯物质临界性质估算 临界性质包括临界温度(Tc)、临界压力(Pc)、临界体 积(Vc)等。在各种临界参数估算法中,比较通用而又可 靠的是基团加和法。 1)Joback法
其所用的估算公式是
Tb Tc 0.584 0.965 ni Tci ( ni Tci ) 2
上页
下页
5.3.2 纯物质正常沸点的估算 正常沸点的实验数据相当丰富,可靠性也高,许多文献中, 有大量实验数据,但仍然有一些物质的Tb值有待估算。正 常沸点较难估算,虽然提出了一些Tb的估算方法,但有实 用价值的只有基团贡献法。
1)Joback法
式中Tb的单位是K,基团贡献值△Tbi见表5-10,通过438种 有机物的数据检验,式(5-15)的平均误差为3.6%。 2)C-G法
5)对称性修正 用键贡献法和基团贡献法估算理想气体熵SӨ时,通常必 须作分子对称性的修正。
对称数为定义是:分子刚性转动时,分子内相同原子 (或基团)出现独立互换的总次数(不得反转)。为便于 计算,通常把分解为外和内,即: =外. 内 计算分子的对称数一些规律 CP
对称性修正只对估算标准熵SӨ和标准生成只有焓GӨf才需 要修正。对于CӨp和HӨf等则不必要
典型的方法如UNIFAC法估算非电解质
5.2.3 基团贡献法中的修正项
分子内构型强烈的影响分子性质的值,而采用纯粹由基团 性质的元贡献值加和,往往不能充分反映分子构型的差异 对分子性质影响的大小。除按基团加和外,常常还要加上 一些修正项,这些修正项常见的有:
1)环式构型修正 n6 以后的环烃每个 -CH2- 具有正常和相同的燃烧热。因此 估算环状结构的化合物的性质时常有修正项,尤其是碳数 少的环。
