2018湖南省普通高中学业水平考试数学试题
2018年湖南省普通高中学业水平考试数学试题

19.(本小题满分 8 分) 如图 5 所示,四棱锥 P-ABCD 的底面是边长为 2 的正方形、PA⊥底面 ABCD.
(1)求证:CD⊥平面 PAD;
2
(2)若 E 为 PD 的中点,三棱锥 C-ADE 的体积为 ,求四棱锥 P-ABCD 的侧面积
3
20.(本小题满分 10 分)
在等差数列an 中,已知 a1 1, a2 a3 5 。
(2) f (x) a b 2
2 sin x
2
cos
x
2
sin(x
)
2
2
2
4
因为 sin(x ) [1,1] ,所以 f (x) 的值域为[1,3] 。 4
机密★启用前
2018 年湖南省普通高中学业水平考试
数学
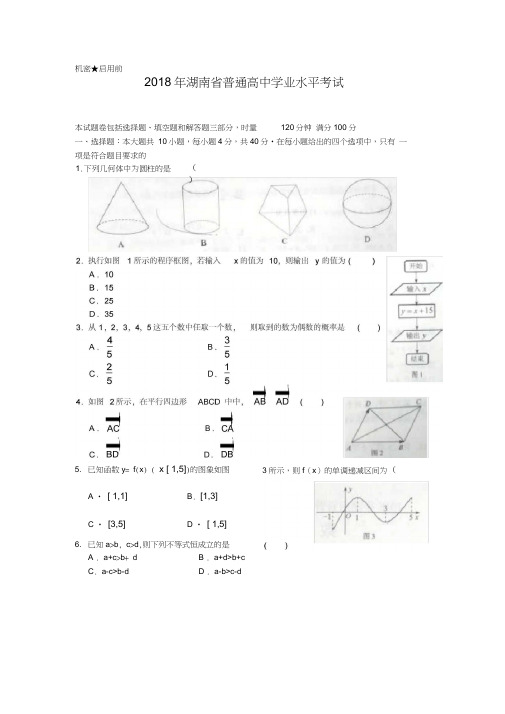
本试题卷包括选择题、填空题和解答题三部分,时量 120 分钟 满分 100 分 一、选择题:本大题共 10 小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有 一项是符合题目要求的 1.下列几何体中为圆柱的是
2.执行如图 1 所示的程序框图,若输入 x 的值为 10,则输出 y 的值为
B. 个单位长度
2
C. 1 个单位长度
D. 个单位长度
4
8.函数
f
(x)
log
( x1) 2
的零点为
A.4
B.3
C.2
D.1
9.在△ABC 中,已知 A=30°,B=45°,AC= 2 ,则 BC=
1
A.
2
2
B.
2
3
C.
2
D.1
10.过点 M(2,1)作圆 C: (x 1)2 y2 2 的切线,则切线条数为
(完整版)2018年湖南省普通高中学业水平考试数学试题(20200814150428)
2018年湖南省普通高中学业水平考试本试题卷包括选择题、填空题和解答题三部分,时量 120分钟 满分100分一、选择题:本大题共 10小题,每小题4分,共40分•在每小题给出的四个选项中,只有 一项是符合题目要求的5. 已知函数y = f (x ) ( x [ 1,5])的图象如图A • [ 1,1]B . [1,3]C • [3,5]D • [ 1,5]6. 已知a >b , c >d ,则下列不等式恒成立的是A . a+c >b + dB . a+d>b+cC . a-c>b-dD . a-b>c-d机密★启用前1.下列几何体中为圆柱的是 ()3所示,则f (x )的单调递减区间为(7.为了得到函数y cos(x4)的图象象只需将 y cosx 的图象向左平移()1 A •丄个单位长度2 1C •丄个单位长度4B .—个单位长度2二、 填空题;本大题共 5小题,每小题4分,共20分, 11. 直线y x 3在y 轴上的截距为 ___________________ 。
12. ______________________ 比较大小:sin25 sin23 (填、”或 N ” 13.已知集合 A 1,2 , B 1,x .若 A 「|B2,则 x= _______ 。
14•某工厂甲、乙两个车间生产了同一种产品,数量分别为 60件、40件,现用分层抽样方法抽取一个容量为 n 的样本进行质量检测,已知从甲车间抽取了 6件产品,则n =。
x 215•设x , y 满足不等等式组y 2 ,贝U z = 2x — y 的最小值为 __________ 。
x y 2三、 解答题:本大题共 5小题,共40分,解答应写出文字说明、证明过程或演步 16. (本小题满分6分)函数 f(x) log 2(x1)的零点为(1 A .-Bi C .乜D . 122210.过点M (:2, 1)作圆 C : (x1)2 y 22的切线, 则切线条数为()A . 0B . 1C . 2D . 3在△ ABC 中, 已知 A = 30 ° B = 45 9.AC = •. 2,贝U BC =( )O4个单位长度7. 为了得到函数y cos(x 4)的图象象只需将y cosx的图象向左平移( )1已知函数f (x) x (x 0)x(1 )求f (1)的值(2)判断函数f (x)的奇偶性,并说明理由.(2)设函数f (x) 2,求f (x)的值域,17. (本小题满分8分)某学校为了解学生对食堂用餐的满意度,从全校在食堂用餐的 取100名学生对食堂用餐的满意度进行评分. 根据学生对食堂用餐满意度的评分,得到如图4所示的率分布直方图, (1) 求顺率分布直方图中 a 的值(2) 规定:学生对食堂用餐满意度的评分不低于80分为满意”试估计该校在食堂用 餐的3000名学生中 满意”的人数。
湖南省普通高中2018年学业水平考试数学试题

2018年湖南省普通高中学业水平考试数学本试题卷包括选择题、填空题和解答题三部分,时量120分钟 满分100分一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.下列几何体中为圆柱的是2.执行如图1所示的程序框图,若输入x 的值为10,则输出y 的值为 A .10 B .15 C .25 D .353.从1,2,3,4,5这五个数中任取一个数,则取到的数为偶数的概率是A .45 B .35 C .25 D .154.如图2所示,在平行四边形ABCD 中中,AB AD += A .AC B .CA C .BD D .DB5.已知函数y =f (x )([1,5]x ∈-)的图象如图3所示,则f (x )的单调递减区间为 A .[1,1]- B .[1,3] C .[3,5] D .[1,5]- 6.已知a >b ,c >d ,则下列不等式恒成立的是 A .a +c >b +d B .a +d >b +c C .a -c >b -d D .a -b >c-d 7.为了得到函数cos()4y x π=+的图象象只需将cos y x =的图象向左平移A .12个单位长度 B .2π个单位长度C .14个单位长度 D .4π个单位长度 8.函数(1)2()log x f x -=的零点为A .4B .3C .2D .1 9.在△ABC 中,已知A =30°,B =45°,AC,则BC =A .12BCD .110.过点M (2,1)作圆C :22(1)2x y -+=的切线,则切线条数为 A .0 B .1 C .2 D .3二、填空题;本大题共5小题,每小题4分,共20分, 11.直线3y x =+在y 轴上的截距为_____________。
12.比较大小:sin25°_______sin23°(填“>”或“<”) 13.已知集合{}{}1,2,1,A B x ==-.若{}2AB =,则x =______。
2018年湖南省普通高中学业水平考试试卷

2018年湖南省普通高中学业水平考试试卷一、选择题(本题包括16小题,每题3分,共48分。
每小题只有一个选项符合题意) 1.发现万有引力定律的科学家是A .爱因斯坦B .卡文迪许C .开普勒D .牛顿 2.下列物理量属于矢量的是A .质量B .功C .重力势能D .力 3.列车员说“火车9点20分到站,停车10分。
”在这句话中 A .“9点20分”是指时刻,“10分”是指时间间隔 B .“9点20分”是指时间,“10分”是指时刻 C .“9点20分”与“10分”均指时刻 D .“9点20分”与“10分”均指时间间隔4.将一个物体从地球送到月球上,该物体在地球上的惯性与在月球上的惯性相比 A .在月球上惯性大 B .在地球上惯性大 C .惯性一样大 D .大小关系无法确定5.有两个共点力,其中一个力的大小是3N ,另一个力的大小是4N ,这两个力的合力的最大值为A .1NB .5NC .7ND .12N6.一位同学从操场中心A 点出发,先向北走了6m 到达C 点,然后向东走了8m 到达B 点,可以算出A 、B 两点间的距离为10m ,如图所示。
则该同学的位移大小和路程分别是 A .10m ,14m B .14m ,10m C .10m ,10m D .14m ,14m7.在同一平直公路上有A 、B 两辆汽车,它们的v-t 图象分别为a 、b ,如图所示,a 线平行于时间轴,b 线为过原点的倾斜直线,根据图象可知A .A 车静止,B 车做匀速直线运动B .A 车静止,B 车做匀加速直线运动C .A 车做匀速直线运动,B 车做匀加速直线运动D .A 车做匀速直线运动,B 车做匀速直线运动8.下列关于质点的说法正确的是A .研究跳水运动员在空中的翻转动作时,运动员可当做质点B .研究航天器绕地球运动的运行轨道时,航天器可当做质点C .研究地球自转时,地球可当做质点D .研究火车车轮的转动时,车轮可当做质点9.开普勒第二定律告诉我们:对任意一个行星来说,它与太阳的连线在相等的时间内扫过相等面积。
2018年湖南省高中数学学业水平考试仿真试卷Word版含解析

2018年湖南省高中数学学业水平考试仿真试卷一、选择题(共10小题,每小题4分,满分40分)1.已知集合M={0,1},集合N满足M∪N={0,1},则集合N共有()个.A.1 B.2 C.3 D.42.直线x+2y+2=0与直线2x+y﹣2=0的交点坐标是()A.(2,﹣2)B.(﹣2,2)C.(﹣2,1)D.(3,﹣4)3.不等式2x+y﹣3≤0表示的平面区域(用阴影表示)是()A.B.C. D.4.已知cosα=﹣,α是第三象限的角,则sinα=()A.﹣B.C.﹣D.5.已知函数f(x)=a x(a>0,a≠1)在[1,2]上的最大值和最小值的和为6,则a=()A.2 B.3 C.4 D.56.在△ABC中,a=b,A=120°,则B的大小为()A.30°B.45°C.60°D.90°7.一支田径队有男运动员49人,女运动员35人,用分层抽样的方法从全体运动员中抽出一个容量为24的样本,则应从男运动员中抽出的人数为()A.10 B.12 C.14 D.168.已知tanα=2,则tan(α﹣)=()A.B.C.D.﹣39.圆x2+y2=1与圆(x+1)2+(y+4)2=16的位置关系是()A.相外切B.相内切C.相交D.相离10.如图,圆O内有一个内接三角形ABC,且直径AB=2,∠ABC=45°,在圆O内随机撒一粒黄豆,则它落在三角形ABC内(阴影部分)的概率是()A.B.C.D.二、填空题(共5小题,每小题4分,满分20分)11.不等式x2﹣5x≤0的解集是.转化为十进制的数为.12.把二进制数10011(2)13.已知函数f(x)=Asinωx(A>0,ω>0)的图象如图所示,则A,ω的值分别是.14.已知函数f(x)=4﹣logx,x∈[2,8],则f(x)的值域是.215.点P是直线x+y﹣2=0上的动点,点Q是圆x2+y2=1上的动点,则线段PQ长的最小值为.三、解答题(共5小题,满分40分)16.如图,甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图:(1)某同学不小心把茎叶图中的一个数字弄污了,看不清了,在如图所示的茎叶图中用m表示,若甲运动员成绩的中位数是33,求m的值;(2)估计乙运动员在这次季后赛比赛中得分落在[20,40]内的概率.17.已知向量=(sinx,1),=(2cosx,3),x∈R.(1)当=λ时,求实数λ和tanx的值;(2)设函数f(x)=•,求f(x)的最小正周期和单调递减区间.18.如图,在三棱锥P﹣ABC中,平面PAB⊥平面ABC,△PAB是等边三角形,AC⊥BC,且AC=BC=2,O、D分别是AB,PB的中点.(1)求证:PA∥平面COD;(2)求三棱锥P﹣ABC的体积.19.已知函数f(x)=2+的图象经过点(2,3),a为常数.(1)求a的值和函数f(x)的定义域;(2)用函数单调性定义证明f(x)在(a,+∞)上是减函数.20.已知数列{an }的各项均为正数,其前n项和为Sn,且an2+an=2Sn,n∈N*.(1)求a1及an;(2)求满足Sn>210时n的最小值;(3)令bn=4,证明:对一切正整数n,都有+++…+<.2018年湖南省高中数学学业水平考试仿真试卷参考答案与试题解析一、选择题(共10小题,每小题4分,满分40分)1.已知集合M={0,1},集合N满足M∪N={0,1},则集合N共有()个.A.1 B.2 C.3 D.4【考点】19:集合的相等.【分析】根据集合的包含关系求出集合N的个数即可.【解答】解:M={0,1},集合N满足M∪N={0,1},则N⊆M,故N=∅,{0},{1},{0,1}共4种可能,故选:D.2.直线x+2y+2=0与直线2x+y﹣2=0的交点坐标是()A.(2,﹣2)B.(﹣2,2)C.(﹣2,1)D.(3,﹣4)【考点】IM:两条直线的交点坐标.【分析】根据题意,联立两直线的方程,解可得x、y的值,即可得交点坐标,即可得答案.【解答】解:根据题意,联立,解可得,即直线x+2y+2=0与直线2x+y﹣2=0的交点坐标是(2,﹣2);故选:A.3.不等式2x+y﹣3≤0表示的平面区域(用阴影表示)是()A.B.C. D.【考点】7B:二元一次不等式(组)与平面区域.【分析】作出不等式对应直线的图象,然后取特殊点代入不等式,判断不等式是否成立后得二元一次不等式表示的平面区域.【解答】解:画出不等式2x+y﹣3≤0对应的函数2x+y﹣3=0的图象,取点(0,0),把该点的坐标代入不等式2x+y﹣3≤0成立,说明不等式2x+y﹣3≤0示的平面区域与点(0,0)同侧,所以不等式2x+y﹣3≤0表示的平面区域在直线2x+y﹣3=0的右下方,并含直线.故选B.4.已知cosα=﹣,α是第三象限的角,则sinα=()A.﹣B.C.﹣D.【考点】GH:同角三角函数基本关系的运用.【分析】利用同角三角函数的基本关系、以及三角函数在各个象限中的符号,求得sinα的值.【解答】解:∵cosα=﹣,α是第三象限的角,则sinα=﹣=﹣,故选:C.5.已知函数f(x)=a x(a>0,a≠1)在[1,2]上的最大值和最小值的和为6,则a=()A.2 B.3 C.4 D.5【考点】49:指数函数的图象与性质.【分析】根据指数函数的单调性在定义域是要么递增,要么递减,即看求解.【解答】解:根据指数函数的性质:当x=1时,f(x)取得最大值,那么x=2取得最小值,或者x=1时,f(x)取得最小值,那么x=2取得最大值.∴a+a2=6.∵a>0,a≠1,∴a=2.故选:A.6.在△ABC中,a=b,A=120°,则B的大小为()A.30°B.45°C.60°D.90°【考点】HP:正弦定理.【分析】由已知利用正弦定理,特殊角的三角函数值可求sinB=,结合B的范围即可得解B 的值.【解答】解:∵a=b,A=120°,∴由正弦定理,可得:sinB=,又∵B∈(0°,60°),∴B=30°.故选:A.7.一支田径队有男运动员49人,女运动员35人,用分层抽样的方法从全体运动员中抽出一个容量为24的样本,则应从男运动员中抽出的人数为()A.10 B.12 C.14 D.16【考点】B3:分层抽样方法.【分析】先求出每个个体被抽到的概率,再用男运动员的人数乘以此概率,即得所求.【解答】解:每个个体被抽到的概率等于=,则应从男运动员中抽出的人数为49×=14,故选:C8.已知tanα=2,则tan(α﹣)=()A.B.C.D.﹣3【考点】GR:两角和与差的正切函数.【分析】由题意直接利用两角差的正切公式,求得要求式子的值.【解答】解:∵tanα=2,则tan(α﹣)==,故选:B.9.圆x2+y2=1与圆(x+1)2+(y+4)2=16的位置关系是()A.相外切B.相内切C.相交D.相离【考点】JA:圆与圆的位置关系及其判定.【分析】求出两个圆的圆心与半径,通过圆心距与半径的关系判断选项即可.【解答】解:圆x2+y2=1的圆心(0,0)半径为1;圆(x+1)2+(y+4)2=16的圆心(﹣1,﹣4),半径为4,圆心距为: =,半径和为5,半径差为:3,(3,5).所以两个圆的位置关系是相交.故选:C.10.如图,圆O内有一个内接三角形ABC,且直径AB=2,∠ABC=45°,在圆O内随机撒一粒黄豆,则它落在三角形ABC内(阴影部分)的概率是()A.B.C.D.【考点】CF:几何概型.【分析】根据题意,计算圆O的面积S圆和△ABC的面积S△ABC,求它们的面积比即可.【解答】解:圆O的直径AB=2,半径为1,所以圆的面积为S圆=π•12=π;△ABC的面积为S△ABC=•2•1=1,在圆O内随机撒一粒黄豆,它落在△ABC内(阴影部分)的概率是P==.故选:D.二、填空题(共5小题,每小题4分,满分20分)11.不等式x2﹣5x≤0的解集是{x|0≤x≤5} .【考点】74:一元二次不等式的解法.【分析】把不等式x2﹣5x≤0化为x(x﹣5)≤0,求出解集即可.【解答】解:不等式x2﹣5x≤0可化为x(x﹣5)≤0,解得0≤x≤5,∴不等式的解集是{x|0≤x≤5}.故答案为:{x|0≤x≤5}.12.把二进制数10011(2)转化为十进制的数为19 .【考点】WC:mod的完全同余系和简化剩余系.【分析】本题的考查点为二进制与十进制数之间的转换,只要我们根据二进制转换为十进制方法逐位进行转换,即可得到答案.=1+1×2+1×24=19【解答】解:10011(2)故答案为:1913.已知函数f(x)=Asinωx(A>0,ω>0)的图象如图所示,则A,ω的值分别是3,2 .【考点】HK:由y=Asin(ωx+φ)的部分图象确定其解析式.【分析】根据图象信息即可求出A,ω的值.【解答】解:根据图象,可知最高点为3,最低点﹣3,∴A=3.从图可以看出周期T=π,即=π,∴ω=2.故答案为:3,2.x,x∈[2,8],则f(x)的值域是[1,3] .14.已知函数f(x)=4﹣log2【考点】34:函数的值域.【分析】由x∈[2,8]上结合对数函数的单调性,即可求出函数的值域.【解答】解:∵函数f(x)=4﹣logx在x∈[2,8]时单调递减,22=3,∴当x=2时函数取最大值4﹣log28=1,当x=8时函数取最小值4﹣log2∴函数f(x)的值域为[1,3],故答案为:[1,3].15.点P是直线x+y﹣2=0上的动点,点Q是圆x2+y2=1上的动点,则线段PQ长的最小值为.【考点】J9:直线与圆的位置关系.【分析】求圆心到直线的距离减去半径可得最小值.【解答】解:圆心(0,0)到直线x+y﹣2=0的距离d==.再由d﹣r=﹣1,知最小距离为1.故答案为:.三、解答题(共5小题,满分40分)16.如图,甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图:(1)某同学不小心把茎叶图中的一个数字弄污了,看不清了,在如图所示的茎叶图中用m表示,若甲运动员成绩的中位数是33,求m的值;(2)估计乙运动员在这次季后赛比赛中得分落在[20,40]内的概率.【考点】CC:列举法计算基本事件数及事件发生的概率;BA:茎叶图.【分析】(1)由茎叶图性质利用中位数定义列出方程,求出m.(2)由篮球运动员乙的季后赛10场得分中有5场得分在区间[20,40]内,能估计乙运动员在一场季后赛比赛中得分落在[20,40]内的概率.【解答】解:(1)由茎叶图性质得:中位数为: =33,解得m=4.(2)∵篮球运动员乙的季后赛10场得分中有5场得分在区间[20,40]内,∴可以估计乙运动员在一场季后赛比赛中得分落在[20,40]内的概率为.17.已知向量=(sinx,1),=(2cosx,3),x∈R.(1)当=λ时,求实数λ和tanx的值;(2)设函数f(x)=•,求f(x)的最小正周期和单调递减区间.【考点】GL:三角函数中的恒等变换应用;9R:平面向量数量积的运算.【分析】(1)根据向量的运算性质,向量相等即可求解.(2)根据函数f(x)=•,求出f(x)的解析式,即可求出f(x)的最小正周期和单调递减区间.【解答】解:(1)向量=(sinx,1),=(2cosx,3),x∈R.当=λ时,可得∴,即tanx=.(2)函数f(x)=•,∴f(x)=2sinxcosx+3=sin2x+3.∴f(x)的最小正周期T=.∵f(x)单调递减.则,k∈Z,得:≤x≤.∴f(x)的单调递减区间为[,],k∈Z.18.如图,在三棱锥P﹣ABC中,平面PAB⊥平面ABC,△PAB是等边三角形,AC⊥BC,且AC=BC=2,O、D分别是AB,PB的中点.(1)求证:PA∥平面COD;(2)求三棱锥P﹣ABC的体积.【考点】LF:棱柱、棱锥、棱台的体积;LS:直线与平面平行的判定.【分析】(1)由O、D分别是AB,PB的中点,得OD∥AP,即可得PA∥平面COD.(2)连接OP,得OP⊥面ABC,且OP=.即可得三棱锥P﹣ABC的体积V==.【解答】解:(1)∵O、D分别是AB,PB的中点,∴OD∥AP又PA⊄平面COD,OD⊂平面COD∴PA∥平面COD.(2)连接OP,由△PAB是等边三角形,则OP⊥AB又∵平面PAB⊥平面ABC,∴OP⊥面ABC,且OP=.∴三棱锥P﹣ABC的体积V==.19.已知函数f(x)=2+的图象经过点(2,3),a为常数.(1)求a的值和函数f(x)的定义域;(2)用函数单调性定义证明f(x)在(a,+∞)上是减函数.【考点】3E:函数单调性的判断与证明;33:函数的定义域及其求法.【分析】(1)把点(2,3)代入函数解析式求出a的值;根据f(x)的解析式,求出它的定义域;(2)用单调性定义证明f(x)在(1,+∞)上是减函数即可.【解答】解:(1)函数f(x)=2+的图象经过点(2,3),∴2+=3,解得a=1;∴f(x)=2+,且x﹣1≠0,则x≠1,∴函数f(x)的定义域为{x|x≠1};(2)用函数单调性定义证明f(x)在(1,+∞)上是减函数如下;设1<x1<x2,则f (x 1)﹣f (x 2)=(2+)﹣(2+)=,∵1<x 1<x 2,∴x 2﹣x 1>0,x 1﹣1>0,x 2﹣1>0, ∴f (x 1)>f (x 2),∴f (x )在(1,+∞)上是减函数.20.已知数列{a n }的各项均为正数,其前n 项和为S n ,且a n 2+a n =2S n ,n ∈N *. (1)求a 1及a n ;(2)求满足S n >210时n 的最小值;(3)令b n =4,证明:对一切正整数n ,都有+++…+<.【考点】8K :数列与不等式的综合;8E :数列的求和.【分析】(1)当n=1时,,由此能求出a 1=1,由a n 2+a n =2S n ,得,从而(a n +a n ﹣1)(a n ﹣a n ﹣1﹣1)=0,进而数列{a n }是首项和公差都为1的等差数列,由此能求出a n =n .(2)求出S n =,由此能求出满足S n >210时n 的最小值.(3)由题意得,从而数列{}是首项和公比都是的等比数列,由此能证明对一切正整数n ,都有+++…+<.【解答】解:(1)∵数列{a n }的各项均为正数,其前n 项和为S n ,且a n 2+a n =2S n ,n ∈N *.∴当n=1时,,且a 1>0,解得a 1=1,∵a n 2+a n =2S n ,①,∴,②①﹣②,得:,整理,得:(a n +a n ﹣1)(a n ﹣a n ﹣1﹣1)=0, ∵a n >0,∴a n ﹣a n ﹣1=1,∴数列{a n }是首项和公差都为1的等差数列, ∴a n =n .(2)∵数列{a n }是首项和公差都为1的等差数列,a n =n .∴S=,n∵S>210,∴,n整理,得n2+n﹣420>0,解得n>20(n<﹣21舍),∴满足S>210时n的最小值是21.n证明:(3)由题意得,则,∴数列{}是首项和公比都是的等比数列,∴+++…+==.故对一切正整数n,都有+++…+<.。
2018届湖南省邵阳市高三学业水平考试模拟考试数学试题Word版含答案

2018届湖南省邵阳市学业水平考试模拟考试高三数学试题一、选择题1.设集合{}{}1223M N ==,,,,则M N ⋃= A. {}12, B. {}2 C. {}23, D. {}123,, 【答案】D【解析】由题意结合并集的定义可得M N ⋃= {}123,,. 本题选择D 选项.2.已知直线l 过点()00,和()31,,则直线l 的斜率为 A. 3 B. 13 C. 13- D. 3- 【答案】B【解析】由斜率公式可得,直线l 的斜率为: 101303k -==-. 本题选择B 选项. 3.sin150=A.1212- D. 【答案】A【解析】由题意可得: ()1sin150sin 18030sin302=-==. 本题选择A 选项.4.某校有学生1500名,其中高二年级500,打算从全校学生中抽取一个容量为30的样本,若考虑用分层抽样,则高二年级应抽取A. 30人B. 20人C. 10人D. 5人 【答案】C【解析】根据分层抽样的特征,可得高二年级应抽取30500101500⨯=人. 本题选择C 选项.点睛:分层抽样的特点:适用于总体由差异明显的几部分组成的情况;分层后,在每一层抽样时可采用简单随机抽样或系统抽样.5.圆224210x y x y +--+=的圆心坐标为A. ()42,B. ()42--,C. ()21,D. ()21--, 【答案】C【解析】由圆的一般方程可得圆心坐标为4222⎛⎫⎪⎝⎭,,即()21,. 本题选择C 选项.6.已知实数x y ,满足约束条件1{0 0x y x y +≤≥≥,则x y -的最大值为A. 1B. 0C. 1-D. 2 【答案】A【解析】画出不等式组表示的平面区域,如图中阴影部分所示: 作直线0x y -=,上下平移,当直线经过点(10A ,)时,目标函数z x y =-取得最大值,10 1.z =-=本题选择A 选项.点睛:求线性目标函数z =ax +by (ab ≠0)的最值,当b >0时,直线过可行域且在y 轴上截距最大时,z 值最大,在y 轴截距最小时,z 值最小;当b <0时,直线过可行域且在y 轴上截距最大时,z 值最小,在y 轴上截距最小时,z 值最大. 7.已知34==⋅=,,a b a b 则向量a 与b 的夹角为 A. 60 B. 30 C. 120 D. 150 【答案】A【解析】由3cos 4θθ===a b a b ,得1cos 2θ=,又[]0180θ∈︒︒,, ∴向量a 与b 的夹角60θ=︒. 本题选择A 选项.8.函数()21xf x =-的零点为A. 1B. 0C. ()10,D. ()00, 【答案】B【解析】函数的零点即相应方程的根.由210x -=得0x =,∴函数()21x f x =-的零点为0.本题选择B 选项.9.在长为3的线段AB 上任取一点P , P 到端点A B ,的距离都大于1的概率为 A.18 B. 12 C. 14 D. 13【答案】D【解析】由题知, P 满足条件的点所在的线段长为1,则所求概率为13P =. 本题选择D 选项.点睛:解答几何概型问题的关键在于弄清题中的考察对象和对象的活动范围.当考察对象为点,点的活动范围在线段上时,用线段长度比计算;当考察对象为线时,一般用角度比计算,即当半径一定时,由于弧长之比等于其所对应的圆心角的度数之比,所以角度之比实际上是所对的弧长(曲线长)之比. 10.若ΔABC 的内角A ,B ,C 的对边a b c ,,为满足222a b c bc =+-,则角A 的大小为 A.π6 B. π3 C. 2π3 D. 5π6【答案】B【解析】由余弦定理得2221cos 222b c a bc A bc bc +-===,又()0πA ∈,, π3A ∴=. 本题选择B 选项.二、填空题11.函数()cos2f x x =的最小正周期为________________. 【答案】π【解析】由周期公式可得函数()cos2f x x =的最小正周期为2ππ2T ==. 12.函数()()lg 1f x x =+的定义域为_________________ . 【答案】()1∞-+,【解析】由10x +>得1x >-,则函数()()lg 1f x x =+的定义域为()1∞-+,.13.在ΔABC 中260AB AC A ===,,,则ΔABC 的面积为_____________ . 【答案】3【解析】11sin 2sin60322ABC S AB AC A ∆==⨯︒==.14.若一个圆锥的三视图如图所示,则该圆锥的体积为______________ .【解析】由三视图可知该圆锥的底面半径为212r ==,高为h =则该圆锥的体积为211ππ1π333V r h ==⨯⨯=. 点睛:(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解;(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.15.阅读如图所示的程序框图,运行相应的程序,则输出的结果为________ .【答案】123【解析】模拟程序运行,可得: 1a =,满足循环条件100a ≤,执行循环体, 223a a =+=,满足循环条件100a ≤,执行循环体, 2211a a =+=,满足循环条件100a ≤,执行循环体, 22123a a =+=,不满足循环条件100a ≤,结束循环,输出的结果为123a 的值.三、解答题16.在等差数列{}n a 中242 4.a a ==,, (1)求数列{}n a 的通项公式;(2)设2n a n b =,求数列{}n b 的前5项和. 【答案】(1) n a n =;(2)62. 【解析】试题分析:(1)由题意求得数列的公差为1,据此可得数列的通项公式为n a n =; (2)由等比数列求和公式可得求数列{}n b 的前5项和是62. 试题解析:(1)∵422a a d =+,∴422d =+,∴1d =,∴()()2222n a a n d n n =+-=+-=. (2)∵2n n b =,∴()12122212n n n S +-==--,∴652262S =-=.即数列{}n b 的前5项和为62.17.如图所示,已知直三棱柱111ABC A B C -中12AB BC AA AB BC E ===⊥,,,为AC 的中点1BC ,交1B C 于点F.(1)证明:直线//EF 平面11ABB A ; (2)求异面直线1AB 与1BC 所成角的大小. 【答案】(1)证明见解析;(2)60°. 【解析】试题分析:(1)由题意可证得1//EF AB ,结合线面平行的判断定理即可证得直线//EF 平面11ABB A ;(2)由题意作出异面直线所成的角,结合空间几何体的结构特征可得异面直线1AB 与1BC 所成角的大小是60°.试题解析:(1)∵E F ,分别为1AC B C ,的中点,∴1//EF AB ,又11111EF ABB A AB ABB A ⊄⊂平面,平面, ∴11//EF ABB A 平面.(2)∵1//AB EF ,∴BFE ∠即为异面直线1AB 与1BC 所成的角或补角,连接BE , ∵12AB BD AA AB ===,⊥BC ,∴11•22BE AC ===111•22EF AB ===111•22BF BC ===∴△BEF 为等边三角形,∴060BFE ∠=,即异面直线11AB BC 与所成的角为060.点睛:(1)平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面问题化归为共面问题来解决,具体步骤如下:①平移:平移异面直线中的一条或两条,作出异面直线所成的角; ②认定:证明作出的角就是所求异面直线所成的角; ③计算:求该角的值,常利用解三角形; ④取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.(2)求异面直线所成的角要特别注意异面直线之间所成角的范围.18.某校从参加邵阳市数学竞赛的学生中随机抽取20名学生的数学成绩(均为整数)整理后分成六[)[)[]4050506090100,,,,,,,画出如图所示的频率分布直方图,观察图形的信息,回答下列问题:(1)求这20名学生中分数在[)7080,内的人数;(2)若从成绩大于或等于80分的学生中随机抽取2人,求恰有1名学生成绩在区间[]90100,内的概率. 【答案】(1) 7人;(2) 25. 【解析】试题分析:(1)由题意首先求得频率值,然后整理计算可得这20名学生中分数在[)7080,内的人数是7人; (2)列出所有可能的事件,由古典概型公式可得恰有1名学生成绩在区间[]90100,内的概率是25. 试题解析:(1)1-0.1-0.15-0.15-0.20-0.05=1-0.65=0.35,0.35⨯20=7, ∴分数在[70,80)内的学生人数为7人. (2)∵0.20+0.05=0.25,0.25⨯20=5,∴分数大于或等于80分的学生人数有5人,(其中[90,100]内的学生有1人).设这5人分别为a b c d e ,,,,,则从中选2人有ab ac ad ae bc bd be cd ce de ,,,,,,,,,,共10中情形,其中恰有1名学生成绩在[90,100]内的有ae be ce de ,,,4种情形, ∴恰有1名学生成绩在区间[90,100]内的概率为42105P ==.19.已知函数()sin2.f x x x x =∈R , (1)求()f x 的单调递增区间;(2) ππ42x ⎡⎤∀∈⎢⎥⎣⎦,恒有()3f x m -<成立,求实数m 的取值范围.【答案】(1) ()π5πππ1212k k k ⎡⎤-+∈⎢⎥⎣⎦Z ,;(2) ()14-,. 【解析】试题分析:(1)整理函数的解析式为()π2sin 23f x x x ⎛⎫=-∈ ⎪⎝⎭R ,,则()f x 的单调递增区间是()π5πππ1212k k k ⎡⎤-+∈⎢⎥⎣⎦Z ,. (2)由题意得到关于实数m 的不等式组,求解不等式组可得实数m 的取值范围是()14-,. 试题解析:(1)∵()πsin22sin 23f x x x x x ⎛⎫==-∈ ⎪⎝⎭R ,,当πππ2π22π232k x k -≤-≤+即π5π2π22π66k x k -≤≤+, 即()π5πππ1212k x k k -≤≤+∈Z 时()f x 单调递增, ∴()f x 的单调递增区间为()π5πππ1212k k k ⎡⎤-+∈⎢⎥⎣⎦Z ,. (2)∵ππ42x ⎡⎤∈⎢⎥⎣⎦,,∴ππ2π2363x ⎡⎤-∈⎢⎥⎣⎦,,∴()[]12f x ∈,, 由()3f x m -<得()33m f x m -<<+,∴31{ 32m m -<+>,,∴14m -<<即()14m ∈-,. 20.已知函数()21ax bf x x +=+是定义在()2a a -,上的奇函数. (1)求()f x 的解析式;(2)证明:函数()f x 在定义域上是增函数; (3)设()()()m h x f x f x =+,是否存在正实数m ,使得函数()h x 在112⎡⎤⎢⎥⎣⎦,内的最小值为2125?若存在,求出m 的值;若存在,请说明理由.【答案】(1) ()()2111x f x x x =∈-+,,;(2)证明见解析;(3)存在4412500m =,使函数()h x 在112⎡⎤⎢⎥⎣⎦,内的最小值为2125. 【解析】试题分析:(1)由题意求得实数a,b 的值,则()()2111xf x x x =∈-+,,; (2)由单调性的定义证明函数的单调性即可; (3)结合函数的解析式分类讨论可得存在4412500m =,使函数()h x 在112⎡⎤⎢⎥⎣⎦,内的最小值为2125. 试题解析:(1)∵2a a -=-,∴1a =,又()00f =,∴0b =, ∴()()2111xf x x x =∈-+,,. (2)设12x x ,为区间()11-,内的任意两个自变量,且12x x <,则()()2121222111x x f x f x x x -=-++=()()22212121221211x x x x x x x x +--++=()()()()121221221211x x x x x x x x -+-++ ()()()()21122212111x x x x xx --=++,∵()()12121111x x x x ∈-∈-,,,,,∴1210x x ->, 又∵12x x <,∴210x x ->,∴()()()()211222121011x x x x x x -->++,即()()21f x f x >,∴()f x 在()11-,上为增函数.(3)由(2)知()f x 在112⎡⎤⎢⎥⎣⎦,内为增函数,∴()2152f x ⎡⎤∈⎢⎥⎣⎦,,令()t f x =,则()2152m h t t t t ⎡⎤=+∈⎢⎥⎣⎦,,.12>时()2152h t ⎛⎫ ⎪⎝⎭,在,上单调递减()min 12h t h ⎛⎫= ⎪⎝⎭,, 解得17100m =,矛盾,舍去;②当2152≤≤时()2125m h t t t =+≥=,, 解得441212125002552m t ⎛⎫==∈ ⎪⎝⎭,,时取等号;③当205<<时()h t ,在2152⎡⎤⎢⎥⎣⎦,上单调递增()min 25h t h ⎛⎫= ⎪⎝⎭,, 解得22125m =,矛盾,舍去. 所以存在4412500m =,使函数()h x 在112⎡⎤⎢⎥⎣⎦,内的最小值为2125. 点睛:判断函数的奇偶性,其中包括两个必备条件:(1)定义域关于原点对称,这是函数具有奇偶性的必要不充分条件,所以首先考虑定义域;(2)判断f (x )与f (-x )是否具有等量关系.在判断奇偶性的运算中,可以转化为判断奇偶性的等价等量关系式(f (x )+f (-x )=0(奇函数)或f (x )-f (-x )=0(偶函数))是否成立.关于奇偶性、单调性、周期性的综合性问题,关键是利用奇偶性和周期性将未知区间上的问题转化为已知区间上的问题.。
湖南数学学考真题(2009-2018)

2018年湖南省普通高中学业水平考试数学试卷一、选择题:本大题共10小题,每小题4分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知等差数列{n a }的前3项分别为2、4、6,则数列{n a }的第4项为A .7B .8C .10D .122.如图是一个几何体的三视图,则该几何体为A .球B .圆柱C .圆台D .圆锥 3.函数)2)(1()(+-=x x x f 的零点个数是A .0B .1C .2D .34.已知集合}2,0,1{-=A ,}3,{x =B ,若}2{=B A ,则x 的值为 A .3 B .2 C .0 D .-15.已知直线1l :12+=x y ,2l :52+=x y ,则直线1l 与2l 的位置关系是 A .重合 B .垂直 C .相交但不垂直 D .平行6.下列坐标对应的点中,落在不等式01<-+y x 表示的平面区域内的是A .(0,0)B .(2,4)C .(-1,4)D .(1,8) 7.某班有50名同学,将其编为1、2、3、…、50号,并按编号从小到大平均分成5组.现用系统抽样方法,从该班抽取5名同学进行某项调查,若第1组抽取的学生编号为3,第2组抽取的学生编号为13,则第4组抽取的学生编号为 A .14 B .23 C .33 D .438.如图,D 为等腰三角形ABC 底边AB 的中点,则下列等式恒成立的是A .0=⋅B .0=⋅C .0=⋅D .0=⋅9.将函数x y sin =的图象向左平移3π个单位长度,得到的图象对应的函数解析式为A .)3sin(π+=x yB .)3sin(π-=x yC .)32sin(π+=x yD .)32sin(π-=x y 10.如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60颗豆子落在阴影部分内,则用随机模拟的方法可以(第2题图)俯视图(第8题图)CABD估计图中阴影部分的面积为A .32B .54C .56D .34二、填空题:本大题共5小题,每小题4分,满分20分. 11.比较大小:5log 2 3log 2 (填“>”或“<”). 12.已知圆4)(22=+-y a x 的圆心坐标为)0,3(,则实数=a .13.某程序框图如图所示,若输入的c b a ,,值分别为3,4,5,则输出的y 值为 .14.已知角α的终边与单位圆的交点坐标为(23,21),则αcos = .15.如图,A ,B 两点在河的两岸,为了测量A 、B 之间的距离,测量者在A 的同侧选定一点C ,测出A 、C 之间的距离是100米,∠BAC=105º,∠ACB=45º,则A 、B 两点之间的距离为 米.三、解答题:本大题共5小题,满分40分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分6分)已知函数)(x f y =(]6,2[-∈x )的图象如图.根据图象写出: (1)函数)(x f y =的最大值; (2)使1)(=x f 的x 值. 17.(本小题满分8分)一批食品,每袋的标准重量是50g ,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位:g ),并得到其茎叶图(如图).(第13题图)(第15题图) (第16题图)(1)求这10袋食品重量的众数,并估计这批食品实际重量的平均数;(2)若某袋食品的实际重量小于或等于47g ,则视为不合格产品,试估计这批食品重量的合格率.18.(本小题满分8分)如图,在四棱柱ABCD-A 1B 1C 1D 1中,D 1D ⊥底面ABCD ,底面ABCD 是正方形,且AB=1,D 1D=2.(1)求直线D 1B 与平面ABCD 所成角的大小; (2)求证:AC ⊥平面BB 1D 1D .19.(本小题满分8分)已知向量a =(x sin ,1),b =(x cos ,1),∈x R . (1)当4π=x 时,求向量a + b 的坐标;(2)若函数=)(x f |a + b |2m +为奇函数,求实数m 的值.4 5 6 6 95 0 0 0 1 1 2(第17题图) (第18题图)A B CD A 1 B 1C 1D 120.(本小题满分10分)已知数列{n a }的前n 项和为a S n n +=2(a 为常数,∈n N *). (1)求1a ,2a ,3a ;(2)若数列{n a }为等比数列,求常数a 的值及n a ;(3)对于(2)中的n a ,记34)(112-⋅-⋅=++n n a a n f λλ,若0)(<n f 对任意的正整数n 恒成立,求实数λ的取值范围.2018年湖南省普通高中学业水平考试数学试卷参考答案二、填空题(每小题4分,满分20分) 11.>; 12. 3; 13.4; 14. 21; 15. 2100. 三、解答题(满分40分)16.解:(1)由图象可知,函数)(x f y =的最大值为2; …………………3分(2)由图象可知,使1)(=x f 的x 值为-1或5. ……………6分 17.解:(1)这10袋食品重量的众数为50(g ), ………………2分 因为这10袋食品重量的平均数为491052515150505049464645=+++++++++(g ), 所以可以估计这批食品实际重量的平均数为49(g ); ……………4分 (2)因为这10袋食品中实际重量小于或等于47g 的有3袋,所以可以估计这批食品重量的不合格率为103,故可以估计这批食品重量的合格率为107. 8分 18.(1)解:因为D 1D ⊥面ABCD ,所以BD 为直线B D 1在平面ABCD 内的射影,所以∠D 1BD 为直线D 1B 与平面ABCD 所成的角, …………………2分又因为AB=1,所以BD=2,在Rt △D 1DB 中,1tan 11==∠BDDD BD D , 所以∠D 1BD=45º,所以直线D 1B 与平面ABCD 所成的角为45º; 4分 (2)证明:因为D 1D ⊥面ABCD ,AC 在平面ABCD 内,所以D 1D ⊥AC , 又底面ABCD 为正方形,所以AC ⊥BD , …………………6分 因为BD 与D 1D 是平面BB 1D 1D 内的两条相交直线,所以AC ⊥平面BB 1D 1D . …………………………8分 19.解:(1)因为a =(x sin ,1),b =(x cos ,1),4π=x ,所以a + b )2,2()2,cos (sin =+=x x ; …………………4分 (2)因为a + b )2,cos (sin x x +=,所以m x m x x x f ++=+++=52sin 4)cos (sin )(2, ……………6分 因为)(x f 为奇函数,所以)()(x f x f -=-,即m x m x ---=++-52sin 5)2sin(,解得5-=m . ……………8分 注:由)(x f 为奇函数,得0)0(=f ,解得5-=m 同样给分.20.解:(1)211+==a S a , ……………………1分 由212a a S +=,得22=a , ……………………2分由3213a a a S ++=,得43=a ; …………………3分 (2)因为21+=a a ,当2≥n 时,112--=-=n n n n S S a ,又{n a }为等比数列,所以11=a ,即12=+a ,得1-=a , …………5分 故12-=n n a ; …………………………………6分 (3)因为12-=n n a ,所以3242)(2-⋅-⋅=n n n f λλ, ………………7分 令n t 2=,则2≥t ,34)2(34)(22---=-⋅-⋅=λλλλt t t n f , 设34)2()(2---=λλt t g ,当0=λ时,03)(<-=n f 恒成立, …………………8分当0>λ时,34)2()(2---=λλt t g 对应的点在开口向上的抛物线上,所以0)(<n f 不可能恒成立, ……………9分当0<λ时,34)2()(2---=λλt t g 在2≥t 时有最大值34--λ,所以要使0)(<n f 对任意的正整数n 恒成立,只需034<--λ,即43->λ,此时043<<-λ,综上实数λ的取值范围为043≤<-λ. …………………………10分说明:解答题如有其它解法,酌情给分.2017年湖南省普通高中学业水平考试数学(真题)本试卷包括选择题、填空题和解答题三部分,共4页,时量120分钟,满分100分。
2018年湖南省普通高中学业水平考试语文数学英语总分

2018年湖南省普通高中学业水平考试语文数学英语总分1、38.These workers ___________ this bridge since one year ago. [单选题] *A.buildB.are buildingC.have built (正确答案)D.built2、The children were all looking forward to giving the old people a happy day. [单选题]*A. 寻找B. 期盼(正确答案)C. 看望D. 继续3、She was seen _____ that theatre just now. [单选题] *A. enteredB. enterC. to enter(正确答案)D. to be entering4、( ) _____ New York _____ London have traffic problems. [单选题] *A. All…andB. Neither….norC. Both…and(正确答案)D. Either…or5、He has two sisters but I have not _____. [单选题] *A. noneB. someC. onesD. any(正确答案)6、I have a _____ every day to keep fit. [单选题] *A. three thousand meter walkB. three-thousands-meters walkC.three-thousand-meters walkD. three-thousand-meter walk(正确答案)7、He often comes to work early and he is _______ late for work. [单选题] *A. usuallyC. oftenD. sometimes8、--Whose _______ are these?? ? ? --I think they are John·s. [单选题] *A. keyB. keyesC. keys(正确答案)D. keies9、If you want to be successful one day, you have to seize every _______ to realize your dream. [单选题] *A. changeB. chance(正确答案)C. chairD. check10、She _______ love cats, but one attacked her and she doesn’t like them anymore. [单选题]*A. got used toB. was used toC. was used for11、Marie is a _______ girl.She always smiles and says hello to others. [单选题] *A. shyB. friendly(正确答案)C. healthyD. crazy12、31.A key ring is used __________ holding the keys. [单选题] *A.toB.inC.for (正确答案)D.with13、64.Would you like to drink ________?[单选题] *A.something else(正确答案)B.anything elseC.else somethingD.else anything14、( ) Some students preferred to stay in the toilet ______ do morning exercises. [单选题] *A in order to notB in not order toC in order not to(正确答案)D not in order to15、I _______ Zhang Hua in the bookstore last Sunday. [单选题] *A. meetB. meetingC. meetedD. met(正确答案)16、Mr. White likes to live in a _______ place. [单选题] *A. quiteB. quiet(正确答案)C. quickD. quietly17、If people _____ overanxious about remembering something, they will forget it. [单选题] *A. will beB. would beC. wereD. are(正确答案)18、10.﹣Could you please sweep the floor?I’m going to cook dinner.﹣__________.I’ll do it at once,Mom.[单选题] *A.I’m afraid notB.You’re kiddingC.It’s a shameD.My pleasure(正确答案)19、Have you done something _______ on the weekends? [单选题] *A. special(正确答案)B. soreC. convenientD. slim20、While I _____ the morning paper, a headline caught my eye.. [单选题] *A. have readB. was reading(正确答案)C. had readD. am reading21、I _____ of her since she left school three years ago. [单选题] *A. didn’t hearB. haven’t heard(正确答案)C. was not hearingD. shall not heard22、He doesn’t smoke and hates women _______. [单选题] *A. smokesB. smokeC. smokedD. smoking(正确答案)23、There is a bank ______ the street. [单选题] *A. on the end ofB. in the end ofC. at the end of(正确答案)D. by the end of24、We are looking forward to _______ you again. [单选题] *A. seeB. sawC. seeing(正确答案)D. seen25、If you get _______, you can have some bread on the table. [单选题] *A. happyB. hungry(正确答案)C. worriedD. sad26、In order to find the missing child, villagers _______ all they can over the past five hours. [单选题] *A. didB. doC. had doneD. have been doing(正确答案)27、He always ______ the teacher carefully in class. [单选题] *A. listensB. listens to(正确答案)C. hearsD. hears of28、---Where’s that report?---I brought it to you ____you were in Mr. Black’s office yesterday. [单选题] *A. ifB. when(正确答案)C. becauseD. before29、()late for the meeting again, Jack! 一Sorry, I won t. [单选题] *A.Don’tB. Be notC.Don't be(正确答案)D.Not be30、_____ whether robots will one day have vision as good as human vision. [单选题] *A. What is not yet knownB. It is not yet known(正确答案)C. As is not yet knownD. This is not yet known。
2018年湖南省普通高中学业水平考试数学试卷Word版含答案

2018年湖南省普通高中学业水平考试数学试卷一、选择题:本大题共10小题,每小题4分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知等差数列{n a }的前3项分别为2、4、6,则数列{n a }的第4项为A .7B .8C .10D .12 2.如图是一个几何体的三视图,则该几何体为A .球B .圆柱C .圆台D .圆锥 3.函数)2)(1()(+-=x x x f 的零点个数是A .0B .1C .2D .34.已知集合}2,0,1{-=A ,}3,{x =B ,若}2{=B A ,则x 的值为 A .3 B .2 C .0 D .-15.已知直线1l :12+=x y ,2l :52+=x y ,则直线1l 与2l 的位置关系是 A .重合 B .垂直 C .相交但不垂直 D .平行6.下列坐标对应的点中,落在不等式01<-+y x 表示的平面区域内的是A .(0,0)B .(2,4)C .(-1,4)D .(1,8)7.某班有50名同学,将其编为1、2、3、…、50号,并按编号从小到大平均分成5组.现用系统抽样方法,从该班抽取5名同学进行某项调查,若第1组抽取的学生编号为3,第2组抽取的学生编号为13,则第4组抽取的学生编号为A .14B .23C .33D .438.如图,D 为等腰三角形ABC 底边AB 的中点,则下列等式恒成立的是A .0=⋅CB CA B .0=⋅AB CDC .0=⋅CD CA D .0=⋅CB CD9.将函数x y sin =的图象向左平移3π个单位长度,得到的图象对应的函数解析式为A .)3sin(π+=x yB .)3sin(π-=x y(第2题图)俯视图(第8题图)CABDC .)32sin(π+=x y D .)32sin(π-=x y 10.如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60颗豆子落在阴影部分内,则用随机模拟的方法可以估计图中阴影部分的面积为A .32B .54C .56D .34二、填空题:本大题共5小题,每小题4分,满分20分. 11.比较大小:5log 2 3log 2 (填“>”或“<”).12.已知圆4)(22=+-y a x 的圆心坐标为)0,3(,则实数=a .13.某程序框图如图所示,若输入的c b a ,,值分别为3,4,5,则输出的y 值为 . 14.已知角α的终边与单位圆的交点坐标为(23,21),则αcos = . 15.如图,A ,B 两点在河的两岸,为了测量A 、B 之间的距离,测量者在A 的同侧选定一点C ,测出A 、C 之间的距离是100米,∠BAC=105º,∠ACB=45º,则A 、B 两点之间的距离为 米.三、解答题:本大题共5小题,满分40分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分6分)已知函数)(x f y =(]6,2[-∈x )的图象如图.根据图象写出: (1)函数)(x f y =的最大值; (2)使1)(=x f 的x 值.(第10题图)(第13题图)(第15题图)(第16题图)一批食品,每袋的标准重量是50g,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位:g),并得到其茎叶图(如图).(1)求这10袋食品重量的众数,并估计这批食品实际重量的平均数;(2)若某袋食品的实际重量小于或等于47g,则视为不合格产品,试估计这批食品重量的合格率.18.(本小题满分8分)如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,且AB=1,D1D=2.(1)求直线D1B与平面ABCD所成角的大小;(2)求证:AC⊥平面BB1D1D.4 5 6 6 95 0 0 0 1 1 2(第17题图)(第18题图)A BCDA1B1C1D1已知向量a =(x sin ,1),b =(x cos ,1),∈x R . (1)当4π=x 时,求向量a + b 的坐标;(2)若函数=)(x f |a + b |2m +为奇函数,求实数m 的值. 20.(本小题满分10分)已知数列{n a }的前n 项和为a S n n +=2(a 为常数,∈n N *). (1)求1a ,2a ,3a ;(2)若数列{n a }为等比数列,求常数a 的值及n a ;(3)对于(2)中的n a ,记34)(112-⋅-⋅=++n n a a n f λλ,若0)(<n f 对任意的正整数n 恒成立,求实数λ的取值范围.2018年湖南省普通高中学业水平考试数学试卷参考答案二、填空题(每小题4分,满分20分) 11.>; 12. 3; 13.4; 14. 21; 15. 2100. 三、解答题(满分40分)16.解:(1)由图象可知,函数)(x f y =的最大值为2; …………………3分(2)由图象可知,使1)(=x f 的x 值为-1或5. ……………6分 17.解:(1)这10袋食品重量的众数为50(g ), ………………2分 因为这10袋食品重量的平均数为491052515150505049464645=+++++++++(g ), 所以可以估计这批食品实际重量的平均数为49(g ); ……………4分(2)因为这10袋食品中实际重量小于或等于47g 的有3袋,所以可以估计这批食品重量的不合格率为103,故可以估计这批食品重量的合格率为107. 8分 18.(1)解:因为D 1D ⊥面ABCD ,所以BD 为直线B D 1在平面ABCD 内的射影,所以∠D 1BD 为直线D 1B 与平面ABCD 所成的角, …………………2分又因为AB=1,所以BD=2,在Rt △D 1DB 中,1tan 11==∠BDDD BD D , 所以∠D 1BD=45º,所以直线D 1B 与平面ABCD 所成的角为45º; 4分 (2)证明:因为D 1D ⊥面ABCD ,AC 在平面ABCD 内,所以D 1D ⊥AC , 又底面ABCD 为正方形,所以AC ⊥BD , …………………6分 因为BD 与D 1D 是平面BB 1D 1D 内的两条相交直线,所以AC ⊥平面BB 1D 1D . …………………………8分 19.解:(1)因为a =(x sin ,1),b =(x cos ,1),4π=x ,所以a + b )2,2()2,cos (sin =+=x x ; …………………4分 (2)因为a + b )2,cos (sin x x +=,所以m x m x x x f ++=+++=52sin 4)cos (sin )(2, ……………6分因为)(x f 为奇函数,所以)()(x f x f -=-,即m x m x ---=++-52sin 5)2sin(,解得5-=m . ……………8分 注:由)(x f 为奇函数,得0)0(=f ,解得5-=m 同样给分.20.解:(1)211+==a S a , ……………………1分由212a a S +=,得22=a , ……………………2分 由3213a a a S ++=,得43=a ; …………………3分 (2)因为21+=a a ,当2≥n 时,112--=-=n n n n S S a ,又{n a }为等比数列,所以11=a ,即12=+a ,得1-=a , …………5分 故12-=n n a ; …………………………………6分 (3)因为12-=n n a ,所以3242)(2-⋅-⋅=n n n f λλ, ………………7分 令n t 2=,则2≥t ,34)2(34)(22---=-⋅-⋅=λλλλt t t n f , 设34)2()(2---=λλt t g ,当0=λ时,03)(<-=n f 恒成立, …………………8分当0>λ时,34)2()(2---=λλt t g 对应的点在开口向上的抛物线上,所以0)(<n f 不可能恒成立, ……………9分当0<λ时,34)2()(2---=λλt t g 在2≥t 时有最大值34--λ,所以要使0)(<n f 对任意的正整数n 恒成立,只需034<--λ,即43->λ,此时043<<-λ,综上实数λ的取值范围为043≤<-λ. …………………………10分说明:解答题如有其它解法,酌情给分.。
2018年湖南省(长郡中学)普通高中学业水平模拟考试(三)数学答案

解析% 分析如图程序框图& 可知* 该程序的作用是计算分段函数"0 & ! +!$
"& &!# #$ ! $ 的函数值! % & #1 ! ## ! '
当#$ 若"0 ! & 则#0槡 !时 & "& #01槡 "舍去' " ! # 当## 若"0 ! & 则#1 !时 & ! 0 & #0 不合题意! " " " 解析% 连接 ' ' ! ,!$ && ( %& % '& ( '& ! ! ! /)*( ' &(( %& ! ! 3)( % ' 为异面直线% ' 和 )* 所成的角& ! 而三角形 ( % ' 为等边三角形& ! 3)( % '0 & * 4 ! ! 解析% 对于 -& 函数的定义域为 + & & ( ! +!$ * 25 " 定义域不关于原点对称& 故 - 为非奇非偶函数'
!
的图 #
"
& 象与# 轴的两个相邻交点的距离等于 ! " & 0 3 $ 0 " $ 若将函数"0+! 的图象向左平移 个单位得到函数 "0/! #" #" 0 & " 的图象& " 9 = >$ 0 " 9 = >$ #2 1 #2 # # #
2018年湖南学考数学真题

机密★启用前2018年湖南省普通高中学业水平考试数学本试题卷包括选择题、填空题和解答题三部分,时量120分钟 满分100分一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.下列几何体中为圆柱的是2.执行如图1所示的程序框图,若输入x 的值为10,则输出y 的值为 A .10 B .15 C .25 D .353.从1,2,3,4,5这五个数中任取一个数,则取到的数为偶数的概率是A .45 B .35 C .25 D .154.如图2所示,在平行四边形ABCD 中中,AB AD += A .AC B .CA C .BD D .DB5.已知函数y =f (x )([1,5]x ∈-)的图象如图3所示,则f (x )的单调递减区间为 A .[1,1]- B .[1,3] C .[3,5] D .[1,5]- 6.已知a >b ,c >d ,则下列不等式恒成立的是 A .a +c >b +d B .a +d >b +c C .a -c >b -d D .a -b >c-d 7.为了得到函数cos()4y x π=+的图象象只需将cos y x =的图象向左平移A .12个单位长度 B .2π个单位长度C .14个单位长度 D .4π个单位长度 8.函数(1)2()log x f x -=的零点为A .4B .3C .2D .1 9.在△ABC 中,已知A =30°,B =45°,AC,则BC =A .12BCD .110.过点M (2,1)作圆C :22(1)2x y -+=的切线,则切线条数为 A .0 B .1 C .2 D .3二、填空题;本大题共5小题,每小题4分,共20分, 11.直线3y x =+在y 轴上的截距为_____________。
12.比较大小:sin25°_______sin23°(填“>”或“<”) 13.已知集合{}{}1,2,1,A B x ==-.若{}2AB =,则x =______。
湖南省普通高中学业水平考试真题清晰

湖南省普通高中学业水平考试真题清晰TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-2018年湖南省普通高中学业水平考试真题本试题卷包括选择题、填空题和解答题三部分,共4页.时量120分钟,满分100分一、选择题:本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列几何体中为圆柱的是 ( )2.执行如图1所示的程序框图,若输入x 的值为10,则输出y 的值为 ( )3.从1,2,3,4,5这五个数中任取一个数,则取到的数为偶数的概率是( ) A.54 B.53C.52D.514.如图2所示,在平行四边形ABCD 中,=+AD AB ( ) A.B.C.D.5.已知函数()x f y =([]5,1-∈x )的图象如图3所示,则()x f 的单调减区间为( )A.[]1,1-B.[]3,1C.[]5,3 D .[]5,1-6.已知d c b a >>,,则下列不等式恒成立的是 ( ) A.d b c a +>+ B.c b d a +>+ C.d b c a ->-D.d c b a ->-7.为了得到函数⎪⎭⎫⎝⎛+=4cos πx y 的图象,只需将x y cos =的图象向左平移( )A.21个单位长度 B.2π个单位长度 C.41个单位长度 D.4π个单位长度8.函数()()1log 2-=x x f 的零点为( )C.2D.19.在ABC ∆中,已知︒=︒=45,30B A ,2=AC ,则=BC ( ) A.21B.22 C.2310.过点()1,2M 作圆C :()2122=+-y x 的切线,则切线条数为 ( )C.2二、填空题:本大题共5小题,每小题4分,共20分。
11.直线3+=x y 在y 轴上的截距为________.12.比较大小:︒25sin ___︒23sin (填“>”或“<”). 13.已知集合{}2,1=A ,{}x B ,1-=,若{}2=B A ,则=x ________. 14.某工厂甲、乙两个车间生产了同一种产品,数量分别是60件、40件,现用分层抽样的方法抽取一个容量为n 的样本进行质量检测,已知从甲车间抽取6件产品,则=n ________.15.设y x ,满足不等式组⎪⎩⎪⎨⎧≥+≤≤222y x y x ,则y x z -=2的最小值为________.三、解答题:本大题共5小题,共40分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机密★启用前
2018年湖南省普通高中学业水平考试
数 学
本试题卷包括选择题、填空题和解答题三部分,时量120分钟 满分100分
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的
1.下列几何体中为圆柱的是 ( )
2.执行如图1所示的程序框图,若输入x 的值为10,则输出y 的值为( ) A .10 B .15 C .25 D .35 3.从1,2,3,4,5这五个数中任取一个数,则取到的数为偶数的概率是( )
A .
45 B .3
5 C .25 D .15
4.如图2所示,在平行四边形ABCD 中中,AB AD +=u u u r u u u r
( )
A .AC u u u r
B .CA u u u r
C .B
D u u u r D .DB u u u r
5.已知函数y =f (x )([1,5]x ∈-)的图象如图3所示,则f (x )的单调递减区间为( ) A .[1,1]- B .[1,3] C .[3,5] D .[1,5]-
6.已知a >b ,c >d ,则下列不等式恒成立的是 ( ) A .a +c >b +d B .a +d >b +c C .a -c >b -d D .a -b >c-d
7.为了得到函数cos()4
y x π
=+的图象象只需将cos y x =的图象向左平移 ( )
A .
12个单位长度 B .2π
个单位长度 C .14个单位长度 D .4
π
个单位长度
8.函数)1(log )(2-=x x f 的零点为( )
A .4
B .3
C .2
D .1
9.在△ABC 中,已知A =30°,B =45°,AC
,则BC =( )
A .
1
2
B
.2 C
.2 D .1
10.过点M (2,1)作圆C :2
2
(1)2x y -+=的切线,则切线条数为( ) A .0 B .1 C .2 D .3
二、填空题;本大题共5小题,每小题4分,共20分, 11.直线3y x =+在y 轴上的截距为_____________。
12.比较大小:sin25°_______sin23°(填“>”或“<”) 13.已知集合{}{}1,2,1,A B x ==-.若{}2A B =I ,则x =______。
14.某工厂甲、乙两个车间生产了同一种产品,数量分别为60件、40件,现用分层抽样方法抽取一个容量为n 的样本进行质量检测,已知从甲车间抽取了6件产品,则n =_____。
15.设x ,y 满足不等等式组⎪⎩
⎪
⎨⎧≥+≤≤222y x y x ,则z =2x -y 的最小值为________。
三、解答题:本大题共5小题,共40分,解答应写出文字说明、证明过程或演步 16.(本小题满分6分)
已知函数1
()(0)f x x x x
=+≠ (1)求(1)f 的值
(2)判断函数()f x 的奇偶性,并说明理由.
某学校为了解学生对食堂用餐的满意度,从全校在食堂用餐的3000名学生中,随机抽取100名学生对食堂用餐的满意度进行评分.根据学生对食堂用餐满意度的评分,得到如图4所示的率分布直方图, (1)求顺率分布直方图中a 的值
(2)规定:学生对食堂用餐满意度的评分不低于80分为“满意”,试估计该校在食堂
用餐的3000名学生中“满意”的人数。
18.(本小题满分8分)
已知向量22
(sin ,cos ),(
,)a x x b ==r r (1)若a b =r r
,求tan x 的值
(2)设函数()2f x a b =⋅+r r
,求()f x 的值域,
如图5所示,四棱锥P -ABCD 的底面是边长为2的正方形、PA⊥底面ABCD . (1)求证:CD⊥平面PAD ; (2)若E 为PD 的中点,三棱锥C -ADE 的体积为2
3
,求四棱锥P -ABCD 的侧面积 20.(本小题满分10分)
在等差数列{}n a 中,已知1231,5a a a =+=。
(1)求n a
(2)设2n a
n n b a =⋅,求数列{}n b 的前n 项和n T
(3)对于(2)中的n T ,设21
2
2n n n a T c +-=,求数列{}n c 中的最大项。
参考答案
二、填空题
11.3 12.> 13.2 14. .10 15.2- 三、解答题 16. 解:(1)f (1)=2 (2)定义域为(,0)(0,)-∞+∞U ,11
()()()f x x x f x x x
-=-+
=-+=-- 所以()f x 为奇函数。
17.解(1)由频率分布直方图的矩形面积和为1可知:
(0.0400.0300.0150.005)101a ++++⨯=
所以0.010a =
(2)样本中不低于80分的频率为(0.0400.030)100.7+⨯=
由样本估计总体可得3000名学生中不低于80分的频率为约为0.7,所以满意的人数
为0.730002100⨯=。
故该校在校食堂用餐的3000名学生中“满意”的人数约为2100人。
18.解:(1)a b =r r
则sin cos 2
x x ==
所以sin tan 1cos x
x x
=
=
(2)()2cos 2sin()2224
f x a b x x x π
=⋅+=++=++r r 因为sin()[1,1]4
x π
+∈-,所以()f x 的值域为[1,3]。
