RLC串联电路课件(1)
合集下载
RLC 电路暂态响应RLC 串联电路下图1 所示的的电路为RLC 串联

(1.33) (1.34) (1.35) (1.36) (1.37)
特征方程变为 方程的两个根为
谐振频率 阻尼系数
通解为es1t和es2t的线性组合
一般解 利用初始化条件可以得出常数A1,A2. 现在让我们来看看α和ω0的物理意义
(1.38) (1.39) (1.40)
RLC 电路.暂态响应
RLC 串联电路
下图 1 所示的的电路为 RLC 串联电路.我们将分析此电路在开关 S 合上后的暂态 特性。
图1 在电路中应用基尔霍夫定律,可以得到描述系统响应的方程
vR+vL+vc=Vs 电路中的电流为
电压 vR 和 vL 由下式给出
i = C dvc dt
vR = iR = RC dvc dt
(1.17)
(1.18) (1.19) (1.20) (1.21)
由vc(t=0)=V0,
dvc(t = dt
0)
=
0
(初始条件下没有电流),我们可以得出方程(1.20)
A1+A2=Vo
(1.22)
得出
jω0 A1 − jω0 A2 = 0
解变为
A1=A2= V0 2
电路中电流为
vc(t)
=
V0 2
参数A1和A2是常数,可以通过系统初始化条件vc(t=0)和
dvc(t = dt
0)
得出。
式子 α 2 − ω02 的值决定着响应的情况。可能发生三种情况。
1. α=ω0, 当s1和s2相等,并且是实数:没有振荡发生。 临界阻尼系统
2. α>ω0,这里s1和s2为不相等的两个实数。没有振荡发生。
vc = Vs + A1es1t + A2es2t
特征方程变为 方程的两个根为
谐振频率 阻尼系数
通解为es1t和es2t的线性组合
一般解 利用初始化条件可以得出常数A1,A2. 现在让我们来看看α和ω0的物理意义
(1.38) (1.39) (1.40)
RLC 电路.暂态响应
RLC 串联电路
下图 1 所示的的电路为 RLC 串联电路.我们将分析此电路在开关 S 合上后的暂态 特性。
图1 在电路中应用基尔霍夫定律,可以得到描述系统响应的方程
vR+vL+vc=Vs 电路中的电流为
电压 vR 和 vL 由下式给出
i = C dvc dt
vR = iR = RC dvc dt
(1.17)
(1.18) (1.19) (1.20) (1.21)
由vc(t=0)=V0,
dvc(t = dt
0)
=
0
(初始条件下没有电流),我们可以得出方程(1.20)
A1+A2=Vo
(1.22)
得出
jω0 A1 − jω0 A2 = 0
解变为
A1=A2= V0 2
电路中电流为
vc(t)
=
V0 2
参数A1和A2是常数,可以通过系统初始化条件vc(t=0)和
dvc(t = dt
0)
得出。
式子 α 2 − ω02 的值决定着响应的情况。可能发生三种情况。
1. α=ω0, 当s1和s2相等,并且是实数:没有振荡发生。 临界阻尼系统
2. α>ω0,这里s1和s2为不相等的两个实数。没有振荡发生。
vc = Vs + A1es1t + A2es2t
《RLC串联电路》课件

仿真软件
Multisim、Simulink等电路仿真 软件,用于模拟RLC串联电路的 行为。
分析仿真结果
根据仿真结果,分析RLC串联电 路的特性和规律,并与实验结果 进行比较。
THANKS
感谢观看
《rlc串联电路》ppt 课件
目录
• RLC串联电路概述 • RLC串联电路的响应特性 • RLC串联电路的阻抗特性 • RLC串联电路的应用 • RLC串联电路的实验与仿真
01
RLC串联电路概述
定义与组成
总结词
RLC串联电路是由电阻(R)、电感(L)和电容(C) 三个元件串联而成的电路。
详细描述
02
RLC串联电路的响的输出从零开 始变化到最终稳态值的过程。
02 描述
瞬态响应是RLC串联电路对突然变化的输入信号 的即时反应,包括电流和电压的超调和振荡。
03 影响因素
电路的阻尼比、激励信号的大小和类型等。
稳态响应
01 定义
在足够长的时间后,电路的输出达到一个稳定状 态,此时的响应称为稳态响应。
RLC串联电路可以作为振荡器的一部分,用于产生特定频率 的交流信号。
详细描述
在振荡器设计中,RLC串联电路通常与放大器配合使用,通 过正反馈和选频网络的作用,产生特定频率的振荡信号。这 种振荡器广泛应用于信号源、测量仪器和电子仪器等领域。
05
RLC串联电路的实验与仿真
实验设备与器材
电源
为电路提供稳定的直流或交流电源。
电路的阻尼比、激励信号 的频率和幅度等。
03
RLC串联电路的阻抗特性
阻抗的定义与计算
阻抗的定义
阻抗是描述电路中阻碍电流通过的物理量,由电 阻、电感和电容共同决定。
RLC串联电路介绍课件

理解RLC串联电 路的物理原理
实验步骤和结果分析
准备实验器材:RLC 串联电路、信号发生 器、示波器等
01
连接实验电路:按照 实验要求连接RLC串 联电路
02
输入信号:使用信号 发生器输入正弦信号
03
06
总结实验结论:根据 实验结果总结RLC串 联电路的特性和规律, 为后续仿真和设计提 供依据
05
零状态响应的求解需要使 用拉普拉斯变换
零状态响应的求解可以帮 助我们分析电路的瞬态响
应特性
全响应
01
零输入响应:电路在零输入 条件下的响应
03
完全响应:电路在任意输入 和任意初始条件下的响应
05
稳态响应:电路在稳态条件 下的响应
02
零状态响应:电路在零状态 条件下的响应
04
瞬态响应:电路在瞬态条件 下的响应
网孔电流法:通过网孔电流方程求解电路中 的电压和电流
叠加定理:将电路中的电压源和电流源分解 为直流和交流两部分,分别求解后再叠加
戴维南定理:将电路中的电压源和电流源等 效为电压源和电阻,简化电路分析
零输入响应
01
零输入响应是指电路在无输 入信号的情况下的响应特性
03
稳态响应是指电路在无输入 信号的情况下,输出信号随 时间的变化情况
信号分析、信号合成、信号检测等
03
RLC串联电路在通信系统中的应用:用于
信号传输、信号处理、信号调制解调等
04
RLC串联电路在电子设备中的应用:用于
信号处理、信号放大、信号滤波等
实验目的和原理
01
02
Hale Waihona Puke 0304验证RLC串联电 路的谐振特性
RLC串联电路课件

Q0
QL
ULI
I2XL
U
2 L
XL
i u XC
I U XC
P0
QC
UI
I2XC
U2 XC
第三章 单相交流电路
• 纯电阻电路电压、电流(数量、相位)关系?
• 纯电感电路电压、电流(数量、相位)关系?
• 纯电容电路电压、电流(数量、相位)关系?
ui
i
ui
ωt
i
ωt
u (a)
u
u ii
(b)
ωt
u
(c)
复习:纯R、纯L、纯C电路比较
i u I U
R
R
i u I U i u I U
XL
XL
XC
XC
P UI I 2R U 2 R
P0
QL U L I I 2 X L
Q0
QL
U
2 L
XL
P0
QC UI I 2 X C
QC
U2 XC
第三章 单相交流电路
将R、L、C 串联起来, 构成
RLC串联电 路,则性 质怎样?
与电流 i 同相,称电路呈电阻性,电路状态称为谐振状态。
【例】 在 RLC 串联电路中,交流电源电压 U = 220 V,频率 f = 50 Hz,R = 30 ,L = 445 mH,C = 32 F。试求:
(1) 电路中旳电流大小 I ; (2) 各元件上旳电压 UR、UL、UC (3) 总电压与电流旳相位差 ; 。
1
解:(1) XL = 2fL 140 ,XC =2fC 100 ,
则: Z R2 ( X L X C )2 50 Ω
则:
I U Z
电路分析基础RLC串联电路

duC 带入上面 dt
此即为RLC串联电路的微分方程。其特征方程为: LCs 2 RCs 1 0 特征根为:
s1,2 R R 1 2 ( )2 2 0 2L 2L LC
通解形式为
uCh ( t ) A1e s1t A2e s2t
X
电容电压的全响应为通解 uCh (t ) 加特解 uCp (t ) ,即:
( 5)
将方程(5)带入方程(4)并进行整理得:
diL 1 ( R1uC R1 R2 iL R2 us ) (6) dt ( R1 R2 ) L
方程(5)、(6)即为要求的电路状态方程。 返回
X
二 高阶动态电路
列写电路的状态方程基本步骤可以总如下: ( 1) 对含有电容支路的节点列写KCL方程; ( 2) 对含有电感支路的回路列写KVL方程; ( 3) 将非状态变量用状态变量和已知量表示; ( 4) 消去非状态变量,将状态方程整理成标准形式。
X
解(续)
uCp ( t ) B 12V 带入微分方程求得: uC ( t ) 的全响应为: uC (t ) iCh (t ) iCp (t ) ( A1 A2t )e t 12
1 1 1 将初始条件 u (0 ) iL (0 ) iL (0 ) 2 1Vs 和 C C 2 uC (0 ) uC (0 ) 10V 带入上式得:
X
解(续)
写成矩阵形式为:
duC1 1 dt R1C1 duC2 0 dt d iL 1 dt L 0 1 R2C 2 1 L 1 0 C1 uC1 1 1 uC2 C2 R2C 2 iL 0 0 1 C1 us 0 i s 0
电路原理课件_第4章_谐振互感三相 (1)

g g 1 IL U ( ) ( j 0C ) U I C j 0 L
g
g
电感电流与电容电流幅值相同,相位差180°
2)并联谐振品质因数
谐振时电路感纳(容 纳)与电导之比。
1 0 L R
IL C Q R 1 1 IR L U
R
1 U 0 L
R 当 Q 0 L
i2 u22
di2 U12 e12 M dt
3)同名端 二个线圈间绕向不同时,产生的互感电压方向不同。
1
di1 0 , 图1:当 i1 增加时 dt 线圈2互感电压方向为 2 2 。 di1 u2 M dt
di1 0, dt 线圈2互感电压方向为 2 2。
i1
2
u1
减小电阻或增大电感可使UL变大。电压放大。
对于电流源:采用并联谐振方法 。
IL R Q并 0 L I S
增大电阻或减小电感可使IL变大。电流放大。
4.2 互感耦合电路
1)互感现象 邻近线圈间由于磁通 的交链,一个线圈电流的 变化会在另一线圈产生感 应电势(互感电势),这 一现象为互感偶合。 线圈1中通以电流
dψ1 dL1i1 di1 L1 线圈1 的自感电势 e11 dt dt dt
用电压降表示 线圈2 的互感电势
di1 U11 e11 L1 dt
互感电压 参考方向
dψ21 dMi1 di1 e21 M dt dt dt
用电压降表示
i1 u11
u21
di1 U 21 e21 M dt
同理: 当 i 2 变化时,引起 的变化, 二个线圈中产生感应电势, 线圈2 的自感电势: 用电压降表示:
RLC串联电路 (1)

( 2)
U L 240 U R 80 X 40 R 13.3 L I 6 I 6 XL 40 U C 180 L 0.13H X 30 2 f 2 3.14 50 C
I 6
C
1 1 0.000106F 2 fX C 2 3.14 50 30
(1)
U L UC
U L UC u 0 i 0 arctan 0 UR
(2)
UL
U L UC
UL + UC
UR
U L UC u 0 i 0 arctan 0 I UR
(3)
U UC UL UR I
U L UC
u 0 i 0 0
1 1 2123 XC 3 10 2 314 150 10 5 10 2fC
Z R 2 ( X L X C )2
1000 2 (4710 2123 ) 2 2773 .5
初相
电路中电压的有效值
X L XC 2590 arctan arctan 68.9 R 1000
UC
U L 超前
I
90
滞后
I
90
例2 在电阻、电感和电容串联电路中,电路中电流为6A,
U R 80V ,UC 180V ,U L 240V
电源频率为50Hz。
试求:(1)电源电压有效值U; (2)电路参数 R、L和C;(3)电流与电压的相位差。
2 2 2 2 解:(1) U U R (U L U C ) 80 (240 180) 100V
U
UC
(二) RLC串联电路的阻抗关系:
RLC串联电路

U 220 I 4.4 A Z 50
第七节
RLC串联电路
复习导入
问题:在纯电阻电路、纯电感电路、纯电容电路中,电路两端的 电压和电流的大小、相位关系分别是怎样的?(设i=Imsinwt)
答:大小关系:纯电阻电路——UR=IR 纯电感电路——UL=IXL
纯电容电路——UC=IXC
相位关系:纯电阻电路:同相 纯电感电路:电压超前电流 纯电容电路:电流超前电压
上式中 叫做阻抗角,体现了总电压与总电流之间的相 位关系,即总电压(超前或滞后或同相或反相)于总电 流
UL> UC,阻抗角φ>0,电压超前电流φ角。 UL< UC,阻抗角φ<0,电压滞后电流φ角。 UL= UC,阻抗角φ=0,电压和电流同相。
二。 RLC串联电路的阻抗: 2 将 U R IR、R L IX L、U C IXC 代入 U U R (U LU C )2
讲授新课
由电阻、电感、电容相串联所组成的电路,叫做R—L— C串联电路。
一、R-L-C串联电路的电压与电流的大小关系 设电路中电流为i = Imsin( t)
uR =RImsin( t), uL=XLImsin( t 90),
uC =XCImsin( t 90)
根据基尔霍夫电压定律(KVL),在任一时刻A、B两端的总 电压u的瞬时值为 u = uR uL uC
RLC串联电路中的有功功率即R上消耗的功率
P URI
四、功率
2、无功功率 由于电感和电容两端的电压在任何时刻都是 反相的,二者的瞬时功率符号也相反。 当电感吸收能量时,电容放出能量; 当电容吸收能量时,电感放出能量; 电路的无功功率为电感和电容上的无功功率 之差。 2
RLC串联

U U R U L UC
P S cos Q S sin
Q QL QC (U L U C ) I UI sin
S UI P Q
2
2
P cos S
电路 名称
电 流 与 电 压 的 关 系
纯电阻交流 纯电感交流 纯电容交流 RLC串联交 纯R、L、C电路与RLC电路比较 电路
U总 U R U L U C
随堂练习 在R-L-C串联电路中,已知电阻R = 40 ,电感L = 191 mH,
电容C=106 F,外加频率为f = 50 Hz、U = 200 V的交流电 压源,试求:
(1) 电路中的电流I; (2) 各元件电压UR、UL、UC;(3) 总电 压与电流的相位差 解(1)先求XL、XC、
在RLC串联电路中,只有电阻是消耗功率的 RLC串联电路中的有功功率即R上消耗的功率
P U R I UI cos
3、无功功率
由于电感和电容两端的电压在任何时刻都是反相的,
二者的瞬时功率符号也相反。 当电感吸收能量时,电容放出能量; 当电容吸收能量时,电感放出能量; 电路的无功功率为电感和电容上的无功功率之差。
p u i p R p L pC
2. 平均功率 P (有功功率)
I
+ R
L C +
UR UL
1 T U P pdt T 0 1 T ( p R p L pC ) dt T 0 2 PR U R I I R
+ +
UC -
2、有功功率
P cos S
Q S sin
《RLC串联电路》课件

电感元件的特点
电感元件的感抗值决定了电路 中通过它的电流和电压的比例, 可以使用基尔霍夫电压定律和 串并联计算方法求解。
电容元件的电容值决定了电路 中通过它的电流和电压的比例, 可以使用基尔霍夫电流定律和 串并联计算方法求解。
RLC串联电路的特点
RLC串联电路具有阻抗和相位角的影响、电流和电压的关系以及相频特性曲线和幅频特性曲线的形状。
1
阻抗和相位角的影响
RLC串联电路中三种元件的阻抗和相
电流和电压的关系
2
位角相互影响,产生并联、串联和谐 振等现象。
RLC串联电路中电流和电压的关系复
杂多样,产生共振、衰减和失真等响
应。
3
相频特性曲线的形状
RLC串联电路中电流和电压的相位差
随频率的变化产生相频特性曲线,具
幅频特性曲线的形状
4
有低通、高通、带通等不同的形状。
3 调节和控制
RLC串联电路被用于机 器人、输出控制和传感 器等工控领域中。
结论
RLC串联电路是电路基础中的重要部分,具有丰富的应用和多种特性。了解RLC电路可以帮助我们更好 地理解和应用电路知识。
电路模型
RLC串联电路模型简单直观, 易于分析和计算。
响应特性
RLC串联电路响应特性丰富 多样,适用于不同的应用和 场合。
《RLC串联电路》PPT课 件
本演示课件包括电路基础知识介绍、电路元件分析和RLC串联电路的特点。
什么是RLC串联电路
RLC串联电路是由电阻、电感和电容三种元件串联组成的电路,是电路基础中的重要部分。
元件的作用和特点
电阻可以调节电路的电流和电压,电感可以滤波和储能,电容可以分频和滤波。
电流和电压的关系
《RLC串联的交流电路》课件

《RLC串联的交流电路》
一、电压与电流关系
i
u = uR + uL + uC
R
uL C
Z=R+j(XL-XC) = z∠φ
返回
Z=R+j(XL-XC) = z∠φ 称为阻抗,单位Ω
总电压与电流之间大小关系
U=Iz
相位关系
φ 角为阻抗角,它等于电压与电流之
间的相位差角。
返回
以电流为参考相量画相量图
φ=0
电压与电流同相,电路呈纯阻 性。
返回
例1在、RLC串联交流电路中,R=15Ω,
L=12mH, 电源电压
,
C=5μF,求:⑴电路中的电流i 和各部分电压
uR ,uL ,uC (2)画相量图。
解: XL=ωL =5000×12×10-3Ω =60Ω
XC=1/ωC =1/5000×5×10-6Ω =40Ω
返回
P=UIcosφ =10×20×1W=200W Q= UIsinφ =10×20×0=0var S=UI=200VA
返回
例4、已知U=100V, ω=314rad/s,I=IC=IL,电
路消耗功率P=866W,试求iL、iC、i 。
i iL iC
u
R C
L
解:设u为参考正弦量 ∵ iL+iC = i 且 I= IC=IL 所以İC 、İL和İ 组成等 边三角形 作相量图:
X1
R1
a
解:Z1=jX1+R1=(j10+2)Ω
X2
X3
Z2=jX2=j10Ω
u
Z3=-jX3=-j5Ω
Zab=Z2∥Z3=-10jΩ
b
=10∠-90°Ω
一、电压与电流关系
i
u = uR + uL + uC
R
uL C
Z=R+j(XL-XC) = z∠φ
返回
Z=R+j(XL-XC) = z∠φ 称为阻抗,单位Ω
总电压与电流之间大小关系
U=Iz
相位关系
φ 角为阻抗角,它等于电压与电流之
间的相位差角。
返回
以电流为参考相量画相量图
φ=0
电压与电流同相,电路呈纯阻 性。
返回
例1在、RLC串联交流电路中,R=15Ω,
L=12mH, 电源电压
,
C=5μF,求:⑴电路中的电流i 和各部分电压
uR ,uL ,uC (2)画相量图。
解: XL=ωL =5000×12×10-3Ω =60Ω
XC=1/ωC =1/5000×5×10-6Ω =40Ω
返回
P=UIcosφ =10×20×1W=200W Q= UIsinφ =10×20×0=0var S=UI=200VA
返回
例4、已知U=100V, ω=314rad/s,I=IC=IL,电
路消耗功率P=866W,试求iL、iC、i 。
i iL iC
u
R C
L
解:设u为参考正弦量 ∵ iL+iC = i 且 I= IC=IL 所以İC 、İL和İ 组成等 边三角形 作相量图:
X1
R1
a
解:Z1=jX1+R1=(j10+2)Ω
X2
X3
Z2=jX2=j10Ω
u
Z3=-jX3=-j5Ω
Zab=Z2∥Z3=-10jΩ
b
=10∠-90°Ω
《电工技术》课件 RLC串联电路中电压电流的相量图及电压三角形

u 220 2 sin ( 314 t 20 )V
求:(1)电流的有效值I与瞬时值 i ; (2) 各部分电压的有效值与瞬时值;
i R uR
u
L uL
C uC
解:(2)计算各部分电压有效值,再利用各元件电压与电流的 相位关系写出瞬时表达式。
UR IR 4.4 30V 132V 电阻电压与电流同相位
L
C
R
?
ar c tan UL UC U
?
四、习题讲解
例 在RLC串联交流电路中,已知:
R 30Ω, L 127mH,C 40μ F
u 220 2 sin ( 314 t 20 )V
求:(1)电流的有效值I与瞬时值 i ; (2) 各部分电压的有效值与瞬时值; (3) ) 画出电压电流的相量图。
而复数阻抗只是一个运算符号。Z 不能加 “•”
I UZ?
i
u Z
?
i
u Z
?
I
U Z
?
三、电压、电流、阻抗之间关系判断
U
? U
2 R
U
2 L
UC2
U I R2 X L XC 2 ?
U IR jX L XC ?
arctan XL XC ?
R
arctan
UL UC UR
?
ar
c
tan
得:uR 132 2 sin ( 314t 73 )V
UL IXL 4.4 40 V 176V 电感电压超前电流900 得: uL 176 2 sin ( 314t 163 )V
UC IX C 4.4 80 352V 电容电压滞后电流900 得: uC 352 2 sin ( 314t 17)V
求:(1)电流的有效值I与瞬时值 i ; (2) 各部分电压的有效值与瞬时值;
i R uR
u
L uL
C uC
解:(2)计算各部分电压有效值,再利用各元件电压与电流的 相位关系写出瞬时表达式。
UR IR 4.4 30V 132V 电阻电压与电流同相位
L
C
R
?
ar c tan UL UC U
?
四、习题讲解
例 在RLC串联交流电路中,已知:
R 30Ω, L 127mH,C 40μ F
u 220 2 sin ( 314 t 20 )V
求:(1)电流的有效值I与瞬时值 i ; (2) 各部分电压的有效值与瞬时值; (3) ) 画出电压电流的相量图。
而复数阻抗只是一个运算符号。Z 不能加 “•”
I UZ?
i
u Z
?
i
u Z
?
I
U Z
?
三、电压、电流、阻抗之间关系判断
U
? U
2 R
U
2 L
UC2
U I R2 X L XC 2 ?
U IR jX L XC ?
arctan XL XC ?
R
arctan
UL UC UR
?
ar
c
tan
得:uR 132 2 sin ( 314t 73 )V
UL IXL 4.4 40 V 176V 电感电压超前电流900 得: uL 176 2 sin ( 314t 163 )V
UC IX C 4.4 80 352V 电容电压滞后电流900 得: uC 352 2 sin ( 314t 17)V
电路设计--RLC串联电路讲解

_
R P
Q
0 L R
0 LI02
RI
2 0
QL0 P
| QC 0 P
|
谐 振 时 电 感(或 电 容)中 无 功 功 率 的 绝 对 值 谐 振 时 电 阻 消 耗 的 有 功功 率
八、功率
谐振时,电路的无功功率为零,这是由于阻抗角为零, 所以电路的功率因数
cos = 1
P(0 ) UI UI QL (0 ) 0 LI 2
R2 X 2
(ω
)
tg
1
ωL
1
ωC
tg 1
XL XC
tg 1
X
R
R
R
2. 电流谐振曲线 谐振曲线:表明电压、电流大小与频率的关系。
幅值关系: I(ω)
U
| Y (ω) | U
R2 (ωL 1 )2 ωC
可见I( )与 |Y( )|相似。
幅频 特性
相频 特性
而这些电压比值可以用分贝表示 dB 20log A 令 /0 将电路的阻抗Z变换为下述形式
Z(
j )
R
j(L
1)
C
R1
jQ(
1
)
UR ()
U
1 Q2 ( 1 )
U R ()
1
U
1 Q2 ( 1 )
上述关系式可以用于不同的RLC串联谐振电路,
UR /U O
Q1 Q2 Q3
Q1
Q2 Q3
1
/0
UR /U
RLC串联交流电路课件
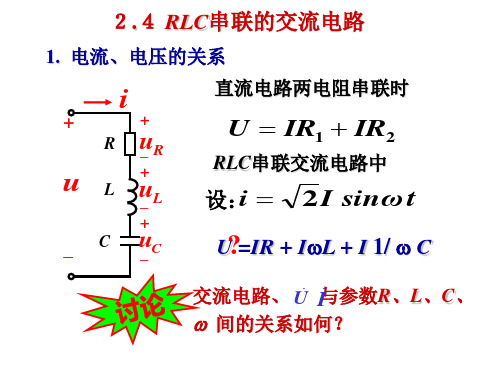
求:A、UO的读数
Uo UC1 U AB
UO 设:U AB 100 0 V
I1
由已知 条件得:
I1 10A 、领先 90°
I2 100
10 52 52
2A
I2 落后于 U AB 45° U C1
I I1 I2
45° I U AB
I2 UO
UC1=I XC1=100V
uC1落后于 i 90°
四.R-L-C串联交流电路 -- 相量图
+
U
_
I
R jXL -jXC
参考相量
+
U_ R U L
+
U_
XL
L
>
U+_C U
U L
UC
XC
U C
U L
(> U C
U
U R I
0 感性)
U L
XL < XC
U L UC U C
U R I
U
( < 0 容性)
U X 由电压三角形可得:
U R
电压 三角形
R
U
tg1
UL UC UR
?
tg 1
L
C
R
?
2.5 阻抗的串联与并联
2.5.1阻抗的串联
I
U U 1 U 2 Z1I Z 2I
+ U
-
+
Z1 -U1
+
Z2
U
-
2
(Z1 Z 2)I
Z Z1 Z2
I U Z
通式: Z Zk Rk j Xk
I 注意:对于阻抗模一般 Z Z 1 Z 2
Z
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 单相交流电路
5.如图3-9所示电路中,当交流电源的电压大小不变而频 率降低时,电压表的读数将( B )。 A.增大 B.减小 C.不变 ω降低→XL =ωL降低→UL=IXL降低 6.RLC串联电路,已知条件如下,只有( A )属电感 性电路。 知识点: A.R=5Ω,XL=7Ω,XC=4Ω XL>XC时,电路为电感性 B.R=5Ω,XL=4Ω,XC=7Ω XL<XC时,电路为电容性 C.R=5Ω,XL=4Ω,XC=4Ω XL=XC时,电路为电阻性 D.R=5Ω,XL=5Ω,XC=5Ω
Z R 2 X 2 称为阻抗
阻抗角
U L UC XL XC arctan arctan UR R
第三章 单相交流电路
知识运用:
1.在RLC串联电路中,正确的关系式为( C) A. U UR UL UC B. U UR UL UC C. U UR (UL UC ) 2 D. U UR UL UC 2.在RLC串联电路中,已知R=3Ω,XL=3Ω,XC=7Ω 则电路的总阻抗为( C) A. 13Ω B.7Ω C. 5 Ω D.10Ω
Q QL QC (U L U C ) I Q UI sin
第三章 单相交流电路
RLC串联电路
四、功率
3、视在功率
电压与电流有效值的乘积,用S表示;
S=UI
单位为伏· 安(V.A)。
视在功率并不代表电路中消耗的功率,它常用于表示电 源设备的容量。 S与P和Q的关系:
第三章 单相交流电路
知识运用:
1.下列不是RLC串联电路发生谐振的特点是(D ) A. 阻抗最小且为纯电阻,即 Z R B.电路中的电流最大,且与电压同相 C.电感与电容两端的电压同相 D.总电压等于电感电压
第三章 单相交流电路
RLC串联电路
四、功率
1、有功功率
在RLC串联电路中,只有电阻是消耗功率的
第三章 单相交流电路
作业: 1. 电阻、电感与电容串联电路参数为 R = 10Ω,L= 0.3 mH,C = 100 pF,外加交 流电压有效值为 U = 10 V,试求在其发生 串联谐振时的f0、Q、UL、 UC 及UR。
第三章 单相交流电路
谢谢 ! 谢谢!
谢谢!
第三章 单相交流电路
S P2 Q2
P S cos
P cos S
第三章 单相交流电路
Q S sin
称为功率因数。
知识运用:
1. 在RLC串联电路中,若XL=XC,则电路的总无功功 率是( A ) A. 0 var B. 10var C. 1W D. 0W
第三章 单相交流电路
RLC串联电路
电压三角形、阻抗三角形和功率三角形
电压相量图
Ux
阻抗三角形
电三章 单相交流电路
返回
RLC串联电路——小结
RLC 电路 电路图 名称 串联电路
频率 电流 与电 压的 关系 相位 电 路 特 点
由R、L、C串联 构成的交流电路
相同 UL>UC,电压超前电流 UL<UC,电压滞后电流 UL=UC,电压与电流同相
RLC串联电路
成武职教中心
RLC串联电路
01 02 电压与电流的关系 电路的性质 串联谐振
03
04
第三章 单相交流电路
功率
RLC串联电路
一、电压与电流的关系
RLC串联电路的总电 压瞬时值等于多个元件 上电压瞬时值之和,即:
u uR uL uC
对应的矢量关系为:
U U R U L UC
第三章 单相交流电路
RLC串联电路
二、电路的性质
3、电阻性电路 当XL=XC时,则UL=UC,阻抗角 0 电路呈电阻性,总阻抗最小,电压与电流同相。 电路的这种状态称为串联谐振。
第三章 单相交流电路
知识运用:
1.交流电路中某元件上的电压和电流分别为
u 12sin(wt 30)V , i 2 sin(wt 60)A
则该元件为( B ) A. 电感性元件 B.电容性元件 C. 电阻性元件 D.纯电感元件 2.以下RLC串联电路中,呈电感性的是( B ) A. R=4Ω,XL=1Ω, XC=2Ω B. R=4Ω,XL=5Ω, XC=2Ω C. R=4Ω, XL=2Ω, XC=3Ω D. R=4Ω, XL=3Ω, XC=5Ω
2 2 2
2
2
2
2
第三章 单相交流电路
RLC串联电路
二、电路的性质
1、电感性电路 当XL>XC时,则UL>UC,阻抗角 0 电路呈电感性,电压超前电流 角。
第三章 单相交流电路
RLC串联电路
二、电路的性质
2、电容性电路 当XL<XC时,则UL<UC,阻抗角 0 电路呈电容性,电压滞后电流 角。
第三章 单相交流电路
3.白炽灯与线圈组成的电路如图3-7所示,由交流电源供 电,如果交流电的频率增大,则线圈的( C )。 A.电感增大 C.感抗增大 B.电感减小 D.感抗减小
4.如图3-8所示RL串联电路中,电压表V1的读数为10V, V2的读数也为10V,则电压表V的读数应为( C )。 A.0V B.10V C.14.1V D.20V
2
2
P cos S
RLC串联电路——小结
串联谐振 1.定义:在RLC串联电路中,发生总电压与电流同相的现象 ,称为谐振。 2.发生谐振的条件:XL=XC 3.发生谐振时的频率:
f
1 0 2π LC
4.串联谐振电路特点: ( 1)阻抗最小,且为纯电阻,即 Z R U I 0 ( 2 ) 电路中的电流最大且与电压同相,即 R ( 3 ) 电感与电容两端电压相等,其大小为总电压的Q倍。
U L UC 0
2 U UR (U LU C ) 2
第三章 单相交流电路
RLC串联电路 电抗、阻抗与阻抗角 将UR=IR,UL=IXL,UC=IXC带入U
2 UR (U LU C ) 2
得 U I R 2 ( X L X C )2 I R 2 X 2 I Z X = XL—XC 称为电抗
数量 有功功率 功率 无功功率 视在功率
第三章 单相交流电路
u uR uL uC
P U R I UI cos
U U R U L UC
P S cos Q S sin
Q QL QC (U L UC ) I UI sin
S UI P Q
RLC串联电路中的有功功率即R上消耗的功率
P U R I UI cos
第三章 单相交流电路
RLC串联电路
四、功率
2、无功功率
由于电感和电容两端的电压在任何时刻都是反相的, 二者的无功功率符号也相反。 当电感吸收能量时,电容放出能量; 当电容吸收能量时,电感放出能量; 电路的无功功率为电感和电容上的无功功率之差。
第三章 单相交流电路
RLC串联电路 一、电压与电流的关系
设 i=Imsinωt,以i为参考矢量作矢量图 uR与i同相,uL超前i 90°,uC滞后i 90°
阴影部分称为 电压三角形,它表明
了RLC串联电路中总
电压与分电压之间的 关系。
U L UC 0
U L UC 0
第三章 单相交流电路
三、串联谐振
1.定义:在RLC串联电路中,发生总电压与电流同相 的现象,称为谐振。 2.发生谐振的条件: XL=XC 1 3.发生谐振时的频率: f 0 2π LC 4.串联谐振电路特点: ( 1)阻抗最小,且为纯电阻,即 Z R U ( 2 ) 电路中的电流最大且与电压同相,即I 0 R ( 3 ) 电感与电容两端电压相等,其大小为总电压的 Q倍。 w0 L 1 Q R w0CR
Q w0 L 1 R w0CR
第三章 单相交流电路
练习:
1.如图3-5所示电路中,电流I等于(A )。 A.5A B.1A C.0A
2.白炽灯与电容器组成的电路如图3-6所示,由交流电源 供电,如果交流电的频率减小,则电容器的( C )。 A.电容增大 B.电容减小 C.容抗增大 D.容抗减小
