第九章梁的弯曲(4)应力状态
梁的弯曲(应力、变形)

2
回顾与比较
内力
应力
F
A
FAy
编辑ppt
T
IP
M
?
?
FS
3
§9-6 梁的弯曲时的应力及强度计算
一、弯曲正应力 Normal stress in bending beam
梁段CD上,只有弯矩,没有剪力--纯弯曲Pure bending
梁段AC和BD上,既有弯矩,又有剪力--剪力弯曲Bending by
transverse force
编辑ppt
4
研究对象:等截面直梁 研究方法:实验——观察——假定
编辑ppt5Leabharlann 实验观察——梁表面变形特征
横线仍是直线,但发生 相对转动,仍与纵线正交
纵线弯成曲线,且梁的 下侧伸长,上侧缩短
以上是外部的情况,内部如何? 想象 —— 梁变形后,其横截面仍为平面,且垂直
x
61.7106Pa61.7MPa
编辑ppt
13
q=60kN/m
A
1m
FAY
C
l = 3m
FS 90kN
M ql /867.5kNm 2
x
2. C 截面最大正应力
120
B
x
180
K
30 C 截面弯矩
z
MC60kN m
FBY
y
C 截面惯性矩
IZ5.83120 5m 4
x 90kN
C max
M C y max IZ
于变形后梁的轴线,只是绕梁上某一轴转过一个角度 透明的梁就好了,我们用计算机模拟 透明的梁
编辑ppt
6
编辑ppt
7
总之 ,由外部去 想象内部 —— 得到
工程力学第九章

下一页 返回
9.4
梁的弯曲变形与刚度
2.
挠度和转角
(1) 挠度 是指梁轴线上的一点在垂直于轴线方向上的位移, 通常用y表示。
一般规定向上的挠度为正,向上的挠度为负。它的单位是mm。 (2) 转角 是指梁的各截面相对原来位置转过的角度,用θ 表
示。
一般规定,逆时针方向的转角为正,顺时针的转角为负。它 的单位是弧度(rad)或度(º)。
远的边缘处。其计算公式为
max
(2) 梁的正应力强度条件为
M max y max M max Iz Wz
M max ≤[σ ] Wz
下一页 返回
max
小
结
max
* FQ S z
(3) 梁横截面上的切应力与切应力强度条件 对矩形截面梁,横截面上的切应力计算公式为 其最大切应力在截面的中性轴上,计算公式为 梁的切应力强度条件为τ max≤[τ ]
上一页 返回
9.2
梁弯曲时正应力强度计算
梁弯曲时正应力强度计算
9.2
为了保证梁在载荷作用下能够正常工作,必须使梁具备足够 的强度。也就是说,梁的最大正应力值不得超过梁材料在单 向受力状态(轴向拉、压情况)下的许用应力值[σ ],即 M max max ≤[σ ] (9.10) Wz 式(9.10)就是梁弯曲时的正应力强度条件。需要指出的是, 式(9.10)只适用于许用拉应力[σ l]和许用压应力[σ y]相等 的材料。如果两者不相等(例如铸铁等脆性材料),为保证梁 的受拉部分和受压部分都能正常工作,应该按拉伸式
上一页 下一页 返回
My Iz
(9.4)
第九章第六节梁弯曲时的应力及强度计算(上课用)

m
V
( Stresses in Beams)
m
m
M
V
m m
只有与剪应力有关的切向内力元素 d V = dA 才能合成剪力
只有与正应力有关的法向内力元素 d FN = dA 才能合成弯矩
剪力V 内力 弯矩M 正应力 剪应力
所以,在梁的横截面上一般
既有 正应力, 又有 剪应力
先观察下列各组图
所以,可作出如下 假设和推断:
1、平面假设:
2.单向受力假设: 各纵向纤维之间互不挤压,纵向纤维均处于单向受拉或受压的状态。 因此梁横截面上只有正应力σ而无剪应力τ
各横向线代表横截面,实验表 明梁的横截面变形后仍为平面。
梁在弯曲变形时,上面部分纵向纤维缩短,下面部分纵向纤维伸长,必 有一层纵向纤维既不伸长也不缩短,保持原来的长度,这一纵向纤维层称为 中性层. 中性层与横截面的交线称为中性轴,中性轴通过截面形心,是一条形心轴。 且与截面纵向对称轴y垂直,将截面分为受拉区及受压区。梁弯曲变形时, 各横截面绕中性轴转动。
(3)横截面上任一点处的剪应力计算公式(推导略)为
V S I zb
Z
V——横截面上的剪力
Iz——整个横截面对中性轴的惯性矩
b——需求剪应力处的横截面宽度 S*Z——横截面上需求剪应力处的水平线 以外(以下或以上)部分面积A*(如图 )对 中性轴的静矩
V
3V 4 y2 (1 2 ) 2bh h
应力状态按主应力分类:
(1)单向应力状态。在三个相对面上三个 主应力中只有一个主应力不等于零。 (2)双向应力状态。在三个相对面上三个 主应力中有两个主应力不等于零。
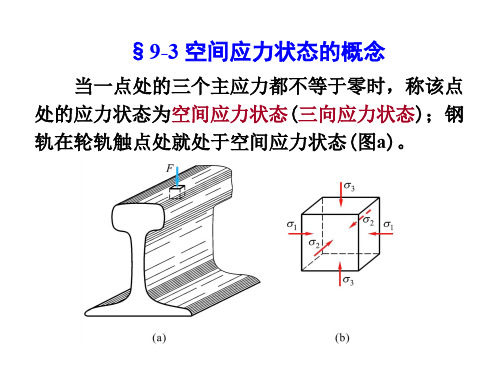
(3)三向应力状态。其三个主应力都不等于零。例 如列车车轮与钢轨接触处附近的材料就是处在三向应 力状态下.
梁的应力

ac
M
⑵、纵向线:由直线变为曲
线,且靠近上部的纤维缩短,
靠近下部的纤维伸长。
b
d
3、假设:
(1)弯曲平面假设:梁变形前原为平面的横截面变形后仍为平 面,且仍垂直于变形后的轴线。
第九章 梁的应力
梁是由许多纵向纤维组成的
凹入一侧纤维缩短
突出一侧纤维伸长
根据变形的连续性可知, 梁弯曲时从其凹入一侧的 纵向线缩短区到其凸出一 侧的纵向线伸长区,中间 必有一层纵向无长度改变
z
A2 20120mm2 y2 80mm
yc
80 2010 120 2080 80 20 120 20
52mm
(2)求截面对中性轴z的惯性矩
Iz
Hale Waihona Puke 80 203 1280 20 422
y
201203 20120 282
12
7.64106 m4
第九章 梁的应力
横截面上应力分布
b
d2
c,m ax
h yt,max yc,max d1
oz y
Oz
y b
t,m ax
中性轴 z 不是横截面的对称轴时,其横截面上最大拉
应力值和最大压应力值为
t,m ax
My t ,m a x Iz
c,m ax
Myc ,m a x Iz
第九章 梁的应力
例 对于图示 T形截面梁,求横截面上的最大拉应力和最大压 应力.已知: I z 290 .6 10 8 m4
d
在弹性范围内, E E Ey ...... (2)
O
O1
A1
B1 x
y
第九章 梁的应力
应力的分布图:
梁的弯曲(应力、变形)

梁的弯曲类型
01
02
03
自由弯曲
梁在受到外力作用时,其 两端不受约束,可以自由 转动。
简支弯曲
梁在受到外力作用时,其 一端固定,另一端可以自 由转动。
固支弯曲
梁在受到外力作用时,其 两端均固定,不能发生转 动。
梁的弯曲应用场景
桥梁工程
桥梁中的梁常常需要进行弯曲变形以承受车辆和 行人等载荷。
稳定性。
06 梁的弯曲研究展望
CHAPTER
新材料的应用研究
高强度材料
随着材料科学的进步,高强度、轻质的新型 材料不断涌现,如碳纤维复合材料、钛合金 等。这些新材料在梁的弯曲研究中具有广阔 的应用前景,能够显著提高梁的承载能力和 刚度。
功能材料
新型功能材料如形状记忆合金、压电陶瓷等, 具有独特的力学性能和功能特性,为梁的弯 曲研究提供了新的思路和解决方案。
反复的弯曲变形可能导致疲劳裂纹的 产生和扩展,影响结构的疲劳寿命。
对使用功能的影响
弯曲变形可能导致结构使用功能受限 或影响正常使用。
04 梁的弯曲分析方法
CHAPTER
理论分析方法
弹性力学方法
01
基于弹性力学理论,通过数学公式推导梁在弯曲状态下的应力
和变形。
能量平衡法
02
利用能量守恒原理,通过计算梁在不同弯曲状态下的能量变化,
详细描述
常见的截面形状有矩形、工字形、圆形等。应根据梁的用途和受力情况选择合适的截面形状。例如, 对于承受较大弯矩的梁,采用工字形截面可以有效地提高梁的承载能力和稳定性。
支撑结构优化
总结词
支撑结构是影响梁弯曲性能的重要因素,合理的支撑结构可以提高梁的稳定性,减小梁 的变形。
第九章应力状态(3,4,5)
s
3
e3
1 E
s
3
s 1
s 2
例 9-17
边长a =0.1 m的铜质立方体,置于刚性很大的 钢块中的凹坑内(图a),钢块与凹坑之间无间隙。 试求当铜块受均匀分布于顶面的竖向荷载F =300 kN时,铜块内的主应力,最大切应力,以及铜块 的体应变。已知铜的弹性模量E =100 GPa,泊松比
1 2
E
sx sy sz
思考: 各向同性材料制成的构件内一点处,
三个主应力为s1=30 MPa,s2=10 MPa,s3=-40
MPa。现从该点处以平行于主应力的截面取出边 长均为a的单元体,试问:(1) 变形后该单元体的 体积有无变化?(2) 变形后该单元体的三个边长之 比有无变化?
弹性,小变形条件下可以
应用叠加原理,故知x方 向的线应变与正应力之
间的关系为
e x
sx
E
sy
E
sz
E
1 E
sx
sy
sz
同理有
e y
1 E
s
y
s x
s z ,e z
1 E
sz
sx
s
最一般表现形式的空间应力状态中有9个应力
分量,但根据切应力互等定理有txy=tyx,tyz=tzy , txz=tzx,因而独立的应力分量为6个,即sx、sy、sz、 tyx、tzy、tzx。
当空间应力状态的三个主应
力s1、s2、s3已知时(图a),与
任何一个主平面垂直的那些斜截
面(即平行于该主平面上主应力
材料力学:第九章 应力状态分析

τx
C
F
Me
d
C
(a)
·
σx
(b)
C
T
F
解:C点所在横截面上的正应力和切应力的分布规律如图 所示, 点所在横截面上的正应力和切应力的分布规律如图b所示 点所在横截面上的正应力和切应力的分布规律如图 所示, 其值为
FN 500 × 103 N σx = = = 63.7 × 106 Pa=63.7MPa π 2 A 0.1m ) ( 4
经整理后得到 )、(2) )、( (1) 由(1)、( )式,可以求出单 ) 元体各个截面上的应力。( 。(即 点 元体各个截面上的应力。(即a点 (2) 处各个方向上的应力) ) 处各个方向上的应力)
∑F = 0
t
τ =τ′
σ α = −τ sin 2α
τ α = τ cos 2α
定义:构件内一点处各个方向上的应力集合, 定义:构件内一点处各个方向上的应力集合,称为该点处的 应力状态。 应力状态。
F F
横截面上只有正应力,且 横截面上只有正应力, 均匀分布 计算公式: 计算公式:
m
σ
F
FN
FN σ= A
等直圆杆扭转时横截面上的应力: 等直圆杆扭转时横截面上的应力:
Me m Me
m
横截面上只有切应力,呈 横截面上只有切应力, 线性分布
T
o
τρ
τmax
T⋅ρ 计算公式: 计算公式: τρ = Ip
R
τ
T 16 M e τ= = WP πd3
为了研究a点处各个方向的应力,围绕a点取一个各边长均为无 为了研究 点处各个方向的应力,围绕 点取一个各边长均为无 点处各个方向的应力 限小的六面体(称为单元体)。 限小的六面体(称为单元体)。 径向截面
第9章 梁的应力

本章主要讨论梁在外力作用下横截面上的应力和强
度条件及其应用。
工程中的弯曲杆件
9.1 梁内正应力、正应力强度条件
9.1.1 纯弯曲时梁内的正应力
纯弯曲:梁的横截面上只有弯矩 而无剪力的弯曲(横截面上只有 正应力而无切应力的弯曲),这 种弯曲称为纯弯曲。
横力弯曲:梁的横截面上既有弯
矩又有剪力的弯曲(横截面上既 有正应力又有切应力的弯曲), 这种弯曲称为横力弯曲。
3 3
压应力
3
3. C截面上最大正应力
C max
MC MC 60 10 6 92.6MPa 2 2 9 Wz bh 6 120 180 10
上压下拉
4.全梁上最大正应力
ql 2 60 32 M max 8 8 67.5kN m M max M max max 2 Wz bh 6
矩形截面:
bh 3 Iz 12
bh 2 Wz 6
圆形截面:
I y Iz
I y Iz
d
4
64
4
Wy Wz W
d
3
32
圆环截面:
D
64
(1 )
4
4
Wy Wz W
D3
32
(1 )
d D
②截面关于中性轴不对称Байду номын сангаас最大拉应力:
y1 yC 96.4mm
y2 200 50 96.4 153.6mm
4、计算弯矩最大截面 上的最大拉应力和最大压应力
拉 max
M max y2 Iz
16 103 153.6 103 1.02 108 1012 24.09 106 Pa 24.09 MPa
(修订)第9章 弯曲应力与弯曲变形-习题解答

第9章 弯曲应力与弯曲变形 习题解答题9 – 1 试计算下列各截面图形对z 轴的惯性矩I z (单位为mm )。
解:(a )mm 317400250500350200400250250500350≈⨯-⨯⨯⨯-⨯⨯=c y()()49323mm 107314002502003171240025050035025031712500350⨯≈⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.I Z (b )mm 431550400800500375550400400800500≈⨯-⨯⨯⨯-⨯⨯=c y()()410323mm 1054615504003754311255040080050040043112800500⨯≈⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.I Z (c )()mm 3060202060506020102060=⨯+⨯⨯⨯+⨯⨯=c y()()46323mm103616020503012602020601030122060⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯+⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.Z I(a)(b) (c)题9-1图题9–2 悬臂梁受力及截面尺寸如图所示。
设q = 60kN/m ,F = 100kN 。
试求(1)梁1– 1截面上A 、B 两点的正应力。
(2)整个梁横截面上的最大正应力和最大切应力。
解:(1)求支反力kN 220100260=+⨯=A F (↑)m kN 32021001260⋅=⨯+⨯⨯=A M ( ) (2)画F S 、M 图(3)求1-1截面上A 、B 两点的正应力 m kN 1305016011001⋅=⨯⨯+⨯=.MF MA 点:MPa 254Pa 1025412150100550101306331=⨯≈⨯⨯⨯==...I y M zA t σB 点:MPa 162Pa 107816112150100*********331=⨯≈⨯⨯⨯==....I y M σzB c (4)求最大正应力和最大切应力M P a 853Pa 10385361501010320623max max =⨯≈⨯⨯==...W M σzM P a 22Pa 10221501010220232363max =⨯≈⨯⨯⋅=⋅=..A F τS 题9 - 3 简支梁受力如图所示。
第九章梁的弯曲应力

一、梁横截面上的正应力
横力 F 弯曲 A a F (+)
V图
纯弯曲 C l D
F
横力 弯曲 B
纯弯曲——梁弯曲变形
时,横截面上只有弯矩
F
a
F 而无剪力(M 0,V 0)。
F
(-)
横力弯曲——梁弯曲变形 时,横截面上既有弯矩又 有剪力(M 0,V 0)。
Fa
M图
(+) Fa
一、梁横截面上的正应力
* z
max
* Vmax Sz Vmax max * Izd ( I z Sz max )d
* 对于工字钢, I z Sz
max
可由型钢表中查得。
3.工字形截面梁的剪应力
V
三、梁的强度条件
1、弯曲正应力强度条件:
max
Mmax [ ] Wz
可解决工程中有关强度方面的三类问题:
3.在进行梁的强度计算时,需注意以下问题:
(1)对于细长梁的弯曲变形,正应力的强度条件是
主要的,剪应力的强度条件是次要的。但对于较粗的
短梁,当集中力较大时,截面上的剪力较大而弯矩较
小,或是薄壁截面梁时,也需要校核剪应力强度。 (2)正应力的最大值发生在横截面的上下边缘,该
正应力最大。
注意:
(3)梁在中性轴的两侧分别受拉或受压,正应力
的正负号(拉或压)可根据弯矩的正负及梁的变形状
态来确定。 (4)必须熟记矩形截面、圆形截面对中性轴的惯 性矩的计算式。
二、梁横截面上的剪(切)应力
1.剪(切)应力分布规律假设
V
A*
(1)各点处的剪(切)应力 都与剪力V方向一致; (2)横截面上距中性轴等距离各点处剪(切)应力大小 相等,即沿截面宽度为均匀分布。 (3)剪(切)应力大小沿截面高度按抛物线规律变化。
应力状态理论

第九章 应力状态理论
三 梁的主应力 主应力迹线
第九章 应力状态理论
(a) )
图 (a)所示矩形截面梁,设任意截 (a)所示矩形截面梁, 所示矩形截面梁 上的Mz Mz> Fs> 面n-n上的Mz>O,Fs>0, 取出五 个点1 5,可求出n 个点1、2、3、4, 5,可求出n-n截 面上五个点的正应力和切应力, 面上五个点的正应力和切应力,这 五个点的单元体如图(b) 所示。 五个点的单元体如图(b) 所示。其 两点为主应力状态, 中1、5两点为主应力状态,其余三 点为非主应力状态, 点为非主应力状态,可求出它们的 主应力和主平面, (c)所示 所示。 主应力和主平面,如图 (c)所示。
公式推导(2) 公式推导(2) 面上的应力: 面上的应力:
用
斜截面截取,此截面上的应力为
τα
第九章 应力状态理论
公式推导 (3) 面上的应力之间的关系: 面上的应力之间的关系:
τβ
即单元体两个相互垂直面上 的正应力之和是一个常数。
τα
即又一次证明了剪应力的互等定理。 即又一次证明了剪应力的互等定理。
一点应力状态的描述
单元体
第九章 应力状态理论
二 平面应力状态分析 — 数解法
第九章 应力状态理论
1.斜截面上的应力 1.斜截面上的应力
已知受力构件中的应力单元体
求垂直于xy面 求垂直于xy面 xy 的任意斜截面 ef上的应力 ef上的应力
第九章 应力状态理论
公式推导使用的符号规定: 公式推导使用的符号规定:
第九章 应力状态理论
2.σmin = ?在何处? 该处 τ = ? 在何处?
max
令
则: 即: 面上有
第九章 应力状态理论
第九章:复杂应力状态及强度理论

杆在周向截面上没有应力。又由切应力互等定理可知, 杆在径向截面上 B 点处应该有与相等的切应力。于是 此单元体各侧面上的应力如图.
第一节:应力状态概念
三、主平面、主应力、应力状态的分类
主单元体:在一般情况下,表示一点处应力状态的应力单元体在其各个表面上同时 存在有正应力和切应力。但是可以证明:在该点处以不同方式截取的各个单元体中, 必有一个特殊的单元体,在这个单元体的侧面上只有正应力而没有切应力。这样的 单元体称为该点处的主应力单元体或主单元体。
sin 2 cos 2
当 450 时, max
当 00 时, max
低碳钢试件扭转破坏是被剪断的,且其抗剪能力低于其抗拉能力。 铸铁试件扭转破坏是被拉断的,且其抗拉能力低于其抗剪能力。
第二节:二向应力状态分析
例 9-3 图示单元体,x =100MPa,x = – 20MPa, y =30MPa。试求:1) =40º的斜截面上的 和 ;2)确定 A 点处的max、max 和它们所在的
由单向应力状态胡克定律可知:主应力 1、 2和 3 单独作用时,分别对 应的纵向线应变为1/E、2/E和 3/E;令横向变形系数 ,则主应力 2 将引起 1 方向相应的线应变为 – 2 /E;其它同理。故 1 由1 的纵向线 应变与 2、3 分别引起的 1 方向相应的横向线应变三项叠加而成。
主应力表示的 广义胡克定律
第三节:三向应力状态分析
第三节:三向应力状态分析
复杂应力状态下一点处的最大应力 1、一点处的最大正应力
设一点处的主应力单元体如图 a 所示,研究证明,当主应力按 1 2 3
排列时,则有
max 1
min 3
第三节:三向应力状态分析
2、一点处的最大切应力
梁的应力及强度计算

Q图
-
2KN
y2=32.8mm由弯矩图可知上部受拉,下部受压
最大拉应力在上边缘
1KNm
s l max
M maxy1 IZ
1106 15.2 25.6 104
59.4MPa 拉
M图
最大压应力在下边缘
s ymax
M maxy2 IZ
1106 32.8 25.6 104
128.1MPa压
23
9 104
:3
144 104
:
4
3
642
2
104
3 72 : 3 144 : 3 64
结论:矩形截面最省料;圆形截面用料最多。
Z
Z
习题8-44
2、横截面上:在与中性轴平行的一条直线上的各点应力相 等。
3、截面上与中性轴距离最远的点应力最大。
横截面上正应力的画法:
M 0
M 0
M
M
smax
smax
第九章 梁的应力及强度计算
公式适用范围: ①弹性范围—正应力小于比例极限; ②精确适用于纯弯曲梁; ③对于横力弯曲的细长梁(跨度与截面高度比L/h>5),上述公 式的误差不大。
20kNm
20kNm
-
-
50 2003 50 200 94.6 1502
12 102106 mm4
+
20kNm
10kN/m
CA 2m
40kN
D 2m 2m
10kN/m
BE 2m
Q图
20kN
20kN
+
+
-
20kN
应力、应力状态分析(习题解答)

8-9 矩形截面梁如图所示,绘出1、2、3、4点的应力单元体,并写出各点的应力计算式。
解:(1)求支反力R A =,R B = (2)画内力图如图所示。
xPl(-)(+)PlMkN ·m)PPy(-)(-)(+)VkN)题8-9图(3) 求梁各点的正应力、剪应力:(4)画各点的应力单元体如图所示。
9-1 试用单元体表示图示构件的A 、B 的应力单元体。
(a )解:(1)圆轴发生扭转变形,扭矩如图所示。
111max 222222333333max 442330,22(')[()]448114()121200(0,0)16ZZZ ZzV pA b hh h hP P b M V S Pl hy I I bb h b h b M SM PlW b h σττστστστ==-=-⋅=-⋅⋅-⋅⨯⨯-⋅=⋅=⋅==⋅⨯⨯⨯⨯⋅=====-=-=⨯⨯80A-+16080T (kN ·m )(2)绘制A 、B 两点的应力单元体:A 、B 两点均在圆轴最前面的母线上,横截面上应力沿铅垂方向单元体如图所示:331601020.21680510.216A A t bB t T Pa kPa W T Pa kPaW τπτπ===⨯===-⨯(b )解:(1)梁发生弯曲变形,剪力、弯矩图如图所示。
-+120VkN)40MkN ·m)+120402060题9-1(b )(2)绘制A 、B 两点的应力单元体:A 点所在截面剪力为正,A 点横截面的剪力为顺时针,同时A 点所在截弯矩为正下拉,而A 点是压缩区的点。
B 点所在截面剪力为负,B 点横截面的剪力为逆时针,同时B 点所在截弯矩为正下拉,而B 点是拉伸区的点。
单元体如图所示:333.3333.60100.0537.50.1200.21212010(0.1200.050.075) 5.6250.1200.20.1201220100.0512.50.1200.2124010(0.1200.05A A A tA z A A tB B B t B z B B t M y Pa MPaI V S Pa MPaI b M y Pa MPaI V S I bστστ⨯=-⋅=-⨯=-⨯⋅⨯⨯⨯⨯=⋅==⋅⨯⨯⨯=⋅=⨯=⨯⋅-⨯⨯⨯⨯=⋅=⋅g g 30.075) 1.8750.1200.20.12012Pa MPa=-⨯⨯9-2(c解:(1)由题意知:30,20.5030ox x y MP MPa MP στσα==-==,,。
工程力学 第九章 梁的应力及强度计算

1、矩形截面梁纯弯曲时的变形观察
现象:
(1)变形后各横向线仍为直线,只是相对旋转了一个角度,且与变形后的梁轴曲线保持垂直,即小矩形格仍为直角;
(2)梁表面的纵向直线均弯曲成弧线,而且,靠顶面的纵线缩短,靠底面的纵线拉长,而位于中间位置的纵线长度不变。
对剪应力的分布作如下假设:
(1)横截面上各点处剪应力均与剪力Q同向且平行;
(2)横截面上距中性轴等距离各点处剪应力大小相。
根据以上假设,可推导出剪应力计算公式:
式中:τ—横截面上距中性轴z距离为y处各点的剪应力;
Q—该截面上的剪力;
b—需求剪应力作用点处的截面宽度;
Iz—横截面对其中性轴的惯性矩;
Sz*—所求剪应力作用点处的横线以下(或以上)的截面积A*对中性轴的面积矩。
应力σ的正负号直接由弯矩M的正负来判断。M为正时,中性轴上部截面为压应力,下部为拉应力;M为负时,中性轴上部截面为拉应力,下部为压应力。
第二节 梁的正应力强度条件
一、弯曲正应力的强度条件
等直梁的最大弯曲正应力,发生在最大弯矩所在横截面上距中性轴最远的各点处,即
对于工程上的细长梁,强度的主要控制因素是弯曲正应力。为了保证梁能安全、正常地工作,必须使梁内最大正应力σmax不超过材料的许用应力[σ],故梁的正应力强度条件为:
圆形截面横梁截面上的最大竖向剪应力也都发生在中性轴上,沿中性轴均匀分布。
其它形状的截面上,一般地说,最大剪应力也出现在中性轴上各点。
结合书P161-162 例8-3进行详细讲解。
五、梁的剪应力强度校核
梁的剪应力强度条件为:
在梁的强度计算时,必须同时满足弯曲正应力强度条件和剪应力强度条件。但在一般情况下,满足了正应力强度条件后,剪应力强度都能满足,故通常只需按正应力条件进行计算。
工程力学 第九章 梁的强度刚度计算

由结果知,梁的强度不满足要求。
返回 下一张 上一张
y2
z
例9-6 试为图示钢轨枕木选择矩形截面。已知矩形截面尺寸的比 例为b:h=3:4,枕木的弯曲许用正应力[]=15.6MPa,许用剪应力 P P 0 0 .2 m 1 .6 m []=1.7MPa,钢轨传给枕木的压力P=49KN。 .2 m
a
M D ya Iz
返回 下一张 上一张
10.7
第二节 梁横截面上的剪应力
一、矩形截面梁:
矩形截面剪应力计算公式: τ沿截面高度按抛物线规律变化:
2Iz 4
3
QS
* z
I zb
bh
4
τ m ax
2 3
y
h 2
, 0 ; y 0 , max
6 Qh 4 bh
校核梁的正应力强度。
解:(1) 内力及抗弯截面模量计算: MC=3.0KN.m; MD=-4.8KN.m
W1 W2
P1
A
a C a
P2
D
a B
y1
z
763 5 .2
146 . 7 cm
3
y1
z
763 8 .8
86 . 7 cm
3
4 .8 k N m
y2
(2)C截面的正应力强度校核:
4 Q 3 A1
max 2
Q A2
返回 下一张 上一张
例9-3 矩形截面简支梁如图,已知:l=2m,h=15cm,b=10cm, h1=3cm,q=3kN/m。试求A支座截面上K点的剪应力及该截面的最 b q 大剪应力。 解:1.求剪力:QA=3kN
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
s 1 30 MPa , 2 0 s
s 3 20 MPa
t max
s1 s 3
2
30 (20) 25 MPa 2
【例9-34】 用应力圆法求:1) a=30o斜截面上的应力;
2) 主应力及其方位;
3) 剪应力极值。
t
40.3
40 sa a
ta D2(-40,20) 20 30 x -45.3 C O
1.断裂原因:最大伸长线应变e1(与应力状态无关); 2.破坏条件: 3.强度准则:
e1 s1 (s 2 s 3 ) s b
s 1 (s 2 s 3 ) [s ]
4.应用情况:符合表面润滑石料的轴向压缩破坏等,不符合 大多数脆性材料的脆性破坏。
四个强度理论 第三强度理论(最大切应力理论)
【例9-35】分析圆轴扭转时的应力状态。
Me
解: ) 围绕圆轴外表面一点取 1
A B
D C
单元体 ABCD: t Mn / Wp
Me
2 s1 0 0 2) t 2 t s3 2 2 t tan2a 0 a 0 45o
s1
s3
45o x t -45o
第九章 梁的弯曲
§9-1 平面弯曲 §9-2 梁的弯曲内力——剪力和弯矩 §9-3 用内力方程法绘制剪力图和弯矩图 §9-4 用微分关系法绘制剪力图和弯矩图 §9-5 用叠加法画弯矩图 §9-6 梁弯曲时的应力及强度计算
§9-7 梁的变形
§9-8 梁的应力状态
§9-8 梁的应力状态
一、应力状态的概念
3) s 1 t ,s 2 0 ,s 3 t
4) 圆 轴 扭 转 时 , 横 截 面 为 纯 剪 切 应 力状态,最大拉、压应力在与轴 线成±45 o 斜截面上,它们数值相 等,均等于横截面上的剪应力;
0
s3
ABCD
s1
分析圆轴扭转时的应力状态
破坏断面
Me
5)对于塑性材料(如低碳钢)抗剪能 力差,扭转破坏时,通常是横截 面上的最大剪应力使圆轴沿横截 面剪断;
s1 s b
s 1 [s ]
3.强度条件:
4.应用情况:符合脆性材料的拉断试验,如铸铁单向拉伸 和扭转中的脆断;但未考虑其余主应力影响且不能用于无拉应 力的应力状态,如单向、三向压缩等。
四个强度理论 第二强度理论(最大伸长线应变理论 )
准则:无论材料处于什么应力状态,发生脆性断裂的
共同原因是单元体中的最大伸长线应变e1达到某个共同极 限值ejx。
y ty t
sy
n a
ta sa
(sa,ta)E
G1t1
2a
D1 (s x ,t x )
2a0 A A1 s1
sx
tx
sx x
tx
B1 O s2
B C D2
s
sy
ty
t
(s y ,t y )
G2 t 2
应力圆与单元体的对应关系
1)点面对应 应力圆上某一点的坐标值对应着单元体上某 一斜截面上的正应力和切应力值。如D1点的坐标 s x ,t.x 2)转向对应 应力圆上由基准点D1到点E的转向和单元体 上由x面到α面的转向一致。
准则:无论在什么样的应力状态下,材料发生屈 服流动的原因都是单元体内的最大切应力tmax达到某 一共同的极限值tjx。 1.屈服原因:最大切应力tmax(与应力状态无关); 2.屈服条件: 3.强度准则:
s1 s 3 s s
s1 s 3 [s ]
4.应用情况:形式简单,符合实际,广泛应用,偏于安全。
二、平面应力分析 三、梁的主应力和主应力迹线 四、强度理论
一、 应力状态的概念
1.一点的应力状态
一点的应力状态:通过构件内某一点所有不同截面 上的应力情况集合。
研究应力状态的目的:找出该点的最大正应力和最 大剪应力数值及所在截面的方位,以便研究构件破 坏原因并进行失效分析。 2.应力状态分类
P A
四个强度理论 第四强度理论(形状改变比能理论)
准则 :不论应力状态如何,材料发生屈服的共同原
因是单元体中的形状改变比能ud 达到某个共同的极限值 udjx。
1.屈服原因:最大形状改变比能ud(与应力状态无关);
2.屈服条件:
2 (s1 s 2 )2 (s 2 s 3 )2 (s 3 s1 )2 2s s
3)倍角对应 应力圆上两点间圆弧的圆心角是单元体上相 应的两个面之间夹角的二倍。
y sy n a
ta sa
t
(sa,ta)E 2a B 2a0 A C D2 (s y ,t y ) sx x tx
D1 (s x ,t x )
ty sx
tx
O
s
sy
ty
t
3.主平面及主应力 由主平面:
tan2a 0
(一) 强度理论简介
四个强度理论
1. 第一类强度理论(以脆性断 裂破坏为标志)
两类强度理论:
2. 第二类强度理论(以塑性 屈服破坏为标志)
四个强度理论
第一强度理论(最大拉应力理论)
准则 :无论材料处于什么应力状态,发生脆性断裂的
共同原因是单元体中的最大拉应力s1达到某个共同极限值 sjx。 1.断裂原因:最大拉应力s1 (与应力状态无关) 2.破坏条件:
2
由s1、s3、0按代数值大小排序得出:s1≥s2≥s3
最大剪应力(切应力):
t
max mix
sx s y 2 t x 2
2
最大剪(切)应力平面与主平面相差45o
t
max min
s max s min 2
【例9-33】求图所示单元体的主应力与主平面,最大切应力。已知
3.强度准则:
1 [(s 1 s 2 ) 2 (s 2 s 3 ) 2 (s 3 s 1 ) 2 ] [s ] 2
4.应用情况:对塑性材料比最大剪应力准则符合实验结果。
强度理论应用
强度准则的统一形式:
s2
s1
s r [s ]
s3
其中:
s r 1 s 1 s s (s s ) 2 3 r2 1 s r 3 s 1 s 3 s 1 [(s s )2 (s s )2 (s s )2 ] 1 2 2 3 3 1 r4 2
P
(1)单元体:
围绕 构 件内 一 点所 截 取的微小正六面体。
单元体
A
(2)应力状态分类
一点处的 应力状态
单向应力状态 平面应力状态 纯剪切应力状态 双向应力状态 空间应力状态 三向应力状态
s s t
简单应 力状态
复杂应 力状态
单向应 力状态
纯剪切 应力状态
三向应 力状态
双向应 力状态
P A s s
sx
sx
tx sy ty x
t sx x
sα
a
dA
sy
a
tα
ty x
tx ty
x
2 2 s y dA dA t t 0:t axdAs(s xsincosa )sina (s y2a sina )cosa 2a t x cos x (t dAcosa )cosa (t dAsina )sina 0 y x 2
P
Me
B
Me
A
t
B
b) 横截面,周向面,直径面各一对
a) 一对横截面,两对纵截面
P C
Me Me
c) 同b),但从 上表面截取
s
t
C
s
P A B
C
sA
A
sA
B
tB
sC
tC C
sC
二、平面应力状态分析
1、平面应力分析的解析法
sy
sx
sx sy
sx
sx tx
ty
tx
sy
ty
任意斜截面上的应力
y
sy t n
Me
Me
Me
6)对于脆性材料(如铸铁、粉笔) 抗拉性能差,扭转破坏时,通常 沿与轴线成45o 的螺旋面发生拉 断。
破坏断面
【例9-36】图示单元体,试求:① a=30o 斜截面上的应力; ②主应力并画出主单元体;③切应力极值。
y ty
t
sy
n a
ta sa
(sa,ta)E
2a B O D2 C 2a0
D1 (s x ,t x )
sx
tx
sx x
tx
A
s
sy
ty
t
(s y ,t y )
应力圆的绘制:
①定坐标及比例尺;
②取x面,定出D1(s x
, tx
)点;取y面,定出D2( s y
, t y )点;
③连D1D2交s轴于C点,以C为圆心,D1D2为直径作圆;
sin 2a t x cos2a
2、平面应力分析的图解法—应力圆
应力圆方程:
sa
s x s y
tx
2 s x s y
s x s y
2
cos2a t x sin 2a
2
2
sin 2a t x cos 2a
2
s s 2 sx s y x y 2 2 sx t x t x 2 2
符号规定:
a —以x轴正向为起始线,逆时针旋转为正,反
之为负。
s —拉为正,压为负。 t —使微元产生顺时针转动趋势为正,反之为负。
【例9-32】 图示单元体各面应力如图所示,试求斜截面上 的应力 s a 、t a 。 【解】已知 s x 30 MPa ,
