重庆中考二次函数专项训练(含答案)

合集下载

2020年重庆中考二次函数最值专题训练(含答案)

2020年重庆中考二次函数最值专题训练类型一、线段的最值问题【例1】（2019•铜仁市模拟）如图，在平面直角坐标系中，已知A（﹣1，0）、C（4，0），BC ⊥x轴于点C，且AC＝BC，抛物线y＝x2+bx+c经过A、B两点．（1）求抛物线的表达式；（2）点E是线段AB上一动点（不与A、B重合），过点E作x轴的垂线，交抛物线于点F，当线段EF的长度最大时，求点E的坐标；解：∵A（﹣1，0）、C（4，0），∴OA＝1，OC＝4，∴AC＝5，∵BC⊥x轴于点C，且AC＝BC，∴B（4，5），将点A和点B的坐标代入抛物线的解析式得：，解得：b＝﹣2，c＝﹣3．∴抛物线的解析式为y＝x2﹣2x﹣3．（2）∵直线AB经过点A（﹣1，0），B（4，5），设直线AB的解析式为y＝kx+b，∴，解得：，∴直线AB的解析式为：y＝x+1，∵二次函数y＝x2﹣2x﹣3，∴设点E（t，t+1），则F（t，t2﹣2t﹣3），∴EF＝（t+1）﹣（t2﹣2t﹣3）＝﹣（t﹣），∴当t＝时，EF的最大值为，∴点E的坐标为（）．【例2】（2019•贺州）如图，在平面直角坐标系中，已知点B的坐标为（﹣1，0），且OA＝OC ＝4OB，抛物线y＝ax2+bx+c（a≠0）图象经过A，B，C三点．（1）求A，C两点的坐标；（2）求抛物线的解析式；（3）若点P是直线AC下方的抛物线上的一个动点，作PD⊥AC于点D，当PD的值最大时，求此时点P的坐标及PD的最大值．解：（1）OA＝OC＝4OB＝4，故点A、C的坐标分别为（4，0）、（0，﹣4）；（2）抛物线的表达式为：y＝a（x+1）（x﹣4）＝a（x2﹣3x﹣4），即﹣4a＝﹣4，解得：a＝1，故抛物线的表达式为：y＝x2﹣3x﹣4；（3）直线CA过点C，设其函数表达式为：y＝kx﹣4，将点A坐标代入上式并解得：k＝1，故直线CA的表达式为：y＝x﹣4，过点P作y轴的平行线交AC于点H，∵OA＝OC＝4，∴∠OAC＝∠OCA＝45°，∵PH∥y轴，∴∠PHD＝∠OCA＝45°，设点P（x，x2﹣3x﹣4），则点H（x，x﹣4），PD＝HP sin∠PFD＝（x﹣4﹣x2+3x+4）＝﹣x2+2x，∵＜0，∴PD有最大值，当x＝2时，其最大值为2，此时点P（2，﹣6）．【例3】（2019•覃塘区三模）如图，抛物线y＝﹣x2+bx+c与x轴交于点A（﹣1，0）和B（3，0），与y轴交于点C（1）求抛物线的表达式；（2）如图1，若点F在线段OC上，且OF＝OA，经入过点F的直线在第一象限内与抛物线交于点D，与线段BC交于点E，求的最大值；（3）如图2，若P为抛物线的顶点，动点Q在抛物线上，当∠QCO＝∠PBC时，请直接写出点Q的坐标．解：（1）函数的表达式为：y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3，则点C（0，3）；（2）过点D作y轴的平行线交BC于点N，将点B、C的坐标代入一次函数表达式并解得：函数BC表达式为：y＝﹣x+3， OF＝OA＝1，则点F（0，1），CF＝2，设点D（x，﹣x2+2x+3），则点N（x，﹣x+3），∵DN∥CF，∴＝＝（﹣x2+2x+3+x﹣3）＝﹣x2+x，∵﹣0，则有最大值，此时x＝，的最大值为；（3）连接PC，点P坐标（1，4），则PC＝，PB＝，BC＝，则△PBC为直角三角形，tan∠PBC＝＝，过点Q作QH⊥y轴于点H，设点Q（x，﹣x2+2x+3），则tan∠HCQ＝tan＝，解得：x＝0或5或﹣1（舍去0），故点Q（﹣1，0）或（5，﹣12）．【练习】1、（2019•河南模拟）如图，抛物线y＝ax2+bx﹣1（a≠0）交x轴于A，B（1，0）两点，交y轴于点C，一次函数y＝x+3的图象交坐标轴于A，D两点，E为直线AD上一点，作EF⊥x轴，交抛物线于点F （1）求抛物线的解析式；（2）若点F位于直线AD的下方，请问线段EF是否有最大值？若有，求出最大值并求出点E的坐标；若没有，请说明理由；解：（1）将y＝0代入y＝x+3，得x＝﹣3．∴点A的坐标为（﹣3，0）．设抛物线的解析式为y＝a（x﹣x1）（x﹣x2），点A的坐标为（﹣3，0），点B的坐标为（1，0）， ∴y＝a（x+3）（x﹣1）．∵点C的坐标为（0，﹣1），∴﹣3a＝﹣1，得a＝，∴抛物线的解析式为y＝x2+x﹣1；（2）设点E的坐标为（m，m+3），线段EF的长度为y，则点F的坐标为（m，m2+m﹣1）∴y＝（m+3）﹣（m2+m﹣1）＝﹣m2+m+4即y＝（m﹣）2+，此时点E的坐标为（，）；2、（2019•安阳二模）如图，直线y＝﹣x+4与x轴，y轴分别交于点B，C，点A在x轴负半轴上，且OA＝OB，抛物线y＝ax2+bx+4经过A，B，C三点．（1）求抛物线的解析式；（2）点P是第一象限内抛物线上的动点，设点P的横坐标为m，过点P作PD⊥BC，垂足为D，用含m的代数式表示线段PD的长，并求出线段PD的最大值．解：（1）由y＝﹣x+4，当x＝0时，y＝4；当y＝0时，x＝4，∴B（4，0），C（0，4），∴OB＝4，∴OA＝OB＝2，∴A（﹣2，0），把A（﹣2，0），B（4，0）代入抛物线y＝ax2+bx+4中，得，解得，∴抛物线的解析式为y＝﹣x2+x+4；（2）∵点P在二次函数y＝﹣x2+x+4图象上且横坐标为m，∴P（m，﹣m2+m+4），过P作PF∥y轴，交BC于F，则F（m，﹣m+4），∴PF＝﹣m2+2m，∵PD⊥AB于点D，∴在Rt△OBC中，OB＝OC＝4，∴∠OCB＝45°，∵PF∥y轴，∴∠PFD＝∠OCB＝45°，∴PD＝PF•sin∠PFD＝（﹣m2+2m）＝﹣（m﹣2）2+，∵0＜m＜4，﹣＜0，∴当m＝2时，PD最大，最大值为．3、（2019•仁寿县模拟）在平面直角坐标系XOY中，抛物线y＝﹣x2+bx+c经过点A（﹣2，0），B（8，0）．（1）求抛物线的解析式；（2）点C是抛物线与y轴的交点，连接BC，设点P是抛物线上在第一象限内的点，PD⊥BC，垂足为点D．是否存在点P，使线段PD的长度最大？若存在，请求出点P的坐标；若不存在，请说明理由；解：（1）把A（﹣2，0），B（8，0）代入抛物线y＝﹣x2+bx+c，，解得：， ∴抛物线的解析式为：y＝﹣x2+x+4；（2）由（1）知C（0，4），∵B（8，0），将点B、C的坐标代入一次函数表达式并解得：直线BC的解析式为：y＝﹣x+4，如图1，过P作PG⊥x轴于G，PG交BC于E，Rt△BOC中，OC＝4，OB＝8，∴BC＝4，在Rt△PDE中，PD＝PE•sin∠PED＝PE•sin∠OCB＝PE，∴当线段PE最长时，PD的长最大，设P（t，﹣t2+t+4），则E（t，﹣t+4），∴PE＝PG﹣EG＝﹣t2+t+4+t﹣4＝﹣（t﹣4）2+4，（0＜t＜8），当t＝4时，PE有最大值是4，此时P（4，6），∴PD═，即当P（4，6）时，PD的长度最大，最大值是；4、（2019•邓州市一模）如图，抛物线y＝ax2+bx+4与x轴交于A，B两点，与y轴交于点C．已知点A（﹣2，0），B（8，0），连接AC，BC．（1）求抛物线的解析式和点C的坐标；（2）点D是直线BC上方抛物线上的一点，过点D作DE⊥BC，垂足为E，求线段DE的长度最大时，点D的坐标；（3）抛物线上是否存在一点P（异于点A，B，C），使S△P AC＝S△PBC？若存在，请直接写出点P的坐标；若不存在，请说明理由．解：（1）把A（﹣2，0），B（8，.0）分别代入y＝ax2+bx+4中得∴抛物线的解析式为y＝，令x＝0，得y＝4．∴点C的坐标为（0，4）；（2）如图1，过点D作DF∥y轴，交BC于点F，则∠DFE＝∠BCO．∵C＝（0，4），B（8，0），∴OC＝4，OB＝8，在Rt△OBC中，BC＝，∴sin∠BCO＝，∴在Rt△DEF中，DE＝DF・sin∠DFE＝DF•sin∠BCO＝，设直线BC的解析式为y＝kx+t，把B（8，0），C（0，4）分别代入，得，解得，∴直线BC的解析式为y＝，设D（m，，则F（m，）∴DF＝，∴DE＝，∵，∴当m＝4时，DE的值最大，最大值为，此时点D的坐标为（4，.6）；（3）存在点P，使S△P AC＝S△PBC，过点C与AB平行的直线交抛物线于P，∵CP∥AB，∴点A、B到CP的距离相等，∴△P AC、△PBC的面积相等，∵C（0，4），把y＝4代入y＝，解得x＝0或x＝6，∴P（6，4），∴使S△P AC＝S△PBC的点P的坐标为（6，4）．类型二、线段和的最值问题【例4】（2019•广安）如图，抛物线y＝﹣x2+bx+c与x轴交于A、B两点（A在B的左侧），与y轴交于点N，过A点的直线l：y＝kx+n与y轴交于点C，与抛物线y＝﹣x2+bx+c的另一个交点为D，已知A（﹣1，0），D（5，﹣6），P点为抛物线y＝﹣x2+bx+c上一动点（不与A、D重合）．（1）求抛物线和直线l的解析式；（2）当点P在直线l上方的抛物线上时，过P点作PE∥x轴交直线l于点E，作PF∥y轴交直线l于点F，求PE+PF的最大值；（3）设M为直线l上的点，探究是否存在点M，使得以点N、C，M、P为顶点的四边形为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．解：（1）将点A、D的坐标代入直线表达式得：，解得：，故直线l的表达式为：y＝﹣x﹣1，将点A、D的坐标代入抛物线表达式，同理可得抛物线的表达式为：y＝﹣x2+3x+4；（2）直线l的表达式为：y＝﹣x﹣1，则直线l与x轴的夹角为45°，即：则PE＝PE，设点P坐标为（x，﹣x2+3x+4）、则点F（x，﹣x﹣1），PE+PF＝2PF＝2（﹣x2+3x+4+x+1）＝﹣2（x﹣2）2+18，∵﹣2＜0，故PE+PF有最大值，当x＝2时，其最大值为18；【例5】（2019•资阳）如图，抛物线y＝﹣x2+bx+c过点A（3，2），且与直线y＝﹣x+交于B、C两点，点B的坐标为（4，m）．（1）求抛物线的解析式；（2）点D为抛物线上位于直线BC上方的一点，过点D作DE⊥x轴交直线BC于点E，点P为对称轴上一动点，当线段DE的长度最大时，求PD+P A的最小值；解：（1）将点B的坐标为（4，m）代入y＝﹣x+，m＝﹣4+＝﹣，∴B的坐标为（4，﹣），将A（3，2），B（4，﹣）代入y＝﹣x2+bx+c，解得b＝1，c＝，∴抛物线的解析式y＝；（2）设D（m，），则E（m，﹣m+），DE＝（）﹣（﹣m+）＝＝﹣（m﹣2）2+2， ∴当m＝2时，DE有最大值为2，此时D（2，），作点A关于对称轴的对称点A'，连接A'D，与对称轴交于点P．PD+PA＝PD+PA'＝A'D，此时PD+PA最小，∵A（3，2），∴A'（﹣1，2），A'D＝＝，即PD+PA的最小值为；类型三、线段差或线段差的绝对值的最值问题【例6】（2019•零陵区一模）如图，已知抛物线y＝ax2﹣4x+c（a≠0）与x轴交于点A（﹣3，0）和点B，与y轴交于点C（0，6）．（1）求抛物线y的函数表达式及点B的坐标；（2）在抛物线的对称轴上是否存在点P使PB﹣PC的值最大？若存在，求出P点的坐标，若不存在，请说明理由；解：（1）函数过点C，则其表达式为：y＝ax2﹣4x+6，将点A的坐标代入上式并解得：a＝﹣2，故抛物线的表达式为：y＝﹣2x2﹣4x+6…①，令y＝0，则x＝1或﹣3，过点B（1，0）；（2）存在，理由：连接BC并延长交函数对称轴于点P，此时，PB﹣PC的值最大，将点B、C的坐标代入一次函数表达式：y＝kx+b得：，故直线BC的表达式为：y＝﹣6x+6，当x＝﹣1时，y＝12，故点P（﹣1，12）；【例7】（2019•安顺）如图，抛物线y＝x2+bx+c与直线y＝x+3分别相交于A，B两点，且此抛物线与x轴的一个交点为C，连接AC，BC．已知A（0，3），C（﹣3，0）．（1）求抛物线的解析式；（2）在抛物线对称轴l上找一点M，使|MB﹣MC|的值最大，并求出这个最大值；解：（1）①将A（0，3），C（﹣3，0）代入y＝x2+bx+c得：，解得：，∴抛物线的解析式是y＝x2+x+3；（2）将直线y＝x+3表达式与二次函数表达式联立并解得：x＝0或﹣4，∵A（0，3），∴B（﹣4，1）①当点B、C、M三点不共线时，|MB﹣MC|＜BC②当点B、C、M三点共线时，|MB﹣MC|＝BC∴当点、C、M三点共线时，|MB﹣MC|取最大值，即为BC的长，过点B作x轴于点E，在Rt△BEC中，由勾股定理得BC＝＝，∴|MB﹣MC|取最大值为；【练习】如图，已知抛物线y＝﹣x2﹣2x+3与x轴交于A、B两点（点A在点B的右侧），与y轴交于C点．（1）求直线BC的解析式；（2）若点P是直线BC上方抛物线上的一点，当△PBC面积的值最大时，在y轴上找一点D，使得|AD ﹣PD|值最大，请求出D点的坐标和|AD﹣PD|的最大值；解：（1）抛物线y＝﹣x2﹣2x+3与x轴交于A、B两点（点A在点B的右侧），与y轴交于C点，令x＝0，则y＝3，∴C（0，3），令y＝0，则，﹣x2﹣2x+3＝0，解得x＝1或﹣3，∴B（﹣3，0），A（1，0），设直线BC的解析式为y＝kx+b，把B（﹣3，0），C（0，3）代入得，解得，∴直线BC的解析式为y＝x+3；（2）设P（x，﹣x2﹣2x+3），∵OB＝3＝OC，∴S四边形OBPC＝S△PDB+S梯形PDOC＝（x+3）（﹣x2﹣2x+3）+×（﹣x）（﹣x2﹣2x+3+3）＝﹣x2﹣3x+ ∴S△PBC＝S四边形OBPC﹣S△BOC＝﹣x2﹣3x+﹣×3×3＝﹣x2﹣3x＝﹣（x+1）2+∴当x＝﹣1时，△PBC面积的值最大，∴P（﹣1，4），∵抛物线的顶点为（﹣1，4），∴P点是抛物线的顶点，∴PB＝P A，要使|AD﹣PD|值最大，则点P、D、B三点在一条直线上，∴设直线PB：y＝mx+n（m≠0），则，解得，∴直线PB：y＝2x+6．当x＝0时，y＝6，则点D的坐标是（0，6）．此时，|AD﹣PD|的最大值为：；类型四、三角形或四边形面积最值问题【例8】（2019•黄埔区一模）在平面直角坐标系xOy中，抛物线y＝﹣x2+bx+c与x轴交于A（﹣3，0），点B（1，0）两点，与y轴交于点C（1）求抛物线的解析式：（2）若点P是抛物线上在第二象限内的一个动点，且点P的横坐标为t，连接PA、PC、AC．①求△ACP的面积S关于t的函数关系式．②求△ACP的面积的最大值，并求出此时点P的坐标．解：（1）∵抛物线y＝﹣x2+bx+c与x轴交于A（﹣3，0），点B（1，0）两点，∴，解得：，∴抛物线的解析式为y＝﹣x2﹣2x+3．（2）①设直线AC的解析式为y＝kx+b，∴，解得：，∴直线AC的解析式为y＝x+3，过点P作PQ∥y轴交直线AC于点Q，设P（t，﹣t2﹣2t+3），Q（t，t+3），∴PQ＝﹣t2﹣2t+3﹣t﹣3＝﹣t2﹣3t，∴S＝S△PQC+S△PQA＝＝＝﹣．②∵S＝﹣，∴t＝﹣时，△ACP的面积最大，最大值是，此时P点坐标为（﹣，）．【例9】（2019•东营）已知抛物线y＝ax2+bx﹣4经过点A（2，0）、B（﹣4，0），与y轴交于点C．（1）求这条抛物线的解析式；（2）如图1，点P是第三象限内抛物线上的一个动点，当四边形ABPC的面积最大时，求点P的坐标；（3）如图2，线段AC的垂直平分线交x轴于点E，垂足为D，M为抛物线的顶点，在直线DE上是否存在一点G，使△CMG的周长最小？若存在，求出点G的坐标；若不存在，请说明理由．解：（1）∵抛物线y＝ax+bx﹣4经过点A（﹣2，0），B（4，0），∴，解得，∴抛物线解析式为y＝x2+x﹣4；（2）如图1，连接OP，设点P（x，），其中﹣4＜x＜0，四边形ABPC的面积为S，由题意得C（0，﹣4），∴S＝S△AOC+S△OCP+S△OBP＝+，＝4﹣2x﹣x2﹣2x+8，＝﹣x2﹣4x+12，＝﹣（x+2）2+16．∵﹣1＜0，开口向下，S有最大值，∴当x＝﹣2时，四边形ABPC的面积最大，此时，y＝﹣4，即P（﹣2，﹣4）．因此当四边形ABPC的面积最大时，点P的坐标为（﹣2，﹣4）．（3），∴顶点M（﹣1，﹣）．如图2，连接AM交直线DE于点G，此时，△CMG的周长最小．设直线AM的解析式为y＝kx+b，且过点A（2，0），M（﹣1，﹣），∴，∴直线AM的解析式为y＝﹣3．在Rt△AOC中，＝2．∵D为AC的中点，∴，∵△ADE∽△AOC，∴，∴，∴AE＝5，∴OE＝AE﹣AO＝5﹣2＝3，∴E（﹣3，0），由图可知D（1，﹣2）设直线DE的函数解析式为y＝mx+n，∴，解得：，∴直线DE的解析式为y＝﹣﹣．∴，解得：，∴G（）．类型五、三角形周长的最值问题【例10】（2019•宜城市模拟）如图，已知抛物线y＝﹣x2+bx+c与一直线相交于A（1，0）、C（﹣2，3）两点，与y轴交于点N，其顶点为D．（1）求抛物线及直线AC的函数关系式；（2）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值及此时点P的坐标；（3）在对称轴上是否存在一点M，使△ANM的周长最小．若存在，请求出M点的坐标和△ANM周长的最小值；若不存在，请说明理由．解：（1）将A（1，0），C（﹣2，3）代入y＝﹣x2+bx+c，得：，解得：，∴抛物线的函数关系式为y＝﹣x2﹣2x+3；设直线AC的函数关系式为y＝mx+n（m≠0），将A（1，0），C（﹣2，3）代入y＝mx+n，得：，解得：，∴直线AC的函数关系式为y＝﹣x+1．（2）过点P作PE∥y轴交x轴于点E，交直线AC于点F，过点C作CQ∥y轴交x轴于点Q，如图1所示．设点P的坐标为（x，﹣x2﹣2x+3）（﹣2＜x＜1），则点E的坐标为（x，0），点F的坐标为（x，﹣x+1）， ∴PE＝﹣x2﹣2x+3，EF＝﹣x+1，EF＝PE﹣EF＝﹣x2﹣2x+3﹣（﹣x+1）＝﹣x2﹣x+2．∵点C的坐标为（﹣2，3），∴点Q的坐标为（﹣2，0），∴AQ＝1﹣（﹣2）＝3，∴S△APC＝AQ•PF＝﹣x2﹣x+3＝﹣（x+）2+．∵﹣＜0，∴当x＝﹣时，△APC的面积取最大值，最大值为，此时点P的坐标为（﹣，）．（3）当x＝0时，y＝﹣x2﹣2x+3＝3，∴点N的坐标为（0，3）．∵y＝﹣x2﹣2x+3＝﹣（x+1）2+4，∴抛物线的对称轴为直线x＝﹣1．∵点C的坐标为（﹣2，3），∴点C，N关于抛物线的对称轴对称．令直线AC与抛物线的对称轴的交点为点M，如图2所示．∵点C，N关于抛物线的对称轴对称，∴MN＝CM，∴AM+MN＝AM+MC＝AC，∴此时△ANM周长取最小值．当x＝﹣1时，y＝﹣x+1＝2，∴此时点M的坐标为（﹣1，2）．∵点A的坐标为（1，0），点C的坐标为（﹣2，3），点N的坐标为（0，3），∴AC＝＝3，AN＝＝，∴C△ANM＝AM+MN+AN＝AC+AN＝3+．∴在对称轴上存在一点M（﹣1，2），使△ANM的周长最小，△ANM周长的最小值为3+．【练习】1、（2018秋•潮南区期末）如图，已知抛物线y＝x2+3x﹣8的图象与x轴交于A，B两点（点A在点B 的右侧），与y轴交于点C．（1）求直线BC的解析式；（2）点F是直线BC下方抛物线上的一点，当△BCF的面积最大时，在抛物线的对称轴上找一点P，使得△BFP的周长最小，请求出点F的坐标和点P的坐标；（3）在（2）的条件下，是否存在这样的点Q（0，m），使得△BFQ为等腰三角形？如果有，请直接写出点Q的坐标；如果没有，请说明理由．解：（1）对于抛物线y＝x2+3x﹣8，令y＝0，得到x2+3x﹣8＝0，解得x＝﹣8或2，∴B（﹣8，0），A（2，0），令x＝0，得到y＝﹣8，∴A（2，0），B（﹣8，0），C（0，﹣8），设直线BC的解析式为y＝kx+b，则有，解得，∴直线BC的解析式为y＝﹣x﹣8．（2）如图1中，作FN∥y轴交BC于N．设F（m，m2+3m﹣8），则N（m，﹣m﹣8）∴S△FBC＝S△FNB+S△FNC＝•FN×8＝4FN＝4[（﹣m﹣8）﹣（m2+3m﹣8）]＝﹣2m2﹣16m＝﹣2（m+4）2+32，∴当m＝﹣4时，△FBC的面积有最大值，此时F（﹣4，﹣12），∵抛物线的对称轴x＝﹣3，点B关于对称轴的对称点是A，连接AF交对称轴于P，此时△BFP的周长最小，设直线AF的解析式为y＝ax+b，则有，解得，∴直线AF的解析式为y＝2x﹣4， ∴P（﹣3，﹣10），∴点F的坐标和点P的坐标分别是F（﹣4，﹣12），P（﹣3，﹣10）．（3）如图2中，∵B（﹣8，0），F（﹣4，﹣12），∴BF＝＝4，①当FQ1＝FB时，Q1（0，0）或（0，﹣24）（虽然FB＝FQ，但是B、F、Q三点一线应该舍去）．②当BF＝BQ时，易知Q2（0，﹣4），Q3（0，4）．③当Q4B＝Q4F时，设Q4（0，m），则有82+m2＝42+（m+12）2，解得m＝﹣4，∴Q4（0，﹣4），∴Q点坐标为（0，0）或（0，4）或（0，﹣4）或（0，﹣4）．2、（2019•昆山市一模）如图，抛物线y＝ax2﹣3ax+c（a≠0）与x轴交于A，B两点，交y轴于点C，其中A（﹣1，0），C（0，3）．（1）求抛物线的解析式；（2）点P是线段BC上方抛物线上一动点（不与B，C重合），过点P作PD⊥x轴，垂足为D，交BC 于点E，作PF⊥直线BC于点F，设点P的横坐标为x，△PEF的周长记为l，求l关于x的函数关系式，并求出l的最大值及此时点P的坐标；（3）点H是直线AC上一点，该抛物线的对称轴上一动点G，连接OG，GH，则两线段OG，GH的长度之和的最小值等于，此时点G的坐标为（，）（直接写出答案．）解：（1）将A、C代入解析式，可得c＝3，a＝ ∴抛物线的解析式为y＝﹣x2+x+3（2）设P（m，﹣m2+m+3），直线BC的解析式为y＝x+3 点E（m，m+3）∴PE＝﹣m2+m+3+m﹣3＝﹣m2+3m∵△OBC∽△PEF ∴＝， ∴l＝﹣m2+m当m＝2时L的最大值为，点P坐标为（2，）（3）如图，作点O关于对称轴的对称点Q（3，0），作QH⊥AC交对称轴于G∵△AOC∽△ABH ∴＝ ∴＝ ∴QH＝∵△GMQ∽△ACO ∴＝ ∴＝ ∴GM＝∴G（，）3、（2019•齐齐哈尔）如图，抛物线y＝x2+bx+c与x轴交于A、B两点，与y轴交于C点，OA＝2，OC＝6，连接AC和BC．（1）求抛物线的解析式；（2）点D在抛物线的对称轴上，当△ACD的周长最小时，点D的坐标为（，﹣5）．（3）点E是第四象限内抛物线上的动点，连接CE和BE．求△BCE面积的最大值及此时点E的坐标；（4）若点M是y轴上的动点，在坐标平面内是否存在点N，使以点A、C、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．解：（1）∵OA＝2，OC＝6 ∴A（﹣2，0），C（0，﹣6）∵抛物线y＝x2+bx+c过点A、C ∴解得： ∴抛物线解析式为y＝x2﹣x﹣6 （2）∵当y＝0时，x2﹣x﹣6＝0，解得：x1＝﹣2，x2＝3∴B（3，0），抛物线对称轴为直线x＝∵点D在直线x＝上，点A、B关于直线x＝对称∴x D＝，AD＝BD∴当点B、D、C在同一直线上时，C△ACD＝AC+AD+CD＝AC+BD+CD＝AC+BC最小设直线BC解析式为y＝kx﹣6 ∴3k﹣6＝0，解得：k＝2 ∴直线BC：y＝2x﹣6∴y D＝2×﹣6＝﹣5 ∴D（，﹣5）（3）过点E作EG⊥x轴于点G，交直线BC与点F设E（t，t2﹣t﹣6）（0＜t＜3），则F（t，2t﹣6）∴EF＝2t﹣6﹣（t2﹣t﹣6）＝﹣t2+3t∴S△BCE＝S△BEF+S△CEF＝EF•BG+EF•OG＝EF（BG+OG）＝EF•OB＝×3（﹣t2+3t）＝﹣（t﹣）2+∴当t＝时，△BCE面积最大∴y E＝（）2﹣﹣6＝﹣∴点E坐标为（，﹣）时，△BCE面积最大，最大值为．（4）存在点N，使以点A、C、M、N为顶点的四边形是菱形．∵A（﹣2，0），C（0，﹣6） ∴AC＝①若AC为菱形的边长，如图3，则MN∥AC且，MN＝AC＝2∴N1（﹣2，2），N2（﹣2，﹣2），N3（2，0）②若AC为菱形的对角线，如图4，则AN4∥CM4，AN4＝CN4设N4（﹣2，n） ∴﹣n＝解得：n＝﹣ ∴N4（﹣2，﹣）综上所述，点N坐标为（﹣2，2），（﹣2，﹣2），（2，0），（﹣2，﹣）．类型六、四边形周长的最值问题【例11】（2019•顺庆区校级自主招生）如图1，抛物线y＝ax2+bx+c（a≠0）的顶点为（1，4），交x轴于A，B两点，交y轴于点D，其中点B的坐标为（3，0）（1）求抛物线的解析式；（2）如图2，过点A的直线与抛物线交于点E，交y轴于点F其中点E的横坐标为2，若直线PQ为抛物线的对称轴，点G为直线PQ上的一动点，则x轴上是否存在一点H使D，G，H，F四点所围成的四边形周长最小？若存在，求出这个最小值及点G，H的坐标；若不存在，请说明理由．解：（1）∵抛物线顶点为（1，4）∴设顶点式y＝a（x﹣1）2+4∵点B（3，0）在抛物线上∴a（3﹣1）2+4＝0 解得：a＝﹣1∴抛物线解析式为y＝﹣（x﹣1）2+4＝﹣x2+2x+3（2）x轴上存在点H使D，G，H，F四点所围成的四边形周长最小．如图，作点F关于x轴对称的对称点F'，连接EF'∵x＝0时，y＝﹣x2+2x+3＝3 ∴D（0，3）∵当y＝0时，﹣x2+2x+3＝0 解得：x1＝﹣1，x2＝3 ∴A（﹣1，0）∵点E在抛物线上且横坐标为2 ∴y E＝﹣22+2×2+3＝3 ∴E（2，3）∴点D、E关于对称轴对称 ∴DG＝EG设直线AE解析式为y＝kx+e ∴解得： ∴直线AE：y＝x+1 ∴F（0，1） ∴F'（0，﹣1），HF＝HF'，DF＝3﹣1＝2∴C四边形DGHF＝DF+DG+GH+FH＝DF+EG+GH+F'H∴当点E、G、H、F'在同一直线上时，C四边形DGHF＝DF+EF'最小∵EF'＝∴C四边形DGHF＝2+2设直线EF'解析式为y＝mx﹣1∴2m﹣1＝3∴m＝2∴直线EF'：y＝2x﹣1当y＝0时，解得x＝∴H（，0）当x＝1时，y＝2﹣1＝1∴G（1，1）∴四边形DGHF周长最小值为2+2，点G坐标为（1，1），点H坐标为（，0）．【练习】1、（2019•深圳）如图抛物线经y＝ax2+bx+c过点A（﹣1，0），点C（0，3），且OB＝OC．（1）求抛物线的解析式及其对称轴；（2）点D、E在直线x＝1上的两个动点，且DE＝1，点D在点E的上方，求四边形ACDE的周长的最小值．（3）点P为抛物线上一点，连接CP，直线CP把四边形CBP A的面积分为3：5两部分，求点P的坐标．解：（1）∵OB＝OC，∴点B（3，0），则抛物线的表达式为：y＝a（x+1）（x﹣3）＝a（x2﹣2x﹣3）＝ax2﹣2ax﹣3a，故﹣3a＝3，解得：a＝﹣1，故抛物线的表达式为：y＝﹣x2+2x+3…①；（2）ACDE的周长＝AC+DE+CD+AE，其中AC＝、DE＝1是常数，故CD+AE最小时，周长最小，取点C关于函数对称点C（2，3），则CD＝C′D，取点A′（﹣1，1），则A′D＝AE，故：CD+AE＝A′D+DC′，则当A′、D、C′三点共线时，CD+AE＝A′D+DC′最小，周长也最小，四边形ACDE的周长的最小值＝AC+DE+CD+AE＝+A′D+DC′＝+A′C′＝+；（3）如图，设直线CP交x轴于点E，直线CP把四边形CBPA的面积分为3：5两部分，又∵S△PCB：S△PCA＝EB×（y C﹣y P）：AE×（y C﹣y P）＝BE：AE，则BE：AE，＝3：5或5：3，则AE＝或，即：点E的坐标为（，0）或（，0），将点E、C的坐标代入一次函数表达式：y＝kx+3，解得：k＝﹣6或﹣2，故直线CP的表达式为：y＝﹣2x+3或y＝﹣6x+3…②联立①②并解得：x＝4或8（不合题意值已舍去），故点P的坐标为（4，﹣5）或（8，﹣45）．2、（2017•日照模拟）如图，抛物线y＝x2﹣2x﹣3与x轴交于A、B两点（点A在点B的左侧），直线l与抛物线交于A，C两点，其中点C的横坐标为2．（1）求A，B两点的坐标及直线AC的函数表达式；（2）P是线段AC上的一个动点（P与A，C不重合），过P点作y轴的平行线交抛物线于点E，求△ACE面积的最大值；（3）若直线PE为抛物线的对称轴，抛物线与y轴交于点D，直线AC与y轴交于点Q，点M为直线PE上一动点，则在x轴上是否存在一点N，使四边形DMNQ的周长最小？若存在，求出这个最小值及点M，N的坐标；若不存在，请说明理由．解：（1）令y＝0，解得x1＝﹣1或x2＝3，∴A（﹣1，0），B（3，0）；将C点的横坐标x＝2代入y＝x2﹣2x﹣3得y＝﹣3，∴C（2，﹣3），∴直线AC的函数解析式是y＝﹣x﹣1，（2）设P点的横坐标为x（﹣1≤x≤2），则P、E的坐标分别为：P（x，﹣x﹣1），E（x，x2﹣2x﹣3），∵P点在E点的上方，PE＝（﹣x﹣1）﹣（x2﹣2x﹣3）＝﹣x2+x+2，∴当x＝时，PE的最大值＝，△ACE的面积最大值＝PE[2﹣（﹣1）]＝PE＝，（3）D点关于PE的对称点为点C（2，﹣3），点Q（0，﹣1）点关于x轴的对称点为K（0，1），连接CK交直线PE于M点，交x轴于N点，可求直线CK的解析式为y＝﹣2x+1，此时四边形DMNQ 的周长最小，最小值＝|CM|+QD＝2+2，求得M（1，﹣1），N（，0）．3、（2017秋•南岸区校级期中）如图1，抛物线y＝x2﹣x﹣3，与x轴交于A和B两点（点A在点B的左侧），与y轴交于点C，过点A的直线与抛物线在第一象限的交点M的横坐标为，直线AM与y 轴交于点D，连接BC、AC．（1）求直线AD和BC的解折式；（2）如图2，E为直线BC下方的抛物线上一点，当△BCE的面积最大时，一线段FG＝4（点F在G的左侧）在直线AM上移动，顺次连接B、E、F、G四点构成四边形BEFG，请求出当四边形BEFG 的周长最小时点F的坐标；解：（1）在抛物线y＝中，令x＝0，得y＝﹣3，∴C（0，﹣3），令y＝0，得，解得x1＝﹣1，x2＝4，∴A（﹣1，0），B（4，0），令x＝，得y＝＝，∴M（，），设直线AD的解析式为y＝k1x+b1，将A（﹣1，0），M（，）代入得，解得，∴直线AD的解析式为y＝x+1．设直线BC的解析式为y＝k2x+b2，将B（4，0），C（0，﹣3）代入，得，解得，∴直线BC的解析式为y＝x﹣3；（2）如图2，过点E作EH∥y轴交BC于H，设E（t，），H（t，），∴HE＝＝∴＝＝＝∵＜0，∴当t＝2时，S△BCE的最大值＝6，此时E（2，），作点B关于直线y＝x+1的对称点B1，连接B1G，过点F作B2F∥B1G，且B2F＝B1G，∴B1（﹣1，5）， ∵FG＝4，且FG在直线y＝x+1上，∴F可以看作是G向左平移4个单位，向下平移4个单位后的对应点，∴B2（﹣5，1），当B2、F、E三点在同一直线上时，BEFG周长最小，设直线B2E解析式为y＝mx+n，将B2（﹣5，1），E（2，）分别代入，得，解得，∴直线B2E解析式为y＝，联立方程组，解得．∴F（，）．类型七、线段与系数线段的和差最值问题【例12】（2018•南岸区模拟）如图1，在平面直角坐标系中，抛物线y＝x2+x﹣与x 轴交于A、B两点（点A在点B的左侧），与y轴交于点C．（1）求抛物线的对称轴和直线AC的解析式；（2）P为直线AC下方抛物线上（不与A、C重合）的一动点，PB交AC于D，当取得最大值时，M为y轴上一动点，N为抛物线对称轴上一动点且MN⊥y轴，求PM+MN+AN的最小值；解：（1）﹣＝﹣1，∴抛物线的对称轴为直线x＝﹣1，令x＝0，y＝﹣，∴C（0，﹣），令y＝0，解得x1＝﹣3，x2＝1，∴A（﹣3，0），B（0，﹣1），设直线AC的解析式为y＝kx+b，则解得∴AC的解析式为y＝﹣x﹣．（2）过点P作y轴的平行线交AC于点H，过点B作y轴的平行线交y轴于点Q，当x＝1时，y＝﹣，∴BQ＝，设点P的坐标为（m，），则点H（m，﹣），∴PH＝﹣﹣（）＝﹣，∵△PHD∽△BDQ，∴，∴＝﹣，此时点P（﹣，﹣），过点P作y轴的对称点P′，则P′（，﹣），将点A向右平移一个单位得到点A′，则点A ′（﹣2，0），连接A′P′，与y轴的交点即为点M，过M作x轴的平行线，与对称轴的交点即为点N，设直线A′P′的解析式为y＝kx+b，，解得，∴y＝﹣x﹣，∴M（0，﹣），N（﹣1，﹣），A′P′＝＝，∴PM+MN+AN的最小值为：1+．【例13】已知二次函数y＝x2﹣x﹣2的图象和x轴交于点A，B，与y轴交于点C，过直线BC的下抛物线上与动点P作PQ∥AC交线段BC于点Q，再过P点作PE⊥x轴于点E，交BC于点D；（1）求直线AC的解析式；（2）求△PQD周长的最大值；（3）当△PQD的周长最大时，在y轴上有两个动点M，N（M在N的上方），且MN＝1，求PN+MN+AM 的最小值．解：（1）对于二次函数y＝x2﹣x﹣2，令x＝0得y＝﹣2，令y＝0，得x2﹣x﹣2＝0，解得x＝﹣1或2， ∴A（﹣1，0），B（2，0），C（0，﹣2），设直线AC的解析式为y＝kx+b，则有，解得，∴直线AC的解析式为y＝﹣2x﹣2．（2）∵B（2，0），C（0，﹣2），∴直线BC的解析式为y＝x﹣2，OB＝OC＝2，∴∠OCB＝∠OBC＝45°，∵PE⊥x轴，∴∠DEB＝90°，∴∠EDB＝∠QDP＝∠EBD＝45°，∵PQ∥AC，∴∠PQC＝∠ACQ，∴∠PQD，∠PDQ是定值，∴PD最长时，△PDQ的最长最大，设P（m，m2﹣m﹣2），则D（m，m﹣2），∴PD＝m﹣2﹣（m2﹣m﹣2）＝﹣m2+2m＝﹣（m﹣1）2+1，∵﹣1＜0，∴m＝1时，PD的值最大，PD最大值为1，此时P（1，﹣2），D（1，﹣1），∴直线PQ的解析式为y＝﹣2x，由，解得，∴Q（，﹣），∴PD＝1，PQ＝，DQ＝ ∴△PDQ的最长的最大值为1++．（3）如图2中，作PP′∥y轴，使得PP′＝MN＝1，连接AP′交y轴于M，此时PN+NM+AM的值最小．由（2）可知P （1，﹣2），∴P ′（1，﹣1），∵A （﹣1，0），∴直线AP ′的解析式为y ＝﹣x ﹣，∴M （0，﹣），N （0，﹣），∴AM ＝＝，PN ＝＝，∴AM +MN +PN 的最小值为+1．【例14】如图，抛物线2142y x x =+-与x 轴交于A 、B （A 在B 的左侧)，与y 轴交于点C ，抛物上的点E 的横坐标为3，过点E 作直线1l ∥x 轴。

重庆市合川区第一中学2020年中考九年级数学典型压轴题专练：二次函数(包含答案)

重庆市合川区第一中学2020 年中考九年级数学典型压轴题专练：二次函数1、已知二次函数y=ax 2﹣ 2ax+c （ a＞ 0）的图象与 x 轴的负半轴和正半轴分别交于A、 B 两点，与 y 轴交于点C，它的极点为P，直线 CP与过点 B 且垂直于x 轴的直线交于点D，且CP： PD=2： 3（1）求 A、 B 两点的坐标；（2）若 tan ∠ PDB= ，求这个二次函数的关系式．2、已知二次函数y=x 2+bx+c 的图象与y 轴交于点C（ 0，﹣ 6），与 x 轴的一个交点坐标是 A （﹣ 2， 0）．（1）求二次函数的分析式，并写出极点 D 的坐标；（2）将二次函数的图象沿x 轴向左平移个单位长度，当y ＜ 0 时，求 x 的取值范围．3、如图，已知抛物线y= ﹣ x2+mx+3与 x 轴交于 A， B 两点，与 y 轴交于点C，点 B 的坐标为（3， 0）（1）求 m的值及抛物线的极点坐标．（2）点 P 是抛物线对称轴l 上的一个动点，当PA+PC的值最小时，求点P 的坐标．4、如图，抛物线y=ax 2+bx﹣ 3（ a≠ 0）的极点为E，该抛物线与x 轴交于 A、 B 两点，与y 轴交于点C，且 BO=OC=3AO，直线 y=﹣x+1 与 y 轴交于点D．（1）求抛物线的分析式；（2）证明：△ DBO∽△ EBC；（3）在抛物线的对称轴上能否存在点 P，使△ PBC是等腰三角形？若存在，请直接写出切合条件的 P 点坐标，若不存在，请说明原因．5、课本中有一个例题：有一个窗户形状如图1，上部是一个半圆，下部是一个矩形，假如制作窗框的资料总长为6m，怎样设计这个窗户，使透光面积最大？这个例题的答案是：当窗户半圆的半径约为0.35m 时，透光面积最大值约为 1.05m2．我们假如改变这个窗户的形状，上部改为由两个正方形构成的矩形，如图2，资料总长仍为6m，利用图3，解答以下问题：（1）若 AB为 1m，求此时窗户的透光面积？（2）与课本中的例题比较，改变窗户形状后，窗户透光面积的最大值有没有变大？请经过计算说明．6、正方形OABC的边长为 4，对角线订交于点P，抛物线L 经过 O、 P、 A 三点，点E 是正方形内的抛物线上的动点．（1）成立适合的平面直角坐标系，①直接写出 O、P、 A 三点坐标；②求抛物线 L 的分析式；（2）求△ OAE与△ OCE面积之和的最大值．[ 根源 :]7、如图，抛物线y=ax 2+bx﹣ 5（ a≠ 0）与x 轴交于点A（﹣ 5， 0）和点B（3， 0），与y 轴交于点 C．（1）求该抛物线的分析式；（2）若点 E 为 x 轴下方抛物线上的一动点，当S△ABE=S△ABC时，求点 E 的坐标；（3）在（ 2）的条件下，抛物线上能否存在点P，使∠BAP=∠ CAE？若存在，求出点P 的横坐标；若不存在，请说明原因．8、如图，已知抛物线y=ax 2+bx+c（ a≠ 0）经过 A（﹣ 1，0）、B（ 3，0）、C（ 0，﹣ 3）三点，直线 l 是抛物线的对称轴．（1）求抛物线的函数关系式；（2）设点P 是直线l 上的一个动点，当点P 到点A、点 B 的距离之和最短时，求点P 的坐标；l 上的动点，且△MAC为等腰三角形，请直接写出全部切合条件的点M （3）点M也是直线的坐标．9、如图1，在平面直角坐标系xOy 中，抛物线y=ax 2+1 经过点A（ 4，﹣ 3），极点为点B，点 P 为抛物线上的一个动点，l 是过点（0，2）且垂直于y 轴的直线，过P 作PH⊥ l ，垂足为 H，连结PO．（1）求抛物线的分析式，并写出其极点 B 的坐标；（2）①当P 点运动到 A 点处时，计算： PO= ，PH= ，由此发现，PO PH（填“＞” 、“＜”或“=”）；②当 P 点在抛物线上运动时，猜想PO与 PH有什么数目关系，并证明你的猜想；（3）如图 2，设点 C（ 1，﹣ 2），问能否存在点 P，使得以 P，O，H为极点的三角形与△ ABC 相像？若存在，求出 P 点的坐标；若不存在，请说明原因．10 、如图，已知抛物线与 x 轴交于 A（﹣ 1 ， 0 ）， B（ 4 ， 0 ），与 y 轴交于 C （ 0 ，﹣ 2 ）．（1 ）求抛物线的解析式；（2 ） H 是 C 关于 x 轴的对称点， P 是抛物线上的一点，当△ PBH 与△ AOC 相似时，求符合条件的 P 点的坐标（求出两点即可）；（3 ）过点 C 作 CD∥ AB， CD 交抛物线于点 D，点 M 是线段 CD 上的一动点，作直线 MN 与线段 AC 交于点 N，与 x 轴交于点 E，且∠ BME=∠ BDC，当 CN 的值最大时，求点 E 的坐标．11、如图，对称轴为直线 x=2 的抛物线 y=x 2+bx+c 与 x 轴交于点 A 和点 B，与 y 轴交于点 C，且点A 的坐标为（﹣ 1， 0）（1）求抛物线的分析式；（2）直接写出 B、 C 两点的坐标；（3）求过 O， B， C 三点的圆的面积．（结果用含π的代数式表示）注：二次函数y=ax2+bx+c （ a≠ 0）的极点坐标为（﹣，）12、在平面直角坐标系中，平行四边形ABOC如图搁置，点A、C 的坐标分别是（0，4）、（﹣1， 0），将此平行四边形绕点O顺时针旋转90°，获得平行四边形A′B′ OC′．（1）若抛物线经过点C、 A、A′，求此抛物线的分析式；（2）点 M时第一象限内抛物线上的一动点，问：当点M在哪处时，△ AMA′的面积最大？最大面积是多少？并求出此时M的坐标；（3）若 P 为抛物线上一动点，N 为 x 轴上的一动点，点Q坐标为（ 1， 0），当 P、N、 B、 Q 构成平行四边形时，求点P 的坐标，当这个平行四边形为矩形时，求点N 的坐标．13、在平面直角坐标系xOy 中，抛物线y=ax2+bx+2 过 B（﹣ 2， 6）， C（ 2， 2）两点．（1）试求抛物线的分析式；（2）记抛物线极点为 D，求△ BCD的面积；（3）若直线 y=﹣x 向上平移 b 个单位所得的直线与抛物线段BDC（包含端点B、 C）部分有两个交点，求 b 的取值范围．14、如图 1（注：与图 2 完整同样），二次函数y= x2+bx+c 的图象与x 轴交于 A（ 3，0），B （﹣ 1， 0）两点，与y 轴交于点C．（1）求该二次函数的分析式；（2）设该抛物线的极点为 D，求△ ACD的面积（请在图 1 中探究）；（3）若点 P， Q同时从 A 点出发，都以每秒 1 个单位长度的速度分别沿AB，AC边运动，其中一点抵达端点时，另一点也随之停止运动，当P，Q运动到 t 秒时，△ APQ沿 PQ所在的直线翻折，点 A 恰巧落在抛物线上 E 点处，请直接判断此时四边形 APEQ的形状，并求出 E 点坐标（请在图 2 中探究）．15、如图，矩形的边 OA在 x 轴上，边 OC在 y 轴上，点 B 的坐标为（ 10， 8），沿直线 OD 折叠矩形，使点 A 正好落在 BC上的 E 处， E 点坐标为（ 6，8），抛物线 y=ax2+bx+c 经过 O、A、 E 三点．（1）求此抛物线的分析式；（2）求 AD 的长；（3）点 P 是抛物线对称轴上的一动点，当△PAD的周长最小时，求点P 的坐标．16、如图，抛物线 L： y=ax 2+bx+c 与 x 轴交于 A、 B（ 3， 0）两点（ A 在 B 的左边），与 y 轴交于点 C（ 0， 3），已知对称轴 x=1．（1）求抛物线L 的分析式；（2）将抛物线L 向下平移h 个单位长度，使平移后所得抛物线的极点落在△OBC内（包含△OBC的界限），求 h 的取值范围；（3）设点 P 是抛物线L 上任一点，点Q在直线 l ：x=﹣ 3 上，△ PBQ可否成为以点P 为直角极点的等腰直角三角形？若能，求出切合条件的点P 的坐标；若不可以，请说明原因．参照答案 :1、解：（ 1）过点 P 作 PE⊥ x 轴于点 E，∵y=ax 2﹣ 2ax+c ，∴该二次函数的对称轴为： x=1，∴O E=1∵OC∥ BD，∴CP： PD=OE：EB，∴OE： EB=2： 3，∴E B= ，∴O B=OE+EB=，∴B（，0）∵A 与 B 对于直线x=1 对称，∴A（﹣，0）；（2）过点 C 作 CF⊥ BD于点 F，交 PE于点 G，令 x=1 代入 y=ax 2﹣2ax+c ，∴y=c ﹣ a，令 x=0 代入 y=ax 2﹣2ax+c ，∴y=c∴P G=a，∵CF=OB= ，∴t an ∠ PDB= ，∴F D=2，∵PG∥ BD∴△ CPG∽△ CDF，∴= =∴PG= ，∴a=，∴y= x2﹣ x+c ，把 A（﹣，0）代入y=x2﹣x+c， [ 根源 : ]∴解得： c=﹣ 1，∴该二次函数分析式为：y= x2﹣x﹣ 1．2、解：（ 1）∵把 C（ 0，﹣ 6）代入抛物线的分析式得：C=﹣6，把 A（﹣ 2，0）代入 y=x 2+bx ﹣6得： b=﹣ 1，∴抛物线的分析式为 y=x 2﹣ x﹣6．∴y= （ x﹣）2﹣．∴抛物线的极点坐标D（，﹣）．（2）二次函数的图形沿x 轴向左平移个单位长度得：y=（ x+2）2﹣．令 y=0 得：（ x+2）2﹣=0，解得： x1=，x2=﹣．∵a＞ 0，∴当 y＜ 0 时， x 的取值范围是﹣＜x＜．3、解：（ 1）把点 B 的坐标为（ 3， 0）代入抛物线y=﹣x2+mx+3得： 0=﹣ 32 +3m+3，解得： m=2，∴y= ﹣ x2+2x+3=﹣（ x﹣ 1）2+4，∴极点坐标为：（ 1， 4）．（2）连结 BC交抛物线对称轴 l 于点 P，则此时 PA+PC的值最小，设直线 BC的分析式为： y=kx+b ，∵点 C（ 0， 3），点 B（ 3，0），∴，解得：，∴直线 BC的分析式为：y= ﹣x+3，当x=1 时， y=﹣1+3=2，∴当 PA+PC的值最小时，求点P 的坐标为：（1， 2）．4、解：（ 1）∵抛物线y=ax2 +bx﹣ 3，∴c= ﹣ 3，∴C（ 0，﹣ 3），∴O C=3，∵BO=OC=3AO，∴BO=3， AO=1，∴B（ 3， 0）， A（﹣ 1， 0），∵该抛物线与x 轴交于 A、 B 两点，∴，∴，∴抛物线分析式为y=x 2﹣ 2x﹣3，（2）由（ 1）知，抛物线分析式为 y=x2 ﹣2x﹣ 3=（ x﹣ 1）2﹣4，∴E（ 1，﹣ 4），∵B（ 3， 0）， A（﹣ 1， 0）， C（ 0，﹣3），∴BC=3 ， BE=2 ，CE= ，∵直线 y=﹣ x+1 与 y 轴交于点 D，∴D（ 0， 1），∵B（ 3， 0），∴O D=1， OB=3，BD=，∴，，，∴，∴△ BCE∽△ BDO，（3）存在，原因：设P（ 1，m），∵B（ 3， 0）， C（ 0，﹣ 3），∴BC=3，PB=，PC=，∵△ PBC是等腰三角形，①当 PB=PC时，∴=，∴m=﹣ 1，∴P（ 1，﹣ 1），②当 PB=BC时，∴3=，∴m=±，∴P（ 1，）或P（1，﹣），③当 PC=BC时，∴3 = ，∴m=﹣ 3±，∴P（ 1，﹣ 3+ ）或 P（ 1，﹣ 3﹣），∴切合条件的P点坐标为 P（ 1，﹣ 1）或 P（ 1，）或 P（ 1，﹣）或 P（ 1，﹣ 3+ ）或 P（ 1，﹣ 3﹣）5、解：（ 1）由已知可得： AD= ，则 S=1×2 m，（2）设 AB=xm，则 AD=3﹣m，∵，∴，设窗户面积为S，由已知得：，当 x= m时，且 x= m在的范围内，，∴与课本中的例题比较，此刻窗户透光面积的最大值变大．6、解：（ 1）以 O点为原点，线段OA所在的直线为x 轴，线段OC所在的直线为y 轴成立直角坐标系，以下图．①∵正方形OABC的边长为 4，对角线订交于点P，∴点 O的坐标为（ 0， 0），点 A 的坐标为（ 4， 0），点 P 的坐标为（ 2，2）．②设抛物线L 的分析式为y=ax 2+bx+c ，∵抛物线L 经过 O、 P、 A 三点，∴有，解得：，∴抛物线L 的分析式为y=﹣+2x．（2）∵点 E 是正方形内的抛物线上的动点，∴设点 E 的坐标为（ m，﹣+2m）（ 0 ＜ m＜ 4），∴S +S = OA?y + 2 2OC?x =﹣m+4m+2m=﹣（ m﹣ 3） +9，△ OAE OCE E E∴当 m=3时，△ OAE与△ OCE面积之和最大，最大值为9．7、解：（1）把 A、 B 两点坐标代入分析式可得，解得，∴抛物线分析式为y= x2+x﹣ 5；2（2）在 y= x + x﹣ 5 中，令 x=0 可得 y=﹣ 5，∴C（ 0，﹣ 5），∵S△ABE=S△ABC，且 E 点在 x 轴下方，∴E 点纵坐标和 C 点纵坐标同样，当 y=﹣ 5 时，代入可得x2+ x=﹣ 5，解得 x=﹣ 2 或 x=0（舍去）， [ 根源 : ] ∴E 点坐标为（﹣2，﹣ 5）；（3）假定存在知足条件的 P 点，其坐标为（ m， m2+ m﹣ 5），如图，连结 AP、CE、 AE，过 E 作 ED⊥ AC于点 D，过 P作 PQ⊥ x 轴于点 Q，则 AQ=AO+OQ=5+m，PQ=| m2+m﹣ 5| ，在 Rt △ AOC中， OA=OC=5，则 AC=5，∠ ACO=∠ DCE=45°，由（ 2）可得 EC=2，在 Rt △ EDC中，可得 DE=DC=，∴AD=AC﹣ DC=5﹣=4，当∠ BAP=∠ CAE时，则△ EDA∽△ PQA，∴=，即=，∴2（ 5+m）或2m+ m﹣5= m+ m﹣ 5=﹣（5+m），当2m﹣5= （ 5+m）时，整理可得2或 m=﹣ 5（与 A 点重合，m+ 4m﹣ 5m﹣ 75=0，解得 m=舍去），当2m﹣5=﹣（ 5+m）时，整理可得2或 m=﹣ 5（与 A 点重合，m+ 4m+11m﹣ 45=0，解得 m=舍去），8、解：（ 1）将 A（﹣ 1， 0）、B（ 3， 0）、 C（ 0，﹣ 3）代入抛物线y=ax2 +bx+c 中，得：，解得：故抛物线的分析式：y=x2﹣ 2x﹣3．（2）当 P 点在 x 轴上， P，A，B 三点在一条直线上时，点P 到点 A、点 B的距离之和最短，此时 x=﹣=1，故 P（ 1， 0）；（3）以下图：抛物线的对称轴为：x=﹣=1，设 M（ 1， m），已知 A（﹣ 1， 0）、C（ 0，﹣3），则：22222 2MA=m+4，MC=（ 3+m） +1=m+6m+10， AC=10；2 2①若 MA=MC，则 MA=MC，得：2 2m+4=m+6m+10，解得： m=﹣ 1，2 2②若 MA=AC，则 MA=AC，得：2m+4=10，得： m=±；2 2③若 MC=AC，则 MC=AC，得：2m+6m+10=10，得： m1=0，m2=﹣ 6；当 m=﹣ 6 时， M、 A、 C 三点共线，构不可三角形，不合题意，故舍去；综上可知，切合条件的M点，且坐标为M（1，）（1，﹣）（1，﹣1）（1，0）．9、（ 1）解：∵抛物线y=ax2 +1 经过点 A（ 4，﹣ 3），∴﹣ 3=16a+1，∴a=﹣， [ 根源 : 学 , 科 , 网 Z,X,X,K]∴抛物线分析式为y=﹣x2+1，极点 B（ 0， 1）．（2）①当 P 点运动到 A 点处时，∵ PO=5， PH=5，∴PO=PH，故答案分别为 5， 5， =．②结论： PO=PH．原因：设点 P 坐标（ m，﹣ m2+1），∵PH=2﹣（﹣m2+1） =m2+1PO=2 = m+1，∴PO=PH．（3）∵ BC==，AC==，AB==4 ∴BC=AC，∵PO=PH，又∵以 P， O， H为极点的三角形与△ABC相像，∴PH与 BC， PO与 AC是对应边，∴=，设点P（m，﹣m2+1），∴=，解得 m=± 1，∴点 P 坐标（ 1，）或（﹣1，）．10 、解：（ 1 ）∵抛物线与 x 轴交于 A（﹣ 1， 0）， B（ 4 ， 0），∴设抛物线的解析式为： y=a （ x+1 ）（ x ﹣ 4 ），把（ 0 ，﹣ 2 ）代入 y=a （ x+1 ）（ x ﹣ 4 ），∴a= ，∴抛物线的解析式为： y= x 2﹣x ﹣ 2 ；（2 ）当△ PBH 与△ AOC 相似时，∴ △ AOC 是直角三角形，∴ △ PBH 也是直角三角形，由题意知： H（ 0 ，2 ），∴ OH=2，∵ A（﹣ 1 ， 0 ）， B（ 4 ，0 ），∴ OA=1， OB=4 ，∴∵ ∠ AOH=∠ BOH，∴ △ AOH∽ △ BOH，∴ ∠ AHO=∠ HBO，∴ ∠ AHO+∠ BHO=∠ HBO+∠ BHO=90 °，∴ ∠ AHB=90 °，设直线 AH 的解析式为： y=kx+b，把A（﹣ 1 ， 0 ）和 H（ 0 ， 2 ）代入 y=kx+b ，∴，∴ 解得，∴直线 AH 的解析式为： y=2x+2，联立，解得： x=1或x=﹣8，当x= ﹣ 1 时，y=0 ，当x=8 时，y=18∴ P 的坐标为（﹣ 1 ， 0 ）或（ 8， 18 ）（ 3 ）过点 M 作 MF⊥ x 轴于点 F，设点 E 的坐标为（ n ， 0 ）， M 的坐标为（ m， 0 ），∵ ∠ BME=∠ BDC，∴ ∠ EMC+∠ BME=∠ BDC+∠ MBD，∴ ∠ EMC=∠ MBD，∵CD∥ x 轴，∴ D 的纵坐标为﹣ 2 ，令 y= ﹣ 2 代入 y= x 2﹣x ﹣ 2 ，∴ x=0或x=3，∴ D（ 3，﹣ 2 ），∵ B（ 4， 0），∴由勾股定理可求得： BD=，∵ M（ m， 0），∴MD=3﹣ m， CM=m（ 0 ≤ m≤ 3 ）∴由抛物线的对称性可知：∠ NCM=∠ BDC，∴△ NCM∽ △ MDB，∴，∴，∴ CN= =﹣（ m﹣）2+ ，∴当 m= 时， CN 可取得最大值，∴此时 M 的坐标为（，﹣ 2 ），∴ MF=2， BF= ， MD=∴由勾股定理可求得： MB= ，∵E（ n， 0），∴ EB=4 ﹣ n，∵CD∥ x 轴，∴ ∠ NMC=∠ BEM，∠ EBM=∠ BMD，∴ △ EMB∽ △ BDM，∴，∴MB2 =MD? EB，∴= ×（ 4 ﹣ n ），∴n= ﹣，∴ E 的坐标为（﹣， 0 ）．11、解：（ 1）由 A（﹣ 1， 0），对称轴为 x=2，可得，解得，∴抛物线分析式为y=x 2﹣ 4x﹣5；（2）由 A 点坐标为（﹣ 1，0），且对称轴方程为 x=2，可知 AB=6，∴OB=5，∴B 点坐标为（ 5， 0），∵y=x 2﹣ 4x﹣ 5，∴C 点坐标为（ 0，﹣ 5）；（3）如图，连结BC，则△ OBC是直角三角形，∴过 O、 B、 C 三点的圆的直径是线段BC的长度，在Rt △ OBC中， OB=OC=5，∴BC=5 ，∴圆的半径为，∴圆的面积为π（）2=π．12、解：（ 1）∵平行四边形 ABOC绕点 O顺时针旋转 90°，获得平行四边形 A′ B′OC′，且点 A 的坐标是（ 0， 4），∴点 A′的坐标为：（ 4， 0），∵点 A、 C的坐标分别是（0， 4）、（﹣ 1， 0），抛物线经过点C、 A、 A′，设抛物线的分析式为：y=ax2+bx+c，∴，解得：，∴此抛物线的分析式为：y=﹣ x2+3x+4；（2）连结 AA′，设直线AA′的分析式为：y=kx+b ，∴，解得：，∴直线 AA′的分析式为：y=﹣ x+4，设点 M的坐标为：（ x，﹣ x2+3x+4），则S△AMA′= × 4×[ ﹣ x2+3x+4﹣（﹣ x+4） ]= ﹣ 2x2+8x=﹣2（ x﹣ 2）2+8，S△AMA′ =8，∴当 x=2 时，△ AMA′的面积最大，最大值∴M的坐标为：（2， 6）；（3）设点 P 的坐标为（ x，﹣ x2+3x+4），当 P， N， B， Q构成平行四边形时，∵平行四边形 ABOC中，点 A、 C的坐标分别是（ 0， 4）、（﹣ 1， 0），∴点 B 的坐标为（ 1， 4），∵点 Q坐标为（ 1， 0）， P 为抛物线上一动点， N为 x 轴上的一动点，①当 BQ为边时， PN∥ BQ， PN=BQ，∵BQ=4，∴﹣ x2+3x+4= ± 4，当﹣ x2+3x+4=4 时，解得： x1=0， x2=3，∴P1（ 0， 4）， P2（ 3，4）；2 ﹣ 4 时，解得： x = ， x = ，当﹣ x +3x+4=3 2∴P3（，﹣ 4）， P4（，﹣ 4）；②当 PQ为对角线时， BP∥ QN， BP=QN，此时 P 与 P ， P 重合；1 2综上可得：点P 的坐标为： P1（ 0， 4）， P2（ 3，4）， P3（，﹣ 4）， P4（，﹣4）；如图 2，当这个平行四边形为矩形时，点N的坐标为：（0， 0）或（ 3， 0）．13、解：（ 1）由题意解得，∴抛物线分析式为y=x2﹣ x+2．（2）∵ y= x2﹣ x+2= （ x﹣1）2+ ．∴极点坐标（1，），∵直线 BC为 y=﹣ x+4，∴对称轴与BC的交点 H（ 1， 3），∴S△BDC=S△BDH+S△DHC=?3+?1=3．（3）由消去y获得x2﹣x+4﹣2b=0，当△ =0 时，直线与抛物线相切，1﹣ 4（ 4﹣2b） =0，∴b= ，当直线 y=﹣x+b 经过点 C 时， b=3，当直线 y=﹣x+b 经过点 B 时， b=5，∵直线 y=﹣x 向上平移 b 个单位所得的直线与抛物线段BDC（包含端点B、C）部分有两个交点，∴＜b≤ 3．[ 根源 : ZXXK]14、解：（ 1）∵二次函数y=x2+bx+c 的图象与 x 轴交于 A（ 3， 0）， B（﹣ 1， 0），∴，解得：，∴y= x2﹣ x﹣ 4；（2）过点 D 作 DM⊥ y 轴于点 M，∵y= x2﹣x﹣ 4=（x﹣1）2﹣，∴点 D（ 1，﹣）、点C（0，﹣4），则S△ACD=S 梯形AOMD﹣ S△CDM﹣ S△AOC= ×（ 1+3）×﹣×（﹣4）× 1﹣× 3× 4=4；（3）四边形APEQ为菱形， E 点坐标为（﹣，﹣）．原因以下如图 2， E 点对于 PQ与 A 点对称，过点Q作， QF⊥ AP于 F，∵A P=AQ=t， AP=EP， AQ=EQ∴A P=AQ=QE=EP，∴四边形 AQEP为菱形，∵FQ∥ OC，∴== ，∴==∴AF= t ， FQ= t ?∴Q（ 3﹣t ，﹣t ），∵E Q=AP=t，∴E（ 3﹣t ﹣ t ，﹣t ），∵E 在二次函数y= x2﹣x﹣ 4 上，∴﹣t=（3﹣t ）2﹣（3﹣t ）﹣ 4，∴t=，或t=0（与A重合，舍去），∴E（﹣，﹣）．15、解：（ 1）∵四边形ABCD是矩形， B（ 10， 8），∴A（ 10， 0），又抛物线经过A、 E、 O三点，把点的坐标代入抛物线分析式可得，解得，∴抛物线的分析式为y=﹣x2+x；（2）由题意可知： AD=DE，BE=10﹣ 6=4， AB=8，设AD=x，则 ED=x， BD=AB﹣ AD=8﹣ x，在 Rt △ BDE中，由勾股定理可知2 2 2 2 2 2，解得 x=5，ED=EB+BD，即 x =4 +（ 8﹣ x）∴AD=5；（3）∵ y=﹣∴其对称轴为x2+x=5，x，∵A、 O两点对于对称轴对称，∴PA=PO，当P、 O、 D 三点在一条直线上时， PA+PD=PO+PD=OD，此时△ PAD的周长最小，如图，连结 OD交对称轴于点 P，则该点即为知足条件的点 P，由（ 2）可知 D点的坐标为（10， 5），设直线 OD分析式为y=kx ，把 D 点坐标代入可得5=10k，解得 k=，∴直线 OD分析式为y= x，令x=5，可得 y= ，∴P 点坐标为（ 5，）．16、解：（ 1）∵抛物线的对称轴x=1， B（3， 0），∴A（﹣ 1， 0）∵抛物线y=ax 2+bx+c 过点 C（ 0，3）∴当 x=0 时， c=3．又∵抛物线y=ax 2+bx+c 过点 A（﹣ 1， 0）， B（ 3， 0）∴，∴∴抛物线的分析式为：y=﹣x2+2x+3；（2）∵C（0，3），B（3，0），∴直线BC分析式为y= ﹣x+3，∵y= ﹣ x2+2x+3=﹣（ x﹣ 1）2+4，∴极点坐标为（ 1， 4）∵对于直线BC：y=﹣ x+1，当 x=1 时， y=2；将抛物线L 向下平移h 个单位长度， [ 根源 : 学 * 科*网 ]∴当 h=2 时，抛物线极点落在BC上；当 h=4 时，抛物线极点落在OB上，∴将抛物线L 向下平移h 个单位长度，使平移后所得抛物线的极点落在△的界限），OBC内（包含△OBC则 2≤ h≤ 4；（3）设 P（ m，﹣ m2+2m+3）， Q（﹣ 3， n），①当 P 点在 x 轴上方时，过 P 点作 PM垂直于 y 轴，交 y 轴与 M点，过 B 点作 BN垂直于 MP 的延伸线于 N 点，以下图：∵B（ 3， 0），∵△ PBQ是以点 P 为直角极点的等腰直角三角形，∴∠ BPQ=90°， BP=PQ，则∠ PMQ=∠ BNP=90°，∠ MPQ=∠ NBP，在△ PQM和△ BPN中，，∴△ PQM≌△ BPN（ AAS），∴PM=BN，∵PM=BN=﹣ m2+2m+3，依据 B 点坐标可得PN=3﹣m，且 PM+PN=6，重庆市合川区第一中学2020年中考九年级数学典型压轴题专练：二次函数(包含答案)2∴﹣ m+2m+3+3﹣ m=6，解得： m=1或 m=0，∴P（ 1， 4）或 P（ 0， 3）．②当 P 点在 x 轴下方时，过 P 点作 PM垂直于 l 于 M点，过 B 点作 BN垂直于 MP的延伸线与N 点，同理可得△ PQM≌△ BPN，∴PM=BN，2∴PM=6﹣（ 3﹣m） =3+m， BN=m﹣2m﹣ 3，2则 3+m=m﹣ 2m﹣ 3，解得 m=或．∴P（，）或（，）．综上可得，切合条件的点P 的坐标是（ 1，4），（ 0，3），（，）和（，）．。

中考数学复习《二次函数》专题训练-附带有参考答案

中考数学复习《二次函数》专题训练-附带有参考答案一、选择题1．下列函数中，是二次函数的是（）A．y=x2+1x B．y=12x(x-1) C．y=-2x-1 D．y=x(x2+1)．2．抛物线y=(x−2)2−3的顶点坐标是（）A．(2，−3)B．(−2，3)C．(2，3)D．(−2，−3)3．把抛物线y=5x2向左平移2个单位，再向上平移3个单位，得到的抛物线是（）A．y=5(x−2)2+3B．y=5(x+2)2−3C．y=5(x+2)2+3D．y=5(x−2)2−34．函数y＝ax2与y＝﹣ax+b的图象可能是（）A． B． C． D．5．函数y=kx2-6x+3的图象与x轴有交点，则k的取值范围是（）A．k<3 B．k<3且k≠0 C．k≤3且k≠0 D．k≤36．若A（−5，y1），B（1，y2），C（2，y3）为二次函数y=x2+2x+m的图象上的三点，则y1，y2，y3的大小关系是（）A．y1<y2<y3B．y2<y3<y1C．y2<y1<y3D．y3<y1<y27．二次函数y＝ax2+bx+c的图象如图所示，对称轴是直线x＝1．下列结论：①b＞0；②当x＞0，y随着x 的增大而增大；③（a+c）2﹣b2＜0；④a+b≥m（am+b）（m为实数）．其中结论正确的个数为（）A．4个B．3个C．2个D．1个8．某服装店购进单价为15元的童装若干件，销售一段时间后发现：当销售价为25元时，平均每天能售出8件，而当销售价每降低2元时，平均每天能多售出4件，为使该服装店平均每天的销售利润最大，则每件的定价为（）A．21元B．22元C．23元D．24元二、填空题9．将二次函数y＝x2－2x化为y＝(x－h)2＋k的形式，结果为10．若抛物线y＝ax2＋bx＋c与x轴的两个交点坐标是（－1，0），（3，0），则此抛物线的对称轴是直线．11．将二次函数y＝x2﹣4x+a的图象向左平移1个单位，再向上平移1个单位，若得到的函数图象与直线y＝2有两个交点，则a的取值范围是.12．飞机着陆后滑行的距离y （单位：m）关于滑行时间t （单位：s）的函数解析式是y=60t-65t2，从飞机着陆至停下来共滑行米．13．已知如图：抛物线y=ax2+bx+c与直线y=kx+n相交于点A(−52，74)、B(0，3)两点，则关于x的不等式ax2+bx+c＜kx+n的解集是三、解答题14．如图，在平面直角坐标系中，一次函数y1=kx−7的图象与二次函数y2=2x2+bx+c的图象交于A(1，−5)、B(3，t)两点.（1）求y1与y2的函数关系式；（2）直接写出当y1<y2时，x的取值范围；（3）点C为一次函数y1图象上一点，点C的横坐标为n，若将点C向右平移2个单位，再向上平移4个单位后刚好落在二次函数y2的图象上，求n的值.15．某品牌服装公司新设计了一款服装，其成本价为60（元/件）.在大规模上市前，为了摸清款式受欢迎状况以及日销售量y（件）与销售价格x（元/件）之间的关系，进行了市场调查，部分信息如表：销售价格x（元/件）80 90 100 110日销售量y（件）240 220 200 180（1）若y与x之间满足一次函数关系，请直接写出函数的解析式（不用写自变量x的取值范围）；（2）若该公司想每天获利8000元，并尽可能让利给顾客，则应如何定价？（3）为了帮助贫困山区的小朋友，公司决定每卖出一件服装向希望小学捐款10元，该公司应该如何定价，才能使每天获利最大？（利润用w表示）16．如图，抛物线y=−x2+bx+c与x轴交于A，B两点（A在B的左侧），与y轴交于点N，过A点的直线：l：y=−x−1与y轴交于点C，与抛物线y=−x2+bx+c的另一个交点为D(5，−6)，已知P点为抛物线y=−x2+bx+c上一动．点（不与A、D重合）．（1）求抛物线的解析式；（2）当点P在直线l上方的抛物线上时，过P点作PE∥x轴交直线l于点E，作PF∥y轴交直线l于点F，求PE+PF的最大值；（3）设M为直线l上的动点，以NC为一边且顶点为N，C，M，P的四边形是平行四边形，直接写出所有符合条件的M点坐标．17．如图是北京冬奥会举办前张家口某小型跳台滑雪训练场的横截面示意图，取某一位置的水平线为x轴，过跳台终点作水平线的垂线为y轴，建立平面直角坐标系，图中的抛物线C1：y=−18x2+32x+32近似表示滑雪场地上的一座小山坡，某滑雪爱好者小张从点O正上方A点滑出，滑出后沿一段抛物线C2：y=−14x2+bx+c 运动．（1）当小张滑到离A处的水平距离为8米时，其滑行高度为10米，求出b，c的值；（2）在(1)的条件下，当小张滑出后离的水平距离为多少米时，他滑行高度与小山坡的竖直距离为是5米？2（3）若小张滑行到坡顶正上方，且与坡顶距离不低于4米，求b的取值范围．18．如图，在平面直角坐标系中，抛物线y=ax2+bx−4与x轴交于A(4，0)、B(−3，0)两点，与y轴交于点C．（1）求这条抛物线所对应的函数表达式．（2）如图①，点D是x轴下方抛物线上的动点，且不与点C重合．设点D的横坐标为m，以O、A、C、D 为顶点的四边形面积为S，求S与m之间的函数关系式．（3）如图②，连结BC，点M为线段AB上一点，点N为线段BC上一点，且BM=CN=n，直接写出当n为何值时△BMN为等腰三角形．参考答案 1．B 2．A 3．C 4．B 5．D 6．B 7．B 8．B9．y =(x −1)2−1 10．x ＝1 11．a ＜5 12．75013．x <−52或x >014．（1）解：把点A(1，−5)代入y 1=kx −7得−5=k −7 ∴y 1=2x −7；把点B(3，t)代入y 1=2x −7中，得t =−1 ∴A(1，−5)把点A 、B 分别代入y 2=2x 2+bx +c 中，得{−2=2+b +c−1=18+3b +c 解得{b =−6c =−1∴y 2=2x 2−6x −1；（2）x <1或x >3（3）解：∵点C 为一次函数y 1图象上一点，∴C(n ，2n −7)将点C 向右平移2个单位，再向上平移4个单位后得到点C ′(n +2，2n −3) 把C ′代入y 2=2x 2−6x −1，得2n −3=2(n +2)2−6(n +2)−1 解得n =±1 所以n 的值为1或-1 15．（1）y=-2x+400（2）解：由题意，得：(x −60)(−2x +400)=8000解得x 1=100，x 2=160 ∵公司尽可能多让利给顾客 ∴应定价100元（3）解：由题意，得w =(x −60−10)(−2x +400)=−2x 2+540x −28000 =−2(x −135)2+8450∵−2<0∴当x =135时，w 有最大值，最大值为8450. 答：当一件衣服定为135元时，才能使每天获利最大. 16．（1）解：∵直线l ：y =−x −1过点A∴A(−1，0)又∵D(5，−6)将点A ，D 的坐标代入抛物线表达式可得：{−1−b +c =0−25+5b +c =−6 解得{b =3c =4．∴抛物线的解析式为：y =−x 2+3x +4．（2）解：如图设点P(x ，−x 2+3x +4) ∵PE ∥x 轴，PF ∥y 轴则E(x 2−3x −5，−x 2+3x +4)，F(x ，−x −1) ∵点P 在直线l 上方的抛物线上∴−1<x <5∴PE =|x −(x 2−3x −5)|=−x 2+4x +5，PF =|−x 2+3x +4−(−x −1)|=−x 2+4x +5 ∴PE +PF =2(−x 2+4x +5)=−2(x −2)2+18． ∴当x =2时，PE +PF 取得最大值，最大值为18．（3）符合条件的M 点有三个：M 1(4，−5)，M 2(2+√14，−3−√14)， M 3(2−√14，−3+√14)． 17．（1）解：由题意可知抛物线C 2：y=−14x 2+bx+c 过点(0， 4)和(8， 10) 将其代入得：{4=c10=−14×82+8b +c解得 ∴b=114，c=4（2）解：由(1)可得抛物线Cq 解析式为： y=−14x 2+114x+4设运动员运动的水平距离为m 米时，运动员与小山坡的竖直距离为52米，依题意得： −14m 2+114m +4−(−18m 2+32m +32)=52解得： m 1=10，m 2=0(舍)故运动员运动的水平距离为10米时，运动员与小山坡的竖直距离为为52米．（3）解：∵抛物线C 2经过点(0， 4) ∴c=4抛物线C 1： y=−18x 2+32x +32=−18(x −6)2+6 当x=6时，运动员到达坡项即−14×62+6b+4≥4+6． ∴b ≥15618．（1）解：把A(4，0)、B(−3，0)代入y =ax 2+bx −4中得{16a +4b −4=09a −3b −4=0解得{a =13b =−13∴这条抛物线所对应的函数表达式为y =13x 2−13x −4．（2）解：当x =0时y =−4∴C(0，−4)当−3<m <0时S =S △ODC +S △OAC =12×4×(−m)+12×4×4=−2m +8当0<m <4时S =S △ODC +S △OAD =12×4×m +12×4×(−13m 2+13m +4)=−23m 2+83m +8．（3）解：n =52，n =2511，n =3011．。

重庆中考二次函数相关的最值问题(含答案)

二次函数相关的最值问题例1. 如图，抛物线y＝－x2－4x＋5与x轴交于点A、B，与y轴交于点C，点D为抛物线的顶点．(1)求直线AC的解析式及顶点D的坐标；(2)若Q为抛物线对称轴上一动点，连接QA、QC，求|QA－QC|的最大值及此时点Q的坐标；(3)连接CD，点P是直线AC上方抛物线上一动点(不与点A、C重合)，过P作PE∥x轴交直线AC于点E，作PF∥CD交直线AC于点F，当线段PE＋PF取最大值时，求点P的坐标及线段EF的长；(4)在(3)问的条件下，将P 向下平移34个单位得到点H ，在抛物线对称轴上找一点L ，在y 轴上找一点K ，连接OL ，LK ，KH ，求线段OL ＋LK ＋KH 的最小值，并求出此时点L(5)在(3)问的条件下，将线段PE 沿着直线AC 的方向平移得到线段P′E′，连接DP′，BE ′，求DP′＋P′E′＋E′B 取最小值时点E′的坐标．针对训练1．如图，直线y＝kx＋b(k、b为常数)分别与x轴、y轴交于点A(－4，0)、B(0，3)，抛物线y＝－x2＋2x＋1与y轴交于点C.(1)求直线y＝kx＋b的解析式；(2)若点P(x，y)是抛物线y＝－x2＋2x＋1上的任意一点，设点P到直线AB的距离为d，求d关于x 的函数解析式，并求d取最小值时点P的坐标；(3)若点E在抛物线y＝－x2＋2x＋1的对称轴上移动，点F在直线AB上移动，求CE＋EF的最小值．2．如图①，已知抛物线y＝－33x2＋2 33x＋3与x轴交于A，B两点(点A在点B的左侧)，与y轴交于点C，点D是点C关于抛物线对称轴的对称点，连接CD，过点D作DH⊥x轴于点H，过点A作AE⊥AC 交DH的延长线于点E.(1)求线段DE的长度；(2)如图②，试在线段AE上找一点F，在线段DE上找一点P，且点M为线段PF上方抛物线上的一点，求当△CPF的周长最小时，△MPF面积的最大值是多少．3．如图，对称轴为直线x＝2的抛物线经过A(－1，0)，C(0，5)两点，与x轴另一交点为B.已知M(0，1)，E(a，0)，F(a＋1，0)，点P是第一象限内的抛物线上的动点．(1)求此抛物线的解析式；(2)若△PCM是以点P为顶点的等腰三角形，求a为何值时，四边形PMEF周长最小？说明理由．4．已知，如图，二次函数y＝ax2＋2ax－3a(a≠0)图象的顶点为H，与x轴交于A、B两点(B点在A点右侧)，点H，B关于直线l：y＝33x＋3对称．(1)求A、B两点坐标，并证明点A在直线l上；(2)求二次函数的解析式；(3)过点B作直线BK∥AH交直线l于点K，M、N分别为直线AH和直线l上的两个动点，连接HN、NM、MK，求HN＋NM＋MK和的最小值．5．如图，在平面直角坐标系中，抛物线y ＝－12x 2＋2x ＋3与x 轴交于A ，B 两点(点A 在点B 左侧)，与y 轴交于点C ，连接BC ，过点A 作AD∥BC 交y 轴于点D.(1)求平行线AD 、BC 之间的距离；(2)点P 为线段BC 上方抛物线上的一动点，当△PCB 的面积最大时，Q 从点P 出发，先沿适当的路径运动到直线BC 上点M 处，再沿垂直于直线BC 的方向运动到直线AD 上的点N 处，最后沿适当的路径运动到点B 处停止．当点Q 的运动路径最短时，求点Q 经过的最短路径的长．6．如图，抛物线y＝－34x2－94x＋3 3交x轴于A、B两点，交y轴于点C，点Q为顶点，点D为点C关于对称轴的对称点．(1)求点D的坐标和tan∠ABC的值；(2)若点P是抛物线上位于点B、D之间的一个动点(不与B、D重合)，在直线BC上有一动点E，在x 轴上有一动点F.当四边形ABPD的面积最大时，一动点G从点P出发以每秒1个单位的速度沿P→E→F的路径运动到点F，再沿线段FA以每秒2个单位的速度运动到A点后停止，当点F的坐标是多少时，动点G 在运动过程中所用时间最少？二次函数相关的最值问题答案例1. 解：(1)∵y ＝－x 2－4x ＋5＝－(x 2＋4x )＋5＝－(x ＋2)2＋9，∴D (－2，9)．当x ＝0时，y ＝5，∴C (0，5)．当y ＝0时，x 1＝1，x 2＝－5，∴A (－5，0)，B (1，0)，∴y AC ＝x ＋5；(2)因为点Q 在抛物线对称轴上，由抛物线对称性知QA ＝QB ，由C (0，5)和B (1，0)可求得y BC ＝－5x ＋5，根据三角形三边关系可知，当点Q ，C ，B 三点共线时，|QB －QC |最大，即|QA －QC |最大，可求直线y BC ＝－5x ＋5与抛物线对称轴交点Q 为(－2，15)，此时|QA －QC |最大值＝BC ＝26.解：(3)过P 作PQ ∥y 轴，交AC 于Q ，再作FM ⊥PQ 于M ，如图①，直线AC ：y ＝x ＋5，设P (t ，－t 2－4t ＋5)，Q (t ，t ＋5)，∴PQ ＝(－t 2－4t ＋5)－(t ＋5)＝－t 2－5t .∵∠PEF ＝∠CAO ＝45°，∴PE ＝PQ ＝－t 2－5t ，∵PF ∥CD ，∴k CD ＝－2＝k PF ，∴tan ∠MPF ＝12，设FM ＝n ＝MQ ，则PM ＝2n ，PQ ＝3n ，PF ＝5n ，即PF ＝53PQ ，∴PE ＋PF ＝(3＋5)n ＝(1＋53)PQ ， ∴当PQ 最大时，PE ＋PF 取最大值，而PQ ＝－t 2－5t ＝PE ＝－⎝ ⎛⎭⎪⎫t ＋522＋254，当t ＝－52时，PE ＋PF 取最大值，此时P ⎝ ⎛⎭⎪⎫－52，354，EF ＝2PM ＝25 26. (4)如图②：在(3)问的条件下，P ⎝ ⎛⎭⎪⎫－52，354， ∴H ⎝ ⎛⎭⎪⎫－52，8，作H 关于y 轴的对称点H 1，作O 关于抛物线对称轴对称点O 1，所以O 1(－4，0)，H 1⎝ ⎛⎭⎪⎫52，8，连接O 1H 1，则O 1H 1长即为OL ＋LK ＋KH 的最小值，直线O 1H 1：y ＝1613x ＋6413， ∴直线O 1H 1与抛物线对称轴交点即为L 点的位置，此时L ⎝⎛⎪⎫－2，3213OL ＋LK ＋KH 的最小值＝O1H 1＝5217；(5)在(3)问的条件下，P ′E ′＝PE 25在线段PE 平移过程中，PE 即P′E′长度不变，将DP′沿P′E′向右平移PE 的长即254个单位，得到D′E′，如图③，则四边形D′DP′E′为平行四边形，故DP′＝D′E′，要使得DP′＋P′E′＋E′B 最小，即DP′＋E′B 最小，即要使D′E′＋E′B 最小，当D′，E ′，B 三点共线时，D ′E ′＋E′B 最小，设D′B 与直线AC 交于点E″.由题意知D′⎝ ⎛⎭⎪⎫174，9，直线BD′：y ＝3613x －3613， ∴E ″⎝ ⎛⎭⎪⎫10123，21623，即点E ′的坐标为(10123，21623)．针对训练：1. 解：(1)∵直线y ＝kx ＋b 经过A (－4，0)、B (0，3)，∴⎩⎪⎨⎪⎧－4k ＋b ＝0，b ＝3，解得⎩⎪⎨⎪⎧k ＝34，b ＝3.∴y ＝34x ＋3.(2)过点P 作PH ⊥AB 于点H ，过点H 作x 轴的平行线MN ，分别过点A 、P 作MN 的垂线段，垂足分别为M 、N .设H (m ，34m ＋3)，则M (－4，34m ＋3)，N (x ，34m ＋3)，P (x ，－x 2＋2x ＋1)． ∵PH ⊥AB ，∴∠PHN ＋∠AHM ＝90°，∵AM ⊥MN ，∴∠MAH ＋∠AHM ＝90°.∴∠MAH ＝∠PHN ，∵∠AMH ＝∠PNH ＝90°，∴△AMH ∽△HNP .∵MA ∥y 轴，∴△MAH ∽△OBA .∴△OBA ∽△NHP .∴NH 3＝PN 4＝PH 5. ∴x －m 3＝（34m ＋3）－（－x 2＋2x ＋1）4＝d 5. 整理得：d ＝45x 2－x ＋85，所以当x ＝58时，d 取最小值，此时P (58，11964)．(3)抛物线的对称轴为直线x ＝1，作点C 关于直线x ＝1的对称点C ′，过点C ′作C ′F ⊥AB 于F .过点F 作JK ∥x 轴，分别过点A 、C ′作AJ ⊥JK 于点J ，C ′K ⊥JK 于点K ，则C ′(2，1)．设F (m ，34m ＋3)， ∵C ′F ⊥AB ，∴∠AFJ ＋∠C ′FK ＝90°，∵C ′K ⊥JK ，∴∠C ′＋∠C ′FK ＝90°，∴∠C ′＝∠AFJ ，∵∠J ＝∠K ＝90°，∴△AFJ ∽△FC ′K .∴AJ FK ＝JF C ′K ，∴34m ＋32－m ＝m ＋434m ＋2，解得m ＝825或m ＝－4(不符合题意，舍去)∴F (825，8125)，∵C ′(2，1)，∴FC ′＝145. 142. 解：(1)对于抛物线y ＝－33x 2＋2 33x ＋3，令x ＝0，得y ＝3，即C (0，3)，D (2，3)，∴DH ＝3，令y ＝0，即－33x 2＋2 33x ＋3＝0，得x 1＝－1，x 2＝3， ∴A (－1，0)，B (3，0)，∵AE ⊥AC ，EH ⊥AH ，∴△ACO ∽△EAH ，∴OC AH ＝OA EH ，即33＝1EH ，解得：EH ＝3，则DE ＝2 3；(2)如图②，找点C 关于DE 的对称点N (4，3)，找点C 关于AE 的对称点G (－2，－3)，连接GN ，交AE 于点F ，交DE 于点P ，即G 、F 、P 、N 四点共线时，△CPF 的周长＝CF ＋PF ＋CP ＝GF ＋PF ＋PN 最小，直线GN 的解析式：y ＝33x －33；直线AE 的解析式：y ＝－33x －33；直线DE 的解析式：x ＝2.联立得：F (0，－33)，P (2，33)，过点M 作y 轴的平行线交FH 于点Q ，设点M (m ，－33m 2＋2 33m ＋3)，则Q (m ，33m －33)(0≤m ≤2)； ∴S △MFP ＝S △MQF ＋S △MQP ＝12MQ ×2＝MQ ＝－33m 2＋33m ＋4 33， ∵对称轴为直线m ＝12，而0≤12≤2，抛物线开口向下， ∴m ＝12时，△MPF 的面积有最大值，为17 312.3. 解：(1)∵对称轴为直线x ＝2，∴设抛物线解析式为y ＝m ′(x －2)2＋k .将A (－1，0)，C (0，5)代入得：⎩⎪⎨⎪⎧9m ′＋k ＝0，4m ′＋k ＝5，解得⎩⎪⎨⎪⎧m ′＝－1，k ＝9，∴y ＝－(x －2)2＋9＝－x 2＋4x ＋5.(2)∵M (0，1)，C (0，5)，△PCM 是以点P 为顶点的等腰三角形，∴点P 的纵坐标为3.令y ＝－x 2＋4x ＋5＝3，解得x ＝2±6.∵点P 在第一象限，∴P (2＋6，3)．四边形PMEF 的四条边中，PM 、EF 长度固定，因此只要ME ＋PF 最小，则四边形PMEF 的周长最小．如图，将点M 向右平移1个单位长度(EF 的长度)，得M 1(1，1)；作点M 1关于x 轴的对称点M 2，则M 2(1，－1)；连接PM 2，与x 轴交于F 点，此时ME ＋PF ＝PM 2最小．设直线PM 2的解析式为y ＝mx ＋n ，将P (2＋6，3)，M 2(1，－1)代入得：⎩⎨⎧（2＋6）m ＋n ＝3，m ＋n ＝－1，解得：m ＝4 6－45，n ＝－4 6＋15， ∴y ＝4 6－45x －4 6＋15. 当y ＝0时，解得x ＝6＋54.∴F (6＋54，0)． ∵a ＋1＝6＋54，∴a ＝6＋14.∴a ＝6＋14时，四边形PMEF 周长最小．4. 解：(1)依题意，得ax 2＋2ax －3a ＝0(a ≠0)，解得x 1＝－3，x 2＝1，∵B 点在A 点右侧，∴A 点坐标为(－3，0)，B 点坐标为(1，0)，证明：∵直线l ：y ＝33x ＋3，当x ＝－3时，y ＝33×(－3)＋3＝0，∴点A 在直线l 上．(2)过顶点H 作HC ⊥AB 交AB 于C 点，∵点H 、B 关于过A 点的直线l ：y ＝33x ＋3对称，∴AH ＝AB ＝4，又∵点H 为抛物线顶点，则点H 在抛物线对称轴上，∴AH ＝BH ＝AB ＝4.在Rt △ACH 中，由勾股定理得CH ＝AH 2－AC 2＝2 3，∴顶点H (－1，2 3)，代入二次函数解析式，解得a ＝－32，∴二次函数解析式为y ＝－32x 2－3x ＋3 32.(3)直线AH 的解析式为y ＝3x ＋3 3，直线BK 的解析式为y ＝3x －3，由⎩⎪⎨⎪⎧y ＝33x ＋3，y ＝3x －3，解得⎩⎨⎧x ＝3，y ＝2 3，即K (3，2 3)，则BK ＝4，∵点H 、B 关于直线AK 对称，∴HN ＋MN 的最小值是MB ，过点K 作KD ⊥x 轴于D ，作点K 关于直线AH 的对称点Q ，连接QK ，交直线AH 于E ，则KE ＝KD ＝2 3，QM ＝MK ，QE ＝EK ＝2 3，AE ⊥QK ，∴BM ＋MK 的最小值是BQ ，即BQ 的长是HN ＋NM ＋MK 的最小值，∵BK ∥AH ，∴∠BKQ ＝∠HEQ ＝90°，由勾股定理得QB ＝8，∴HN ＋NM ＋MK 的最小值为8.5. 解：(1)令y ＝0，即－12x 2＋2x ＋3＝0，解得：x 1＝－2，x 2＝3 2，∴A (－2，0)，B (3 2，0)，∵当x ＝0时，y ＝3，∴C (0，3)，在Rt △BOC 中，BO ＝3 2，CO ＝3，∴BC ＝3 3，∴sin ∠CBO ＝CO BC ＝33. 因为AD ∥BC ，∴sin ∠BAD ＝sin ∠CBO ＝33. 过B 作BH ⊥AD 于点H ，∴sin ∠BAD ＝BH AB ＝33，∴BH ＝4 63； ∴平行线AD 、BC 间的距离为43 6. (2)过P 作PQ ∥y 轴，交BC 于点Q ，设P (m ，－12m 2＋2m ＋3)，∵直线BC ：y ＝－22x ＋3，∴Q (m ，－22m ＋3)， ∴S △PCB ＝12·PQ ·(x B －x C )＝3 22(－12m 2＋3 22m )，当m ＝3 22时，S △CPB 最大，此时，P (3 22，154)．取点B 关于AD 的对称点B ′，将B ′沿B ′B 方向平移4 63个单位长度得B ′′，此时B ′′与点H (5 23，－83)重合．连接HP ，交BC 于点M ，点M 即为所求．∴(PM ＋NM ＋BN )最小＝PH ＋MN ＝593712＋4 63.6. 解：(1)令－34x 2－94x ＋3 3＝0，解得x 1＝－4 3，x 2＝3，∴A (－4 3，0)，B (3，0)，在y ＝－34x 2－94x ＋3 3中，令x ＝0，则y ＝3 3， ∴C (0，3 3)，∴OC ＝3 3，BO ＝3，在Rt △COB 中，∴tan ∠ABC ＝OC OB＝3，由y ＝－34x 2－94x ＋3 3知，对称轴直线为x ＝－3 32，∴点D (－3 3，3 3)；(2)由B (3，0)，D (－3 3，3 3)可得直线BD 解析式：y ＝－34x ＋3 34，过P 作PK ⊥x 轴交BD 于点K ，设P (m ，－34m 2－94m ＋3 3)，则K (m ，－34m ＋3 34)， S 四边形ABPD ＝S △ABD ＋S △PBD ，S △ABD 是定值，∴S 四边形ABPD 最大时，即S △PBD 最大． S △PBD ＝12(x B －x D )(y P －y K )＝－32m 2－3 3m ＋272，当m ＝－b 2a ＝－3时，S △PBD 最大，此时点P 坐标为(－3，9 32)．作点P (－3，9 32)关于直线BC 的对称点P ′(－310，24 35)，以A 为顶点，在x 轴下方作∠BAT ＝30°，过P ′作直线AT 的垂线分别交BC 、x 轴于点E 、F ，此时，点G 在运动过程中所用时间最少，3 10－245，0)．点F坐标为(－。

2024重庆中考复习第25题-二次函数综合题

2024重庆中考复习第25题-二次函数综合题2024年重庆中考复习第25题为一道关于二次函数的综合题。

由于题目没有具体给出，我将为您提供一道关于二次函数的综合题，并给出一个详细的解答，希望能对您的复习有所帮助。

题目：已知函数f(x) = ax^2 + bx + c，其中a、b、c均为实数，且a ≠ 0。

已知f(1) = 0，f(3) = 0，f(4) = 6、求函数f(x)的表达式。

解答：根据题目已知条件，我们可以列出以下方程组：1)f(1)=0：a(1)^2+b(1)+c=0a+b+c=0--(1)2)f(3)=0：a(3)^2+b(3)+c=09a+3b+c=0--(2)3)f(4)=6：a(4)^2+b(4)+c=616a+4b+c=6--(3)现在我们有一个包含三个未知数（a，b，c）的方程组。

我们可以通过解这个方程组来求出函数f(x)的表达式。

首先，我们可以通过方程(1)和方程(2)的消元法得到一个新的方程。

(2)-(1)得：9a+3b+c-(a+b+c)=08a+2b=04a+b=0--(4)然后，我们可以通过方程(4)和方程(3)的消元法得到另一个新的方程。

(4)×4得：16a+4b=0将这个方程代入到方程(3)中，得到：16a+4b+c=6将16a+4b=0代入到上式，得到：c=6现在我们已经得到了a、b和c的值。

将这些值代入到函数f(x) =ax^2 + bx + c中，即可得到函数f(x)的表达式。

将a=-1、b=4和c=6代入到函数f(x)中，得到：f(x)=-x^2+4x+6所以，函数f(x)的表达式为f(x)=-x^2+4x+6以上就是针对2024年重庆中考复习第25题的一道关于二次函数的综合题的解答。

希望能对您的复习有所帮助。

如果您有任何其他问题，请随时提问。

重庆中考数学25题二次函数专项训练：平行四边形的存在性

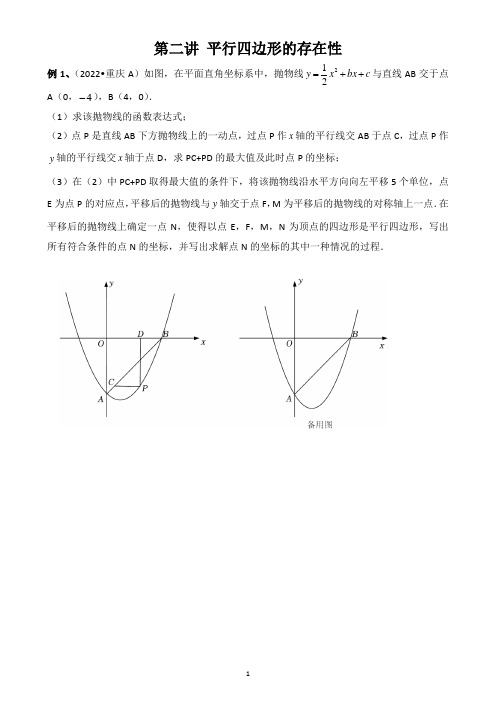
第二讲平行四边形的存在性例1、（2022•重庆A ）如图，在平面直角坐标系中，抛物线c bx x y ++=221与直线AB 交于点A （0，4-），B （4，0）．（1）求该抛物线的函数表达式；（2）点P 是直线AB 下方抛物线上的一动点，过点P 作x 轴的平行线交AB 于点C ，过点P 作y 轴的平行线交x 轴于点D ，求PC+PD 的最大值及此时点P 的坐标；（3）在（2）中PC+PD 取得最大值的条件下，将该抛物线沿水平方向向左平移5个单位，点E 为点P 的对应点，平移后的抛物线与y 轴交于点F ，M 为平移后的抛物线的对称轴上一点．在平移后的抛物线上确定一点N ，使得以点E ，F ，M ，N 为顶点的四边形是平行四边形，写出所有符合条件的点N 的坐标，并写出求解点N 的坐标的其中一种情况的过程．练习1、（2022•重庆B ）如图，在平面直角坐标系中，抛物线c bx x y ++-=243与x 轴交于点A （4，0），与y 轴交于点B （0，3）．（1）求抛物线的函数表达式；（2）点P 为直线AB 上方抛物线上一动点，过点P 作PQ⊥x 轴于点Q ，交AB 于点M ，求PM+56AM 的最大值及此时点P 的坐标；（3）在（2）的条件下，点P′与点P 关于抛物线c bx x y ++-=243的对称轴对称．将抛物线c bx x y ++-=243向右平移，使新抛物线的对称轴l 经过点A ．点C 在新抛物线上，点D 在l 上，直接写出所有使得以点A 、P′、C 、D 为顶点的四边形是平行四边形的点D 的坐标，并把求其中一个点D 的坐标的过程写出来．练习2、如图1，抛物线)0(2≠++=a c bx ax y 与x 轴交于A （4-，0），B （1，0）两点，交y 轴于点C （0，3）．（1）求抛物线的解析式；（2）如图2，点P 为直线AC 上方且抛物线对称轴左侧的抛物线上一点，过点P 作x 轴的平行线交抛物线于点D ，过点P 作y 轴的平行线交AC 于点H ，求PD+PH 的最大值及此时点P 的坐标；（3）把抛物线)0(2≠++=a c bx ax y 向右平移23个单位，再向上平移165个单位得新抛物线，在新抛物线对称轴上找一点M ，在新抛物线上找一点N ，直接写出所有使得以点A ，C ，M ，N 为顶点的四边形是平行四边形的点M 的坐标，并把求其中一个点M 的坐标的过程写出来．练习3、（选讲）在平面直角坐标系中，抛物线)0(32≠++=a bx ax y 与x 轴的交点为A(1-，0)，B(3，0)，与y 轴交于点C ．（1）求抛物线的函数解析式；（2）如图1，连接AC ，BC ，P 是第一象限内抛物线上一动点，过点P 作PT ⊥x 轴交BC 于点T ，过点P 作PR//AC 与BC 交于点R ．求△PRT 的周长的最大值以及此时点P 的坐标；（3）如图2，将抛物线沿CA 方向平移，使得新抛物线'y 刚好经过点A ，设M 为新抛物线上一点，N 为原抛物线对称轴上一点，当点B ，C ，M ，N 组成的四边形为平行四边形时，直接写出点N 的纵坐标．自我巩固1、（2021•重庆B ）如图，在平面直角坐标系中，抛物线)0(42≠-+=a bx ax y 与x 轴交于点A （1-，0），B （4，0），与y 轴交于点C ．（1）求该抛物线的解析式；（2）直线l 为该抛物线的对称轴，点D 与点C 关于直线l 对称，点P 为直线AD 下方抛物线上一动点，连接PA ，PD ，求⊥PAD 面积的最大值．（3）在（2）的条件下，将抛物线)0(42≠-+=a bx ax y 沿射线AD 平移24个单位，得到新的抛物线1y ，点E 为点P 的对应点，点F 为1y 的对称轴上任意一点，在1y 上确定一点G ，使得以点D ，E ，F ，G 为顶点的四边形是平行四边形，写出所有符合条件的点G 的坐标，并任选其中一个点的坐标，写出求解过程．。

重庆中考二次函数的综合题22-40题

二次函数的综合题22、如图，抛物线y=21x 2+bx+c 与直线y=kx+m 交于A （4,2）B （0，-1）. ⑴ 求抛物线与直线的解析式；⑵ 设点C 为抛物线的顶点，求△ABC 的面积；⑶ 若点D 是直线l 下方抛物线上的一个动点，点D 的横坐标为m ，求△ABD 的最大面积及求此时点D 的坐标.23、已知抛物线y=-x 2+bx+c 过点A （4,0）、B （1,3），顶点为C. ⑴ 求该抛物线的解析式，并写出该抛物线的对称轴和顶点坐标； ⑵ 求△ABC 的面积；⑶ 记该抛物线的对称轴为直线l ，设抛物线上的点P （m ，n ）在第四象限，点P 关于直线l 对称的点为E ，点E 关于x 轴的对称点为点F ，若四边形OFAP 的面积为20，求点P 的坐标.24、如图，已知抛物线c bx ax y ++=2（a ≠0）经过A （-1，0），B （4，0），C （0，2）三点.⑴ 求这条抛物线的解析式；⑵ E 为抛物线上的动点，当以A 、B 、E 为顶点的三角形与△COB 相似时，求点E 的坐标； ⑶ 若将直线BC 平移，使其经过点A ，且与抛物线相交于点D ，连接BD ，求∠BDA 的度数.25、如图，抛物线322--=x x y 与x 轴交于点A 、B 两点（点A 在点B 的左边），与y 轴交于点C ，点D 是抛物线的顶点. ⑴ 求B 、C 、D 三点的坐标；⑵ 连接BC 、BD 、CD ，若点P 为抛物线上一动点，设点P 的横坐标为m ，当△B C D△P B CS S =时，求m 的值（点P 不与点D 重合）；⑶ 连接AC ，将△AOC 沿x 轴正方向平移，设移动距离为a ，当点A 和点B 重合时，停止运动，设运动过程中△AOC 与△BOC 重叠部分的面积为S ，请直接写出S 与a 之间的函数关系式，并写出相应的自变量a 的取值范围.26、如图⑴，抛物线52++=bx ax y （a ≠0）与x 轴交于A 、B 两点，与y 轴交于点C ，直线AC 的解析式为5+=x y ，抛物线的对称轴与x 轴交于点E ，点D （-2，-3）在对称轴上.⑴ 求抛物线的解析式；⑵ 如图⑴，若点M 是线段OE 上一点（点M 不与点O 、E 重合），过点M 作MN ⊥x 轴，交抛物线于点N ，记点N 关于抛物线的对称轴的对称点为点F ，点P 是线段MN 上一点，且满足MN=4MP ，连接FN 、FP ，作QP ⊥PF 交x 轴于点Q ，且满足PF=PQ ，求点Q 的坐标；⑶ 如图⑵，过点B 作BK ⊥x 轴交直线AC 于点K ，连接DK 、AD ，点H 是DK 的中点，点G 是线段AK 上任意一点，将△DGH 沿GH 翻折得△D ¹GH ，求当KG 为何值时，△D ¹GH 与△KGH 重叠部分的面积是△DGK 面积的41.图⑴ 图⑵备用图27、如图，二次函数y=ax 2+bx （a≠0）的图象经过点A （1，4），对称轴是直线x=-23 ，线段AD 平行于x 轴，交抛物线于点D ．在y 轴上取一点C （0，2），直线AC 交抛物线于点B ，连结OA ，OB ，OD ，BD ．（1）求该二次函数的解析式；（2）求点B 坐标和坐标平面内使△EOD ∽△AOB 的点E 的坐标；（3）设点F 是BD 的中点，点P 是线段DO 上的动点，问PD 为何值时，将△BPF 沿边PF 翻折，使△BPF 与△DPF 重叠部分的面积是△BDP 的面积的41？28、如图，二次函数c bx ax y ++=2的图象与x 轴交于A （-1，0）、B （3，0），与y 轴交于C （0，-3），顶点为D.连接BC 、BD 、AC 、CD.将△AOC 绕点O 逆时针旋转90°得△MOB.⑴ 求抛物线的解析式及直线BD 的解析式；⑵ ① 操作一：动点P 从点M 出发到x 轴上的点N ，又到抛物线的对称轴上的点Q ，再回到y 轴上的点C ，当四边形MNQC 的周长最小时，则四边形MNQC 的最小周长为，此时，tan ∠OMN=② 操作二：将△AOC 旋转过程中，A 的对应点1A ，点C 的对应点1C ，当 O 1A ⊥AC 时，求直线O 1C 与抛物线的交点的坐标；⑶ 将△BOM 沿y 轴的负半轴以每秒1个单位的速度平移，当BM 过点D 时停止平移，设平移的时间为t 秒，△BOM 与△BCD 的重叠部分的面积为S ，请直接写出S 与t 的函数关系式及相应的t 的取值范围29、如图⑴，抛物线52++=bx ax y （a ≠0）与x 轴交于A 、B 两点，与y 轴交于点C ，直线AC 的解析式为5+=x y ，抛物线的对称轴与x 轴交于点E ，点D （-2，-3）在对称轴上.（1）求此抛物线的解析式；（2）如图（1），若点M 是线段OE 上一点（点M 不与点O 、E 重合），过点M 作MN轴，交抛物线于点N ，记点N 关于抛物线对称轴的对称点为点F ，点P 是线段MN 上一点，且满足MN=4MP ，连接FN 、FP ，作QP PF 交轴于点Q ，且满足PF=PQ ，求点Q 的坐标；（3）如图（2），过点B 作BK轴交直线AC 于点K ，连接DK 、AD ，点H 是DK 的中点，点G 是线段AK 上任意一点，将DGH 沿GH 边翻折得，求当KG为何值时，与重叠部分的面积是DGK 面积的.30、已知如图，抛物线33122+--=x x y 与x 轴相交于点A 、B ，与y 轴相交于点C ，点D 为抛物线的顶点，抛物线的对称轴与x 轴相交于点E.⑴ 如图① 点F 是直线AC 上方抛物线上的一个动点，过点F 作FG ∥x 轴，交直线AC 与点G ，求线段FG 的最大值；⑵ 如图② 点P 为x 轴下方、对称轴左侧抛物线上的一点，连接PA ，以线段PA 为边作等腰直角三角形PAQ ，当点Q 在抛物线对称轴上时，求点P 的坐标；⑶ 如图③ 将线段AB 绕点A 顺时针旋转30°，与y 轴相交于点M ，连接BM.点S 是线段AM 的中点，连接OS ，得△OSM.若点N 是线段BM 上一动点，连接SN ，将△SMN 绕点S 逆时针旋转60°得到△SOT ，延长TO 交BM 于点K.若△KTM 的面积等于△ABM 的面积的121，求线段MN 的长.31、如图1，已知抛物线c bx x y ++=23经过点A （3，0），点B （-1，0），与y 轴负半轴交于点C ，连接BC 、AC ⑴ 求抛物线的解析式；⑵ 在抛物线上是否存在点P ，使得以A 、B 、C 、P 为顶点的四边形的面积等于△ABC 的面积的23倍？若存在，求出点P 的坐标；若不存在，请说明理由. ⑶ 如图2，直线BC 与抛物线的对称轴交于点K ，将直线AC 绕点C 按顺时针方向旋转°α，旋转中直线A ´C 与抛物线的另一个交点为M.求在旋转过程中△MCK 为等腰三角形时点M 的坐标.32、已知，抛物线33163310332+-=x x y 与x 轴交于点A 、B 两点，与y 轴交于点C.⑴ 设抛物线的顶点为P ，点M 为抛物线BP 之间的一动点，求四边形ABMP 面积的最大值； ⑵ 把△APB 翻折，使点P 落在线段AB 上（不与A 、B 重合），记作P ´,折痕为EF ，设 AP ´=x ，PE=y ，求y 关于x 的函数关系式，并写出自变量x 的取值范围；⑶ 当点P ´在线段AB 上运动但不与A 、B 重合时，能否使△BFP ´为直角三角形？若能，请求出此时点P ´的坐标；若不能，请你说明理由.33、如图，若二次函数363632--=x x y 的图象与x 轴交于点A 、B 两点，与直线x y 3=交于C 、D 两点，抛物线的顶点为E.⑴ 若点F 在y 轴正半轴上，且使得△AEF 的面积为235，求点F 的坐标； ⑵ 点M 为线段CD 上一点，过点M 作MN ∥x 轴，交抛物线对称轴右侧部分于点N ，当线段MN 的长度取得最大值时，求tan ∠MAB 的值⑶ 如图② 点G 在直线x y 3=上，其横坐标与B 点的横坐标相同.点A 关于直线x y 3=的对称点A ´（此时点A ´会落在抛物线上),连接AA ´，交直线x y 3=于点H ，连接AG 、A ´G.已知点P 在线段AG 上，点Q 在线段A ´G 上，且AP=2GQ ，连接PQ 、QH 、PH ，若将△APH 和△A ´QH 分别沿PH 、QH 翻折，恰好使得翻折后A 点和A ´点的对称点都落在直线PQ 上，求此时线段AP 的长.34、如图，抛物线42-+=bx ax y 与x 轴交于A 、B 两点，与y 轴交于点C ，对称轴是直线x=25，直线421-=x y 经过B 、C 两点. ⑴ 求抛物线的解析式；⑵ 若在对称轴右侧的抛物线上有一点P ，过点P 作PD ⊥直线BC ，垂足为D ，当∠PBD=∠ACO 时，求出点P 的坐标；⑶ 如图2，过点C 作CE ∥x 轴交抛物线于点E ，连接AE ，点F 是线段CE 上的动点，过点F 作FG ⊥x 轴，交AE 于H ，垂足为点G ，将△EFH 沿直线AE 翻折，得到△EMH ，连接GM.是否存在这样的点F ，使△GHM 是等腰三角形？若存在，求出对应的EF 的长度；若不存在，请说明理由35、已知抛物线c bx x y ++-=23与x 轴交于点A （1，0）、B （3，0），与y 轴相交于点C ，抛物线的顶点为D.⑴ 求b 、c 的值及顶点D 的坐标；⑵ 如图1，点E 是线段BC 上的一点，且BC=3BE ，点F （0，m ）是y 轴正半轴上一点，连接BF 、EF ，EF 交线段OB 于点G ，OF ：OG=2：3，求△FEB 的面积；⑶ 如图2，P 为线段BC 上一动点，连接DP ，将△DBP 绕点D 顺时针旋转60°得△DB ´P ´，（点B 的对应点是B ´，点P 的对应点是P ´），DP ´交y 轴于点M ，N 为MP ´的中点，连接PP ´、NO ，延长NO 交BC 于点Q ，连接QP ´，若△PP ´Q 的面积是△BOC 面积的91，求线段BP 的长.36、如图①所示，抛物线c bx ax y ++=2过A 、D 、C 三点，其中D （0，32）、C （6，32），已知CB ⊥AB ，AD ⊥DB ，点P 是边BC 上的动点（点P 不与点B 、C 重合），过点P 作直线PQ ∥BD ，交CD 边于点Q ，再把△PQC 沿着直线PQ 对折，点C 的对应点为R.⑴ 求抛物线的解析式及R 落在BD 上时CP 的长；⑵ 当点R 刚好落在线段AB 上时，如图②，若此时将△所得的点R 在线段AB 上移动，问在移动过程中是否存在某一时刻，使得△ADR 为等腰三角形？若存在，求出AR 的长度；若不存在，请说明理由；⑶ 当点R 落在BD 上时（如图③），点M 为BC 边上一动点，连接QM ，将△CQM 绕点Q 顺时针旋转60°，得到△RQH.延长HR 交直线CB 于点K.若△HMK 的面积等于23.求CM 的长.37、如图，二次函数322--=x x y 的图象与x 轴交于A 、B 两点，与y 轴交于点C ，顶点为D.⑴ 点E （2213+，m ）是抛物线上的一点，求∠AOE 的度数； ⑵ 动点P 在线段OB 上以每秒1个单位的速度从O 点出发向B 点运动，同时动点Q 在线段BC 上以每秒2个单位的速度从C 点向B 点运动，设运动时间为t ，求△OPQ 面积的最大值和对应的时间t 的值；⑶ 当△OPQ 面积最大时，直线PQ 与抛物线在第四象限相交于点N ，在直线AN 上有一动点M ，M 点关于x 轴的对称点为M ₁，M 关于y 轴的对称点为M ₂，是否存在M 点使 △D M M 21为直角三角形？若存在，求出M 点的坐标，若不存在，请说明理由.38、如图，抛物线3332332-+=x x y 交x 轴于点A 、B ，交y 轴于点C. ⑴ 求抛物线的对称轴及△ABC 的面积；⑵ 如图1，已知点Q （0，3），点P 是直线AC 下方抛物线上的一动点，连接PQ 交直线AC 于点K ，连接BQ 、BK.当点P 使得△BQK 周长最小时，请求出△BQK 周长的最小值和此时点P 的坐标；⑶ 如图2，线段AC 水平向右移动的线段FE （点A 的对应点是F ，点C 的对应点E ），将△ACF 沿CF 翻折得△CFA ´，连接A ´E ，是否存在点F ，使得△CEA ´是直角三角形？若存在，请求出点F 的坐标；若不存在，请说明理由39、已知，如图，在平面直角坐标系中，点A 坐标为（4，0），点B 的坐标为（0，-4），C 为y 轴负半轴上一点，且OC=AB ，抛物线c bx x y ++=22的图象经过A 、C 两点. ⑴ 求此抛物线的解析式；⑵ 将∠OAB 的顶点A 沿AB 平移，在平移过程中，保持∠OAB 的大小不变，顶点A 记为A 1，一边AB 记为A 1B ₁，A 1与B 重合时停止平移.A 1B 1与y 轴交于点D.当△A 1OD 是以A 1D 为腰的等腰三角形时，求点A 1的坐标；⑶ 在⑵问的条件下，直线A 1B 1与x 轴交于点E ，P 为⑴中抛物线上一动点，直线PA 1交x 轴于点G ，在直线EB 1下方的抛物线上是否存在一点P ，使得△PDA 1与△GEA 1的面积之比为()221+：1.若存在，求点P 的坐标；若不存在，请说明理由.40、如图，在平面直角坐标系xoy 中，矩形ABCD 的边AB 在x 轴上，且AB=3，BC=23，直线323-=x y 经过点C ，交y 轴于点G.⑴ 求C 、D 的坐标；⑵ 已知抛物线顶点在323-=x y 上，且经过点C 、D ，若抛物线于y 轴交于点M ，连接MC ，设点Q 是线段下方此抛物线上一点，当点Q 运动到什么位置时，△MCQ 的面积最大？求出此时点Q 的坐标和面积的最大值.⑶ 将⑵中抛物线沿着直线323-=x y 平移，平移后的抛物线交y 轴于点F ，顶点为E （顶点在y 轴右侧），平移后是否存在这样的抛物线，使△EFG 为等腰三角形？若存在，求出此时抛物线的解析式；若不存在，请说明理由.。

2020重庆中考复习数学第12题二次函数专题训练二含答案

2020年重庆中考复习二次函数专题训练二1．（2020•南岸区校级模拟）如图所示，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与y 轴的一个交点坐标为（0，3），其部分图象如图所示，下列结论：①abc＜0；②4a+c＞0；③方程ax2+bx+c＝3的两个根是x1＝0，x2＝2；④方程ax2+bx+c＝0有一个实根大于2；⑤当x＜0时，y随x增大而增大．其中结论正确的个数是（）A．4个B．3个C．2个D．1个解：抛物线开口向下，a＜0，对称轴为x＝1＞0，a、b异号，因此b＞0，与y轴交点为（0，3），因此c＝3＞0，于是abc＜0，故结论①是正确的；由对称轴为x ＝﹣＝1得2a+b＝0，当x＝﹣1时，y＝a﹣b+c＜0，所以a+2a+c＜0，即3a+c ＜0，又a＜0，4a+c＜0，故结论②不正确；当y＝3时，x1＝0，即过（0，3），抛物线的对称轴为x＝1，由对称性可得，抛物线过（2，3），因此方程ax2+bx+c＝3的有两个根是x1＝0，x2＝2；故③正确；抛物线与x轴的一个交点（x1，0），且﹣1＜x1＜0，由对称轴x＝1，可得另一个交点（x2，0），2＜x2＜3，因此④是正确的；根据图象可得当x＜0时，y随x增大而增大，因此⑤是正确的；正确的结论有4个，故选：A．2．（2019秋•沙坪坝区校级月考）如图，二次函数y＝ax2+bx+c的图象经过点A（﹣3，0），其对称轴为直线x＝﹣1，有下列结论：①abc＜0；②a+b+c＜0；③5a+4c＜0；④4ac﹣b2＞0；⑤若P （﹣5，y1），Q（m，y2）是抛物线上两点，且y1＞y2，则实数m的取值范围是﹣5＜m＜3．其中正确结论的个数是（）A．1 B．2 C．3 D．4解：①观察图象可知：a＞0，b＞0，c＜0，∴abc＜0，∴①正确；②当x＝1时，y＝0，即a+b+c ＝0，∴②错误；③对称轴x＝﹣1，即﹣＝﹣1得b＝2a，当x ＝时，y＜0，即a +b+c＜0，即a+2b+4c＜0，∴5a+4c＜0．∴③正确；④因为抛物线与x轴有两个交点，所以△＞0，即b2﹣4ac＞0，∴4ac﹣b2＜0．∴④错误；⑤∵（﹣5，y1）关于直线x＝﹣1的对称点的坐标是（3，y1），∴当y1＞y2时，﹣5＜m＜3．∴⑤正确．故选：C3．如图是二次函数y＝ax2+bx+c（a，b，c是常数，且a≠0）图象的一部分，它与x轴的一个交点A在点（2，0）和点（3，0）之间，图象的对称轴是x＝1，对于下列说法：①ab＜0；②2a+b＝0；③3a+c＞0；④a+b≥m（am+b）（m为实数）；⑤当﹣1＜x＜3时，y＞0，其中正确的是（）A．①②④B．①②⑤C．②③④D．③④⑤解：①∵对称轴在y轴右侧，∴a、b异号，∴ab＜0，故正确；②∵对称轴x ＝﹣＝1，∴2a+b＝0；故正确；③∵2a+b＝0，∴b＝﹣2a，∵当x＝﹣1时，y＝a﹣b+c＜0，∴a﹣（﹣2a）+c＝3a+c＜0，故错误；④根据图示知，当x＝1时，有最大值；当m≠1时，有am2+bm+c≤a+b+c，所以a+b≥m（am+b）（m为实数）．故正确．⑤如图，当﹣1＜x＜3时，y不只是大于0．故错误．故选：A．4．（2019秋•九龙坡区校级期中）如图，抛物线y＝ax2+bx+c（a≠0）过点（3，0），且对称轴为直线x＝1．下列说法，其中正确的是（）①abc＜0 ②b2﹣4ac＞0；③a﹣b+c＜0；④b﹣c ＞2a A．①②B．①③④C．②④ D．①②④解：∵抛物线y＝ax2+bx+c（a≠0）与x轴交于点（3，0），其对称轴为直线x＝1，∴抛物线y＝ax2+bx+c（a≠0）与x轴交于点（3，0）和（﹣1，0），且b＝﹣2a，由图象知：a＜0，c＞0，b＞0，b2﹣4ac＞0，∴abc＜0故结论①②正确；∵抛物线y＝ax2+bx+c（a≠0）与x轴交于点（﹣1，0），∴a﹣b+c＝0，故结论③错误；∵a﹣b+c＝0，a＜0，∴2a﹣b+c＜0，∴b﹣c＞2a，故结论④正确；故结论正确的有①②④，故选：D．5．（2019秋•涪陵区校级月考）已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的结论有（）①abc＜0；②2a+b＝0；③b2﹣4ac＜0；④9a+3b+c＞0；⑤c+8a＜0．A．1个B．2个C．3个D．4个解：∵图象的开口向下，与y轴的交点在y轴的正半轴上，对称轴是直线x＝1，∴a＜0，c＞0，﹣＝1，即2a+b＝0，b＞0，∴abc＜0，故①②正确；∵抛物线的图象和x轴有两个交点，∴b2﹣4ac＞0，故③错误；∵抛物线的图象的对称轴是直线x＝1，和x轴的一个交点坐标是（﹣1，0），∴另一个交点坐标是（3，0），即当x＝3时，y＝a×32+b×3+c＝0，故④错误；∵2a+b＝0，即b＝﹣2a，代入解析式得：y＝ax2﹣2ax+c，当x＝3时，y＝9a﹣6a+c＝3a+c＝0，∵a＜0，∴3a+c+5a＝8a+c＜0，故⑤正确；即正确的有3个，故选：C．6．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，其对称轴为直线x＝﹣1，与x轴的交点为（x1，0）、（x2，0），其中0＜x1＜1，有下列结论：①abc＞0；②﹣3＜x2＜﹣2；③4a﹣2b+c＜﹣1；④a﹣b＞am2+bm（m≠﹣1）；⑤a ＞；其中，正确的结论有（）A．5 B．4 C．3 D．2解：①对称轴在y轴左侧，则ab同号，c＜0，故abc＜0，故错误；②对称轴为直线x＝﹣1，0＜x1＜1，则﹣3＜x2＜﹣2，正确；③对称轴为直线x＝﹣1，则b＝2a，4a﹣2b+c＝c＜﹣1，故正确；④x＝﹣1时，y＝ax2+bx+c＝a﹣b+c，为最小值，故a﹣b+c＜am2+bm+c，故错误；⑤x＝1时，y＝a+b+c＝3a+c＞0，即3a＞﹣c，而c＜﹣1，故a ＞，正确；故选：C．7．（2019•重庆模拟）如图，二次函数y＝ax2+bx+c的图象与x轴交于A，B（﹣1，0）两点，与y 轴交于点C，则下列四个结论：①ac＜0；②2a+b＝0；③﹣1＜x＜3时，y＜0；④4a+c＜0．其中所有正确结论的序号是（）A．①②④B．①③④C．①②③D．②③④解：∵抛物线开口向下，∴a＜0，∵抛物线与y轴相交于正半轴，∴c＞0，则ac＜0，即①正确，该二次函数的对称轴为：x ＝﹣＝1，整理得：2a+b＝0，即②正确，∵抛物线对称轴为x＝1，点B的坐标为：（﹣1，0），则点A的坐标为：（3，0），由图象可知：当1＜x＜3时，y＞0，即③错误，由图象可知，当x＝﹣1时，函数值为0，把x＝﹣1代入y＝ax2+bx+c得：a﹣b+c＝0，∵b＝﹣2a，∴3a+c＝0，∵a＜0，∴4a+c＜0 即④正确，正确结论的序号是①②④，故选：A．8．如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，且经过点（﹣1，0），下列四个结论：①如果点（﹣，y1）和（2，y2）都在抛物线上，那么y1＜y2；②b2﹣4ac＞0；③m（am+b）＜a+b（m≠1的实数）；④＝﹣3；其中正确的有（）A．4个B．3个C．2个D．1个解：∵对称轴为直线x＝1，∴﹣＝1，∴b＝﹣2a，∵经过点（﹣1，0），∴a﹣b+c＝0，∴c＝﹣3a，∴y＝ax2+bx+c＝a（x2﹣2x﹣3），由图象可知，a ＜0；①将点（﹣，y1）和（2，y2）分别代入抛物线解析式可得y1＝﹣a，y2＝﹣3a，∴y1＜y2；②由图象可知，抛物线与x轴有两个不同的交点，∴△＝b2﹣4ac＞0；③由图象可知，当x＝1时，函数有最大值1，∴对任意m，则有m（am+b）＜a+b；②＝＝﹣3；∴①②③④正确，故选：A．9．已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，并且关于x的一元二次方程ax2+bx+c﹣m ＝0没有实数根，下列结论：①abc＞0；②a﹣b+c＜0；③m＞﹣2；④二次函数y＝ax2+bx+c （a≠0），最小值为﹣2，其中正确的个数有（）A．1 B．2 C．3 D．4解：①对称轴在y轴右侧，则ab＜0，而c＜0，故abc＞0正确，符合题意；②当x＝﹣1时，y＝a﹣b+c＞0，故原选项错误，不符合题意；③关于x的一元二次方程ax2+bx+c﹣m＝0没有实数根，即y＝ax2+bx+c与y＝m没有交点，故m ＜﹣2，原选项错误，不符合题意；④从图象看二次函数y＝ax2+bx+c（a≠0）的最小值为﹣2，故符合题意；故选：B．10．（2019秋•曾都区期末）二次函数y＝ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为（1，﹣4a），点A（4，y1）是该抛物线上一点，若点D（x2，y2）是抛物线上任意一点，有下列结论：①4a﹣2b+c＞0；②若y2＞y1，则x2＞4；③若0≤x2≤4，则0≤y2≤5a；④若方程a（x+1）（x﹣3）＝﹣1有两个实数根x1和x2，且x1＜x2，则﹣1＜x1＜x2＜3．其中正确结论的个数是（）A．1个B．2个C．3个D．4个解：①∵二次函数y＝ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为（1，﹣4a），∴x ＝，且﹣4a＝a+b+c，∴b＝﹣2a，c＝﹣3a，∴4a﹣2b+c＝4a+4a﹣3a＝5a＞0（∵抛物线开口向上，则a＞0），于是①的结论正确；②∵点A（4，y1）关于直线x＝1的对称点为（﹣2，y1），∴当y2＞y1，则x2＞4或x2＜﹣2，于是②错误；③当x＝4时，y1＝16a+4b+c＝16a﹣8a﹣3c＝5a，∴当﹣1≤x2≤4，则﹣4a≤y2≤5a，于是③错误；④∵方程a（x+1）（x﹣3）＝﹣1有两个实数根x1和x2，且x1＜x2，∴抛物线y＝a（x+1）（x﹣3）与直线y＝﹣1交点的坐标（x1，﹣1）和（x2，﹣1），∵抛物线y＝a（x+1）（x﹣3）＝0时，x＝﹣1或3，即抛物线y＝a（x+1）（x﹣3）＝0与x轴的两个交点坐标分别为（﹣1，0）和（3，0），∴﹣1＜x1＜x2＜3，于是④正确．故选：B．11．（2020•下陆区模拟）抛物线y＝ax2+bx+c的对称轴为直线x＝﹣1，图象过（1，0）点，部分图象如图所示，下列判断中：其中正确的个数是（）①abc＞0；②b2﹣4ac＞0；③9a﹣3b+c＝0；④若点（﹣2.5，y1），（﹣0.5，y2）均在抛物线上，则y1＞y2；⑤5a﹣2b+c＜0．A．2个B．3个C．4个D．5个解：①由图象开口向上，则a＞0，故b＞0，∵c＜0，∴abc＜0，故①错误．②∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，故②正确．③∵抛物线与x轴的一个交点是（1，0），对称轴是x＝﹣1，∴抛物线与x轴的另一个交点是（﹣3，0），∴9a﹣3b+c＝0，故③正确．④∵点（﹣0.5，y2）在抛物线上，对称轴为x＝﹣1，∴（﹣1.5，y2）也在抛物线上，∵﹣1.5＞﹣2.5，且（﹣1.5，y2），（﹣2.5，y1）都在对称轴的左侧，∴y1＞y2，故④正确．⑤∵抛物线对称轴x＝﹣1，经过（1，0），∴﹣＝﹣1，a+b+c＝0，∴b＝2a，c＝﹣3a，∴5a﹣2b+c＝5a﹣4a﹣3a＝﹣2a＜0，∴⑤正确．故正确的判断是②③④⑤共4个．故选：C．12．（2020•成华区模拟）已知抛物线y＝ax2+bx+c的对称轴为直线x＝2，与x轴的一个交点坐标为（4，0）其部分图象如图所示，下列结论其中结论正确的是（）①抛物线过原点；②4a+b＝0；③a﹣b+c＜0；④抛物线线的顶点坐标为（2，b）⑤当x＜2时，y随x增大而增大A．①②③B．③④⑤C．①②④D．①④⑤解：①∵抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝2，与x轴的一个交点坐标为（4，0），∴抛物线与x轴的另一交点坐标为（0，0），结论①正确；②∵抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝2，且抛物线过原点，∴﹣＝2，c＝0，∴b＝﹣4a，c＝0，∴4a+b＝0，结论②正确；③∵当x＝﹣1时，y值为正，∴a﹣b+c＞0，结论③错误；④当x＝2时，y＝ax2+bx+c＝4a+2b+c＝（4a+b+c）+b＝b，∴抛物线的顶点坐标为（2，b），结论④正确；⑤观察函数图象可知：当x＜2时，y随x增大而减小，结论⑤错误．综上所述，正确的结论有：①②④．故选：C．13．（2020•枣阳市校级模拟）已知二次函数y＝ax2+bx+c的图象如图所示，有以下结论：①a+b+c＜0；②a﹣b+c＞1；③abc＞0；④9a﹣3b+c＜0；⑤c﹣a＞1．其中所有正确结论的序号是（）A．①②B．①③④C．①②③④D．①②③④⑤解：由图象可知，a＜0，c＝1，对称轴x ＝﹣＝﹣1，∴b＝2a，①∵当x＝1时，y＜0，∴a+b+c＜0，故正确；②∵当x＝﹣1时，y＞1，∴a﹣b+c＞1，故正确；③abc＝2a2＞0，故正确；④由图可知当x＝﹣3时，y＜0，∴9a﹣3b+c＜0，故正确；⑤c﹣a＝1﹣a＞1，故正确；∴①②③④⑤正确，故选：D．14．（2020•凉山州一模）二次函数y＝ax2+bx+c的图象如图所示、则下列结论：①abc＞0；②a﹣5b+9c＞0；③3a+c＜0，正确的是（）A．①③B．①②C．①②③D．②③解：①∵抛物线的对称轴在y轴的左侧，∴ab＞0，由图象可知：c＞0，∴abc＞0，故①正确；③∵x ＝﹣＝﹣1，∴b＝2a，∴a﹣5b+9c＝9c﹣9a＝9（c﹣a）＞0，故②正确，③∵x ＝﹣＝﹣1，∴b＝2a，由图象可知：9a﹣3b+c＜0，∴9a﹣6a+c＜0，即3a+c＜0，故③正确；故选：C．15．（2020•龙岗区模拟）如图，二次函数y＝ax2+bx+c（a≠0）图象经过点（﹣1，2），下列结论中正确的有（）①4a﹣2b+c＜0；②2a﹣b＜0；③a+c＜1；④b2+8a＞4ac，A．1个B．2个C．3个D．4个解：①由函数的图象可得：当x＝﹣2时，y＜0，即y＝4a﹣2b+c＜0，故①正确；②由函数的图象可知：抛物线开口向下，则a＜0；抛物线的对称轴大于﹣1，即x ＝﹣＞﹣1，得出2a﹣b＜0，故②正确；③已知抛物线经过（﹣1，2），即a﹣b+c＝2（1），由图象知：当x＝1时，y＜0，即a+b+c＜0（2），联立（1）（2），得：a+c＜1，故③正确；④由于抛物线的对称轴大于﹣1，所以抛物线的顶点纵坐标应该大于2，即：＞2，由于a＜0，所以4ac﹣b2＜8a，即b2+8a＞4ac，故④正确，故选：D．16．（2019秋•铁锋区期末）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点（﹣3，0），其对称轴为直线x ＝﹣，结合图象分析下列结论：①abc＞0；②3a+c＞0；③当x＜0时，y随x的增大而增大：④若m，n（m＜n）为方程a（x+3）（x﹣2）+3＝0的两个根，则m＜﹣3且n＞2：⑤＜0，其中正确的结论有（）A．2个B．3个C．4个D．5个解：∵抛物线y＝ax2+bx+c（a≠0）与x轴交于点（﹣3，0），其对称轴为直线x ＝﹣∴抛物线y＝ax2+bx+c（a≠0）与x轴交于点（﹣3，0）和（2，0），且a＝b由图象知：a＜0，c＞0，b＜0，∴abc＞0，故结论①正确；∵抛物线y＝ax2+bx+c（a≠0）与x轴交于点（﹣3，0），∴9a﹣3b+c＝0∵a＝b，∴c＝﹣6a，∴3a+c＝﹣3a＞0，故结论②正确；∵当x ＜﹣时，y随x 的增大而增大；当﹣＜x＜0时，y随x的增大而减小，故结论③错误；∵抛物线y＝ax2+bx+c（a≠0）与x轴交于点（﹣3，0）和（2，0），∴y＝ax2+bx+c＝a（x+3）（x﹣2）∵m，n（m＜n）为方程a（x+3）（x﹣2）+3＝0的两个根∴m，n（m＜n）为方程a（x+3）（x﹣2）＝﹣3的两个根∴m，n（m＜n）为函数y＝a（x+3）（x﹣2）与直线y＝﹣3的两个交点的横坐标结合图象得：m＜﹣3且n＞2，故结论④成立；∵当x ＝﹣时，y ＝＞0，∴＜0，故结论⑤正确；故选：C．。

重庆备战中考数学二次函数培优易错试卷练习(含答案)

一、二次函数真题与模拟题分类汇编（难题易错题）1．如图，抛物线y＝﹣x2﹣2x+3的图象与x轴交于A、B两点(点A在点B的左边)，与y轴交于点C，点D为抛物线的顶点．(1)求点A、B、C的坐标；(2)点M(m，0)为线段AB上一点(点M不与点A、B重合)，过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，可得矩形PQNM．如图，点P在点Q左边，试用含m的式子表示矩形PQNM的周长；(3)当矩形PQNM的周长最大时，m的值是多少？并求出此时的△AEM的面积；(4)在(3)的条件下，当矩形PMNQ的周长最大时，连接DQ，过抛物线上一点F作y轴的平行线，与直线AC交于点G(点G在点F的上方)．若FG＝22DQ，求点F的坐标．【答案】(1)A(﹣3，0)，B(1，0)；C(0，3) ；(2)矩形PMNQ的周长＝﹣2m2﹣8m+2；(3) m＝﹣2；S＝12；(4)F(﹣4，﹣5)或(1，0)．【解析】【分析】（1）利用函数图象与坐标轴的交点的求法，求出点A，B，C的坐标；（2）先确定出抛物线对称轴，用m表示出PM，MN即可；（3）由（2）得到的结论判断出矩形周长最大时，确定出m，进而求出直线AC解析式，即可；（4）在（3）的基础上，判断出N应与原点重合，Q点与C点重合，求出DQ＝DC＝2，再建立方程（n+3）﹣（﹣n2﹣2n+3）＝4即可．【详解】(1)由抛物线y＝﹣x2﹣2x+3可知，C(0，3)．令y＝0，则0＝﹣x2﹣2x+3，解得，x＝﹣3或x＝l，∴A(﹣3，0)，B(1，0)．(2)由抛物线y＝﹣x2﹣2x+3可知，对称轴为x＝﹣1．∵M(m，0)，∴PM＝﹣m2﹣2m+3，MN＝(﹣m﹣1)×2＝﹣2m﹣2，∴矩形PMNQ的周长＝2(PM+MN)＝(﹣m2﹣2m+3﹣2m﹣2)×2＝﹣2m2﹣8m+2．(3)∵﹣2m2﹣8m+2＝﹣2(m+2)2+10，∴矩形的周长最大时，m＝﹣2．∵A(﹣3，0)，C(0，3)，设直线AC的解析式y＝kx+b，∴303k bb-+=⎧⎨=⎩解得k＝l，b＝3，∴解析式y＝x+3，令x＝﹣2，则y＝1，∴E(﹣2，1)，∴EM＝1，AM＝1，∴S＝12AM×EM＝12．(4)∵M(﹣2，0)，抛物线的对称轴为x＝﹣l，∴N应与原点重合，Q点与C点重合，∴DQ＝DC，把x＝﹣1代入y＝﹣x2﹣2x+3，解得y＝4，∴D(﹣1，4)，∴DQ＝DC∵FG＝，∴FG＝4．设F(n，﹣n2﹣2n+3)，则G(n，n+3)，∵点G在点F的上方且FG＝4，∴(n+3)﹣(﹣n2﹣2n+3)＝4．解得n＝﹣4或n＝1，∴F(﹣4，﹣5)或(1，0)．【点睛】此题是二次函数综合题，主要考查了函数图象与坐标轴的交点的求法，待定系数法求函数解析式，函数极值的确定，解本题的关键是用m表示出矩形PMNQ的周长．2．某宾馆客房部有60个房间供游客居住，当每个房间的定价为每天200元时，房间可以住满．当每个房间每天的定价每增加10元时，就会有一个房间空闲．对有游客入住的房间，宾馆需对每个房间每天支出20元的各种费用．设每个房间每天的定价增加x元．求：（1）房间每天的入住量y（间）关于x（元）的函数关系式；（2）该宾馆每天的房间收费p（元）关于x（元）的函数关系式；（3）该宾馆客房部每天的利润w（元）关于x（元）的函数关系式；当每个房间的定价为每天多少元时，w有最大值？最大值是多少？【答案】（1）y=60-10x ；（2）z=-110x 2+40x+12000；（3）w=-110x 2+42x+10800，当每个房间的定价为每天410元时，w 有最大值，且最大值是15210元．【解析】试题分析：（1）根据题意可得房间每天的入住量=60个房间﹣每个房间每天的定价增加的钱数÷10；（2）已知每天定价增加为x 元，则每天要（200+x ）元．则宾馆每天的房间收费=每天的实际定价×房间每天的入住量；（3）支出费用为20×（60﹣10x ），则利润w =（200+x ）（60﹣10x ）﹣20×（60﹣10x ），利用配方法化简可求最大值．试题解析：解：（1）由题意得： y =60﹣10x （2）p =（200+x ）（60﹣10x ）=﹣2110x +40x +12000 （3）w =（200+x ）（60﹣10x ）﹣20×（60﹣10x ） =﹣2110x +42x +10800 =﹣110（x ﹣210）2+15210 当x =210时，w 有最大值．此时，x +200=410，就是说，当每个房间的定价为每天410元时，w 有最大值，且最大值是15210元．点睛：求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法．本题主要考查的是二次函数的应用，难度一般．3．如图①，在平面直角坐标系xOy 中，抛物线y=ax 2+bx+3经过点A(-1，0) 、B(3，0) 两点，且与y 轴交于点C.（1）求抛物线的表达式；（2）如图②，用宽为4个单位长度的直尺垂直于x 轴，并沿x 轴左右平移，直尺的左右两边所在的直线与抛物线相交于P 、 Q 两点（点P 在点Q 的左侧），连接PQ ，在线段PQ 上方抛物线上有一动点D ，连接DP 、DQ.①若点P 的横坐标为12-，求△DPQ 面积的最大值，并求此时点D 的坐标； ②直尺在平移过程中，△DPQ 面积是否有最大值？若有，求出面积的最大值；若没有，请说明理由.【答案】（1）抛物线y=-x 2+2x+3；（2）①点D （ 31524，）；②△PQD 面积的最大值为8【解析】分析：（1）根据点A 、B 的坐标，利用待定系数法即可求出抛物线的表达式；（2）（I ）由点P 的横坐标可得出点P 、Q 的坐标，利用待定系数法可求出直线PQ 的表达式，过点D 作DE ∥y 轴交直线PQ 于点E ，设点D 的坐标为（x ，-x 2+2x+3），则点E 的坐标为（x ，-x+54），进而即可得出DE 的长度，利用三角形的面积公式可得出S △DPQ =-2x 2+6x+72，再利用二次函数的性质即可解决最值问题；（II ）假设存在，设点P 的横坐标为t ，则点Q 的横坐标为4+t ，进而可得出点P 、Q 的坐标，利用待定系数法可求出直线PQ 的表达式，设点D 的坐标为（x ，-x 2+2x+3），则点E 的坐标为（x ，-2（t+1）x+t 2+4t+3），进而即可得出DE 的长度，利用三角形的面积公式可得出S △DPQ =-2x 2+4（t+2）x-2t 2-8t ，再利用二次函数的性质即可解决最值问题．详解：（1）将A （-1，0）、B （3，0）代入y=ax 2+bx+3，得：309330a b a b -+⎧⎨++⎩＝＝，解得：12a b -⎧⎨⎩＝＝， ∴抛物线的表达式为y=-x 2+2x+3．（2）（I ）当点P 的横坐标为-12时，点Q 的横坐标为72， ∴此时点P 的坐标为（-12，74），点Q 的坐标为（72，-94）．设直线PQ 的表达式为y=mx+n ，将P （-12，74）、Q （72，-94）代入y=mx+n ，得： 17247924m n m n ⎧-+⎪⎪⎨⎪+-⎪⎩＝＝，解得：154m n -⎧⎪⎨⎪⎩＝＝， ∴直线PQ 的表达式为y=-x+54．如图②，过点D 作DE ∥y 轴交直线PQ 于点E ，设点D的坐标为（x，-x2+2x+3），则点E的坐标为（x，-x+54），∴DE=-x2+2x+3-（-x+54）=-x2+3x+74，∴S△DPQ=12DE•（x Q-x P）=-2x2+6x+72=-2（x-32）2+8．∵-2＜0，∴当x=32时，△DPQ的面积取最大值，最大值为8，此时点D的坐标为（32，154）．（II）假设存在，设点P的横坐标为t，则点Q的横坐标为4+t，∴点P的坐标为（t，-t2+2t+3），点Q的坐标为（4+t，-（4+t）2+2（4+t）+3），利用待定系数法易知，直线PQ的表达式为y=-2（t+1）x+t2+4t+3．设点D的坐标为（x，-x2+2x+3），则点E的坐标为（x，-2（t+1）x+t2+4t+3），∴DE=-x2+2x+3-[-2（t+1）x+t2+4t+3]=-x2+2（t+2）x-t2-4t，∴S△DPQ=12DE•（x Q-x P）=-2x2+4（t+2）x-2t2-8t=-2[x-（t+2）]2+8．∵-2＜0，∴当x=t+2时，△DPQ的面积取最大值，最大值为8．∴假设成立，即直尺在平移过程中，△DPQ面积有最大值，面积的最大值为8．点睛：本题考查了待定系数法求二次（一次）函数解析式、二次（一次）函数图象上点的坐标特征、三角形的面积以及二次函数的最值，解题的关键是：（1）根据点的坐标，利用待定系数法求出二次函数表达式；（2）（I）利用三角形的面积公式找出S△DPQ=-2x2+6x+72；（II）利用三角形的面积公式找出S△DPQ=-2x2+4（t+2）x-2t2-8t．4．已知，抛物线y=x2+2mx(m为常数且m≠0）．（1）判断该抛物线与x轴的交点个数，并说明理由．（2）若点A（-n+5，0），B(n-1，0)在该抛物线上，点M为抛物线的顶点，求△ABM的面积．（3）若点（2，p)，（3，g），（4，r)均在该抛物线上，且p<g<r，求m的取值范围．【答案】（1）抛物线与x轴有2个交点，理由见解析；（2）△ABM的面积为8；（3）m的取值范围m>-2.5【解析】【分析】（1）首先算出根的判别式b 2-4ac 的值，根据偶数次幂的非负性，判断该值一定大于0，从而根据抛物线与x 轴交点个数与根的判别式的关系即可得出结论；（2）根据抛物线的对称性及A,B 两点的坐标特点求出抛物线的对称轴直线为x=2.从而再根据抛物线对称轴直线公式建立方程，求解算出m 的值，进而求出抛物线的解析式，得出A,B,M 三点的坐标，根据三角形的面积计算方法，即可算出答案；（3）方法一（图象法）：根据抛物线的对称轴直线及开口方向判断出当对称轴在直线x=3的右边时，显然不符合题目条件；当对称轴在直线x=2的左边时，显然符合题目条件（如图2），从而列出不等式得出m 的取值范围；当对称轴在直线x=2和x=3之间时，满足3-（-m)>-m-2即可（如图3），再列出不等式得出m 的取值范围，综上所述，求出m 的取值范围；方法二（代数法）：将三点的横坐标分贝代入抛物线的解析式，用含m 的式子表示出p,g,r ，再代入 p<g<r 即可列出关于m 的不等式组，求解即可。

重庆名校二次函数综合试题精练(有答案)

重庆名校函数综合试题精练1、（南开中学2008中考模拟）如图，已知抛物线223y x bx c =-++与y 轴交于点C ，与x 轴交与A 、B 两点（点A 在点B 的左侧），且OA =1，OC =2 （1）求抛物线的解析式及对称轴；（2）点E 是抛物线在第一象限内的一点，且tan 1EOB ∠=，求点E 的坐标；（3）在抛物线的对称轴上，是否存在点P ，使得PBE ∆为等腰三角形？若存在，请求出点P 的坐标；若不存在，请说明理由。

2．（2008年南开5月模拟）已知，抛物线2y ax bx c =++与x 轴交于(1,0)A -和(2,0)B 两点，与y 轴交于(0,2)C -。

（1）求这条抛物线的解析式和抛物线顶点M 的坐标；（2）求四边形ABMC 的面积；（3）在对称轴的右侧的抛物线上是否存在点P ，使PAC ∆为直角三角形？若存在，求出所有符合条件的点P 的坐标，若不存在，请说明理由。

（备用图）xx(26题图)3.（一中2009年5月模拟）如图，直线33+=x y 分别交x 轴、y 轴于B 、A 两点，抛物线L ：c bx ax y ++=2的顶点G 在x 轴上，且过(0，4)和(4，4)两点.（1）求抛物线L 的解析式；（2）抛物线L 上是否存在这样的点C ，使得四边形ABGC 是以BG 为底边的梯形，若存在，请求出C 点的坐标，若不存在，请说明理由.（3）将抛物线L 沿x 轴平行移动得抛物线L 1，其顶点为P ，同时将△PAB 沿直线AB 翻折得到△DAB，使点D 落在抛物线L 1上. 试问这样的抛物线L 1是否存在，若存在，求出L 1对应的函数关系式，若不存在，说明理由．4.（南开中学2009年5月中考模拟）如图1，矩形OABC 的顶点O 为原点，点E 在AB 上，把CBE ∆沿CE 折叠，使点B 落在OA 边上的点D 处，点A D 、坐标分别为(10,0)和(6,0)，抛物线215y x bx c =++过点C B 、. (1)求C B 、两点的坐标及该抛物线的解析式；(2)如图2，长、宽一定的矩形PQRS 的宽1PQ =，点P 沿(1)中的抛物线滑动，在滑动过程中x PQ //轴，且RS 在PQ 的下方，当P 点横坐标为-1时，点S 距离x 轴511个单位，当矩形PQRS 在滑动过程中被x 轴分成上下．．两部分的面积比为2:3时，求点P 的坐标； (3)如图3，动点M N 、同时从点O 出发，点M 以每秒3个单位长度的速度沿折线ODC 按C D O →→的路线运动，点N 以每秒8个单位长度的速度沿折线OCD 按D C O →→的路线运动，当M N 、两点相遇时，它们都停止运动．设M N 、同时从点O 出发t 秒时，OMN ∆的面积为S ．①求出S 与t 的函数关系式，并写出t 的取值范围：②设0S 是①中函数S 的最大值，那么0S = .5.（一中）已知二次函数2y x bx c =++的图象过点A （-3，0）和点B （1，0），且与y 轴交于点C ，D 点在抛物线上且横坐标是 -2。

重庆中考复习12题(二次函数与系数)专题训练

二次函数图象与系数的关系1．已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（）A．a＞0 B．b＜0 C．c＜0 D．a+b+c＞02．（2011•雅安）已知二次函数y=ax2+bx+c的图象如图，其对称轴x=﹣1，给出下列结果①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a﹣b+c＜0，则正确的结论是（）A．①②③④B．②④⑤C．②③④D．①④⑤3．（2011•孝感）如图，二次函数y=ax2+bx+c的图象与y轴正半轴相交，其顶点坐标为（），下列结论：①ac＜0；②a+b=0；③4ac﹣b2=4a；④a+b+c＜0．其中正确结论的个数是（）A．1 B．2 C．3 D．44．已知二次函数y=ax2+bx+c的图象如图所示，对称轴为直线x=1，则下列结论正确的是（）A．ac＞0 B．方程ax2+bx+c=0的两根是x1=﹣1，x2=3 C．2a﹣b=0D．当x＞0时，y随x的增大而减小第1题图第2题图第3题图第4题图5．（2011•泸州）已知二次函数y=ax2+bx+c（a，b，c为常数，a≠0）的图象如图所示，有下列结论：①abc＞0，②b2﹣4ac＜0，③a﹣b+c＞0，④4a﹣2b+c＜0，其中正确结论的个数是（）A．1 B．2 C．3 D．46．（2011•兰州）如图所示的二次函数y=ax2+bx+c的图象中，刘星同学观察得出了下面四条信息：（1）b2﹣4ac＞0；（2）c＞1；（3）2a﹣b＜0；（4）a+b+c＜0．你认为其中错误的有（）A．2个B．3个C．4个D．1个7．（2011•昆明）抛物线y=ax2+bx+c（a≠0）的图象如图所示，则下列说法正确的是（）A．b2﹣4ac＜0 B．abc＜0 C．D．a﹣b+c＜08．（2011•鸡西）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，现有下列结论：①b2﹣4ac＞0 ②a＞0 ③b＞0 ④c＞0 ⑤9a+3b+c＜0，则其中结论正确的个数是（）A．2个B．3个C．4个D．5个第5题图第6题图第7题图第8题图24. 如图,四边形ABCD是边长为2的正方形，点G是BC延长线上一点，连结AG，点E、F分别在AG上，连接BE、DF，∠1=∠2 ，∠3=∠4. （1）证明：△AB E≌△DAF；（2）若∠AGB=30°，求EF的长.9．（2011•广西）已知：二次函数y=ax 2+bx+c （a≠0）的图象如图所示，下列结论中：①abc＞0；②2a+b＜0；③a+b＜m （am+b ）（m≠1的实数）；④（a+c ）2＜b 2；⑤a＞1．其中正确的项是（） A ．①⑤ B ．①②⑤ C ．②⑤ D ．①③④10．（2010•梧州）已知二次函数y=ax 2+bx+c 的图象如图所示，那么下列判断不正确的是（）A ．ac ＜0B ．a ﹣b+c ＞0C ．b=﹣4aD ．关于x 的方程ax 2+bx+c=0的根是x 1=﹣1，x 2=511．（2010•天津）已知二次函数y=ax 2+bx+c （a≠0）的图象如图所示，有下列结论：①b 2﹣4ac ＞0；②abc ＞0；③8a+c ＞0；④9a+3b+c ＜0其中，正确结论的个数是（） A ．1 B ．2 C ．3 D ．412．（2009•芜湖）如图所示是二次函数y=ax 2+bx+c 图象的一部分，图象过A 点（3，0），二次函数图象对称轴为x=1，给出四个结论：①b 2＞4ac ；②bc ＜0；③2a+b=0；④a+b+c=0，其中正确结论是（） A ．②④ B ．①③ C ．②③ D ．①④第9题图第10题图第11题图第12题图13．（2009•随州）如图是某二次函数的图象，将其向左平移2个单位后的图象的函数解析式为y=ax 2+bx+c （a≠0），则下列结论中正确的有（）（1）a ＞0；（2）c ＜0；（3）2a ﹣b=0；（4）a+b+c ＞0． A ．1个 B ．2个 C ．3个 D ．4个14．已知二次函数y=ax 2+bx+c （a≠0）的图象如图所示，则下列结论：①ac ＞0；②方程ax 2+bx+c=0的两根之和大于0；③y 随x 的增大而增大；④a ﹣b+c ＜0，其中正确的个数（） A ．4个 B ．3个 C ．2个 D ．1个15．二次函数y=ax 2+bx+c （a≠0）的图象如图所示，对称轴是直线x=1，则下列四个结论错误的是（）A ．c ＞0B ．2a+b=0C ．b 2﹣4ac ＞0 D ．a ﹣b+c ＞016．（2009•南宁）已知二次函数y=ax 2+bx+c （a≠0）的图象如图所示，有下列四个结论：①b ＜0；②c ＞0；③b 2﹣4ac ＞0；④a ﹣b+c ＜0，其中正确的个数有（） A ．1个 B ．2个 C ．3个 D ．4个第13题图第14题图第15题图第16题图17．（2009•济宁）小强从如图所示的二次函数y=ax 2+bx+c 的图象中，观察得出了下面五条信息：（1）a ＜0；（2）c ＞1；（3）b ＞0；（4）a+b+c ＞0；（5）a ﹣b+c ＞0．你认为其中正确信息的个数有（） A ．2个 B ．3个 C ．4个 D ．5个第17题图。

重庆备战中考数学二次函数培优易错试卷练习(含答案)

重庆备战中考数学二次函数培优易错试卷练习(含答案)一、二次函数1．已知，点M为二次函数y＝﹣（x﹣b）2+4b+1图象的顶点，直线y＝mx+5分别交x轴正半轴，y轴于点A，B．（1）判断顶点M是否在直线y＝4x+1上，并说明理由．（2）如图1，若二次函数图象也经过点A，B，且mx+5＞﹣（x﹣b）2+4b+1，根据图象，写出x的取值范围．（3）如图2，点A坐标为（5，0），点M在△AOB内，若点C（14，y1），D（34，y2）都在二次函数图象上，试比较y1与y2的大小．【答案】（1）点M在直线y＝4x+1上；理由见解析；（2）x的取值范围是x＜0或x＞5；（3）①当0＜b＜12时，y1＞y2，②当b＝12时，y1＝y2，③当12＜b＜45时，y1＜y2．【解析】【分析】（1）根据顶点式解析式，可得顶点坐标，根据点的坐标代入函数解析式检验，可得答案；（2）根据待定系数法，可得二次函数的解析式，根据函数图象与不等式的关系：图象在下方的函数值小，可得答案；（3）根据解方程组，可得顶点M的纵坐标的范围，根据二次函数的性质，可得答案．【详解】（1）点M为二次函数y＝﹣（x﹣b）2+4b+1图象的顶点，∴M的坐标是（b，4b+1），把x＝b代入y＝4x+1，得y＝4b+1，∴点M在直线y＝4x+1上；（2）如图1，直线y＝mx+5交y轴于点B，∴B点坐标为（0，5）又B在抛物线上，∴5＝﹣（0﹣b）2+4b+1＝5，解得b＝2，二次函数的解析是为y＝﹣（x﹣2）2+9，当y＝0时，﹣（x﹣2）2+9＝0，解得x1＝5，x2＝﹣1，∴A（5，0）．由图象，得当mx+5＞﹣（x﹣b）2+4b+1时，x的取值范围是x＜0或x＞5；（3）如图2，∵直线y＝4x+1与直线AB交于点E，与y轴交于F，A（5，0），B（0，5）得直线AB的解析式为y＝﹣x+5，联立EF，AB得方程组415 y xy x=+⎧⎨=-+⎩，解得45215 xy⎧=⎪⎪⎨⎪=⎪⎩，∴点E（45，215），F（0，1）．点M在△AOB内，1＜4b+1＜215，∴0＜b＜45．当点C，D关于抛物线的对称轴对称时，b﹣14＝34﹣b，∴b＝12，且二次函数图象开口向下，顶点M在直线y＝4x+1上，综上：①当0＜b＜12时，y1＞y2，②当b＝12时，y1＝y2，③当12＜b＜45时，y1＜y2．【点睛】本题考查了二次函数综合题，解（1）的关键是把点的坐标代入函数解析式检验；解（2）的关键是利用函数图不等式的关系：图象在上方的函数值大；解（3）的关键是解方程组得出顶点M 的纵坐标的范围，又利用了二次函数的性质：a ＜0时，点与对称轴的距离越小函数值越大．2．如图，抛物线y=ax 2+bx+c 与x 轴交于点A 和点B （1，0），与y 轴交于点C （0，3），其对称轴l 为x=﹣1．（1）求抛物线的解析式并写出其顶点坐标；（2）若动点P 在第二象限内的抛物线上，动点N 在对称轴l 上．①当PA ⊥NA ，且PA=NA 时，求此时点P 的坐标；②当四边形PABC 的面积最大时，求四边形PABC 面积的最大值及此时点P 的坐标．【答案】（1）y=﹣（x+1）2+4，顶点坐标为（﹣1，4）；（2）①点P 2﹣1，2）；②P （﹣32，154）【解析】试题分析：（1）将B 、C 的坐标代入已知的抛物线的解析式，由对称轴为1x =-即可得到抛物线的解析式；（2）①首先求得抛物线与x 轴的交点坐标，然后根据已知条件得到PD=OA ，从而得到方程求得x 的值即可求得点P 的坐标；②ΔOBC ΔAPD ABCP C =PDO S S S S ++四边形梯形，表示出来得到二次函数，求得最值即可．试题解析：（1）∵抛物线2y ax bx c =++与x 轴交于点A 和点B （1，0），与y 轴交于点C （0，3），其对称轴l 为1x =-，∴0{312a b c c b a++==-=-，解得：1{23a b c =-=-=，∴二次函数的解析式为223y x x =--+=2(1)4x -++，∴顶点坐标为（﹣1，4）；（2）令2230y x x =--+=，解得3x =-或1x =，∴点A （﹣3，0），B （1，0），作PD ⊥x 轴于点D ，∵点P 在223y x x =--+上，∴设点P （x ，223x x --+）， ①∵PA ⊥NA ，且PA=NA ，∴△PAD ≌△AND ，∴OA=PD ，即2232y x x =--+=，解得21（舍去）或x=21-，∴点P （21-，2）；②设P(x ，y)，则223y x x =--+，∵ΔOBC ΔAPD ABCP C =PDO S S S S ++四边形梯形=12OB•OC+12AD•PD+12(PD+OC)•OD=11131+(3)(3)()222x y y x ⨯⨯⨯+++-=333222x y -+ =2333(23)222x x x -+--+=239622x x --+=23375()228x -++， ∴当x=32-时，ABCP S 四边形最大值=758，当x=32-时，223y x x =--+=154，此时P （32-，154）．考点：1．二次函数综合题；2．二次函数的最值；3．最值问题；4．压轴题．3．如图，在平面直角坐标系中，二次函数2y ax bx c =++交x 轴于点()4,0A -、()2,0B ，交y 轴于点()0,6C ，在y 轴上有一点()0,2E -，连接AE .（1）求二次函数的表达式；（2）若点D 为抛物线在x 轴负半轴上方的一个动点，求ADE ∆面积的最大值；（3）抛物线对称轴上是否存在点P ，使AEP ∆为等腰三角形，若存在，请直接写出所有P 点的坐标，若不存在请说明理由.【答案】（1）二次函数的解析式为233642y x x =--+；（2）当23x =-时，ADE ∆的面积取得最大值503；（3）P点的坐标为()1,1-，()1,11-±，()1,219--±.【解析】分析：（1）把已知点坐标代入函数解析式，得出方程组求解即可；（2）根据函数解析式设出点D坐标，过点D作DG⊥x轴，交AE于点F，表示△ADE的面积，运用二次函数分析最值即可；（3）设出点P坐标，分PA=PE，PA=AE，PE=AE三种情况讨论分析即可．详解：（1）∵二次函数y=ax2+bx+c经过点A（﹣4，0）、B（2，0），C（0，6），∴16404206a b ca b cc-+=⎧⎪++=⎨⎪=⎩，解得：34326abc⎧=-⎪⎪⎪=-⎨⎪=⎪⎪⎩，所以二次函数的解析式为：y=233642x x--+；（2）由A（﹣4，0），E（0，﹣2），可求AE所在直线解析式为y=122x--，过点D作DN⊥x轴，交AE于点F，交x轴于点G，过点E作EH⊥DF，垂足为H，如图，设D（m，233642m m--+），则点F（m，122m--），∴DF=233642m m--+﹣（122m--）=2384m m--+，∴S△ADE=S△ADF+S△EDF=12×DF×AG+12DF×EH=12×DF ×AG +12×DF ×EH =12×4×DF =2×（2384m m --+） =23250233m -++（）， ∴当m =23-时，△ADE 的面积取得最大值为503．（3）y =233642x x --+的对称轴为x =﹣1，设P （﹣1，n ），又E （0，﹣2），A （﹣4，0），可求PA PE AE =，分三种情况讨论：当PA =PE n =1，此时P （﹣1，1）；当PA =AE =n =，此时点P 坐标为（﹣1，）；当PE =AE =n =﹣2P 坐标为：（﹣1，﹣2）．综上所述：P 点的坐标为：（﹣1，1），（﹣1，1，﹣2）．点睛：本题主要考查二次函数的综合问题，会求抛物线解析式，会运用二次函数分析三角形面积的最大值，会分类讨论解决等腰三角形的顶点的存在问题时解决此题的关键．4．某商场经营某种品牌的玩具，购进时的单价是3元，经市场预测，销售单价为40元时，可售出600个；销售单价每涨1元，销售量将减少10个设每个销售单价为x 元．（1）写出销售量y （件）和获得利润w （元）与销售单价x （元）之间的函数关系；（2）若玩具厂规定该品牌玩具销售单价不低于44元，且商场要完成不少于540件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？【答案】（1）y ＝﹣10x+1000；w=﹣10x 2+1300x ﹣30000（2）商场销售该品牌玩具获得的最大利润是8640元．【解析】【分析】（1）利用销售单价每涨1元，销售量将减少10个即可表示出y ＝600﹣10（x ﹣40），再利用w= y•（x ﹣30）即可表示出w 与x 之间的关系式；（2）先将w ＝﹣10x 2+1300x ﹣30000变成顶点式，找到对称轴，利用函数图像的增减性确定在44≤x≤46范围内当x ＝46时有最大值，代入求值即可解题.【详解】解：（1）依题意，易得销售量y （件）与销售单价x （元）之间的函数关系：y ＝600﹣10（x ﹣40）＝﹣10x+1000获得利润w （元）与销售单价x （元）之间的函数关系为：w ＝y•（x ﹣30）＝（1000﹣10x ）（x ﹣30）＝﹣10x 2+1300x ﹣30000（2）根据题意得，x≥14时且1000﹣10x≥540，解得：44≤x≤46w ＝﹣10x 2+1300x ﹣30000＝﹣10（x ﹣65）2+12250∵a ＝﹣10＜0，对称轴x ＝65∴当44≤x≤46时，y 随x 的增大而增大∴当x ＝46时，w 最大值＝8640元即商场销售该品牌玩具获得的最大利润是8640元．【点睛】本题考查了二次函数的实际应用，难度较大，求解二次函数与利润之间的关系时,需要用代数式表示销售数量和销售单价，熟悉二次函数顶点式的性质是解题关键.5．如图，已知抛物线2(0)y ax bx c a =++≠的对称轴为直线1x =-，且抛物线与x 轴交于A 、B 两点，与y 轴交于C 点，其中(1,0)A ，(0,3)C .（1）若直线y mx n =+经过B 、C 两点，求直线BC 和抛物线的解析式；（2）在抛物线的对称轴1x =-上找一点M ，使点M 到点A 的距离与到点C 的距离之和最小，求出点M 的坐标；（3）设点P 为抛物线的对称轴1x =-上的一个动点，求使BPC ∆为直角三角形的点P 的坐标.【答案】（1）抛物线的解析式为223y x x =--+，直线的解析式为3y x =+.（2）(1,2)M -；（3）P 的坐标为(1,2)--或(1,4)-或317(+-或317()--. 【解析】分析：（1）先把点A ，C 的坐标分别代入抛物线解析式得到a 和b ，c 的关系式，再根据抛物线的对称轴方程可得a 和b 的关系，再联立得到方程组，解方程组，求出a ，b ，c 的值即可得到抛物线解析式；把B 、C 两点的坐标代入直线y=mx+n ，解方程组求出m 和n 的值即可得到直线解析式；（2）设直线BC 与对称轴x=-1的交点为M ，此时MA+MC 的值最小．把x=-1代入直线y=x+3得y 的值，即可求出点M 坐标；（3）设P（-1，t），又因为B（-3，0），C（0，3），所以可得BC2=18，PB2=（-1+3）2+t2=4+t2，PC2=（-1）2+（t-3）2=t2-6t+10，再分三种情况分别讨论求出符合题意t值即可求出点P的坐标．详解：（1）依题意得：1 23baa b cc⎧-=-⎪⎪++=⎨⎪=⎪⎩，解得：123abc=-⎧⎪=-⎨⎪=⎩，∴抛物线的解析式为223y x x=--+.∵对称轴为1x=-，且抛物线经过()1,0A，∴把()3,0B-、()0,3C分别代入直线y mx n=+，得303m nn-+=⎧⎨=⎩，解之得：13mn=⎧⎨=⎩，∴直线y mx n=+的解析式为3y x=+.（2）直线BC与对称轴1x=-的交点为M，则此时MA MC+的值最小，把1x=-代入直线3y x=+得2y=，∴()1,2M-.即当点M到点A的距离与到点C的距离之和最小时M的坐标为()1,2-.（注：本题只求M坐标没说要求证明为何此时MA MC+的值最小，所以答案未证明MA MC+的值最小的原因）.（3）设()1,P t-，又()3,0B-，()0,3C，∴218BC=，()2222134PB t t=-++=+，()()222213610PC t t t=-+-=-+，①若点B为直角顶点，则222BC PB PC+=，即：22184610t t t++=-+解得：2t=-，②若点C为直角顶点，则222BC PC PB+=，即：22186104t t t+-+=+解得：4t=，③若点P为直角顶点，则222PB PC BC+=，即：22461018t t t++-+=解得：1317t+=2317t-=.综上所述P 的坐标为()1,2--或()1,4-或3171,⎛⎫+- ⎪ ⎪⎝⎭或3171,⎛⎫-- ⎪ ⎪⎝⎭. 点睛：本题综合考查了二次函数的图象与性质、待定系数法求函数（二次函数和一次函数）的解析式、利用轴对称性质确定线段的最小长度、难度不是很大，是一道不错的中考压轴题．6．如图，已知顶点为(0,3)C -的抛物线2(0)y ax b a =+≠与x 轴交于A ，B 两点，直线y x m =+过顶点C 和点B ．（1）求m 的值；（2）求函数2(0)y ax b a =+≠的解析式；（3）抛物线上是否存在点M ，使得15MCB ∠=︒？若存在，求出点M 的坐标；若不存在，请说明理由．【答案】（1）﹣3；（2）y 13=x 2﹣3；（3）M 的坐标为（3632）．【解析】【分析】（1）把C （0，﹣3）代入直线y ＝x +m 中解答即可；（2）把y ＝0代入直线解析式得出点B 的坐标，再利用待定系数法确定函数关系式即可；（3）分M 在BC 上方和下方两种情况进行解答即可．【详解】（1）将C （0，﹣3）代入y ＝x +m ，可得：m ＝﹣3；（2）将y ＝0代入y ＝x ﹣3得：x ＝3，所以点B 的坐标为（3，0），将（0，﹣3）、（3，0）代入y ＝ax 2+b 中，可得：390b a b =-⎧⎨+=⎩，解得：133a b ⎧=⎪⎨⎪=-⎩，所以二次函数的解析式为：y 13=x 2﹣3；（3）存在，分以下两种情况：①若M 在B 上方，设MC 交x 轴于点D ，则∠ODC ＝45°+15°＝60°，∴OD ＝OC •tan30°3=设DC 为y ＝kx ﹣33，0），可得：k 3= 联立两个方程可得：233133y x y x ⎧=-⎪⎨=-⎪⎩，解得：121203336x x y y ⎧=⎧=⎪⎨⎨=-=⎪⎩⎩，所以M 1（36）；②若M 在B 下方，设MC 交x 轴于点E ，则∠OEC ＝45°-15°＝30°，∴OE ＝OC •tan60°＝3设EC 为y ＝kx ﹣3，代入（30）可得：k 3= 联立两个方程可得：233133y x y x ⎧=-⎪⎪⎨⎪=-⎪⎩，解得：12120332x x y y ⎧=⎧=⎪⎨⎨=-=-⎪⎩⎩，所以M 23，﹣2）．综上所述M 的坐标为（33，6）或（3，﹣2）．【点睛】此题是一道二次函数综合题，熟练掌握待定系数法求函数解析式等知识是解题关键．7．如图，在平面直角坐标系xOy 中，A 、B 为x 轴上两点，C 、D 为y 轴上的两点，经过点A 、C 、B 的抛物线的一部分C 1与经过点A 、D 、B 的抛物线的一部分C 2组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点C 的坐标为（0，），点M 是抛物线C 2：2y mx 2mx 3m =--（m ＜0）的顶点．（1）求A 、B 两点的坐标；（2）“蛋线”在第四象限上是否存在一点P ，使得△PBC 的面积最大？若存在，求出△PBC 面积的最大值；若不存在，请说明理由；（3）当△BDM 为直角三角形时，求m 的值．【答案】（1）A （，0）、B （3，0）．（2）存在．S △PBC 最大值为2716 （3）2m 2=-或1m =-时，△BDM 为直角三角形．【解析】【分析】（1）在2y mx 2mx 3m =--中令y=0，即可得到A 、B 两点的坐标．（2）先用待定系数法得到抛物线C 1的解析式，由S △PBC = S △POC + S △BOP –S △BOC 得到△PBC 面积的表达式，根据二次函数最值原理求出最大值．（3）先表示出DM 2，BD 2，MB 2，再分两种情况：①∠BMD=90°时；②∠BDM=90°时，讨论即可求得m 的值．【详解】解：（1）令y=0，则2mx 2mx 3m 0--=，∵m ＜0，∴2x 2x 30--=，解得：1x 1=-，2x 3=．∴A （，0）、B （3，0）．（2）存在．理由如下：∵设抛物线C 1的表达式为()()y a x 1x 3=+-（a 0≠），把C （0，32-）代入可得，12a =． ∴Ｃ1的表达式为：()()1y x 1x 32=+-，即213y x x 22=--．设P （p ，213p p 22--）， ∴ S △PBC = S △POC + S △BOP –S △BOC =23327p 4216--+（）． ∵3a 4=-<0，∴当3p 2=时,S △PBC 最大值为2716．（3）由C 2可知： B （3，0），D （0，3m -），M （1，4m -），∴BD 2=29m 9+，BM 2=216m 4+，DM 2=2m 1+．∵∠MBD<90°, ∴讨论∠BMD=90°和∠BDM=90°两种情况：当∠BMD=90°时，BM 2+ DM 2= BD 2，即216m 4+＋2m 1+=29m 9+，解得：12m 2=-,22m 2=(舍去)．当∠BDM=90°时，BD 2+ DM 2= BM 2，即29m 9+＋2m 1+=216m 4+，解得：1m 1=-，2m 1=(舍去) ．综上所述，2m =-或1m =-时，△BDM 为直角三角形．8．如图，抛物线y ＝ax 2+bx+c 经过A （﹣3，0），B （1，0），C （0，3）三点．（1）求抛物线的函数表达式；（2）如图1，P 为抛物线上在第二象限内的一点，若△PAC 面积为3，求点P 的坐标；（3）如图2，D 为抛物线的顶点，在线段AD 上是否存在点M ，使得以M ，A ，O 为顶点的三角形与△ABC 相似？若存在，求点M 的坐标；若不存在，请说明理由．【答案】（1）y ＝﹣x 2﹣2x+3；（2）点P 的坐标为（﹣1，4）或（﹣2，3）；（3）存在，（32-，32）或（34-，94），见解析. 【解析】【分析】（1）利用待定系数法，然后将A 、B 、C 的坐标代入解析式即可求得二次函数的解析式；（2））过P 点作PQ 垂直x 轴，交AC 于Q ，把△APC 分成两个△APQ 与△CPQ ，把PQ 作为两个三角形的底，通过点A ，C 的横坐标表示出两个三角形的高即可求得三角形的面积．（3）通过三角形函数计算可得∠DAO=∠ACB ，使得以M ，A ，O 为顶点的三角形与△ABC 相似，则有两种情况，∠AOM=∠CAB=45°，即OM 为y=-x ，若∠AOM=∠CBA ，则OM 为y=-3x+3，然后由直线解析式可求OM 与AD 的交点M ．【详解】（1）把A （﹣3，0），B （1，0），C （0，3）代入抛物线解析式y ＝ax 2+bx+c 得 93003a b c a b c c -+=⎧⎪++=⎨⎪=⎩，解得123a b c =-⎧⎪=-⎨⎪=⎩，所以抛物线的函数表达式为y ＝﹣x 2﹣2x+3．（2）如解（2）图1，过P 点作PQ 平行y 轴，交AC 于Q 点，∵A （﹣3，0），C （0，3），∴直线AC 解析式为y ＝x+3，设P 点坐标为（x ，﹣x 2﹣2x+3．），则Q 点坐标为（x ，x+3），∴PQ ＝﹣x 2﹣2x+3﹣（x+3）＝﹣x 2﹣3x ．∴S △PAC ＝1PQ A 2O ⋅， ∴()213332x x --⋅=，解得：x 1＝﹣1，x 2＝﹣2．当x ＝﹣1时，P 点坐标为（﹣1，4），当x ＝﹣2时，P 点坐标为（﹣2，3），综上所述：若△PAC 面积为3，点P 的坐标为（﹣1，4）或（﹣2，3），（3）如解（3）图1，过D 点作DF 垂直x 轴于F 点，过A 点作AE 垂直BC 于E 点，∵D 为抛物线y ＝﹣x 2﹣2x+3的顶点，∴D 点坐标为（﹣1，4），又∵A （﹣3，0），∴直线AC 为y ＝2x+4，AF ＝2，DF ＝4，tan ∠PAB ＝2，∵B （1，0），C （0，3）∴tan ∠ABC ＝3，BC 10，sin ∠ABC 310BC 解析式为y ＝﹣3x+3． ∵AC ＝4，∴AE ＝AC•sin ∠ABC ＝3104610BE 210， ∴CE ＝3105， ∴tan ∠ACB ＝2AE CE =， ∴tan ∠ACB ＝tan ∠PAB ＝2，∴∠ACB ＝∠PAB ，∴使得以M ，A ，O 为顶点的三角形与△ABC 相似，则有两种情况，如解（3）图2Ⅰ．当∠AOM ＝∠CAB ＝45°时，△ABC ∽△OMA ，即OM 为y ＝﹣x ，设OM 与AD 的交点M （x ，y ）依题意得：3y x y x =-⎧⎨=+⎩，解得3232x y ⎧=-⎪⎪⎨⎪=⎪⎩，即M 点为（32-，32）． Ⅱ．若∠AOM ＝∠CBA ，即OM ∥BC ，∵直线BC 解析式为y ＝﹣3x+3．∴直线OM 为y ＝﹣3x ，设直线OM 与AD 的交点M （x ，y ）．则依题意得：33y x y x =-⎧⎨=+⎩，解得3494x y ⎧=-⎪⎪⎨⎪=⎪⎩，即M 点为（34-，94），综上所述：存在使得以M ，A ，O 为顶点的三角形与△ABC 相似的点M ，其坐标为（32-，32）或（34-，94）．【点睛】本题结合三角形的性质考查二次函数的综合应用，函数和几何图形的综合题目，要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．9．我们知道，经过原点的抛物线解析式可以是()2y=ax bx a 0+≠。

重庆中考数学25题二次函数专项训练之三角形的存在性

第一讲三角形的存在性问题例1、如图，抛物线822++-=x x y 与x 轴交于A 、B 两点，过点A 的直线2+=x y 与抛物线交于点C ，与y 轴交于点D ．（1）求△ABC 的面积；（2）若点P 为直线AC 上方抛物线上的动点，求点P 到直线AC 距离的最大值；（3）将抛物线沿射线AC 的方向平移23个单位长度，平移后的顶点记作M ，原抛物线的顶点关于新抛物线的对称轴的对称点记作N ，E 为直线AC 上的动点，是否存在点E ，使得以M 、N 、E 为顶点的三角形是等腰三角形？若存在，请直接写出点E 的坐标；若不存在，请说明理由．与y 轴交于点C ，对称轴交抛物线于点Q ，交x 轴于点M ．其中点A （﹣2，0），点B （4，0）．（1）求抛物线的解析式；（2）如图2，连接BC ，在第一象限的抛物线上有一点P ，且点P 位于对称轴右侧，过P 作PD△BC 于点D ，PE△MQ 于点E ，求5PD+PE 的最大值及此时点P 的坐标．（3）将抛物线向右平移2个单位长度后得到新抛物线1y ，新抛物线1y 与原抛物线相交于点N ，在新抛物线1y 的对称轴上有一点H ，点F 为1y 与x 轴正半轴的交点，若△NFH 是以NH 为腰的等腰三角形，请直接写出点H 的坐标，并写出求解其中一个H 点的过程．与y轴交于点B，其中点B坐标为（0，﹣4），点C坐标为（2，0）．（1）求此抛物线的函数解析式．（2）点D是直线AB下方抛物线上一个动点，连接AD、BD，探究是否存在点D，使得△ABD 的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由．（3）点P为该抛物线对称轴上的动点，使得△PAB为直角三角形，请求出点P的坐标．练习2、已知抛物线c bx ax y ++=2与x 轴交于A （2-，0）、B （6，0）两点，与y 轴交于点C （0，3-）．（1）求抛物线的表达式；（2）点P 在直线BC 下方的抛物线上，连接AP 交BC 于点M ，当AMPM 最大时，求点P 的坐标及AM PM 的最大值；（3）在（2）的条件下，过点P 作x 轴的垂线l ，在l 上是否存在点D ，使△BCD 是直角三角形，若存在，请直接写出点D 的坐标；若不存在，请说明理由．自我巩固1、如图，抛物线343832++-=x x y 与x 轴相交于点A ，点B （A 在B 的左侧），与y 轴相交于点C ，连接AC ，BC ．（1）求△ABC 的面积；（2）如图，点P 是第一象限内抛物线上的动点，过点P 作PE△y 轴，交直线BC 于点E ，当PE+54CE 有最大值时，求PE+54CE 的最大值与点P 的坐标；（3）将抛物线343832++-=x x y 向右平移2个单位得到新抛物线y ′，点F 为原抛物线y 与新抛物线y ′的交点，点M 是原抛物线y 对称轴上一点，当△AFM 是以FM 为腰的等腰三角形时，直接写出点M 的坐标．。

重庆中考专题第十题(最新的哟)二次函数

1. 如图，抛物线y=ax 2+bx+c 图象，则下列结论中:①abc>0;②2a+b<0;③a>31;④c<1.其中正确的结论是 . A.①②③ B.①③④ C.①②④ D.②③④2. 已知:如图,抛物线y=ax 2+bx+c 的图象如图所示，则下列结论：①abc>0； ②2=++c b a ;③a>21; ④b>1.其中正确的结论是 .A.①②B.②③C.③④D.②④3. 已知：如图所示，抛物线y=ax 2+bx+c 的对称轴为x=-1，则下列结论正确的个数是 . ①abc>0 ②a+b+c>0 ③c>a ④2c>bA.①②③④B.①③④C.①②④D.①②③4. 已知二次函数y ＝ax 2＋bx ＋c 的图象与x 轴交于点（-2，0），（x 1，0），且1<x 1<2，与y 轴的正半轴的交点在点（0，2）的上方.下列结论：①a<b ＜0；②2a+c ＞0；③4a ＋c ＜0；④2a-b+1>0.其中正确结论的个数为 . A1个 B2个 C3个 D4个5. 已知:如图所示,抛物线y=ax 2+bx+c 的对称轴为x=-1，且过点(1,-2),则下列结论正确的个数是 . ①abc>0 ②bca +>-1 ③b<-1 ④5a-2b<0 A.①②③④ B.①③④ C.①②④ D.①②③ 6. 已知:如图所示,抛物线y=ax 2+bx+c 的图象如图所示，下列结论：①a<-1;②-1<a<0;③a+b+c<2;④0<b<1.其中正确的个数是 .A.①④B.②③④C.①③④D.②③7. 二次函数y=ax 2+bx+c 的图象如图所示,则a 、b 、c 的大小关系是 . A.a>b>c B.a>c>bC.a>b=cD.a 、b 、c 的大小关系不能确定8. 如图，抛物线y=ax 2+bx+c 图象与x 轴交于A(x 1,0)、B(x 2,0)两点,则下列结论中: ①2a+b<0; ②a<-1;③a+b+c>0; ④0<b 2-4a<5a 2.其中正确的结论有个. A.1个 B.2个 C.3个 D.4个9. 已知:如图所示,抛物线y=ax 2+bx+c 的对称轴为x=-1，与x 轴交于A 、B 两点，交y 轴于点C ，且OB=OC ，则下列结论正确的个数是 . ①b=2a ②a-b+c>-1 ③0<b 2-4ac<4 ④ac+1=b A.1个 B.2个 C.3个 D.4个10. 二次函数y=ax 2+bx+c 的图象如图所示,则在下列各不等式中:①abc<0;②(a+c)2-b 2<0;③b>2a+2c;④3a+c<0.其中正确的个数是 .(1,-2)-1Oyx-1xO1yy O-1xA O2-12yB xxB-1ACyO-1O 1x2y2 -1┙ ┙┙┙3 1y xy-1Ox(2,1)Oyx1A.1个B. 2个C.3个D.4个。

二次函数压轴题集锦带答案(2024年中考真题)

二次函数压轴题集锦带答案(2024年中考真题)1.(24年安徽中考)已知物线2y x bx =-+(b 为常数)的顶点横坐标比抛物线22y x x =-+的顶点横坐标大1. (1)求b 的值；(2)点11(,)A x y 在抛物线22y x x =-+上,点11(,)B x t y h ++在抛物线2y x bx =-+上. (i)若3h t =,且10,0x t >,求h 的值； (ii)若 11x t =-,求h 的最大值.2.(24年包头中考)如图,在平面直角坐标系中,抛物线22yx bxc 与x 轴相交于()1,0A ,B 两点(点A 在点B 左侧),顶点为()2,M d ,连接AM ．(1)求该抛物线的函数表达式;(2)如图1,若C 是y 轴正半轴上一点,连接,AC CM ．当点C 的坐标为10,2⎛⎫ ⎪⎝⎭时,求证:ACM BAM ∠=∠;(3)如图2,连接BM ,将ABM 沿x 轴折叠,折叠后点M 落在第四象限的点M '处,过点B 的直线与线段AM '相交于点D ,与y 轴负半轴相交于点E ．当87BD DE =时,3ABD S △与2M BD S '△是否相等？请说明理由．3.(24年成都中考)如图,在平面直角坐标系xOy 中,抛物线()2:230L y ax ax a a =-->与x 轴交于,A B 两点(点A 在点B 的左侧),其顶点为C ,D 是抛物线第四象限上一点. (1)求线段AB 的长(2)当1a =时,若ACD ∆的面积与ABD ∆的面积相等,求tan ABD ∠的值:(3)延长CD =交x =轴于点E =,当AD DE =时,将ADB ∆沿DE 方向平移得到A EB ''∆.将抛物线L 平移得到抛物线L ',使得点A ',B '都落在抛物线L '上.试判断抛物线L '与L 是否交于某个定点.若是,求出该定点坐标;若不是,请说明理由.4.(24年重庆中考)如图,在平面直角坐标系中,抛物线()240y ax bx a =++≠经过点()1,6-,与y 轴交于点C ,与x 轴交于A B ，两点(A 在B 的左侧),连接tan 4AC BC CBA ∠=，，．(1)求抛物线的表达式(2)点P 是射线CA 上方抛物线上的一动点,过点P 作PE x ⊥轴,垂足为E ,交AC 于点D ．点M 是线段DE 上一动点,MN y ⊥轴,垂足为N ,点F 为线段BC 的中点,连接AM NF ，．当线段PD 长度取得最大值时,求AM MN NF ++的最小值(3)将该抛物线沿射线CA 方向平移,使得新抛物线经过(2)中线段PD 长度取得最大值时的点D ,且与直线AC 相交于另一点K ．点Q 为新抛物线上的一个动点,当QDK ACB ∠∠=时,直接写出所有符合条件的点Q 的坐标．5.(24年浙江中考)已知二次函数2y x bx c =++(b ,c 为常数)的图象经过点(2,5)A -,对称轴为直线12x =-.(1)求二次函数的表达式(1)若点(1,7)B 向上平移2个单位长度,向左平移(0)m m >个单位长度后,恰好落在2y x bx c =++的图象上,求m 的值(3)当2≤a ≤n 时,二次函数2y x bx c =++的最大值与最小值的差为94,求n 的取值范围.6.(24年呼伦贝尔中考)如图,在平面直角坐标系中,二次函数()20y ax bx c a =++≠的图像经过原点和点()4,0A ．经过点A 的直线与该二次函数图象交于点()1,3B ,与y 轴交于点C ．(1)求二次函数的解析式及点C 的坐标;(2)点P 是二次函数图象上的一个动点,当点P 在直线AB 上方时,过点P 作PE x ⊥轴于点E ,与直线AB 交于点D ,设点P 的横坐标为m ． ①m 为何值时线段PD 的长度最大,并求出最大值;①是否存在点P ,使得BPD △与AOC 相似．若存在,请求出点P 坐标;若不存在,请说明理由．7.(24年广州中考)已知抛物线232:621(0)G y ax ax a a a =--++>过点()1,2A x 和点()2,2B x ,直线2:l y m x n =+过点(3,1)C ,交线段AB 于点D ,记CDA 的周长为1C ,CDB △的周长为2C ,且122C C =+．(1)求抛物线G 的对称轴 (2)求m 的值(3)直线l 绕点C 以每秒3︒的速度顺时针旋转t 秒后(045)t ≤<得到直线l ',当l AB '∥时,直线l '交抛物线G 于E ,F 两点． ①求t 的值①设AEF △的面积为S ,若对于任意的0a >,均有S k ≥成立,求k 的最大值及此时抛物线G 的解析式．8.(24年绥化中考)综合与探究如图,在平面直角坐标系中,已知抛物线2y x bx c =-++与直线相交于A ,B 两点,其中点()3,4A ,()0,1B ．(1)求该抛物线的函数解析式．(2)过点B 作BC x ∥轴交抛物线于点C ,连接AC ,在抛物线上是否存在点P 使1tan tan 6BCP ACB ∠=∠．若存在,请求出满足条件的所有点P 的坐标;若不存在,请说明理由．(提示:依题意补全图形,并解答)(3)将该抛物线向左平移2个单位长度得到()2111110y a x b x c a =++≠,平移后的抛物线与原抛物线相交于点D ,点E 为原抛物线对称轴上的一点,F 是平面直角坐标系内的一点,当以点B ,D ,E ,F 为顶点的四边形是菱形时,请直接写出点F 的坐标．9.(24年上海中考)在平面直角坐标系中,已知平移抛物线213y x =后得到的新抛物线经过50,3A ⎛⎫- ⎪⎝⎭和(5,0)B ．(1)求平移后新抛物线的表达式(2)直线x m =(0m >)与新抛物线交于点P,与原抛物线交于点Q ． ①如果PQ 小于3,求m 的取值范围①记点P 在原抛物线上的对应点为P ',如果四边形P BPQ '有一组对边平行,求点P 的坐标．10.(24年乐山中考)在平面直角坐标系xOy 中,我们称横坐标、纵坐标都为整数的点为“完美点”．抛物线222y ax ax a =-+(a 为常数且0a >)与y 轴交于点A ．(1)若1a =,求抛物线的顶点坐标;(2)若线段OA (含端点)上的“完美点”个数大于3个且小于6个,求a 的取值范围;(3)若抛物线与直线y x =交于M ,N 两点,线段MN 与抛物线围成的区域(含边界)内恰有4个“完美点”,求a 的取值范围．11.(24年甘肃武威中考)如图1,抛物线()2y a x h k =-+交x 轴于O,()4,0A 两点,顶点为(2,B ．点C 为OB 的中点．(1)求抛物线2()y a x h k =-+的表达式;(2)过点C 作CH OA ⊥,垂足为H,交抛物线于点E ．求线段CE 的长．(3)点D 为线段OA 上一动点(O 点除外),在OC 右侧作平行四边形OCFD ．①如图2,当点F 落在抛物线上时,求点F 的坐标;①如图3,连接BD ,BF ,求BD BF +的最小值．12.(24年枣庄中考)在平面直角坐标系xOy 中,点()2,3P -在二次函数()230y ax bx a =+->的图像上,记该二次函数图像的对称轴为直线x m =．(1)求m 的值(2)若点(),4Q m -在23y ax bx =+-的图像上,将该二次函数的图像向上平移5个单位长度,得到新的二次函数的图像．当04x ≤≤时,求新的二次函数的最大值与最小值的和(3)设23y ax bx =+-的图像与x 轴交点为()1,0x ,()()212,0x x x <．若2146x x <-<,求a 的取值范围．13.(24年四川广安中考)如图,抛物线223y x bx c =-++与x 轴交于A ,B 两点,与y 轴交于点C ,点A 坐标为(1,0)-,点B 坐标为(3,0)．(1)求此抛物线的函数解析式．(2)点P 是直线BC 上方抛物线上一个动点,过点P 作x 轴的垂线交直线BC 于点D ,过点P 作y 轴的垂线,垂足为点E ,请探究2PD PE +是否有最大值？若有最大值,求出最大值及此时P 点的坐标;若没有最大值,请说明理由．(3)点M 为该抛物线上的点,当45∠=︒MCB 时,请直接写出所有满足条件的点M 的坐标．14.(24年四川南充中考)已知抛物线2y x bx c =-++与x 轴交于点()1,0A -,()3,0B ．(1)求抛物线的解析式;(2)如图1,抛物线与y 轴交于点C ,点P 为线段OC 上一点(不与端点重合),直线PA ,PB 分别交抛物线于点E ,D ,设PAD 面积为1S ,PBE △面积为2S ,求12S S 的值; (3)如图2,点K 是抛物线对称轴与x 轴的交点,过点K 的直线(不与对称轴重合)与抛物线交于点M ,N ,过抛物线顶点G 作直线l x ∥轴,点Q 是直线l 上一动点．求QM QN +的最小值．15.(24年四川泸州中考)如图,在平面直角坐标系xOy 中,已知抛物线23y ax bx =++经过点()3,0A ,与y 轴交于点B,且关于直线1x =对称．(1)求该抛物线的解析式;(2)当1x t -≤≤时,y 的取值范围是021y t ≤≤-,求t 的值;(3)点C 是抛物线上位于第一象限的一个动点,过点C 作x 轴的垂线交直线AB 于点D,在y 轴上是否存在点E,使得以B,C,D,E 为顶点的四边形是菱形？若存在,求出该菱形的边长;若不存在,说明理由．16.(24年河北中考)如图,抛物线21:2C y ax x =-过点(4,0),顶点为Q ．抛物线22211:()222C y x t t =--+-(其中t 为常数,且2t >),顶点为P ．(1)直接写出a 的值和点Q 的坐标．(2)嘉嘉说:无论t 为何值,将1C 的顶点Q 向左平移2个单位长度后一定落在2C 上．淇淇说:无论t 为何值,2C 总经过一个定点．请选择其中一人的说法进行说理．(3)当4t =时①求直线PQ 的解析式.①作直线l PQ ∥,当l 与2C 的交点到x 轴的距离恰为6时,求l 与x 轴交点的横坐标．(4)设1C 与2C 的交点A,B 的横坐标分别为,A B x x ,且A B x x <．点M 在1C 上,横坐标为()2B m m x ≤≤．点N 在2C 上,横坐标为()A n x n t ≤≤．若点M 是到直线PQ 的距离最大的点,最大距离为d ,点N 到直线PQ 的距离恰好也为d ,直接用含t 和m 的式子表示n.17.(24年武汉中考)抛物线215222y x x =+-交x 轴于A ,B 两点(A 在B 的右边),交y 轴于点C ．(1)直接写出点A ,B ,C 的坐标(2)如图(1),连接AC ,BC ,过第三象限的抛物线上的点P 作直线PQ AC ∥,交y 轴于点Q ．若BC 平分线段PQ ,求点P 的坐标(3)如图(2),点D 与原点O 关于点C 对称,过原点的直线EF 交抛物线于E ,F 两点(点E 在x 轴下方),线段DE 交抛物线于另一点G ,连接FG ．若90EGF ∠=︒,求直线DE 的解析式．18.(24年四川德阳中考)如图,抛物线2y x x c =-+与x 轴交于点()1,0A -和点B ,与y 轴交于点C ．(1)求抛物线的解析式;(2)当02x <≤时,求2y x x c =-+的函数值的取值范围;(3)将拋物线的顶点向下平移34个单位长度得到点M ,点P 为抛物线的对称轴上一动点,求PA PM +的最小值．19.(24年湖北中考)如图,二次函数23y x bx =-++交x 轴于(1,0)A -和B ,交y 轴于C .(1)求b 的值.(2)M 为函数图像上一点,满足MAB ACO ∠=∠,求M 点的横坐标.(3)将二次函数沿水平方向平移,新的图像记为L ,L 与y 轴交于点D ,记DC d =,记L 顶点横坐标为n .①求d 与n 的函数解析式.②记L 与x 轴围成的图像为,U U 与ABC ∆重合部分(不计边界)记为W ,若d 随n 增加而增加,且W 内恰有2个横坐标与纵坐标均为整数的点,直接写出n 的取值范围。

重庆中考二次函数25题专题

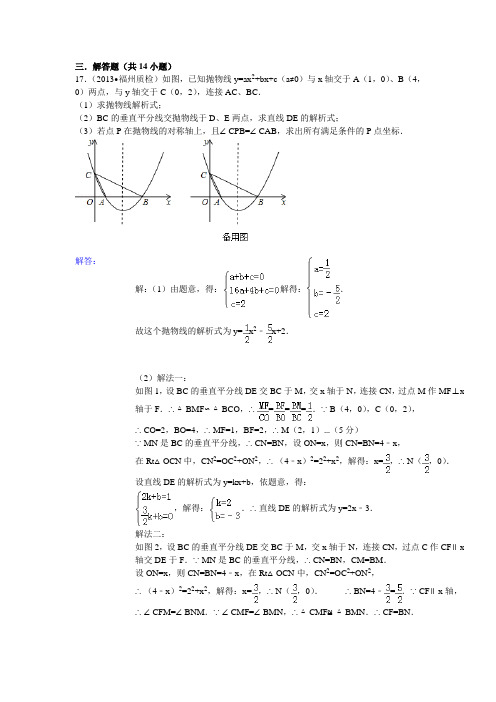
三．解答题（共14小题）17．（2013•福州质检）如图，已知抛物线y=ax2+bx+c（a≠0）与x轴交于A（1，0）、B（4，0）两点，与y轴交于C（0，2），连接AC、BC．（1）求抛物线解析式；（2）BC的垂直平分线交抛物线于D、E两点，求直线DE的解析式；（3）若点P在抛物线的对称轴上，且∠CPB=∠CAB，求出所有满足条件的P点坐标．）由题意，得：解得：y=﹣，∴===x=，∴（，解得：，∴，﹣．∵，，解得：x x+2x=（GA=的坐标为（，﹣，∴NH==1=，点的坐标为（，﹣）或（，18．如图，抛物线y=ax+bx+3与x轴交于A（﹣1，0）、B （3，0）两点，与y轴交于点C，此抛物线的对称轴与抛物线相交于点P，与直线BC相交于点M，连接PB．（1）求点C坐标以及该抛物线的关系式；（2）连接AC，在x轴下方的抛物线上有点D，使S△ABD=S△ABC，求点D的坐标；（3）抛物线上是否存在点Q，使△QMB与△PMB的面积相等？若存在，直接写出点Q的坐标；若不存在，说明理由；（4）在第一象限、对称轴右侧的抛物线上是否存在一点R，使△RPM与△RMB的面积相等？若存在，直接写出点R的坐标；若不存在，说明理由．解得：×，∴±，﹣联立，解得：或）或或﹣=1+C（5，8）两点，点D是抛物线顶点，E是对称轴与直线AC的交点，F与E关于点D对称．（1）求抛物线的解析式；（2）求证：∠AFE=∠CFE；（3）在抛物线的对称轴上是否存在点P，使△AFP与△FDC相似？若有，请求出所有符合条件的点P的坐标；若没有，请说明理由．，解得，===只需=之间）或（点20．如图，抛物线y=ax+bx过点A（4，0）正方形OABC的边BC与抛物线的一个交点为D，点D的横坐标为3，点M在y轴的负半轴上，直线L过点D、M两点且与抛物线的对称轴将于点H，tan∠OMD=．（1）写出D点坐标（3，4），a=﹣，b=，抛物线的对称轴为x=2．（2）求M点坐标，H点坐标；（3）如果点Q是抛物线对称轴上一个动点，那么是否存在点Q使得以点O、M、Q、H为顶点的四边形是平行四边形？若存在，求出点Q的坐标；若不存在，请说明理由．得，解得=，得解得21．（2011•莆田）已知抛物线y=ax+bx+c的对称轴为直线x=2，且与x轴交于A、B两点，与y轴交于点C，其中A（1，0），C（0，﹣3）．（1）求抛物线的解析式；（2）若点P在抛物线上运动（点P异于点A）．①如图1．当△PBC面积与△ABC面积相等时．求点P的坐标；②如图2．当∠PCB=∠BCA时，求直线CP的解析式．）由题意，得，解得解方程组，得解方程组得），（（∴，∴∴的解析式为22．（2005•山西）矩形OABC在直角坐标系中的位置如图所示，A、C两点的坐标分别为A （6，0）、C（0，3），直线y=x与BC边相交于点D．（1）求点D的坐标；（2）若抛物线y=ax2+bx经过D、A两点，试确定此抛物线的表达式；（3）P为x轴上方（2）中抛物线上一点，求△POA面积的最大值；（4）设（2）中抛物线的对称轴与直线OD交于点M，点Q为对称轴上一动点，以Q、O、M为顶点的三角形与△OCD相似，求符合条件的Q点的坐标．xx得解之得﹣+＜×==3。

重庆中考二次函数相关的存在性问题习题练习(含答案)

2018届重庆中考复习：二次函数相关的存在性问题习题练习（含答案）一．等腰三角形存在性问题：例1．如图①，抛物线y ＝ax 2－6x ＋c 与x 轴交于点A(－5，0)、B(－1，0)，与y 轴交于点C(0，－5)，点P 是抛物线上的动点，连接PA 、PC ，PC 与x 轴交于点D.(1)求该抛物线所对应的函数解析式；(2)过点P 作y 轴的平行线交x 轴于点H ，交直线E ，如图②.①若∠APE＝∠CPE，求证：AE EC ＝37；②△APE 能否为等腰三角形？若能，请求出此时点P 的坐标；若不能，请说明理由．针对训练：1．如图①，抛物线y＝ax2＋bx＋4交x轴于A、B两点(点A在点B左侧)，交y轴于点C，连接AC、BC，其中CO＝BO＝2AO.(1)求抛物线的解析式；(2)点Q为直线BC上方的抛物线上一点，过点Q作QE∥AC交BC于E，作QN⊥x轴于N，交BC于M，当△EMQ 的周长L最大时，求点Q的坐标及L的最大值；(3)如图②，在(2)的结论下，连接AQ分别交BC于F，交OC于G，四边形BOGF从F开始沿射线FC平移，同时点P从C开始沿折线CO－OB运动，且点P的运动速度为四边形BOGF平移速度的2倍，当点P到达B 点时，四边形BOGF停止运动．设四边形BOGF平移过程中对应的图形为B1O1G1F1，当△PFF1为等腰三角形时，求B1F的长度．2．如图，在平面直角坐标系中，抛物线y ＝－12x 2＋2x ＋3与x 轴交于A ，B 两点(点A 在点B 左侧)，与y 轴交于点C ，连接BC ，过点A 作AD∥BC 交y 轴于点D.现将抛物线以每秒3个单位长度的速度沿射线AD 方向平移，抛物线上的点A 、C 平移后的对应点分别记作A′、C′，当△A′C′B 是以C′B 为底边的等腰三角形时，将等腰△A′C′B 绕点D 逆时针旋转α°(0°<α<180°)，记旋转中的△A′C′B 为△A′′C′′B′，若直线A′′C′′与y 轴交于点K ，直线A ′′C ′′与直线AD 交于点I ，则△DKI 是否能为等腰三角形？若能，求出所有符合条件的KI 的长；若不能，说明理由．三角形全等、相似存在性问题：例2．如图，矩形OABC 的边OA 、OC 分别在x 轴、y 轴的正半轴上，且OA ＝1，OC ＝2，以O 为直角顶点作Rt △COD ，OD ＝3.已知二次函数y ＝x 2＋52x －32的图象过D 、B 两点，连接BD ，E 为射线DB 上的一点，过E 作EH⊥x 轴于H ，点P 为抛物线对称轴上一点，且在x 轴上方，点Q 在第二象限的抛物线上，是否存在P 、Q 使得以P 、O 、Q 为顶点的三角形与△DEH 全等？若存在，请求出点Q 的坐标，如果不存在，请说明理由．针对训练：1．如图，抛物线与x轴交于A(－1，0)、B(3，0)两点，与y轴交于点C(0，－3)，设抛物线的顶点为D.(1)求该抛物线的解析式与顶点D的坐标；(2)以B、C、D为顶点的三角形是直角三角形吗？为什么？(3)探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCD相似？若存在，请指出直接写出点P的坐标；若不存在，请说明理由．2．如图，已知一条直线过点(0，4)，且与抛物线y＝14x2交于A，B两点，其中点A的横坐标是－2.(1)求这条直线的解析式及点B的坐标．(2)在x轴上是否存在点C，使得△ABC是直角三角形？若存在，求出点C的坐标，若不存在，请说明理由．3．如图，已知抛物线y ＝15x 2＋85x －4与x 轴交于A 、B 两点，与y 轴交于C 点，且A(2，0)，C(0，－4)，直线l ：y ＝－12x －4与x 轴交于D 点，点P 是抛物线y ＝15x 2＋85x －4上的一动点，过点P 作PE⊥x 轴，垂足为E ，交直线l 于点F.过点P 作PH⊥y 轴，垂足为H ，连接AC ，PC ，试问当P 点横坐标为何值时，使得以点P ，C ，H 为顶点的三角形与△ACD 相似？4．如图，已知抛物线y ＝－x 2＋2x ＋3与x 轴交于A 、B 两点，与y 轴交于点C ，顶点为D ，点N 在抛物线上，其横坐标为52.连接CN ，点P 为直线CN 上的动点，点Q 在抛物线上，连接CQ 、PQ 得△CPQ，当△CPQ 为等腰直角三角形时，求线段CP 的长度．与四边形有关的存在性问题：例3．如图，抛物线y＝x2－2x－3与x轴交A、B两点(A点在B点左侧)，直线l与抛物线交于A、C 两点，其中C点的横坐标为2.(1)求A、B两点的坐标及直线AC的函数表达式；(2)P是线段AC上的一个动点，过P点作y轴的平行线交抛物线于E点，求线段PE长度的最大值；(3)点G是抛物线上的动点，在x轴上是否存在点F，使以A、C、F、G四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的F点坐标；如果不存在，请说明理由．1．如图，抛物线y＝a(x＋1)2＋4(a≠0)与x轴交于A，C两点，与直线y＝x－1交于A，B两点，直线AB与抛物线的对称轴交于点E.连接CE，将△CEB补成矩形，使△CEB上的两个顶点成为矩形一边的两个顶点，第三个顶点落在矩形这一边的对边上，求出矩形未知顶点的坐标．2．如图，抛物线y＝x2＋2x－3交x轴于点A，B.点C是点A关于点B的对称点，点F是线段BC的中点，直线l过点F且与y轴平行．在直线l上取点M，在抛物线上取点N，使以点A，C，M，N为顶点的四边形是平行四边形，求点N的坐标．3．如图，在平面直角坐标系xOy 中，抛物线y ＝ax 2－2ax －3a(a ＜0)与x 轴交于A 、B 两点(点A 在点B 的左侧)，经过点A 的直线l ：y ＝kx ＋b 与y 轴负半轴交于点C ，与抛物线的另一个交点为D ，且CD ＝4AC. (1)直接写出点A 的坐标，并求直线l 的函数表达式(其中k 、b 用含a 的式子表示)； (2)点E 是直线l 上方的抛物线上的一点，若△ACE 面积的最大值为54，求a 的值；(3)设P 是抛物线的对称轴上的一点，点Q 在抛物线上，以点A 、D 、P 、Q 为顶点的四边形能否成为矩形？若能，求出点P 的坐标；若不能，请说明理由．二次函数相关的存在性问题答案等腰三角形存在性问题：例1. 解：(1)∵抛物线y ＝ax 2－6x ＋c 过点B(－1，0)、 C(0，－5)．∴⎩⎪⎨⎪⎧a ＋6＋c ＝0，c ＝－5，解得⎩⎪⎨⎪⎧a ＝－1，c ＝－5.∴该抛物线为y ＝－x 2－6x －5. (2)①证明：∵PE∥y 轴，∴PH ⊥AO ， ∴∠AHP ＝∠DHP＝90°.又∵PH＝PH ，∠APE ＝∠CPE， ∴△AHP ≌△DHP ，∴AH ＝DH.设点P(x ，－x 2－6x －5)，∴AH ＝DH ＝x －(－5)＝x ＋5，PH ＝－x 2－6x －5.由PE∥y 轴，得PH DH ＝CODO，则－x 2－6x －5x ＋5＝5－2x －5.∵x ＋5≠0，∴x ＋1＝52x ＋5，解得x 1＝－72，x 2＝0(不符合)．∴OH ＝72，AH ＝32，∴AE EC ＝AH HO ＝37.②能，分三种情况讨论．Ⅰ、若PA ＝PE.由OA ＝OC ＝5，得∠AEP＝∠PAE＝∠ACO＝45°，∴∠APE ＝90°.此时点P 与点B 重合． ∴此时点P 的坐标为(－1，0)．Ⅱ、若AP ＝AE.由题意，可得∠APE＝∠AEP＝45°，又∵PH⊥AO，∴AH ＝PH ，即－x 2－6x －5＝x ＋5. 解得x 1＝－2，x 2＝－5(不符合)．则y ＝3，则点P 的坐标为(－2，3)．Ⅲ、∵点A 、C 的坐标为(－5，0)、(0，－5)．∴直线AC 的解析式为y ＝－x －5.∴点E 的坐标为(x ，－x －5)．若AE ＝PE ，则PE ＝|－x 2－6x －5－(－x －5)|＝|－x 2－5x|. 又AE ＝2AH ＝2(x ＋5)，则－x 2－5x ＝2(x ＋5)或x 2＋5x ＝2(x ＋5)， (x ＋5)(2＋x)＝0或(x ＋5)(2－x)＝0.解得：x 1＝－2，x 2＝－5(不符合)，x 3＝2，x 4＝－5(不符合)．当x 1＝－2时，y 1＝6 2－7，当x 3＝2时，y 3＝－6 2－7. ∴此时点P 的坐标为(－2，6 2－7)或(2，－6 2－7)．综上所述可得点P 的坐标为(－2，3)、(－1，0)、(－2，6 2－7)或(2，－6 2－7)．针对训练：1. 解：(1)当x ＝0时，y ＝4，则C(0，4)， ∴OC ＝4.又∵OC＝OB ＝2OA ， ∴OB ＝4，OA ＝2，∴B(4，0)，A(－2，0)．∴⎩⎪⎨⎪⎧16a ＋4b ＋4＝0，4a －2b ＋4＝0，∴⎩⎪⎨⎪⎧a ＝－12，b ＝1.∴抛物线的解析式为y ＝－12x 2＋x ＋4.(2)∵B(4，0)，C(0，4)，∴直线BC 的解析式为y ＝－x ＋4. ∴∠MBN ＝∠NMB＝∠QME＝45°，延长QE 交y 轴于R. 又∵EQ∥AC，OC ∥QM ，∴∠EQM ＝∠CRQ＝∠ACO，∴tan ∠EQM ＝tan ∠ACO ＝OA OC ＝12.如图，过E 作EH⊥QM 于H ，设EH ＝m ，则QH ＝2m ，EQ ＝5m ，MH ＝m ，EM ＝2m ，∴QM ＝3m ，∴m ＝13QM.设Q(x ，－12x 2＋x ＋4)，则M(x ，－x ＋4)，∴L ＝3＋2＋53QM ＝3＋2＋53⎣⎢⎡⎦⎥⎤（－12x 2＋x ＋4）－（－x ＋4）＝3＋2＋53(－12x 2＋2x) ＝－3＋2＋56(x －2)2＋6＋2 2＋2 53，又∵0<x<4，∴当x ＝2时，L max ＝6＋2 2＋2 53，∴Q(2，4)．(3)∵Q(2，4)，A(－2，0)，∴AQ 的解析式为y ＝x ＋2，∴G(0，2)，F(1，3)， ∴BF ＝B 1F 1＝3 2，△CFG 为等腰三角形．设FF 1＝2t ，则PC ＝2t.∴F 1(1－t ，t ＋3)，当P 在线段CO 上运动时，则0<t≤2且P(0，4－2t)①若FP ＝FF 1时，则1＋(1－2t)2＝2t 2，∴t 1＝t 2＝1，∴FF 1＝2t ＝2，∴B 1F ＝B 1F 1－FF 1＝2 2；②若PF ＝PF 1时，则1＋(1－2t)2＝(1－t)2＋(1－3t)2，∴t 1＝0，t 2＝23.又∵0<t≤2，∴t ＝23.∴FF 1＝2t ＝2 23，∴B 1F ＝B 1F 1－FF 1＝7 23； ∴B 1F ＝B 1F 1－FF 1＝4－2 2. 综上所述：B 1F ＝7 23，5 22，2 2或4－2 2.③若F 1P ＝F 1F 时，则(1－t)2＋(1－3t)2＝2t 2，∴t 1＝t 2＝12.∴FF 1＝2t ＝22，∴B 1F ＝B 1F 1－FF 1＝5 22；当P 在线段OB 上运动时，则2<t<4且P(2t －4，0)．∵∠F 1FP>90°，∴要使△PFF 1为等腰三角形，则只有FP ＝FF 1，∴9＋(2t －5)2＝2t 2，∴t ＝5±2 2. 又∵2<t<4，∴t ＝5－2 2， ∴FF 1＝2t ＝5 2－4，2. 解：令y ＝0，－12x 2＋2x ＋3＝0.解得x 1＝－2，x 2＝3 2.∴A(－2，0)，B(3 2，0)．∵当x ＝0时，y ＝3，∴C(0，3)． 3－00－3 2＝－22，∵AD ∥BC ，∴tan ∠BAD ＝22.设A′(2t －2，－t)则C′(2t ，3－t)，当△A′C′B 是以C′B 为底边的等腰三角形时，(2t －4 2)2＋t 2＝11，∴t 1＝3(舍去)，t 2＝73.∴A ′(4 23，－73)，C ′(7 23，23)．设直线A′C′的表达式为y ＝kx ＋b ，将A′，C ′的坐标代入解得k ＝3 22，b ＝－193.∴y ＝3 22x －193.D(0，－1)到直线A′C′：y ＝3 22x －193的距离d ＝16 2233.① 如图①，DK ＝DI ，∠KDI 为钝角，KI ＝32（33＋11）33.②如图②，DK ＝DI ，∠KDI 为锐角，KI ＝32（33－11）33.如图③，KD ＝KI 或ID ＝IK ，KI ＝8 1111.综上所述，△KDI 为等腰三角形，符合条件的KI 的长为32（ 33＋ 11）33、32（ 33－ 11）33、8 1111.三角形全等、相似存在性问题：例2：解：设直线BD 的解析式为y ＝mx ＋n ，把B(1，2)，D(－3，0)代入BD的解析式得到y ＝12x ＋32.①若△OPQ≌△DHE.过点P 作PT⊥y 轴于T ，过点Q 作QS⊥PT 于S.如图①.则有∠POQ＝∠HDE，∠OPQ ＝∠DHE＝90°，则有PQ PO ＝tan ∠POQ ＝tan ∠HDE ＝AB AD ＝12.易证△QSP∽△PTO，从而可得SQ ＝SP ＝PQ ＝1，∴SQ ＝12TP ，SP ＝12TO.∵x P ＝－522×1＝－54，∴PT ＝54，SQ ＝58.设OT ＝p ，则有SP ＝p 2，则Q(－54－p 2，p －58)，代入二次函数解析式，并整理得p 2－4p －394＝0.解得p ＝4±552，∵点Q 在第二象限，∴－54－p 2＜0且p －58＞0，∴p ＞58，∴p ＝4＋552.此时Q(－9＋554，11＋4 558)． ②若△QPO≌△DHE，同①可得Q(－54－2p ，p －52)，代入二次函数解析式，并整理得4p 2－p －916＝0，解得p 3＝1＋108，p 4＝1－108(舍)，此时Q(－6＋104，－19－108)(舍)．③若△PQO≌△DHE，过点Q 作QS⊥x 轴于S ，过点P 作PT⊥QS 于T.如图②.易证△PTQ∽△QSO，从而可得PT QS ＝PQ QO ＝DHHE＝2.设PT ＝p ，则有QS ＝p 2，∴点Q 的坐标为(－54－p ，p2)，代入抛物线y ＝x 2＋52x －32，结合p ＞0，可得p ＝1＋5 24，从而可得Q(－6＋5 26，1＋5 28)．④若△OQP≌△DHE，同③可得Q(－9＋654，4＋652)．综上所述，满足题意的点Q 为：(－9＋554，11＋4 558)或(－9－654，4＋652)或Q(－6－5 24，1＋5 28)．针对训练：1. 解：(1)设该抛物线的解析式为y ＝ax 2＋bx ＋c ，由抛物线与y 轴交于点C(0，－3)，可知c ＝－3.把A(－1，0)、B(3，0)代入，得⎩⎪⎨⎪⎧a －b －3＝0，9a ＋3b －3＝0，解得⎩⎪⎨⎪⎧a ＝1，b ＝－2.∴抛物线的解析式为y ＝x 2－2x －3.∵y＝x 2－2x －3＝(x －1)2－4， ∴顶点D 的坐标为(1，－4)．(2)以B 、C 、D 为顶点的三角形是直角三角形．如图①，过点D 分别作x 轴、y 轴的垂线，垂足分别为E 、F.在Rt △BOC 中，OB ＝3，OC ＝3，∴BC 2＝OB 2＋OC 2＝32＋32＝18.在Rt △CDF 中，DF ＝1，CF ＝OF －OC ＝4－3＝1，∴CD 2＝CF 2＋DF 2＝12＋12＝2.在Rt △BDE 中，DE ＝4，BE ＝OB －OE ＝3－1＝2，∴BD 2＝BE 2＋ED 2＝22＋42＝20.∴BC 2＋CD 2＝BD 2，故△BCD 为直角三角形．(3)存在．连接AC ，可知Rt △COA ∽Rt △BCD ，得符合条件的点P 为(0，0)．如图②，过A 作AP 1⊥AC 交y 轴正半轴于P 1，可知Rt △CAP 1∽Rt △COA ∽Rt △BCD ，求得符合条件的点为P 1(0，13)．过C 作CP 2⊥AC 交x 轴正半轴于P 2，可知Rt △P 2CA ∽Rt △COA ∽Rt △BCD ，求得符合条件的点为P 2(9，0)．∴综上所述，点P 的坐标为(0，0)或(0，13)或(9，0)．2. 解：(1)∵点A 是直线与抛物线的交点，且横坐标为－2，∴y ＝14×(－2)2＝1，∴A 点的坐标为(－2，1)，设直线的解析式为y ＝kx ＋b ，将(0，4)，(－2，1)代入得⎩⎪⎨⎪⎧b ＝4，－2k ＋b ＝1，解得⎩⎪⎨⎪⎧k ＝32，b ＝4.∴直线的解析式为y ＝32x ＋4.∵直线与抛物线相交，∴32x ＋4＝14x 2，解得x ＝－2或x ＝8，当x ＝8时，y ＝16， ∴点B 的坐标为(8，16)；(2)如图，过点B 作BG∥x 轴，过点A 作AG∥y 轴，交点为G ，∵由A(－2，1)，B(8，16)可求得AB 2＝AG 2＋BG 2＝325.设点C(m ，0)，同理可得AC 2＝(m ＋2)2＋12＝m 2＋4m ＋5， BC 2＝(m －8)2＋162＝m 2－16m ＋320.①若∠BAC＝90°，则AB 2＋AC 2＝BC 2，即325＋m 2＋4m ＋5＝m 2－16m ＋320，解得：m ＝－12；②若∠ACB＝90°，则AB 2＝AC 2＋BC 2，即325＝m 2＋4m ＋5＋m 2－16m ＋320，解得：m ＝0或m ＝6；③若∠ABC＝90°，则AB 2＋BC 2＝AC 2，即m 2＋4m ＋5＝m 2－16m ＋320＋325，解得：m ＝32；∴点C 的坐标为(－12，0)，(0，0)，(6，0)，(32，0)．3. 解：(1)由题意知A(2，0)，C(0，－4)，对于y ＝－12x －4，令y ＝0，解得x ＝－8，∴D(－8，0)，∴OD ＝8.∵A(2，0)、C(0，－4)，∴AD ＝2－(－8)＝10.∵AC 2＝22＋42＝20，DC 2＝82＋42＝80，AD 2＝100，设P(n ，15n 2＋85n －4)，CH ＝|15n 2＋85n|，以P 、C 、H 为顶点的三角形与△ACD 相似，分两种情况：ⅰ)当△ACD∽△CHP 时，AC CD ＝CHHP，即2 54 5＝－15n 2－85n －n 或2 54 5＝15n 2＋85n －n ，解得n 1＝0(舍)，n 2＝－5.5，或n 3＝0(舍)，n 4＝－10.5；ⅱ)当△ACD∽△PHC 时，AC CD ＝PHHC，即2 54 5＝－n －15n 2－85n 或2 54 5＝－n 15n 2＋85n ，解得n 5＝0(舍)，n 6＝2，或n 7＝0(舍)，n 8＝－18；综上所述，当P 点横坐标为－5.5或－10.5或2或－18时，以P 、C 、H 为顶点的三角形与△ACD 相似．4. 解：把x ＝52代入y ＝－x 2＋2x ＋3，得y ＝74.∴N(52，74)．∵C(0，3)，∴直线CN 的解析式为y ＝－12x ＋3.设P(x ，－12x ＋3)，显然C 不可能为直角顶点，①当点P 为直角顶点，且在线段CN 上时：∵PC ＝PQ ，∴Q(32x ，x 2＋3)．∴－94x 2＋3x ＋3＝x2＋3，解得x ＝109或x ＝0.∴P 1(109，229)或P 1(0，3)(舍)．∴CP 1＝⎝ ⎛⎭⎪⎫1092＋（3－229）2＝5 59. ②当点P 为直角顶点，且在CN 延长线上时：∵PC ＝PQ ，∴Q(x 2，－32x ＋3)，∴－14x 2＋x ＋3＝－32x ＋3，解得x ＝10或x ＝0(舍)，∴P 2(10，－2)，∴CP 2＝（10）2＋（3＋2）2＝5 5.③当点Q 为直角顶点，且在直线CN 上方的抛物线上时：∵CQ ＝PQ ，∴Q(34x ，3＋14x)，∴－916x 2＋32x ＋3＝3＋14x ，解得x ＝209或x ＝0(舍)．∴P 3(209，179)，∴CP 3＝10 59.④当点Q 为直角顶点，且在直线CN 下方的抛物线上时：∵CQ ＝PQ ，∴Q(x 4，－34x ＋3)．∴－116x 2＋12x ＋3＝－34x ＋3，∴P 4(20，－7)，∴CP 4＝10 5.综上所述，CP 的长度为5 59，5 5，10 59，10 5.与四边形有关的存在性问题：例3. 解：(1)令y ＝0，解得x 1＝－1或x 2＝3， ∴A(－1，0)，B(3，0)；将C 点的横坐标x ＝2代入y ＝x 2－2x －3，得y ＝－3， ∴C(2，－3)．∴直线AC 的函数解析式是y ＝－x －1. (2)设P 点的横坐标为x(－1≤x≤2)，则P 、E 的坐标分别为：P(x ，－x －1)，E(x ，x 2－2x －3)． ∵P 点在E 点的上方，∴PE ＝(－x －1)－(x 2－2x －3)＝－x 2＋x ＋2＝－(x －12)2＋94.∴当x ＝12时，PE 的最大值为94.(3)①如图①，AF 为平行四边形的边时，AF 綊GC ∵G(0，－3)，GC ＝2，∴AF ＝2，∵A(－1，0)， ∴F 1(－3，0)，F 2(1，0)；②如图②，AF 为平行四边形的对角线时，则平行四边形ACFG 的对称中心为AF 中点，且这个对称中点在x 轴上，而顶点G 与C 也关于这个对称中心成中心对称，因为y C ＝－3，所以y G ＝3，对y ＝x 2－2x －3，令y ＝3，即x 2－2x －3＝3，解得x ＝1±7，所以G(1＋7，3)，G ′(1－7，3)，所以对称中心为(3＋72，0)或(3－72，0)，故F 3(4＋7，0)，F 4(4－7，0)．综上所述，存在4个这样的点F ，分别是F 1(－3，0)，F 2(1，0)，F 3(4＋7，0)，F 4(4－7，0)．针对训练：1. 解：∵由题意知A(1，0)，把它代入y ＝a(x ＋1)2＋4，得a ＝－1，∴抛物线的解析式为y ＝－(x ＋1)2＋4，即y ＝－x 2－2x ＋3.解方程－x 2－2x ＋3＝x －1得x 1＝1(舍)，x 2＝－4，∴B(－4，－5)．由－x 2－2x ＋3＝0，得x 1＝－3，x 2＝1(舍去)． ∴C(－3，0)．∵C(－3，0)，E(－1，－2)，B(－4，－5)， ∴CE ＝2 2，BE ＝3 2，CB ＝26. ∴∠CEB ＝90°.(i)以BC 为对角线，点E 矩形的顶点时，如图①所示，易求得直线CD 的解析式为y ＝x ＋3，直线BD 的解析式为y ＝－x －由⎩⎪⎨⎪⎧y ＝x ＋3，y ＝－x －9得⎩⎪⎨⎪⎧x ＝－6，y ＝－3.此时D(－6，－3)．(ii)以BC 为边，点E 在BC 对边上时，如图②所示，过点B 作y 轴的平行线交x 轴于点N ，过点M 作MT⊥BN.由面积关系得BM ＝6 2613.由△BTM∽△CNB，得BT CN ＝MT BN ＝BM BC. ∴BT ＝613，MT ＝3013.∴M(－2213，－7113)．过点F 作FK⊥x 轴于点K ，由△FKC∽△PNB，得FK CN ＝CK BN ＝FC CB .∴FK ＝613，CK ＝3013.∴F(－913，－613)． ∴当B ，E 在矩形同一边时，未知点的坐标为D(－6，－3)，当B ，C 在矩形同一边时，未知点的坐标为M(－2213，－7113)，F(－913，－613)．2. 解：∵x 2＋2x －3＝0， ∴A(－3，0)，B(1，0)．∵点C 是点A 关于点B 的对称点， ∴点C 的坐标是C(5，0)．∵点F 是线段BC 的中点，B(1，0)，C(5，0)， ∴点F 的坐标为F(3，0)．∵直线l 过点F 且与y 轴平行， ∴直线l 的函数表达式为x ＝3.∵点M 在直线l 上，点N 在抛物线上，∴设点M 的坐标为M(3，m)，点N 的坐标为N(n ，n 2＋2n －3)． ∵A(－3，0)，C(5，0)，∴AC ＝8. 分情况讨论：①若线段AC 是以点A ，C ，M ，N 为顶点的平行四边形的边，则MN∥AC，且MN ＝AC ＝8.当点N 在点M 的左侧时，MN ＝3－n.∴3－n ＝8，解得n ＝－5.∴N 点的坐标为N(－5，12)．当点N 在点M 的右侧时，MN ＝n －3.∴n－3＝8，解得n ＝11.∴N 点的坐标为N(11，140)． ②若线段AC 是以点A ，C ，M ，N 为顶点的平行四边形的对角线，由“点C 与点A 关于点B 中心对称”知：点M 与点N 关于点B 中心对称．故⎩⎪⎨⎪⎧3＋n ＝2，m ＋n 2＋2n －3＝0，解得⎩⎪⎨⎪⎧n ＝－1，m ＝4，即点N 的坐标为(－1，－4)．综上所述，当点N 的坐标为(－5，12)，(11，40)，(－1，－4)时，以点A ，C ，M ，N 为顶点的四边形是平行四边形．3. 解：(1)A(－1，0)；∵直线l 经过点A ，∴0＝－k ＋b ，解得b ＝k.∴直线l 的表达式为y ＝kx ＋k.令ax 2－2ax －3a ＝kx ＋k ，即ax 2－(2a ＋k)x －3a －k ＝0. ∵CD ＝4AC ，∴点D 的横坐标为4.∴－3－ka＝－1×4，∴k ＝a.∴直线l 的函数表达式为y ＝ax ＋a.(2)如图，过点E 作EF∥y 轴，交直线l 于点F.设E(x ，ax 2－2ax －3a)，则F(x ，ax ＋a)．EF ＝ax 2－2ax －3a －(ax ＋a)＝ax 2－3ax －4a. S △ACE ＝S △AFE －S △CFE ＝12(ax 2－3ax －4a)(x ＋1)－12(ax 2－3ax －4a)x努力的你，未来可期!拼搏的你，背影很美！＝12(ax 2－3ax －4a)＝12a(x －32)2－258a ， ∴△ACE 面积的最大值为－258a. ∵△ACE 面积的最大值为54， ∴－258a ＝54，解得a ＝－25.(3)令ax 2－2ax －3a ＝ax ＋a ，即ax 2－3ax －4a ＝0，解得x 1＝－1，x 2＝4.∴D(4，5a)．∵y ＝ax 2－2ax －3a ，∴抛物线的对称轴为x ＝1.设P(1，m)，①若AD 是矩形的一条边，则Q(－4，21a)．∴m＝21a ＋5a ＝26a ，则P(1，26a)．∵四边形ADPQ 为矩形，∴∠ADP ＝90°.∴AD 2＋PD 2＝AP 2，∴52＋(5a)2＋(1－4)2＋(26a －5a)2＝(－1－1)2＋(26a)2，即a 2＝17，∵a ＜0，∴a ＝－77，∴P 1(1，－26 77)．②若AD 是矩形的一条对角线，则线段AD 的中点坐标为(32，5a 2)，Q(2，－3a)， m ＝5a －(－3a)＝8a ，则P(1，8a)．∵四边形APDQ 为矩形，∴∠APD ＝90°.∴AP 2＋PD 2＝AD 2.∴(－1－1)2＋(8a)2＋(1－4)2＋(8a －5a)2＝52＋(5a)2，即a 2＝14， ∵a ＜0，∴a ＝－12.∴P 2(1，－4)．综上所述，以点A 、D 、P 、Q 为顶点的四边形能成为矩形，点P的坐标为(1，－26 77)或(1，－4)．。

《二次函数压轴题》(共59题)2022年中考专练附答案(重庆专用)

【分析】（1）先确定点F的位置，可设点N（m，m2﹣2m﹣3），则点F（m，2m﹣6），可得|NF|＝（2m﹣6）﹣（m2﹣2m﹣3）＝﹣m2+4m﹣3，根据二次函数的性质得m 2时，NF取到最大值，此时MN取到最大值，此时HF＝2，此时F（2，﹣2），在x轴上找一点K（，0），连接CK，过点F作CK的垂线交CK于点J点，交y轴于点P，sin∠OCK ，直线KC的解析式为：y ，从而得到直线FJ的解析式为：y 联立解出点J（，）得FP PC的最小值即为FJ的长，且|FJ| 最后得出|HF+FP PC|min ；
【解析】解：（1）如图1
∵抛物线y＝x2﹣2x﹣3与x轴交于点A，B（点A在点B的左侧），交y轴于点C
∴令y＝0解得：x1＝﹣1，x2＝3，令x＝0，解得：y＝﹣3，
∴A（﹣1，0），B（3，0），C（0，﹣3）
∵点D为抛物线的顶点，且 1， 4
∴点D的坐标为D（1，﹣4）
∴直线BD的解析式为：y＝2x﹣6，
故直线AB的表达式为：y＝x﹣1，
过点P作y轴的平行线交AB于点H，
设点P（x，x2+4x﹣1），则H（x，x﹣1），
△PAB面积S PH×（xB﹣xA）（x﹣1﹣x2﹣4x+1）×（0+3） x2 x，
∵ 0，故S有最大值，当x 时，S的最大值为；
（3）抛物线的表达式为：y＝x2+4x﹣1＝（x+2）2﹣5，
（2）首先利用待定系数法求出点D′坐标，设N（1，n），∵C（0，2 ），D′（5，），则NC2＝1+（n﹣2 ）2，D′C2＝52+（ 2 ）2，D′N2＝（5﹣1）2+（ n）2，分三种情形分别构建方程求出n的值即可解决问题．

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1、（12分）如图, 已知抛物线c bx x y ++=221与y 轴相交于C ，与x 轴相交于A 、B ，点A 的坐标为（2，0），点C 的坐标为（0，-1）.（1）求抛物线的解析式；（2）点E 是线段AC 上一动点，过点E 作DE ⊥x 轴于点D ，连结DC ，当△DCE 的面积最大时，求点D 的坐标；（3）在直线BC 上是否存在一点P ，使△ACP 为等腰三角形，若存在，求点P 的坐标，若不存在，说明理由.解：（1）∵二次函数c bx x y ++=221的图像经过点A （2，0）C(0,－1) ∴⎩⎨⎧-==++1022c c b 解得： b =－21 c =－1-------------------2分 ∴二次函数的解析式为121212--=x x y --------3分（2）设点D 的坐标为（m ，0）（0＜m ＜2）∴ OD =m ∴AD =2-m由△AD E ∽△AOC 得，OC DE AO AD = --------------4分 ∴122DE m =- ∴DE =22m ------------------------------------5分 ∴△CDE 的面积=21×22m -×m =242m m +-=41)1(412+--m 当m =1时，△CDE 的面积最大∴点D 的坐标为（1，0）--------------------------8分（3）存在由(1)知：二次函数的解析式为121212--=x x y 设y=0则1212102--=x x 解得：x 1=2 x 2=－1 ∴点B 的坐标为（－1，0） C （0，－1）备用图题图26设直线BC 的解析式为：y =kx ＋b∴ ⎩⎨⎧-==+-10b b k 解得：k =-1 b =-1 ∴直线BC 的解析式为: y =－x －1在Rt △AOC 中，∠AOC=900 OA=2 OC=1由勾股定理得：AC=5∵点B(－1,0) 点C （0，－1）∴OB=OC ∠BCO=450①当以点C 为顶点且PC=AC=5时，设P(k , －k －1)过点P 作PH ⊥y 轴于H∴∠HCP=∠BCO=450CH=PH=∣k ∣ 在Rt △PCH 中k 2+k 2=()25 解得k 1=210， k 2=－210 ∴P 1（210，－1210-） P 2（－210，1210-）---10分 ②以A 为顶点，即AC=AP=5设P(k , －k －1)过点P 作PG ⊥x 轴于GAG=∣2－k ∣ GP=∣－k －1∣在Rt △APG 中 AG 2＋PG 2=AP 2（2－k )2+(－k －1)2=5解得：k 1=1,k 2=0(舍)∴P 3(1, －2) ----------------------------------11分③以P 为顶点，PC=AP 设P(k , －k －1)过点P 作PQ ⊥y 轴于点QPL ⊥x 轴于点L∴L(k ,0)∴△QPC 为等腰直角三角形PQ=CQ=k由勾股定理知CP=PA=2k∴AL=∣k -2∣, PL=｜－k －1｜在Rt △PLA 中 (2k)2=(k －2)2＋(k ＋1)2解得：k =25∴P 4(25,－27) ------------------------12分2、（本题满分12分）已知抛物线2y x bx c =++交x 轴于A (1,0)、B (3,0)两点，交y 轴于点C ，其顶点为D ．（1）求b 、c 的值并写出抛物线的对称轴；（2）连接BC ，过点O 作直线OE ⊥BC 交抛物线的对称轴于点E ．求证：四边形ODBE 是等腰梯形；（3）抛物线上是否存在点Q ，使得△OBQ 的面积等于四边形ODBE 的面积的31？若存在，求点Q 的坐标；若不存在，请说明理由． 2、（1）求出：4-=b ，3=c ，抛物线的对称轴为：x=2(2) 抛物线的解析式为342+-=x x y ，易得C 点坐标为（0，3），D 点坐标为（2，-1）设抛物线的对称轴DE 交x 轴于点F ，易得F 点坐标为（2，0），连接OD ，DB ，BE∵∆OBC 是等腰直角三角形，∆DFB 也是等腰直角三角形，E 点坐标为（2，2），∴∠BOE= ∠OBD= 45 ∴OE ∥BD∴四边形ODBE 是梯形 ………………5分在ODF Rt ∆和EBF Rt ∆中，OD=5122222=+=+DF OF ，BE=5122222=+=+FB EF∴OD= BE∴四边形ODBE 是等腰梯形 ………………7分(3) 存在， ………………8分由题意得：29332121=⨯⨯=⋅=DE OB S ODBE 四边形 ………………9分设点Q 坐标为（x ，y ），由题意得：y y OB S OBQ 2321=⋅=三角形=23293131=⨯=ODBE S 四边形 ∴1±=y当y=1时，即1342=+-x x ，∴ 221+=x ， 222-=x ，∴Q 点坐标为（2+2，1）或(2-2，1) ………………11分当y=-1时，即1342-=+-x x ， ∴x=2，∴Q 点坐标为（2，-1）综上所述，抛物线上存在三点Q 1（2+2，1），Q 2 (2-2，1) ，Q 3（2，-1）使得OBQ S 三角形=ODBE S 四边形31． ………………12分3、（11分）如图，已知抛物线(1)233(0)y a x a =-+≠经过点(2)A -，0，抛物线的顶点为D ，过O 作射线OM AD ∥．过顶点D 平行于x 轴的直线交射线OM 于点C ，B 在x 轴正半轴上，连结BC ．（1）求该抛物线的解析式；（2）若动点P 从点O 出发，以每秒1个长度单位的速度沿射线OM 运动，设点P 运动的时间为()t s ．问当t 为何值时，四边形DAOP 分别为平行四边形？直角梯形？等腰梯形？（3）若OC OB =，动点P 和动点Q 分别从点O 和点B 同时出发，分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为t ()s ，连接PQ ，当t 为何值时，四边形BCPQ 的面积最小？并求出最小值及此时PQ 的长．解：（1）抛物线2(1)33(0)y a x a =-+≠经过点(20)A -，， 309333a a ∴=+∴=- ························· 1分 ∴二次函数的解析式为：232383333y x x =-++ ·············· 3分（2）D 为抛物线的顶点(133)D ∴，过D 作DN OB ⊥于N ，则33DN =， 2233(33)660AN AD DAO =∴=+=∴∠=，° ·············· 4分OM AD ∥EF Q 1 Q 3Q 2 M C D P①当AD OP =时，四边形DAOP 是平行四边形66(s)OP t ∴=∴= ············· 5分②当DP OM ⊥时，四边形DAOP 是直角梯形过O 作OH AD ⊥于H ，2AO =，则1AH =（如果没求出60DAO ∠=°可由Rt Rt OHA DNA △∽△求1AH =）55(s)OP DH t ∴=== ·························· 6分 ③当PD OA =时，四边形DAOP 是等腰梯形26244(s)OP AD AH t ∴=-=-=∴=综上所述：当6t =、5、4时，对应四边形分别是平行四边形、直角梯形、等腰梯形． 7分（3）由（2）及已知，60COB OC OB OCB ∠==°，，△是等边三角形则6262(03)OB OC AD OP t BQ t OQ t t =====∴=-<<，，，过P 作PE OQ ⊥于E，则2PE = ···················· 8分116(62)222BCPQ S t ∴=⨯⨯⨯-⨯=2322t ⎫-+⎪⎝⎭··························· 9分当32t =时，BCPQ S·················· 10分 ∴此时33393324444OQ OP OE QE PE ==∴=-==，=，PQ ∴=== ·············· 11分4．（本小题满分13分）如图，抛物线经过(40)(10)(02)A B C -，，，，，三点．（1）求出抛物线的解析式；（2）P 是抛物线上一动点，过P 作PM x ⊥轴，垂足为M ，是否存在P 点，使得以A ，P ，M 为顶点的三角形与OAC △相似？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由；（3）在直线AC 上方的抛物线上有一点D ，使得DCA △的面积最大，求出点D 的坐标．解：（1）该抛物线过点(02)C -，，∴可设该抛物线的解析式为22y ax bx =+-．将(40)A ，，(10)B ，代入，得1642020a b a b .+-=⎧⎨+-=⎩，解得1252a b .⎧=-⎪⎪⎨⎪=⎪⎩， ∴此抛物线的解析式为215222y x x =-+-． ··············· （3分）（2）存在． ······························ （4分）如图，设P 点的横坐标为m ，则P 点的纵坐标为215222m m -+-，当14m <<时， 4AM m =-，215222PM m m =-+-．又90COA PMA ∠=∠=°，∴①当21AM AO PM OC ==时， APM ACO △∽△，即21542222m m m ⎛⎫-=-+- ⎪⎝⎭．解得1224m m ==，（舍去），(21)P ∴，． ················ （6分） ②当12AM OC PM OA ==时，APM CAO △∽△，即2152(4)222m m m -=-+-．解得14m =，25m =（均不合题意，舍去）∴当14m <<时，(21)P ，． ······················ （7分）类似地可求出当4m >时，(52)P -，． ·················· （8分）当1m <时，(314)P --，．综上所述，符合条件的点P 为(21)，或(52)-，或(314)--，． ········ （9分）（3）如图，设D 点的横坐标为(04)t t <<，则D 点的纵坐标为215222t t -+-．过D 作y 轴的平行线交AC 于E ．由题意可求得直线AC 的解析式为122y x =-． ············· （10分） E ∴点的坐标为122t t ⎛⎫- ⎪⎝⎭，．2215112222222DE t t t t t ⎛⎫∴=-+---=-+ ⎪⎝⎭． ············ （11分）22211244(2)422DAC S t t t t t ⎛⎫∴=⨯-+⨯=-+=--+ ⎪⎝⎭△．∴当2t =时，DAC △面积最大．(21)D ∴，．5.如图，二次函数的图象经过点D(0，397)，且顶点C 的横坐标为4，该图象在x 轴上截得的线段AB 的长为6.⑴求二次函数的解析式；⑵在该抛物线的对称轴上找一点P ，使PA+PD 最小，求出点P 的坐标；⑶在抛物线上是否存在点Q ，使△QAB 与△ABC 相似？如果存在，求出点Q 的坐标；如果不存在，请说明理由．⑴设二次函数的解析式为：y=a(x-h)2+k∵顶点C 的横坐标为4，且过点(0，397)∴y=a(x-4)2+k k a +=16397 ………………①又∵对称轴为直线x=4，图象在x 轴上截得的线段长为6 ∴A(1，0)，B(7，0) ∴0=9a+k ………………② 由①②解得a=93，k=3－∴二次函数的解析式为：y=93(x-4)2－3⑵∵点A 、B 关于直线x=4对称 ∴PA=PB∴PA+PD=PB+PD ≥DB∴当点P 在线段DB 上时PA+PD 取得最小值 ∴DB 与对称轴的交点即为所求点P 设直线x=4与x 轴交于点M∵PM ∥OD ，∴∠BPM=∠BDO ，又∠PBM=∠DBO ∴△BPM ∽△BDO∴BO BM DO PM = ∴3373397=⨯=PM ∴点P 的坐标为(4，33)⑶由⑴知点C(4，3-)，又∵AM=3，∴在Rt △AMC 中，cot ∠ACM=33，∴∠ACM=60o，∵AC=BC ，∴∠ACB=120o①当点Q 在x 轴上方时，过Q 作QN ⊥x 轴于N 如果AB=BQ ，由△ABC ∽△ABQ 有 BQ=6，∠ABQ=120o，则∠QBN=60o∴QN=33，BN=3，ON=10，此时点Q(10，33)，如果AB=AQ ，由对称性知Q(-2，33) ②当点Q 在x 轴下方时，△QAB 就是△ACB ，此时点Q 的坐标是(4，3-)，经检验，点(10，33)与(-2，33)都在抛物线上综上所述，存在这样的点Q ，使△QAB ∽△ABC点Q 的坐标为(10，33)或(-2，33)或(4，3-)．6、(12分) 如图，抛物线与x 轴交于A （－1，0）、B （3，0）两点，与y 轴交于点C （0，－3），设抛物线的顶点为D ．（1）求该抛物线的解析式与顶点D 的坐标；（2）以B 、C 、D 为顶点的三角形是直角三角形吗？为什么？（3）探究坐标轴上是否存在点P ，使得以P 、A 、C 为顶点的三角形与△BCD 相似？若存在，请指出符合条件的点P 的位置，并直接写出点P 的坐标；若不存在，请说明理由．解：（1）设该抛物线的解析式为c bx ax y ++=2，由抛物线与y 轴交于点C （0，－3）,可知3-=c .即抛物线的解析式为32-+=bx ax y ． ………………………1分把A （－1，0）、B （3，0）代入, 得30,9330.a b a b --=⎧⎨+-=⎩解得2,1-==b a .∴ 抛物线的解析式为y = x 2－2x －3． ……………………………………………3分 ∴ 顶点D 的坐标为()4,1-. ……………………………………………………4分说明：只要学生求对2,1-==b a ，不写“抛物线的解析式为y = x 2－2x －3”不扣分. （2）以B 、C 、D 为顶点的三角形是直角三角形. ……………………………5分理由如下：过点D 分别作x 轴、y 轴的垂线，垂足分别为E 、F.在Rt △BOC 中，OB=3，OC=3，∴ 182=BC . …………………………6分在Rt △CDF 中，DF=1，CF=OF-OC=4-3=1，∴ 22=CD . …………………………7分在Rt △BDE 中，DE=4，BE=OB-OE=3-1=2，∴ 202=BD . …………………………8分 ∴ 222BD CD BC =+，故△BCD 为直角三角形. …………………………9分（3）连接AC ，可知Rt △COA ∽ Rt △BCD ，得符合条件的点为O （0，0）． ………10分过A 作AP 1⊥AC 交y 轴正半轴于P 1，可知Rt △CAP 1 ∽ Rt △COA ∽ Rt △BCD ，求得符合条件的点为)31,0(1P ． …………………………………………11分过C 作CP 2⊥AC 交x 轴正半轴于P 2，可知Rt △P 2CA ∽ Rt △COA ∽ Rt △BCD ，求得符合条件的点为P 2（9，0）． …………………………………………12分 ∴符合条件的点有三个：O （0，0），)31,0(1P ，P 2（9，0）.7、如图，抛物线21y ax bx =++与x 轴交于两点A （－1，0），B （1，0），与y 轴交于点C ． (1)求抛物线的解析式；(2)过点B 作BD ∥CA 与抛物线交于点D ，求四边形ACBD 的面积；(3)在x 轴下方的抛物线上是否存在一点M ，过M 作MN ⊥x 轴于点N ，使以A 、M 、N 为顶点的三角形与△BCD 相似？若存在，则求出点M 的坐标；若不存在，请说明理由．解：（1）解：（1）把A (1,0)- B (1,0)代入21y ax bx =++得：1010a b a b -+=⎧⎨++=⎩ 解得：10a b =-⎧⎨=⎩ 21y x ∴=-+………………………………………………………………………3分（2）令0x =，得1y = ∴()0,1C ……………………………………………4分∵OA=OB=OC=1 ∴∠BAC=∠ACO=∠BCO=∠ABC =45 ∵BD ∥CA ， ∴∠AB D=∠BA C 45=︒过点D 作DE ⊥x 轴于E ，则∆BDE 为等腰直角三角形令OE k = ()0k >，则1DE k =+ ∴(),1D k k --- ∵点D 在抛物线21y x ∴=-+上 ∴ ()211k k --=--+解得12k =，21k =-（不合题意，舍去） ()2,3D -- ∴DE=3(说明：先求出直线BD 的解析式，再用两个解析式联立求解得到点D 的坐标也可)∴四边形ACBD 的面积S =12AB •OC +12AB •DE 112123422=⨯⨯+⨯⨯=………………………………7分（说明：也可直接求直角梯形ACBD 的面积为4）(3)存在这样的点M ……………………………………………………………………8分∵∠ABC=∠ABD=45 ∴∠DBC=90 ∵MN ⊥x 轴于点N ， ∴∠ANM=∠DBC =90 在Rt △BOC 中，OB=OC=1 有2 在Rt △DBE 中，BE=DE=3 有BD=32设M 点的横坐标为m ，则M ()2,1m m -+ ①点M 在y 轴左侧时，则1m <- (ⅰ) 当∆A MN ∽∆CDB 时，有AN MNBC BD=∵21,1AN m MN m =--=-即 2232=解得：1m =-（舍去） 22m =- 则()2,3M --(ⅱ) 当∆AMN ∽∆DCB 时，有AN MNBD BC=2322=解得11m =-（舍去） 223m =（舍去）…………10分② 点M 在y 轴右侧时，则1m > (ⅰ) 当∆AMN ∽∆DCB 时，有AN MNBD BC= ∵21,1AN m MN m =+=-∴ 2322=解得11m =-（舍去） 243m =∴47,39M ⎛⎫-⎪⎝⎭ (ⅱ) 当∆A MN ∽∆CDB 时，有AN MNBC BD=即 211232m m +-=解得：11m =-（舍去） 24m = ∴()4,15M -∴M 点的坐标为()()472,3,,,4,1539⎛⎫---- ⎪⎝⎭…………………………12分8、在直角坐标系xOy 中，设点A （0，t ），点Q （t ，b ）。

重庆中考二次函数专项训练(含答案)

2020年重庆中考二次函数最值专题训练(含答案)

重庆市合川区第一中学2020年中考九年级数学典型压轴题专练：二次函数(包含答案)

中考数学复习《二次函数》专题训练-附带有参考答案

重庆中考二次函数相关的最值问题(含答案)

2024重庆中考复习第25题-二次函数综合题

重庆中考数学25题二次函数专项训练：平行四边形的存在性

重庆中考二次函数的综合题22-40题

2020重庆中考复习数学第12题二次函数专题训练二含答案

重庆备战中考数学 二次函数 培优易错试卷练习(含答案)

重庆名校二次函数综合试题精练(有答案)

重庆中考复习12题(二次函数与系数)专题训练

重庆备战中考数学 二次函数 培优易错试卷练习(含答案)

重庆中考数学25题二次函数专项训练之三角形的存在性

重庆中考专题第十题(最新的哟)二次函数

二次函数压轴题集锦带答案(2024年中考真题)

重庆中考二次函数25题专题

重庆中考二次函数相关的存在性问题习题练习(含答案)

《二次函数压轴题》(共59题)2022年中考专练附答案(重庆专用)

重庆备战中考数学二次函数培优易错试卷练习(含答案)

重庆备战中考数学二次函数培优易错试卷练习(含答案)