如何用梅逊公式求传递函数
梅逊公式

+ G1(s) + H(s) F(s)
A(s)
G2(s)
Y(s)
1
R(s) E(s)
G1(s)
A(s)
1
G2(s)
Y(s)
1 Y(s)
-H(s)
回章首 回节首 14
R(s) -
-
H2 (s) G2(s) G3(s) Y(s)
+
G1(s)
+
+
H1 (s) -1
-H2 (s) R(s) 1 G1(s) G2(s) G3(s) Y(s) 1 Y(s)
回章首
回节首
5
前向通路传输:在前向通路中 , 各支路传输的乘积。 如图中abc和ade。 回路传输:回路中各支路传输的 乘积。 如图中的df和g。
回章首
回节首
6
2. 信号流图的基本性质
1) 信号在支路上只能沿箭头单向传 递,后一节点对前一节点没有负载 效应。 2) 支路表示了一个信号对另一信号 的关系,支路传输相应于比例系数, 信号经支路时,被乘以支路传输变 为另一信号。 如图中x2经支路b变换为x3=bx2 , 经支路d变换为x4=dx2 。
回章首
回节首
21
解: 有三条前向通路, 前向通路的增益分别为
n3
p1 G1G2 G3G4 G5 p2 G1G6 G4 G5 p3 G1G2 G7
有四个独立的回路,分别为
L1 G2 G3G4 G5 H 2 L2 G6 G4 G5 H 2
在四个回路中,L3与L4不接触。
L3 G2 G7 H 2 L4 G4 H1
回章首
回节首
7
3) 节点可以把所有输入支路的信 号相加(注意:是相加而不是相减), 并把总的信号传递到所有输出支 路。 如图中节点 x2=ax1+fx4 如果此反馈为负反馈,则将“-” 号表示在传输 f 上,即信号流图上 f变为-f,此时x2=ax1+(-f)x4
用梅逊公式求传递函数

C(s) R(s)
1
G1(s)G2 (s) G1(s)G2 (s)H (s)
Φr(s)为输入信号r(t)作用下系统的闭环传递函数。此时系统输出的 拉氏变换式为
C
(s)
r
(s)R(s)
1
G1(s)G2 (s) G1(s)G2 (s)H
(s)
R(s)
7
2). 扰动 n(t)作用下系统的闭环传递函数
在下图(a)所示的反馈系统中,为求取r(t)作用下系统的闭环传递 函数,可令n(t)=0。
R(s)
E(s)
- B(s)
G1(s)
N(s)
+
C(s)
G2(s)
H(s)
(a)
R(s)
- B(s)
G1(s)
C(s) G2(s)
H(s)
(b)
6
由图(b)求得输出C(t)和输入r(t)之间的传递函数为
r
(s)
用梅逊(S.J.Mason)公式求传递函数
梅逊公式一般形式为
n
Pk k
(s) k1
式中 (s)为待求的总传递函数。
称为特征式,且
其中
1 Li Li L j Li L j Lk Li ——所有不同回路传递函数之和。 Li L j ——所有两两互不接触回路的回路传递函数乘积之和。 Li L j Lk ——所有三个互不接触回路的回路传递函数乘积之和。
n
(s)
N
(s)
1
G1
G2 (s) (s)G2 (s)H
(s)
N
(s)
自动控制原理 第六课 动态结构图 梅逊公式
§2-4 传递函数定义控制系统的传递函数为 在零初始条件下 ,输出信号的拉氏变换与输入 信号的拉氏变换之比。
表示为Y ( s ) bm s m + bm -1 s m -1 + ... + b1 s + b0 G( s) = = n , n ³ m (2-95) n -1 U (s) s + a n -1 s + ... + a1 s + a0系统的输出可表示为传递函数与控制输入的乘积Y ( s) = G ( s) × U ( s)(2-96)U(s)G(s)Y(s)回章首回节首12-4-3 控制系统的传递函数 1.复数阻抗U R (s) Z R ( s) = =R I R (s)(2-100)ZC ( s) =UC (s) 1 = I C ( s ) Cs(2-101)U L ( s) Z L ( s) = = Ls I L (s)回章首 回节首(2-102)22.典型环节 (1) 比例环节G(s) = Uo (s) =K Ui (s)(2) 积分环节G( s) = Uo ( s) 1 = Ui ( s) Ts(3) 微分环节U o (s) G (s) = = ts U i (s)3(4) 一阶惯性环节U o ( s) 1 G( s ) = = U i ( s) Ts + 1(5) 二阶振荡环节G( s) = U o ( s) 1 = 2 2 U i ( s ) T s + 2xTs + 1(6) 延迟环节G( s) = U o (s) = e -ts U i ( s)4画结构图时,所依据的原则是信号流通关系。
下面以实例来说明。
[例2-25] 已知两级RC网络如图2-33所示,作出该系 统的结构图。
解 设一个中间变量为电容C1 的电压Ux, 采 用复 数阻抗法顺序写出各 算子代数方程和方块图如下:回章首回节首5(1) U i ( s ) - U x ( s ) = U R1 ( s )(2) U R1 ( s ) × 1 = I ( s) R1(3) I ( s ) - I 2 ( s ) = I1 ( s )( 4) I 1 ( s ) × 1 = U x ( s ) C1 s(5) U x ( s ) - U o ( s ) = U R2 ( s )回章首回节首6(6) U R2 ( s ) × 1 = I 2 ( s ) R2 (7 ) I 2 ( s ) × 1 = U o ( s ) C2 s将各基本环节的方块按照信号流通方向连接起来 就可以得到如图2-33所示的系统方块图。
梅逊公式的应用

系统信号流图及梅逊公式
②
-
1/G2(s) G2(s) H1(s)
①
H2(s) Y0 G4(s)
+
Xi(s)
+
G1(s)
+
X0(s)
-
-
-
G3(s)
③ ④
第二步、消去反馈回路①,另相加点(比较点)③前移
1/G2 H2
Xi(s)
+
G1
②
+
③
G3(1+G2H1)/G2G4
X0(s)
G2G4 /(1+G2 H1 )
P1=G1G2G3 G4G5; ; P2=G1G4G5G6; P3=G1G2G7
有4个反馈回路,其传递函数分别为:L1=−G4H1; L2=−G2G7H2; L3=−G4G5G6H2; L4=−G2G3G4G5H2; 有1个互不接触的反馈回路,即: L b L c G 4 H 1G 2 G 7 H 2
k
由梅逊公式求得系统的传递函数为:
G (s) G 1 G 2 G 3 G 4 G 5 G 1 G 4 G 5 G 6 G 1 G 2 G 7 (1 G 4 H 1 ) 1 G 4 H 1 G 2 G 7 H 2 G 4 G 5 G 6 H 2 G 2 G 3 G 4 G 5 H 2 G 4 H 1G 2 G 7 H 2
-
④
2.6
第三步、消去并联回路③和反馈回路②
系统信号流图及梅逊公式
Xi(s)
+
G1
G2G4-(1+G2H1)/G2G4
G2G4 /(1+G2 H1 + G2G4)
X0(s)
24-56控制系统的传递函数及信号流图和梅逊公式

《自动控制理论》
§2.6 信号流图和梅逊公式的应用
例2-9 利用梅逊公式,求:C(s)/R(s)
G7
G6R(s)Fra bibliotekG1+ -
G2
G3
+
+
G4
-
G5
+
+ C ( s)
H1
H2
解:画出该系统的信号流程图
G6
R ( s ) G1
G2 G3
G7
G4 G5
1 C (s)
H1
H2
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
R(s) +
1 R1 -
A
_
+
B
1 C1s
C +
D _
1 R2
E
1 C2s
C ( s)
解:信号流图
1 R1 1 C1s
1
C
1
R( s )
1
A
D
1 R2
1 C2 s
1
C ( s)
B 1
E
1
R( s )
1
A
《自动控制理论》 E B
C
1
1 R1
1 C1s
1 D
1 R2
1 C2 s
1
C ( s)
1
Xj ( s ) Gkj( s ) Xk ( s ),
k 1
n
j 1,2, , n
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
信号流图的基本组成单元有两个:节点和支路。 节点表示系统中的变量; 两变量之间的因果关系用一被称为支路的有向线段 来表示,支路的方向用箭头标明,信号只能沿箭头 指向单向传递。 两变量间的因果关系又称增益,标明在相应的支 路旁。
控制系统的传递函数及信号流图和梅逊公式
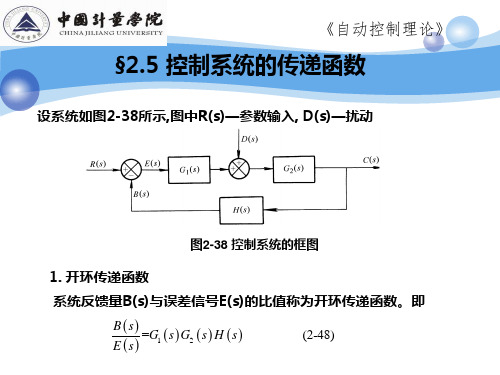
1 Ln LrLsLt
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
例2-7 试用梅逊公式求系统的闭环传递函数 C(S)
R(S)
图2-45 例2-7图
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
解: P1 G1G2G3.
路 开通路—通路与任一节点相交不多于一次
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
闭通路—通路的终点也是通路的起点,并且与任何其它节 点相交不多于一次
6)前向通路—从输入节点到输出节点的通路上,通过任何节 点不多于一次,此通路自然保护区为前向通路
7)回路—就是闭环通路 8)不接触回路—如果一些回路间没有任何公共节点 9)前向通路增益—在前向通路中多支路增益的乘积。 10)回路增益—回路中多支路增益的乘积。
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
信号流图的性质 (1)信号流图只适用于线性系统。 (2)支路表示一个信号对另一个信号的函数关系;信 号只能沿着支路上的箭头指向传递 (3)在节点上可以把所有输入支路的信号叠加,并把 相加后的信号传送到所有的输出支路。
(4)具有输入和输出支路的混合节点,通过增加一个具 有单位增益的支路,可以把它作为输出节点来处理。 (5)对于一个给定的系统,其信号流图不是唯一的, 这是由于描述的方程可以表示为不同的形式。
参考输入误差的传递函数为
CR(s) ER(s)G1(s)G2(s)
CR(s)
G1( s )G 2( s )
R(s) 1 G1(s)G2(s)H (s)
ER(s)G1(s)G2(s)
7梅逊公式闭环传递函数

§2.7 信号流图和梅逊公式
§2.7.1 信号流图与结构图的对应关系
信号流图
相加 相乘 节点的吸收 反馈回环
结构图
并联 串联 中间变量的消除 反馈
(1)信号流图 结构图 · 将节点转换为代表变量的有向信号线; · 将支路转换为表示传递函数的方框;
X(s) G(s) Y(s)
X(s) G(s)
G1G2G3G4 G1G2G4 G2G3G4G5 G2G4G5 G3G4G6 G2G4G6 H 2 ( s ) 1 G2 H 2 G1G2G3G4 H 1 G1G2G4 H 1
Mason 公式(6)
例 6 求传递函数 C(s)/R(s), C(s)/N(s)
控制系统结构图
结构图:
X(s)
G(s)
信号流图:
1
E(s) G(s)
Y(s)
-1
信号流图的作用:利用梅逊公式直接求出系 统的传递函数。
§2.7 信号流图和梅逊公式
§2.7.1 信号流图与结构图的对应关系
信号流图
源节点 汇节点 混合节点 支路 支路增益 前向通路 回路 互不接触回路
结构图
输入信号 输出信号 比较点,引出点 环节 环节传递函数
Y(s)
(1)信号流图 结构图 · 具有两个以上输入支路的节点,附加一个相加点; · 具有两个以上输出支路的节点,附加一个分支点。
1 E(s) - H(s) G1(s) E(s) G3(s) E(s) G1(s)
E(s)
1 H(s)
G3(s) G2(s)
G2(s)
(1)信号流图 结构图
控制系统信号流图
例 2 求C(s)/R(s)
1 [ G1G2 H1 G2G3 H 2 G1G2G3 G4 H 2 G1G4 ]
自动控制原理-梅逊公式例题

= 1 + H 1 + G1 + G2 + G1G2 − G3 H 1
P1 = G1G2 P2 = −G3
∆ 2 = 1 + H1
∆1 = 1
G1G2 − G3 (1 + H 1 ) Φ( s ) = 1 + H 1 + G1 + G2 + G1G2 − G3 H 1
Mason 公式(5) )
例 5 求传递函数 C(s)/R(s)
P1 = G1G2G3G4G5G6
∆1 = 1
G1G2G3G4G5Байду номын сангаас6 Φ( s ) = 1 + G2G3 H 2 + G4G5 H 3 + G3G4 H 4 + G1G2G3G4G5G6 H 1 + G2G3G4G5 H 2 H 3
Mason 公式(2) )
例 2 求传递函数 C(s)/R(s)
§2.6 控制系统的传递函数
1. 开环传递函数
2. 输入 r(t) 作用下的闭环传递函数
控制系统的传递函数
3. 干扰 n(t) 作用下的闭环传递函数
4. 系统的总输出 C(s) 及总误差 E(s)
控制系统的传递函数 (例) 例
系统结构图如右图所示, 例7 系统结构图如右图所示, 求当输入 干扰 r(t) = 1(t) n(t) =δ(t) δ c’(0) = 0 和总误差e(t)。 时系统的总输出 c(t) 和总误差 。 求解
控制系统结构图
例6 求 C(s)/R(s), C(s)/N(s)
∆ = 1 − [ − G2 H − G1G2 − G1G3 ] + G1G2G3 H
= 1 + G2 H + G1G2 + G1G3 + G1G2G3 H
2.7 梅逊公式

△1= 1
∑Pk△k= P1△1= G1 G2 G3 G4G5 G6 将中△与第K条前向通道相接触 条前向通道相接触( △k:将中△与第 条前向通道相接触(有 重合部分)回路所在项去掉之后的余子式。 重合部分)回路所在项去掉之后的余子式。
例:试用梅逊公式求传函C(S)/R(S)。 试用梅逊公式求传函 。
一、梅逊公式
∑Pk△k C(s) : G(S)= R(s) = i G = G1 G3 2 △ 1、G(S):从输入通道到输出通道总的传递 、 : H1 H2 H3 函数(总增益)。 函数(总增益)。 2、△:称为系统主特征式 、 △=1- ∑La+ ∑LbLc-∑LdLeLf+…
所有单独回路增益 回路增益之和 ∑La — 所有单独回路增益之和 ∑LbLc—所有两两互不接触回路增益乘积之和 所有两两互不接触回路增益乘积之和 ∑LdLeLf—所有三个互不接触回路增益乘积之和 所有三个互不接触回路增益乘积之和
R G1 G2 1 H2 G3 H4 H1 4 G4 C
2 H3
G5
G6 3
解: 3、G(S) 、
△=1+G2G3H2 +G4G5H3 +G3G4H4 +G1G2G3G4G5G6H1+G2G3G4G5H2 H3
∑Pk△k= P1△1= G1 G2 G3 G4G5 G6 ∑Pk△k C(s) : G(S)= R(s) = i = △
= G1 G2 G3 G4G5 G6
n
△
应用梅逊公式, 应用梅逊公式,将大大简化结构 变换的计算。 变换的计算。但当系统结构较复 杂时,容易将前向通道、 杂时,容易将前向通道、回路数 及余子式判断错,需格外注意。 及余子式判断错,需格外注意。
例:试用梅逊公式求传函C(S)/R(S)。 试用梅逊公式求传函 。 G4 4 G3 2 H2
第二章 传递函数-梅逊公式
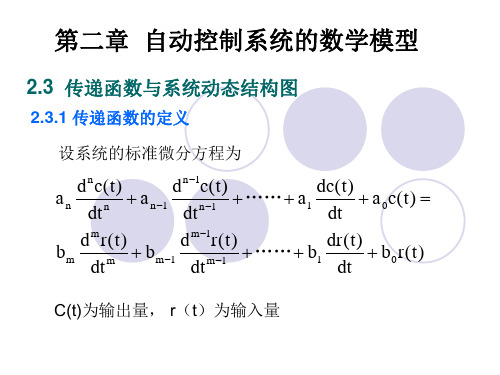
点
上图所示的是
G(s)
(s
(s 1)(s 2) 3)(s 2 2s
2)
的零、极点分布图。
2.2 传递函数
比
比例环节(无惯性环节): c(t)=kr(t)
例
传递函数:G(S)=C(S)/R(S)=k
c(t)
环
阶跃响应:R(S)=1/S
r(t)
节
C(S)=kR(S)=k/S C(t)=k
0
R(s) 1 G(s)H(s)
R(s)
C(s)
Φ(s)
同理 E(s) R(s) B(s)(正反馈时) (s)= C(s) G(s)
R(s) 1 G(s)H(s)
闭环传递函数的通式为
前向通道的传递函数
(s) 1闭环的开环传递函数
负反馈时,分母项取“+”;正反馈时,取 “-”
(1)前向通道:G(s)
传递函数为: G(S)= Uc(S)/ Uc(S) =1/(TS)=k/S
2.2 传递函数
惯 性
惯性环节:Tdc(t)/dt + c(t)=kr(t) 传递函数: G(S)=C(S)/R(S)=k/(TS+1)
当T=∞时,惯性 环节近似为积分 环节;当T=0时,
环 节
阶跃响应: R(S)=1/S C(t)=k(1-e-1/T) C(S)=kR(S)
a
n
sn1
1
……
a1s
a
0
R(s)
传递函数,记作G(s)
传递函数的定义:对线性定常系统(环节),在零初 始条件下,输出量的拉氏变换与输入量的拉氏变换之比, 记作G(s)
G(s)
C(s) R(s)
|零初始条件
信号与系统7_梅森公式的证明及应用

电子工程系 无22班 喻浩 赵欣 肖元章 马存庆 蔡金蝉
梅森公式
梅森公式的回顾
大家都知道,用梅逊公式可不必简化信号流图而直接求得
从输入节点到输出节点之间的总传输。(即总传递函数)
其表达式为:P
1
n k 1
Pk k
式中: P 总传输(即总传递函数);
n 从输入节点到输出节点的前向通道总数;
回路传输乘积之和;
k 第k个前向通道的特征式的余子式;其值为 中除去与
第k个前向通道接触的回路后的剩余部分;
梅森公式的推导
梅森公式的推导(先 用一个一般性的图来证明)
如右图已知信号流图如图所 示,所对应的代数方程为
V1 mV1 lV3 bR
f
m
h
R1
Ⅰ
b
l
Ⅱ
V3
k
Ⅲ
Ⅳ
C
V1 d Ⅴ e V2 1
和
1 m bR l 2 g fR e (1 m) fR debR dlfR gbR
d 0 1 [bde f (1 m dl) bg]R
梅森公式的推导
根据克莱姆法则得
C
V2
2
1 (m
[bde f (1 m dl) bg]R dl ke h gkl) mh dlh
j,k
而△值就是
1 Li Lj Lk 1 (m dl ke h gkl) mh dlh mke
i
j,k
可见,传递函数的分母△取决于信号流图的拓扑结构特征。
梅森逊公式的推导
1 Li Lj Lk 1 (m dl ke h gkl) mh dlh mke
自动控制原理 梅森公式求系统传递函数

P1 G1G2G3 P2 G1G4
4 H2 1 4
L4 G4H2 L5 G1G4
8
R(s)
-
G4
A
G1
G2
-B
H1
G3 H2
C C(s)
P1 G1G2G3 1 1
P2 G1G4 2 1
C(S) P(S) P11 P22
P11 P22
E(s) R(s)
1 1 G1(s)G2(s)H (s)
扰动作用下,系统误差传递函数:
eN (s)
E(s) N (s)
1
G2 (s)H (s) G1(s)G2(s)H (s)
根据线性叠加原理,系统总误差为:
E(s) e (s)R(s) eN (s)N(s)
13
例:试求如图所示系统的传递函数C(s)/R(s)
23
练习
已知系统的结构如图,求传递函数 Y , Y , Y
R1 R2 R3
G2
R3
R1
-
G1
-
G
-
3
H2
R2
H1
解 Y
G1G3 G2G3
R1 1 G3 H G 2 3 H1G1G3 H1G2G3
Y
G1G3 G2G3
R2 1 G3 H G 2 3 H1G1G3 H1G2G3
(s)
N
(s)
根据线性叠加原理,系统总输出 :
C(s)
C(s)
CN
(s)
G2 (s)[G1(s)R(s) N (s)] 1 G1(s)G2(s)H (s)
02 数学模型 - 10梅逊公式

第二章控制系统的数学模型第10讲梅逊公式王燕舞梅逊(Mason)公式◆梅逊(Mason)公式是美国麻省理工学院S.J. Mason于20世纪50年代提出的。
借助于梅逊公式,不经任何结构变换,便可以得到系统的传递函数。
•∑L i :所有回路(n 条)的回路增益之和。
•∑L i L j :所有两两互不接触回路(n 2条)的回路增益乘积之和。
•∑L i L j L k :所有三三互不接触回路(n 3条)的回路增益乘积之和。
•P k :从输入节点到输出节点第k 条前向通路的增益。
•Δk :在Δ中,将与第k 条前向通路相接触的回路除去后所余下的部分的Δ ,称为余子式。
•m :从输入节点到输出节点所有前向通路的条数。
∆∆=∑=m k kk P s G 1)(+-+-=∆∑∑∑321111n kj i n j i n i L L L L L L ◆梅逊公式的表达式为:•G(s):待求的总传递函数。
•Δ称为特征式,◆梅逊公式的证明:参见:1.Samuel J. Mason, “Feedback theory-Some properties ofsignal flow graphs,” Proc. IRE, vol. 41, no. 9, pp. 1144-1 156, Sept. 1953.2.Samuel J. Mason, “Feedback theory-Further properties ofsignal flow graphs,” Proc. IRE, vol. 44, no. 7, pp. 920-926, July 1956.3.W.K. Chen, “Applied Graph Theory, Graphs and ElectricalNetworks,” North-Holland, Amsterdam, 1976.4.陈景明, “S.J. Mason讯号流图增益公式的另一个证明,” 吉林大学自然科学学报, no. 4, pp. 137-146, 1979.G 3H 2G 2G 1G 4H 1CR G 5G 6H 4H 3-H 2G 2G 3-H 4G41G 6G 5-H 3CB E F G x 3H IR A 1G 1-H 11结构图信号流图求图示控制系统的传递函数。
§25闭环传递函数§26 梅逊公式

P G GG 1 1 2 3
P G G 2 1 4
1 1
2 1
G G G G G 1 2 3 1 4 ( s ) G G H G G H G G G G H G G 1 2 1 2 3 2 1 2 3 4 2 1 4
Mason 公式(3)
例 3 求传递函数 C(s)/R(s)
例1
求C(s)/R(s)
( G G H )( G G H ) 1 [ G G H G3G4 H4 G G G G G G H G5 H ] 2 3 2 4 5 3 2 3 2 G 1 2 3 4 5 6 1 4 3
1 G G H G G H G G H G G G G G G H G G G G H H 2 3 2 4 5 3 3 4 4 1 2 3 4 5 6 1 2 3 4 5 2 3
§2.5 控制系统的传递函数
<2、扰动输入作用下的误差传递函数 令R(s) =0,可求出误差对扰动作用的闭环传递函数,简称扰动误差传递函数,即
N(s)
<3、控制输入和扰动同时作用下系统的总误差 利用叠加原理可求出系统在控制输入和扰动输入同时作用下系统的总误差为
不难发现,四种闭环传递函数 Φ(s)、Φn(s)、 Φe(s)、Φen(s) 具有相同的分母即 =1+ G(s)H(s)。这正是闭环控制系统的本质特征。通常把这 个分母多项式称为闭环系统的特征多项式。1+ G(s)H(s) 称为闭环系统的特征方 程。特征方程的根称为闭环系统的根或极点。
(1)结构图 信号流图
(2)结构图 信号流图
§2.6.2 梅逊(Mason)增益公式
G(s) PΔ Δ
k k 1
如何用梅逊公式求传递函数

G7
+
-
G2
H2
H1
G7
G2 1
G3
1
H2
G8
H1
G3
+
++
+
G4
C
G8
为节点
注意:①信号流
G4
1
图与结构图的对
C 应关系;②仔细
确定前向通道和
回路的个数。
作业:2-12,2-13
23
小结
小结
信号流图的组成;术语; 信号流图的绘制和等效变换; 梅逊公式极其应用; 信号流图和结构图之间的关系。
Sunday, March 22, 2020
24
P3 G1G2G8G4
P4 G5G2G3G4 P5 G5G2G7G4 P6 G5G2G8G4
P7 G6G3G4 P8 G6G8G4 P9 G6H 2G2G7G4
Sunday, March 22, 2020
22
梅逊公式||例2-15
对应的结构图为:
G6
G5
R
-
G1
G6
G5
1
R
1
G1
Sunday, March 22, 2020
第四节 控制系统的信号流图
Sunday, March 22, 2020
1
信号流图的概念
信号流图可以表示系统的结构和变量传送过程中的数学关 系。它也是控制系统的一种数学模型。在求复杂系统的传递函 数时较为方便。
一、信号流图及其等效变换
组成:信号流图由节点和支路组成。见下图:
R1
N
1
E G1 P
G2
Q
15
梅逊公式||例2-13
2.4 系统信号流图及梅逊公式

Fc(s)
cs
例 :绘制如图所示系统的方块图
R1 i1(t) ui(t) C1
A
R2
i2(t)
uA(t)
u0(t)
C2
U i s - U A s = R1 I 1 s
拉氏变换后方程组
U A s - U 0 s = R2 I 2 s 1 I2 s = U0 s c2 s
Ө(t)
D
f(t)
P74 2-25 已知:f(t)为输入力,θ(t) 为轴的输出转角,弹簧刚度k,轴的 转动惯量J,阻尼系数D,轴的半径r, 求系统的传递函数。
解:该系统可以看作是一个质量、弹簧、 阻尼系统。
对于质量,这里用转动惯量J来代替。 对J、k、D分别列方程,有
J t f t r TK TD
1 I1 s - I 2 s = UA s c1 s
各环节的方块图如下所示。
Ui s -U A s = R1 I1 s
Ui(s)
+
1/R1
I1(s)
1 I1 s I 2 s UA s c1s
I1(s)
TK K t TD D t
J t f t r K t D t J t D t K t f t r
拉氏变换后,得 2 Js s Ds s K s F s r
X0(s)
H(S)
-H(s)
从图中可以我们可以定义: 通路:沿支路箭头方向穿过各相连支路的路径。 节点:用来表示变量或信号的点,像输 回路:起点与终点重合且与任何节点 前向通路:从输入节点到输出节点的通路上通 入节点、输出节点、比较点以及引出点, 支路:定向线段,箭头表明信号的流向, 相交不多于一次的通路。 过任何节点不多于一次的通路。 标明有传递函数。 用符号“。”表示。
梅逊公式

2-7 结构图等效变换及梅逊公式求传递函数时,需要对微分方程组(或变换方程组)进行消元,最后仅剩下输入、输出两个变量,因此中间变量的传递过程得不到反映。
若采用结构图,它就能形象地表明输入信号在系统或元件中的传递过程。
另外,下面将会看到,利用结构图,也便于求取传递函数。
所以,结构图在控制理论中应用十分广泛。
一、结构图在第2-6节中,我们曾采用消元法求得图2-24所示RC 网络的传递函数。
这里,我们采用结构图的方法求其传递函数。
RC 网络的微分方程组如下:⎪⎩⎪⎨⎧=+=⎰idt C u u Ri u c cr 1对上两式进行拉氏变换,得)()()(s U s RI s U c r +=或[])()()(1s I s U s U Rc r =- (2-54) )(1)(s I Css U r =(2-55)方程(2-54)可用图2-29)(a 表示,方程(2-55)可用图2-29)(b 表示。
将图2-29)(a )(b 按信号传递方向结合起来,网络的输入量置于图示的左端,输出量置于最右端,并将同一变量的信号连在一起,如图2-30)(a 所示,即得RC 网络结构图。
对图2-30)(a 进行所谓“等效变换”就可得出网络传递函数,因此网络结构就更为简单,如图2-30)(b 所示。
关于结构图等效变换的方法将另作介绍。
(1)建立控制系统各元、部件的微分方程。
(2)对各元、部件的微分方程进行拉氏变换,并做出各元、部件的结构图。
(3)按系统中各信号的传递顺序,依次将各元件结构图连接起来,便得到系统的结构图。
下面以图1-7所示随动系统为例。
把组成该系统各元部件的微分方程(2-18)进行拉氏变换,可得方程组(2-56e a ~),其中比较元件 )()()(s s s c r θθθε-=(2-56a ) 电位器 )()(1s K s U εεθ= (2-56b ) 放大器 )()(2s U k s U ε=(2-56c ) 电动机 )()()1(s U K s s T s m m =+εθ(2-56d ) 减速器)(1)(s is c θθ=(2-56e )各元、部件的结构图如图2-31所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M c ( s)
Gm
Gu
( s )
Gf
先在结构图上标出节点,如上图所示。然后画出信号流图 M c 如下图所示。 G
1
G1
G2
G3
Gu
m
1
ug
ue
u1
u2
G
f
ua
8
Thursday, November 15, 2018
例2: 已知结构图如下,可在结构图上标出节点,如上图所示。 然后画出信号流图如下图所示。
Thursday, November 15, 20182信号流图的术语X1
G1
X2
X3
G2
H1
G3
H3 G4
X4 X5
G5
X6
H2
X9
G6X 7 G7
X8
[几个术语]:
输入节点(源点):只有输出支路的节点。如:X1,X9。 输出节点(阱点):只有输入支路的节点。如: X8。 混合节点:既有输入支路又有输出支路的节点。如: X2,X3,X4,X5,X6,X7。混合节点相当于结构图中的信号相加点和分 支点。它上面的信号是所有输入支路引进信号的叠加。 通路:沿支路箭头方向穿过各个相连支路的路线,起始点和 终点都在节点上。若通路与任一节点相交不多于一次,且起点 和终点不是同一节点称为开通路。起点在源点,终点在阱点的 开通路叫前向通路。
Thursday, November 15, 2018
7
信号流图的绘制
[信号流图的绘制]: 根据结构图 列出系统各环节的拉氏方程,按变量间的数学关系绘制 例1:速度控制系统的结构图为: u1 ( s) u g ( s ) ue ( s ) ua ( s ) u2 ( s )
u f ( s)
G1
G2
f R1
Ⅳ V3 k C Ⅱ b Ⅲ V1 d Ⅴ e V2 1 g Ⅰ
m
h l
V1 mV 1 lV3 bR C V2 gV1 hV2 eV3 fR
V3 dV1 kV2
按方程可绘制信号流图。
Thursday, November 15, 2018
10
梅逊公式
二、梅逊增益公式
L L L
d e f
回路传输乘积之和;
所有互不接触回路中,每次取其中三个
k 第k个前向通道的特征余子式;其值为 中除去与第k个
前向通道接触的回路后的剩余部分。
Thursday, November 15, 2018
Thursday, November 15, 2018
11
梅逊公式
1 La Lb Lc Ld Le Lf ...(正负号间隔)
式中: La 流图中所有不同回路的回路传输之和; 路传输乘积之和;
b c
1 n P Pk k k 1
L L 所有互不接触回路中,每次取其中两个回
信号流图的概念
信号流图可以表示系统的结构和变量传送过程中的数学关 系。它也是控制系统的一种数学模型。在求复杂系统的传递函 数时较为方便。 一、信号流图及其等效变换 组成:信号流图由节点和支路组成。见下图:
N 1 R 1 E G1 P G2 Q 1
R( s ) E ( s ) G1 ( s) C -
N (s) + C (s) G2 (s)
用梅逊公式可不必简化信号流图而直接求得从输入节点到 输出节点之间的总传输。(即总传递函数)
n 1 其表达式为:P Pk k k 1 式中: P 总传输(即总传递函数);
n 从输入节点到输出节点的前向通道总数;
Pk 第k个前向通道的总传输;
流图特征式;其计算公式为:
Thursday, November 15, 2018
3
信号流图的术语
X1
G1
X2
X3
G2
H1
G3
H3 G4
X4 X5
G5
X6
H2
X9
G6X 7 G7
X8
回路(闭通路):通路与任一节点相交不多于一次,但起点和终 点为同一节点的通路称为回路。 互不接触回路:回路之间没有公共节点时,这种回路称为互 不接触回路。 通路传输(增益):通路中各支路传输的乘积称为通路传输或通 路增益。前向通路中各支路传输的乘积称为前向通路传输或前 向通路增益。 回路传输(增益):回路上各支路传输的乘积称为回路传输或回 路增益。 4 Thursday, November 15, 2018
H
H (s)
Thursday, November 15, 2018
1
信号流图的概念
节点:节点表示信号,输入节点表示输入信号,输出节点 表示输出信号。 支路:连接节点之间的线段为支路。支路上箭头方向表示 信号传送方向,传递函数标在支路上箭头的旁边,称支路传输。
x
G
y
x
G
y
上图中, 两者都具有关系: y( s) G( s) x( s)。支路对节点x来说 是输出支路,对节点y来说是输入支路。
2
混合支路的清除:
ad
x4
bd
bc
x1 ac x1
x2 x4
1 1 b
x3 ac
x2 bc
ab
自回路的消除:
a
b x3
1
x1
x2
b
x1 x3 b x4
x1
ab
x3
x4
Thursday, November 15, 2018
6
信号流图的性质
信号流图的性质
节点表示系统的变量。一般,节点自左向右顺序设置,每 个节点标志的变量是所有流向该节点的信号之代数和,而 从同一节点流向各支路的信号均用该节点的变量表示。 支路相当于乘法器,信号流经支路时,被乘以支路增益而 变换为另一信号。 信号在支路上只能沿箭头单向传递,即只有前因后果的因 果关系。 对于给定的系统,节点变量的设置是任意的,因此信号流图 不是唯一的。
信号流图的等效变换
串联支路合并:
x1
a
x2
a
b
x3
x1
ab
x3
并联支路的合并:
x1
b
x2
x1
ab
x2
回路的消除:
x1 x2
a
b
c
x3
x1
b a 1 bc
x2
x3
Thursday, November 15, 2018
5
信号流图的等效变换
x4 ad b x1 c x2 x3
x1 a c b x3 x4 x
k m
R (S )
g
V1
b
d l f
V3
e h
C (S ) V2
f
Ⅳ V3 k C Ⅱ b Ⅲ V1 d Ⅴ e V2 1 g Ⅰ
m
h l
R1
Thursday, November 15, 2018
9
信号流图的绘制
例2: 按微分方程拉氏变换后 的代数方程所表示的变量间 数学关系绘制。如前例所对 应的代数方程为:
