北京大学 数学分析(I)期末考试 2011
2011年普通高等学校招生全国统一考试北京文科数学和理科数学整编卷详细解析(精品回顾)

绝密★使用完毕前2011年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分。
考试时间长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合P={x ︱x 2≤1},M={a }.若P ∪M=P,则a 的取值范围是(A )(-∞, -1] (B )[1, +∞) (C )[-1,1] (D )(-∞,-1] ∪[1,+∞) (2)复数212i i-=+(A )i(B )-i(C )(D )4355i--4355i -+(3)在极坐标系中,圆ρ=-2sin θ的圆心的极坐标系是(A)(B) (C) (1,0)(1,)2π(1,2π-(D)(1,)π(4)执行如图所示的程序框图,输出的s 值为(A )-3 (B )-12(C )13(D )2(5)如图,AD ,AE ,BC 分别与圆O 切于点D ,E ,F ,延长AF 与圆O 交于另一点G 。
给出下列三个结论:AD+AE=AB+BC+CA ;○1回归往日精品,再现今日辉煌AF·AG=AD·AE○2③△AFB ~△ADG 其中正确结论的序号是(A )①② (B )②③ (C )①③ (D )①②③(6)根据统计,一名工作组装第4件某产品所用的时间(单位:分钟)为(A ,C 为常数)。
已知工人组装第4件产品用时30分钟,组装第A 件产品用时15分钟,那么C 和A 的值分别是(A )75,25 (B )75,16 (C )60,25 (D )60,16 (7)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是(A) 8 (B) (C)10 (D) (8)设,,,.记为平行四边形()0,0A ()4,0B ()4,4C t +()(),4D t t R ∈()N t ABCD 内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数的值域为()N t(A ) (B ) {}9,10,11{}9,10,12(C ) (D ) {}9,11,12{}10,11,12第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
北京大学2010-2011高数D期末试卷答案

课程名称:高等数学(D )2010 -2011 学年第(1)学期期末 试卷 本试卷共 九 道大题,满分 100 分 答案请写在答题本上,试卷上答题无效。
考试结束后请将试卷、答题本一起交给监考老师。
一、 判断题(给出简单解释,每题3分,共5题)1. 对于多元函数,可导必可微,可微必可导。
(错,需要偏导数连续)2. 所有的初等函数在其定义域的任意子集上都是可求定积分的。
(错,广义积分)3. 若函数(,)z f x y =在点00(,)x y 处偏导数都为0,则函数在该点处必取得极值。
(错)4. 若函数()f x 在 [a,b]上可导,则函数在[a,b]上有最大值与最小值。
(对)5. 若区间[,][,]c d a b ⊆,则必有()()bda c f x dx f x dx ≥⎰⎰。
(对)二、选择题(不需要写过程,每题3分,共5题)1. 当0x +→ B )(A ) 1- (B )ln(1 (C 1 (D )1-2.设1D I σ=,222()D I x y d σ=+⎰⎰,2223()D I x y d σ=+⎰⎰,其中}1),{(22≤+=y x y x D ,则(D )(A ) 123I I I >> (B )213I I I >>(C )312I I I >> (D )321I I I >>3. 设f(x)为不恒等于零的奇函数,且)0(f '存在,则函数xx f x g )()(= (D ) (A )在x=0处左极限不存在 (B )有跳跃间断点x=0(C )在x=0处右极限不存在 (D )有可去间断点x=04. 设函数()f x 在(,)-∞+∞上连续, 则()d f x dx ⎡⎤⎣⎦⎰等于( B ). (A) ().f x (B) ().f x dx (C) ().f x C + (D) ().f x dx '5. 设43()()()d d I f x dx f x dx f x dx dx dx '=++⎰⎰⎰存在, 则I =( D ). (A) 0. (B) ().f x (C) 2().f x (D) 2().f x C +三、填空题((不需要写过程,每题3分,共5题))1. 设a>0,,x a x g x f 其他若,10,0,)()(≤≤⎩⎨⎧==而D 表示全平面,则⎰⎰-=D dxdy x y g x f I )()(= a 2 2.设()f x =在[1, 4]上使Lagrange(拉格朗日)中值定理成立的ξ=___9/4__.3. 二元函数22a r c s i n (2)l n ()z x y x y =--+-的定义域为:{}222(,)|13,D x y x y x y =≤+≤>4. 函数22(,)2()f x y x y x y =-+-的驻点为: (-1,-1)5. ()()1ln cos 1lim1sin 2x x x π→-=- 24π- 四、计算下列不定积分(每题4分,共20分)1. ()3cos x x dx -⎰=C x x x x d x xdx ++-=--⎰⎰322sin 31sin 2sin )sin 1( 2.⎰C x x x dx +-=--⎰2222111)1(213.dx=2222sec cos sin 1tan sec sin sin sin tdt t d t dt C C t t t t t ===-+=+⎰⎰⎰ 4. 32sin 1cos x x dx x ++⎰2234sin cos 322sec 2tan 2222cos 23(tan )2tan 3tan 3tan 2tan 22222sin 23tan 23tan ln cos 2222cos 2x x x x x dx x dx dx x x x x x x xd dx x dx dx x x x x x x d x C x +==+=+=-+=-=++⎰⎰⎰⎰⎰⎰⎰⎰ 5. 3sin 2cos sin cos x x x x e dx x--⎰=C xe xe dx e x e dx e xe dx e x e xde x d e x xd ex x x x x x x x x x x +--=--+-=---=------------⎰⎰⎰⎰⎰⎰cos cos cos cos 1sin sin sin sin sin sin sin sin sin sin sin sin 五、求抛物线22y px =及其在点(,)2p p 处的法线所围成的图形的面积。
2011年北京市高考数学试卷(理科)答案与解析

2011年北京市高考数学试卷(理科)参考答案与试题解析一、选择题(共8小题,每小题5分,满分40分)1.(5分)(2011•北京)已知集合P={x|x2≤1},M={a}.若P∪M=P,则a的取值范围是()A.(﹣∞,﹣1]B.[1,+∞)C.[﹣1,1]D.(﹣∞,﹣1]∪[1,+∞)【考点】集合关系中的参数取值问题.【专题】集合.【分析】通过解不等式化简集合P;利用P∪M=P⇔M⊆P;求出a的范围.【解答】解:∵P={x|x2≤1},∴P={x|﹣1≤x≤1}∵P∪M=P∴M⊆P∴a∈P﹣1≤a≤1故选:C.【点评】本题考查不等式的解法、考查集合的包含关系:根据条件P∪M=P⇔M⊆P是解题关键.2.(5分)(2011•北京)复数=()A.i B.﹣i C.D.【考点】复数代数形式的混合运算.【专题】数系的扩充和复数.【分析】将分子、分母同乘以1﹣2i,再按多项式的乘法法则展开,将i2用﹣1代替即可.【解答】解:==i故选A【点评】本题考查复数的除法运算法则:分子、分母同乘以分母的共轭复数;再按多项式的乘法法则展开即可.3.(5分)(2011•北京)在极坐标系中,圆ρ=﹣2sinθ的圆心的极坐标系是()A.B.C.(1,0)D.(1,π)【考点】简单曲线的极坐标方程.【专题】直线与圆;坐标系和参数方程.【分析】先在极坐标方程ρ=﹣2sinθ的两边同乘以ρ,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得直角坐标系,再利用直角坐标方程求解即可.【解答】解:将方程ρ=﹣2sinθ两边都乘以p得:ρ2=﹣2ρsinθ,化成直角坐标方程为x2+y2+2y=0.圆心的坐标(0,﹣1).∴圆心的极坐标故选B.【点评】本题考查点的极坐标和直角坐标的互化,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互,能在极坐标系中用极坐标刻画点的位置.4.(5分)(2011•北京)执行如图所示的程序框图,输出的s值为()A.﹣3 B.﹣C.D.2【考点】循环结构.【专题】算法和程序框图.【分析】i=0,满足条件i<4,执行循环体,依此类推,当i=4,s=2,此时不满足条件i<4,退出循环体,从而得到所求.【解答】解:i=0,满足条件i<4,执行循环体,i=1,s=满足条件i<4,执行循环体,i=2,s=﹣满足条件i<4,执行循环体,i=3,s=﹣3满足条件i<4,执行循环体,i=4,s=2不满足条件i<4,退出循环体,此时s=2故选:D【点评】根据流程图计算运行结果是算法这一模块的重要题型,处理的步骤一般为:分析流程图,从流程图中即要分析出计算的类型,又要分析出参与计算的数据建立数学模型,根据第一步分析的结果,选择恰当的数学模型解模.算法和程序框图是新课标新增的内容,在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题.5.(5分)(2011•北京)如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O 交于另一点G.给出下列三个结论:①AD+AE=AB+BC+CA;②AF•AG=AD•AE③△AFB~△ADG其中正确结论的序号是()A.①②B.②③C.①③D.①②③【考点】与圆有关的比例线段.【专题】直线与圆.【分析】根据从圆外一点引圆的两条切线,切线长相等,得到第一个说法是正确的,根据切割线定理知道第二个说法是正确的,根据切割线定理知,两个三角形△ADF~△ADG,得到第三个说法错误.【解答】解:根据从圆外一点引圆的两条切线,切线长相等,有CE=CF,BF=BD,∴AD+AE=AB+BC+CA,故①正确,∵AD=AE,AE2=AF•AG,∴AF•AG=AD•AE,故②正确,根据切割线定理知△ADF~△ADG故③不正确,综上所述①②两个说法是正确的,故选A.【点评】本题考查与圆有关的比例线段,考查圆的切线长定理,考查圆的切割线定理,考查切割线构成的两个相似的三角形,本题是一个综合题目.6.(5分)(2011•北京)根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为(A,C为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是()A.75,25 B.75,16 C.60,25 D.60,16【考点】函数解析式的求解及常用方法.【专题】函数的性质及应用.【分析】首先,x=A的函数值可由表达式直接得出,再根据x=4与x=A的函数值不相等,说明求f(4)要用x<A对应的表达式,将方程组联解,可以求出C、A的值.【解答】解:由题意可得:f(A)==15,所以c=15而f(4)==30,可得出=30故=4,可得A=16从而c=15=60故答案为D【点评】分段函数是函数的一种常见类型,解决的关键是寻找不同自变量所对应的范围,在相应区间内运用表达式加以解决.7.(5分)(2011•北京)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是()A.8 B. C.10 D.【考点】由三视图求面积、体积.【专题】立体几何.【分析】三视图复原的几何体是一个三棱锥,根据三视图的图形特征,判断三棱锥的形状,三视图的数据,求出四面体四个面的面积中,最大的值.【解答】解:三视图复原的几何体是一个三棱锥,如图,四个面的面积分别为:8,6,,10,显然面积的最大值,10.故选C.【点评】本题是基础题,考查三视图复原几何体的知识,考查几何体的面积,空间想象能力,计算能力,常考题型.8.(5分)(2011•北京)设A(0,0),B(4,0),C(t+4,4),D(t,4)(t∈R).记N(t)为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数N(t)的值域为()A.{9,10,11}B.{9,10,12} C.{9,11,12} D.{10,11,12}【考点】集合的含义.【专题】集合.【分析】分别由t=0,1,2求出N(t),排除错误选项A,B,D,从而得到正确选项.【解答】解:当t=0时,▱ABCD的四个顶点是A(0,0),B(4,0),C(4,4),D(0,4),符合条件的点有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),共九个,N(t)=9,故选项D不正确.当t=1时,▱ABCD的四个顶点是A(0,0),B(4,0),C(5,4),D(1,4),同理知N(t)=12,故选项A不正确.当t=2时,▱ABCD的四个顶点是A(0,0),B(4,0),C(6,4),D(2,4),同理知N(t)=11,故选项B不正确.故选C.【点评】本题考查集合的性质和应用,解题时要注意排除法的合理运用.本题中取整点是个难点,常用的方法是,先定横(或纵)坐标,在定纵(横)坐标,以确定点的个数,如果从图形上看,就是看直线x=r(r是整数)上有几个整点在四边形内.二、填空题(共6小题,每小题5分,满分30分)9.(5分)(2011•北京)在△ABC中.若b=5,,tanA=2,则sinA=;a=2.【考点】正弦定理;同角三角函数间的基本关系.【专题】解三角形.【分析】由tanA的值,利用同角三角函数间的基本关系求出cosA的平方,然后由A的范围,再利用同角三角函数的基本关系求出sinA的值,然后再利用正弦定理,由sinA,sinB及b 的值即可求出a的值.【解答】解:由tanA=2,得到cos2A==,由A∈(0,π),得到sinA==,根据正弦定理得:=,得到a===2.故答案为:;2【点评】此题考查学生灵活运用同角三角函数间的基本关系以及正弦定理化简求值,是一道中档题.10.(5分)(2011•北京)已知向量=(,1),=(0,﹣1),=(k,).若与共线,则k=1.【考点】平面向量共线(平行)的坐标表示.【专题】平面向量及应用.【分析】利用向量的坐标运算求出的坐标;利用向量共线的坐标形式的充要条件列出方程,求出k的值.【解答】解:∵与共线,∴解得k=1.故答案为1.【点评】本题考查向量的坐标运算、考查向量共线的坐标形式的充要条件:坐标交叉相乘相等.11.(5分)(2011•北京)在等比数列{a n}中,a1=,a4=﹣4,则公比q=﹣2;|a1|+|a2|+…+|a n|=.【考点】等比数列的性质;等比数列的前n项和.【专题】等差数列与等比数列.【分析】先利用等比数列的通项公式求得公比;|a n|是以a1为首项,|q|为公比,进而利用等比数列的求和公式求解.【解答】解:q===﹣2,|a1|+|a2|+…+|a n|==故答案为:﹣2,【点评】本题主要考查了等比数列的性质.考查了对等比数列的通项公式和求和公式的灵活运用.12.(5分)(2011•北京)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有14个.(用数字作答)【考点】计数原理的应用.【专题】算法和程序框图.【分析】本题是一个分类计数问题,首先确定数字中2和3 的个数,当数字中有1个2,3个3时,当数字中有2个2,2个3时,当数字中有3个2,1个3时,写出每种情况的结果数,最后相加.【解答】解:由题意知本题是一个分类计数问题,首先确定数字中2和3 的个数,当数字中有1个2,3个3时,共有C41=4种结果,当数字中有2个2,2个3时,共有C42=6种结果,当数字中有3个2,1个3时,共有有C41=4种结果,根据分类加法原理知共有4+6+4=14种结果,故答案为:14【点评】本题考查分类计数原理,是一个数字问题,这种问题一般容易出错,注意分类时要做到不重不漏,本题是一个基础题,也是一个易错题,易错点在数字中重复出现的数字不好处理.13.(5分)(2011•北京)已知函数若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是(0,1).【考点】根的存在性及根的个数判断.【专题】函数的性质及应用.【分析】要求程f(x)=k有两个不同的实根是数k的取值范围,根据方程的根与对应函数零点的关系,我们可以转化为求函数y=f(x)与函数y=k交点的个数,我们画出函数的图象,数形结合即可求出答案.【解答】解:函数的图象如下图所示:由函数图象可得当k∈(0,1)时方程f(x)=k有两个不同的实根,故答案为:(0,1)【点评】本题考查的知识点是根的存在性及根的个数判断,其中根据方程的根与对应函数零点的关系,将方程问题转化为函数问题是解答的关键.14.(5分)(2011•北京)曲线C是平面内与两个定点F1(﹣1,0)和F2(1,0)的距离的积等于常数a2(a>1)的点的轨迹.给出下列三个结论:①曲线C过坐标原点;②曲线C关于坐标原点对称;③若点P在曲线C上,则△F1PF2的面积不大于a2.其中,所有正确结论的序号是②③.【考点】轨迹方程.【专题】圆锥曲线的定义、性质与方程.【分析】由题意曲线C是平面内与两个定点F1(﹣1,0)和F2(1,0)的距离的积等于常数a2(a>1),利用直接法,设动点坐标为(x,y),及可得到动点的轨迹方程,然后由方程特点即可加以判断.【解答】解:对于①,由题意设动点坐标为(x,y),则利用题意及两点间的距离公式的得:⇔[(x+1)2+y2]•[(x﹣1)2+y2]=a4(1)将原点代入验证,此方程不过原点,所以①错;对于②,把方程中的x被﹣x代换,y被﹣y 代换,方程不变,故此曲线关于原点对称.②正确;对于③,由题意知点P在曲线C上,则△F1PF2的面积=a2sin∠F1PF2,≤a2,所以③正确.故答案为:②③.【点评】此题重点考查了利用直接法求出动点的轨迹方程,并化简,利用方程判断曲线的对称性及利用解析式选择换元法求出值域.三、解答题(共6小题,满分80分)15.(13分)(2011•北京)已知函数.(Ⅰ)求f(x)的最小正周期:(Ⅱ)求f(x)在区间上的最大值和最小值.【考点】三角函数的周期性及其求法;两角和与差的余弦函数;三角函数的最值.【专题】三角函数的图像与性质.【分析】(Ⅰ)利用两角和公式和二倍角公式对函数的解析式进行化简整理后,利用正弦函数的性质求得函数的最小正周期.(Ⅱ)利用x的范围确定2x+的范围,进而利用正弦函数的单调性求得函数的最大和最小值.【解答】解:(Ⅰ)∵,=4cosx()﹣1=sin2x+2cos2x﹣1=sin2x+cos2x=2sin(2x+),所以函数的最小正周期为π;(Ⅱ)∵﹣≤x≤,∴﹣≤2x+≤,∴当2x+=,即x=时,f(x)取最大值2,当2x+=﹣时,即x=﹣时,f(x)取得最小值﹣1.【点评】本题主要考查了三角函数的周期性及其求法,三角函数的最值.解题的关键是对函数解析式的化简整理.16.(14分)(2011•北京)如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.(Ⅰ)求证:BD⊥平面PAC;(Ⅱ)若PA=AB,求PB与AC所成角的余弦值;(Ⅲ)当平面PBC与平面PDC垂直时,求PA的长.【考点】直线与平面垂直的判定;点、线、面间的距离计算;用空间向量求直线间的夹角、距离.【专题】空间位置关系与距离.【分析】(I)由已知条件可得ACBD,PABD,根据直线与平面垂直的判定定理可证(II)结合已知条件,设AC与BD的交点为O,则OB⊥OC,故考虑分别以OB,OC为x 轴、y轴,以过O且垂直于平面ABCD的直线为z轴,建立空间直角坐标系,设PB与AC所成的角为θ,则,代入公式可求(III)分别求平面PBC的法向量,平面PDC的法向量由平面PBC⊥平面PDC可得从而可求t即PA【解答】解:(I)证明:因为四边形ABCD是菱形,所以AC⊥BD,又因为PA⊥平面ABCD,所以PA⊥BD,PA∩AC=A所以BD⊥平面PAC(II)设AC∩BD=O,因为∠BAD=60°,PA=AB=2,所以BO=1,AO=OC=,以O为坐标原点,分别以OB,OC为x轴、y轴,以过O且垂直于平面ABCD的直线为z 轴,建立空间直角坐标系O﹣xyz,则P(0,﹣,2),A(0,﹣,0),B(1,0,0),C(0,,0)所以=(1,,﹣2),设PB与AC所成的角为θ,则cosθ=|(III)由(II)知,设,则设平面PBC的法向量=(x,y,z)则=0,所以令,平面PBC的法向量所以,同理平面PDC的法向量,因为平面PBC⊥平面PDC,所以=0,即﹣6+=0,解得t=,所以PA=.【点评】本小题主要考查空间线面关系的垂直关系的判断、异面直线所成的角、用空间向量的方法求解直线的夹角、距离等问题,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力17.(13分)(2011•北京)以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.(Ⅰ)如果X=8,求乙组同学植树棵数的平均数和方差;(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y 的分布列和数学期望.(注:方差,其中为x1,x2,…x n的平均数)【考点】茎叶图;众数、中位数、平均数;极差、方差与标准差;离散型随机变量的期望与方差.【专题】概率与统计.【分析】(Ⅰ)根据所给的数据,把所有数据相加再除以4写出这组数据的平均数,再利用所给的方差的公式,做出这组数据的方差.(Ⅱ)根据所给的变量写出随机变量可能的取值,结合变量对应的事件写出变量的概率,写出分布列,做出期望值.【解答】解:(Ⅰ)当X=8,乙组同学植树棵数是8,8,9,10,平均数是=,方差为+=;(Ⅱ)当X=9时,甲组同学的植树棵数是9,9,11,11;乙组同学的植树棵数是9,8,9,10,分别从甲和乙两组中随机取一名同学,共有4×4=16种结果,这两名同学植树的总棵数Y可能是17,18,19,20,21,事件Y=17,表示甲组选出的同学植树9棵,乙组选出的同学植树8棵,∴P(Y=17)=P(Y=18)=P(Y=19)=P(Y=20)=,P(Y=21)=Y 17 18 19 20 21P 0。
北京西城区2011届高三第一学期期末考试(数学理)

北京市西城区2010—2011学年度高三第一学期期末考试数学(理)试题第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知全集U =R ,集合{10}A x x =+<,{30}B x x =-<,那么集合()U C A B =( )A .{13}x x -≤<B .{13}x x -<<C .{1}x x <-D .{3}x x >2.已知点(1,1)A -,点(2,)B y ,向量=(1,2)a ,若//AB a ,则实数y 的值为 ( )A .5B .6C .7D .8 3.已知ABC ∆中,1,a b ==45B =,则角A 等于( )A .150B .90C .60D .30 4.在极坐标系中,过点(1,0)并且与极轴垂直的直线方程是( ) A .cos ρθ= B .sin ρθ=C .cos 1ρθ=D .sin 1ρθ=5.阅读右面程序框图,如果输出的函数值在区间11[,]42内,则输入的实数x 的取值范围是( ) A .(,2]-∞- B .[2,1]--C .[1,2]-D .[2,)+∞6.设等比数列{}n a 的前n 项和为n S ,若0852=+a a ,则下列式子中数值不能确定的是( )A .35a a B .35S S C .nn a a 1+ D .nn S S 1+ 7.如图,四边形ABCD 中,1AB AD CD ===,BD =BD CD ⊥.将四边形ABCD 沿对角线BD 折成四面体A BCD '-,使平面A BD '⊥平面BCD ,则下列结论正确的是( ) A .A C BD '⊥B .90BAC '∠=C .CA '与平面A BD '所成的角为30D .四面体A BCD '-的体积为138.对于函数①1()45f x x x =+-,②21()log ()2x f x x =-,③()cos(2)cos f x x x =+-,判断如下两个命题的真假:命题甲:()f x 在区间(1,2)上是增函数;命题乙:()f x 在区间(0,)+∞上恰有两个零点12,x x ,且121x x <. 能使命题甲、乙均为真的函数的序号是A .①B .②C .①③D .①②第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9.i 为虚数单位,则22(1i)=+______. 10.在5(2)x +的展开式中,2x 的系数为_____.11.若实数,x y 满足条件10,2,1,x y x y x -+≥⎧⎪+≥⎨⎪≤⎩则2x y +的最大值为_____.ABCD12.如图所示,过圆C 外一点P 做一条直线与圆C 交于A B ,两点,2BA AP =,PT 与圆C 相切于T 点.已知圆C 的半径为2,30CAB ∠=,则PT =_____.13.双曲线22:1C x y -=的渐近线方程为_____;若双曲线C 的右顶点为A ,过A 的直线l 与双曲线C 的两条渐近线交于,P Q 两点,且2PA AQ =,则直线l 的斜率为_____.14.在平面直角坐标系中,定义1212(,)d P Q x x y y =-+-为两点11(,)P x y ,22(,)Q x y 之间的“折线距离”.则坐标原点O 与直线20x y +-=上一点的“折线距离”的最小值是____;圆221x y +=上一点与直线20x y +-=上一点的“折线距离”的最小值是____.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数2()22sin f x x x =-.(Ⅰ)若点(1,P 在角α的终边上,求()f α的值;(Ⅱ)若[,]63x ππ∈-,求()f x 的值域.16.(本小题满分13分)如图,在三棱柱111ABC A B C -中,侧面11ABB A ,11ACC A 均为正方形,∠=90BAC ,点D 是棱11B C 的中点.(Ⅰ)求证:1A D ⊥平面11BB C C ;(Ⅱ)求证:1//AB 平面1A DC ; (Ⅲ)求二面角1D A C A --的余弦值.17.(本小题满分13分) 一个袋中装有6个形状大小完全相同的小球,球的编号分别为1,2,3,4,5,6. (Ⅰ)若从袋中每次随机抽取1个球,有放回的抽取2次,求取出的两个球编号之和为6的概率;(Ⅱ)若从袋中每次随机抽取2个球,有放回的抽取3次,求恰有2次抽到6号球的概率;(Ⅲ)若一次从袋中随机抽取3个球,记球的最大编号为X ,求随机变量X 的分布列. 18.(本小题满分13分)已知椭圆12222=+by a x (0>>b a )的右焦点为2(3,0)F ,离心率为e .(Ⅰ)若2e =,求椭圆的方程;(Ⅱ)设直线y kx =与椭圆相交于A ,B 两点,,M N 分别为线段22,AF BF 的中点.若A BC C 1B 1A 1D坐标原点O 在以MN 为直径的圆上,且2322≤<e ,求k 的取值范围. 19.(本小题满分14分) 已知函数21()(21)2ln ()2f x ax a x x a =-++∈R . (Ⅰ)若曲线()y f x =在1x =和3x =处的切线互相平行,求a 的值; (Ⅱ)求()f x 的单调区间;(Ⅲ)设2()2g x x x =-,若对任意1(0,2]x ∈,均存在2(0,2]x ∈,使得12()()f x g x <,求a 的取值范围.20.(本小题满分14分)已知数列}{n a ,{}n b 满足n n n a a b -=+1,其中1,2,3,n =.(Ⅰ)若11,n a b n ==,求数列}{n a 的通项公式;(Ⅱ)若11(2)n n n b b b n +-=≥,且121,2b b ==.(ⅰ)记)1(16≥=-n a c n n ,求证:数列}{n c 为等差数列; (ⅱ)若数列}{na n中任意一项的值均未在该数列中重复出现无数次.求首项1a 应满足的条件.参考答案(理科) 2011.1一、选择题:本大题共8小题,每小题5分,共40分.二、填空题:本大题共6小题,每小题5分,共30分. 9.i - 10.80 11.412.3 13.0x y ±=,3± 142注:13、14题第一问2分,第二问3分. 三、解答题:(本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.) 15.(本小题满分13分)解:(Ⅰ)因为点(1,P 在角α的终边上,所以sin 2α=-,1cos 2α=, ………………2分所以22()22sin cos 2sin f αααααα=-=- ………………4分21()2(3222=-⨯-⨯-=-. ………………5分(Ⅱ)2()22sin f x x x =-cos 21x x =+- ………………6分2sin(2)16x π=+-, ………………8分因为[,]63x ππ∈-,所以65626πππ≤+≤-x , ………………10分所以1sin(2)126x π-≤+≤, ………………11分所以()f x 的值域是[2,1]-. ………………13分16.(本小题满分13分)(Ⅰ)证明:因为侧面11ABB A ,11ACC A 均为正方形, 所以11,AA AC AA AB ⊥⊥,所以1AA ⊥平面ABC ,三棱柱111ABC A B C -是直三棱柱. ………………1分 因为1A D ⊂平面111A B C ,所以11CC A D ⊥, ………………2分 又因为1111A B AC =,D 为11B C 中点,所以111A D B C ⊥. ……………3分 因为1111CC B C C =,所以1A D ⊥平面11BB C C . ……………4分 (Ⅱ)证明:连结1AC ,交1A C 于点O ,连结OD , 因为11ACC A 为正方形,所以O 为1AC 中点,又D 为11B C 中点,所以OD 为11AB C ∆中位线, 所以1//AB OD , ………………6分 因为OD ⊂平面1A DC ,1AB ⊄平面1A DC , 所以1//AB 平面1A DC . ………………8分(Ⅲ)解: 因为侧面11ABB A ,11ACC A 均为正方形, 90BAC ∠=, 所以1,,AB AC AA 两两互相垂直,如图所示建立直角坐标系A xyz -. 设1AB =,则111(0,10),(1,0,0),(0,0,1),(,,1)22C B AD ,.1111(,,0),(0,11)22A D AC ==-,, ………………9分 设平面1A DC 的法向量为=()x,y,z n ,则有1100A D AC ⋅=⎧⎨⋅=⎩n n ,00x y y z +=⎧⎨-=⎩, x y z =-=-, 取1x =,得(1,1,1)=--n . ………………10分又因为AB ⊥平面11ACC A ,所以平面11ACC A 的法向量为(1,00)AB =,,………11分cos ,3AB AB AB⋅〈〉===n n n , ………………12分 因为二面角1DA C A --是钝角, 所以,二面角1D A C A --的余弦值为3-. ………………13分17.(本小题满分13分) 解:(Ⅰ)设先后两次从袋中取出球的编号为,m n ,则两次取球的编号的一切可能结果),(n m 有6636⨯=种, ………………2分其中和为6的结果有(1,5),(5,1),(2,4),(4,2),(3,3),共5种, 则所求概率为536. ………………4分 (Ⅱ)每次从袋中随机抽取2个球,抽到编号为6的球的概率152613C p C ==.………………6分所以,3次抽取中,恰有2次抽到6号球的概率为2223122(1)3()()339C p p -=⨯=. ………………8分(Ⅲ)随机变量X 所有可能的取值为3,4,5,6. (9)分33361(3)20C P X C ===, 23363(4)20C P X C ===, 243663(5)2010C P X C ====,2536101(6)202C P X C ====. ………………12分所以,随机变量X 的分布列为:分18、(本小题满分13分)解:(Ⅰ)由题意得3c c a=⎧⎪⎨=⎪⎩a = ………………2分结合222a b c =+,解得212a =,23b =. ………………3分所以,椭圆的方程为131222=+y x . ………………4分(Ⅱ)由22221,,x y a b y kx ⎧+=⎪⎨⎪=⎩得222222()0b a k x a b +-=.设1122(,),(,)A x y B x y .所以2212122220,a b x x x x b a k-+==+, ………………6分 依题意,OM ON ⊥,易知,四边形2OMF N 为平行四边形,所以22AF BF ⊥, ………………7分 因为211(3,)F A x y =-,222(3,)F B x y =-,所以222121212(3)(3)(1)90F A F B x x y y k x x ⋅=--+=++=. ………………8分即222222(9)(1)90(9)a a k a k a --++=+-, ………………9分 将其整理为 4222424218818111818a a k a a a a -+==---+-. ………………10分因为2322≤<e,所以a ≤<21218a ≤<. ………………11分 所以218k ≥,即2(,(,]44k ∈-∞-+∞. ………………13分 19.(本小题满分14分)解:2()(21)f x ax a x '=-++(0)x >. ………………2分 (Ⅰ)(1)(3)f f ''=,解得23a =. ………………3分(Ⅱ)(1)(2)()ax x f x x--'=(0)x >. ………………5分 ①当0a ≤时,0x >,10ax -<,在区间(0,2)上,()0f x '>;在区间(2,)+∞上()0f x '<,故()f x 的单调递增区间是(0,2),单调递减区间是(2,)+∞. ………………6分 ②当102a <<时,12a>,在区间(0,2)和1(,)a +∞上,()0f x '>;在区间1(2,)a上()0f x '<,故()f x 的单调递增区间是(0,2)和1(,)a +∞,单调递减区间是1(2,)a.…………7分③当12a =时,2(2)()2x f x x -'=, 故()f x 的单调递增区间是(0,)+∞.………8分④当12a >时,102a <<, 在区间1(0,)a 和(2,)+∞上,()0f x '>;在区间1(,2)a上()0f x '<,故()f x 的单调递增区间是1(0,)a 和(2,)+∞,单调递减区间是1(,2)a. ………9分(Ⅲ)由已知,在(0,2]上有max max ()()f x g x <. ………………10分 由已知,max ()0g x =,由(Ⅱ)可知, ①当12a ≤时,()f x 在(0,2]上单调递增, 故max ()(2)22(21)2ln 2222ln 2f x f a a a ==-++=--+, 所以,222ln 20a --+<,解得ln 21a >-,故1ln 212a -<≤.……………11分 ②当12a >时,()f x 在1(0,]a 上单调递增,在1[,2]a上单调递减, 故max 11()()22ln 2f x f a a a==---.由12a >可知11ln ln ln 12ea >>=-,2ln 2a >-,2ln 2a -<,所以,22ln 0a --<,max ()0f x <, ………………13分 综上所述,ln 21a >-. ………………14分20.(本小题满分14分)解:(Ⅰ)当2≥n 时,有121321()()()n n n a a a a a a a a -=+-+-++-1121n a b b b -=++++ …………2分2(1)11222n n n n -⨯=+=-+. ………………3分又因为11=a 也满足上式,所以数列}{n a 的通项为2122n n na =-+.……………4分 (Ⅱ)(ⅰ)因为对任意的n ∈*N 有5164321n n n n n n n b b b b b b b ++++++====, …………5分所以 1656161661626364n n n n n n n n n n c c a a b b b b b b ++--++++-=-=+++++111221722=+++++=(1)n ≥,所以数列}{n c 为等差数列. ………………7分 (ⅱ)设)0(6≥=+n a c i n n ,(其中i 为常数且}6,5,4,3,2,1{∈i ),所以1666661626364657(0)n n n i n i n i n i n i n i n i n i c c a a b b b b b b n +++++++++++++++-=-=+++++=≥所以数列}{6i n a +均为以7为公差的等差数列. ………………9分设6777(6)7766666666i i k i i k i ii k a a a a k f k i i k i k i k+++--+====+++++, (其中i k n +=6)0(≥k ,i 为}6,5,4,3,2,1{中的一个常数),当76i i a =时,对任意的i k n +=6有n a n 76=; ………………10分当76i ia ≠时, 17771166()()6(1)666(1)6i i k k ii ia a i f f a k i k i k i k i +---=-=--++++++ 76()()6[6(1)](6)i i a k i k i -=-+++………………11分①若76i ia >,则对任意的k ∈N 有k k f f <+1,所以数列}6{6i k a i k ++为单调减数列;②若76i ia <,则对任意的k ∈N 有k k f f >+1,所以数列}6{6i k a i k ++为单调增数列;………………12分综上:设集合741111{}{}{}{}{}{}632362B =--74111{,,,,}63236=--,当B a ∈1时,数列}{na n中必有某数重复出现无数次. 当B a ∉1时,}6{6ik a ik ++ )6,5,4,3,2,1(=i 均为单调数列,任意一个数在这6个数列中最多出现一次,所以数列}{na n中任意一项的值均未在该数列中重复出现无数次……14分。
2011年西城区高一上学期数学期末测试及答案(北区)

北京市西城区2010 — 2011学年度第一学期期末试卷(北区)高一数学 2011.1试卷满分:150分 考试时间:120分钟A 卷 [必修 模块4] 本卷满分:100分一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1. 若角α是第四象限的角,则( )A. sin 0α>B. cos 0α>C. tan 0α>D. cot 0α> 2. 若向量a = (1, 1),b = (2, 1-),则2-a b 等于 ( )A. (0,3)B. (0,2)C. (1,2)-D. (1,3)- 3. 已知1cos 3a =,则cos(3π)a +的值等于( ) A. 13-B. 13C. 3-D. 3 4. 设x ∈R ,向量a =(1, x -1),b =(-2,x ),若a ^b ,则实数x 等于( ) A.-2或1 B. -2或-1 C. 2或1 D. 2或-1 5. 函数()2cos sin f x x x =是( )A. 最小正周期为2π的偶函数B. 最小正周期为2π的奇函数C. 最小正周期为π的偶函数D. 最小正周期为π的奇函数6. 如图,D 是ABC V 的边AB 的中点,则向量CD uu u r等于( )A. 12BC BA +uu u r uu rB. 12BC BA -uu u r uu rC. 12BC BA -+uu u r uu rD. 12BC BA --uu u r uu rAD CB7. 对于向量,,a b c 和实数λ,下列说法中正确的是( ) A. 若0a b?,则0a =或 0b = B. 若0l =a ,则0l =或0a =C. 若22a b =,则a b =或 a b =- D. 若a b a c ? ,则b c =8. 为了得到函数πcos(2)3y x =+的图象,只需将函数cos2y x =的图象( ) A. 向左平移π6个长度单位 B. 向右平移π6个长度单位 C. 向左平移π3个长度单位 D. 向右平移π3个长度单位9. 设向量a , b 的长度分别为2和3,且π,3=〈〉a b ,则|a +b |等于 ( ) A. 13B. C. 19 D.10. 设向量2222(cos ,sin ),(cos ,sin )x x x x ==-a b ,函数()f x =⋅a b ,则函数()f x 的图象 ( )A. 关于点(π,0)中心对称B. 关于点π(,0)2中心对称C. 关于点π(,0)4中心对称 D. 关于点(0,0)中心对称二、填空题:本大题共6小题,每小题4分,共24分. 把答案填在题中横线上. 11. sin 390的值等于_________.12. 若向量(12)=-,a 与向量(,4)x b =平行,则实数x =______________. 13. 不等式cos 0x >的解集为___________________ .14. 若向量,a b 满足||||1==a b ,a 与b 的夹角为120,则()⋅+a a b =__________. 15. 设角θ的终边经过点(3,4)-,则πsin()4θ+=___________ . 16. 函数π()sin(π)6f x x =+, x ∈R 的部分图象如右图所示. 设P 是图象上的最高点,M , N 是图象与x 轴的交点,则tan MPN ∠=______________.三、解答题:本大题共3小题,共36分. 解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)设函数sin ()tan xf x x=. (Ⅰ)求函数()f x 的定义域; (Ⅱ)已知π(0,)2α∈,且2()3f α=,求π()3f α+的值.18.(本小题满分12分)在平面直角坐标系xOy 中,点A (0,2) ,B (-1,-1), C (2,3). (Ⅰ)求BAC ∠的的大小;(Ⅱ)求以线段AB , AC 为邻边的平行四边形两条对角线的长.19.(本小题满分12分)已知函数2()sin cos f x x x x ωωω=+(0ω>)图象的两相邻对称轴间的距离为2π. (Ⅰ)求ω的值;(Ⅱ)求函数()f x 的单调减区间;(Ⅲ)若对任意12π,02x x ⎡⎤∈⎢⎥⎣⎦,都有12|()()|f x f x m -<,求实数m 的取值范围.B 卷 [学期综合] 本卷满分:50分一、填空题:本大题共5小题,每小题4分,共20分.把答案填在题中横线上. 1. 2lg 2lg 25+的值等于 .2. 已知函数3,1,(),1,x x f x x x ⎧≤=⎨->⎩若()2f x =,则x = .3. 定义域为(0,)+∞的函数f (x )对于任意正实数x 1, x 2满足f (x 12x ) = f (x 1)+f (x 2). 则f (x )的解析式可以是______________.(写出一个符合条件的函数即可)4. 设f (x )是定义在R 上的偶函数,若()f x 在[0,)+∞是增函数,且(2)0f =,则不等式(1)0f x +>的解集为____________________.5. 某学校要召开学生代表大会,规定各班每10人推选一名代表 ,当各班人数除以10的余数大于6时再增选一名代表. 已知各班可推选代表人数y 与该班人数x 之间的函数关系可以表示为[]10x ay += ([x ]表示不大于x 的最大整数,a ∈N ),那么其中a =__________.二、解答题:本大题共3小题,共30分.解答应写出文字说明,证明过程或演算步骤. 6. (本小题满分10分)设函数1()11f x x =--. (Ⅰ) 求函数()f x 的定义域和值域; (Ⅱ) 证明函数()f x 在(1,)+∞上为减函数.7. (本小题满分10分)已知函数()||()()f x x x a a =⋅+∈R 是奇函数. (Ⅰ)求a 的值;(Ⅱ)设0b >,若函数()f x 在区间[,]b b -上最大值与最小值的差为b ,求b 的值.8.(本小题满分10分)一般地,我们把函数1110()()n n n n h x a x a x a x a n --=++++∈N 称为多项式函数,其中系数01,,,n a a a ∈ R .设 (),()f x g x 为两个多项式函数,且对所有的实数x 等式[()][()]f g x g f x =恒成立. (Ⅰ) 若2()3,()(0)f x x g x kx b k =+=+ .○1 求()g x 的表达式; ○2 解不等式()()5f x g x ->.(Ⅱ)若方程()()f x g x =无实数解,证明方程[()][()]f f x g g x =也无实数解.北京市西城区2010 — 2011学年度第一学期期末试卷(北区)高一数学参考答案及评分标准 2011.1A 卷 [必修 模块4] 满分100分一、选择题:本大题共10小题,每小题4分,共40分.1. B2. A3. A4. D5. D6. C7. B8. A9. D 10. C 二、填空题:本大题共6小题,每小题4分,共24分.11.12 12. 2- 13. ππ{|2π2π+,}22x k x k k -<<∈Z 14. 1215. 1016. 43三、解答题:本大题共3小题,共36分.17.(Ⅰ)解:要使函数()f x 有意义,只要使tan 0x ≠, 所以函数()f x 的定义域为{|x x ∈R 且π,2k x k ≠∈Z}. ----------------4分 (Ⅱ)解:由sin tan cos xx x=,得()cos f x x =, -----------------5分 所以 2()cos 3f αα==,因为 π(0,)2α∈,所以sin α==. ----------------7分 所以ππππ()cos()cos cos sin sin 3333f αααα+=+=- ---------------10分2132=⨯=. ----------------12分 18.(Ⅰ)解:由题意,得(1,3),(2,1)AB AC =--=, -----------------2分 所以cos ||||AB ACBAC AB AC ⋅∠=⋅--------------------------4分2==. --------------------------5分 所以135BAC ∠=. -------------------------6分 (Ⅱ)解:设以线段AB , AC 为邻边的平行四边形的另一个顶点为D , 则两条对角线分别为,BC AD .根据向量加减法的几何意义,得 (1,2),(3,4)AD AB AC BC AC AB =+=-=-=,------------------------9分所以 ||||5AD BC === ,即以线段AB , AC 5.-------12分19.(Ⅰ)解:1cos 2()sin 222x f x x ωω-=+ --------------------------2分112cos 222x x ωω=-+π1sin 262x ω⎛⎫=-+ ⎪⎝⎭. ------------4分由题意,得函数()f x 的最小正周期为π,且0ω>, 所以2ππ2ω=,解得1ω=. ------------------------5分 (Ⅱ)解:由(Ⅰ)得π1()sin 262f x x ⎛⎫=-+ ⎪⎝⎭. 所以当ππ3π2π+22π262k x k -+≤≤时,()f x 单调递减, -----------------------7分 故()f x 的单调递减区间是π5ππ+π36k k ⎡⎤+⎢⎥⎣⎦,,其中k ∈Z . -------------------8分 (Ⅲ)由π02x ≤≤,得ππ5π2666x --≤≤, 所以1πsin 2126x ⎛⎫-- ⎪⎝⎭≤≤, 所以π130sin 2622x ⎛⎫-+ ⎪⎝⎭≤≤,即302()f x ≤≤, 且当π3x =时,()f x 取最大值32;当0x =时,()f x 取最小值0. ----------10分 所以对任意12π,02x x ⎡⎤∈⎢⎥⎣⎦,都有1233|()()||0|22f x f x -≤-≤, 且当1π3x =,20x =时,12|()()|f x f x -取到最大值32, 因为对任意12π,02x x ⎡⎤∈⎢⎥⎣⎦,都有12|()()|f x f x m -<成立, 所以32m >. --------------------------12分B 卷 [学期综合] 满分50分一、填空题:本大题共5小题,每小题4分,共20分.1. 22. 3log 23. 答案不唯一,如()lg f x x =,2()log f x x =等4. {|1,3}x x x ><-或5. 3 二、解答题:本大题共3小题,共30分.6.(Ⅰ)解:要使函数()f x 有意义,只要使10x -≠,所以函数()f x 的定义域为{|,1}x x x ∈≠R 且. ------------------------2分 由反比例函数1y x =的图象和性质,知 11x ∈-R 且101x ≠-, 所以函数1()11f x x =--的值域为{|y y ∈R ,且1}y ≠- . ------------------4分 (Ⅱ)证明:设12x x ,是(1)+∞,上的两个任意实数,且12x x <,则120x x x ∆=-<, 1212121111()()(1)(1)1111y f x f x x x x x ∆=-=---=----- 2112(1)(1)x x x x -=--. ------------------------7分因为121x x <<, 所以 210x x ->,1210,10x x ->->, 从而0y ∆>,所以函数()f x 在(1)+∞,上为减函数. -----------------------10分 7.(Ⅰ)解:因为函数()f x 的定义域为R , 且为奇函数,所以(1)(1)f f -=- ,即 1(1)a a -=-+, 解得 0a = .验证可得0a =时,()f x 是奇函数. --------------------------4分(Ⅱ)解:由(Ⅰ),得 22,0,()||,0.x x f x x x x x ⎧≥⎪=⋅=⎨-<⎪⎩ -------------------------5分则当0x ≥时,()0f x ≥,且()f x 在[0,]b 上为增函数;当0x <时,()0f x <,且()f x 在[,0)b -上为增函数.所以当x b =时,()f x 取到最大值2b ;当x b =-时,()f x 取到最小值2b -.----------------------8分由题意,得22()b b b --=,解得12b =或0b =(舍), 故当12b =时,函数()f x 在区间[,]b b -上最大值与最小值的差为b .-----------10分 8.(Ⅰ)解:因为[()][()]f g x g f x =,所以22()3(3)kx b k x b ++=++, ---------------------------1分即2222233k x kbx b kx k b +++=++, 因为上式对所有的实数x 都成立,且0k ≠,所以22,20,33.k k kb b k b ⎧=⎪=⎨⎪+=+⎩解得1,0k b ==.所以 ()g x x =. ----------------------------3分 不等式()()5f x g x ->,即为235x x +->,解得 2x > 或 1x <-.答:○1 ()g x 的表达式为()g x x =; ○2 不等式()()5f x g x ->的解集为{|2x x >或1}x <-. --------------------------5分(Ⅱ)证明:设函数()()()F x f x g x =-,因为方程()()f x g x =无实数解,所以函数()F x 的图象或者恒在x 轴上方,或者恒在x 轴下方,即()F x 恒大于零或者恒小于零, -------------------------7分 不妨假设()0F x > ,即()()0f x g x ->,因为[()][()]f g x g f x =,所以 [()][()]{[()][()]}{[()][()]}f f x g g x f f x g f x g f x g g x -=-+-,{[()][()]}{[()][()]}f f x g f x f g x g g x =-+- [()][()]0F f x F g x =+>.故方程[()][()]f f x g g x =也无实数解. ----------------------10分。
北京大学数学科学学院《高等代数I》期末试题及答案【完整版】

北京大学数学科学学院期末试题考试科目 高等代数I 考试时间 姓 名 学 号一.(10分)设F 4 = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------i 1i 11111i 1i 11111, F 2 = ⎥⎦⎤⎢⎣⎡-1111, D 2 = ⎥⎦⎤⎢⎣⎡i 001.1) 求矩阵C , 使得 ⎥⎦⎤⎢⎣⎡-2222D I D I ⎥⎦⎤⎢⎣⎡22F 00F C = F 4 ; 2) 求F 4 的逆矩阵.解: 1) 比较 ⎥⎦⎤⎢⎣⎡-2222D I D I⎥⎦⎤⎢⎣⎡22F 00F =⎥⎦⎤⎢⎣⎡-=222222F D F F D F ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------i i 111111i i 111111 与 F 4 得 C =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000001001000001. 2) 由 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------i 1i 11111i 1i 11111⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------i 1i 11111i 1i 11111⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=4000040000400004知 414F 41F =-.二. (10分)设n 阶方阵A n = ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡010010100110010 . 记θ = π / ( n+1 ) .1) 对1 ≤ j ≤ n, 证明 α j = [ sin( j θ ) sin( 2 j θ ) . . . sin( n j θ ) ] T是A n 的特征向量 ;2) 对 a ∈ R , 求矩阵a I + A n 的行列式. 解: 1) 对每个 1 ≤ j ≤ n, 我们有⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-++=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡)θj n sin()θj 3sin()θj 2sin()θj sin(θ)2cos(j )θj 1)(n sin()θj 4sin()θj 2sin()θj 3sin()θj sin()θj sin(2)θj n sin()θj 3sin()θj 2sin()θj sin(01001010011001即 A n α j = 2cos( j θ ) α j .于是α j ( 1 ≤ j ≤ n ) 是A n 的特征向量, 它们对应的特征值2cos( j θ ) ( 1 ≤ j ≤ n )互异.2) a I + A n 的特征值为a + 2cos( j θ ) ( 1 ≤ j ≤ n ) , 故| a I + A n | = ( a + 2cos θ ) ( a + 2cos( 2θ ) ) ...( a + 2cos( n θ ) ) .三. (10分)设A : XA X 是R 4到R 3的线性映射, 其中A = ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡110110101101.1) 求A 的秩 r 及可逆矩阵P , Q , 使得 A = P ⎥⎦⎤⎢⎣⎡0I rQ , 这里 I r 是r 阶单位矩阵.2) 求R 4的一组基α 1 , α 2 , α 3 , α 4 与 R 3的一组基β 1 , β 2 , β 3 ,使得 A α i = β i , ∀ 1 ≤ i ≤ r 且 A α i = 0 , ∀ i > r . 解: 1)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1000010010101101000000100001101010001000010101101101010001110110101101于是A 的秩为 2 , 可取 P = ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡101010001, Q = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000010010101101. 2) 在上式两边右乘Q -1 =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---1000010*********, 得A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---0000001000011010100011000010010101101. 令α 1 , α 2 , α 3 , α 4 依次为Q -1的列向量, β 1 , β 2 , β 3 依次为P 的列向量, 则有 A α 1 = β 1 , A α 2 = β 2 , A α 3 = 0 , A α 4 = 0 . 三.(32分)填空题 .1.设 B, C, D 是n 阶矩阵, 其中D 可逆, 则⎥⎦⎤⎢⎣⎡-D CB C D B 1的秩 = n . ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡---D C 00D C B C D B I 0D B I 11,⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡-D 000I D C 0ID C 0012. 当t < - 1/4 时, 二次型 f = 5 t x 2 + t y 2 – z 2 + 2 t xy + 2 x z 负定 ; 当t >0 时, 二次型 f 的正、负惯性指数分别是 2 与 1 . 通过成对行列变换, 二次型 f 的矩阵可化为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-1000t 0001t 41000t t 0t 1t 51010t t 1t t 5f 负定 ⇔ 4 t + 1 < 0 且t < 0 ⇔ t < – 1 / 4f 的正、负惯性指数分别是 2 与 1 ⇔ 4 t + 1 > 0 且t > 0 ⇔ t > 0 .3. 已知 A = ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--12222121231 是行列式为1的正交矩阵, 则线性变换X A X 是绕单位向量α = 的旋转, 旋转角为 .解特征方程组 ( A – I ) X = 0 , 得特征值1 的特征子空间基底 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡011. 于是α = ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡±01121. 取与α垂直的向量β = ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-011, 由A β =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-41131 求得β与A β 夹角的余弦值为 ( β, A β )/ ( | β| | A β| )= 1/3 . 故旋转角为 arccos( 1 / 3 ).4. 在欧氏空间R 4中,子空间 < ( 1,0,0,0) T, ( 0,1,0,0 ) T> 到⎩⎨⎧==+1x 2x x 321的解集合的最小距离是 1 .四. (18分)设f ( x 1 , x 2 , x 3 ) = 8 x 12 –7 x 22 + 8 x 32 + 8 x 1 x 2 – 2 x 1 x 3 + 8 x 2 x 3 . (1) 将 f 写成 X T A X 的形式, 并求A 的特征值与特征向量; (2) 求正交矩阵 P 及对角矩阵D , 使得 A = P D P T .解: (1) []⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---==321321Tx x x 841474148x x x X A X f8λ4147λ49λ09λ8λ4147λ4148λ|A λI |---+-+--=---+---=-)9λ()9λ()3249λ()9λ(7λ4187λ4009λ22+-=---=---+--=A 的特征值为λ = 9 (二重), – 9 . 对λ = 9解齐次方程组 ( A – 9 I ) X = 0 :⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----0000001411414164141 通解为x 1 = 4 x2 - x3 , x 2 、x 3为自由变量. 解的向量形式⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡101x 014x x x x 4x x x x 323232321于是α1 = [ 1 0 -1 ] T , α2 = [ 4 1 0 ] T 构成λ = 9特征子空间的一组基. 对λ = -9解齐次方程组 ( A + 9 I ) X = 0 :⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--00041010100036901741000212174117414241417 通解为 x 1 = x 3 , x 2 = - 4 x 3 , x 3为自由变量. 解的向量形式:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡141x x 4x x x x x 3333321于是α3 = [ 1 -4 1 ] T 构成λ = -9特征子空间的一组基. (2) 将α1 = [ 1 0 -1 ] T , α2 = [ 4 1 0 ] T 正交化: 令 β1 = α1 ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-=21210124014β)β,β()β,α(αβ1111222 再单位化:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==21231β||β||1γ,10121β||β||1γ222111 将α3 = [ 1 -4 1 ] T 也单位化: .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=141231γ3 γ1 , γ2 , γ3 构成R 3 的标准正交基, P = [ γ1 γ2 γ3 ] =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--23132212343102313221为正交矩阵, 且.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==T 3T 2T1321Tγγγ999]γγγ[P D P A五.(10分)设β是欧氏空间R n 的单位向量, V 是子空间 < β > 的正交补. (1) 求矩阵A , 使得对任意列向量X ∈ R n , AX 是X 向V 所作的正交投影; (2) 求正交矩阵B , 使得线性变换 X B X 是R n 关于V 的镜面反射. 解: (1) 对任意列向量X ∈ R n , X 在一维子空间 < β > 上的正交投影为 ( X , β ) β = β βT X .于是X 在正交补 < β >⊥上的正交投影为X – ( X , β ) β = X – β βT X = ( I – β βT ) X .故所求矩阵为A = I – β βT .(2) 向量X ∈ R n , 关于 < β >⊥ 的镜面反射为X – 2 ( X , β ) β = X – 2 β βT X = ( I – 2 β βT ) X . 故所求正交矩阵为B = I – 2 β βT .六.(10分)判断对错, 正确的请给出证明, 错误的举出反例.1) 若A 是实对称矩阵, B 是实反对称矩阵, 则A + i B 的特征多项式在复数域上的根都是实数. 正确.证明: 设λ是A + i B 在复数域上的特征值, α是属于λ的复特征向量, 即 ( A + i B ) α = λ α , α ≠ 0 .则有 αT ( A – i B ) = λ αT , TT αλ)B i A (α=+.于是 ααλα)B i A (αααλTTT=+=, 由α ≠ 0 知0ααT≠, 于是 λλ=, λ 为实数.2) 在数域K 上, 若 n 阶方阵A 有 n + 1 个特征向量, 且其中任意 n 个都线性无关, 则 A 一定是数量矩阵. 正确.若A 不是数量矩阵, 则A 的特征子空间维数都小于n. 又因为A 有 n 个 线性无关的特征向量, A 可对角化, 故A 的特征子空间的维数之和等于n. 任给n + 1 个特征向量, 必存在A 的一个特征子空间 V , 包含其中至少 dim V + 1≤ n 个特征向量, 这dim V + 1 个特征向量线性相关, 矛盾!。
北京大学数学科学学院【数学分析 I】课程习题集(参考 谢惠民 数学分析习题课讲义)

或任意 n ≥ N 有 则仍有矛盾. 从而 c = 1.
1 ∈ (c − ϵ, c + ϵ) .
an
解. 取 M > 1 使得
[
]
1
a1, a2 ∈
,M M
.
则归纳易知任意
n
有
an
∈
[
1 M
,
M ],
从而
α = lim sup an, β = lim inf an
n→∞
n→∞
均为正数, 且 α ≥ β. 又从两个方向分别导出不等式, 可得出 αβ = 1. 取 {ank }∞ k=1 收敛于 α, 易证
4
证明. 只须证 α < c < β 的情形. 找 p1 < q1 < p2 < q2 < · · · 使得
xpl > c > xqm (l = 1, 2, . . . ; m = 1, 2, . . .). 又存在 pj ≤ rj < qj (j = 1, 2, . . .) 使得
此时
xrj ≥ c ≥ xrj+1.
lim
k→∞
ank −1
=
lim
k→∞
ank −2
=
β.
而 2
ank−3 = ank−1 − ank−2 (nk > 3).
左式关于 k 的上极限不大于 α, 但右式关于 k 的极限为 2α − β > α, 矛盾.
问题 4 (08 上期中). 设 {an}∞ n=1 为单调递增的正整数列. 证明: 数列
cn = max(bn+1, bn) (n = 1, 2, . . .).
则 {cn}∞ n=1 不增且有下界, 故其下确界 c 为其极限值 (显然 c ≥ 1), 从而任 意 ϵ > 0, 存在 N 使得任意 n ≥ N 有
北京大学高等代数 I_2011 期末答案

北京大学数学学院期末试题2011-2012学年第一学期考试科目 高等代数I 考试时间 2012年1月3日姓 名 学 号一. (10分)已知n 阶方阵A =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡111011001 , B =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡n 321332122211111 . 求矩阵X , 使得 A X = B .解: 对矩阵 [ A | B ] 作初等行变换⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-→⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡1n 2101110022101101110001011110001n 3211111033211112221001111110001⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡→⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-→100010000110010011100010111100012n 1001100011001001110001011110001故 X =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡100110111 .二.(15分)设 A : X A X 是R 3上的线性变换, 其中A = ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡200211011.(1) 求线性变换 A 像空间的维数和一组基;(2) 求矩阵A 的特征值与特征向量;(3) 判断矩阵A 能否对角化并说明理由.解: (1) 在标准基下, A 像空间就是矩阵A 的列空间, 它的一组基为 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡220011,, 维数是2 .(2)A 的特征值为λ = 2 (代数二重), 0 .对λ = 2解齐次方程组 ( A - 2 I ) X = 0 :⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--000100011000211011通解为x 1 = x 2 , x 3 = 0 , x 2 为自由变量. 写成向量形式⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡0110222321x x x x x x α1 = [ 1 1 0 ] T 构成λ = 2特征子空间的一组基.22)2λ(λ)λ2λ()2λ(1λ111λ)2λ(2λ0021λ1011λλ-=--=-----=------=-|A I |对λ = 0解齐次方程组 A X = 0 :⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000100011200211011通解为x 1 = - x 2 , x 3 = 0 , x 2 为自由变量. 写成向量形式⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡0110222321x x x x x xα1 = [ -1 1 0 ] T 构成λ = 0特征子空间的一组基.(3) 由于特征值 λ = 2特征子空间的维数1小于其代数重数2,A 不能否对角化.三.(35分)填空题 (多选) .1.已知3阶矩阵A 的特征值为 1, 1/2 , 0 , 相应的特征向量为[ 1 0 1 ] T , [ 0 1 0 ] T , [ 1 2 0 ] T , 则 2 A 3 – 3 A 2 = .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-101121010100121010100002100010012101011// 2. 设A = . 当t 取 不等于1的值 时, 存在矩阵B ,使得 AB = I . 当t 取 1 时, 存在非零矩阵C , 使得 C A = 0 .3. 当 -4/5 < t < 0 时, 三元二次型x 2 + y 2 + 5 z 2 + 2 t x y – 2 x z + 4 y z 正定.4. 设α是n 维欧氏空间里的单位列向量 , 则 | I – 5 α αT | = - 4 . 注: 可计算行列式或利用 | I m –A B | = | I n –B A | .5. 在实数域上,以下诸矩阵的相抵分类是 {A,B,D},{C},⎥⎦⎤⎢⎣⎡+421211t t相似分类是 {A,D},{B},{C} , 合同分类是 {A},{B},{C},{D}.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=000010212D 103010001C 010131010B 101010101A ,,,6. 以下说法正确的有 (a)(b)(c)(d) (多选).a) 如果两个实对称矩阵相似, 它们也一定合同;b) 实方阵都能写成P Q 的形式, 其中P 是实对称矩阵, Q 是正交矩阵 c) 每个矩阵都能写成P J 的形式, P 是可逆矩阵, J 是行简化阶梯矩阵 d) 实方阵都能写成Q R 的形式, Q 是正交矩阵, R 是上三角矩阵四.(12分)判断对错, 正确的请给出证明, 错误的举出反例.1) 在包含n (n>1)个向量的向量组中, 若任意n - 1 个向量都线性 无关, 则整个向量组也线性无关.解: 此命题错误. 例如, 考察向量组 ⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡0201,, 其中由任意一个 向量构成的部分组都线性无关, 但整个向量组线性相关.2) 设A 是m ⨯ n 矩阵. 若存在矩阵B 与C, 使得 BA = I n , AC = I m , 则必有m = n , 且 B = C .解: 此命题正确. 由矩阵乘法的结合律, 有C = ( BA ) C = B ( AC ) = B , 于是 m = n.五.(20分)设 f = 2 x 1 x 2 + 2 x 1 x 3 + 2 x 2 x 3 是三元二次型.(1) 将 f 写成 X T A X 的形式, 并求A 的特征值与特征向量;(2) 求正交矩阵P 及对角矩阵D, 使得A = P D P T ;(3) 求二次齐次函数 f ( x 1 , x 2 , x 3 ) 在单位球面 x 12 + x 22 + x 32 = 1上的最大、最小值, 并确定在何处取到.解: (1) []⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==321321T AX X f x x x x x x 011101110A 的特征值为λ = - 1 (代数二重), 2 .对λ = - 1解齐次方程组 ( A + I ) X = 0 :⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000000111111111111通解为x 1 = - x 2 - x 3 , x 2 、x 3为自由变量. 写成向量形式⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡101011323232321x x x x x x x x xα1 = [ -1 1 0 ] T , α2 = [ -1 0 1 ] T 构成λ = -1特征子空间的一组基. 对λ = 2解齐次方程组 ( A - 2 I ) X = 0 :⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---000110101000112121211121112通解为 x 1 = x 3 , x 2 = x 3 , x 3为自由变量. 向量形式:)2λ()1λ()2λλ()1λ(1λ0011λ112λ1λλ101λ111λλ111λ111λλ22-+=--+=+-----=+------=------=-|A I |⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1113333321x x x x x x x 于是α3 = [ 1 1 1 ] T 构成λ = 2特征子空间的一组基.(2) 将α1 = [ -1 1 0 ] T , α2 = [ -1 0 1 ] T 正交化:令β1 = α1 ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=-=2112101121101β)β,β()β,α(αβ1111222 再单位化:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==21161β||β||1γ,01121β||β||1γ222111 将α3 = [ 1 1 1 ] T 也单位化: .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=11131γ3 γ1 , γ2 , γ3 构成R 3 的标准正交基, P = [ γ1 γ2 γ3 ] 为正交矩阵, 且.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--==T 3T 2T 1321γγγ211]γγγ[T P D P A (3) 做正交替换X = P Y ,f = X T A X = Y T P T A P Y = Y T D Y = - y 12 - y 22 + 2 y 32 . 由于P 正交, x 12 + x 22 + x 32 = 1 当且仅当 y 12 + y 22 + y 32 = 1.当 y 12 + y 22 + y 32 = 1时,f = - y 12 - y 22 + 2 y 32 ≤ 2( y 12 + y 22 + y 32 ) = 2,等号成立当且仅当 y 3 = ±1, y 1 = y 2= 0, 即X 取λ = 2特征子空间中的单位向量 ± γ3时成立.类似地, 当 y 12 + y 22 + y 32 = 1时,f = - y 12 - y 22 + 2 y 32 ≥ - ( y 12 + y 22 + y 32 ) = -1,等号成立当且仅当X 取λ = -1特征子空间中的单位向量时成立.六.(8分)设 A 是一个n 阶正定矩阵, 其 ( i , j ) 元记为a i j .证明: a 11 a 22 . . . a nn ≥ | A | .证法1. 对 n 应用数学归纳法.当 n = 1 时, A = a 11 = | A | , 命题成立.以下设命题对n -1成立, 考察A 是n 阶矩阵的情况.记A =⎥⎦⎤⎢⎣⎡-nn αT αα1n A , 其中A n-1是n - 1阶正定矩阵, α是 n - 1 维列向量. 对 A 做成对的行,列分块运算, 得⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-----αααααα1-1-n 1n 1-1-n 1n 1n 1-1-n 1n A 00A 1A 0I A 1A 0I T T T T nn T nn αα 于是 | A | = | A n-1 | ( a nn - αT A n-1-1 α ) .由归纳假设, | A n-1 | ≤ a 11 a 22 . . . a n-1n-1 . 又由A n-1 正定知A n-1 的特征值都 > 0, 于是实对称矩阵A n-1-1的特征值也都大于0, 故A n-1-1 也正定. 特别地, 有αT A n-1-1 α ≥ 0 .综上所述, | A | = | A n-1 | ( a nn - αT A n-1-1 α )≤ a 11 a 22 . . . a n-1n-1 a nn .故命题对所有n ≥成立.证法2. 利用Cholesky 分解: 每个正定矩阵A都可写成A = L T L,其中L是对角元都> 0的实上三角矩阵.设L 的( i , j ) 元为b i j , 则有a j j = b1 j2+ b2 j2 + … +b j j2 ≥b j j2 .故 a 11 a22 . . . a nn ≥b112 b222. . . b nn2 = | L T L | =| A |.。
北京大学2010年数学分析试题及解答

|Pn(x) − Pm(x)| < ε.
因为 I 为无穷区间, 因此当 n > m ⩾ Nε 时, |Pn(x) − Pm(x)| 为常数. 设
|PNε (x) − Pn(x)| = cn, n > N,
于是 {cn} 为有界数列, 必有收敛子列 {cnk }∞ k=1, 设
结合 |PNε (x) − Pnk (x)| = cnk , 令 k → ∞ 得
2ε
∫1
3 + |t − t0| η0
∫1
0
xt0+θ(t−t0)(ln x)2
η0
xa(ln x)2 · f (x) dx
· f (x) dx
η0
θ ∈ (0, 1)
因此存在正数 δ <
ε
{∫ 1 , 其中 M = max
3M
η0
xa(ln x)2 · f (x)
} dx, 1 . 当 |t − t0| < δ 时, 就有
ε
{∫ A0 , 其中 M = max
3M
0
xb(ln x)2 · f (x)
} dx, 1 . 当 |t − t0| < δ 时, 就有
|J2(t) − J2(t0)| < ε.
这说明 J2(t) 在 [a, b] 上连续, 由 [a, b] 的任意性知 J2(t) 在 (−1, 1) 上连续. 因此 J(t) = J1(t) + J2(t) 在 (−1, 1) 上连续.
ε <,
∀t ∈ [a, b].
A
3
于是 ∀t, t0 ∈ [a, b]
∫ +∞
∫ +∞
|J2(t) − J2(t0)| =
北京大学数学分析期末试题

1. 讨论下列函数序列或函数项级数在指定区间的一致收敛性:
+∞ 1
(1)
, x ∈ (−∞, +∞);
n2 + x2n源自1+∞ sin x sin nx
(2)
√
, x ∈ [0, +∞);
n=1 n + x2
(3) fn(x) = nαx(1 − x)n, α ∈ R, x ∈ [0, 1].
x
8. p(x)是周期为2π的连续函数, ω是实数但不是整数, 求证: p(x) sin ωxdx有界.
0
2. 求下列幂级数的收敛半径和收敛域:
(1)
+∞
n! n2n
xn;
n=1
+∞
(2)
2nxn2 .
n=1
3. 求下列函数的Fourier级数:
(1) f (x) = x cos x, −π ≤ x < pi; (2) f (x) = sin4 x.
1
2
4. 设函数fn(x)(n = 1, 2, · · · )在[0, 1]上具有连续导函数, 并且{fn(x)}在[0, 1]上一致有 界. 证明: 如果{fn(x)}在区间[a, b]上点点收敛到f (x), 则{fn(x)}在[a, b]上必定一致 收敛到f (x).
5. 设函数f (x)和g(x)以2π为周期, 且在[−π, π]上可积. 证明: f (x)与g(x)的Fourier级数
π
相等的充分必要条件是 |f (x) − g(x)|dx = 0.
−π
b
6. 设f (x)是[a, b]上的连续函数, 满足: f (x)x3ndx = 0, n = 0, 1, 2, · · · . 证明在[a, b]上
2011年北京市高考数学试卷(文科)答案与解析

2011年北京市高考数学试卷(文科)参考答案与试题解析一、选择题(共8小题,每小题5分,满分40分)1.(5分)(2011•北京)已知全集U=R,集合P={x|x2≤1},那么∁U P=()A.(﹣∞,﹣1]B.[1,+∞)C.[﹣1,1]D.(﹣∞,﹣1)∪(1,+∞)【考点】补集及其运算.【专题】集合.【分析】先求出集合P中的不等式的解集,然后由全集U=R,根据补集的定义可知,在全集R 中不属于集合P的元素构成的集合为集合A的补集,求出集合P的补集即可.【解答】解:由集合P中的不等式x2≤1,解得﹣1≤x≤1,所以集合P=[﹣1,1],由全集U=R,得到C U P=(﹣∞,1)∪(1,+∞).故选D【点评】此题属于以不等式的解集为平台,考查了补集的运算,是一道基础题.2.(5分)(2011•北京)复数=()A.i B.﹣i C.D.【考点】复数代数形式的混合运算.【专题】数系的扩充和复数.【分析】将分子、分母同乘以1﹣2i,再按多项式的乘法法则展开,将i2用﹣1代替即可.【解答】解:==i故选A【点评】本题考查复数的除法运算法则:分子、分母同乘以分母的共轭复数;再按多项式的乘法法则展开即可.3.(5分)(2011•北京)如果那么()A.y<x<1 B.x<y<1 C.1<x<y D.1<y<x【考点】对数函数的单调性与特殊点.【专题】函数的性质及应用.【分析】本题所给的不等式是一个对数不等式,我们要先将不等式的三项均化为同底根据对数函数的单调性,即可得到答案.【解答】解:不等式可化为:又∵函数的底数0<<1故函数为减函数∴x>y>1故选D【点评】本题考查的知识点是对数函数的单调性与特殊点,其中根据对数函数的性质将对数不等式转化为一个整式不等式是解答本题的关键.4.(5分)(2011•北京)若p是真命题,q是假命题,则()A.p∧q是真命题B.p∨q是假命题C.﹁p是真命题D.﹁q是真命题【考点】复合命题的真假.【专题】简易逻辑.【分析】根据题意,由复合命题真假表,依次分析选项即可作出判断.【解答】解:∵p是真命题,q是假命题,∴p∧q是假命题,选项A错误;p∨q是真命题,选项B错误;¬p是假命题,选项C错误;¬q是真命题,选项D正确.故选D.【点评】本题考查复合命题的真假情况.5.(5分)(2011•北京)某四棱锥的三视图如图所示,该四棱锥的表面积是()A.32 B.16+16 C.48 D.16+32【考点】由三视图求面积、体积.【专题】立体几何.【分析】根据所给的三视图得到四棱锥的高和底面的长和宽,首先根据高做出斜高,做出对应的侧面的面积,再加上底面的面积,得到四棱锥的表面积.【解答】解:由题意知本题是一个高为2,底面是一个长度为4的正方形的四棱锥,过顶点向底面做垂线,垂线段长是2,过底面的中心向长度是4的边做垂线,连接垂足与顶点,得到直角三角形,得到斜高是2,∴四个侧面积是,底面面积是4×4=16,∴四棱锥的表面积是16+16,故选:B.【点评】本题考查有三视图求表面积和体积,考查由三视图得到几何图形,考查简单几何体的体积和表面积的做法,本题是一个基础题.6.(5分)(2011•北京)执行如图所示的程序框图,若输入A的值为2,则输入的P值为()A.2 B.3 C.4 D.5【考点】循环结构.【专题】算法和程序框图.【分析】根据输入A的值,然后根据S进行判定是否满足条件S≤2,若满足条件执行循环体,依此类推,一旦不满足条件S≤2,退出循环体,求出此时的P值即可.【解答】解:S=1,满足条件S≤2,则P=2,S=1+=满足条件S≤2,则P=3,S=1++=满足条件S≤2,则P=4,S=1+++=不满足条件S≤2,退出循环体,此时P=4故选:C【点评】本题主要考查了当型循环结构,循环结构有两种形式:当型循环结构和直到型循环结构,当型循环是先判断后循环,直到型循环是先循环后判断.7.(5分)(2011•北京)某车间分批生产某种产品,每批的生产准备费用为800元.若每批生产x件,则平均仓储时间为天,且每件产品每天的仓储费用为1元.为使平均每件产品的生产准备费用与仓储费用之和最小,每批应生产产品()A.60件B.80件C.100件D.120件【考点】函数模型的选择与应用.【专题】函数的性质及应用.【分析】若每批生产x件,则平均仓储时间为天,可得仓储总费用为,再加上生产准备费用为800元,可得生产x件产品的生产准备费用与仓储费用之和是=元,由此求出平均每件的生产准备费用与仓储费用之和,再用基本不等式求出最小值对应的x值【解答】解:根据题意,该生产x件产品的生产准备费用与仓储费用之和是=这样平均每件的生产准备费用与仓储费用之和为(x为正整数)由基本不等式,得当且仅当时,f(x)取得最小值、可得x=80时,每件产品的生产准备费用与仓储费用之和最小故答案为B【点评】本题结合了函数与基本不等式两个知识点,属于中档题,运用基本不等式时应该注意取等号的条件,才能准确给出答案.8.(5分)(2011•北京)已知点A(0,2),B(2,0).若点C在函数y=x2的图象上,则使得△ABC的面积为2的点C的个数为()A.4 B.3 C.2 D.1【考点】抛物线的应用.【专题】函数的性质及应用.【分析】本题可以设出点C的坐标(a,a2),求出C到直线AB的距离,得出三角形面积表达式,进而得到关于参数a的方程,转化为求解方程根的个数(不必解出这个跟),从而得到点C的个数.【解答】解:设C(a,a2),由已知得直线AB的方程为,即:x+y﹣2=0点C到直线AB的距离为:d=,有三角形ABC的面积为2可得:=|a+a2﹣2|=2得:a2+a=0或a2+a﹣4=0,显然方程共有四个根,可知函数y=x2的图象上存在四个点(如上面图中四个点C1,C2,C3,C4)使得△ABC的面积为2(即图中的三角形△ABC1,△ABC2,△ABC3,△ABC4).故应选:A【点评】本题考查了截距式直线方程,点到直线的距离公式,三角形的面积的求法,就参数的值或范围,考查了数形结合的思想二、填空题(共6小题,每小题5分,满分30分)9.(5分)(2011•北京)在△ABC中.若b=5,,sinA=,则a=.【考点】正弦定理.【专题】解三角形.【分析】直接利用正弦定理,求出a 的值即可.【解答】解:在△ABC中.若b=5,,sinA=,所以,a===.故答案为:.【点评】本题是基础题,考查正弦定理解三角形,考查计算能力,常考题型.10.(5分)(2011•北京)已知双曲线(b>0)的一条渐近线的方程为y=2x,则b=2.【考点】双曲线的简单性质.【专题】圆锥曲线的定义、性质与方程.【分析】利用双曲线的标准方程写出其渐近线方程是解决本题的关键,根据已知给出的一条渐近线方程对比求出b的值.【解答】解:该双曲线的渐近线方程为,即y=±bx,由题意该双曲线的一条渐近线的方程为y=2x,又b>0,可以得出b=2.故答案为:2.【点评】本题考查根据双曲线方程求解其渐近线方程的方法,考查学生对双曲线标准方程和渐近线方程的认识和互相转化,考查学生的比较思想,属于基本题型.11.(5分)(2011•北京)已知向量=(,1),=(0,﹣1),=(k,).若与共线,则k=1.【考点】平面向量共线(平行)的坐标表示.【专题】平面向量及应用.【分析】利用向量的坐标运算求出的坐标;利用向量共线的坐标形式的充要条件列出方程,求出k的值.【解答】解:∵与共线,∴解得k=1.故答案为1.【点评】本题考查向量的坐标运算、考查向量共线的坐标形式的充要条件:坐标交叉相乘相等.12.(5分)(2011•北京)在等比数列{a n}中,a1=,a4=﹣4,则公比q=﹣2;a1+a2+…+a n=.【考点】等比数列的性质;等比数列.【专题】等差数列与等比数列.【分析】根据等比数列的性质可知,第4项比第1项得到公比q的立方等于﹣8,开立方即可得到q的值,然后根据首项和公比,根据等比数列的前n项和的公式写出此等比数列的前n 项和S n的通项公式,化简后即可得到a1+a2+…+a n的值.【解答】解:q3==﹣8∴q=﹣2;由a1=,q=﹣2,得到:等比数列的前n项和S n=a1+a2+…+a n==.故答案为:﹣2;【点评】此题考查学生掌握等比数列的性质,灵活运用等比数列的前n项和公式化简求值,是一道基础题.13.(5分)(2011•北京)已知函数若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是(0,1).【考点】根的存在性及根的个数判断.【专题】函数的性质及应用.【分析】要求程f(x)=k有两个不同的实根是数k的取值范围,根据方程的根与对应函数零点的关系,我们可以转化为求函数y=f(x)与函数y=k交点的个数,我们画出函数的图象,数形结合即可求出答案.【解答】解:函数的图象如下图所示:由函数图象可得当k∈(0,1)时方程f(x)=k有两个不同的实根,故答案为:(0,1)【点评】本题考查的知识点是根的存在性及根的个数判断,其中根据方程的根与对应函数零点的关系,将方程问题转化为函数问题是解答的关键.14.(5分)(2011•北京)设A(0,0),B(4,0),C(t+4,3),D(t,3)(t∈R).记N(t)为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则N(0)=6,N(t)的所有可能取值为6、7、8.【考点】二元一次不等式(组)与平面区域.【专题】不等式的解法及应用.【分析】作出平行四边形,结合图象得到平行四边形中的整数点的个数.【解答】解:当t=0时,平行四边形ABCD内部的整点有(1,1);(1,2);(2,1);(2,2);(3,1);(3,2)共6个点,所以N(0)=6作出平行四边形ABCD将边OD,BC变动起来,结合图象得到N(t)的所有可能取值为6,7,8故答案为:6;6,7,8【点评】本题考查画可行域、考查数形结合的数学思想方法.三、解答题(共6小题,满分80分)15.(13分)(2011•北京)已知函数.(Ⅰ)求f(x)的最小正周期:(Ⅱ)求f(x)在区间上的最大值和最小值.【考点】三角函数的周期性及其求法;两角和与差的余弦函数;三角函数的最值.【专题】三角函数的图像与性质.【分析】(Ⅰ)利用两角和公式和二倍角公式对函数的解析式进行化简整理后,利用正弦函数的性质求得函数的最小正周期.(Ⅱ)利用x的范围确定2x+的范围,进而利用正弦函数的单调性求得函数的最大和最小值.【解答】解:(Ⅰ)∵,=4cosx()﹣1=sin2x+2cos2x﹣1=sin2x+cos2x=2sin(2x+),所以函数的最小正周期为π;(Ⅱ)∵﹣≤x≤,∴﹣≤2x+≤,∴当2x+=,即x=时,f(x)取最大值2,当2x+=﹣时,即x=﹣时,f(x)取得最小值﹣1.【点评】本题主要考查了三角函数的周期性及其求法,三角函数的最值.解题的关键是对函数解析式的化简整理.16.(13分)(2011•北京)以下茎叶图记录了甲、乙两组各四名同学的植树棵树.乙组记录中有一个数据模糊,无法确认,在图中以X表示.(1)如果X=8,求乙组同学植树棵树的平均数和方差;(注:方差,其中的平均数)(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.【考点】茎叶图;众数、中位数、平均数;极差、方差与标准差.【专题】概率与统计.【分析】(1)根据所给的这组数据,利用求平均数的公式,把所有的数据都相加,再除以4,得到平均数,代入求方差的公式,做出方差.(2)本题是一个等可能事件的概率.分别从甲、乙两组中随机选取一名同学,共有16种结果,满足条件的事件是这两名同学的植树总棵数为19,可以列举出共有4种结果,根据等可能事件的概率公式得到结果.【解答】解:(1)当X=8时,由茎叶图可知乙组同学的植树棵树是8,8,9,10,∴平均数是,方差是+=.(2)由题意知本题是一个等可能事件的概率.若X=9,分别从甲、乙两组中随机选取一名同学,共有16种结果,满足条件的事件是这两名同学的植树总棵数为19,包括:(9,10),(11,8),(11,8),(9,10)共有4种结果,∴根据等可能事件的概率公式得到P=.【点评】本题考查一组数据的平均数和方差,考查等可能事件的概率,考查利用列举法来列举出符合条件的事件数和满足条件的事件数,本题是一个文科的考试题目.17.(14分)(2011•北京)如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.(Ⅰ)求证:DE∥平面BCP;(Ⅱ)求证:四边形DEFG为矩形;(Ⅲ)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.【考点】直线与平面平行的判定;空间中直线与直线之间的位置关系.【专题】空间位置关系与距离;立体几何.【分析】(Ⅰ)根据两个点是两条边的中点,得到这条线是两条边的中位线,得到这条线平行于PC,根据线面平行的判定定理,得到线面平行.(Ⅱ)根据四个点是四条边的中点,得到中位线,根据中位线定理得到四边形是一个平行四边形,根据两条对角线垂直,得到平行四边形是一个矩形.(Ⅲ)做出辅助线,证明存在点Q到四面体PABC六条棱的中点的距离相等,根据第二问证出的四边形是矩形,根据矩形的两条对角线互相平分,又可以证出另一个矩形,得到结论.【解答】证明:(Ⅰ)∵D,E分别为AP,AC的中点,∴DE∥PC,∵DE⊄平面BCP,∴DE∥平面BCP.(Ⅱ)∵D,E,F,G分别为AP,AC,BC,PB的中点,∴DE∥PC∥FG,DG∥AB∥EF∴四边形DEFG为平行四边形,∵PC⊥AB,∴DE⊥DG,∴四边形DEFG为矩形.(Ⅲ)存在点Q满足条件,理由如下:连接DF,EG,设Q为EG的中点,由(Ⅱ)知DF∩EG=Q,且QD=QE=QF=QG=EG,分别取PC,AB的中点M,N,连接ME,EN,NG,MG,MN,与(Ⅱ)同理,可证四边形MENG为矩形,其对角线交点为EG的中点Q,且QM=QN=EG,∴Q为满足条件的点.【点评】本题考查直线与平面平行的判定,考查三角形中位线定理,考查平行四边形和矩形的判定及性质,本题是一个基础题.18.(13分)(2011•北京)已知函数f(x)=(x﹣k)e x.(Ⅰ)求f(x)的单调区间;(Ⅱ)求f(x)在区间[0,1]上的最小值.【考点】利用导数研究函数的单调性;利用导数求闭区间上函数的最值.【专题】导数的综合应用.【分析】(I)求导,令导数等于零,解方程,跟据f′(x)f(x)随x的变化情况即可求出函数的单调区间;(Ⅱ)根据(I),对k﹣1是否在区间[0,1]内进行讨论,从而求得f(x)在区间[0,1]上的最小值.【解答】解:(Ⅰ)f′(x)=(x﹣k+1)e x,令f′(x)=0,得x=k﹣1,f′(x)f(x)随x的变化情况如下:x (﹣∞,k﹣1)k﹣1 (k﹣1,+∞)f′(x)﹣0 +f(x)↓﹣e k﹣1↑∴f(x)的单调递减区间是(﹣∞,k﹣1),f(x)的单调递增区间(k﹣1,+∞);(Ⅱ)当k﹣1≤0,即k≤1时,函数f(x)在区间[0,1]上单调递增,∴f(x)在区间[0,1]上的最小值为f(0)=﹣k;当0<k﹣1<1,即1<k<2时,由(I)知,f(x)在区间[0,k﹣1]上单调递减,f(x)在区间(k﹣1,1]上单调递增,∴f(x)在区间[0,1]上的最小值为f(k﹣1)=﹣e k﹣1;当k﹣1≥1,即k≥2时,函数f(x)在区间[0,1]上单调递减,∴f(x)在区间[0,1]上的最小值为f(1)=(1﹣k)e;综上所述f(x)min=.【点评】此题是个中档题.考查利用导数研究函数的单调性和在闭区间上的最值问题,对方程f’(x)=0根是否在区间[0,1]内进行讨论,体现了分类讨论的思想方法,增加了题目的难度.19.(14分)(2011•北京)已知椭圆G:=1(a>b>0)的离心率为,右焦点为(2,0),斜率为1的直线l与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(﹣3,2).(Ⅰ)求椭圆G的方程;(Ⅱ)求△PAB的面积.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程.【专题】圆锥曲线的定义、性质与方程.【分析】(Ⅰ)根据椭圆离心率为,右焦点为(,0),可知c=,可求出a的值,再根据b2=a2﹣c2求出b的值,即可求出椭圆G的方程;(Ⅱ)设出直线l的方程和点A,B的坐标,联立方程,消去y,根据等腰△PAB,求出直线l方程和点A,B的坐标,从而求出|AB|和点到直线的距离,求出三角形的高,进一步可求出△PAB的面积.【解答】解:(Ⅰ)由已知得,c=,,解得a=,又b2=a2﹣c2=4,所以椭圆G的方程为.(Ⅱ)设直线l的方程为y=x+m,由得4x2+6mx+3m2﹣12=0.①设A,B的坐标分别为(x1,y1),(x2,y2)(x1<x2),AB的中点为E(x0,y0),则x0==﹣,y0=x0+m=,因为AB是等腰△PAB的底边,所以PE⊥AB,所以PE的斜率k=,解得m=2.此时方程①为4x2+12x=0.解得x1=﹣3,x2=0,所以y1=﹣1,y2=2,所以|AB|=3,此时,点P(﹣3,2).到直线AB:y=x+2距离d=,所以△PAB的面积s=|AB|d=.【点评】此题是个中档题.考查待定系数法求椭圆的方程和椭圆简单的几何性质,以及直线与椭圆的位置关系,同时也考查了学生观察、推理以及创造性地分析问题、解决问题的能力.20.(13分)(2011•北京)若数列A n:a1,a2,…,a n(n≥2)满足|a k+1﹣a k|=1(k=1,2,…,n﹣1),则称A n为E数列,记S(A n)=a1+a2+…+a n.(Ⅰ)写出一个E数列A5满足a1=a3=0;(Ⅱ)若a1=12,n=2000,证明:E数列A n是递增数列的充要条件是a n=2011;(Ⅲ)在a1=4的E数列A n中,求使得S(A n)=0成立得n的最小值.【考点】数列的应用.【专题】点列、递归数列与数学归纳法.【分析】(Ⅰ)根据题意,a2=±1,a4=±1,再根据|a k+1﹣a k|=1给出a5的值,可以得出符合题的E数列A5;(Ⅱ)从必要性入手,由单调性可以去掉绝对值符号,可得是A n公差为1的等差数列,再证充分性,由递增数列的性质得出不等式,再利用同向不等式的累加,可得a k+1﹣a k=1>0,A n是递增数列;(Ⅲ)由|a k+1﹣a k|=1,可得a k+1≥a k﹣1,再结合已知条件a1=4,可得n的最小值.【解答】解:(Ⅰ)0,1,0,1,0是一个满足条件的E数列A5(答案不唯一,0,﹣1,0,﹣1,0或0,±1,0,1,2或0,±1,0,﹣1,﹣2或0,±1,0,﹣1,0都满足条件的E数列A5)(Ⅱ)必要性:因为E数列A n是递增数列所以a k+1﹣a k=1(k=1,2, (1999)所以A n是首项为12,公差为1的等差数列.所以a2000=12+(2000﹣1)×1=2011充分性:由于a2000﹣a1999≤1a1999﹣a1998≤1…a2﹣a1≤1,所以a2000﹣a1≤1999,即a2000≤a1+1999又因为a1=12,a2000=2011所以a2000≤a1+1999故a k+1﹣a k=1>0(k=1,2,…,1999),即A n是递增数列.综上所述,结论成立.(Ⅲ)对首项为4的E数列A n,由于a2≥a1﹣1=3a3≥a2﹣1≥2…a8≥a7﹣1≥﹣3…所以a1+a2+…+a k>0(k=2,3,…,8),所以对任意的首项为4的E数列A n,若S(A n)=0,则必有n≥9,又a1=4的E数列A9:4,3,2,1,0,﹣1,﹣2,﹣3,﹣4满足S(A9)=0,所以n的最小值是9.【点评】本题以数列为载体,考查了不等式的运用技巧,属于难题,将题中含有绝对值的等式转化为不等式是解决此题的关键.。
2011年高考北京卷理科数学解析版

2011年高考(北京卷)理科数学解析版第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知集合2{|1}P x x =≤,{}M a =,若P M P = ,则a 的取值范围是 A. (,1]-∞- B. [1,)+∞ C. [1,1]- D. (,1]-∞- [1,)+∞ 【命题意图】本题考查一元二次不等式解法、集合运算,是简单题.【解析】:2{|1}{|11}P x x x x =≤=-≤≤,[1,1]P M P a =⇒∈- ,选C 。
2.复数i 212i-=+ A. iB. i -C. 43i 55-- D. 43i 55-+ 【命题意图】本题考查复数的运算,是简单题.【解析】:i 212ii -=+,选A 。
3.在极坐标系中,圆2sin ρθ=-的圆心的极坐标是A. (1,)2πB. (1,)2π-C. (1,0)D. (1,)π【命题意图】本题考查极坐标方程与直角坐标系下方程的互化及点互化,是简单题.【解析】:222sin (1)1x y ρθ=-⇒++=,圆心直角坐标为(0,-1),极坐标为(1,)2π-,选B 。
4.执行如图所示的程序框图,输出的s 的值为 A. 3- B. 12-C. 13D. 2【命题意图】本题考查程序框图,是简单题.【解析】:循环操作4次时S 的值分别为11,,3,232--,选D 。
5.如图,AD 、AE 、BC 分别与圆O 切于点D 、E 、F ,延长AF 与圆O 交于另一点G ,给出下列三个结论: ①CA BC AB AE AD ++=+; ②AE AD AG AF ⋅=⋅; ③ADG AFB ∽△△.其中正确的结论的序号是( )A .①②B .②③C .①③D .①②③ 【命题意图】本题考查集合选讲的相关知识,是容易题.【解析】:①正确。
由条件可知,BD=BF ,CF=CE ,可得CA BC AB AE AD ++=+。
北京大学1996-2011、2013年数学分析考研真题(缺2012年)

∫
1
0
则反常积分 ∫ f ( x) g ( x) d x( ) f ( x) d x ,∫ g ( x) d x 都存在,
0 0
1
1
A.收敛, B.发散, C.不一定收敛, D.一定不收敛。 4.若 lim nan = 1 ,则
n →∞
∑a
n =1
∞
n
( )
A.发散, B.收敛, C.不一定收敛, D.绝对收敛。 5.设 f ( x, y ) 在区域 {( x, y ) : x 2 + y 2 < 1} 上有定义,若存在偏导数
五、 (15 分)求第二型曲面积分
∫∫ ( x d y d z + cos y d z d x + d x d y) ,其中 S 为
S
x2 + y 2 + z 2 = 1 的外侧。
六、 (20 分)设 x = f (u , v) , y = g (u , v) ,w = w( x, y ) 有二阶连续偏导数,满足
− x2
)
, (a 2 + α 2 ≠ 0)
2π n+ n + ⋅⋅⋅ + sin π ) 2. lim( n →∞ n + 1 1 1 n+ n+ n 2 sin
3. lim
n →∞ 0
π
∫ (1 − x )
n n
1
2 n
dx
4. lim 1 + a , (a > 0)
n →∞
三、 (45 分)求解下列命题: 1.求级数
北京大学 2002 年研究生入学考试试题
考试科目:数学分析 一、 (10 分)求极限: lim(
数学分析I(实验班)课

Mathematical analysis (I) is one of the most important courses for the students who wish to study the mathematics and related subjects. The course mainly includes the theory of limits of sequence of numbers and functions; derivatives and differentials of real functions. The course is a basis for Mathematical analysis (II) and (III) and for many courses such as differential equations; differential geometry, functions of one complex variable; real analysis, probability; basic physics, etc. The course provides the training for the mathematical thinking and skills.
开课院系
数学科学学院
通选课领域
是否属于艺术与美育
否ቤተ መጻሕፍቲ ባይዱ
平台课性质
平台课类型
授课语言
中文
教材
数学分析,伍胜健,北京大学;
参考书
教学大纲
本课程是数学类各专业最重要的基础课之一。内容主要包括极限论、一元微分学。本课程是数学分析(II)(III)的基础, 同时是许多后继课程如微分方程、微分几何、复变函数、实变函数、概率论、基础物理、理论力学等学习的基础。数学分析(I)将提供大学数学的基本能力及思维方法的训练重要课程。具有良好的数学分析(I)的基础对于今后的学习和研究起着关键的作用。
《数学分析》第三版全册课后答案 (1)

4、一阶微分方程 (3x 4 xy)dx 2 x dy 0 的通解(可以用隐函数表达)为 5、设二阶可微函数 f ( x, y) 满足 .
专业:
2 f 2 f 2 f y , x y , x, 则 f ( x, y) 的表达形式为 x 2 xy y 2
得分
评阅人
(2) f ( x, y) 在 (0, 0) 点的可微性.
2、 (本题 7 分)设函数 f ( x ) 在0, 上有界且连续, f (0) 0, 讨论函数
F ( y)
0
yf ( x) dx 的连续性. x2 y 2
得分
评阅人
三、计算题 II(共 4 小题,共 40 分)
第 2 页(共
3 页)
------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------
1、 (本题 10 分)设定义在 (0, ) 上的函数 f 满足下列三个条件: (1) x 0, f ( x) 0, f (1) 1; (2) f ( x 1) xf ( x), x 0; (3) ln f 是 (0, ) 上的凸函数. 证明: (1) f ( x) lim
n x n! ; n x( x 1) ( x n)
(2)验证欧拉积分 ( x) 也满足题述的三个条件,并由此证明 f ( x) ( x).
2 2、 (本题 10 分)设 u ( x, y ) 在 R 上连续,对任意 r 0 ,证明:等式
2011年北京高考数学答案解析(理科)
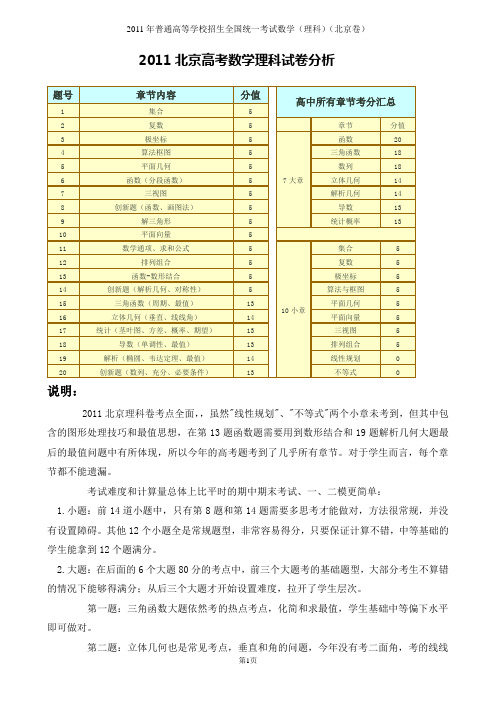
2011北京高考数学理科试卷分析题号章节内容分值高中所有章节考分汇总1 集合 52 复数 5 章节分值3 极坐标 57大章函数204 算法框图5 三角函数185 平面几何 5 数列186 函数(分段函数) 5 立体几何147 三视图 5 解析几何148 创新题(函数、画图法) 5 导数139 解三角形 5 统计概率1310 平面向量 511 数学通项、求和公式 510小章集合 512 排列组合 5 复数 513 函数-数形结合 5 极坐标 514 创新题(解析几何、对称性) 5 算法与框图 515 三角函数(周期、最值)13 平面几何 516 立体几何(垂直、线线角)14 平面向量 517 统计(茎叶图、方差、概率、期望)13 三视图 518 导数(单调性、最值)13 排列组合 519 解析(椭圆、韦达定理、最值)14 线性规划020 创新题(数列、充分、必要条件)13 不等式0说明:2011北京理科卷考点全面,,虽然"线性规划"、"不等式"两个小章未考到,但其中包含的图形处理技巧和最值思想,在第13题函数题需要用到数形结合和19题解析几何大题最后的最值问题中有所体现,所以今年的高考题考到了几乎所有章节。
对于学生而言,每个章节都不能遗漏。
考试难度和计算量总体上比平时的期中期末考试、一、二模更简单:1.小题:前14道小题中,只有第8题和第14题需要多思考才能做对,方法很常规,并没有设置障碍。
其他12个小题全是常规题型,非常容易得分,只要保证计算不错,中等基础的学生能拿到12个题满分。
2.大题:在后面的6个大题80分的考点中,前三个大题考的基础题型,大部分考生不算错的情况下能够得满分;从后三个大题才开始设置难度,拉开了学生层次。
第一题:三角函数大题依然考的热点考点,化简和求最值,学生基础中等偏下水平即可做对。
第二题:立体几何也是常见考点,垂直和角的问题,今年没有考二面角,考的线线角更简单,基础弱的学生甚至可以用几何向量法做出这三问,顺利拿到14分。
北京大学数学分析I期中考试试题

北京大学数学科学学院数学分析I期中考试题目
共七道大题,满分101分,时间110分钟
2018.11.15 8:00-9:50
一.(本题30分)判断下列极限是否存在。
(1
(2)
(3)
二.(本题36分)下列问题若回答是,请给出证明;若回答否,请给出反例。
(1)若和在上均一致连续,问在是否一致连续?
(2)若和在上均一致连续,问在是否一致连续?
(3)若和在,且问在
否一致连续?
(4)设在上连续,且一致连续,问是否一致连续?
三.(本题10分)设
证明:此数列当时,极限存在,并求其值。
四.(本题10分)假设是定义在上的函数,,如果存在一个定义
在上的连续函数使得单调上升,证明:可以取到与之间的任
一实数。
五.(本题5分)设是定义在整个实数轴上的连续函数.
证明:函数方程
六.(本题5分)设,如果极限
其中是在上的最大值,证明:
七.(本题5分)设是定义在实数轴上最小正周期为无理数的连续函数,
证明:当时,数列的极限不存在。
2011ans2022

北京大学数学学院期末试题2010-2011学年第二学期考试科目高等代数II 考试时间2011年6月15日姓名学号一.判断对错, 正确的请给出简要证明, 错误的举出反例. (24分)1)只要A是幂零矩阵, 就有| I + A | = 1 .正确.A可写成U J U-1的形式, J是A的Jordan 标准型. 由于A幂零, J的对角元都是0 . 于是| I + A | = | I + U J U-1 | = | I + J | = 1 .2)设F 5是包含5个元素的有限域, A为F 5上的方阵.若A满足3 A 3 + A 2 + 2A = I , 则A可以在F 5上对角化.正确.由于A的最小多项式m ( x )是x 3+ 2x 2 – x – 2 = ( x + 2)( x 2 – 1 ) = ( x + 2)( x + 1 ) ( x– 1 )的因式, m ( x )是F 5上不同的一次因式的乘积. A可对角化.3)若线性变换A满足Ker A ∩Im A= { 0 } , 则A 2= A .不正确.例如, R上的线性变换α 2α即不满足此命题.4)若A是实矩阵, 满足A T = – A , 则I + A 一定可逆.正确.反对称实矩阵的特征值都是纯虚数或0, 不可能是–1 .二. 填空题(20分)1) 在 R[ x 1 , x 2 , x 3 ]中, 由全体 10次齐次多项式和零多项式构成的实线性空间的维数是_66C 212=_; 其中由全体 10次齐次对称多项式和零多项式构成的线性子空间的维数是_14_. 2) 已知α 1 , α 2 , α 3 , α 4是欧氏空间R 4的标准正交基, 其中 α 1 = [ 1 0 0 0 ] T , α 2 = [ 0 0 1 0 ] T , 且 α 3 与 [ 1 1 1 1 ] T 的夹角 为45 º, 则α 4 =_][210210-±_.3) 以下诸矩阵的相似等价类的分类为 { A , C } , { B , D }__.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000230000310003A , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1202030112310003B ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1001030001300003C , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000030010310103D三.(10分)已知 R 3 上的对称双线性函数 f ( α , β ) 在基底α 1 , α 2 , α 3 下的度量矩阵为 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----532311211 .1) 判断 f ( α , β ) 能否构成R 3 上的内积;2) 求基底 β1 , β2 , β3 , 使得 f 在此基下的度量矩阵是对角矩阵. 解: 1) 由于[],0011532311211011=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=++)αα,αα(2121 但 ,0αα21≠+ f ( α , β ) 不构成内积;2) 对以下矩阵做成对的行列变换, 得⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡------→⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡------→⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡------→⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡------→⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-------110010211100010001101211110010001101211110100001111110100211111532311211 [][].313211321αα,ααα,αα,α,α+-++-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--2110010211 于是, 在新基底313211αα,ααα,α+-++-2 下, f 的度量矩阵是 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-100010001.四.(24分)已知 A 是实线性空间 V 上的线性变换, 且在基底α 1 , α 2 , α 3 , α 4 下的矩阵为 A = .1) 求A 的特征多项式与最小多项式 ;2) 求 V 的根子空间分解, 写出每个根子空间的基底; 3) 求 V 的一组基, 使得A 的矩阵为 Jordan 标准型. 解: 1) A 的特征多项式为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-100122210010101310122110311001222100101013-------=---------=-x x x x x x x x A xI )(||321111321))(())((--=-----=x x x x x x注意到A - 2I = 的秩 = 3, ker( A - 2I )的维数 = 1 ;( A - 2I ) 2 = 的秩 = 2, ker( A - 2I ) 2的维数 = 2 ;( A - 2I ) 3= 的秩 = 1, ker( A - 2I ) 3的维数 = 3 .于是有ker( A - 2I ) ⊂ ker( A - 2I ) 2 ⊂ ker( A - 2I ) 3 = ker( A - 2I ) 4 = . . .故 A 的最小多项式为 . 2) 全空间可以分解为根子空间的直和:V = Ker( A - 2I ) 3 ⊕ Ker( A - I ) .由以上计算可知 ( A - 2I ) 3 α 1 = 0, 但 ( A - 2I ) 2 α 1 = – α 3 ¹ 0 . 于是 α 1 , ( A - 2I ) α 1 = α 1 + α 3 – α 4 , ( A - 2I ) 2 α 1 = – α 3 是根子空间 Ker( A - 2I ) 3 的一组基底. 另一方面, 对矩阵A – I 做初等行变换, 得A - I =( A – I ) X = 0 解的公式为 , x 4是自由变量.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---1001202100101011⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----0010101100100000⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-0010000000100000≠≠321))((--x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-0001212100001012⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡→0000212010100001⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡→0000010010100001⎪⎩⎪⎨⎧=-==003421x x x x( A – I ) 的解空间为< > ,于是α 2 – α 4 是根子空间 Ker( A - I ) 的一组基底. 3) 由以上讨论可知, 在基底( A - 2I ) 2 α 1 , ( A - 2I ) α 1 , α 1 , α 2 – α 4下, A 的矩阵为Jordan 标准型 . 由[ (A - 2I ) 2 α1 ,(A - 2I ) α1 , α1 , α2 –α4 ] = [ α1 , α2 , α3 , α4 ]可知五.(12分)设β1 , β2 , β3 与 γ 1 , γ 2 , γ 3分别是矩阵 B = ⎥⎦⎤⎢⎣⎡110101与 C = ⎥⎦⎤⎢⎣⎡--101111 的列向量. 求欧氏空间R 2上的线性变换A (写出标准基下的矩阵), 使得∑=-31i 2i i ||||γβA 取到最小值.解: 记线性变换A 在标准基下的矩阵为 A = ⎥⎦⎤⎢⎣⎡d c b a , 记 βi = ⎥⎦⎤⎢⎣⎡'i i b b , γ i = ⎥⎦⎤⎢⎣⎡'i i c c , 3i 1≤≤. 则⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1010004444321x x x x x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-1010⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000020001200012⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---10100011100001101101000111000011012121210100011100001101001222100101013-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-∑=-31i 2i i ||||γβA =∑=-+31i 2)'(i i i c bb ab +∑=-+31i 2)'(i i i c db cb . (*)欲求A , 使得(*)式取到最小值, 只需分别求 a , b 与 c , d , 使得等号右边的两个求和式各取到最小值. 注意到右边第一个求和式取最小值当且仅当 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡'''321321b b b b b b b a 是 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321c c c 在子空间 >⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡<''',321321b b b b b b 上的正交投影, 即[ a , b ] T 是方程组 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡32121c c c x x B B B T 的解. 解此方程组,,⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡20111110101211221x x得 .,343221-==x x 取到的最小值为.3111131111110341013222=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡ 类似地, (*)式右边第二个和式取最小值当且仅当⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡'''321321b b b d b b b c 是 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡'''321c c c 在 >⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡<''',321321b b b b b b 上的正交投影, 即[ c , d ] T是方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡'''32121c c c x x B B B T 的解. 解此方程组,⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡12101110101211221x x 得 .,0121==x x 取到的最小值为 0. 于是, 当A 在标准基下的矩阵为 A = ⎥⎦⎤⎢⎣⎡-013432 时, ∑=-31i 2i i ||||γβA 取到最小值 1/3.六. 设A 是欧氏空间R n 上的正交变换. 证明: 1)(3分)A 的每个复特征值 λ 都满足 | λ | = 1 ;2)(7分)R n 可分解成有限个1维与2维A -子空间的直和. 证:设A 在欧氏空间R n 的一组标准正交基下的矩阵为A . 则A 是正交矩阵且与A 有相同的(复)特征值. 以下对矩阵A 进行讨论.1) 设 λ 是A 的一个复特征值, α是相应的复特征向量. 由 A α = λ α , 可得 TTTαλA α=. 于是 TTTααλλαα=A A . 注意到A 是正交矩阵且α ≠ 0, 我们有 | λ | = 1 .2) 对欧氏空间的维数应用数学归纳法:当 n = 1或2时命题显然成立. 设命题对维数 < n 的欧氏空间 成立, 以下考察n 维欧氏空间的情况. 设 λ 是A 的一个复特征值.若 λ 是实数, 则 λ = ± 1. 设V 1 = < α >, α是 λ 的一个实特征向量. 对任意β ∈ V 1⊥, 有 λ ( A β , α ) = ( A β , A α ) = ( β , α ) = 0 ,于是A β ∈V 1⊥. 注意到线性变换 γ → A γ 限制在不变子空间V 1⊥上, 是欧氏空间V1⊥上的正交变换. 由归纳假设, V1⊥可分解为1维与2维A-子空间的直和. 于是R n = V1⊕ V1⊥也可分解为1维与2维A-子空间的直和.以下设λ = u + i v 不是实数( u, v∈R, v ≠ 0), 设α1 + i α2是λ的复特征向量( α1, α2 ∈R n ). 由A ( α1 + i α2 ) = ( u + i v ) ( α1 + i α2 ) = ( u α1 – v α2 ) + i ( v α1 + u α2 ) 得 A α1 = u α1 – v α2, A α2= v α1 + u α2 .于是V2 = < α1 , α2 > = < Aα1 , Aα2 > 是A-不变子空间.对任意β∈V2⊥, 有( Aβ , Aαi ) = ( β , αi ) = 0 , 1 ≤ i ≤ 2, 于是A β∈V2⊥. 故V2⊥也是A-不变子空间. 由归纳假设, V2⊥可分解为1维与2维A-子空间的直和. 于是R n = V2⊕ V2⊥也可分解为1维与2维A-子空间的直和.。
