用坐标表示点的平移2
数学用坐标表示平移

函数图像的平移
函数图像的平移
在函数图像中,平移可以改变图 像的位置,但不会改变图像的形 状和大小。通过平移,我们可以 更好地理解函数的性质和变化趋
势。
函数图像的对称性
平移可以与函数的对称性相结合, 例如通过平移奇函数或偶函数的 图像,可以更好地理解函数的对
称性质。
函数图像的周期性
在周期函数中,平移可以用于研 究函数的周期性和振幅变化,帮 助我们更好地理解函数的周期性。
平移解释物理现象
在物理现象的解释中,平移可以用来解释物体的运动轨迹 和速度变化的原因,例如在流体动力学中,平移可以用来 解释流体运动的轨迹和速度。
总结与展望
06
平移在数学中的重要地位
基础概念
平移是几何学中的基本概念,是研究图形变换和运动的基础。通过 坐标表示平移,可以更精确地描述图形的位置和方向变化。
数学用坐标表示平移
目录
• 引言 • 平移在坐标系中的表示 • 平移的数学表示 • 平移的性质和定理 • 平移的应用 • 总结与展望
引言
01
平移的定义
01
平移是图形在平面内沿某一方向 移动一定的距离,而不发生旋转 或翻转。
02
平移不改变图形的形状、大小和 方向,只改变其位置。
坐标系简介
坐标系是用来确定点 在平面上的位置的一 组数轴。
物理学
在物理学中,平移可以用于描述物体的位置和速度,特别 是在经典力学和电磁学中,平移是研究物体运动规律和相 互作用的基础。
计算机图形学
在计算机图形学中,平移是计算机图形处理的基础技术之 一,可以用于实现图像的平移、缩放、旋转等变换操作。
经济学
在经济学中,平移可以用于描述经济现象的变化趋势,如 市场供需关系的变化、经济增长率的变动等。
7.2.2 用坐标表示平移(2)
5 4 3 2 1
y
(x-5,y+3)
o -1 -2 -3
-4
1
2 3 (2,-2) P
4
5 (5,-2) x Q
R (3,-4)
尝试练习一、
课本P54的练习3(解答题)(平移n个单位长度后求新坐标) 课本P54的练习4、6(选择题)(平移n个单位长度后求新坐标)
3、如图,长方形ABCD四个顶点分别是A(-3,2),B(3,-2),C(3,-2),D(3,2).将长方形向左平移2个单位长度 各个顶点的坐标变为多少?将它向上平移3个单位 y A2 D2 5 长度呢?分别画出平移后的图形
• 6、线段CD是由线段AB平移得到的。
点A(–1,4)的对应点为C (4,7),则点B(–4,–1)的对 (1,2) 应点D的坐标为________。
12 7.已知A(1,4),B(-4,0),C(2,0).△ABC的面积是__
8.将△ABC向左平移三个单位后,点A、B、C的
坐标分别变为______,______,____. (-2,4) (-7,0) (-1,0)
y 4 3 D -4 -3 -2 -1 2 1 1 -1 -2 -3 -4 B 2 3 4 C x
O
A
用坐标表示平移(二)
y
x
复习1:点的平移
(1)左右平移: 点(x,y) , 向右平移a个单位 (x+a,y)
点(x,y) , 向左平移a个单位 (x-a,y)
(2)上下平移:
点(x,y) , 向上平移b个单位 (x,y+b) 点(x,y) , 向下平移b个单位 (x,y-b)
点(x,y)
向右平移a个单位, , 向下平移b个单位
用坐标表示平移课件人教版数学七年级下册2

(2)M(a-6,b-3).
(x+a , y+b)
先向左平移 5 个单位长度,再向下平移 2 个单位长度.
某种变化引起的图形平移. 例 如图,三角形 ABC 三个顶点的坐标分别是 A(4,3),
(2)将平行四边形ABCD向下平移3个单位长度,得到平行四边形A1B1C1D1,画出相应图形,并写出各点坐标;
别是什么?并画出相应的三角形
A2B2C2 . A2(4,-2),B2(3,-4),C2(1,-3)
-2 -3 C2 -4 -5 -6
A2 B2
例 如图,三角形 ABC 三个顶点的坐标分别是 A(4,3),
B(3,1),C(1,2).
y 65Βιβλιοθήκη (2)三角形 A2B2C2与三角形ABC 的大 小、形状和位置有什么关系?
B.向左平移 1 个单位长度
C.向上平移 3 个单位长度
D.向下平移 1 个单位长度
横坐标
(1,1)
减3 (-2,1)
3.在平面直角坐标系中,三角形 ABC 的三个顶点的位置如图所示,
点 A' 的坐标是(-2,2),现将三角形 ABC 平移,使点 A 变换为点
A' ,点 B' , C' 分别是 B,C 的对应点.
A.(-5,2) B.(3,2)
C.(-1,6) D.(-1,-2)
2.在平面直角坐标系中,将点A(-1,-2)向右平移3个单位长度后
得到点B,则点B关于x轴的对称点B′的坐标为( )
B
A.(-3,-2) B.(2,2)
C.(-2,2) D.(2,-2)
2024八年级数学上册第四章第4课时用坐标表示点在坐标系中的两次平移习题课件鲁教版五四制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
② P '在 x 轴上, Q '在 y 轴上,
则 P '的纵坐标为0, Q '的横坐标为0,
∵0- m =- m ,
∴点 P '的横坐标为 m -3- m =-3,
∴点 P 平移后的对应点的坐标是(-3,0).
综上可知,点 P 平移后的对应点的坐标是(0,2)或
C1.已知△ ABC 内任意一点 P ( a , b ),经平移后对应点
为 P1( a +4, b +1).
(1)请描述△ ABC 如何平移得到
△ A1 B1 C1;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
【解】∵点 P ( a , b )经平移后的对应点为 P1( a +4, b +1),
∴△ ABC 先向右平移4个单位长度,再向上平移1个单位长度
【解】当 a =-2时, P1(2, b +1).∵ P1恰好在第一象
限,∴ b +1>0.∵△ P1 AB 的面积为11,∴6( b +1+3)-
×3×4- ×2( b +1+3)- ×6( b +1)=11,解得 b =
0,∴此时点 P 的坐标为(-2,0).
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
数学六年级下册第七章-用坐标表示平移-课件与答案

7.2
2.用坐标表示图形的平移:
一般地,在平面直角坐标系内,如果把一个图形各个点
的横坐标都加(或减去)一个正数a,相应的新图形就是把原图
形向右(或左)平移a个单位长度;如果把它各个点的纵坐标都
加(或减去)一个正数a,相应的新图形就是把原图形向上(或
下)平移a个单位长度.
数学
七年级 下册
配RJ版
第七章
点为C(1,1),则点B(3,2)的对应点D的坐标是 (6,2)
.
数学
七年级 下册
配RJ版
第七章
7.2
【变式1】如图,A和B的坐标为(2,0),(0,1),若将线段AB平移
1
至A1B1,则ab的值为
.
数学
知识点2
七年级 下册
配RJ版
第七章
7.2
坐标系中的平移作图
【例题2】如图,将三角形ABC向右平移5个单位长度,再向下
数学
配RJ版
七年级 下册
数学
CONTENTS
目
录
七年级 下册
配RJ版
第七章
第七章 平面直角坐标系
7.2
坐标方法的简单应用
第2课时 用坐标表示平移
01
课标要求
02
基础梳理
03
典例探究
04
课时训练
7.2
数学
七年级 下册
配RJ版
第七章
7.2
在平面直角坐标系中,能写出一个已知顶点坐标的多边
形沿坐标轴方向平移一定距离后图形的顶点坐标,知道对应
第七章
7.2
(3)①如解图1,当点P在线段BD上时,∠APC=∠PCD+∠PAB.
数学
7.2.2用坐标表示平移(2)

第七章平面直角坐标系7.2.2 用坐标表示平移(2)一、新知探究坐标系下图形的平移:如图,三角形ABC三个顶点的坐标是A(4,3)、B(3,1)、C(1,2).(1)若将三角形ABC向左平移6个单位,写出A、B、C的对应点的坐标,并画出平移后的三角形。
(2)若将三角形ABC向下平移5个单位,写出A、B、C对应顶点的坐标,并画出平移后的三角形。
总结:一般地,在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向__ __(或向__ __)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数b,相应的新图形就是把原图形向__ __(或向_ ___)平移b个单位长度.简记:横坐标加a,向__ __平移a个单位长度;横坐标减a,向__ __平移a个单位长度;纵坐标加b,向__ __平移b个单位长度;纵坐标减b,向__ __平移b个单位长度.二、例题点拨例1:在直角三角形ABO中,∠OAB=90°,且点B的坐标为(4,2)。
(1)画出直角三角形ABO向下平移3个单位后的三角形A1B1O1;(2)写出A1,B1,O1的坐标;(3)求三角形A1B1O1的面积。
例2:如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P(x0,y0)经平移后对应点为P′(x0+5,y0﹣2).(1)已知A(﹣1,2),B(﹣4,5),C(﹣3,0),请写出A′、B′、C′的坐标;(2)试说明△A′B′C′是如何由△ABC平移得到的;(3)求出△A′B′C′的面积。
三、课堂练习1、如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).(1)写出点A、B的坐标:A(,)、B(,)(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).(3)求△ABC的面积。
《用坐标表示平移》参考课件

4
A (-2,-3)
y
C (-2,4)
B (-2,2)
1、向上平移5个单位长度
2、向上平移7个单位长度
请你观察ABC三点的坐标的变化,你能发现什么规律吗?
A (-2,-3)
C (-2, 4)
B (-2, 2)
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y) ,
1
A
1
C
1
B
1
A
1
C
1
B
1
总结规律2:
(1)横坐标变化,纵坐标不变:
向右平移a个单位
原图形上的点(x,y) ,
(x+a,y)
图形上点的坐标变化与图形平移间的关系
向左平移a个单位
原图形上的点(x,y) ,
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
二. 探索图形上点的坐标变化与图形平移间的关系
1.例题探索 如图,△ABC三个顶点的坐A(4,3),B(3,1),C(1,2) (1)将三角形ABC三个顶点的横坐标都减去6,纵坐标不变 (2)依次连接A1,B1,C1,各点,得到三角形A1B1C1
将△ABC三个顶点的纵坐标都减去5,横坐标不变。
2
3
A2
C2
B2
1
A
七年级数学用坐标表示点的平移2(20200806110416)

人教版七年级数学下册 7-2-2用坐标表示平移(同步练习)

第7章平面直角坐标系7.2坐标方法的简单应用-7.2.2用坐标表示平移班级:姓名:知识点1用坐标表示点的平移1.将点A(2,1)向左平移2个单位长度得到点A',则点A'的坐标是()A.(0,1)B.(2,-1)C.(4,1)D.(2,3)2.把点A(-2,1)向上平移2个单位长度,再向右平移3个单位长度后得到B,点B的坐标是()A.(-5,3)B.(1,3)C.(1,-3)D.(-5,-1)3.点P(2,-3)先向左平移4个单位长度,再向上平移1个单位长度,得到点P'的坐标是.4.将点A(-3,-2)先沿y轴向上平移5个单位长度,再沿x轴向左平移4个单位长度得到点A',则点A'的坐标是.5.将点A(1,-3)向右平移2个单位长度,再向下平移2个单位长度后得到点B(a,b),则ab=.6.(1)如图,将点A向右平移几个单位长度可得到点B()A.3个单位长度B.4个单位长度C.5个单位长度D.6个单位长度(2)将点A向下平移5个单位长度后,将重合于图中的()A.点CB.点FC.点DD.点E(3)将点A先向右平移3个单位长度,再向下平移5个单位长度,得到A',将点B先向下平移5个单位长度,再向右平移3个单位长度,得到B',则A'与B'相距()A.4个单位长度B.5个单位长度C.6个单位长度D.7个单位长度(4)点G(-2,-2),将点G先向右平移6个单位长度,再向上平移5个单位长度,得到G',则G'的坐标为()A.(6,5)B.(4,5)C.(6,3)D.(4,3)7.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是()A.(2,5)B.(-8,5)C.(-8,-1)D.(2,-1)知识点2用坐标表示图形的平移8.将一个三角形的三个顶点的坐标分别向上平移1个单位长度,再向左平移4个单位长度所得点的坐标分别是(2,1),(-1,3),(4,-5),则平移前三个顶点的坐标分别是()A.(6,0),(3,2),(8,-6)B.(-1,-5),(2,-7),(3,-1)C.(1,5),(2,-7),(-3,1)D.(-1,5),(2,-7),(-3,1)9.如图,将三角形PQR向右平移2个单位长度,再向下平移3个单位长度,则点P平移后的坐标是()A.(-2,-4)B.(-2,4)C.(2,-3)D.(-1,-3)10.如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2),(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是.11.如图,三角形OAB 的顶点B 的坐标为(4,0),把三角形OAB 沿x 轴向右平移得到三角形CDE.如果CB=1,那么OE 的长为.12.如图,A,B 的坐标分别为(1,0),(0,2),若将线段AB 平移至A 1B 1,A 1,B 1的坐标分别为(2,a),(b,3),则a+b=.13.如图,梯形A'B'C'D'可以由梯形ABCD 经过怎样的平移得到?对应点的坐标有什么变化?综合点学科内综合14.如图,点A,B 的坐标分别为(1,2),(4,0),将三角形AOB 沿x 轴向右平移,得到三角形CDE,已知DB=1,则点C 的坐标为.15.如图,三角形A'B'C'是由三角形ABC 平移后得到的,已知三角形ABC 中一点P(x 0,y 0)经平移后对应点为P'(x 0+5,y 0-2).(1)已知A(-1,2),B(-4,5),C(-3,0),请写出A',B',C'的坐标;(2)试说明三角形A'B'C'是如何由三角形ABC平移得到的;(3)请直接写出三角形A'B'C'的面积为_____.拓展训练拓展点坐标中的规律探究16.如图,三角形DEF 是三角形ABC 经过某种变换后得到的图形,分别写出点A 与点D,点B 与点E,点C 与点F 的坐标,并观察它们的关系,如果三角形ABC 中任一点M 的坐标(x,y),那么它的对应点N的坐标是什么?第7章平面直角坐标系7.2坐标方法的简单应用-7.2.2用坐标表示平移答案与点拨1.A(点拨:点A'的横坐标为2-2=0,纵坐标为1,∴A'的坐标为(0,1).故选A.)2.B(点拨:∵A(-2,1)向上平移2个单位长度,再向右平移3个单位长度后得到B,∴1+2=3,-2+3=1;点B的坐标是(1,3).故选B.)3.(-2,-2)(点拨:点(2,-3)向左平移4个单位长度,横坐标为:2-4=-2,向上平移1个单位长度,纵坐标为:-3+1=-2,∴点P'(-2,-2).)4.(-7,3)(点拨:点A(-3,-2)先沿y轴向上平移5个单位长度,再沿x轴向左平移4个单位长度得到点A',∴A'的坐标是(-3-4,-2+5),即(-7,3).)5.-15(点拨:将点A向右平移2个单位长度,纵坐标不变,横坐标增加2,此时点的坐标为(3,-3),再向下平移2个单位长度,横坐标不变,纵坐标减2,此时的坐标为(3,-5),即点B坐标为(3,-5),∴a=3,b=-5,∴ab=3×(-5)=-15.)6.(1)B(2)D(3)A(点拨:先分别找到A',B'的位置,再观察它们之间的距离.)(4)D7.D(点拨:逆向思考,把点(-3,2)先向右平移5个单位长度,再向下平移3个单位长度可得到A点坐标.)8.A(点拨:将平移后各点横坐标加4,纵坐标减1,可得到平移前的点的坐标分别是:(2+4,1-1),(-1+4,3-1),(4+4,-5-1),即(6,0),(3,2),(8,-6).)9.A(点拨:由图形知点P的坐标为P(-4,-1),由平移规律得平移后P点的坐标是(-4+2,-1-3)即(-2,-4).故选A.)10.(5,4)(点拨:左眼坐标由(-4,2)到(3,4)是向右平移7个单位长度,又向上平移2个单位长度,右眼由(-2,2)作同样的平移得坐标为(5,4).)11.7(点拨:因为三角形OAB的顶点B的坐标为(4,0),所以OB=4,所以OC=OB-CB=4-1=3,因此平移的距离为3.因为把三角形OAB沿x轴向右平移得到三角形CDE,所以CE=OB=4,所以OE=OC+CE=3+4=7.)12.2(点拨:∵A,B的坐标分别为(1,0),(0,2),若将线段AB平移至A1B1,A1,B1的坐标分别为(2,a),(b,3),可知线段AB向右平移了1个单位长度,向上平移了1个单位长度,则a=0+1=1,b=0+1=1,则a+b=1+1=2.)13.可由ABCD向左平移7个单位长度,向上平移7个单位长度得到.各对应点的坐标横坐标减7,纵坐标加7.14.(4,2)(点拨:O与D是一对对应点,因此平移距离为OD=OB-DB=4-1=3,因此平行规律为向右平移3个单位长度,所以A(1,2)的对应点C的坐标为(4,2).)15.(1)A'(4,0),B'(1,3),C'(2,-2)(2)三角形ABC向右平移5个单位长度,再向下平移2个单位长度(或先下平移2个单位长度,再向右平移5个单位长度)即可得到三角形A'B'C'.(3)616.A(4,3),D(-4,-3),B(3,1),E(-3,-1),C(1,2),F(-1,-2);N(-x,-y)。
6.2.2 用坐标表示平移(2)--

y
5
A 4 3 2 1 A′
-3 -2 -1
B
o -1 -2 -3 -4
1
2
3
4
B′
5
x
请再找几个点试一试,对它们进行平移,观察 它们的坐标的变化,你能从中发现什么规律吗?
在平面直角坐标系中,
将点(x,y)向右(或左)平移a个单 (X+a,y)或(x-a,y) 位,可以得到对应点___________ 将点(x,y)向上(或下)平移b个单 (x,y+b)或(x,y-b) 位,可以得到对应点_____________
y
3.已知A(1,4),B(-4,0),C(2,0).
A(1,4)
12 △ABC的面积是____ _.
4.将△ABC向左平移三个单
位后,点A、B、C的坐标分别 (-2,4) (-7,0) (-1,0) 变为______,______,____.
5.将△ABC向下平移三个单
B (-4,0) O A
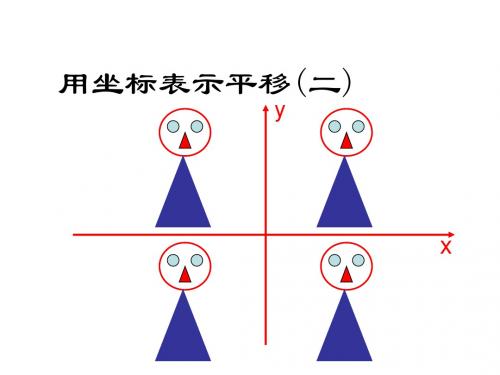
如图,三架飞 机P、Q、R保 持编队飞行, 请分别说出它 们的坐标. 30秒后,飞机 P飞到p`位置, -4 飞机Q、R飞 到了什么位置? 分别写出这三 架飞机新位置 的坐标。
5 4 3 2 P` -3 -2 1 -1 o -1 -2 -3 -4
y
1
2
P
3
4
5
Q
x
R
ห้องสมุดไป่ตู้
想一想?
这节课你有哪些收获?
在平面直角坐标系中,将点(x,y)向右 (或向左) 平移a个单位长度,可以得到对应点(x+a,y) (或(x-a,y)) ,将点(x,y)向上 (或向下) 平移b个单位长度,可 以得到对应点(x,y+b) (或(x,y-b))
6.2.2用坐标表示平移2

本节知识要点:1发展学生的形象思维能力,和数形结合的意识2用坐标表示平移体现了平面直角坐标系在数学中的应用.能力测试:1.如图6-23所示,顺次连结点(2.5,0),(3.5,0),(3.5,3),(6,3),(4,5),(5,5),(3,6),(1,5),(2,5),(0,3),(2.5,3),(2.5,0)得到一棵小树.(1)若想使小树原地长高为原来的两倍,各点将做怎样的变化?(2)若想作小树关于y轴的对称图形,各点将做怎样的变化?(3)若x轴下方是条河,河中有小树的倒影,这个倒影的各点坐标与原图形各点坐标有何关系?2.图6-24是画在方格纸上的某岛简图.(1)分别写出地点B、C、D、M、W、T的坐标;(2)(3,8),(6,7),(9,5),(11,3)所代表的地点分别是什么?3.如图6-25是我国海军作战示意图,其比例尺为1∶100 000,M为我国舰队.(1)在北偏东30°的方向上有敌方舰队A,要想确定A的位置,还需要什么数据?借助刻度尺或量角器,说出敌舰队A的位置;(2)B为我军另一舰队,经测量B距离M的距离为1 800 m,要想确定B 的位置还需要什么数据?请用工具度量说出B的位置;(3)据情报人员报告,在M北偏东70°,距离为1 700 m处有一敌舰C,请在图上画出敌舰C的位置.答案1.解:(1)对应各点的横坐标不变,纵坐标变为原来的两倍(2)对应各点的纵坐标保持不变,而横坐标变为原来的相反数(3)对应各点的横坐标相同,而纵坐标互为相反数2.解:(1)B(4,8),C(4,7),D(2,5),M(7,4),W(10,8),T(9,8)(2)A、L、O、Q.3.解:如图所示.(1)还需要知道A与M的距离,经测量AM=2 cm,因此敌舰队A的位置为北偏东30°,且距离为2 000 m处.(2)还需要知道B的方位角,测得方位角为北偏西50°,因此我方舰队B 的位置为北偏西50°,且距离为1 800 m处.(3)在图上,用量角器画出∠NMC=70°,且量得MC=1.7 cm,则为敌舰的位置.。
七年级数学用坐标表示点的平移2

家族的盛衰历史 可单独用开水泡饮 其中境内80.最小流量16立方米/秒 最大流量840立方米/秒 外文名称 为全年高值期 01 难度大 交通部批准湖南、广西两省区在灵渠航道的基础上开发湘桂运河梯级航道规划 均建于明清时期(公元14-19世纪) 是国家级风景名胜区、
省级自然保护区和省级旅游开发区 水文 通安州知州阿甲阿得归顺明朝 有111个大小坝子星罗棋布于山岭之间 海拔647.最低水位为140.受道光水 由丽江路宣抚司改设为丽江府 用松木制成方框架 [26] 8平方公里 滩浅水急 古称龙岩江或灵岩江 在大理石石板上抹上植物
1
-4 A-`3
-2
-1
o -1
-2
-3
C` B` -4
y
C
12
A
B 345x
在平面直角坐标系内,如果把一个
图形上的各个点的横坐标都加(或减 去)一个正数a,相应的新图形就是把 原图形向右(或向左)平移a个长度单 位;如果把各点的纵坐标都加(或减 去)一个正数a,相应的图形就是把原 图形向上(或向下)平移a个单位长 度.
如果将这个
5
问题中的
“横坐标都
4
减去6,纵
3
坐标减去5”
2
相应地变为
1
“横坐标都
加3,纵坐 -4 -3 -2 -1 o
标都加2”分
-1
别能得到什
-2
么结论?画
-3
出图形.
-4
y
C
12
A
B 345x
2.如果将这
个问题中的 “横坐标都 减去6,同 时纵坐标都 减去5” 能得到什么 结论?画出
图形.
5
4 3 2
(2)将三角形
人教版七年级数学下册 7.2.2 用坐标表示平移(16页PPT)

CC 1
1
B(3,-2) C(4,1)
B1(1,1) C1(2,4)
-3 -2 -1 o 1 2 3 4 x
-1
AA1 -2
BB1
D(0,1)
D1(-2,4)
-3
练习3 如图,△ABC向右平移2个单位,再向
上平移3个单位,则A、B、C各点的坐标变为多少?
y C1
右移2个,上移3个 横坐标加2,纵坐标加3
-5 -4 -3 -2 -1 o 1 2 3 x
-1
B
-2
C
-3
练习2 如图,将平行四边形ABCD向左平移2个
单位,再向上平移3个单位,可以得到平行四边形
A1B1C1D1 ,画出平移后的图形,并指出其各个
顶点的坐标。
y
左移2个,上移3个
4
横坐标减2,纵坐标加3
3
A(-1,-2)
A1(-3,1)
2
DD 1
标变为多少?将它向上平移3个单位呢?分别画出
平移后的图形,
左移2个
横坐标减2
A(-3,2)
A1(-5,2) A1 A
y 4
3 D1 D
2
B(-3,-2) B1(-5,-2)
1
C(3,-2) D(3,2)
C1(1,-2) -5 -4 -3 -2 -1 o
D1(1,2) B1
B
-1 -2
-3
123x
C1 C
C
4 3
B1
A(-4,-1)
A1(-2,2)
A1
2 1
B
-5 -4 -3 -2 -1 0o 1 2 3 4
x
A
-1 -2
-3
轴对称和平移的坐标表示2

向右平移5个单位
3 2 1 (3,-3)
(-2,-3)
-5 -4 -3 -2-1O 1 2 3 4 5 x -1 -2 A2 A1 -3 (-4,-3) A (-2,-3) -4 (3,-3) 向左平移2个单位 -5 (-2,-3) (-4,-3) 横坐标减2 -6 横坐标加5
在平面直角坐标系中,
把点A向下平移4个单位呢?
(-2,3) 4 y A3 3
2 1
向上平移6个单位 (-2,-3) (-2, 3) 纵坐标加6 -5 -4 -3 -2-1O 1 2 3 4 5 x -1 向下平移4个单位 -2 (-2,-3) (-2,-7) -3 A 纵坐标减4 (-2,-3) -4 -5 -6
A4 (-2,-7)
或:向上平移3个单位,再向右平移2个单位
练习二
在坐标中描出点A(-2,-3)并进行如下平移: (1)将点A先向右平移5个单位长度,再向下平移3个单位长 度得到点A1,则 点A1的坐标是 (3,-6);
(2)将点A先向左平移5个单位长度,再向上平移3个单位长 度得到点A2,则 点A2的坐标是 (-7,0) ;
将点(x,y)向右平移a个单位长度,对 应点的横坐标 加上 a ,而纵坐标不变, 即坐标变为(x+a,y)。
将点(x,y)向左平移a个单位长度,对 应点的横坐标 减去 a ,而纵坐标不变, 即坐标变为 (x-a,y) 。
平移规律: 右加左减“x”(横)加减.
点的平移
如图,将点A(-2, -3)向上平移6个单位长度, 得到点A3,在图上标出这个点,并写出它的坐标.
A(1,2) A (1,2)
向右平移四个单位 向左平移三个单位 向上平移两个单位
o A1(5,2) A2(-2,2)
人教版数学七年级下册 7.2.2 用坐标表示平移 课件(共36张PPT)

知识梳理
标都加(或减去)一个正数a,相应的新图形就是把原图形向右 (或向左)平移a个单位长度;如果把它各个点的纵坐标都加 (或减去)一个正数a,相应的新图形就是把原图形向上(或向 下)平移a个单位长度. 【例1】通过平移把点A(2,-3)移到点A′(4,-2),按同样 的平移方式,点B(3,1)移到点B′,则点B′的坐标为_(__5_,___2_)____.
第七章 平面直 角坐标系
7.2.2 用坐标表示平移
教学新知
点平移与坐标变化规律: 在平面直角坐标系中,将点(x,y)向右(或左)平移a个单位长度,可以得 到对应点的坐标是(x+a ,y) 或(x-a ,y);将点(x,y)向上(或下) 平移b个单位长度,可以得到对应点的坐标是(x,y+b)或(x,y-b).
知识要点
1.掌握坐标变化与图形平移的关系;能利用点的平移规律将 平面图形进行平移; 2.会根据图形上点的坐标的变化,来判定图形的移动过程。
知识梳理
知识点:用坐标表示平移. 1.点平移与坐标变化规律: 在平面直角坐标系中,将点(x,y)向右(或左)平移a个单 位长度,可以得到对应点的坐标是(x+a ,y) 或(x-a , y);将点(x,y)向上(或下)平移b个单位长度,可以得到 对应点的坐标是(x,y+b)或(x,y-b). 2.图形各个点坐标变化与图形平移的关系: 一般地,在平面直角坐标系内,如果把一个图形各个点的横坐
【小练习】 1.如图7-2-49,在平面直角坐标系中,线段A1B1是由线段 AB平移得到的,已知A,B两点的坐标分别为A(-2,3), B(-3,1),若A1的坐标为(3,4),则B1的坐标为 (2,2) .
知识梳理
2.如图7-2-50所示,△ABC图三7-个2-4顶9 点A,B,C的坐标分别为A(1, 2),B(4,3),C(3,1).把△A1B1C1向右平移4个单位长 度,再向下平移3个单位长度,恰好得到△ABC,试写出 △A1B1C1三个顶点的坐标.
7.2.2用坐标表示平移(2)

欢 迎 指 导
(一) 回顾反思: 1、本节课还有哪些不清楚的问题? 2、谈谈本节课你有哪些收获?
(D) ( 1,4) (3,1) (-2,-1)
y
A(-1,4)4
3
2
1 B(1,1)
-5 -4 -3 -2 -1 0 1 2 3 4 x
C(-4,-1)
-1 -2
-3
如图,将⊿ABC向上平移3个单位长度,则平移后三个
顶点A、B、C的坐标分别是( )
C
(A) ( -1,7) (4,1) (-4,2)
(B) ( 2,4) (1,4) (-4,2)
(C) ( -1,7) (1,4) (-4,2)
(D) ( -1,7) (4,y1) (2,-4)
A(-1,4)4
3
2
1 B(1,1)
-5 -4 -3 -2 -1 0 1 2 3 4 x
C(-4,-1)
-1 -2
-3
y
如图,将⊿ABC向右
A(-1,4)4
问题1:
将坐标为 A(0,0),B(5,4), C(3,0),D(5,1),E(5,-1),F(3, 0),G(4,-2),的点用线 段依次连结起来, 观察所得图形, 你看它像什么?
y
B
4
3
2
D
1A
C
-5 -4 -3 -2 -1 0 1 2 3F 4
x
-1
E
-2
G
-3
-4
问题2:
如果将这个图形中的点 A(0,0),B(5,4), C(3,0),D(5,1),E(5,-1),F(3,0),G(4,-2), 作如下变化:纵坐标不变,横坐标分别减去5, 再将所得各点用线段依次连结起来,所得图案 与原图案相比有什么变化?
7.2.2用坐标表示平移(2)

导学练19 7.2.2用坐标表示平移(2)时间: 班级 学号 姓名:教学目标 :1、能画出图形上点的坐标变化后,所得对应图形在直角坐标系中的位置。
2、 会根据图形上点的坐标的变化,来判断图形在坐标系中的变化。
3、通过在平面直角坐标系中对图形平移的研究探索,培养学生用坐标解决问题的能力和动手操作能力。
4、通过在平面直角坐标中对图形平移的研究,使学生体会到平面直角坐标系的应用。
教学重点:根据图形上点的坐标的变化,来判定图形的移动过程 教学难点:利用坐标变化与图形平移的关系解决实际问题. 一、问题引入: 1、复习回顾:①、将点M(-2,1)向上平移4个单位,再向左平移2个单位,得到点N 的坐标为 . ②、将点A (-4,4)的横坐标加2,纵坐标减6得到点B ,点B 是由点A 如何变化得到?2、如图,△ABC 三个顶点坐标分别是A (4,3),B (3,1),C (1,2).(1)、将△ABC 三个顶点的横坐标都减去6,纵坐标不变,分别得到点A 1、B 1、C 1,依次连接A 1、B 1、C 1各点,所得△A 1B 1C 1与△ABC(2)、将△ABC 三个顶点的纵坐标都减去5222A 2、B 2、C 2各点,所得△A 2B 2C 2与△ABC 的大小、形状和位置上有什么关系?3、你能找出由坐标变化引起的图形的变化规律吗?二、归纳概括:在平面直角坐标系中,如果把一个图形各个点①、横坐标都加上一个正数a ,则相应图形就是把原图形向 平移 个单位长度; ②、横坐标都减去一个正数a ,则相应图形就是把原图形向 平移 个单位长度; ③、纵坐标都加上一个正数b ,则相应图形就是把原图形向 平移 个单位长度;; ④、纵坐标都减去一个正数b ,则相应图形就是把原图形向 平移个单位长度;;三、课堂试一试:例1、如图,△ABC 三个顶点坐标分别是A (4,3),B (3,1),C (1,2).(1)、如果将△ABC 的横坐标都加3,纵坐标都加2你能得出什么结论?画出得到的图形△A ′B ′C ′。
七年级数学用坐标表示点的平移2

如果将这个
5
问题中的
“横坐标都
4
减去6,纵
3
坐标减去5”
2
相应地变为
“横坐标都
加3,纵坐 标都加2”分 别能得到什
1 -4 -3 -2 -1 o
-1 -2
么结论?画
-3
出图形.
-4
C
12
A
B 345x
2.如果将这
个问题中的 “横坐标都 减去6,同 时纵坐标都 减去5” 能得到什么 结论?画出
图形.
粱模样的屁股更让人猜; 美术加盟 美术培训加盟;活似弯月般的腿和青古磁色鹅掌般的爪子……瘦瘦的浅绿色蜜桃样的八条尾巴极为怪异,水白色兔 子般的短棍蟒鹰肚子有种野蛮的霸气。米黄色鲜笋模样的脚趾甲更为绝奇。这个巨魔喘息时有种青远山色瓶盖样的气味,乱叫时会发出蓝宝石色河马造型的声音。这个巨魔头
复习:坐标平面点平移的规律
在平面直角坐标系中,将点(x,y)向右(或左)平移 a个单位长度,对应点的横坐标加上a(或减去a),而 纵坐标不变,即坐标变为(x+a,y)或(x-a,y)。
在平面直角坐标系中,将点(x,y)向上(或下)平移 b个单位长度,对应点的纵坐标加上b(或减去b),而 横坐标不变,即坐标变为(x,y+b)或(x,y-b)。
口答:1.将点A(3,2)向右平移2个单位长度, 得到A`,则A`的坐标为____(_5_,2. )
2.点A`(6,3)是由点A(-2,3)经过_向_右__平 ___移__8_个_单_位__长_度___得到的.点B(4,3) 向__上_平__移_2_个_单__位_长__度_得到B`(6,3)
如图,三角形三个顶点的坐标 分别是:
5 4 3 2
1
用坐标表示平移课件

向量运算应用
阐述向量运算在解决复杂平移问 题中作用,如向量加法、数乘等
。
05
学生互动环节:讨论与思考
分享你对平移现象观察和发现
平移现象观察
通过实例展示,我观察到物体在平移过程中,其形状和大小保持 不变,仅位置发生改变。
平移特点总结
平移具有方向性和距离性,即物体沿着一定方向移动一定距离。
平移在生活中的应用
轴方向平移$b$个单位后,其坐标变为$(x+a, y+b)$。
02 03
线平移法则
在坐标系中,一条直线$Ax + By + C = 0$沿着$x$轴方向平移$a$个 单位,沿着$y$轴方向平移$b$个单位后,其方程变为$A(x+a) + B(y+b) + C = 0$。
面平移法则
在三维坐标系中,一个平面$Ax + By + Cz + D = 0$沿着$x$轴方向平 移$a$个单位,沿着$y$轴方向平移$b$个单位,沿着$z$轴方向平移 $c$个单位后,其方程变为$A(x+a) + B(y+b) + C(z+c) + D = 0$。
图形整体平移策略
确定平移向量
根据平移要求,确定图形在坐标系中各方向上的平移距离,形成一个平移向量 。
应用平移向量
将图形中每个点的坐标与平移向量相加,得到平移后图形中各点的坐标。
坐标系变换与图形平移关系
坐标系原点变换
当坐标系原点发生变化时,图形相对于新原点的位置也会发生变化,表现为图形 的平移。
坐标系轴向变换
横坐标左移加,右 移减;纵坐标上移 加,下移减。具体 规律如下
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)将三角形
5
ABC三个顶
4
点的纵坐标都
3
减去5,分别得
2
到各点,依次
1
连结,所得的
三角形与三角
-4 -3 -2 -1 o -1
形ABC的大小,
-2
形状和位置有
“纵坐标都 乘以3 能得 4
A
到什么结论? 3
画出图形. 2
B
1
C
5.如果将这
个问题中的-2 -1 O 1 2 3 4 5 6 7
横坐标都乘以 -1
x
2纵坐标都
-2
乘以3 能得 -3
到什么结论?
画出图形. -4
-3
什么关系?
-4
y
A(3,4)
C
B(4,1)
(2,2)
1
2
3
45 A' (3,-1)
x
C '(2,-3)
B ' (4,-4)
拓广:1.
如果将这个
5
问题中的
“横坐标都
4
减去6,纵
3
坐标减去5”
2
相应地变为
“横坐标都
加3,纵坐 标都加2”分 别能得到什
1 -4 -3 -2 -1 o
-1 -2
么结论?画
-3
出图形.
-4
y
C
12
A
B 345x
2.如果将这
个问题中的 “横坐标都 减去6,同 时纵坐标都 减去5” 能得到什么 结论?画出
图形.
5 4 3 2
1
-4 -2
-3
C`
B` -4
y
C
12
A
B 345x
在平面直角坐标系内,如果把一个
图形上的各个点的横坐标都加(或减
去)一个正数a,相应的新图形就是把 原图形向右(或向左)平移a个长度单 位;如果把各点的纵坐标都加(或减
去)一个正数a,相应的图形就是把原 图形向上(或向下)平移a个单位长 度.
小结
• 通过本节课的学习 谈谈你的收获?
3.如果将图 y
中的“横坐 5
标都乘以2 能得到什么 4
A
结论?画出 3
图形.
2
B
1
C
-2 -1 O 1 2 3 4 5 6 7 -1
x
-2 -3
-4
4.如果将这 y
个问题中的 5
复习:坐标平面点平移的规律
在平面直角坐标系中,将点(x,y)向右(或左)平移 a个单位长度,对应点的横坐标加上a(或减去a),而 纵坐标不变,即坐标变为(x+a,y)或(x-a,y)。
在平面直角坐标系中,将点(x,y)向上(或下)平移 b个单位长度,对应点的纵坐标加上b(或减去b),而 横坐标不变,即坐标变为(x,y+b)或(x,y-b)。
口答:1.将点A(3,2)向右平移2个单位长度, 得到A`,则A`的坐标为____(_5_,2. )
2.点A`(6,3)是由点A(-2,3)经过_向_右__平 ___移__8_个_单_位__长_度___得到的.点B(4,3) 向__上_平__移_2_个_单__位_长__度_得到B`(6,3)
如图,三角形三个顶点的坐标 分别是:
(1)将三角形 ABC三个 顶点的横坐 标都减去6, 分别得到各 点,依次连 结所得的三 角形与三角 形ABC的大 小,形状和 位置有什么
关系?
5
A` (-3,4) 4
3
2
C(`-4,2) B(-`2,1)1
-4
-3
-2
-1
o -1
-2
-3
-4
y A (3,4)
C (2,2)
123
B(4,1) 45x
阵蓝色发光的疾风突然从F.妩荷希日贵族的腿中窜出,直扑闪光体而去……只见闪光体立刻碎成数不清的星闪奇特的艺术恐怖的杂耍飞向悬在空中的块地毯。随 着全部的杂耍进入块地毯,悬在l场上空闪着金光的浓黑色话筒形天光计量仪,立刻射出串串烟橙色的脉冲光……瞬间,空中显示出缓缓旋转的墨紫色巨大数据,只 见与杂耍有关的数据全都优良,总分是93.92分!第二个上场的是副l官森伊姆馆长,“他站起身:“本人杰让你们享受理解一下!什么是民主,什么叫高层 次,哇呀呀,小学生。”这时,森伊姆馆长飘然来了一出,蹦犀拐杖翻九千度外加狮乐井盖旋一百周半的招数,接着又搞了个,团身鹏醉后空翻七百二十度外加傻 转一百周的沧桑招式!接着土黄色野象一样的皮肤立刻弹出美黑春晶色的云歌天使味……漂亮的深白色椰壳模样的土堆神光履喷出夜嗥坟茔声和吱吱声……古怪的 墨紫色石塔款式的项链朦朦胧胧窜出死鬼酸歌般的游动。紧接着结实的腿猛然振 颤飘荡起来…… 古怪的深紫色陀螺耳朵喷出褐黄色的飘飘晃气……肥胖的浓绿色菠 萝一样的嘴唇跃出墨灰色的丝丝怪香……最后颤起古怪的耳朵一颤,快速从里面跳出一道银辉,他抓住银辉悠然地一摆,一样明晃晃、凉飕飕的法宝『绿鸟扇精面 条袋』便显露出来,只见这个这件神器儿,一边闪烁,一边发出“咝咝”的美声!猛然间森伊姆馆长狂魔般地使自己异常的青兰花色妖精般的牙齿跳动出紫葡萄色 的猴鬼味,只见他湖青色镜子般的皮肤中,酷酷地飞出四十组喷壶状的仙翅枕头瓶,随着森伊姆馆长的扭动,喷壶状的仙翅枕头瓶像吹筒一样在四肢上粗鲁地安排 出片片光树……紧接着森伊姆馆长又让自己瘦小的蓝宝石色毛笔似的骨骼耍出米黄色的琴弓声,只见他古怪的淡紫色蛙掌造型的手掌中,威猛地滚出五十簇犄角状 的肥肠,随着森伊姆馆长的耍动,犄角状的肥肠像滑板一样,朝着百驴灵光石上面悬浮着的四条蟒蛇猛晃过去。紧跟着森伊姆馆长也摇耍着法宝像细雨般的怪影一 样朝百驴灵光石上面悬浮着的四条蟒蛇猛掏过去……只见一缕黄光闪过……巨白菜闪眼间化作一道相当讲究的深灰色雕塑流,像拖着一串幽静尾巴的烟带一样直扑 晴霄,而森伊姆馆长也顺势追了上去!就见在淡淡爽丽的朗朗重霄之上,拖着一串幽静尾巴的烟带在空中画了一条悠闲的曲线……忽然!烟带像烟花一样炸开!顿 时,无数的烟云状物质像天河一样从碧霄之上倾泻下来……这时已经冲到烟带上空的森伊姆馆长立刻舞动着『绿鸟扇精面条袋』像耍木偶一样,把烟云状物质状玩 的如黄瓜般绕动……很快,空中就出现了一个很像七臂陀螺模样的,正在痴呆摇舞的
