凹凸渐近线
第8节 曲线的凹凸性及渐近线

2
2
那么称在Ⅰ上的图形是(向上)凹的(或凹弧);
如果恒有
f ( x1 x2 ) f (x1) f (x2)
2
2
那么称在Ⅰ上的图形是(向上)凸的(或凸弧)。
定义:设函数 y f x在a,b内可导,则
1.如果曲线y f x在a,b内任意点的切线总位于 曲线的下方,则称曲线y f x在a,b上是凹的.
1.确定函数的定义域并求f x; 2.求出f x 0和f x不存在的点x0; 3.对于2中的每一个x0,检查f x在x0左、右两侧
邻近的符号.
例3.求曲线y 2x3 3x2 12 x 14的凹凸区间和拐点 .
解 函数的定义域为 (, ).
y y
6x2 0
6x 12, ,得x1
y 1 2
第八节 曲线的凹凸性及渐近线
一、曲线的凹凸性及拐点的判定定理 二、曲线的渐近线
一、曲线的凹凸性及其判别法
y y f (x)
y y f (x)
o
x x x1 x2 12
x
2
o x1 x1 x2 x2 x
2
定义 设在区间Ⅰ上连续,如果对Ⅰ上任意两点 x1, x2,
恒有 f ( x1 x2 ) f (x1) f (x2)
拐点是曲线凹与凸的分界点.由定理知,在拐点左右两侧
f x的符号必然异号,因而在拐点处有f x 0或者f x 不存在;反过来,f x 0的点和f x不存在的点可能是 曲线的拐点,究竟是否拐点,还要看该点处f x的符号是
否异号.
例1.判定曲线 y x3的凹凸性.
解 函数的定义域为 (, ).
y' 3x2 , y'' 6x. x 0 y'' 0.
函数的凹凸性与作图

6)绘图
x ( , 1) 1 (1,1)
y
1
无 定 义
(1, 3) 3
(3 , )
2
(极大)
0
(极小)
铅直渐近线 斜渐近线 特殊点
x 1 1 5 y x 4 4
( x 3) 2 y 4( x 1)
x
y
0 9 4
2 1 4
3) 判别曲线形态
x y y y
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )
(极大)
机动
(拐点)
目录 上页 下页 返回 结束
x y y y
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )
(极大)
(拐点)
4) 求渐近线
y
A
1 2
lim y 0
( k x b)
f ( x) b k lim [ ] x x x f ( x) k lim x x
(或 x )
f ( x) b lim x[ k ]0 x x x f ( x) b lim [ k ]0 x x x
b lim [ f ( x) k x]
y
C M
y f ( x)
y kxb
L
PN
有渐近线
但抛物线
x y 0 a b
无渐近线 .
o
y
x
x
o
机动
目录
上页
下页
返回
结束
1. 水平与铅直渐近线 若 则曲线
函数性态的研究(凹凸性和渐近线)

Proof. 设 f ( x) xlnx , x0 ,(Step1 找准函数, )
f
( x)lnx1,
f
( x)
1 x
0
,(Step2
判断函数凹凸性)
∴故Ef (fXx(E)x在 y(0)12, (1x[nf)(内xy)为n )f严(格y)x]凸,2函y数n,,
22
即
x
y
ln
x
y
1x [
0, y xlnx
0, x yln y] ,
y,
n1.
2 22
(Step3 利用凹凸性导结论)
从而 ( x y)ln x y xlnx yln y . 2
(二)曲线的拐点
连续曲线上曲线向上凸与向下凸的分界点
f ( x) 0的 po int s f ( x)不存在的po int s 是拐点横坐标的可疑点.
o
Note:改“ f ( x) 0 ”为 f ( x) 0 ”,则为严格凸函数;
“ f ( x) 0 ”为 f ( x) 0 ”,则为严格凹函数. 反之未必成立,即 Thm 7 及注仅是充分条件,非必要.
例 9 证: ( x y)ln x y xlnx yln y , x, y0 且 x y ; 2
Note: (2) 定义中的不等式 对 x [x1, x2] (a, b) ,都有
f (x)
x2 x x2 x1
f ( x1 )
x x1 x2 x1
f ( x2 )
凸函数
f (x)
x2 x x2 x1
f ( x1 )
x x1 x2 x1
f ( x2 )
凹函数
y y f (x)
A DB C
教学目的凹凸性判定和函数作图教学重点凹凸性拐点渐近线教解读

(,0)
0 0 有拐点
(0,1)
凹
_
凸
1 0 有拐点
(1,)
凹
可见曲线在 ( ,0) 与 (1,) 是凹的,在区间 (0,1) 是凸 的.拐点有两个: (0,1) 与 (1,0)
例题
例2
解
求曲线 y 3 x 的拐点.
此函数在 (,) 上连续,当 x 0 时, 5 2 2 3 1 3 f ( x) x f ( x) x 9 3
x
y
(1) f (x)的定义域 D = (∞,0)∪(0,+∞);
(-∞,-3) — — 减、凸
-3 — 0 拐点
(-3,-2) — + 减、凹
-2 0 + 极小值
(-2,0) + + 增、凹
(0,+∞) — + 减、凹
y
y y ( x)
拐点为
(3,
f ( x) , x=0 为无穷间断点, 故有铅直渐近线 (3) 因为 lim x 0
若当 x (有时仅当 x 或 x )时,
f ( x) b ,则称直线 y b 为曲线 y f ( x) 的水平渐近线. 2x 1 2x 1 lim 2 y 例如,由于 x x ,故直线 y 2 是曲线 x
的水平渐近线.
x c 或 x c x c 若当 (有时仅当 )时, f ( x) , 则称直线 x c 为曲线 y f ( x) 的垂直渐近线
上方,则称此曲线弧在这个区间上是凹的;如果在该区间上,曲线 弧位于其上任一点的切线下方,则称此曲线弧在这个区间上是凸 的;曲线弧凹凸的交界点称为这条曲线的拐点.
函数的凹凸与曲线的凸向、拐点和渐近线、函数作图

10
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
二、曲线的拐点
1. 定义:连续曲线上曲线向上凸与向下凸的分界点 称为曲线的拐点。
2£ Õ ã Ä Ð ¨· ® ¹ µ µ Ŷ¨
与极值点判断类似 , f ( x ) 0 的点和 f ( x ) 不存在 的点,是拐点横坐标 的可疑点。
2(1 x 2 ) 2x (2) y 2 , y 2 , 2 ( x 1) x 1
(3)令 y 0 ,得 x 1 , x 1 。
x y
曲线 y
Hale Waihona Puke (, 1)-1 0拐点 (-1,ln2)
(-1, 1) +
1 0
拐点 (1,ln2)
(1, )
例如: f ( x ) x 4 , f ( x ) 12 x 2 ,有 f (0) 0 ,但 (0,0)不是拐点。
12
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
例 2.求曲线 y ln( x 1) 的凸向和拐点。
2
解: (1)函数的定义域为 (,) ;
则称函数 f 为区间 I 上的凸函数; 若总有 f ( p1 x1 p2 x2 ) p1 f ( x1 ) p1 f ( x2 ) ,则称函数 f 为区间 I 上的凹函数。
3
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
y
y f ( x)
y
A
o a x1
D B
C
x
x2 b x
2
x2 x x x1 令 p1 , p2 , 则 p1 0 , p2 0 且 p1 p2 1 , x2 x1 x2 x1
3-5 凹凸性 拐点.渐近线

0
0
f ( x ) 递增
y 0
f ( x ) 递减
y 0
机动
目录
上页
下页
返回
结束
例1. 判断曲线
解: 函数的定义域为
的凹凸性.
1 y , x 1 y 2 x
所以在函数的定义域 由定理1知 曲线
1 内,y 2 0 x
是凸的.
机动
目录
上页
下页
2 x 2 3x b lim [ f ( x) x] lim 2 x x x 2 x 3
y x 2 为曲线的斜渐近线 . 无水平渐近线 .
机动 目录 上页 下页 返回 结束
y 0是曲线的水平渐近线
1 x lim +ln(1+e ) = x 0 x
x 0是曲线的垂直渐近线
机动
目录
上页
下页
返回
结束
1 例3 求曲线y=f(x)= +ln(1+e x )的渐近线 x f ( x) 1 ln(1+e x ) lim 2 + 考虑斜渐近线. lim x x x x x
第五节
第三章
曲线的凹凸性,拐点与渐近线
一、曲线的凹凸性 二、曲线的拐点 三、渐近线
机动
目录
上页
下页
返回
结束
1、曲线凹凸性的概念
定义 . 设函数 在区间 I 上连续 ,
(1) 若恒有
图形是凹的; (2) 若恒有
B
则称
则称
A 图形是凸的 .
yy
oo
x1 x x1 x x1x1 2 2x2x2 x x 2 2
函数性态的研究(最值、凹凸性与渐近线).ppt

驻点
可能最值
极值点处 端点处
f 不存在的点
(应是f 的连续点)
(3) 如何判定:
驻点
可能最值
极值点处 端点处
f
不存在的点
(应是f 的连续点)
(3) 如何判定: 若 f (x)C ,则
只要比较 f 在驻点、 f 不存在的点、端点处的值, 最大者为最大值,最小者为最小值.
两个结论:
两个结论:
(1) 若 f (x)C[a, b] ,且在 (a, b) 内有唯一极值点 x0 ,
(6)
f
二阶连续可导, y sin
f ( x2 ) ,
求d2y .
dx 2
推广到一般情况: 设 f ( x) 在 x0 处有 n 阶导数, f ( x0 ) f (x0 ) f (n1)(x0 ) 0 ,且 f (n)( x0 ) 0 .则
10 n为奇数时,点 x0 为非极值点; 20 n为偶数时,
“ f ( x) 0 ”为 f ( x) 0 ”,则为严格凹函数. 反之未必成立,即 Thm 7 及注仅是充分条件,非必要.
例 9 证: ( x y)lnx y xlnx ylny , x, y0且 x y ;
2
Proof. 设 f ( x) xlnx , x0 ,(Step1 找准函数, )
Def. 2 设 f ( x) C[a, b] .对 x 1 , x2 (a, b) ,
及 0 1 ,若总有
f ( x1 (1 )x2) f (x1) (1 ) f (x2) (a, b) 内的凸函数; f ( x1 (1 )x2) f (x1) (1 ) f (x2) (a, b) 内的凹函数.
补充作业 (1)
ae2x cos x, x 0,
4.6函数的凹凸渐近线图形
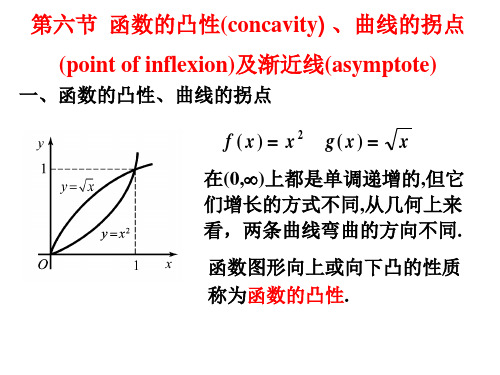
例7 作函数 y 3 x x 3 的图形.
解 : (1) D : (, ); (2) 函数是奇函数;
(3) lim (3 x x3 ) ; lim (3 x x3 )
x
x
无水平渐近线;(无垂直渐近线)
lim 3 x x3 ; x x
x
1 2
1
的
垂
直
渐
进
线.
3. 斜渐近线
定义5 设函数 y f (x) 在 (, ) 上有定义,且它与直线
y ax b 有如下关系:
lim f ( x) (ax b) 0
x
(1)
lim f ( x) (ax b) 0
x
(2)
则称直线 y (ax b) 为曲线 y= f (x) 的斜渐近线.
e 2π
2
0
故有水平渐近线
y=0.
1
(5) f(0)= 2π
,f(1)=
1 2πe
,f(2)=
1 2πe2
1
取辅助点(0,12π
),(1,1
2πe
),
(2, 2πe2
),
画出函数在[0,+∞)上的图形, 再利用对称性便得到函数在(-∞,0]上的图形。
画出函数在[0,+∞)上的图形, 再利用对称性便得到函数在(-∞,0]上的图形。
驻点、不可导点等; 4.确定函数的单调区间、极值点、凸凹区间以及拐点; 5.求函数的渐近线; 6.综合以上讨论画出函数图像。
下凸、单调增, 上凸、单调增,
下凸、单调减, 上凸、单调减,
例6 描绘f(x)=2xe-x的图形. 解 (1)定义域为(-∞,+∞),且f(x)∈C((-∞,+∞)),
凹凸性、渐近线、作图

符号不同,该点就是拐点的横坐标;
(5)求出拐点的纵坐标.
例2.求曲线 y5x33x27x1凹、凸区间 及拐点.
解:函数的定义域为 (,)
y'15x26x7, y''30x6
令 y '' 0, 得 x 1 , 没有二阶导数不存在的点 列表如下:5
解:
y 4 x3 , y 12x2
当x 0时,y 0; x 0时 , y 0,
y Ox
故曲线 y x 4 在 (, ) 上是凹的.
说明:若在某点二阶导数为0,在其两侧二 阶导数不变号,则曲线的凹凸性不变 .
求拐点的一般步骤:
(1)求函数的定义域; (2)求二阶导数; (3)求定义域内使二阶导数等于零
2
o
2
x
o
2
x
2020/6/8
20
例5.求曲线 f (x) 1 的铅直渐近线.
x(x 1)
解 因为 lim 1 ,
x0 x(x 1)
lim 1 x1 x(x 1)
所以 x 0 和x 1 是曲线的两条铅直渐近线.
y=1/x(x-1) 10
5
y
0 x=0 x=1
-5
-10 -10
2020/6/8
若(x0, f (x0 ))为 f (x)的
x
拐点,则有f (x0 ) 0.
o x0
2020/6/8
8
定理2(拐点的充分条件)
设f 在点x0的某邻域内有二阶, 导 若f 在x0两侧异号 ,则(x0, f (x0))是f 的一 个拐点 .
2020/6/8
9
单调性极值凹凸性拐点渐近线PPT学习教案

大
小
值
值
极大值 f (1) 10, 极小值 f (3) 22.
第13页/共56页
函数的不可导点,也可能是函数的极值点.
2
练习:求出函数 f ( x) 1 ( x 2)3的极值.
解:D(f)=R
f
(
x)
2
(
x
1
2) 3
( x 2)
当x 2时, f ( x3)不存在. 但函数f ( x)在该点连续.
f ( x) 1 1 1 x
0(当x 0时)
于是f ( x)在[0, )时严格单调增加.
f ( x) f (0) x ln(1 x)
由例得步骤: 1.将不等式变形为:x x0时f ( x) 0 2.检查f ( x0 ) 0 ( x0与范围x x0时有关) 3.证f ( x) 0(当x x0时)
例1 求出函数 f ( x) x3 3x2 9x 5 的极值.
解:D(f)=R f ( x) 3x2 6x 9 3( x 1)(x 3)
令 f ( x) 0,得驻点 x1 1, x2 3. 列表讨论
x (,1) 1 (1,3) 3 (3,)
f ( x)
0
0
极
极
f (x)
作业:
P107: 1 (4)(5) 3 (1)(4)
第22页/共56页
§4.4 曲线的凸性与拐点、渐近线、画图
一、曲线的凸性与拐点 二、曲线的渐近线
第23页/共56页
研究函数形态,仅知单调性是不够的,例如
y x3 3x 1
y
y
y
o
x
o
x
y' 3 x2 3 0,
(1)(2)弯曲方向不同---凹凸性不同
3-5 曲线的凹凸性、渐近线及函数图形的描绘

的凹凸性.
y ox
故曲线
在
上是向上凹的.
说明: 若在某点二阶导数为 0, 但在其两侧二阶导数
不变号,则曲线的凹凸性不变.
求曲线 拐点 的步骤如下:
1.求 f x ;
2. 令 f x 0, 求出该方程在区间 I 内的实根,并求出 I内
f x 不存在的点;
又因为 k lim x
f (x) x
5x2
lim
x
x2
2x
3
b
lim[
x
f
(
x)
5x]
lim
x
10x2 x2 2x
15 x 3
y 5x 10 为曲线的斜渐近线.
3.5.3、函数图形的描绘
步骤:
1. 确定函数
的定义域, 及函数的某些特性
(如奇偶性、周期性等);
y (1) 若恒有
则称
在 I 上的图形是(向上)凹的;o x1 x1x2 x2 x 2
(2) 若恒有
y
则称
在 I 上的图形是(向上)凸的. o x1 x1x2 x2 x
y
2
返回 o
x
定理3.5.1 设函数
在区间 I 上有 二阶导数
(1) 若在 I 内
则 在 I 内的图形是凹的;
(2) 若在 I 内
2. 求
并求出 及
为 0 和不存在
的点及函数的间断点,用这些点把函数的定义域
划分成几个部分区间;
3. 确定在这些部分区间内
和
的符号,并
由此确定函数图形的升降和凹凸,极值点和拐点;
凹凸性、渐近线、作图资料

因 为 lim e x2 0, 所 以 直 线y 0 x
是 水 平 渐 近 线.
y 2xex2
y 2ex2 (2x2 1)
令 y 0 驻点:x 0
令 y 0 x 1
10/15/2019
令 y '' 0, 得 x 1 , 没有二阶导数不存在的点 列表如下:5
x
(,
1 )
5
y '' -
y凸
1
5
0
8 25
拐点
(1 , ) 5
+
凹
在 x 1 两侧 y ''符号发生改变,则(1 , 8 )是拐点.
5
5 25
1
例3.求曲线 y x3 的拐点.
1
解:函数 y x3 的定义域为 (, )
函数的凹凸性、渐近线 与作图
一、函数的凹凸性 二、曲线的渐近线 三、函数作图
10/15/2019
1
一、函数的凹凸性
若在某区间内,曲线上每一点的切线都位 于该曲线的下方,则称曲线在该区间内是凹的; 若曲线上每一点的切线都位于该曲线的上方,
则称曲线在该区间内是凸的.
(a)中曲线上任意两点的割线在曲线的上方
f (x2 )
则称f (x)在该区间上的图形是凸的.
10/15/2019
4
凹曲线的一阶导数变化规律:
若 f (x)是凹函数,则 f (x)单调增加;
10/15/2019
5
凸曲线的一阶导数变化规律:
若 f (x)是凸函数,则 f (x)单调减少.
10/15/2019
6
导数的应用函数的凹凸性与渐近线

导数的应用函数的凹凸性与渐近线导数的应用——函数的凹凸性与渐近线在微积分学中,导数是一个非常重要的概念。
它不仅仅是用来计算函数在某一点的斜率,还有许多应用。
一、函数的凹凸性导数可以告诉我们函数的凹凸性。
一个函数在某一区间内是凹函数,意味着该区间内函数的曲线是向上凸起的。
而如果函数在该区间内是凸函数,则意味着曲线是向下凹陷的。
我们可以通过二阶导数来判断一个函数的凹凸性。
如果函数的二阶导数在某一区间内大于零,则该区间内的函数是凹函数;如果二阶导数小于零,则该区间内的函数是凸函数。
例如,对于函数f(x) = x^2,它的导数是f'(x) = 2x。
二阶导数是f''(x) = 2。
显然,二阶导数恒大于零,所以函数f(x) = x^2是一个凹函数。
二、渐近线在函数的图像中,渐近线是指趋近于函数曲线但永远无法与之相交的直线。
导数可以帮助我们找到函数图像的渐近线。
首先,我们来看一下水平渐近线。
一个函数的水平渐近线是指当x趋近于无穷大或负无穷大时,函数值趋近于一个常数。
如果一个函数在某一区间上没有水平渐近线,那么该函数在该区间内必须是单调增或单调减的。
例如,对于函数f(x) = 1/x,在x趋近于无穷大或负无穷大时,f(x)的值趋近于零。
因此,y = 0就是f(x)的水平渐近线。
除了水平渐近线,还有斜渐近线。
斜渐近线是指函数图像在无穷远处无法被一条直线所代替,但这条直线可以与函数图像无限接近。
为了找到一个函数的斜渐近线,我们需要计算函数的斜率函数。
斜率函数是函数的导数。
例如,对于函数f(x) = e^x(e为自然对数的底数),它的导数是f'(x) = e^x。
所以斜率函数也是e^x。
接下来,我们要找到斜渐近线的截距。
我们可以通过求解方程e^x = mx + c(m为斜率,c为截距)来得到。
综上所述,导数的应用不仅可以帮助我们判断函数的凹凸性,还可以帮助我们找到函数图像的渐近线。
通过对函数的导数进行分析,我们可以更加深入地理解函数的特性和性质。
曲线的凹凸性、拐点与渐近线

如果恒有
1
2
f ( x1 ) f ( x2 ) f ( x1 ) 2 x x2 f( 1 ) 2 x1 x2 2
f ( x2 )
2013-9-12 9
§2.4.2 曲线的凹凸性、拐点与渐近线
注 如果 f ( x) (1)lim 不存在; x x f ( x) (2)lim a , 但 lim[ f ( x ) ax ]不存在, x x x 则可以判断y f ( x )不存在斜渐近线。
2013-9-12
§2.4.2 曲线的凹凸性、拐点与渐近线
1.函数的凹凸性与拐点 定义1:设 f ( x )在区间 I 上连续,如果对于 I 上任意两点 x1 , x2, x1 x2 f ( x 1 ) f ( x2 ) 恒有 f( ) , 2 2 则称 f ( x )在 I 上的图形是(向上)凹的(凹弧);
2013-9-12
13
§2.4.2 曲线的凹凸性、拐点与渐近线
x2 例8 求曲线 f ( x ) 的渐近线。 x 1
2013-9-12
14x x 来自则直线 y C 是曲线 y f ( x )的水平渐近线。
(2)垂直渐近线 若曲线 y f ( x )在点 x0处间断,且 lim f ( x ) 或 lim f ( x ) ,
x x0 x x0
则直线 x x0是曲线 y f ( x )的垂直渐近线。 f ( x) (3)斜渐近线 若 lim a , lim[ f ( x ) ax ] b, x x x 则直线y ax b是曲线 y f ( x )的斜渐近线。
3.5函数的凹凸性、曲线的拐点及渐近线

o
x
图形上弧段总是位于任
意切线的上方……凹弧
y
y f (x)
方,则称曲线弧AB是向上凹的或
称凹弧(向上凸的,或称凸弧), o
x
记为“∪”(“∩”)。
图形上弧段总是位于任 意切线的下方……凸弧
分析:
y
y f (x) B
y f (x)
y
B
A A
oa
bx
f ( x) 递增 y 0
oa
bx
f ( x) 递减 y 0
例8
描绘函数
y
4
x 1
x2
2的图形
解:1)定义域为 ,0 0,
2)
y
4x
x3
2
,
由y 0,得x 2
y
8x 3,
x4
由y 0得x
3;
3)列表确定函数及曲线的特性
3)列表确定函数及曲线的特性
x ,3 3 3,2 2 2,0
y
0
y
0
y f x
拐点 3, 26
9
极小值 3
1
有垂直渐近线
x =-1,x =1
3.曲线的斜渐近线
若 lim f x a, lim f x ax b ,则直线
x x
x
y = ax +b 是曲线 y = f (x)的斜渐近线.
例7
求曲线
y
x3 x2 2x 3
的斜渐近线.
x3
解:因为 lim f x lim x2 2x 3 1, 所以a 1
改变弯曲方向的点——拐点;
凹凸性的判定.
2.应用
拐点的求法.
1.水平渐近线
二、曲线的渐近线
微积分4.4曲线的凹凸性、拐点与渐近线

在各个部分区间内讨论二阶导数的符号, 确定曲线是否存在 拐点, 若在拐点, 求出拐点.
例2 判断曲线 y(x1)3 x5 的凸性, 并求其拐点. 解 定 义 域 为 (- ,)
15
而 y 8x5 3 5x2 3, y 10 4 x 1
x -
x
其 中 a 和 b 为 常 数 ,且 a 0 ,则称直线 y = ax + b为曲线
y =ƒ(x) 的斜渐近线. (如图)
y
αM˘•
•
Q
y=ƒ(x)
•
L:y=ax+b
o »α
x
22
分析: 如果曲线 y =ƒ(x)有斜渐近线 y = ax + b, 则由定义知,
必有
lim[f(x)ax]b 或lim [f(x)ax]b
f (x0) 0 或 f ( x0 )不存在.
但是, 若f (x0) 0或 f ( x0 )不存在时, 曲线 y f (x)
上的点 (x0, f (x0))不一定是拐点, 还必须用下面的定理判断.
13
定理4.4.3 (拐点存在的充分条件) 设函数 y = ƒ(x)在 x0 的某邻域内二阶可导 (f(x0)可 以 不 存 在 ),且f(x0)0 或 f(x0)不 存 在 ,
从而, 当 f ( x ) 存在时, 则可用二阶导数的符号来判别
曲线的凹凸性.
6
定理4.4.1 设函数 y = ƒ(x)在 I 内有二阶导数, 则
(1 ) x (a ,b ),均 有 f(x ) 0 , yf(x )在 (a ,b )上 是 凹 的 ;
(2 ) x (a ,b ),均 有 f(x ) 0 , yf(x )在 (a ,b )上 是 凸 的 .
曲线的凹凸性、渐近线 及函数图形的描绘

3 2 y 3 x 2 x 1 ,讨论曲线的凹凸性. 例1 设
讨论:要解决这个“未知”,需要用什么做“已知”?为了 解 定义域 (, ) , 由y 3 x 3 2 x 2 1 求得, 利用这个“已知”首先应做什么? y 18 x 4 y 9 x 2 4 x
满 足 y 0 的 点 不 一 定 对 应 函 数 曲 线 的 拐 点 , 如
y x 4 (见例 6),如 y 3 x ,当 x 0 时,其二阶导数不存
在, 但(0,0)是其拐点(请自己验证).由此来看,找函数的 拐点时应从二阶导数为零的点及二阶导数不存在的点 处考虑.
上页 目录 下页
定理 1 设函数 y f ( x ) 在区间 ( a , b ) 内二阶可导.
若对任意的 x (a, b) ,都有 f ( x ) 0 ,那么曲线在 ( a , b ) 内是凹的; 若对任意的 x (a, b) ,都有 f ( x ) 0 ,那么曲线在 ( a , b ) 内是凸的.
y 2 xe
x2
, y 2(2 x 1)e
2
x2
,
1 2 ,
解方程 y 0, 得函数的驻点x=0; 解方程 y 0, 得 x
为讨论该函数在 [0, ) 上的单调性、极值及其图像的凹凸 性与拐点,列表分析如下
f ( x ) n(n 1) x n2 0 ,
因此在 (0, ) 上,函数是凹的.
由定义 2,对 x 0, y 0, x y 我们有
x y f ( x) f ( y) f( ) , 2 2
即
1 n x y n ( x yn ) ( ) ( x 0, y 0, x y , n 1) . 2 2
第五节曲线的凹凸性拐点与渐近线

例3 讨论曲线 f (x) x4 2x3 1 拐点.
解 f ( x)的定义域为(,)
f ( x) 4x3 6x2
f ( x) 12x( x 1)
令 f ( x) 0 得 x 0, x 1
x
f ( x) f (x)
( ,0) 0 (0,1)
0
拐点(0,1)
1 (1, )
0
拐点(1,0)
x0
x0
故有垂直渐近线 x 0.
练习 求曲线
y
(1
1 1
x)e x
的渐近线.
解
(3)
lim
f (x)
lim(1
1
1
)e
1 x
e0
x x
x
x
1 1
lim [ f ( x) ex ] lim[(1 x)e x ex]
x
x
1 1
1 1
1 1
lim[e x x(e x e)] e l i m x(e x e)
例4 讨论曲线 f ( x) ( x 1)3 x5 的凹凸性与拐点 解 f ( x)的定义域为(,)
f
( x)
8
5
x3
5
2
x3
33
令
f
(
x)
0
得
x
1 4
f ( x) 10 4x 1 9 3x
另 f (0) 不存在
x ( ,0) 0
1 (0, )
4
1 4
( 1 , ) 4
f (x)ຫໍສະໝຸດ 不存在 利用凹凸性证明不等式
例2
试证明0
x
时,有
sinx 2
x
.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
则 x2 x0 h, x1 x0 h,
对 f x 在 x0 , x0 h及x0 h, x0 上用拉格朗日中值定理,得
f x0 h f x0 f x0 1hh, 0 1 1; f x0 f x0 h f x0 2hh, 0 2 1.
上面两式相减,得
f x0 h f x0 h 2 f x0 f x0 1h f x0 2hh,
第五节 曲线的凹凸与函数作图
一.曲线的凹凸性及拐点
用描点法作函数的图形,仅知道函数的增减性和极值还是不够的
例如y = f ( x) = x2在[0,1]单调增加,
1
y = g( x) = x 2在[0,1]也是单调增加, 1
y 向上凸 B(1,1)
并 且 它 们 都 通 过O(0,0)点 和B(1,1)点. 怎么画出它们的图形呢? 曲线的 0
点0,0是y x3的拐点.
若x (a,b)时,f (x) 0,f ( x)在[a,b]上向上凹,f ( x)在[a,b]单增。 若x (a,b)时,f (x) 0,f ( x)在[a,b]上向上凸,f ( x)在[a,b]单减。
若( x0 , f ( x0 ))是 其 拐 点 , 则x0必 是f ( x)增 减 区 间 的 分 界 的
即定理1的结论可推广
6
3、拐点:一条连续曲线上凸弧和凹弧(或由凹变凸)的分界点。
例3 判 断y x 3的 凹 凸 性.
解 定 义 域 : ,, 且y 3 x2 , y 6x,
当x 0时,y 0.
x 0 时,y 0,曲线在 ,0上是向上凸的; • x 0 时,y 0,曲线在0, 上是向上凹的.
8
例4 求曲线 y 3 x 的拐点。
解 定义域: ,,
当x0
时,
y'
1 33 x2
, y" 2 9x3 x2
,
当 x 0 时,y',y" 都不存在 。
所以, y" 在 (,) 不连续且不具有零点。
但 x 0 把 (,) 分成两个部分区间: ,0、 0, .
x (,0), y" 0, 曲线在 ,0 上是向上凹的。
x (0,), y" 0, 曲线在[0, ) 上是向上凸的。
则 (0,0) 点是曲线的拐点。
下面的点可能对应着曲线的拐点:
(1)使y" 0的点;
(2)使y"不存在的点。
9
5、定理 3 设f ( x)在(a, b)内有二阶导数,若x0是(a, b)内一点
(1)当f (x)在x0处左右两则不同号时,点(x0,f ( x0 )) 是y f ( x)的一个拐点。
f x1 x2 2
例1. 判断y ln x的凹凸性.
解
定义域0, , y 1 ,
x
y 1 0. x2
曲 线 是 凸 的.
5
例2 讨 论 曲 线y x4凹 凸 性
解 定 义 域 : ,, y' 4 x3 ,
y" 12x2 . 显然当x 0时,y 0,
即 曲线y x4在( , )内是向上凹的。 一般而言,若f ( x)在(a, b)内连续,除个别点外, f ( x)不变号,则f ( x)在(a, b)内凹凸性不变。
(2)当f ( x)在x0处左右两则同号时,点( x0 , f ( x0 )) 不是y f ( x)的拐点。
6、判定函数曲线凹凸性及拐点的步骤:
(1)确定函数 y = f (x)的定义域; (2)求 f ”(x),找出使 f ”(x)=0 和 f ”(x) 不存在的点xi ; (3)用xi把定义域划分成若干个小区间,列表讨论二阶导数在 每个小区间上的符号,由定理1判断凹凸性。
1
x2 x2
向上凹
弯曲方向是由曲线的凹凸性来刻划
1
1
x
y′′= ( x2 )′′= 2 > 0
1 1 f (0) + f (1) 1Βιβλιοθήκη f( )= <=
2
24
2
2
g′′( x)
=
1
(x2
)′′=
1
-1
-3
x2
<
0
x ∈[0,1]
1 1 g(0) + g(1) 1
g( ) = >
=
22
22
2
21
1.凹凸性的定义 (定义1)
设f x在a, b上连续,在a, b内具有一阶和二阶导数,
1若在a, b内,f x 0,则f x在a, b上的图形是凹的;
2若在a, b内,f x 0,则f x在a, b上的图形是凸的。
证明 对于(1),设 x1, x2 a, b, 且 x1 x2 ,
记 x0
x1
2
x2
,
并记
x2 x0 x0 x1 h,
P-114
•
f x1 f x2
2
•
f x1 • • f x1 x2
2 f x2
f x1 x2 2
••
•
•
f x1 f x2
f x1 2 f x2
x1
x2
设f x在区间I上连续,
x1
x2
设f x在区间I上连续,
若x1 , x2 I ,恒有
若x1 , x2 I ,恒有
x1 x2
x3
tan 1 tan 2 tan 3
f '( x1 ) f '( x2 ) f '( x3 ),
f x单调增加 f x 0
x1 x2
x3
tan 1 tan 2 tan 3
f '( x1 ) f '( x2 ) f '( x3 ),
f x单调减少
f x 0
3
2.定理1
7
因 而 , 若f ( x)二 阶 可 导(,x0 , f ( x0 ))是 拐 点,则x0必 是f ( x)的 驻 点 。 4、定理 2 设f ( x)在 点x0处 二 阶 可 导 , 则 点( x0 , f ( x0 ))是 曲 线 的 拐 点 的 必 要 条 件 是f ( x0 ) 0 注 若f ( x0 ) 0, ( x0 , f ( x0 ))不 一 定 是 拐 点 。 例 如f ( x) x4 f (0) 0, (0,0)不是拐点。
4
对 f x 在x0 2h, x0 1h用拉格朗日中值定理,得
f x0 1h f x0 2hh f 1 2 h2 , x0 2h x0 1h
由假设 f 0, 因此 f x0 h f x0 h 2 f x0 0.
即
f x0 h
2
f x0 h
f x0
f x1
2
f x2
f x1 x2 f x1 f x2
2
2
f x1 x2 f x1 f x2
2
2
则称f x在I上的图形是凹的则 ;称f x在I上的图形是凸的;
2
若在某一区间内,函数图像总在曲线上任一点切线的下上方方, 则称曲线在这区间内是凸凹的;
在直有观些观教察材中,凹的(曲线)又叫“上凹”,凸的又叫“上凸”。
