1《圆的标准方程》课件1.ppt
合集下载
圆的标准方程完整ppt课件

解决与圆有关的切线问题
圆的方程可以用来求解与圆有关的切线问题,如切线方程、切点坐 标等。
圆的方程在物理问题中的应用
描述圆形运动轨迹
在物理学中,圆的方程可以用来描述物体做圆周运动时的轨迹。
计算圆形运动的物理量
利用圆的方程,可以计算物体做圆周运动时的线速度、角速度、向 心加速度等物理量。
解决与圆有关的物理问题
切线与半径垂直
切线垂直于经过切点的 半径。
切线长定理
从圆外一点引圆的两条 切线,它们的切线长相
等。
04
圆的方程在实际问题中的应用
圆的方程在几何问题中的应用
确定圆的位置和大小
通过圆的方程,可以准确地确定圆心的坐标和半径的长度,从而 确定圆的位置和大小。
判断点与圆的位置关系
利用圆的方程,可以判断一个点是否在圆上、圆内或圆外,从而解 决相关的几何问题。
3
解决与圆有关的经济问题
圆的方程还可以用来解决一些与圆有关的经济问 题,如圆形区域的经济发展、圆形市场的竞争等 。
05
圆的方程与其他知识点的联系
圆的方程与直线方程的关系
直线与圆的位置关系
通过比较圆心到直线的距离与半径的大小关系,可以确定直线与 圆是相切、相交还是相离。
切线方程
当直线与圆相切时,切线的斜率与圆心和切点的连线垂直,由此 可以求出切线的方程。
根据两点间距离公式,有 $OP = sqrt{(x - a)^{2} + (y
- b)^{2}}$。
将 $OP = r$ 代入上式,得到 $(x - a)^{2} + (y - b)^{2} =
r^{2}$。
方程中参数的意义
$a, b$
01
圆心坐标,表示圆心的位置。
圆的方程可以用来求解与圆有关的切线问题,如切线方程、切点坐 标等。
圆的方程在物理问题中的应用
描述圆形运动轨迹
在物理学中,圆的方程可以用来描述物体做圆周运动时的轨迹。
计算圆形运动的物理量
利用圆的方程,可以计算物体做圆周运动时的线速度、角速度、向 心加速度等物理量。
解决与圆有关的物理问题
切线与半径垂直
切线垂直于经过切点的 半径。
切线长定理
从圆外一点引圆的两条 切线,它们的切线长相
等。
04
圆的方程在实际问题中的应用
圆的方程在几何问题中的应用
确定圆的位置和大小
通过圆的方程,可以准确地确定圆心的坐标和半径的长度,从而 确定圆的位置和大小。
判断点与圆的位置关系
利用圆的方程,可以判断一个点是否在圆上、圆内或圆外,从而解 决相关的几何问题。
3
解决与圆有关的经济问题
圆的方程还可以用来解决一些与圆有关的经济问 题,如圆形区域的经济发展、圆形市场的竞争等 。
05
圆的方程与其他知识点的联系
圆的方程与直线方程的关系
直线与圆的位置关系
通过比较圆心到直线的距离与半径的大小关系,可以确定直线与 圆是相切、相交还是相离。
切线方程
当直线与圆相切时,切线的斜率与圆心和切点的连线垂直,由此 可以求出切线的方程。
根据两点间距离公式,有 $OP = sqrt{(x - a)^{2} + (y
- b)^{2}}$。
将 $OP = r$ 代入上式,得到 $(x - a)^{2} + (y - b)^{2} =
r^{2}$。
方程中参数的意义
$a, b$
01
圆心坐标,表示圆心的位置。
圆的方程课件PPT

2.点与圆的位置关系 设点 P 到圆心的距离为 d,圆的半径为 r,则点与圆的位置有 如表所示的对应关系.
位置关系 点在圆外 点在圆上 点在圆内
d 与 r 的关系 ___d_>_r___ ___d_=__r__ ___d_<_r___
自主探究 探究 1:方程(x-a)2+(y-b)2=r2(a,b,r∈R)表示一个圆吗? 为什么?
解:
法一:设圆的方程为(x-a)2+(y-b)2=r2(r>0).
则b5=-0a,2+2-b2=r2, 3-a2+-2-b2=r2.
a=4, 解得b=0,
r= 5.
∴所求圆的方程为(x-4)2+y2=5.
法二:
∵圆过 A(5,2),B(3,-2)两点, ∴圆心一定在线段 AB 的中垂线上. AB 中垂线的方程为 y=-12(x-4), 令 y=0,得 x=4.即圆心坐标 C(4,0), ∴r=|CA|= 5-42+2-02= 5, ∴所求圆的方程为(x-4)2+y2=5.
【答案】未必表示圆,当 r≠0 时,表示圆心为(a,b),半径 为|r|的圆;当 r=0 时,表示一个点(a,b).
探究 2:由圆的标准方程可以得到圆的哪些几何特征? 【答案】由圆的标准方程可直接得到圆的圆心坐标和半径.
预习测评 1.若一圆的标准方程为(x-1)2+(y+5)2=3,则此圆的圆心和 半径分别是( ) A.(-1,5), 3 B.(1,-5), 3 C.(-1,5),3 D.(1,-5),3
错解:由题意可知圆心在直线 y=2x 上,且在线段 AB 的垂直 平分线 x=2 上,由xy==22,x, 可得圆心 C(2,4),r=|AC|= 17, ∴圆 C 的方程为(x-2)2+(y-4)2=17.
必修2《圆的标准方程》1(人教版)PPT课件

极坐标方程与标准方程的关系
通过极坐标与直角坐标的转换公式 $x = rcostheta, y = rsintheta$, 可以将极坐标方程转换为标准方程。
标准方程 $x^2 + y^2 + Dx + Ey + F = 0$ 可以通过配方转换为极坐标方 程。
极坐标方程的应用
描述圆的形状和大小。 解决与圆相关的几何问题,如求圆的面积、周长等。
圆的几何意义
01
02
03
04
圆是中心对称图形,对称中心 是圆心。
圆也是轴对称图形,任何经过 圆心的直线都是它的对称轴。
圆的周长与直径的比值是一个 常数,这个常数叫做圆周率π
。
圆的面积与半径的平方成正比 ,比例系数是π。
2023
PART 02
圆的标准方程
REPORTING
标准方程的形式
圆的标准方程为: $(x - a)^{2} + (y b)^{2} = r^{2}$
切线的定义
与圆有且仅有一个公共点 的直线。
切线的性质
切线与半径垂直,且切点 到圆心的距离等于半径长 。
切线的判定方法
若直线与圆有公共点,且 过该点的半径与直线垂直 ,则该直线为圆的切线。
2023
PART 06
圆的综合应用
REPORTING
圆与直线的位置关系
相离
直线与圆没有交点,即圆心到直 线的距离大于圆的半径。
$(x - a)^{2} + (y - b)^{2} = r^{2}$
标准方程的应用
用于判断点与圆的位置关系 用于求解与圆有关的轨迹问题
用于求解圆的切线方程 用于解决与圆相关的最值问题
2023
选择必修 第二章 2.4.1 圆的标准方程 课件(共26张PPT)

究位置关系、距离
等问题
新知引入
类比直线方程的研究过程,如何研究圆的方程呢?
圆
平面直角坐标系
圆的方程
代数运算
利用圆的方程,研究
圆有关的位置关系、
几何度量等问题
新知探究
在平面直角坐标系中,如何确定一个圆?
如图,在平面直角坐标系中,⨀A的圆心A的坐标为(a,b),半径为r,M(x,y)为
圆上任意一点,⨀A就是以下点的集合
多边形和圆是平面几何中的两类基本图形.建立直线的方程后,我们可以运
用它研究多边形这些“直线形”,解决边所在直线的平行或垂直、边与边的交
点以及点到线段所在直线的距离等问题.类似地,为了研究圆的有关性质,解决
与圆有关的问题,我们首先需要建立圆的方程.
我国的墨子云:圆,一中同长也.
意思:圆有一个圆心,圆心到圆周上各点的距离(即半径)都相等.
程①.于是
(5 − )2 +(1 − )2 = 2 ,
൞(7 − )2 +(−3 − )2 = 2 ,.
(2 − )2 +(−8 − )2 = 2
知新探究
【例2】△ABC的三个顶点分别是A(5,1),B(7,-3),C(2,-8),
求△ABC的外接圆的标准方程.
解: 即
2 + 2 − 10 − 2 + 26 = 2 ,
心A间的距离为r,点M就在⨀A上.
这时,我们把上述方程称为圆心为A,半径为r的圆
的标准方程(standard equation of thecircle).
半径r
圆的几何要素: 圆心(a,b)
圆心在坐标原点,
半径为r的圆的标准
三个独立条件求a,b,r确定一个圆的方程.
等问题
新知引入
类比直线方程的研究过程,如何研究圆的方程呢?
圆
平面直角坐标系
圆的方程
代数运算
利用圆的方程,研究
圆有关的位置关系、
几何度量等问题
新知探究
在平面直角坐标系中,如何确定一个圆?
如图,在平面直角坐标系中,⨀A的圆心A的坐标为(a,b),半径为r,M(x,y)为
圆上任意一点,⨀A就是以下点的集合
多边形和圆是平面几何中的两类基本图形.建立直线的方程后,我们可以运
用它研究多边形这些“直线形”,解决边所在直线的平行或垂直、边与边的交
点以及点到线段所在直线的距离等问题.类似地,为了研究圆的有关性质,解决
与圆有关的问题,我们首先需要建立圆的方程.
我国的墨子云:圆,一中同长也.
意思:圆有一个圆心,圆心到圆周上各点的距离(即半径)都相等.
程①.于是
(5 − )2 +(1 − )2 = 2 ,
൞(7 − )2 +(−3 − )2 = 2 ,.
(2 − )2 +(−8 − )2 = 2
知新探究
【例2】△ABC的三个顶点分别是A(5,1),B(7,-3),C(2,-8),
求△ABC的外接圆的标准方程.
解: 即
2 + 2 − 10 − 2 + 26 = 2 ,
心A间的距离为r,点M就在⨀A上.
这时,我们把上述方程称为圆心为A,半径为r的圆
的标准方程(standard equation of thecircle).
半径r
圆的几何要素: 圆心(a,b)
圆心在坐标原点,
半径为r的圆的标准
三个独立条件求a,b,r确定一个圆的方程.
12.2(1)圆的标准方程省公开课一等奖全国示范课微课金奖PPT课件

方程. 3.已知圆 C 的直径的两个端点是 A(1, 2) , B(3, 4) ,求圆 C 的轨迹方程. 4.已知圆的直径的两个端点是 A(x1, y1) , B(x2, y2) ,求圆的轨迹方程. 5.圆过点 (1, 2) ,且与两坐标轴相切,求圆的轨迹方程.
第8页
如图,求以 C 1,2 为圆心,且和直线 l : 2x 3y 5 0 相切的圆的方程.
第4页
例 3 :(书 P38—例 3)
如图,已知 M x0, y0 O 为圆 C :x2 y2 r2 上一点,求过点 M 的圆 C 的切线
l 的方程.
第5页
例 4:(书 P38—例 2) 造船时,在船体放样中, 要画出甲板圆弧线,由于 这条圆弧线的半径很大, 无法在钢板上用圆规画 出,因此需要先求出这条 圆弧线的方程,再用描点 法画出圆弧线,如图,已 知 圆 弧 AB 的 半 径 r 29 米,圆弧 AB 所对的弦长 l 12 米,以米为单位,建 立适当的坐标系,并求圆 弧 AB 的方程(答案中数据 精确到 0.001米)
第6页
(三)课堂练习 练 1:(书 P39/练习 12.2(1)). 练 2:若直线 x y r 和圆 x2 y2 r(r 0) 相切,求实数 r 的值.
(四)课堂小结
第7页Biblioteka 三、巩固练习 1.练习册 P21/习题 12.2( A 组)——1,2,3,4,5.
2. 求过点 A(2, 3) ,B(2, 5) 且圆心在直线 x 2y 3 0 上的圆的轨迹
____________________________________
2.圆 x2 y2 r2 上的点 x0, y0 处的切线方程: __________________________________________
第8页
如图,求以 C 1,2 为圆心,且和直线 l : 2x 3y 5 0 相切的圆的方程.
第4页
例 3 :(书 P38—例 3)
如图,已知 M x0, y0 O 为圆 C :x2 y2 r2 上一点,求过点 M 的圆 C 的切线
l 的方程.
第5页
例 4:(书 P38—例 2) 造船时,在船体放样中, 要画出甲板圆弧线,由于 这条圆弧线的半径很大, 无法在钢板上用圆规画 出,因此需要先求出这条 圆弧线的方程,再用描点 法画出圆弧线,如图,已 知 圆 弧 AB 的 半 径 r 29 米,圆弧 AB 所对的弦长 l 12 米,以米为单位,建 立适当的坐标系,并求圆 弧 AB 的方程(答案中数据 精确到 0.001米)
第6页
(三)课堂练习 练 1:(书 P39/练习 12.2(1)). 练 2:若直线 x y r 和圆 x2 y2 r(r 0) 相切,求实数 r 的值.
(四)课堂小结
第7页Biblioteka 三、巩固练习 1.练习册 P21/习题 12.2( A 组)——1,2,3,4,5.
2. 求过点 A(2, 3) ,B(2, 5) 且圆心在直线 x 2y 3 0 上的圆的轨迹
____________________________________
2.圆 x2 y2 r2 上的点 x0, y0 处的切线方程: __________________________________________
圆的标准方程1.ppt

得 r= 3 1-4 3-7 =16
因此圆的方程是
32+-42
x-1 +y-3
=
5
25
2
2 256
解:
因为圆心在y轴上,圆心的坐标是(0,b),圆的半径是 r,那么圆的方程是
x2+(y-b)2=r2
因为点(10,0)和(0,4)在圆上。于是得方程组
0 2 +4-b2=r2
10
2
+0-b2=r2
1 ) 写 出 过 圆 x2+y2=13 上 一 点 M ( 2 , 3 )的切线的方程。
2)已知圆x2+y2=3,求过点(-3,0)的圆的切 线方程。
小结
1)圆心为C(a,b),半径为r的圆的标准方程是
x a2 y b2 r 2;当圆心在原点时,a=0,b=0,那么圆的
方程就是x2+y2=r2。
x-22+y2=10
例2; 2) 如图是某圆拱桥的一孔圆拱的示意图,该圆拱的
跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱 支撑,求支柱A2P2的长度(精确到0.01m)
y
P2 P
x
A
A1 A2 O A3 A4 B
Y
例3:已知圆的方程是x2+y2=r2,求
经过圆上一点M(xo,yo)的切线
M
的方程
O
X
解得 b=-10.5,r2=14.52
所以这个圆的方程是 x2+y+10.52=14.52
解: 因为圆心在X轴上,圆心的坐标是(a,0),圆的
半径是r,那么圆的方程是 (x-a)2+y2=r2
因为点(-1,1)和(1,3)在圆上。于是得方程组
-1-a2+12=r2 1-a2+32=r2
《圆的标准方程》课件

《圆的标准方程》PPT课 件
欢迎来到《圆的标准方程》PPT课件!在这个课件中,我们将介绍圆的基本概 念、标准方程的一般形式以及圆心和半径的含义。让我们开始探索圆的奥秘 吧!
什么是圆的标准方程
圆的标准方程是描述圆形的方程式。它使用平面直角坐标系中的变量来表示 圆的位置和半径。了解圆的标准方程可以帮助我们解决各种与圆相关的数学 问题。
多边形
圆可以与多边形的外接圆或内切 圆相交或相切。
圆的重要性及应用领域
1 数学基础
圆是几何学的基本概念之一,对于数学的发展起到了重要的推动作用。
2 物理学
圆的运动和旋转是物理学中许多现象的基础,如行星的轨道和自转。
3 计算机科学
圆的标准方程在计算机图形学中用于绘制圆形的图像和动画。
圆的标准方程与其他方程型的比较
圆的标准方程在物理学中的应用
物理学中的许多现象可以用圆的标准方程进行建模和描述。例如,行星的轨道可以用圆形或椭圆 形来表示,而物体的旋转运动也可以用圆的方程来描述。
圆的标准方程在工程 中用于设计圆形物体 的尺寸和位置。
通过圆的标准方程解决方程组
圆的标准方程可以与其他方程组合使用,解决多元方程组中与圆有关的问题。例如,我们可以通 过圆的标准方程和直线方程的系统来求解直线和圆的交点。
圆和其他图形的关系
1
三角形
2
圆可以与三角形的外接圆或内切
圆有关。
3
矩形
圆可以与矩形相切或包围,形成 有趣的图案。
步骤2
将圆心的坐标(h, k)代入圆的标准方程的x 和y的变量位置。
步骤4
整理方程,得到圆的标准方程。
圆的一般方程和标准方程之间 的关系
圆的一般方程和标准方程都可以用来表示圆形,但它们的形式不同。一般方 程是多项式形式,而标准方程是平方项的和。通过变换,可以将一般方程转 化为标准方程,反之亦然。
欢迎来到《圆的标准方程》PPT课件!在这个课件中,我们将介绍圆的基本概 念、标准方程的一般形式以及圆心和半径的含义。让我们开始探索圆的奥秘 吧!
什么是圆的标准方程
圆的标准方程是描述圆形的方程式。它使用平面直角坐标系中的变量来表示 圆的位置和半径。了解圆的标准方程可以帮助我们解决各种与圆相关的数学 问题。
多边形
圆可以与多边形的外接圆或内切 圆相交或相切。
圆的重要性及应用领域
1 数学基础
圆是几何学的基本概念之一,对于数学的发展起到了重要的推动作用。
2 物理学
圆的运动和旋转是物理学中许多现象的基础,如行星的轨道和自转。
3 计算机科学
圆的标准方程在计算机图形学中用于绘制圆形的图像和动画。
圆的标准方程与其他方程型的比较
圆的标准方程在物理学中的应用
物理学中的许多现象可以用圆的标准方程进行建模和描述。例如,行星的轨道可以用圆形或椭圆 形来表示,而物体的旋转运动也可以用圆的方程来描述。
圆的标准方程在工程 中用于设计圆形物体 的尺寸和位置。
通过圆的标准方程解决方程组
圆的标准方程可以与其他方程组合使用,解决多元方程组中与圆有关的问题。例如,我们可以通 过圆的标准方程和直线方程的系统来求解直线和圆的交点。
圆和其他图形的关系
1
三角形
2
圆可以与三角形的外接圆或内切
圆有关。
3
矩形
圆可以与矩形相切或包围,形成 有趣的图案。
步骤2
将圆心的坐标(h, k)代入圆的标准方程的x 和y的变量位置。
步骤4
整理方程,得到圆的标准方程。
圆的一般方程和标准方程之间 的关系
圆的一般方程和标准方程都可以用来表示圆形,但它们的形式不同。一般方 程是多项式形式,而标准方程是平方项的和。通过变换,可以将一般方程转 化为标准方程,反之亦然。
《圆的标准方程》课件1 (北师大版必修2)

半径 r =_____ (2) C:(x+1)2+(y-1)2=10, 圆心坐标是________, 半径 r =_____ (3) C:(x-1)2+(y+5)2=3, 圆心坐标是________, 半径 r =_____
(4) 圆心为原点半径为 5的圆的方程________ , (5) 圆心为 3,4),半径为4的圆的方程_________ (
即有
(x1-a) 2 + (y1-b) 2 = r
这说明点P1(x1,y1)在以C(a, b)为圆心,r为半径的圆上.
方程(x-a) 2 +
(y-b) 2 = r2 (r>0)
叫做以(a,b)为圆心, r为半径的圆的标准方程.
练习: (1) C:(x-3)2+(y+2)2=9, 圆心坐标是_______,
Y
A
0
2.7
B
X
3.求圆心在直线2 x-y-3=0上,且经过点( 5, 2) 和点( 3, -2)的圆的方程.
6
4
2
A( 5 ,2 )
-10 -5 5 10
-2
B( 3, -2 )
-4
-6
课堂检测: 1.写出下列各圆的方程:
(1)圆心在原点,半径为6;
(2)经过点P( 6, 3 ),圆心为C(2, -2). 2.求以点C( -1 ,-5) 为圆心,并且和y轴相 切的圆的方程. 3.已知点A(-4 ,-5 ),B(6, -1),求以线段AB 为直径的圆的方程.课堂源自结1.圆的标准方程 (x-a)
2+
(y-b) =
2
2 r
(r>0)
2.会用待定系数法求出圆的基本 量a、b、r, 从而求出圆的标准方 程.
圆的标准方程 圆的一般方程 教学课件(共39张PPT)高中数学北师大版(2019)选择性必修第一册

(, )
r
由两点间的距离公式得
x
a
2
y b
2
r,
(, )
O
将上式两边平方得 x a
2
y b
2
r 2 .①
x
思考一下
以方程①的解为坐标点一定在圆 C 上吗?
设以方程①的任意解 x, y 为坐标的点记为点 Q ,
因为 x, y 是方程①的解,代入方程①可得: x a 2 y b 2 r 2
10
D +3E
20
4 D+2 E
F050ຫໍສະໝຸດ 5D 5EF0
解得 D
F
2, E
0
4, F
2
2
x
+
y
故所求圆的方程为
20 ,
2x
4y
20
0.
例 5:讨论方程 x +y
2
2
x 3
解: 将原方程组整理为 1 2 x2
当
2
y2 表示的是什么图形?
1 y2
2
0,
6x 9
1 时,方程(1)是一元一次方程 6x 9
思考交流
对于点 Px0 , y0 和圆 C : x a 2 y b 2 r 2 ,由圆的标准方程的概念,可知点 P
在圆 C 上的充要条件是 x0 a2 y0 b2 r 2 .
2
2
当点 P 不在圆 C 上时,一定有 x0 a y0 b r 2 ,此时,存在以下两种情况:
PC r
x0 a 2 y0 b2
r
x0 a y0 b r 2
圆的标准方程ppt课件

_____5______.
解析:圆 C : x2 y2 25 的圆心为C(0,0) ,半径r = 5 , 因为 AC (8 0)2 (6 0)2 10 5 ,所以点 A 在圆外, 所以 AP 的最小值为 AC r 10 5 5 ,故答案为:5.
总结一下
圆的标准方程
6.已知 A2,2、 B2,6 ,则以 AB 为直径的圆的标准方程为_x_2____.y4 2 8
解析:线段 AB 的中点坐标为0, 4 , AB 2 22 2 62 4 2 ,
所以,所求圆的半径为 2 2 ,故所求圆的标准方程为 x2 y 42 8 .
7.已知点 A(8, 6) 与圆C : x2 y2 25 ,P 是圆 C 上任意一点,则 AP 的最小值是
求圆的标准方程的两种方法
1.待定系数法.先设圆的标准方法 x a 2 y b 2 r2 ,再根据条件列出关于 a, b,r 的三个独立方程,通过解方程组求出 a,b,r 的值,从而得到圆的标准方程, 如例题 2 的解法.这是一种代数解法. 2.直接求解法.先根据题目条件求出圆心和半径,直接写出圆的标准方程,如例 3 的解法,这种解法往往需要圆的几何性质.
例 3 已知圆心为 C 的圆经过 A(1,1) ,B(2 ,2) 两点,且圆心 C 在直线l : x y 1 0 上, 求此圆的标准方程.
分析:设圆心 C 的坐标为 a,b .由已知条件可知, CA CB ,且a b 1 0 , 由此可以求出圆心坐标和坐标.
解:解法1:
设圆心 C 的坐标为 (a ,b) . 因为圆心 C 在直线 l : x y 1 0 上,所以 a b 1 0 .① 因为 A,B 是圆上两点,所以| CA| | CB | . 根据两点间距离公式,有 (a 1)2 (b 1)2 (a 2)2 (b 2)2 , 即 a 3b 3 0 .② 由①②可得 a 3,b 2 . 所以圆心 C 的坐标是 (3, 2) . 圆的半径 r | AC | (1 3)2 (1 2)2 5 .
解析:圆 C : x2 y2 25 的圆心为C(0,0) ,半径r = 5 , 因为 AC (8 0)2 (6 0)2 10 5 ,所以点 A 在圆外, 所以 AP 的最小值为 AC r 10 5 5 ,故答案为:5.
总结一下
圆的标准方程
6.已知 A2,2、 B2,6 ,则以 AB 为直径的圆的标准方程为_x_2____.y4 2 8
解析:线段 AB 的中点坐标为0, 4 , AB 2 22 2 62 4 2 ,
所以,所求圆的半径为 2 2 ,故所求圆的标准方程为 x2 y 42 8 .
7.已知点 A(8, 6) 与圆C : x2 y2 25 ,P 是圆 C 上任意一点,则 AP 的最小值是
求圆的标准方程的两种方法
1.待定系数法.先设圆的标准方法 x a 2 y b 2 r2 ,再根据条件列出关于 a, b,r 的三个独立方程,通过解方程组求出 a,b,r 的值,从而得到圆的标准方程, 如例题 2 的解法.这是一种代数解法. 2.直接求解法.先根据题目条件求出圆心和半径,直接写出圆的标准方程,如例 3 的解法,这种解法往往需要圆的几何性质.
例 3 已知圆心为 C 的圆经过 A(1,1) ,B(2 ,2) 两点,且圆心 C 在直线l : x y 1 0 上, 求此圆的标准方程.
分析:设圆心 C 的坐标为 a,b .由已知条件可知, CA CB ,且a b 1 0 , 由此可以求出圆心坐标和坐标.
解:解法1:
设圆心 C 的坐标为 (a ,b) . 因为圆心 C 在直线 l : x y 1 0 上,所以 a b 1 0 .① 因为 A,B 是圆上两点,所以| CA| | CB | . 根据两点间距离公式,有 (a 1)2 (b 1)2 (a 2)2 (b 2)2 , 即 a 3b 3 0 .② 由①②可得 a 3,b 2 . 所以圆心 C 的坐标是 (3, 2) . 圆的半径 r | AC | (1 3)2 (1 2)2 5 .
圆的标准方程ppt课件

通过配方,可以将其 转化为标准形式,进 而确定圆心和半径。
一般形式下圆的方程 为 $x^2+y^2+Dx+Ey +F=0$,其中 $D^2+E^2-4F>0$。
拓展延伸
与直线方程联立,可以求解交点。
极坐标形式下圆的方程及其求解 方法
极坐标形式下圆的方程为 $rho=a(1+costheta)$或 $rho=a(1+sintheta)$,其中
圆的面积
S = πr²。
弧长与扇形面积计算
ห้องสมุดไป่ตู้弧长公式
l = θ/360° × 2πr,其中θ 为圆心角的度数。
扇形面积公式
S = θ/360° × πr²,其中θ 为圆心角的度数。
弓形面积计算
弓形面积 = 扇形面积 - 三 角形面积,其中三角形面 积可通过底和高计算得出。
02 圆的标准方程及其推导
数学建模竞赛
在数学建模竞赛中,圆的方程常常作为数学模型的基础,用于解决 各种实际问题,如城市规划、交通流量分析等。
06 总结回顾与拓展延伸
总结回顾本次课程重点内容
01
圆的标准方程的定义和形式
02
圆心和半径的确定方法
03
圆的方程与直线方程联立求解交点
04
圆的方程在实际问题中的应用
拓展延伸
一般形式下圆的方程 及其求解方法
圆的要素
圆心、半径。
03
圆的表示方法
一般用圆心和半径表示,如圆O(r)。
圆心、半径与直径
01
02
03
圆心
圆的中心,用字母O表示。
半径
连接圆心和圆上任意一点 的线段,用字母r表示。
1《圆的标准方程》课件1.ppt
( y 0b) ( y 0b) ( y 0b)
2 2 2
r ,P在圆外, r ,P在圆上, r ,P在圆内。
2
⑵( x 0 a )
⑶( x 0 a )
例5 已知隧道的截面是半径是4m的 半圆,车辆只能在道路的中心线一侧 行驶,一辆宽为2.7m,高为3m的货车 能不能驶入这个隧道?
例6 已知圆的方程是x y r ,求经过圆上一点 y M x , y 的切线的方程。 解:如图⑵,设切线的斜率 k , P(x,y) 半径OM的斜率为 k ,因为圆的 M(x0,y0) 切线垂直于过切点的半径,于是
小结:⑴ x
M
0
, 0
0
y
0
在x
2
y
2
r 上时,过 M 的切线为
0
2
x x r 2 2 M x , y ( x a ) ( y b ) 2 ⑵ 在 r 上时,过 M x , y b )( y b ) r 2
点M适合的条件可表示为
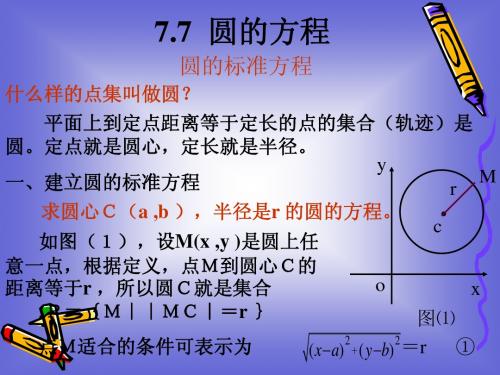
(x a)
2
( y b)
2
=r
①
①式两边平方,得 ② 方程②就是圆心为C (a ,b ),半径为r 的圆的方程,我 们把它叫做圆的标准方程。 特别的,如果圆心在原点,这时 a 0 , b 0 ,那么 2 2 2 y r 圆的方程是 x 二、圆的标准方程的应用 例1 写出下列各圆的方程: ⑴圆心在原点,半径是3; ⑵圆心在点 C 3 , 4 ,半径是 5 ; ⑶经过点 P 5 ,1 ,圆心在点 C 8 , 3 。 2 2 2 2 y 9 ⑵( x 3) ( y 4) 5 答:⑴ x 2 2 ( y 3) 2 5 ⑶ ( x 8) 点评:⑶中,可先用两点距离公式求圆的半径,或设 2 2 2 x 8 y 3 r,用待定系数法求解。
圆的标准方程公开课一等奖课件

例题1
已知圆O的半径为5cm,弦AB长为8cm,P是弦AB所对的优弧上的一个动点,则PC+PD的最 小值为_______.
分析
根据垂径定理和勾股定理求出圆心O到弦AB的距离,再利用切线长定理求出PC+PD的最小值。
解答
过点O作OE⊥AB于点E,连接OA,则AE=BE=1/2AB=4cm。在Rt△AOE中,OA=5cm, AE=4cm,根据勾股定理得OE=3cm。因为P是优弧上的一个动点,所以当PC和PD为切线时, PC+PD的值最小。根据切线长定理得PC=PD,所以PC+PD=2OE=6cm。故答案为6cm。
典型例题分析与解答
01
例题1
已知圆的标准方程为 $(x - 2)^{2} + (y + 1)^{2} = 9$,求圆心坐标
和半径。
03
例题2
将一般方程 $x^{2} + y^{2} - 4x + 6y + 12 = 0$ 化为标准方程,并指
出圆心坐标和半径。
02
解析
直接对比标准方程形式,可得圆心 坐标为 $(2, -1)$,半径 $r = sqrt{9} = 3$。
圆的标准方程公开课一等奖课件
contents
目录
• 圆的基本概念与性质 • 圆的标准方程及其推导 • 直线与圆的位置关系判断 • 圆的对称性与中心对称性探究 • 复杂图形中涉及圆的问题解决方法 • 总结回顾与拓展延伸
01
圆的基本概念与性质
圆的定义及基本要素
圆的定义:平面上所有与定点 (圆心)距离等于定长(半径) 的点的集合。
04
圆的对称性与中心对称性 探究
圆的对称性表现形式
图形对称
已知圆O的半径为5cm,弦AB长为8cm,P是弦AB所对的优弧上的一个动点,则PC+PD的最 小值为_______.
分析
根据垂径定理和勾股定理求出圆心O到弦AB的距离,再利用切线长定理求出PC+PD的最小值。
解答
过点O作OE⊥AB于点E,连接OA,则AE=BE=1/2AB=4cm。在Rt△AOE中,OA=5cm, AE=4cm,根据勾股定理得OE=3cm。因为P是优弧上的一个动点,所以当PC和PD为切线时, PC+PD的值最小。根据切线长定理得PC=PD,所以PC+PD=2OE=6cm。故答案为6cm。
典型例题分析与解答
01
例题1
已知圆的标准方程为 $(x - 2)^{2} + (y + 1)^{2} = 9$,求圆心坐标
和半径。
03
例题2
将一般方程 $x^{2} + y^{2} - 4x + 6y + 12 = 0$ 化为标准方程,并指
出圆心坐标和半径。
02
解析
直接对比标准方程形式,可得圆心 坐标为 $(2, -1)$,半径 $r = sqrt{9} = 3$。
圆的标准方程公开课一等奖课件
contents
目录
• 圆的基本概念与性质 • 圆的标准方程及其推导 • 直线与圆的位置关系判断 • 圆的对称性与中心对称性探究 • 复杂图形中涉及圆的问题解决方法 • 总结回顾与拓展延伸
01
圆的基本概念与性质
圆的定义及基本要素
圆的定义:平面上所有与定点 (圆心)距离等于定长(半径) 的点的集合。
04
圆的对称性与中心对称性 探究
圆的对称性表现形式
图形对称
人教A版高中数学必修二4.1.1 圆的标准方程 课件(共16张PPT)
设圆的标准方程为(x-a)2+(y-b)2=r2。
六.小结
1.圆心是 A(a,b),半径为r的圆A的标准方程是(x–a)2+(y–b )2=r2 2.点M(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系
几何法 先求出点M与圆心A的距离d
(1)若点M在圆A上,则d=r; (2)若点M在圆A内,则 d<r; (3)若点M在圆A外,则 d>r.
数与形,本是相倚依 焉能分作两边飞 数无形时少直觉 形少数时难入微 数形结合百般好 隔离分家万事休 切莫忘,几何代数统一体 永远联系莫分离
—— 华罗庚
O
平面直角坐标系
数
直线方程 1.点斜式方程 ������ − ������������ = ������(������ − ������������)
r2
③
展开平方后,
(x–2)2+(y+3)2=y25.
① ②得:a 2b 8 0
A(5,1)
③-②得:a b 1 0
几
解得a=2,b=-3,r=5.
代
何
O M
(6,-1) x B(7,-3)
∴ △ABC的外接圆方程为
数
(x–2)2+(y+3)2=25.
法
C(2,-8)
kAB 2
(1 a)2 (1 b)2 r 2
(2 a)2 (2 b)2 r 2
ab1 0
a 3 解得 b 2
r 5
∴圆C方程是(x-3)2+(y-2)2=25.
代
何
O
x
数
法
C
六.小结
1.圆心是 A(a,b),半径为r的圆A的标准方程是(x–a)2+(y–b )2=r2 2.点M(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系
几何法 先求出点M与圆心A的距离d
(1)若点M在圆A上,则d=r; (2)若点M在圆A内,则 d<r; (3)若点M在圆A外,则 d>r.
数与形,本是相倚依 焉能分作两边飞 数无形时少直觉 形少数时难入微 数形结合百般好 隔离分家万事休 切莫忘,几何代数统一体 永远联系莫分离
—— 华罗庚
O
平面直角坐标系
数
直线方程 1.点斜式方程 ������ − ������������ = ������(������ − ������������)
r2
③
展开平方后,
(x–2)2+(y+3)2=y25.
① ②得:a 2b 8 0
A(5,1)
③-②得:a b 1 0
几
解得a=2,b=-3,r=5.
代
何
O M
(6,-1) x B(7,-3)
∴ △ABC的外接圆方程为
数
(x–2)2+(y+3)2=25.
法
C(2,-8)
kAB 2
(1 a)2 (1 b)2 r 2
(2 a)2 (2 b)2 r 2
ab1 0
a 3 解得 b 2
r 5
∴圆C方程是(x-3)2+(y-2)2=25.
代
何
O
x
数
法
C
圆的标准方程精品课件

3
证明
设P和Q是圆上关于任意直线l对称的两点,则 AP=BQ,且PO=QO。由于PQ与l垂直,所以 △APO≌△BQA,从而证明了P和Q关于l对称。
06 圆的实际应用
生活中的圆的应用
交通工具
车轮、自行车轮胎、火车 铁轨等都采用了圆形的结 构,使得运动更加平稳和 高效。
建筑学
建筑物的窗户、门洞、柱 基等常采用圆形或圆弧形, 不仅美观大方,而且符合 结构力学原理。
圆的弦长定理
总结词
弦长与半径的关系
详细描述
在圆中,通过圆心的弦被平分,并且弦长等于两个半径之和。如果弦不经过圆心,则弦长小于两个半径之和。这 个定理用于计算弦的长度以及与半径之间的关系。
04 圆的面积与周长
圆的面积计算公式
圆的面积计算公式
$S = pi r^{2}$,其中$S$表示圆的面积,$r$表示圆的半径。
圆的标准方程的图形表示
以圆心为坐标原点,以半径为长度单 位,在平面直角坐标系中画出的圆形。
圆的标准方程推导
推导过程
通过将圆上任一点的坐标表示为$(x, y)$,利用点到圆心 的距离等于半径的性质,将圆的方程转化为标准形式。
推导步骤
设圆上任一点$P(x, y)$,圆心$O(h, k)$,半径为$r$,则 $OP = r$,即$sqrt{(x - h)^{2} + (y - k)^{2}} = r$,平 方两边得到标准方程。
自然界
自然界中许多物体呈现圆 形或类圆形,如星球、花 朵、叶子等。
02 圆的标准方程
圆的标准方程形式
圆的标准方程
圆的标准方程的应用
$(x - h)^{2} + (y - k)^{2} = r^{2}$, 其中$(h, k)$是圆心坐标,$r$是半径。
圆的标准方程ppt课件

M3 (3,3)是否在这个圆上。(课本85页)
解:圆心为A(2,-3),半径为5的圆的标准方程是
y
M3
( − ) + ( + ) =
把点M1(5,-7)代入圆得
把点M2(-2,-1)代入圆得
把点M3(3,3)代入圆得
(5-2)2+(-7+3)2=25,M1在圆上
(-2-2)2+(-1+3)2=20<25,M2在圆内
课堂小结
回顾两点间的距离公式
B(x2 ,y2)
定点到定点的距离
A(x1 ,y1)
知识回顾
知识探究
例题剖析
课堂小结
巩固练习
圆心(0,0)
圆心(0,0)
圆心(a,b)
半径 1
半径 r
半径 r
1
p(x ,y)
r
p(x ,y)
(a,b)
( − ) +( − ) =
( − ) +( − ) =
y
O
圆的标准方程的特点
1、明确给出了圆心坐标和半径;2、确定圆的
标准方程必须具备三个独立条件,即a、b、r。
3、是关于x,y的二元二次方程。
M(x,y)
A
(a,b)
x
知识回顾
例题剖析
知识探究
巩固练习
课堂小结
例1、 求圆心A(2,-3),半径为5的圆的标准方程,并判断点M1(5,-7),M2 (-2,-1),
P={M| |MA|=r},
y
根据两点间的距离公式,点M的坐标(x,y)满足的条件可以表示为
( − ) + ( − )
= r
两边平方,得
解:圆心为A(2,-3),半径为5的圆的标准方程是
y
M3
( − ) + ( + ) =
把点M1(5,-7)代入圆得
把点M2(-2,-1)代入圆得
把点M3(3,3)代入圆得
(5-2)2+(-7+3)2=25,M1在圆上
(-2-2)2+(-1+3)2=20<25,M2在圆内
课堂小结
回顾两点间的距离公式
B(x2 ,y2)
定点到定点的距离
A(x1 ,y1)
知识回顾
知识探究
例题剖析
课堂小结
巩固练习
圆心(0,0)
圆心(0,0)
圆心(a,b)
半径 1
半径 r
半径 r
1
p(x ,y)
r
p(x ,y)
(a,b)
( − ) +( − ) =
( − ) +( − ) =
y
O
圆的标准方程的特点
1、明确给出了圆心坐标和半径;2、确定圆的
标准方程必须具备三个独立条件,即a、b、r。
3、是关于x,y的二元二次方程。
M(x,y)
A
(a,b)
x
知识回顾
例题剖析
知识探究
巩固练习
课堂小结
例1、 求圆心A(2,-3),半径为5的圆的标准方程,并判断点M1(5,-7),M2 (-2,-1),
P={M| |MA|=r},
y
根据两点间的距离公式,点M的坐标(x,y)满足的条件可以表示为
( − ) + ( − )
= r
两边平方,得
圆的标准方程ppt课件完整版x

圆的基本要素
圆心、半径、直径、弧、弦等。
圆心、半径与直径
01
02
03
圆心
圆的中心,用字母O表示 。
半径
连接圆心和圆上任意一点 的线段,用字母r表示。
直径
通过圆心且两端点都在圆 上的线段,用字母d表示 ,且d=2r。
圆的周长和面积公式
圆的周长公式
C=2πr,其中π为圆周率,约等于3.14159。
圆的面积公式
02
其中,$(a, b)$ 为圆心坐标,$r$ 为圆的半径。
标准方程中各参数意义
$a$ 和 $b$ 分别表 示圆心的横坐标和纵 坐标。
$(x - a)^{2}$ 和 $(y - b)^{2}$ 分别表示 点 $(x, y)$ 到圆心 $(a, b)$ 的水平和垂 直距离的平方。
$r$ 表示圆的半径, 即从圆心到圆上任一 点的距离。
分析物体的受力情况
在某些物理问题中,可以通过分析物体运动轨迹的形状(如圆形 或椭圆形)来推断物体所受的力。
其他领域应用举例
工程测量
在工程测量中,经常需要确定一 些圆形结构(如管道、井盖等) 的位置和大小,这时可以利用圆 的方程来进行精确测量和计算。
经济学
在经济学中,有时会用圆形来表示 市场供需平衡的状态,通过圆的方 程可以分析市场价格的波动和变化 趋势。
3. 将以上两部分相加,并加 上常数项 12,得到 $(x 2)^{2} + (y + 3)^{2} = 1$ 。
04
05
4. 从中可以看出,圆心坐标 为 $(2, -3)$,半径 $r = 1$
。
03
圆的图像与性质分析
圆心位置对图像影响
圆心决定圆的位置
圆心、半径、直径、弧、弦等。
圆心、半径与直径
01
02
03
圆心
圆的中心,用字母O表示 。
半径
连接圆心和圆上任意一点 的线段,用字母r表示。
直径
通过圆心且两端点都在圆 上的线段,用字母d表示 ,且d=2r。
圆的周长和面积公式
圆的周长公式
C=2πr,其中π为圆周率,约等于3.14159。
圆的面积公式
02
其中,$(a, b)$ 为圆心坐标,$r$ 为圆的半径。
标准方程中各参数意义
$a$ 和 $b$ 分别表 示圆心的横坐标和纵 坐标。
$(x - a)^{2}$ 和 $(y - b)^{2}$ 分别表示 点 $(x, y)$ 到圆心 $(a, b)$ 的水平和垂 直距离的平方。
$r$ 表示圆的半径, 即从圆心到圆上任一 点的距离。
分析物体的受力情况
在某些物理问题中,可以通过分析物体运动轨迹的形状(如圆形 或椭圆形)来推断物体所受的力。
其他领域应用举例
工程测量
在工程测量中,经常需要确定一 些圆形结构(如管道、井盖等) 的位置和大小,这时可以利用圆 的方程来进行精确测量和计算。
经济学
在经济学中,有时会用圆形来表示 市场供需平衡的状态,通过圆的方 程可以分析市场价格的波动和变化 趋势。
3. 将以上两部分相加,并加 上常数项 12,得到 $(x 2)^{2} + (y + 3)^{2} = 1$ 。
04
05
4. 从中可以看出,圆心坐标 为 $(2, -3)$,半径 $r = 1$
。
03
圆的图像与性质分析
圆心位置对图像影响
圆心决定圆的位置
圆的方程ppt课件

圆的方程
圆的标准方 程
一、知识梳理 1. 圆的方程
标准方程
走进教材
(x—a)²+(y—b)²=r²(r>0)
圆心 半径为r
一般方程
x²+y²+Dx+Ey+F=0
条 件 :D²+E²—4F>0 圆心:
半径:
2.点与圆的位置关系 点M(x₀,y₀) 与圆(x—a)²+(y-b)²=r²的位置关系. (1)若M(x₀,yo) 在圆外,则(x₀—a)²+(y₀—b)²> r². (2)若M(x₀,yo) 在圆上,则(x₀—a)²+(yo—b)²= r². (3)若M(xo,yo)在圆内,则(x₀—a)²+(y₀—b)²<
解得k=±√3
所 的最大值为 √3
图1
(2)y-x 可看作是直线y=x+b 在y轴上的截距,当直线y=x+b 与圆相切时,
纵截距b取得最大值或最小值,此时
解得b=-2±√6
所以y-x 的最大值-2+ √6,最小值-2- √6
(3)x²+y² 表示圆上的一点与原点距离的平方,由平面几何知识知, 在原点与圆心连线与圆的两个交点处取得最大值和最小值 又圆心与原点的距离为(2-0)²+(0-0)²=2
答案:C
求圆的方程的两种方法 (1)直接法
根据圆的几何性质,直接求出圆心坐标和半径,进而得方程。 (2)待定系数法
①若已知条件与圆(a,b) 和半径r 有关,则设圆的标准方程,依据已知条件列出 关于a,b,r 的方程组,从而求得圆的方程。 ②已知条件没有明确给出圆心或半径,则选择圆的一般方程,依据已知条件列出 关于D,E,F 的程组,得圆的方程。
圆的标准方 程
一、知识梳理 1. 圆的方程
标准方程
走进教材
(x—a)²+(y—b)²=r²(r>0)
圆心 半径为r
一般方程
x²+y²+Dx+Ey+F=0
条 件 :D²+E²—4F>0 圆心:
半径:
2.点与圆的位置关系 点M(x₀,y₀) 与圆(x—a)²+(y-b)²=r²的位置关系. (1)若M(x₀,yo) 在圆外,则(x₀—a)²+(y₀—b)²> r². (2)若M(x₀,yo) 在圆上,则(x₀—a)²+(yo—b)²= r². (3)若M(xo,yo)在圆内,则(x₀—a)²+(y₀—b)²<
解得k=±√3
所 的最大值为 √3
图1
(2)y-x 可看作是直线y=x+b 在y轴上的截距,当直线y=x+b 与圆相切时,
纵截距b取得最大值或最小值,此时
解得b=-2±√6
所以y-x 的最大值-2+ √6,最小值-2- √6
(3)x²+y² 表示圆上的一点与原点距离的平方,由平面几何知识知, 在原点与圆心连线与圆的两个交点处取得最大值和最小值 又圆心与原点的距离为(2-0)²+(0-0)²=2
答案:C
求圆的方程的两种方法 (1)直接法
根据圆的几何性质,直接求出圆心坐标和半径,进而得方程。 (2)待定系数法
①若已知条件与圆(a,b) 和半径r 有关,则设圆的标准方程,依据已知条件列出 关于a,b,r 的方程组,从而求得圆的方程。 ②已知条件没有明确给出圆心或半径,则选择圆的一般方程,依据已知条件列出 关于D,E,F 的程组,得圆的方程。
圆的标准方程PPT完美课件

(3) 注意圆的平面几何知识的运用以及应用圆的方程 解决实际问题。
圆的标准方程PPT完美课件
圆的标准方程PPT完美课件
•
1应该认识到,阅读是学校教育的重要 组成部 分,一 个孩子 如果在 十多年 的教育 历程中 没有养 成阅读 的习惯 、兴趣 和能力 ,一旦 离开校 园,很 可能把 书永远 丢弃在 一边, 这样的 结果一 定是我 们所有 的教育 工作者 不想看 到的。
5
(3)已知点A(2,3),B(4,9), 圆以线段AB为直径;
待定系数法 关键:求圆心和半径
类比于直线 方程求法
(1) (x-1)2+(y-3)2 = 9
(2) (x-1)2+(y+1)2 = 5 或 (x-1)2+(y-3)2 = 5
(3) (x-3)2+(y-6)2=10
圆的标准方程PPT完美课件
圆的标准方程PPT完美课件
圆的标准方程PPT完美课件
[点与圆的位置关系]
例题4、设圆 C : (x a)2 ( y 1)2 2a
(a 0,且a 1), 则坐标原点的位置是( A)。
(A) 在圆外 (B) 在圆上 (C)在圆内 (D) 与a的取值有关而无法确定.
圆的标准方程PPT完美课件
圆的标准方程PPT完美课件
•
10保尔身上的人格特征或完美的精神 操守: 自我献 身的精 神、坚 定不移 的信念 、顽强 坚韧的 意志
•
11把记叙、描写、抒情和议论有机地 融合为 一体, 充满诗 情画意 。如描 写百草 园的景 致,绘 声绘色 ,令人 神往。
•
12简·爱人生追求有两个基本旋律:富 有激情 、幻想 、反抗 和坚持 不懈的 精神; 对人间 自由幸 福的渴 望和对 更高精 神境界 的追求 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例6 已知圆的方程是x M x 0 , y 的切线的方程。 0 解:如图⑵,设切线的斜率 k , 半径OM的斜率为 k 1 ,因为圆的 切线垂直于过切点的半径,于是
2
2 2 y r ,求经过圆上一点
y
P(x,y) M(x0,y0) o x
k
1
y ∵k x
1
k
1
0
∴
k
0
x y
0 0
x , y 在(xa)2 ( yb)2 r 2 上时,过 M x , y
0
0 0 0
பைடு நூலகம்
y
r
2
;
r
2
上时,过 M的切线为
三、课堂练习
练习1 2 3
四、小结 五、作业
习题2.2(1) 1 2 3
经过点M的切线方程是 图⑵ 2 整理,得 x0 x y0 y r 当点M在坐标轴上时,可以验证上面的方程同样适 用。 思考:是否可以用平面几何的知识求此切线方程。
0 0 0
y y
x y x x
0
小结:⑴ M
x , y 在x
0 0
2
y
2
xx
0
y
0
⑵M
圆的切线方程为 ( x 0 a)( x a) ( y b)( y b) r 2 0
7.7 圆的方程
圆的标准方程
什么样的点集叫做圆? 平面上到定点距离等于定长的点的集合(轨迹)是 圆。定点就是圆心,定长就是半径。 y M 一、建立圆的标准方程 r 求圆心C(a ,b ),半径是r 的圆的方程。 c 如图(1),设M(x ,y )是圆上任 意一点,根据定义,点M到圆心C的 o 距离等于r ,所以圆C就是集合 x P={M||MC|=r } 图⑴
点M适合的条件可表示为
( xa)
2
( y b)
2
=r
①
①式两边平方,得 2 2 2 ( y b) r ( xa) ② 方程②就是圆心为C (a ,b ),半径为r 的圆的方程,我 们把它叫做圆的标准方程。 特别的,如果圆心在原点,这时 a 0, b 0,那么 2 2 2 y r 圆的方程是 x 二、圆的标准方程的应用 例1 写出下列各圆的方程: ⑴圆心在原点,半径是3; ⑵圆心在点 C 3,4,半径是 5 ; ⑶经过点 P5,1 ,圆心在点 C 8,3。 2 2 y 9 ⑵( x3)2 ( y 4)2 5 答:⑴ x 2 2 ( y 3) 25 ⑶ ( x8) 点评:⑶中,可先用两点距离公式求圆的半径,或设 2 2 2 x 8 y 3 r,用待定系数法求解。
d r 3 1 4 3 7
2
∴圆的方程为 x 1 y 3
2
3
4
2
2
16 5
256 25
例4 已知圆O的方程为 x 1 y 1 ,判断下面的点在 4 圆内、圆上、还是圆外? A1,1 B0,1 C 0,3
2 2
例2 ⑵ x 4 ⑶x
2
说出下列圆的圆心坐标和半径长:
2
2
⑴ x3
y 1
y2 2
y2 2 4 ;
2
7 ;
答:⑴圆心 (3,2), 半径为2; ⑵圆心 (4, 2 ),半径为 7 ; ⑶圆心 (0,1),半径为4
16.
例3 求以C 1,3 为圆心,并且和直线 3x 4 y 7 0 相切的圆的方程。 解:∵圆与直线 3x 4 y 7 0 相切, ∴圆心C 1,3 到 3x 4 y 7 0的距离
r
⑴( x0a) ( y 0b)
2
2
r r r
2
,P在圆外, ,P在圆上, ,P在圆内。
⑵( x0a) ( y 0b)
⑶( x0a) ( y 0b)
2
2 2
2
例5 已知隧道的截面是半径是4m的 半圆,车辆只能在道路的中心线一侧 行驶,一辆宽为2.7m,高为3m的货车 能不能驶入这个隧道?
解:①∵11
2
11
2
4 ,∴点 A
在圆上;
②∵ 01 11 1 4,∴点 B在圆内;
2 2
③∵ 01
小结: P
0
2
31
2
,∴点 C 在圆外。 5 4
2 2
( x0 , y ) 与圆( x a) 2 ( y b) 2 2 的关系判断:
